《相似》全章复习与巩固--知识讲解(提高)

合集下载

九年级数学下册第27章《相似》复习课说课稿

2.探究式教学法：引导学生通过观察、实验、猜想、验证等方式，自主探究相似图形的性质，培养学生的探究能力和创新思维。
3.互动式教学法：通过提问、讨论、合作等方式，激发学生的思维，促进师生之间、生生之间的互动交流。
选择这些方法的理论依据是：情境教学法能够将抽象的数学知识具体化，帮助学生建立数学与现实世界的联系；探究式教学法能够激发学生的内在动机，培养他们的自主学习能力；互动式教学法能够促进学生之间的信息交流和思维碰撞，提高学习的实效性。
（2）课堂反馈：在讲解完一个知识点后，让学生即时反馈学习效果，教师据此进行针对性讲解。
2.生生互动：
（1）小组讨论：将学生分成小组，针对特定问题进行讨论，培养学生的合作精神和批判性思维。
（2）合作探究：在探究活动中，让学生相互协作，共同解决问题，提高学生的实践操作能力和团队协作能力。
开篇直接输出，以下是教学过程设计的内容：
4.互联网资源：如在线测量工具、数学软件等，用于实际问题的探究和解决。
这些媒体资源在教学中的作用是：提高学生对相似图形性质的理解和掌握，增强学习的直观性和互动性，以及提高教学效率。
（三）互动方式
我计划设计以下师生互动和生生互动的环节：
1.师生互动：
（1）课堂提问：通过提问引导学生思考，及时了解学生对知识点的理解和掌握情况。
九年级数学下册第27章《相似》复习课说课稿
一、教材分析
（一）内容概述
本节课为九年级数学下册第27章《相似》复习课，是学生在掌握了平面几何的基本知识后，对相似图形的进一步理解和应用。本章内容在整个课程体系中起到了承前启后的作用，为后续学习立体几何打下基础。主要知识点包括：
1.相似图形的定义和性质：相似图形的形状相同，大小不同，对应边成比例，对应角相等。

九年级数学《相似-小结》教案

《第27章相似》复习课教学设计1.教材内容义务教育课程标准实验教科书（人教版）《数学》九年级下册第27章相似的全章复习。

2.知识背景分析本章隶属于“空间与图形”领域，本章共有三节内容第1节图形的相似主要介绍相似图形，相似多边形的概念，并探索相似多边形的性质；第2节相似三角形主要研究相似三角形的判定方法、相似三角形在测量中的应用及相似三角形的周长和面积；第3节位似研究了一种特殊的相似－位似，研究了位似图形的画法及平面直角坐标系中的位似变化。

本节课是在学习前三节的基础上进行的，通过对一些图形性质的探索、证明等，进一步发展学生的探究能力，培养学生的逻辑思维能力等。

3.学情背景分析教学对象是九年级学生，学生的逻辑思维能力得到了一定的发展。

本章正处于学生对于掌握的推理论证方法的进一步巩固和提高阶段，要求学生能熟练运用综合法证明命题，熟悉探索法德推理过程，因此在教学中要注意多帮助学生复习已有的知识，做到以新带旧，新旧结合。

要加强解题思路的分析，帮助学生树立已知与未知，简单与复杂，特殊与一般在一定的条件下可以转换的思想，使学生学会把未知化为已知，把复杂问题化为简单问题，把一般问题化为特殊问题的思考方法。

通过小结对于学生推理证明的训练，进一步提高学生的逻辑思维能力和分析解决问题的能力。

4.学习目标4.1知识与技能目标（1）通过复习,梳理本章知识,构建知识网络.（2）通过具体实例认识图形的相似，探索相似图形的性质，知道相似多边形的对应角相等，对应边成比例，面积的比等于对应边的比的平方。

（3）了解两个三角形相似的概念，探索两个三角形相似的条件。

（4）了解图形的位似，能够利用位似将一个图形放大或缩小。

（5）通过典型实例观察和认识现实生活中物体的相似，使学生综合运用图形的相似解决一些实际问题。

（5）在同一直角坐标系中，感受图形变换后点的坐标的变化特点。

4.2过程与方法目标经历小结的过程，使学生学会建立本章的知识结构图。

相似知识点复习

60°60°60°相似三角形知识点1 比例的性质基本性质：bc ad d c b a =⇔=::；．合比性质：ddc b b ad c b a ±=±⇒=．等比性质：如果)0(≠++++====n f d b n m f e d c b a ，那么ban f d b m e c a =++++++++ ．例题1若线段a ，b ，c ，d 成比例，其中a=5㎝，b=7㎝，c=4㎝，则,d= ． 3已知4x －5y=0，则（x ＋y ）∶（x －y ）的值为．知识点2 黄金分割把线段AB 分成两条线段)(,BC AC BC AC >，且使AC 是BC AB 和的比例中项，叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点，其中AB AC 215-=≈0.618AB ．例题 1已知点C 是线段AB 的黄金分割点,且AC>BC,则AC ∶AB= .知识点3 相似三角形判定①两角对应相等，两个三角形相似②两边对应成比例且夹角相等，两三角形相似 ③三边对应成比例，两三角形相似④如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角形相似⑤平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似⑥直角三角形被斜边上的高分成的两个直角三角形和原三角形相似知识点4 相似三角形性质①相似三角形的对应角相等 ②相似三角形的对应边成比例③相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比 ④相似三角形周长的比等于相似比⑤相似三角形面积的比等于相似比的平方知识点5 相似三角形常见的图形知识点6 相似高级模型① 双垂直模型及其变形② 大角夹半角相似模型:如上右图。

知识点7 位似图形(1)概念：如果两个多边形不仅相似，而且对应顶点的连线相交于一点，这样的图形叫做位似图形．这个点叫做位似中心．(2)性质：位似图形上任意一对对应点到位似中心的距离之比等于位似比．120°60°45°相似三角形解题思路：把证明三角形全等的思想方法迁移到相似三角形中来；对一些出现频率较高的图形，要善于归纳和记忆；对相似三角形的判定思路要善于总结，形成一整套完整的判定方法．如：(1)“平行线型”相似三角形，基本图形见上节图．“见平行，想相似”是解这类题的基本思路；(2)“相交线型”相似三角形，如上图．其中各图中都有一个公共角或对顶角．“见一对等角，找另一对等角或夹等角的两边成比例”是解这类题的基本思路；A C DBE ABC DE变式2图 H MDEF GCBA提高题专题提升一、相似的性质1.如图,DE ∥BC ，AD ∶BD=2∶3，则ΔADE 的面积∶四边形DBCE 的面积=_________。

专题27.46 《相似》全章复习与巩固(培优篇)(专项练习)-2022-2023学年九年级数学下册基

专题27.46《相似》全章复习与巩固（培优篇）（专项练习）一、单选题1．已知AB ＝2，点P 是线段AB 上的黄金分割点，且AP ＞BP ，则AP 的长为（）A B 1 C 352D ．32．如图，在△ABC 中，已知MN△BC ，DN△MC ．小红同学由此得出了以下四个结论：△AN CN ＝AM AB ；△AD DM＝AM MB ；△AM MB ＝AN CN ；△AD AM ＝ANAC .其中正确结论的个数为( )A ．1个B ．2个C ．3个D ．4个3．我们把宽与长的比等于黄金比)的矩形称为黄金矩形.如图,在黄金矩形ABCD ()AB BC <中,ABC ∠的平分线交AD 边于点E ,EF BC ⊥于点F ,则下列结论错误．．的是（）A ．AE DEAD AE= B ．CF BFBF BC= C ．AE BEBE BC= D ．DE ABEF BC= 4．如图，正方形ABCD 中，AB=12，点E 在边BC 上，BE=EC ，将△DCE 沿DE 对折至△DFE ，延长EF 交边AB 于点G ，连接DG 、BF ，给出下列结论：△△DAG△△DFG ；△BG=2AG ；△△EBF△△DEG ；△S △BEF =725.其中正确结论的个数是（）A ．1B ．2C ．3D ．45．正方形ABCD 的边长为1cm ，E 、F 分别是BC 、CD 的中点，连接BF 、DE ，则图中阴影部分的面积是( )cm 2．A ．B ．C ．D ．6．如图，已知在等腰Rt △ABC 中，△ACB ＝90°，AD 为BC 边的中线，过点C 作CE △AD 于点E ，交AB 于点F ．若AC ＝2，则线段EF 的长为（）A ．35B C D ．237．如图，在矩形ABCD 中，点E 是对角线上一点，连接AE 并延长交CD 于点F ，过点E 作EG △AE 交BC 于点G ，若AB ＝8，AD ＝6，BG ＝2，则AE ＝（）A B C D 8．如图，在平面直角坐标系中，已知()20A -，，()04B ，，点C 与坐标原点O 关于直线AB对称．将ABC 沿x 轴向右平移，当线段AB 扫过的面积为20时，此时点C 的对应点1C 的坐标为（）A ．7855⎛⎫ ⎪⎝⎭，B ．9855⎛⎫ ⎪⎝⎭，C ．1855⎛⎫- ⎪⎝⎭，D ．1655⎛⎫- ⎪⎝⎭，9．如图，将矩形ABCD 折叠，使点D 落在AB 上点D ′处，折痕为AE ；再次折叠，使点C 落在ED ′上点C ′处，连接FC ′并延长交AE 于点G ．若AB =8，AD =5，则FG 长为（）A ．BC ．203D ．410．如图，在平面直角坐标系中，点A 、点B 在x 轴上，OB =5，OA =2，点C 是y 轴上一动点，连接AC ，将AC 绕点A 顺时针方向旋转60︒得到AD ，连接BD ，则BD 的最小值为（）A ．72B ．52C D 二、填空题11．如图，////AC EF DB ，若8AC =，12BD =，则EF =________．12．如图，在ABC 中，90BAC ∠=︒，4AB AC ==，点D 是BC 边上一点，且3BD CD =，连接AD ，并取AD 的中点E ，连接BE 并延长，交AC 于点F ，则EF 的长为________．13．如图，在ABC 中，90,8,6,ACB AC BC AD ∠=︒==为边BC 上的中线，BE 是ABC 的角平分线，,AD BE 交于点F ．则EF 的长为______．14．如图，AD BC ⊥，垂足为C ，BF BC ⊥，点P 为线段BC 上一动点，连接AP ，过D 作DE AP ⊥交BF 于E ，连接PE ，若4AC BC ==，1CD =，则PE 长的最小值为______．15．如图，在矩形ABCD 中，AB ＝3，BC ＝4，将矩形ABCD 绕点C 按顺时针方向旋转α角，得到矩形A ′B ′CD ′，B ′C 与AD 交于点E ，AD 的延长线与A ′D ′交于点F ．当矩形A 'B 'CD '的顶点A '落在CD 的延长线上时，则EF ＝_____．16．如图，Rt △ABC 中，△ACB =90°，AC =BC ，D 、E 分别在AC 、BC 上，CE =AD ，CG △DE 于点F ，FE =1，FG =3，则AC =______．17．如图，在菱形ABCD 中，ABC ∠是锐角，过点A 作AE BC ⊥于点E ，作EAF ABC ∠=∠，交CD 于点F ．连接EF 、BD ，若25ABCD S =菱形，25EF BD =，则AEF 的面积为_____．18．如图，平面直角坐标系中有正方形ABCD 和正方形EFGH ，若点A 和点E 的坐标分别为(2,3)-，(1,1)-，则两个正方形的位似中心的坐标是__________．三、解答题19．所谓黄金分割，指的是把长为L 的线段分为两部分，使其中较长部分对于全部之比，． (1 )如图△，在ABC 中，△A ＝36°，AB AC =，△ACB 的平分线CD 交腰AB 于点D ．请你根据所学知识证明：点D 为腰AB 的黄金分割点：(2) 如图△，在Rt ABC △中，△ACB ＝90°，CD 为斜边AB 上的高，AD BD >，1AB =，若点D 是AB 的黄金分割点，求BC 的长，20．如图，在等边ABC 中，D 是BC 的中点，过点A 作AE BC ∥，且AE DC =，连接CE ．(1) 求证：四边形ADCE 是矩形；(2) 连接BE 交AD 于点F ，连接CF ．若4AB =，求CF 的长．21．已知菱形ABCD 中，E 是BC 边上一点． (1) 在BC 的右侧求作AEF ，使得EF BD ∥，且12EF BD =；（要求：尺规作图，不写作法，保留作图痕迹）(2) 在（1）的条件下，若12EAF ABC ∠=∠，求证：AE =．22．已知不等臂跷跷板AB 长为3米，当AB 的一端点A 碰到地面时，（如图1）点B 离地高1.5米；当AB 的另一端点B 碰到地面时，（如图2）点A 离地高1米，求跷跷板AB 的支撑点O 到地面的距离为多少米？23．如图1．已知四边形ABCD 是矩形．点E 在BA 的延长线上．. AE AD EC =与BD 相交于点G ，与AD 相交于点,.F AF AB =()1求证：BD EC ⊥；()2若1AB =，求AE 的长；()3如图2，连接AG ，求证：EG DG -=．24．如图1，在矩形ABCD 中，P 为CD 边上一点（DP ＜CP ），△APB=90°．将△ADP 沿AP 翻折得到△AD′P ，PD′的延长线交边AB 于点M ，过点B 作BN△MP 交DC 于点N ．（1）求证：AD 2=DP•PC ；（2）请判断四边形PMBN 的形状，并说明理由；（3）如图2，连接AC，分别交PM，PB于点E，F．若DPAD =12，求EFAE的值．参考答案1．B【分析】根据黄金分割点的定义和AP＞BP得出AB，代入数据即可得出AP 的长度．解：由于P为线段AB＝2的黄金分割点，且AP ＞BP ，则AP ×21．故选：B ．【点拨】本题考查了黄金分割．应该识记黄金分割的公式：较短的线段=原线段的352，较长的线段=． 2．C解：△△MN △ BC ，△ AN ：CN = AM ：BM ，该项错误；△△DN △ MC ，△ AD ：DM = AN ：NC ，再由（1）得 AD ：DM = AM ：BM ，该项正确；△根据（1）知，此项正确；△根据（2）知，此项正确．所以正确的有3个，故选C ．点睛：本题考查平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．3．C【分析】先根据矩形的性质、角平分线的性质、正方形的判定可得四边形ABFE 是正方形，再根据正方形的性质可得AE EF AB BF ===，再根据黄金矩形的定义逐项判断即可得．解：四边形ABCD 是矩形， 90,A ABC AD BC ∴∠=∠=︒=，EF BC ⊥，即90BFE ∠=︒，∴四边形ABFE 是矩形，BE 是ABC ∠的平分线，且,?EA AB EF BC ⊥⊥， AE EF ∴=，∴四边形ABFE 是正方形，AE EF AB BF ∴===，又四边形ABCD 是黄金矩形，且AB BC <，AB BC ∴=设1)(0)AB a a =≠，则2BC a =，1),2AE EF BF AB a AD BC a ∴======，(3,(3DE AD AE a CF BC BF a ∴=-==-=，1)BE a ，则AB B A A C E D ==DE AE ==，即AE DEAD AE=，选项A 正确；CF BF AB BF BC BC == 即 CF BF BF BC=，选项B 正确；AE BE BE B C 即 AE BE BE BC≠，选项C 错误；AE DE DE AB EF BC===，则选项D 正确；故选：C ．【点拨】本题考查了矩形的性质、角平分线的性质、正方形的判定与性质，掌握理解黄金矩形的定义是解题关键．4．C【分析】根据正方形的性质和折叠的性质可得AD=DF ，△A=△GFD=90°，于是根据“HL”判定Rt△ADG△Rt△FDG ，再由GF+GB=GA+GB=12，EB=EF ，△BGE 为直角三角形，可通过勾股定理列方程求出AG=4，BG=8，进而求出△BEF 的面积，再由△BEF 是等腰三角形，而△GED 显然不是等腰三角形，判断△是错误的，即可得答案．解：如图，由折叠可知，DF=DC=DA ，△DFE=△C=90°， △△DFG=△A=90°，在Rt△ADG 和Rt△FDG 中，AD DFDG DG =⎧⎨=⎩， △Rt△ADG△Rt△FDG ，故△正确； △正方形边长是12， △BE=EC=EF=6，设AG=FG=x ，则EG=x+6，BG=12﹣x ，由勾股定理得：EG2=BE2+BG2，即：（x+6）2=62+（12﹣x）2，解得：x=4△AG=GF=4，BG=8，BG=2AG，故△正确；BE=EF=6，△BEF是等腰三角形，易知△GED不是等腰三角形，故△错误；△S△GBE=12×6×8=24，S△BEF：S△BGE=EF：EG，△S△BEF=610×24=725，故△正确．综上可知正确的结论是3个．故选C．【点拨】本题考查了相似三角形的判定和性质、图形的翻折变换的性质和正方形的性质，全等三角形的判定与性质，勾股定理，三角形的面积计算，熟练掌握相似三角形的判定和性质是解题关键.5．B解：试题分析：阴影部分的面积可转化为两个三角形面积之和，根据角平分线定理，可知阴影部分两个三角形的高相等，正方形的边长已知，故只需将三角形的高求出即可，根据△DON△△DEC可将△ODC的高求出，进而可将阴影部分两个三角形的高求出．连接AC，过点O作MN△BC交AB于点M，交DC于点N，PQ△CD交AD于点P，交BC于点Q△AC为△BAD的角平分线，△OM=OP，OQ=ON；设OM=OP=h1，ON=OQ=h2，△ON△BC△，即，解得△OM=OP故选B.考点：角平分线的性质，三角形的面积公式，相似三角形的判定和性质点评：解题的关键是读懂题意及图形，正确作出辅助线，将阴影部分分成几个规则图形面积相加或相减求得．6．B【分析】过点B作BH△BC，交CF的延长线于H，由勾股定理可求AD的长，由面积法可求CE，由“AAS”可证△ACD△△CBH，可得CD＝BH＝1，AD＝CH△ACF△△BHF，可得BH FHAC FC=＝12，可求CF的长，即可求解．解：如图，过点B作BH△BC，交CF的延长线于H，△AD为BC边的中线，AC＝BC＝2，△CD＝BD＝1，△AD△11S22ACDAC CD AD CE =⨯⨯=⨯⨯，△CE，△△ADC +△BCH ＝90°，△BCH +△H ＝90°，△△ADC ＝△H ，在△ACD 和△CBH 中，90ADC H ACD CBH AC BC ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩，△△ACD △△CBH （AAS ），△CD ＝BH ＝1，AD ＝CH△AC △BC ，BH △BC ，△AC △BH ，△△ACF △△BHF ， △BH FH AC FC=＝12，△CF△EF ＝CF ﹣CE ，故选：B ．【点拨】本题考查了相似三角形判定和性质，全等三角形的判定和性质，勾股定理，等腰直角三角形的性质，添加恰当辅助线构造全等三角形是解题的关键．7．B【分析】过点E 作AB 的平行线，分别交,AD BC 于点,M N ，先根据矩形的性质与判定可得四边形ABNM 和四边形CDMN 都是矩形，设(0)EM x x =>，则8EN x =-，再根据相似三角形的判定证出DEM DBA ，根据相似三角形的性质可得34x DM =，从而可得336,444x AM x GN =-=-，然后根据相似三角形的判定证出AEM EGN ，根据相似三角形的性质可得x 的值，最后在Rt AEM △中，利用勾股定理即可得．解：如图，过点E 作AB 的平行线，分别交,AD BC 于点,M N ，四边形ABCD 是矩形，8,6AB AD ==，6,90,BC AD BAD AD BC ∴==∠=︒，∴四边形ABNM 是矩形，8,90MN AB AME ENG ∴==∠=∠=︒，同理可得：四边形CDMN 是矩形，DM CN ∴=，设(0)EM x x =>，则8EN MN EM x =-=-，EM AB ，DEMDBA ∴， DM EM DA BA∴=，即68DM x =，解得34x DM =， 34x CN ∴=，364AM AD DM x =-=-， 2BG =，344x GN BC BG CN ∴=--=-， 90,AME EG AE ∠=︒⊥，90EAM AEM GEN AEM ∴∠+∠=︒=∠+∠，EAM GEN ∴∠=∠，在AEM △和EGN △中，90AME ENG EAM GEN ∠=∠=︒⎧⎨∠=∠⎩， AEM EGN ∴，AM EM EN GN ∴=，即3643844x x x x -=--，解得4825=x 或8x =，经检验，4825=x 是所列分式方程的根，且符合题意；8x =不是所列分式方程的根，舍去，483114,625425EM AM x ∴==-=，AE ∴=== 故选：B ．【点拨】本题考查了矩形的判定与性质、相似三角形的判定与性质等知识点，通过作辅助线，构造相似三角形是解题关键．8．B【分析】连接AA 1、BB 1，过C 点作CE △x 轴于E 点，过B 点作BD △CE ，交EC 的延长线于点D ，根据A (-2，0)、B (0，4)，OA =2，OB =4，进而得到AC =2，BC =4，再证Rt △DBC △Rt △ECA ，得到422BD CD BC CE AE AC ====，设AE =x ，则有CD =2x ，OE =AO +AE =2+x ，在Rt △ACE 中，222AC CE AE =+，即有22222()2x x +=+，解方程求出x ，即可求出AE ，则C 点坐标可求，再根据AB 扫过的面积为20，求得15AA =，可知△ABC 向右平移了5个单位，则问题得解．解：平移后的效果如图，连接AA 1、BB 1，过C 点作CE △x 轴于E 点，过B 点作BD △CE ，交EC 的延长线于点D ，根据平移的性质可知AA 1=BB 1，且11//AA BB ，即有四边形11AA BB 是平行四边形．△CE △x 轴，BD △CE ，△△D =△CEA =90°，根据对称的性质可知△AOB △△ACB ，△△ACB =△AOB =90°，AO =AC ，OB =BC ，△A (-2，0)、B (0，4)，△OA =2，OB =4，△AO =AC =2，OB =BC =4，△△ACB =90°=△D ，△△DCB +△ACE =90°，△DCB +△DBC =90°，△△ACE =△CBD ，△Rt △DBC △Rt △ECA ， △422BD CD BC CE AE AC ====，设AE =x ，则有CD =2x ，△OE =AO +AE =2+x ，△△D =△CEA =90°=△AOB ，△四边形OBDE 是矩形，△BD =OE ，即BD =2+x ， △422BD CD BC CE AE AC ====， △222BD x CE +==， △在Rt △ACE 中，222AC CE AE =+，△有22222()2x x +=+，解得65x =，（负值舍去）， △65AE =， △1625OE x =+=，2825x CE +==， △C 点坐标为168()55-，，根据平移的性质可知直线AB 扫过的图形为是平行四边形11AA BB ，△根据题意有1120AA BB S =平行四边形，△11114AA BB S AA OB AA =⨯=平行四边形，△1420AA =，△15AA =，△可知△ABC向右平移了5个单位，△C168()55-，也向右平移了5个单位才得到C1，△即169555 -+=，△C1点坐标为98 () 55，，故选：B．【点拨】本题考查了平移的性质、平行四边形的判定与性质、勾股定理、相似三角形的判定与性质、一元二次方程的应用等知识，求出C点的坐标是解答本题的关键．9．C【分析】过点G作GI△AB，GH△ED'，垂足分别为I、H，由折叠的性质可得C′E=5-4=1，在Rt△EFC′中，设FC′=x，则EF=3-x，由勾股定理得：12+（3-x）2=x2，解得：x=53，再证明△BC′D'△△C′GH，设C′H=3m，则GH=4m，C′G=5m，则HD'=GI=AI=4-3m，ID'=5-（4-3m）=1+3m=GH=4m，可得到C′G=5m=5，从而解决问题．解：由折叠的性质得，△AD'E=△D=90°，AD=AD'，又△△DAB=90°，△四边形ADED'是矩形，△AD=AD'，△四边形ADED'是正方形，过点G作GI△AB，GH△ED'，垂足分别为I、H，△AD'ED是正方形，△AD=DE=ED'=AD'=5，BC=BC′=5，△C=△BC′F=90°，FC=FC′，△D'B=EC=8-5=3，在Rt△C′BD'中，C′D'=4，△C′E=5-4=1，在Rt△EFC′中，设FC′=x，则EF=3-x，由勾股定理得：12+（3-x）2=x2，解得：x=53，△△BC′D'+△GC′H=90°，△GC′H+△C′GH=90°，△△BC′D'=△C′GH，又△△GHC′=△BD'C′=90°，△△BC′D'△△C′GH，△C′H：GH：C′G=BD'：C′D'：BC′=3：4：5，设C′H=3m，则GH=4m，C′G=5m，△HD'=GI=AI=4-3m，ID'=5-（4-3m）=1+3m=GH=4m，解得：m=1，△C′G=5m=5，△FG=203；故选：C．【点拨】本题主要考查了矩形的性质，正方形的判定与性质，翻折的性质，勾股定理，相似三角形的判定与性质等知识，作辅助线构造三角形相似是解题的关键．10．A【分析】构造等边三角形OAE，过点E作AE△EF，垂足为E，交x轴于点F，截取ED=OC,证明△AOC△△AED，得到AC=AD，且△CAD=60°，从而得到点D在直线EF上，过点B作BD△EF，此时BD最小．解：构造等边三角形OAE，过点E作AE△EF，垂足为E，交x轴于点F，截取ED=OC,△等边三角形OAE，△AO=AE，△OAE=△AOE=60°，△ED=OC, △AED=△AOC=90°，△△AOC△△AED，△AC =AD ，且△CAD =60°，△点D 在直线EF 上，过点B 作BD △EF ，此时BD 最小，△OB =5，OA =2，△AE∥BD ，△OEF =△OFE =30°，△OF =OE =OA =AE =2，AB =3，△F A =4，FB =7，AE FA BD FB=， △247BD =，解得BD =72，故选A ．【点拨】本题考查了等边三角形的判定和性质，三角形相似的判定和性质，三角形全等的判定和性质，垂线段最短，熟练掌握三角形相似的判定，垂线段最短原理是解题的关键．11．245【分析】根据平行线AC△EF 分线段成比例得到.EF BF CA AB =同理EF AF DB AB =，则由比例的性质得到DB EF BF DB AB -=，根据等量代换推知EF DB EF CA DB-=，所以把相关数据代入即可求得EF 的值．解：如图,△AC △EF ，△.EF BF CA AB= 又△EF △DB ， △EF AF DB AB=，则由比例的性质知,DB EF AB AF DB AB --= 即DB EF BF DB AB -=， △EF DB EF CA DB-=， △AC =8，BD =12，△12812EF EF -= △EF =245. 故答案是：245. 【点拨】考查平行线分线段成比例定理：一组平行线截两条直线，所截的线段对应成比例.12【分析】利用△ABC 是直角三角形构造直角坐标系，过点D 作DM △AC 于M ，过点D 作DN △AB 于N ，利用图中各线段的长度，再结合一次函数、中点坐标公式可以求出图中各点的坐标，即可求出EF 的长．解：根据△BAC =90°可知△ABC 是直角三角形，则以直角△ABC 的顶点A 点为坐标原点O ，以AC 为x 轴，以AB 为y 轴构造直角坐标系，过点D 作DM △AC 于M ，过点D 作DN △AB 于N ，如图，由AB =AC =4，可知B 点坐标为(4,0)，C 点坐标为(0,4)，则直线BC 的解析式为4y x =-，△BD =3CD ，△4CD =BC ，△DM △AC ，DN △AB ，△有MD AB ∥，MD AB ∥，则有CD CM MD BC CA AB ==，即有：14CD CM MD BC CA AB ===，则可求得D 点坐标为：(1,3)，又△E 点为AD 中点，△根据中点坐标公式又E 点坐标为：13(,)22，则直线BE 的解析式为：31277y x =-+，则易得F 点坐标为：12(0,)7，则EF 的长度为：EF =【点拨】本题考查了运用直角坐标系求线段的长度的问题，设计根据点的坐标求解一次函数解析式、中点坐标公式、线段长度公式等知识，利用直角三角形的特点构建直角坐标系是解答本题的关键．13【分析】过点E 作EG △AB ，垂足为G ，证明△CBE △△GBE ，求得CE ，EG ，AE 的长，过点F 作FO △AC ，垂足为O ，利用平行线分线段成比例定理求解即可．解：△90,8,6,ACB AC BC ∠=︒==，过点E 作EG △AB ，垂足为G ，△BE 是ABC 的角平分线，△△CBE =△GBE ，△△C =△BGE =90°，BE =BE ，△△CBE △△GBE ，△BC =BG =6，EC =EG ，设CE =x ，则EG =x ，AE =8-x ,AG =AB -BG =4,在直角三角形AEG 中，根据勾股定理，得222AE EG AE =+，即222(8)4x x -=+，解得x =3，△CE =3，AE =5，过点F 作FO △AC ，垂足为O ，90ACB ∠=︒，△FO∥BC ， △OF OE BC CE =， △623OF BC OE CE ===即FO =2OE ， △AD 是中线，BC =6，△CD =3，△FO∥DC ， △8OF AE OE DC +=， △2538OE OE +=，解得OE =1513，在直角三角形OEF 中，22225EF EO OF EO =+=，△EF．【点拨】本题考查了勾股定理，三角形全等，平行线分线段成比例定理，中线，角的平分线，构造辅助线实施全等证明，平行线分线段成比例证明是解题的关键．14【分析】设DE 交AP 于点Q ，DE 交BC 于点H ，根据DE AP ⊥，确定点Q 在以AD 为直径的圆周上运动，得到当点Q 与点P 重合时，PE 最小，此时，点Q 、点P 与点H 重合，取AD 的中点O ，连接OP ，利用勾股定理求出CP ，再证明△CDP △△BPE ，利用勾股定理求出答案．解：设DE 交AP 于点Q ，DE 交BC 于点H ，△DE AP ⊥，△90AQD EQP ∠=∠=︒，△点Q 在以AD 为直径的圆周上运动，当点Q 与点P 重合时，PE 最小，此时，点Q 、点P 与点H 重合，取AD 的中点O ，连接OP ，△52OA OD OP ===，32OC =,△2CP ==， △AD △BF ，△△CPD △△BPE ，△2BP CP ==，△△CDP △△BPE ，△PE PD =【点拨】此题考查图形中的动点问题，勾股定理，全等三角形的判定及性质，相似三角形的判定，正确理解点Q 的位置与点P 的位置确定PE 的最小值位置是解题的关键．15．154##334 【分析】根据矩形的性质得90D '∠=︒，根据勾股定理得222=+A C A D CD '''，再证明A DF A D C '''△∽△得A D DF A D CD''''=，证明CDE CB A ''△∽△得CD ED CB A B '''=，分别计算DF 和DE 的长即可得解．解：△四边形ABCD 是矩形，矩形ABCD 绕点C 按顺时针方向旋转α角，得到矩形A ′B ′CD ′， △90D '∠=︒，=4AD A D BC ''==，3CD CD AB '===，在Rt A CD ''△中，=90D '∠︒，△222=+A C A D CD ''''，△5A C '=，2A D '=，△=DA F CA D '''∠∠，=90A DF D ''∠∠=︒，△A DF A D C '''△∽△，△A D DF A D CD ''''=， △243DF =， △DF 32=，同理可得CDE CB A ''△∽△， △CD ED CB A B '''=， △343ED =， △ED 94=， △EF ＝ED +DF 154=，故答案为：154．【点拨】本题考查了矩形的性质，相似三角形的判定与性质，解题的关键是掌握这些知识点．16．【分析】过点D 作DT △AD 交AB 于点T ，连接ET ，连接CT 交DE 于点M ，通过推导角度可知CT =CG ，且四边形DTEC 为矩形，设CF 为x ，表示出DF ，利用相似可求出x ，进而可得结果．解：过点D 作DT △AD 交AB 于点T ，连接ET ，连接CT 交DE 于点M ，△Rt △ABC 中，△ACB =90°，AC =BC ，△△A =△B =45°，△DT △AD ，△△ADT 为等腰直角三角形，△CE =AD ，△DT =CE ，△DT ∥CE ，△DCE =90°，△四边形DTEC 为矩形，△DE =CT ，设△BCG =α，则△CDE =α，△△DCT =α，△△CTB =45°+α，△△CGT =45°+α，△CT =CG ，△DE =CG ，设CF =x ,则DE =CG =x +3，△DF =x +2，△△CFE △△DFC ， △CF EF DF CF=，即2CF EF DF =⋅， △22x x =+，解得x =2或x =-1（舍），△CF =2，△DF =4，CE =AD△CD△AC故答案为：【点拨】本题考查三角形与四边形综合知识，需要同学们熟练掌握等腰直角三角形的性质、矩形的性质、相似三角形的性质与判定，选择适当的辅助线将AD =CE 这一条件联系起来是解题关键．17．8【分析】连接AC ，设2CE a =，由菱形的性质和AE BC ⊥可证()ABE ADF ASA ≌，由全等三角形的性质可得BE DF =，从而推出CEF CBD ∠=∠，由相似三角形的判定得出CEF CBD ∽△△，所以25EC EF BC BD，所以5AB AD BC a ===，3BE a =，利用勾股定理得4AE a =，然后再证明FAE ABC △∽△，由相似三角形的性质得1625AEF ABC S S =△△，即可求解．解：连接AC ，设2CE a =，△四边形ABCD 是菱形，AE BC ⊥，△AB AD DC BC ===， AD BC ∥，ABC ADC ∠=∠，CBD CDB ∠=∠，90AEB =︒∠，△90DAE AEB ∠=∠=︒，△90ABC BAE EAF DAF ∠+∠=∠+∠=︒，△EAF ABC ∠=∠，△BAE DAF ∠=∠，在ABE △和ADF 中，BAE DAF AB ADABE ADF ∠=∠⎧⎪=⎨⎪∠=∠⎩， △()ABE ADF ASA ≌，△BE DF =，AE AF =，△CE CF =，△CEF CFE ∠=∠，△CBD CDB ∠=∠，BCD ECF ∠=∠， △()11802CEF ECF ∠=︒-∠，()11802CBD BCD ∠=︒-∠， △CEF CBD ∠=∠，△CEF CBD ∽△△， △25ECEF BC BD ， △5BC a =，△5AB AD BC a ===，523BE BC EC a a a =-=-=，△4AE a ==，△4AF AE a ==，△45AF AE BA BC ==，又△FAE ABC ∠=∠，△FAE ABC △∽△，△22416525AEF ABC S AE a S BC a ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭△△， △四边形ABCD 是菱形，25ABCD S =菱形， △12522ABC ADC ABCD S S S ===△△菱形， △161625825252AEF ABC S S ==⨯=△△．故答案为：8．【点拨】本题是相似综合题，考查了菱形的性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，等腰三角形的性质等知识．掌握菱形的性质和等腰三角形的性质，证明三角形全等和三角形相似是解题的关键．18．1(,0)4或3(4,-)2 【分析】根据位似变换中对应点的坐标的变化规律．因而本题应分两种情况讨论，一种是点A 和E 是对应顶点，B 和F 是对应顶点；另一种是点A 和G 是对应顶点，C 和E 是对应顶点．解：△平面直角坐标系中有正方形ABCD 和正方形EFGH ，点A 和点E 的坐标分别为(2,3)-，(1,1)-，△(2,0)B -，(2,1)H -，(2,0)G ，（1）当点A 和E 是对应顶点，B 和F 是对应顶点时，位似中心就是AE 与BF 的交点，如图所示：连接AE ，交x 轴于点N ，点N 即为两个正方形的位似中心，设AE 所在直线解析式为：y kx b =+，把(2,3)A -，(1,1)E -代入得：故321k b k b=-+⎧⎨-=+⎩，解得：4313k b ⎧=-⎪⎪⎨⎪=⎪⎩，故4133y x =-+；当0y =时，即41033x =-+，解得14x =，即点坐标为1(4，0)， ∴两个正方形的位似中心的坐标是：1(4，0)．（2）当点A 和G 是对应顶点，B 和H 是对应顶点时，位似中心就是AG 与BH 的交点，如图所示：连接AG ，DF ，BH ，CE 并延长交于点M ，设AG 所在直线解析式为：y kx b =+，把(2,3)A -，(2,0)G 代入得：故3202k b k b =-+⎧⎨=+⎩，解得：3432k b ⎧=-⎪⎪⎨⎪=⎪⎩，故3342y x =-+；设BH 所在直线解析式为：y mx n =+，把(2,0)B -，(2,1)H -代入得：1412m n ⎧=-⎪⎪⎨⎪=-⎪⎩，故1142y x =--，联立直线BH 、AG 得方程组：33421142y x y x ⎧=-+⎪⎪⎨⎪=--⎪⎩，解得：432x y =⎧⎪⎨=-⎪⎩，故3(4,)2M -，综上所述：两个正方形的位似中心的坐标是：1(4，0)或3(4,)2-．故答案为：1(4，0)或3(4,)2-．【点拨】此题主要考查了位似图形的性质以及函数交点求法以及位似变化中对应点的连线一定经过位似中心．注意：本题应分两种情况讨论．根据点的对应关系利用一次函数求直线的交点是解题关键．19．(1)证明见分析(2)2【分析】（1）根据三角形内角和定理，等边对等角，等角对等边确定BC =AD ，△BCD =△A ，根据相似三角形的判定定理和性质即可证明．（2）根据黄金分割的定义求出BD 的长度，根据相似三角形的判定定理和性质求出BC 2，进而即可求出BC 的长度．（1）证明：△在ABC 中，△A ＝36°，AB AC =， △180722A B ACB ︒-∠∠=∠==︒． △CD 为△ACB 的平分线， △1362ACD BCD ACB ∠∠=∠︒==， △△ACD =△BCD =△A ．△AD =DC ．△18072BDC B BCD ∠=︒-∠-∠=︒．△△BDC =△B ，△BDC >△BCD ．△DC =BC ，BC >BD ．△BC =AD ．△AD >BD ．△CBD ABC ∠=∠，△CBD ABC ∽△△． △BC BD BA BC=，即AD BD BA AD =． △点D 是腰AB 的黄金分割点．（2）解：△点D 是AB 的黄金分割点，AD BD >，△AD BD AB AD ==．△1AB =，△2AD =．△1BD =．△90ACB ∠=︒，CD 是△ABC 斜边上的高，△90ACB CDB ∠=∠=︒．△ABC CBD ∠=∠，△ACB CDB ∽△△． △AB BC CB BD=．△)2114BC AB BD =⋅==． △2BC =．【点拨】本题考查三角形内角和定理，等边对等角，等角对等边，相似三角形的判定定理和性质，综合应用这些知识点是解题关键．20．(1)见分析【分析】（1）由AE BC ∥，AE DC =，可得四边形ADCE 是平行四边形，由ABC 是等边三角形，D 是BC 的中点，得到△ADC ＝90°，结论得证；（2）由等边三角形的三线合一求得BD ，在Rt ABD △中，由勾股定理得AD ，BE ，由AD EC ，D 为BC 的中点，得到F 为BE 的中点，△BCE 是直角三角形，由斜边上中线等于斜边的一半得到答案．（1）证明：△AE BC ∥，AE DC =，△四边形ADCE 是平行四边形．△ABC 是等边三角形，D 是BC 的中点，△AD BC ⊥．△90ADC ∠=︒．△四边形ADCE 是矩形．（2）解：如图，△ABC 是等边三角形，4AB =，△4BC AB ==．△D 是BC 的中点，△2BD =．在Rt ABD △中，90ADB ∠=︒，△AD =△四边形ADCE 为矩形，△==EC AD 90ECB ∠=︒，AD EC ∥．△BE =△AD EC ∥，D 为BC 的中点， △1==BF BD FE DC． △F 为BE 的中点．△△BCE 是直角三角形，△12==CF BE 【点拨】此题考查了矩形判定和性质、等边三角形的性质、平行四边形的判定、平行线分线段成比例、直角三角形的性质、勾股定理等知识，熟练掌握相关图形的性质和判定是解题的关键．21．(1)见分析；(2)见分析.【分析】（1）连接AC 交BD 于O ，在BC 右侧作△CEF =△CBD ，再在射线EF 截取EF =OB ，连接AE 、AF ，即可得△AEF ；（2）延长EF 交AD 延长线于点G ，先证明四边形BEGD 是平行四边形，可得EG =BD =2EF ，△G =△CBD ，（1）解：如图，连接AC 交BD 于O ，在BC 右侧作△CEF =△CBD ，再在射线EF 截取EF =OB ，连接AE 、AF ，则△AEF 即为所要求作的三角形，再证~EAF EGA ，可得EF AE AE EG=，最后证得结果；（2）证明：延长EF 交AD 延长线于点G ，△四边形ABCD 是菱形，△AD //BC∥又△EF //BD ，EF =12BD ，△四边形BEGD 是平行四边形，△EG =BD =2EF ，△G =△CBD ，又△在菱形ABCD 中，△CBD =12△ABC ，12EAF ABC ∴∠=∠， EAF G ∴∠=∠，又△AEF GEA ∠=∠，~EAF EGA ∴，EF AE AE EG∴=， 2222AE EF EG EF EF EF ∴=⋅=⋅=，AE ∴=；【点拨】本题考查作图-复杂作图、相似三角形的性质与判定、菱形的性质、平行四边形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．22．跷跷板AB 的支撑点O 到地面的距离为0.6米．【分析】过点B 作BN ⊥AH 于点N ，AM ⊥BH 于点M ，直接利用相似三角形的判定与性质分别得出OH AO BN AB=，OH BO AM AB =，即可得出答案．解：如图所示：过点B 作BN ⊥AH 于点N ，AM ⊥BH 于点M ，可得HO ∥BN ，则△AOH ∽△ABN ，故OH AO BN AB=， ∵AB 长为3米，BN 长为1.5米， ∴1.53OH AO =， ∴2OH OA =同理可得：△BOH ∽△BAM ，则OH BO AM AB=， ∵AB 长为3米，AM 长为1米， ∴313OH AO -=，即3213OH OH -= ∴OH ＝0.6，答：跷跷板AB 的支撑点O 到地面的距离为0.6米．【点拨】此题主要考查了相似三角形的应用，正确得出比例式，建立方程是解题关键．23．（1）见分析；（2；（3）见分析【分析】（1）由矩形的形及已知证得△EAF△△DAB ，则有△E=△ADB ，进而证得△EGB=90º即可证得结论；（2）设AE=x ，利用矩形性质知AF△BC ，则有EA AF EB BC=，进而得到x 的方程，解之即可；（3）在EF 上截取EH=DG ，进而证明△EHA△△DGA ，得到△EAH=△DAG ，AH=AG ，则证得△HAG 为等腰直角三角形，即可得证结论．解：（1）△四边形ABCD 是矩形，△△BAD=△EAD=90º，AO=BC ，AD△BC ，在△EAF 和△DAB ，AE AD EAF DAB AF AB =⎧⎪∠=∠⎨⎪=⎩，△△EAF△△DAB(SAS)，△△E=△BDA ，△△BDA+△ABD=90º，△△E+△ABD=90º，△△EGB=90º，△BG△EC ；（2）设AE=x ，则EB=1+x ，BC=AD=AE=x ，△AF△BC ，△E=△E ，△△EAF△△EBC ， △EA AF EB BC =，又AF=AB=1， △11x x x=+即210x x --=，解得：x =x =（舍去）即；（3）在EG 上截取EH=DG ，连接AH ，在△EAH 和△DAG ，AE AD HEA GDA EH DG =⎧⎪∠=∠⎨⎪=⎩，△△EAH△△DAG(SAS)，△△EAH=△DAG ，AH=AG ，△△EAH+△DAH=90º，△△DAG+△DAH=90º，△△HAG=90º，△△GAH 是等腰直角三角形，△222AH AG GH +=即222AG GH =，，△GH=EG -EH=EG -DG ，△EG DG -=．【点拨】本题主要考查了矩形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、直角定义、相似三角形的判定与性质、解一元二次方程等知识，涉及知识面广，解答的关键是认真审题，提取相关信息，利用截长补短等解题方法确定解题思路，进而推理、探究、发现和计算．24．（1）证明见分析；（2）四边形PMBN 是菱形，理由见分析；（3）49EF AE = 【分析】（1）过点P 作PG△AB 于点G ，易知四边形DPGA ，四边形PCBG 是矩形，所以AD=PG ，DP=AG ，GB=PC ，易证△APG△△PBG ，所以PG 2=AG•GB ，即AD 2=DP•PC ；（2）DP△AB ，所以△DPA=△PAM ，由题意可知：△DPA=△APM ，所以△PAM=△APM ，由于△APB -△PAM=△APB -△APM ，即△ABP=△MPB ，从而可知PM=MB=AM ，又易证四边形PMBN 是平行四边形，所以四边形PMBN 是菱形；（3）由于12DP AD =，可设DP=k ，AD=2k ，由（1）可知：AG=DP=k ，PG=AD=2k ，从而求出GB=PC=4k ，AB=AG+GB=5k ，由于CP△AB ，从而可证△PCF△△BAF ，△PCE△△MAE ，从而可得59AF AC ＝，513AE AC ＝，从而可求出EF=AF -AE=59AC -513AC =20117AC ，从而可得2041175913AC EF AE AC ==．解：（1）过点P 作PG△AB 于点G ，△易知四边形DPGA，四边形PCBG是矩形，△AD=PG，DP=AG，GB=PC△△APB=90°，△△APG+△GPB=△GPB+△PBG=90°，△△APG=△PBG，△△APG△△PBG，△PG GB AG PG＝，△PG2=AG•GB，即AD2=DP•PC；（2）△DP△AB，△△DPA=△PAM，由题意可知：△DPA=△APM，△△PAM=△APM，△△APB-△PAM=△APB-△APM，即△ABP=△MPB△AM=PM，PM=MB，△PM=MB，又易证四边形PMBN是平行四边形，△四边形PMBN是菱形；（3）由于12 DPAD，可设DP=k，AD=2k，由（1）可知：AG=DP=k，PG=AD=2k，△PG2=AG•GB，△4k2=k•GB，△GB=PC=4k，AB=AG+GB=5k，△CP△AB，△△PCF△△BAF，△45 CF PCAF AB==，△59 AFAC＝，又易证：△PCE△△MAE，AM=12AB=52k,△48552CE PC kAE AM k===△513 AEAC＝，△EF=AF-AE=59AC-513AC=20117AC，△2041175913ACEFAE AC==.【点拨】本题考查相似三角形的综合问题，涉及相似三角形的性质与判定，菱形的判定，直角三角形斜边上的中线的性质等知识，综合程度较高，需要学生灵活运用所学知识．。

《相似》单元复习

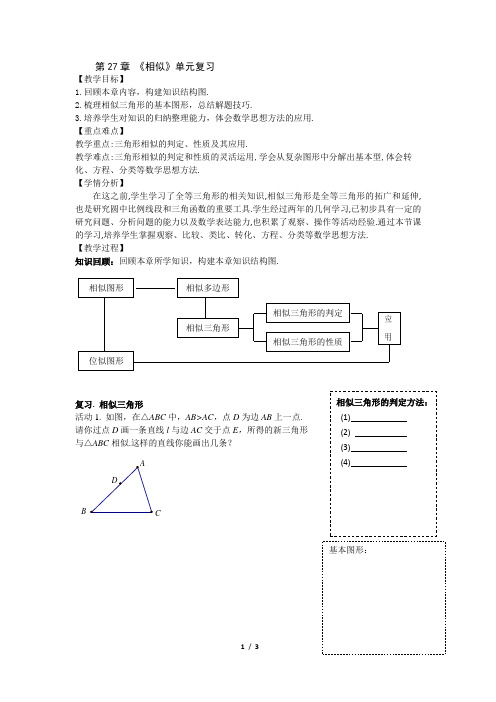
第27章《相似》单元复习【教学目标】1.回顾本章内容，构建知识结构图.2.梳理相似三角形的基本图形，总结解题技巧.3.培养学生对知识的归纳整理能力，体会数学思想方法的应用. 【重点难点】教学重点:三角形相似的判定、性质及其应用.教学难点:三角形相似的判定和性质的灵活运用,学会从复杂图形中分解出基本型,体会转化、方程、分类等数学思想方法. 【学情分析】在这之前,学生学习了全等三角形的相关知识,相似三角形是全等三角形的拓广和延伸,也是研究圆中比例线段和三角函数的重要工具.学生经过两年的几何学习,已初步具有一定的研究问题、分析问题的能力以及数学表达能力,也积累了观察、操作等活动经验.通过本节课的学习,培养学生掌握观察、比较、类比、转化、方程、分类等数学思想方法. 【教学过程】知识回顾：回顾本章所学知识，构建本章知识结构图.复习. 相似三角形活动1. 如图，在△ABC 中，AB>AC ，点D 为边AB 上一点.请你过点D 画一条直线l 与边AC 交于点E ，所得的新三角形与△ABC 相似.这样的直线你能画出几条？CB基本图形：活动2.如图，∠ACB =90°，CD ⊥AB 于D ，BD =3，，求 .找一找：图中有几对相似三角形？你是如何思考的？活动3. 如图，B 、C 、P 共线，AB ⊥BC ，DC ⊥BC ，AP ⊥PD .若PC =1 ，CD =2，PB =6，则AB 的长为 . P变题1：如图，B 、C 、P 共线，AB ⊥BC ，DC ⊥BC ，BC =7，CD =2，AB =3. 若在边BC 上有点P ,使△P AB 与△PCD 相似，则符合条件的点P 有个.P基本图形：基本图形：变题2：在等腰△ABC中，∠BAC=90°，AB=AC=1，点D是BC边上的一个动点(不与B、C 重合).在AC上取一点E，使∠ADE=45°.设BD=x，AE=y.请你尝试设计一个问题.【课堂小结】通过本节课的复习，你有哪些收获？有哪些新的认识？你还有什么疑惑吗？。

《相似》全章复习与巩固--知识讲解(基础).docx

撰稿：赵炜审稿：杜少波【学习目标】1、了解比例的基本性质，线段的比、成比例线段；2、通过具体实例认识图形的相似，探索相似图形的性质，理解相似多边形对应角相等、对应边成比例、周长的比等于相似比、面积的比等于相似比的平方，探索并常握相似三角形的判定方法，并能利用这些性质和判定方法解决生活中的一些实际问题；3、了解图形的位似，能够利用位似将一个图形放大或缩小，在同一直角坐标系中，感受位似变换后点的坐标的变化；4、结合相似图形性质和判定方法的探索和证明，进一步培养推理能力，发展逻辑思维能力和推理论证的表达能力，以及综合运用知识的能力，运用学过的知识解决问题的能力.【知识网络】积比等于相似比的平方他似图形］【要点梳理】要点一、相似图形及比例线段1.相似图形：在数学上，我们把形状相同的图形称为相似图形(sim 订ar figures). 要点诠释：(1)相似图形就是指形状相同，但大小不一定相同的图形；(2)“全等”是“相似”的一种特殊情况，即当“形状相同”且“大小相同”时，两个图形全等；2.相似多边形如果两个多边形的对应角相等，对应边的比相等，我们就说它们是相似多边形.要点诠释：(1)相似多边形的定义既是判定方法，又是它的性质.（2）相似多边形对应边的比称为相似比.3.比例线段：对于四条线段自、b 、c 、d,如果其中两条线段的比与另两条线段的比相等, 如臼:我们就说《相似》全章复习与巩固知识讲解(基础)相似图形卜|相似多边形卜对应角相等奸应边紛谕等?周长比等于相似比面积比寧于才a 似比的平方相似三角形的识别?判定方法］t ?判定方法2 } 1判定方法3 }彳判定方湖”I 相似三角形相似三角形的特征应玄的财壽对应高的比、对应中线的比、对应角平分线的比等于相似比1周长比等于相似比相似图形的应用这四条线段是成比例线段，简称比例线段.要点诠释：（1）若a: ire: d ,则ad二be；（d也叫第四比例项）（2）若a: b=b\ c ,贝ijb' =ac （.b称为&、u的比例中项）.要点二、相似三角形1.相似三角形的判定：判定方法（一）：平行于三角形一边的直线和其他两边相交，所构成的三角形和原三角形相似.判定方法（二）：如果两个三角形的三组对应边的比相等，那么这两个三角形相似.判定方法（三）：如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似.要点诠释：此方法要求用三角形的两边及其夹角来判定两个三角形相似，应用时必须注意这个角必须是两边的夹角，否则，判断的结果可能是错误的.判定方法（四）：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似.要点诠释：要判定两个三角形是否相似，只需找到这两个三角形的两个对应角相等即可，对于直角三角形而言，若有一个锐角对应相等，那么这两个三角形相似.2.相似三角形的性质：（1）相似三角形的对应角相等，对应边的比相等；（2）相似三角形中的重要线段的比等于相似比；相似三角形对应高，对应屮线，对应角平分线的比都等于相似比.要点诠释：要特别注意“对应”两个字，在应用时，要注意找准对应线段.（3）相似三角形周长的比等于相似比；（4）相似三角形面积的比等于相似比的平方。

初三上期末复习——相似

B
∴∠ADC=90°，∴∠DCA+∠DAC=90°，
DC
∴∠EBC+∠DCA=90°，∴∠BGC =180°－
(∠EBC+∠DCA)=90°，∴AC⊥BH.
(2) 若 ∠ABC=45°，⊙O 的直径等于 10，BD = 8，
求 CE 的长．解：∵∠BDA=180°－∠ADC=90°， ∠ABC=45°，∴∠BAD=45°，
期末复习相似
相似
考点讲练
考点一相似三角形的判定和性质
针对训练
1．如图所示,当满足下列条件之一时，都可判定
△ADC ∽△ACB．
(1) ∠ACD =∠B
；
(2) ∠ACB =∠ADC
；
(3)
AD AC AC AB
或
AC2 = AD ·AB.
A
D
B
C
1. △ABC 的三边长分别为 5，12，13，与它相似的 △DEF 的最小边长为 15，则 △DEF 的其他两条边长为 36 和 39．
方形的一边在 BC 上，其余两个顶点分别在 AB、AC 上，
这个正方形零件的边长是多少？
解：设正方形 EFHG 为加工成的
A
正方形零件，边 GH 在 BC 上，顶点 E、F 分别在AB、
EM F
AC上，△ABC 的高 AD 与边 EF 相交于点 M，设正方形的 B G D H C 边长为 x mm.
A
GH
E
O
∴ BD = AD.∵ BD Βιβλιοθήκη 8，∴ AD = 8.B
DC
在 Rt△ADC中，AD = 8，AC = 10，
由勾股定理得 DC = 6，则 BC = BD + DC = 14.

中考数学专题复习精品讲义相似

专题复习精品讲义第二十七章相似本章小结小结1 本章概述本章内容是对三角形知识的进一步认识，是通过许多生活中的具体实例来研究相似图形．在全等三角形的基础上，总结出相似三角形的判定方法和性质，使学过的知识得到巩固和提高．在学习过程中，通过大量的实践活动来探索三角形相似的条件，并应用相似三角形的性质及判定方法来研究和解决实际问题．在研究相似三角形的基础上学习位似图形，知道位似变换是特殊的相似变换．小结2 本章学习重难点【本章重点】通过具体实例认识图形的相似，探索相似图形的性质，掌握相似多边形的对应角相等，对应边成比例，面积的比等于相似比的平方．了解两个三角形相似的概念，探索两个三角形相似的条件．【本章难点】通过具体实例观察和认识生活中物体的相似，利用图形的相似解决一些实际问题．【学习本章应注意的问题】通过生活中的实例认识物体和图形的相似，探索并认识相似图形的特征，掌握相似多边形的对应角相等，对应边成比例以及面积的比与相似比的关系，能利用相似三角形的性质解决一些简单的实际问题，了解图形的位似，能利用位似将一个图形放大或缩小，会建立坐标系描述点的位置，并能表示出点的坐标．小结3 中考透视图形的相似在中考中主要考查：(1)了解比例的基本性质，了解线段的比及成比例线段．(2)认识相似图形，了解相似多边形的对应角相等，对应边成比例，面积比等于相似比的平方．(3)了解两个三角形相似的概念，掌握两个三角形相似的条件，能利用图形的相似解决一些实际问题．(4)了解图形的位似，能利用位似将一个图形放大或缩小．相似是平面几何中重要的内容，在近几年的中考中题量有所增加，分值有所增大，且题型新颖，如阅读题、开放题、探究题等．由于相似图形应用广泛，且与三角形、平行四边形联系紧密，估计在今后中考的填空题、选择题中将会注重相似三角形的判定与性质等基础知识的考查，并在解答题中加大知识的横向与纵向联系．具体考查的知识点有相似三角形的判定、相似三角形的性质、相似三角形的实际应用、图形的放大与缩小等．知识网络结构图专题总结及应用一、知识性专题专题1 比例线段【专题解读】解决有关比例线段的问题时，常常利用三角形相似来求解．例1 如图27－96所示，A，B，D，E四点在⊙O上，AE，BD的延长线相交于点C，AE＝8，OC＝12，∠EDC＝∠BAO．

《图形的相似》全章复习与巩固(知识讲解)九年级数学上册基础知识讲与练(北师大版)

专题4.48 《图形的相似》全章复习与巩固（知识讲解）【学习目标】1、了解比例的基本性质，线段的比、成比例线段；2、通过具体实例认识图形的相似，探索相似图形的性质，理解相似多边形对应角相等、对应边成比例、周长的比等于相似比、面积的比等于相似比的平方，探索并掌握相似三角形的判定方法，并能利用这些性质和判定方法解决生活中的一些实际问题；3、了解图形的位似，能够利用位似将一个图形放大或缩小，在同一直角坐标系中，感受位似变换后点的坐标的变化；4、结合相似图形性质和判定方法的探索和证明，进一步培养推理能力，发展逻辑思维能力和推理论证的表达能力，以及综合运用知识的能力，运用学过的知识解决问题的能力.【要点梳理】【知识点一】成比例线段1、定义：四条线段,,,a b c d 中，如果a 与b 的比等于c 与d 的比，即a cb d =，那么这四条线段,,,a bcd 叫做成比例线段，简称比例线段。

2、性质：（1）基本性质：如果a c b d=，那么ad bc =；反之，若ad bc =(),,,0a b c d 都不等于，那么a c b d= （2）等比性质：如果()==0a c m b d n b d n =+++≠，那么a c m a b d n b +++=+++ （3）合比性质：如果a c b d =，那么a b c d b d ++=，a b c d b d--= 【知识点二】平行线分线段成比例1、定理：两条直线被一组平行线所截，所得的对应线段成比例2、推论：平行于三角形一边的直线与其他两边相交，截得的对应线段成比例【知识点三】相似多边形1、定义：各角分别相等，各边成比例的两个多边形叫做相似多边形。

相似多边形对应边的比叫做相似比2、性质：相似多边形的周长比等于相似比，面积比等于相似比的平方【知识点四】相似三角形1、定义：三角分别相等，三边成比例的两个三角形叫做相似三角形2、判定：（1）两角分别相等的两个三角形相似（2）两边成比例且夹角相等的两个三角形相似（3）三边成比例的两个三角形相似3、性质：（1）相似三角形的对应角相等，对应边成比例（2）相似三角形对应高的比，对应中线的比，对应角平分线的比都等于相似比（3）相似三角形的周长比等于相似比，面积比等于相似比的平方【知识点五】黄金分割点C 把线段AB 分成两条线段AC 和BC ()AC BC >，如果AC BC AB AC=，那么称线段AB 被点C 黄金分割，点C 叫做线段AB 的黄金分割点，AC 与AB 的比叫做黄金比，即:0.618:1AC AB ≈【知识点六】位似图形1、定义：一般的，如果两个相似多边形任意一组对应顶点P ,'P 所在的直线都经过同一点O ，且有'OP =()0k OP k ⋅≠，那么这样的两个多边形叫做位似多边形，点O 叫做位似中心2、性质：位似图形上任意一对对应点到位似中心的距离之比等于相似比3、画图步骤：（1）尺规作图法：① 确定位似中心；②确定原图形中的关键点关于中心的对应点；③描出新图形（2）坐标法：在平面直角坐标系中，将一个多边形每个顶点的横坐标、纵坐标都乘于同一个数()0k k ≠，所对应的图形与原图形位似，位似中心是坐标原点，它们的相似比为k【典型例题】类型一、成比例线段和平行线分线段成比例1．已知三条线段 a b c ，，满足 1324a b c ，且 17a b c ．（1）求 a b c ，，的值；（2）若线段 d 是线段 a 和 b 的比例中项，求 d 的值．1324ab c k ，用含的方程，解方程求出k 的值，从而可求出d 是线段 a 和 b 的比例中项，可得到1324ab c k，c+1=4k 即c=4k -11=17使计算更加简便．【变式1】已知:2:3,:3:4a b b c ==，且26a b c +-=，求,,a b c 的值【答案】4a =，6b =，8c =．【分析】根据比的性质，可得a ，b ，c 用k 表示，根据解方程，可得k 的值，即可得答案．解：∴:2:3a b =，:3:4b c =，∴设2a k =，3b k =，4c k =，∴()22346k k k ⋅+-=，整理得：36k =　，解得：2k =，∴24a k ==，36b k ==，48c k ==．【点拨】本题考查了比例的性质，利用比例的性质得出2a k =，3b k =，4c k =是解题关键．【变式2】如图所示，以长为2的定线段AB 为边作正方形ABCD ，取AB 的中点P ，连接PD ，在BA 的延长线上取点F ，使PF PD =，以AF 为边作正方形AMEF ，点M 在AD 上．（1）求AM DM ，的长；（2）点M 是AD 的黄金分割点吗？为什么？【答案】（1）AM =51-，DM =35-；（2）是，理由见分析Rt APD 中，2PD AD =AP PD -=35=-． 51-，DM AD 的黄金分割点．DM 的长，然后求得线段AM 和AD ，DM 和AM 之间的比，根据黄金分割的概念进行判断．2．如图，已知AD∴BE∴CF ，它们以此交直线l 1、l 2于点A 、B 、C 和D 、E 、F ．若25DE EF =，AC=14，（1）求AB 的长．（2）如果AD=7，CF=14，求BE 的长．【答案】(1) 4 10 (2) 9【点拨】本题考查平行线分线段成比例的知识，解题的关键是掌握三条平行线截两条直线，所得的对应线段成比例．【变式1】如图，已知AD//BE//CF，它们依次交直线1l、2l于点A、B、C和点D、E、F，且AB=6，BC=8．（1）求DEDF的值；（2）当AD=5，CF=19时，求BE的长．3∴AG//DF，AD//BE//CF，比例；熟练掌握平行线分线段成比例，通过作辅助线运用平行线分线段成比例求出BH是解决问题的关键．【变式2】如图，在ABC ∆中，点D 是边AB 上的一点.（1）请用尺规作图法，在ABC ∆内，求作ADE ∠，使ADE B ∠=∠，DE 交AC 于E ；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，若2AD DB =，求AE EC的值.AE(2)∴ADE B ∠=∠，规作一个角等于已知角的作图方法是解题的关键.类型二、相似三角形判定和性质3．如图，在ABC 中，90ACB ∠=︒，CD 是边AB 上的中线，EF 垂直平分CD ，分别交AC ，BC 于E ，F ，连接DE ，DF ．(1) 求证：OCE OFD ∽△△．(2) 当7AE =，24BF =时，求线段EF 的长．【答案】(1)见分析(2)25EF =【分析】（1）如图（见分析），先根据线段垂直平分线的性质可得90EOC DOF ∠=∠=︒，ED EC =，FD FC =，再根据三角形全等的判定定理证出EDF ECF ≅，根据全等三角形的性质可得12∠=∠，从而可得421∠=∠=∠，然后根据相似三角形的判定即可得证；（2）如图（见分析），延长FD 至G ，使DG DF =，连接AG ，EG ，先根据线段垂直平分线的判定与性质可得EG EF =，再根据三角形全等的判定定理证出ADG BDF ≅△△，根据全等三角形的性质可得24AG BF ==，7B ∠=∠，然后根据平行线的判定与性质可得90EAG ∠=︒，最后在Rt AEG △中，利用勾股定理即可得．（1）证明：∴EF 垂直平分CD ，∴90EOC DOF ∠=∠=︒，ED EC =，FD FC =，在EDF 和ECF △中，ED EC FD FC EF EF =⎧⎪=⎨⎪=⎩，∴()EDF ECF SSS ≅，∴12∠=∠，∴90ACB ∠=︒，90EOC ∠=︒，∴233490∠+∠=∠+∠=︒，∴421∠=∠=∠，在OCE △和OFD △中，9014EOC DOF ∠=∠=︒⎧⎨∠=∠⎩， ∴OCE OFD ．（2）解：如图，延长FD 至G ，使DG DF =，连接AG ，EG ．则ED 垂直平分FG ，CD 是边∴AD BD =在ADG 和BDF 中，65DG DF AD BD =⎧⎪∠=∠⎨⎪=⎩，∴(ADG BDF SAS ≅△△24AG BF ==，7∠AG BC ，180EAG =︒-∠2AE =+25=．【点拨】本题考查了相似三角形的判定、线的判定与性质等知识点，较难的是题（2），构造全等三角形和直角三角形是解题关键．【变式1】如图，四边形ABCD 中，AC 平分∴DAB ，∴ADC=∴ACB=90°，E 为AB 的中点，（1）求证：AC 2=AB•AD ；（2）求证：CE∴AD ；（3）若AD=4，AB=6，求的值．AC7=．∴AF4【变式2】如图，在∴ABC中，（1）求作：∴BAD=∴C，AD交BC于D．（用尺规作图法，保留作图痕迹，不要求写作法）．（2）在（1）条件下，求证：AB2=BD•BC．【答案】（1）作图见分析；（2）证明见分析；【分析】（1）∴以C为圆心，任意长为半径画弧，交CB、CA于E、F；∴以A为圆心，CE长为半径画弧，交AB于G；∴以G为圆心，EF长为半径画弧，两弧交于H；∴连接AH并延长交BC于D，则∴BAD=∴C；（2）证明∴ABD∴∴CBA，然后根据相似三角形的性质得到结论．解：（1）如图，∴BAD为所作；（2）∴∴BAD=∴C，∴B=∴B∴∴ABD∴∴CBA，∴AB：BC=BD：AB，∴AB2=BD•BC．【点拨】本题考查了基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．也考查了相似三角形的判定与性质．4．如图，在ABC中，过点C作CD//AB，E是AC的中点，连接DE并延长，交AB于点F，交CB的延长线于点G，连接AD，CF()1求证：四边形AFCD是平行四边形．()2若GB 3=，BC 6=，3BF 2=，求AB 的长．即可证AEF ∴CED ，从而得证GBF ∴GCD 得GB GC )1E 是AC 的中点，CE =，AB//CD ，AFE CDE ∠∠∴=，在AEF 和CED 中，AFE CDE AEF CED AE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，AEF ∴∴(CED AAS AF CD ∴=，又AB//CD ，即AF/∴四边形AFCD 是平行四边形；)2AB//CD ，GBF ∴∴GCD ，GB BF GC CD ∴=，即33+解得：9CD 2=，四边形AFCD 是平行四边形，9交AC于点F.求证：(1) ∴ABF∴∴BED；(2) 求证：AC BD BE DE=.（1）用直尺和圆规在BC边上取一点E，使AB=AE，连结AE；（保留作图痕迹，不写作法）（2）在（1）的前提下，求证：AE=CD；∠EAD=∠D；（3）若点E为BC的中点，连接BD，交AE于F，直接写出EF：FA的值．【答案】（1）见分析（2）证明见分析（3）1:2分析：(1)以点A为圆心，AB为半径作圆，该圆与BC的交点即为所求的点E;(2)根据平行四边形的对边互相平行可得AD∴BC，再根据两直线平行，内错角相等可得∴AEB=∴EAD,根据等边对等角可得∴ABE=∴AEB,即可得证；(3)由四边形ABCD是平行四边形，可证得∴BEF∴∴AFD即可求得EF∴FA的值．解：（1）如图所示：；（2）证明：在平行四边形ABCD中，AD∠BC，∠∠AEB=∠EAD，∠AE=AB，∠∠ABE=∠AEB，∠∠B=∠EAD，∠∠B=∠D，∠∠DAE=∠D；（3）解：∠四边形ABCD是平行四边形，∠AD∠BC，AD=BC，∠∠BEF∠∠AFD，∠=，∠E为BC的中点，∠BE=BC=AD，∠EF：FA=1：2．【点拨】此题考查了相似三角形的判定与性质与平行四边形的性质，熟练掌握平行四边形的性质是关键．5．如图，在ABC 中，点D 、点E 分别在AC 、AB 上，点P 是BD 上的一点，联结EP 并延长交AC 于点F ，且A EPB ECB ∠=∠=∠．(1)求证：BE BA BP BD ⋅=⋅；(2)若90ACB ∠=︒，求证：CP BD ⊥．【答案】(1)见分析(2)见分析）先证明ABC ∴△，再证明PBC ∴CBD ，得到）证明：A EPB ∠=∠ABD =∠，PBE ∴∴ABD △，∴BE BP BD BA=BE BA BP BD ∴⋅=⋅．（2）证明：A ECB ∠=∠ABC ∴∴CBE △，BC BA BE BC∴=， 2BE BA BC ∴⋅=，又∴BE BA BP BD ⋅=⋅，2BC BP BD ∴=⋅，BC BP PBC ∠=PBC ∴△∴CBD ，90ACB ∠=︒，90BPC BCD ∴∠=∠=CP BD ∴⊥．【点拨】此题考查相似三角形的判定与性质，比例列出相应的比例式，再经过适当的变形使所得的比例式符合“两边成比例且夹角相等”的形式．【变式1】已知ADE C ∠=∠，AG 平分BAC ∠交DE 于F ，交BC 于G ． (1) 求证：ADF ∽ACG ；(2) 连接DG ，若DG AC ∥，25AF AG =，6AD =，求CE 的长度．）的结果和平行线的性质证明BAC ∽BAC ，进而可得ADG 为等腰三角形，最后证明ADE ∽△并结合相应的计算即可解答．）证明：AG 平分CAG =∠，又ADE C ∠=∠，ADF ∴∽ACG ；（2）解：ADF ∽ACG ， 25AD AF AC AG ∴==， 5152AC AD ∴==， DG AC ∥，AGD CAG ∴∠=∠，BDG ∽BAC ，BG DG BC AC ∴=， AG 平分∴∴DAG =∴AGD ∴∠∴ADG 为等腰三角形，DG AD ∴=BG DG BC AC ∴=解得：BD =ADE ∠=ADE ∴∽△AD AE AC AB ∴=25AE AB ∴=CE AC ∴=【点拨】本题考查了相似三角形的判定和性质、角平分线的性质、平行线的性质、等腰三角形的判定和性质，解决本题的关键是掌握以上的定理并熟练的运用．【变式2】如图，∴A ＝∴C ＝∴EDF ，CF ＝4，CD ＝AD ＝6；(1) 求AE 的长．(2) 求证：∴ADE ∴∴DFE ．似三角形性质列出比例式进行求解是解题的关键．类型三、相似三角形拓展与提升6．已知∴ABC中，∴ACB＝90°，AC＝BC＝4cm，点P从点A出发，沿AB方向以每秒2cm的速度向终点B运动，同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，设运动的时间为t秒．(1)如图∴，若PQ∴BC，求t的值；(2)如图∴，将∴PQC沿BC翻折至∴P′QC，当t为何值时，四边形QPCP′为菱形？Rt PDQ中，结合四边形（1）解：（∴∴ACB ＝90°，AC ＝BC ＝4cm ，22442（cm BQ ＝t cm ，cm ，BPQ BAC ∴∽，∴BP BA ＝BQ BC ， ∴422442t t -=，解得：t ＝2，∴当t ＝2时，PQ ∴BCAP t ，BQ tcm =，(04)t <90C ∠=cm ，ABC ∴∆为直角三角形，45A B ∠，APE ∴∆和PBD ∆为等腰直角三角形，四边形Rt PDQ 中，四边形QPCP PQ PC =，()24t +-=43=，2t =段垂直平分线的性质，用方程的思想解决问题是解本题的关键．【变式1】已知，点E 、F 、G 、H 分别在正方形ABCD 的边AB 、BC 、CD 、AD 上．(1)如图1，当四边形EFGH 是正方形时，求证：AE AH AB +=；(2)如图2，已知AE AH =，CF CG =，当AE 、CF 的大小有_________关系时，四边形EFGH 是矩形；(3)如图3，AE DG =，EG 、FH 相交于点O ，:4:5OE OF =，已知正方形ABCD 的边长为16，FH 长为20，当OEH △的面积取最大值时，判断四边形EFGH 是怎样的四边形？证明你的结论．【答案】(1)见分析(2)AE CF =(3)平行四边形，证明见分析【分析】（1）利用平行四边形的性质证得BEF AHE ∠=∠，根据角角边证明AEH BFE △≌△．（2）当AE CF =，证得AEH FCG △≌△，EBF △是等腰直角三角形，∴HEF =∴EFG =90°，即可证得四边形EFGH 是矩形．（3）利用正方形的性质证得AEGD 为平行四边形，过点H 作HM BC ⊥，垂足为点M ，交EG 于点N ，由平行线分线段成比例，设4OE x =，5OF x =，HN h =，则可表示出HN ，从而把∴OEH 的面积用x 的代数式表示出来，根据二次函数求出最大值，则可得OE =OG ，OF =OH ，即可证得平行四边形．解：（1）∴四边形ABCD 为正方形，∴90A B ∠=∠=︒，∴90AEH AHE ∠+∠=°．∴四边形EFGH 为正方形，∴EH EF =，90HEF ∠=︒，∴90AEH BEF ∠+∠=︒，∴BEF AHE ∠=∠．在AEH △和BFE △中，∴90A B ∠=∠=︒，AHE BEF ∠=∠，EH FE =，∴AEH BFE △≌△．∴AH BE =．∴AE AH AE BE AB +=+=；（2）AE CF =；证明如下：∴四边形ABCD 为正方形，∴90A B ∠=∠=︒，AB =BC =AD =CD ，∴AE =AH ，CF =CG ，AE =CF ，∴AH =CG ，∴AEH FCG △≌△，∴EH =FG ．∴AE =CF ，∴AB －AE =BC －CF ，即BE =BF ，∴EBF △是等腰直角三角形，∴∴BEF =∴BFE =45°，∴AE =AH ，CF =CG ，∴∴AEH =∴CFG =45°，∴∴HEF =∴EFG =90°，∴EH ∴FG ，【点拨】此题考查了正方形的性质，矩形的判定和平行四边形的性质与判定，平行线分线段成比例定理，全等三角形的判定与性质，等腰三角形的性质，二次函数的最值，有一定的综合性，解题的关键是熟悉这些知识并灵活运用．【变式2】已知点E 在正方形ABCD 的对角线AC 上，正方形AFEG 与正方形ABCD 有公共点A ．(1)如图1，当点G 在AD 上，F 在AB(2)将正方形AFEG 绕A 点逆时针方向旋转9(0)0αα︒<<︒，如图2，求：CE DG 的值为多少；(3)AB =2AG AD =，将正方形AFEG 绕A 逆时针方向旋转(0360)αα︒<<︒，当C ，G ，E 三点共线时，请直接写出DG 的长度．进而证明GAD EAC ∽，根据相似三角形的性质即可求解；）分两种情况画出图形，证明股定理即可得出答案．）解：正方形AFEG GE DC ∥AG AE DG EC = 四边形正方形AFEG 绕A 点逆时针方向旋转9(0)0αα︒<<︒，AG AD AE AC =GAD EAC ∴∽∴2AC CE DG AD==，（3）解：∴如图，AB 2,,G E C 三点共线，Rt AGC △CE GC ∴=由（2）可知GAD EAC ∽，∴2CE AC DG DA==， (8283816CE AC ⨯-=由（2）知△ADG∴∴ACE，勾股定理，旋转的性质，综合运用以上知识是解题的关键．类型三、位似7．如图，在6×8的网格图中，每个小正方形边长均为1，点O和∴ABC的顶点均为小正方形的顶点.∴以O为位似中心，在网格图中作∴A′B′C′，使∴A′B′C′和∴ABC位似，且位似比为1：2∴连接∴中的AA′，求四边形AA′C′C的周长.（结果保留根号）（2）AA ′=1，CC ′=2．位置是解题关键．【变式一】如图，在平面直角坐标系中，已知∴ABC 三个顶点的坐标分别为A （2，4），B （1，1），C （5，2）．(1)以点B 为位似中心，在网格内画出∴ABC 的位似∴A 1BC 1，使得∴A 1BC 1与∴ABC 的位似比为2；(2)直接写出点A 1的坐标和∴A 1BC 1的面积．【答案】(1)见分析(2)()13,7A ，22【分析】(1) 以点B 为位似中心，使得∴A 1BC 1与∴ABC 的位似比为2，延长BA 到A 1，使BA 1=2BA ，延长BC 到C 1，使BC 1=2BC ，再顺次连接即可；（2）利用割补法求解可得．(2)如图所示A ()3,7【变式二】如图，ABC 在平面直角坐标系内，三个顶点的坐标分别为()1,3A ，()2,1B ，()5,2C （正方形网格中，每个小正方形的边长为1），以点O 为位似中心，把ABC 按相似比2：1放大，得到对应A B C '''．(1)请在第一象限内画出A B C '''；(2)若以点A 、B 、C 、D 为顶点的四边形是平行四边形，请直接写出满足条件的点D 的坐标．【答案】(1)见分析(2)()14,4D ；()26,0D ；()32,2D -【分析】（1）根据点O 为位似中心，()1,3A ，()2,1B ，()5,2C ，把ABC 按相似比2：1放大，得到对应A B C '''，求出点'A ，'B ，'C 的坐标，在网格中描点顺次连线即得；（2）设D (x ,y )，根据平行四边形的对角线互相平分与()1,3A ，()2,1B ，()5,2C ，得到当AC 为对角线时， x +2=1+5，y +1=2+3，推出x =4，y =4，得到()14,4D ；当BC 是对角线时，推出x +1=2+5，x =6，y +3=1+2，y =0，得到()26,0D ，当AB 为对角线时，推出x +5=1+2，x =-2，y +2=3+1，y =2，得到()32,2D -．解：(1)∴点O 为位似中心，ABC 按相似比2：1放大，得到对应A B C '''，A B C，如图；在网格图中顺次连接各点得到'''(2)设D(x,y)，()2,2D()D-4,46,0D()角形的定义及画法，平行四边形对角线的性质和线段中点坐标公式．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《相似》全章复习与巩固--知识讲解（提高）【学习目标】 1、了解比例的基本性质，线段的比、成比例线段； 2、通过具体实例认识图形的相似，探索相似图形的性质，理解相似多边形对应角相等、对应边成比例、周长的比等于相似比、面积的比等于相似比的平方，探索并掌握相似三角形的判定方法，并能利用这些性质和判定方法解决生活中的一些实际问题； 3、了解图形的位似，能够利用位似将一个图形放大或缩小，在同一直角坐标系中，感受位似变换后点的坐标的变化； 4、结合相似图形性质和判定方法的探索和证明，进一步培养推理能力，发展逻辑思维能力和推理论证的表达能力，以及综合运用知识的能力，运用学过的知识解决问题的能力. 【知识网络】

【要点梳理】要点一、相似图形及比例线段 1．相似图形：在数学上，我们把形状相同的图形称为相似图形(similar figures). 要点诠释： (1) 相似图形就是指形状相同，但大小不一定相同的图形； (2) “全等”是“相似”的一种特殊情况，即当“形状相同”且“大小相同”时，两个图形全等； 2.相似多边形如果两个多边形的对应角相等，对应边的比相等，我们就说它们是相似多边形．要点诠释：（1）相似多边形的定义既是判定方法，又是它的性质．（2）相似多边形对应边的比称为相似比. 3. 比例线段：对于四条线段a、b、c、d，如果其中两条线段的比与另两条线段的比相等，如a:b=c:d，我们就说这四条线段是成比例线段，简称比例线段．要点诠释：（1）若a:b=c:d ，则ad=bc；（d也叫第四比例项）（2）若a:b=b:c ，则2b =ac（b称为a、c的比例中项）．要点二、相似三角形 1. 相似三角形的判定: 判定方法（一）：平行于三角形一边的直线和其他两边相交，所构成的三角形和原三角形相似. 判定方法（二）：如果两个三角形的三组对应边的比相等，那么这两个三角形相似. 判定方法（三）：如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似. 要点诠释：此方法要求用三角形的两边及其夹角来判定两个三角形相似，应用时必须注意这个角必须是两边的夹角，否则，判断的结果可能是错误的. 判定方法（四）：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似. 要点诠释：要判定两个三角形是否相似，只需找到这两个三角形的两个对应角相等即可，对于直角三角形而言，若有一个锐角对应相等，那么这两个三角形相似. 2. 相似三角形的性质：（1）相似三角形的对应角相等，对应边的比相等；（2）相似三角形中的重要线段的比等于相似比；相似三角形对应高，对应中线，对应角平分线的比都等于相似比. 要点诠释：要特别注意“对应”两个字，在应用时，要注意找准对应线段. (3) 相似三角形周长的比等于相似比；（4）相似三角形面积的比等于相似比的平方。 3.相似多边形的性质：（1）相似多边形的对应角相等，对应边的比相等．（2）相似多边形的周长比等于相似比．（3）相似多边形的面积比等于相似比的平方．要点三、位似 1.位似图形定义: 如果两个图形不仅是相似图形，而且每组对应点所在的直线都经过同一点，那么这样的两个图形叫做位似图形，这个点叫做位似中心． 2.位似图形的性质: （1）位似图形的对应点和位似中心在同一条直线上；（2) 位似图形的对应点到位似中心的距离之比等于相似比；（3）位似图形中不经过位似中心的对应线段平行. 要点诠释： (1）位似图形与相似图形的区别：位似图形是一种特殊的相似图形，而相似图形未必能构成位似图形. （2）位似变换中对应点的坐标变化规律:在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k.

要点四、黄金分割 1.定义：如图，将一条线段AB分割成大小两条线段AP、PB，若小段与大段的长度之比等于大段的长度与全长之比，即ABAPAPPB（此时线段AP叫作线段PB、AB的比例中项），则P点就是线段AB的黄金分割点（黄金点），这种分割就叫黄金分割．

2.黄金三角形：顶角为36°的等腰三角形，它的底角为72°，恰好是顶角的2倍，人们称这种三角形为黄金三角形．黄金三角形性质：底角平分线将其腰黄金分割．要点五、射影定理在Rt△ABC中，∠ACB=90°，CD⊥AB于D， ∴△ABC∽△ACD∽△CBD（“角角”）

∴BDADCD2；

ABADAC2； ABBDBC2（射影定理）； CDABBCAC（等积）．

【典型例题】类型一、相似三角形【高清课堂:相似专题复习高清ID号： 394502 关联的位置名称（播放点名称）：例1-2】

1. 已知：如图，∠ABC=∠CDB=90°，AC=a，BC=b，当BD与a、b之间满足怎样的关系时，这两个三角形相似？

【答案与解析】 ∵AC=a，BC=b，

∴AB=22ab， ①当△ABC∽△BDC时， BDBCABAC,

即22babBDa. ②当△ABC∽△CDB时， BDBCCBAC，

即2bBDa. 【总结升华】相似三角形中未明确对应点和对应边时，要注意分类讨论. 举一反三【变式】如图，在矩形ABCD中，AB=6，BC=8,沿直线MN对折，使A、C重合，直线MN交AC于O.（1）求证：△COM∽△CBA；（2）求线段OM的长度.

【答案】（1）证明： A与C关于直线MN对称，

∴ACMN，∴∠COM=90°，在矩形ABCD中，∠B=90°， ∴∠COM=∠B ，又∠ACB=∠ACB， ∴△COM∽△CBA ，（2）在Rt△CBA中，AB=6，BC=8， ∴AC=10 ，∴OC=5， △COM∽△CBA， ∴OCOM=

BCAB，

∴OM=154.

2. 如图，在△ABC中，∠C＝90°，将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC＝6，NC＝23，则四边形MABN的面积是（） A．63 B．123 C．183 D．243 【答案】C；【解析】由MC＝6，NC＝23，∠C＝90°得S△CMN=63，再由翻折前后△CMN≌△DMN得对应高相等；由MN∥AB得△CMN∽△CAB且相似比为1:2，故两者的面积比为1:4，从而得S△CMN：S四边形MABN=1:3，故选C. 【总结升华】本题综合考查了直角三角形的面积算法、翻折的性质、由平行得相似的三角形相似的判定方法、相似图形的面积比等于相似比的平方等一些类知识点.知识点丰富；考查了学生综合运用知识来解决问题的能力.难度较大.

类型二、相似三角形的综合应用 3.（2015•上海）已知，如图，平行四边形ABCD的对角线相交于点O，点E在边BC的延长线上，且OE=OB，连接DE．（1）求证：DE⊥BE；（2）如果OE⊥CD，求证：BD•CE=CD•DE．

【答案与解析】证明：（1）∵四边形ABCD是平行四边形，

∴BO=BD， ∵OE=OB， ∴OE=BD， ∴∠BED=90°， ∴DE⊥BE；

（2）∵OE⊥CD ∴∠CEO+∠DCE=∠CDE+∠DCE=90°， ∴∠CEO=∠CDE， ∵OB=OE，

DACB∴∠DBE=∠CDE， ∵∠BED=∠BED， ∴△BDE∽△DCE，

∴， ∴BD•CE=CD•DE．【总结升华】本题考查了相似三角形的判定和性质，直角三角形的判定和性质，平行四边形的性质，熟记定理是解题的关键．

4. （2016•杭州）如图，在△ABC中，点D，E分别在边AB，AC上，∠AED=∠B，射线AG分别交线段DE，BC于点F，G，且．（1）求证：△ADF∽△ACG；（2）若，求的值．

【思路点拨】（1）欲证明△ADF∽△ACG，由可知，只要证明∠ADF=∠C即可．（2）利用相似三角形的性质得到=，由此即可证明．【答案与解析】（1）证明：∵∠AED=∠B，∠DAE=∠DAE， ∴∠ADF=∠C，

∵=， ∴△ADF∽△ACG．（2）解：∵△ADF∽△ACG，

∴=，

又∵=， ∴=， ∴=1．【总结升华】本题考查相似三角形的性质和判定、三角形内角和定理等知识，记住相似三角形的判定方法是解决问题的关键，属于基础题中考常考题型．举一反三：【变式】（2015•湘潭）如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．（1）求证：△BDE∽△BAC；（2）已知AC=6，BC=8，求线段AD的长度．

【答案与解析】证明：（1）∵∠C=90°，△ACD沿AD折叠， ∴∠C=∠AED=90°， ∴∠DEB=∠C=90°， ∵∠B=∠B， ∴△BDE∽△BAC；（2）由勾股定理得，AB=10．由折叠的性质知，AE=AC=6，DE=CD，∠AED=∠C=90°． ∴BE=AB﹣AE=10﹣6=4，在Rt△BDE中，由勾股定理得， DE2+BE2=BD2，即CD2+42=（8﹣CD）2，解得：CD=3，在Rt△ACD中，由勾股定理得AC2+CD2=AD2，即32+62=AD2，解得：AD=．【高清课堂: 相似专题复习高清ID号： 394502 关联的位置名称（播放点名称）：例7】

5. 如图，已知在梯形ABCD中，AD//BC，AD=2，BC=4，点M是AD的中点，△MBC是等边三角形．（1）求证：梯形ABCD是等腰梯形．（2）动点P、Q分别在线段BC和MC上运动，且∠MPQ=60°保持不变．设PC=x，MQ=y，求y与x的函数关系式．

【答案与解析】（1）∵MBC△是等边三角形