解三角形习题
中考《解直角三角形》复习练习题及答案
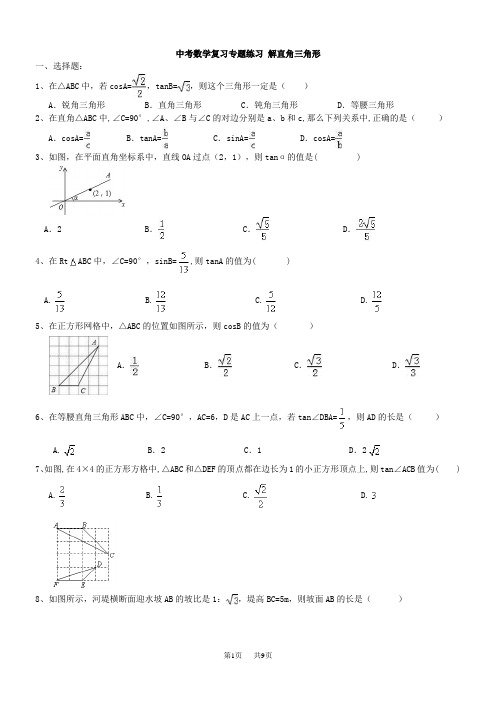
中考数学复习专题练习解直角三角形一、选择题:1、在△ABC中,若cosA=,tanB=,则这个三角形一定是()A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形2、在直角△ABC中,∠C=90°,∠A、∠B与∠C的对边分别是a、b和c,那么下列关系中,正确的是()A.cosA= B.tanA= C.sinA= D.cosA=3、如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )A.2 B. C. D.4、在Rt ABC中,∠C=90°,sinB=,则tanA的值为( )A. B. C. D.5、在正方形网格中,△ABC的位置如图所示,则cosB的值为()A. B. C. D.6、在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,则AD的长是()A. B.2 C.1 D.27、如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB值为( )A. B. C. D.8、如图所示,河堤横断面迎水坡AB的坡比是1:,堤高BC=5m,则坡面AB的长是()A.10mB.mC.15m D.m9、如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )A.4米B.6米C.12米D.24米10、如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连接BD,则tan∠DBC的值为( )A. B.-1 C.2- D.11、如图,已知的三个顶点都在方格图的格点上,则的值为( )A. B. C. D.12、如图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于()A. B. C. D.二、填空题:13、在△ABC中,∠A,∠B都是锐角,若sinA=,cosB=,则∠C=________.14、已知在Rt△ABC中,∠C=90°,AB=15,cosB=,则BC= .15、如图,先锋村准备在坡角为α=30°山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为______米.16、如图,菱形ABCD的边长为15,sin∠BAC=,则对角线AC的长为______.17、如图,正方形ABCD的边长为4,点M在边DC上,M、N两点关于对角线AC对称,若DM=1,则tan∠ADN= .18、如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(+) tan+tan.(填“>”“=”“<”)19、如图在四边形ABCD中,∠ACB=∠BAD=105°,∠B=∠D=45°若 AD=,则AB=__________20、如图所示的半圆中,是直径,且,,则的值是.21、如图,在菱形ABCD中,DE⊥AB,,BE=2,则________.22、如图,在中,是边边上的中线,如果,tanB值是________23、如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为米.24、如图,在顶角为30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°.根据图形计算tan15°= .三、简答题:25、在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,且c=,若关于x的方程(+b)x2+2ax+(-b)=0有两个相等的实数根,方程2x2-(10sin A)x+5sin A=0的两个实数根的平方和为6,求△ABC的面积.26、已知:如图,正方形ABCD中,点E为AD边的中点,联结CE. 求cos∠ACE和tan∠ACE的值.27、如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.(1)求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);(2)求海轮在B处时与灯塔C的距离(结果保留整数).(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)28、如图,河流两岸a,b互相平行,C,D是河岸a上间隔50m的两个电线杆.某人在河岸b上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=60°,求河流的宽度CF的值.(结果精确到个位)29、张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:≈1.732)30、如图,在正方形ABCD中,点E、F分别是BC、CD的中点,DE交AF于点M,点N为DE的中点.(1)若AB=4,求△DNF的周长及sin∠DAF的值;(2)求证:2AD•NF=DE•DM.31、中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?说明理由.(≈1.732)参考答案1、A.2、C.3、B.4、D.5、B.6、B.7、B.8、A.9、B.10、A.11、D.12、B.13、答案为:60°14、答案为:9.15、答案为:(米).16、答案为24.17、答案为:4.3 18、答案为:>. 19、答案为:.20、答案为: ;21、答案为:2 ;22、答案为:23、答案为:137.24、答案为:2﹣.25、解:∵方程(5+b)x2+2ax+(5-b)=0有两个相等的实数根,且c=5,∴△=(2a)2-4(c+b)(c-b)=0,∴a2+b2=c2,则△ABC为直角三角形,且∠C=90°.设x1,x2是方程2x2-(10sin A)x+5sin A=0的两个根,则根据根与系数的关系有x1+x2=5sin A,x1·x2=sin A.∴x12+x22=(x1+x2)2-2x l·x2=(5sin A)2-2×sin A=6,解得sinA=或sinA=-(舍去),∴a=csin A=3,b==4,S△ABC=ab==18.26、解:过点作于点,∵四边形是正方形,∴平分,.∴,.∵是中点,∴.设,则,,.在Rt△AEF中,,.∴.∴,.27、【解答】解:(1)过C作AB的垂线,设垂足为D,根据题意可得:∠1=∠2=42°,∠3=∠4=55°,设CD的长为x海里,在Rt△ACD中,tan42°=,则AD=x•tan42°,在Rt△BCD中,tan55°=,则BD=x•tan55°,∵AB=80,∴AD+BD=80,∴x•tan42°+x•tan55°=80,解得:x≈34.4,答:海轮在航行过程中与灯塔C的最短距离是34.4海里;(2)在Rt△BCD中,cos55°=,∴BC=≈60海里,答:海轮在B处时与灯塔C的距离约为60海里.28、【解答】解:过点C作CE∥AD,交AB于E∵CD∥AE,CE∥AD∴四边形AECD是平行四边形∴AE=CD=50m,EB=AB﹣AE=50m,∠CEB=∠DAB=30°又∠CBF=60°,故∠ECB=30°∴CB=EB=50m∴在Rt△CFB中,CF=CB•sin∠CBF=50•sin60°≈43m答:河流的宽度CF的值为43m.29、解:如图,过B作BE⊥CD交CD延长线于E,∵∠CAN=45°,∠MAN=30°,∴∠CAB=15°∵∠CBD=60°,∠DBE=30°,∴∠CBD=30°,∵∠CBE=∠CAB+∠ACB,∴∠CAB=∠ACB=15°,∴AB=BC=20,在Rt△BCE中,∠CBE=60°,BC=20,∴CE=BCsin∠CBE=20×BE=BCcos∠CBE=20×0.5=10,在Rt△DBE中,∠DBE=30°,BE=10,∴DE=BEtan∠DBE=10×,∴CD=CE﹣DE=≈11.5,答:这棵大树CD的高度大约为11.5米.30、:(1)解:∵点E、F分别是BC、CD的中点,∴EC=DF=×4=2,由勾股定理得,DE==2,∵点F是CD的中点,点N为DE的中点,∴DN=DE=×2=,NF=EC=×2=1,∴△DNF的周长=1++2=3+;在Rt△ADF中,由勾股定理得,AF===2,所以,sin∠DAF===;(2)证明:在△ADF和△DCE中,,∴△ADF≌△DCE(SAS),∴AF=DE,∠DAF=∠CDE,∵∠DAF+∠AFD=90°,∴∠CDE+∠AFD=90°,∴AF⊥DE,∵点E、F分别是BC、CD的中点,∴NF是△CDE的中位线,∴DF=EC=2NF,∵cos∠DAF==,cos∠CDE==,∴=,∴2AD•NF=DE•DM.31、【解答】解:过A作AD⊥CF于D,由题意得∠CAG=15°,∴∠ACE=15°,∵∠ECF=75°,∴∠ACD=60°,在Rt△ACD中,sin∠ACD=,则AD=AC•sin∠ACD=250≈433米,433米>400米,∴不需要改道.答:消防车不需要改道行驶.。
必修5解三角形知识点和练习题(含答案)

【译文】玉露凋伤枫树林,——白露凋伤了漫山遍野的枫林,巫山巫峡气萧森。
——巫山巫峡的气象满目萧瑟阴森。
江间波浪兼天涌,——峡中的江水波涛滚滚汹涌连天,塞上风云接地阴。
——塞上风云漫卷密布天地一片阴沉。
丛菊两开他日泪,——秋菊已开两度回想他日再流泪,孤舟一系故园心。
——孤舟靠岸系绳也系着我游子的故园心。
寒衣处处催刀尺,——深秋季节处处都在为游子征夫赶制寒衣,白帝城高急暮砧。
——傍晚白帝城头传来急促的捶布声。
【译文】群山万壑赴荆门,——千山万壑逶迤不断奔赴荆门山,生长明妃尚有村。
——这里遗留有生长明妃的香溪村。
一去紫台连朔漠,——一别汉宫便与北方荒漠连一起,独留青冢向黄昏。
——最后只留下青冢向着漠漠黄昏。
画图省识春风面,——画工曾经辨识昭君美丽的面容,(却因一己私欲致使昭君嫁匈奴),环佩空归月夜魂。
——只有死后魂灵徒然在月夜归来。
千载琵琶作胡语,——千年以来琵琶弹奏的胡地乐曲,分明怨恨曲中论。
——还分明倾诉着她内心的怨恨情。
【译文】风急天高猿啸哀,-- 风急天高猿猴啼叫显得十分悲哀,渚清沙白鸟飞回。
-- 水清沙白的河洲上空鸟儿在盘旋。
无边落木萧萧下,-- 无边无际的树木萧萧地飘下落叶,不尽长江滚滚来。
-- 望不到头的长江水滚滚奔腾而来。
万里悲秋常作客,-- 悲对秋景感慨万里漂泊常年为客,百年多病独登台。
-- 一生当中疾病缠身今日独上高台。
艰难苦恨繁霜鬓,-- 历尽了艰难苦恨白发长满了双鬓,潦倒新停浊酒杯。
-- 穷困潦倒偏又暂停了浇愁的酒杯向量知识点的归纳一、知识梳理:(1)本章要点梳理:1.向量加法的几何意义:起点相同时适用平行四边形法则(对角线),首尾相接适用“蛇形法则”,特别注意:)(21→→+ACAB表示△ABC的边BC的中线向量.向量减法的几何意义:起点相同适用三角形法则,(终点连结而成的向量,指向被减向量),||AB表示A、B两点间的距离;以、为邻边的平行四边形的两条对角线分别表示向量+、-(或-).2.理解单位向量、平行向量、垂直向量的意义。
解三角形练习题和答案

解三角形练习题1.在ABC 中,a ,b ,c分别为角A ,B ,C 所对边,若 a 2b cosC ,则此三角形一定是()A.等腰直角三角形B. 直角三角形C. 等腰三角形D. 等腰或直角三角形2. 在△ABC 中,角A, B,C 的对边边长分别为 a 3,b 5,c 6,则bc cos A ca cos B ab cosC 的值为A.38 B.37 C .36 D .353.有四个关于三角函数的命题:p :x R, 12sinx2+ 2cosx2=12p : x, y R, sin( x y) sin x sin y2p : x 0, , 3 1 cos22xsin x p4 : sin x cos y x y2其中假命题的是(A)p,1 p (B)4p ,2p (3)4p ,1p (4)3p ,2p34.已知ABC 的内角 A ,B ,C 所对的边分别为a,b ,c,若1n s i A ,b 3sin B,则a等于.35. 在△ABC中,已知边 c 10 , c os A b 4cos B a 3,求边a、b 的长。
6.已知A 、B 、C 为ABC 的三内角,且其对边分别为a、b 、c,若(Ⅰ)求 A ;1 cos B cosC sin B sin C .2(Ⅱ)若a 2 3, b c 4 ,求ABC 的面积.7.已知△ABC 的内角A, B,C 的对边分别为a, b, c ,其中c 2 ,又向量m(1 , cosC ) ,n( cosC , 1) ,m·n=1.(1)若 A 45 ,求a的值;(2)若a b 4,求△ABC 的面积.14.已知:△ABC中角A、B、C 所对的边分别为a、b、c 且sin A cos B sin B cos A sin 2C .(1) 求角 C 的大小;(2) 若a, c,b成等差数列,且CA CB 18,求 c 边的长.5.已知ABC 的三个内角A、B、C所对的边分别为a、b、c ,向量m (4, 1),A2n (cos ,cos 2 A) ,且2(1)求角 A 的大小;7 m n .2(2)若a 3,试求当b c取得最大值时ABC 的形状.10.在ABC中, 5 4cos A , sin B .13 5(Ⅰ)求cosC 的值;(Ⅱ)设BC 15 ,求ABC的面积.2 x7..已知f (x) 2 sin xcos x 2 3 cos 1 3,x[0, ]2⑴求f (x) 的最大值及此时x的值;⑵求f (x) 在定义域上的单调递增区间。
解三角形经典练习题集锦(附答案)之欧阳家百创编

解三角形欧阳家百(2021.03.07)一、选择题1.在△ABC 中,若0030,6,90===B a C ,则b c -等于( )A .1B .1-C .32D .32-2.若A 为△ABC 的内角,则下列函数中一定取正值的是( )A .A sinB .A cosC .A tanD .Atan 13.在△ABC 中,角,A B 均为锐角,且,sin cos B A >则△ABC 的形状是( ) A .直角三角形 B .锐角三角形 C .钝角三角形 D .等腰三角形4.等腰三角形一腰上的高是3,这条高与底边的夹角为060,则底边长为( ) A .2 B .23C .3D .32 5.在△ABC 中,若B a b sin 2=,则A 等于( )A .006030或B .006045或C .0060120或D .015030或6.边长为5,7,8的三角形的最大角与最小角的和是( )A .090B .0120C .0135D .0150 二、填空题1.在Rt △ABC 中,090C =,则B A sin sin 的最大值是_______________。
2.在△ABC中,若=++=A c bc b a 则,222_________。
3.在△ABC 中,若====a C B b 则,135,30,200_________。
4.在△ABC 中,若sin A ∶sin B ∶sin C =7∶8∶13,则 C =_____________。
5.在△ABC 中,,26-=AB 030C =,则AC BC +的最大值是________。
三、解答题1.在△ABC 中,若,cos cos cos C c B b A a =+则△ABC 的形状是什么?2.在△ABC 中,求证:)cos cos (aAb Bc ab ba -=- 3.在锐角△ABC中,求证:C B A C B A cos cos cos sin sin sin ++>++。
解三角形基础练习题(含答案)

解三角形基础练习题(含答案)一、选择题:1、在ABC ∆中,已知8a =,60B =︒,75C =︒,则b 的值为( C )A. B. C. D.3232、在ABC ∆中,15a =,10b =,60A =︒,则cos B =( B )3、在ABC ∆中,222a c b ab -+=,则C =( A )A.60︒B.45︒或135︒C.120︒D.30︒4、在△ABC 中,若60A ∠=,45B ∠=,BC =AC = BA. B. C. D. 25、已知ABC ∆中,C B A ∠∠∠,,的对边分别为a,b,c 若a=c=26+且75A ∠=,则b=AA. 2 B .4+ C .4— D 6、若△ABC 的内角,,,A B C 满足6sin 4sin 3sin A B C ==,则cos B =( D )A B .34C D .1116 7、在△ABC 中,若222sin sin sin A B C +<,则△ABC 的形状是(A )A 、钝角三角形B 、直角三角形C 、锐角三角形D 、不能确定二、填空题:8、在△ABC 中,若a=3,b=3,∠A=3π,则∠C 的大小为_________。
【答案】︒909、在△ABC 中,已知∠BAC=60°,∠ABC=45°,3=BC ,则AC=_______.【答案】2.10、设△ABC 的内角A B C 、、 的对边分别为a b c 、、,且1cos 4a b C ==1,=2,,则sin B = 【答案】41511、在三角形ABC 中,角A,B,C 所对应的长分别为a ,b ,c ,若a=2 ,B=6π,则b= .【答案】2.12、在△ABC 中,三边a 、b 、c 所对的角分别为A 、B 、C ,若2220a b c +-+=,则角C 的大小为 .34π(或135)13、△ABC 的三个内角A 、B 、C 所对边的长分别为a 、b 、c ,已知2,3a b ==,则sin sin()A A C =+ .2314、 若△ABC 的面积为3,BC=2,C=︒60,则边AB 的长度等于_____________. 解析:12sin 603,22s AC AC =⋅⋅⋅==, 所以△ABC 为等边三角形,故边AB 的长度等于2.答案应填2.15:在ABC ∆中,已知6:5:4)(:)(:)(=+++b a a c c b ,则ABC ∆中最大内角 。
解三角形(提升)练习题(含答案)

解三角形练习(提升)(含答案)一、选择题1、在△ABC 中,a, b, c 分别是内角 A , B , C 所对的边,若 c cos A b ,则△ABC 形状为 CA.一定是锐角三角形 B . 一定是钝角三角形C . 一定是直角三角形D . 可能是锐角三角形, 也可能是钝角三角形2、在△ABC 中,角A、B、C 的对边分别为a、b、c,若(a2+c2-b2)tanB= 3ac , 则角 B 的值为(D )A. B. C.或6 3 6 56D.3或233、在△ABC中,AB 3 ,A 45 ,C 75 ,则BC (A)A.3 3 B. 2 C.2D.3 34、在ABC 中,02 xA 60 ,且最大边长和最小边长是方程x 7 11 0的两个根,则第三边的长为( C )A.2 B.3 C.4 D.55、在△ABC中,根据下列条件解三角形,则其中有二个解的是 DA、b 10, A 45 ,C70B、a 60, c 48, B 60C、a 7,b 5,A 80D、a 14, b 16, A 456、长为5、7、8 的三角形的最大角与最小角之和为( B )A 90°B 120°C 135°D 150°二、填空题:7、如图,在△ABC 中,D 是边AC 上的点,且AB AD ,2 A B 3BD ,BC 2BD ,则s in C 的值为___________。
6 68、如图,△ABC 中,AB=AC=2 ,BC= 2 3 ,点D 在BC 边上,∠ADC=4°5,则AD 的长度等于______。
解析:在△ABC 中,AB=AC=2 ,BC= 2 3 中,ACB ABC 30 ,而∠ADC=4°5,AC ADsin 45 sin 30, AD 2 ,答案应填 2 。
9、在△ABC中,若tan1A ,C 150 ,BC 1,则AB .3110答案210、在锐角△ABC 中,BC=1,B=2A,则AC的值等于________,AC 的取值范围为________.cos A解析:由正弦定理BC=sin AAC,则sin BAC=cos ABC s in B=sin Acos A2BCsin Bsin 2A=2.由A+B+C=π得3A+C=π,即C=π-3A.π0< A<2由已知条件:π0<2 A<2,解得ππ<A< .由AC=2cos A 知2<AC< 3.6 4π 0<π-3A<2答案:2 ( 2,3)三、解答题:11、在△ABC 中,内角A,B,C 对边的边长分别是a,b,c ,已知c 2,C .3 (Ⅰ)若△ABC的面积等于 3 ,求a,b ;(Ⅱ)若sin B 2sin A,求△ABC的面积.解:(Ⅰ)由余弦定理得, 2 2 4a b ab ,又因为△ABC的面积等于 3 ,所以12ab sin C 3 ,得ab 4.联立方程组2 2 4a b ab,解得a 2,b 2.ab 4,(Ⅱ)由正弦定理,已知条件化为 b 2a,联立方程组2 2 4a b ab,解得b 2a,2 3a ,34 3b .3所以△ABC的面积 1 sin 2 3S ab C .2 312、在ABC中,若c osB b cosC 2a c(1)求角B的大小(2)若b 13 ,a c 4,求ABC的面积2 a2c2b解:(1)由余弦定理得2a 2ac2b2cb2a c2 2 2化简得: a c b ac2ab2∴2 2 2a cb ac 1cos B∴B=120°2ac 2ac 22 2 2(2)b a c 2ac cos B 2 ac ac1∴13 (a c) 2 2 ( )2∴ac=3 ∴S ABC 12ac sin B3 3413、某市电力部门某项重建工程中,需要在A、B 两地之间架设高压电线,因地理条件限制,不能直接测量A、B两地距离. 现测量人员在相距 3 km的C 、D 两地(假设A、B 、C 、D 在同一平面上),测得∠A CB 75 ,BCD 45 ,ADC 30 ,ADB 45 (如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是A、B 距离的43倍,问施工单位至少应该准备多长的电线?A解:在ACD 中,由已知可得,CAD 30B 所以,AC 3km⋯⋯⋯754545在BCD 中,由已知可得,CBD 6030CDsin 75 sin(45 30 ) 6 2 4由正弦定理,BC 3 sin 75 6 2 sin 60 2cos 75 cos(45 30 ) 6 2 4在ABC中,由余弦定理 2 2 2 cosAB AC BC AC BC BCA2 6 2 2 6 23 ( ) 2 3 cos75 52 2所以,AB 5 施工单位应该准备电线长4 53.答:施工单位应该准备电线长435 km.3。
解直角三角形练习题(带答案)

解直角三角形—题集1.如图,在地面上的点处测得树顶的仰角为度,米,则树高为( ).A.米B.米C.米D.米【答案】A【解析】米.【标注】【知识点】仰角与俯角2.如图,斜坡,坡顶到水平地面的距离为米,坡底为米,在处,处分别测得顶部点的仰角为,,求的长度.(结果保留根号).【答案】的长度为米.【解析】设米,则米,由题意得,四边形为矩形,∴,在中,∴ ,在中,,∴,∴,解得,,∴.答:的长度为米.【标注】【知识点】仰角与俯角A.的值越小,梯子越陡B.的值越小,梯子越陡C.的值越小,梯子越陡D.陡缓程度与的函数值无关3.如图,梯子跟地面的夹角为,关于的三角函数值与梯子的倾斜程度之间,叙述正确的是().【答案】B【标注】【知识点】坡度4.某地的一座人行天桥如图所示,天桥高为米,坡面的坡度为,文化墙在天桥底部正前方米处(的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为.(1)(2)若新坡面坡角为,求坡角度数.有关部门规定,文化墙距天桥底部小于米时应拆除,天桥改造后,该文化墙是否需要拆除?请说明理由.(参考数据:,)【答案】(1)(2).该文化墙需要拆除,证明见解析.【解析】(1)(2)∵新坡面坡角为,新坡面的坡度为,∴,∴.作于点,则米,∵新坡面的坡度为,∴,解得,米,∵坡面的坡度为,米,∴米,∴米,又∵米,∴米米,故该文化墙需要拆除.【标注】【知识点】坡度游船港口海警船北(1)(2)5.一艘观光游船从港口以北偏东的方向出港观光,航行海里至处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东方向,马上以海里每小时的速度前往救援.求点到直线的距离.求海警船到达事故船处所需的大约时间.(温馨提示:,)【答案】(1)(2)海里.小时.【解析】游船港口海警船北(1)(2)如图,过点作交延长线于.在中,∵,,海里,∴点到直线距离海里.在中,∵,,∴(海里),∴海警船到达事故船处所需的时间大约为:(小时).【标注】【知识点】方位角在锐角三角函数中的应用6.一副直角三角板按如图所示放置,点在的延长线上,,,,,,则的长为 .【答案】【解析】过点作于点,在中,,,,∴.∵,∴.,在中,,,∴,∴,∴.【标注】【知识点】三角板拼接问题7.如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧与墙平行且距离为米,一辆小汽车车门宽为米,当车门打开角度为时,车门是否会碰到墙? .(填“是”或“否”)请简述你的理由 .(参考数据:,,).【答案】否 ; 点到的距离小于与墙的距离【解析】过点作,垂足为点,如图.在中,∵,米,∴米,∵汽车靠墙一侧与墙平行且距离为米,∴车门不会碰到墙(点到的距离小于与墙的距离).故答案为:否;点到的距离小于与墙的距离.【标注】【知识点】测量物体之间的距离8.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为米,坡面上的影长为米.已知斜坡的坡角为,同一时刻,一根长为米、垂直于地面放置的标杆在地面上的影长为米,求树的高度.【答案】米.【解析】延长交延长线于点,则,作于,在中,,,∴(米),(米),在中,∵同一时刻,一根长为米、垂直于地面放置的标杆在地面上的影长为米,(米),,∴(米),∴(米),在中,(米),故答案为:米.【标注】【知识点】影子问题(1)(2)9.如图,在中,,点是边的中点,,.求和的长.求的值.【答案】(1)(2),..【解析】(1)(2)∵点是边的中点,且∴.∵,∴.∵在中,,,∴.在中,,,∴.故,.如图,作交于点.∵在中,,,∴设,,由勾股定理可得,解得,∴.在中,∵,,∴.即.【标注】【知识点】解直角三角形的综合应用10.如图,在四边形中,,于点,已知,,,求的长.【答案】.【解析】过点作于.∵在中,,,∴,.∵,,∴,∵,∴.∴在中,,,∴,.又∵在中,,,.∴.【标注】【知识点】解直角三角形的综合应用11.如图,在中,,,=, ,求.【答案】.【解析】 在中,,,,,,由勾股定理得:,∵,∴,∵∴,,∴.【标注】【知识点】解直角三角形的综合应用。
解三角形练习题和答案

解三角形 【2 】演习题1.在ABC ∆中,a ,b ,c 分离为角A ,B ,C 所对边,若C b a cos 2=,则此三角形必定是()A.等腰直角三角形B. 直角三角形C. 等腰三角形D. 等腰或直角三角形2.在△ABC 中,角,,A B C 的对边边长分离为3,5,6a b c ===,则cos cos cos bc A ca B ab C ++的值为A .38B .37C .36D .353.有四个关于三角函数的命题:1p :∃x ∈R, 2sin 2x +2cos 2x =122p : ,x y R ∃∈, sin()sin sin x y x y -=- 3p : ∀x ∈[]0,π1cos 2sin 2x x -=4p : sin cos 2x y x y π=⇒+= 个中假命题的是 (A )1p ,4p (B )2p ,4p (3)1p ,3p (4)2p ,3p4.已知ABC ∆的内角A ,B ,C 所对的边分离为a ,b ,c ,若31sin =A ,B b sin 3=,则a 等于. 5.在△ABC 中,已知边10c =, cos 4cos 3A bB a ==,求边a.b 的长. 6.已知A .B .C 为ABC ∆的三内角,且其对边分离为a .b .c ,若21sin sin cos cos =-C B C B . (Ⅰ)求A ;(Ⅱ)若4,32=+=c b a ,求ABC ∆的面积.7.已知△ABC 的内角C B A ,,的对边分离为c b a ,,,个中2=c ,又向量m )cos ,1(C =,n )1,cos (C =,m ·n =1.(1)若45A =︒,求a 的值;(2)若4=+b a ,求△ABC 的面积.8.已知:△ABC 中角A .B .C 所对的边分离为a .b .c 且sin cos sin cos sin 2A B B A C ⋅+⋅=.(1)求角C 的大小;(2)若,,a c b 成等差数列,且18CA CB ⋅=,求c 边的长.9.已知ABC ∆的三个内角A.B.C 所对的边分离为a b c 、、,向量(4,1),m =-2(cos ,cos 2)2A n A =,且72m n ⋅= . (1)求角A 的大小;(2)若a =试求当b c ⋅取得最大值时ABC ∆的外形.10.在ABC ∆中,54sin ,135cos =-=B A . (Ⅰ)求C cos 的值; (Ⅱ)设15=BC ,求ABC ∆的面积.11..已知31cos 32cos sin 2)(2--+=x x x x f ,]2,0[π∈x⑴求)(x f 的最大值及此时x 的值;⑵求)(x f 在界说域上的单调递增区间.12.已知角(0,)απ∈,向量(2,cos )m α=,2(cos ,1)n α=,且1m n ⋅=,()cos f x x x =+.(Ⅰ)求角α的大小;(Ⅱ)求函数()f x α+ 的单调递减区间.解三角形演习题答案1.C2.D .由余弦定理得222222222cos cos cos 222b c a c a b a b c bc A ca B ab C bc ca ab bc ca ab +-+-+-++=++ 222222222222352222b c a c a b a b c a b c +-+-+-++=++==,∴选项为D . 3. A【解析】因为2sin 2x +2cos 2x =1,故1p 是假命题;当x =y 时,2p 成立,故2p 是真命题=sinx |,因为x ∈[]0,π,所以,|sinx |=sinx,3p 准确;当x =4π,y =94π时,有sin cos x y =,但2x y π+>,故4p 假命题,选A . 4.33 5.解:由cos cos A b B a =,sinB sinA b a =,可得cos sin cos sin A B B A =,…………………….4分 变形为sinAcosA=sinBcosB,∴sin2A=sin2B, …………….6分又∵a ≠b, ∴2A=π-2B, ∴A+B=2π. ∴△ABC 为直角三角形. ………….8分由a 2+b 2=102和43b a =,解得a=6, b=8.………….12分6.解:(Ⅰ)21sin sin cos cos =-C B C B 21)cos(=+∴C B ………………………………2分 又π<+<C B 0 ,3π=+∴C B …………………4分π=++C B A ,32π=∴A ………………………………6分 (Ⅱ)由余弦定理A bc c b a cos 2222⋅-+=得 32cos 22)()32(22π⋅--+=bc bc c b ………………………………8分 即:)21(221612-⋅--=bc bc ,4=∴bc ………………………………10分 ∴323421sin 21=⋅⋅=⋅=∆A bc S ABC ………………………………12分 7.解:(1)∵mn 1cos 2cos cos ==+=C C C ∴21cos =C 0180C ︒<<︒∴60C =︒…………………………………2分由正弦定理得,2sin 45sin 60a =︒︒,……………………………………………4分 ∴362322==a ,………………………………………………………………6分(2)∵2=c ,60C ∠=︒,222cos604a b ab ∴+-︒=,∴422=-+ab b a ,…………………………………………………………8分又∵4=+b a ,∴16222=++ab b a ,∴4=ab ,………………………10分 ∴3sin 21==∆C ab S ABC .……………………………………………………12分8.解:(1) ∵sin cos sin cos sin 2A B B A C ⋅+⋅=∴sin()sin 2A B C +=,------------------------------------2分 ∵,sin()sin A B C A B C π+=-∴+=∴sin sin 22sin cos C C C C ==,-----------------------------4分∵0C π<<∴sin 0C > ∴1cos 2C =∴.3C π= --------------------------------6分 (2)由,,a c b 成等差数列,得.2b a c +=----------------------------7分∵18CA CB ⋅=,即.36,18cos ==ab C ab ----------------------------------------9分 由余弦弦定理ab b a C ab b a c 3)(cos 22222-+=-+=, 36,3634222=⨯-=∴c c c ,.6=∴c ---------------------------12分9.解:(1)由2(4,1),(cos ,cos 2)2A m n A =-= 24cos cos 22A m n A ⋅=-21cos 4(2cos 1)2A A +=⋅-- 22cos 2cos 3A A =-++……………………………………3分 又因为77,2cos 322m n A A ⋅=++=2所以-2cos 解得1cos 2A =………………………5分0,3A A ππ<<∴=……………………7分(Ⅱ)在2222cos ,ABC a b c bc A a ∆=+-=中,且222122b c bc ∴=+-⋅22b c bc =+-.…………………………………9分 222,32b c bc bc bc +≥∴≥-,即3,bc ≤当且仅当b c b c ==⋅取得最大值,……………………12分 又由(Ⅰ)知,,33A B C ππ=∴==………………………………13分所以,ABC ∆为正三角形 ………………………………14分10.解:(Ⅰ)由54sin ,135cos =-=B A ,得53cos ,1312sin ==B A .----2分 ∵π=++C B A ,∴)cos()](cos[cos B A B A C +-=+-=π-----4分6563)sin sin cos (cos =--=B A B A .-----6分 (Ⅱ)由6563cos =C ,得6513sin =C ,------8分由正弦定理得13sin sin =⨯=AB BC AC .-----10分 所以ABC ∆的面积1sin 2S BC AC C =⨯⨯⨯246516131521=⨯⨯⨯=.----12分 11.解:⑴1)32sin(2)(-+=πx x f -----------3分 20π≤≤x 34323πππ≤+≤∴x 当232ππ=+x 时,即12π=x 时,1max =y -----------6分 ⑵由2323πππ≤+≤x 得120π≤≤x)(x f ∴在界说域上的单调递增区间]12,0[π-----------12分 12.解:(Ⅰ)∵(2,cos )m α=,2(cos ,1)n α=,且1m n ⋅=,∴22cos cos 1αα+=………………………………………2分即22cos cos 10αα+-=∴1cos 2α=或cos 1α=-, ………………4分∵角(0,)απ∈,∴1cos 23παα=⇒=, …………………………………6分(Ⅱ)∵1()cos cos )2sin()26f x x x x x x π=+=+=+…………8分 ∴()()2sin()2sin()2cos 3632f x f x x x x ππππα+=+=++=+=……10分 ∴函数()f x α+ 的单调递减区间为[2,2]k k πππ+k Z ∈………………12分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.在△ABC 中,已知2B =A +C ,则B =( ) A .30° B .45° C .60° D .90°2.在△ABC 中,若∠A =60°,∠B =45°,BC =32,则AC =( ) A .4 3 B .2 3 C. 3 D.323.在△ABC 中,a =15,b =10,A =60°,则cos B 等于( ) A .-223 B.223 C .-63 D.634.在△ABC 中,若角A ,B ,C 对应的三边分别是a ,b ,c ,则下列关于正弦定理的叙述或变形中错误的是( )A .a ∶b ∶c =sin A ∶sinB ∶sinC B .a =b ⇔sin 2A =sin 2B C.asin A =b +c sin B +sin CD .正弦值较大的角所对的边也较大5.在△ABC 中,a =bsin A ,则△ABC 一定是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .等腰三角形 二、填空题6.(2015·北京卷)在△ABC 中,a =3,b =6,∠A =2π3,则∠B =________. 7.在△ABC 中,已知a ∶b ∶c =4∶3∶5,则2sin A -sin B sin C =________. 8.在△ABC 中,若B =30°,AB =23,AC =2,则AB 边上的高是________. 三、解答题9.在△ABC 中,若acos A =bcos B ,试判断△ABC 的形状.10.在△ABC 中,已知c =10,cos A cos B =b a =43,求a 、b 及△ABC 的内切圆半径.1.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c.若3a =2b ,则2sin2B -sin2Asin2A 的值为( )A.19B.13 C .1 D.722.设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c.若a =3,sin B =12,C =π6,则b =________. 3.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知A -C =90°,a +c =2b ,求C.A 级 基础巩固 一、选择题1.(2016·天津卷)在△ABC 中,若AB =13,BC =3,∠C =120°,则AC =( ) A .1 B .2 C .3 D .42.在△ABC 中,已知acos A +bcos B =ccos C ,则△ABC 是( ) A .等腰三角形 B .直角三角形C .等腰直角三角形D .等边三角形 3.在△ABC 中,有下列结论:①若a2>b2+c2,则△ABC 为钝角三角形; ②若a2=b2+c2+bc ,则∠A 为60°;③若a2+b2>c2,则△ABC 为锐角三角形; ④若A ∶B ∶C =1∶2∶3,a ∶b ∶c =1∶2∶3. 其中正确的个数为( ) A .1 B .2 C .3 D .44.在△ABC 中,B =π4,BC 边上的高等于13BC ,则cos A =( ) A.31010 B.1010 C .-1010D .-310105.在△ABC 中,若2cos Bsin A =sin C ,则△ABC 的形状一定是( ) A .等腰直角三角形 B .直角三角形 C .等腰三角形 D .等边三角形 二、填空题6.在△ABC 中,若(a +c)(a -c)=b(b +c),则∠A =________.7.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c.已知b -c =14a ,2sin B =3sin C ,则cos A 的值为________.8.三角形的一边长为14,这条边所对的角为60°,另两边长之比为8∶5,则这个三角形的面积是________. 三、解答题9.在△ABC 中,已知sin2 B -sin2 C -sin2 A =3sin Asin C ,求B 的度数.10.在△ABC 中,BC =a ,AC =b ,且a ,b 是方程x2-23x +2=0的两根,2cos(A +B)=1 (1)求角C 的度数; (2)求AB 的长. B 级 能力提升1.在△ABC 中,sin2 A 2=c -b2c ,则△ABC 的形状为( ) A .正三角形 B .直角三角形 C .等腰直角三角形D .等腰三角形2.在△ABC 中,AB =2,AC =6,BC =1+3,AD 为边BC 上的高,则AD 的长是________. 3.如图所示,已知在四边形ABCD 中,AD ⊥CD ,AD =10,AB =14,∠BDA =60°,∠BCD =135°,求BC 的长.一、选择题1.已知三角形的三边长分别是a ,b ,a2+b2+ab ,则此三角形中最大的角是( ) A .30° B .60° C .120°D .150° 2.在△ABC 中,有下列关系式: ①asin B =bsin A ; ②a =bcos C +ccos B ; ③a2+b2-c2=2abcos C ; ④b =csin A +asin C. 一定成立的有( )A .1个B .2个C .3个D .4个3.在△ABC 中,A =60°,AB =2,且△ABC 的面积为32,则BC 的长为( ) A.32 B.3 C .2 3 D .24.锐角三角形ABC 中,sin A 和cos B 的大小关系是( ) A .sin A =cos B B .sin A <cos B C .sin A >cos B D .不能确定5.在△ABC 中,b =8,c =3,A =60°,则此三角形外接圆面积为( ) A.1963 B.196π3 C.493 D.49π3 二、填空题6.若锐角△ABC 的面积为103,且AB =5,AC =8,则BC 等于________.7.(2015·北京卷)在△ABC 中, a =4,b =5,c =6,则sin 2Asin C =________.8.(2016·全国Ⅱ卷)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若cos A =45,cos C =513,a =1,则b =________. 三、解答题9.在△ABC 中,已知sin2 B -sin2 C -sin2 A =3sin Asin C .求B 的度数. 10.在△ABC 中,BC =5,AC =3,sin C =2sin A. (1)求AB 的值; (2)求sin ⎝⎛⎭⎫2A -π4.B 级 能力提升1.在△ABC 中,∠ABC =π4,AB =2,BC =3,则sin ∠BAC 等于( )A.1010B.105C.31010D.552.在平面四边形ABCD 中,∠A =∠B =∠C =75°,BC =2,则AB 的取值范围是________. 3.(2016·全国Ⅰ卷)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2cos C(acos B +bcos A)=c. (1)求C ;(2)若c =7,△ABC 的面积为332,求△ABC 的周长.一、选择题1.有一长为1公里的斜坡,它的倾斜角为20°,现要将倾斜角改成10°,则斜坡长为( ) A .1 B .2sin 10° C .2cos 10° D .cos 20°2.如图所示为起重机装置示意图.支杆BC =10 m ,吊杆AC =15 m ,吊索AB =519 m ,起吊的货物与岸的距离AD 为( )A .30 m B.1523mC .15 3 mD .45 m3.甲骑电动自行车以24 km/h 的速度沿着正北方向的公路行驶,在点A 处望见电视塔在电动车的北偏东30°方向上,15 min 后到点B 处望见电视塔在电动车的北偏东75°方向上,则电动车在点B 时与电视塔S 的距离是( )A .6 kmB .3 3 kmC .3 2 kmD .3 km4.设A 、B 两点在河的两岸,要测量两点之间的距离,测量者在A 的同侧,在河岸边选定一点C ,测出AC 的距离是100 m ,∠BAC =60°,∠ACB =30°,则A 、B 两点的距离为( ) A .40 m B .50 m C .60 m D .70 m5.两灯塔A 、B 与海洋观察站C 的距离都等于2 2 km ,灯塔A 在观察站C 的北偏东30°,灯塔B 在观察站C 南偏东60°,则A 、B 之间的距离为( ) A .2 km B .3 km C .4 km D .5 km 二、填空题6.已知两座灯塔A 和B 与海洋观察站C 的距离相等,灯塔A 在观察站C 的北偏东40°,灯塔B 在观察站C 的南偏东60°,则灯塔A 在灯塔B 的________.7.已知A ,B ,C 三地,其中A ,C 两地被一个湖隔开,测得AB =3 km ,B =45°,C =30°,则A 、C 两地的距离为________.8.在△ABC 中,若b =2,B =30°,C =135°,则a =________. 三、解答题9.要测量对岸两点A、B之间的距离,选取相距 3 km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.10.如图所示,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1°)?1.如图所示,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A—C—B 行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10 km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走(结果精确到0.1 km;参考数据;2≈1.41,3≈1.73)()A.3.4 km B.2.3 kmC.5 km D.3.2 km2.如图所示,一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距塔68海里的M处,下午2时到达这座灯塔的东南方向的N处,则这只船航行的速度为________海里/时.3.如图所示,港口B在港口O正东方向120海里处,小岛C在港口O北偏东60°方向,且在港口B北偏西30°方向上.一艘科学家考察船从港口O出发,沿北偏东30°的OA方向以20海里/时的速度行驶,一艘快艇从港口B出发,以60海里/时的速度驶向小岛C,在C 岛装运补给物资后给考察船送去.现两船同时出发,补给物资的装船时间为1小时,则快艇驶离港口B后,最少要经过多少小时才能和考察船相遇?一、选择题1.某人向正东走了x km 后向右转了150°,然后沿新方向走了3 km ,结果离出发点恰好 3 km ,那么x 的值是( )A. 3 B .2 3 C .3 D .23或 3 2.在200 m 高的山顶上,测得山下一塔塔顶与塔底的俯角分别为30°,60°,则塔高为( ) A.4003 mB.40033mC.2033mD.2003m3.在静水中划船的速度是每分钟40 m ,水流的速度是每分钟20 m ,如果船从岸边A 处出发,沿着与水流垂直的航线到达对岸,那么船前进的方向指向河流的上游并与河岸垂直的方向所成的角为( ) A.π4 B.π3 C.π6 D.512π4.要测量底部不能到达的东方明珠电视塔的高度,在黄浦江西岸选择甲、乙两观测点,在甲、乙两点测得塔顶的仰角分别为45°,30°,在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°,甲、乙两地相距500米,则电视塔在这次测量中的高度是( ) A .1002米B .400米C .2003米D .500米5.在△ABC 中,A =60°,且最大边长和最小边长是方程x2-7x +11=0的两个根,则第三边的长为( )A .2B .3C .4D .5 二、填空题6.如图,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得M 点的仰角∠MAN =60°,C 点的仰角∠CAB =45°以及∠MAC =75°;从C 点测得∠MCA =60°.已知山高BC =100 m ,则山高MN =________m.7. 一蜘蛛沿东北方向爬行x cm 捕捉到一只小虫,然后向右转105°,爬得10 cm 捕捉到另一只小虫,这时它向右转135°爬行可回到它的出发点,那么x =________cm.8.如图所示,一船在海上自西向东航行,在A 处测得某岛M 位于北偏东α,前进m 海里后在B 处测得该岛位于北偏东β,已知该岛周围n 海里范围内(包括边界)有暗礁,现该船继续东行,当α与β满足条件__________时,该船没有触礁危险.三、解答题9.甲船在A 处,乙船在A 的南偏东45°方向,距A 有9海里的B 处,并以20海里/时的速度沿南偏西15°方向行驶,若甲船以28海里/时的速度行驶,用多少小时能最快追上乙船? 10.如下图所示,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧远处一山顶D 在西偏北15°的方向上,行驶5 km 后到达B 处,测得此山顶在西偏北25°的方向上,仰角为8°,求此山的高度CD(精确到1 m).B 级 能力提升1.在某个位置测得某山峰仰角为θ,对着山峰在地面上前进600 m 后测得仰角为2θ,继续在地面上前进200 3 m 以后测得山峰的仰角为4θ,则该山峰的高度为( ) A .200 m B .300 m C .400 m D .100 3 m2.一架飞机在海拔8 000 m 的高度飞行,在空中测出前下方海岛两侧海岸俯角分别是30°和45°,则这个海岛的宽度为________m.3.我炮兵阵地位于地面A 处,两观察所分别位于地面C 和D 处,已知CD =6 km ,∠ACD =45°,∠ADC =75°,目标出现于地面点B 处时,测得∠BCD =30°,∠BDC =15°(如图所示),求我炮兵阵地到目标的距离.第一章解三角形 1.2 应用举例第3课时三角形中的几何计算A 级 基础巩固 一、选择题1.在△ABC 中,a ,b ,c 分别是角A 、B 、C 的对边,a =5,b =4,cos C =45,则△ABC 的面积是( )A .8B .6C .4D .22.在△ABC 中,三边a ,b ,c 与面积S 的关系式为a2+4S =b2+c2,则角A 为( ) A .45° B .60° C .120° D .150°3.在△ABC 中,A =60°,AB =1,AC =2,则S △ABC 的值为( ) A.12 B.32 C.3 D .2 34.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,a =1,B =π3,当△ABC 的面积等于3时,tan C 等于( )A. 3 B .- 3 C .-2 3 D .-25.在△ABC 中,已知b2-bc -2c2=0,且a =6,cos A =78,则△ABC 的面积等于( ) A.152 B.15 C .2 D .36.△ABC 中,下述表达式:①sin(A +B)+sin C ; ②cos(B +C)+cos A 表示常数的是________. 7.在△ABC 中,已知a -b =4,a +c =2b ,且最大角为120°,则该三角形的周长为________. 8.在△ABC 中,若A =60°,b =16,此三角形的面积S =2203,则a 的值为________. 三、解答题9.某市在进行城市环境建设时,要把一个三角形的区域改造成一个公园,经过测量得到这个三角形区域的三条边长分别为70 m ,90 m ,120 m ,这个区域面积是多少?10.在△ABC 中,c =22,a>b ,tan A +tan B =5,tan A ·tan B =6,试求a ,b 及△ABC 的面积. .B 级 能力提升1.在△ABC 中,若cos B =14,sin C sin A =2,且S △ABC =154,则b 等于( ) A .4 B .3 C .2 D .12.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c.已知a =23,c =22,1+tan A tan B =2cb ,则角C 的值为________.3.已知△ABC 的面积为1,tan B =12,tan C =-2,求△ABC 的各边长以及△ABC 外接圆的面积.。
