2013年莆田市高中毕业班教学质量检查理科试卷(word)
福建省莆田市2013年初中毕业班质量检查数学试题(WORD版) 2
4.方茴说:“可能人总有点什么事,是想忘也忘不了的。
”5.方茴说:“那时候我们不说爱,爱是多么遥远、多么沉重的字眼啊。
我们只说喜欢,就算喜欢也是偷偷摸摸的。
”6.方茴说:“我觉得之所以说相见不如怀念,是因为相见只能让人在现实面前无奈地哀悼伤痛,而怀念却可以把已经注定的谎言变成童话。
”7.在村头有一截巨大的雷击木,直径十几米,此时主干上唯一的柳条已经在朝霞中掩去了莹光,变得普普通通了。
8.这些孩子都很活泼与好动,即便吃饭时也都不太老实,不少人抱着陶碗从自家出来,凑到了一起。
9.石村周围草木丰茂,猛兽众多,可守着大山,村人的食物相对来说却算不上丰盛,只是一些粗麦饼、野果以及孩子们碗中少量的肉食。
1.“噢,居然有土龙肉,给我一块!”2.老人们都笑了,自巨石上起身。
而那些身材健壮如虎的成年人则是一阵笑骂,数落着自己的孩子,拎着骨棒与阔剑也快步向自家中走去。
莆田2013年初中毕业班质量检测数 学(满分:150分;考试时间:120分钟)友情提醒:本试卷分为“试题”和“答题卡”两部分,答题时,请按答题卡中的“注意事项”认真作答。
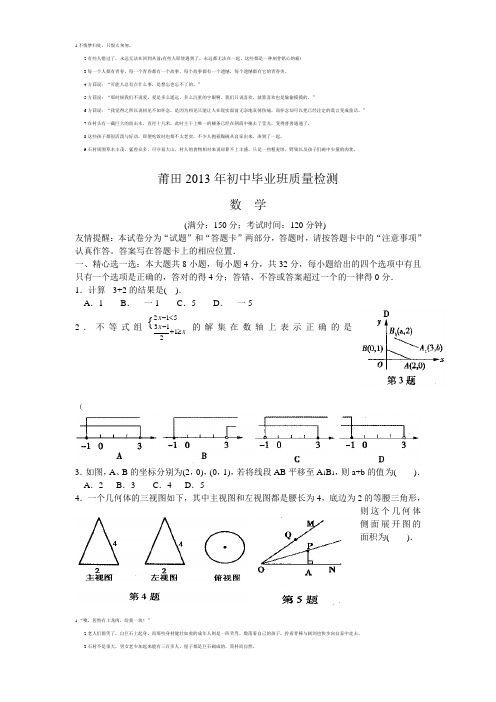
答案写在答题卡上的相应位置.一、精心选一选:本大题共8小题,每小题4分,共32分,每小题给出的四个选项中有且只有一个选项是正确的,答对的得4分;答错、不答或答案超过一个的一律得0分. 1.计算 -3+2的结果是( ).A .1B . 一1C .5D . 一5 2.不等式组5121213{<-≥+-x xx 的解集在数轴上表示正确的是(3.如图,A 、B 的坐标分别为(2,0),(0,1),若将线段AB 平移至A 1B 1,则a+b 的值为( ). A .2 B .3 C .4 D .54.一个几何体的三视图如下,其中主视图和左视图都是腰长为4,底边为2的等腰三角形,则这个几何体侧面展开图的面积为( ).4.方茴说:“可能人总有点什么事,是想忘也忘不了的。
”5.方茴说:“那时候我们不说爱,爱是多么遥远、多么沉重的字眼啊。
2013届福建省泉州市普通中学高中毕业班质量检查_理科数学(含参考答案及评分标准)

2013届泉州市普通中学高中毕业班质量检查理科数学试题参考解答及评分标准说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数.选择题和填空题不给中间分.一、选择题:本大题考查基础知识和基本运算.每小题5分,满分50分.1. B 2.B 3.C 4.A 5.D 6. B 7.A 8.D 9.C 10.C【解析】:1、∵1242x <<⇒12222x -<<⇒-1< x <2,∴选B.2、∵19379991822(a a )(a a )S ++===,,∴选B. 3、∵OB 1=b ,OF 2=c ,四边形B 1F 1B 2F 2是正方形,∴b =c ,∵222a b c =+,∴222a c =,选C.4、对于B ,α与β可平行、可成任意角;对于C ,α与β可平行、可成任意角;对于D ,α⊥β.5、由已知得24T π=,∴ω=4;14f ()π=⇒4242k ππ⨯+ϕ=π+⇒22k πϕ=π-,k ∈Z ,∵|ϕ|<π,∴2πϕ=-,选D.6、∵2f (x )sin x |x |=+,∴f (x )是非奇非偶函数,排除A 、C ;又∵当x > 0时,221f (x )cos x '=+,令0f (x )'>解得3388k x k πππ-<<π+,k ∈Z∴f (x )在(0,38π)上递增,从而选B.7、由已知函数f (x )=11x +得A n (n ,11n +) ,则直线O A n 的斜率为n tan θ=11n(n )+=111nn -+,∴1tan θ+2tan θ+…+n tan θ=111n -+,选A.8、∵目标函数z O A O P ==x +2y ,作出可行域,由图象可得:最优解为点(0,1),∴2m ax z =,则选D.9、记“甲袋中取出1个球是红球”为事件A ,“甲袋中取出1个球是白球”为事件B ,“乙袋中取出1个球是红球”为事件C ,“乙袋中取出1个球是白球”为事件D , ∵f (n )=P(AC +BD)= P(A)P(C)+P(B)P(D)=2135151n n n ⨯+⨯++=13251n n +⨯+=11(3)51n -+ n ∈N +∴f (n ) 随着n 的增大而增大,则f (n ) 的最小值为f (1)=1/2,选C.10、由已知得 R +∀ξ∈,x D ∃∈,使得| f (x ) -1|<ξ恒成立⇔ f (x )为“敛1函数”. 分别从四个函数图象去观察,可以发现①不满足上述条件(注意定义域),∴选C.二、填空题:本大题考查基础知识和基本运算.每小题4分,满分20分.11.12. 15 ; 13. y=lnx +1 (或y=ln|x|+1) ; 14. 3 ; 15. 4个③和1个⑤【解析】:11、z=(+(3-1)i= 2i . 12、∵16216()rrr r T C xx--+=-=3626(1)r r rC x--,∴r = 4 时,44416(1)15T C +=-=13、∵y=f (x )的导函数为y=1x,∴f (x )= lnx +c (或f (x )= ln|x|+c ),(c 为常数);…………①又过曲线y=f (x )上点P(0x ,0y )的切线方程为y -0y =1x (x -0x ),化简得 x -0x y +0x (0y -1)=0,对比已知直线l 的方程得0x =e ,0y =2,代入①式 解得 c=1,则 f (x )= lnx +1(或 f (x )= ln|x|+c ).14、由已知直线与已知圆相切,得1=⇒221a b +=;根据已知得 |AB|2=2214ba+=(2214ba+)(22b a +)≥(1+2)2=9,(柯西不等式)∴当222a b ==23时,|AB| 的最小值为3.15、略三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.16. 本小题主要考查三角函数的性质、两角和与差的三角函数公式、解三角形以及数列等基础知识,考查运算求解能力,考查函数与方程思想、数学结合思想.满分13分. 解:(I )∵a 、b 、c 成等差,且公差为2,∴a=c -4,b=c -2 ………………1分又∵∠MCN=23π,∴cosC=12-,由余弦定理得 c 2=a 2+b 2+ab , ………………4分即c 2=( c -4)2+(c -2)2+( c -4) (c -2),整理得 c 2-9c +14 = 0,解得c=7或2 ………5分 又∵ a =c -4>0, ∴ c=7 ………6分 (II )在△ABC 中,由已知及正弦定理得2233ab csin sin()sin===ππθ-θ,………8分 ∴b=2sin θ,a =2sin(3π-θ),则△ABC 的周长f (θ)=a +b +c=2[sin(3π-θ)+sin θ],化简得 f (θ)=2sin(3πθ+)………11分∵θ∈(0,3π), ∴3πθ+∈(3π,23π) ………12分则当 θ=6π时,f (θ)m ax =2………13分17. 本题主要考查概率与统计和独立性检验、频率估计概率、样本估计总体等统计思想方法,考查数据处理能力、运算求解能力以及应用用意识,考查函数与方程思想、必然与或然思想.满分13分. 解:(I )设“甲机床生产一件零件获得的利润”为X 元,它的分布列为 ……… 3分则有E(X)= -350+750+34050⨯=12450=6225≈2.48 (元)∴甲机床生产一件零件的利润的数学期望为2.48元 ……… 6分 (II )由已知表中数据可得,样本频数2×2列联表 如下……… 9分计算K 2=21004020301050507030()⨯-⨯⨯⨯⨯=10021≈4.762 ……… 11分考察参考数据,并注意到3.841<4.762<5.024,因此可知:约有95%的把握认为“零件优等品与否和所用机床有关”. ……… 13分18.本题考查直线与直线、直线与平面、平面与平面的位置关系,空间向量、函数等基础知识,考查空间想象能力、推理论证能力及运算求解能力,考查化归与转化思想、数形结合思想、函数与方程思想及应用意识. 满分13分.解:(Ⅰ)在图1中,取BE 中点F ,由已知得DF AB=DC ,BF=FE=EC=1,∴DE ⊥BC (1)分在图2中,DE ⊥BE ,DE ⊥CE ,∴∠BEC 是二面角B —DE —C 的平面角, (2)分∵∠BEC 是直二面角,∴ BE ⊥CE (3)分则分别以EB 、EC 、ED 为x 、y 、z 轴,点E 为原点,建立空间直角坐标系E —xyz , 根据已知得E(0,0,0),A(1,0,B(2,0,0),C(0,1,0), (4)分设平面AEC 的法向量为n = (x ,y ,z), ∴00EA n EC n ⎧=⎪⎨=⎪⎩, 即0x y ⎧+=⎪⎨=⎪⎩,取n 0,-1), ……… 5分又平面ABED 的一个法向量为m= (0,1,0), (6)分∴m·n= 0, 则 平面AEC ⊥平面ABED (7)分(II )由已知得 点G(-1,0, 设M(x ,y ,0),则G M=(x +1,y , (9)∵直线GM与平面ACE所成交为60°,∴sin60°=|G M n||G M||n| (10)分12|x)++=⇒(x+2)2= (x+1)2+y2+3,化简得y2=2x (11)分又|MB|2=(x-2)2+y2=x2-2x+4=(x-1)2+3 (12)分∴当x=1时,|MB|M到点B………13分19.本小题考查抛物线的标准方程、圆锥曲线的性质、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、数形结合思想、化归与转化思想等.满分13分.解:(Ⅰ)由已知及抛物线的定义得|MF|=5=42p+,∴p=2 (2)分∴抛物线C的方程为y2=4x. ………3分又点M抛物线C上,∴2t=4×4 ,∵t > 0,∴M (4,4) ………4分(II)由已知可设直线1l的方程为y-4=1k(x-4)∵直线1l与抛物线C交于两点M、A,∴1k≠0 ………5分由y-4=1k(x-4)与y2=4x联立,消去x得1k y2-4y+16(1-1k)=0. ………6分设A (1x,1y),则由韦达定理得1y+4=14k,1y×4=11161(k)k-………7分∴1y=14k-4=114(1)k-,1x=214y=2114(1)k-,则A (2114(1)k-,114(1)k-),…8分同理 B (2214(1)k-,214(1)k-), (9)则直线AB的斜率3k =122212114[(1)(1)]114[(1)(1)]k k k k ------=121212111111(2)()k k k k k k -+--=121112k k +- ………10分(i )若1k +2k = 0,则1211k k +=1212k k k k +=0,∴3k =12- (11)分(ii )∵31k =1211k k +-2, ∴1211k k +-31k =2 (定值) ………13分20. 本题主要考查函数、导数、零点、算法初步等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、数形结合思、化归与转想化思想、分类与整合思想.满分14分.解: ∵3()=1n f x x nx -- ( x > 0 ), ∴()n f x '=32x -n , ………1分(Ⅰ)3()f x '=32x -3=0 ,得x=1; 当x>1时,3()f x '>0;当0<x<1时,3()f x '<0, ………3分∴当x=1时,3()f x 取得唯一的一个极小值-3,无极大值 ………4分(II )函数()n f x………5分 证明如下:∵()n f x '=32x -n ( x > 0 ), 令()n f x '>0⇒,∵当n ∈N *∴函数()n f x7分又∵n f=311--=-<0,n f=311-=->0∴n fn f < 0,则函数()n f x (8)分综上,函数()n f x (9)分(III )程序框图的算法功能是:找出最小的正整数n ,使()n f x 的零点n a满足2n a +≥ (10)分∵()2n f +=3122--=8+-1 关于n 单调递增∴当n=1,2,3时,()2n f +< 0 =()n n f a ;当n ≥4时,()2n f +> 0 =()n n f a (11)分又∵函数()n f x∴当n=1,2,3时,2n a <;当n ≥42n a ≥ (13)分∴ 输出的n 值为4 …………………14分21.(1)选修4—2:矩阵与变换本题主要考查矩阵与变换等基础知识,考查运算求解能力及函数与方程思想.满分7分.解:(Ⅰ)复合变换090R σ 对应的矩阵为AB=10101021100012-⎛⎫⎛⎫-⎛⎫ ⎪⎪=⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,………… 3分 ∴复合变换090R σ 的坐标变换公式为12x y y x '=-⎧⎪⎨'=⎪⎩ , ………… 4分 (II )设圆C 上任意一点P (x ,y )在变换090Rσ 的作用下所得点P '(x ',y ')由(Ⅰ)得12x yy x '=-⎧⎪⎨'=⎪⎩ 解得2x y y x '=⎧⎨'=-⎩, ………… 5分代入圆C :221x y +=,得2241x y ''+=,∴曲线C '的方程为2241x y += ………… 7分(2)选修4—4:坐标系与参数方程本题主要考查曲线的参数方程、直线的极坐标方程等基础知识,考查运算求解能力以及化归与转化思想,满分7分.解:(Ⅰ)由2x ty =-⎧⎪⎨=⎪⎩,消去参数t 得0y +-=, ∴直线l 的平面直角坐标方程为y +-=………… 3分 (II )直线l 与x 轴、y 轴的交点为P(2,0)、Q(0,,∴线段PQ 中点M 的直角坐标为(1,则ρ=2,tan θM 在第一象限, ………… 5分 ∴点M 的极坐标为(2,3π), ………… 6分直线OM 的极坐标方程为 θ=3π (R ρ∈) ………… 7分(3)选修4—5;不等式选讲本题主要考查绝对值的含义、柯西不等式等基础知识,考查运算求解能力以及推理论证能力,考查函数与方程思想. 满分7分.解:(Ⅰ)∵不等式|x -2|>1的解集为{x| x<1或 x>3} ………… 1分 ∴由已知得,不等式 20x ax b -+>的解集为{x| x<1或 x>3}从而1、3是方程20x ax b -+=的两根 ………… 2分 由韦达定理得 a =4 ,b=3 ………… 3分 (II )函数()f x 的定义域为[3,5],且显然有 y>0 由柯西不等式可得:)2≤(42+3222)=50 (5)分当且仅当时等号成立 …………6分即10725x =时,函数()f x (7)分。
莆田市高中毕业班教学质量检查试卷.docx

2016年莆田市高中毕业班教学质量检查试卷数 学(文科)第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是 符合题目要求的.(1)若复数z=2(1)1i i-+,则|z|=(A)8 (B)22 (C)2 (D)2(2)已知集合A={x|x 2一x-6 >0),B={x|-1≤x ≤4),则A I B=(A)[一l,3) (B)(3,4] (C)[一1,2) (D)(2,4](3)已知函数f(x)= sin (2ωx 一4π)(ω>0)的最小正周期为π,则函数f(x)的图象 (A)关于点(8π,0)对称 (B)关于直线x=8π对称(C)关于点(一4π,0)对称 (D)关于直线x=一4π对称(4)设M 是△ABC 所在平面内的一点,若AB uu u r +AC uuur =2AM uuu r ,|BC uu u r |=2,则MB uuu r ·MC uuur =(A) -1 (B)1 (C) -2 (D)2(5)已知函数2,0()21,0x x ax x f x x ⎧-+>⎪=⎨-≤⎪⎩有两个零点,则实数a 的取值范围为(A)(一∞,0) (B)(0,1] (C)(0,+∞) (D)[0,+∞)(6)执行如图所示的程序框图,欲使输出的S>11,则输入整数n 的最 小值为(A)3 (B)4 (C)5 (D)6(7)盒中共有形状大小完全相同的5个球,其中有2个红球和3个白 球.若从中随机取2个球,则概率为35的事件是 (A)都不是红球 (B)恰有1个红球 (C)至少有1个红球 (D)至多有1个红球(8)已知等比数列{a n }为递增数列,其前n 项和为S n .若S 3=7,a 2=2, 则 a 3 +a 4 +a 5= (A)74 (B 78(C) 28 (D) 56(9)已知点P 在双曲线22216x y a -=1的右支上,F 为双曲线的左焦点,Q 为线段PF 的中点,D 为坐标原点.若|OQ|的最小值为1,则双曲线的离心率为(A)1715 (B)1517 (C)35 (D)53(10)已知某几何体的三视图如图所示,则该几何体的体积为(A)83π (B)3π (C)103π (D) 113π(11)已知F 为抛物线y 2 =4x 的焦点,点A ,B 在抛物线上,O 为坐标原点.若AF uuu r +2BF uu u r=0,则△OAB 的面积为(A)328 (B)324 (C)322(D)32 (12)已知函数f(x)=|log 3(x+1)|,实数m ,n 满足一1<m<n ,且f(m)=f(n).若f(x)在 [m 2,n]上的最大值为2,则nm= (A) -6 (B) -8 (C) -9 (D) -12第Ⅱ卷本卷包括必考题和选考题两部分.第(13)题一第(21)题为必考题,每个试题考生都必须 作答.第(22)题~第(24)题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分,共20分. (13)已知数列{a n }满足a 1=1,a n+1+2a n+1-a n =0,则a 4=____.(14)若变量x ,y ,满足约束条件10210,30x x y x y -≥⎧⎪--≤⎨⎪+-≤⎩则z=x -y 的最小值为__ .(15)若一个长方体内接于表面积为4π的球,则这个长方体的表面积的最大值是 (16)已知函数f(x)=x 2+bx+1满足f(一x )=f(x+1),若存在实数t ,使得对任意实 数x ∈[l ,m],都有f(x+t )≤x 成立,则实数m 的最大值为 三、解答题:解答应写出文字说明、证明过程或演算步骤. (17)(本小题满分12分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且sin 3cos 0a B b A -=. (I)若cos C=45,求cos(A+C); (Ⅱ)若b+c=5,A=7,求△ABC 的面积,(18)(本小题满分12分)某企业对其生产的一批产品进行检测,得 出每件产品中某种物质含量(单位:克) 的频率分布直方图如图所示.(I)估计产品中该物质含量的中位数及 平均数(同一组数据用该区间的中 点值作代表);(Ⅱ)规定产品的级别如下表:若生产1件A 级品可获利润100元,生产1件B 级品可获利润50元,生产1件C 级品亏损50元.现管理人员从三个等级的产品中采用分层抽样的方式抽取10件产品,试用样本估计生产1件该产品的平均利润. (19)(本小题满分12分)如图,在四棱锥P-ABCD 中,底面ABCD 是正方形,侧面PAD 是边长为2的正三角形, PD ⊥CD ,E ,F 分别为PC ,AD 的中点. (I)求证:平面CEF ⊥平面ABCD : (Ⅱ)求三棱锥P-BDE 的体积.(20)(本小题满分12分)动圆P 过点M( -1,O),且与圆N :x 2+y 2 -2x -15 =0内切,记圆心P 的轨迹为曲线τ。
2013年福建省普通高中毕业班质量检查数学(文)试卷及答案.

2013年福建省普通高中毕业班质量检查文 科 数 学本试卷分第1卷(选择题)和第Ⅱ卷(非选择题).本试卷共5页.满分150分.考试时间120分钟.注意事项:1.答题前,考生先将自己的姓名、准考证号填写在答题卡上.2.考生作答时,将答案答在答题卡上.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.在草稿纸、试题卷上答题无效.3.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.4.保持答题卡卡面清洁,不折叠、不破损.考试结束后,将本试卷和答题卡一并交回.参考公式:样本数据x 1,x 2, …,x n 的标准差 锥体体积公式V =31Sh 其中x 为样本平均数 其中S 为底面面积,h 为高 柱体体积公式球的表面积、体积公式 V =Sh24S R =π,343V R =π其中S 为底面面积,h 为高其中R 为球的半径第Ⅰ卷(选择题 共60分)一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数1i z =-,z 为z 的共轭复数,则下列结论正确的是A .1i z =--B .1+i z =-C .2z =D .z =2.已知,0a b c >≠,则下列不等式一定成立的是 A .22a b >B .ac bc >C .a c b c +>+D .a b c c> 3.执行如图所示的程序框图,若输入的x 值为2,则输出的x 值为A .3B .8C .9D .63 4.“1x =”是“210x -=”的A.充分而不必要条件 B.必要而充分不条件 C.充要条件 D.既不充分也不必要条件5.函数2cos 22y x x x ππ⎛⎫=-≤≤ ⎪⎝⎭的图象是6.已知集合{}|28M x x =-≤≤,{}2|320N x x x =-+≤,在集合M 中任取一个元素x ,则 “x MN ∈”的概率是A .110B .16C .310D .127.已知1F ,2F 是椭圆C 的两个焦点,焦距为4.若P 为椭圆C 上一点,且12PF F ∆的周长为14,则椭圆C 的离心率e 为 A .15 B .25 C .45D .5A BCD8.若变量,x y 满足约束条件310,3110,2,x y x y y --≥⎧⎪+-≤⎨⎪≥⎩则2z x y =-的最小值为A .4B .1C .0D .1- 9.设,m n 为两条不同的直线,βα,是两个不同的平面,下列命题正确的是 A .若β//,//m n m ,则β//n B .若αα//,//n m ,则n m // C .若β⊥m n m ,//,则β⊥n D .若n m n m //,,βα⊂⊂,则βα// 10.已知点()0,0O ,()1,2A ,()3,2B ,以线段AB 为直径作圆C ,则直线:30l x y +-=与圆C 的位置关系是A .相交且过圆心B .相交但不过圆心C .相切D .相离 11.已知点()()()0000167n O ,,A ,,A ,,点()1212n A ,A ,,A n ,n -∈≥N 是线段0n A A 的n 等分点,则011+n n OA OA OA OA -+++等于A .5nB .10nC .()51n +D .()101n + 12.定义两个实数间的一种新运算“*”:()l g1010,x yx y *=+,x y ∈R .对任意实数,,a b c ,给出如下结论:①()()c b a c b a ****=; ②a b b a **=; ③()()()**a b c a c b c +=++; 其中正确的个数是A . 0B .1C .2D .3第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡相应位置. 13.一支田径队有男运动员28人,女运动员21人,现按性别用分层抽样的方法,从中抽取14位运动员进行健康检查,则男运动员应抽取________人. 14.在ABC ∆中,角,,A B C 所对的边分别为,,a b c .已知3a =,8b =,C=3π,则c = .15.若函数2,0,()ln ,0x a x f x x x ⎧-≤=⎨>⎩有两个不同的零点,则实数a 的取值范围是 . 16.观察下列等式:12133+=; 781011123333+++=; 16171920222339333333+++++=; …则当m n <且,m n ∈N 表示最后结果.313232313333n n m m ++--++++= (最后结果用,m n 表示最后结果). 三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)某工厂生产,A B 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:由于表格被污损,数据y x ,看不清,统计员只记得x y <,且,A B 两种元件的检测数据的平均值相等,方差也相等. (Ⅰ)求表格中x 与y 的值;(Ⅱ)若从被检测的5件B 种元件中任取2件,求2件都为正品的概率. 18.(本小题满分12分)已知函数()sin cos f x x x =+,x ∈R . (Ⅰ)求12f π⎛⎫⎪⎝⎭的值; (Ⅱ)试写出一个函数()g x ,使得()()cos2g x f x x =,并求()g x 的单调区间. 19.(本小题满分12分)某几何体111C B A ABC -的三视图和直观图如图所示. (Ⅰ)求证:平面11AB C ⊥平面11AAC C ; (Ⅱ)若E 是线段1AB 上的一点,且满足1111191C B A ABC C AA E V V --=,求AE 的长.20.(本小题满分12分)某工业城市按照“十二五”(2011年至2015年)期间本地区主要污染物排放总量控制要求,进行减排治污.现以降低SO 2的年排放量为例,原计划“十二五”期间每年的排放量都比上一年减少0.3万吨,已知该城市2011年SO 2的年排放量约为9.3万吨, (Ⅰ)按原计划,“十二五”期间该城市共排放SO 2约多少万吨?(Ⅱ)该城市为响应“十八大”提出的建设“美丽中国”的号召,决定加大减排力度.在2012年刚好按原计划完成减排任务的条件下,自2013年起,SO 2的年排放量每年比上一年减少的百分率为p ,为使2020年这一年的SO 2年排放量控制在6万吨以内,求p 的取值范围.(参考数据9505.0328≈,9559.0329≈). 21.(本小题满分12分)已知函数()2e xf x ax bx =++.(Ⅰ)当0,1a b ==-时,求()f x 的单调区间; (Ⅱ)设函数()f x 在点()(),P t f t ()01t <<处的切线为l ,直线l 与y 轴相交于点Q .若点Q 的纵坐标恒小于1,求实数a 的取值范围. 22.(本小题满分14分)某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线2:2E y px =,在抛物线上任意画一个点S ,度量点S的坐标俯视图侧(左)视图正(主)视图1A(),S S x y ,如图.(Ⅰ)拖动点S ,发现当4S x =时,4S y =,试求抛物线E 的方程;(Ⅱ)设抛物线E 的顶点为A ,焦点为F ,构造直线SF 交抛物线E 于不同两点S 、T ,构造直线AS 、AT 分别交准线于M 、N 两点,构造直线MT 、NS .经观察得:沿着抛物线E ,无论怎样拖动点S ,恒有MT //NS .请你证明这一结论.(Ⅲ)为进一步研究该抛物线E 的性质,某同学进行了下面的尝试:在(Ⅱ)中,把“焦点F ”改变为其它“定点(),0G g ()0g ≠”,其余条件不变,发现“MT 与NS 不再平行”.是否可以适当更改(Ⅱ)中的其它条件,使得仍有“MT //NS ”成立?如果可以,请写出相应的正确命题;否则,说明理由.2013年福建省普通高中毕业班质量检查 文科数学试题参考解答及评分标准说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分. 三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数.选择题和填空题不给中间分.一、选择题:本大题考查基础知识和基本运算.每小题5分,满分60分. 1.D 2.C 3.B 4.A 5.B 6.A 7.B 8.A 9.C 10.B 11.C 12.D二、填空题:本大题考查基础知识和基本运算.每小题4分,满分16分.13.8; 14.7; 15.01a <≤; 16.22n m -.三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17.本小题主要考查古典概型、统计等基础知识,考查数据处理能力、运算求解能力以及应用意识,考查必然与或然思想等.满分12分.解:(Ⅰ)因为11=+7+75+9+95=8=858555x x x y ⋅⋅+⋅+⋅+A B (7),(6+), 由=x x A B,得17x y +=. ① ………………………………………2分因为222211=1+1+0.25+1+2.25=1.1=4+8+0.25+0.25+855x y ⎡⎤--⎣⎦A B ,s ()s ()(), 由22=A Bs s ,得228+8=1x y --()(). ② …………………………………………4分由①②解得89x y =⎧⎨=⎩,,或98.x y =⎧⎨=⎩,因为x y <, 所以8x y ==. ………………………………………6分(Ⅱ) 记被检测的5件B 种元件分别为12345,,,,B B B B B ,其中2345,,,B B B B 为正品, 从中任取2件,共有10个基本事件,列举如下:()12,B B ,()13,B B ,()14,B B ,()15,B B ,()23,B B , ()24,B B ,()25,B B ,()34,B B ,()35,B B ,()45,B B , ………………………………………8分记“2件都为正品”为事件C ,则事件C 包含以下6个基本事件:()23,B B ,()24,B B ,()25,B B ,()34,B B ,()35,B B ,()45,B B .……………………………10分所以63()105P C ==,即2件都为正品的概率为35. ………………………………………12分 18.本小题主要考查三角函数的图象与性质、两角和与差三角公式、二倍角公式、三角函数的恒等变换等基础知识,考查运算求解能力,考查化归与转化思想等.满分12分.解法一:(Ⅰ)因为())4f x x π=+,………………………………………3分所以121243f ππππ⎛⎫⎛⎫=+==⎪ ⎪⎝⎭⎝⎭……………………………6分 (Ⅱ)()cos sin g x x x =-. …………………………………………………………7分 下面给出证明:因为()()22(cos sin )(sin cos )cos sin cos2,g x f x x x x x x x x =-+=-=所以()cos sin g x x x =-符合要求.……………………………………………………9分又因为()cos sin 4g x x x x π⎛⎫=-=+ ⎪⎝⎭,…………………………………………10分由222,4k x k πππππ+<+<+得3722,44k x k ππππ+<<+ 所以()g x 的单调递增区间为372244k k ππππ⎛⎫++ ⎪⎝⎭,k ∈Z .………………………………11分又由224k x k ππππ<+<+,得32244k x k ππππ-<<+, 所以()g x 的单调递减区间为32244k k ππππ⎛⎫-+⎪⎝⎭,,k ∈Z .………………………………12分 解法二:(Ⅰ)因为()21s i n 2,fx x =+⎡⎤⎣⎦所以231s i n 1262f ππ⎡⎤⎛⎫=+= ⎪⎢⎥⎝⎭⎣⎦,………………………………3分又因为0,12f π⎛⎫>⎪⎝⎭所以12f π⎛⎫=⎪⎝⎭6分 (Ⅱ)同解法一. 解法三:(Ⅰ)sin cos sin cos 1212123434f πππππππ⎛⎫⎛⎫⎛⎫=+=-+-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭sincoscossincoscossinsin34343434ππππππππ=-++…………………3分112222=-++=………………………………6分 (Ⅱ)同解法一.注:若通过()()cos 2xg x f x =得到()g x 或由()()(cos sin )(cos sin )g x f x x x x x =+-两边同时约去()f x 得到()g x 不扣分.19.本小题主要考查三视图、直线与直线、直线与平面、平面与平面的位置关系,几何体的体积等基础知识;考查空间想象能力、推理论证能力、运算求解能力;考查函数与方程思想、数形结合思想、化归与转化思想.满分12分.解法一:(Ⅰ)由三视图可知,几何体111C B A ABC -为三棱柱,侧棱1111C B A AA 底面⊥,1111C A C B ⊥,且41==AC AA ,2=BC .………………………………………2分 1111C B A AA 平面⊥ ,11111111,C B AA C B A C B ⊥∴⊂平面, …………………3分 11111111,A C A AA C A C B =⊥ ,1111ACC A C B 平面⊥∴.……………………5分又1111C AB C B 平面⊂ , C C AA C AB 1111平面平面⊥∴.………………………6分 (Ⅱ)过点E 作11//C B EF 交1AC 于F ,由(Ⅰ)知,11ACC A EF 平面⊥,即EF 为C AA E 1-三棱锥的高. ………7分1111191C B A ABC C AA E V V --= ,,9131111AA S EF S ABC C AA ⋅=⋅∴∆∆ ……………………8分1111442443292EF ⎛⎫⎛⎫∴⨯⨯⨯⨯=⨯⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭,解得32=EF .……………………9分在Rt ABC ∆中,AB ===,在1Rt ABB ∆中,16AB ===,……………………10分由111C B EF AB AE =, ……………………11分 得22326C B EFAB AE 111=⨯=⋅=. ……………………12分解法二:(Ⅰ)同解法一.(Ⅱ)过点E 作11//C B EF 交1AC 于F ,由(Ⅰ)知,11ACC A EF 平面⊥,即EF 为C AA E 1-三棱锥的高. ………7分11111111133C AA B C B A A C B A ABC V V V ---== ,111111113191C AA B C B A ABC C AA E V V V ---==∴ ………8分,313131111111C B S EF S C AA C AA ⋅⨯=⋅∴∆∆,3111C B EF =∴ ………9分 在AB C Rt ∆中,5224AB 2222=+=+=BC AC ,在1ABB Rt ∆中,()6452AB 222121=+=+=BB AB ,……………………10分由111C B EFAB AE =, ……………………11分 得2AB 31AE 1==. ……………………12分 20.本小题主要考查等差数列、等比数列等基础知识,考查运算求解能力和应用意识,考查函数与方程思想.满分12分.解:(Ⅰ)设“十二五”期间,该城市共排放SO 2约y 万吨,依题意,2011年至2015年SO 2的年排放量构成首项为9.3,公差为0.3-的等差数列,……………3分 所以()55159.3(0.3)=43.52y ⨯-=⨯+⨯-(万吨). 所以按计划“十二五”期间该城市共排放SO 2约43.5万吨.……………………6分 (2)由已知得, 2012年的SO 2年排放量9.60.32=9-⨯(万吨),……………………7分所以2012年至2020年SO 2的年排放量构成首项为9,公比为1p -的等比数列,…………………9分由题意得891p ⨯-()<6,即1p -<832, 所以10.9505p -<,解得 4.95%p >.所以SO 2的年排放量每年减少的百分率p 的取值范围4.95%1p <<<……………………12分21.本小题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查分类与整合思想、数形结合思想、化归与转化思想.满分12分.解:(Ⅰ)当0,1a b ==-时,()e x f x x =-,()e 1xf x '=-,……………………1分所以,当(,0x ∈-∞时,()0f x '<;当(0,x ∈+∞时,()0f x '>;……………………3分所以函数()f x 的单调递减区间为(),0-∞,单调递增区间为(0,)+∞.……………………4分(Ⅱ)因为()2xf x e ax b '=++,所以()(),P t f t 处切线的斜率()2tk f t e at b '==++,所以切线l 的方程为()()()22t t y e at bt e at b x t -++=++-,令0x =,得()21ty t e a t=-- ()01t << (5)分当01t <<时,要使得点Q 的纵坐标恒小于1,只需()211tt e at --<,即()2110tt e at -++>()01t <<.……………… 6分令()()211tg t t e at =-++,则()()2t g t t e a '=+,………………………………………………………… 7分 因为01t <<,所以1t e e <<, ①若21a ≥-即12a ≥-时,20te a +>, 所以,当()0,1t ∈时,()0g t '>,即()g t 在()0,1上单调递增, 所以()(0)0g t g >=恒成立,所以12a ≥-满足题意.………………………………8分 ②若2a e ≤-即2e a ≤-时,20te a +<,所以,当()0,1t ∈时,()0g t '<,即()g t 在()0,1上单调递减,所以()(0)0g t g <=,所以2ea ≤-不满足题意.………………………………………9分 ③若21e a -<<-即122e a -<<-时,0ln(2)1a <-<.则t 、()g t '、()g t 的关系如下表:所以()()l n (2)00g a g -<=,所以22a -<<-不满足题意.………………………………11分 综合①②③,可得,当12a ≥-时,()0g t >()01t <<时,此时点Q 的纵坐标恒小于1.…………12分22.本小题主要考查抛物线的标准方程、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想、数形结合思想等.满分14分.解法一:(Ⅰ)把4S x =,4S y =代入22y px =,得248p =,……………………2分所以2p =,………………………………………………………………………3分因此,抛物线E 的方程24y x =.…………………………………………………4分(Ⅱ)因为抛物线E 的焦点为()1,0F ,设()()1122,,,S x y T x y , 依题意可设直线:1l my x =-,由241y x my x ⎧=⎨=-⎩,得2440y my --=,则121244.y y m y y +=⎧⎨⋅=-⎩, ①……………………6分又因为11:AS y l y x x =,22:AT yl y x x =,所以111,y M x ⎛⎫-- ⎪⎝⎭,221,y N x ⎛⎫-- ⎪⎝⎭,所以12211,y MT x y x ⎛⎫=++⎪⎝⎭,21121,y NS x y x ⎛⎫=++ ⎪⎝⎭, ……………………7分 又因为()()1221121211y y y x y x x x ⎛⎫⎛⎫++-++ ⎪ ⎪⎝⎭⎝⎭……………………………………8分 2221121241411144y y y y y y ⎛⎫⎛⎫⎛⎫⎛⎫=++-++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭22122112*********4y y y y y y y y y y ⎛⎫⎛⎫=+++-+++ ⎪ ⎪⎝⎭⎝⎭()21121212144y y y y y y y y -=-+()22121212164y y y y y y ⎛⎫-=- ⎪⎝⎭, ②把①代入②,得()221212121604y y y y y y ⎛⎫--= ⎪⎝⎭, (10)分即()()12211212110y y y x y x x x ⎛⎫⎛⎫++-++= ⎪ ⎪⎝⎭⎝⎭,所以//MT NS ,又因为M 、T 、N 、S 四点不共线,所以MT //NS .……………………………………………11分(Ⅲ)设抛物线2:4E y x =的顶点为A ,定点()(),00G g g ≠,过点G 的直线l 与抛物线E 相交于S 、T 两点,直线AS 、AT 分别交直线x g =-于M 、N 两点,则MT //NS .……………………14分解法二:(Ⅰ)同解法一.(Ⅱ)因为抛物线E 的焦点为()1,0F ,设()()221122,2,,2S t t T t t ,……………………5分依题意,可设直线:1ST l my x =-,由241y x my x ⎧=⎨=-⎩得2440y my --=, 则1212224,224,t t m t t +=⎧⎨⋅=-⎩所以12124,1.t t m t t +=⎧⎨⋅=-⎩ (7)分又因为2:2AS l y t x =-,1:2AT l y t x =-, 所以()21,2M t -,()11,2N t -,………………………………………………………………………10分所以MT k =,0NS k =,………………………………………………………………………………10分又因为M 、T 、N、S四点不共线,所以MT //NS .…………………………………………………11分(Ⅲ)同解法一. 解法三:(Ⅰ)同解法一.(Ⅱ)因为抛物线E 的焦点为()1,0F ,设()()1122,,,S x y T x y , 依题意,设直线:1l my x =-,由241y xmy x ⎧=⎨=-⎩得2440y my --=,则121244y y my y +=⎧⎨⋅=-⎩,…………………………………………6分 又因为11:AS y l y x x =,22:AT yl y x x =,所以111,y M x ⎛⎫-- ⎪⎝⎭,221,y N x ⎛⎫-- ⎪⎝⎭, 又因为212y y x ⎛⎫-- ⎪⎝⎭221122224404y y y y y x y +=+=,……………………………………9分 所以212y y x =-,所以NS 平行于x 轴; 同理可证MT 平行于x 轴;又因为M、T、N、S四点不共线,所以MT//NS.…………………………………………………11分(Ⅲ)同解法一.…………………………………………………14分。
福建省莆田市高三毕业班教学质量检查数学(理)试题含解析.docx

2015年福建省莆田市高考数学一模试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给岀的四个选项中,只 有一项是符合题目要求的.把答案填涂在答题卡相应位置.1.下列函数中,为奇函数的是( )A. y=x+lB. y=x 2C. y=2xD. y=x|x|2. 己知曲R,复数z= (a-2i ) (1+i ) (i 为虚数单位)在复平面内对应的点为M,贝『沪0〃是“点M 在第四象限〃的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件3. 若a>0, b>0, a+b=l,则『=丄+丁的最小值是()a bA. 2 B ・ 3 C. 4 D. 5兀71IT兀A. x= --T-B. x=——C. x=—D. x=—24 8 45. 某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,俯视图是半径为 1的半圆,则其侧视图的面积是()4. 函数 y=sin (2x)图象的一条对称轴方程为(兀侧视图僻視图A冷B. C. 1 D. V36.阅读如图所示的程序框图,运行相应的程序,若输岀的貞的值等于126,则判断框中的①可以是( )【开始]S-0J-1「2束IA. i>4?B. i>5?C. i>6?D. i>7?7.若直线y=kx - k交抛物线y2=4x于A, B两点,且线段AB中点到y轴的距离为3,则|AB|= ( )A. 12B. 10C. 8D. 68.学校将5个参加知识竞赛的名额全部分配给高一年级的4个班级,其中甲班级至少分配2个名额,其它班级可以不分配或分配多个名额,则不同的分配方案共有( )A. 20 种B. 24 种C. 26 种D. 30 种9.常用以下方法求函数y=[f (x) ]g(x>的导数:先两边同取以e为底的对数(#2.71828..., 为自然对数的底数)得lny=g (x) Inf (x),再两边同时求导,得(x) Inf (x) +g(x) *[lnf (x) ]\ 即y~[f (x) ]g(x>{g# (x) Inf (x) +g (x) *[lnf (x) ]}运用此方法可以求函数h (x) =x x (x>0)的导函数.据此可以判断下列各函数值中最小的是( ) 1112A. h (三)B. h (-)C. h (三)D. h (-)3 e 2 e10.如图,AABC所在平面上的点P n (nGN*)均满足ZSPnAB与APnAC的而积比为3; 1, P^A 寺J吒(2Xn+l) P^C (其中,风}是首项为1的正项数列),则X5等于i=i+l( )A. 65B. 63C. 33D. 31二、填空题:本大题共5小题,每小题4分,共20分.把答案填写在答题卡的相应位置.11.集合A={x| ・1Vx<3}, B={x|x<l),贝ij AnB= _____________ .12.某工厂的某种型号的机器的使用年限x和所支出的维修费用y (万元)的统计资料如表:根据上表数据可得y与x之I'可的线性回归方程]=0.7x+?,据此模型估计,该机器使用年限y a 为14年时的维修费用约为_____________ 万元.(O^x^l13.向区域o<y< 1内随机投点,则该点与坐标原点连线的斜率大于1的概率[y>x2为____________ .2 214.已知圆O: x2+y2=l和双曲线C:七-七=1(a>0,b>0).若对双曲线C上任意一a b点A (点A在圆O外),均存在与圆O外切且顶点都在双曲线C上的菱形ABCD,则-a 1庐-------------- .fr胃7(\A x/15. 定义:fx] (xeR)表示不超过x 的最大整数.例如[1.5]=1, [-0.5]=- 1.给出下列结论: ① 函数y=Lsinx]是奇函数;② 函数y=[sinx]是周期为2n 的周期函数; ③ 函数y=[sinx] - cosx 不存在零点;④ 函数 y=[sinx]+[cosx]的值域是{・ 2, - 1, 0, 1}.其中正确的是 ____________ ・(填上所有正确命题的编号)三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.把 答案填在答题卡相应位置.16. 已知数列{如}的首项为1,前n 项和Sn 满足寸瓦fSn- pH (n>2). (I) 求Sn 与数列{%}的通项公式;(11)设恥盘 5贰),求使不等式叽+…也遗成立的最小正整数n ・一个周期内的图象时,列表并填入的部分数据如下表:X ① 23H5 3Hf (x)1「I(I )请直接写出①处应填的值,并求函数f (X )在区间,亏]上的值域;(II ) AABC 的内角 A, B, C 所对的边分别为 a, b, c,f (A+—) =1, b+c=4, a=^/7>求A ABC 的血积.17.已知函数 (o )>0)经化简后利用〃五点法〃画其在某f (x) =V^sinu )xcosu )x - cos?18. 甲、乙两位选手为为备战我市即将举办的“推广妈祖文化•印象莆田〃知识竞赛活动,进行针对性训练,近8次的训练成绩如下(单位:分): 甲 83 81 93 79 78 84 88 94 乙 87 89 89 77 74 78 88 98(I )依据上述数据,从平均水平和发挥的稳定程度考虑,你认为应派哪位选手参加?并说 明理rti ;(II )本次竞赛设置A 、B 两问题,规定:问题A 的得分不低于80分时答题成功,否则答 题失败,答题成功可获得价值100元的奖品,问题B 的得分不低于90分吋答题成功,否则 答题失败,答题成功可获得价值300元的奖品.答题顺序可自由选择,但答题失败则终止答 题.选手答题问题A, B 成功与否互不影响,且以训练成绩作为样本,将样本频率视为概率, 请问在(I )中被选中的选手应选择何种答题顺序,使获得的奖品价值更高?并说明理由.19. 如图,边长为2的正方形ABCD 绕AB 边所在直线旋转一定的角度(小于180。
【物理】福建省莆田一中2013届高三高考模拟试题03

莆田一中2013届高三理科综合物理模拟考试卷2013.5.28 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷。
第Ⅰ卷为必考题,第Ⅱ卷包括必考题和选考题两部分满分300分,考试时间150分钟可能用到的相对分子质量:H:1 C:12 N:14 O: 16 Na:23 Ba:137 S:.32 Fe:56第Ⅰ卷(选择题共108分)本卷共18题,每小题6分,共108分。
在每小题给出的四个选项中,只有一个选项符合题目要求。
13.如图(a)、(b)所示,当图中a、b两端与e、f两端分别加上220 V的交流电压时,测得c、d间与g、h间的电压均为110 V.若分别在c、d两端与g、h两端加上110 V的交流电压,则a、b与e、f间的电压为A.220 V,220 VB. 110 V,110 VC. 220 V,110 VD.220 V,014. 据报道,嫦娥二号探月卫星其环月飞行的高度距离月球表面100km,所探测到的有关月球的数据将比环月飞行高度为200km的嫦娥一号更加详细。
若两颗卫星环月运行均可视为匀速圆周运动,运行轨道如图所示。
则正确的是:A.嫦娥二号环月运行的周期比嫦娥一号更长B.嫦娥二号环月运行的角速度比嫦娥一号更大C.嫦娥二号环月运行时向心加速度比嫦娥一号更小D.嫦娥二号环月运行时线速度比嫦娥一号更小15. 沿x轴正向传播的一列简谐横波在t=0时刻的波形如图所示,P为介质中的一个质点,其平衡位置位于x=1.5m处,该波的传播速度为2.5m/s ,则t=0.8s时刻,质点PA.位置在x=3.5m处B.位移沿+y方向C.速度沿+y方向D.加速度沿+y方向16.如图所示,竖直直线为某点电荷Q 所产生的电场中的一条电场线,M 、N 是其上的两个点。
另有一带电小球q 自M 点由静止释放后开始运动,到达N 点时速度恰变为零。
由此可以判定A .Q 必为正电荷,且位于N 点下方B .M 点的电场强度小于N 点的电场强度C .M 点的电势高于N 点的电势D .q 在M 点的电势能大于在N 点的电势能17.如图所示,光滑水平平台上有一个质量为m 的物体,地面上的人用跨过定滑轮的绳子向右拉动物体,不计绳和滑轮的质量、滑轮的大小及滑轮的摩擦,人手离滑轮到竖直高度始终为h ,所分析的运动过程中,人的初位置在A 点,当人以速度v 从A 匀速运动到B 时,人离滑轮的水平距离为x ,下列说法正确的是A .在该运动过程中,物块向右做匀加速运动B .人运动到BC .在该运动过程中,人对物块做的功为212mvD .在该运动过程中,人对物块做的功为22222()mv x h x +18. 如图所示,一根轻质弹簧上端固定的,下端挂一质量为m 0的平盘,盘中有一物体,质量为m ,当盘静止时,弹簧的长度比其自然长度伸长了l ,现向下拉盘使弹簧再伸长△l 后停止,然后松手放开,设弹簧总处在弹性限度以内,则刚松手时盘对物体的支持力等于第Ⅱ卷必考部分N Mm 0g m m llB )(1 .0+∆+)(mg 1 .)(llA ∆+mgC.l l ∆gm m ll)( .D 0+∆本卷共10题,共157分。
福建省莆田市2013届高三数学上学期期末考试试题 理 新人教A版
2013届莆田第二十四中学高高三上学期期末考试理科数学〔总分为:150分, 时间:120分钟〕须知事项:1.答题前填写好自己的姓名、班级、座号等信息 2.请将答案正确填写在答题卡上第I 卷〔选择题共50分〕一、选择题:本大题共10小题,每一小题5分,共50分,在每一小题给出的四个选项中,只有一项为哪一项符合题目要求的. 1.0α<<π,且3tan 4α=,如此cos α等于〔〕 A .35-B .35C .45-D .452.假设等差数列{}n a 的前5项和525S =,如此3a 等于〔〕 A .3B .4C .5D .63.)(0360sin 2log 的值是〔〕 A .21B .23C .21-D .23-4.随机变量X 服从正态分布N (3,41),且P 〔X >27〕=0.1587,如此P (25≤X ≤27)=〔〕A .0.6588B .0.6883C .0.6826D .0.65865.右图给出一个算法的程序框图,该程序框图的功能是〔〕A .找出a 、b 、c 三个数中最大的数B .找出a 、b 、c 三个数中最小的数C .找出a 、b 、c 三个数中第二大的数D .把c 的值赋给a6.命题p :“x >0,如此a =1是x +ax≥2的充分必要条件〞,命题q :“∃x 0∈R,02020>-+x x 〞,如此如下命题正确的答案是( )A .命题“p ∧q 〞是真命题B .命题 “p ∧(⌝q )〞是真命题C .命题“(⌝p )∧q 〞是真命题D .命题“(⌝p )∧(⌝q )〞是真命题8.假设函数f (x )=sin2x +a cos2x 图象的一条对称轴方程为6x π=-,如此实数a 的值为( )A .BC .7.假设l m n 、、是空间中互不一样的直线,αβ、是不重合的两平面,如此如下命题中为真命题的是( )A .假设//,,l n αβαβ⊂⊂,如此//l nB .假设,l αβα⊥⊂,如此l β⊥C .假设,l n m n ⊥⊥,如此//l mD .假设,//l l αβ⊥,如此αβ⊥9.函数 f 〔x 〕的定义域为R ,其导函数f '〔x 〕的图象如图所 示,如此对于任意x 1,x 2∈R ( x 1≠x 2),如下结论正确的答案是〔〕 ①f 〔x 〕< 0恒成立;②(x 1-x 2)[ f 〔x 1〕-f 〔x 2〕] < 0; ③(x 1-x 2) [ f 〔x 1〕-f 〔x 2〕] > 0;④⎪⎭⎫⎝⎛+221x x f >12()()2f x f x ; ⑤⎪⎭⎫⎝⎛+221x x f <12()()2f x f x . A .①③ B .①③④ C .②④ D .②⑤ 10.椭圆)0(12222>>=+b a b y a x 的焦点为1F 和2F ,过点1F 的直线l 交椭圆于Q P ,两点,22,0PQ PF PQ PF =⋅=且,如此椭圆的离心率为〔〕A .12-B .36-C .236-D .263- 第2卷〔非选择题共100分〕二、填空题:本大题共5小题,每一小题4分,共20分,把答案填在答题卡相应位置. 11.复数122i ,43i z z =+=-在复平面内的对应点分别为点A 、B ,如此A 、B 的中点所对应的复数是.12.向量a = (1,2),b = (x ,1),c = a + b ,d = a - b ,假设c //d ,如此实数x 的值等于13.在531⎪⎪⎭⎫⎝⎛+x x 的展开式中的常数项为p ,如此=+⎰dx p x )3(10214.假设函数x x a x x f ln )(+-=〔a 为常数〕在定义域上是增函数,如此实数a 的取值范围是15.假设自然数n 使得作加法(1)(2)n n n ++++运算均不产生进位现象,如此称n 为“给力数〞,例如:32是“给力数〞,因323334++不产生进位现象;23不是 “给力数〞,因232425++产生进位现象.设小于1000的所有“给力数〞的各个数位上的数字组成集合A ,如此用集合A 中的数字可组成无重复数字的三位偶数的个数为_______________三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤. 16.〔本小题总分为13分〕某工厂共有工人40人,在一次产品大检查中每人 的产品合格率〔百分比〕绘制成频率分布直方图, 如下列图.(Ⅰ) 求合格率在[50,60〕内的工人人数; (Ⅱ)为了了解工人在本次大检查中产品不合格的情况,从合格率在[50,70〕内的工人中随机选取3人的合格率进展分析,用X 表示所选工人合格率在[ 60,70〕内的人数,求X 的分布列和数学期望.17.〔本小题总分为13分〕设函数)(cos sin 32sin cos )(22R x x x x x x f ∈+-=的最大值为M ,最小正周期为T . 〔1〕求M 、T ;〔2〕假设有10个互不相等的正数i x 满足),10,,2,1(10,)( =<=i x M x f i i π且求1210x x x +++的值.18.〔此题总分为13分〕在如图的多面体中,EF ⊥平面AEB ,AE EB ⊥,//AD EF ,//EF BC ,24BC AD ==,3EF =,2AE BE ==,G 是BC 的中点.(Ⅰ) 求证://AB平面DEG;(Ⅱ) 求二面角C DF E--的余弦值.19.(本小题总分为13分)如图,某旅游区拟在公路l〔南北向〕旁开发一个抛物线形的人工湖,湖沿岸上每一点到公路l的距离与到A处的距离相等,并在湖中建造一个三角形的游乐区MNC,三个顶点CNM,,都在湖沿岸上,直线通道MN经过A处。
2013年中考物理试题莆田
2013年莆田市初中毕业班质量检查试卷物理(满分:100分;考试时间:90分钟)注意:本试卷分为“试题”和“答题卡”两部分,答题时请按答题卡中的“注意事项”要求认真作答,答案写在答题卡上的相应位置。
一、单项选择题(每小题2分,共20分)1.人们在家中利用天线能接收到电视塔发射载有电视信号的( )A.超声波 B.次声波 c.电磁波 D.可见光2.新鲜的菠菜放两天就“蔫”了,其中水分的减少主要是因为水发生了( )A.液化 B.升华 C.凝固 D.蒸发3.据中央电视台“智力快车”节目介绍,蜜蜂飞行与空气摩擦能产生静电,因此蜜蜂在飞行中就可以吸引带正电的花粉。
关于飞行中的蜜蜂,以下说法正确的是( )A.蜜蜂带负电 B.蜜蜂带正电 C.空气不带电 D.空气带负电4.有一种新型“隐形坦克”,它先通过摄像机把坦克身后的景象自动拍摄下来,再用投影仪把拍摄到的画面同步投射在反光效果极佳的特制坦克外壳上,让敌人看到的只是一片“风景”,而决不会想到如此“风景”之下竟隐匿着战争利器。
关于“隐形坦克”,以下说法正确的是( )A.为了能在各个方向隐形,坦克表面发生的是光的反射B.摄像机的镜头相当于一个凹透镜C.隐形逼真的原因是坦克外壳涂上了吸光材料D.坦克手看到的始终是倒立、等大的实像5.下列关于水的理解,正确的是( )A.0℃的水内能为零 B.水温降低,内能一定减小C.水受热时,体积变大,密度变大 D.30℃的水比20~C的水所含的热量多6.一个滑轮组经改进后提高了机械效率,用它将同一物体匀速提升同样的高度,改进后与改进前相比( )A.有用功减少,总功减少 B.有用功增加,总功增加C.有用功不变,总功不变 D.有用功不变,总功减少7.如图是一种新型“风光互补”景观照明灯。
它“头顶”小风扇,“肩扛”光电池板,“腰挎”照明灯,“脚踩”蓄电池。
对于上述照明灯,下列解释合理的是( )A.光电池板是将电能转化为光能B.照明灯是将内能转化为电能C.小风扇利用风力发电,将机械能转化为电能D.蓄电池夜晚放电,将电能转化为化学能8.火车进站时,人若越过安全线,有可能被吸进轨道而发生危险,因此在火车站台上候车的乘客应站在安全线以外,因为火车通过时,人体与车辆之间( )A.空气流速比外侧快,压强减小 B.空气流速比外侧快,压强增大c.空气流速比外侧慢,压强减小 D.空气流速比外侧慢,压强增大9.如下图所示,下列用电器的额定电流最接近5 A的是( )A.家用电冰箱 B.电视机 C.节能灯 D.电压力锅10.如图所示的电蚊拍,具有灭蚊和照明等功能。
2013年福建省莆田市中考数学试题(含答案)
福建省莆田市2013年中考数学试卷一、精心选一选:本大题共8小题,每小题4分,共32分。
每小题给出的四个选项中有且只有一个选项是符合题目要求的,答对的得4分,答错、不答或答案超过一个的一律得0分。
1.2013的相反数是()A.2013 B.﹣2013 C.D.﹣2.下列运算正确的是()A.(a+b)2=a2+b2B.3a2﹣2a2=a2C.﹣2(a﹣1)=﹣2a﹣1 D.a6÷a3=a23.对于一组统计数据:2,4,4,5,6,9.下列说法错误的是()A.众数是4 B.中位数是5 C.极差是7 D.平均数是54.如图,一次函数y=(m﹣2)x﹣1的图象经过二、三、四象限,则m的取值范围是()A.m>0 B.m<0 C.m>2 D.m<25.如图是一个圆柱和一个长方体的几何体,圆柱的下底面紧贴在长方体的上底面上,那么这个几何体的俯视图可能是()A.B.C.D.6.如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于()A.55°B.70°C.125°D.145°7.如图,△ABC内接于⊙O,∠A=50°,则∠OB C的度数为()A.40°B.50°C.80°D.100°8.下列四组图形中,一定相似的是()A.正方形与矩形B.正方形与菱形C.菱形与菱形D.正五边形与正五边形二、细心填一填:本大题共8小题,每小题4分,共32分)9.不等式2x﹣4<0的解集是.10.小明同学在“百度”搜索引擎中输入“中国梦”,搜索到相关的结果个数约为8650000,将这个数用科学记数法表示为.11.如图,点B、E、C、F在一条直线上,AB∥DE,BE=CF,请添加一个条件,使△ABC≌△DEF.12.已知在R t△ABC中,∠C=90°,sinA=,则tanB的值为.13.(4分)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,5,1,2.则最大的正方形E的面积是.14.(4分)经过某个路口的汽车,它可能继续直行或向右转,若两种可能性大小相同,则两辆汽车经过该路口全部继续直行的概率为.15.(4分)如图,正方形ABCD的边长为4,点P在DC边上且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为.16.(4分)统计学规定:某次测量得到n个结果x1,x2,…,x n.当函数y=++…+取最小值时,对应x的值称为这次测量的“最佳近似值”.若某次测量得到5个结果9.8,10.1,10.5,10.3,9.8.则这次测量的“最佳近似值”为.三、耐心做一做:本大题共9小题,共86分。
福建省莆田市2013年初中毕业、升学考试数学试题(word版_含答案)
24、 (2013莆田)解:(1)∵抛物线y=ax 2+bx+c 与x 轴交于点A (﹣3,0)和点B (1,0),∴抛物线解析式为y=a (x+3)(x ﹣1)=ax 2+2ax ﹣3a ,∵y=a (x+3)(x ﹣1)=a (x 2+2x ﹣3)=a (x+1)2﹣4a, ∴顶点D 的坐标为(﹣1,﹣4a ); (2)如图1,①设AC 与抛物线对称轴的交点为E .∵抛物线y=ax 2+2ax ﹣3a 与y 轴交于点C , ∴C 点坐标为(0,﹣3a ).设直线AC 的解析式为:y=kx+t ,则:,解得:,∴直线AC 的解析式为:y=﹣ax ﹣3a ,∴点E 的坐标为:(﹣1,﹣2a ), ∴DE=﹣4a ﹣(﹣2a )=﹣2a ,∴S △ACD =S △CDE +S △ADE =×DE ×OA=×(﹣2a )×3=﹣3a ,∴﹣3a=3,解得a=﹣1,∴抛物线的解析式为y=﹣x 2﹣2x+3;②∵y=﹣x 2﹣2x+3, ∴顶点D 的坐标为(﹣1,4),C (0,3), ∵A (﹣3,0),∴AD 2=(﹣1+3)2+(4﹣0)2=20,CD 2=(﹣1﹣0)2+(4﹣3)2=2, AC 2=(0+3)2+(3﹣0)2=18,∴AD 2=CD 2+AC 2, ∴∠ACD=90°, ∴tan ∠DAC===,∵∠PAB=∠DAC , ∴tan ∠PAB=tan ∠DAC=.如图2,设y=﹣x 2﹣2x+3=﹣(x+1)2+4向右平移后的抛物线解析式为y=﹣(x+m )2+4,两条抛物线交于点P ,直线AP 与y 轴交于点F . ∵tan ∠PAB===,∴OF=1,则F 点的坐标为(0,1)或(0,﹣1). 分两种情况: (Ⅰ)如图2①,当F 点的坐标为(0,1)时,直线AF 的解析式为y=x+1,由,解得,(舍去),∴P 点坐标为(,),将P 点坐标(,)代入y=﹣(x+m )2+4,得=﹣(+m )2+4,解得m 1=﹣,m 2=1(舍去),∴平移后抛物线的解析式为y=﹣(x ﹣)2+4; (Ⅱ)如图2②,当F 点的坐标为(0,﹣1)时, 直线AF 的解析式为y=﹣x ﹣1,由,解得,(舍去),∴P 点坐标为(,﹣),将P 点坐标(,﹣)代入y=﹣(x+m )2+4,得﹣=﹣(+m )2+4,解得m 1=﹣,m 2=1(舍去), ∴平移后抛物线的解析式为y=﹣(x ﹣)2+4;综上可知,平移后抛物线的解析式为y=﹣(x ﹣)2+4或y=﹣(x ﹣)2+4.点评:此题是二次函数的综合题,考查了待定系数法求函数的解析式,二次函数的性质,勾股定理的逆定理,三角函数的定义,三角形的面积、两函数交点坐标的求法,函数平移的规律等知识,综合性较强,有一定难度,解题的关键是方程思想、数形结合思想与分类讨论思想的应用.25.(14分)(2013•莆田)解:(1)证明:若AC=BC,则△ABC为等腰直角三角形,如答图1所示,连接OD,则CD⊥AB,又∵DM⊥DN,∴∠1=∠2.在△AND与△CDM中,∴△AND≌△CDM(ASA),∴DM=DN.∵∠4+∠1=90°,∠1+∠3=90°,∴∠4=∠3,∵∠1+∠3=90°,∠3+∠5=90°,∴∠1=∠5,在△NED与△DFM中,∴△NED≌△DFM(ASA),∴NE=DF.∵△ANE为等腰直角三角形,∴AE=NE,∴AE=DF.(2)①答:AE=DF.证法一:由(1)证明可知:△DEN∽△MFD,∴,即MF•EN=DE•DF.同理△AEN∽△MFB,∴,即MF•EN=AE•BF.∴DE•DF=AE•BF,∴(AD﹣AE)•DF=AE•(BD﹣DF),∴AD•DF=AE•BD,∴AE=DF.证法二:如答图2所示,过点D作DP⊥BC于点P,DQ⊥AC于点Q.∵D为AB中点,∴DQ=PC=PB.易证△DMF∽△NDE,∴,易证△DMP∽△DNQ,∴,∴;易证△AEN∽△DPB,∴,∴,∴AE=DF.②答:DF=kAE.证法一:由①同理可得:DE•DF=AE•BF,∴(AE﹣AD)•DF=AE•(DF﹣BD)∴AD•DF=AE•BD∵BD=kAD∴DF=kAE.证法二:如答图3,过点D作DP⊥BC于点P,DQ⊥AC于点Q.易证△AQD∽△DPB,得,即PB=kDQ.由①同理可得:,∴;又∵,∴,∴DF=kAE.点评:本题是几何探究与证明综合题,考查了相似三角形与全等三角形的判定与性质.题中三个结论之间逐级递进,体现了从特殊到一般的数学思想.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
蓝园高级中学2013届高三年理科数学综合试卷(35)
一、选择题:本大题共10小题,每小题5分,共50分.
1.设全集1,2,3,4,5,6,2,4,6,2,3,5UAB,则AUBð等于( )
A.3,5 B.4,6 C.1,2,3,5 D.1,2,4,6
2.已知平面向量,1,2,1axb,若//ab,则实数x的值等于( )
A.2 B.-2 C.12 D.12
3.“1x”是“ln0x”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要
4.阅读如图所示的程序框图,运行相应的程序。若输入xi(i为虚数单位),
则输出的结果是( )
A.1 B.i C.-1 D.i
5.若某几何体的正视图、侧视图、俯视图完全相同,则该几何体的正视图不可
..
能.的是( )
6.任意画一个正方形,再将这个正方体各边的中点相连得到第二个正方
形,依此类推,这样一共画了4个正方形,如图所示。若向图形中随机投
一点,则所投点落在第四个正方形的概率是( )
A.24 B.14 C.18 D.116
7.抛物线24yx与过其焦点且垂直于x轴的直线的直线相交于A、B两
点,其准线与x轴的交点为M,则过,,MAB三点的圆的标准方程是( )
A.225xy B.2211xy C.2212xy D.2214xy
8.在ABC中,角,,ABC所对的边分别为,,abc。若1,2ab,且1CACB,则sinA的
值是( )
A.12 B. 24 C.34 D.2114
9.若不等式组31,31,0yxykxy表示的平面区域是一个等腰三角形区域,则直线1ykx
的倾斜角的大小是( )
A.030 B. 0030,75 C.0030,120 D.0075,120
10.对于函数fx,xD,若满足对任意正数,总存在正数,使得对任意12,xxD,
12
xx
,只要12xx,就有12fxfx,则称函数fx在定义域D内具有性质P。
下列四个函数:①2,0,2fxxx; ②1,0,2fxxx;
③2,0,2xfxx; ④24,0,,02.xfxxx
其中在定义域内具有性质P的函数的序号是( )
A.①② B.①③ C.②④ D.③④
二、填空题:本大题共5小题,每小题4分,共20分.把答案填写在答题卷的相应位置.
11.若1cos,0,2,则cos2 。
12.23abbc的展开式中22abc的系数是 。
13.已知a、b为实数,0ab,若函数1()sin12xxfxabab是奇函数,则1f的
最小值是 。
14.一组数据如茎叶图所示。若从中剔除2个数据,使得新数据组的平均数不变且方差最小,则剔
除的2个数据的积等于 。
15.已知P是双曲线22221(0,0)xyabab右支上异于顶点的一点,1F、2F分别是双曲线的左、
2
右焦点,M是12PFF的内切圆的圆心。若121212MPFMPFMFFSSS,则ba 。
三、解答题:本大题共6小题,共80分.
16.(本小题满分13分)
数列na的前n项和为nS,对*nN,点,nna恒在直线()2fxxk上,点,nnS恒在抛
物线2()gxaxx上,其中,ka为常数。
(1)求数列na的通项公式;
(2)求直线()fx与抛物线()gx所围成的封闭图形的面积。
17.(本小题满分13分)
某数学兴趣小组共10名学生,参加一次只有5道填空题的测试。填空第i题的难度计算公式为iiRPN(其
中iR为答对该题的人数,N为参加测试的总人数)。该次测试每道填空题的考前预估难度'ip及考后实测难
度iP的数据如下表:
题号 1 2 3 4 5
考前预估难度'ip
0.9 0.8 0.7 0.6 0.4
考后实测难度iP
0.8 0.8 0.7 0.7 0.2
(1)定义描述填空题难度预估值与实测值偏离程度的统计量为
222
*'''
11221nn
SpPpPpPn
,若
*
0.01S
,则称填空题的难度预估是合理
的,否则为不合理。请你判断该次测试中填空题的难度预估是否合理?并说明理由;
(2)从该小组中随机抽取2个考生,记被抽取的考生中第5题答对的人数为,求的分布列及
数学期望。
18.(本小题满分13分)
已知a为实数,函数3221()(2)3fxxxaax。
(1)当1a时,求函数()fx在0x处的切线方程;
(2)若函数()fx在区间1,2上单调递减,求(3)f的取值范围。
19.(本小题满分13分)
如图,正方体ABCD-A1B1C1D1的棱长为2,P为棱CD上的一点,且三棱锥A- CP D1的体积为23。
(1)求CP的长;
(2)求直线AD与平面APD1所成的角的正弦值;
(3)请直接写出正方体的棱上满足C1M∥平面APD1的所.有.点M的位置,并
任选其中的一点予以证明。
20.(本小题满分14分)
已知直线32230xy过椭圆2222:1(0)xyEabab的两个
顶点。
(1)求椭圆E的标准方程;
(2)F为椭圆E的左焦点,且P ),(00yx椭圆上的动点,过点M)0,41(0x作直线PF的垂线,垂足
为N,当0x变化时,线段PN的长度是否为定值?若是,请写出这个
定值,并证明你的结论;若不是,请说明理由。
21.(本小题满分14分)
湄洲湾港被誉为“世界不多,中国少有”的天然良港。港口各泊位
每天的水深(水面与洋底的距离)()fx(单位:米)与时间x(单位:小时)的函数关系近似地
满足()sin(,0,02)6fxAxBAB。在通常情况下,港口各泊位能正常进行额
定吨位的货船的装卸货任务,而当货船的吨位超过泊位的额定吨位时,货船需在涨潮时驶入航道,
靠近码头卸货,在落潮时返回海洋。
该港口某五万吨级泊位接到一艘七万吨货船卸货的紧急任务,货船将凌晨0点在该泊位开始卸货。
已知该泊位当天的最低水深12米,最大水深20米,并在凌晨3点达到最大水深。
(1)求该泊位当天的水深f(x)的解析式;
(2)已知该货船的吃水深度(船底与水面的距离)为12。5米,安全条例规定,当船底与洋底距
离不足1。5米时,货船必须停止卸货,并将船驶向较深的水域。据测算,一个装卸小队可使货船
吃水深度以每小时0。1米的速度减少。
(Ⅰ)如果只安排一装卸小队进行卸货,那么该船在什么时间必须停止卸货,并将船驶向较深的水
域(精确到小时)?
(Ⅱ)如果安排三个这样的装卸小队同时执行该货船的卸货任务,问能否连续不间断的完成卸货任
务?说明你的理由。
