2017第一学期高三理科期中考试
2017届高三上学期期中考试(理)数学试卷

四川省成都市石室中学2017届高三上学期期中考试数学(理)试卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一个是符合题目要求的. 1.若复数z 满足i 12i z =+,其中i 为虚数单位,则在复平面上复数z 对应的点的坐标为( ) A .(2,1)--B .(2,1)-C .(2,1)D .(2,1)-2.“2log (23)1x -<”是“48x >”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件 3.已知随机变量,E M 服从正态分布(1,1)N ,若(3)0.976P ξ<=,则(13)P ξ-<<=( )A .0.952B .0.942C .0.954?D .0.9604、若数列{}n a 的前n 项和为2n S kn n =+,且1039,a =则100a =( ) A .200B .199C .299D .3995.若π(0,)2α∈,若π4cos()65α+=,则πsin(2)6α+的值为( )ABCD6、在平面直角坐标系xOy 中,已知ABC ∆的顶点(0,4)A 和(0,4)C -,顶点B 在椭圆221925x y+=上,则sin()sin sin A C A C+=+( )A .35B .45C .54D .537.若,x y 满足4,20,24,x y x y x y +≤⎧⎪-≥⎨⎪+≥⎩则43y z x -=-的取值范围是( )A .(,4][3,)-∞-+∞UB .(,2][1,)-∞--+∞UC .[2,1]--D .[4,3]-8.从0,1,2,3,4,5,6这七个数字中选两个奇数和两个偶数,组成没有重复数字的四位数的个数为( ) A .432B .378C .180D .3629.已知函数()sin()(0,0π)f x x ωϕωϕ=+><<的最小正周期是π,将函数()f x 图象向左平移π3个单位长度后所得的函数过点π(,1)6-,则函数()sin()f x x ωϕ=+( )A .在区间ππ[,]63-上单调递减B .在区间ππ[,]63-上单调递增C .在区间ππ[,]36-上单调递减D .在区间ππ[,]36-上单调递增10.在ABC △中,D 是BC 中点,E 是AB 中点,CE 的交AD 于点,F 若EF u u u r,AB AC λμ=+u u u r u u u r 则λμ+=( ) A .16-B .16C .13-D .111.如图,在棱长为1的正方体1111ABCD A B C D -中,点E 是棱BC 的中点,点F 在棱1CC 上,且12CF FC =,P 是侧面四边形11BCC B 内一点(含边界),若1A P //平面AEF ,则直线1A P 与面11BCC B 所成角的正弦值的取值范围是( )A.B.C. D. 12.若存在两个正实数,x y ,使得等式2(2e )(ln ln )0x a y x y x +--=成立,其中e 为自然对数的底数,则实数a 的取值范围为( )A .11[,]2e-B .2(0,]eC .2(,0)[,)e-∞+∞U D .11(,)[,)2e -∞-+∞U二、填空题:本大题共4小题,每小题5分.13.已知()f x 是定义在R 上的奇函数,且当0x <时,()2x f x =,则4(log 9)f 的值为__________. 14.已知61()x ax+展开式的常数项是160,则由曲线2y x =和a y x =围成的封闭图形的面积为________________.15.若点O和点(F 分别是双曲线2221(0)x y a a-=>的对称中心和左焦点,点P 为双曲线右支上任意一点,则221PFOP +的取值范围为________________.16.定义在(0,)+∞上的函数()f x 满足:(1)当1,12x ⎡⎫∈⎪⎢⎣⎭时,13()|2|22f x x =--;(2)(2)2()f x f x =.设关于x 的函数()()F x f x a =-的零点从小到大一次为1x ,2x ,…,n x ,….若1(,1)2a ∈,则F1A C122n x x x +++=…________________.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)已知向量22,cos ),(1,2cos ),m x x n x =+=u r r 设函数()f x m n =u r rg .(Ⅰ)求函数()f x 的最小正周期及在ππ(,]62-上的值域;(Ⅱ)在ABC △中,,,a b c 分别是角,,A B C 的对边,若()4,4f A b ==,ABC ∆a 的值. 18.(本小题满分12分)如图,四边形ABCD是矩形,1,AB AD =E 是AD 的中点,BE 与AC 交于点F ,GF ⊥平面ABCD . (Ⅰ)求证:AF ⊥面BEG ;(Ⅱ)若AF FG =,求二面角E AG B --所成角的余弦值.19.(本小题满分12分)近年来我国电子商务行业迎来发展的新机遇.2016年双十一期间,某购物平台的销售业绩高达516亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.7,对服务的好评率为0.8,其中对商品和服务都做出好评的交易为120次.(Ⅰ)先完成关于商品和服务评价的2×2列联表,再判断能否在犯错误的概率不超过0.005的前提下,认为商品好评与服务好评有关?(Ⅱ)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量X :①求对商品和服务全好评的次数X 的分布列; ②求X 的数学期望和方差. 附临界值表:2K 的观测值:2()()()()()n ad bc k a b c d a c b d -=++++(其中n a b c d =+++)关于商品和服务评价的2×2列联表:GFEDCBA20.(本小题满分12分)已知椭圆Γ:221x y a b+=(0a b >>)的左顶点为A ,右焦点为2F ,过点2F 作垂直于x 轴的直线交该椭圆于,M N 两点,直线AM 的斜率为12.(Ⅰ)求椭圆Γ的离心率;(Ⅱ)若AMN △的外接圆在点M 处的切线与椭圆交于另一点D ,2F MD △的面积为67,求椭圆Γ的标准方程.21.(本小题满分12分)已知函数2e )))(((1x f x x ax a =-∈-R (Ⅰ)当1a ≤时,求()f x 的单调区间;(Ⅱ)当(0,)x ∈+∞时,()y f x '=的图象恒在32(1)y ax x a x -=+-的图象上方,求a 的取值范围.22.(本小题满分10分)选修4-4:坐标系与参数方程已知直线l 过点(1,0)且倾斜角为α,在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系,曲线M 的方程为2sin 4cos 0.ρθθ+=(1)写出曲线M 的直角坐标方程及直线l 的参数方程; (2)若直线l 与曲线M 只有一个公共点,求倾斜角α的值.。
2017朝阳高三第一学期期中理科考试

北京市朝阳区2017-2018学年度第一学期高三年级期中统一考试数学试卷(理工类) 2017.11(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1. 已知集合{|1}A x x =>,2{|log 1}B x x =>,则A B =A. {|1}x x >B. {|12}x x <<C. {|2}x x >D. {|0}x x >2. 已知实数,x y 满足条件2,2,6,x y x y ≥⎧⎪≥⎨⎪+≤⎩则2x y +的最大值为A. 12B. 10C. 8D. 63.要得到函数πsin(2)3y x =-的图象,只需将函数sin y x =的图象上所有的点 A. 先向右平移π3个单位长度,再将横坐标伸长为原来的2倍,纵坐标不变 B. 先向右平移π6个单位长度,横坐标缩短为原来的12倍,纵坐标不变 C. 横坐标缩短为原来的12倍,纵坐标不变,再向右平移π6个单位长度 D. 横坐标变伸长原来的2倍,纵坐标不变,再向右平移π3个单位长度 4. 已知非零平面向量,a b ,则“+=+a b a b ”是“存在非零实数λ,使λb =a ”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件5.已知n S 是等差数列{}n a (n *∈N )的前n 项和,且564S S S >>,以下有四个命题: ①数列{}n a 中的最大项为10S ②数列{}n a 的公差0d <③100S > ④110S <其中正确的序号是( )A. ②③B. ②③④C. ②④D. ①③④6. 如图,在直角梯形ABCD 中,AB //CD ,AD DC ⊥,E 是CD 的中点1DC =,2AB =,则EA AB ⋅=B. C.1 D.1-7. 袋子里有编号为2,3,4,5,6的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,再让甲、乙分别推断这两个球的编号. 甲说:“我无法确定.”乙说:“我也无法确定.”甲听完乙的回答以后,甲说:“我现在可以确定两个球的编号了.”根据以上信息, 你可以推断出抽取的两球中A .一定有3号球 B.一定没有3号球 C.可能有5号球 D.可能有6号球8. 已知函数()sin(cos )f x x x =-与函数()cos(sin )g x x x =-在区间(0)2π,都为减函数,设123,,(0)2x x x π∈,,且11cos x x =,22sin(cos )x x =,33cos(sin )x x =,则123,,x x x 的大小关系是( )A. 123x x x <<B. 312x x x <<C. 213x x x <<D. 231x x x <<第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.9. 执行如下图所示的程序框图,则输出i 的值为 .(第9题图)10. 已知1x >,且1x y -=,则1x y+的最小值是 . 11. 已知函数1211(),,22()1log ,.2x x f x x x ⎧≤⎪⎪=⎨⎪>⎪⎩若()f x 的图象与直线y kx =有两个不同的交点,则实数k 的取值范围为 .12. 已知函数()f x 同时满足以下条件:① 定义域为R ;② 值域为[0,1];③ ()()0f x f x --=.试写出一个函数解析式()f x = .13. 某罐头生产厂计划制造一种圆柱形的密封铁皮罐头盒,其表面积为定值S . 若罐头盒的底面半径为r ,则罐头盒的体积V 与r 的函数关系式为 ;当r = 时,罐头盒的体积最大.14. 将集合=M {}1,2,3,...,15表示为它的5个三元子集(三元集:含三个元素的集合)的并集,并且这些三元子集的元素之和都相等,则每个三元集的元素之和为 ;请写出满足上述条件的集合M 的5个三元子集 . (只写出一组)三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15. (本小题满分13分)已知数列{}n a 的前n 项和为n S (n *∈N ),满足21n n S a =-. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列{}n b 满足12=log n n b a ,求数列{}n b 的前n 项和n T .16. (本小题满分13分) 已知函数π()2sin cos()3f x x x =⋅-.(Ⅰ)求函数()f x 的最小正周期; (Ⅱ)当π[0,]2x ∈时,求函数()f x 的取值范围.17. (本小题满分13分)在ABC △中,π4A =,c b= (Ⅰ)试求tan C 的值;(Ⅱ)若5a =,试求ABC △的面积.18. (本小题满分14分)已知函数2()()e x f x x ax a -=-+⋅,a ∈R .(Ⅰ)求函数()f x 的单调区间;(Ⅱ)设()()g x f x '=,其中()f x '为函数()f x 的导函数.判断()g x 在定义域内是否为单调函数,并说明理由.19. (本小题满分14分) 已知函数12()ln e e x f x x x=--. (Ⅰ)求曲线()y f x =在点()1,(1)f 处的切线方程; (Ⅱ)求证:1ln e x x≥-; (Ⅲ)判断曲线()y f x =是否位于x 轴下方,并说明理由.20. (本小题满分13分)数列12,,,n a a a 是正整数1,2,,n 的任一排列,且同时满足以下两个条件:①11a =;②当2n ≥时,1||2i i a a +-≤(1,2,,1i n =- ).记这样的数列个数为()f n .(I )写出(2),(3),(4)f f f 的值;(II )证明(2018)f 不能被4整除.。
山东省烟台市2017届高三(上)期中数学试卷(理科)(解析版).doc

2016-2017学年山东省烟台市高三(上)期中数学试卷(理科)参考答案与试题解析一、选择题:本大题共10个小题,每小题5分,共50分.每小题给出的四个选项中只有一项是符合题目要求的,把正确选项的代号涂在答题卡上.1.已知全集U={1,2,3,4,5},M={3,4,5},N={2,3},则集合(∁U N)∩M=()A.{2} B.{1,3} C.{2,5} D.{4,5}【考点】交、并、补集的混合运算.【分析】求出N的补集,然后求解交集即可.【解答】解:全集U={1,2,3,4,5},N={2,3},则集合∁U N={1,4,5},M={3,4,5},集合(∁U N)∩M={4,5}.故选:D.2.已知向量与不平行,且||=||≠0,则下列结论中正确的是()A.向量与垂直B.向量与垂直C.向量与垂直D.向量与平行【考点】数量积判断两个平面向量的垂直关系;平行向量与共线向量.【分析】求出()•()=0,从而得到与垂直.【解答】解:∵向量与不平行,且||=||≠0,∴()•()==||2﹣||2=0,∴与垂直.故选:A.3.已知函数f(x)=1g(1﹣x)的值域为(﹣∞,0),则函数f(x)的定义域为()A.[0,+∞] B.(0,1)C.[﹣9,+∞)D.[﹣9,1)【考点】函数的定义域及其求法.【分析】由函数f(x)=1g(1﹣x)的值域为(﹣∞,0),则lg(1﹣x)<0,即有0<1﹣x <1,解得即可得到函数的定义域.【解答】解:由函数f(x)=1g(1﹣x)的值域为(﹣∞,0),则lg(1﹣x)<0,∴0<1﹣x<1,解得,0<x<1.则函数f(x)的定义域为:(0,1).故选:B.4.如果a>b,那么下列不等式中正确的是()A.B.a2>b2C.lg(|a|+1)>lg(|b|+1)D.2a>2b【考点】不等式的基本性质.【分析】通过取特殊值判断A、B、C,根据指数的性质判断D.【解答】解:若a>b,对于A:a=0,b=﹣1,时,无意义,错误;对于B,C:若a=1,b=﹣2,不成立,错误;对于D:2a>2b,正确;故选:D.5.曲线y=x3与直线y=x所围成图形的面积为()A.B.C.1 D.2【考点】定积分在求面积中的应用.【分析】先求出曲线y=x3与y=x的交点坐标,得到积分的上下限,然后利用定积分求出第一象限所围成的图形的面积,根据图象的对称性可求出第三象限的面积,从而求出所求.【解答】解:曲线y=x3与y=x的交点坐标为(0,0),(1,1),(﹣1,﹣1)曲线y=x3与直线y=x在第一象限所围成的图形的面积是==根据y=x3与y=x都是奇函数,关于原点对称,在第三象限的面积与第一象限的面积相等∴曲线y=x3与y=x所围成的图形的面积为故选B6.若x,y满足且z=2x+y的最大值为4,则k的值为()A.B.C.D.【考点】简单线性规划.【分析】根据已知的约束条件画出满足约束条件的可行域,再用目标函数的几何意义,求出求出直线2x+y=4与y=0相交于B(2,0),即可求解k值.【解答】解:先作出不等式组对应的平面区域,直线kx﹣y+3=0过定点(0,3),∵z=2x+y的最大值为4,∴作出直线2x+y=4,由图象知直线2x+y=4与y=0相交于B(2,0),同时B也在直线kx﹣y+3=0上,代入直线得2k+3=0,即k=,故选:A.7.设函数f(x)=xsinx+cosx的图象在点(t,f(t))处切线的斜率为k,则函数k=g(t)的图象大致为()A.B. C.D.【考点】函数的图象.【分析】由已知可得k=g(t)=f′(x)=xcosx,分析函数的奇偶性及x∈(0,)时,函数图象的位置,利用排除法,可得答案.【解答】解:∵函数f(x)=xsinx+cosx的图象在点(t,f(t))处切线的斜率为k,∴k=g(t)=f′(x)=sinx+xcosx﹣sinx=xcosx,函数为奇函数,图象关于原点对称,排除B,C,当x∈(0,)时,函数值为正,图象位于第一象限,排除D,故选:A.8.将函数y=sin(ωx+φ)(ω>0,|φ|<π的图象向左平移个单位,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为y=sinx,则y=sin(ωx+φ)图象上离y轴距离最近的对称中心为()A.(,0)B.(π,0)C.(﹣,0)D.(﹣,0)【考点】函数y=Asin(ωx+φ)的图象变换.【分析】函数y=sin(ωx+φ)(ω>0,|φ|<π的图象向左平移个单位,得到函数y=sin[ω(x+)+φ]的图象;再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=sin(ωx+ω+φ)的图象;由解析式相同求出ω、φ的值,然后根据正弦函数的对称中心求出函数y=sin(ωx+φ)的对称中心,进而求出离y轴距离最近的对称中心.【解答】解:将函数y=sin(ωx+φ)(ω>0,|φ|<π的图象向左平移个单位,得到函数y=sin[ω(x+)+φ]的图象;再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=sin(ωx+ω+φ)的图象;∴函数y=sin(ωx+ω+φ)的图象与函数y=sinx的图象相同∴,φ=0解得:ω=2,φ=∴y=sin(ωx+φ)=sin(2x)由2x=kπ得2x=k(k∈Z)当k=﹣1时,x=﹣∴离y轴距离最近的对称中心为(﹣,0).故选C.9.已知△ABC外接圆的半径为2,圆心为O,且,则=()A.12 B.13 C.14 D.15【考点】平面向量数量积的运算.【分析】由条件便可得出AB⊥AC,O为斜边的中点,再根据,即可得出,进而得出的值,从而求出的值.【解答】解:根据条件,AB⊥AC,O为BC中点,如图所示:;∴△ABO为等边三角形,,,,;∴.故选A.10.在实数集R上定义一种运算“*”,对于任意给定的a、b∈R,a*b为唯一确定的实数,且具有性质:(1)对任意a、b∈R,a*b=b*a;(2)对任意a、b∈R,a*0=a;(3)对任意a、b∈R,(a*b)*c=c*(ab)+(a*c)+(c*b)﹣2c.关于函数f(x)=x*的性质,有如下说法:①在(0,+∞)上函数f(x)的最小值为3;②函数f(x)为奇函数;③函数f(x)的单调递增区间为(﹣∞,﹣1),(1,+∞).其中所有正确说法的个数为()A.0 B.1 C.2 D.3【考点】抽象函数及其应用.【分析】根据条件在③中令c=0得到a*b=ab+a+b从而得到f(x)的表达式,结合函数的奇偶性,单调性和最值的性质分别进行判断即可.【解答】解:①由新运算“*”的定义③令c=0,则(a*b)*0=0*(ab)+(a*0)+(0*b)=ab+a+b,即a*b=ab+a+b∴f(x)=x*=1+x+,当x>0时,f(x)=x*=1+x+≥1+2=1+2=3,当且仅当x=,即x=1时取等号,∴在(0,+∞)上函数f(x)的最小值为3;故①正确,②函数的定义域为(﹣∞,0)∪(0,+∞),∵f(1)=1+1+1=3,f(﹣1)=1﹣1﹣1=﹣1,∴f(﹣1)≠﹣f(1)且f(﹣1)≠f(1),则函数f(x)为非奇非偶函数,故②错误,③函数的f′(x)=1﹣,令f′(x)=0则x=±1,∵当x∈(﹣∞,﹣1)或(1,+∞)时,f′(x)>0∴函数f(x)的单调递增区间为(﹣∞,﹣1)、(1,+∞).故③正确;故正确的是①③,故选:C二、填空题,本大题共5个小题,每小题5分,共25分.11.已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为a<﹣3或a >6.【考点】函数在某点取得极值的条件.【分析】先求出函数的导数,根据函数有极大值和极小值,可知导数为0的方程有两个不相等的实数根,通过△>0,即可求出a的范围.【解答】解:函数f(x)=x3+ax2+(a+6)x+1,所以函数f′(x)=3x2+2ax+(a+6),因为函数有极大值和极小值,所以方程f′(x)=0有两个不相等的实数根,即3x2+2ax+(a+6)=0有两个不相等的实数根,∴△>0,∴(2a)2﹣4×3×(a+6)>0,解得:a<﹣3或a>6故答案为:a<﹣3或a>612.平面向量与的夹角为60°,||=1,=(3,0),|2+|=.【考点】平面向量数量积的运算.【分析】由条件可以得到,从而进行数量积的运算便可求出的值,从而便可得出的值.【解答】解:根据条件,,;∴;∴.故答案为:.13.设函数f(x)=若f(a)>a,则实数a的取值范围是(﹣∞,﹣1).【考点】其他不等式的解法.【分析】先根据分段函数的定义域选择好解析式,分a≥0时,和a<0时两种情况求解,最后取并集.【解答】解:当a≥0时,,解得a<﹣2,矛盾,无解当a<0时,,a<﹣1.综上:a<﹣1∴实数a的取值范围是(﹣∞,﹣1).故答案为:(﹣∞,﹣1)14.若cos(75°﹣a)=,则cos(30°+2a)=.【考点】两角和与差的余弦函数;三角函数的化简求值.【分析】由条件利用诱导公式,求出sin(15°﹣α)的值,再利用二倍角的余弦公式求得cos (30°﹣2α)的值.【解答】解:∵cos(75°﹣α)=sin(15°+α)=,则cos(30°+2α)=1﹣2sin2(15°+α)=1﹣2×=.故答案为:.15.若定义在R上的偶函数f(x)满足f(x﹣1)=f(x+1).且当x∈[﹣1,0]时,f(x)=﹣x2+1,如果函数g(x)=f(x)﹣a|x|恰有8个零点,则实数a的值为8﹣2.【考点】根的存在性及根的个数判断.【分析】由函数f(x)满足f(x+1)=﹣f(x),变形得到函数的周期,由周期性即可求得函数在某一段上的解析式,代入进行计算即可得出答案.【解答】解:由f(x+1)=f(x﹣1),则f(x)=f(x﹣2),故函数f(x)为周期为2的周期函数.∵函数g(x)=f(x)﹣a|x|恰有8个零点,∴f(x)﹣a|x|=0在(﹣∞,0)上有四个解,即f(x)的图象(图中黑色部分)与直线y=a|x|(图中红色直线)在(﹣∞,0)上有4个交点,如图所示:又当x∈[﹣1,0]时,f(x)=﹣x2+1,∴当直线y=﹣ax与y=﹣(x+4)2+1相切时,即可在(﹣∞,0)上有4个交点,∴x2+(8﹣a)x+15=0,∴△=(8﹣a)2﹣60=0.∵a>0,∴a=8﹣2.故答案为:8﹣2.三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.16.已知函数f(x)=cos2x,g(x)=sinxcosx.(1)若直线x=a是函数y=f(x)的图象的一条对称轴,求g(2a)的值;(2)若0≤x≤,求h(x)=f(x)+g(x)的值域.【考点】三角函数的最值.【分析】(1)利用二倍角公式化简函数的表达式,通过直线x=a是函数y=f(x)的图象的一条对称轴,求出a,然后求g(2a)的值;(2)化简h(x)=f(x)+g(x)为正弦函数类型,利用角的范围求出相位的范围,然后去函数值域.【解答】解:(1),其对称轴为,因为直线线x=a是函数y=f(x)的图象的一条对称轴,所以,又因为,所以即.(2)由(1)得=∵,∴,∴.所以h(x)的值域为.17.设△ABC的内角A、B、C的对应边分别为a、b、c,若向量=(a﹣b,1)与向量=(a﹣c,2)共线,且∠A=120°.(1)a:b:c;(2)若△ABC外接圆的半径为14,求△ABC的面积.【考点】正弦定理.【分析】(1)利用向量共线的性质可得2b=a+c,设a=b﹣d,c=b+d,由余弦定理解得d=﹣,进而可得a=,c=,从而可求a:b:c.(2)由正弦定理可求a,由(1)可求b,c的值,利用三角形面积公式即可计算得解.【解答】解:(1)∵向量与向量共线,可得:,∴2b=a+c,设a=b﹣d,c=b+d,由已知,cosA=﹣,即=﹣,d=﹣,从而a=,c=,∴a:b:c=7:5:3.(2)由正弦定理=2R,得a=2RsinA=2×14×=14,由(1)设a=7k,即k=2,所以b=5k=10,c=2k=6,所以S△ABC=bcsinA=×10×6×=45,所以△ABC的面积为45.18.如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米.(1)当x,y为何值时?游客体验活动区APQ的面积最大,并求最大面积;(2)当x,y为何值时?线段|PQ|最小,并求最小值.【考点】余弦定理;正弦定理.【分析】(1)由已知利用三角形面积公式,基本不等式可得,即可得解.(2)利用已知及余弦定理可得PQ2=x2+y2﹣2xycos120°=(x﹣100)2+30000,根据二次函数的图象和性质即可解得线段|PQ|最小值.【解答】(本题满分为14分)解:(1)因为:AP=x,AQ=y且x+y=200,…2分所以:.…4分当且仅当x=y=100时,等号成立.所以:当x=y=100米时,平方米.…6分(2)因为:PQ2=x2+y2﹣2xycos120°=x2+y2+xy…8分=x2+2+x=x2﹣200x+40000=(x﹣100)2+30000.…10分所以:当x=100米,线段米,此时,y=100米.…12分答:(1)当AP=AQ=100米时,游客体验活动区APQ的面积最大为平方米.(2)当AP=AQ=100米时,线段|PQ|最小为.…14分.19.已知函数f(x)=log()满足f(﹣2)=1,其中a为实常数.(1)求a的值,并判定函数f(x)的奇偶性;(2)若不等式f(x)>()x+t在x∈[2,3]上恒成立,求实数t的取值范围.【考点】函数恒成立问题.【分析】(1)根据f(﹣2)=1,构造方程,可得a的值,结合奇偶性的宝义,可判定函数f (x)的奇偶性;(2)若不等式f(x)>()x+t在x∈[2,3]上恒成立,则t<log()﹣()x 在x∈[2,3]上恒成立,构造函数求出最值,可得答案.【解答】解:(1)∵函数f(x)=log()满足f(﹣2)=1,∴log()=1,∴=,解得:a=﹣1,∴f(x)=log()的定义域(﹣∞,﹣1)∪(1,+∞)关于原点对称;又∵f(﹣x)=log()=log()=﹣log()=﹣f(x),故函数f(x)为奇函数;(2)若不等式f(x)>()x+t在x∈[2,3]上恒成立,则t<log()﹣()x在x∈[2,3]上恒成立,设g(x)=log()﹣()x,则g(x)在[2,3]上是增函数.∴g(x)>t对x∈[2,3]恒成立,∴t<g(2)=﹣.20.设函数f(x)=xe x﹣ae2x(a∈R)(I)当a≥时,求证:f(x)≤0.(II)若函数f(x)有两个极值点,求实数a的取值范围.【考点】利用导数研究函数的极值;利用导数求闭区间上函数的最值.【分析】(Ⅰ)利用分析法,构造函数g(x)=x﹣ae x,利用导数和函数的最值的关系即可求出,(Ⅱ)函数f(x)有两个极值点,等价于y=f'(x)有两个变号零点,即方程有两个不相同的根,构造函数,利用导数求出函数的最值,问题得以解决.【解答】解:(I)证明:f(x)=xe x﹣ae2x=e x(x﹣ae x)∵e x>0,只需证:当即可﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣,g(x)=x﹣ae x,g'(x)=1﹣ae x=0∴,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣,﹣﹣﹣﹣﹣﹣,∴当从而当时,f(x)≤0﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(II)f'(x)=(x+1)e x﹣2ae2x=e x(x+1﹣2ae x)函数f(x)有两个极值点,等价于y=f'(x)有两个变号零点即方程有两个不相同的根﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣设,,x∈(﹣∞,0),h'(x)>0,h(x)递增;x∈(0,+∞),h'(x)<0,h(x)递减﹣﹣﹣﹣﹣﹣﹣﹣,h(x)max=h(0)=1,h(﹣1)=0﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣,x>﹣1,h(x)>0,x→+∞,h(x)→0,x→﹣∞,h(x)→﹣∞当有两个交点方程有两个不相同的根,函数f(x)有两个极值点﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣21.已知函数f(x)=(2﹣a)lnx++2ax(a∈R).(Ⅰ)当a=0时,求f(x)的极值;(Ⅱ)当a<0时,求f(x)单调区间;(Ⅲ)若对任意a∈(﹣3,﹣2)及x1,x2∈[1,3],恒有(m+ln3)a﹣2ln3>|f(x1)﹣f (x2)|成立,求实数m的取值范围.【考点】利用导数求闭区间上函数的最值;函数恒成立问题;利用导数研究函数的单调性;利用导数研究函数的极值.【分析】(Ⅰ)当a=0时,f(x)=2lnx+,求导,令f′(x)=0,解方程,分析导数的变化情况,确定函数的极值;(Ⅱ)当a<0时,求导,对导数因式分解,比较两根的大小,确定函数f(x)单调区间;(Ⅲ)若对任意a∈(﹣3,﹣2)及x1,x2∈[1,3],恒有(m+ln3)a﹣2ln3>|f(x1)﹣f (x2)|成立,求函数f(x)的最大值和最小值,解不等式,可求实数m的取值范围.【解答】解:(Ⅰ)依题意知f(x)的定义域为(0,+∞),当a=0时,f(x)=2lnx+,f′(x)=﹣=,令f′(x)=0,解得x=,当0<x<时,f′(x)<0;当x≥时,f′(x)>0又∵f()=2﹣ln2∴f(x)的极小值为2﹣2ln2,无极大值.(Ⅱ)f′(x)=﹣+2a=当a<﹣2时,﹣<,令f′(x)<0 得0<x<﹣或x>,令f′(x)>0 得﹣<x<;当﹣2<a<0时,得﹣>,令f′(x)<0 得0<x<或x>﹣,令f′(x)>0 得<x<﹣;当a=﹣2时,f′(x)=﹣≤0,综上所述,当a<﹣2时f(x),的递减区间为(0,﹣)和(,+∞),递增区间为(﹣,);当a=﹣2时,f(x)在(0,+∞)单调递减;当﹣2<a<0时,f(x)的递减区间为(0,)和(﹣,+∞),递增区间为(,﹣).(Ⅲ)由(Ⅱ)可知,当a∈(﹣3,﹣2)时,f(x)在区间[1,3]上单调递减,当x=1时,f(x)取最大值;当x=3时,f(x)取最小值;|f(x1)﹣f(x2)|≤f(1)﹣f(3)=(1+2a)﹣[(2﹣a)ln3++6a]=﹣4a+(a﹣2)ln3,∵(m+ln3)a﹣ln3>|f(x1)﹣f(x2)|恒成立,∴(m+ln3)a﹣2ln3>﹣4a+(a﹣2)ln3整理得ma>﹣4a,∵a<0,∴m<﹣4恒成立,∵﹣3<a<﹣2,∴﹣<﹣4<﹣,∴m≤﹣2016年12月20日。
2017届高三数学上学期期中试题理

2017届高三数学上学期期中试题理数学试卷(理)注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
其中第Ⅰ卷满分60分,第Ⅱ卷满分90分。
本试卷满分150分,考试时间为120分钟。
2、答卷前,考生务必将自己的姓名、班级、写在答题卡上。
3、将第Ⅰ卷选出答案后,和第二卷答案都写在答题卡相应标号位置,答错位置不得分。
第Ⅰ卷一、选择题(每题只有一个正确选项,每题5分共60分)1. 若集合,则等于( ){}{}Ax x y y B x x N x A ∈-==>-+∈=,4,0452B A ⋃A. B. C. D.B {}4,2,1{}4,3,2,1{}4,3,2,1,0,1-2.若tan α=,则cos2α+2sin 2α等于()43A .B .C . 1D .2548256425163.已知△ABC 中,的对边分别为.若,且,则()A . 2B .C .D .4.曲线与直线及所围成的封闭图形的面积为()x y 2=1-=x y 4=xA. B. C. D.2ln 22ln 2-2ln 4-2ln 24-5.给出如下四个命题:①若“”为假命题,则均为假命题;q p ∧q p ,②命题“若”的否命题为“若”;122,b ->>a b a 则122,a -≤≤bb a 则 ③命题“任意”的否定是“存在”;01,2≥+∈x R x 01,200<+∈x R x④函数在处导数存在,若p :;q :x=x0是的极值点,则是的必要条件,但不是的充分条件;其中真命题的个数是()()f x 0x =x ()00/=x f ()f x p q qA.1B.2C.3D. 46.已知=(1,sin2x),=(2,sin2x),其中x ∈(0,π),若,则tanx的值等于() A .-1 B . 1 C .D .→a →b ||||||→→→←=⋅b a b a227.已知是平面内两个互相垂直的单位向量,若向量满足,则||的最大值是().←←b a ,0)()(=-⋅-→→←←c b c aA . 1B . 2C .D .2228.某班文艺晚会,准备从A,B 等8个节目中选出4个节目,要求:A,B。
中学2017届高三上学期期中考试理科综合化学试题(附答案)

2017届潮师高中高三级期中考试理科综合-化学试题可能用到的相对原子质量:H-1 C-12 O-16 Mg-24 Cu-64 Fe-56 Br-807.设N A表示阿伏加德罗常数值,下列说法正确的是A.1L 0.1mol/L的NaHCO3溶液中HCO3-和CO32-离子数之和为0.1N AB.标准状况下,22.4L C2H4与C3H6混合气体所含有分子数为N AC.1mol Na2O2与足量的CO2反应转移的电子数为2N AD.18g NH+4所含的电子数11N A8.用N A表示阿伏加德罗常数的值,下列叙述中不正确的是A.分子总数为N A的NO2和CO2混合气体中含有的氧原子数为2N AB.28g乙烯和环丁烷(C4H8)的混合气体中含有的碳原子数为2N AC.常温常压下,92g的NO2和N2O4混合气体含有的原子数为6N AD.常温常压下,22.4L氯气与量的镁粉充分反应,转移的电子数为2N A9.下列各组离子,在溶液中能大量共存、加入NaOH溶液后加热既有气体放出又有沉淀生成的一组是A.Ba2+、NO3-、NH4+、Cl-B.Ca2+、HCO3-、NH4+、AlO2-C.K+、Ba2+、Cl-、HSO3-D.Mg2+、NH4+、SO42-、K+10.下列离子方程式书写正确的是A.将铁放入氯化铁溶液中:Fe + Fe3+ === 2Fe2+B.向新制的氢氧化亚铁中加入足量的稀硝酸:Fe(OH)2 +2H+=== Fe2++2H2O C.将少量的二氧化硫通入氢氧化钠溶液中:SO2 +2OH-=== SO32-+H2OD.向氯化铝溶液中加入过量的氢氧化钠溶液:Al3+ +3OH- === Al(OH)3↓11. 高铁酸钾是一种高效绿色水处理剂,其工业制备的反应原理为:2Fe(OH)3 + 3KClO + 4KOH =2K2FeO4 + 3KCl + 5H2O,下列说法正确的是A.ClO−做还原剂B.Fe(OH)3在反应中被还原C.高铁酸钾中铁的化合价为+7 D.制备1molK2FeO4时转移3 mol 电子12.在酸性条件下,向含铬废水中加入FeSO4 ,可将有害的Cr2O72-转化为Cr3+,然后再加入熟石灰调节溶液的pH,使Cr3+转化为Cr(OH)3沉淀,而从废水中除去。
2017届 浙江省温州中学高三上学期期中理科数学试卷及答案
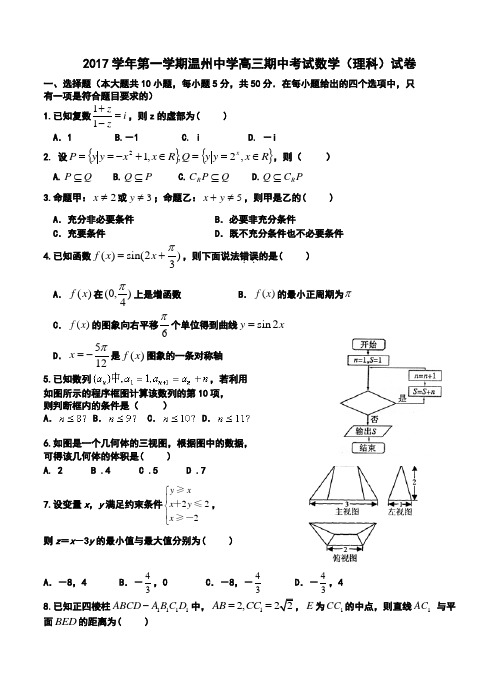
2017学年第一学期温州中学高三期中考试数学(理科)试卷一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只 有一项是符合题目要求的) 1.已知复数11zi z+=-,则z 的虚部为( ) A .1 B.-1 C. i D. -i2. 设{}{}R x y y Q R x x y y P x ∈==∈+-==,2,,12,则( ) A.Q P ⊆ B.P Q ⊆ C.Q P C R ⊆D.P C Q R ⊆3.命题甲:2≠x 或3≠y ;命题乙:5≠+y x ,则甲是乙的( ) A .充分非必要条件 B .必要非充分条件C .充要条件D .既不充分条件也不必要条件 4.已知函数()sin(2)3f x x π=+,则下面说法错误..的是( ) A .()f x 在(0,)4π上是增函数 B .()f x 的最小正周期为πC .()f x 的图象向右平移6π个单位得到曲线sin 2y x =D .512x π=-是()f x 图象的一条对称轴5.已知数列,若利用 如图所示的程序框图计算该数列的第10项, 则判断框内的条件是( ) A . B . C . D .6.如图是一个几何体的三视图,根据图中的数据, 可得该几何体的体积是( )A. 2 B .4 C .5 D .7 7.设变量x ,y 满足约束条件222y x x y x ⎧⎪⎨⎪⎩≥+≤≥-,则z =x -3y 的最小值与最大值分别为( )A .-8,4B .-34,0 C .-8,-34 D .-34,4 8.已知正四棱柱1111ABCD A BC D -中,12,AB CC ==E 为1CC 的中点,则直线1AC 与平面BED 的距离为( )A .2B ..1 9.函数y =给定的数中可能是该等比数列的公比的是( )A .13B .2C .3 D1 10.定义域为R 的偶函数)(x f 满足对x R ∀∈,有)1()()2(f x f x f -=+,且当]3,2[∈x 时,18122)(2-+-=x x x f ,若函数)1|(|log )(+-=x x f y a 在),0(+∞上至少有三个零点,则a 的取值范围是 ( ) A .)22,0( B .)33,0( C .)55,0( D .)66,0( 二、填空题(本大题共7小题,每小题4分,共28分)11.已知焦点在y轴上的双曲线的焦距为则双曲线的标准方程为12.已知实数a b 、满足21a b +=,则2a ab +的最大值为 13.已知数列{}n a 是单调递增的等差数列, 从7654321,,,,,,a a a a a a a 中取走任意三项, 则剩下四项依然构成单调递增的等差数列的概率= 14.若椭圆中心为坐标原点,焦点在x 轴上,过点(1,12)作圆22+=1x y 的切线,切点分别为,A B ,直线AB 恰好经过椭圆的右焦点和上顶点,则椭圆方程是15.如图,在半径为1的扇形AOB 中,︒=∠60AOB ,C 为弧上的动点,AB 与OC 交于点P ,则OP BP ⋅的最小值是16.若9290129(23)x a a x a x a x +=++++ ,则213579(3579)a a a a a ++++-2(2a +2468468)=a a a ++17.椭圆22a x +22b y =1(a>b>0)上一点A 关于原点的对称点为B ,F 为其右焦点,若AF ⊥BF ,设∠ABF=α,且α∈[12π,4π],则该椭圆离心率的取值范围为第15题图2017学年第一学期温州中学高三期中考试数学(理科)答题卷一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只 有一项是符合题目要求的) 1 2 3 4 5 6 7 8 9 10二、填空题(本大题共7小题,每小题4分,共28分)11. 12. 13. 14. 15. 16. 17. 三、解答题(本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤) 18.已知ABC ∆的内角,,A B C 所对边分别为,,a b c ,且1cos 2a C cb +=. (1)求角A 的大小;(2)若2bc =,求边长a 的最小值.19.已知n S 是数列{}n a 的前n 项和,且对任意n N +∈,有21143(21)3n n n a S +-=+, (1)求4n n a ⎧⎫⎨⎬⎩⎭的通项公式; (2)求数列22n n a -⎧⎫⎨⎬⎩⎭的前n 项和n T .20.如图在四棱锥P ABCD -中,底面ABCD 是边长为a 的正方形, 侧面PAD ⊥底面ABCD,且2PA PD AD ==, 设E 、F 分别为PC 、BD 的中点. (1) 求证:EF //平面PAD ; (2) 求证:面PAB ⊥平面PDC ; (3) 求二面角B PD C --的正切值.BA21.如图,已知曲线221:1(||1)C x y x +=<,22:81(||1)C x y x =+≥,动直线l 与1C 相切,与2C 相交于,A B 两点,曲线2C 在,A B 处的切线相交于点M .(1)当MA MB ⊥时,求直线l 的方程;(2)试问在y 轴上是否存在两个定点12,T T ,当直线12,MT MT 斜率存在时,两直线的斜率 之积恒为定值?若存在,求出满足的12,T T 点 坐标;若不存在,请说明理由.M第21题图22.已知函数1()x a x f x e-=(a 为常数).(1)当0a>时,求()f x 的极值;(2) 设函数32()g x x ax x =-+,若[]1,1x ∈-时,()()f x g x ≤恒成立,求a 的取值范围.2017学年第一学期温州中学高三期中考试数学(理科)参考答案一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只 有一项是符合题目要求的) 1 2 3 4 5 6 7 8 9 10 ACBABAADBB二、填空题(本大题共7小题,每小题4分,共28分)11. 2212x y -= 12. 1413. 17 14. 22154x y += 15. 116- 16. 28185⋅17. 23⎣⎦三、解答题(本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤) 18. 解:(1)1sin cos sin sin sin()sin cos cos sin 2A C CB AC A C A C +==+=+ ∴1sin cos sin 2C A C =,∴ 1cos 23A A π=⇒= (2) 222222cos 22a b c bc A b c bc bc bc bc =+-=+-≥-==a ≥边长a19. 解:(1)当1n =时,311143(21)3a S -=+ 得13a = 当2n ≥时 由21143(21)3n n n a S +-=+ ①BA得2111143(21)3n n n a S ----=+ ② ①-②得2114432n n n n a a a ----= 即21142n n n a a --=+化为111442n n n n a a --=+ 数列4n n a ⎧⎫⎨⎬⎩⎭是以34为首项,以12为公差的等差数列,311(1)44224n n a n n =+-⨯=+ 11424n n a n =+ (2)由(1)得:2(21)22nn n a n -=+ 231325272(21)2(21)2n n n T n n -=⋅+⋅+⋅++-⋅++⋅ 23412325272(21)2(21)2n n n T n n +⋅=⋅+⋅+⋅++-⋅++⋅ 34116222(21)2n n n T n ++-=++++-+⋅ 1(21)22n n T n +=-⋅+20. 法一:(Ⅰ)证明:ABCD 为平行四边形 连结AC BD F = ,F 为AC 中点,E 为PC 中点∴在CPA ∆中EF //PA且PA ⊆平面PAD ,EF ⊄平面PAD ∴PAD EF 平面// (Ⅱ)证明:因为面PAD ⊥面ABCD 平面PAD 面ABCD AD =ABCD 为正方形,CDAD ⊥,CD ⊂平面ABCD所以CD ⊥平面PAD ∴CD PA ⊥又PA PD AD ==,所以PAD ∆是等腰直角三角形, 且2PAD π∠=即PA PD ⊥ CD PD D = ,且CD 、PD ⊆面ABCD PA ⊥面PDC又PA ⊆面PAB 面PAB ⊥面PDC (Ⅲ) 【解】:设PD 的中点为M ,连结EM ,MF ,则EM PD ⊥由(Ⅱ)知EF ⊥面PDC , EF PD ⊥,PD ⊥面EFM ,PD MF ⊥,EMF ∠是二面角B PD C --的平面角Rt FEM ∆中,124EF PA == 1122EM CD a ==4tan 12EF EMF EM a ∠===故所求二面角的正切值为2 法二:如图,取AD 的中点O , 连结OP ,OF .∵PA PD =, ∴PO AD ⊥. ∵侧面PAD ⊥底面ABCD ,PAD ABCD AD ⋂=平面平面,∴PO ABCD ⊥平面,而,O F 分别为,AD BD 的中点,∴//OF AB , 又ABCD 是正方形,故OF AD ⊥. ∵PA PD AD ==,∴PA PD ⊥,2a OP OA ==.以O 为原点,直线,,OA OF OP 为,,x y z 轴建立空间直线坐标系,则有(,0,0)2a A ,(0,,0)2a F ,(,0,0)2a D -,(0,0,)2a P ,(,,0)2a B a ,(,,0)2aC a -. ∵E 为PC 的中点, ∴(,,)424a a aE -(Ⅰ)证明:易知平面PAD 的法向量为(0,,0)2a OF = 而(,0,)44a aEF =- ,且(0,,0)(,0,)0244a a aOF EF ⋅=⋅-= , ∴EF //平面PAD(Ⅱ)证明:∵(,0,)22a a PA =- ,(0,,0)CD a =∴(,0,)(0,,0)022a a PA CD a ⋅=-⋅= ,∴PA CD ⊥,从而PA CD ⊥,又PA PD ⊥,PD CD D = ,∴PA PDC ⊥平面,而PA PAB ⊂平面,∴平面PAB ⊥平面PDC .(Ⅲ) 由(Ⅱ)知平面PDC 的法向量为(,0,)22a aPA =- .设平面PBD 的法向量为(,,)n x y z = .∵(,0,),(,,0)22a a DP BD a a ==-,∴由0,0n DP n BD ⋅=⋅= 可得002200a a x y z a x a y z ⎧⋅+⋅+⋅=⎪⎨⎪-⋅+⋅+⋅=⎩,令1x =,则1,1y z ==-, 故(1,1,1)n =-∴cos ,n PA n PA n PA⋅<>===, 即二面角B PD C --的余弦值为3所以二面角B PD C --的正切值为221.(1)设半圆1C 上的切点00(,)P x y ,直线00:1AB l x x y y +=,1122(,),(,)A x y B x y 002181x x y y x y +=⎧⇒⎨=+⎩2000880y x x x y +--=得:0128y x x y --=。
2017届江苏省南通中学高三上学期期中考试数学(理)试卷
A B CO(第12题)2017届高三上学期数学期中测试(理科)本试卷分为数学I(必做题)和数学II(附加题)两部分.共200分,考试用时150分钟.数学I(必做题 共160分)一、填空题:本大题共14小题,每小题5分,共计70分. 1.已知集合{}=2,3,4A ,{}=2B a a +,,若=AB B ,则A B =ð ▲ .2.命题“2,10x x x ∃∈-+R ≤”的否定是 ▲ . 3.函数0.2log y x =的定义域为 ▲ .4.若角α的终边经过点P (a ,2a )(a<0),则cos α= ▲ . 5.设n S 是等比数列{}n a 的前n 项的和,若3620a a +=,则36S S 的值是 ▲ . 6.如图,在正方形ABCD 中,点E 是DC 的中点,点F 是BC 的一个三等分点,那么EF = ▲ .(用AB 和AD 表示)7.已知命题p :|x -a |<4,命题q :(x -1)(2-x )>0,若p 是q 的必要不充分条件,则实数a 的取值范围是 ▲ .8.已知直线01=+-y x 与曲线ln y x a =-相切,则a 的值为 ▲ . 9.在△ABC 中,BC =1,B =π3,△ABC 的面积S =3,则边AC 等于 ▲ .10.已知函数f (x )=⎩⎪⎨⎪⎧-x 2+2x ,x >0,0,x =0,x 2+mx ,x <0是奇函数且函数f (x )在区间[-1,a -2]上单调递增,则实数a 的取值范围为 ▲ .11.函数y =2sin ⎝⎛⎭⎫2x -π6与y 轴最近的对称轴方程是 ▲ . 12.如图,点O 为△ABC 的重心,且OA OB ⊥,4AB =,则AC BC ⋅的值为 ▲ .13.已知n S 为数列{}n a 的前n 项和,11a =,2(1)n n S n a =+,若关于正整数n 的不等式222n n a ta t -≤的解集中的整数解有两个,则正实数t 的取值范围为 ▲ .14.已知函数2+1, 1,()(), 1,a x x f x x a x ⎧-⎪=⎨->⎪⎩≤ 函数()2()g x f x =-,若函数()()y f x g x =- 恰有4个零点,则实数a 的取值范围是 ▲ .二、解答题:本大题共6小题,共计90分. 解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分) 已知向量(sin(),1)2a x ωϕ=+,(1,cos())2b x ωϕ=+(0,0)4πωϕ><<,记函数()()()f x a b a b =+⋅-.若函数()y f x =的周期为4,且经过点1(1,)2M .(1)求ω的值;(2)当11x -≤≤时,求函数()f x 的最值.16.(本小题满分14分)设公差不为零的等差数列{}n a 的前5项的和为55,且2674,,9a a a a +-成等比数列. (1)求数列{}n a 的通项公式. (2)设数列4(6)(4)n n n b a a =--,求证:数列{}n b 的前n 项和12n S <.17.(本小题满分14分)如图,在ABC ∆中,角,,A B C 的对边分别为,,a b c ,(sin cos )a b C C =+. (Ⅰ)求ABC ∠; (Ⅱ)若=2A π∠,D 为ABC ∆外一点,2DB =,1DC =,求四边形ABDC 面积的最大值.18.(本小题满分16分)BACD如图,某城市有一块半径为40 m 的半圆形绿化区域(以O 为圆心,AB 为直径),现计划对其进行改建.在AB 的延长线上取点D ,OD =80 m ,在半圆上选定一点C ,改建后的绿化区域由扇形区域AOC 和三角形区域COD 组成,其面积为S m 2.设∠AOC =x rad .(1)写出S 关于x 的函数关系式S (x ),并指出x 的取值范围; (2)试问∠AOC 多大时,改建后的绿化区域面积S 取得最大值.19. (本小题满分16分) 已知函数2()22a f x ax a x-=++-(0)a >. (1)当1a =时,求函数()f x 在点(2,(2))f 处的切线方程; (2)求函数()f x 的单调区间;(3)若()2ln f x x ≥在[1,)+∞上恒成立,求a 的取值范围.20.(本题满分16分)已知数列}{n a 的前n 项和为n S ,且4=+n n a S ,∈n N * (1)求数列}{n a 的通项公式;(2)已知32+=n c n (∈n N *),记=n d n C n a c log +(0>C 且1≠C ),是否存在这样的常数C ,使得数列}{n d 是常数列,若存在,求出C 的值;若不存在,请说明理由.(3)若数列}{n b ,对于任意的正整数n ,均有2221123121+-⎪⎭⎫ ⎝⎛=++++--n a b a b a b a b nn n n n 成立,求证:数列}{n b 是等差数列.数学II(附加题 共40分)ABOCD(第18题)21. (本小题满分10分)设矩阵A =⎣⎢⎡⎦⎥⎤1 -23 -7的逆矩阵为1-A ,矩阵B 满足AB =⎣⎢⎡⎦⎥⎤31,求1-A ,B .22.(本小题满分10分) 设矩阵1221A ⎡⎤=⎢⎥⎣⎦,求矩阵A 的逆矩阵的特征值及对应的特征向量.23.(本小题满分10分)已知曲线C 的极坐标方程为 ρ=2cos θ,直线l 的极坐标方程为 ρ sin(θ+π6)=m .若直线l 与曲线C 有且只有一个公共点,求实数m 的值.24. (本小题满分10分)在平面直角坐标系xOy 中,已知曲线C :⎩⎪⎨⎪⎧x =4cos θy =3sin θ(θ为参数,θ∈R ),直线l :⎩⎨⎧x =3+22t ,y =-3+22t (t 为参数,t ∈R ),求曲线C 上的动点P 到直线l 的距离的最小值.参考答案:2017届高三上学期数学期中测试(理科)本试卷分为数学I(必做题)和数学II(附加题)两部分.共200分,考试用时150分钟.数学I(必做题 共160分)一、填空题:本大题共14小题,每小题5分,共计70分. 1.已知集合{}=2,3,4A ,{}=2B a a +,,若=AB B ,则A B =ð ▲ .{}32.命题“2,10x x x ∃∈-+R ≤”的否定是 ▲ .2,10x x x ∀∈-+>R 3.函数0.2log y x =的定义域为 ▲ .(0,1]4.若角α的终边经过点P (a ,2a )(a<0),则cos α= ▲ .55-5.设n S 是等比数列{}n a 的前n 项的和,若3620a a +=,则36S S 的值是 ▲ .2 6.如图,在正方形ABCD 中,点E 是DC 的中点,点F 是BC 的一个三等分点,那么EF = ▲ .(用AB 和AD 表示)1223AB AD -7.已知命题p :|x -a |<4,命题q :(x -1)( 2-x )>0,若p 是q 的必要不充分条件,则实数a 的取值范围是________.[-2,5]8.已知直线01=+-y x 与曲线ln y x a =-相切,则a 的值为 ▲ .2- 9.在△ABC 中,BC =1,B =π3,△ABC 的面积S =3,则边AC 等于 ▲ .1310.已知函数f (x )=⎩⎪⎨⎪⎧-x 2+2x ,x >0,0,x =0,x 2+mx ,x <0是奇函数且函数f (x )在区间[-1,a -2]上单调递增,则实数a 的取值范围为 ▲ .(1,3].11.函数y =2sin ⎝⎛⎭⎫2x -π6与y 轴最近的对称轴方程是 ▲ .6x π=-12.如图,点O 为△ABC 的重心,且OA OB ⊥,4AB =,则AC BC ⋅的值为▲ .3213.已知n S 为数列{}n a 的前n 项和,11a =,2(1)n n S n a =+,若关于正整数n 的不等式222n n a ta t -≤的解集中的整数解有两个,则正实数t 的取值范围为 ▲ .3(1,)214.已知函数2+1, 1,()(), 1,a x x f x x a x ⎧-⎪=⎨->⎪⎩≤ 函数()2()g x f x =-,若函数()()y f x g x =- 恰有4个零点,则实数a 的取值范围是 ▲ .23a <≤二、解答题:本大题共6小题,共计90分. 解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)已知向量(sin(),1)2a x ωϕ=+,(1,cos())2b x ωϕ=+(0,0)4πωϕ><<,记函数()()()f x a b a b =+⋅-.若函数()y f x =的周期为4,且经过点1(1,)2M .(1)求ω的值;(2)当11x -≤≤时,求函数()f x 的最值.15.解:(1)2222()()()sin ()cos ()cos(2)22f x a b a b a b x x x ωωϕϕωϕ=+⋅-=-=+-+=-+ ………………4分由题意得:周期24T πω==,故2πω=………………6分(2)∵图象过点1(1,)2M ,1cos(2)22πϕ∴-+=即1sin 22ϕ=,而04πϕ<<,故26πϕ=,则()cos()26f x x ππ=-+. ………………10分 当11x -≤≤时,23263x ππππ-≤+≤1cos()1226x ππ∴-≤+≤ ∴当13x =-时,min ()1f x =-,当1x =时,max 1()2f x =. ………………14分16.(本小题满分14分)设公差不为零的等差数列{}n a 的前5项的和为55,且2674,,9a a a a +-成等比数列.(1)求数列{}n a 的通项公式.(2)设数列4(6)(4)n n n b a a =--,求证:数列{}n b 的前n 项和12n S <.16.解:(1)设等差数列的的首项为1a ,公差为d ,则112111154555722(56)()(39)a d a d a d a d a d a d ⨯⎧+==⎧⎪⇒⎨⎨=⎩⎪+++=++-⎩或1110a d =⎧⎨=⎩(舍去) 故数列{}n a 的通项公式为72(1)n a n =+-即25n a n =+.………… 7分 (2)由(1)25n a n =+, 得11111()(6)(4)(21)(21)22121n n n b a a n n n n ===----+-+.…………10分12111111[(1)()()]23352121n n S b b b n n =+++=-+-++--+111(1)2212n =-<+. ………14分17.(本小题满分14分)如图,在ABC ∆中,角,,A B C 的对边分别为,,a b c ,(sin cos )a b C C =+. (Ⅰ)求ABC ∠; (Ⅱ)若=2A π∠,D 为ABC ∆外一点,2DB =,1DC =,求四边形ABDC 面积的最大值.17.解:(Ⅰ)在ABC ∆中,∵(sin cos )a b C C =+,∴sin sin (sin cos )A B C C =+, ……………………………………………1分 ∴sin()sin (sin cos )B C B C C π--=+,∴sin(+)sin (sin cos )B C B C C =+,……………………………………………2分 ∴sin cos cos sin sin sin sin cos B C B C B C B C +=+, ……………………… 3分 ∴cos sin sin sin B C B C =,又∵(0,)C ∈π,故sin 0C ≠, ……………………………………………4分BACD∴cos sin B B =,即tan 1B =. ……………………………………………5分 又(0,)B ∈π,∴4B π=. ……………………………………………6分 (Ⅱ)在BCD ∆中,2DB =,1DC =,222=12212cos BC D +-⨯⨯⨯54cos D =-. ………………………………7分又=2A π,由(Ⅰ)可知4ABC π∠=, ∴ABC ∆为等腰直角三角形, …………………………………………8分21115cos 2244ABC S BC BC BC D ∆=⨯⨯⨯==-, ……………………………… 9分又1sin sin 2BDC S BD DC D D ∆=⨯⨯⨯=, ……………………………………10分∴55cos sin 2sin()444ABDC S D D D π=-+=+-四边形. ……………………12分 ∴当=4D 3π时,四边形ABDC 的面积有最大值,最大值为524+.………14分18.(本小题满分16分)如图,某城市有一块半径为40 m 的半圆形绿化区域(以O 为圆心,AB 为直径),现计划对其进行改建.在AB 的延长线上取点D ,OD =80 m ,在半圆上选定一点C ,改建后的绿化区域由扇形区域AOC 和三角形区域COD 组成,其面积为S m 2.设∠AOC =x rad .(1)写出S 关于x 的函数关系式S (x ),并指出x 的取值范围; (2)试问∠AOC 多大时,改建后的绿化区域面积S 取得最大值.18.(本小题满分16分)解:(1)因为扇形 AOC 的半径为 40 m ,∠AOC =x rad ,所以 扇形AOC 的面积S 扇形AOC =x ·OA 22=800x ,0<x <π. …………… 2分在△COD 中,OD =80,OC =40,∠COD =π-x ,所以△COD 的面积S △COD =12·OC ·OD ·sin ∠COD =1600sin(π-x )=1600sin x .………………… 5分从而 S =S △COD +S 扇形AOC =1600sin x +800x ,0<x <π. …………………7分 (2)由(1)知, S (x )=1600sin x +800x ,0<x <π.S ′(x )=1600cos x +800=1600(cos x +12). ……………… 9分ABOCD(第18题)由 S ′(x )=0,解得x =2π3.从而当0<x <2π3时,S ′(x )>0;当2π3<x <π时, S ′(x )<0 .因此 S (x )在区间(0,2π3)上单调递增;在区间(2π3,π)上单调递减. …………… 14分所以 当x =2π3,S (x )取得最大值.答:当∠AOC 为2π3时,改建后的绿化区域面积S 最大.……………… 16分19. (本小题满分16分) 已知函数2()22a f x ax a x-=++-(0)a >. (Ⅰ)当1a =时,求函数()f x 在点(2,(2))f 处的切线方程; (Ⅱ)求函数()f x 的单调区间;(Ⅲ)若()2ln f x x ≥在[1,)+∞上恒成立,求a 的取值范围. 19.解:(1)当 1=a 时,1()=-f x x x ,21()1f x x'=+ …………2分 3(2),2=f 5(2)4f '= …………3分所以,函数()f x 在点(2,(2))f 处的切线方程为35(2)24-=-y x 即:5440--=x y …………4分 (Ⅱ)函数的定义域为:{|0}≠x x2'222(2)()(0)-+-=-=>a ax a f x a a x x …………6分当02<≤a 时,'()0≥f x 恒成立,所以,()f x 在(,0)-∞和(0,)+∞上单调递增 当2>a 时,令'()0=f x ,即:220+-=ax a ,1222,--=-=a a x x a a'()0,>f x 21;或><x x x x '()0,<f x 1200或<<<<x x x x , 所以,()f x 单调递增区间为22(,)(,)和---∞-+∞a a a a,单调减区间为22(,0))和(0,---a a a a. …………10分 (Ⅲ)因为()2ln ≥f x x 在[1,)+∞上恒成立,有2222ln 0(0)-++--≥>a ax a x a x在[1,)+∞上恒成立.所以,令2()222ln -=++--a g x ax a x x, 则2'2222222(1)[(2)]()---+-+-=--==a ax x a x ax a g x a x x x x . 令'()0,=g x 则1221,-==-a x x a若21--=a a,即1=a 时,'()0≥g x ,函数()g x 在[1,)+∞上单调递增,又(1)0=g 所以,()2ln ≥f x x 在[1,)+∞上恒成立; 若21-->a a ,即1<a 时,当2(0,1),(,)-∈-+∞a x a时,'()0,()>g x g x 单调递增; 当2(1,)-∈-a x a时,'()0<g x ,()g x 单调递减 所以,()g x 在[1,)+∞上的最小值为2()--a g a, 因为(1)0,=g 所以2()0--<a g a不合题意. 21,--<a a 即1>a 时,当2(0,),(1,)-∈-+∞a x a时,'()0,()>g x g x 单调递增, 当2(,1)-∈-a x a时,'()0,()<g x g x 单调递减, 所以,()g x 在[1,)+∞上的最小值为(1)g 又因为(1)0=g ,所以()2ln ≥f x x 恒成立综上知,a 的取值范围是[1,)+∞. …………16分20.(本题满分16分)已知数列}{n a 的前n 项和为n S ,且4=+n n a S ,∈n N * (1)求数列}{n a 的通项公式;(2)已知32+=n c n (∈n N *),记=n d n C n a c log +(0>C 且1≠C ),是否存在这样的常数C ,使得数列}{n d 是常数列,若存在,求出C 的值;若不存在,请说明理由.(3)若数列}{n b ,对于任意的正整数n ,均有2221123121+-⎪⎭⎫ ⎝⎛=++++--n a b a b a b a b nn n n n 成立,求证:数列}{n b 是等差数列. 20.解:(1)114a a -=,所以21=a ………………1分由4=+n n a S 得2≥n 时,411=+--n n a S两式相减得,12-=n n a a ,211=-n n a a …………2分 数列}{n a 是以2为首项,公比为21的等比数列, 所以n n a -=22(*N n ∈) ……………4分(2)由于数列}{n d 是常数列n d =n C n a c log +2log )2(32C n n -++= ……………6分=2log 2log 232C C n n -++2log 23)2log 2(C C n ++-=为常数,只有02log 2=-C ;解得2=C ,此时7=n d ………8分 (3)2221123121+-⎪⎭⎫ ⎝⎛=++++--n a b a b a b a b nn n n n ……① 1=n ,1232111-=-=a b ,其中21=a ,所以 211-=b …10分 当2≥n 时, 2121111332211+-⎪⎭⎫ ⎝⎛=++++-----n a b a b a b a b n n n n n ② …12分 ②式两边同时乘以21得, 41212123121+-⎪⎭⎫ ⎝⎛=++++---n a b a b a b a b n n n n n ③ …14分 ①式减去③得,431--=n a b n ,所以838--=n b n 且811-=-+n n b b 所以数列}{n b 是以21-为首项,公差为81-的等差数列. …16分数学II(附加题 共40分)21. (本小题满分10分)设矩阵A =⎣⎢⎡⎦⎥⎤1 -23 -7的逆矩阵为1-A ,矩阵B 满足AB =⎣⎢⎡⎦⎥⎤31,求1-A ,B .21.解:因为A =⎣⎢⎡⎦⎥⎤1 -23 -7,所以|A |=⎪⎪⎪⎪⎪⎪1 -23 -7=-7+6=-1. 由逆矩阵公式得,A -1=⎣⎢⎡⎦⎥⎤7 -23 -1. …5分 因为AB =⎣⎢⎡⎦⎥⎤31,所以B =A -1AB =⎣⎢⎡⎦⎥⎤7 -23 -1 ⎣⎢⎡⎦⎥⎤31=⎣⎢⎡⎦⎥⎤19 8.…………………………10分22.(本小题满分10分)设矩阵1221A ⎡⎤=⎢⎥⎣⎦,求矩阵A 的逆矩阵的特征值及对应的特征向量. 答案:矩阵A 的逆矩阵为12332133⎡⎤-⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦,则特征多项式为221421()()3933f λλλλ=+-=+- 令()0f λ=,解得1211,3λλ=-=,设特征向量为x y ⎡⎤⎢⎥⎣⎦,则12332133x x y y ⎡⎤-⎢⎥⎡⎤⎡⎤⋅=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥-⎢⎥⎣⎦, 易算得特征值11λ=-对应的一个特征向量为11⎡⎤⎢⎥-⎣⎦,同理可得特征值213λ=对应的一 个特征向量为11⎡⎤⎢⎥⎣⎦................................................(10分)23.(本小题满分10分)已知曲线C 的极坐标方程为 ρ=2cos θ,直线l 的极坐标方程为 ρ sin(θ+π6)=m .若直线l 与曲线C 有且只有一个公共点,求实数m 的值.23.解:曲线C 的极坐标方程为 ρ=2cos θ,化为直角坐标方程为x 2+y 2=2x .即(x -1)2+y 2=1,表示以(1,0)为圆心,1为半径的圆. …………………… 3分 直线l 的极坐标方程是 ρ sin(θ+π6)=m ,即12ρcos θ+32ρsin θ=m , 化为直角坐标方程为x + 3y -2m =0. ………………… 6分因为直线l 与曲线C 有且只有一个公共点,所以|1-2m |2=1,解得m =-12或m =32. 所以,所求实数m 的值为-12 或 32. ……………… 10分24. (本小题满分10分)在平面直角坐标系xOy 中,已知曲线C :⎩⎪⎨⎪⎧x =4cos θy =3sin θ(θ为参数,θ∈R ),直线l :⎩⎨⎧x =3+22t ,y =-3+22t(t 为参数,t ∈R ),求曲线C 上的动点P 到直线l 的距离的最小值.21.C .解:将直线l 的参数方程⎩⎨⎧x =3+22ty =-3+22t化为普通方程为x -y -6=0. 因为点P 在曲线C :⎩⎪⎨⎪⎧x =4cos θy =3sin θ(θ为参数)上,所以设P (4cos θ,3sin θ). 点P 到直线l 的距离d =|4cos θ-3sin θ-6|2=|5cos(θ+φ)-6|2,其中tan φ=34,φ是锐角. 所以当cos(θ+φ)=1时,d min =22. 所以点P 到直线l 的距离的最小值为22.…………………………………10分。
2017届德州市高三上学期期中考试数学理科试题及答案
! " # $! # #
,-" + | ,&" } # ä* ,#( ááááááááááááááááááá ' 7 !! L "# #" ,
áááááááááááááááááááááááááááááá ( 7 ,% ( @ "# (% |' J®45}
$ #&, % vGP¬J¤N' A )+# ! %áááááááááááááááááááááá $ 7 , ,% $ @#& &## # -"!! @
AB'C $ DE % F5 ! G ' H $ I ( H%
!"#$ %& '()*+,
9 &'( !](. # ;<( ) $ .) D^_>?L\>(EF ! " <( "$! #% .!!% -!'% 0!(% *!)% 0!$% -!9% *!/% .!,% .!# "% *
, #& ' )&')" *% # ' ( .% ) !) 0% )
! * "tuv T%wN' xyz% #% {V * @| #% ,! +* &! " # #4( # # # } iv~ $ # %jk* +!& &! $ & : 6 +" "# # # #4! ,## ; * , ! VB-.%'l * , % s" # -% " ! ! *% " ( # ! .% ( ! # 0% # !
山东省德州市2017届高三上学期期中数学试卷(理科) 含解析
2016-2017学年山东省德州市高三(上)期中数学试卷(理科)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.A={x|x是小于9的质数},B={x|x是小于9的正奇数},则A∩B的子集个数是()A.32 B.16 C.8 D.42.不等式x2﹣2|x|﹣3<0的解集是()A.(﹣3,3)B.(﹣3,1)C.(﹣3,0)∪(0,3) D.(﹣1,0)∪(0,1) 3.已知,x∈(0,π),则tanx=()A.B.C.D.4.已知命题;命题,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件5.已知向量=(1,m),=(3,﹣2),且(+)⊥,则m=()A.﹣8 B.﹣6 C.6 D.86.为了得到函数的图象,只需把y=3sinx上所有的点()A.先把横坐标缩短到原来的倍,然后向左平移个单位B.先把横坐标缩短到原来的2倍,然后向左平移个单位C.先把横坐标缩短到原来的2倍,然后向左右移个单位D.先把横坐标缩短到原来的倍,然后向右平移个单位7.已知函数,若x0是方程f(x)=0的根,则x0∈()A. B. C. D.8.已知x,y满足约束条件,目标函数z=x2+y2的最小值为()A.13 B. C.D.9.设f(x)是定义在R上的偶函数,对任意的x∈R,都有f(x+4)=f(x),且当x∈[﹣2,0]时,,若在区间(﹣2,6]内关于x的方程f(x)﹣log a(x+2)=0(0<a<1)恰有三个不同的实数根,则a的取值范围是()A. B.C.D.10.已知f(x)的定义域是(0,+∞),f’(x)为f(x)的导函数,且满足f(x)<f'(x),则不等式f(2)的解集是()A.(﹣∞,2)∪(1,+∞) B.(﹣2,1)C.(﹣∞,﹣1)∪(2,+∞) D.(﹣1,2)二、填空题(每题5分,满分25分,将答案填在答题纸上)11.已知f(x)的定义域为[﹣1,1],则函数的定义域为.12.设函数f(x)对x≠0的实数满足,那么=.13.在Rt△ABC中,∠A=90°,AB=AC=1,点E是AB的中点,点D满足,则=.14.若正数a,b满足,则的最小值为.15.定义:f1(x)=f(x),当n≥2且x∈N*时,f n(x)=f(f n(x)),对于函数f(x)定义﹣1域内的x0,若正在正整数n是使得f n(x0)=x0成立的最小正整数,则称n是点x0的最小正周期,x0称为f(x)的n~周期点,已知定义在[0,1]上的函数f(x)的图象如图,对于函数f(x),下列说法正确的是(写出所有正确命题的编号)①1是f(x)的一个3~周期点;②3是点的最小正周期;③对于任意正整数n,都有f n()=;④若x0∈(,1],则x0是f(x)的一个2~周期点.三、解答题(本大题共6小题,共75分。
重庆市璧山中学2017届高三上学期期中考试理科综合试题含答案
璧山中学2016-2017学年上期高2017级期中考试理科综合能力测试第I卷一、选择题:本大题共21小题。
在1~17题给出的四个选项中,只有一项是符合题目要求的;第18~21题有多项符合题目要求,全部选对的得6分,选对但不全的得3分,有选错的得0分.1.关于细胞论述,下列说法错误的是()A.原核细胞中的DNA分子都是裸露存在的B.观察到有核糖体等多种细胞器,一定是细胞的亚显微结构图C.原核细胞和真核细胞只有一种共有的细胞器D。
若细胞中没有核膜,一定是原核细胞结构图2. 有种细菌会在人类的细胞之间快速转移,使人患脑膜炎.其原因是该菌的一种名为InIC的蛋白可通过阻碍人类细胞中的Tuba蛋白的活性,使细胞膜更易变形而有利于细菌的转移.下列叙述正确的是( )A.该菌的遗传物质主要是DNAB.Tuba蛋白和InIC蛋白的合成均需要内质网的加工C.该菌使人类细胞发生变形,说明细胞膜具有一定的流动性D.该菌在人类的细胞之间快速转移依赖于细胞膜的选择透过性3。
右图为某同学画的洋葱根尖分生区细胞处于分裂间期时的模式8图,根据此图得出的结论,错误的是( )A.被称为有机物合成“车间”的结构是5B.图中出现了两处明显的错误,体现在结构2和4上C.能发生碱基互补配对的细胞结构有9、4、3、6D.在细胞分裂后期,7的活动会增强,合成结构84.将新鲜苔藓植物叶片放入有少量红墨水、浓度为30 %的KNO3溶液中,过一段时间后显微镜下观察到苔藓细胞如图所示,请据图判断,错误的是()A.此时苔藓细胞可能正在吸水B.①处为红色,②处为无色,③处为绿色C.高温加热后的苔藓细胞重复实验,会看到整个细胞是红色D.用一定浓度的蔗糖溶液代替KNO3溶液,实验中观察的结果不同5.将耐碱性的单细胞藻类,放入盛有一定体积和浓度的碳酸氢钠溶液中培养(如甲图所示)。
光照充足,每隔5分钟收集一次甲数据绘制出乙图曲线1,则乙图曲线2是指改变甲图中何种条件后气体量的变化( )A.①B.②C.③D.②或③6.关于细胞分化、衰老、凋亡和癌变的叙述错误有()①个体发育过程中细胞的衰老对于生物体都是有害的②正常细胞癌变后在体外培养可无限增殖③由造血干细胞分化成红细胞的过程是可逆的④癌细胞容易在体内转移,与其细胞膜上糖蛋白等物质减少无关⑤人胚胎发育过程中尾的消失是细胞凋亡的结果⑥原癌基因和抑癌基因的突变是细胞癌变的内因⑦低温引起的细胞冻伤和死亡属于细胞坏死A.4个 B.3个 C.2个 D.1个7.化学与人类生产、生活、社会可持续发展密切相关,下列说法正确的是()A.“滴水石穿,绳锯木断”不包含化学变化B.“天宫一号"中使用的碳纤维,是一种新型有机高分子材料C.二氧化硅可用于光纤通信、单晶硅可用于光电转换D.淀粉、油脂和蛋白质都是高分子化合物8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
3
(20)(本小题满分 12 分) 在平面直角坐标系 xOy 中, 椭圆 C : 在椭圆 C 上. (1)求椭圆 C 的方程; (2)若点 A 、 B 都在椭圆 C 上,且 AB 中点 M 在线段 OP (不包括端点)上.求
AOB 面积的最大值.
2 x2 y 2 , 且点 P(2,1) 2 1(a b 0) 的离心率 e 2 2 a b
4
17.题满分 12 分) 已知数列 {an } 为等差数列, Sn 为其前 n 项和,若 a3 20 , 2S3 S4 8 . (1)求数列 {an } 的通项公式; (2)设 bn
1 (n N* ) , Tn b1 b2 bn ,求 Tn . Sn 1
(21)(本小题满分 12 分) 设函数 f ( x) ex ln x 1 ,其中 e 是自然对数的底数 (1)求证:函数 f ( x) 存在极小值; (2)若 x [ , ) ,使得不等式
1 2
ex m ln x 0 成立,求实数 m 的取值范围. x x
(22)(本小题满分 10 分)选修 4-4:坐标系与参数方程 已知极坐标的极点在平面直角坐标系的原点 O 处,极轴与 x 轴的正半轴重合,
(16)如图,在正方形 OABC 内,阴影部分是由两曲线 y
x , y x 2 (0 x 1)
围成,在正方形内随机取一点,且此点取自阴影部分的概率是 a, 则函数 f x 1
log3 x( x a) 的值域为 x ( ) ( x a ) 3
.
2
三.解答题:解答应写出文字说明,证明过程或演算步骤。
1 1 −������
C.{2,6} )
D.{2,3}
3.函数������ ������ = A.[1 ,+∞)
的定义(
B.(1,+∞) C.(-∞,1 ] ) C. )
1 2
D.(-∞,1)
4.计算:log 2 12-log 2 3=( A. -2 B. 0
D 2
5.直线 x+3y+3=0 的斜率是(
x2 y 2 1 (a 0, b 0) 的渐近线与抛物线 y x2 1 仅有两个交 a 2 b2
点,则该双曲线的离心率为
.
(15) 已知曲线 f x x ln x 在点 1, f 1 处的切线与曲线 y x2 a 相切, 则a _________.
是两个不同平面,下列命题中正确的是() B 若 L⊥α,L⊥β,则 α// β D 若 α⊥β,L//α,则L⊥β
A 若 L//α, L//β 则 α//β C 若 L⊥α,L //β 则 α// β,
二.填空题题:(本大题共 4 小题,每小题 5 分,共 20 分)
(13)在四面体 P ABC 中, PC 平面 ABC ,AB=AC=2,BC=PC= 2 2 ,则 该四面体外接球的表面积为 (14) 设双曲线 .
18)(本小题满分 12 分) 自 2016 年 1 月 1 日起,我国全面二孩政策正式实施,这次人口与生育政策的历 史性调整,使得“要不要再生一个”,“生二孩能休多久产假”等问题成为千千万万 个家庭在生育决策上避不开的话题. 为了解针对产假的不同安排方案形成的生育 意愿,某调查机构随机抽取了 200 户有生育二胎能力的适龄家庭进行问卷调查, 得到如下数据: 产假安排(单位:周) 14 15 16 17 18 有生育意愿家庭数 4 8 16 20 26
且长度单位相同.直线 l 的极坐标方程为: sin( ) 3 ,若点 P 为曲线 3
x 2 2 cos , (为参数) 上的动点,其中参数 0, 2 . C: y 2 sin
(1)试写出直线 l 的直角坐标方程及曲线 C 的普通方程; (2)求点 P 到直线 l 距离的最大值.
(1)若用表中数据所得的频率代替概率,面对产假为 14 周与 16 周,估计某家 庭有生育意愿的概率分别为多少? (2)假设从 5 种不同安排方案中,随机抽取 2 种不同安排分别作为备选方案, 然后由单位根据单位情况自主选择.①求两种安排方案休假周数和不低于 32 周 的概率; ②如果用 表示两种方案休假周数之和. 求随机变量 的分布列及数学期望. (19)(本小题满分 12 分) 如图,在四棱锥 P—ABCD 中, 面PAB 面ABCD , PA PB 3 ,且四边形 P 0 ABCD 为菱形, AD 2 , BAD 60 . (1)求证: AB PD ; (2)求平面 PAB 与平面 PCD 所成的二面角的余弦值。 A B C
A.
−3
1
B.
1 3
C. 2 )
D .1
6.设向量a = 2sin θ, 2cos θ , , 则 a =( A. 8 B. 4 C. 2
D. 1 )
7.下列函数在其定义域内单调递减的是( A.y=− x
2 1BΒιβλιοθήκη y=2xc.y=1 X 2
D.y = x 2 )
8.各项均为正数的等比数列{an }中,若a1 = 1,a5 =4,a3 =( A.2 B.-2 X 2 + 1, x ≤ 1
隆江中学 6-2017 学年度第一学期高三期中考试
(理科试卷) 一、选择题(本大题共 12 小题,每小题 5 分,共 60 分) 1.设 i 为负数单位,则复数(3+4i)i= ( A.-4i-3 B.-4+3i C.4+3i ) D4-3i
2.已知集合 A={1,2,3,4},B={2,4,6},则 A∩B=( ) A.{1,2} B.{2,4}
2 X
C. 2 , ������ > 1 ,则 f(f(1))=
D.− 2
9.设函数 f(x)= A.1
B.2
C.3
1
D.4
10 .已知 a∈ ℝ,则“a> 2”是“a2 >2a 的 A 充分不要条件, C.充要条件 B.必要不充分条件 D.既不充分也不必要条件 x+y≤1 11.已知变量 x,满足约束条件 x − y ≤ 1,则 Z=x+2y 的最小 x+1≥0 值 ( A.3 12.设 L 为直线 ) B,.1 C.-5 D.-6
