中考总复习专题:二次函数与相似的结合
二次函数与相似三角形的结合

提问:二次函数解析式 三种表达式
分类讨论
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分 别交于点P,N. ①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M 的坐标;
方法一、
N
B P A
0
M
解(2):当∠NBP=90°时
由题意可知: tan∠NBC=tan∠BAO=
举一反三
1、在平面直角坐标系中,二次函数图象的顶点坐标为 C(4,0),且与x轴的两个交点间的距离为6. (1)求二次函数的解析式; (2)在x轴上方的抛物线上,是否存在点Q,使得以 Q,A,B为顶点的三角形与△ABC相似?如果存在,请 求出点Q的坐标;如果不存在,请说明理由.
y
OA
B
x
C
课后作业
热点、二次函数与相似三角形的 存在性问题
例题1
(2017年河南中考第23题)
如图,直线y= 于点B,抛物线
2
3 y
x
c与x轴交于点A(3,0),与y轴交 4 x2 bx c 经过点A,B.
(1)求点B的坐标和3抛物线的解析式;
中恰有一点是其它两点所连线段的中点(三点重合除外)称M,P,N三点为 “共谐点”。请直接写出使得M,P,N三点成为“共谐点”的m的值。
x1 (0 舍)
x2 11 8
即m(11 ,0) 8
①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M 的坐标;
方法一、
当∠BNM=90°时,设M(m,0),N(m,
4 3
m
2
10 3
)m
2
由图可知:
4 m2 10 m 2 2
专题24 二次函数与相似三角形存在问题-2022中考数学之二次函数重点题型专题(全国通用版)(原卷版

专题24 二次函数与相似三角形存在问题1.(2021—2022浙江省宁波市九年级开学考试)如图,抛物线与x 轴交于1,0A 、()3,0B -两点,与y 轴交于点()0,3C ,设抛物线的顶点为D .坐标轴上有一动点P ,使得以P 、A 、C 为顶点的三角形与BCD △相似.则点P 的坐标______.2.(2021·云南腾冲·中考一模)如图,抛物线212y x bx c =-++经过点()2,0A -和点()4,0B ,与y 交于点C ,顶点为D ,连接AC 、BC ,BC 与抛物线的对称轴l 交于点E . (1)求该抛物线的函数表达式;(2)点P 是第一象限抛物线上的动点,连接PB ,PC ,当四边形OBPC 面积取最大值时,求点P 的坐标;(3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以M ,N ,E 为顶点的三角形与OBC 相似?若存在,求点M 的坐标;若不存在,请说明理由.3.(2021·浙江诸暨·九年级期末)如图,已知Rt ABC 中,30BAC ∠=︒,90C ∠=︒,A 点坐标为(1,0)-,B 点坐标为(3,0),抛物线1y 的顶点记为Q ,且经过ABC 的三个顶点A 、B 、C (点A 在点B 左侧,点C 在x 轴下方).抛物线2y 也交x 轴于点A 、B ,其顶点为P .(1)求C 点的坐标和抛物线1y 的顶点Q 的坐标. (2)当AP CP +的值最小时,求抛物线2y 的解析式.(3)设点M 是抛物线1y 上的一个动点,且位于其对称轴的右侧.若PQM 是与ABC 相似的三角形,求抛物线2y 的顶点P 的坐标.4.(2020—2021湖南长郡中学九年级月考)在平面直角坐标系中,抛物线2y ax bx c =++(0a ≠)与x 轴的两个交点分别为A 、B ,与y 轴相交于点C ,点A (2-,0),4BO AO =,连接BC ,tan ∠OCB =2.(1)求该抛物线的解析式;(2)设点P 是抛物线上在第一象限内的动点(不与C 、B 重合),过点P 做PD ⊥BC ,垂足为点D .①点P 在运动过程中,线段PD 的长度是否存在最大值?若存在,请求出点D 的坐标;若不存在,请说明理由;②以P 、D 、C 为顶点的三角形与△COA 相似时,求出点P 的坐标.5.(2021·山东临沭·九年级期末)如图,已知抛物线24y ax bx =++与x 轴交于(2,0)A -,(4,0)B 两点,与y 轴交于点C ,其顶点为D ,连接BC 与抛物线的对称轴l 交于点E .(1)求抛物线的表达式并写出该抛物线的对称轴;(2)在直线BC 上方的抛物线上找一点P ,使得PBC ∆的面积最大,求出此时点P 的坐标; (3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M N E 、、为顶点的三角形与OBC ∆相似?若存在,求出点M 的坐标;若不存在,请说明理由.6.(2021·湖南·长沙市九年级期中)如图,已知抛物线26y ax bx =++经过两点(1,0)A -,(3,0)B ,C 是抛物线与y 轴的交点.(1)求抛物线的解析式;(2)点(,)P m n 在平面直角坐标系第一象限内的抛物线上运动,直线CP 与x 轴交于点Q ,当BQC BCO ∠=∠时,求此时P 点坐标;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得90CNM ∠=︒,且CMN ∆与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.7.(2021·广东·佛山市九年级期末)如图,抛物线2y x bx c =-++与x 轴交于点()1,0A -,()3,0B ,与y 轴交于点C .点D 是直线BC 上方抛物线上一动点. (1)求抛物线的解析式;(2)如图1,连接BD 、CD ,设点D 的横坐标为m ,BCD △的面积为s .求s 与m 的函数关系式,并求出s 的最大值;(3)如图2,点E 坐标为()20,,过点D 作DF BC ⊥于F ,连接CD 、CE ,是否存在点D ,使得CDF 与CEO 相似?若存在,请直接写出点D 的坐标:若不存在,请说明理由.8.(2021·云南·昆明市九年级月考)如图1,已知二次函数()241y x b b =--++的图象与一次函数5y kx =+的图象相交于点A ,B ,其中点A 在x 轴的正半轴上,点B 在y 轴上,点M 为二次函数图象的顶点. (1)求点M 的坐标及k 的值;(2)根据图象,直接写出关于x 的不等式25()41kx x b b +≤--++的解集______;(3)如图2,抛物线对称轴为直线x b =与直线AB 交于C ,在直线AB 上是否存在点P ,使得点M 、C 、P 组成的三角形与AOB ∆与相似,若存在,请求出满足条件的所有点P 坐标;若不存在,说明理由.9.(2021·江苏·景山中学九年级月考)如图1,二次函数214y x x =-+的图像与x 轴交于点O 、点A ,顶点为B , 点M 、N 的坐标分别为(0 ,m )、(0 ,n ). (1)求点B 的坐标.(2)如图2,将函数图像在y 轴左侧部分沿x 轴翻折,图像其余部分保持不变,得到的新图像记为G .①过点M 作y 轴的垂线l ,当m 时,直线l 与图像G 有且只有两个交点. ②请求出翻折后图像的函数关系式.(3)如图3,点Q 是第二象限内图像上的动点,当m >1 ,n <0,且∠QMB =90°时,是否存在点M ,使得△QMB 与△ABN 相似.若存在,请求出点M 的坐标;若不存在,说明理由.10.(2021·广东·深圳市中考模拟预测)如图,二次函数()2680y ax ax a =-+≠的图象经过点A ,B ,C 三点,且4OB OC OA ==,点D 在抛物线上,//CD x 轴.(1)请求出抛物线的解析式. (2)点P 为y 轴右侧抛物线上一点.①如图①,若OP 平分COD ∠,OP 交CD 于点E ,求点P 的坐标.②如图②,抛物线上一点F 的横坐标为2,直线CF 交x 轴于点G ,过点P 作直线CF 的垂线,垂足为Q ,若PCQ CGO ∽△△,求点Q 的坐标.11.(2021·湖南宁乡·九年级期末)如图,在平面直角坐标系xoy 中,直线:2l y x =-与x 轴、y 轴分别交于点A 和点B ,抛物线2y x bx c =++经过点B ,且与直线l 的另一个交点为(6,)C n .(1)求n 的值和抛物线的解析式;(2)已知点P 是抛物线上位于,B C 之间的一动点(不与点,B C 重合),设点P 的横坐标为,a 当a 为何值时,∆APC 的面积最大,并求出其最大值;(3)在y 轴上是否存在点M ,使以点,,B M C 为顶点的三角形与∆BAO 相似?若存在,直接写出点M 的坐标(不用说理);若不存在,请说明理由.12.(2021·辽宁丹东·中考一模)如图1,在平面直角坐标系中,抛物线232y ax x c =-+()0a ≠与x 轴交于A ,B 两点,A 点坐标为()40-,,与y 轴交于点C ,且C 点坐标为()02,. (1)求抛物线的函数表达式;(2)点D 为第二象限内抛物线上的一个动点,过点D 作DE x ⊥轴于点E ,交AC 于点F ,当线段CD CF =时,求点D 的坐标;(3)在(2)的条件下,设抛物线上点A 与点D 之间有一点P (包括A 、D 两点),在线段EA 上是否存在点Q ,使得以P 、Q 、E 为顶点的三角形与ABC 相似?如果存在,请求出点Q 的坐标;如果不存在,请说明理由;(4)设过点C 的射线与CA 的夹角为α,且1tan 3α=,请直接写出该射线与抛物线的交点M 的坐标.13.(2021·山东阳谷·中考一模)如图1,一次函数的图象与两坐标轴分别交于A ,B 两点,且B 点坐标为()0,4,以点A 为顶点的抛物线解析式为()22y x =-+.(1)求一次函数的解析式;(2)如图2,将抛物线的顶点沿线段AB 平移,此时抛物线顶点记为C ,与y 轴交点记为D ,当点C 的横坐标为-1时,求抛物线的解析式及D 点的坐标;(3)在(2)的条件下,线段AB 上是否存在点P ,使以点B ,D ,P 为顶点的三角形与AOB 相似,若存在,求出所有满足条件的P 点坐标;若不存在,请说明理由.。
2024年中考数学总复习:二次函数(附答案解析)

2024年中考数学总复习:二次函数一.选择题(共25小题)1.抛物线y=(x+1)2﹣1的对称轴是()A.直线x=0B.直线x=1C.直线x=﹣1D.直线y=12.将抛物线y=﹣x2+2向左平移2个单位,再向下平移3个单位,得到抛物线解析式为()A.y=﹣(x+2)2﹣1B.y=﹣(x﹣2)2﹣1C.y=﹣(x+2)2+5D.y=﹣(x﹣2)2+53.已知二次函数y=kx2+2x+1的图象与x轴有交点,则k的取值范围是()A.k<1且k≠0B.k≤1C.k≥1D.k≤1且k≠0 4.把抛物线y=x2+bx+2的图象向右平移3个单位,再向上平移2个单位,所得到的图象的解析式为y=x2﹣4x+7,则b=()A.2B.4C.6D.85.已知点(﹣3,y1),(2,y2),(−12,y3)都在函数y=x2﹣1的图象上,则()A.y2<y1<y3B.y1<y3<y2C.y1<y2<y3D.y3<y2<y1 6.二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:①当x>﹣1时,y的值随x值的增大而增大;②a﹣b+c>0;③4a+b=0;④9a+c>3b;其中正确的结论是()A.①B.②C.③D.④7.已知二次函数y=3(x﹣1)2+k的图像上有三点A(√2,y1),B(3,y2),A(0,y3),则y1,y2,y3为的大小关系为()A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y2>y3>y18.A(−12,y1),B(1,y2),C(4,y3)三点都在二次函数y=﹣(x﹣1)2+k的图象上,则y1,y2,y3的大小关系为()A.y1<y2<y3B.y1<y3<y2C.y3<y1<y2D.y3<y2<y1第1页(共17页)。
中考备考数学总复习第12讲二次函数(含解析)
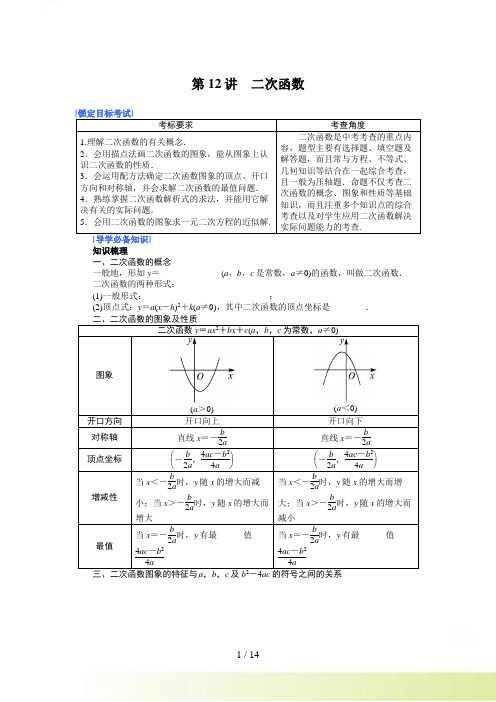
第12讲 二次函数[锁定目标考试]考标要求考查角度1.理解二次函数的有关概念. 2.会用描点法画二次函数的图象,能从图象上认识二次函数的性质. 3.会运用配方法确定二次函数图象的顶点、开口方向和对称轴,并会求解二次函数的最值问题. 4.熟练掌握二次函数解析式的求法,并能用它解决有关的实际问题. 5.会用二次函数的图象求一元二次方程的近似解. 二次函数是中考考查的重点内容,题型主要有选择题、填空题及解答题,而且常与方程、不等式、几何知识等结合在一起综合考查,且一般为压轴题.命题不仅考查二次函数的概念、图象和性质等基础知识,而且注重多个知识点的综合考查以及对学生应用二次函数解决实际问题能力的考查.[导学必备知识]知识梳理一、二次函数的概念一般地,形如y =______________(a ,b ,c 是常数,a ≠0)的函数,叫做二次函数. 二次函数的两种形式:(1)一般形式:____________________________;(2)顶点式:y =a (x -h )2+k (a ≠0),其中二次函数的顶点坐标是________.二、二次函数的图象及性质二次函数y =ax 2+bx +c (a ,b ,c 为常数,a ≠0) 图象(a >0)(a <0) 开口方向 开口向上 开口向下对称轴 直线x =-b 2a 直线x =-b 2a顶点坐标 ⎝⎛⎭⎫-b 2a ,4ac -b 24a ⎝⎛⎭⎫-b 2a ,4ac -b 24a增减性 当x <-b 2a 时,y 随x 的增大而减小;当x >-b 2a 时,y 随x 的增大而增大 当x <-b 2a时,y 随x 的增大而增大;当x >-b 2a时,y 随x 的增大而减小最值 当x =-b 2a 时,y 有最______值4ac -b 24a 当x =-b 2a 时,y 有最______值4ac -b 24a三、二次函数图象的特征与a ,b ,c 及b 2-4ac 的符号之间的关系四、二次函数图象的平移抛物线y=ax2与y=a(x-h)2,y=ax2+k,y=a(x-h)2+k中|a|相同,则图象的________和大小都相同,只是位置不同.它们之间的平移关系如下:五、二次函数关系式的确定1.设一般式:y=ax2+bx+c(a≠0).若已知条件是图象上三个点的坐标,则设一般式y=ax2+bx+c(a≠0),将已知条件代入,求出a,b,c的值.2.设交点式:y=a(x-x1)(x-x2)(a≠0).若已知二次函数图象与x轴的两个交点的坐标,则设交点式:y=a(x-x1)(x-x2)(a≠0),将第三点的坐标或其他已知条件代入,求出待定系数a,最后将关系式化为一般式.3.设顶点式:y=a(x-h)2+k(a≠0).若已知二次函数的顶点坐标或对称轴方程与最大值或最小值,则设顶点式:y=a(x-h )2+k (a ≠0),将已知条件代入,求出待定系数化为一般式.六、二次函数与一元二次方程的关系1.二次函数y =ax 2+bx +c (a ≠0),当y =0时,就变成了ax 2+bx +c =0(a ≠0).2.ax 2+bx +c =0(a ≠0)的解是抛物线与x 轴交点的________.3.当Δ=b 2-4ac >0时,抛物线与x 轴有两个不同的交点;当Δ=b 2-4ac =0时,抛物线与x 轴有一个交点;当Δ=b 2-4ac <0时,抛物线与x 轴没有交点.4.设抛物线y =ax 2+bx +c 与x 轴两交点坐标分别为A (x 1,0),B (x 2,0),则x 1+x 2=________,x 1·x 2=________.自主测试1.下列二次函数中,图象以直线x =2为对称轴,且经过点(0,1)的是( )A .y =(x -2)2+1B .y =(x +2)2+1C .y =(x -2)2-3D .y =(x +2)2-32. 如图所示的二次函数y=ax 2+bx+c 的图象中,刘星同学观察得出了下面四个结论:(1)b 2-4ac >0;(2)c >1;(3)2a-b <0;(4)a+b+c <0.你认为其中错误的有( )A .2个B .3个C .4个D .1个3.当m =__________时,函数y =(m -3)xm 2-7+4是二次函数.4.(上海)将抛物线y =x 2+x 向下平移2个单位,所得新抛物线的表达式是________.5.(广东珠海)如图,二次函数y =(x -2)2+m 的图象与y 轴交于点C ,点B 是点C 关于该二次函数图象的对称轴对称的点.已知一次函数y =kx +b 的图象经过该二次函数图象上点A (1,0)及点B .(1)求二次函数与一次函数的解析式;(2)根据图象,写出满足kx +b ≥(x -2)2+m 的x 的取值范围.[探究重难方法]考点一、二次函数的图象及性质【例1】 (1)二次函数y =-3x 2-6x +5的图象的顶点坐标是( )A .(-1,8)B .(1,8)C .(-1,2)D .(1,-4)(2)已知抛物线y =ax 2+bx +c (a >0)的对称轴为直线x =1,且经过点(-1,y 1),(2,y 2),试比较y 1和y 2的大小:y 1________y 2.(填“>”“<”或“=”)解析:(1)抛物线的顶点坐标可以利用顶点坐标公式或配方法来求.∵-b 2a=--62×(-3)=-1, 4ac -b 24a =4×(-3)×5-(-6)24×(-3)=8, ∴二次函数y =-3x 2-6x +5的图象的顶点坐标是(-1,8).故选A .(2)点(-1,y1),(2,y2)不在对称轴的同一侧,不能直接利用二次函数的增减性来判断y1,y2的大小,可先根据抛物线关于对称轴的对称性,然后再用二次函数的增减性即可.设抛物线经过点(0,y3),∵抛物线对称轴为直线x=1,∴点(0,y3)与点(2,y2)关于直线x=1对称.∴y3=y2.∵a>0,∴当x<1时,y随x的增大而减小.∴y1>y3.∴y1>y2.答案:(1)A(2)>方法总结1.将抛物线解析式写成y=a(x-h)2+k的形式,则顶点坐标为(h,k),对称轴为直线x=h,也可应用对称轴公式x=-b2a ,顶点坐标⎝⎛⎭⎪⎫-b2a,4ac-b24a来求对称轴及顶点坐标.2.比较两个二次函数值大小的方法:(1)直接代入自变量求值法;(2)当自变量在对称轴两侧时,看两个数到对称轴的距离及函数值的增减性判断;(3)当自变量在对称轴同侧时,根据函数值的增减性判断.触类旁通1已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是()A.a>0 B.当x>1时,y随x的增大而增大C.c<0 D.3是方程ax2+bx+c=0的一个根考点二、利用二次函数图象判断a,b,c的符号【例2】如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a +b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是__________.(只要求填写正确命题的序号)解析:由图象可知过(1,0),代入得到a+b+c=0;根据-b2a=-1,推出b=2a;根据图象关于对称轴对称,得出与x轴的交点是(-3,0),(1,0);由a-2b+c=a-2b-a-b=-3b<0,根据结论判断即可.答案:①③方法总结根据二次函数的图象确定有关代数式的符号,是二次函数中的一类典型的数形结合问题,具有较强的推理性.解题时应注意a决定抛物线的开口方向,c决定抛物线与y轴的交点,抛物线的对称轴由a,b共同决定,b2-4ac决定抛物线与x轴的交点情况.当x=1时,决定a+b+c的符号,当x=-1时,决定a-b+c的符号.在此基础上,还可推出其他代数式的符号.运用数形结合的思想更直观、更简捷.触类旁通2小明从如图的二次函数y=ax2+bx+c的图象中,观察得出了下面五个结论:①c<0;②abc>0;③a-b+c>0;④2a-3b=0;⑤c-4b>0,你认为其中正确的结论有()A.2个 B.3个C.4个 D.5个考点三、二次函数图象的平移【例3】二次函数y=-2x2+4x+1的图象怎样平移得到y=-2x2的图象()A.向左平移1个单位,再向上平移3个单位B.向右平移1个单位,再向上平移3个单位C.向左平移1个单位,再向下平移3个单位D.向右平移1个单位,再向下平移3个单位解析:首先将二次函数的解析式配方化为顶点式,然后确定如何平移,即y=-2x2+4x+1=-2(x-1)2+3,将该函数图象向左平移1个单位,再向下平移3个单位就得到y=-2x2的图象.答案:C方法总结二次函数图象的平移实际上就是顶点位置的变换,因此先将二次函数解析式转化为顶点式确定其顶点坐标,然后按照“左加右减、上加下减”的规律进行操作.触类旁通3将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数解析式是()A.y=(x-1)2+2 B.y=(x+1)2+2 C.y=(x-1)2-2 D.y=(x+1)2-2考点四、确定二次函数的解析式【例4】如图,四边形ABCD是菱形,点D的坐标是(0,3),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.(1)求A,B,C三点的坐标;(2)求经过A,B,C三点的抛物线的解析式.解:(1)由抛物线的对称性可知AE=BE.∴△AOD≌△BEC.∴OA=EB=EA.设菱形的边长为2m,在Rt△AOD中,m2+(3)2=(2m)2,解得m=1.∴DC=2,OA=1,OB=3.∴A ,B ,C 三点的坐标分别为(1,0),(3,0),(2,3). (2)解法一:设抛物线的解析式为y =a (x -2)2+3,代入A 的坐标(1,0),得a =- 3. ∴抛物线的解析式为y =-3(x -2)2+ 3.解法二:设这个抛物线的解析式为y =ax 2+bx +c ,由已知抛物线经过A (1,0),B (3,0),C (2,3)三点,得⎩⎪⎨⎪⎧ a +b +c =0,9a +3b +c =0,4a +2b +c =3,解这个方程组,得⎩⎪⎨⎪⎧ a =-3,b =43,c =-3 3.∴抛物线的解析式为y =-3x 2+43x -3 3.方法总结 用待定系数法求二次函数解析式,需根据已知条件,灵活选择解析式:若已知图象上三个点的坐标,可设一般式;若已知二次函数图象与x 轴两个交点的横坐标,可设交点式;若已知抛物线顶点坐标或对称轴与最大(或小)值,可设顶点式.触类旁通4 已知抛物线y =-12x 2+(6-m 2)x +m -3与x 轴有A ,B 两个交点,且A ,B 两点关于y 轴对称.(1)求m 的值;(2)写出抛物线的关系式及顶点坐标.考点五、二次函数的实际应用【例5】 我市某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对该特产的销售收益为:每投入x 万元,可获得利润P =-1100(x -60)2+41(万元).当地政府拟在“十二·五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的收益为:每投入x 万元,可获利润Q =-99100(100-x )2+2945(100-x )+160(万元). (1)若不进行开发,求5年所获利润的最大值是多少;(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少;(3)根据(1)、(2),该方案是否具有实施价值?解:(1)当x =60时,P 最大且为41万元,故五年获利最大值是41×5=205(万元).(2)前两年:0≤x ≤50,此时因为P 随x 的增大而增大,所以x =50时,P 值最大且为40万元,所以这两年获利最大为40×2=80(万元).后三年:设每年获利为y 万元,当地额为x 万元,则外地额为(100-x )万元,所以y =P +Q =⎣⎡⎦⎤-1100(x -60)2+41+⎝⎛⎭⎫-99100x 2+2945x +160=-x 2+60x +165=-(x -30)2+1 065,表明x =30时,y 最大且为1 065,那么三年获利最大为1 065×3=3 195(万元),故五年获利最大值为80+3 195-50×2=3 175(万元).(3)有极大的实施价值.方法总结 运用二次函数的性质解决生活和实际生产中的最大值和最小值问题是最常见的题目类型,解决这类问题的方法是:1.列出二次函数的关系式,列关系式时,要根据自变量的实际意义,确定自变量的取值范围.2.在自变量取值范围内,运用公式法或配方法求出二次函数的最大值和最小值. 触类旁通5一玩具厂去年生产某种玩具,成本为10元/件,出厂价为12元/件,年销售量为2万件.今年计划通过适当增加成本来提高产品档次,以拓展市场.若今年这种玩具每件的成本比去年成本增加0.7x 倍,今年这种玩具每件的出厂价比去年出厂价相应提高0.5x 倍,则预计今年年销售量将比去年年销售量增加x 倍(本题中0<x ≤11).(1)用含x 的代数式表示,今年生产的这种玩具每件的成本为__________元,今年生产的这种玩具每件的出厂价为__________元;(2)求今年这种玩具的每件利润y (元)与x 之间的函数关系式;(3)设今年这种玩具的年销售利润为w 万元,求当x 为何值时,今年的年销售利润最大?最大年销售利润是多少万元?注:年销售利润=(每件玩具的出厂价-每件玩具的成本)×年销售量.[品鉴经典考题]1.(湖南株洲)如图,已知抛物线与x 轴的一个交点为A (1,0),对称轴是x =-1,则抛物线与x 轴的另一个交点坐标是( )A .(-3,0)B .(-2,0)C .x =-3D .x =-2 2.(湖南郴州)抛物线y =(x -1)2+2的顶点坐标是( )A .(-1,2)B .(-1,-2)C .(1,-2)D .(1,2)3. (湖南娄底)已知二次函数y =x 2-(m 2-2)x -2m 的图象与x 轴交于点A (x 1,0)和点B (x 2,0),x 1<x 2,与y 轴交于点C ,且满足1x 1+1x 2=12.(1)求这个二次函数的解析式;(2)探究:在直线y =x +3上是否存在一点P ,使四边形P ACB 为平行四边形?如果有,求出点P 的坐标;如果没有,请说明理由.4.(湖南长沙)在长株潭建设两型社会的过程中,为推进节能减排,发展低碳经济,我市某公司以25万元购得某项节能产品的生产技术后,再投入100万元购买生产设备,进行该产品的生产加工.已知生产这种产品的成本价为每件20元.经过市场调研发现,该产品的销售单价定在25元到30元之间较为合理,并且该产品的年销售量y (万件)与销售单价x (元)之间的函数关系式为y =⎩⎪⎨⎪⎧40-x ,25≤x ≤30,25-0.5x ,30<x ≤35(年获利=年销售收入-生产成本-成本).(1)当销售单价定为28元时,该产品的年销售量为多少万件?(2)求该公司第一年的年获利W (万元)与销售单价x (元)之间的函数关系式,并说明的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?(3)第二年,该公司决定给希望工程捐款Z 万元,该项捐款由两部分组成:一部分为10万元的固定捐款;另一部分则为每销售一件产品,就抽出一元钱作为捐款.若除去第一年的最大获利(或最小亏损)以及第二年的捐款后,到第二年年底,两年的总盈利不低于67.5万元,请你确定此时销售单价的范围.5. (湖南湘潭)如图,抛物线y =ax 2-32x -2(a ≠0)的图象与x 轴交于A ,B 两点,与y 轴交于C 点,已知B 点坐标为(4,0).(1)求抛物线的解析式;(2)试探究△ABC 的外接圆的圆心位置,并求出圆心坐标;(3)若点M 是线段BC 下方的抛物线上一点,求△MBC 的面积的最大值,并求出此时M 点的坐标.[研习预测试题]1.抛物线y =x 2-6x +5的顶点坐标为( )A .(3,-4)B .(3,4)C .(-3,-4)D .(-3,4)2.由二次函数y =2(x -3)2+1,可知( )A .其图象的开口向下B .其图象的对称轴为直线x =-3C .其最小值为1D .当x <3时,y 随x 的增大而增大3.已知函数y =(k -3)x 2+2x +1的图象与x 轴有交点,则k 的取值范围是( )A .k <4B .k ≤4C .k <4且k ≠3D .k ≤4且k ≠34.如图,平面直角坐标系中,两条抛物线有相同的对称轴,则下列关系正确的是( )(第4题图) A .m =n ,k >h B .m =n ,k <h C .m >n ,k =hD .m <n ,k =h5.如图,已知二次函数y =x 2+bx +c 的图象经过点A (-1,0),B (1,-2),该图象与x 轴的另一交点为C ,则AC 长为__________.(第5题图)6.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:x …-2-1012…y …04664…从上表可知,下列说法中正确的是__________.(填写序号)①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;③抛物线的对称轴是直线x=1 2;④在对称轴左侧,y随x增大而增大.7.抛物线y=-x2+bx+c的图象如图所示,若将其向左平移2个单位,再向下平移3个单位,则平移后的解析式为__________.8.长江中下游地区发生了特大旱情,为抗旱保丰收,某地政府制定了农户购买抗旱设备的补贴办法,其中购买Ⅰ型、Ⅱ型抗旱设备所的金额与政府补贴的额度存在下表所示的函数对应关系.(1)分别求y1和y2的函数解析式;(2)有一农户同时对Ⅰ型、Ⅱ型两种设备共10万元购买,请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.9.如图,已知二次函数L1:y=x2-4x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C.(1)写出二次函数L 1的开口方向、对称轴和顶点坐标;(2)研究二次函数L 2:y =kx 2-4kx +3k (k ≠0).①写出二次函数L 2与二次函数L 1有关图象的两条相同的性质;②若直线y =8k 与抛物线L 2交于E ,F 两点,问线段EF 的长度是否发生变化?如果不会,请求出EF 的长度;如果会,请说明理由. 参考答案【知识梳理】一、ax 2+bx +c (1)y =ax 2+bx +c (a ,b ,c 是常数,a ≠0) (2)(h ,k )二、小 大三、y 轴 左 右四、形状六、2.横坐标 4.-b a c a导学必备知识自主测试1.C2.D ∵抛物线与x 轴有两个交点,∴b 2-4ac >0;与y 轴交点在(0,0)与(0,1)之间,∴0<c <1,∴(2)错;∵-b 2a >-1,∴b 2a<1,∵a <0,∴2a <b ,∴2a -b <0; 当x =1时,y =a +b +c <0,故选D.3.-3 由题意,得m 2-7=2且m -3≠0,解得m =-3.4.y =x 2+x -2 因为抛物线向下平移2个单位,则y 值在原来的基础上减2,所以新抛物线的表达式是y =x 2+x -2.5.解:(1)由题意,得(1-2)2+m =0,解得m =-1,∴y =(x -2)2-1.当x =0时,y =(0-2)2-1=3,∴C (0,3).∵点B 与C 关于直线x =2对称,∴B (4,3).于是有⎩⎪⎨⎪⎧ 0=k +b ,3=4k +b ,解得⎩⎪⎨⎪⎧ k =1,b =-1.∴y =x -1.(2)x 的取值范围是1≤x ≤4.探究考点方法触类旁通1.D触类旁通2.C ∵抛物线开口向上,∴a >0;∵抛物线与y 轴交于负半轴,∴c <0;对称轴在y 轴右侧,a ,b 异号,故b <0,∴abc >0.由题图知当x =-1时,y >0,即a -b +c >0.对称轴是直线x =13, ∴-b 2a =13,即2a +3b =0; 由⎩⎪⎨⎪⎧a -b +c >0,2a +3b =0,得c -52b >0. 又∵b <0,∴c -4b >0.∴正确的结论有4个.触类旁通3.A 因为将二次函数y =x 2向右平移1个单位,得y =(x -1)2,再向上平移2个单位后,得y =(x -1)2+2,故选A.触类旁通4.解:(1)∵抛物线与x 轴的两个交点关于y 轴对称,∴抛物线的对称轴即为y 轴.∴-6-m 22×⎝⎛⎭⎫-12=0. ∴m =±6.又∵抛物线开口向下,∴m -3>0,即m >3. ∴m =6.(2)∵m =6,∴抛物线的关系式为y =-12x 2+3,顶点坐标为(0,3). 触类旁通5.解:(1)(10+7x ) (12+6x )(2)y =(12+6x )-(10+7x )=2-x .(3)∵w =2(1+x )(2-x )=-2x 2+2x +4,∴w =-2(x -0.5)2+4.5.∵-2<0,0<x ≤11,∴当x =0.5时,w 最大=4.5(万元).答:当x 为0.5时,今年的年销售利润最大,最大年销售利润是4.5万元. 品鉴经典考题1.A 点A 到对称轴的距离为2,由抛物线的对称性知,另一个交点的横坐标为-3,所以另一个交点坐标为(-3,0).2.D3.解:(1)由已知得x 1+x 2=m 2-2,x 1x 2=-2m .∵1x 1+1x 2=12,即x 1+x 2x 1x 2=12, ∴m 2-2-2m =12, 解得m =1或m =-2.当m =1时,y =x 2+x -2,得A (-2,0),B (1,0);当m =-2时,y =x 2-2x +4,与x 轴无交点,舍去.∴这个二次函数的解析式为y =x 2+x -2.(2)由(1)得A (-2,0),B (1,0),C (0,-2).假设存在一点P ,使四边形P ACB 是平行四边形,则PB ∥AC 且PB =AC ,根据平移知识可得P (-1,2),经验证P (-1,2)在直线y =x +3上,故在直线y =x +3上存在一点P (-1,2),使四边形P ACB 为平行四边形.4.解:(1)当x =28时,y =40-28=12.所以,产品的年销售量为12万件.(2)①当25≤x ≤30时,W =(40-x )(x -20)-25-100=-x 2+60x -925=-(x -30)2-25,故当x =30时,W 最大为-25,即公司最少亏损25万元;②当30<x ≤35时,W =(25-0.5x )(x -20)-25-100=-12x 2+35x -625=-12(x -35)2-12.5,故当x =35时,W 最大为-12.5,及公司最少亏损12.5万元,综上所述,的第一年,公司亏损,最少亏损是12.5万元;(3)①当25≤x ≤30时,W =(40-x )(x -20-1)-12.5-10=-x 2+61x -862.5, 令W =67.5,则-x 2+61x -862.5=67.5,化简得x 2-61x +930=0,x 1=30,x 2=31,此时,当两年的总盈利不低于6.75万元时,x =30.②当30<x ≤35时,W =(25-0.5x )(x -20-1)-12.5-10=-12x 2+35.5x -547.5, 令W =67.5,则-12x 2+35.5x -547.5=67.5, 化简得x 2-71x +1 230=0,x 1=30,x 2=41,此时,当两年的总盈利不低于67.5万元时,30<x ≤35.所以,到第二年年底,两年的总盈利不低于67.5万元,此时销售单价的范围是30≤x ≤35.5.解:(1)将点B (4,0)代入y =ax 2-32x -2(a ≠0)中,得a =12.∴抛物线的解析式为y =12x 2-32x -2. (2)∵当12x 2-32x -2=0时,解得x 1=4,x 2=-1, ∴A 点坐标为(-1,0),则OA =1.∵当x =0时,y =12x 2-32x -2=-2,∴C 点坐标为(0,-2),则OC =2.在Rt △AOC 与Rt △COB 中,OA OC =OC OB =12, ∴Rt △AOC ∽Rt △COB .∴∠ACO =∠CBO .∴∠ACB =∠ACO +∠OCB =∠CBO +∠OCB =90°.∴△ABC 为直角三角形.∴△ABC 的外接圆的圆心为AB 中点,其坐标为⎝⎛⎭⎫32,0.(3)连接OM .设M 点坐标为⎝⎛⎭⎫x ,12x 2-32x -2,则S △MBC =S △OBM +S △OCM -S △OBC =12×4×⎝⎛⎭⎫-12x 2+32x +2+12×2×x -12×2×4 =-(x -2)2+4.∴当x =2时,△MBC 的面积有最大值为4,点M 的坐标为(2,-3).研习预测试题1.A 2.C3.D 由题意,得22-4(k -3)≥0,且k -3≠0,解得k ≤4且k ≠3,故选D.4.A5.3 ∵把A (-1,0),B (1,-2)代入y =x 2+bx +c 得⎩⎪⎨⎪⎧1-b +c =0,1+b +c =-2,解得⎩⎪⎨⎪⎧b =-1,c =-2,∴y =x 2-x -2,解x 2-x -2=0得x 1=-1,x 2=2, ∴C 点坐标为(2,0),∴AC =3.6.①③④ 由图表可知当x =0时,y =6;当x =1时,y =6,∴抛物线的对称轴是直线x =12,③正确;∵抛物线与x 轴的一个交点为(-2,0),对称轴是直线x =12,∴抛物线与x 轴的另一个交点为(3,0),①正确;由图表可知,在对称轴左侧,y 随x 增大而增大,④正确;当x =12时,y 取得最大值,②错误. 7.y =-x 2-2x 由题中图象可知,对称轴为直线x =1,所以-b -2=1,即b =2.把点(3,0)代入y =-x 2+2x +c ,得c =3.故原图象的解析式为y =-x 2+2x +3,即y =-(x -1)2+4,然后向左平移2个单位,再向下平移3个单位,得y =-(x -1+2)2+4-3,即y =-x 2-2x .8.解:(1)由题意,得5k =2,∴k =25,∴y 1=25x ;⎩⎪⎨⎪⎧ 4a +2b =2.4,16a +4b =3.2,∴⎩⎨⎧ a =-15,b =85,∴y 2=-15x 2+85x . (2)设该农户t 万元购Ⅱ型设备,(10-t )万元购Ⅰ型设备,共获补贴Q 万元.∴y 1=25(10-t )=4-25t ,y 2=-15t 2+85t . ∴Q =y 1+y 2=4-25t -15t 2+85t =-15t 2+65t +4=-15(t -3)2+295.∴当t =3时,Q 最大=295. ∴10-t =7.即7万元购Ⅰ型设备,3万元购Ⅱ型设备,能获得最大补贴金额,最大补贴金额为5.8万元.9.解:(1)二次函数L 1的开口向上,对称轴是直线x =2,顶点坐标(2,-1).(2)①二次函数L 2与L 1有关图象的两条相同的性质:对称轴为直线x =2或顶点的横坐标为2;都经过A (1,0),B (3,0)两点.②线段EF 的长度不会发生变化.∵直线y =8k 与抛物线L 2交于E ,F 两点,∴kx 2-4kx +3k =8k ,∵k ≠0,∴x 2-4x +3=8,解得x 1=-1,x 2=5.∴EF =x 2-x 1=6,∴线段EF 的长度不会发生变化.。
2023年中考数学压轴题专题04 二次函数与相似问题-【含答案】

专题4二次函数与相似问题函数中因动点产生的相似三角形问题一般有三个解题途径①求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
相似三角形常见的判定方法:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;这是判定三角形相似的一种基本方法.相似的基本图形可分别记为“A”型和“X”型,如图所示在应用时要善于从复杂的图形中抽象出这些基本图形.(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.判定定理“两边及其夹角法”是常用的解题依据,一般分三步:寻找一组等角,分两种情况列比例方程,解方程并检验.如果已知∠A=∠D,探求△ABC与△DEF相似,只要把夹∠A和∠D的两边表示出来,按照对应边成比例,分AB DEAC DF=和AB DFAC DE=两种情况列方程.应用判定定理“两角法”解题,先寻找一组等角,再分两种情况讨论另外两组对应角相等.应用判定定理“三边法”解题不多见,根据三边对应成比例列连比式解方程(组).还有一种情况,讨论两个直角三角形相似,如果一组锐角相等,其中一个直角三角形的锐角三角比是确定的,那么就转化为讨论另一个三角形是直角三角形的问题.【例1】(2022•贵港)如图,已知抛物线y=﹣x2+bx+c经过A(0,3)和B(,﹣)两点,直线AB与x轴相交于点C,P是直线AB上方的抛物线上的一个动点,PD⊥x轴交AB于点D.(1)求该抛物线的表达式;(2)若PE∥x轴交AB于点E,求PD+PE的最大值;(3)若以A,P,D为顶点的三角形与△AOC相似,请直接写出所有满足条件的点P,点D的坐标.【例2】.(2022•衡阳)如图,已知抛物线y=x2﹣x﹣2交x轴于A、B两点,将该抛物线位于x轴下方的部分沿x轴翻折,其余部分不变,得到的新图象记为“图象W”,图象W交y轴于点C.(1)写出图象W位于线段AB上方部分对应的函数关系式;(2)若直线y=﹣x+b与图象W有三个交点,请结合图象,直接写出b的值;(3)P为x轴正半轴上一动点,过点P作PM∥y轴交直线BC于点M,交图象W于点N,是否存在这样的点P,使△CMN与△OBC相似?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.【例3】.(2022•桂林)如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y 轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.(1)直接写出A,B,C三点的坐标;(2)求CP+PQ+QB的最小值;(3)过点P作PM⊥y轴于点M,当△CPM和△QBN相似时,求点Q的坐标.【例4】(2022•玉林)如图,已知抛物线:y=﹣2x2+bx+c与x轴交于点A,B(2,0)(A在B的左侧),与y轴交于点C,对称轴是直线x=,P是第一象限内抛物线上的任一点.(1)求抛物线的解析式;(2)若点D为线段OC的中点,则△POD能否是等边三角形?请说明理由;(3)过点P作x轴的垂线与线段BC交于点M,垂足为点H,若以P,M,C为顶点的三角形与△BMH相似,求点P的坐标.1.(2020秋•兴城市期末)如图,抛物线y=ax2+bx+4经过A(4,0),B(﹣1,0)两点,与y轴交于点C,D为第一象限抛物线上的动点,连接AC,BC,DA,DB,DB与AC相交于点E.(1)求抛物线的解析式;(2)如图1,设△ADE的面积为S1,△BCE的面积为S2,当S1=S2+5时,求点D的坐标;(3)如图2,过点C作CF∥x轴,点M是直线CF上的一点,MN⊥CF交抛物线于点N,是否存在以C,M,N为顶点的三角形与△BCO相似?若存在,请直接写出点M的坐标,若不存在,请说明理由.2.(2020秋•郴州期末)已知抛物线y=x2﹣3x+与x轴交于A,B两点(点A在点B的左边).(1)求A,B两点的坐标;(2)如图1,若点D是抛物线上在第四象限的点,连接DA并延长,交y轴于点P,过点D作DE⊥x轴于点E.当△APO与△ADE的面积比为=时.求点D的坐标;(3)如图2,抛物线与y轴相交于点F.若点Q是线段OF上的动点,过点Q作与x轴平行的直线交抛物线于M,N两点(点M在点N的左边).请问是否存在以Q,A,M为顶点的三角形与△QNA相似?若存在,求出点Q的坐标;若不存在,请说明理由.3.(2020秋•长垣市期末)如图1,抛物线y=x2+bx+c与x轴、y轴分别交于点B(6,0)和点C(0,﹣3).(1)求抛物线的解析式;(2)点P是直线BC下方抛物线上一动点,其横坐标为m,连接PB、PC,当△PBC的面积为时,求m 值;(3)如图2,点M是线段OB上的一个动点,过点M作x轴的垂线l分别与直线BC和抛物线交于D,E 两点,是否存在以C,D,E为顶点的三角形与△BDM相似,若存在,请直接写出点M的坐标;若不存在,请说明理由.4.(2021秋•邹城市期末)如图,已知抛物线y=x2+2x的顶点为A,直线y=x+2与抛物线交于B,C两点.(1)求A,B,C三点的坐标;(2)作CD⊥x轴于点D,求证:△ODC∽△ABC;(3)若点P为抛物线上的一个动点,过点P作PM⊥x轴于点M,则是否还存在除C点外的其他位置的点,使以O,P,M为顶点的三角形与△ABC相似?若存在,请求出这样的P点坐标;若不存在,请说明理由.5.(2021秋•攸县期末)如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.①求点M和点N的坐标;②在抛物线的对称轴上找一点Q,使|AQ﹣BQ|的值最大,请直接写出点Q的坐标;③是否存在点P,使四边形MNPD为菱形?并说明理由;(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.6.(2022•禹城市模拟)如图,抛物线经过A(4,0),B(1,0),C(0,﹣2)三点.(1)求出抛物线的解析式;(2)P是抛物线在第一象限上的一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M 为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;=S△ABC,直接写出点D (3)若抛物线上有一点D(点D位于直线AC的上方且不与点B重合)使得S△DCA的坐标.7.(2022•祥云县模拟)如图,已知抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),交y轴于点C(0,3),点M是该抛物线上第一象限内的一个动点,ME垂直x轴于点E,交线段BC于点D,MN∥x轴,交y轴于点N.(1)求抛物线y=ax2+bx+c的表达式;(2)若四边形MNOE是正方形,求该正方形的边长;(3)连结OD,AC,抛物线上是否存在点M,使得以C,O,D为顶点的三角形与△ABC相似,若存在,请求出点M的坐标,若不存在,请说明理由.8.(2022•松江区校级模拟)如图,抛物线y=x2﹣bx+c过点B(3,0),C(0,﹣3),D为抛物线的顶点.(1)求抛物线的解析式以及顶点坐标;(2)连接BC,CD,DB,求∠CBD的正切值;(3)点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点,连接BE,直线BE与对称轴交于点M,在(2)的条件下,点P是抛物线对称轴上的一点,是否存在点P使△CDB和△BMP相似,若存在,求点P坐标,若不存在,请说明理由.9.(2022•平江县一模)如图,抛物线y=ax2+bx+8与x轴交于A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求该抛物线的函数表达式;(2)点P是第一象限内抛物线上的动点,连接PB,PC,设四边形PBOC和△AOC的面积分别为S四边形PBOC ,记S=S四边形PBOC﹣S△AOC,求S最大值点P的坐标及S的最大值;和S△AOC(3)点N是对称轴l右侧抛物线上的动点,在射线ED上是否存在点M,使得以点M,N,E为顶点的三角形与△BOC相似?若存在,求点M的坐标;若不存在,请说明理由.10.(2022•莱州市一模)如图①,在平面直角坐标系中,抛物线y=x2+c经过点A(4,3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,﹣2)且垂直于y轴的直线,连接PO.(1)求抛物线的表达式,并求出顶点B的坐标;(2)试证明:经过点O的⊙P与直线l相切;(3)如图②,已知点C的坐标为(1,2),是否存在点P,使得以点P,O及(2)中的切点为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.11.(2022•巩义市模拟)已知,二次函数y=ax2+bx﹣3的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于C点,点A的坐标为(﹣1,0),且OB=OC.(1)求二次函数的解析式;(2)当0≤x≤4时,求二次函数的最大值和最小值分别为多少?(3)设点C'与点C关于该抛物线的对称轴对称.在y轴上是否存在点P,使△PCC'与△POB相似,且PC 与PO是对应边?若存在,求出点P的坐标;若不存在,请说明理由.12.(2022•澄迈县模拟)在平面直角坐标系中,抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.(1)求该抛物线的函数表达式及顶点C的坐标;(2)设该抛物线上一动点P的横坐标为t.①在图1中,当﹣3<t<0时,求△PBO的面积S与t的函数关系式,并求S的最大值;②在图2中,若点P在该抛物线上,点E在该抛物线的对称轴上,且以A,O,P,E为顶点的四边形是平行四边形,求点P的坐标;③在图3中,若P是y轴左侧该抛物线上的动点,过点P作PM⊥x轴,垂足为M,是否存在点P使得以点P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.13.(2022•丰南区二模)如图①、②,在平面直角坐标系中,一边长为2的等边三角板CDE恰好与坐标系中的△OAB重合,现将三角板CDE绕边AB的中点G(G点也是DE的中点),按顺时针方向旋转180°到△C′ED的位置.(1)直接写出C′的坐标,并求经过O、A、C′三点的抛物线的解析式;(2)点P在第四象限的抛物线上,求△C′OP的最大面积;(3)如图③,⊙G是以AB为直径的圆,过B点作⊙G的切线与x轴相交于点F,抛物线上是否存在一点M,使得△BOF与△AOM相似?若存在,请求出点M的坐标;若不存在,请说明理由.14.(2022•莱芜区三模)如图,在平面直角坐标系中,一次函数y=﹣x+3的图象与x轴交于点A,与y轴交于点B,二次函数y=x2+bx+c的图象经过A和点C(0,﹣3).(1)求二次函数的表达式;(2)如图1,平移线段AC,点A的对应点D落在二次函数在第一象限的图象上,点C的对应点E落在直线AB上,直接写出四边形ACED的形状,并求出此时点D的坐标;(3)如图2,在(2)的条件下,连接CD,交x轴于点M,点P为直线CD下方抛物线上一个动点,过点P作PF⊥x轴,交CD于点F,连接PC,是否存在点P,使得以点P,C,F为顶点的三角形与△COM相似?若存在,求出线段FP的长度;若不存在,请说明理由.15.(2022•临清市三模)如图,抛物线y=﹣x2+bx+c的顶点D坐标为(1,4),且与x轴相交于A,B两点(点A在点B的左侧,与y轴相交于点C,点E在x轴上方且在对称轴左侧的抛物线上运动,点F在抛物线上并且和点E关于抛物线的对称轴对称,作矩形EFGH,其中点G,H都在x轴上.(1)求抛物线解析式;(2)设点F横坐标为m,①用含有m的代数式表示点E的横坐标为(直接填空);②当矩形EFGH为正方形时,求点G的坐标;③连接AD,当EG与AD垂直时,求点G的坐标;(3)过顶点D作DM⊥x轴于点M,过点F作FP⊥AD于点P,直接写出△DFP与△DAM相似时,点F 的坐标.16.(2022•成都模拟)如图①,已知抛物线y=﹣(x﹣1)2+k交x轴于A,B两点,交y轴于点C,P是抛物线上的动点,且满足OB=3OA.(1)求抛物线的解析式;(2)若点P在第一象限,直线y=x+b经过点P且与直线BC交于点E,设点P的横坐标为t,当线段PE 的长度随着t的增大而减小时,求t的取值范围;(3)如图②,过点A作BC的平行线m,与抛物线交于另一点D.点P在直线m上方,点Q在线段AD 上,若△CPQ与△AOC相似,且点P与点O是对应点,求点P的坐标.17.(2022•东莞市校级一模)在平面直角坐标系xOy中,已知抛物线y=﹣x2+2kx+2k2+1与x轴的左交点为A,右交点为B,与y轴的交点为C,对称轴为直线l,对于抛物线上的两点(x1,y1),(x2,y2)(x1<k<x2),当x1+x2=2时,y1﹣y2=0恒成立.(1)求该抛物线的解析式;(2)点M是第二象限内直线AC上方的抛物线上的一点,过点M作MN⊥AC于点N,求线段MN的最大值,并求出此时点M的坐标;(3)点P是直线l右侧抛物线上的一点,PQ⊥l于点Q,AP交直线l于点F,是否存在这样的点P,使△PQF与△ACO相似?若存在,请求出点P的坐标,若不存在,请说明理由.18.(2022•碑林区校级模拟)如图,Rt△ABC中,∠ACB=90°,AB=8,AC=4,以AB所在直线为x轴建立平面直角坐标系,若C(0,2).(1)请直接写出A、B的坐标;(2)求经过A、B、C三点的抛物线表达式;(3)l为抛物线对称轴,P是直线l右侧抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△ABC全等,求满足条件的点P,点E的坐标.【例1】(2022•贵港)如图,已知抛物线y=﹣x2+bx+c经过A(0,3)和B(,﹣)两点,直线AB与x轴相交于点C,P是直线AB上方的抛物线上的一个动点,PD⊥x轴交AB于点D.(1)求该抛物线的表达式;(2)若PE∥x轴交AB于点E,求PD+PE的最大值;(3)若以A,P,D为顶点的三角形与△AOC相似,请直接写出所有满足条件的点P,点D的坐标.【分析】(1)直接利用待定系数法,即可求出解析式;(2)先求出点C的坐标,然后证明Rt△DPE∽Rt△AOC,再由二次函数的最值性质,求出答案;(3)根据题意,可分为两种情况进行分析:当△AOC∽△APD时;当△AOC∽△DAP时;分别求出两种情况的点的坐标,即可得到答案.【解析】(1)将A(0,3)和B(,﹣)代入y=﹣x2+bx+c,,解得,∴该抛物线的解析式为y=﹣x2+2x+3;(2)设直线AB的解析式为y=kx+n,把A(0,3)和B(,﹣)代入,,解得,∴直线AB的解析式为y=﹣x+3,当y=0时,﹣x+3=0,解得:x=2,∴C点坐标为(2,0),∵PD⊥x轴,PE∥x轴,∴∠ACO=∠DEP,∴Rt△DPE∽Rt△AOC,∴,∴PE=PD,∴PD+PE=PD,设点P的坐标为(a,﹣a2+2a+3),则D点坐标为(a,﹣a+3),∴PD=(﹣a2+2a+3)﹣(﹣a+3)=﹣(a﹣)2+,∴PD+PE=﹣(a﹣)2+,∵﹣<0,∴当a=时,PD+PE有最大值为;(3)①当△AOC∽△APD时,∵PD⊥x轴,∠DPA=90°,∴点P纵坐标是3,横坐标x>0,即﹣x2+2x+3=3,解得x=2,∴点D的坐标为(2,0);∵PD⊥x轴,∴点P的横坐标为2,∴点P的纵坐标为:y=﹣22+2×2+3=3,∴点P的坐标为(2,3),点D的坐标为(2,0);②当△AOC∽△DAP时,此时∠APG=∠ACO,过点A作AG⊥PD于点G,∴△APG∽△ACO,∴,设点P的坐标为(m,﹣m2+2m+3),则D点坐标为(m,﹣m+3),则,解得:m=,∴D点坐标为(,1),P点坐标为(,),综上,点P的坐标为(2,3),点D的坐标为(2,0)或P点坐标为(,),D点坐标为(,1).【例2】(2022•衡阳)如图,已知抛物线y=x2﹣x﹣2交x轴于A、B两点,将该抛物线位于x轴下方的部分沿x轴翻折,其余部分不变,得到的新图象记为“图象W”,图象W交y轴于点C.(1)写出图象W位于线段AB上方部分对应的函数关系式;(2)若直线y=﹣x+b与图象W有三个交点,请结合图象,直接写出b的值;(3)P为x轴正半轴上一动点,过点P作PM∥y轴交直线BC于点M,交图象W于点N,是否存在这样的点P,使△CMN与△OBC相似?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.【分析】(1)令x=0和翻折的性质可得C(0,2),令y=0可得点A、B的坐标,利用待定系数法即可求出图象W的解析式;(2)利用数形结合找出当y=﹣x+b经过点C或者y=﹣x+b与y=x2﹣x﹣2相切时,直线y=﹣x+b与新图象恰好有三个不同的交点,①当直线y=﹣x+b经过点C(0,2)时,利用一次函数图象上点的坐标特征,即可求出b值;②当y=﹣x+b与y=x2﹣x﹣2相切时,联立一次函数解析式和抛物线解析式,利用根的判别式Δ=0,即可求出b值.综上即可得出结论;(3)先确定△BOC是等腰直角三角形,分三种情况:∠CNM=90°或∠MCN=90°,分别画图可得结论.【解析】(1)当x=0时,y=﹣2,∴C(0,2),当y=0时,x2﹣x﹣2=0,(x﹣2)(x+1)=0,∴x1=2,x2=﹣1,∴A(﹣1,0),B(2,0),设图象W的解析式为:y=a(x+1)(x﹣2),把C(0,2)代入得:﹣2a=2,∴a=﹣1,∴y=﹣(x+1)(x﹣2)=﹣x2+x+2,∴图象W位于线段AB上方部分对应的函数关系式为:y=﹣x2+x+2(﹣1<x<2);(2)由图象得直线y=﹣x+b与图象W有三个交点时,存在两种情况:①当直线y=﹣x+b过点C时,与图象W有三个交点,此时b=2;②当直线y=﹣x+b与图象W位于线段AB上方部分对应的函数图象相切时,如图1,﹣x+b=﹣x2+x+2,x2﹣2x+b﹣2=0,Δ=(﹣2)2﹣4×1×(b﹣2)=0,∴b=3,综上,b的值是2或3;(3)∵OB=OC=2,∠BOC=90°,∴△BOC是等腰直角三角形,如图2,CN∥OB,△CNM∽△BOC,∵PN∥y轴,∴P(1,0);如图3,CN∥OB,△CNM∽△BOC,当y=2时,x2﹣x﹣2=2,x2﹣x﹣4=0,∴x1=,x2=,∴P(,0);如图4,当∠MCN=90°时,△OBC∽△CMN,∴CN的解析式为:y=x+2,∴x+2=x2﹣x﹣2,∴x1=1+,x2=1﹣(舍),∴P(1+,0),综上,点P的坐标为(1,0)或(,0)或(1+,0).【例3】(2022•桂林)如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.(1)直接写出A,B,C三点的坐标;(2)求CP+PQ+QB的最小值;(3)过点P作PM⊥y轴于点M,当△CPM和△QBN相似时,求点Q的坐标.【分析】(1)由y=﹣x2+3x+4可得A(﹣1,0),B(4,0),C(0,4);(2)将C(0,4)向下平移至C',使CC'=PQ,连接BC'交抛物线的对称轴l于Q,可知四边形CC'QP是平行四边形,及得CP+PQ+BQ=C'Q+PQ+BQ=BC'+PQ,而B,Q,C'共线,故此时CP+PQ+BQ最小,最小值为BC'+PQ的值,由勾股定理可得BC'=5,即得CP+PQ+BQ最小值为6;(3)由在y=﹣x2+3x+4得抛物线对称轴为直线x=﹣=,设Q(,t),则P(,t+1),M(0,t+1),N(,0),知BN=,QN=t,PM=,CM=|t﹣3|,①当=时,=,可解得Q(,)或(,);②当=时,=,得Q(,).【解析】(1)在y=﹣x2+3x+4中,令x=0得y=4,令y=0得x=﹣1或x=4,∴A(﹣1,0),B(4,0),C(0,4);(2)将C(0,4)向下平移至C',使CC'=PQ,连接BC'交抛物线的对称轴l于Q,如图:∵CC'=PQ,CC'∥PQ,∴四边形CC'QP是平行四边形,∴CP=C'Q,∴CP+PQ+BQ=C'Q+PQ+BQ=BC'+PQ,∵B,Q,C'共线,∴此时CP+PQ+BQ最小,最小值为BC'+PQ的值,∵C(0,4),CC'=PQ=1,∴C'(0,3),∵B(4,0),∴BC'==5,∴BC'+PQ=5+1=6,∴CP+PQ+BQ最小值为6;(3)如图:由在y=﹣x2+3x+4得抛物线对称轴为直线x=﹣=,设Q(,t),则P(,t+1),M(0,t+1),N(,0),∵B(4,0),C(0,4);∴BN=,QN=t,PM=,CM=|t﹣3|,∵∠CMP=∠QNB=90°,∴△CPM和△QBN相似,只需=或=,①当=时,=,解得t=或t=,∴Q(,)或(,);②当=时,=,解得t=或t=(舍去),∴Q(,),综上所述,Q的坐标是(,)或(,)或(,).【例4】(2022•玉林)如图,已知抛物线:y=﹣2x2+bx+c与x轴交于点A,B(2,0)(A在B的左侧),与y轴交于点C,对称轴是直线x=,P是第一象限内抛物线上的任一点.(1)求抛物线的解析式;(2)若点D为线段OC的中点,则△POD能否是等边三角形?请说明理由;(3)过点P作x轴的垂线与线段BC交于点M,垂足为点H,若以P,M,C为顶点的三角形与△BMH相似,求点P的坐标.【分析】(1)把点B(2,0)代入y=﹣2x2+bx+c中,再由对称轴是直线x=列方程,两个方程组成方程组可解答;(2)当△POD是等边三角形时,点P在OD的垂直平分线上,所以作OD的垂直平分线与抛物线的交点即为点P,计算OD≠PD,可知△POD不可能是等边三角形;(3)分种情况:①当PC∥x轴时,△CPM∽△BHM时,根据PH的长列方程可解答;②②如图3,△PCM ∽△BHM,过点P作PE⊥y轴于E,证明△PEC∽△COB,可得结论.【解析】(1)由题意得:,解得:,∴抛物线的解析式为:y=﹣2x2+2x+4;(2)△POD不可能是等边三角形,理由如下:如图1,取OD的中点E,过点E作EP∥x轴,交抛物线于点P,连接PD,PO,∵C(0,4),D是OD的中点,∴E(0,1),当y=1时,﹣2x2+2x+4=1,2x2﹣2x﹣3=0,解得:x1=,x2=(舍),∴P(,1),∴OD≠PD,∴△POD不可能是等边三角形;(3)设点P的坐标为(t,﹣2t2+2t+4),则OH=t,BH=2﹣t,分两种情况:①如图2,△CMP∽△BMH,∴∠PCM=∠OBC,∠BHM=∠CPM=90°,∴tan∠OBC=tan∠PCM,∴====2,∴PM=2PC=2t,MH=2BH=2(2﹣t),∵PH=PM+MH,∴2t+2(2﹣t)=﹣2t2+2t+4,解得:t1=0,t2=1,∴P(1,4);②如图3,△PCM∽△BHM,则∠PCM=∠BHM=90°,过点P作PE⊥y轴于E,∴∠PEC=∠BOC=∠PCM=90°,∴∠PCE+∠EPC=∠PCE+∠BCO=90°,∴∠BCO=∠EPC,∴△PEC∽△COB,∴=,∴=,解得:t1=0(舍),t2=,∴P(,);综上,点P的坐标为(1,4)或(,).1.(2020秋•兴城市期末)如图,抛物线y=ax2+bx+4经过A(4,0),B(﹣1,0)两点,与y轴交于点C,D为第一象限抛物线上的动点,连接AC,BC,DA,DB,DB与AC相交于点E.(1)求抛物线的解析式;(2)如图1,设△ADE的面积为S1,△BCE的面积为S2,当S1=S2+5时,求点D的坐标;(3)如图2,过点C作CF∥x轴,点M是直线CF上的一点,MN⊥CF交抛物线于点N,是否存在以C,M,N为顶点的三角形与△BCO相似?若存在,请直接写出点M的坐标,若不存在,请说明理由.【分析】(1)运用待定系数法将A(4,0),B(﹣1,0)代入y=ax2+bx+4,解方程组即可求得答案;(2)根据题意,当S1=S2+5,即S△ABD=S△ABC+5,设D(x,y),表示出△ABD和△ABC的面积,列方程求解即可;(3)分情况讨论,列出三角形相似的三种情况,画出相应图形,设M(m,4),则N(m,﹣m2+3m+4),运用相似三角形性质,建立方程求解即可.【解析】(1)∵抛物线y=ax2+bx+4经过A(4,0),B(﹣1,0)两点,∴,解得:,∴y=﹣x2+3x+4;(2)∵抛物线y=﹣x2+3x+4与y轴交于点C,令x=0,则y=4,∴C(0,4),∵S1=S2+5,∴S1+S△AEB=S2+S△AEB+5,=S△ABC+5,即S△ABD∵A(4,0),B(﹣1,0),∴AB=5,设D(x,y),∴×5×y=×5×4+5,∴y=6,∴﹣x2+3x+4=6,解得:x1=1,x2=2,∴D1(1,6),D2(2,6);(3)设M(m,4),则N(m,﹣m2+3m+4),①如图2,△BOC∽△NMC,则=,∴=,解得:m=0(舍去),m=,经检验,m=是原方程的解,∴M(,4);②如图3,△BOC∽△CMN,则=,∴=,解得:m=0(舍去),m=﹣1,经检验,m=﹣1是原方程的解,∴M(﹣1,4);③如图4,△BOC∽△NMC,则=,∴=,解得:m=0(舍去),m=,经检验,m=是原方程的解,∴M(,4);④如图5,△BOC∽△CMN,则=,∴=,解得:m=0(舍去),m=7,经检验,m=7是原方程的解,∴M(7,4);综上所述,点M的坐标为(,4)或(﹣1,4)或(,4)或(7,4).2.(2020秋•郴州期末)已知抛物线y=x2﹣3x+与x轴交于A,B两点(点A在点B的左边).(1)求A,B两点的坐标;(2)如图1,若点D是抛物线上在第四象限的点,连接DA并延长,交y轴于点P,过点D作DE⊥x轴于点E.当△APO与△ADE的面积比为=时.求点D的坐标;(3)如图2,抛物线与y轴相交于点F.若点Q是线段OF上的动点,过点Q作与x轴平行的直线交抛物线于M,N两点(点M在点N的左边).请问是否存在以Q,A,M为顶点的三角形与△QNA相似?若存在,求出点Q的坐标;若不存在,请说明理由.【分析】(1)在抛物线解析式中,令y=0则可求得A、B的坐标;(2)证明△AOP∽△AED,根据相似三角形面积的比等于对应边的比的平方列比例式可得AE=2,从而得点D的横坐标为3,代入抛物线的解析式可得点D的坐标;(3)如图2所示,若以Q,A,M为顶点的三角形与△QNA相似,有两种情况,但是∠QAM与∠QAN不可能相等,所以最后只存在一种情况:△AQM∽△NQA,列比例式可得结论.【解析】(1)当y=0时,x2﹣3x+=0,解得:x1=1,x2=5,∴A(1,0),B(5,0);(2)∵DE⊥x轴,∴∠AED=90°,∴∠AOP=∠AED=90°,∵∠OAP=∠DAE,∴△AOP∽△AED,∴==,∴=,∵OA=1,∴AE=2,∴OE=3,当x=3时,y=﹣3×3+=﹣2,∴D(3,﹣2);(3)如图2,设Q(0,m),当x=0时,y=,∴F(0,),∵点Q是线段OF上的动点,∴0≤m≤,当y=m时,x2﹣3x+=m,x2﹣6x+5﹣2m=0,x=3,∴x1=3+,x2=3﹣,∴QM=3﹣,QN=3+,在Rt△AOQ中,由勾股定理得:AQ=,∵∠AQM=∠AQN,∴当△AQM和△AQN相似只存在一种情况:△AQM∽△NQA,∴,∴AQ2=NQ•QM,即1+m2=(3+)(3﹣),解得:m1=﹣1+,m2=﹣1﹣(舍),∴Q(0,﹣1+).3.(2020秋•长垣市期末)如图1,抛物线y=x2+bx+c与x轴、y轴分别交于点B(6,0)和点C(0,﹣3).(1)求抛物线的解析式;(2)点P是直线BC下方抛物线上一动点,其横坐标为m,连接PB、PC,当△PBC的面积为时,求m 值;(3)如图2,点M是线段OB上的一个动点,过点M作x轴的垂线l分别与直线BC和抛物线交于D,E 两点,是否存在以C,D,E为顶点的三角形与△BDM相似,若存在,请直接写出点M的坐标;若不存在,请说明理由.【分析】(1)根据点A、B的坐标,利用待定系数法即可求出该抛物线的函数关系式;(2)根据点P是直线BC下方抛物线上一动点,其横坐标为m,表示PH的长,根据三角形的面积列方程解出即可得出结论;(3)先根据两三角形相似判断出∠CED=∠BMD=90°或∠DCE=∠DMB=90°,进而分两种情况讨论即可得出结论.【解析】(1)把点B(6,0)和点C(0,﹣3)代入得:,解得:,∴抛物线的解析式为;(2)设直线BC的解析式为:y=ax+n,由点B(6,0)和C(0,﹣3)得:,解得:,∴直线BC的解析式为,如图1,过点P作y轴的平行线交BC于点H,∵点P的坐标为(m,),PH∥y轴,∴点H的坐标为(m,),∴PH=y H﹣y P=﹣()=﹣,x B﹣x C=6﹣0=6,=PH×6=(﹣)×6=﹣=,∵S△PBC解得:m1=1,m2=5,∴m值为1或5;(3)如图2,∵∠CDE=∠BDM,△CDE与△BDM相似,∴∠CED=∠BMD=90°或∠DCE=∠DMB=90°,设M(x,0),①当∠CED=∠BDM=90°,∴CE∥AB,∵C(0,﹣3),∴点E的纵坐标为﹣3,∵点E在抛物线上,∴x2﹣x﹣3=﹣3.∴x=0(舍)或x=5,∴M(5,0);②当∠DCE=∠DMB=90°,∵OB=6,OC=3,∴BC==3,由(2)知直线BC的关系式为y=x﹣3,∴OM=x,BM=6﹣x,DM=3﹣x,由(2)同理得ED=﹣+3x,∵DM∥OC,∴,即,∴CD=,∴BD=BC﹣CD=﹣x,∵△ECD∽△BMD,∴,即=,∴=x(3﹣x)2,x(6﹣x)(1﹣x)=0,x1=0(舍),x2=6(舍),x3=1,∴M(1,0);综上所述:点M的坐标为(5,0)或(1,0).4.(2021秋•邹城市期末)如图,已知抛物线y=x2+2x的顶点为A,直线y=x+2与抛物线交于B,C两点.(1)求A,B,C三点的坐标;(2)作CD⊥x轴于点D,求证:△ODC∽△ABC;(3)若点P为抛物线上的一个动点,过点P作PM⊥x轴于点M,则是否还存在除C点外的其他位置的点,使以O,P,M为顶点的三角形与△ABC相似?若存在,请求出这样的P点坐标;若不存在,请说明理由.【分析】(1)将抛物线配方后可得顶点A的坐标,将抛物线和一次函数的解析式联立方程组,解出可得B 和C的坐标;(2)先根据两点的距离计算AB、BC、AC的长,根据勾股定理的逆定理可得:∠ABC=90°,最后根据两边的比相等且夹角为90度得两三角形相似;(3)存在,设M(x,0),则P(x,x2+2x),表示OM=|x|,PM=|x2+2x|,分两种情况:有=或=,根据比例式代入可得对应x的值,计算点P的坐标即可.【解答】(1)解:y=x2+2x=(x+1)2﹣1,∴顶点A(﹣1,﹣1);由,解得:或∴B(﹣2,0),C(1,3);(2)证明:∵A(﹣1,﹣1),B(﹣2,0),C(1,3),∴AB==,BC==3,AC==2,∴AB2+BC2=AC2,==,∴∠ABC=90°,∵OD=1,CD=3,∴=,∴,∠ABC=∠ODC=90°,∴△ODC∽△ABC;(3)存在这样的P点,设M(x,0),则P(x,x2+2x),∴OM=|x|,PM=|x2+2x|,当以O,P,M为顶点的三角形与△ABC相似时,有=或=,由(2)知:AB=,CB=3,①当=时,则=,当P在第二象限时,x<0,x2+2x>0,∴,解得:x1=0(舍),x2=﹣,当P在第三象限时,x<0,x2+2x<0,∴=,解得:x1=0(舍),x2=﹣,②当=时,则=3,同理代入可得:x=﹣5或x=1(舍),综上所述,存在这样的点P,坐标为(﹣,﹣)或(﹣,)或(﹣5,15).5.(2021秋•攸县期末)如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.①求点M和点N的坐标;②在抛物线的对称轴上找一点Q,使|AQ﹣BQ|的值最大,请直接写出点Q的坐标;③是否存在点P,使四边形MNPD为菱形?并说明理由;(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.【分析】(1)①函数的对称轴为:x=﹣=,故点M(,),即可求解;②设抛物线与x轴左侧的交点为R(﹣1,0),则点A与R关于抛物线的对称轴对称,连接RB并延长交抛物线的对称轴于点Q,则点Q为所求,即可求解;③四边形MNPD为菱形,首先PD=MN,即(﹣2x2+2x+4)﹣(﹣2x+4)=,解得:x=或(舍去),故点P(,1),而PN==≠MN,即可求解;(2)分∠DBP为直角、∠BDP为直角两种情况,分别求解即可.【解析】(1)①函数的对称轴为:x=﹣=,故点M(,),当x=时,y=﹣2x+4=3,故点N(,3);②设抛物线与x轴左侧的交点为R(﹣1,0),则点A与R关于抛物线的对称轴对称,连接RB并延长交抛物线的对称轴于点Q,则点Q为所求,将R、B的坐标代入一次函数表达式:y=kx+b并解得:直线RB的表达式为:y=4x+4,当x=时,y=6,故点Q(,6);③不存在,理由:设点P(x,﹣2x+4),则点D(x,﹣2x2+2x+4),MN=﹣3=,四边形MNPD为菱形,首先PD=MN,即(﹣2x2+2x+4)﹣(﹣2x+4)=,解得:x=或(舍去),故点P(,1),而PN==≠MN,故不存在点P,使四边形MNPD为菱形;(2)当点P的横坐标为1时,则其坐标为:(1,2),此时点A、B的坐标分别为:(2,0)、(0,4),①当∠DBP为直角时,以B、P、D为顶点的三角形与△AOB相似,则∠BAO=∠BDP=α,tan∠BAO==2=tanα,则sinα=,PA=,PB=AB﹣PA=2﹣=,则PD==,故点D(1,);②当∠BDP为直角时,以B、P、D为顶点的三角形与△AOB相似,则BD∥x轴,则点B、D关于抛物线的对称轴对称,故点D(1,4),综上,点D的坐标为:(1,4)或(1,),将点A、B、D的坐标代入抛物线表达式:y=ax2+bx+c并解得:y=﹣2x2+2x+4或y=﹣x2+3x+4.6.(2022•禹城市模拟)如图,抛物线经过A(4,0),B(1,0),C(0,﹣2)三点.(1)求出抛物线的解析式;(2)P是抛物线在第一象限上的一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M 为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;=S△ABC,直接写出点D (3)若抛物线上有一点D(点D位于直线AC的上方且不与点B重合)使得S△DCA的坐标.。
中考专题:二次函数函数的存在性问题(相似三角形)

二次函数函数的存在性问题(相似三角形)1、)如图,已知抛物线与x 交于A(-1,0)、E(3,0)两点,与y 轴交于点B(0,3)。
(1)求抛物线的解析式; (2)设抛物线顶点为D ,求四边形AEDB 的面积; (3)△AOB 与△DBE 是否相似?如果相似,请给以证明;如果不相似,请说明理由。
2、)矩形OABC 在平面直角坐标系中位置如图所示,A C 、两点的坐标分别为(60)A ,,(03)C -,, 直线34y x =-与BC 边相交于D 点. (1)求点D 的坐标; (2)若抛物线294y ax x =-经过点A ,试确定此抛物线的表达式; (3)设(2)中的抛物线的对称轴与直线OD 交于点M ,点P 为对称轴上一动点,以P O M 、、为顶点的三角形与OCD △相似,求符合条件的点P 的坐标.3、)如图,已知抛物线y =34x 2+bx +c 与坐标轴交于A 、B 、C 三点, A 点的坐标为(-1,0)过点C 的直线y =34tx -3与x 轴交于点Q ,点P 是线段BC 上的一个动点,过P 作PH⊥OB 于点H .若PB =5t , 且0<t <1.(1)填空:点C 的坐标是_ _,b = _,c =_ _;(2)求线段QH 的长(用含t 的式子表示);(3)依点P 的变化,是否存在t 的值,使以P 、H 、Q 为顶点的三角形与△COQ 相似?若存在,求出所有t 的值;若不存在,说明理由.4、)已知,如图1,过点()01E -,作平行于x 轴的直线l ,抛物线214y x =上的两点A B 、的横坐标分别为-1和4,直线AB 交y 轴于点F ,过点A B 、分别作直线l 的垂线,垂足分别为点C 、D ,连接CF DF 、. (1)求点A B F 、、的坐标; (2)求证:CF DF ⊥; (3)点P 是抛物线214y x =对称轴右侧图象上的一动点,过点P 作PQ PO ⊥交x 轴于点Q ,是否存在点P 使得OPQ △与CDF △相似?若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.5、如图,抛物线经过(40)(10)(02)A B C -,,,,,三点.(1)求出抛物线的解析式;(2)P 是抛物线上一动点,过P 作PM x ⊥轴,垂足为M ,是否存在P 点,使得以A ,P ,M 为顶点的三角形与OAC △相似?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由; (3)在直线AC 上方的抛物线上有一点D ,使得DCA △的面积最大,求出点D 的坐标.6、)如图,ABCD 在平面直角坐标系中,6AD =,若OA 、OB 的长是关于x 的一元二次方程27120x x -+=的两个根,且OA OB >.(1)求sin ABC ∠的值. (2)若E 为x 轴上的点,且163AOE S =△,求经过D 、E 两点的直线的解析式,并判断AOE △与DAO △是否相似?(3)若点M 在平面直角坐标系内,则在直线AB 上是否存在点F ,使以A 、C 、F 、M 为顶点的四边形为菱形?若存在,请直接写出F 点的坐标;若不存在,请说明理由.答案1、(09贵州安顺)解:(1) ∵抛物线与y 轴交于点(0,3),∴设抛物线解析式为)0(32≠++=a bx ax y (1′) 根据题意,得⎩⎨⎧=++=+-033903b a b a ,解得⎩⎨⎧=-=21b a∴抛物线的解析式为322++-=x x y (5′) (2)由顶点坐标公式得顶点坐标为(1,4) 设对称轴与x 轴的交点为F∴四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形 =111()222AO BO BO DF OF EF DF ⋅++⋅+⋅=11113(34)124222⨯⨯++⨯+⨯⨯=9(3)相似如图,==∴====∴2220BD BE +=, 220DE = 即: 222BD BE DE +=,所以BDE ∆是直角三角形 ∴90AOB DBE ∠=∠=︒,且AO BO BD BE ==∴AOB ∆∽DBE ∆ 2、(09青海)解:(1)点D 的坐标为(43)-,.(2)抛物线的表达式为23984y x x =-. (3)抛物线的对称轴与x 轴的交点1P 符合条件. ∵OA CB ∥, ∴1POM CDO ∠=∠. ∵190OPM DCO ∠=∠=°, ∴1Rt Rt POM CDO △∽△. ∵抛物线的对称轴3x =, ∴点1P 的坐标为1(30)P ,. 过点O 作OD 的垂线交抛物线的对称轴于点2P . ∵对称轴平行于y 轴, ∴2P MO DOC ∠=∠.∵290POM DCO ∠=∠=°, ∴21Rt Rt P M O DOC △∽△∴点2P 也符合条件,2OP M ODC ∠=∠. ∴121390PO CO P PO DCO ==∠=∠=,°, ∴21Rt Rt P PO DCO △≌△. ∴124PP CD ==.∵点2P 在第一象限,∴点2P 的坐标为2P (34),, ∴符合条件的点P 有两个,分别是1(30)P ,,2P (34),3、(09广西钦州) 解:(1)(0,-3),b =-94,c =-3. (2)由(1),得y =34x 2-94x -3,它与x 轴交于A ,B 两点,得B (4,0). ∴OB =4,又∵OC =3,∴BC =5. 由题意,得△B HP ∽△BOC ,∵OC ∶OB ∶BC =3∶4∶5 , ∴HP ∶HB ∶BP =3∶4∶5 , ∵PB =5t ,∴HB =4t ,HP =3t . ∴OH =OB -HB =4-4t . 由y =34tx -3与x 轴交于点Q ,得Q (4t ,0). ∴OQ =4t . ①当H 在Q 、B 之间时, QH =OH -OQ =(4-4t )-4t =4-8t . ②当H 在O 、Q 之间时,QH =OQ -OH =4t -(4-4t )=8t -4. 综合①,②得QH =|4-8t |;(3)存在t 的值,使以P 、H 、Q 为顶点的三角形与△COQ 相似. ①当H 在Q 、B 之间时,QH =4-8t , 若△QHP ∽△COQ ,则QH ∶CO =HP ∶OQ ,得483t -=34tt, ∴t =732. 若△PHQ ∽△COQ ,则PH ∶CO =HQ ∶OQ ,得33t =484t t -,即t 2+2t -1=0.∴t 11,t 21(舍去).②当H 在O 、Q 之间时,QH =8t -4.若△QHP ∽△COQ ,则QH ∶CO =HP ∶OQ , 得843t -=34t t ,∴t =2532.若△PHQ ∽△COQ ,则PH ∶CO =HQ ∶OQ , 得33t =844t t -,即t 2-2t +1=0.∴t 1=t 2=1(舍去).综上所述,存在t 的值,t 11,t 2=732,t 3=2532.4、(09福建莆田)(1)解:方法一,如图1,当1x =-时,14y =;当4x =时,4y = ∴1A ⎛⎫- ⎪⎝⎭1,4 ()44B , 设直线AB 的解析式为y kx b =+则1444k b k b ⎧-+=⎪⎨⎪+=⎩ 解得341k b ⎧=⎪⎨⎪=⎩∴直线AB 的解析式为314y x =+ ,当0x =时,1y = ()01F ∴, 方法二:求A B 、两点坐标同方法一,如图2,作FG BD ⊥,AH BD ⊥,垂足分别为G 、H ,交y 轴于点N ,则四边形FOMG 和四边形NOMH 均为矩形,设FO x =图3BGF BHA △∽△ BG FG BH AH ∴= 441544x -∴=-解得1x = ()0F ∴,1(2)证明:方法一:在Rt CEF △中,1,2CE EF == 22222125CF CE EF ∴=+=+=CF ∴在Rt DEF △中,42DE EF ==, 222224220DF DE EF ∴=+=+= DF ∴=由(1)得()()1141C D ---,,,, 5CD ∴=, 22525CD ∴== 222CF DF CD ∴+=90CFD ∴∠=° ∴CF DF ⊥方法二:由 (1)知5544AF AC ===,AF AC ∴= 同理:BF BD = ACF AFC ∴∠=∠AC EF ∥ ACF CFO ∴∠=∠ AFC CFO ∴∠=∠ 同理:BFD OFD ∠=∠ 90CFD OFC OFD ∴∠=∠+∠=° 即CF DF ⊥(3)存在. 如图3,作PM x ⊥轴,垂足为点M 又PQ OP ⊥ Rt Rt OPM OQP ∴△∽△ PM OMPQ OP∴= PQ PM OP OM ∴= 设()2104P x x x ⎛⎫> ⎪⎝⎭,,则214PM x OM x ==,①当RtRt QPO CFD △∽△时,12PQ CF OP DF === 21142xPM OM x ∴== 解得2x = ()121P ∴, ②当Rt Rt OPQ CFD △∽△时,2PQ DF OP CF === 2142xPM OM x ∴==解得8x = ()2816P ∴, 综上,存在点()121P ,、()2816P ,使得OPQ △与CDF △相似.(图2)5、(09山东临沂)解:(1)该抛物线过点(02)C -,,∴可设该抛物线的解析式为22y ax bx =+-.将(40)A ,,(10)B ,代入,得1642020a b a b .+-=⎧⎨+-=⎩,解得1252a b .⎧=-⎪⎪⎨⎪=⎪⎩,∴此抛物线的解析式为215222y x x =-+-.(2)存在.如图,设P 点的横坐标为m , 则P 点的纵坐标为215222m m -+-, 当14m <<时, 4AM m =-,215222PM m m =-+-. 又90COA PMA ∠=∠=°, ∴①当21AM AO PM OC ==时, APM ACO △∽△, 即21542222m m m ⎛⎫-=-+- ⎪⎝⎭. 解得1224m m ==,(舍去),(21)P ∴,.②当12AM OC PM OA ==时,APM CAO △∽△,即2152(4)222m m m -=-+-. 解得14m =,25m =(均不合题意,舍去) ∴当14m <<时,(21)P ,. 类似地可求出当4m >时,(52)P -,. 当1m <时,(314)P --,. 综上所述,符合条件的点P 为(21),或(52)-,或(314)--,. (3)如图,设D 点的横坐标为(04)t t <<,则D 点的纵坐标为215222t t -+-. 过D 作y 轴的平行线交AC 于E . 由题意可求得直线AC 的解析式为122y x =-.E ∴点的坐标为122t t ⎛⎫- ⎪⎝⎭,. 2215112222222DE t t t t t ⎛⎫∴=-+---=-+ ⎪⎝⎭.22211244(2)422DAC S t t t t t ⎛⎫∴=⨯-+⨯=-+=--+ ⎪⎝⎭△.∴当2t =时,DAC △面积最大.(21)D ∴,. 6、(09牡丹江)(1)解27120x x -+=得1243x x ==,,OA OB >, 43OA OB ∴==,在Rt AOB △中,由勾股定理有5AB = 4sin 5OA ABC AB ∴∠== (2)∵点E 在x 轴上,163AOES =△ 11623AO OE ∴⨯= 83OE ∴= 880033E E ⎛⎫⎛⎫∴- ⎪ ⎪⎝⎭⎝⎭,或, 由已知可知D (6,4) 设DE y kx b =+,当803E ⎛⎫⎪⎝⎭,时有46803k b k b =+⎧⎪⎨=+⎪⎩解得65165k b ⎧=⎪⎪⎨⎪=-⎪⎩∴61655DEy x =- 同理803E ⎛⎫- ⎪⎝⎭,时,6161313DE y x =+ 在AOE △中,89043AOE OA OE ∠===°,, 在AOD △中,9046OAD OA OD ∠===°,, OE OAOA OD= AOE DAO ∴△∽△ (3)满足条件的点有四个123475224244(38)(30)1472525F F F F ⎛⎫⎛⎫----- ⎪ ⎪⎝⎭⎝⎭,;,;,;,。
中考数学考点17二次函数综合题总复习(解析版)
二次函数综合题【命题趋势】在中考中.二次函数综合题每年必考点.特别是跟几何结合.经常在压轴题中出现。
【中考考查重点】一、线段问题二、面积问题三、等腰、直角三角形问题四、特殊四边形问题五、相似三角形问题六、与角度有关问题考点一:线段问题1.(2021秋•龙沙区期末)如图.抛物线y=ax2+bx+c与x轴交于A(﹣1.0).B(3.0)两点.与y轴交于点C(0.3).抛物线的顶点为D.连接BC.P为线段BC上的一个动点(P不与B、C重合).过点P作PF∥y轴.交抛物线于点F.交x轴于点G.(1)求抛物线的解析式;(2)当PG=2PF时.求点P的坐标;【答案】(1)y=﹣x2+2x+3 (2)P(.)【解答】解:(1)将A(﹣1.0).B(3.0).C(0.3)代入y=ax2+bx+c.∴.∴.∴y=﹣x2+2x+3;(2)设直线BC的解析式为y=kx+b'.∴.∴.∴y=﹣x+3.设P(t.﹣t+3).则F(t.﹣t2+2t+3).G(t.0).∴PG=﹣t+3.PF=﹣t2+2t+3+t﹣3=﹣t2+3t.∵PG=2PF.∴﹣t+3=﹣2t2+6t.∴t=或t=3(舍).∴P(.);考点二:面积问题2.(2021秋•梅里斯区期末节选)如图.在平面直角坐标系中.已知直线y=x﹣2与x轴交于点A.与y轴交于点B.过A、B两点的抛物线y=ax2+bx+c与x轴交于另一点C(﹣1.0).(1)求抛物线的解析式和顶点坐标;(2)探究:在抛物线上直线AB下方是否存在一点P.使△ABP面积最大?若存在.请求出点P的坐标.若不存在.请说明理由;【答案】(1)y=x2﹣x﹣2 .(.﹣)(2)P(2.﹣3)【解答】解:(1)直线y=x﹣2与x轴交于点A.与y轴交于点B.∴A(4.0)、B(0.﹣2).将A、B、C点坐标分别代入二次函数解析式y=ax2+bx+c.∴.∴.∴二次函数解析式为:y=x2﹣x﹣2.化成顶点式为:y=(x﹣)2﹣.∴抛物线的顶点坐标为(.﹣);(2)存在.理由如下:设P点坐标为(x.x2﹣x﹣2)(0<x<4).过点P作PD⊥AC于点D.交AB于点E.则E的坐标表示为(x.x﹣2).∴S△ABP==×4×(x﹣2﹣x2+x+2)=﹣x2+4x=﹣(x﹣2)2+4.∵a=﹣1<0.∴当x=2时S△ABP有最大值.求得P(2.﹣3);考点三:等腰、直角三角形问题3.(2021秋•龙凤区校级期末)如图.已知抛物线y=ax2+bx﹣8的图象与x轴交于A(2.0)和B(﹣8.0).与y轴交于点C.(1)求该抛物线的解析式;(2)点F是直线BC下方抛物线上的一点.当△BCF的面积最大时.在抛物线的对称轴上找一点P.使得△BFP的周长最小.请求出点F的坐标和点P的坐标;(3)在(2)的条件下.是否存在这样的点Q(0.m).使得△BFQ为等腰三角形?如果有.请直接写出点Q的坐标;如果没有.请说明理由.【答案】(1)(2)F(﹣4.﹣12).P(﹣3.﹣10)(3)Q1(0.﹣4)或或或Q4(0.0).【解答】解:(1)将A(2.0)、B(﹣8.0)代入解析式.得.解得:.∴.(2)当x=0时.y=﹣8.∴C(0.﹣8).设直线BC的解析式为y=kx+b.则.解得:.∴直线BC的解析式为y=﹣x﹣8.设.如图1.作FG垂直于x轴交BC于G.则G(n.﹣n﹣8).∴.∵=4FG.∴当FG取得最大值时.S△BCF取得最大值.∴当时.FG取得最大值8.S△BCF取得最大值32.∴F(﹣4.﹣12).作F关于对称轴对称的点F'.∴F'(﹣2.﹣12).当F'、B、P共线时.PB+PF有最小值.此时C△BFP有最小值.设y BF'=ax+b.则.解得:.∴y BF'=﹣2x﹣16.又∵x p=﹣3.∴P(﹣3.﹣10).综上所述.F(﹣4.﹣12).P(﹣3.﹣10).(3)存在.理由如下.①如图2.以BF为底边时.点Q1在BF的中垂线上.∴BF的中垂线与y轴交点即为所求.连接BQ1.FQ1.作FN垂直于y轴.∵Q1B=Q1F.设OQ1=t.则Q1N=12﹣t.∵FN=4.BO=8..∴42+(12﹣t)2=82+t2.解得:t=4.∴Q1(0.﹣4);②以BF为腰时..(i)当BF=BQ2时.设OQ2=s.则.∴160=82+s2.解得:.当时..当时.;(ii)当BF=FQ4时:∵B(﹣8.0).F(﹣4.﹣12).O(0.0).∴F在线段BO的中垂线上.∴FB=FO.∴Q4(0.0);由Q4关于N点对称得Q5(0.﹣24).∵FN⊥y轴.∴FO=BF=FQ5.但此时B、F、Q5三点共线.不合题意;综上所述.点Q的坐标为Q1(0.﹣4)或或或Q4(0.0).4.(2021秋•黄埔区期末)如图.抛物线y=mx2﹣4mx﹣5m(m>0)与x轴交于A、B两点.与y轴交于C点.(1)求抛物线顶点M的坐标(用含m的代数式表示).A.B两点的坐标;(2)是否存在使△BCM为直角三角形的抛物线?若存在.请求出;若不存在.请说明理由.【答案】(1)A.B两点的坐标为(﹣1.0)、(5.0)(2)和【解答】解:(1)∵y=m(x﹣2)2﹣9m.∴抛物线顶点M的坐标为(2.﹣9m).∵抛物线与x轴交于A、B两点.∴当y=0时.mx2﹣4mx﹣5m=0.∵m>0.∴x2﹣4x﹣5=0.解得x1=﹣1.x2=5.∴A.B两点的坐标为(﹣1.0)、(5.0).(2)存在使△BCM为直角三角形的抛物线.过点C作CN⊥DM于点N.则△CMN为直角三角形.CN=OD=2.DN=OC=5m.∴MN=DM﹣DN=4m.∴CM2=CN2+MN2=4+16m2.在Rt△OBC中.BC2=OB2+OC2=25+25m2.在Rt△BDM中.BM2=BD2+DM2=9+81m2.①如果△BCM是直角三角形.且∠BMC=90°时.CM2+BM2=BC2.即4+16m2+9+81m2=25+25m2.解得.∵m>0.∴.∴存在抛物线使得△BCM是直角三角形;②如果△BCM是直角三角形.且∠BCM=90°时.BC2+CM2=BM2.即25+25m2+4+16m2=9+81m2.解得.∵m>0.∴.∴存在抛物线使得△BCM是Rt△;③∵25+25m2>4+16m2.9+81m2>4+16m2.∴以∠CBM为直角的直角三角形不存在.综上.存在抛物线和使△BCM是直角三角形.特考点四:特殊四边形问题5.(2021秋•龙江县期末节选)已知抛物线y=ax2+bx+3的图象与x轴相交于点A和点B(1.0).与y轴交于点C.连接AC.有一动点D在线段AC上运动.过点D作x轴的垂线.交抛物线于点E.交x轴于点F.AB=4.设点D的横坐标为m.(1)求抛物线的解析式;(2)当m=﹣2时.在平面内是否存在点Q.使以B.C.E.Q为顶点的四边形为平行四边形?若存在.请直接写出点Q的坐标;若不存在.请说明理由.【答案】(1)y=﹣x2﹣2x+3 (2)Q点为(3.0)或(﹣1.0)或(﹣3.6)【解答】解:(1)∵点B(1.0).AB=4.∴A(﹣3.0).将B(1.0).A(﹣3.0)代入y=ax2+bx+3.∴.∴.∴y=﹣x2﹣2x+3;(2)存在.理由如下:∵m=﹣2.∴E(﹣2.3).设Q(n.t).①当BC为平行四边形的对角线时..解得.∴Q(3.0);②当BE为平行四边形的对角线时..解得.∴Q(﹣1.0);③当BQ为平行四边形的对角线时..解得.∴Q(﹣3.6);综上所述:当Q点为(3.0)或(﹣1.0)或(﹣3.6)时.以B.C.E.Q为顶点的四边形为平行四边形.6.(2021秋•江西月考)如图.抛物线y=﹣x2+3x+m与x轴的一个交点为A(4.0).另一交点为B.且与y轴交于点C.连接AC.(1)求m的值及该抛物线的对称轴;(2)若点P在直线AC上.点Q是平面内一点.是否存在点Q.使以点A、点B、点P、点Q为顶点的四边形为正方形?若存在.请直接写出Q点的坐标;若不存在.请说明理由.【答案】(1)m=4 y=﹣(x﹣)2+(2)(4.5)或(.﹣).【解答】解:(1)把A(4.0)代入二次函数y=﹣x2+3x+m得:∴﹣16+12+m=0.解得:m=4.∴二次函数的解析式为:y=﹣x2+3x+4=﹣(x﹣)2+.∴二次函数对称轴为直线x=;(2)存在.理由:①当AB是正方形的边时.此时.对应的正方形为ABP′Q′.∵A(4.0).AB=5.∴点Q′的坐标为(4.5);②当AB是正方形的对角线时.此时.对应的矩形为APBQ.∵AB、PQ是正方形对角线.∴线段AB和线段PQ互相垂直平分.∴点Q在抛物线对称轴上.且到x轴的距离为.∴点Q的坐标为(.﹣).故点Q的坐标为(4.5)或(.﹣).考点五:相似三角形问题7.(2021秋•建华区期末节选)抛物线y=x2+bx+c经过A、B(1.0)、C(0.﹣3)三点.点D 为抛物线的顶点.连接AD、AC、BC、DC.(1)求抛物线的解析式;(2)在线段AC上找一点M.使△AOM∽△ABC.请你直接写出点M的坐标;【答案】(1)y=x2+2x﹣3 (2)(.)【解答】解(1)∵抛物线y=x2+bx+c经过B(1.0)、C(0.﹣3).∴.解得.∴抛物线的解析式为:y=x2+2x﹣3.(2)∵△AOM∽△ABC.∴∠AOM=∠ABC.∴OM∥BC.设直线BC的解析式为y=mx+n.直线OM的解析式为y=mx.∴.解得.∴直线BC的解析式为y=3x﹣3.直线OM的解析式为y=3x.联立.解得.∴点M的坐标为(.);考点六:与角度有关的问题8.(2021秋•郧西县期末)如图.抛物线y=ax2+bx﹣3与x轴交于点A(1.0)、B(3.0).与y 轴交于点C.连接AC.BC.(1)求抛物线的函数解析式;(2)Q为抛物线上一点.若∠ACQ=45°.求点Q的坐标.【答案】(1)y=﹣x2+4x﹣3 (2)Q(.)【解答】(1)把A(1.0)、B(3.0)代入y=ax2+bx﹣3.得.解得.∴抛物线的解析式是y=﹣x2+4x﹣3.(2)如图2.点Q在抛物线上.且∠ACQ=45°.过点A作AD⊥CQ于点D.过点D作DF⊥x轴于点F.过点C作CE⊥DF于点E.∵∠ADC=90°.∴∠DAC=∠DCA=45°.∴CD=AD.∵∠E=∠AFD=90°.∴∠ADF=90°﹣∠CDE=∠DCE.∴△CDE≌△DAF(AAS).∴DE=AF.CE=DF.∵∠E=∠OFE=∠COF=90°.∴四边形OCEF是矩形.∴OF=CE.EF=OC=3.设DE=AF=n.∵OA=1.∴CE=DF=OF=n+1.∵DF=3﹣n.∴n+1=3﹣n.解得n=1.∴DE=AF=1.∴CE=DF=OF=2.∴D(2.﹣2).设直线CQ的函数解析式为y=px﹣3.则2p﹣3=﹣2.解得p=.∴直线CD的函数解析式为y=x﹣3.由.得.(不符合题意.舍去).∴点Q的坐标为(.)3.(2021•郴州)将抛物线y=ax2(a≠0)向左平移1个单位.再向上平移4个单位后.得到抛物线H:y=a(x﹣h)2+k.抛物线H与x轴交于点A.B.与y轴交于点C.已知A(﹣3.0).点P是抛物线H上的一个动点.(1)求抛物线H的表达式;(2)如图1.点P在线段AC上方的抛物线H上运动(不与A.C重合).过点P作PD⊥AB.垂足为D.PD交AC于点E.作PF⊥AC.垂足为F.求△PEF的面积的最大值;(3)如图2.点Q是抛物线H的对称轴l上的一个动点.在抛物线H上.是否存在点P.使得以点A.P.C.Q为顶点的四边形是平行四边形?若存在.求出所有符合条件的点P的坐标;若不存在.说明理由.【答案】(1)y=﹣(x+1)2+4 (2)m=﹣时.S△PEF最大值=×()2=(3)P的坐标为(2.﹣5)或(﹣4.﹣5)或(﹣2.3)【解答】解:(1)由题意得抛物线的顶点坐标为(﹣1.4).∴抛物线H:y=a(x+1)2+4.将A(﹣3.0)代入.得:a(﹣3+1)2+4=0.解得:a=﹣1.∴抛物线H的表达式为y=﹣(x+1)2+4;(2)如图1.由(1)知:y=﹣x2﹣2x+3.令x=0.得y=3.∴C(0.3).设直线AC的解析式为y=mx+n.∵A(﹣3.0).C(0.3).∴.解得:.∴直线AC的解析式为y=x+3.设P(m.﹣m2﹣2m+3).则E(m.m+3).∴PE=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m=﹣(m+)2+.∵﹣1<0.∴当m=﹣时.PE有最大值.∵OA=OC=3.∠AOC=90°.∴△AOC是等腰直角三角形.∴∠ACO=45°.∵PD⊥AB.∴∠ADP=90°.∴∠ADP=∠AOC.∴PD∥OC.∴∠PEF=∠ACO=45°.∵PF⊥AC.∴△PEF是等腰直角三角形.∴PF=EF=PE.∴S△PEF=PF•EF=PE2.∴当m=﹣时.S△PEF最大值=×()2=;(3)①当AC为平行四边形的边时.则有PQ∥AC.且PQ=AC.如图2.过点P作对称轴的垂线.垂足为G.设AC交对称轴于点H.则∠AHG=∠ACO=∠PQG.在△PQG和△ACO中..∴△PQG≌△ACO(AAS).∴PG=AO=3.∴点P到对称轴的距离为3.又∵y=﹣(x+1)2+4.∴抛物线对称轴为直线x=﹣1.设点P(x.y).则|x+1|=3.解得:x=2或x=﹣4.当x=2时.y=﹣5.当x=﹣4时.y=﹣5.∴点P坐标为(2.﹣5)或(﹣4.﹣5);②当AC为平行四边形的对角线时.如图3.设AC的中点为M.∵A(﹣3.0).C(0.3).∴M(﹣.).∵点Q在对称轴上.∴点Q的横坐标为﹣1.设点P的横坐标为x.根据中点公式得:x+(﹣1)=2×(﹣)=﹣3.∴x=﹣2.此时y=3.∴P(﹣2.3);综上所述.点P的坐标为(2.﹣5)或(﹣4.﹣5)或(﹣2.3).1.(2021秋•长兴县月考)如图.在平面直角坐标系xOy中.抛物线y=﹣x2+bx+c与x轴交于A(1.0)和B(3.0).点D为线段BC上一点.过点D作y轴的平行线交抛物线于点E.连结BE.(1)求抛物线的解析式;(2)当△BDE为直角三角形时.求线段DE的长度;(3)在抛物线上是否存在这样的点P.使得∠ACP=45°.若存在.求出点P的坐标;若不存在.请说明理由.【答案】(1)y=﹣x2+4x﹣3 (2)DE的长度为2 (3)P(.﹣)【解答】解:(1)∵抛物线y=﹣x2+bx+c与x轴交于A(1.0)和B(3.0).∴.解得:.∴抛物线的解析式为y=﹣x2+4x﹣3.(2)令x=0.则y=﹣3.∴C(0.﹣3).设直线BC的解析式为y=kx+n.∴.解得:.∴直线BC的解析式为y=x﹣3.∵点D为线段BC上一点.∴设D(m.m﹣3).则点E(m.﹣m2+4m﹣3).∴DE=(﹣m2+4m﹣3)﹣(m﹣3)=﹣m2+3m.∵B(3.0).C(0.﹣3).∴OB=OC=3.∴∠OBC=∠OCB=45°.∵DE∥y轴.∴∠EDB=∠OCB=45°.∴点D不可能是直角的顶点.①当点B为直角的顶点时.设DE交x轴于点F.∵∠BDE=45°.∠EBD=90°.∴∠DEB=45°.∴△BED为等腰直角三角形.∴EF=FD=DE.∵DF=3﹣m.∴3﹣m=(﹣m2+3m).解得:m=2或3(m=3不合题意.舍去).∴m=2.∴DE=﹣22+3×2=﹣4+6=2.②当点E为直角顶点时.此时边EB在x轴上.点E与点A重合.∴m=1.∴DE=﹣12+3×1=﹣1+3=2.综上.当△BDE为直角三角形时.线段DE的长度为2.(3)在抛物线上存在点P.使得∠ACP=45°.理由:∵A(1.0).∴OA=1.∴ABOB﹣OA=2.∴AC==.延长CP交x轴于点F.如图.由(2)知:∠OBC=∠OCB=45°.∴∠AFC+∠FCB=45°.∵∠ACP=45°.∴∠ACB+∠FCB=∠ACP=45°.∴∠AFC=∠ACB.∵∠F AC=∠CAB.∴△AFC∽△ACB.∴.∴.∴AF=5.∴OF=OA+AF=6.∴F(6.0).设直线CF的解析式为y=dx+e.∴.解得:.∴直线FC的解析式为y=x﹣3.∴.解得:..∴点P的坐标为(.﹣).2.(2021秋•新荣区月考)如图1.在平面直角坐标系中.二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1.0).B(4.0).与y轴交于C(0.4).(1)求该二次函数的解析式.(2)二次函数位于x轴上方的图象上是否存在点P.使得S△BOP=6S△AOC?如果存在.请求出点P的坐标;若不存在.请说明理由.(3)如图2.D为线段BC上的一个动点.过点D作DE∥y轴.交二次函数的图象于点E.求线段DE长度的最大值.【答案】(1)y=﹣x2+3x+4 (2)P(1.6)或P(2.6)(3)当m=2时.ED有最大值4【解答】解:(1)将点A(﹣1.0).B(4.0).C(0.4)代入y=ax2+bx+c.得.解得.∴y=﹣x2+3x+4;(2)存在.理由如下:∵A(﹣1.0).B(4.0).C(0.4).∴OB=4.AO=1.CO=4.∴S△ACO=×1×4=2.∵S△BOP=6S△AOC.∴S△BOP=12.设P(t.﹣t2+3t+4).∴S△BOP=12=×4×(﹣t2+3t+4).解得t=1或t=2.∴P(1.6)或P(2.6);(3)设直线BC的解析式为y=kx+b.∴.解得.∴y=﹣x+4.设D(m.﹣m+4).则E(m.﹣m2+3m+4).∴ED=﹣m2+3m+4+m﹣4=﹣m2+4m=﹣(m﹣2)2+4.∵D为线段BC上的一个动点.∴0≤m≤4.∴当m=2时.ED有最大值41.(2021•内江)如图.抛物线y=ax2+bx+c与x轴交于A(﹣2.0)、B(6.0)两点.与y轴交于点C.直线l与抛物线交于A、D两点.与y轴交于点E.点D的坐标为(4.3).(1)求抛物线的解析式与直线l的解析式;(2)若点P是抛物线上的点且在直线l上方.连接P A、PD.求当△P AD面积最大时点P 的坐标及该面积的最大值;(3)若点Q是y轴上的点.且∠ADQ=45°.求点Q的坐标.【答案】(1)y=﹣x2+x+3,y=x+1 (2)△P AD的面积的最大值为.P(1.)(3)Q的坐标为(0.)或(0.﹣9)【解答】解:(1)∵抛物线y=ax2+bx+c与x轴交于A(﹣2.0)、B(6.0)两点.∴设抛物线的解析式为y=a(x+2)(x﹣6).∵D(4.3)在抛物线上.∴3=a(4+2)×(4﹣6).解得a=﹣.∴抛物线的解析式为y=﹣(x+2)(x﹣6)=﹣x2+x+3.∵直线l经过A(﹣2.0)、D(4.3).设直线l的解析式为y=kx+m(k≠0).则.解得..∴直线l的解析式为y=x+1;(2)如图1中.过点P作PK∥y轴交AD于点K.设P(m.﹣m2+m+3).则K(m.m+1).∵S△P AD=•(x D﹣x A)•PK=3PK.∴PK的值最大值时.△P AD的面积最大.∵PK=﹣m2+m+3﹣m﹣1=﹣m2+m+2=﹣(m﹣1)2+.∵﹣<0.∴m=1时.PK的值最大.最大值为.此时△P AD的面积的最大值为.P(1.).(3)如图2中.将线段AD绕点A逆时针旋转90°得到AT.则T(﹣5.6).设DT交y轴于点Q.则∠ADQ=45°.∵D(4.3).∴直线DT的解析式为y=﹣x+.∴Q(0.).作点T关于AD的对称点T′(1.﹣6).则直线DT′的解析式为y=3x﹣9.设DQ′交y轴于点Q′.则∠ADQ′=45°.∴Q′(0.﹣9).综上所述.满足条件的点Q的坐标为(0.)或(0.﹣9).2.(2021•西藏)在平面直角坐标系中.抛物线y=﹣x2+bx+c与x轴交于A.B两点.与y轴交于点C.且点A的坐标为(﹣1.0).点C的坐标为(0.5).(1)求该抛物线的解析式;(2)如图(甲).若点P是第一象限内抛物线上的一动点.当点P到直线BC的距离最大时.求点P的坐标;(3)图(乙)中.若点M是抛物线上一点.点N是抛物线对称轴上一点.是否存在点M使得以B.C.M.N为顶点的四边形是平行四边形?若存在.请求出点M的坐标;若不存在.请说明理由.【答案】(1)y=﹣x2+4x+5 (2)P(.)(3)M的坐标为:(3.8)或(﹣3.﹣16)或(7.﹣16)【解答】解:(1)将A的坐标(﹣1.0).点C的坐(0.5)代入y=﹣x2+bx+c得:.解得.∴抛物线的解析式为y=﹣x2+4x+5;(2)过P作PD⊥x轴于D.交BC于Q.过P作PH⊥BC于H.如图:在y=﹣x2+4x+5中.令y=0得﹣x2+4x+5=0.解得x=5或x=﹣1.∴B(5.0).∴OB=OC.△BOC是等腰直角三角形.∴∠CBO=45°.∵PD⊥x轴.∴∠BQD=45°=∠PQH.∴△PHQ是等腰直角三角形.∴PH=.∴当PQ最大时.PH最大.设直线BC解析式为y=kx+5.将B(5.0)代入得0=5k+5.∴k=﹣1.∴直线BC解析式为y=﹣x+5.设P(m.﹣m2+4m+5).(0<m<5).则Q(m.﹣m+5).∴PQ=(﹣m2+4m+5)﹣(﹣m+5)=﹣m2+5m=﹣(m﹣)2+.∵a=﹣1<0.∴当m=时.PQ最大为.∴m=时.PH最大.即点P到直线BC的距离最大.此时P(.);(3)存在.理由如下:抛物线y=﹣x2+4x+5对称轴为直线x=2.设M(s.﹣s2+4s+5).N(2.t).而B(5.0).C(0.5).①以MN、BC为对角线.则MN、BC的中点重合.如图:∴.解得.∴M(3.8).②以MB、NC为对角线.则MB、NC的中点重合.如图:∴.解得.∴M(﹣3.﹣16).③以MC、NB为对角线.则MC、NB中点重合.如图:.解得.综上所述.M的坐标为:(3.8)或(﹣3.﹣16)或(7.﹣16).3.(2021•湘潭)如图.一次函数y=x﹣图象与坐标轴交于点A、B.二次函数y=x2+bx+c图象过A、B两点.(1)求二次函数解析式;(2)点B关于抛物线对称轴的对称点为点C.点P是对称轴上一动点.在抛物线上是否存在点Q.使得以B、C、P、Q为顶点的四边形是菱形?若存在.求出Q点坐标;若不存在.请说明理由.【答案】(1)y=x2﹣x﹣(2)Q的坐标为:(1.﹣)或(﹣1.0)或(3.0)【解答】解:(1)在y=x﹣中.令x=0得y=﹣.令y=0得x=3.∴A(3.0).B(0.﹣).∵二次函数y=x2+bx+c图象过A、B两点.∴.解得.∴二次函数解析式为y=x2﹣x﹣;(2)存在.理由如下:由二次函数y=x2﹣x﹣可得其对称轴为直线x==1.设P(1.m).Q(n.n2﹣n﹣).而B(0.﹣).∵C与B关于直线x=1对称.①当BC、PQ为对角线时.如图:此时BC的中点即是PQ的中点.即.解得.∴当P(1.﹣).Q(1.﹣)时.四边形BQCP是平行四边形.由P(1.﹣).B(0.﹣).C(2.﹣)可得PB2==PC2.∴PB=PC.∴四边形BQCP是菱形.∴此时Q(1.﹣);②BP、CQ为对角线时.如图:同理BP、CQ中点重合.可得.解得.∴当P(1.0).Q(﹣1.0)时.四边形BCPQ是平行四边形.由P(1.0).B(0.﹣).C(2.﹣)可得BC2=4=PC2.∴四边形BCPQ是菱形.∴此时Q(﹣1.0);③以BQ、CP为对角线.如图:BQ、CP中点重合.可得.解得.∴P(1.0).Q(3.0)时.四边形BCQP是平行四边形.由P(1.0).B(0.﹣).C(2.﹣)可得BC2=4=PC2.∴四边形BCQP是菱形.∴此时Q(3.0);综上所述.Q的坐标为:(1.﹣)或(﹣1.0)或(3.0).4.(2021•济南)抛物线y=ax2+bx+3过点A(﹣1.0).点B(3.0).顶点为C.(1)求抛物线的表达式及点C的坐标;(2)如图1.点P在抛物线上.连接CP并延长交x轴于点D.连接AC.若△DAC是以AC为底的等腰三角形.求点P的坐标;(3)如图2.在(2)的条件下.点E是线段AC上(与点A.C不重合)的动点.连接PE.作∠PEF=∠CAB.边EF交x轴于点F.设点F的横坐标为m.求m的取值范围.【答案】(1)y= ﹣(x﹣1)2+4 ,C(1.4)(2)P()(3)﹣1<m≤【解答】解:(1)将点A(﹣1.0).点B(3.0)代入y=ax2+bx+3得:.解得:.∴抛物线的表达式为y=﹣x2+2x+3.∵y=﹣x2+2x+3=﹣(x﹣1)2+4.∴顶点C(1.4).(2)设AC交y轴于点F.连接DF.过点C作CE⊥x轴于点E.如图.∵A(﹣1.0).C(1.4).∴OA=1.OE=1.CE=4.∴OA=OE.AC==2.∵FO⊥AB.CE⊥AB.∴FO∥CE.∴OF=CE=2.F为AC的中点.∵△DAC是以AC为底的等腰三角形.∴DF⊥AC.∵FO⊥AD.∴△AFO∽△FDO.∴.∴.∴OD=4.∴D(4.0).设直线CD的解析式为y=kx+m.∴.解得:.∴直线CD的解析式为y=﹣.∴.解得:..∴P().(3)过点P作PH⊥AB于点H.如下图.则OH=.PH=.∵OD=4.∴HD=OD﹣OH=.∴PD==.∴PC=CD﹣PD=5﹣=.由(2)知:AC=2.设AF=x.AE=y.则CE=2﹣y.∵DA=DC.∴∠DAC=∠C.∵∠CAB+∠AEF+∠AFE=180°.∠AEF+∠PEF+∠CEP=180°.又∵∠PEF=∠CAB.∴∠CEP=∠AFE.∴△CEP∽△AFE.∴.∴.∴x=﹣+y=﹣+.∴当y=时.x即AF有最大值.∵OA=1.∴OF的最大值为﹣1=.∵点F在线段AD上.∴点F的横坐标m的取值范围为﹣1<m≤.1.(2021•宝鸡模拟)如图.已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1.0)和B.与y轴交于点C(0.3).(1)求此抛物线的解析式及点B的坐标;(2)设抛物线的顶点为D.连接CD、DB、CB、AC.①求证:△AOC∽△DCB;②在坐标轴上是否存在与原点O不重合的点P.使以P、A、C为顶点的三角形与△DCB 相似?若存在.请直接写出点P的坐标;若不存在.请说明理由.【答案】(1)B(3.0)(2)①略.②点P的坐标为(9.0)或(0.﹣).【解答】解:(1)把A(﹣1.0)、C(0.3)代入y=﹣x2+bx+c.得.解得.∴此抛物线的解析式为y=﹣x2+2x+3.当y=0时.则﹣x2+2x+3=0.解得x1=﹣1.x2=3.∴B(3.0).(2)①如图1.∵y=﹣x2+2x+3=﹣(x﹣1)2+4.∴抛物线的顶点D的坐标为(1.4).∵B(3.0).C(0.3).∴CD2=12+(4﹣3)2=2.CB2=32+32=18.BD2=(3﹣1)2+42=20.∴CD2+CB2=BD2=20.∴△DCB是直角三角形.且∠DCB=90°.∴∠AOC=∠DCB=90°.∵CD=.CB==3.OA=1.OC=3.∴==.==.∴=.∴△AOC∽△DCB.②存在.如图2.点P在x轴上.△COP∽△DCB.且∠COP=∠DCB=90°.∠OPC=∠CBD.∴=.∴OP===9.∴P(9.0);如图3.点P在y轴上.△P AC∽△DCB.且∠P AC=∠DCB=90°.∠ACP=∠CBD.∴.∵AC===.BD==.∴CP===.∴OP=﹣3=.∴P(0.﹣).综上所述.点P的坐标为(9.0)或(0.﹣).2.(2021•中山市模拟)如图.抛物线y=﹣x﹣3与x轴交于A.B两点(点A在点B的左侧).与y轴交于点C.直线l与抛物线交于A.D两点.与y轴交于点E.点D的坐标为(4.﹣3).(1)请直接写出A.B两点的坐标及直线l的函数表达式;(2)若点P是抛物线上的点.点P的横坐标为m(m≥0).过点P作PM⊥x轴.垂足为M.PM 与直线l交于点N.当点N是线段PM的三等分点时.求点P的坐标;(3)若点Q是y轴上的点.且∠ADQ=45°.求点Q的坐标.【答案】(1)y=﹣x﹣1 (2)P的坐标为(3.﹣)或(0.﹣3)(3)点Q的坐标为(0.9)或(0.﹣)【解答】解:(1)令y=0.得y=x2﹣x﹣3=0.解得.x=﹣2.或x=6.∴A(﹣2.0).B(6.0).设直线l的解析式为y=kx+b(k≠0).则.解得..∴直线l的解析式为y=﹣x﹣1;(2)如图1.根据题意可知.点P与点N的坐标分别为P(m.m2﹣m﹣3).N(m.﹣m ﹣1).∴PM=﹣m2+m+3.MN=m+1.NP=﹣m2+m+2.分两种情况:①当PM=3MN时.得﹣m2+m+3=3(m+1).解得.m=0.或m=﹣2(舍).∴P(0.﹣3);②当PM=3NP时.得﹣m2+m+3=3(﹣m2+m+2).解得.m=3.或m=﹣2(舍).∴P(3.﹣);∴综上所述:P的坐标为(3.﹣)或(0.﹣3);(3)∵直线l:y=﹣x﹣1与y轴交于点E.∴点E的坐标为(0.﹣1).分两种情况:①如图2.当点Q在y轴的正半轴上时.记为点Q1.过Q1作Q1H⊥AD于点H.则∠Q1HE=∠AOE=90°.∵∠Q1EH=∠AEO.∴△Q1EH∽△AEO.∴.即.∴Q1H=2HE.∵∠Q1DH=45°.∠Q1HD=90°.∴Q1H=DH.∴DH=2EH.∴HE=ED.连接CD.∵C(0.﹣3).D(4.﹣3).∴CD⊥y轴.∴ED===2.∴HE=ED=2.Q1H=2EG=4.∴Q1E==10.∴Q1O=Q1E﹣OE=9.∴Q1(0.9);②如图3.当点Q在y轴的负半轴上时.记为点Q2.过Q2作Q2G⊥AD于G.则∠Q2GE=∠AOE=90°.∵∠Q2EG=∠AEO.∴△Q2GE∽△AOE.∴.即.∴Q2G=2EG.∵∠Q2DG=45°.∠Q2GD=90°.∴∠DQ2G=∠Q2DG=45°.∴DG=Q2G=2EG.∴ED=EG+DG=3EG.由①可知.ED=2.∴3EG=2.∴EG=.∴Q2G=.∴EQ2==.∴OQ2=OE+EQ2=.∴Q2(0.﹣).综上.点Q的坐标为(0.9)或(0.﹣).3.(2020•长春模拟)如图.抛物线y=﹣x2+bx+c与x轴交于点A(1.0)、B(3.0)(点A在点B的左边).与y轴交于点C.过点C作CD∥x轴.交抛物线于点D.过点D作DE∥y轴.交直线BC于点E.点P在抛物线上.过点P作PQ∥y轴交直线CE于点Q.连接PB.设点P 的横坐标为m.PQ的长为d.(1)求抛物线对应的函数表达式;(2)求直线BC的函数表达式;(3)当0<m<4时.求d关于m的函数关系式;(4)当△PQB是等腰三角形时.直接写出m的值.【答案】(1)y=﹣x2+4x﹣3 (2)y=x﹣3(3)当0<m<3时.PQ=﹣m2+3m.当3≤m<4时.PQ=m2﹣3m;(4)m=1或2或±【解答】解:(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(1.0)、B(3.0).∴解得:∴抛物线解析式为:y=﹣x2+4x﹣3;(2)∵抛物线y=﹣x2+4x﹣3与y轴交于点C.∴点C(0.﹣3)设直线BC解析式为:y=kx﹣3.∴0=3k﹣3∴k=1.∴直线BC解析式为:y=x﹣3;(3)∵设点P的横坐标为m.PQ∥y轴.∴点P(m.﹣m2+4m﹣3).点Q(m.m﹣3).当0<m<3时.PQ=d=﹣m2+4m﹣3﹣(m﹣3)=﹣m2+3m.当3≤m<4时.PQ=d=(m﹣3)﹣(﹣m2+4m﹣3)=m2﹣3m;(4)B(3.0).点C(0.﹣3).∴OB=OC=3.∴∠OCB=∠OBC=45°.∵PQ∥OC.∴∠PQB=45°.若BP=PQ.∴∠PQB=∠PBQ=45°.∴∠BPQ=90°.即点P与点A重合.∴m=1.若BP=QB.∴∠BQP=∠BPQ=45°.∴∠QBP=90°.∴BP解析式为:y=﹣x+3.∴解得:.∴m=2;若PQ=QB.∴(3﹣m)2+(m﹣3﹣0)2=(﹣m2+3m)2.或(3﹣m)2+(m﹣3﹣0)2=(m2﹣3m)2.∴m=±.综上所述:m=1或2或±4.(2021•黄冈二模)如图.抛物线y=ax2+bx+2(a<0)与x轴交于点A(﹣1.0)和点B(2.0).与y轴交于点C.(1)求该抛物线的函数解析式;(2)如图1.连接BC.点D是直线BC上方抛物线上的点.连接OD、CD.OD交BC于点F.当S△COF:S△CDF=2:1时.求点D的坐标;(3)如图2.点E的坐标为(0.﹣1).在抛物线上是否存在点P.使∠OBP=2∠OBE?若存在.请直接写出符合条件的点P的坐标;若不存在.请说明理由.【答案】(1)y=﹣x2+x+2 (2)D(1.2)(3)点P的坐标为()或(﹣)【解答】解:(1)∵A(﹣1.0).B(2.0).∴把A(﹣1.0).B(2.0)代入y=ax2+bx+2得..解得..∴该抛物线的函数解析式为y=﹣x2+x+2;(2)如图1.过点D作DH∥y轴交BC于点H.交x轴于点G.∵抛物线y=﹣x2+x+2与y轴交于点C.设直线BC解析式为y=kx+b.则.解得.∴直线BC解析式为y=﹣x+2.∵S△COF:S△CDF=2:1.∴OF:DF=2:1.∵DH∥OC.∴△OFC∽△DFH.∴=2.∴OC=2DH.设D(a.﹣a2+a+2).则H(a.﹣a+2).∴DH=﹣a2+a+2﹣(﹣a+2)=﹣a2+2a.∴2=2(﹣a2+2a).解得a=1.∴D(1.2).(3)①当点P在x轴上方时.在y轴上取点G(0.1).连接BG.则∠OBG=∠OBE.过点B作直线PB交抛物线于点P.交y轴于点M.使∠GBM=∠GBO.则∠OBP=2∠OBE.过点G作GH⊥BM.∵E(0.﹣1).∴OE=OG=GH=1.设MH=x.则MG=.在Rt△OBM中.OB2+OM2=MB2.∴(+1)2+4=(x+2)2.解得:x=.故MG===.∴OM=OG+MG=1+=.∴点M(0.).将点B(2.0)、M(0.)的坐标代入一次函数表达式y=mx+n..解得:.∴直线BM的表达式为:y=﹣x+.∴.解得:x=或x=2(舍去).∴点P(.);②当点P在x轴下方时.作点M(0.)关于x轴的对称点N(0.﹣).求得直线BN的解析式为y=x﹣.∴.解得.x=﹣或x=2(舍去).∴点P(﹣.﹣);综合以上可得.点P的坐标为()或(﹣).5.(2021•阳东区模拟)如图.已知抛物线y=﹣x2+bx+c与x轴相交于点A(﹣1.0).与y轴相交于点N(0.3).抛物线的顶点为D.经过点A的直线y=kx+1与抛物线y=﹣x2+bx+c 相交于点C.(1)求抛物线的解析式;(2)若P是抛物线上位于直线AC上方的一个动点.设点P的横坐标为t.过点P作y轴的平行线交AC于M.当t为何值时.线段PM的长最大.并求其最大值;(3)若抛物线的对称轴与直线AC相交于点B.E为直线AC上的任意一点.过点E作EF ∥BD交抛物线于点F.以B.D.E.F为顶点的四边形能否为平行四边形?若能.请直接写出点E的坐标;若不能.请说明理由.【答案】(1)y=﹣x2+2x+3 (2)t=时.线段PM的长最大.PM最大值=(3)E的坐标为(0.1)或(.)或(.).【解答】解:(1)∵抛物线y=﹣x2+bx+c与直线相交于A(﹣1.0).N(0.3)两点.∴.解得.∴抛物线的解析式为y=﹣x2+2x+3;(2)如图1.将A(﹣1.0)代入直线AC的解析式为y=kx+1.得﹣k+1=0.解得k=1.∴直线AC:y=x+1.∵点P的横坐标为t.且PM∥y轴.∴P(t.﹣t2+2t+3).M(t.t+1).∵点P在直线AC上方的抛物线上.∴﹣1<t<3.∴PM=﹣t2+2t+3﹣(t+1)=﹣t2+t+2=﹣(t﹣)2+.∵﹣1<0.且﹣1<<3.∴当t=时.线段PM的长最大.PM最大值=;(3)能.设点E的横坐标为t.则点F的横坐标为t.当﹣1<t<3.如图2.由(2)得.EF=﹣t2+t+2;∵y=﹣x2+2x+3=﹣(x﹣1)2+4.∴该抛物线的对称轴为直线x=1.顶点D的坐标为(1.4).直线AC:y=x+1.当x=1时.y=2.∴B(1.2).∴BD=4﹣2=2.∵EF∥BD.∴当EF=BD=2时.四边形BDNG是平行四边形.∴﹣t2+t+2=2.解得t1=0.t2=1(不符合题意.舍去).对于直线y=x+1.当x=0时.y=1.∴E(0.1);当x<﹣1或x>3时.如图3.EF∥BD或E′F′∥BD.则EF=(t+1)﹣(﹣t2+2t+3)=t2﹣t﹣2.∴t2﹣t﹣2=2.解得t1=.t2=.直线y=x+1.当x=时.y=;当x=时.y=.∴E(.).E′(.).综上所述.点E的坐标为(0.1)或(.)或(.).。
最新九年级数学中考专题训练:二次函数综合压轴题(相似三角形问题)
2023年九年级数学中考专题训练:二次函数综合压轴题(相似三角形问题)1.已知,二次函数23y ax bx =+-的图象与x 轴交于A ,B 两点(点A 在点B 的左边),与y 轴交于C 点,点A 的坐标为()1,0-,且OB OC =.(1)求二次函数的解析式;(2)当04x ≤≤时,求二次函数的最大值和最小值分别为多少?(3)设点C '与点C 关于该抛物线的对称轴对称.在y 轴上是否存在点P ,使PCC '△与POB 相似,且PC 与PO 是对应边?若存在,求出点P 的坐标;若不存在,请说明理由.2.如图1,抛物线234y x x =-++与x 轴交于A 、B 两点(A 在B 的左侧),与y 轴交于点C ,连接,AC BC .(1)求ABC 的面积;(2)如图2,点P 为直线上方抛物线上的动点,过点P 作PD AC ∥交直线BC 于点D ,过点P 作直线PE x ∥轴交直线BC 于点E ,求PD PE +的最大值及此时P 的坐标;(3)在(2)的条件下,将原抛物线234y x x =-++沿射线AC 方向平移M 是新抛物线与原抛物线的交点,N 是平面内任意一点,若以P 、B 、M 、N 为顶点的四边形是平行四边形,请直接写出点N 的坐标.3.已知抛物线2y x bx c =++与x 轴交于()()1030A B ,、,两点,且与y 轴的公共点为点C ,设该抛物线的顶点为D .(1)求抛物线的表达式,并求出顶点D 的坐标;(2)若点P 为抛物线上一点,且满足PB PC =,求点P 的横坐标;(3)连接CD BC ,,点E 为线段BC 上一点,过点E 作EF CD ⊥交CD 于点F ,若12=DF CF ,求点E 的坐标.4.如图1,在平面直角坐标系中,点O 为坐标原点,抛物线24y ax bx =++与x 轴交于点A 、B (点A 在点B 左侧),与y 轴交于点C ,直线4y x =-+经过B 、C 两点,4OB OA =.(1)求抛物线的解析式;(2)如图2,点P 为第四象限抛物线上一点,过点P 作PD x ⊥轴交BC 于点D ,垂足为N ,连接PC 交x 轴于点E ,设点P 的横坐标为t ,PCD 的面积为S ,求S 与t 的函数关系式;(3)在(2)的条件下,如图3,过点P 作PF PC ⊥交y 轴于点F ,PF PE =.点G 在抛物线上,连接PG ,45CPG ∠=︒,连接BG ,求直线BG 的解析式.5.如图1,已知二次函数2y ax bx c =++的图象的顶点为()0,1D ,且经过点()2,2A .(1)求二次函数的解析式;(2)过点A 的直线与二次函数图象的另一交点为B ,与y 轴交于点C ,若BDC 的面积是ADC △的两倍,求直线AB 的解析式;(3)如图2,已知(),0E m ,是x 轴上一动点(E ,O 不重合),过E 的两条直线1l ,2l 与二次函数均只有一个交点,且直线1l ,2l 与y 轴分别交于点M 、N .对于任意的点E ,在y 轴上(点M 、N 上方)是否存在一点()0,F t ,使N FEM F E △∽△恒成立.若存在,求出t 的值;若不存在,请说明理由.6.如图,抛物线y 2b c x ++与x 轴交于点A 、B ,点A 、B 分别位于原点的左、右两侧,BO =3AO =3,过点B 的直线与y 轴正半轴和抛物线的交点分别为C 、D ,BC.(1)求b、c的值;(2)求直线BD的直线解析式;(3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当△ABD与△BPQ相似时,请直接写出所有满足条件的点Q的坐标.7.如图1,抛物线与坐标轴分别交于A(-1,0),B(3,0),C(0,3).(1)求抛物线解析式;(2)抛物线上是否存在点P,使得△CBP=△ACO,若存在,求出点P的坐标,若不存在,说明理由;(3)如图2,Q是△ABC内任意一点,求DQ EQ QFAD BE CF++的值.8.如图所示,平面直角坐标系中,二次函数y=a(x+2k)(x﹣k)图象与x轴交于A、B两点,抛物线对称轴为直线x=﹣2;(1)求k 的值;(2)点C 为抛物线上一点,连接BC 、AC ,作CD △x 轴于D ,当△BCA =90°时,设CD 长度为d ,求d 与a 的函数关系式;(3)抛物线顶点为S ,作S T 垂直AB 于T ,点Q 为第一象限抛物线上一点,连接AQ 交S T 于点P ,过B 作x 轴的垂线交AQ 延长线于点E ,连接OE 交BQ 于点G ,过O 作OE 的垂线交AQ 于点F ,若OF =OG ,tan△ABQ =2时,连接S Q ,求证:S Q =S P .9.已知抛物线23y x bx =-++的图象与x 轴相交于点A 和点B ,与y 轴交于点C ,图象的对称轴为直线=1x -.连接AC ,有一动点D 在线段AC 上运动,过点D 作x 轴的垂线,交抛物线于点E ,交x 轴于点F .设点D 的横坐标为m .(1)求AB 的长度;(2)连接AE CE 、,当ACE △的面积最大时,求点D 的坐标; (3)当m 为何值时,ADF △与CDE 相似.10.如图,抛物线28y ax bx =++与x 轴交于()2,0A -和点()8,0B ,与y 轴交于点C ,顶点为D ,连接AC ,BC ,BC 与抛物线的对称轴l 交于点E .(1)求该抛物线的函数表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,设四边形PBOC 和AOC 的面积分别为PBOC S 四边形和AOCS,记AOC PBOC S S S =-△四边形,求S 最大值点P 的坐标及S 的最大值;(3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与BOC 相似?若存在,求点M 的坐标;若不存在,请说明理由.11.如图,抛物线24y ax bx =+-经过点()1,0C -,点()4,0B ,交y 轴于点A ,点H 是该抛物线上第四象限内的一个动点,HE △x 轴于点E ,交线段AB 于点D ,HQ △y 轴,交y 轴于点Q .(1)求抛物线的函数解析式.(2)若四边形HQOE 是正方形,求该正方形的面积.(3)连接OD 、AC ,抛物线上是否存在点H ,使得以点O 、A 、D 为顶点的三角形与△ABC 相似,若存在,请直接写出点H 的坐标,若不存在,请说明理由.12.如图,已知抛物线2y ax x c =-+的对称轴为直线x =1,与x 轴的一个交点为()10A -,,顶点为B .点()5C m ,在抛物线上,直线BC 交x 轴于点E .(1)求抛物线的表达式及点E 的坐标; (2)连接AB ,求△B 的余切值;(3)点G 为线段AC 上一点,过点G 作CB 的垂线交x 轴于点M (位于点E 右侧),当△CGM 与△ABE 相似时,求点M 的坐标.13.如图所示,抛物线2=23y x x --与x 轴相交于A 、B 两点,与y 轴相交于点C ,点M 为抛物线的顶点.(1)求点C 及顶点M 的坐标.(2)若点N 是第四象限内抛物线上的一个动点,连接BN 、CN ,求BCN △面积的最大值. (3)直线CM 交x 轴于点E ,若点P 是线段EM 上的一个动点,是否存在以点P 、E 、O 为顶点的三角形与ABC 相似.若存在,求出点P 的坐标;若不存在,请说明理由.14.如图,抛物线L 1:y =ax 2﹣2x +c (a ≠0)与x 轴交于A 、B (3,0)两点,与y 轴交于点C (0,﹣3),抛物线的顶点为D .抛物线L 2与L 1关于x 轴对称.(1)求抛物线L 1与L 2的函数表达式;(2)已知点E 是抛物线L 2的顶点,点M 是抛物线L 2上的动点,且位于其对称轴的右侧,过M 向其对称轴作垂线交对称轴于P ,是否存在这样的点M ,使得以P 、M 、E 为顶点的三角形与△BCD 相似,若存在请求出点M 的坐标,若不存在,请说明理由.15.综合与探究如图,抛物线212y x bx c =-++与x 轴交于A ,B 两点,与y 轴交于点C ,点B ,C 的坐标分别为(2,0),(0,3),点D 与点C 关于x 轴对称,P 是直线AC 上方抛物线上一动点,连接PD 、交AC 于点Q .(1)求抛物线的函数表达式及点A 的坐标; (2)在点P 运动的过程中,求PQ :DQ 的最大值;(3)在y 轴上是不存在点M ,使45AMB ∠=︒?若存在,请直接写出点M 的坐标;若不存在,请说明理由.16.如图,已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -,()3,0B ,与y 轴的交点()0,6C .(1)求抛物线的解析式;(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动,设PBC 的面积为S ,求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得△CMN =90°,且∆CMN 与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.17.如图(1),直线y =-x +3与x 轴、y 轴分别交于点B (3,0)、点C (0,3),经过B 、C 两点的抛物线2y x bx c =++与x 轴的另一个交点为A ,顶点为P .(1)求该抛物线的解析式与点P 的坐标;(2)当0<x <3时,在抛物线上求一点E ,使△CBE 的面积有最大值; (3)连接AC ,点N 在x 轴上,点M 在对称轴上,△是否存在使以B 、P 、N 为顶点的三角形与△ABC 相似?若存在,请求出所有符合条件的点N 的坐标;若不存在,请说明理由;△是否存在点M ,N ,使以C 、P 、M 、N 为顶点的四边形是平行四边形?若存在,请直接写出点M 的坐标;若不存在,请说明理由. (图(2)、图(3)供画图探究)18.如图,已知抛物线213222y x x =-++与x 轴交于点A 、B ,与y 轴交于点C .(1)则点A 的坐标为_________,点B 的坐标为_________,点C 的坐标为_________;(2)设点11(,)P x y ,22(,)Q x y (其中12x x >)都在抛物线213222y x x =-++上,若121x x =+,请证明:12y y >;(3)已知点M 是线段BC 上的动点,点N 是线段BC 上方抛物线上的动点,若90CNM ∠=︒,且CMN 与OBC △相似,试求此时点N 的坐标.参考答案:1.(1)2=23y x x --(2)函数的最大值为5,最小值为4-(3)存在,(0,9)P -或9(0,)5P -2.(1)10;(2)最大值为4,()2,6P ; (3)N 点坐标为113,24⎛⎫ ⎪⎝⎭或345,24⎛⎫- ⎪⎝⎭或53,24⎛⎫- ⎪⎝⎭.3.(1)243y x x =-+,()21-,(2)⎝⎭或⎝⎭(3)207,99⎛⎫ ⎪⎝⎭4.(1)254y x x =-+ (2)32122S t t =-+ (3)416y x =-5.(1)2114y x =+ (2)312y x =-或132y x =-+ (3)存在,=2t6.(1)132b c ⎧=-⎪⎪⎨⎪=-⎪⎩(2)y=+(3)Q 1(,0)、Q 2(0)、Q 3,0)、Q 4(,0) 7.(1)223y x x =-++(2)存在,1217(,),(1,4)24P P - (3)DQ EQ QF AD BE CF ++的值为18.(1)k =4 (2)1d a=-9.(1)4(2)(32-,32-) (3)当2m =-或1m =-时ADF △与CDE 相似10.(1)21382y x x =-++ (2)()4,12P ,最大值为56(3)存在,()3,8,(3,5,()3,1111.(1)234y x x =--(2)6+(3)存在,点H 的坐标为1684,525⎛⎫- ⎪⎝⎭或521,24⎛⎫- ⎪⎝⎭12.(1)21322y x x =--;E (2,0) (2)3(3)M 点的坐标为(5,0)或(7,0)13.(1)C 点坐标为(0,-3),顶点M 的坐标为(1,-4);(2)278(3)P 点的坐标为39(,)44--或(-1,-2).14.(1)抛物线L 1:2=23y x x --,抛物线L 2:223y x x =-++; (2)435(,)39M 或(4,5)M -.15.(1)211322y x x =--+,A (-3,0); (2)316; (3)存在,M (0,6)或(0,-6)16.(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<,S 的最大值是274 (3)存在,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M (3,0),N (0,﹣32)17.(1)243y x x =-+,顶点坐标为P (2,-1) (2)33,24E ⎛⎫- ⎪⎝⎭(3)△存在,()10,0N 或27,03N ⎛⎫ ⎪⎝⎭;△存在,点M 的坐标为(2,2);(2,-4);(2,4)18.(1)(-1,0),(4,0),(0,2);(3)点N 的坐标为(32,258)或(3,2).。
初三中考数学专题复习:二次函数综合题(相似三角形问题)含答案
中考数学专题复习:二次函数综合题(相似三角形问题)1.如图①,二次函数y =﹣x 2+bx +c 的图象与x 轴交于点A (﹣1,0)、B (3,0),与y 轴交于点C ,连接BC ,点P 是抛物线上一动点.(1)求二次函数的表达式.(2)当点P 不与点A 、B 重合时,作直线AP ,交直线BC 于点Q ,若①ABQ 的面积是①BPQ 面积的4倍,求点P 的横坐标.(3)如图①,当点P 在第一象限时,连接AP ,交线段BC 于点M ,以AM 为斜边向①ABM 外作等腰直角三角形AMN ,连接BN ,①ABN 的面积是否变化?如果不变,请求出①ABN 的面积;如果变化,请说明理由.2.如图,二次函数2314y x bx =++的图像经过点()8,3A ,交x 轴于点B ,C (点B 在点C 的左侧),与y 轴交于点D .(1)填空:b = ______;(2)点P 是第一象限内抛物线上一点,直线PO 交直线CD 于点Q ,过点P 作x 轴的垂线交直线CD 于点T ,若PQ QT =,求点P 的坐标;(3)在x 轴的正半轴上找一点E ,过点E 作AE 的垂线EF 交y 轴于F ,若AEF 与EFO △相似,求OE 的长.3.如图,已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -,()3,0B ,与y 轴的交点()0,6C .(1)求抛物线的解析式;(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动,设PBC 的面积为S ,求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得①CMN =90°,且∆CMN 与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.4.如图,抛物线L 1:y =ax 2﹣2x +c (a ≠0)与x 轴交于A 、B (3,0)两点,与y 轴交于点C (0,﹣3),抛物线的顶点为D .抛物线L 2与L 1关于x 轴对称.(1)求抛物线L 1与L 2的函数表达式;(2)已知点E 是抛物线L 2的顶点,点M 是抛物线L 2上的动点,且位于其对称轴的右侧,过M 向其对称轴作垂线交对称轴于P ,是否存在这样的点M ,使得以P 、M 、E 为顶点的三角形与△BCD 相似,若存在请求出点M 的坐标,若不存在,请说明理由.5.如图,在平面直角坐标系中,已知直线4y x =+与x 轴、y 轴分别相交于点A 和点C ,抛物线21y x kx k =++-的图象经过点A 和点C ,与x 轴的另一个交点是点B .(1)求出此抛物线的解析式; (2)求出点B 的坐标;(3)若在y 轴的负半轴上存在点D .能使得以A ,C ,D 为顶点的三角形与①ABC 相似,请求出点D 的坐标.6.如图1,已知抛物线23y ax bx =++经过点()1,5D ,且交x 轴于A ,B 两点,交y 轴于点C ,已知点()1,0A -,(),P m n 是抛物线在第一象限内的一个动点,PQ BC ⊥于点Q .(1)求抛物线的解析式;(2)当PQ =m 的值;(3)是否存在点P ,使BPQ 与BOC 相似?若存在,请求出P 点的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,直线y =12x +2与x 轴交于点A ,与y 轴交于点C .抛物线y =ax 2+bx +c的对称轴是x=-32且经过A、C两点,与x轴的另一交点为点B.(1)求二次函数y=ax2+bx+c的表达式;(2)点P为线段AB上的动点,求AP+2PC的最小值;(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与①ABC 相似?若存在,求出点M的坐标;若不存在,请说明理由.8.如图,抛物线y=−x2+bx+c与x轴相交于A(−1,0),B(3,0)两点,与y轴交于点C,顶点为点D,抛物线的对称轴与BC相交于点E,与x轴相交于点F.(1)求抛物线的函数关系式;(2)连结DA,求sin A的值;(3)若点H线段BC上,BOC与BFH△相似,请直接写出点H的坐标.9.如图,抛物线y=1-2x2+bx+c与x轴交于点A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,当S △PBC =720S △ABC 时,求点P 的坐标; (3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与①OBC 相似?若存在,求点M 的坐标;若不存在,请说明理由.10.如图,抛物线23y ax bx =++与x 轴交于1,0A 、()3,0B -两点,与y 轴交于点C ,设抛物线的顶点为D .(1)求该抛物线的表达式与顶点D 的坐标; (2)试判断BCD △的形状,并说明理由;(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与BCD △相似?若存在,请求出点P 的坐标;若不存在,请说明理由.11.如图,抛物线y =ax 2﹣2ax ﹣3a (a ≠0)与x 轴交于点A ,B .与y 轴交于点C .连接AC ,BC .已知ABC 的面积为2.(1)求抛物线的解析式;(2)平行于x 轴的直线与抛物线从左到右依次交于P ,Q 两点.过P ,Q 向x 轴作垂线,垂足分别为G ,H .若四边形PGHQ 为正方形,求正方形的边长;(3)抛物线上是否存在一点N ,使得①BCN =①CAB ﹣①CBA ,若存在,请求出满足条件N 点的横坐标,若不存在请说明理由.12.如图,二次函数2y x bx c =-++的图像与x 轴交于点A (-1,0),B (2,0),与y 轴相交于点C .(1)求这个二次函数的解析式;(2)若点M 在此抛物线上,且在y 轴的右侧.①M 与y 轴相切,过点M 作MD ①y 轴,垂足为点D .以C ,D ,M 为顶点的三角形与①AOC 相似,求点M 的坐标及①M 的半径长.13.如图,在平面直角坐标系中,抛物线2()0y ax bx c ac =++≠与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C .若线段OA OB OC 、、的长满足2OC OA OB =⋅,则这样的抛物线称为“黄金”抛物线.如图,抛物线22(0)y ax bx a =++≠为“黄金”抛物线,其与x 轴交点为A ,B (其中B 在A 的右侧),与y 轴交于点C .且4OA OB =(1)求抛物线的解析式;(2)若P 为AC 上方抛物线上的动点,过点P 作PD AC ⊥,垂足为D . ①求PD 的最大值;①连接PC ,当PCD 与ACO △相似时,求点P 的坐标.14.如图,在平面直角坐标系xOy 中,已知抛物线2y x bx c =++与x 轴交于点A 、B 两点,其中1,0A ,与y 轴交于点()0,3C .(1)求抛物线解析式;(2)如图1,过点B 作x 轴垂线,在该垂线上取点P ,使得①PBC 与①ABC 相似,请求出点P 坐标;(3)如图2,在线段OB 上取一点M ,连接CM ,请求出12CM BM +最小值.15.如图,抛物线y =ax 2+k (a >0,k <0)与x 轴交于A ,B 两点(点B 在点A 的右侧),其顶点为C ,点P 为线段OC 上一点,且PC =14OC .过点P 作DE ①AB ,分别交抛物线于D ,E 两点(点E 在点D 的右侧),连接OD ,DC .(1)直接写出A ,B ,C 三点的坐标;(用含a ,k 的式子表示) (2)猜想线段DE 与AB 之间的数量关系,并证明你的猜想;(3)若①ODC =90°,k =﹣4,求a 的值.16.如图,抛物线223y x bx c =++与x 轴交于A ,B 两点,与y 轴交于C 点,连接AC ,已知B (﹣1,0),且抛物线经过点D (2,﹣2).(1)求抛物线的表达式;(2)若点E 是抛物线上第四象限内的一点,且2ABES=,求点E 的坐标;(3)若点P 是y 轴上一点,以P ,A ,C 三点为顶点的三角形是等腰三角形,求P 点的坐标.17.如图,在直角坐标系xOy 中,抛物线y =ax 2+bx +2(a ≠0)与x 轴交于点A (﹣1,0)和B (4,0),与y 轴交于点C ,点P 是抛物线上的动点(不与点A ,B ,C 重合).(1)求抛物线的解析式;(2)当点P 在第一象限时,设①ACP 的面积为S 1,①ABP 的面积为S 2,当S 1=S 2时,求点P 的坐标; (3)过点O 作直线l ①BC ,点Q 是直线l 上的动点,当BQ ①PQ ,且①BPQ =①CAB 时,请直接写出点P 的坐标.18.如图,在平面直角坐标系xOy中,直线y=﹣x+3与两坐标轴交于A、B两点,抛物线y=x2+bx+c 过点A和点B,并与x轴交于另一点C,顶点为D.点E在对称轴右侧的抛物线上.(1)求抛物线的函数表达式和顶点D的坐标;(2)若点F在抛物线的对称轴上,且EF①x轴,若以点D,E,F为顶点的三角形与①ABD相似,求出此时点E的坐标;(3)若点P为坐标平面内一动点,满足tan①APB=3,请直接写出①P AB面积最大时点P的坐标及该三角形面积的最大值.19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴交于点C,且OC=2OB=6OA=6,点P是第一象限内抛物线上的动点.(1)求抛物线的解析式;(2)连接BC与OP,交于点D,当S△PCD:S△ODC的值最大时,求点P的坐标;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N.使①CMN=90°,且①CMN与①BOC 相似,若存在,请求出点M、点N的坐标.20.如图,抛物线y=x2+bx+12(b<0)与x轴交于A,B两点(A点在B点左侧),且OB=3OA.(1)请直接写出b=,A点的坐标是,B点的坐标是;(2)如图(1),D点从原点出发,向y轴正方向运动,速度为2个单位长度/秒,直线BD交抛物线于点E,若BE=5DE,求D点运动时间;(3)如图(2),F点是抛物线顶点,过点F作x轴平行线MN,点C是对称轴右侧的抛物线上的一定点,P 点在直线MN上运动.若恰好存在3个P点使得①P AC为直角三角形,请求出C点坐标,并直接写出P点的坐标.答案1.(1)y =﹣x 2+2x +3.(2)P 352或 (3)①ABN 的面积不变,为4.2.(1)2-(2)5⎛ ⎝⎭或5⎛ ⎝⎭(3)4或493.(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<,S 的最大值是274 (3)存在,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M (3,0),N (0,﹣32)4.(1)抛物线L 1:223y x x =--,抛物线L 2:2y x 2x 3=-++;(2)435(,)39M 或(4,5)M -.5.(1)254y x x =++(2)点B 的坐标为(-1,0)(3)点D 的坐标是(0,-203) 6.(1)215322y x x =-++ (2)1或5(3)存在;P (53,529)7.(1)抛物线表达式为:213222y x x =--+;(2)AP +2PC 的最小值是4;(3)存在M(0,2)或(-3,2)或(2,-3)或(5,-18),使得以点A 、M 、N 为顶点的三角形与ABC 相似.8.(1)y =-x 2+2x +3(3)点H 的坐标为(1,2)或(2,1)9.(1)21382y x x =++ (2)P 1(1,10.5),P 2(7,4.5)(3)存在,(3,8)或(3,5或(3,11)30.(1)y =﹣x 2﹣2x +3,(﹣1,4);(2)直角三角形,理由见解析;(3)存在,(0,0)或(0,﹣13)或(-9,0)11.(1)y =﹣13x 2+23x +1(2)﹣6﹣(3)存在,5或11712.(1)22y x x =-++; (2)M 的坐标为(12,94),(32, 54 ),(3,-4),①M 的半径长为12或32或313.(1)213222y x x =--+(2)①PD ①P 坐标为(3,2)-或325()28,-14.(1)243y x x =-+(2)P 点坐标为()3,9或()3,215.(1)点A 、B 、C 的坐标分别为(、、(0,k ) (2)DE =12AB(3)a =1316.(1)224233y x x =--(2)E ,-1)(3)P 点的坐标(0,2)或(02)或(0,﹣2或(0,54)17.(1)213222y x x =-++ (2)点P 的坐标为(103,139)(3)点P 的坐标为(32,﹣2)或(32,﹣2)或(173,﹣509)18.(1)y =x 2﹣4x +3,(2,﹣1)(2)(5,8)或(73,89-)(3)①P AB ,此时P )19.(1)y =﹣2x 2+4x +6 (2)点P 的坐标为(32,152) (3)存在,M 、N 的坐标分别为(3,0)、(0,﹣32)或(94,398)、(0,38)或(1,8)、(0,172)或(74,558)、(0,838)20.(1)﹣8,(2,0),(6,0)(2)3秒或212秒 (3)C 点坐标为(143,﹣329),P 点的坐标为(103,﹣4)或(﹣103,﹣4)或(11027,﹣4)。
专题61 二次函数背景下的相似三角形问题(解析版)-中考数学解题大招复习讲义
模型介绍在坐标系中确定点,使得由该点及其他点构成的三角形与其他三角形相似,即为“相似三角形存在性问题”.【相似判定】判定1:三边对应成比例的两个三角形是相似三角形;判定2:两边对应成比例且夹角相等的两个三角形是相似三角形;判定3:有两组角对应相等的三角形是相似三角形.以上也是坐标系中相似三角形存在性问题的方法来源,根据题目给的已知条件选择恰当的判定方法,解决问题.【题型分析】通常相似的两三角形有一个是已知的,而另一三角形中有1或2个动点,即可分为“单动点”类、“双动点”两类问题.【思路总结】根据相似三角形的做题经验,可以发现,判定1基本是不会用的,这里也一样不怎么用,对比判定2、3可以发现,都有角相等!所以,要证相似的两个三角形必然有相等角,关键点也是先找到一组相等角.然后再找:思路1:两相等角的两边对应成比例;思路2:还存在另一组角相等.事实上,坐标系中在已知点的情况下,线段长度比角的大小更容易表示,因此选择方法可优先考虑思路1.一、如何得到相等角?二、如何构造两边成比例或者得到第二组角?搞定这两个问题就可以了.例题精讲【例1】.如图,抛物线y=﹣x2+x+2交x轴于点A,B,交y轴于点C,点M是第一象限内抛物线上一点,过点M作MN⊥x轴于点N.若△MON与△BOC相似,求点M的横坐标.解:∵抛物线y=﹣x2+x+2交x轴于点A,B,交y轴于点C,∴当y=0时,0=﹣x2+x+2,解得x1=﹣1,x2=4,∴OB=4,当x=0时,y=2,∴OC=2,∵点M是第一象限内抛物线上一点,∴设M(m,﹣m2+m+2),∵MN⊥x轴,∴ON=m,MN=﹣m2+m+2,∠ONM=90°,∵∠BOC=90°,∴∠BOC=∠ONM,∵△MON与△BOC相似,∴或,∴=或=,∴m=或m=﹣1+(负值舍去),∴点M的横坐标为或﹣1+.变式训练【变1-1】.如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,(1)求出此抛物线的解析式、对称轴以及B点坐标;(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.解:(1)由x=0得y=0+4=4,则点C的坐标为(0,4);由y=0得x+4=0,解得x=﹣4,则点A的坐标为(﹣4,0);把点C(0,4)代入y=x2+kx+k﹣1,得k﹣1=4,解得:k=5,∴此抛物线的解析式为y=x2+5x+4,∴此抛物线的对称轴为x=﹣=﹣.令y=0得x2+5x+4=0,解得:x1=﹣1,x2=﹣4,∴点B的坐标为(﹣1,0).(2)∵A(﹣4,0),C(0,4),∴OA=OC=4,∴∠OCA=∠OAC.∵∠AOC=90°,OB=1,OC=OA=4,∴AC==4,AB=OA﹣OB=4﹣1=3.∵点D在y轴负半轴上,∴∠ADC<∠AOC,即∠ADC<90°.又∵∠ABC>∠BOC,即∠ABC>90°,∴∠ABC>∠ADC.∴由条件“以A、C、D为顶点的三角形与△ABC相似”可得△CAD∽△ABC,∴=,即=,解得:CD=,∴OD=CD﹣CO=﹣4=,∴点D的坐标为(0,﹣).【例2】.如图,抛物线y=x2+bx+c与x轴交于A(1,0),B两点,与y轴交于点C(0,3).(1)求该抛物线的表达式;(2)过点B作x轴的垂线,在该垂线上取一点P,使得△PBC与△ABC相似,请求出点P的坐标.解:(1)把C(0,3)代入y=x2+bx+c,得c=3,∴y=x2+bx+3,把A(1,0)代入y=x2+bx+3,得1+b+3=0,解得b=﹣4,∴该抛物线的表达式为y=x2﹣4x+3.(2)当点P在点B上方时,如图1,PB=AB,∵PB⊥x轴,∴∠ABP=90°,抛物线y=x2﹣4x+3,当y=0时,则x2﹣4x+3=0,解得x1=1,x2=3,∴B(3,0),∴OB=OC=3,PB=AB=3﹣1=2,∵∠BOC=90°,∴∠OBC=∠OCB=45°,∴∠PBC=∠ABC=45°,∵==1,∴△PBC∽△ABC,此时点P的坐标为(3,2);如图2,△PBC∽△CBA,且∠CBP=∠ABC=45°,∠BCP=∠BAC,∴=,∵BC2=OB2+OC2=32+32=18,BA=2,∴BP===9,此时点P的坐标为(3,9);当点P在点B下方时,∠PBC=135°,∠BAC=∠AOC+∠ACO=90°+∠ACO<135°,此时△PBC与△ABC不相似,综上所述,点P的坐标为(3,2)或(3,9).变式训练【变2-1】.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,且过点D(2,﹣3).点P、Q是抛物线y=ax2+bx+c上的动点.(1)求抛物线的解析式;(2)当点P在直线OD下方时,求△POD面积的最大值.(3)直线OQ与线段BC相交于点E,当△OBE与△ABC相似时,求点Q的坐标.解:(1)函数的表达式为:y=a(x+1)(x﹣3),将点D坐标代入上式并解得:a=1,故抛物线的表达式为:y=x2﹣2x﹣3…①;(2)设点P(m,m2﹣2m﹣3),①当点P在第三象限时,设直线PD与y轴交于点G,设点P(m,m2﹣2m﹣3),将点P、D的坐标代入一次函数表达式:y=sx+t并解得:直线PD的表达式为:y=mx﹣3﹣2m,则OG=3+2m,S△POD=×OG(x D﹣x P)=(3+2m)(2﹣m)=﹣m2+m+3,②当点P在第四象限时,设PD交y轴于点M,=×OM(x D﹣x P)=﹣m2+m+3,同理可得:S△POD=﹣m2+m+3,综上,S△POD有最大值,当m=时,其最大值为;∵﹣1<0,故S△POD(3)∵OB=OC=3,∴∠OCB=∠OBC=45°,∵∠ABC=∠OBE,故△OBE与△ABC相似时,分为两种情况:①当∠ACB=∠BOQ时,AB=4,BC=3,AC=,过点A作AH⊥BC于点H,S△ABC=×AH×BC=AB×OC,解得:AH=2,则sin∠ACB==,则tan∠ACB=2,则直线OQ的表达式为:y=﹣2x…②,联立①②并解得:x=或﹣,故点Q(,﹣2)或(﹣,2),②∠BAC=∠BOQ时,tan∠BAC==3=tan∠BOQ,则点Q(n,﹣3n),则直线OQ的表达式为:y=﹣3x…③,联立①③并解得:x=,故点Q(,)或(,);综上,当△OBE与△ABC相似时,Q的坐标为:(,﹣2)或(﹣,2)或(,)或(,).1.抛物线y=﹣x2平移后的位置如图所示,点A,B坐标分别为(﹣1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D.(1)求平移后的抛物线的解析式和点D的坐标;(2)∠ACB和∠ABD是否相等?请证明你的结论;(3)点P在平移后的抛物线的对称轴上,且△CDP与△ABC相似,求点P的坐标.解:(1)∵将抛物线y=﹣x2平移,平移后的抛物线与x轴交于点A(﹣1,0)和点B(3,0),∴平移后的抛物线的表达式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3,即y=﹣x2+2x+3,∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4);(2)∠ACB与∠ABD相等,理由如下:如图,∵y=﹣x2+2x+3,∴点x=0时,y=3,即C点坐标为(0,3),又∵B(3,0),∠BOC=90°,∴OB=OC,∠OBC=∠OCB=45°.在△BCD中,∵BC2=32+32=18,CD2=12+12=2,BD2=22+42=20,∴BC2+CD2=BD2,∴∠BCD=90°,∴tan∠CBD===,∵在△AOC中,∠AOC=90°,∴tan∠ACO==,∴tan∠ACO=tan∠CBD,∴∠ACO=∠CBD,∴∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD;(3)∵点P在平移后的抛物线的对称轴上,而y=﹣x2+2x+3的对称轴为x=1,∴可设P点的坐标为(1,n).∵△ABC是锐角三角形,∴当△CDP与△ABC相似时,△CDP也是锐角三角形,∴n<4,即点P只能在点D的下方,又∵∠CDP=∠ABC=45°,∴D与B是对应点,分两种情况:①如果△CDP∽△ABC,那么=,即=,解得n=,∴P点的坐标为(1,);②如果△CDP∽△CBA,那么=,即=,解得n=,∴P点的坐标为(1,).综上可知P点的坐标为(1,)或(1,).2.如图,已知△ABC中,∠ACB=90°,以AB所在直线为x轴,过c点的直线为y轴建立平面直角坐标系.此时,A点坐标为(﹣1,0),B点坐标为(4,0)(1)试求点C的坐标;(2)若抛物线y=ax2+bx+c过△ABC的三个顶点,求抛物线的解析式;(3)点D(1,m)在抛物线上,过点A的直线y=﹣x﹣1交(2)中的抛物线于点E,那么在x轴上点B的左侧是否存在点P,使以P、B、D为顶点的三角形与△ABE相似?若存在,求出P点坐标;若不存在,说明理由.解:(1)在Rt△ABC中,∠ACB=90°,OC⊥AB,由射影定理,得:OC2=OA•OB=4,即OC=2,∴C(0,2);(2)∵抛物线经过A(﹣1,0),B(4,0),C(0,2),可设抛物线的解析式为y=a(x+1)(x﹣4)(a≠0),则有:2=a(0+1)(0﹣4),a=﹣,∴y=﹣(x+1)(x﹣4)=﹣x2+x+2;(3)存在符合条件的P点,且P(,0)或(﹣,0).根据抛物线的解析式易知:D (1,3),联立直线AE 和抛物线的解析式有:,解得,,∴E (6,﹣7),∴tan ∠DBO ==1,即∠DBO =45°,tan ∠EAB ==1,即∠EAB =45°,∴∠DBA =∠EAB ,若以P 、B 、D 为顶点的三角形与△ABE 相似,则有两种情况:①△PBD ∽△BAE ;②△PBD ∽△EAB .易知BD =3,EA =7,AB =5,由①得:,即,即PB =,OP =OB ﹣PB =,由②得:,即,即P ′B =,OP ′=OB ﹣BP ′=﹣,∴P (,0)或(﹣,0).3.如图已知直线y =x +与抛物线y =ax 2+bx +c 相交于A (﹣1,0),B (4,m )两点,抛物线y =ax 2+bx +c 交y 轴于点C (0,﹣),交x 轴正半轴于D 点,抛物线的顶点为M .(1)求抛物线的解析式;(2)设点P 为直线AB 下方的抛物线上一动点,当△PAB 的面积最大时,求△PAB 的面积及点P 的坐标;(3)若点Q 为x 轴上一动点,点N 在抛物线上且位于其对称轴右侧,当△QMN 与△MAD相似时,求N点的坐标.解:(1)将点B(4,m)代入y=x+,∴m=,将点A(﹣1,0),B(4,),C(0,﹣)代入y=ax2+bx+c,解得a=,b=﹣1,c=﹣,∴函数解析式为y=x2﹣x﹣;(2)设P(n,n2﹣n﹣),则经过点P且与直线y=x+垂直的直线解析式为y=﹣2x+n2+n﹣,直线y=x+G(n2+n﹣,n2+n+),∴GP=(﹣n2+3n+4),当n=时,GP最大,此时△PAB的面积最大,∴P(,﹣),∵AB=,PG=,∴△PAB的面积=××=;(3)∵M(1,﹣2),A(﹣1,0),D(3,0),∴AM=2,AD=4,MD=2,∴△MAD是等腰直角三角形,∵△QMN与△MAD相似,∴△QMN是等腰直角三角形,设N(t,t2﹣t﹣)①如图1,当MQ⊥QN时,N(3,0);②如图2,当QN⊥MN时,过点N作NR⊥x轴,过点M作MS⊥RN交于点S,∵QN=MN,∠QNM=90°,∴△MNS≌△NMS(AAS)∴t﹣1=﹣t2+t+,∴t=±,∴t>1,∴t=,∴N(,1﹣);③如图3,当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点M作MR ∥x轴,与过Q点的垂线分别交于点S、R;∵QN=MQ,∠MQN=90°,∴△MQR≌△QNS(AAS),∴SQ=QR=2,∴t+2=1+t2﹣t﹣,∴t=5,∴N(5,6);④如图4,当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,过点N作x轴的平行线,与两垂线交于点R、S;∵QN=MN,∠MNQ=90°,∴△MNR≌△NQS(AAS),∴SQ=RN,∴t2﹣t﹣=t﹣1,∴t=2±,∵t>1,∴t=2+,∴N(2+,1+);综上所述:N(3,0)或N(2+,1+)或N(5,6)或N(,1﹣).4.如图,已知抛物线经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.(1)直接写出:b=2,c=1;(2)过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP 的面积最大时,求点P的坐标;(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似,若存在,直接写出点Q的坐标,若不存在,请说明理由.解:(1)将点A(0,1),B(﹣9,10)代入,∴,解得,∴抛物线的解析式为,∴b=2,c=1,故答案为:2,1;(2)∵AC∥x轴,A(0,1),∴,∴x1=﹣6,x2=0,∴C(﹣6,1),∵A(0,1),B(﹣9,10),∴直线AB的解析式为y=﹣x+1,设点,则E(m,﹣m+1),∴,∵AC⊥EP,AC=6,=S△AEC+S△APC∴S四边形AECP=×AC×EF+=×AC×(EF+PF)=×AC×PE=×6×(﹣m2﹣3m)=﹣m2﹣9m=﹣(m+)2+,∵﹣6<m<0,当时,四边形AECP,此时点;(3)存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似,理由如下:∵,∴P(﹣3,﹣2),∴PF=y F﹣y P=3,CF=x F﹣x C=3,∴PF=CF,∴∠PCF=45°.同理可得:∠EAF=45°,∴∠PCF=∠EAF,∴在直线AC上存在满足条件的Q,设Q(t,1),∵A(0,1),B(﹣9,10),C(﹣6,1),∴,AC=6,,以C,P,Q为顶点的三角形与△ABC相似,①当△CPQ∽△ABC时,∴,∴,∴t=﹣4,∴Q(﹣4,1);②当△CQP∽△ABC时,∴,∴,∴t=3,∴Q(3,1);综上所述:Q点坐标为(﹣4,1)或(3,1).5.已知抛物线经过点A(﹣2,0),B(0,﹣4),与x轴交于另一点C,连接BC.(1)求抛物线的解析式;=S△PBC,求直线AP的表达式;(2)如图,P是第一象限内抛物线上一点,且S△PBO(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请直接写出点D的坐标;若不存在,请说明理由.解:(1)把点A(﹣2,0),B(0、﹣4)代入抛物线y=x2+bx+c中得:,解得:,∴抛物线的解析式为:y=x2﹣x﹣4;(2)当y=0时,x2﹣x﹣4=0,解得:x=﹣2或4,∴C(4,0),如图1,过O作OE⊥BP于E,过C作CF⊥BP于F,设PB交x轴于G,=S△PBC,∵S△PBO∴,∴OE=CF,易得△OEG≌△CFG,∴OG=CG=2,设P(x,x2﹣x﹣4),过P作PM⊥y轴于M,tan∠PBM===,∴BM=2PM,∴4+x2﹣x﹣4=2x,x2﹣6x=0,x1=0(舍),x2=6,∴P(6,8),∴AP的解析式为:y=x+2,BC的解析式为:y=x﹣4,∴AP∥BC;(3)以A,B,C,E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE,四种,其中△ABE重合,不符合条件,△ACE不能构成三角形,∴当△ABE与以A,B,C,E中的三点为顶点的三角形相似,存在两个三角形:△ABC 和△BCE,①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,∵∠BAE=∠BAC,∠ABE≠∠ABC,∴∠ABE=∠ACB=45°,∴△ABE∽△ACB,∴,∴,∴AE=,OE=﹣2=∴E(,0),∵B(0,﹣4),∴BE:y=3x﹣4,则x2﹣x﹣4=3x﹣4,x1=0(舍),x2=8,∴D(8,20);②当△ABE与以B,C、E中的三点为顶点的三角形相似,如图3,此时E在C的左边,∵∠BEA=∠BEC,∴当∠ABE=∠BCE时,△ABE∽△BCE,∴==,设BE=2m,CE=4m,Rt△BOE中,由勾股定理得:BE2=OE2+OB2,∴,3m2﹣8m+8=0,(m﹣2)(3m﹣2)=0,m1=2,m2=,∴OE=4m﹣4=12或,∵OE=<2,∠AEB或∠BEC是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,如图4,∴E(﹣12,0);同理得BE的解析式为:y=﹣x﹣4,﹣x﹣4=x2﹣x﹣4,x=或0(舍)∴D(,﹣);同理可得E在C的右边时,△ABE∽△BCE,∴=,设AE=2m,BE=4m,Rt△BOE中,由勾股定理得:BE2=OE2+OB2,∴,3m2+2m﹣5=0,(m+)(3m﹣)=0,m1=﹣,m2=,∴OE=﹣12(舍)或,∵OE=<4,∠BEC是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,综上,点D的坐标为(8,20)或(,﹣6.如图,已知抛物线y =ax 2+bx +6经过两点A (﹣1,0),B (3,0),C 是抛物线与y 轴的交点.(1)求抛物线的解析式;(2)点P (m ,n )在平面直角坐标系第一象限内的抛物线上运动,直线CP 与x 轴交于点Q ,当∠BQC =∠BCO 时,求此时P 点坐标;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得∠CNM =90°,且△CMN 与△OBC 相似,如果存在,请求出点M 和点N 的坐标.解:(1)把A(﹣1,0),B(3,0)代入y=ax2+bx+6得:,解得,∴抛物线的解析式为y=﹣2x2+4x+6;(2)由y=﹣2x2+4x+6得C(0,6),∴OC=6,当Q在x轴正半轴,如图:∵∠BQC=∠BCO,且∠COB=∠QOC,∴△COB∽△QOC,∴=,即=,∴OQ=12,∴Q(12,0),设直线CQ解析式为y=kx+6,则0=12k+6,∴k=﹣,即直线CQ为y=﹣x+6,由得(与C重合,舍去)或,∴P(,),当Q在x轴负半轴,如图:同理可得:△BOC∽△BCQ,∴=,即BC2=OB•BQ,而OC=6,OB=3,∴BC=3,∴(3)2=3×BQ,∴BQ=15,∴Q(﹣12,0),设直线CQ为y=mx+6,则0=﹣12m+6,解得m=,∴直线CQ为y=x+6,由得(舍去)或,∴P(,),综上所述,P点坐标为(,)或(,),(3)设M(t,﹣2t2+4t+6),则N(0,﹣2t2+4t+6),∴MN=|t|,CN=|2t2﹣4t|,∵OC=6,OB=3,∴OC=2OB,∵△CMN与△OBC相似,∴MN=2CN或CN=2MN,①MN=2CN时,如图:∴|t|=2|2t2﹣4t|,解得t=或t=或t=0(舍去),∴M(,),N(0,)或M(,),N(0,);②CN=2MN时,如图:∴|2t2﹣4t|=2|t|,解得t=0(舍去)或t=3(M与B重合,舍去)或t=1,∴M(1,8),N(0,8),综上所述,M(,),N(0,)或M(,),N(0,)或M(1,8),N(0,8).7.如图,抛物线与x轴交于A,B两点,点A,B分别位于原点的左、右两侧,BO=3AO=3,过点B的直线与y轴正半轴和抛物线的交点分别为点C,D,.(1)求b,c的值;(2)求直线CD的函数解析式;(3)求∠ADB的度数;(4)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上,当△ABD与△BPQ 相似时,请直接写出所有满足条件的点Q的坐标.解:(1)∵点A,B分别位于原点的左、右两侧,BO=3AO=3,∴A(﹣1,0),B(3,0),把A(﹣1,0),B(3,0)代入y=x2+bx+c,得,解得:,∴b=﹣,c=﹣;(2)如图1,过点D作DE⊥AB于E,则∠DEB=∠COB=90°,∴DE∥OC,∴=,∵BC=CD,OB=3,∴=,∴OE=,∴点D横坐标为﹣,当x=﹣时,y=×(﹣)2﹣×(﹣)﹣=+1,∴点D坐标为(﹣,+1),设直线BD的函数解析式为y=kx+n,把B(3,0),D(﹣,+1)代入,得,解得:,∴直线BD的函数解析式为y=﹣x+;(3)如图2,连接AC,∵直线BD的函数解析式为y=﹣x+,∴C(0,),∵A(﹣1,0),D(﹣,+1),∴AC2=OA2+OC2=12+()2=4,则AC=2,BC2=OB2+OC2=32+()2=12,则BC=2,∴AB=3﹣(﹣1)=4,∴AC2+BC2=AB2,∴∠ACB=90°,∴∠ACD=180°﹣90°=90°,∵BC=CD,∴CD=2,∴tan∠ADB===1,∴∠ADB=45°;(4)在△ABD中,tan∠ABD==,∴∠ABD=30°,∵∠ADB=45°,∴∠BAD=180°﹣(∠ABD+∠ADB)=180°﹣(30°+45°)=105°,∵CD=2,BC=CD=2,∴BD=BC+CD=2+2,由(3)知:AC=CD=2,∠ACD=90°,AB=4,∴AD=2,∵y=x2﹣x﹣,∴对称轴为直线x=1.∵点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上,∴∠PBQ<90°,∴分两种情况:①当∠PBQ=∠ABD=30°时,如图3,设对称轴与x轴交于点M,则M(1,0),∴BM=3﹣1=2,∴PM=BM•tan∠PBQ=2×tan30°=,∵点P在抛物线的对称轴上且在x轴下方,∴P(1,﹣),BP===,∵△ABD与△BPQ相似,且∠PBQ=∠ABD,∴=或=,∴=或=,∴BQ=或BQ=,∴Q(,0)或(,0);②当∠PBQ=∠ADB=45°时,如图4,∵PM=BM•tan∠PBQ=2tan45°=2,∴P(1,﹣2),∴BP=2,∵△ABD与△BPQ相似,且∠PBQ=∠ADB,∴=或=,∴=或=,∴BQ=2﹣2或2+2,∴Q(5﹣2,0)或(1﹣2,0);综上所述,点Q的坐标为Q(,0)或Q(,0)或Q(5﹣2,0)或Q(1﹣2,0).8.在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,﹣2).(1)求抛物线的函数表达式;(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,求的最大值;(3)如图2,连接AC,BC,过点O作直线l∥BC,点P,Q分别为直线l和抛物线上的点,试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△CAB?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.解:(1)设抛物线的解析式为y=a(x+1)(x﹣4).将C(0,﹣2)代入得:﹣4a=﹣2,解得a=,∴抛物线的解析式为y=(x(x﹣4),即y=x2﹣x﹣2.(2)过点D作DG⊥x轴于点G,交BC于点F,过点A作AK⊥x轴交BC的延长线于点K,∴AK∥DG,∴△AKE∽△DFE,∴=.设直线BC的解析式为y=kx+b1,∴,解得,∴直线BC的解析式为y=x﹣2,∵A(﹣1,0),∴y=﹣﹣2=﹣,∴AK=,设D(m,m2﹣m﹣2),则F(m,m﹣2),∴DF=m﹣2﹣m2+m+2=﹣m2+2m.∴==﹣(m﹣2)2+.∴当m=2时,有最大值,最大值是.(3)符合条件的点P的坐标为(,)或(,).∵l∥BC,∴直线l的解析式为y=x,设P(a1,),①当点P在直线BQ右侧时,如图2,过点P作PN⊥x轴于点N,过点Q作QM⊥直线PN于点M,∵A(﹣1,0),C(0,﹣2),B(4,0),∴AC=,AB=5,BC=2,∵AC2+BC2=AB2,∴∠ACB=90°,∵△PQB∽△CAB,∴==,∵∠QMP=∠BNP=90°,∴∠MQP+∠MPQ=90°,∠MPQ+∠BPN=90°,∴∠MQP=∠BPN,∴△QPM∽△PBN,∴===,∴QM=,PM=(a1﹣4)=a1﹣2,∴MN=a1﹣2,ON﹣QM=a1﹣=a1,∴Q(a1,a1﹣2),将点Q的坐标代入抛物线的解析式得×(a1)2﹣×a1﹣2=a1﹣2,解得a1=0(舍去)或a1=.∴P(,).②当点P在直线BQ左侧时,由①的方法同理可得点Q的坐标为(a1,2).此时点P的坐标为(,).综上所述,符合条件的点P的坐标是(,)或(,).9.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c 经过点A,B.(1)求点B的坐标和抛物线的解析式;(2)M为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;(3)将抛物线在0≤x≤3之间的部分记为图象L,将图象L在直线y=t上方部分沿直线y=t翻折,其余部分保持不动,得到一个新的函数图象,记这个函数的最大值为a,最小值为b,若a﹣b≤3,请直接写出t的取值范围.解:(1)将(3,0)代入y=﹣x+c得0=﹣2+c,解得c=2,∴y=﹣x+2.将x=0代入y=﹣x+2得y=2,∴点B坐标为(0,2).将(3,0),(0,2)代入y=﹣x2+bx+c得,解得,∴y=﹣x2+x+2.(2)如图,当BM∥AM时满足题意,点B,N关于抛物线对称轴对称,∵y=﹣x2+x+2,∴抛物线对称轴为直线x=﹣=,∴点N坐标为(,2),∴点M坐标为(,0).如图,当∠NBP=90°时符合题意,作NC⊥y轴于点C,则N(m,﹣m2+m+2),∵∠NBC+∠ABO=∠ABO+∠BAO=90°,∴∠NBC=∠BAO,∴△BCN∽△AOB,∴=,即,解得m=,∴点M坐标为(,0).综上所述,点M坐标为(,0)或(,0).(3)∵y=﹣x2+x+2=﹣(x﹣)2+,∴抛物线顶点坐标为(,),∴翻折后顶点坐标为(,2t﹣),当点A为最低点时,t﹣0≤3,解得t≤3,令t﹣(2t﹣)=3,解得t=,∴≤t≤3.10.如图所示,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴相交于点C,B、C两点的坐标分别为(1,0)、(0,﹣3),直线y=kx+3k经过点A,与y轴交于点D.(1)求抛物线的函数表达式;(2)点E是抛物线上一动点(不与点C重合),连接AE,过点E作EF⊥x轴,垂足为F,若△AEF是等腰直角三角形,求点E的坐标;(3)在(2)的条件下,若在直线y=kx+3k上存在一点G使得△DFG与△AOC相似,求出k的值.解:(1)∵直线y=kx+3k经过点A,则点A的坐标为(﹣3,0),将点A、B、C的坐标代入抛物线表达式得:,解得,故抛物线的表达式为y=x2+2x﹣3;(2)设点E的坐标为(x,x2+2x﹣3),则AF=|x+3|,EF=|x2+2x﹣3|,∵△AEF是等腰直角三角形,∴AF=EF,∴|x2+2x﹣3|=|x+3|,∴x=﹣3(舍去)或x=0(舍去)或x=2,故点E的坐标为(2,5);(3)∵CO=BO=3,故△AOC为等腰直角三角形,当△DFG与△AOC相似时,则△DFG为等腰直角三角形,显然∠DFG不可能为直角,∵直线y=kx+3k与y轴交于点D D(0,3k),由(2)知,点F(2,0),①当∠FDG为直角时,∵点G在直线AD上,故在∠FDG的前提下,总能找到GD=DF,故只需要DF⊥AD即可,在等腰Rt△FDG中,由直线AD的表达式为:y=kx+3k,则tan∠DOA=k,而tan∠DFO====,解得k=±;②当∠FGD为直角时,如下图,过点G作MN∥y轴,交x轴于点N,交过点D与x轴的平行线于点M,则DG=GF,设点G的坐标为(t,kt+3k),则MD=﹣t,MG=3k﹣tk﹣3k=﹣kt;GN=kt+3k,FN=2﹣t,∵∠MGD+∠FGN=90°,∠FGN+∠GFN=90°,∴∠MGD=∠GFN,∵∠GMD=∠FNG=90°,GD=FG,∴△GMD≌△FNG(AAS),∴MD=GN,MG=NF,即﹣t=kt+3k且﹣kt=2﹣t,解得k=2或﹣;当∠DFG=90°时,过点G作GH⊥x轴于H,则△ODF≌△HFG,∴GH=OF=2,HF=OD=3k,∵y=﹣2时,﹣2=kx+3k,∴x=,∴2+=3k,解得k=2或﹣综上,k=±或2或﹣.11.如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣x﹣1交于点C.(1)求抛物线解析式及对称轴;(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N 的坐标,若不存在,请说明理由.解:(1)把A(﹣2,0),B(4,0)代入抛物线y=ax2+bx﹣1,得解得∴抛物线解析式为:y=∴抛物线对称轴为直线x=﹣(2)存在使四边形ACPO的周长最小,只需PC+PO最小∴取点C(0,﹣1)关于直线x=1的对称点C′(2,﹣1),连C′O与直线x=1的交点即为P点.设过点C′、O直线解析式为:y=kx∴k=﹣∴y=﹣则P点坐标为(1,﹣)(3)当△AOC∽△MNC时,如图,延长MN交y轴于点D,过点N作NE⊥y轴于点E∵∠ACO=∠NCD,∠AOC=∠CND=90°∴∠CDN=∠CAO由相似,∠CAO=∠CMN∴∠CDN=∠CMN∵MN⊥AC∴M、D关于AN对称,则N为DM中点设点N坐标为(a,﹣a﹣1)由△EDN∽△OAC∴ED=2a∴点D坐标为(0,﹣)∵N为DM中点∴点M坐标为(2a,)把M代入y=,解得a=0(舍去)或a=4∴a=4则N点坐标为(4,﹣3)当△AOC∽△CNM时,∠CAO=∠NCM∴CM∥AB则点C关于直线x=1的对称点C′即为点M由(2)M为(2,﹣1)∴由相似CN=,MN=由面积法求N到MC距离为则N点坐标为(,﹣)∴N点坐标为(4,﹣3)或(,﹣)12.抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.(1)求出抛物线L的解析式;(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D,F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点,若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.解:(1)由题意知,解得:,∴抛物线L的解析式为y=﹣x2+2x+1;(2)如图1,∵y=kx﹣k+4=k(x﹣1)+4,∴当x=1时,y=4,即该直线所过定点G坐标为(1,4),∵y=﹣x2+2x+1=﹣(x﹣1)2+2,∴点B(1,2),则BG=2,=1,即S△BNG﹣S△BMG=BG•(x N﹣1)﹣BG•(x M﹣1)=1,∵S△BMN∴x N﹣x M=1,由得x2+(k﹣2)x﹣k+3=0,解得:x==,则x N=、x M=,由x N﹣x M=1得=1,∴k=±3,∵k<0,∴k=﹣3;(3)如图2,设抛物线L 1的解析式为y =﹣x 2+2x +1+m ,∴C (0,1+m )、D (2,1+m )、F (1,0),设P (0,t ),①当△PCD ∽△FOP 时,,∴,∴t 2﹣(1+m )t +2=0①;②当△PCD ∽△POF 时,,∴,∴t =(m +1)②;(Ⅰ)当方程①有两个相等实数根时,Δ=(1+m )2﹣8=0,解得:m =2﹣1(负值舍去),此时方程①有两个相等实数根t 1=t 2=,方程②有一个实数根t =,∴m =2﹣1,此时点P 的坐标为(0,)和(0,);(Ⅱ)当方程①有两个不相等的实数根时,把②代入①,得:(m +1)2﹣(m +1)2+2=0,解得:m =2(负值舍去),此时,方程①有两个不相等的实数根t 1=1、t 2=2,方程②有一个实数根t =1,∴m=2,此时点P的坐标为(0,1)和(0,2);综上,当m=2﹣1时,点P的坐标为(0,)和(0,);当m=2时,点P的坐标为(0,1)和(0,2).13.设抛物线y=ax2+bx﹣2与x轴交于两个不同的点A(﹣1,0)、B(m,0),与y轴交于点C,且∠ACB=90度.(1)求m的值和抛物线的解析式;(2)已知点D(1,n)在抛物线上,过点A的直线y=x+1交抛物线于另一点E.若点P 在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标;(3)在(2)的条件下,△BDP的外接圆半径等于或.解:(1)令x=0,得y=﹣2,∴C(0,﹣2),∵∠ACB=90°,CO⊥AB,∴△AOC∽△COB,∴OA•OB=OC2∴OB=,∴m=4,将A(﹣1,0),B(4,0)代入y=ax2+bx﹣2,得,∴抛物线的解析式为y=x2﹣x﹣2.(2)D(1,n)代入y=x2﹣x﹣2,得n=﹣3,由,得,,∴E(6,7),过E作EH⊥x轴于H,则H(6,0)∴AH=EH=7∴∠EAH=45°过D作DF⊥x轴于F,则F(1,0)∴BF=DF=3∴∠DBF=45°∴∠EAH=∠DBF=45°∴∠DBH=135°,90°<∠EBA<135°则点P只能在点B的左侧,有以下两种情况:①若△DBP1∽△EAB,则∴BP1===∴OP1=4﹣=,∴P1(,0).②若△DBP2∽△BAE,则∴BP2===∴OP2=﹣4=∴P2(﹣,0).综合①、②,得点P的坐标为:P1(,0)或P2(﹣,0).(3)或.如图所示:先作△BPD的外接圆,过P作直径PM,连接DM,作DF⊥x轴于F.∵∠PMD=∠PBD,∠DFP=∠PDM,∴△PMD和△FBD相似,∴,∴PD===,DF=3,BD==3,∴PM==,∴△BPD的外接圆的半径=;同理可求出当P点在x轴的负半轴上时,△BPD的外接圆的半径=.14.如图1,在平面直角坐标系中,抛物线y=x2+x﹣与x轴交于点A、B(点A在点B右侧),点D为抛物线的顶点,点C在y轴的正半轴上,CD交x轴于点F,△CAD绕点C顺时针旋转得到△CFE,点A恰好旋转到点F,连接BE.(1)求点A、B、D的坐标;(2)求证:四边形BFCE是平行四边形;(3)如图2,过顶点D作DD1⊥x轴于点D1,点P是抛物线上一动点,过点P作PM⊥x轴,点M为垂足,使得△PAM与△DD1A相似(不含全等).①求出一个满足以上条件的点P的横坐标;②直接回答这样的点P共有几个?解:(1)令x2+x﹣=0,解得x1=1,x2=﹣7.∴A(1,0),B(﹣7,0).由y=x2+x﹣=(x+3)2﹣2得,D(﹣3,﹣2);(2)证明:∵DD1⊥x轴于点D1,∴∠COF=∠DD1F=90°,∵∠D1FD=∠CFO,∴△DD1F∽△COF,∴=,∵D(﹣3,﹣2),∴D1D=2,OD1=3,∵AC=CF,CO⊥AF∴OF=OA=1∴D1F=D1O﹣OF=3﹣1=2,∴=,∴OC=,∴CA=CF=FA=2,∴△ACF是等边三角形,∴∠AFC=∠ACF,∵△CAD绕点C顺时针旋转得到△CFE,∴∠ECF=∠AFC=60°,∴EC∥BF,∵EC=DC==6,∵BF=6,∴EC=BF,∴四边形BFCE是平行四边形;(3)∵点P是抛物线上一动点,∴设P点(x,x2+x﹣),①当点P在B点的左侧时,∵△PAM与△DD1A相似,∴或=,∴=或=,解得:x1=1(不合题意舍去),x2=﹣11或x1=1(不合题意舍去)x2=﹣;当点P在A点的右侧时,∵△PAM与△DD1A相似,∴=或=,∴=或=,解得:x1=1(不合题意舍去),x2=﹣3(不合题意舍去)或x1=1(不合题意舍去),x2=﹣(不合题意舍去);当点P在AB之间时,∵△PAM与△DD1A相似,∴=或=,∴=或=,解得:x1=1(不合题意舍去),x2=﹣3(不合题意舍去)或x1=1(不合题意舍去),x2=﹣;综上所述,点P的横坐标为﹣11或﹣或﹣;②由①得,这样的点P共有3个.15.如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A(,0),在第一象限内与直线y=x交于点B(2,t).(1)求这条抛物线的表达式;(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,①求点M的坐标;②在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.解:(1)∵B(2,t)在直线y=x上,∴t=2,∴B(2,2),把A、B两点坐标代入抛物线解析式可得,解得,∴抛物线解析式为y=2x2﹣3x;(2)如图1,过C作CD∥y轴,交x轴于点E,交OB于点D,过B作BF⊥CD于点F,∵点C是抛物线上第四象限的点,∴可设C(t,2t2﹣3t),则E(t,0),D(t,t),∴OE=t,BF=2﹣t,CD=t﹣(2t2﹣3t)=﹣2t2+4t,=S△CDO+S△CDB=CD•OE+CD•BF=(﹣2t2+4t)(t+2﹣t)=﹣2t2+4t,∴S△OBC∵△OBC的面积为2,∴﹣2t2+4t=2,解得t1=t2=1,∴C(1,﹣1);(3)①设MB交y轴于点N,如图2,∵B(2,2),∴∠AOB=∠NOB=45°,在△AOB和△NOB中,∴△AOB≌△NOB(ASA),∴ON=OA=,∴N(0,),∴可设直线BN解析式为y=kx+,把B点坐标代入可得2=2k+,解得k=,∴直线BN的解析式为y=x+,联立直线BN和抛物线解析式可得,解得(舍去)或,∴M(﹣,),②∵C(1,﹣1),∴∠COA=∠AOB=45°,且B(2,2),∴OB=2,OC=,∵△POC∽△MOB,∴==2,∠POC=∠BOM,当点P在第一象限时,如图3,过M作MG⊥y轴于点G,过P作PH⊥x轴于点H,∵∠COA=∠BOG=45°,∴∠MOG=∠POH,且∠PHO=∠MGO,∴△MOG∽△POH,∴===2,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数与相似的结合题型一:动点在线段上如图,平面直角坐标系xOy 中,已知(1,0)B -,一次函数5y x =-+的图像与x 轴、y 轴分别交于点A 、C 两点,二次函数2y x bx c =-++的图像经过点A 、点B ;(1)求这个二次函数的解析式;(2)点P 是该二次函数图像的顶点,求△APC 的面积;(3)如果点Q 在线段AC 上,且△ABC 与△AOQ 相似,求点Q 的坐标;如图,抛物线22y ax ax c =++(0)a >与x 轴交于(3,0)A -、B 两点(A 在B 的左侧),与y 轴交于点(0,3)C -,抛物线的顶点为M ;(1)求a 、c 的值; (2)求tan MAC ∠的值;(3)若点P 是线段AC 上一个动点,联结OP ;问是否存在点P ,使得以点O 、C 、P 为顶点的三角形与△ABC 相似?若存在,求出P 点坐标;若不存在,请说明理由; 如图,已知抛物线2y ax x c =-+的对称轴为直线x =1,与x 轴的一个交点为A (-1,0),顶点为B . 点C (5,m )在抛物线上,直线BC 交x 轴于点E . (1) 求抛物线的表达式及点E 的坐标; (2) 联结AB ,求∠B 的正切值;(3) 点G 为线段AC 上一点,过点G 作CB 的垂线交x 轴于点M (位于点E 右侧),当△CGM 与△ABE 相似时,求点M 的坐标. 【参考答案】24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(3)小题5分)解:(1)∵抛物线2y ax x c =-+的对称轴为直线x =1,∴12a =. ∵抛物线与x 轴的一个交点为A (-1,0),∴32c =-. ∴抛物线的表达式为21322y x x =--.………………………………………………(2分) ∴顶点B (1,-2).…………………………………………………………………(1分) ∵点C (5,m )在抛物线上,∴6m =. ∴C 点坐标为(5,6). 设直线BC 的表达式为y =kx +b (k ≠0),xyAB EC O (第24题图)则652k b k b=+⎧⎨-=+⎩,∴2,4.k b =⎧⎨=-⎩即BC 的表达式为y =2x -4.∴E (2,0).……………………………………………………………………………(1分)(2)作CH ⊥x 轴,垂足为H ,作BP ⊥x 轴,垂足为P , ∵C (5,6),A (-1,0),∴CH =6=AH . ∴∠CAH=45°. ∵B (1,-2),A (-1,0),∴BP =2=AP .∴∠BAP=45°. ∴∠CAB=90°. …………………………………………………………………………(1分)∵CH =6=AH ,CH ⊥x 轴,∴AC =∵BP =2=AP ,BP ⊥x 轴,∴AB =∴tan 3.ACB AB∠==…………………………………………………………………(2分) (3)∵∠CAB=90°,∴∠B +∠ACB =90°. ∵GM ⊥BC ,∴∠CGM +∠ACB =90°.∴∠CGM =∠B . ………………………………(1分) ∵△CGM 与△ABE 相似,∴∠BAE =∠CMG 或∠BAE =∠MCG . 情况1:当∠BAE =∠CMG 时, ∵∠BAE =45°,∴∠CMG =45°. ∵GM ⊥BC ,∴∠MCE =45°.∴∠MCE =∠EAB .∵∠AEB =∠CEM ,∴△ABE ∽△CME . ……………………………………………(1分)∴BE AEEM CE =.即EM =∴EM =5. ∴M (7,0). ……………………………(1分) 情况2:当∠BAE =∠MCG 时,∵∠BAE =∠CAM ,∴∠MCG =∠CAM .∴MC =MA . ………………………………(1分) 设M (x ,0),∵C (5,6),A (-1,0),∴222(1)(5)6.x x +=-+∴x=5.∴M (5,0). …………………………………………………………………………(1分) 题型二:动点在线段的延长线上如图7,已知抛物线32++-=bx x y 与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C ,且OC OB =,点D 是抛物线的顶点,直线AC 和BD 交于点E 。
(1)求点D 的坐标;(2)联结BC CD 、,求DBC ∠的余切值;(3)设点M 在线段CA 延长线上,如果EBM △和ABC △相似,求点M 的坐标。
【答案】(1)D 1,4()(2)3(3)63,)55-(- 【解析】(1)∵抛物线2y 3x bx =-++与轴的交于点A 和点B (点A 在点B 的左侧) , 与y 轴交于点C ,)3,0(C ,且OC OB =,)0,3(B(2)OB OC =∵45OCB OBC ∴∠=∠=︒y=45DC 。
∴∠;(3)由223y x x =-++,可得,在AOC 和BCD 中,3CO BCAO CD==, 又ACO CBD ∴∠=∠;ACB ACO OCB E CBD ∠=∠+=∠+∠ 当EBM ABC ∆∆和相似时,可知E CBA ∠=∠;又点在线段的延长线上,ACB EBA ∠=∠,可得EMB ACB ∠=∠; 由题意,得直线的表达式为y 33x =+;设(,33)M x x +.2(3)(33)18x x ∴-++=,解得126,05x x =-=(舍去)∴点M 的坐标是63,)55-(-题型三:动点在对称轴上如图,抛物线c bx x y ++-=2经过点)0,3(B ,)3,0(C ,D 为抛物线的顶点。
(1)求抛物线的解析式及顶点坐标;(2)点C 关于抛物线c bx x y ++-=2的对称点为E 点,联结BC ,BE ,求CBE ∠的正切值;(3)点M 是抛物线对称轴上一点,且△DMB 和△BCE 相似,求点M 的坐标。
【答案】(1)322++-=x x y ;)4,1(D (2)21(3) ()2,1-M 或⎪⎭⎫⎝⎛32,1M【解析】(1)∵抛物线c bx x y ++-=2经过点)0,3(B ,)3,0(C∴⎩⎨⎧==++-339c c b 可解得⎩⎨⎧==32c b ∴ 322++-=x x y 顶点坐标)4,1(D (2)过点E 作EH 垂直于BC 交于点H ∵点C 与点E 关于对称轴1=x 对称 ∴)3,2(E ,2=CE ,CE 平行于x 轴 在等腰直角三角形ECH 中,2=CE在直角三角形EHB 中,22=-=CH BC BH ,2=EH∴CBE ∠的正切值为21 (3)设抛物线对称轴1=x 交x 轴与点F∵在直角三角形DFB 中,4=DF ,2=BF ∴点M 在点D 的下方∴当DMB ∆与BCE ∆相似时,有下列两种情况:•当BE BCDB DM = 时,即 102352=DM 可解得6=DM ‚当BC BE DB DM = 时,即 231052=DM 可解得310=DM 综上所述: ()2,1-M 或⎪⎭⎫⎝⎛32,1M2)动点在平移后的对称轴上在平面直角坐标系中,点)0,4(A 是抛物线c x ax y ++=22上的一点,将此抛物线向下平移6个单位以后经过点)2,0(B ,平移后的新抛物线的顶点记为C ,新抛物线的对称轴和线段AB 的交点记为P 。
(1)求平移后得到的新抛物线的表达式,并求出点C 的坐标;(2)求CAB ∠的正切值;(3)如果点Q 是新抛物线对称轴上的一点,且BCQ △和ACP △相似,试求点Q 的坐标。
【答案】(1)222++-=x x y ;)3,1(C (2)1tan 3CAB ∠=(3))25,1(1Q 或)1,1(2-Q 【解析】(1)∵点)0,4(A 是抛物线c x ax y ++=22上的一点,代入得:0816=++c a ①又∵抛物线向下平移6个单位以后经过点)2,0(B ,平移后的抛物线解析式为:622-++=c x ax y 。
代入得:8,26==-c c ②,由①②得:8,1=-=c a平移后得到的新抛物线的表达式:222++-=x x y ,顶点)3,1(C(2)∵)0,4(A 、)2,0(B 、)3,1(C ,易得52,23,2===BA CA CB由勾股定理逆定理得ABC △是直角三角形,31tan ==∠CA CB CAB (3)设抛物线对称轴与x 轴相交于点H 易得45=∠=∠ACP BCP ,23,23,2===CP CA CB ∴点Q 只能在对称轴点C 的下方,BCQ △和ACP △相似,有以下两种情况: 综上,)25,1(1Q 或)1,1(2-Q 题型四:动点在某直线上如图,已知抛物线22y ax x c =-+经过ABC ∆的三个顶点,其中点(0,1)A ,点(9,10)B ,AC x ∥轴.(1)求这条抛物线的解析式; (2)求tan ABC ∠的值;(3)若点D 为抛物线的顶点,点E 是直线AC 上一点,当CDE ∆与ABC ∆相似时,求点E 的坐标.【参考答案】24.解:(1)∵抛物线22y ax x c =-+经过点(0,1)A 和点(9,10)B∴1811810c a c =⎧⎨-+=⎩……………………………………………………1分解得131a c ⎧=⎪⎨⎪=⎩………………………………………………………………2分∴这条抛物线的解析式为21213y x x =-+………………………………1分 (2)过点B 作BH AC ⊥,垂足为H9BH AH ==∴又90BHA ∠=︒HAB ∴△是等腰直角三角形45HAB ∠=︒∴………………………………………………………1分AC x ∥轴,(0,1)A ,点C 也在该抛物线上过点C 作CG AB ⊥,垂足为点Gsin 45CG AC =︒=∴1分又∵在Rt △ABH中,sin 45BHAB ==︒∴BG ==…………………………………………………1分(第24题图)∴在Rt △BCG 中,1tan 2CG ABC BG ∠==……………………………1分 (3)过点D 作DK AC ⊥,垂足为K ∵点D 是抛物线21213y x x =-+的顶点∴(3,2)D -………………1分 ∴3CK DK ==又∵90CKD ∠=︒∴△CDK 是等腰直角三角形 又∵45BAC ∠=︒∴DCK BAC ∠=∠………………………………………………………1分 ∴当△CDE 与△ABC 相似时,存在以下两种情况:1︒AC EC AB CD ==9232∴∴EC=2(4,1)E ∴……………1分2︒AC DCAB EC =32=92EC∴∴EC=9(3,1)E -∴…………1分 题型五:动点在x 轴上如图9,在平面直角坐标系xoy 中,顶点为M 的抛物线2(0y ax bx a =+>)经过点A 和x 轴正半轴上的点B ,AO OB == 2,0120AOB ∠=. (1)求这条抛物线的表达式; (2)联结OM ,求AOM ∠的大小;(3)如果点C 在x 轴上,且△ABC 与△AOM 相似,求点C 的坐标.2019年青浦一模24】已知,如图8,在平面直角坐标系中,抛物线142+-=ax ax y 与x 轴正半轴交于点A 和点B ,与y 轴交于点C ,且OC OB 3=,点P 是第一象限内的点,联结BC ,△PBC 是以BC 为斜边的等腰直角三角形.(1)求这个抛物线的表达式; (2)求点P 的坐标;(3)点Q 在x 轴上,若以P O Q 、、为顶点的三角形与以点B A C 、、为顶点的三角形相似,求点Q 的坐标. 【答案】(1)134312+-=∴x x y (2))2,2(P ∴(3)点Q 坐标为)0,2(-或)0,4(- MA B Oy图9【解析】(1)由题意可得)1,0(C33==∴OC OB )0,3(B ∴代入142+-=ax ax y 得31=a 134312+-=∴x x y(2)过点P 作轴轴x PF y PE ⊥⊥, (3)PBC ∆ 为等腰直角三角形 (4)PB PC =∴(5)︒=∠+∠=∠+∠90CPF FPB CPF EPC(6)FPB EPC ∠=∠∴)(AAS PFB Rt PCE Rt ∆∆∴≌BF EC =∴ (7)可证四边形PEOF 为正方形BF OB OC EC -=+∴3,1==OB OC(8)BF EC -=+∴31,解得1==BF EC 2==∴OF OE P 在第一象限内)2,2(P ∴ (9)2,2==AB AC )0,1(),1,0(A C OA OC =∴,可得AOC ∆为等腰直角三角形︒=∠∴45OAC ︒=∠∴135CAB ,则点Q 在y 轴左侧i.CAB OP Q ∆∆∽1ABCA OP OQ =1,222221=⨯=⋅=AB CA OP OQ )0,2(1-∴Q ii.CAB POQ ∆∆∽2ABCA OQ OP =2 42222=⨯=⋅=ACABOP OQ )0,4(2-∴Q若点Q 在y 轴右侧,不存在综上所述:点Q 坐标为)0,2(-或)0,4(-在平面直角坐标系xOy 中,抛物线2+c y x bx =-+与x 轴相交点(1,0)A -和点B ,与y 轴相交于点(0,3)C ,抛物线的顶点为点D ,联结AC ,BC ,DB DC 。
