材料力学第十一章
合集下载
材料力学刘鸿文版全套课件
M (x)
M (x)
N ( x)
N ( x)
T (x)
T (x)
V
L
FN 2 (x)dx 2EA
L
M 2 (x)dx 2EI
L
T 2 (x)dx 2GIP
所有的广义力均以静力方式，按一定比例由O增加至最终值。任一广义位移 与
整个力系有关，但与其i 相应的广义力 呈线性关系。
Fi
产生位移1 , 2 ,, i ,
变形能的增加量：
V
1 2
Fi
i
F11 F2 2
Fi i
略去二阶小量，则：
V F11 F2 2 Fi i
如果把原有诸力看成第一组力，把 Fi 看作第二组力，根据互等
F F 功的互等定理:
1 12
2 21
若F1 F2，则得
位移互等定理:
12 21
例：求图示简支梁C截面的挠度。
F
B2
wC1
解：由功的互等定理 F wC1 M B2
得：F
wC1
M
Fl 2 16EI
由此得：wC1
Ml2 16E I
例：求图示悬臂梁中点C处的铅垂位移C 。
有效应力集中因数 理论应力集中因数
K
1
d
1
K
或
K
1
d
1 K
K
max n
目录
2.零件尺寸的影响——尺寸因数
( 1)d 1
查看表11.1
( 1 )d 光滑零件的疲劳极限
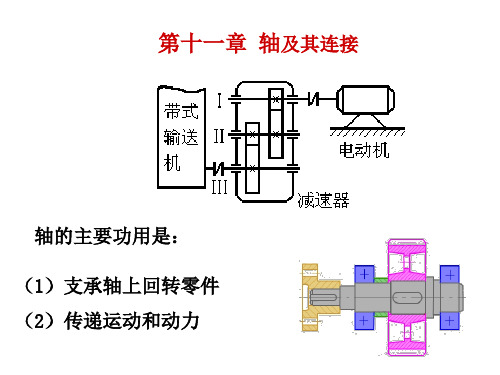
第十一章 轴及其连接
轴上的槽用盘铣刀或指状铣刀 加工；轮毂槽用拉刀或插刀加工。
②导键和滑键
用于动联接，即轴与轮毂之间有相对轴向移 动的联接。滑键用于轴上零件轴向移动量较大的 场合。
（2）半园键
半园键的侧面为工作面，对中良好，用于静 联接。 特点：键能在槽中摆动，装配 方便，适用于锥形轴与轮毂的 联接。缺点是对轴的强度削弱 较大。只适宜轻载联接。需要 用两个半圆键时，一般安置在 轴的同一条母线上。
d
r
r
D
D
h
11.2.2 轴的制造和轴上零件的装拆
1.轴的加工工艺性
(1)为减少加工时换刀时间及装夹工件时间，同一 根轴上所有圆角半径、倒角尺寸、退刀槽宽度 应尽可能统一；当轴上有两个以上键槽时，应 置于轴的同一条母线上，以便一次装夹后就能 加工。
(2)轴上的某轴段需磨削时，应留有砂轮的越程槽； 需切制螺纹时，应留有退刀槽。
84 82 Ⅰ
45H7/k6
b) 轴承、齿轮的定位及轴段主要尺寸——
根据轴的受力，选取一对7211C滚动轴承正装，其尺寸为d×D×B＝ 55mm×100mm×21mm, 配合段轴径 dⅢ-Ⅳ=dⅥ-Ⅶ=55mm(k6)。左端 轴承采用轴肩作轴向定位，由手册确定轴肩处直径 dⅤ-Ⅵ≥64mm，配 合轴段长LⅥ-Ⅶ=23mm；右端采用轴套作轴向定位。 23 23 21 21 84 100 Ⅱ Ⅰ 82
主要失效形式是工作面的过度磨损，通常按工作面
上的压力进行条件性的强度校核计算。
（2）平键联接的强度条件 普通平键的挤压强度条件为:
p
2000T / d 2000T p lk dlk
导向平键和滑键联接的强度条件为：
p
式中
2000T p kld
交变应力
材料力学
疲劳失效机理
第十一章 交变应力
金属材料裂纹 疲劳源 裂纹扩展 光滑区 脆断 粗糙区
材料力学
第十一章 交变应力
§11-2 交变应力的循环特征、应力幅 和平均应力
应力循环：应力每重复变化一次，称为一个应力循环。 完成一个应力循环所需的时间T ，称为一个周期。
o
t
材料力学
第十一章 交变应力
材料力学
构件尺寸的影响
第十一章 交变应力
构件尺寸越大，疲劳极限越 低。如受扭转大、小二圆截面试 件，如二者的最大剪应力相同， 则大试件横截面上的高应力区比 小试件的大。即大试件中处于高 应力状态的晶粒比小试件的多， 故引发疲劳裂纹的机会也多。
材料力学
第十一章 交变应力
构件表面质量的影响
构件上的最大应力常发生于表层，疲劳裂纹也多生成于 表层。故构件表面的加工缺陷（划痕、擦伤）等将引起应力 集中，降低疲劳极限。
a
max
min
o
a
m
t 应力幅度
平均应力
max：最大应力
min：最小应力
a
m
材料力学
第十一章 交变应力
a a
max min
o
m
min 循环特征： r max
m
t
1 a max min 2
1 max min 2
如:机车车轴
材料力学
2.脉动循环
min 0
第十一章 交变应力
1 1 m max min max 2 2 1 1 a max min max 2 2
《材料力学 第2版》_顾晓勤第11章第6节 提高构件疲劳强度的措施
构件上少开孔口，特别是在承受最大拉应力的表 面上尽量不开孔口。若必须开设时，尽量使用圆 形或椭圆形孔口。对于轴上开孔之处，可将孔开 穿，以降低应力集中的影响。
为减小应力集中影响， 设计焊接件时，要求使 焊缝尽量远离高应力区 域，尽量避免焊缝的交 汇，对焊缝进行磨削加 工使焊缝平滑，角焊缝 采用坡口焊。
尽量避免构件表面受到机械碰伤（如刀痕、打记 号）和化学损伤（如腐蚀、氧化脱碳、生锈等）。
ห้องสมุดไป่ตู้
第 6 节 提高构件疲劳强度的措施 第十一章 动载荷和疲劳
提高构件表面层的强度，是提高构件疲劳强度的 重要措施。生产上通常采用表面热处理（如高频 淬火）、化学处理（如表面渗碳或氮化）和表面 机械强化（如滚压、喷丸）等方法，使构件表面 层强度提高。
第 6 节 提高构件疲劳强度的措施 第十一章 动载荷和疲劳
一、合理选材
为提高疲劳强度，应选择对应力集中敏感性低的 材料。在各种钢材中，通常情况下强度极限较低 的材料，对应力集中的敏感性也较低，相同外形 尺寸改变处的有效应力集中因数也较低，其构件 的疲劳强度也较高。
静强度设计时希望强度极限较高的材料，而考虑 疲劳强度时宜选择强度极限较低的材料，设计时 要对二者的要求相权衡，以确定合适的材料。
第 6 节 提高构件疲劳强度的措施 第十一章 动载荷和疲劳
三、提高构件表面质量
构件弯曲或扭转时表层的应力一般较大，加上构 件表面的切削刀痕又将引起应力集中，故容易形 成疲劳裂纹。降低表面粗糙度，可以减弱切削刀 痕引起的应力集中，从而提高构件的疲劳强度。 特别是高强度构件，对应力集中较敏感，只有采 用精加工方法，才能有利于发挥材料的高强度性 能。此外，应尽量避免构件表面的机械损伤和化 学腐蚀。
选材还需要考虑工作环境。例如，在低温下工作 的构件，应选择韧性更好的材料；在腐蚀环境中 工作的构件，应选择耐腐蚀性强的材料；等等。
为减小应力集中影响， 设计焊接件时，要求使 焊缝尽量远离高应力区 域，尽量避免焊缝的交 汇，对焊缝进行磨削加 工使焊缝平滑，角焊缝 采用坡口焊。
尽量避免构件表面受到机械碰伤（如刀痕、打记 号）和化学损伤（如腐蚀、氧化脱碳、生锈等）。
ห้องสมุดไป่ตู้
第 6 节 提高构件疲劳强度的措施 第十一章 动载荷和疲劳
提高构件表面层的强度，是提高构件疲劳强度的 重要措施。生产上通常采用表面热处理（如高频 淬火）、化学处理（如表面渗碳或氮化）和表面 机械强化（如滚压、喷丸）等方法，使构件表面 层强度提高。
第 6 节 提高构件疲劳强度的措施 第十一章 动载荷和疲劳
一、合理选材
为提高疲劳强度，应选择对应力集中敏感性低的 材料。在各种钢材中，通常情况下强度极限较低 的材料，对应力集中的敏感性也较低，相同外形 尺寸改变处的有效应力集中因数也较低，其构件 的疲劳强度也较高。
静强度设计时希望强度极限较高的材料，而考虑 疲劳强度时宜选择强度极限较低的材料，设计时 要对二者的要求相权衡，以确定合适的材料。
第 6 节 提高构件疲劳强度的措施 第十一章 动载荷和疲劳
三、提高构件表面质量
构件弯曲或扭转时表层的应力一般较大，加上构 件表面的切削刀痕又将引起应力集中，故容易形 成疲劳裂纹。降低表面粗糙度，可以减弱切削刀 痕引起的应力集中，从而提高构件的疲劳强度。 特别是高强度构件，对应力集中较敏感，只有采 用精加工方法，才能有利于发挥材料的高强度性 能。此外，应尽量避免构件表面的机械损伤和化 学腐蚀。
选材还需要考虑工作环境。例如，在低温下工作 的构件，应选择韧性更好的材料；在腐蚀环境中 工作的构件，应选择耐腐蚀性强的材料；等等。
哈尔滨工程大学力学基础课件第11章
2
Ni2li U U i i 1 i 1 2 EA i
m m
(11-3)
2.圆轴扭转
M
M
A
j
M
l
o
(a)
j
B
j
对于圆轴的扭转，当外力偶矩由零开始 逐渐增加至最终值M时，扭转角也由零逐渐 增至最终值。在线弹性范围内，M与 的关 系也是一条斜直线，如图所示。 1 (b) W M
O
解：
由图b可以看出，截面mn上 的扭矩和弯矩分别为
A
P
dj
R
j
m n
(b)
M n PR(1 cos j )
M PR sin j
p
A
j
m
dj
R
例3:图示半圆形等截面曲杆位于 水平面内，在A点受铅垂力P的 作用，求A点的垂直位移。
变形能为: 2
dU
M n Rdj M 2 Rdj 2GI p 2 EI P 2 R 3 (1 cos j ) 2 dj P 2 R 3 sin j dj 2GI p 2 EI
3P R P R 4GI p 4 EI
2 3 2 3
dj
j
m n
(b)
由此求得:
A
3PR PR 2GI p 2 EI
3 3
11.2 莫尔定理
莫尔定理是一种能够求 解在复杂载荷作用下的结构 任一处广义位移的有效工具。 现在以梁为例，利用变 形能的概念和特性来导出莫 尔定理。 假设梁在外力1 ,2 …… 作用下发生弯曲变形，如图a 所示。今要确定在上述外力 作用下，梁上任意一点C的 挠度 。
p
A
p
o
p
(a)
Ni2li U U i i 1 i 1 2 EA i
m m
(11-3)
2.圆轴扭转
M
M
A
j
M
l
o
(a)
j
B
j
对于圆轴的扭转，当外力偶矩由零开始 逐渐增加至最终值M时，扭转角也由零逐渐 增至最终值。在线弹性范围内，M与 的关 系也是一条斜直线，如图所示。 1 (b) W M
O
解：
由图b可以看出，截面mn上 的扭矩和弯矩分别为
A
P
dj
R
j
m n
(b)
M n PR(1 cos j )
M PR sin j
p
A
j
m
dj
R
例3:图示半圆形等截面曲杆位于 水平面内，在A点受铅垂力P的 作用，求A点的垂直位移。
变形能为: 2
dU
M n Rdj M 2 Rdj 2GI p 2 EI P 2 R 3 (1 cos j ) 2 dj P 2 R 3 sin j dj 2GI p 2 EI
3P R P R 4GI p 4 EI
2 3 2 3
dj
j
m n
(b)
由此求得:
A
3PR PR 2GI p 2 EI
3 3
11.2 莫尔定理
莫尔定理是一种能够求 解在复杂载荷作用下的结构 任一处广义位移的有效工具。 现在以梁为例，利用变 形能的概念和特性来导出莫 尔定理。 假设梁在外力1 ,2 …… 作用下发生弯曲变形，如图a 所示。今要确定在上述外力 作用下，梁上任意一点C的 挠度 。
p
A
p
o
p
(a)
第课弯曲应力
6
第十一章 弯曲应力
伽利略最早提出了梁的问题
马略特梁截面应力分布 上的假设有所改进
胡克正确描述了梁的变 形，但没有深入
伯努利提出平面假设 “伯努利梁”
纳维正确地确定了梁的 中性层位置，最后解决
了梁的线性理论
铁木辛柯在梁横向振动微分
方程中考虑了旋转惯性和剪
力, “铁木辛柯梁”
7
伽利略对梁问题的研究
已知 = (D+) / 2、E、截面尺寸，可应
用下述关系求应力与内力
变形->应力->内力：
y
E
y
max
E
ymax
变形->内力->应力：
M maxW
1 M
EIz
max
M W
29
第十一章 弯曲应力
2. 应力计算
max
E
ymax
ymax
2
1.0 103 m
第十一章 弯曲应力
第十一章 弯 曲 应 力
§5-1 §5-2 附录A
引言 弯曲正应力 截面几何性质
5
§11-1 引言
第十一章 弯曲应力
梁的理论在材料力学中占有突出的位置，在任何一本 材料力学教材中都是最重要的部分。
从1638年伽利略在《关于两门新科学的对话》提出梁 的问题开始…。此后，马略特、胡克、伯努利、纳维、 欧拉、圣维南等著名力学家都对梁的问题进行了研究。 到1921年铁木辛柯梁对动力学问题的完善，前后历经 近400年的时间…
y
dx
yd d
y
第11章 弯曲应力
工程力学—材料力学 工程力学 材料力学 （3）切应力分布规律及最大切应力 ）
第十一章 弯曲应力
S z∗ =
则
∫ y ' dA = ∫
A' y
h/2
b h2 2 y1bdy1 = − y 2 4
FSZ∗ F b h2 2 F h2 2 τ = s = s ⋅ − y = s ⋅ − y bIz bIz 2 4 2Iz 4
整理得
FSZ∗ τ == s bIz
——矩形截面梁弯曲时横截面上切应力计算公式。 矩形截面梁弯曲时横截面上切应力计算公式。 矩形截面梁弯曲时横截面上切应力计算公式
S z∗ =
∫ y ' dA
A'
——横截面上 以外部分面积对中性轴 的静钜。 横截面上3-3以外部分面积对中性轴 静钜。 横截面上 以外部分面积对中性轴z的 东北大学秦皇岛分校
M(x)+Fsd x
东北大学秦皇岛分校
工程力学—材料力学 工程力学 材料力学 z
F3 F1
第十一章 弯曲应力
M F1 = ∫ σ 1dA = A' Iz MS z∗ ∫A ' y 'dA = I z
τ'
dx
τ
y
x
F2
F2 =
∫σ
A'
2
dA
( M + Fs d x ) = ∫ y ' dA Iz A' = ( M + Fs d x ) Iz
Iz为整个截面对z轴之惯性矩；b 为y点处截面宽度。 轴之惯性矩； 点处截面宽度。
东北大学秦皇岛分校
工程力学—材料力学 工程力学 材料力学 （2）几种常见截面的最大弯曲剪应力 工字钢截面： ① 工字钢截面：
工程力学课件 第11章 动载荷、冲击载荷、交变应力简介
1.1.1 电路பைடு நூலகம்组成
交变应力的变化特点可用最小应力与最大应力的比值r表示， 称为循环特征（应力比）即
它的可能取值范围为
在五个特征量
中，只有两个是独立的，即只要已知其中的任意两个特征量， 就可求出其他的量。如果
工程力学
12
称为脉动循环交变应力，其循环特征r＝0。 当
1.1.1 电路的组成
r＝1 交变应力统称为非对称循环交变应力。
对于以等加速度作直线运动构件，只要确定其上各点的加速度a, 就可以应用达朗贝尔原理施加惯性力，如果为集中质量m，则惯性力 为集中力。
如果是连续分布质量，则作用在质量微元上的惯性力为
工程力学
2
然后，按照弹性 静力学中的方法对构
1.件1进.1行电应力路分的析和组强成 度与刚度的计算。以 图中的起重机起吊重 物为例，在开始吊起 重物的瞬时，重物具 有向上的加速度a，重 物上便有方向向下的 惯性力，如式(11-1) 所示。
其中
分别称为静应力(staticsstress)和动应力(dynamicsstress)。
工程力学
4
第二节 冲击载荷
一、基本假定 1.1.1具电有一路定的速度组的成运动物体，向着静止的构件冲击时，冲击物的
速度在很短的时间内发生了很大变化，即：冲击物得到了很大的负 值加速度。这表明，冲击物受到与其运动方向相反的很大的力作用。 同时，冲击物也将很大的力施加于被冲击的构件上，这种力在工程 上称为“冲击力”或“冲击载荷”。
③假设冲击过程中没有其他形式的能量转换，机械能量守恒定 理仍成立。
工程力学
5
二、自由落体冲击 1.1.1设电一简路支的梁(组线弹成性体)受自由落体冲击如图11.3所示，试分析
交变应力的变化特点可用最小应力与最大应力的比值r表示， 称为循环特征（应力比）即
它的可能取值范围为
在五个特征量
中，只有两个是独立的，即只要已知其中的任意两个特征量， 就可求出其他的量。如果
工程力学
12
称为脉动循环交变应力，其循环特征r＝0。 当
1.1.1 电路的组成
r＝1 交变应力统称为非对称循环交变应力。
对于以等加速度作直线运动构件，只要确定其上各点的加速度a, 就可以应用达朗贝尔原理施加惯性力，如果为集中质量m，则惯性力 为集中力。
如果是连续分布质量，则作用在质量微元上的惯性力为
工程力学
2
然后，按照弹性 静力学中的方法对构
1.件1进.1行电应力路分的析和组强成 度与刚度的计算。以 图中的起重机起吊重 物为例，在开始吊起 重物的瞬时，重物具 有向上的加速度a，重 物上便有方向向下的 惯性力，如式(11-1) 所示。
其中
分别称为静应力(staticsstress)和动应力(dynamicsstress)。
工程力学
4
第二节 冲击载荷
一、基本假定 1.1.1具电有一路定的速度组的成运动物体，向着静止的构件冲击时，冲击物的
速度在很短的时间内发生了很大变化，即：冲击物得到了很大的负 值加速度。这表明，冲击物受到与其运动方向相反的很大的力作用。 同时，冲击物也将很大的力施加于被冲击的构件上，这种力在工程 上称为“冲击力”或“冲击载荷”。
③假设冲击过程中没有其他形式的能量转换，机械能量守恒定 理仍成立。
工程力学
5
二、自由落体冲击 1.1.1设电一简路支的梁(组线弹成性体)受自由落体冲击如图11.3所示，试分析
第十一章 动荷载 交变应力
FNd Fd A2 D 2 2 4
qd
qd
Fd d m m n n FNd FNd (c)
D d 2
于是，横截面上的正应力 d 为
FNd 2 D 2 d A 4
材料力学教学课件 2019年4月2日星期二
11
第11章
动荷载 · 交变荷载
例题：直径 d=100mm 的圆轴，一端有重量 P=0.6kN 、 直径 D=400mm 的飞轮，以均匀转速 n=1000r/min 旋 转（图 a)。现因在轴的另一端施加了掣动的外力偶矩 Me ，而在 t=0.01s 内停车。若轴的质量与飞轮相比很 小而可以略去不计，试求轴内最大动切应力d,max 。 解：飞轮的惯性力矩为
则
Δd Kd Δst
(e)
将上式两边乘以 E/l 后得
d Kd st
(1)
当 h0 时，相当于P 骤加在杆件上，这时
Kd 2
对于实际情况，以上计算是偏于安全的。
材料力学教学课件 2019年4月2日星期二
24
第11章
动荷载 · 交变荷载
D 例题：钢吊索AC的下端挂一重量为P=20kN C 的重物(图a)，并以等速度 v=1m/s 下降。 当吊索长度为 l=20m 时，滑轮D突然被卡 (a) A 住。试求吊索受到的冲击荷载 Fd 及冲击 Δd 应力 d 。已知吊索内钢丝的横截面面积 Fd A=414mm2，材料的弹性模量E=170GPa， D C 滑轮的重量可略去不计。若在上述情况下 ，在吊索与重物之间安置一个刚度系数 k=300kN/m 的弹簧，则吊索受到的冲击荷 (b) A Δst 载又是多少？ l P
解出 d 的两个根，取其中大于 st 的那个根，即得
2h Δd Δst (1 1 ) Δst 2h 引用记号 K d (1 1 ) Δst
qd
qd
Fd d m m n n FNd FNd (c)
D d 2
于是，横截面上的正应力 d 为
FNd 2 D 2 d A 4
材料力学教学课件 2019年4月2日星期二
11
第11章
动荷载 · 交变荷载
例题：直径 d=100mm 的圆轴，一端有重量 P=0.6kN 、 直径 D=400mm 的飞轮，以均匀转速 n=1000r/min 旋 转（图 a)。现因在轴的另一端施加了掣动的外力偶矩 Me ，而在 t=0.01s 内停车。若轴的质量与飞轮相比很 小而可以略去不计，试求轴内最大动切应力d,max 。 解：飞轮的惯性力矩为
则
Δd Kd Δst
(e)
将上式两边乘以 E/l 后得
d Kd st
(1)
当 h0 时，相当于P 骤加在杆件上，这时
Kd 2
对于实际情况，以上计算是偏于安全的。
材料力学教学课件 2019年4月2日星期二
24
第11章
动荷载 · 交变荷载
D 例题：钢吊索AC的下端挂一重量为P=20kN C 的重物(图a)，并以等速度 v=1m/s 下降。 当吊索长度为 l=20m 时，滑轮D突然被卡 (a) A 住。试求吊索受到的冲击荷载 Fd 及冲击 Δd 应力 d 。已知吊索内钢丝的横截面面积 Fd A=414mm2，材料的弹性模量E=170GPa， D C 滑轮的重量可略去不计。若在上述情况下 ，在吊索与重物之间安置一个刚度系数 k=300kN/m 的弹簧，则吊索受到的冲击荷 (b) A Δst 载又是多少？ l P
解出 d 的两个根，取其中大于 st 的那个根，即得
2h Δd Δst (1 1 ) Δst 2h 引用记号 K d (1 1 ) Δst
第十一章 超静定问题
第十一章超静定问题————材料力学教案第十一章超静定问题静不定结构也称为超静定结构，和相应的静定结构相比，具有强度高、刚度大的优点，因此工程实际中的结构大多是静不定结构。
本章主要介绍静不定结构的定义、静不定次数的判断以及静不定结构的求解方法，重点介绍用力法求解静不定结构。
§11-1概述1.静不定结构的概念在各种受力情况下的支座约束力和内力，仅利用静力学平衡方程就可全部求得，这类结构称为静定结构。
例如图11-1a所示的被车削工件，图11-2a所示的桁架都是静定结构。
它们上面作用的载荷和支座约束力构成平面一般力系，有3个独立的平衡方程，正好可解出3个未知的支座约束力，其内力也可由截面法或节点法所列的平衡方程求得。
为了满足构件对强度、刚度的要求，常常会增加一些约束。
例如为了提高图11-1a所示工件的车削精度，在自由端B处增加了一个尾架，见图11-1b。
这样未知的支座约束力由原来的3个增加到4个，仅仅利用平衡方程已不能求出全部的支座约束力，这类结构称为外静不定结构。
又如图11-2a所示桁架中增加了一个杆BD，见图11-2b，虽然支座约束力仍为3个，仍能由静力学平衡方程确定，但是杆件的内力却不能全部由平衡方程求出，这类结构称为内静不定结构。
此外，还有的结构既是外静不定的，又是内静不定的，见图11-2c。
凡是用静力学平衡方程无法求出全部支座约束力和内力的结构，统称为静不定结构或静不定系统。
在图11-1a及11-2a所示结构中，原有的约束对于维持结构的平衡是必要的，充分的。
而由于其他原因在静定结构上增加的约束，如图11-1b中的尾架，图11-2b中的杆肋以及图11-2c中的杆BD和D处的水平支座链杆，对于结构的平衡来说，则是多余的。
因此称它们为“多余约束”，相应的支座约束力或内力，则称为“多余约束力”。
当然“多余约束”对工程实际来说并非多余，它们都是为了提高强度或刚度而加上去的。
图11-1图11-2图11-42.静不定次数1）外静不定结构首先由约束的性质确定支座约束力所含未知量的数目，再根据结构所受到的力系的性质确定独立平衡方程的数目，二者之差即为结构的静不定次数。