03.图像
三次函数的性质和图像

投资决策分析:在金融领域,三次函数可以用于分析投资组合的风险和回 报,以及股票价格的预测。
资源分配问题:在资源分配问题中,三次函数可以用来解决如何将有限的 资源分配到各个领域,以最大化整体效益的问题。
在其他领域的应用
物理学:三次函数在描述物理现象和解决物理问题中有着广泛的应用,例如振动、波动、 热传导等。
经济学:三次函数在经济学中用于描述经济现象和预测经济趋势,例如预测股票价格、 消费需求等。
生物学:三次函数在生物学中用于描述生长曲线、繁殖率等,例如描述细菌生长、动物 繁殖等。
计算机科学:三次函数在计算机科学中用于图像处理、信号处理等,例如图像的缩放、 旋转和平移等。
05
三次函数与其他函数的 比较
感谢您的观看
汇报人:XX
单调性
单调递增:当导数大于0时,函数在对应区间内单调递增 单调递减:当导数小于0时,函数在对应区间内单调递减 单调性的判断:通过求导数并分析导数的符号来判断单调性 单调性的应用:利用单调性研究函数的极值、最值等问题
极值点
极值点的定义:三次函数图像上函数值发生变化的点 极值点的位置:函数图像上凹凸部分的分界点 极值点的求法:通过导数求出极值点的横坐标,再代入原函数求出纵坐标 极值点的性质:极值点处的函数值大于或小于其邻近点的函数值
与指数函数的比较
定义域:三次函数 定义域为全体实数, 而指数函数定义域 为正实数
函数值:三次函数 在定义域内连续且 可导,而指数函数 在定义域内连续但 不可导
单调性:三次函数 可以具有单调递增 、递减或先增后减 等变化趋势,而指 数函数在定义域内 单调递增
奇偶性:三次函数 既可能是奇函数也 可能是偶函数,而 指数函数是偶函数
函数的图像特征

函数图像的参 数影响
参数对函数图像形状的影响
斜率:斜率越大, 函数图像越陡峭
截距:截距越大, 函数图像越远离 原点
正负号:正负号 决定函数图像的 上升或下降趋势
幂指数:幂指数 越大,函数图像
越接近原点
常数项:常数项 影响函数图像的
起始位置
导数:导数决定 函数图像的凹凸
性
参数对函数图像位置的影响
翻转变换
翻转变换的定义:将 函数图像沿x轴或y轴 进行翻转
翻转变换的类型:包 括x轴翻转、y轴翻转 和原点翻转
翻转变换的应用:在 解决实际问题中,如 物理、工程等领域, 经常需要对函数图像 进行翻转变换
翻转变换的性质:翻 转变换不改变函数的 单调性、奇偶性、周 期性等性质
函数图像的对称性
轴对称:函数图像关于x轴、y轴或原点对称 旋转对称:函数图像关于某一点旋转一定角度后与原图像重合 反射对称:函数图像关于某一点或直线反射后与原图像重合 平移对称:函数图像关于某一点或直线平移一定距离后与原图像重合
圆函数:y=f(x)=x^2
开口方向:向上
形状:对称的抛物线
渐近线:y=x和y=-x
顶点:(0,0)
极值:(0,0)是最大值和最小值
函数图像的坐 标轴关系
截距
截距的定义:函数图像与x轴或y轴的交点 截距的作用:确定函数图像的位置和形状 截距的计算:通过函数解析式求解 截距的应用:解决实际问题,如物理、工程等领域
双曲线函数:y=a/x^2,其中a>0
形状:开口向上或向下,取决于a的 正负
顶点:(0,a)或(0,-a),取决于a的正 负
渐近线:y=x和y=-x,与x轴相交于 (0,a)和(0,-a)
焦点:(0,±a/2),取决于a的正负
专题03 速度图像和计算-备战八年级物理上学期期中真题分类汇编(原卷版)

专题03 速度计算和图像一、单选题1.(2022秋·山东临沂·八年级统考期中)某物体从地面上某一点出发沿直线运动,其s-t 图象如图所示。
对物体的运动情况进行分析,得出结论不正确的是()A.物体在6s内运动的路程为15mB.以地球为参照物,物体在中间2s内静止C.物体在前2s内和后2s内的速度相等D.物体在6s内的平均速度为2.5m/s2.(2022秋·河南周口·八年级校考期中)在某校举办的机器人模拟救援比赛中,甲、乙两机器人同时从同一地点出发,沿直线匀速运动到10m远的目的地,它们运动的路程随时间变化的图像如图所示。
下列说法正确的是()A.甲的速度大小为4m/s B.乙的速度大小为2m/sC.甲的运动时间比乙多1s D.甲的运动时间比乙少2s3.(2022秋·广东深圳·八年级深圳市海湾中学校考期中)如图所示,表示物体做匀速直线运动的是()A.B.C.D.4.(2022秋·湖南娄底·八年级校联考期中)关于速度,以下说法正确的是()A.运动路程越长,速度越大B.运动时间越短,速度越大C.相同时间内,通过的路程越长,速度越大D.通过相同的路程,所用时间越长,速度越大5.(2022秋·湖北宜昌·八年级校考期中)如图为“测量物体运动的平均速度”的实验,小车从A点运动到C点的过程中,下列说法正确的是()A.小车在这个过程中做匀速直线运动B.为了测量小车在BC段的平均速度,可以将小车从B点由静止释放C.斜面应保持较大的坡度,以便于测量时间D.在测量小车到达B点的时间时,过了B点才停止计时,则AB段的平均速度会偏小6.(2022秋·湖南常德·八年级统考期中)一辆汽车在从甲地到乙地的过程中,若前半程的平均速度为15m/s,后半程的速度为30m/s,则物体在整个运动过程中的平均速度为()A.20m/s B.24m/s C.22.5m/s D.25m/s二、填空题7.(2022春·山东泰安·九年级统考期中)如图所示是甲、乙两车运动的s—t图象,当两车从同一地点,同时、同向做匀速直线运动时,以甲车为参照物,乙车是(填“静止”或“运动”)的;当时间t= s时,两车相距8m。
专题03 函数图像的压轴真题训练(解析版)-2023年中考数学解答题压轴真题汇编
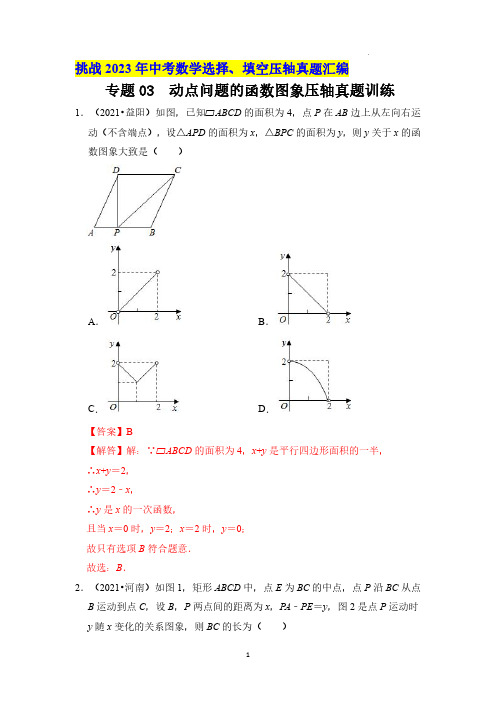
挑战2023年中考数学选择、填空压轴真题汇编专题03动点问题的函数图象压轴真题训练1.(2021•益阳)如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是()A.B.C.D.【答案】B【解答】解:∵▱ABCD的面积为4,x+y是平行四边形面积的一半,∴x+y=2,∴y=2﹣x,∴y是x的一次函数,且当x=0时,y=2;x=2时,y=0;故只有选项B符合题意.故选:B.2.(2021•河南)如图1,矩形ABCD中,点E为BC的中点,点P沿BC从点B运动到点C,设B,P两点间的距离为x,PA﹣PE=y,图2是点P运动时y随x变化的关系图象,则BC的长为()A.4B.5C.6D.7【答案】C【解答】解:由函数图象知:当x=0,即P在B点时,BA﹣BE=1.利用三角形两边之差小于第三边,得到P A﹣PE≤AE.∴y的最大值为AE,∴AE=5.在Rt△ABE中,由勾股定理得:BA2+BE2=AE2=25,设BE的长度为t,则BA=t+1,∴(t+1)2+t2=25,即:t2+t﹣12=0,∴(t+4)(t﹣3)=0,由于t>0,∴t+4>0,∴t﹣3=0,∴t=3.∴BC=2BE=2t=2×3=6.故选:C.3.(2022•鞍山)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4cm,CD⊥AB,垂足为点D,动点M从点A出发沿AB方向以cm/s的速度匀速运动到点B,同时动点N从点C出发沿射线DC方向以1cm/s的速度匀速运动.当点M停止运动时,点N也随之停止,连接MN.设运动时间为ts,△MND的面积为Scm2,则下列图象能大致反映S与t之间函数关系的是()A.B.C.D.【答案】B【解答】解:∵∠ACB=90°,∠A=30°,AB=4,∴∠B=60°,BC=AB=2,AC=BC=6,∵CD⊥AB,∴CD=AC=3,AD=CD=3,BD=BC=,∴当M在AD上时,0≤t≤3,MD=AD﹣AM=3﹣t,DN=DC+CN=3+t,∴S=MD•DN=(3﹣t)(3+t)=﹣t2+,当M在BD上时,3<t≤4,MD=AM﹣AD=t﹣3,∴S=MD•DN=(t﹣3)(3+t)=t2﹣,故选:B.4.(2022•菏泽)如图,等腰Rt△ABC与矩形DEFG在同一水平线上,AB=DE =2,DG=3,现将等腰Rt△ABC沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰Rt△ABC与矩形DEFG 的重合部分面积记为y,则能大致反映y与x的函数关系的图象为()A.B.C.D.【答案】B【解答】解:如图,作CH⊥AB于点H,∵AB=2,△ABC是等腰直角三角形,∴CH=1,当0≤x≤1时,y=×2x•x=x2,当1<x≤3时,y==1,当3<x≤4时,y=1﹣=﹣(x﹣3)2+1,故选:B.5.(2022•鄂尔多斯)如图①,在正方形ABCD中,点M是AB的中点,点N 是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为()A.B.2C.D.【答案】A【解答】解:如图,连接AC交BD于点O,连接NC,连接MC交BD于点N′.∵四边形ABCD是正方形,∴O是BD的中点,∵点M是AB的中点,∴N′是△ABC的重心,∴N′O=BO,∴N′D=BD,∵A、C关于BD对称,∴NA=NC,∴AN+MN=NC+MN,∵当M、N、C共线时,y的值最小,∴y的值最小就是MC的长,∴MC=2,设正方形的边长为m,则BM=m,在Rt△BCM中,由勾股定理得:MC2=BC2+MB2,∴20=m2+(m)2,∴m=4,∴BD=4,∴a=N′D=BD=×4=,故选:A.6.(2021•鞍山)如图,△ABC是等边三角形,AB=6cm,点M从点C出发沿CB方向以1cm/s的速度匀速运动到点B,同时点N从点C出发沿射线CA方向以2cm/s的速度匀速运动,当点M停止运动时,点N也随之停止.过点M 作MP∥CA交AB于点P,连接MN,NP,作△MNP关于直线MP对称的△MN′P,设运动时间为ts,△MN′P与△BMP重叠部分的面积为Scm2,则能表示S与t之间函数关系的大致图象为()A.B.C.D.【答案】A【解答】解:如图1中,当点N′落在AB上时,取CN的中点T,连接MT.∵CM=t(cm),CN=2t(cm),CT=TN,∴CT=TN=t(cm),∵△ABC是等边三角形,∴∠C=∠A=60°,∴△MCT是等边三角形,∴TM=TC=TN,∴∠CMN=90°,∵MP∥AC,∴∠BPM=∠A=∠MPN=60°,∠BMP=∠C=60°,∠C+∠CMP=180°,∴∠CMP=120°,△BMP是等边三角形,∴BM=MP,∵∠CMP+∠MPN=180°,∴CM∥PN,∵MP∥CN,∴四边形CMPN是平行四边形,∴PM=CN=BM=2t,∴3t=6,∴t=2,如图2中,当0<t≤2时,过点M作MK⊥AC于K,则MK=CM•sin60°=t,∴S=•(6﹣t)•t=﹣t2+t.如图3中,当2<t≤6时,S=•MQ•PQ=×(6﹣t)×(6﹣t)=×(6﹣t)2,观察图象可知,选项A符合题意,故选:A.7.(2021•威海)如图,在菱形ABCD中,AB=2cm,∠D=60°,点P,Q同时从点A出发,点P以1cm/s的速度沿A﹣C﹣D的方向运动,点Q以2cm/s 的速度沿A﹣B﹣C﹣D的方向运动,当其中一点到达D点时,两点停止运动.设运动时间为x(s),△APQ的面积为y(cm2),则下列图象中能大致反映y与x之间函数关系的是()A.B.C.D.【答案】A【解答】解:∵四边形ABCD为菱形,∴AB=BC=CD=DA=2cm,∠B=∠D=60°.∴△ABC、△ACD都是等边三角形,∴∠CAB=∠ACB=∠ACD=60°.如图1所示,当0≤x≤1时,AQ=2xcm,AP=xcm,作PE⊥AB于E,∴PE=sin∠PAE×AP=(cm),∴y=AQ•PE=×2x×=,故D选项不正确;如图2,当1<x≤2时,AP=xcm,CQ=(4﹣2x)cm,作QF⊥AC于点F,∴QF=sin∠ACB•CQ=(cm),∴y===,故B选项不正确;如图3,当2<x≤3时,CQ=(2x﹣4)cm,CP=(x﹣2)cm,∴PQ=CQ﹣CP=2x﹣4﹣x+2=(x﹣2)cm,作AG⊥DC于点G,∴AG=sin∠ACD•AC=×2=(cm),∴y===.故C选项不正确,故选:A.8.(2021•日照)如图,平面图形ABD由直角边长为1的等腰直角△AOD和扇形BOD组成,点P在线段AB上,PQ⊥AB,且PQ交AD或交于点Q.设AP=x(0<x<2),图中阴影部分表示的平面图形APQ(或APQD)的面积为y,则函数y关于x的大致图象是()A.B.C.D.【答案】D【解答】解:当Q在AD上时,即点P在AO上时,有0<x≤1,此时阴影部分为等腰直角三角形,∴y=,该函数是二次函数,且开口向上,排除B,C选项;当点Q在弧BD上时,补全图形如图所示,阴影部分的面积等于等腰直角△AOD的面积加上扇形BOD的面积,再减去平面图形PBQ的面积即减去弓形QBF的面积,设∠QOB=θ,则∠QOF=2θ,=﹣S△QOF,∴,S弓形QBF=﹣=﹣,当θ=45°时,AP=x=1+≈1.7,S弓形QBFy=+﹣(﹣)=≈1.14,=﹣=﹣,当θ=30°时,AP=x≈1.87,S弓形QBFy=+﹣(﹣)=≈1.24,当θ=60°时,AP=x≈1.5,y≈0.98,在A,D选项中分别找到这两个特殊值,对比发现,选项D符合题意.故选:D.法二、当1<x<2时,即P在OB之间时,设∠QOD=θ,则θ∈(0,),则PQ=cosθ,OP=sinθ,则弧QD的长为θπ,此时S阴影=+θπ+sinθcosθ=+θ+sin2θ,∴y随x的增大而增大,而且增加的速度越来越慢,分析四个选项中的图象,只有选项D符合.故选:D.9.(2021•辽宁)如图,在矩形ABCD中,AB=6,AD=4,E是CD的中点,射线AE与BC的延长线相交于点F,点M从A出发,沿A→B→F的路线匀速运动到点F停止.过点M作MN⊥AF于点N.设AN的长为x,△AMN的面积为S,则能大致反映S与x之间函数关系的图象是()A.B.C.D.【答案】B【解答】解:如图,∵E是CD的中点,∴CE=DE,∵四边形ABCD是矩形,∴∠D=∠DCF=90°,AD=BC=4,在△ADE与△FCE中,,∴△ADE≌△FCE(SAS),∴CF=AD=4,∴BF=CF+BC=8,∴AF=,当点M在AB上时,在Rt△AMN和Rt△AFB中,tan∠NAM=,∴NM=x=x,∴△AMN的面积S=×x×x=x2,∴当点M在AB上时,函数图象是开口向上、经过原点的抛物线的一部分;当点M在BF上时,如图,AN=x,NF=10﹣x,在Rt△FMN和Rt△FBA中,tan∠F=,∴=﹣,∴△AMN的面积S==﹣,∴当点M在BF上时,函数图象是开口向下的抛物线的一部分;故选:B.10.(2021•苏州)如图,线段AB=10,点C、D在AB上,AC=BD=1.已知点P从点C出发,以每秒1个单位长度的速度沿着AB向点D移动,到达点D后停止移动.在点P移动过程中作如下操作:先以点P为圆心,PA、PB 的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面,设点P的移动时间为t(秒),两个圆锥的底面面积之和为S,则S关于t的函数图象大致是()A.B.C.D.【答案】D【解答】解:∵AB=10,AC=BD=1,∴CD=10﹣1﹣1=8,∵PC=t,∴AP=t+1,PB=8﹣t+1=9﹣t,设围成的两个圆锥底面圆半径分别为r和R则:2πr=;.解得:r=,R=,∴两个圆锥的底面面积之和为S===,根据函数关系式可以发现该函数图象是一个开口向上的二次函数.故选:D.11.(2021•甘肃)如图1,在△ABC中,AB=BC,BD⊥AC于点D(AD>BD).动点M从A点出发,沿折线AB→BC方向运动,运动到点C停止.设点M的运动路程为x,△AMD的面积为y,y与x的函数图象如图2,则AC的长为()A.3B.6C.8D.9【答案】B【解答】解:由图2知,AB+BC=2,∵AB=BC,∴AB=,∵AB=BC,BD⊥AC,∴AC=2AD,∠ADB=90°,在Rt△ABD中,AD²+BD²=AB²=13①,设点M到AC的距离为h,=AD•h,∴S△ADM∵动点M从A点出发,沿折线AB→BC方向运动,∴当点M运动到点B时,△ADM的面积最大,即h=BD,由图2知,△ADM的面积最大为3,∴AD•BD=3,∴AD•BD=6②,①+2×②得,AD²+BD²+2AD•BD=13+2×6=25,∴(AD+BD)²=25,∴AD+BD=5(负值舍去),∴BD=5﹣AD③,将③代入②得,AD(5﹣AD)=6,∴AD=3或AD=2,∵AD>BD,∴AD=3,∴AC=2AD=6,故选:B.12.(2021•百色)如图,矩形ABCD各边中点分别是E、F、G、H,AB=2,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是()A.B.C.D.【答案】D【解答】解:①当M点运动在AE段,+S△GHD﹣S△EOM﹣S△GPS,此时S=S△HAE∵四边形ABCD是矩形,直线l⊥AB,H、E、F、G为AD、AB、BC、CD的中点,=S△GHD,S△EOM=S△GPS,∴AH=AD==1,AE=AB=,S△HAE﹣2S△EOM,∴S=2S△HAE=AE•AH=;∴S△HAE∵直线l⊥AB,∴∠OME=∠A=90°,∠HEA=∠OEM,∴△HAE∽△OME,∴,∴OM=,又∵ME=AE﹣AM=﹣x,∴OM=ME=,=,∴S△EOM﹣2S△EOM=,∴S=2S△HAE此时,对应抛物线开口向下;②当M点运动到在BE段,+S△GHD+S△EO1M1+S△GP1S1,此时,S=S△HAE+2S△EO1M1,即S=2S△HAE与①同理,O1M1=,又∵M1E=AM1﹣AE=x﹣,∴O1M1=M1E=,=,∴S△EO1M1+2S△EO1M1=,∴S=2S△HAE此时,对应抛物线开口向上,故选:D.13.(2021•鄂尔多斯)如图①,在矩形ABCD中,H为CD边上的一点,点M 从点A出发沿折线AH﹣HC﹣CB运动到点B停止,点N从点A出发沿AB运动到点B停止,它们的运动速度都是1cm/s,若点M、N同时开始运动,设运动时间为t(s),△AMN的面积为S(cm2),已知S与t之间函数图象如图②所示,则下列结论正确的是()①当0<t≤6时,△AMN是等边三角形.②在运动过程中,使得△ADM为等腰三角形的点M一共有3个.③当0<t≤6时,S=.④当t=9+时,△ADH∽△ABM.⑤当9<t<9+3时,S=﹣3t+9+3.A.①③④B.①③⑤C.①②④D.③④⑤【答案】A【解答】解:由图②可知:点M、N两点经过6秒时,S最大,此时点M在点H处,点N在点B处并停止不动,如图,①∵点M、N两点的运动速度为1cm/s,∴AH=AB=6cm,∵四边形ABCD是矩形,∴CD=AB=6cm.∵当t=6s时,S=9cm2,∴×AB×BC=9.∴BC=3cm.∵当6≤t≤9时,S=且保持不变,∴点N在B处不动,点M在线段HC上运动,运动时间为(9﹣6)秒,∴HC=3cm,即点H为CD的中点.∴BH=cm.∴AB=AH=BH=6cm,∴△ABM为等边三角形.∴∠HAB=60°.∵点M、N同时开始运动,速度均为1cm/s,∴AM=AN,∴当0<t≤6时,△AMN为等边三角形.故①正确;②如图,当点M在AD的垂直平分线上时,△ADM为等腰三角形:此时有两个符合条件的点;当AD=AM时,△ADM为等腰三角形,如图:当DA=DM时,△ADM为等腰三角形,如图:综上所述,在运动过程中,使得△ADM为等腰三角形的点M一共有4个.∴②不正确;③过点M作ME⊥AB于点E,如图,由题意:AM=AN=t,由①知:∠HAB=60°.在Rt△AME中,∵sin∠MAE=,∴ME=AM•sin60°=tcm,∴S=AN×ME=cm2.∴③正确;④当t=9+时,CM=cm,如图,由①知:BC=3cm,∴MB=BC﹣CM=2cm.∵AB=6cm,∴tan∠MAB=,∴∠MAB=30°.∵∠HAB=60°,∴∠DAH=90°﹣60°=30°.∴∠DAH=∠BAM.∵∠D=∠B=90°,∴△ADH∽△ABM.∴④正确;⑤当9<t<9+3时,此时点M在边BC上,如图,此时MB=9+3﹣t,∴S=×AB×MB=×6×(9+3﹣t)=27+9﹣3t.∴⑤不正确;综上,结论正确的有:①③④.故选:A.14.(2021•通辽)如图,在矩形ABCD中,AB=4,BC=3,动点P,Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P,Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接PQ.设点P的运动路程为x,PQ2为y,则y关于x的函数图象大致是()A.B.C.D.【答案】C【解答】解:当0≤x≤3时,在Rt△APQ中,∠QAP=90°,AP=AQ=x,∴PQ2=2x2.∴y=PQ2=2x2;当3≤x≤4时,DQ=x﹣3,AP=x,∴y=PQ2=32+32=18;当4≤x≤7时,CP=7﹣x,CQ=7﹣x,∴y=PQ2=CP2+CQ2=2x2﹣28x+98.故选:C.15.(2021•湖北)如图,AC为矩形ABCD的对角线,已知AD=3,CD=4,点P沿折线C﹣A﹣D以每秒1个单位长度的速度运动(运动到D点停止),过点P作PE⊥BC于点E,则△CPE的面积y与点P运动的路程x间的函数图象大致是()A.B.C.D.【答案】D【解答】解:∵BC∥AD,∴∠ACB=∠DAC,∵∠PEC=∠D=90°,∴△PCE∽△CAD,∴==,∵AD=3,CD=4,∴AC==5,∴当P在CA上时,即当0<x≤5时,PE==x,CE==x,∴y=PE•CE==x2,当P在AD上运动时,即当5<x≤8时,PE=CD=4,CE=8﹣x,∴y=PE•CE=×4×(8﹣x)=16﹣2x,综上,当0<x≤5时,函数图象为二次函数图象,且y随x增大而增大,当5<x≤8时,函数图象为一次函数图象,且y随x增大而减小,故选:D.16.(2021•衡阳)如图1,菱形ABCD的对角线AC与BD相交于点O,P、Q 两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P的运动路线为O﹣A﹣D﹣O,点Q的运动路线为O﹣C﹣B﹣O.设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,当点P在A﹣D段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为厘米.【答案】(2+3)【解答】解:由图分析易知:当点P从O→A运动时,点Q从O→C运动时,y不断增大,当点P运动到A点,点Q运动到C点时,由图象知此时y=PQ=2cm,∴AC=2cm,∵四边形ABCD为菱形,∴AC⊥BD,OA=OC==cm,当点P运动到D点,Q运动到B点,结合图象,易知此时,y=BD=2cm,∴OD=OB=BD=1cm,在Rt△ADO中,AD===2(cm),∴AD=AB=BC=DC=2cm,如图,当点P在A﹣D段上运动,点P运动到点E处,点Q在C﹣B段上运动,点Q运动到点F处时,P、Q两点的距离最短,此时,OE=OF==,AE=CF===,∴当点P在A﹣D段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为:(cm),故答案为:(2+3).17.(2021•武汉)如图(1),在△ABC中,AB=AC,∠BAC=90°,边AB 上的点D从顶点A出发,向顶点B运动,同时,边BC上的点E从顶点B出发,向顶点C运动,D,E两点运动速度的大小相等,设x=AD,y=AE+CD,y关于x的函数图象如图(2),图象过点(0,2),则图象最低点的横坐标是.【答案】﹣1【解答】解:∵图象过点(0,2),即当x=AD=BE=0时,点D与A重合,点E与B重合,此时y=AE+CD=AB+AC=2,∵△ABC为等腰直角三角形,∴AB=AC=1,过点A作AF⊥BC于点F,过点B作NB⊥BC,并使得BN=AC,如图所示:∵AD=BE,∠NBE=∠CAD,∴△NBE≌△CAD(SAS),∴NE=CD,又∵y=AE+CD,∴y=AE+CD=AE+NE,当A、E、N三点共线时,y取得最小值,如图所示,此时:AD=BE=x,AC=BN=1,∴AF=AC•sin45°=,\又∵∠BEN=∠FEA,∠NBE=∠AFE∴△NBE∽△AFE∴,即,解得:x=,∴图象最低点的横坐标为:﹣1.故答案为:.18.(2022•营口)如图1,在四边形ABCD中,BC∥AD,∠D=90°,∠A=45°,动点P,Q同时从点A出发,点P以cm/s的速度沿AB向点B运动(运动到B点即停止),点Q以2cm/s的速度沿折线AD→DC向终点C运动,设点Q的运动时间为x(s),△APQ的面积为y(cm2),若y与x之间的函数关系的图象如图2所示,当x=(s)时,则y=cm2.【答案】【解答】解:过点D作DE⊥AB,垂足为E,在Rt△ADE中,∵∠AED=90°,∠EAD=45°,∴,∵点P的速度为cm/s,点Q的速度为2cm/s,∴AP=x,AQ=2x,∴,在△APQ和△AED中,=,∠A=45°,∴△AED∽△APQ,∴点Q在AD上运动时,△APQ为等腰直角三角形,∴AP=PQ=x,∴当点Q在AD上运动时,y=AP•AQ=×x×x=x2,由图像可知,当y=9此时面积最大,x=3或﹣3(负值舍去),∴AD=2x=6cm,当3<x≤4时,过点P作PF⊥AD于点F,如图:=S△APF+S四边形PQDF﹣S△ADQ,此时S△APQ在Rt△APF中,AP=x,∠PAF=45°,∴AF=PF=x,FD=6﹣x,QD=2x﹣6,=x2+(x+2x﹣6)•(6﹣x)﹣×6×(2x﹣6),∴S△APQ即y=﹣x2+6x,当x=时,y=﹣()2+6×=,故答案为:.。
三角函数的图像及性质-人教版高中数学

知识图谱-正弦函数的图像及性质-余弦函数的图像及性质-正切函数的图像及性质-正弦型函数的图像变换正弦函数有关的值域问题正弦函数有关的单调性问题正弦函数有关的对称问题正弦型函数的图像变换利用图像求解析式余弦函数的性质余弦函数有关的值域问题余弦函数有关的单调性问题余弦函数有关的对称问题正切函数有关的值域问题正切函数有关的单调性问题正切函数有关的对称问题第03讲_三角函数的图像及性质错题回顾正弦函数的图像及性质知识精讲一. 三角函数线设角的顶点在坐标原点,始边与轴非负半轴重合,终边与单位圆相交于点,过作垂直于轴于则点是点在轴上的正射影.由三角函数的定义知,点的坐标为即其中单位圆与轴的正半轴交于点,单位圆在点的切线与的终边或其反向延长线相交于点,则我们把有向线段叫做的余弦线、正弦线、正切线.有向线段为正弦线有向线段为余弦线有向线段为正切线二. 在直角坐标系中作点由单位圆中的正弦线知识,我们只要已知一个角的大小,就能用几何方法作出对应的正弦值的大小来,思考一下,如何用几何方法在直角坐标系中作出点.我们能否借助上面作点的方法在直角坐标系中作出正弦函数,的图像呢?1. 用几何方法作的图像我们知道,作函数的图像的步骤是:列表、描点、连结;如果我们用列表法得出各点的坐标,就会因各点的纵坐标都是查三角函数表得到的数值不够精确,使得描点后画出的图像误差也大,为克服这一不足,我们用前面作点的几何方法来描点,从而使图像的精确度有了提高.我们先作在上的图像,具体分为如下五个步骤:(1)作直角坐标系,并在直角坐标系中轴左侧画单位圆.(2)把单位圆分成12等份(等份越多,画出的图像越精确).过单位圆上的各分点作轴的垂线,可以得到对应于0,,,…角的正弦线.(3)找横坐标:把轴上从到()这一段分成12等分.(4)找纵坐标:将正弦线对应平移,即可指出相应12个点.(5)连线:用平滑的曲线将12个点依次从左到右连接起来,即得的图像.2. 五点法作的简图在作正弦函数的图像时,我们描述了12个点,但其中起关键作用的是函数与轴的交点及最高点和最低点这五个点,它们的坐标依次是,,,,,只要指出这五个点,的图像的形状就基本确定了;找出这五个关键点,然后用光滑的曲线将它们连结起来,就得到函数的简图,这种作图的方法称为“五点法”作图.3. 作正弦曲线的图像.因为终边相同的角的三角函数值相等,所以函数的图像与函数的图像的形状完全一样,只是位置不同,于是我们只要将函数的图像向左、右平移(每次个单位长度),就可以得到正弦函数数的图像,如图.正弦函数的图像叫做正弦曲线.三. 正弦三角函数的性质增;减;三点剖析一. 方法点拨1. 用五点法做出图像的方法:设,分别令为这五个点,相应的值分别为,根据的值求出相应的值,然后在坐标系中画出相应的点坐标,最后用圆滑的曲线画出图像.题模精讲题模一正弦函数有关的值域问题例1.1、如图,某港口一天6时到18时的水渠变化曲线近似满足函数y=3sin(x+φ)+k.据此函数可知,这段时间水深(单位:m)的最大值为______.例1.2、函数f(x)=sin(2x-)在区间[0,]上的最小值是()A、-1B、-C、D、0例1.3、已知函数f(x)=sin(ωx+),(ω>0)的最小正周期为π.(1)求ω和f()的值;(2)求函数f(x)的最大值及相应x的集合.题模二正弦函数有关的单调性问题例2.1、已知ω∈N+,函数f(x)=sin(ωx+)在(,)上单调递减,则ω= .题模三正弦函数有关的对称问题例3.1、若函数是偶函数,则实数a的值为__________.例3.2、设点P是函数f(x)=sinωx的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值,则f(x)的最小正周期是()A、2πB、πC、D、随堂练习随练1.1、函数f(x)=-sin2x+的值域为____.随练1.2、函数f(x)=sinx-cos2x的最大值是____.随练1.3、函数f(x)=3sin(2x+)的部分图象如图所示.(Ⅰ)写出f(x)的最小正周期及图中x0,y0的值;(Ⅱ)求f(x)在区间[-,-]上的最大值和最小值.随练1.4、若函数f(x)=sin(ωx+φ),其中,两相邻对称轴的距离为,为最大值,则函数f(x)在区间[0,π]上的单调增区间为()A、B、C、和D、和随练1.5、已知函数y=2sin(-4x).(Ⅰ)求函数的周期及单调区间;(Ⅱ)求函数的最大值及最小值并写出取最值时自变量x的集合.随练1.6、已知f(x)=sin(x-φ)+cos(x-φ)为奇函数,则φ的一个取值()A、0B、πC、D、随练1.7、若,是偶函数,则的值为________.随练1.8、将函数的图像向左平移个单位,若所得图像与原图像重合,则的值不可能等于().A、4B、6C、8D、12随练1.9、若将函数的图象向右平移个单位,所得图象关于轴对称,则的最小正值是_________.余弦函数的图像及性质知识精讲一. 函数称之为余弦函数正弦函数变换为余弦函数的方法:正弦函数图像整体向左平移个单位,既可得到余弦函数图像.二. 余弦函数的图像三.余弦函数的性质1. 定义域:2. 值域:3. 奇偶性:偶函数4. 最小正周期:5. 单调区间:单调递增区间单调递减区间6. 对称轴:7. 对称中心:三点剖析一. 方法点拨1. 用正弦图像转换成余弦图像的方法:图像整体向左平移个单位即可得到,正弦函数图像经过原点,而当余弦函数图像经过最高点,故正弦函数是奇函数,而余弦函数是偶函数.2. 余弦函数图像的平移和转换可参考正弦函数图像的方法.题模精讲题模一余弦函数的性质例1.1、求函数的定义域例1.2、的定义域是_________.例1.3、已知函数,求的定义域.题模二余弦函数有关的值域问题例2.1、定义域为R的函数f(x)=a-2bcosx(b>0)的最大值为,最小值为-,求a,b的值.例2.2、在同一平面直角坐标系中,函数y=cos(+)(x∈[0,2π])的图象和直线y=的交点个数是()A、0B、1C、2D、4例2.3、阅读下面材料:根据两角和与差的正弦公式,有sin(α+β)=sinαcosβ+cosαsinβ…①sin(α-β)=sinαcosβ-cosαsinβ…②由①+②得sin(α+β)+sin(α-β)=2sinαcosβ…③令α+β=A,α-β=B 有α=,β=代入③得sinA+sinB=2sin cos.(1)利用上述结论,试求sin15°+sin75°的值.(2)类比上述推证方法,根据两角和与差的余弦公式,证明:cosA+cosB=2 cos•cos.(3)求函数y=cos2x•cos(2x+)x∈[0,]的最大值.题模三余弦函数有关的单调性问题函数y=cos(2x+)+2的单调递减区间是()A、[2kπ-,2kπ+](k∈Z)B、[2kπ+,2kπ+](k∈Z)C、[kπ-,kπ+](k∈Z)D、[kπ+,kπ+](k∈Z)例3.2、函数,其单调性是()A、在上是增函数,在上是减函数B、在上是增函数,在上是减函数C、在上是增函数,在上是减函数D、在上是增函数,在上是减函数例3.3、已知x∈[0,π],f(x)=sin(cosx)的最大值为a,最小值为b;g(x)=cos (sosx)的最大值为c,最小值为d,则a,b,c,d的大小关系是()A、b<d<c<a B、d<b<c<aC、b<d<a<cD、d<b<a<c题模四余弦函数有关的对称问题已知函数f(x)=cos(ωx+φ)+1(ω>0)的图象的一条对称轴为直线x=,且f()=1,则ω的最小值为()A、2B、4C、6D、8例4.2、同时具有性质“①最小正周期是π,②图象关于直线x=对称;③在[-,]上是增函数”的一个函数是()A、y=sin(+)B、y=cos(2x+)C、y=sin(2x-)D、y=cos(2x-)例4.3、已知函数f(x)=3sin(ωx-)(ω>0)和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若x∈[0,],则f(x)的取值范围是____.随堂练习随练2.1、函数的定义域是()A、()B、()C、()D、()随练2.2、函数的定义域为,则的定义域为__________随练2.3、已知函数的定义域为,则函数的定义域是_________.随练2.4、函数的最大值是______,最小值是______.随练2.5、函数的最小正周期和最大值分别为()A、B、C、D、随练2.6、已知函数f(x)=sin2x,g(x)=cos(2x+),直线x=t(t∈R).与函数f (x),g(x)的图象分别交于M、N两点.(1)当t=时,求|MN|的值;(2)求|MN|在t∈[0,]时的最大值.随练2.7、函数y=cos2x在下列哪个区间上是减函数()A、[-,]B、[,]C、[0,]D、[,π]随练2.8、求函数的单调递减区间随练2.9、求y=2cos的单调区间.随练2.10、将函数y=cos(x-)的图象上的各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移个单位,所得函数的图象的一条对称轴为()A、x=B、x=C、x=D、x=π随练2.11、若f(x)=Asin(ωx+φ)+1(ω>0,|φ|<π)对任意实数t,都有f(t+)=f(-t+).记g(x)=Acos(ωx+φ)-1,则g()=()A.-B.C.-1D.1正切函数的图像及性质知识精讲一.形如的函数称之为正切函数二.正切函数的图像类似正弦曲线的作法,我们先作正切函数在一个周期上的图象,下面我们利用正切线画出函数,的图象,作法如下:1.作直角坐标系,并在直角坐标系轴左侧作单位圆.2.把单位圆右半圆分成8等份,分别在单位圆中作出正切线.3.描点. (横坐标是一个周期的8等分点,纵坐标是相应的正切线).4. 连线.根据正切函数的周期性,我们可以把上述图象向左、右扩展,得到正切函数,的图象,并把它叫做正切曲线.三. 正切函数的性质1. 定义域:2. 值域:3. 周期性:正切函数是周期函数,周期是.4. 奇偶性:,正切函数是奇函数,正切曲线关于原点对称.5. 单调性:由正切曲线图象可知:正切函数在开区间内都是增函数.6. 中心对称点:四.正弦余弦正切函数的性质综合增减增减增三点剖析一.注意事项1. 正切函数图像的定义域为,值域为全体实数,不同于正弦函数和余弦函数定义域是全体实数,值域是.2. 关于的最小正周期,最小正周期为,而正弦和余弦函数的最小正周期为3. 切记正切函数必须说是在定义域内单调递增,而不能说是在全体实数内单调递增.4. 正切函数图像的中心对称点是,不同于正弦函数图像和余弦函数图像,对称轴只是与轴的交点.5.正切函数图像没有对称轴.题模精讲题模一正切函数有关的值域问题例1.1、求函数的定义域、值域例1.2、求函数的值域例1.3、求函数在区间上的值域题模二正切函数有关的单调性问题例2.1、函数f(x)=tan(x+)的单调增区间为()A、(kπ-,kπ+),k∈ZB、(kπ,(k+1)π),k∈ZC、(kπ-,kπ+),k∈Z D、(kπ-,kπ+),k∈Z例2.2、已知函数y=tanωx在(-,)上是减函数,则()A、0<ω≤1B、-1≤ω<0C、ω≥1D、ω≤-1例2.3、求函数的周期和单调区间题模三正切函数有关的对称问题例3.1、函数y=2tan(3x-)的一个对称中心是()A、(,0)B、(,0)C、(-,0)D、(-,0)例3.2、下列函数既是偶函数,又在(0,π)上单调递增的是()A、y=|sinx|B、y=tan|x|C、y=cosxD、y=-cosx例3.3、在下列函数中,同时满足:①在上递增;②以为周期;③是奇函数的是()A、B、C、D、随堂练习随练3.1、若<θ<,则下列不等式中成立的是()A、sinθ>cosθ>tanθB、cosθ>tanθ>sinθC、tanθ>sinθ>cosθD、tanθ>cosθ>sinθ随练3.2、若直线x=(-1≤k≤1)与函数y=tan(2x+)的图象不相交,则k=()A、B、-C、或-D、-或随练3.3、求函数的定义域随练3.4、求函数的定义域随练3.5、,,的大小关系是()A、B、C、D、随练3.6、下列函数在区间上是减函数的是()B、A、D、随练3.7、求函数单调区间随练3.8、下列函数中,在区间(0,)上为增函数且以π为周期的函数是()B、y=sinxA、y=sinC、y=-tanxD、y=-cos2x随练3.9、下列函数中,周期为1且为奇函数的是()A、y=1-sin2πxB、y=tanπxD、y=cos2πx-sin2πxC、y=cos(πx+)正弦型函数的图像变换知识精讲一. 的图象函数的图象可以用下面的方法得到:先把的图象上所有点向左或向右平行移动个单位;再把所得各点的横坐标缩短或伸长到原来的倍(纵坐标不变);再把所得的各点的纵坐标伸长或缩到原来的倍(横坐标不变),从而得到的图象.当函数表示一个振动量时:叫做振幅;叫做周期;叫做频率;叫做相位,叫做初相.上面是一种函数的平移缩放的过程,可以用这种方法来把一种三角函数转换成另外一种三角函数.下面把这个过程分解一下:1. 相位变换要得到函数的图象,可以令,也就是原来的变成了现在的,相当于减小了,即可以看做是把的图象上的各点向左或向右平行移动个单位而得到的.这种由的图象变换为的图象的变换,使相位由变为,我们称它为相位变换.它实质上是一种左右平移变换.2. 周期变换要得到函数的图象,令,即现在的缩小到了原来的倍,就可以看做是把的图象上的各点的横坐标缩短或伸长到原来的倍(纵坐标不变)得到,由的图象变换为的图象,其周期由变为,这种变换叫周期变换.周期变换是一种横向的伸缩.3. 振幅变换要得到的图象,令,即相当于变为原来的倍,也就是把的图象上的各点的纵坐标伸长或缩短到原来的倍(横坐标不变)而得到的.这种变换叫做振幅变换.振幅变换是一种纵向的伸缩.二. 三角函数图象变换函数图象平移基本结论小结如下:;;;;这些新的解析式可以由图象上任意一点变换后的对应关系得出,以左移个单位的解析式变化为例:设为左移个单位后所得图象上的任意一点,则将P右移个单位得到的必在的图象上,故,又点任意,故的图象左移个单位得到的新的函数的解析式为:.三. 由图像确定函数的解析式1. 求:由图像确定函数的最大值和最小值,则.2. 求:确定函数的周期(相邻对称轴或相邻零点间的距离是,相邻最值与平衡位置间距离是,),则.3. 求的常用方法:(1)代入法:把图像上的一个已知点代入(此时已知)或代入图像与直线的交点求解(此时要注意交点在上升区间上还是在下降区间上).(2)五点法:确定的值时,往往以寻找“五点法”中的第一零点作为突破口.具体如下:“第一点”(即图像上升时与轴的交点)为;“第二点”(即图像的“峰点”)为;“第三点”(即图像下降时与轴的交点)为;“第四点”(即图像的“谷点”);“第五点”为;说明:当不能确定周期时,往往要根据图像与轴的交点,先求函数变换可以用下图表示:三点剖析一. 注意事项1. 相位变换中,注意的系数,系数不为1时,是对进行平移而不是初相;2. 周期变换中,沿轴缩短倍,沿轴伸长倍;3. 振幅变换中,,沿轴缩短倍,,沿轴伸长倍;4. 由图像确定函数的解析式三步走.二. 必备公式三角函数图像平移和转换的公式题模精讲题模一正弦型函数的图像变换例1.1、将函数f(x)=sin(ωx+φ)(ω>0,-≤φ<)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到y=sinx的图象,则f()=____.例1.2、将函数y=sin(x+)(x∈R)的图象上所有的点向左平移个单位长度,再把图象上各点的横坐标扩大到原来的2倍,则所得的图象的解析式为()A、y=sin(2x+)(x∈R)B、y=sin(+)(x∈R)C、y=sin(-)(x∈R)D、y=sin(+)(x∈R)题模二利用图像求解析式例2.1、函数f(x)=2sin(ωx+φ)(ω>0,﹣<φ<)的部分图象如图所示,则ω,φ的值分别是()A、B、C、D、例2.2、若函数f(x)=Asin(ωx+φ)的部分图象如图所示,其中A>0,ω>0,0<φ<,则f(x)=()A、2sin(x+)B、2sin(2x+)C、sin(2x+)D、2sin(2x+)例2.3、函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的部分图象如图所示,将y=f(x)的图象向右平移个单位后得到函数y=g(x)的图象.则函数y=g(x)的单调增区间为()A、[kπ-,kπ+],k∈Z B、[kπ+,kπ+],k∈ZC、[kπ-,kπ+],k∈Z D、[kπ+,kπ+],k∈Z随堂练习随练4.1、把函数y=sin(2x-)的图象上的所有点向右平移个单位,再把所有点的横坐标缩短到原来的一半,而把所有点的纵坐标伸长到原来的4倍,所得图象的表达式是()A、y=4sin4xB、y=4sin(4x-)C、y=4sin(4x+)D、y=4sin(4x-)随练4.2、若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标缩小到原来的,再将整个图象向右平移个单位,沿y轴向下平移1个单位,得到函数y= sinx的图象,则函数y=f(x)是()A、y=sin(x-)+1B、y=sin(x+)+1C、y=sin(x+)+1D、y=sin(x-)+1随练4.3、=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,KL=1,则f()的值为()A、-B、-C、D、随练4.4、如图为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象,则函数解析式为()A、y=3sin(2x+)B、y=3sin(2x-)C、y=3sin(2x+)D、y=3sin(2x-)随练4.5、已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的部分图象如图所示.(Ⅰ)求函数f(x)的解析式;(Ⅱ)若x∈[0,],求f(x)的值域;(Ⅲ)若f(x0)=,-<x0<,将函数y=f(x)图象向右平移个单位长度得到函数y=g(x)的图象,求g(x0)的值.自我总结课后作业作业1、函数y=sinx(≤x≤π)的值域为()A、[,1]B、[-1,1]C、[,]D、[,1]作业2、函数f(x)=cos2x+2sinx(x∈[0,])的值域是____.作业3、已知函数y=sinx的定义域为[a,b],值域为[-1,],则b-a的值不可能是()A、B、C、πD、作业4、已知ω>0,函数f(x)=sin(ωx+)在(,π)上单调递减.则ω的取值范围是()A、[,]B、[,]C、(0,]D、(0,2]作业5、已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<)的部分图象如图所示.(1)求函数y=f(x)的解析式;(2)求函数y=f(x)的单调增区间;(3)求方程f(x)=0的解集.作业6、函数()是R上的偶函数,则等于()A、0B、C、D、作业7、若f(x)=asin(x+)+3sin(x-)是偶函数,则a=____.作业8、的定义域是____________.作业9、函数y=2cos(x-)的最小值是____.作业10、函数在区间上的最大值为________,最小值为________.作业11、函数的值域是()A、B、C、D、作业12、函数的值域是______.作业13、已知,求函数的值域作业14、函数y=cos2x在下列哪个区间上是减函数()A、[-,]B、[,]C、[0,]D、[,π]作业15、函数()A、在上递增B、在上递增,在上递减C、在上递减D、在上递减,在上递增作业16、若,比较,,这三者之间的大小.作业17、定义在R上的函数满足,设,,,则a,b,c大小关系是_____.作业18、函数y=3cos(2x+)的图象()A、关于点(-,0)对称B、关于点(,0)对称C、关于直线x=对称D、关于直线x=对称作业19、函数f(x)=3cos(2x+φ)的图象关于点(,0)成中心对称,则φ的最小正值为____.作业20、若,对任意实数都有,且,则实数的值等于()B、A、C、或1D、或3作业21、函数的定义域为()A、B、C、D、作业22、求函数的定义域作业23、函数的单调增区间为__________.作业24、已知函数y=tanωx在(-,)上是减函数,则()A、0<ω≤1B、-1≤ω<0C、ω≥1D、ω≤-1作业25、函数f(x)=x2-tan(-α)•x+1在[,+∞)上单调递增,则α的取值范围是()A、[kπ-,kπ+π),(k∈Z)B、(kπ-π,kπ+],(k∈Z)C、(-π,+∞)(k∈Z)D、(-∞,kπ+],(k∈Z)作业26、已知则的中心对称点为_______作业27、函数y=tan(13x+14π)是()A、周期为的偶函数B、周期为的奇函数C、周期为的偶函数D、周期为的奇函数作业28、右图是函数y=Asin(ωx+φ)(x∈R)在区间[-,]上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点()A、向左平移个单位长度,再把所得各点的横坐标缩短到原来的,纵坐标不变B 、向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C、向左平移个单位长度,再把所得各点的横坐标缩短到原来的,纵坐标不变D、向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变作业29、要得到函数y=sin(4x﹣)的图象,只需将函数y=sin4x的图象()A、向左平移单位B、向右平移单位C、向左平移单位D、向右平移单位作业30、要得到的图象,只需把y=sin2x的图象()A、向左平移个单位长度B、向右平移个单位长度C、向左平移个单位长度D、向右平移个单位长度作业31、已知函数y=Asin(ωx+φ)+B(A>0,ω>0,|φ|<)的周期为T,在一个周期内的图象如图所示,则正确的结论是()A、A=3,T=2πB、B=-1,ω=2C、T=4π,φ=-D、A=3,φ=作业32、如图曲线对应的函数是()A、y=|sinx|B、y=sin|x|C、y=-sin|x|D、y=-|sinx|作业33、已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的图象如图所示,则函数的解析式为f(x)=____.。
三角函数的定义、图像和性质

极值点:函数 在其周期内取 得最大值和最 小值的点,即 最值点的横坐 标
0 4
诱导公式
三角函数的诱导 公式是三角函数 性质的重要组成 部分,它可以帮 助我们简化复杂 的三角函数计算。
添加标题
诱导公式包括正 弦、余弦和正切 的诱导公式,它 们可以通过三角 函数的周期性和 对称性推导出来。
添加标题
奇偶性
奇函数:满足f(-x)=-f(x) 的函数
偶函数:满足f(-x)=f(x) 的函数
奇偶性的判断方法:根据 定义来判断
奇偶性在三角函数中的应 用:判断函数的图像对称
性
最值和零点
最大值和最小 值:三角函数 在其周期内可 以达到的最大 和最小值
0 1
零点:函数值 为零的点,即 解方程的根
0 2
周期性:三角 函数图像呈现 周期性变化, 每个周期内存 在一个最大值 和一个最小值
利用诱导公式, 我们可以将任意 角的三角函数转 化为锐角或0到 360度之间的角的 三角函数,从而
简化计算。
添加标题
诱导公式在三角 函数的图像和性 质中有着广泛的 应用,可以帮助 我们更好地理解 三角函数的性质
和图像。
添加标题
THANK YOU
汇报人:XX
三角函数的定义、 图像和性质
汇报人:XX
目录
01 三 角 函 数 的 定 义 02 三 角 函 数 的 图 像 03 三 角 函 数 的 性 质
01
三角函数的定义
正弦函数
定义:正弦函数是三角函数的一种,定义为y=sinx,x∈R。 图像:正弦函数的图像是一个周期函数,形状类似于波浪。 性质:正弦函数具有一些重要的性质,如奇偶性、周期性、单调性等。
图像的信息量和信息冗余编码技术
种基于信息冗余编码技术的数据存储方案。
信息冗余编码技术的优缺点
优点
信息冗余编码技术可以提高数据的鲁棒性和可靠性,使得数 据在传输和存储过程中能够更好地抵抗噪声和数据丢失。此 外,信息冗余编码技术还可以提高数据的容错性和纠错能力 ,从而降低传输和存储过程中的错误率。
缺点
信息冗余编码技术会增加数据的传输和存储开销,因为需要 传输更多的数据。此外,信息冗余编码技术也会增加解码的 复杂度,因为需要解码更多的数据。因此,在实际应用中需 要根据具体需求进行权衡和选择。
冗余数据是指与原始图像数据重复或无关的数据,这些数据在解码时可以被丢弃,而不会影响图像的完整性。信息冗余编码 技术通过将原始图像数据编码成包含冗余数据的码字,来提高图像的鲁棒性。
信息冗余编码技术的应用
01
信道编码
在数字通信中,信道编码是一种常见的信息冗余编码技术。通过在发送
端对数据进行冗余编码,可以在接收端对数据进行纠错和恢复,从而提
图像信息量的计算方法
直方图法
通过统计图像像素值的分布情况 来计算信息量,像素值分布越均 匀,信息量越大。
信息熵法
基于信息论中的熵概念,计算图 像中包含的信息量。熵越大,信 息量越大。
图像信息量的影响因素
图像分辨率
分辨率越高,细节表现 越丰富,信息量越大。
色彩深度
色彩深度越高,像素值 的范围越广,信息量越
图像压缩编码技术的优缺点
优点
能够大大减少图像数据的存储空间和传输时间,提高数据处理的效率;能够保 持图像的质量和分辨率;能够提供更好的视觉效果和用户体验。
缺点
可能会损失部分数据,导致图像质量的下降;对于一些复杂的图像或动态图像, 压缩效果可能不理想;需要耗费一定的计算资源和时间进行压缩和解压缩操作。ຫໍສະໝຸດ 图像压缩编码技术的发展趋势
函数及其图象函数的图像函数的图象
02
函数的图像
函数图像的概念
1 2
函数图像
将函数表达式中自变量与因变量之间的关系用 图形表示出来。
坐标系
在平面直角坐标系中,以横轴表示自变量,纵 轴表示因达式的性质,图像呈现不同形状, 如直线、曲线、折线等。
绘制函数图像的方法
描点法
根据函数表达式,求出一些自变量对应的因变量值,然后在坐标系上描出对 应的点,最后用平滑的曲线或直线将这些点连接起来。
图示法
利用计算器或编程语言,直接在计算机上绘制出函数图像。
函数图像的变换
复合变换
以上变换可以同时进行,也可以多次进行 。
平移
将函数图像沿横轴或纵轴方向移动一定距 离。
伸缩
将函数图像按比例进行缩放,可以是横向 或纵向。
旋转
将函数图像按一定角度顺时针或逆时针旋 转一定角度。
翻折
将函数图像以某一条直线或点为对称中心 进行翻折。
VS
图像特征
对数函数的图像在坐标系中呈现出“双曲 线+直线”的形式,当底数$a>1$时,函 数图像在第一象限,当底数$0<a<1$时 ,函数图像在第四象限。
04
函数图像的应用
利用函数图像求解方程
图像法
通过观察函数图像的交点或切 线等方法,求解方程的根。
交点法
根据两个函数图像的交点坐标 ,求解方程的根。
零点法
通过函数图像与x轴交点的横坐 标,求解方程的根。
利用函数图像研究函数性质
01
02
观察法
分析法
通过观察函数图像的形状、趋势和特 征,得出函数的性质。
通过对函数图像的局部和整体分析, 得出函数的性质。
03
计算法
二值化
用于显示的灰度图像通常用每个采样像素8 bits的非线性尺度来保存,这样可以有256种灰度(8bits就是2 的8次方=256)。这种精度刚刚能够避免可见的条带失真,并且非常易于编程。在医学图像与遥感图像这些技术 应用中经常采用更多的级数以充分利用每个采样10或12 bits的传感器精度,并且避免计算时的近似误差。在这 样的应用领域流行使用16 bits即个组合(或种颜色)。
根据阈值选取的不同,二值化的算法分为固定阈值和自适应阈值。比较常用的二值化方法则有:双峰法、P 参数法、迭代法和OTSU法等。
图像分割
图像分割
在计算机视觉领域,图像分割(Segmentation)指的是将数字图像细分为多个图像子区域(像素的集合) (也被称作超像素)的过程。图像分割的目的是简化或改变图像的表示形式,使得图像更容易理解和分析。图像 分割通常用于定位图像中的物体和边界(线,曲线等)。更精确的,图像分割是对图像中的每个像素加标签的一 个过程,这一过程使得具有相同标签的像素具有某种共同视觉特性。
二值图像
二值图像
二值图像是每个像素只有两个可能值的数字图像。人们经常用黑白、B&W、单色图像表示二值图像,但是也 可以用来表示每个像素只有一个采样值的任何图像,例如灰度图像等。
二值图像经常出现在数字图像处理中作为图像掩码或者在图像如激光打印机、传真机、单色计算机显示器等都可以处理二值图像。
图像分割的结果是图像上子区域的集合(这些子区域的全体覆盖了整个图像),或是从图像中提取的轮廓线 的集合(例如边缘检测)。一个子区域中的每个像素在某种特性的度量下或是由计算得出的特性都是相似的,例 如颜色、亮度、纹理。邻接区域在某种特性的度量下有很大的不同。
图像符号的特性及其意义解构
3、寓意特性
图像符号的寓意特性是其独特魅力所在,通过隐喻、象征、暗示等手法,传达 出特定的文化内涵和价值观。例如,和平鸽是和平的象征,而玫瑰则代表爱情。 这些寓意特性使得图像符号在文化传承和社会交流中扮演了重要角色。
图像符号的意义解构
1、文化意义
图像符号作为文化载体的形式之一,具有丰富的文化意义。它不仅可以传达特 定的文化观念和信仰,还可以展示一个民族或地区的文化传统和特色。例如, 中国的太极图象征着对立统一与和谐平衡的哲学思想,龙和凤则被视为中华民 族的图腾和文化象征。
相互模仿
在叙事活动中,图像与文字之间存在着相互模仿的关系。具体而言,图像的视 觉性可以激发读者的想象力,帮助他们更好地理解和感受故事的情感与意境; 而文字的理性化则能够深度阐释图像的内涵,为读者提供更加全面和深入的视 角。
例如,在一部小说中,作者可能会用一些描述性的语言来呈现一幅生动的画面。 这些语言描述可以帮助读者在脑海中浮现出相应的场景,从而更好地理解和感 受故事情节的发展。同时,小说中的插图或配图也可以进一步强化这些场景的 真实感和代入感,使读者更加深入地沉浸在故事情境之中。
图像符号特性
图像作为一种符号形式,具有形象性和直观性。与文字不同,图像可以直接呈 现事物的外观和形象,如实地再现现实世界中的各种景象。图像的这种形象性 使其在传达信息时更加简洁明了,同时更容易引起观众的共鸣和情感反应。此 外,图像还具有概括性,可以通过对细节的省略或突出,概括出事物的关键特 征,进而引导观众对整体意义进行理解和想象。
文字符号特性
文字作为一种符号形式,具有概念性和理性化。文字可以对现实世界中的事物 进行抽象描述和概念化,以便更准确地表达思想、情感和信息。与图像不同, 文字的表达方式更加间接和内敛,它需要读者具备一定的文化背景和知识储备 才能正确理解。此外,文字还具有普遍性,它是世界上使用范围最广的符号系 统之一,可以跨越地域和文化的界限,为不同的人群所共同理解和接受。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广播电视技术基础 第 - 17 - 页 作者:洪 强 黄志浩 华侨大学中文系广电教研室 - 17 - 第三章 图 像 图像做为电视系统传输的一种信息成分,它影响着电视设备的原理和使用方法。图像转化成的电信号是一种较为复杂的信号,相对于广播系统中的声音,图像在处理上有诸多困难,这也是导致电视制作设备相当昂贵的原因。本节主要对电视机图像的由来进行分析。完成对于图像的认识。
第一节 黑白电视图像 黑白电视图像在电视系统中最早实现,随后才出现了彩色的电视图像、高清晰电视图像及研制中的立体电视图像。它的原理是认识其它电视图像的基础。 一、静止的黑白图像 静止的黑白图像范围很广,报纸上图片、黑白的照片、黑白的电视画面都是其中一种,它们是如何让人感觉出其中的影像呢? 用放大镜看报纸中的图片,我们可以发现原来图片中的影像是由小黑点与剩下的“白点”拼成的。在一个平面上的不同位置,分布着不同疏密的黑点,从宏观上综合起来就形成有人、有物的图像。 这些小黑点(小白点)称为像素,一个报纸的图片就是由许许多多像素组成。其实黑白照片也一样,只不过它的像素很小,用显微镜才能看到。从黑白照片和报纸中的黑白图片效果比较来看,当然照片影像细腻,细节清晰,所以,其中的道理是:像素越多,图像越清晰。 当然,二者在形成影像上还有一个大的差异,照片有黑白,还有中间不同程度的灰色像素。 黑白电视图像也是这样,显像管的荧光屏上的图像也是由许许多多的像素组成。 二、活动的黑白图像 要获得活动的影像,这和人的一种视觉现象有关。 人看东西有一种“视觉残留”(也叫“视觉惰性”)现象,即当两个画面在人眼前依次出现,只要它们之间的时间差不到0.1秒,人会感觉不到两个画面的存在,只会把两个画面的内容联系起来,看为一个画面。显然,当连续的几个画面内容是一个运动物体在这段时间内的运动片断时,视觉暂留把它们一联系起来,人就会看到活动的物体影像。 这种现象在我国古代发明的走马灯中就有运用。在一个旋转灯的四面,贴上4 幅马在奔跑过程中四种状态的图画,当灯转起来时,就会看到一个运动着的马;英国的一位摄影家也做过这种实验:为了获得马在奔跑时各个阶段精确的照片,他把8个照相机放在路的一侧,每个照相机的快门均用一细线连着,细线横过道路;当马跑过时,便自动启动各台照相机,这样就得到了8张马在奔跑时的照片,用于连续放映时用。 黑白电影也就是这个原理,它是利用摄影机的精确机械运动,使一组胶片感光,最后再用同样速度的放映机播放在银幕上,现在电影的每秒播放画面24个,也就是说每秒要求24格胶片记录,1小时就要用掉86400格胶片。 电影在放映中,要求每一个胶片是静止的,这样才能有好的画面效果。这样就存在一个换片格的问题。具体的做法是:在胶片前方有一个片门的结构,在放片格时打开,播放完后片门关上,此时银幕是黑色的,直到 图15 电影播放示意 下一格胶片运动到放映灯前稳定后,片门再次打开。所以,在看电影时,观众有三分之一的时间是看一个黑色的银幕。因为视觉残留,人无法察觉出这些“黑幕”。 但即使每秒给人眼看到24格画面还是不够好,运动的连续性当然是没有问题,但是在人眼对于亮度闪烁的觉察比1/24更快。电影的“黑幕”和图像的时间间隔是1/24秒,这样人就会感到画面一直在闪烁,这是不好的观看效果。据测定,只有时间间隔小于1/48秒时,人眼才不能觉察闪烁。但是,要再提广播电视技术基础 第 - 18 - 页 作者:洪 强 黄志浩 华侨大学中文系广电教研室 - 18 - 高每秒片格数会带来成本的大幅度上升,因此不现实。 因此,电影中采用一种技术,在每一个画格放映时,片门开关两次。这样就相当于每格画面放映两次,虽然只有24格画面,投放到银幕上的却有48次,这样就克服了亮度的闪烁。 三、黑白电视成像原理 电视图像的形成比电影要复杂。电影可以一次把一整幅图像投在银幕上。而电视做不到。电视是以电信号为信息载体,受到时间的局限。它每个时刻只能在荧光屏上成一个点,使一个象素发光。因此,电视图像要采用扫描成像法,像撒豆子一样将像素一逐行排列,最终构成一幅画面,如下图所示: 图16 扫描成像原理图
图中实线表示行扫描的正程,此时电子束打在荧光屏上,使像素发光,这是显示图像的部分,这相当于电影放映机片门打开的时段;图中的虚线表示行扫描的逆程,这是使电子束回到起始点的过程,此时显像管会控制电子束,使之无法到达显像管形成发光点,这很象是电影放映机片门关闭的时段;图中的粗虚线表示场扫描的逆程,这段时间内,电子束回到一场的起始点,此时显像管也会控制电子束,使之无法到达显像管形成发光,这是真正对应电影的片门关闭的时段。 扫描成像的方法: 1、让电子束打在荧光屏上,形成一个亮点(像素)。这个亮点的亮度与电信号在这时的幅度对应; 2、随着时间的变化,控制电子束从左到右扫描,依次使荧光屏上的这一行像素发光; 3、到一行的结束点时,电子束回扫,同时显像管发出截止电压,使此时的电子束无法到达荧光屏,这段时间称为“行消隐期”; 4、一行一行扫描到整个屏幕的右下角时,完成一幅电视图像的显示。电子束回扫,回到屏幕的左上角,此时显像管又发出截止电压,使此时的电子束无法到达荧光屏,这个这段时间为“场消隐期”。 完成以上的扫描工作后,电视就为观众提供了一个电视画面,这一个完整的电视画面称为“1帧”。对于中国的电视制式而言,电视每秒提供25帧画面,所以能够满足运动连续性的需要。但是同样的问题是无法克服亮度的闪烁(电视在场消隐期时,电子束打不到荧光屏,此时屏幕是不发光的,每次不到1/25秒屏幕就要变黑一次)。因此电视也要提高每秒提供的画面数量。和电影一样,电视也采用同一幅画面显示两次的方法,不过电视是采用“隔行扫描”来实现的。 隔行扫描的含义是:第一次电视先扫描1、3、5、7„„这些奇数行,到达屏幕右下角时完成一幅电视画面的重放,但此时的一幅画面不完整,与一帧画面不同,我们给它一个新的名称:“场”。此时完成了奇数场的重放,而后进入场消隐期;第二次再扫描2、4、6、8„„这些偶数行,最终形成偶数场,两场一起构成电视画面一帧的全部信息,由于时间间隔很短,人也一样不能觉察这种合成过程。 随着电视技术的提高,近期还出现了“逐行扫描”技术,将原先只扫描半数行的“场”改为完全扫描的帧,这就和电影一样一幅画面出现两次,从而消除了闪烁现象。 中国的电视制式要求电视的长宽比为4:3,屏幕从上到下共625行组成,每秒要求提供50场(25帧)电视画面。这些指标对于其它的电视制式不一定相同。 广播电视技术基础 第 - 19 - 页 作者:洪 强 黄志浩 华侨大学中文系广电教研室 - 19 - 第二节 彩色电视图像
对于黑白电视而言,画面只有一种信息成份。只要荧光屏上海一点的发光程度与电信号强度对应,一幅由明暗像素构成的画面就可以形成。但对于彩色的电视画面来说,像素却是要呈现出无穷多种的颜色,因此相对要复杂一些。 一、彩色电视图像的形成 (一)三基色原理 要求每一个像素根据条件发出无穷多种颜色来,这是不现实的,但这又是形成彩色电视画面的要求。有一个很重要的原理帮助了这个问题的解决。 三基色原理的内容是:自然界虽然有无穷多种颜色,但它们可以被分解成三种基本颜色:红(R)、绿(G)、蓝(B)的组合。只要三者在大小、比例上有所不同,颜色就不一样。 这样,彩色电视信号只要告诉每一个像素应该表达出红、绿、蓝的各自份量,就可以实现无限多种颜色的重放。 (二)彩色显像管 和黑白电视显像管不同的是,彩色显像管的屏幕上每一个像素都是由三种荧光粉组成,即红色荧光粉、绿色荧光粉和蓝色荧光粉组成,它们在电子束打击时,会发出红、绿、蓝三种色光;电子束也由黑白电视机的单束变成三束(三支电子枪),分别反映红、绿、蓝三种电信号的大小,在工厂调试时已经精确调整到:反映红色信号的电子束只能打中红色荧光粉、反映绿色信号的电子束只能打中绿色荧光粉、反映蓝色信号的电子束只能打中蓝色荧光粉。 这样,彩色电视信号中的红、绿、蓝三种电信号就指挥着屏幕上每一象素的红、绿、蓝比例。 (三)人眼的空间混色能力 彩色电视屏幕上的像素是非常小的,人在观看时,无法分辨出它们。这时,每一个像素中的红、绿、蓝三种颜色就无法被分开,人会把它们混合起来,形成一种颜色的感觉。 这样,随着每个像素中三色的份量不同,人就看到了无限多种色彩。由这一个个有色彩的像素最终就能拼成一幅彩色的电视画面。 二、彩色电视信号的组成 电视信号从物理图像上看是一种电流的波动,它的频率范围是0~6MHz,比声音信号的范围大300倍。0Hz的电视图像是全屏单色或单一亮度,6MHz的电视图像是画面中每一像素都与邻近像素不同的图像。计算方法是: 625×625×4/3 ×25×1/2。 电视信号的合成过程(以彩色电视信号为例):
1、R、C、B三基色信号首先被转化成亮度信号Y和两个色差信号R-Y、B-Y,通称“分量视频信号”这一步转化是为了信号传输的方便。转化的原理是亮度方程:Y=0.3R+0.59G+0.11B; 2、进一步把两个色差信号R-Y和B-Y编码色度信号成C,与亮度信号Y组成所谓的“准分量视频信号” ,俗称“S端子信号”; 3、最后将亮度信号Y与色度信号C混合成复合视频信号Video,而后加入消隐信号、同步信号,再与声音信号Audio 一起合成全电视信号。 广播电视技术基础 第 - 20 - 页 作者:洪 强 黄志浩 华侨大学中文系广电教研室 - 20 - 三、彩色电视制式 (一)什么是电视制式 多种电视制式并存,是当前电视系统中的一个突出现象。同样利用电信号传输和还原声音和图像,方法可以有许多种,只要在本系统中都遵循这种方法,便形成了一种电视制式。打个比喻:同样一件货物,要从产地送到用户手中,要进行包装才能保证质量和运输,但这种包装的方法有多种多样,只要能完成传输就可以。这种货物到了用户的手中,解开包装的方法要按包装的方法反向进行才可以,所以,采用一种电视制式的国家,从它的摄像机(包装)、录像机(存放和二次包装)、电视机(解开包装)的全过程,都要以这个标准进行。这就形成一种制式。 从历史的发展来看,由于电视对政治、经济、文化有很大的影响,研究过程中各国家、各产家互相保秘密,结果就形成各自为政、各个用各人的系统的局面。这种状况给电视节目的交流带来很大的不便。 (二)电视制式的种类 全世界的电视制式有许多种。 黑白制式:这是黑白电视时代就已出现,主要的种类有D、I、M、BG等制式,我国使用D制、英国、我国香港等地使用I制,我国台湾、日本、美国使用M制。它们之间的差别是: (1)声音处理方法不同,D制6.5MHz,I制6.0MHz,M制4.5MHz播放节目时互相听不到对方的声音; (2)图像处理方法不同,D制625行50场/秒,M制525行60场/秒,这样播放对方节目时图像就会垂直滚动和水平扭曲。 彩色制式:到了彩色电视时代,为了实现彩色的重放,世界上又出现了三种主要的彩色电视制式。 (1)NTSC制:1953年美国研制,全称“National Television System Committee(国家电视制式委员会)”,技术命名“正交平衡调幅制”,彩色副载波频率为3.5795MHz。特点是:后期制作处理简单,信号的调制与解码简单,每行色度信号按同一方式传送,不存在“行顺序效应”,亮度与色度串扰低,但对相位失真敏感,远距离传输、信号不稳易造成色调失真。这种制式的使用国家有:美国、日本、加拿大、墨西哥、菲律宾和台湾地区; (2)PAL制:1962年德国研制,全称“Phase Alternation Line(相位逐行交变)”,技术命名“逐行倒相正交平衡调幅制” ,彩色副载波频率为4.4336MHz。特点是:后期制作处理简单,但信号的调制与解码较复杂。修正了NTSC制式因相位敏感导致的色彩失真问题,但特有的“梳状滤波器”也可能会引起大面积的“彩色爬行现象”和半帧频闪烁现象,导致色彩清晰度下降。使用这种制式的国家有:中国、德国、英国、荷兰、意大利、阿根廷、澳大利亚、印度、泰国等,我国香港地区也是PAL制; (3)SECAM制:1966年研制,全称“Séquential Couleur à Mémoire(顺序传送色彩与存储)”,使用双彩色副载波4.40625MHz、4.25MHz。修正了PAL制式中的色彩串扰和闪烁问题,但彩色调制与解调兼容性差,彩色垂直分辨率低,后期制作处理困难。使用这种制式的国家有:法国、希腊、埃及、摩洛哥、突尼斯、叙利亚、独联体和东欧一些国家。 因此,现在的电视制式要综合考虑黑白制式和彩色制式,如我国的电视制式是PAL—D制,香港地区是PAL—I制,两种制式仍不能互通(无声);美国和我国台湾的电视制式是NTSC—M制,与前面的制式有很大不同(无声、无色、滚动)。 (三)电视制式的兼容 1、用制式转换器,把其它制式的电视节目转换成自己系统的电视制式。 这个过程实际上是先用别人的方法拆开包装,再把信号用自己的方法重新包装。这种方法多用于有线电视台转播境外节目、播放境外节目带。制转换器一般较为昂贵,但转换后,干家万户使用就很方便; 2、对于个人使用,可以用多制式的录像机和电视机。 带有多制式功能的设备实际上就是具有多种的解包装能力的机种,它的内部有多套电路。机器先识别信号的制式(或是由人工调节),而后把信号转到相应的解码电路去处理。
