01-有理数的意义—初中数学知识点解读与提高
初一数学《有理数》04节:有理数的加减法知识点解读与提高

有理数的加减法(基础)要点一、有理数的加法1.定义:把两个有理数合成一个有理数的运算叫作有理数的加法.2.法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0;(3)一个数同0相加,仍得这个数.利用法则进行加法运算的步骤:(1)判断两个加数的符号是同号、异号,还是有一个加数为零,以此来选择用哪条法则.(2)确定和的符号(是“+”还是“-”).(3)求各加数的绝对值,并确定和的绝对值(加数的绝对值是相加还是相减).3.运算律:交换加数的位置时,不要忘记符号.要点二、有理数的减法1.定义:已知两个数的和与其中一个加数,求另一个加数的运算,叫做减法,例如:(-5)+?=7,求?,减法是加法的逆运算.(1)任意两个数都可以进行减法运算.(2)几个有理数相减,差仍为有理数,差由两部分组成:①性质符号;②数字即数的绝对值.2.法则:减去一个数,等于加这个数的相反数,即有:()a b a b -=+-.将减法转化为加法时,注意同时进行的两变,一变是减法变加法;二变是把减数变为它的相反数”.如:有理数加法运算律加法交换律文字语言两个数相加,交换加数的位置,和不变符号语言a+b=b+a 加法结合律文字语言三个数相加,先把前两个数相加,或者先把后两个数相加,和不变符号语言(a+b)+c=a+(b+c)1.掌握有理数加法的意义,法则及运算律,并会使用运算律简算;2.掌握有理数减法的法则和运算技巧,认识减法与加法的内在联系;3.熟练将加减混合运算统一成加法运算,理解运算符号和性质符号的意义,运用加法运算律合理简算,并会解决简单的实际问题.要点三、有理数加减混合运算将加减法统一成加法运算,适当应用加法运算律简化计算.类型一、有理数的加法运算.计算:(1)(+20)+(+12);(2)1223⎛⎫⎛⎫-+-⎪ ⎪⎝⎭⎝⎭;(3)(3)(+2)+(-11);(4)(-3.4)+(+4.3);(5)(-2.9)+(+2.9);(6)(6)(-5)+0.(1)(2)属于同一类型,用的是加法法则的第一条;(3)(4)属于同一类,用的是加法法则的第二条;(5)用的是第二条:互为相反数的两个数相加得0;(6)用的是法则的第三条.(1)(+20)+(+12)=+(20+12)=+32=32;(2)12121123236⎛⎫⎛⎫⎛⎫-+-=-+=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(3)(+2)+(-11)=-(11-2)=-9(4)(-3.4)+(+4.3)=+(4.3-3.4)=0.9(5)(-2.9)+(+2.9)=0;(6)(-5)+0=-5.【变式1】计算:113343⎛⎫⎛⎫-++⎪ ⎪⎝⎭⎝⎭【答案】111113333433412⎛⎫⎛⎫⎛⎫-++=+-=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭【变式2】计算:(1)(+10)+(-11);(2)⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭12-1+-23【答案】(1)(+10)+(-11)=﹣(11-10)=﹣1;(2)类型二、有理数的减法运算.计算:(1)(-32)-(+5);(2)(+2)-(-25).此题是有理数的减法运算,先按照减法法则将减法转化为加法,再按照有理数的加法进行计算.法一:绝对值不等的异号两数相加,是有理数加法的难点,在应用法则时,一定要先确定符号,再计算绝对值.⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭1212341-1+-=-1+=-1+=-22323666法二:(1)原式=-32-5=-32+(-5)=-37;(2)原式=2+25=27【变式】若()﹣(﹣2)=3,则括号内的数是()A.﹣1B.1C.5D.﹣5B.根据题意得:3+(﹣2)=1,则1﹣(﹣2)=3.类型三、有理数的加减混合运算.计算:3.8+4﹣(+6)+(﹣8)根据有理数的加减混合运算的方法:有理数加减法统一成加法,求解即可解:原式=(3.8﹣6.8)+(4﹣8)=﹣3﹣4=﹣7,【变式】用简便方法计算:(1)(-2.4)+(-4.2)+(-3.8)+(+3.1)+(+0.8)+(-0.7)(2)2)324(83)65()851(43-++-+-+(1)原式=[(-3.8)+(-4.2)]+[(-2.4)+(-0.7)+(+3.1)]+(+0.8)=-8+0.8=-7.2(2)原式=(2-1-4)+(34-58-56+38-23)=-3+[68-58+38+(-56-46)]=-3-1=-4类型四、有理数的加减混合运算在实际中的应用.邮递员骑车从邮局出发,先向南骑行2km 到达A 村,继续向南骑行3km 到达B 村,然后向北骑行9km 到C 村,最后回到邮局.(1)以邮局为原点,以向北方向为正方向,用1cm 表示1km,画出数轴,并在该数轴上表示出A、B、C 三个村庄的位置;(2)C 村离A 村有多远?(3)邮递员一共骑了多少千米?(1)以邮局为原点,以向北方向为正方向用1cm算式中的“+”或“-”既可以看作运算符号按法则进行计算,也可以看作是性质符号按多重符号化简进行计算.本题考查了有理数的加减混合运算的知识,如果在一个式子里,有加法也有减法,根据有理数减法法则,把减法都转化成加法,并写成省略括号的和的形式.表示1km,按此画出数轴即可;(2)可直接算出来,也可从数轴上找出这段距离;(3)邮递员一共骑了多少千米?即数轴上这些点的绝对值之和.解:(1)依题意得,数轴为:;(2)依题意得:C点与A 点的距离为:2+4=6(千米);(3)依题意得邮递员骑了:2+3+9+4=18(千米).【变式1】华英中学七年级(14)班的学生分成五组进行答题游戏,每组的基本分为100分,答对一题加50分,答错一题扣50分,游戏结束后各组的得分如下表:(1)第一名超过第二名多少分?(2)第一名超过第五名多少分?由表看出:第一名350分,第二名150分,第五名-400分.(1)350-150=200(分)(2)350-(-400)=350+400=750(分)答:第一名超过第二名200分;第一名超过第五名750分.【变式2】某产粮专业户出售粮食8袋,每袋重量(单位:千克)如下:197,202,197,203,200,196,201,198.计算出售的粮食总共多少千克?法一:以200(千克)为基准,超过的千克数记作正数,不足的千克数记作负数,则这8个数的差的累计是:(-3)+(+2)+(-3)+(+3)+0+(-4)+(+1)+(-2)=-6200×8+(-6)=1594(千克)答:出售的粮食共1594千克.法二:197+202+197+203+200+196+201+198=1594(千克)答:出售的粮食共1594千克.【巩固练习】一、选择题1.某市一天的最高气温为2℃,最低气温为﹣8℃,那么这天的最高气温比最低气温高()A.﹣10℃B.﹣6℃C.10℃D.6℃2.若等式0□1=﹣1成立,则□内的运算符号为()A.+B.﹣C.×D.÷3.两个有理数相加,和小于其中一个加数而大于另一个加数,需满足()A.两个数都是正数B.两个数都是C.一个是正数,另一个是负数D.至少有一个数是零4.下列说法中正确的是A.正数加负数,和为0B.两个正数相加和为正;两个负数相加和为负C.两个有理数相加,等于它们的绝对值相加D.两个数的和为负数,则这两个数一定是负数第1组第2组第3组第4组第5组100150350-400-100本题主要考查了学生有实际生活中对数轴的应用能力,只要掌握数轴的基本知识即可.5.下列说法正确的是()A.零减去一个数,仍得这个数B.负数减去负数,结果是负数C.正数减去负数,结果是正数D.被减数一定大于差6.某粮店出售的三种品牌的面粉袋上,分别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差()A.0.8kg B.0.6kg C.0.5kg D.0.4kg7.-3+5的相反数是().A.2B.-2C.-8D.8二、填空题8.有理数,,a b c在数轴上对应点位置如图所示,用“>”或“<”(1)|a|______|b|;(2)a+b+c______0:(3)a-b+c______0;(4)a+c______b;(5)c-b______a.8.计算:|﹣2|+2=________.9.某月股票M开盘价20元,上午10点跌1.6元,下午收盘时又涨了0.4元,则股票这天的收盘价是_______.10.列出一个满足下列条件的算式:(1)所有的加数都是负数,和为-5,________;(2)一个加数是0,和是-5________;(3)至少有一个加数是正整数,和是-5,________.11.数学活动课上,王老师给同学们出了一道题:规定一种新运算“☆”对于任意两个有理数a和b,有a☆b=a-b+1,请你根据新运算,计算(2☆3)☆2的值是.12.计算(﹣3)+(﹣9)的结果为.三、解答题14.计算题(1)232(1)(1)(1.75)343-----+-(2)132.1253(5)(3.2)58-+---+(3)21772953323+---(4)231321234243--++-+(5)2312()()3255---+--+-15.已知:|a|=2,|b|=3,求a+b的值.16.某人用400元购买了8套儿童服装,准备以一定价格出售,如果以每套儿童服装55元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,﹣3,+2,+1,﹣2,﹣1,0,﹣2.(单位:元)(1)当他卖完这八套儿童服装后是盈利还是亏损?(2)盈利(或亏损)了多少钱?【答案与解析】一、选择题1.【答案】C【解析】解:2﹣(﹣8)=2+8=10℃.故选C.2.【答案】B3.【答案】C【解析】举例验证.4.【答案】B【解析】举反例:如5+(-2)=+3≠0,故A 错;如:(-2)+(-3)≠|-2|+|-3|,故C错;如(+2)+(-8)=-6,故D错误.5.【答案】C【解析】举反例逐一排除.6.【答案】B【解析】因为最低重量为24.7kg,最大重量为25.3kg,故质量最多相差25.3-24.7=0.6kg.7.【答案】B二、填空题8.【答案】<,<,>,>,>【解析】由图可知:b a c>>,且0,0b a c<<>,再根据有理数的加法法则可得答案.9.【答案】4.10.【答案】18.8元【解析】跌1.6元记为-1.6元,涨0.4元记为+0.4元,故有收盘价为20+(-1.6)+0.4-18.8.11.【答案】(1)(-2)+(-3)=-5(2)(-5)+0=-5(3)2+(-7)=-5【解析】答案不唯一.12.【答案】-1【解析】(2☆3)☆2=(2☆3)-2+1=2-3+1-2+1=-113.【答案】-12.【解析】同号两数相加的法则是取相同的符号,并把绝对值相加.原式=﹣(3+9)=﹣12.三、解答题13.【解析】(1)原式22(1)(1.75 1.75)133=-++-+=;(2)原式131[3(3.2)][(5) 2.125]3584=+-++---=(3)原式217297719)533326=+---=-(4)原式223311()()12334422=-++-++-=-(5)原式23122312231283[()][()]32553255325530 =------=--------=----=-(6)原式=12342001200220032004-+-++-+-+15.【解析】由题意知:a=±2,b=±3,所以要分四种情况代入求值.∵|a|=2,∴a=±2,∵|b|=3,∴b=±3.当a=+2,b=+3时,a+b=(+2)+(+3)=+5;当a=+2,b=-3时,a+b=(+2)+(-3)=-1;当a=-2,b=+3时,a+b=(-2)+(+3)=+1;当a=-2,b=-3时,a+b=(-2)+(-3)=-5.16.【解析】解:根据题意得(1)2﹣3+2+1﹣2﹣1+0﹣2=﹣3,(12)(34)(20032004)110021002 =-++-+++-+=⨯=55×8+(﹣3)=437元,∵437>400,∴卖完后是盈利;(2)437﹣400=37元,故盈利37元.有理数的加减法(提高)要点一、有理数的加法1.定义:把两个有理数合成一个有理数的运算叫作有理数的加法.2.法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0;(3)一个数同0相加,仍得这个数.利用法则进行加法运算的步骤:(1)判断两个加数的符号是同号、异号,还是有一个加数为零,以此来选择用哪条法则.(2)确定和的符号(是“+”还是“-”).(3)求各加数的绝对值,并确定和的绝对值(加数的绝对值是相加还是相减).3.运算律:交换加数的位置时,不要忘记符号.要点二、有理数的减法1.定义:已知两个数的和与其中一个加数,求另一个加数的运算,叫做减法,例如:(-5)+?=7,求?,减法是加法的逆运算.(1)任意两个数都可以进行减法运算.(2)几个有理数相减,差仍为有理数,差由两部分组成:①性质符号;②数字即数的绝对值.2.法则:减去一个数,等于加这个数的相反数,即有:()a b a b -=+-.将减法转化为加法时,注意同时进行的两变,有理数加法运算律加法交换律文字语言两个数相加,交换加数的位置,和不变符号语言a+b=b+a加法结合律文字语言三个数相加,先把前两个数相加,或者先把后两个数相加,和不变符号语言(a+b)+c=a+(b+c)1.掌握有理数加法的意义,法则及运算律,并会使用运算律简算;2.掌握有理数减法的法则和运算技巧,认识减法与加法的内在联系,体会其中蕴含的转化的思想;3.熟练地将加减混合运算统一成加法运算,理解运算符号和性质符号的意义,运用加法运算律合理简算,并且会解决简单的实际问题.一变是减法变加法;二变是把减数变为它的相反数”.如:要点三、有理数加减混合运算将加减法统一成加法运算,适当应用加法运算律简化计算.类型一、有理数的加法运算.阅读下题的计算方法.计算.解:原式===0+(﹣)=﹣上面这种解题方法叫做拆项法,按此方法计算:.根据拆项法,可把整数结合在一起,分数结合在一起,再根据有理数的加法,可得答案.解:原式=[(﹣2011)+(﹣)]+[(﹣2010)+(﹣)]+[4022+]+[(﹣1)+(﹣)]=[(﹣2011)+(﹣2010)+4022+(﹣1)]+[(﹣)+(﹣)++(﹣)]=0+(﹣)=﹣.【变式1】计算:(1)-721+1061;(2)(-21)+(-7.3);(3)141+(-231);(4)751+(-3.8)+(-7.2)【答案】(1)原式=11112(107)(97)(1)262623+-=-+-=;(2)原式=(0.57.3)7.8-+=-;(3)(3)原式=111(21)13412--=-;(4)原式=7.27.2 3.80 3.8 3.8--=-=-【变式2】计算:11511236⎛⎫-++- ⎪⎝⎭1151151151111(11)1236236236⎡⎤⎛⎫⎛⎫⎛⎫-++-=--++-=-++-++-=-⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦【变式3】计算:11(6)(3.3)(3)(6)(0.3)(8)(6)(16)644⎛⎫⎛⎫++++-+++-+++++++-+-⎪ ⎪⎝⎭⎝⎭解法一:11(6)(3.3)(3)(6)(0.3)(8)(6)(16)644⎛⎫⎛⎫++++-+++-+++++++-+-⎪ ⎪⎝⎭⎝⎭11(6)(3)(0.3)(8)(6)(3.3)(6)(16)644⎡⎤⎡⎤⎛⎫⎛⎫=++++++++++++-+-+-+-⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦→同号的数一起先加(23.55)(31.55)8=++-=-.本题考查了有理数的加法,拆项法是解题关键.解法二:11(6)(3.3)(3)(6)(0.3)(8)(6)(16)644⎛⎫⎛⎫++++-+++-+++++++-+- ⎪ ⎪⎝⎭⎝⎭11(6)6[(3.3)(3)(0.3)][(6)(6)][(16)(8)]44⎡⎤⎛⎫⎛⎫=++++-+-+++++-+++-++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦→同分母,互为相反数的数,或几个数可以凑整的数分别结合相加000(8)8=+++-=-.类型二、有理数的减法运算.(1)2-(-3);(2)0-(-3.72)-(+2.72)-(-4);(3)41373⎛⎫+- ⎪⎝⎭.此题是有理数的减法运算,先按照减法法则将减法转化为加法,再按照有理数的加法进行计算.本题可直接利用有理数的减法法则进行计算.(1)2-(-3)=2+3=5(2)原式=0+3.72+(-2.72)+4=(0+4)+(3.72-2.72)=4+1=5(3)原式=411416(3)(3)2733721+-=--=-类型三、有理数的加减混合运算.计算:(1)-3.72-1.23+4.18-2.93-1.25+3.72;(2)11-12+13-15+16-18+17;(3)1113.76395684.7621362--+--+(4)51133.464 3.872 1.54 3.376344+---+++(5)1355354624618-++-;(6)132.2532 1.87584+-+(1)观察各个加数,可以发现-3.72与3.72互为相反数,把它们分为一组;4.18、-2.93与-1.25的和为0,把它们分为一组可使计算简便.解:-3.72-1.23+4.18-2.93-1.25+3.72=(-3.72+3.72)+(4.18-2.93-1.25)-1.23=0+0-1.23=-1.23(2)把正数和负数分别分为一组.解:11-12+13-15+16-18+17=(11+13+16+17)+(-12-15-18)=57+(-45)=12(3)仔细观察各个加数,可以发现两个小数的和是-1,两个整数的和是29,三个分数通分后也不难算.故把整数、分数、小数分别分为一组.解:1113.7639568 4.7621362--+--+111(3.76 4.76)(521)(3968)362=-+--++-+1(6)2922=-+-+=(4)3.46和1.54的和为整数,把它们分为一组;-3.87与3.37的和为-0.5,把它们分为一组;546与13-易于通分,把它们分为一组;124-与34同分母,把它们分为一组.算式中的“+”或“-”既可以看作运算符号按法则进行计算,也可以看作是性质符号按多重符号化简进行计算.解:51133.464 3.872 1.54 3.376344+---+++5113(3.46 1.54)(3.873.37)(4)(2)6344=++-++-+-+115(0.5)4(1) 4.537.522=+-++-=+=(5)先把整数分离后再分组.解:1355354624618-++-1355354624618=--++++--1355(3546)()24618=-++-+-++-1827301036-++-=+2936=注:带分数中的整数与分数分离时,如果这个数是负数,那么分离得到的整数与分数都是负数,例如113322-=--.(6)如果按小数、整数分组,效果似乎不是很好.可先将小数和分数统一后再考虑分组.解:132.2532 1.87584+-+(2.25 2.75)(3.125 1.875)=-++0.55 4.5=-+=【变式】5.6+[0.9+4.4﹣(﹣8.1)].解:原式=5.6+0.9+4.4+8.1=19.类型四、有理数的加减混合运算在实际中的应用.“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话.(1)现有1,2,3,4,5,6,7,8,9共九个数字,请将它们分别填入图1的九个方格中,使得第行的三个数、每列的三个数、斜对角的三个数之和都等于15;(2)通过研究问题(1),利用你发现的规律,将3,5,﹣7,1,7,﹣3,9,﹣5,﹣1这九个数字分别填入图2的九个方格中,使得横、竖、斜对角的所有三个数的和都相等.解:(1)15÷3=5,∴最中间的数是5,其它空格填写如图1;(2)如图2所示.计算多个有理数相加时,必须先审题,分析特点,寻找规律,然后再去计算.注意在交换加数的位置时,要连同符号一起交换.本题考查了有理数加法,熟知“九宫图”的填法是解题的关键.【变式】某产粮专业户出售粮食8袋,每袋重量(单位:千克)如下:197,202,197,203,200,196,201,198.计算出售的粮食总共多少千克?法一:以200(千克)为基准,超过的千克数记作正数,不足的千克数记作负数,则这8个数的差的累计是:(-3)+(+2)+(-3)+(+3)+0+(-4)+(+1)+(-2)=-6200×8+(-6)=1594(千克)答:出售的粮食共1594千克.法二:197+202+197+203+200+196+201+198=1594(千克)答:出售的粮食共1594千克.【巩固练习】一、选择题1.某地一天的最高气温是12℃,最低气温是2℃,则该地这天的温差是()A﹣10℃B.10℃C.14℃D.﹣14℃2.比﹣1小2015的数是()A.﹣2014B.2016C.﹣2016D.20143.如果三个数的和为零,那么这三个数一定是().A.两个正数,一个负数B.两个负数,一个正数C.三个都是零D.其中两个数之和等于第三个数的相反数4.若0,0a b ><,a b <,则a 与b 的和是()A.B.C. D..5.下列判断正确的是()A.两数之差一定小于被减数.B.若两数的差为正数,则两数都为正数.C.零减去一个数仍得这个数.D.一个数减去一个负数,差一定大于被减数.6.某粮店出售的三种品牌的面粉袋上,分别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg 的字样,从中任意拿出两袋,它们的质量最多相差()A.0.8kg B.0.6kg C.0.5kg D.0.4kg 二、填空题7.有理数,,a b c 在数轴上对应点位置如图所示,用“>”或“<”填空:(1)|a |______|b |;(2)(2)a +b +c ______0:(3)a -b +c ______0;(4)a +c ______b ;(5)c -b ______a .8.小明存折中原有450元,取出260元,又存入150元,现在存折中还有______元.9.若a ,b 为整数,且|a-2|+|a -b|=1,则a+b=________.10.某地的冬天,半夜的温度是-5︒C,早晨的温度是-1︒C,中午的温度是4︒C.则(1)早晨的温度比半夜的温度高________度;(2)早晨的温度比中午的温度低________度.11.北京与纽约的时差为-13(负号表示同一时刻纽约时间比北京时间晚).如果现在是北京时间15:00,那么纽约时间是______________12.数学活动课上,王老师给同学们出了一道题:规定一种新运算“☆”对于任意两个有理数a和b,有a☆b=a-b+1,请你根据新运算,计算(2☆3)☆2的值是.三、解答题13.计算题(1)3401(1)(5)|4|77⎡⎤⎛⎫⎛⎫+-----+--+-⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦;(2)2121 02133434⎛⎫⎛⎫⎛⎫-++---+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(3)44444 999999999999999 55555 ++++(4)1+(-2)+(-3)+4+5+(-6)+(-7)+8+…+97+(-98)+(-99)+100的值.(5)11111 8244880120 ++++;(6)2312()() 3255 ---+--+-14.数轴上到原点的距离小于3的整数的个数为x,不大于3的正整数的个数为y,绝对值等于3的整数的个数为z,求:x+y+z的值.15.股民李星星在上周星期五以每股11.2元买了一批股票,下表为本周星期一到星期五该股票的涨跌情况求:(1)本周星期三收盘时,每股的钱数.(2)李星星本周内哪一天把股票抛出比较合算,为什么?【答案与解析】一、选择题1.【答案】B.2.【答案】C【解析】解:根据题意得:﹣1﹣2015=﹣2016,故选C.3.【答案】D【解析】若0a b c++=,则a b c+=-或b c a+=-或a c c+=-,所以D正确.4.【答案】D【解析】(a b+)的符号与绝对值较大的b一致为负的,并用较大的绝对值减去较小的绝对值,即有()b a--.5.【答案】D【解析】A错误,反例:2-(-3)=5,而5>2;B不对,反例:2-(-3)=5,而-3为负数;C错误,0-2=-2,0-(-2)=2,所以零减去一个数得这个数的相反数.6.【答案】B【解析】因为最低重量为24.7kg,最大重量为25.3kg,故质量最多相差25.3-24.7=0.6kg.星期一二三四五每股涨跌/元+0.4+0.45﹣0.2+0.25﹣0.4二、填空题7.【答案】<,<,>,>,>【解析】由图可知:b a c >>,且0,0b a c <<>,再根据有理数的加法法则可得答案.8.【答案】340【解析】450﹣260+150=290+150=340(元).9.【答案】2,6,3或5【解析】当|a-2|=1,|a -b|=0时,得:a+b=6或2;当|a-2|=0,|a -b|=1时,得:a+b=3或5;10.【答案】(1)4(2)5【解析】(1)-1-(-5)=4(2)-1-(+4)=-511.【答案】2:00【解析】15:00+(-13)=2:00.12.【答案】-1【解析】(2☆3)☆2=(2☆3)-2+1=2-3+1-2+1=-1三、解答题13.【解析】(1)原式341[15]45(5)1077=--+-++=--=(2)原式212102133434⎛⎫⎛⎫⎛⎫=-+++++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭21212133434=-++-2211213213183344⎛⎫⎛⎫=-++-=-+=- ⎪ ⎪⎝⎭⎝⎭(3)原式=1111101001000100005555⎡⎤⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+-++-++-++- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦⎣⎦11000005⎡⎤⎛⎫++- ⎪⎢⎥⎝⎭⎣⎦11111(10100100010000100000)55555⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++++-+-+-+-+- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦111110(1)111109=+-=.(4)1+(-2)+(-3)+4+5+(-6)+(-7)+8+…+97+(-98)+(-99)+100=[1+(-2)+(-3)+4]+[5+(-6)+(-7)+8]+…+[97+(-98)+(-99)+100]=0+0++…+0=0.(5)111111111182448801202446688101012++++=++++⨯⨯⨯⨯⨯111111*********()()22446688101012221224=-+-+-+-+-=-=(6)原式23122312231283[()][()]32553255325530=------=--------=----=-14.【解析】解:根据数轴,到原点的距离小于3的整数为0,±1,±2,即x=5,不大于3的正整数为1,2,3,即y=3,绝对值等于3的整数为3,﹣3,即z=2,所以x+y+z=10.15.【解析】解:(1)根据题意得:11.2+0.4+0.45+(﹣0.2)=11.85(元),则本周星期三收盘时,该只股票每股为11.85元;(2)根据题意得:11.2+0.4+0.45+(﹣0.2)+0.25=12.1(元),则本周该只股票最高价12.1元出现在周四,李星星本周四把股票抛出比较好.。
人教版初中数学知识点总结【完整版】

人教版初中数学知识点全总结第一章有理数1、有理数:无限不循环小数和开根开不尽的数叫无理数;整数和分数统称有理数.注意:0 即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;有理数: 零、负整数、负分数、正分数、正整数2、数轴是规定了原点、正方向、单位长度的一条直线.3、相反数: (1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0 的相反数还是 0;(2)相反数的和为 0 a+b=0 a、b 互为相反数.4、绝对值:绝对值和我们学过的加、减、乘、除一样,是一种运算,运算符号通常用||表示。
这种运算的意义是:一个正数和0的绝对值是它本身,一个负数的绝对值是它的相反数。
总之,一个数的绝对值是非负数。
用代数式表示为:|a|=a(a>0) |a|=-a(a<0) |a|=0(a=0)在数轴上,一个数的绝对值表示为代表这个数的点到原点的距离。
如:|-5|表示在数轴上代表-5 的点与原点的距离,即|-5|=5。
5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比 0 大,负数永远比 0 小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数> 0,小数-大数< 0.6.互为倒数:乘积为 1 的两个数互为倒数;注意:0 没有倒数;若 a≠0,那么 a 的倒数是1 ;若 ab=1 a、 ab 互为倒数;若ab=-1 a、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与 0 相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b)+c=a+(b+c).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即 a-b=a+(-b).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba;(2)乘法的结合律:(ab)c=a(bc);(3)乘法的分配律:a(b+c)=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,即无意义 .13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当 n 为正奇数时: (-a)n=-an 或(a -b)n=-(b-a)n , 当 n 为正偶数时: (-a)n =an 或 (a-b)n=(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:这是一种记数的方法。
七年级有理数的知识点概念

七年级有理数的知识点概念有理数在我们的生活中无处不在,正负号、分数、小数等等都属于有理数范畴。
在初中数学中,有理数的学习是十分重要的一环,从基础概念到实际运用,都需要对有理数有深刻的认识。
一、有理数的定义和表示有理数是整数和分数的集合,可以用分数表示,也可以用十进制小数表达,具体的表示方式有下面两种:1. 分数表示方式:用两个整数(其中分母不能为零)表示一个有理数,形如 $\frac{a}{b}$ ($ a,b \in \mathrm{Z},b\neq 0$)。
2. 小数表示方式:完全体现出有理数的大小和正负性,小数点左边是整数,右边是一个有限或无限循环小数。
二、有理数的比较有理数的大小比较可以根据小数的大小比较,也可以将其化为同分母的分数后比较分子的大小,方法如下:1. 分数比较法:将两个有理数化做相等分母后,比较两个分数的分子大小,分数越大,所代表的有理数就越大。
2. 小数比较法:将两个有理数化为小数后,比较小数的大小即可。
三、有理数的加减法1. 两个有理数同号相加,绝对值求和,符号不变。
2. 两个有理数异号相加,绝对值取差,符号取大数的符号。
3. 有理数的加减可以转化为同加、同减,例如 $a + b - c = a - c + b$。
四、有理数的乘除法1. 两个有理数同号,积为正;异号,积为负。
2. 有理数的乘除可以转化为同乘、同除,例如 $\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}$。
3. 有理数的乘方,负次方为分母次幂,正次方为分子次幂,例如 $a^{-2} = \frac{1}{a^2}$。
五、有理数的绝对值有理数的绝对值是一个非负的有理数,表示有理数到零点的距离,正负号不起作用。
六、有理数的倒数有理数的倒数是这个数与 $1$ 的商的倒数,即 $\frac{a}{b}$ 的倒数是 $\frac{b}{a}$。
人教版初中数学知识点全总结(完美打印版)

七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容。
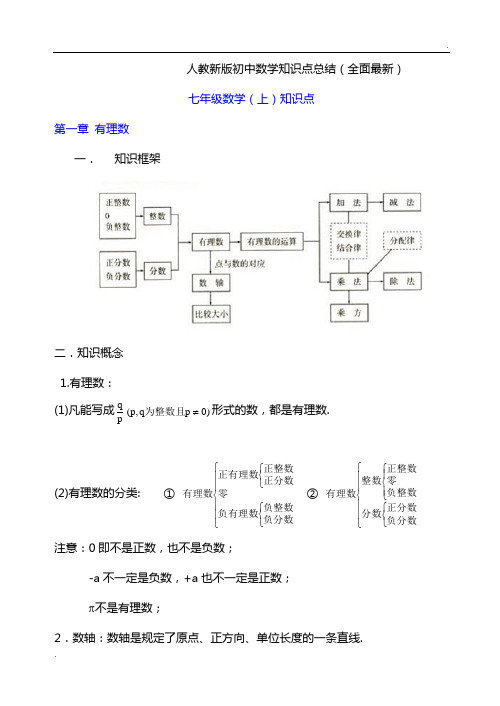
第一章 有理数一、知识框架二.知识概念1。
有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;—a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5。
有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数—小数 > 0,小数—大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔ a 、b 互为倒数;若ab=—1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数。
人教最新版初中数学知识点总结(全面)
人教新版初中数学知识点总结(全面最新)七年级数学(上)知识点第一章有理数一.知识框架二.知识概念1.有理数:(1)凡能写成)0pq,p(pq≠为整数且形式的数,都是有理数.(2)有理数的分类: ①⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数②⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数注意:0即不是正数,也不是负数;-a不一定是负数,+a也不一定是正数;π不是有理数;2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,互为相反数,即a 和- a 互为相反数; 0的相反数还是0; (2) a+b=0 ⇔ a 、b 互为相反数. 4.绝对值:(1)绝对值的意义是数轴上表示某数的点离开原点的距离;(2) ⎪⎩⎪⎨⎧<-=>=)0()0(0)0(a a a a a a 或⎩⎨⎧<-≥=)0a (a )0a (a a 或⎩⎨⎧≤->=)0()0(a a a a a ; 正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数; 绝对值的问题经常分类讨论,零既可以和正数一组也可以和负数一组; 5.有理数比大小:两个负数比大小,绝对值大的反而小; 数轴上的两个数,右边的数总比左边的数大; 大数-小数 > 0,小数-大数 < 0. 6.倒数:乘积为1的两个数互为倒数; 注意:0没有倒数;若 a ≠0,那么a 的倒数是a1; 若ab=1⇔ a 、b 互为倒数; 若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b)+c=a+(b+c).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定,负因数为奇数个时乘积为负,负因数为偶数个时乘积为正.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba;(2)乘法的结合律:(ab)c=a(bc);(3)乘法的分配律:a(b+c)=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;a.注意:零不能做除数,无意义即13.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;14.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n为正奇数时: (-a)n=-a n或(a -b)n=-(b-a)n, 当n为正偶数时: (-a)n =a n 或(a-b)n=(b-a)n .15.科学记数法:把一个大于10的数记成a×10n的形式,(其中1≤a<10)这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.第二章整式的加减一.知识框架二.知识概念1.单项式:数字或字母的乘积叫单项式.2.单项式的系数与次数:单项式中不为零的数字因数,叫单项式的系数;单项式中所有字母指数的和,叫单项式的次数.3.多项式:几个单项式的和叫多项式.4.多项式的项数与次数:多项式中所含单项式的个数就是多项式的项数,每个单项式叫多项式的项;多项式里,次数最高项的次数叫多项式的次数。
初中数学知识点全总结(齐全)
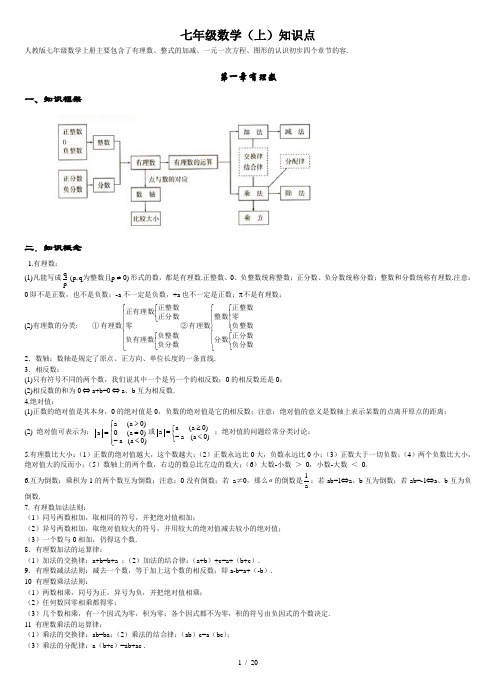
七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的容.第一章 有理数一、知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (p q≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数; (2)有理数的分类: ①⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数②⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数. 4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离; (2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (aa ;绝对值的问题经常分类讨论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0. 6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔a 、b 互为倒数;若ab=-1⇔a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值; (3)一个数与0相加,仍得这个数. 8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ). 9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘; (2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定. 11 有理数乘法的运算律: (1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc ); (3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a .13.有理数乘方的法则:(1)正数的任何次幂都是正数; (2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n . 14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法. 16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字. 18.混合运算法则:先乘方,后乘除,最后加减.本章容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
初中数学有理数知识点总结
0 既不是正数,也不是负数。
最小的正整数是 1,最大的负整数是-1。
(2)正数和负数表示相反意义的量。
5、利用肯定值比较大小
2、有理数的概念及分类
两个正数比较:肯定值大的那个数大;
3、有关数轴
两个负数比较:先算出它们的肯定值,肯定值大的反而小。
(1)数轴的三要素:原点、正方向、单位长度。数轴是一条直线。
第一步:确定积的符号 第二步:肯定值相乘 10、乘积的符号确实定 几个有理数相乘,因数都不为 0 时,积的符号由负因数的个数确 定:当负因数有奇数个时,积为负; 当负因数有偶数个时,积为正。几个有理数相乘,有一个因数为零, 积就为零。 11、倒数:乘积为 1 的两个数互为倒数,0 没有倒数。 正数的倒数是正数,负数的倒数是负数。(互为倒数的两个数符号 肯定相同) 倒数是本身的只有 1 和-1。
魏
第2页共2页
肯定值较大的加数的符号相同,和的肯定值等于加数中较大的肯定值
(2)相反数:符号不同、肯定值相等的两个数互为相反数。
魏
第1页共2页
本文格式为 Word 版,下载可任意编辑
减去较小的肯定值;当两个加数肯定值相等时,两个加数互为相反数, 和为零.
(3)一个数同零相加,仍得这个数. 加法的交换律:a+b=b+a 加法的结合律:(a+b)+c=a+(b+c) 7、有理数减法:减去一个数,等于加上这个数的相反数。 8、在把有理数加减混合运算统一为最简的形式,负数前面的加号 可以省略不写. 例 如 : 14+12+(-25)+(-17) 可 以 写 成 省 略 括 号 的 形 式 : 14+12 -25-17,可以读作“正 14 加 12 减 25 减 17”,也可以读作“正 14、正 12、负 25、负 17 的和.” 9、有理数的乘法 两个数相乘,同号得正,异号得负,再把肯定值相乘;任何数与 0 相乘都得 0。
初中数学知识点全总结
- 1 - 数学知识点 第一章 有理数 一、知识框架
二.知识概念 1.有理数: (1)凡能写成)0pq,p(pq为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a不一定是负数,+a也不一定是正数;不是有理数;
(2)有理数的分类: ① 负分数负整数负有理数零正分数正整数正有理数有理数 ② 负分数正分数分数负整数零正整数整数有理数 2.数轴:数轴是规定了原点、正方向、单位长度的一条直线. 3.相反数: (1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)相反数的和为0 a+b=0 a、b互为相反数. 4.绝对值: (1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;
(2) 绝对值可表示为:)0a(a)0a(0)0a(aa或)0a(a)0a(aa ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.
6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a≠0,那么a的倒数是a1;若ab=1 a、b互为倒数;若ab=-1 a、b互为负倒数. - 2 -
7. 有理数加法法则: (1)同号两数相加,取相同的符号,并把绝对值相加; (2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值; (3)一个数与0相加,仍得这个数. 8.有理数加法的运算律: (1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b)+c=a+(b+c). 9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b). 10 有理数乘法法则: (1)两数相乘,同号为正,异号为负,并把绝对值相乘; (2)任何数同零相乘都得零; (3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定. 11 有理数乘法的运算律: (1)乘法的交换律:ab=ba;(2)乘法的结合律:(ab)c=a(bc); (3)乘法的分配律:a(b+c)=ab+ac .
精华—初中数学知识点总结(人教版)
精华—初中数学知识点总结(人教版)人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章有理数一.知识框架二.知识概念1.有理数:(1)凡能写成形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a不一定是负数,+a也不一定是正数;不是有理数;(2)有理数的分类: ① ②2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 a+b=0 a、b互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点分开原点的间隔;(2) 绝对值可表示为:或;绝对值的问题经常分类讨论;5.有理数比大小:〔1〕正数的绝对值越大,这个数越大;〔2〕正数永远比0大,负数永远比0小;〔3〕正数大于一切负数;〔4〕两个负数比大小,绝对值大的反而小;〔5〕数轴上的两个数,右边的数总比左边的数大;〔6〕大数-小数> 0,小数-大数< 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;假设a≠0,那么的倒数是;假设ab=1 a、b互为倒数;假设ab=-1 a、b互为负倒数.7. 有理数加法法那么:〔1〕同号两数相加,取一样的符号,并把绝对值相加;〔2〕异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;〔3〕一个数与0相加,仍得这个数.8.有理数加法的运算律:〔1〕加法的交换律:a+b=b+a ;〔2〕加法的结合律:〔a+b〕+c=a+〔b+c〕.9.有理数减法法那么:减去一个数,等于加上这个数的相反数;即a-b=a+〔-b〕.10 有理数乘法法那么:〔1〕两数相乘,同号为正,异号为负,并把绝对值相乘;〔2〕任何数同零相乘都得零;〔3〕几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:〔1〕乘法的交换律:ab=ba;〔2〕乘法的结合律:〔ab〕c=a〔bc〕;〔3〕乘法的分配律:a〔b+c〕=ab+ac .12.有理数除法法那么:除以一个数等于乘以这个数的倒数;注意:零不能做除数,.13.有理数乘方的法那么:〔1〕正数的任何次幂都是正数;〔2〕负数的奇次幂是负数;负数的偶次幂是正数;注意:当n为正奇数时: (-a)n=-an或(a -b)n=-(b-a)n , 当n 为正偶数时: (-a)n =an 或 (a-b)n=(b-a)n .14.乘方的定义:〔1〕求一样因式积的运算,叫做乘方;〔2〕乘方中,一样的因式叫做底数,一样因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的准确位:一个近似数,四舍五入到那一位,就说这个近似数的准确到那一位.17.有效数字:从左边第一个不为零的数字起,到准确的位数止,所有数字,都叫这个近似数的有效数字.请判断以下题的对错,并解释.1.近似数25.0的准确度与近似数25一样.2.近似数4千万与近似数4000万的准确度一样.3.近似数660万,它准确到万位.有三个有效数字.4.用四舍五入法得近似数6.40和6.4是相等的.5.近似数3.7x102与近似数370的准确度一样.1、错。
初中数学知识点大全(完整版)
第一册第一章有理数1.1正数和负数以前学过的0以外的数前面加上负号“一”的书叫做负数以前学过的0以外的数叫做正数。
数0既不是正数也不是负数,0是正数与负数的分界。
在同一个问题中,分别用正数和负数表示的量具有相反的意义1.2有理数1.2.1有理数正整数、0、负整数统称整数,正分数和负分数统称分数。
整数和分数统称有理数。
1.2.2数轴规定了原点、正方向、单位长度的直线叫做数轴。
数轴的作用:所有的有理数都可以用数轴上的点来表达。
注意事项:⑴数轴的原点、正方向、单位长度三要素,缺一不可⑵同一根数轴,单位长度不能改变。
一般地,设是一个正数,则数轴上表示a的点在原点的右边,是a个单位长度;表示数-a的点在原点的左边,与原点的距离是 1.2.3相反数只有符号不同的两个数叫做互为相反数。
数轴上表示相反数的两个点关于原点对称。
与原点的距离a个单位长度。
在任意一个数前面添上号,新的数就表示原数的相反数。
124绝对值一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值。
一个正数的绝对值是它的本身;一个负数的绝对值是它的相反数;0的绝对值是0。
在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数。
比较有理数的大小:⑴正数大于0,0大于负数,正数大于负数。
⑵两个负数,绝对值大的反而小。
1.3有理数的加减法1.3.1有理数的加法有理数的加法法则:⑴同号两数相加,取相同的符号,并把绝对值相加。
⑵绝对值不相等的饿异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0。
⑶一个数同0相加,仍得这个数。
两个数相加,交换加数的位置,和不变。
加法交换律:a + b = b + a三个数相加,先把前面两个数相加,或者先把后两个数相加,和不变。
加法结合律:(a + b) + c= a+ (b + c)1.3.2有理数的减法有理数的减法可以转化为加法来进行有理数减法法则:减去一个数,等于加这个数的相反数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有理数的意义要点一、正数与负数像+3、+1.5、、+584等大于0的数,叫做正数;像-3、-1.5、、-584等在正数前面加“-”号的数,叫做负数.(1)一个数前面的“+”“-”是这个数的性质符号,“+”常省略,但“-”不能省略.(2)用正数和负数表示具有相反意义的量时,哪种为正可任意选择,但习惯把“前进、上升”等规定为正,而把“后退、下降”等规定为负.(3)0既不是正数也不是负数,它是正数和负数的分界线.要点二、有理数的分类(1)按整数、分数的关系分类:(2)按正数、负数与0的关系分类:(1)有理数都可以写成分数的形式,整数也可以看作是分母为1的数.(2)分数与有限小数、无限循环小数可以互化,所以有限小数和无限循环小数可看作分数,但无限不循环小数不是分数,例如.(3)正数和零统称为非负数;负数和零统称为非正数;正整数、0、负整数统称整数.类型一、正数与负数:中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么﹣80元表示()A.支出20元 B.收入20元C.支出80元 D.收入80元在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.C解:根据题意,收入100元记作+100元,则﹣80表示支出80元.故选:C.12+12-π1.掌握用正负数表示实际问题中具有相反意义的量;2.理解正数、负数、有理数的概念;3. 掌握有理数的分类方法,初步建立分类讨论的思想.【变式1】一种大米的质量标识为“(50±0.5)千克”, 则下列各袋大米中质量不合格的是( )A .50.0千克B .50.3千克C .49.7千克D .49.1千克D .解:“50±0.5千克”表示最多为50.5千克,最少为49.5千克.【变式2】(1)如果收入300元记作+300元,那么支出500元用___________ 表示,0元表示__________ .(2)若购进50本书,用-50本表示,则盈利30元如何表示?(1) -500元;既没有收入也没有支出. (2) 不是一对具有相反意义的量,不能表示.【变式3】如果60m 表示“向北走60m ”,那么“向南走40m ”可以表示为( ).A .-20mB .-40mC .20mD .40mB: 体育课上,华英学校对九年级男生进行了引体向上测试,以能做7个为标准,超过的次数记为正数,不足的次数记为负数,其中8名男生成绩如下:2,-1,0,3,-2,-3,1,0 (1) 这8名男生有百分之几达到标准? (2) 他们共做了多少引体向上?(1)由题意可知:正数或0表示达标,而正数或0的个数共有5个,所以百分率为:;答:这8名男生有62.5%达到标准.(2)(7+2)+(7-1)+7+(7+3)+(7-2)+(7-3)+(7+1)+7=56(个) 答:他们共做了引体向上56个.类型二、有理数的分类: 下面说法中正确的是( ). A . 非负数一定是正数.B . 有最小的正整数,有最小的正有理数.C .一定是负数.D .正整数和正分数统称正有理数.D5100%62.5%8⨯=a -本题考查了正数和负数,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量一定要先弄清“基准”是什么.(A) 不对,因为非负数还包括0;(B) 最小的正整数为1,但没有最小的正有理数;(C)不对,当为负数或0时,则为正数或0,而不是负数;(D)对【变式1】 判断题:(1)0是自然数,也是偶数.( ) (2)0既可以看作是正数,也可以看成是负数.( ) (3)整数又叫自然数.( ) (4)非负数就是正数,非正数就是负数.( )√, ,,【变式2】下列四种说法,正确的是( ). (A)所有的正数都是整数 (B)不是正数的数一定是负数(C)正有理数包括整数和分数 (D)0不是最小的有理数D: 请把下列各数填入它所属于的集合的大括号里.1, 0.0708, -700, -3.88, 0, 3.14159265, , . 正整数集合:{ …},负整数集合:{ …},整数集合: { …},正分数集合:{ …}, 负分数集合:{ …}, 分数集合: { …}, 非负数集合:{ …}, 非正数集合:{ …}.正整数: 1;负整数:-700;整数:1,0,-700;正分数:0.0708,3.14159265,;负分数: -3.88,;分数:0.0708,3.14159265,,-3.88,;非负数: 1,0.0708, 3.14159265,0,;非正数:-700, -3.88, 0,a a -⨯⨯⨯723-723-723-723-一个有理数既有性质符号,又有除性质符号外的数值部分,两者合在一起才表示这个有理数.填数的方法有两种:一种是逐个考察,一一进行填写;二是逐个填写相关的集合,从给出的数中找出属于这个集合的数.此外注意几个概念:非负数包括0和正数;非正数包括0和负数.【变式】在有理数、﹣5、3.14中,属于分数的个数共有个.2.类型三、探索规律: 某校生物教师李老师在生物实验室做实验时,将水稻种子分组进行发芽试验:第1组取3粒,第2组取5粒,第3组取7粒,第4组取9粒,.按此规律,那么请你推测第n组应该有种子是粒.()第1组取3粒,第2组取5粒,第3组取7粒,第4组取9粒,,由此我们观察到的粒数与组数之间有一定关系:,,,,,按此规律,第n组应该有种子数()粒.【变式1】有一组数列:2,-3,2,-3,2,-3,,根据这个规律,那么第2010个数是:-3【变式2】观察下列有规律的数:根据其规律可知第9个数是:12+n1123+⨯=1225+⨯=1327+⨯=1429+⨯=12+n,,301,201,121,61,21901研究一列数的排列规律时,其中的数与符号往往都与序数有关.【巩固练习】一、选择题1. 下列语句正确的()个(1)带“﹣”号的数是负数;(2)如果a为正数,则﹣a一定是负数;(3)不存在既不是正数又不是负数的数;(4)0℃表示没有温度.A. 0B. 1C. 2D. 32.关于数“0”,以下各种说法中,错误的是 ( ) A.0是整数 B.0是偶数C.0是正整数 D.0既不是正数也不是负数3.如果规定前进、收入、盈利、公元后为正,那么下列各语句中错误的是 ( )A.前进-18米的意义是后退18米B.收入-4万元的意义是减少4万元C.盈利的相反意义是亏损D.公元-300年的意义是公元后300年4.一辆汽车从甲站出发向东行驶50千米,然后再向西行驶20千米,此时汽车的位置是 ( ) A.甲站的东边70千米处B.甲站的西边20千米处C.甲站的东边30千米处C.甲站的西边30千米处5.在有理数中,下面说法正确的是()A.身高增长和体重减轻是一对具有相反意义的量B.有最大的数C.没有最小的数,也没有最大的数D.以上答案都不对6.下列各数是正整数的是()A.-1 B.2 C.0.5 D. 2二、填空题1.如果用+4米表示高出海平面4米,那么低于海平面5米可记作.2.在数中,非负数是______________;非正数是__________.3.把公元2008年记作+2008,那么-2008年表示 .4.既不是正数,也不是负数的有理数是 .5.如果向东行驶10米,记作+10米,那么向西行驶20米,记作__________米.6.是整数而不是正数的有理数是 .7.既不是整数,也不是正数的有理数是 .8.一种零件的长度在图纸上是()毫米,表示这种零件的标准尺寸是毫米,加工要求最大不超过毫米,最小不小于毫米.三、解答题1.说出下列语句的实际意义.(1)输出-12t (2)运进-5t (3)浪费-14元(4)上升-2m (5)向南走-7m2.下面两个圈分别表示负数集和分数集,请把下列6个数填入这两个圈中合适的位置.﹣28%,,﹣2014,3.14,﹣(+5),﹣0.cm2.1kg2.103.002.0 10+-3.随着人们的生活水平的提高,家用轿车越来越多地进入普通家庭.小明家买了一辆小轿车,他连续记录了7天中每天行驶的路程,以50km 为标准,多于50km 的记为“+”,不足50km 的记为“﹣”,刚好50km 的记为“0”,记录数据如下表:(1)请你估计小明家的小轿车一月(按30天计)要行驶多少千米?(2)若每行驶100km 需用汽油8L ,汽油每升7.14元,试求小明家一年(按12个月计)的汽油费用是多少元?4.观察下面依次排列的一列数,它的排列有什么规律?请接着写出后面的两个数,你能说出第2011个数是什么吗?(1)1,-2,3,-4,5,-6,7,-8, , ,... ,... (2)-1,,-,,,,, , ,... ,...【答案与解析】一、选择题1.【答案】B 【解析】(1)带“﹣”号的数不一定是负数,如﹣(﹣2),错误;(2)如果a 为正数,则﹣a 一定是负数,正确;(3)0既不是正数也不是负数,故不存在既不是正数又不是负数的数此表述错误;(4)0℃表示没有温度,错误. 综上,正确的有(2),共一个.2.【答案】C【解析】0既不是正数也不是负数,但0是整数,是偶数,是自然数.3. 【答案】D【解析】D 错误,公元-300年的意义应该是公元前300年.4. 【答案】 C【解析】画个图形有利于问题分析,向东50千米然后再向西20千米后显然此时汽车在甲站的东边30千米处.5.【答案】C【解析】A 错误,因为身高与体重不是具有相反意义的量;B 错误,没有最大的数也没有最小数;C 对.6. 【答案】B二、填空题1.【答案】﹣5米2.【答案】0.5,100,0,;,0,-45【解析】正数和零统称为非负数,负数和零统称为非正数,零既不是正数也不是负数.21314151-6171-112122-时间第一天第二天第四天第五天第六天第七天路程(km ) ﹣8 ﹣11 0 ﹣16 +41 +83.【答案】公元前2008年【解析】正负数表示具有相反意义的量.4.【答案】0【解析】既不是正数也不是负数的数只有零.5.【答案】-20. 【解析】解:∵向东行驶10米,记作+10米,∴向西行驶20米,记作﹣20米, 故答案为:﹣20.6.【答案】负整数和0【解析】整数包括正整数和负整数,又因为不是正数,所以只能是负整数和0.7.【答案】负分数【解析】不是整数,则只能是分数,又不是正数,所以只能是负分数.8.【答案】10,,【解析】表示的数的范围为:大于,而小于,即大于而小于. 三、解答题 1. 【解析】(1)输出-12t 表示输入12t ; (2)运进-5t 表示运出5t ; (3)浪费-14元表示节约14元; (4)上升-2m 表示下降2m ;(5)向南走-7m 表示向北走7m. 提示:“-”表示相反意义的量.2.【解析】3.【解析】解:(1)=50,50×30=1500(km ).答:小明家的小轿车一月要行驶1500千米; (2)×8×7.14×12=10281.6(元),答:小明家一年的汽油费用是10281.6元.4.【解析】(1)9,-10,…,2011,…(2)10.039.9803.002.010+--(100.02)(10+0.03)9.9810.03111,,...,, (892011)--。
