基于核主成分分析(KPCA)的一种食品评价模型
基于核主成分分析和深度置信网络的暂态稳定评估

基于核主成分分析和深度置信网络的暂态稳定评估#唐文权,徐武,文聪,郭兴(云南民族大学电气信息工程学院,云南昆明650500)摘要:针对电力系统暂态稳定评估实时性较差以及错误率较高的问题,提岀了一种核主成分分析结合深度置信网络的暂态稳定评估方法。
首先,构造了一组电力系统暂态稳定的特征向量;然后,基核主成分分析法对向行提取,向以及余,将的向量传输至深度置信网络;最后,进行训练分析,训程包括预训练和微调,优化网络,提深度置信网络评估精度。
1039系统结 ,该方法可以输的,余,暂态稳定性评估的错误率时间,、电力系统的稳态状态。
关键词:电力系统暂态稳定评估;核主成分分析;特征降维;深度置信网络中图分类号:TM712文献标志码:A文章编号:1673-6540(2021)01-0046-07doi:10.12177/emca.2020.1%5Transient Stability Assessment Based on Kernel Principal ComponentAnalysis and Deep BelieS Network*TANG Wenquan+XU%)WEN Cong,GUO Xing(School of Electrical and Information Technology,Yunnan Minzu University,Kunming650500,China)Abstract:Aiming ai the problems of poos real-time performance and high eiros rate of powcs system transieni stability assessment,a method of transient stability assessment based on kerneC principa-component analysit combined with deep belief network is proposed.Firstly,a set of eigenvectoio reflecting the transient stabOity of power system is constructed.Secondly,the feature vector set is extracted based on kernel principa-component analysis,and the dimensionlity of featura vector is reduced and the redundant features ara filtered.The reduced eicenvectors ara transmitted1w the deep belief network.Finally,training analysis is corried out.The training process includes pretraining and fine tuning t optimize network parameters,and then the evaluation accuacy of deep confidencc network is irnpaved.The sirnulation resultr of NewEngland10-machine39-bus system showthat the method can afective-y aeducethedimenKionayit,oeinputdata,aemoveaedundanteeatuaeK,aeducetheeaoaaateand teKttimeoetaanKient stability assessment,as well as accurate-y and quicky judge the steady state of power system.Key words:power system transiee:stability assessment;kernel principal componeet analysis;featrrr dimensionality reeuction;deep belief network引去复杂性,准确、快速评估电力系统暂态稳定愈发困⑴。
【国家自然科学基金】_核主成分分析(kpca)_基金支持热词逐年推荐_【万方软件创新助手】_20140801
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
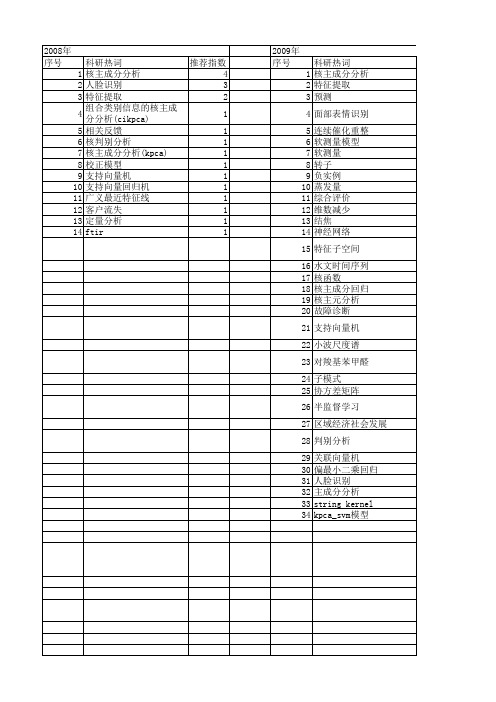
科研热词 推荐指数 核主成分分析 4 人脸识别 3 特征提取 2 组合类别信息的核主成分分析(cikpca) 1 相关反馈 1 核判别分析 1 核主成分分析(kpca) 1 校正模型 1 支持向量机 1 支持向量回归机 1 广义最近特征线 1 客户流失 1 定量分析 1 ftir 1
推荐指数 6 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
Байду номын сангаас
53 kpca 54 ifkpca
1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
高校人文社会学科科研实力综合评价研究——基于核主成分分析和实证研究法

高校人文社会学科科研实力综合评价研究——基于核主成分分析和实证研究法沈一岚;王志刚【摘要】In this paper,the comprehensive strength of scientific research was evaluated by the kernel principal component analysis and empirical research,collecting relevant data of humanities and social sciences in some colleges and universities in 31 provinces and autonomous regions in 2013.Kernel principal component analysis (KPCA) was used to explore the nonlinear relationship of data and increase the contribution rate of the first principal component,aiming at the problems of weight determination and information extraction in PCA.By adopting the idea of "subjective" transformation,this paper put forward the viewpoint of increasing importance right and constructs the empirical research model.The comprehensive analysis model of kernel principal component analysis and empirical research was given to comprehensively evaluate the scientific research strength of university humanities and social sciences.%收集了2013年31个省市自治区部分高校有关人文社会学科科研方面的相关数据,利用核主成分分析法和实证研究法对科研实力进行综合评价.针对主成分分析在权重系数确定和信息提取等方面存在的问题,利用核主成分分析(KPCA)探究了数据的非线性关系并提高第一主成分贡献率;采用“主观化”改造的思路,提出增加重要性权等观点,构建了实证研究模型;给出了核主成分分析与实证研究相结合的理实综合分析模型对高校人文社会学科科研实力进行综合评价.【期刊名称】《安徽师范大学学报(自然科学版)》【年(卷),期】2017(040)001【总页数】7页(P20-26)【关键词】核主成分分析;实证研究;综合评价;科研实力【作者】沈一岚;王志刚【作者单位】海南大学数学系,海南海口 570228;海南大学数学系,海南海口570228【正文语种】中文【中图分类】O212.4主成分分析是对复杂系统进行统计分析的一种有效方法,它以最小的信息丢失为前提,利用降维思想将多个变量综合成少数几个变量(即主成分),以达到简化数据,揭示变量间关系的目的,每个主成分都是原始变量的线性组合,且所含的信息互不重叠[1-2].主成分分析广泛应用于多指标的综合评价体系中,例如,陈宝等[3]通过提取政府投入、经济政策和社会政策的主成分,实证分析对政府综合效率改进构成显著性影响的因素;刘丽萍等[4]将主成分和门限方法有效结合,提出了基于主成分正交补门限方法的DCC模型;徐顽强等[5]建立了主成分分析的省域科技创新体系评价模型;王思哲[7]等将主成分应用于葡萄酒指标评价体系,对葡萄酒进行分类研究,并建立了酿酒葡萄和葡萄酒理化指标之间的关系.随着研究问题的深入,主成分分析在应用中也存在很多问题,例如,采用以方差贡献率为权重构造综合得分函数,看似可以提高信息含量(提高方差贡献率),但其实是一种错觉;在进行综合评价时,采用指标值与权重线性加权的方法来确定评价系数,忽视了指标数据与评价系数之间非线性映射的关系,有必要对传统主成分的“线性化”进行改进;主成分分析强调评价理论中的客观性,主观性任务还有待补充,权系数按性质可分为重要性权和信息量权两大类,重要性权属于主观赋权,信息量权属于客观赋权,主成分分析采用的是信息量权,未考虑重要性权,因而会影响综合评价效果.核主成分分析是处理指标数据与评价系数之间非线性关系的一种有效方法,现已引起了学者的广泛关注.例如,程砚秋等[8]探究了基于核主成分分析的生态评价模型及其应用;苏治等[9]给出了核主成分遗传算法与SVR选股模型改进方法;潘文砚[10]对2012年我国30个省(自治区、直辖市)的低碳经济进行综合评价,找出影响我国低碳经济发展水平的关键因素,对核主成分分析法不能判断关键影响因素的问题进行了补充.核主成分分析进行综合评价时存在的缺陷是未能考虑权重的重要性,得出的评价结论也有待进一步完善和深化.针对主成分分析和核主成分分析综合评价时存在的问题,本文主要目的是利用核主成分分析和实证研究法对2013年31个省市自治区部分高校有关人文社会学科科研实力进行评价研究.首先,通过收集相关数据,利用主成分分析法和核主成分分析比较研究科研综合实力,结果表明,核主成分分析(KPCA)在处理数据的非线性关系和提高第一主成分贡献率等方面明显优于主成分分析;其次,采用“主观化”改造的思路,提出增加重要性权等观点,构建了实证研究模型;最后,给出了核主成分分析与实证分析相结合的理实综合分析模型对高校人文社会学科科研实力做出了综合评价.1.1 核主成分评价基本原理主成分分析是最为经典的特征提取方法,通过对原始数据加工处理,简化问题处理的难度,起到了降维作用.但主成分分析是线性映射方法,降维后是由线性映射生成,忽略了数据之间高于二阶的相互关系,所以提取的特征并不是最优,这在一定程度上影响了主成分分析的效果.核主成分分析是线性主成分的非线性扩展算法,它采用非线性的方法提取主成分,其基本思想是通过某种隐式方式将输入空间映射到某个高维空间(又称特征空间) ,并在特征空间中实现主成分分析,其中的内积运算采用核函数来代替.假定样本空间的样本点(x1,x2,L,xN),定义非线性变换Φ:RN→F,x→X将其映射到特征空间F的样本点(Φ(x1),Φ(x2),L,Φ(xN)),假定满足中心化条件则F空间中样本协方差矩阵为其中xj的M个指标构成M维列向量,求出C的特征值(λ≥0)和非零特征向量v. Cv=λv所有v都可以表示为(Φ(x1),Φ(x2),L,Φ(xN))的线性张量,即存在系数αi(i=1,2,L,N),使得将(1)、(3)代人(2),并用Φ(xk)(k=1,2,L,N)同乘以(2)式两边,得到N个等价方程:定义N×N对称矩阵K,Kij=(Φ(xi)∘Φ(xj)),则(4)式等价于:NλKα=K2α简化为Nλα=Kα,求解可得相应的特征值和特征向量.为了确保特征向量vk(k=1,2,L,N)为单位向量,还需要对αk进行规范化则样本x在F空间的第k个向量vk上的投影为:将核函数替换内积,有:).核主成分分析与主成分分析有本质区别,前者基于样本,后者基于指标;前者的特征数目仅为输入样本的维数,而后者可提取的特征数目与输入样本数目是相等的,核主成分分析可以最大限度地抽取指标信息.利用核主成分分析处理的一般步骤为:(1)将样本点(x1,x2,L,xN)按照指标(每个xi有M个指标)写成(M×N)数据矩阵.(2)选定核函数,并利用给定的参数计算核矩阵.本文的实际应用中采用了以下两种核函数:多项式函数K(xi,xj)=(xixj+1)p和高斯径向函数|.(3)计算核矩阵的特征值λ1,λ2,L,λM和相应的特征向量v1,v2,L,vM,并将特征值按降序排列,对特征向量进行正交化,得到α1,α2,L,αM.(4)计算特征值的累积贡献率B1,B2,L,BM,根据指定的提取率p,若Bl≥p,则提取l个主成分α1,α2,L,αl.(5)综合评价函数F(x)计算综合评价得分并排序.其中ωk表示第k个主成分的贡献率.1.2 数据实验本文收集了2013年31个省市自治区部分高校有关人文社会学科科研方面的相关数据.首先采用主成分分析方法研究上述31个省份的7个主要指标,第一主成分的方差贡献率为85.625%,得到PCA评价系数与排名2.我们采用核主成分分析算法,通过对原始数据进行中心化处理,发掘其中的非线性关系,得到表1的排序结果. 运用优化方法选取参数的合适值.选取多项式核函数K(x,y)=[s(x*y)+c]d对数据评价,通过对核参数进行了适当的选取,可以最大限度地提高贡献率,例如,当s=0.05,c=0,d=5时,第一主成分的贡献率为99.979%,它的降维效果明显优于主成分分析. 利用PCA综合排名的前5位别是北京、江苏、湖北、山东和广东,后5位分别是海南、贵州、宁夏、青海和西藏;利用KPCA综合排名的前5位别是北京、江苏、湖北、广东和上海,后5位分别是海南、贵州、宁夏、青海和西藏,结果较为吻合.我们采用高斯径向函数作为核函数,对数据进行评价(见表2),通过优化选取相关参数时,第一主成份的贡献率为97.12%,不及多项式核函数,此时综合排名结果前5位分别是北京、江苏、山东、湖北、西藏,显然与实际有出入,可能是由于高斯径向函数并不能正确提取指标中的信息,但是多项式核函数局部性差,所以可以考虑使用混合核函数.核主成分分析不仅可以利用合理的核函数解决变量间的非线性关系,而且在一定程度上提高了第一主成分的贡献率,但其权重系数确定方面也存在缺陷,我们借鉴科学计量学、统计学等相关理论,运用文献资料分析法、层次分析法、比较研究法结合专家意见在计算机软件辅助计算下构建了各地区高校人文社会学科科研水平的评价指标体系.在评价人文社会学科成果方面,不能简单的把工程计量方法搬到人文社会学科领域来.为充分反映科研成果的质量,本研究突破了理论研究中仅考虑各影响因素在综合评价中所占权重的弊端,从“常规指标”——用于了解各省份高校人文社会学科科研的基本和整体情况和“附加指标”——从研究的重大标志性成果来评价其研究水平这两个方面对科研水平做综合评价,这样设置指标既兼顾数量又突出质量.根据各省份高校人文社会学科所研究的科研目标和科研实际情况,结合专家意见,从科研平台与基础条件建设和成果产出两方面考察各省份高校人文社会学科综合实力.建立指标体系(见图1).考虑到研究需要具有广泛适应性的方法,在构建科研评价指标体系确定权重时采用萨蒂教授创立的最具代表性的层次分析法(AHP法),绘出科研绩效评价的递阶层次结构图2.基于人文社会学科综合实力评价,王晓丽[11]提出了建议和完善基于CSSCI的同行专家评议制、公正内行的评价专家队伍和公正公开的评价监督机制,确保人文社会学科研究评价程序的有效性和公正性.通过Benchmarking的方法,参照国内外对科研水平的评价方式并结合专家意见,用计算机Expert Chlice对专家所写判断矩阵进行计算,并采用权重算术平均法对各专家评判结果进行修正与剔除,最终得到各指标权重(见表3、表4).下面我们将表3和表4的数据进行处理.第一步,假设一级指标有m项,二级指标有n项,三级指标有l项,则各二、三级指标的实际数据分别如下表示:二级指标:x11,x12, (x1)x21,x22,…,x2n,(这里m=2,n=3);三级指标:x221,x222.第二步,分别将研究机构三级指标数据xmnl除以标准值对应量Smnl,即指标对应于标准值的比例,通过计算fmnl完成对指标的无量纲化,再将该比值乘上指标相应的权重,可得指标xmnl对应的分值.具体如下:第三步,考虑到只有第二项二级指标有三级指标,将第二项二级指标的三级指标各项所得分值fmnl分别相加,即可得到第二项二级指标的分值I22,其余二级指标算法同第二步,详细如下:第四步,将各项二级指标所得分值相加,即为科研平台与基础条件建设分值M,后五项二级指标所得分值相加,即为基础性成果分值N.M与N相加的和乘以100即为常规指标得分f11+f12+f13=Mf21+f22+f23=NF=M+N第五步,计算附加指标得分F2.将研究机构附加指标数据y除以标准值对应量S,即指标对应于标准值得比例,通过计算f完成对指标的无量纲化.再将该比值乘上该指标对应的总分数20即可得到指标对应的分值.具体如下:第六步,将常规指标得分F1与附加指标得分F2相加,即可得到综合分F=F1+F2. 第七步,将各研究机构的指标数据根据上述六个步骤进行处理,再将所得总分可算出各省市研评价综合得分见表5.结合上述两种方法采用理实结合的评价思路,通过敏感度分析前后排名的结果可以发现总体趋势保持一致,可以求取综合评价函数进行综合评价.3.1 敏感度分析先将主客观评价方法所得排名(见表2和表3)根据公式yi=31-xi+1(xi为地区i的排名)数量化.记β为权重,综合评价函数为z=β*m1+(1-β)*m2,此处对其取不同的值,其综合评价分数见表,敏感分析图如图4.由图4看出综合权重的变化对排名影响的敏感度较低,故主客观评价模型比较合理.3.2 综合评价函数的建立对于地区把主观评价数据和客观评价数据都转化为对应的模糊集合,并对所有评价指标的模糊集合的对应项进行加权平均求和得到该项的对应数据,后把所有评价数据集成构成最终评价结果的模糊集[12].记地区Di客观评价值为:{(district1,δ1),(district2,δ2),…,(district31,δ31)},记地区Di主观评价值为:{(district1,γ1),(district2,γ2),…,(district31,δ31)},记λ1和λ2分别为客观和主观评价信息的权重,那么,关于地区Di的综合评价值仍未基准等级集合的模糊集,记为:{(district1,λ1+δ1+λ2γ1),(district2,λ1δ2+λ2γ2),…,(district31,λ1δ31+λ2γ31)}建立优化模型求解权重系数λ1和λ2使得所有地区的综合评价值之和最大化.再将主客观信息权重进行归一化处理,得即综合评价函数为z=0.46m1+0.54m2,得各地区高校科研水平综合评分和排名见表7.本文的主要工作在于,首先,针对主成分分析综合评价存在的问题,利用核主成分分析法(KPCA)不仅可以利用合理的核函数解决变量间的非线性关系,而且在一定程度上提高了第一主成分的贡献率(从86.625%提高到99.975%);其次,无论是核主成分分析还是主成分分析,在其权重系数确定方面都存在缺陷(未考虑权重的重要性),实证研究法是以层次分析法为工具,总结国内外相关文献,综合各专家意见,以兼顾数量又突出质量为突破点,从常规指标和附加指标这两个方面对科研水平做出综合评价;再次,针对核主成分分析法在指标权重确定方面的不足之处,从信息量权和重要性权两方面进行完善,提出了一种基于传统主成分分析的新型评价方法对各省份高校人文社会学科科研作出了较为全面的评价.【相关文献】[1] 王志刚.应用随机过程[M].合肥:中国科学技术大学出版社,2009.[2] 薛薇.SPSS统计分析方法及应用(第三版)[M].北京:电子工业出版社,2013.[3] 陈宝,李湛.中国政府效率改进的影响因素与中国政府改革——基于主成分分析的研究[J].当代经济科学,2011,33(6):57-63.[4] 刘丽萍,马丹,白万平.大维数据的动态条件协方差阵的估计及其应用[J].统计研究,2015,32(6):105-112.[5] 徐顽强,周晓婷.基于主成分分析法的省域科技创新体系评价模型构建[J].科技管理研究,2016(6):52-57.[6] 李靖华.主成分分析用于多指标评价的方法研究——主成分评价[J].管理工程学报,2002,18(1):39-43.[7] 王思哲,王志刚,何勇.基于数据挖掘技术的葡萄酒评价体系研究[J].应用数学进展,2015,4(4):376-384.[8] 程砚秋,迟国泰.基于核主成分分析的生态评价模型及其应用研究[J].中国管理科学,2011,19(3):182-192.[9] 苏治,傅晓媛.核主成分遗传算法与SVR选股模型改进[J].统计研究,2013,30(5):54-62.[10] 潘文砚,王宗军.基于核主成分分析的低碳经济发展水平评价研究[J].金融与经济,2016(4):55-60.[11] 王晓丽.高校人文社会学科研究机构科研绩效评价体系构建研究[D].浙江:浙江大学,2013.[12] 于佳.期刊等级评价的主客观信息集成方法研究[D].沈阳:沈阳工业大学,2015.。
kpca例题

kpca例题含解答KPCA(Kernel Principal Component Analysis,核主成分分析)是一种非线性降维方法KPCA (Kernel Principal Component Analysis,核主成分分析)是一种非线性降维方法,它通过将原始数据映射到高维空间,然后在高维空间中进行主成分分析来实现降维。
下面是一个关于KPCA的例题及解答:例题:假设我们有一组二维数据点,如下所示:(1,2),(2,3),(3,4),(4,5)我们希望使用KPCA将这些数据点降维到一维空间。
请问如何选择合适的核函数和参数?解答:首先,我们需要选择一个核函数。
常用的核函数有线性核、多项式核、高斯径向基核(RBF)等。
在这个例子中,我们可以选择线性核或RBF核。
接下来,我们需要确定核函数的参数。
对于线性核,参数为0;对于RBF核,参数为σ(标准差)。
我们可以分别尝试这两种核函数和参数组合,然后比较降维后的效果。
例如,我们可以尝试使用线性核和RBF核,参数分别为0和1。
1. 使用线性核:由于线性核实际上就是普通的PCA,所以降维后的数据点仍然是原数据点。
因此,我们可以认为线性核在这个例子中没有起到作用。
2. 使用RBF核:我们将数据点映射到高维空间,然后在高维空间中进行主成分分析。
这里我们选择σ=1作为RBF核的参数。
降维后的数据点可以通过以下公式计算:γ= (x -μ)^T K^+ y其中,x是原始数据点,y是降维后的数据点,μ是数据的均值向量,K^+是K的伪逆矩阵。
计算得到降维后的数据点为:(-1, -1),(-1, 0),(0, 1),(1, 1)可以看到,使用RBF核和σ=1作为参数时,数据点成功地被降维到了一维空间。
因此,我们可以选择RBF核和σ=1作为这个例子中的参数。
基于KPCA-DFNN海洋微生物发酵过程软测量建模

基于KPCA-DFNN海洋微生物发酵过程软测量建模孙丽娜;黄永红;蒋星红;冯培燕【摘要】针对海洋微生物发酵过程中关键生物参量(基质浓度、菌体浓度、产物浓度等)在线测量困难,离线化验滞后大,难以实现实时控制的问题,提出了一种基于核主元分析(KPCA)与动态模糊神经网络(DFNN)相结合的软测量方法;以典型的海洋微生物-海洋蛋白酶发酵过程为例,通过KPCA提取输入数据空间中的非线性主元,将提取的主元作为DFNN的输入,基质浓度、菌体浓度、相对酶活作为DFNN的输出,建立了基于KPCA-DFNN的海洋蛋白酶发酵过程生物参量软测量模型;仿真结果表明,KPCA-DFNN模型比DFNN和PCA-DFNN建模的测量精度高,跟踪性能强,能很好地满足发酵过程中生物参量的测量要求.【期刊名称】《计算机测量与控制》【年(卷),期】2018(026)007【总页数】4页(P41-43,98)【关键词】海洋微生物;生物参量;核主元分析;动态模糊神经网络【作者】孙丽娜;黄永红;蒋星红;冯培燕【作者单位】苏州工业园区职业技术学院,江苏苏州215123;江苏大学电气信息工程学院,江苏镇江212013;苏州工业园区职业技术学院,江苏苏州215123;苏州工业园区职业技术学院,江苏苏州215123【正文语种】中文【中图分类】TP2730 引言海洋微生物作为微生物的一类,因其生存的海洋具有特殊的环境,故其所产生的酶与其他微生物所产生的酶相比具有更加独特的性质,如耐低温,耐碱性,PH作用范围宽等,这使得海洋微生物在食品加工、酶工业、添加剂和医药等发酵行业具有极大的开发潜力和应用前景[1-5]。
在海洋微生物发酵过程中,为保证发酵产物的品质和质量,需要实时检测一系列生物参数,尤其是基质浓度、菌体浓度及产物浓度(酶活)。
当前,在线测量仪器仅能检测发酵过程中某些物理和化学参数,还没有成熟实用的仪器来测量这些关键生物参数[6-8]。
在此背景下,许多关于微生物发酵过程中生物参数的软测量方法应运而生,其中,基于神经网络[9]的预测方法成为软测量领域的研究热点。
基于改进型主成分分析法的食品供应商评价模型研究

一
篇论文 , 随后便弓 起学术界的普遍关注 。一直 以来 , I 国内外
学者已经作 出了大量 的研究 , 现有 文献对供应商评价的模型 , 主要有定性 和定量两种方法 , 定性 方法主要是概念型 、 经验型
的研究 , 通过直观判 断与协商 等途径 , 建立供应商选择 和评 价
指标体 系, 定量方法 是采用仿 真研究 和数学模 型分析 , 涉 主要
【 要】 摘 根据食品行业的特点建立供应商评价指标体 系, 利用改进型主成分分析法 消除评价指标之间相关影 响, 减少指标选 择 的工作量, 并通过专家打分及相关 的评价指标建立判别模 型对备选 的供应商进行筛选 , 然后选择最优的供应商。 最后通过实例 分析验证了该方法 的有效性 , 对企业选择物流供应商具有一定参考价值 。 【 关键词】 食品 ; 供应商评价 ; 改进型主成分分析 【 中图分类-]24  ̄F 2. 0 【 文献标识码】 A 【 文章编-] 0 — 5 X 2 1 )8 06 — 3  ̄ 1 5 1 2 ( 00 0 —{ 2 0 0 )
一
Ke wo d :fo s p le v u t n i rv dpr cpa o o e t n yi y r s od;u pir a ai ;mp oe i il c mp n n a ss el o n al
PCA与KPCA简介
第二章 主成分分析1. 主成分分析的基本原理统计学上PCA 的定义为用几个较少的综合指标来代替原来较多的指标,而这些较少的综合指标既能尽多地反映原来较多指标的有用信息,且相互之间又是无关的。
作为一种建立在统计最优原则基础上的分析方法,主成分分析具有较长的发展历史。
在1901年,Pearson 首先将变换引入生物学领域,并重新对线性回归进行了分析,得出了变换的一种新形式。
Hotelling 于1933年则将其与心理测验学领域联系起来,把离散变量转变为无关联系数。
在概率论理论建立的同时,主成分分析又单独出现,由Karhunen 于1947年提出,随后Loeve 于1963年将其归纳总结。
因此,主成分分析也被称为K -L 变换[1]。
PCA 运算就是一种确定一个坐标系统的直交变换,在这个新的坐标系统下,变换数据点的方差沿新的坐标轴得到了最大化。
这些坐标轴经常被称为是主成分。
PCA 运算是一个利用了数据集的统计性质的特征空间变换,这种变换在无损或很少损失了数据集的信息的情况下降低了数据集的维数。
PCA 的基本原理如下:给定输入数据矩阵m n X ⨯ (通常m n >),它由一些中心化的样本数据1{}m i i x =构成,其中n i x R ∈且10m i i x==∑ (2-1)PCA 通过式(2-2)将输入数据矢量i x 变换为新的矢量T i i s U x = (2-2)其中:U 是一个n n ⨯正交矩阵,它的第i 列i U 是样本协方差矩阵11nT i i i C x x n ==∑ (2-3) 的第i 个本征矢量。
换句话说,PCA 首先求解如下的本征问题1,...,i i i u Cu i n λ= = (2-4)其中λ是C 的一个本征值,i u 是相应的本征矢量。
当仅利用前面的P 个本征矢量时(对应本征值按降序排列),得矩阵T S U X = 。
新的分量S 称为主分量[2]。
最大特征值λ对应的最大特征向量u 就是第一个主成分,这个特征向量就是数据有最大方差分布的方向。
基于主成分分析的苹果品质综合评价
基于主成分分析的苹果品质综合评价随着消费者对水果品质的不断追求和对食品安全的关注,苹果品质的综合评价成为越来越多果业企业所关注的课题。
传统的评价方法主要依赖人工观察和经验判断,无法客观、量化地评价苹果的品质。
一、数据采集首先,需要采集与苹果品质相关的各项指标数据。
这些指标可以分为两类:一类是直接测量的物理参数,如果径、果重、硬度等;另一类是感官评价指标,如外表色泽、口感、风味等。
通常情况下,采集的数据越多,评价结果越客观可信。
二、数据预处理在数据采集的基础上,需要对数据进行预处理。
预处理的目的是去除噪声数据、调整数据的量纲和标准化数据。
这样可以有效地提高主成分分析的精度和可靠性。
具体预处理方法包括:1.去除异常值。
通过箱线图等方法判断数据是否异常,将异常值剔除或进行修正。
2.调整数据的量纲。
将不同指标的数据值调整到相同的量级。
3.标准化数据。
将各指标数据按照均值为0、标准差为1的标准分布进行标准化处理。
三、主成分分析主成分分析的目标是将多个变量信息降维为几个代表性的主成分,从而实现对苹果品质的综合评价。
PCA算法通过对原数据的协方差矩阵进行特征值分解,计算出若干个主成分。
每个主成分代表了原数据中一部分的信息,具有以下特点:1.主成分之间不相关,即它们彼此独立。
2.第一主成分所包含的信息最多,第二主成分所包含的信息次之,以此类推。
3.通过选取前几个主成分,可以保留大部分数据的信息,从而实现数据降维。
根据PCA算法的计算结果,可以得出若干个主成分的系数,从而计算出每个苹果的主成分得分。
这些主成分得分可以用于综合评价每个苹果品质的好坏程度。
四、评价结果分析在得到每个苹果的综合评价结果后,需要对数据进行进一步的分析和比较。
常见的方法包括单因素方差分析、聚类分析、因子分析等。
单因素方差分析可以帮助分析每个主成分与苹果品质的相关性,以确定不同主成分对苹果品质的贡献程度。
聚类分析可以将苹果按照品质相似性进行归类,找出品质较好的苹果的共性特点,并为果业企业提供有针对性的管理建议。
核主成分分析在线性分类问题中的应用
核主成分分析在线性分类问题中的应用在机器学习领域中,线性分类问题是常见的一种问题。
核主成分分析(Kernel Principal Component Analysis,简称KPCA)是一种非常重要的无监督降维技术,可以有效地解决线性分类问题。
本文将介绍KPCA及其在线性分类问题中的应用。
1、KPCA的基本原理PCA(Principal Component Analysis)是一种无监督的数据降维技术,它可以将高维数据集映射到低维空间中,同时保留原始数据集的大部分信息。
但是,在某些情况下,PCA不能够很好地处理非线性数据。
KPCA是基于PCA的思想,通过使用非线性核函数来增强PCA的非线性能力。
核函数可以将数据映射到高维空间中,使得原始非线性数据在高维空间中变得线性可分。
2、KPCA的算法流程KPCA的算法流程包括以下几个步骤:(1)选择核函数,并基于核函数计算样本之间的相似度矩阵。
(2)利用相似度矩阵计算中心化Kernel Gram矩阵K。
(3)对Kernel Gram矩阵K进行特征值分解,得到特征值和特征向量。
(4)根据特征向量将原始数据映射到新的低维空间中。
3、KPCA在线性分类问题中的应用KPCA最常用的应用之一是在线性分类问题中。
当线性分类问题不能被简单地解决时,KPCA可以通过映射原始数据到高维空间中,使得数据在高维空间中变得线性可分。
具体来说,在线性分类问题中,我们通常会遇到以下两种情况:(1)类别之间的边界不是线性可分的。
(2)样本数目相对于特征数目是相对较小的。
对于第一种情况,我们可以使用核函数将数据映射到高维空间中。
在高维空间中,数据可能是线性可分的。
对于第二种情况,我们可以使用KPCA对数据进行降维,从而减小特征数目,加强数据分析的可靠性。
4、KPCA的实现在Python中,我们可以使用Scikit-learn库来实现KPCA。
下面是一个简单的代码示例:```pythonfrom sklearn.decomposition import KernelPCAimport numpy as np# 构造随机数据集np.random.seed(0)X = np.random.rand(100, 5)# 将数据集映射到高维空间kpca = KernelPCA(n_components=2, kernel='rbf')X_kpca = kpca.fit_transform(X)# 输出结果print(X_kpca.shape)```在上面的代码中,我们使用Scikit-learn库中的KernelPCA类来实现KPCA。
基于主成分分析的苹果品质综合评价
基于主成分分析的苹果品质综合评价
苹果品质是一个综合性的评价指标,主要包括外观、风味和口感等方面。
为了对苹果品质进行综合评价,可以借助主成分分析方法。
主成分分析是一种通过线性变换将原始变量转化为一组新变量的方法,这组新变量被称为主成分。
主成分是原始变量的线性组合,具有以下特点:第一主成分能够解释原始变量中最大的方差,第二主成分能够解释剩下的最大方差,以此类推。
通过主成分分析,可以将原始变量的维度降低,从而减少变量间的相关性,提取出影响苹果品质的主要因素。
苹果品质综合评价可以从以下几个方面展开:
一、外观评价。
外观评价主要包括果形、果色、果皮光泽度等指标。
可以通过对这些指标进行量化,并进行主成分分析,得到一组新的主成分。
二、风味评价。
风味是苹果品质的核心指标之一,主要包括香气、口感等方面。
对于风味评价可以设计一套标准的评分系统,通过专家对苹果的风味进行评分,然后进行主成分分析,得到一组新的主成分。
将上述三组主成分进行综合加权,得到主成分综合评价值。
权重可以根据实际情况进行确定,可以根据消费者需求和市场需求进行调整。
最终,根据主成分综合评价值可以对苹果品质进行高中低档的划分,帮助消费者更好地选择适合自己口味的苹果。
基于主成分分析的苹果品质综合评价能够客观地反映苹果的外观、风味和口感等方面的品质,为消费者提供更全面的苹果选择参考。
该方法也可为苹果生产和销售企业提供品质改进和市场调整的依据,促进苹果产业的发展。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V一>:啦西(z。)。
l—l
通讯作者:王来生(1954一),男,博士,教授,研究方向:运筹学与管理 学。北京市清华东路17号 中国农业大学理学院数学系,100083。
下面定义z×z矩阵K, 其中Ki一 (中(zi)・①(z,)),可以得到从Ka—K2a,其中口一(口1,
口。…嘞)T。容易证明上式等价于及口一№,对于主成分
1
求得特征值为:A-≥Az≥…A。>o,其对应的单位特征 向量为
一}2 p唧2慝,
2.1
模型原理[3・41 首先将原空间的数据通过非线性变换
①:RN—F,z一①(z) 投影到特征空间F;假定特征空间的满足西(z。),
f
①(z。),…,中(z,),满足>:①(z。)一o,非线性PcA就可
主成分分析(PCA)模型‘1]
抽取,只需计算一个测试点①(z)在F的特征向量∥上
Email wanglaish@sina.com。
万方数据 万方数据 万方数据 维特征空间,然后在这个高维特征空间中进行线性主成分分析。通过核技巧,不必知道非线性变换的具体形式,只要选取适 当的核及其参数,就可使第一主成分的贡献率达到85%以上,从而能有效地避免主成分分析(PCA)只能处理线性问题和 降维效果不明显的弊端。在对豆腐乳的品质进行评价时,得到了较理想的评价效果。
关键词:核主成分分析;综合评价;豆腐乳;感官品质;理化性质
中图分类号:伸39
o
文献标识码:A
文章编码:l002—6819(2004)ZK一0236一03 则
引
言
s—R一÷x’x,
主成分分析[13(PCA)是将多个变量综合成少数变 量的一种多元统计方法,为解决多指标综合评价提供 了一种很好的方法,可以有效地处理变量间的线性关 系。但现实指标间的关系往往是非线性的,采用线性 PCA方法可能出现各指标贡献率过于分散的情况。主 成分的所谓综合,实际上是对变量间共性的一种提取, 因此要综合相关性不大的变量,采用线性主成分分析 法是不妥的,文献[2]中的作者对其作了改进,提出了 一种非线性主成分分析法。而本文给出了一种核主成 分分析(KPCA)的评价模型[3_5],它将观察变量空间 通过一个非线性变换垂映射到高维特征空间F,在F中 进行线性主成分分析,通过核技巧,KPCA评价方法只 需在原空间进行点积运算,而不必知道中的具体形式。 文献[6]中豆腐乳感官的评定因素有17个,理化性质 的评定因素有19个,影响因素较多,若用主成分分析, 各主成分的贡献率过于分散,降维效果不明显,另外, 选取主成分的个数不同,可能会得到不同的评价结果。 本文采用核主成分分析,只要选取适当的核,就可使第 一主成分的贡献率达到85%,从而取得较好的评价效 果。
A(①(z女)・V)一(面(z女)・瓦V),(志一1,2…Z),
s一(si),sd=÷∑(z。一i)(巧一i)
。d兰1
而相关系数阵为
R—c托h
y一一了季芋≥亏
中国农业大学理学院数学系,
且存在系数使得
£
收稿日期:2003—11一03
修订日期:2004一04—20
作者简介:徐义田(1970一),男,山东人,讲师,硕士生,研究方向:运 筹与优化。北京市清华东路17号
设z。∈R一(志一1,2,……Z)为样本数据向量,将原
百
Z
以看作在F中对矩阵
始变量z。,zz,…,z。标准化,求出其样本协方差阵:
耳一÷∑中(z,)①(z,)丁
进行线性主成分分析。 显然K的所有特征值A(A≥o)和特征向量V满足: AV—KV,其所有解均在西(z。),垂(z。),…,西(z,)张成 的子空间内,因此有
第20卷
236
增刊 7月
农业工程学报
Transactions of the CSAE
V01.20
Suppl 2004
2004年
Julyl
基于核主成分分析【KPCA)的一种食品评价模型
徐义田,王来生※
(中国农业大学理学院,北京100083)
摘
要:该文提出了一种新的食品评价模型:核主成分分析(KPcA)。它通过一个非线性变换,首先将原变量空间映射到高
