立体几何初步空间几何与点线面单元过关检测卷(三)含答案人教版高中数学考点大全辅导班专用
苏州十六中必修第二册第三单元《立体几何初步》检测题(含答案解析)

一、选择题1.设m ,n 是两条不同直线,α,β是两个不同的平面,下列命题正确的是( ) A .//m α,//n β且//αβ,则//m nB .m α⊂,n α⊂,//m β,//n β,则//αβ C .m α⊥,n β⊂,m n ⊥,则αβ⊥D .m α⊥,n β⊥且αβ⊥,则m n ⊥2.古代数学名著《数学九章》中有云:“有木长三丈,围之八尺,葛生其下,缠木两周,上与木齐,问葛长几何?”意思为:圆木长3丈,圆周为8尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺(注:1丈即10尺)( ) A .30尺 B .32尺 C .34尺 D .36尺 3.如图所示,AB 是⊙O 的直径,VA 垂直于⊙O 所在的平面,点C 是圆周上不同于A ,B 的任意一点,M ,N 分别为VA ,VC 的中点,则下列结论正确的是( )A .MN //ABB .MN 与BC 所成的角为45° C .OC ⊥平面VACD .平面VAC ⊥平面VBC 4.已知平面α内一条直线l 及平面β,则“l β⊥”是“αβ⊥”的( )A .充分必要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件 5.如图所示,在正方体1111ABCD A B C D -中,O 是11B D 的中点,直线1A C 交平面11AB D 于点M ,则下列结论正确的是( )A .,,A M O 三点共线B .1,,,A M O A 不共面C .,,,A M C O 不共面D .1,,,B B O M 共面6.已知平面α,β,γ和直线l ,下列命题中错误的是( )A .若αβ⊥,//βγ,则αγ⊥B .若αβ⊥,则存在l α⊂,使得//l βC .若a γ⊥,βγ⊥,l αβ=,则l γ⊥D .若αβ⊥,//l α,则l β⊥7.菱形ABCD 的边长为3,60B ∠=,沿对角线AC 折成一个四面体,使得平面ACD ⊥平面ABC ,则经过这个四面体所有顶点的球的表面积为( )A .15πB .12πC .8πD .6π8.在长方体1111ABCD A B C D -中,P 为BD 上任意一点,则一定有( )A .1PC 与1AA 异面B .1PC 与1A C 垂直 C .1PC 与平面11ABD 相交D .1PC 与平面11AB D 平行 9.设α、β是两个不同的平面,m 、n 是两条不同的直线,下列说法正确的是( )A .若α⊥β,α∩β=m ,m ⊥n ,则n ⊥βB .若α⊥β,n ∥α,则n ⊥βC .若m ∥α,m ∥β,则α∥βD .若m ⊥α,m ⊥β,n ⊥α,则n ⊥β10.边长为2的正方形ABCD 沿对角线AC 折叠使得ACD 垂直于底面ABC ,则点C 到平面ABD 的距离为( )A .263B 23C 22D 6 11.下列命题中正确的个数有( )个①不共面的四点中,其中任意三点不共线②依次首位相接的四条线段必共面③若点,,,A B C D 共面,点,,,A B C E 共面,则点,,,,A B C D E 共面④若直线,a b 共面,直线,a c 共面,则直线,b c 共面A .1B .2C .3D .412.长方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E 为AB 的中点,3CE =,53cos 9ACE ∠=,且四边形11ABB A 为正方形,则球O 的直径为( ) A .4 B .51C .4或51D .4或5 13.在正方形SG 1G 2G 3中,E 、F 分别是G 1G 2及G 2G 3的中点,D 是EF 的中点,现在沿SE 、SF 及EF 把这个正方形折成一个四面体,使G 1、G 2、G 3三点重合,重合后的点记为G ,那么,在四面体S ﹣EFG 中必有( )A .SG ⊥△EFG 所在平面B .SD ⊥△EFG 所在平面C .GF ⊥△SEF 所在平面D .GD ⊥△SEF 所在平面14.用一个平行于圆锥底面的平面截这个圆锥,截得的圆台上、下底面的面积之比为1:16,截去的圆锥的母线长是3cm ,则圆台的母线长是( )A .9cmB .10cmC .12cmD .15cm二、解答题15.如图,BC 为圆O 的直径,D 为圆周上异于B 、C 的一点,AB 垂直于圆O 所在的平面,BE AC ⊥于点E ,BF AD ⊥于点F .(1)求证:BF AC ⊥;(2)若2AB BC ==,60CBD ∠=︒,求三棱锥B DEF -的体积.16.在如图所示的几何体中,侧面CDEF 为正方形,底面ABCD 中,//AB CD ,222AB BC DC ===,30BAC ∠=,AC FB ⊥.(1)求证:AC ⊥平面FBC ;(2)线段AC 上是否存在点M ,使//EA 平面FDM ?证明你的结论.17.如图,直三棱柱ABC -A 1B 1C 1中,AA 1=2,A 1C =25,AB =2,∠BAC =60°.(1)求三棱锥A 1-ABC 的表面积;(2)证明:在线段A 1C 上存在点M ,使得AC ⊥BM ,并求1A M MC的值. 18.如图所示的四棱锥E -ABCD 中,底面ABCD 为矩形,AE =EB =BC =2,AD ⊥平面ABE ,且CE 上的点F 满足BF ⊥平面ACE .(1)求证:AE ∥平面BFD ;(2)求三棱锥C -AEB 的体积.19.如图,在长方形ABCD 中,4AB =,2AD =,点E 是DC 的中点.将ADE 沿AE 折起,使平面ADE ⊥平面ABCE ,连结DB 、DC 、EB .(1)求证:AD ⊥平面BDE ;(2)点M 是线段DA 的中点,求三棱锥D MEC -的体积.20.如图,已知多面体111ABCA B C ,1A A ,1B B ,1C C 均垂直于平面ABC ,120ABC ∠=︒,14A A =,11C C =,12AB BC B B ===.(1)证明:1AB ⊥平面111A B C ;(2)求直线1AC 平面1ABB 所成的角的正弦值.21.如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,PCD 为等边三角形,平面PAC ⊥平面PCD ,,3,5PA CD CD AD ⊥==.(1)设G ,H 分别为PB ,AC 的中点,求证://GH 平面PAD ;(2)求证:PA ⊥平面PCD ;(3)求三棱锥-D PAC 的体积.22.如图,在直三棱柱ABC -A 1B 1C 1中,AB ⊥侧面BB 1C 1C ,E 是CC 1上的中点,且BC =1,BB 1=2.(1)证明:B 1E ⊥平面ABE ;(2)若三棱锥A -BEA 1的体积是33,求异面直线AB 和A 1C 1所成角的大小. 23.在斜三棱柱111ABC A B C -中,AB AC ⊥,1B C ⊥平面ABC ,且2AB AC ==,123AA =.(Ⅰ)求证:平面1AB C ⊥平面11ABB A ;(Ⅱ)求直线1BC 与平面11ABB A 所成角的正弦值.24.如图,在梯形ABCD 中,//BC AD ,E 在AD 上,且2BC BE ED ===.沿BE 将ABE △折起,使得AB CE .(1)证明:AD CE ⊥;(2)若在梯形ABCD 中,π3ADC ∠=,折起后π3ABD ∠=,点A 在平面BCDE 内的射影H 为线段BD 的一个四等分点(靠近点B ),求三棱锥D ABC -的体积. 25.已知四棱锥P ABCD -的底面ABCD 是菱形,PD ⊥平面ABCD ,2AD PD ==,60DAB ∠=,F ,G 分别为PD ,BC 中点,AC BD O =.(Ⅰ)求证:FG ∥平面PAB ;(Ⅱ)求三棱锥A PFB -的体积;26.如图,在棱长为1的正方体1111ABCD A B C D -中,点O 是BD 中点.(1)求证:平面11BDD B ⊥平面1C OC ;(2)求二面角1C BD C --的正切值.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】对每一个命题逐一判断得解.【详解】对于A ,若m ∥α,n ∥β且α∥β,说明m 、n 是分别在平行平面内的直线,它们的位置关 系应该是平行或异面或相交,故A 不正确;对于B ,若“m ⊂α,n ⊂α,m ∥β,n ∥β”,则“α∥β”也可能α∩β=l ,所以B 不成立. 对于C ,根据面面垂直的性质,可知m ⊥α,n ⊂β,m ⊥n ,∴n ∥α,∴α∥β也可能α∩β=l ,也可能α⊥β,故C 不正确;对于D ,由m ⊥α,n ⊥β且α⊥β,则m 与n 一定不平行,否则有α∥β,与已知α⊥β矛盾,通过平移使得m 与n 相交,且设m 与n 确定的平面为γ,则γ与α和β的交线所成的角即 为α与β所成的角,因为α⊥β,所以m 与n 所成的角为90°,故命题D 正确. 故答案为D【点睛】本题考查直线与平面平行与垂直,面面垂直的性质和判断的应用,考查逻辑推理能力和空间想象能力.2.C【分析】由题意,圆柱的侧面展开图是矩形,葛藤长是两个矩形相连所成矩形的对角线的长,画出图形,即可求出葛藤长.【详解】由题意,圆柱的侧面展开图是矩形,葛藤长是两个矩形相连所成矩形的对角线的长. 如图所示矩形ABCD 中,30AD =尺,2816AB =⨯=尺, 所以葛藤长2222301634AC AD AB =+=+=尺.故选:C .【点睛】本题考查圆柱的侧面展开图,考查学生的空间想象能力,属于基础题. 3.D解析:D【分析】由中位线性质,平移异面直线即可判断MN 不与AB 平行,根据异面直线平面角知MN 与BC 所成的角为90°,应用反证知OC 不与平面VAC 垂直,由面面垂直的判定知面VAC ⊥面VBC ,即可知正确选项.【详解】M ,N 分别为VA ,VC 的中点,在△VAC 中有//MN AC ,在面ABC 中AB AC A =,MN 不与AB 平行;AC BC C =,知:MN 与BC 所成的角为90BCA ∠=︒;因为OC ⋂面VAC C =,OC 与平面内交线,AC VC 都不垂直,OC 不与平面VAC 垂直; 由VA ⊥面ABC ,BC ⊂面ABC 即VA BC ⊥,而90BCA ∠=︒知AC BC ⊥,AC VA A ⋂=有BC ⊥面VAC ,又BC ⊂面VBC ,所以面VAC ⊥面VBC ; 故选:D【点睛】本题考查了异面直线的位置关系、夹角,以及线面垂直的性质,面面垂直判定的应用,属于基础题.4.B解析:B根据面面垂直和线面垂直的定义,结合充分条件和必要条件的定义进行判断即可.【详解】解:由面面垂直的定义知,当“l ⊥β”时,“α⊥β”成立,当αβ⊥时,l β⊥不一定成立,即“l β⊥”是“αβ⊥”的充分不必要条件,故选:B .【点睛】本题考查命题充分性和必要性的判断,涉及线面垂直和面面垂直的判定,属基础题. 5.A解析:A【分析】连接11,A C AC ,利用两个平面的公共点在一条直线上可判断点共线.【详解】连接11,A C AC ,则11//A C AC ,11,,,A C C A ∴四点共面,1A C ∴⊂平面11ACC A ,1M AC ∈,M ∴∈平面11ACC A ,M ∈平面11AB D ,∴点M 在平面11ACC A 与平面11AB D 的交线上,同理点O 在平面11ACC A 与平面11AB D 的交线上,,,A M O ∴三点共线,故A 正确;,,A M O 三点共线,且直线与直线外一点可确定一个平面,1,,,A M O A ∴四点共面,,,,A M C O 四点共面,故B ,C 错误;1BB 平面11AB D ,OM ⊂平面11AB D ,1B ∈平面11AB D 且1B OM ,1BB ∴和OM 是异面直线,1,,,B B O M ∴四点不共面,故D 错误.故选:A.本题主要考查空间中点的共线问题,此类题一般证明这些点同在两个不同的平面内,根据两平面的公共点在一条直线上即可判断.6.D解析:D【分析】根据面面垂直的判定定理即可判断A 正确;根据线面平行的判定定理可知B 正确; 根据面面垂直的性质定理可知C 正确;根据线面垂直的判定定理可知D 错误.【详解】对于A ,因为αβ⊥,所以存在直线a ⊂α,使a ⊥β,又β∥γ,所以a ⊥γ,有α⊥γ,正确;对于B ,α⊥β,设α∩β=m ,则在平面α内存在不同于直线m 的直线l ,满足l ∥m , 根据线面平行的判定定理可知,l ∥β,正确;对于C ,过直线l 上任意一点作直线m ⊥γ,根据面面垂直的性质定理可知,m 既在平面α又在平面β内,所以直线l 与直线m 重合,即有l ⊥γ,正确;对于D ,若α⊥β,l ∥α,则l ⊥β不一定成立,D 错误.故选:D .【点睛】本题主要考查线面位置关系的判断,考查学生的逻辑推理能力,属于中档题. 7.A解析:A【分析】首先根据已知条件找到四面体外接球的球心,再求出半径,即可得到球体的表面积.【详解】如图所示,1O ,2O 分别为ABC 和DAC △的外接圆圆心,因为菱形ABCD ,60B ∠=,所以ABC 和DAC △为等边三角形.设E 为AC 的中点,连接DE ,BE ,则DE AC ⊥,BE AC ⊥,又因为平面ACD ⊥平面ABC AC =,所以DE ⊥平面ABC .分别过1O ,2O 作垂直平面ABC 和平面ACD 的直线,则交点O 为四面体ABCD 外接球的球心.因为2233332⎛⎫==-= ⎪⎝⎭EB DE ,四边形12OO EO 为矩形, 所以123==O B DO ,1213===O E O E OO . 所以外接圆半径为()223153=22⎛⎫+⎪ ⎪⎝⎭,表面积为15π. 故选:A【点睛】 本题主要考查四面体外接球的表面积,根据题意确定外接球的球心为解题关键,属于中档题.8.D解析:D【分析】取P 为BD 的中点可判断A 、B 、C 选项的正误;证明平面1//BC D 平面11AB D ,可判断D 选项的正误.【详解】如下图所示:对于A 选项,当点P 为BD 的中点时,1PC ⊂平面11AAC C ,则直线1PC 与1AA 相交,A 选项错误;对于B 选项,当点P 为BD 的中点时,1AC P ∠为锐角,1PC 与1A C 不垂直,B 选项错误;对于C 选项,当点P 为BD 的中点时,连接11A C 、11B D 交于点O ,则O 为11A C 的中点, 在长方体1111ABCD A B C D -中,11//AA CC 且11AA CC =,则四边形11AAC C 为平行四边形,11//AC AC ∴且11AC A C =,O 、P 分别为11A C 、AC 的中点,则1//AP OC 且1AP OC =,∴四边形1OAPC 为平行四边形,1//PC AO ∴,AO ⊂平面11AB D ,1PC ⊄平面11AB D ,1//PC ∴平面11AB D ,C 选项错误; 对于D 选项,在长方体1111ABCD A B C D -中,11//BB DD 且11BB DD =,则四边形11BB D D 为平行四边形,11//BD B D ∴,BD ∴⊄平面11AB D ,11B D ⊂平面11AB D ,//BD ∴平面11AB D ,同理可证1//BC 平面11AB D ,1BD BC B ⋂=,∴平面1//BC D 平面11AB D ,1PC ⊂平面1BC D ,1//PC ∴平面11AB D .D 选项正确.故选:D.【点睛】本题考查空间中直线与直线、直线与平面位置关系的判断,考查推理能力,属于中等题. 9.D解析:D【分析】根据直线、平面平行垂直的关系进行判断.【详解】由α、β是两个不同的平面,m 、n 是两条不同的直线,知:在A 中,若α⊥β,α∩β=m ,m ⊥n ,则n 与β相交、平行或n ⊂β,故A 错误; 在B 中,若α⊥β,n ∥α,则n 与β相交、平行或n ⊂β,故B 错误; 在C 中,若m ∥α,m ∥β,则α与β相交或平行,故C 错误;在D 中,若m ⊥α,m ⊥β,则α∥β,∴若n ⊥α,则n ⊥β,故D 正确.故选:D.【点睛】本题考查命题真假的判断,考查空间中线线、线面、面面间的益关系等基础知识,考查运算求解能力,是中档题.10.A解析:A【分析】取AC 的中点O ,连接DO 和BO ,由等腰三角形的性质得出DO AC ⊥,可求出DO 和BO 的长,再由平面ACD ⊥平面ABC ,根据面面垂直的性质可得DO ⊥平面ABC ,进而得到DO OB ⊥,利用勾股定理即可求出BD ,最后利用等体积法得出C ABD D ABC V V --=,进而求出点C 到平面ABD 的距离.【详解】解:取AC 的中点O ,连接DO 和BO ,则DO AC ⊥,BO AC ⊥,由于四边形ABCD 是边长为2的正方形,2AD CD AB BC ∴====, 则222222AC =+=,()22222DO BO ==-=,由题知,平面ACD ⊥平面ABC ,且交线为AC ,而DO ⊂平面ACD ,则DO ⊥平面ABC ,又BO ⊂平面ABC ,所以DO BO ⊥,∴在Rt BOD 中,()()22222BD =+=,∴ABD △是等边三角形,则122sin 6032ABD S =⨯⨯⨯=△, 则在Rt ABC 中,12222ABC S =⨯⨯=, 设点C 到平面ABD 的距离为d , 则C ABD D ABC V V --=,即1133ABD ABC S d S DO ⋅=⋅△△, 即:1132233d ⨯=⨯⨯,解得:263d =, 即点C 到平面ABD 的距离为263. 故选:A.【点睛】本题考查利用等体积法求点到面的距离,还涉及面面垂直的性质和棱锥的体积公式,考查推理证明和运算能力.11.A解析:A【分析】假设存在三点共线,则四个点必共面,可判断①;借助空间四边形可判断②;当A ,B ,C 共线时,可判断③;由共面不具有传递性可判断④【详解】①正确,可以用反证法证明,假设存在三点共线,则四个点必共面,与不共面的四点矛盾;②不正确,例如空间四边形的四个顶点就不共面;③不正确,A ,B ,C 共线时,这两平面有三个公共点A ,B ,C ;④不正确,共面不具有传递性,若直线,a b 共面,直线,a c 共面,则直线,b c 可能异面. 故选:A【点睛】本题考查了空间中点线面的位置关系判断,考查了学生综合分析,空间想象,逻辑推理能力,属于中档题12.C解析:C【分析】设2AB x =,则AE x =,29BC x =-,由余弦定理可得222539392393x x x =++-⨯⨯+⨯,求出x ,即可求出球O 的直径. 【详解】 根据题意,长方体内接于球O 内,则球的直径为长方体的体对角线,如图作出长方体1111ABCD A B C D -:设2AB x =,则AE x =,29BC x =-,由余弦定理可得:2225393923939x x x =++-⨯+,∴1x =6, ∴2AB =,22BC =O 4484++=;或26AB =3BC =,球O 2424351++=故选:C .【点睛】本题考查球的直径的计算方法,考查余弦定理,考查计算能力和分析能力,属于常考题. 13.A解析:A【分析】在正方形SG 1G 2G 3中,有S G 1⊥G 1E ,在折叠后其垂直关系不变,所以有SG ⊥EG.同理有有SG ⊥FG ,再由线面垂直的判定定理证明.【详解】在正方形SG 1G 2G 3中,因为S G 1⊥G 1E ,所以在四面体中有SG ⊥EG.又因为S G 3⊥G 3F ,所以在四面体中有SG ⊥FG ,且GEGF G =, 所以 SG ⊥△EFG 所在平面.故选:A【点睛】本题主要考查折叠问题及线面垂直的判定定理,还考查了推理论证的能力,属于中档题. 14.A解析:A【分析】计算得到12:1:4r r =,根据相似得到3134l =+,计算得到答案. 【详解】圆台上、下底面的面积之比为1:16,则12:1:4r r =.设圆台母线长为l ,根据相似得到:3134l =+,故9l =. 故选:A .【点睛】本题考查了圆台的母线长,意在考查学生的计算能力和空间想象能力. 二、解答题15.(1)证明见解析;(2 【分析】(1)易证得CD ⊥平面ABD ,由线面垂直性质可得CD BF ⊥,利用线面垂直判定定理可证得BF ⊥平面ACD ,由线面垂直性质证得结论;(2)利用勾股定理可求得,AD BD 长,在ABD △中,利用面积桥可求得BF ,进而得到BDF S ;由等腰三角形三线合一可知E 为AC 中点,由此确定E 到平面ABD 的距离;利用体积桥和三棱锥体积公式可求得结果.【详解】(1)AB 垂直于圆O 所在平面BCD ,CD ⊂平面BCD ,AB CD ∴⊥, BC 为圆O 的直径,CD BD ∴⊥, 又,BD AB ⊂平面ABD ,AB BD B =,CD平面ABD , BF ⊂平面ABD ,CD BF ∴⊥,又BF AD ⊥,AD CD D =,,AD CD ⊂平面ACD ,BF ∴⊥平面ACD , AC ⊂平面ACD ,BF AC ∴⊥.(2)2BC =,60CBD ∠=︒,CD BD ⊥,1BD ∴=,由AB ⊥平面BCD ,CD ⊂平面BCD 知:AB BD ⊥,AD ∴==,11122ABD S AB BD AD BF BF ∴=⋅=⋅==,解得:5BF =,DF ∴===111225BDF S DF BF ∴=⋅==, AB BC =,BE AC ⊥,E ∴为AC 中点,由(1)知:CD ⊥平面ABD ,E ∴到平面ABD 的距离为12CD =,13B DEF E BDF BDF V V S --∴===. 【点睛】 方法点睛:立体几何求解三棱锥体积的问题常采用体积桥的方式,将所求三棱锥转化为底面面积和高易求的三棱锥体积的求解问题.16.(1)证明见解析;(2)M 为AC 的中点,证明见解析.【分析】(1)本题首先可通过正弦定理得出90ACB ∠=以及AC BC ⊥,然后根据AC FB ⊥以及线面垂直的判定即可证得结果;(2)本题首先可取AC 的中点M ,连接CE 、MN ,然后通过三角形中位线的性质得出//EA MN ,最后通过线面平行的判定即可得出结果.【详解】(1)因为30BAC ∠=,2AB =,1BC =, 所以sin sin AB BC ACB BAC =∠∠,即211sin 2ACB ,解得sin 1ACB ∠=,90ACB ∠=,AC BC ⊥,因为AC FB ⊥,BC FB B ⋂=,所以AC ⊥平面FBC .(2)当M 为AC 的中点时,//EA 平面FDM .证明如下:如图,取AC 的中点M ,连接CE ,与DF 交于点N ,连接MN ,因为四边形CDEF 为正方形,所以N 为CE 的中点,因为M 是AC 的中点,所以//EA MN ,因为MN ⊆平面FDM ,EA ⊄平面FDM ,所以//EA 平面FDM .【点睛】关键点点睛:本题考查线面垂直与线面平行的判定,若直线与平面内的两条相交直线都垂直,则线面垂直,若平面外一条直线平行平面内一条直线,则线面平行,考查数形结合思想,是中档题.17.(1)6+23+26;(2)证明见解析;13. 【分析】(1)可先证明1A B ⊂平面1A AB 得出1BC A B ⊥,即可求出三棱锥A 1-ABC 各个面的面积,得出表面积;(2)在平面ABC 内,过点B 作BN AC ⊥,垂足为N ,过N 作1//MN A A 交1A A 于M ,连接BM ,即可得出.【详解】(1)2,4,=60=23AB AC BAC BC BC AB ==∠∴∴⊥,,,1A A ⊥平面ABC ,BC ⊆平面ABC ,1BC AA ∴⊥,1A A AB A =,BC ∴⊥平面1A AB ,1A B ⊂平面1A AB ,1BC A B ∴⊥,112223262A BC S ∴=⨯= 1=232ABC S AB BC ∴⋅⋅=,111==22A AB S A A AB ⋅,111=42A AC S A A AC =⋅, 则表面积=6+23+26S(2)证明:在平面ABC 内,过点B 作BN AC ⊥,垂足为N ,过N 作1//MN A A 交1A A 于M ,连接BM ,1A A ⊥AC ,1//MN A A ,AC MN ∴⊥,MN BN N =,∴AC ⊥平面MBN .又BM ⊂平面MBN ,∴AC BM ⊥.在直角BAN 中,cos 1, 3.=∠==-=AN AB BAC NC AC AN 111//.3,∴==A M AN MN A A MC NC 【点睛】 本题考查三棱柱表面积的求解,解题的关键是得出1BC A B ⊥以便求出各个面的面积,考查点的存在性问题,解题关键是正确利用线面垂直关系作出辅助线.18.(1)证明见解析;(2)43. 【分析】(1)由ABCD 为矩形,易得G 是AC 的中点,又BF ⊥平面ACE ,BC =BE ,则F 是EC 的中点,从而FG ∥AE ,再利用线面平行的判定定理证明.(2)根据AD ⊥平面ABE ,易得AE ⊥BC ,再由BF ⊥平面ACE ,得到AE ⊥BF ,进而得到AE ⊥平面BCE ,然后由C AEB A BCE V V --=求解.【详解】(1)如图所示:因为底面ABCD 为矩形,所以AC ,BD 的交点G 是AC 的中点,连接FG ,∵BF ⊥平面ACE ,则CE ⊥BF ,而BC =BE ,∴F 是EC 的中点,∴FG ∥AE .又AE ⊄平面BFD ,FG ⊂平面BFD ,∴AE ∥平面BFD .(2)∵AD ⊥平面ABE ,AD ∥BC ,∴BC ⊥平面ABE ,则AE ⊥BC .又BF ⊥平面ACE ,则AE ⊥BF ,∴AE ⊥平面BCE .∴三棱锥C -AEB 的体积11142223323C AEB A BCE BCE V V S AE --⎛⎫==⋅=⨯⨯⨯⨯= ⎪⎝⎭△. 【点睛】方法点睛:1、判断或证明线面平行的常用方法:(1)利用线面平行的定义,一般用反证法;(2)利用线面平行的判定定理(a ⊄α,b ⊂α,a ∥b ⇒a ∥α),其关键是在平面内找(或作)一条直线与已知直线平行,证明时注意用符号语言的叙述;(3)利用面面平行的性质定理(α∥β,a ⊂α⇒a ∥β);(4)利用面面平行的性质(α∥β,a ⊄β,a ∥α⇒a ∥β).19.(1)证明见解析;(2)3. 【分析】(1)先利用勾股定理得出AE BE ⊥,再利用面面垂直的性质定理得到BE ⊥平面ADE ,进而得到AD BE ⊥,利用线面垂直的判定定理即可得证;(2)利用1122D MEC M DEC A DEC D AEC V V V V ----===,取AE 的中点O ,连接DO ,用面面垂直的性质定理得到DO ⊥平面ABCE ,利用体积公式求解即可.【详解】(1)证明:∵2AD DE ==,90ADE ∠=︒, ∴AE BE ==,4AB =,∴222AE BE AB +=,∴AE BE ⊥,又平面ADE ⊥平面ABCE , 平面ADE平面ABCE AE =, ∴BE ⊥平面ADE ,又AD ⊂平面ADE ,所以AD BE ⊥,又AD DE ⊥,DE BE E ⋂=,所以AD ⊥平面BDE.(2)∵M 是线段DA 的中点, ∴1122D MEC M DEC A DEC D AEC V V V V ----===, 取AE 的中点O ,连接DO ,∵DA DE =∴DO AE ⊥,又平面DAE ⊥平面ABCE ,∴DO ⊥平面ABCE , 又2DO =,1sin13522AEC S AE EC =⨯⨯⨯︒=, ∴122233D AEC V -=⨯=, ∴23D MEC V -=. 【点睛】方法点睛: 证明线面垂直的常用方法:利用线面垂直的判定定理;利用面面垂直的性质定理;利用面面平行的性质;利用垂直于平面的传递性.20.(1)证明见解析;(239 【分析】(1)由已知条件可得2221111A B AB AA +=,2221111AB B C AC +=,则111AB A B ⊥,111AB B C ⊥,再利用线面垂直的判定定理可证得结论; (2)如图,过点1C 作111C D A B ⊥,交直线11A B 于点D ,连接AD ,可证得1C D ⊥平面1ABB ,从而1C AD ∠是1AC 与平面1ABB 所成的角,然后在1Rt C AD 求解即可【详解】(1)证明: 由2AB =,14AA =,12BB =,1AA AB ⊥,1BB AB ⊥得11122AB A B ==,所以2221111A B AB AA +=,由111AB A B ⊥.由2BC =,12BB =,11CC =,1BB BC ⊥,1CC BC ⊥得115B C =, 由2AB BC ==,120ABC ∠=︒得23AC =,由1CC AC ⊥,得113AC =,所以2221111AB B C AC +=,故111AB B C ⊥,又11111A B B C B =,因此1AB ⊥平面111A B C .(2)解 如图,过点1C 作111C D A B ⊥,交直线11A B 于点D ,连接AD . 由1AB ⊥平面111A B C ,1AB ⊂平面1ABB ,得平面111A B C ⊥平面1ABB ,由111C D A B ⊥,得1C D ⊥平面1ABB , 所以1C AD ∠是1AC 与平面1ABB 所成的角. 由115B C =,1122AB =,1121AC = 得1116cos 7C A B ∠=,111sin 7C A B ∠=, 所以13C D =,故11139sin C D C AC AD ∠==. 因此,直线1AC 与平面1ABB 所成的角的正弦值是3913.【点睛】关键点点睛:此题考查线面垂直的判定和线面角的求法,解题的关键是通过过点1C 作111C D A B ⊥,交直线11A B 于点D ,连接AD ,然后结合条件可证得1C AD ∠是1AC 与平面1ABB 所成的角,从而在三角形中求解即可,考查推理能力和计算能力,属于中档题 21.(1)证明见解析;(2)证明见解析;(3)33【分析】(1)通过证明//GH PD 来证得//GH 平面PAD .(2)取PC 的中点M ,连接DM ,根据面面垂直的性质定理证得DM ⊥平面PAC ,由此证得DM PA ⊥,结合PA CD ⊥证得PA ⊥平面PCD . (3)利用D PAC A PCD V V --=求得三棱锥-D PAC 的体积. 【详解】(1)连BD ,则H 为BD 中点,因为G 为BP 中点,故GH //PD , 由于GH ⊂/平面PAD ,PD ⊂平面PAD ,所以GH //平面PAD .(2)取PC 中点M ,连DM ,则DM PC ⊥,因为PCD ⊥平面PAD ,则DM ⊥平面PAC ,所以DM PA ⊥, 又PA CD ⊥,DMCD D =,所以PA ⊥平面PCD .(3)因为PA ⊥平面PCD ,所以PA PD ⊥,所以224PA AD PD =-=,213433334D PAC A PCD V V --==⨯⨯⨯=.【点睛】要证明线面平行,则先证线线平行.要证明线面垂直,可通过面面、线线垂直相互转化来证明.22.(1)证明见解析;(2)30. 【分析】(1)由AB ⊥侧面BB 1C 1C 可得1AB B E ⊥,由勾股定理可得1BE B E ⊥,即可证明; (2)由11//A B AB 可得111C A B ∠即为异面直线AB 和A 1C 1所成角,由等体积法可求得AB 长度,即可求出角的大小. 【详解】 (1)AB ⊥侧面BB 1C 1C ,1B E ⊂侧面BB 1C 1C ,1AB B E ∴⊥,BC =1,BB 1=2,E 是CC 1上的中点,12BE B E ∴=22211BE B E BB +=,1BE B E ∴⊥,AB BE B ⋂=,∴B 1E ⊥平面ABE ;(2)11//A B AB ,111C A B ∴∠即为异面直线AB 和A 1C 1所成角,且1A 到平面ABE 的距离等于1B 到平面ABE 的距离,由(1)B 1E ⊥平面ABE ,故B 1E 的长度即为1B 到平面ABE 的距离, 由AB ⊥侧面BB 1C 1C 可得AB ⊥BE ,则111111332A BEA A ABE ABE V V S B E AB --==⋅=⨯⨯=,解得AB =则11A B AB == 在111Rt A B C △中,1111111tan B C C A B A B ∠===11130A C B ∴∠=, 即异面直线AB 和A 1C 1所成角为30. 【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角. 23.(Ⅰ)证明见解析;(Ⅱ)6. 【分析】(Ⅰ)通过1B C AB ⊥和AB AC ⊥可得AB ⊥平面1AB C ,即得证; (Ⅱ)设11BC B C O =,作1OE AB ⊥于E ,连结BE ,可得EBO ∠为1BC 与平面11ABB A 所成角,求出相关长度即可求解.【详解】(Ⅰ)证明:∵1B C ⊥平面ABC ,∴1B C AB ⊥, 又AB AC ⊥,1AC B C C ⋂=, 所以AB ⊥平面1AB C ,AB ⊂平面11ABB A ,所以平面1AB C ⊥平面11ABB A ; (Ⅱ)设11BC B C O =,作1OE AB ⊥于E ,连结BE ,∵平面1AB C ⊥平面11ABB A 于1AB ,∴OE ⊥平面11ABB A , ∴EBO ∠为1BC 与平面11ABB A 所成角,由已知2AB AC ==,123BB =,得12B C =,122B A =, ∴223BO BC OC =+=,在等腰直角1AB C 中,22OE =, 所以2sin OE EBO OB ∠==,即1BC 与平面11ABB A 所成角的正弦值为26. 【点睛】方法点睛:求线面角或面面角的常用方法,根据图形结构常用建立坐标系利用向量法求解或直接用几何法求解,向量法的往往更简单有效. 24.(1)证明见解析;(2)3V =. 【分析】(1)设BD 与EC 交于点O ,连接AO ,由四边形BCDE 为菱形,可得BD EC ⊥,再利用线面垂直的判定定理即可证明. (2)求出四棱锥A BCDE -的高为32,即三棱锥A BCD -的高,再利用等体积法即可求解. 【详解】(1)设BD 与EC 交于点O ,连接AO .因为BC BE ED ==,//BC DE ,所以四边形BCDE 为菱形, 所以BD EC ⊥,又AB EC ⊥,ABBD B =,所以EC ⊥平面ABD ,因为AD ⊂平面ABD ,所以EC AD ⊥. (2)因为在菱形BCDE 中,π3EDC ∠=,2BC BE ==, 所以2CE =,23BD =.因为H 为线段BD 的一个四等分点(靠近点B ),所以1342BH BD ==. 因为AH ⊥平面BCDE ,所以AH ⊥ BD , 又π3ABD ∠=,所以3tan 2AH BH ABD =∠=,所以四棱锥A BCDE -的高为32. 即三棱锥D ABC -的高为32. 易得BCD 的面积11231322BCDSBD OC =⋅=⨯⨯=, 所以三棱锥D ABC -的体积1333322A BCD D ABC V V --==⨯⨯=. 【点睛】方法点睛:本题考查了证明异面直线垂直以及求三棱锥的体积,常用方法如下: (1)证明线线垂直的常法:①利用特殊图形中的垂直关系;②利用等腰三角形底边中线的性质;③利用勾股定理的逆应用;④利用直线与平面垂直的性质. (2)求体积的常用方法:①直接法;②割补法;③等体积法. 25.(Ⅰ)证明见解析;(Ⅱ)3. 【分析】(Ⅰ)通过证明平面//OFG 平面PAB ,进一步得出结论; (Ⅱ)利用等体积法即1124A PFB A PDB P ABCD V V V ---==,进一步求出答案. 【详解】(Ⅰ)如图,连接OF ,OG ∵O 是BD 中点,F 是PD 中点,∴//OF PB ,而OF ⊂/平面PAB ,PB ⊂平面PAB , ∴//OF 平面PAB ,又∵O 是AC 中点,G 是BC 中点,∴//OG AB ,而OG ⊂/平面PAB ,AB 平面PAB ,∴//OG 平面PAB ,又OGOF O =∴平面//OFG 平面PAB ,即//FG 平面PAB .(Ⅱ)∵PD ⊥底面ABCD ,∴PD AO ⊥,又四边形ABCD 为菱形, ∴BD AO ⊥,又AD DB D =,∴AO ⊥平面PDB ,而F 为PD 的中点,∴111122sin 60224433A PFB A PDB P ABCD V V V ︒---===⨯⨯⨯⨯⨯=. 【点睛】本题主要考查立体几何的知识点,属于中档题. 立体几何常用的三种解题方法为: (1)分割法; (2)补形法; (3)等体积法.26.(1)证明见解析;(2. 【分析】(1)在正方体1111ABCD A B C D -中,易证1,C O BD CO BD ⊥⊥,由线面垂直的判定定理得到BD ⊥平面1C OC ,然后再利用面面垂直的判定定理证明.(2)由(1)知BD ⊥平面1C OC ,且平面1C BD ⋂平面CBD BD =,得到1C OC ∠是二面角1C BD C --的平面角 ,然后在1Rt C OC ∆中求解. 【详解】(1)∵在正方体1111ABCD A B C D -中, 点O 是BD 中点 , 又11BC DC = , BC DC = ,∴ 1,C O BD CO BD ⊥⊥11,C O CO O C O =⊂平面1,C OC CO ⊂平面1C OC ,BD ∴⊥平面1C OC ,又∵BD ⊂平面11BDD B , ∴平面11BDD B ⊥平面1C OC .… (2)由(1)知:平面1C BD ⋂平面CBD BD =,11,C O BD C O ⊥⊂半平面1;,C BD CO BD CO ⊥⊂ 半平面;CBD所以1C OC ∠是二面角1C BD C --的平面角则在正方体1111ABCD A B C D -中11,2C C OC ==∴在1Rt C OC ∆中,11tan C CC OC OC∠==故二面角1C BD C -- .【点睛】本题主要考查线面垂直,面面垂直的判定定理以及二面角的求法,还考查了逻辑推理和运算求解的能力,属于中档题.。
立体几何初步空间几何与点线面单元过关检测卷(四)附答案人教版高中数学考点大全辅导班专用
高中数学专题复习
《立体几何初步空间几何与点线面》单元过关检
测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I 卷(选择题)
请点击修改第I 卷的文字说明 评卷人
得分 一、选择题
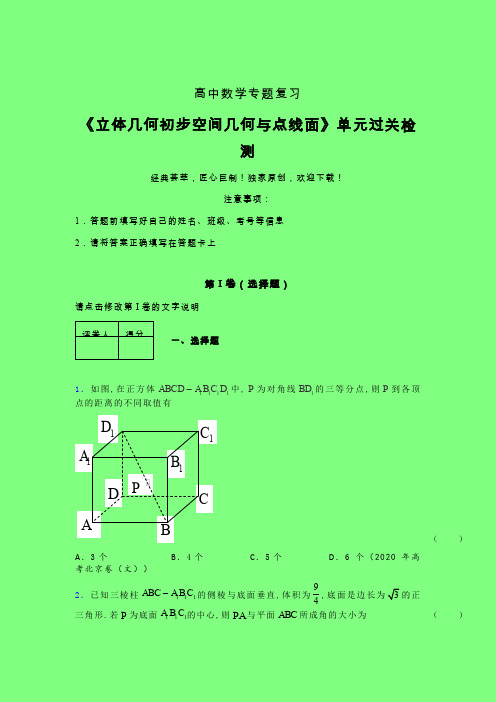
1.如图,在正方体1111ABCD A B C D -中,P 为对角线1BD 的三等分点,则P 到各顶点的距离的不同取值有 ( ) A .3个
B .4个
C .5个
D .6个(2020年高考北京卷(文))
2.已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94
,底面是边长为3的正三角形.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为 ( ) 1D 1B P
D 1C
C B
A 1A。
立体几何初步空间几何与点线面单元过关检测卷(四)附答案人教版高中数学高考真题汇编
高中数学专题复习
《立体几何初步空间几何与点线面》单元过关检
测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I 卷(选择题)
请点击修改第I 卷的文字说明 评卷人
得分 一、选择题
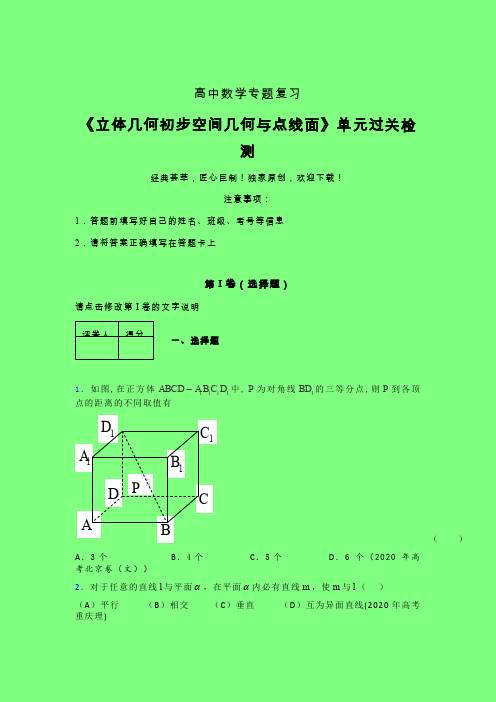
1.如图,在正方体1111ABCD A B C D -中,P 为对角线1BD 的三等分点,则P 到各顶点的距离的不同取值有 ( ) A .3个
B .4个
C .5个
D .6个(2020年高考北京卷(文))
2.对于任意的直线l 与平面α,在平面α内必有直线m ,使m 与l ( )
(A )平行 (B )相交 (C )垂直 (D )互为异面直线(2020年高考重庆理) 1D 1B P
D 1C
C B
A 1A。
厦门市必修第二册第三单元《立体几何初步》检测(包含答案解析)

一、选择题1.在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,15AA =,则V 的最大值是( )A .4πB .92πC .1256πD .323π 2.球面上有,,,A B C D 四个点,若,,AB AC AD 两两垂直,且4AB AC AD ===,则该球的表面积为( )A .803πB .32πC .42πD .48π 3.如图,梯形ABCD 中,AD ∥BC ,1AD AB ==,AD AB ⊥,45BCD ∠= ,将ABD ∆沿对角线BD 折起.设折起后点A 的位置为A ',并且平面A BD '⊥平面BCD . 给出下面四个命题: ①A D BC '⊥;②三棱锥A BCD '-的体积为22; ③CD ⊥平面A BD ';④平面A BC '⊥平面A DC '.其中正确命题的序号是( )A .①②B .③④C .①③D .②④ 4.如图所示,AB 是⊙O 的直径,VA 垂直于⊙O 所在的平面,点C 是圆周上不同于A ,B 的任意一点,M ,N 分别为VA ,VC 的中点,则下列结论正确的是( )A .MN //ABB .MN 与BC 所成的角为45° C .OC ⊥平面VACD .平面VAC ⊥平面VBC5.如图,在长方体1111ABCD A B C D -中,13,2,4AA AB AD ===,点M 是棱AD 的中点,点N 在棱1AA 上,且满足12AN NA =,P 是侧面四边形11ADD A 内的一动点(含边界),若1//C P 平面CMN ,则线段1C P 长度的取值范围是( )A .[3,17]B .[2,3]C .[6,22]D .[17,5] 6.已知三棱锥A BCD -中,侧面ABC ⊥底面BCD ,ABC 是边长为3的正三角形,BCD 是直角三角形,且90BCD ∠=︒,2CD =,则此三棱锥外接球的体积等于( )A .43πB .323πC .12πD .643π 7.菱形ABCD 的边长为3,60B ∠=,沿对角线AC 折成一个四面体,使得平面ACD ⊥平面ABC ,则经过这个四面体所有顶点的球的表面积为( )A .15πB .12πC .8πD .6π8.直三棱柱111ABC A B C -的6个顶点在球O 的球面上.若3AB =,4AC =.AB AC ⊥,112AA =,则球O 的表面积为( )A .1694πB .169πC .288πD .676π 9.半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的棱长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.一个二十四等边体的各个顶点都在同一个球面上,若该球的表面积为16π,则该二十四等边体的表面积为( )A .123+B .183+C .2483+D .363+10.点M ,N 分别是棱长为2的正方体1111ABCD A B C D -中棱BC ,1CC 的中点,动点P 在正方形11BCC B (包括边界)内运动.若1//PA 面AMN ,则1PA 的长度范围是( )A .2,5⎡⎤⎣⎦B .32,52⎡⎤⎢⎥⎣C .32,32⎡⎤⎢⎥⎣⎦D .[]2,311.棱长为2的正方体1111ABCD A B C D -中,,E F 分别是棱11C D 和11C B 的中点,则经过点,,B E F 的平面截正方体所得的封闭图形的面积为( )A .92B .310C .32D .10 12.已知,a b 是两条直线,,αβ是两个平面,则a b ⊥的一个充分条件是( ) A .a α⊥,b β//,αβ⊥B .a α⊥,b β⊥,//αβC .a α⊂,b β⊥,//αβD .a α⊂,b β//,αβ⊥13.下列命题中正确的个数有( )个①不共面的四点中,其中任意三点不共线②依次首位相接的四条线段必共面③若点,,,A B C D 共面,点,,,A B C E 共面,则点,,,,A B C D E 共面④若直线,a b 共面,直线,a c 共面,则直线,b c 共面A .1B .2C .3D .414.设l 是直线,α,β是两个不同的平面,下列命题正确的是( )A .若//l α,//l β,则//αβB .若αβ⊥,//l α,则l β⊥C .若αβ⊥,l α⊥,则//l βD .若//l α,l β⊥,则αβ⊥ 二、解答题15.如图所示的四棱锥E -ABCD 中,底面ABCD 为矩形,AE =EB =BC =2,AD ⊥平面ABE ,且CE 上的点F 满足BF ⊥平面ACE .(1)求证:AE ∥平面BFD ;(2)求三棱锥C -AEB 的体积.16.如图所示,在四面体ABCD 中,点P ,Q ,R 分别为棱BC ,BD ,AD 的中点,AB BD ⊥,2AB =,3PR =,22CD =.(1)证明://CD 平面PQR ;(2)证明:平面ABD ⊥平面BCD .17.如图,在正三棱柱111ABC A B C -中,233AB =,12A A =,D ,E ,F 分别为线段AC ,1A A ,1C B 的中点.(1)证明://EF 平面ABC ;(2)求直线1C B 与平面BDE 所成角的正弦值.18.如图,在三棱柱111ABC A B C -中,1CC ⊥面ABC ,2AC BC ==,22AB =,14CC =,M 是棱1CC 上一点.(1)若,M N 分别是1CC ,AB 的中点,求证://CN 面1AB M ;(2)若132C M =,求二面角1A B M C --的大小. 19.如图,已知AF ⊥平面ABCD ,四边形ABEF 为矩形,四边形ABCD 为直角梯形,90DAB ∠=︒,//AB CD ,2AD AF CD ===,4AB =.(1)求证:AC ⊥平面BCE ;(2)求三棱锥E BCF -的体积.20.如图,在组合体中,ABCD -A 1B 1C 1D 1是一个长方体,P -ABCD 是一个四棱锥.AB =2,BC =3,点P ∈平面CC 1D 1D 且PD =PC =2(1)证明:PD ⊥平面PBC ;(2)求直线PA 与平面ABCD 所成角的正切值;(3)若AA 1=a ,当a 为何值时,PC //平面AB 1D .21.如图,四面体ABCD 中,O ,E 分别是BD 、BC 的中点,2CA CB CD BD ====,2AB AD ==.(1)求证:AO ⊥平面BCD ;(2)若G 为AO 上的一点,且2AG GO =,求证://AC 平面GDE .22.如图,四面体ABCD 中,点E ,F 分别为线段AC ,AD 的中点,平面EFNM ⋂平面BCD MN =,90CDA CDB ∠=∠=︒,DH AB ⊥,垂足为H .(1)求证://EF MN;(2)求证:平面CDH⊥平面ABC.23.如图,棱长为2的正方体ABCD—A1B1C1D1,E、F分别为棱B1C1、BB1中点,G在A1D 上且DG=3GA1,过E、F、G三点的平面α截正方体.(1)作出截面图形并求出截面图形面积(保留作图痕迹);(2)求A1C1与平面α所成角的正弦值. (注意:本题用向量法求解不得分)24.如图,在五面体ABCDEF中,FA⊥平面ABCD,AD//BC//FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=12 AD.(I )证明:平面AMD ⊥平面CDE ;(II )求二面角A ﹣CD ﹣E 的余弦值.25.已知四棱锥P ABCD -的底面ABCD 是菱形,PD ⊥平面ABCD ,2AD PD ==,60DAB ∠=,F ,G 分别为PD ,BC 中点,AC BD O =.(Ⅰ)求证:FG ∥平面PAB ;(Ⅱ)求三棱锥A PFB -的体积;26.如图甲,边长为2的正方形ABCD 中,E 是AB 边的中点,F 是BC 边上的一点,对角线AC 分别交DE 、DF 于M 、N 两点,将DAE ∆及DCF ∆折起,使A 、C 重合于G 点,构成如图乙所示的几何体.(1)求证:GD EF ⊥;(2)若EF ∥平面GMN ,求三棱锥G EFD -的体积G EFD V -.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】先保证截面圆与ABC 内切,记圆O 的半径为r ,由等面积法得()68AC AB BC r ++=⨯,解得2r .由于三棱柱高为5,此时可以保证球在三棱柱内部,球的最大半径为2,由此能求出结果.【详解】解:如图,由题意可知,球的体积要尽可能大时,球需与三棱柱内切.先保证截面圆与ABC 内切,记圆O 的半径为r , 则由等面积法得1111 (682222)ABC S AC r AB r BC r =++=⨯⨯△, 所以()68AC AB BC r ++=⨯,又因为6AB =,8BC =,所以10AC =,所以2r.由于三棱柱高为5,此时可以保证球在三棱柱内部,若r 增大,则无法保证球在三棱柱内,故球的最大半径为2,所以3344322333V r πππ==⋅=. 故选:D .【点评】本题考查球的最大体积的求法,考查空间想象能力,属于中档题.2.D解析:D【分析】分析:首先求得外接球半径,然后求解其表面积即可.详解:由题意可知,该球是一个棱长为4的正方体的外接球,设球的半径为R ,由题意可得:()22222444R =++,据此可得:212R =,外接球的表面积为:2441248S R πππ==⨯=.本题选择D 选项.点睛:与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径. 3.B解析:B【分析】利用折叠前四边形ABCD 中的性质与数量关系,可证出BD DC ⊥,然后结合平面A BD ' ⊥平面BCD ,可得CD ⊥平面A BD ',从而可判断①③;三棱锥'A BCD -的体积为113226⋅=,可判断②;因为CD ⊥平面A BD ',从而证明CD A B '⊥,再证明'A B ⊥平面A DC ',然后利用线面垂直证明面面垂直.【详解】①90,BAD AD AB ︒∠==,45ADB ABD ︒∴∠=∠=,//,45AD BC BCD ︒∠=,BD DC ∴⊥,平面A BD ' ⊥平面BCD ,且平面A BD '平面BCD BD =, CD 平面A BD ',A D '⊂平面A BD ',CD A D '∴⊥,若A D BC '⊥则A D '⊥面BCD ,则A D '⊥BD ,显然不成立, 故A D BC '⊥不成立,故①错误;②棱锥'A BCD -的体积为1132⋅=,故②错误; ③由①知CD ⊥平面A BD ',故③正确;④由①知CD ⊥平面A BD ',又A B '⊂平面A BD ',CD A B '∴⊥, 又A B A D ''⊥,且'A D 、CD ⊂平面A DC ',A D CD D '=,A B '∴⊥平面A DC ',又A B '⊂平面'A BC ,∴平面'A BC ⊥平面A DC ',故④正确.故选:B .【点睛】本题通过折叠性问题,考查了面面垂直的性质,面面垂直的判定,考查了体积的计算,关键是利用好直线与平面、平面与平面垂直关系的转化,也要注意利用折叠前后四边形ABCD 中的性质与数量关系.4.D解析:D【分析】由中位线性质,平移异面直线即可判断MN 不与AB 平行,根据异面直线平面角知MN 与BC 所成的角为90°,应用反证知OC 不与平面VAC 垂直,由面面垂直的判定知面VAC ⊥面VBC ,即可知正确选项.【详解】M ,N 分别为VA ,VC 的中点,在△VAC 中有//MN AC ,在面ABC 中AB AC A =,MN 不与AB 平行;AC BC C =,知:MN 与BC 所成的角为90BCA ∠=︒;因为OC ⋂面VAC C =,OC 与平面内交线,AC VC 都不垂直,OC 不与平面VAC 垂直; 由VA ⊥面ABC ,BC ⊂面ABC 即VA BC ⊥,而90BCA ∠=︒知AC BC ⊥,AC VA A ⋂=有BC ⊥面VAC ,又BC ⊂面VBC ,所以面VAC ⊥面VBC ; 故选:D【点睛】本题考查了异面直线的位置关系、夹角,以及线面垂直的性质,面面垂直判定的应用,属于基础题.5.C解析:C【分析】首先找出过点1C 且与平面CMN 平行的平面,然后可知点P 的轨迹即为该平面与侧面四边形11ADD A 的交线段,进而可以利用解三角形的知识求出线段1C P 长度的取值范围.【详解】 如图所示:,取11A D 的中点G ,取MD 的中点E ,1A G 的中点F ,1D D 的三等分点H 靠近D ,并连接起来.由题意可知1//C G CM ,//GH MN ,所以平面1//C GH 平面CMN .即当点P 在线段GH 上时,1//C P 平面CMN .在1H C G 中,2212222C G =+=2212222C H =+=22GH =, 所以1H C G 为等边三角形,取GH 的中点O ,1226C O ==故线段1C P 长度的取值范围是6,22].故选:C .【点睛】本题主要考查线面平行,面面平行的判定定理和性质定理的应用,以及解三角形,意在考查学生的逻辑推理能力和数学运算能力,属于中档题.6.B解析:B【分析】把三棱锥放入长方体中,根据长方体的结构特征求出三棱锥外接球的半径,再计算三棱锥外接球的体积.【详解】三棱锥A BCD -中,侧面ABC ⊥底面BCD ,把该三棱锥放入长方体中,如图所示;且333AM AB ==; 设三棱锥外接球的球心为O ,则2233333AG AM ==⨯=,112OG CD ==, 所以三棱锥外接球的半径为22221(3)2R OA OG AG ==+=+=, 所以三棱锥外接球的体积为3344232333R V πππ===. 故选:B .【点睛】本题考查了三棱锥外接球的体积计算问题,也考查了数形结合与转化思想,是中档题. 7.A解析:A【分析】首先根据已知条件找到四面体外接球的球心,再求出半径,即可得到球体的表面积.【详解】如图所示,1O ,2O 分别为ABC 和DAC △的外接圆圆心,因为菱形ABCD ,60B ∠=,所以ABC 和DAC △为等边三角形.设E 为AC 的中点,连接DE ,BE ,则DE AC ⊥,BE AC ⊥,又因为平面ACD ⊥平面ABC AC =,所以DE ⊥平面ABC .分别过1O ,2O 作垂直平面ABC 和平面ACD 的直线,则交点O 为四面体ABCD 外接球的球心.因为22333322⎛⎫==-= ⎪⎝⎭EB DE ,四边形12OO EO 为矩形,所以12==O B DO 1212===O E O E OO .2,表面积为15π. 故选:A【点睛】 本题主要考查四面体外接球的表面积,根据题意确定外接球的球心为解题关键,属于中档题.8.B解析:B【分析】由于直三棱柱111ABC A B C -的底面ABC 为直角三角形,我们可以把直三棱柱111ABC A B C -补成四棱柱,则四棱柱的体对角线是其外接球的直径,求出外接球的直径后,代入外接球的表面积公式,即可求出该三棱柱的外接球的表面积.【详解】解:将直三棱柱补形为长方体1111ABEC A B E C -,则球O 是长方体1111ABEC A B E C -的外接球.所以体对角线1BC 的长为球O 的直径.因此球O 的外接圆直径为213R ==,故球O 的表面积24169R ππ=.故选:B.【点睛】本题主要考查球的内接体与球的关系、球的半径和球的表面积的求解,考查运算求解能力,属于基础题型.9.C解析:C【分析】通过二十四等边体的外接球表面积求得半径,进而计算出二十四等边体的边长,进而计算出二十四等边体的表面积.【详解】由于二十四等边体的外接球表面积为16π,设其半径为r ,则2416r π=π,解得2r .设O 为球心,依题意可知四边形,,,A B C D 分别为正方体侧棱的中点,所以ABCD 正方形,由于2OA OB OC OD ====,所以四边形ABCD 是正方形,AB ==所以二十四等边体的边长为2.所以二十四等边体的边长的表面积为122622sin 823π⨯⨯+⨯⨯⨯⨯2483=+.故选:C【点睛】本小题主要考查几何体外接球有关计算,考查空间想象能力,属于中档题.10.B解析:B【分析】取11B C ,1B B 中点E ,F ,得平面1A EF ∥平面AMN .进而得到点P 的轨迹为线段EF ,又因为1A EF 为等腰三角形,进而便可得出答案.【详解】取11B C ,1B B 中点E ,F , 连接1A E 、1A F .则1A E ∥AM .EF ∥MN .又因为1A E EF E ⋂= .所以平面1A EF ∥平面AMN .又因为动点P 在正方形11BCC B (包括边界)内运动,所以点P 的轨迹为线段EF .又因为正方体1111ABCD A B C D -的棱长为2,所以115A E A F ==2EF = 所以1A EF 为等腰三角形.故当点P 在点E 或者P 在点F 处时,此时1PA 5当点P 为EF 中点时,1PA 22232(5)()22-= . 故选:B.【点睛】本题主要考查点、线、面间的距离问题,考查学生的运算能力及推理转化能力,属于中档题目,解决本题的关键是通过构造平行平面寻找点P 的位置.11.A解析:A【分析】画出所截得的封闭图形,根据正方体的性质可求.【详解】如图所示,经过点,,B E F 的平面截正方体所得的封闭图形为四边形BDEF .,E F 分别是棱11C D 和11C B 的中点,//EF BD ∴,且12EF BD =. 正方体棱长为2,22,2BD EF ∴==∴四边形BDEF 是一个等腰梯形.在1Rt BB F 中,22215BF =+= 2232522⎛⎫-= ⎪ ⎪⎝⎭. 所以梯形BDEF 的面积为322+229222⨯=. 故选:A .【点睛】本题考查正方体的性质,属于基础题.12.C解析:C【分析】在A 中,a 与b 可以成任意角;在B 中a 与b 是平行的;在C 中,可得b α⊥,从而得到a b ⊥;在D 中,可得a 与b 可以成任意角,从而得到正确结果.【详解】由a ,b 是两条不同的直线,,αβ是两个不同的平面,在A 中,a α⊥,b β//,αβ⊥,因为b 的方向不确定,则a 与b 可以成任意角,故A 错误;在B 中,a α⊥,b β⊥,//αβ,根据对应的性质可知,可知a 与b 是平行的,故B 错误;在C 中,由a α⊂,b β⊥,//αβ,可知b α⊥,由线面垂直的性质可知a b ⊥,故C 正确;在D 中,a α⊂,b β//,αβ⊥,可得a 与b 可以成任意角,故D 错误.故选:C.【点睛】该题考查线线垂直的充分条件的判断,考查空间中线线、线面、面面间的位置关系等基础知识,在解题的过程中,注意结合图形去判断,属于中档题目.13.A解析:A【分析】假设存在三点共线,则四个点必共面,可判断①;借助空间四边形可判断②;当A ,B ,C 共线时,可判断③;由共面不具有传递性可判断④【详解】①正确,可以用反证法证明,假设存在三点共线,则四个点必共面,与不共面的四点矛盾;②不正确,例如空间四边形的四个顶点就不共面;③不正确,A ,B ,C 共线时,这两平面有三个公共点A ,B ,C ;④不正确,共面不具有传递性,若直线,a b 共面,直线,a c 共面,则直线,b c 可能异面. 故选:A【点睛】本题考查了空间中点线面的位置关系判断,考查了学生综合分析,空间想象,逻辑推理能力,属于中档题14.D解析:D【分析】利用空间线线、线面、面面的位置关系对选项进行逐一判断,即可得到答案.A.若//l α,//l β,则α与β可能平行,也可能相交,所以不正确.B.若αβ⊥,//l α,则l 与β可能的位置关系有相交、平行或l β⊆,所以不正确.C.若αβ⊥,l α⊥,则可能l β⊆,所以不正确.D.若//l α,l β⊥,由线面平行的性质过l 的平面与α相交于l ',则ll ',又l β⊥.所以l β'⊥,所以有αβ⊥,所以正确.故选:D【点睛】本题考查面面平行、垂直的判断,线面平行和垂直的判断,属于基础题. 二、解答题15.(1)证明见解析;(2)43. 【分析】(1)由ABCD 为矩形,易得G 是AC 的中点,又BF ⊥平面ACE ,BC =BE ,则F 是EC 的中点,从而FG ∥AE ,再利用线面平行的判定定理证明.(2)根据AD ⊥平面ABE ,易得AE ⊥BC ,再由BF ⊥平面ACE ,得到AE ⊥BF ,进而得到AE ⊥平面BCE ,然后由C AEB A BCE V V --=求解.【详解】(1)如图所示:因为底面ABCD 为矩形,所以AC ,BD 的交点G 是AC 的中点,连接FG ,∵BF ⊥平面ACE ,则CE ⊥BF ,而BC =BE , ∴F 是EC 的中点,∴FG ∥AE .又AE ⊄平面BFD ,FG ⊂平面BFD ,∴AE ∥平面BFD .(2)∵AD ⊥平面ABE ,AD ∥BC ,∴BC ⊥平面ABE ,则AE ⊥BC .又BF ⊥平面ACE ,则AE ⊥BF ,∴AE ⊥平面BCE .∴三棱锥C -AEB 的体积11142223323C AEB A BCE BCE V V S AE --⎛⎫==⋅=⨯⨯⨯⨯= ⎪⎝⎭△.方法点睛:1、判断或证明线面平行的常用方法:(1)利用线面平行的定义,一般用反证法;(2)利用线面平行的判定定理(a ⊄α,b ⊂α,a ∥b ⇒a ∥α),其关键是在平面内找(或作)一条直线与已知直线平行,证明时注意用符号语言的叙述;(3)利用面面平行的性质定理(α∥β,a ⊂α⇒a ∥β);(4)利用面面平行的性质(α∥β,a ⊄β,a ∥α⇒a ∥β).16.(1)证明见解析;(2)证明见解析.【分析】(1)推导出//PQ DC ,由此能证明//CD 平面PQR .(2)推导//RQ AB ,//PQ CD ,且12RQ AB =,12PQ CD =,从而RQ BD ⊥,PQ RQ ⊥,进而RQ ⊥平面BCD ,由此能证明平面ABD ⊥平面BCD .【详解】证明:(1)点P ,Q 分别为棱BC ,BD 的中点,//PQ DC ∴,PQ ⊂平面PQR ,CD ⊂/平面PQR ,//CD ∴平面PQR .(2)点P ,Q ,R 分别为棱BC ,BD ,AD 的中点,//RQ AB ∴,//PQ CD ,且12RQ AB =,12PQ CD =, AB BD ⊥,RQ BD ∴⊥,2AB =,3PR =,22CD =.112RQ AB ∴==,122PQ CD ==, 222PQ QR PR ∴+=,PQ RQ ∴⊥,BD PQ Q ⋂=,RQ ∴⊥平面BCD ,RQ ⊂平面ABD ,∴平面ABD ⊥平面BCD .【点睛】思路点睛:证明线面平行、面面垂直的常见思路:(1)证明线面平行的思路:通过三角形中位线或者证明平行四边形说明线线平行或者证明面面平行;(2)证明面面垂直的思路:证明线面垂直结合面面垂直的判定定理完成证明.17.(1)证明见解析;(2)33. 【分析】(1)取BC 的中点G ,连结AG ,FG ,易得四边形AEFG 是平行四边形,从而//EF AG ,然后利用线面平行的判定定理证明.(2)以D 为坐标原点,建立空间直角坐标系,分别求得1BC 的坐标和平面BDE 的一个法向量(),,n a b c =,再由111sin cos ,n BC n BC n BC θ⋅=<>=⋅求解.【详解】(1)如图,取BC 的中点G ,连结AG ,FG .在1BCC 中,因为F 为1C B 的中点,所以1//FG C C ,112FG C C =. 在三棱柱111ABC A B C -中,11//A A C C ,11A A C C =,且E 为1A A 的中点,所以//FG EA ,FG EA =.所以四边形AEFG 是平行四边形.所以//EF AG .因为EF ⊄平面ABC ,AG ⊂平面ABC ,所以//EF 平面ABC .(2)以D 为坐标原点,如图所示建立空间直角坐标系,因为23AB =1BD =, 所以()0,0,0D ,()0,1,0B ,13C ⎫⎪⎝⎭,3E ⎛⎫ ⎪⎝⎭, 所以131,2BC ⎛⎫=- ⎪⎝⎭,()0,1,0DB =,3DE ⎛⎫=- ⎪⎝⎭, 设平面BDE 的一个法向量为(),,n a b c =,则00DB n DE n ⎧⋅=⎨⋅=⎩,即0303b ac =⎧⎪⎨-+=⎪⎩, 取3a =,则1c =,所以(3,0,1)n =, 所以1113312cos ,||||1643n BC n BC n BC ⋅+<>===⋅, 直线1C B 与平面BDE 所成角为θ,则θ与1,n BC <>或它的补角互余, 所以11133sin cos ,n BC n BC n BC θ⋅=<>==⋅. 【点睛】方法点睛:利用向量求线面角的方法:(1)分别求出斜线和它所在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角);(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角. 18.(1)证明见解析;(2)4π. 【分析】(1)连接A 1B 交AB 1于P ,根据平行四边形AA 1B 1B 的性质,结合三角形中位线定理,可得NP 与CM 平行且相等,从而四边形MCNP 是平行四边形,可得CN ∥MP ,再结合线面平行的判定定理,得到CN ∥平面AB 1M ;(2)以C 为原点,CA ,CB ,CC 1分别为x 轴,y 轴,z 轴建立空间直角坐标系如图,根据题意得到C 、A 、、B 1、M 各点的坐标,从而得到向量AB 、1B M 的坐标,再利用垂直向量数量积为零的方法,列方程组可求出平面AMB 1的法向量n =(5,﹣3,4),结合平面MB 1C 的一个法向量CA =(2,0,0),利用空间两个向量的夹角公式,得到n 与CA 的夹角,即得二面角A ﹣MB 1﹣C 的大小.【详解】(1)连结A 1B 交AB 1于P .因为三棱柱ABC -A 1B 1C 1,所以P 是A 1B 的中点. 因为M ,N 分别是CC 1,AB 的中点,所以NP // CM ,且NP = CM ,所以四边形MCNP 是平行四边形,所以CN //MP .因为CN ⊄平面AB 1M ,MP ⊂平面AB 1M ,所以CN //平面AB 1M .(2)因为AC =BC =2,22AB =, 所以由勾股定理的逆定理知BC ⊥AC .又因为CC 1⊥平面ABC ,以C 为原点,CA ,CB ,CC 1分别为x 轴,y 轴,z 轴建立空间直角坐标系C-xyz .因为132C M =,所以C (0,0,0),A (2,0,0),B 1(0,2,4),5(0,0,)2M ,5(2,0,)2AM =-, 13(0,2,)2B M =--. 设平面1AMB 的法向量(,,)n x y z =,则0n AM ⋅=,10n B M ⋅=. 即5(2,0,)(,,)=023(0,2,)(,,)=0.2x y z x y z ⎧-⋅⎪⎪⎨⎪--⋅⎪⎩,,令5x =,则3,4y z =-=,即(5,3,4)n =-.又平面MB 1C 的一个法向量是=(2,0,0)CA ,所以2cos ,>=||||n CA n CA n CA ⋅<=. 由图可知二面角A-MB 1-C 为锐角,所以二面角A-MB 1-C 的大小为4π.【点睛】关键点睛:解题关键在于由勾股定理的逆定理知BC ⊥AC .又因为CC 1⊥平面ABC ,进而 以C 为原点,CA ,CB ,CC 1分别为x 轴,y 轴,z 轴建立空间直角坐标系,进而利用法向量计算二面角,难度属于中档题19.(1)证明见解析;(2)83.【分析】(1)先证明AC ⊥BE ,再取AB 的中点M ,连接CM ,经计算,利用勾股定理逆定理得到AC ⊥BC ,然后利用线面垂直的判定定理证得结论;(2)利用线面垂直的判定定理证得CM ⊥平面BEF ,即为所求三棱锥的高,进而计算得到其体积.【详解】解:(1)证明:∵四边形ABEF 为矩形∴//AF BE∵AF ⊥平面ABCD ∴BE ⊥平面ABCD∵AC ⊂平面ABCD ∴AC BE ⊥.如图,取AB 的中点M ,连接CM ,∴122AM AB DC === ∵//AM DC ,90MAD ∠=︒,2AM DC AD === ∴四边形ADCM 是正方形.∴90ADC ∠=︒∴222448C AD DC =+=+=,222448BC CM BM =+=+= ∵4AB =∴222AC BC AB +=∴ABC 是直角三角形∴AC BC ⊥. ∵BCBE B =,BC 、BE ⊂平面BCE ∴AC ⊥平面BCE(2)由(1)知:CM AB ⊥∵AF ⊥平面ABCD ,CM ⊂平面ABCD ∴AF CM ⊥∵AF AB A ⋂=,AF 、AB 平面ABEF∴CM ⊥平面ABEF ,∴CM ⊥平面BEF即:CM 是三棱锥C BEF -的高 ∴11182243323E BCF C BEF BEF V V CM S --==⋅=⨯⨯⨯⨯=△ 【点睛】本题考查线面垂直的证明,棱锥的体积的计算,属基础题.在利用线面垂直的判定定理证明线面垂直时一定要将条件表述全面,“两个垂直,一个相交”不可缺少.20.(1)证明见解析;(210;(3)当a =2时,PC //平面AB 1D . 【分析】(1)先证PD ⊥PC ,再由线面垂直的性质证得BC ⊥PD ,运用线面判定方法即可证明结果;(2)由题意先作出线面角,运用勾股定理计算三角形边长,最后求出线面角得正切值;(3)运用线面平行得判定定理证明即可.【详解】(1)证明:∵PD =PC =2,CD =AB =2,∴△PCD 为等腰直角三角形,所以PD ⊥PC .又∵ABCD -A 1B 1C 1D 1是一个长方体,∴ BC ⊥平面CC 1D 1D ,而P ∈平面CC 1D 1D , ∴ PD ⊂平面CC 1D 1D ,所以BC ⊥PD .又∵PC ∩BC =C ,∴ PD ⊥平面PBC .(2)如图,过P 点作PE ⊥CD ,连接AE .∵平面ABCD ⊥平面PCD ,所以PE ⊥平面ABCD ,∴∠PAE 就是直线PA 与平面ABCD 所成的角.又∵PD =PC 2,PD ⊥PC ,所以PE =1,DE =1,所以2223110AE AD DE =+=+=∴10tan 10PE PAE AE ∠=== ∴直线PA 与平面ABCD 10 (3)当a =2时,PC //平面AB 1D .理由如下:连接C 1D ,∵a =2,∴四边形CC 1D 1D 是一个正方形,∴∠C 1DC =45°,而∠PDC =45°,∴∠PDC =90°,所以C 1D ⊥PD .又∵PC ⊥PD ,C 1D 与PC 在同一个平面内,∴PC //C 1D .又∵C 1D ⊂平面AB 1C 1D∴PC //平面AB 1C 1D∴PC //平面AB 1D .【点睛】方法点睛:在证明线面垂直或者线面平行时运用其判定定理进行证明,找线线垂直的方法有:(1)运用勾股定理逆定理;(2)已知线面垂直,由其性质得线线垂直;(3)在圆中直径所对的圆周角(4)三角形相似找线线平行的方法有:(1)有中点找中点,构造三角形中位线或者平行四边形;(2)线面平行的性质定理;(3)直线平行的条件(同位角、内错角等知识).21.(1)证明见解析;(2)证明见解析.【分析】(1)连结OC ,根据等腰三角形的性质得出AO BD ⊥和CO BD ⊥,利用勾股定理的逆定理得出90AOC ︒∠=,则AO OC ⊥,最后根据线面垂直的判定定理,即可证明AO ⊥平面BCD ;(2)连接DE 交OC 于点H ,由BCD △为正三角形,得出H 为BCD △重心,最后通过线面平行的判定,即可证明//AC 平面GDE .【详解】证明:(1)证明:O ,E 分别是BD 、BC 的中点,连结OC ,∵,BO DO AB AD ==,∴AO BD ⊥,∵,BO DO BC CD ==,∴CO BD ⊥,在AOC △中,由已知可得1,AO CO ==2AC =,∴222AO CO AC +=,∴90AOC ︒∠=,即AO OC ⊥,∵BD OC O ⋂=,,BD OC ⊂平面BCD ,∴AO ⊥平面BCD ;(2)证明:连接DE 交OC 于点H ,∵BCD △正三角形,,O E 分别为,BD BC 的中点,∴H 为BCD △重心,∴2CH HO =且2AG GO =, ∴AG CH GO HO=,∴//AC GH ,∴GH ⊂平面GDE ,AC ⊄平面GDE , ∴//AC 平面GDE .【点睛】关键点点睛:本题考查等腰三角形的性质、线面垂直和线面平行的判定定理,熟练掌握三角形的重心的性质是解题的关键.22.(1)证明见解析;(2)证明见解析.【分析】本题考查线面平行与线面垂直的判定,难度不大.(1)利用线面平行的判定定理证得//EF 平面BCD ,进而利用线面平行的性质定理证得; (2)利用线面垂直的判定定理证得CD ⊥平面ADB ,进而证得AB ⊥平面CDH ,然后由面面垂直判定定理证得结论.【详解】证明:(1)因为点E 、F 分别为线段AC 、AD 的中点,EF ∴为ACD △的中位线,则//EF CD ,CD ⊂平面BCD ,EF ⊄平面BCD ,//EF ∴平面BCD ,又EF ⊂平面EFNM ,平面EFNM ⋂平面BCD MN =,//EF MN ∴;(2)90CDA CDB ∠=∠=︒,CD DA ∴⊥,CD DB ⊥,DA DB D ⋂=,DA ⊂平面ADB ,DB ⊂平面ADB , CD 平面ADB ,CD AB ∴⊥又DH AB ⊥,DH CD D ⋂=,DC ⊂平面DCH ,DH ⊂平面DCH ,AB ∴⊥平面CDH ,AB ⊂平面ABC ,∴平面CDH ⊥平面ABC.【点睛】要证线线平行,常常先证线面平行,综合利用线面平行的判定与性质进行证明;要证面面垂直,常常先证线面垂直,而要证线面垂直,又常常先证另一个线面垂直.23.(1)截面见解析,面积为2;(2)12. 【分析】(1)先根据线面平行的性质定理确定出,EF MN 的位置关系,再根据,EF MN 的长度关系确定出,M N 的位置,从而截面的形状可确定以及截面面积可求;(2)记11ME AC H =,通过线面垂直证明1A HG ∠即为所求的线面角,从而计算出11A C 与平面α所成角的正弦值.【详解】(1)如图截面为矩形EFNM :因为//EF 平面11ADD A ,且平面EFNM平面11ADD A MN =,所以//EF MN , 又因为111111////,==22EF BC AD EF BC AD ,且3DG GA =,所以可知111//,2MN AD MN AD =, 所以//,MN EF MN EF =,所以可知,M N 为棱111,AA A D 的中点, 所以四边形EFNM 为矩形,且112,2EF ME =+==,所以截面EFNM 的面积为22;(2)记11ME AC H =,连接GH ,如图所示: 因为//NF AB ,AB ⊥平面11AA D D ,所以NF ⊥平面11AA D D ,又1AG ⊂平面11AA D D ,所以1NF A G ⊥, 由(1)知1//MN AD 且11A D AD ⊥,所以1MN A D ⊥,所以1MN AG ⊥,且MN NF N =,1A G ⊥平面EFNM ,所以11A C 与平面α所成角为1A HG ∠, 因为111222442AG A D ===,111122A H AC ==1111sin 2A G A HG A H ∠==,所以11A C 与平面α所成角的正弦值为12. 【点睛】 方法点睛:求解线面角的正弦值的两种方法:(1)几何法:通过线面垂直的证明,找到线面角,通过长度的比值即可计算线面角的正弦值;(2)向量法:求解出直线的方向向量和平面的法向量,根据直线的方向向量与平面法向量夹角的余弦值的绝对值等于线面角的正弦值求解出结果.24.(I)证明见解析;(II)3 . 【分析】(I )取AD 的中点P ,连结EP PC ,,MP ,利用平行四边形及线面垂直的性质定理证明,,PE PC AD 相互垂直,从而可证明EC 与,MP MD 垂直,然后可得线面垂直,面面垂直;(II )取Q CD 为的中点,连结,PQ EQ ,可得EQP ∠为二面角A CD E --的平面角,在Rt EPQ △中求得其余弦值.【详解】(Ⅰ)证明:取AD 的中点P ,连结EP PC ,.则EFAP =,∵//FE AP =,∴四边形FAPE 是平行四边形,∴//FA EP =,同理,//AB PC =.又∵FA ⊥平面ABCD ,∴EP ⊥平面ABCD ,而PC AD ,都在平面ABCD 内,∴.EP PC EP AD ⊥⊥,由AB AD ⊥,可得PC AD ⊥,设FA a =,则2.EP PC PD a CD DE EC a ======,所以△ECD 为正三角形.∵DC DE =且M 为CE 的中点,∴DM CE ⊥.连结MP ,则.MP CE ⊥PM ∩MD =M ,而PM ,MD 在平面AMD 内 ,∴CE ⊥平面AMD而CE ⊂平面CDE ,所以平面AMD ⊥CDE .(Ⅱ)解:取Q CD 为的中点,连结,PQ EQ ,∵CE DE =,∴.EQ CD ⊥∵PC PD =,∴PQ CD ⊥∴EQP ∠为二面角A CD E --的平面角.由(Ⅰ)可得, 62EP PQ EQ a PQ a ==⊥,,. 于是在Rt EPQ △中,3cos 3PQ EQP EQ ∠==. ∴二面角A CD E --的余弦值为3. 【点睛】 方法点睛:本题考查证明面面垂直,考查求二面角.求二面角的几何方法:一作二证三计算,一作:作出二面角的平面角;二证:证明所作的角是二面角的平面角;三计算:在三角形中求出这个角(这个角的余弦值).25.(Ⅰ)证明见解析;(Ⅱ)33 . 【分析】(Ⅰ)通过证明平面//OFG 平面PAB ,进一步得出结论;(Ⅱ)利用等体积法即1124A PFB A PDB P ABCD V V V ---==,进一步求出答案. 【详解】(Ⅰ)如图,连接OF ,OG ∵O 是BD 中点,F 是PD 中点,∴//OF PB ,而OF ⊂/平面PAB ,PB ⊂平面PAB ,∴//OF 平面PAB ,又∵O 是AC 中点,G 是BC 中点,∴//OG AB ,而OG ⊂/平面PAB ,AB平面PAB ,∴//OG 平面PAB ,又OG OF O =∴平面//OFG 平面PAB ,即//FG 平面PAB .(Ⅱ)∵PD ⊥底面ABCD ,∴PD AO ⊥,又四边形ABCD 为菱形,∴BD AO ⊥,又ADDB D =,∴AO ⊥平面PDB ,而F 为PD 的中点, ∴1111322sin 60224433A PFB A PDB P ABCD V V V ︒---===⨯⨯⨯⨯⨯=. 【点睛】本题主要考查立体几何的知识点,属于中档题. 立体几何常用的三种解题方法为: (1)分割法;(2)补形法;(3)等体积法.26.(1)证明见解析;(2)13; 【分析】 (1)想要证明线线垂直,就得先证明线面垂直,由于E ,F 两点都是中点,故想到取中点,构造两组线线垂直,由线面垂直的判定定理知,平面DGH ,由线面垂直的性质知,GD EF ⊥;(2)求解三棱锥的体积问题,我们通常采用等体积法,将已知的三棱锥转变成一个我们容易求解的三棱锥来求解,由于本题中,所以,平面GEF ,显然,三棱锥的高解决了,故有G EFD V -=D GEF V -=13【详解】证明:取EF 的中点为H,连接DH,GH ,在中,GE=GF ,H 是中点,,在中,DE=DF ,H 是中点, 故,, 所以平面DGH ,即GD EF ⊥. (2)EF ∥平面GMN 知,F 是BC 边上的中点,故有GE GF ⊥,在直角三角形GEF 中,GE=GF=1,故EF=,又因为, 所以,平面GEF ,故此时三棱锥的高为DG ,值是2, G EFD V -=D GEF V -=13。
立体几何第二章空间点线面的位置关系单元测试题(含详细答案解析)

第二章综合素能检测本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.直线l1∥l2,在l1上取3个点,在l2上取2个点,由这5个点能确定平面的个数为错误!()A.5B.4C.9D.1[答案] D[解析]由经过两条平行直线有且只有一个平面可知分别在两平行直线上的5个点只能确定一个平面.2.教室内有一直尺,无论怎样放置,在地面总有这样的直线,使得它与直尺所在直线错误!()A.平行B.垂直C.相交D.异面[答案] B[解析]当直尺垂直于地面时,A不对;当直尺平行于地面时,C不对;当直尺位于地面上时,D不对.3.已知m、n是两条不同直线,α、β是两个不同平面,则下列命题正确的是错误!()A.若α、β垂直于同一平面,则α与β平行B.若m、n平行于同一平面,则m与n平行C.若α、β不平行...与β平行的直线...,则在α内不存在D.若m、n不平行...垂直于同一平面...,则m与n不可能[答案] D[解析]A项,α、β可能相交,故错误;B项,直线m、n的位置关系不确定,可能相交、平行或异面,故错误;C项,若m⊂α,α∩β=n,m∥n,则m∥β,故错误;D项,假设m、n垂直于同一平面,则必有m∥n,所以原命题正确,故D项正确.4.已知α、β是两个平面,直线l⊄α,l⊄β,若以①l⊥α;②l∥β;③α⊥β中两个为条件,另一个为结论构成三个命题,则其中正确的命题有错误!()A.①③⇒②;①②⇒③B.①③⇒②;②③⇒①C.①②⇒③;②③⇒①D.①③⇒②;①②⇒③;②③⇒①[答案] A[解析]因为α⊥β,所以在β内找到一条直线m,使m⊥α,又因为l⊥α,所以l∥m.又因为l⊄β,所以l∥β,即①③⇒②;因为l∥β,所以过l可作一平面γ∩β=n,所以l∥n,又因为l⊥α,所以n⊥α,又因为n⊂β,所以α⊥β,即①②⇒③.5.如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,若过C1作C1H⊥平面ABC,垂足为H,则点H一定在导学号 92180601()A.直线AC上B.直线AB上C.直线BC上D.△ABC的内部[答案] B[解析]∵∠BAC=90°,∴BA⊥AC.又∵BC1⊥AC,∴AC⊥平面ABC1,∴平面ABC⊥平面ABC1.∵平面ABC∩平面ABC1=AB,∴C1在面ABC上的射影在直线AB上.6.设直线l⊂平面α,过平面α外一点A与l,α都成30°角的直线有错误!() A.1条B.2条C.3条D.4条[答案] B[解析]如图,和α成30°角的直线一定是以A为顶点的圆锥的母线所在直线,当∠ABC=∠ACB=30°且BC∥l时,直线AC,AB都满足条件,故选B.7.(2016·浙江文)已知互相垂直的平面α、β交于直线l.若直线m、n满足m∥α,n⊥β,则错误!()A.m∥l B.m∥nC.n⊥l D.m⊥n[答案] C[解析]选项A,只有当m∥β或m⊂β时,m∥l;选项B,只有当m⊥β时,m∥n;选项C,由于l⊂β,∴n⊥l;选项D,只有当m∥β或m⊂β时,m⊥n,故选C.8.(2016·南安一中高一检测)如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱BC 和棱CC1的中点,则异面直线AC与MN所成的角为错误!()A.30°B.45°C.60°D.90°[答案] C[解析]如图,连接A1C1、BC1、A1B.∵M、N分别为棱BC和棱CC1的中点,∴MN∥BC1。
立体几何初步空间几何与点线面单元过关检测卷(一)附答案新人教版高中数学名师一点通

高中数学专题复习
《立体几何初步空间几何与点线面》单元过关检
测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
请点击修改第I卷的文字说明
评卷人得分
一、选择题
1.已知平面α外不共线的三点A,B,C到α的距离都相等,则正确的结论是( )
A.平面ABC必平行于α
B.平面ABC必与α相交
C.平面ABC必不垂直于α
D.存在△ABC的一条中位线平行于α或在α内(2020陕西理)
2.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是
A.16πB.20πC.24πD.32π(2020全国1理)
3.连结球面上两点的线段称为球的弦.半径为4的球的两条弦AB、CD的长度分别等于27、43,M、N分别为AB、CD的中点,每条弦的两端都在球面上运动,有下列四个命题:
①弦AB、CD可能相交于点M ②弦AB、CD可能相交于点N
③MN的最大值为5 ④MN的最小值为l
其中真命题的个数为
A.1个 B.2个 C.3个 D.4个(2020江西理)。
立体几何初步空间几何与点线面单元过关检测卷(一)含答案人教版高中数学考点大全艺考生专用
高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.已知正四棱柱1111ABCD A B C D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于 ( )A .23 B .33C .23D .13(2020年普通高等学校招生统一考试大纲版数学(理)WOR D 版含答案(已校对)) 2.设有直线m 、n 和平面α、β。
下列四个命题中,正确的是 A.若m ∥α,n ∥α,则m ∥nB.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βC.若α⊥β,m ⊂α,则m ⊥βD.若α⊥β,m ⊥β,m ⊄α,则m ∥α (2020湖南理)(D )3.一个与球心距离为1的平面截球所得的圆面面积为π,则球的表面积为 (A )π28 (B )π8(C )π24(D )π4(2020全国1理)4.在正四面体P —ABC 中,D ,E ,F 分别是AB ,BC ,CA 的中点,下面四个结论中不成立的是(A)BC∥平面PDF (B )DF ⊥平面PAE(C)平面PDF ⊥平面ABC (D)平面PAE ⊥平面ABC(2020北京理) 5.设α、β 为两个不同的平面,l 、m 为两条不同的直线,且l ⊂α,m ⊂β,有如下的两个命题:①若α∥β,则l ∥m ;②若l ⊥m ,则α⊥β.那么( )(A) ①是真命题,②是假命题 (B) ①是假命题,②是真命题 (C) ①②都是真命题 (D) ①②都是假命题(2020浙江文) 6.到两互相垂直的异面的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是 (A ) 直线 (B ) 椭圆(C ) 抛物线(D ) 双曲线(2020重庆理)7.在下列命题中,真命题是( ) A .若直线m 、n 都平行于平面α,则m ∥nB .设α—l —β是直二面角,若直线m ⊥l ,则m ⊥βC .若直线m 、n 在平面α内的射影依次是一个点和一条直线,且m ⊥n ,则n 在α内或n 与α平行D .设m 、n 是异面直线,若m 与平面α平行,则n 与α相交(2020上海4) 18.没有公共点的两条直线的位置关系是-------------------------------------------------------------( )(A)异面 (B)平行 (C)异面或平行 (D)不确9.如果用a 记某三角形两边中点的连线,用α记过该三角形第三边的一个平面,那么必有( )(A)a α∥ (B)a α⊂ (C)a α⊄ (D)a a αα⊂∥或10.设四棱锥P ABCD -的底面不是平行四边形,用平面α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面α( ) A .不存在B .只有1个C .恰有4个D .有无数多个第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人得分二、填空题PABC DE(第1611.(理科做) 如图,在三棱锥A BCD -中,AB BCD ⊥平面, 90DBC ∠=,2BC BD ==,1AB =,则BC 和平面AC D 所成角的正弦值为 ▲ .12.长方体1111ABCD A B C D -中,13,2AB BC AA ===,则四面体11A BC D 的体积为13.已知正四棱锥S ABCD -中,23SA =,那么当该棱锥的体积最大时,它的高为 .14.已知n m ,是两条不同的直线,βα,为两个不同的平面,有下列四个命题: ①若βα⊥⊥n m ,,m ⊥n ,则βα⊥; ②若n m n m ⊥,//,//βα,则βα//; ③若n m n m ⊥⊥,//,βα,则βα//; ④若βαβα//,//,n m ⊥,则n m ⊥. 其中正确的命题是(填上所有正确命题的序号)____▲____.15.已知正三棱锥的底面边长为6,侧棱长为5,则此三棱锥的体积为_________. 16.在矩形ABCD 中,2AB =, 3BC =,以BC 边所在直线为轴旋转一周,则形成的几何体的侧面积为 . 12π 评卷人得分三、解答题17.(本小题满分14分)在四棱锥P -ABCD 中,AB ∥DC ,AB ⊥平面PAD , PD =AD ,AB =2DC ,E 是PB 的中点.求证:(1)CE ∥平面PAD ; (2)平面PBC ⊥平面PAB .(第11题理科EFABCDPPABC DE(第16FM【证】(1)(方法1)取PA 的中点F ,连EF ,DF .…… 2分 因为E 是PB 的中点,所以EF // AB ,且12EF AB =.因为AB ∥CD ,AB =2D C ,所以EF ∥CD ,……………… 4分EF CD =,于是四边形DCEF 是平行四边形,从而CE ∥DF ,而CE ⊄平面PAD ,DF ⊂平面PAD , 故CE ∥平面PAD . …………………… 7分 (方法2)取AB 的中点M ,连EM ,C M . ……………… 2分 因为E 是PB 的中点,所以EM // PA .因为AB ∥CD ,AB =2D C ,所以CM // AD .……………… 4分 因为EM ⊄平面PAD ,PA ⊂平面PAD , 所以EM ∥平面PAD .同理,CM ∥平面PAD . 因为EMCM M =,EM CM ⊂,平面CEM ,所以平面CEM ∥平面PAD .而CE ⊂平面PAD ,故CE ∥平面PAD .……………………… 7分(2)(接(1)中方法1)因为PD =AD ,且F 是PA 的中点,所以DF PA ⊥. 因为AB ⊥平面PAD ,DF ⊂平面PAD,所以DF AB ⊥. ……………………… 10分 因为CE ∥DF ,所以CE PA ⊥,CE AB ⊥. 因为PA AB ⊂,平面PAB ,PAAB A =,所以CE ⊥平面PAB .因为CE ⊂平面PBC ,所以平面PBC⊥平面PAB . ………………………… 14分18.如图,四棱锥P ABCD -的底面为矩形,2AB =,1BC =,,E F 分别是,A B P C 的中点,DE PA ⊥. (Ⅰ)求证:EF平面PAD ;(Ⅱ)求证:平面PAC ⊥平面PDE .(本小题满分14分)19.如图,四面体P ABC -中,,,PA AC PC BC M ⊥⊥为PB 的中点,D 为AB 的中点,且AMB 为正三角形。
立体几何初步空间几何与点线面单元过关检测卷(四)附答案人教版高中数学考点大全艺考生专用
高中数学专题复习
《立体几何初步空间几何与点线面》单元过关检
测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I 卷(选择题)
请点击修改第I 卷的文字说明 评卷人
得分 一、选择题
1.设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是
( )
A .若αβ⊥,m α⊂,n β⊂,则m n ⊥
B .若//αβ,m α⊂,n β⊂,则//m n
C .若m n ⊥,m α⊂,n β⊂,则αβ⊥
D .若m α⊥,//m n ,//n β,则αβ⊥(2020年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))
2.设A 、B 、C 、D 是空间四个不同的点,在下列命题中,不正确...的是( )
(A )若AC 与BD 共面,则AD 与BC 共面
(B )若AC 与BD 是异面直线,则AD 与BC 是异面直线
(C) 若AB =AC ,DB =DC ,则AD =BC
(D) 若AB =AC ,DB =DC ,则AD ⊥BC (2020北京文)
一、
3.在下列关于直线l 、m 与平面α、β的命题中,真命题是( )
(A)若l ⊂β且α⊥β,则l ⊥α. (B) 若l ⊥β且α∥β,则l ⊥α.
(C) 若l ⊥β且α⊥β,则l ∥α. (D) 若α∩β=m 且l ∥m,则l ∥α. (2020上海理)。
人教版数学高一第一章空间几何体单元测试精选(含答案)3
【答案】 2 1 3 4 2
评卷人 得分
三、解答题
试卷第 8页,总 11页
40.一张长为10cm ,宽为 5cm 的矩形纸,以它为侧面卷成一个圆柱,求该圆柱的体积.
125
【答案】
cm3 或 125
cm3 .
π
2π
41.如图所示,在四边形 ABCD 中, A0, 0 , B 1,0 , C 2,1 , D 0,3 ,将四边
A.等边三角形
B.直角三角形
C.三边中只有两边相等的等腰三角形
D.三边互不相等的三角形
【答案】A
8.如图所示,观察四个几何体,其中判断正确的是( ).
A.(1)是棱台 C.(3)是棱锥 【答案】C
B.(2)是圆台 D.(4)不是棱柱
试卷第 2页,总 11页
9.一个球的内接正方体的表面积为 54,则球的表面积为( )
1
PB1= A1B1,则多面体 P-BCC1B1 的体积为( )
4
A.
8 3
C.4
【答案】B
16
B.
3
D.5
评卷人 得分
二、填空题
27.圆台的上底面半径为 2,下底面半径为 3,截得此圆台的圆锥的高为 6,则此圆台
的体积为____________.
【答案】 38 π 3
28.已知在三棱锥 P ABC 中,侧面与底面所成的二面角相等,则点 P 在平面 ABC 内的射影一定是 ABC 的__________心.
所示),则其侧视图的面积是 ( )
A.4 3cm2
B.2 3 cm2
C.8 cm2
D.4 cm2
【答案】A 21.若一个圆柱的正视图与其侧面展开图相似,则这个圆柱的侧面积与全面积之比为( )
立体几何初步空间几何与点线面单元过关检测卷(四)含答案人教版高中数学考点大全
高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.设直线l ⊂平面α,过平面α外一点A 与,l α都成030角的直线有且只有:( D )(A)1条 (B)2条 (C)3条 (D)4条(2020四川理)2.如图,l A B A B αβαβαβ⊥=∈∈,,,,,到l 的距离分别是a 和b ,AB与αβ,所成的角分别是θ和ϕ,AB 在αβ,内的射影分别是m 和n ,若a b >,则( )A Ba bl αβA .m n θϕ>>,B .m n θϕ><,C .m n θϕ<<,D .m n θϕ<>,(2020陕西理)3.设三棱柱ABC-A 1B 1C 1的体积为V ,P 、Q 分别是侧棱AA 1、CC 1上的点,且PA=QC 1,则四棱锥B-A PQC 的体积为( ) (A )16V (B )14V (C )13V (D )12V (2020全国3文)4.对于不重合的两个平面βα与,给定下列条件: ①存在平面γ,使得α、β都垂直于γ; ②存在平面γ,使得α、β都平等于γ; ③存在直线α⊂l ,直线β⊂m ,使得m l //; ④存在异面直线l 、m ,使得.//,//,//,//βαβαm m l l 其中,可以判定α与β平行的条件有( ) A .1个B .2个C .3个D .4个(2020重庆文)5.下列命题正确的是( )A 、若两条直线和同一个平面所成的角相等,则这两条直线平行B 、若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C 、若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D 、若两个平面都垂直于第三个平面,则这两个平面平行6.已知平面βα,和直线,给出条件:①α//m ;②α⊥m ;③α⊂m ;④βα⊥;⑤βα//.(i )当满足条件 时,有β//m ;(ii )当满足条件 时,有β⊥m . (填所选条件的序号)(2020湖南文15)7.下列命题中正确的有---------------------------------------------------------------------------------( )①三点确定一个平面;②两两相交的三条直线必在同一平面内;③任意三点都不共线的空间四点必共面;④空间三条相交于同一点的直线在同一平面内 (A) 1个 (B) 2个 (C) 3个 (D) 08.αβ∥,直线a α⊂,点B β∈,则β内过点B 的所有直线中-------------------------------( )(A)不一定存在与a 平行的直线 (B)只有两条与a 平行的直线 (C)存在无数条与a 平行的直线 (D)存在唯一一条与a 平行的直9.过直线外一点与直线平行的平面有----------------------------------------------------------------( )(A) 1个 (B)无数个 (C)不存在 (D)以上均不对10.若干个棱长为2、3、5的长方体,依相同方向拼成棱长为90的正方体,则正方体的一条对角线贯穿的小长方体的个数是( ) A .64 B .66C .68D .70第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人得分二、填空题11.(理)正三棱柱ABC -A 1B 1C 1中,AB =AA 1=2, 则A 1C 与BC 1所成角的余弦值为______.1.已知点(0,2)A 和圆2236:(6)(4)5C x y -+-=,一条光线从A 点出发,射到x 轴后沿圆的切线方向反射,则这条光线从A 点到切点所经过的路程 12.若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 .13.已知直线,m n 与平面,αβ,给出下列四个命题:①若//,//m n αα,则//m n ;②若//,m n αα⊥,则n m ⊥;③若n m m ⊥⊥,α,则α//n ;若,,//α⊥n n m 则α⊥m ,其中正确..命题的个数..是__________;14.设b a ,是两条不同直线,,αβ是两个不同平面,给出下列四个命题: ①若,,a b a α⊥⊥b α⊄,则//b α; ②若//,a ααβ⊥,则a β⊥; ③若,a βαβ⊥⊥,则//a α或a α⊂; ④若,,a b a b αβ⊥⊥⊥则αβ⊥. 其中正确的命题是 ▲ (请把所有正确命题的序号都填上). 15.已知正四棱锥的体积是48c m 3,高为4c m , 则该四棱锥的侧面积是 ▲ c m 2.16.已知线段AB 在平面α外,A 、B 两点到平面α的距离分别为1和3,则线段AB 的中点到平面α的距离为 . 评卷人得分三、解答题17. 【2020高考辽宁理第19题】如图,ABC ∆和BCD ∆所在平面互相垂直,且2AB BC BD ===,0120ABC DBC ∠=∠=,E 、F 分别为AC 、DC 的中点. (1)求证:EF BC ⊥;(2)求二面角E BF C --的正弦值.易得1331(0,,),(,,0)2222E F,所以33(,0,),(0,2,0)22EF BC=-=,因此0EF BC⋅=,从而得(方法二)由题意,以B 为坐标原点,在平面DBC 内过B 左垂直BC 的直线为x 轴,BC 所在直线为y 轴,在平面ABC 内过B 作垂直BC 的直线为z 轴,建立如图所示的空间直角坐标系.易得B (0,0,0),A (0,-1,3),D (3,-1,0),C (0,2,0),因而1331(0,,),(,,0)2222E F ,所以33(,0,),(0,2,0)22EF BC =-=,因此0EF BC ⋅=,从而EF BC ⊥,所以EF BC ⊥.18.在正方体ABCD -A 1B 1C 1D 1中,E 为AB 的中点, F 为A 1A 的中点,求证:(1)E 、C 、D 1、F 四点共面; (2)CE 、D 1F 、DA 三线共点.证明:(1)如图所示,分别连结EF 、A 1B 、D 1C . ∵E 、F 分别是AB 和A A 1的中点,∴EF 綊12A 1B .又A 1D 1綊B 1C 1綊BC ,∴四边形A 1D 1CB 为平行四边形. ∴A 1B ∥CD 1,从而EF ∥CD 1. ∴ EF 与CD 1确定一个平面. ∴E 、F 、D 1、C 四点共面.(2)∵EF 綊12CD 1,∴直线D 1F 和CE 必相交,BADCFE(第16设D 1F ∩CE =P .∵P ∈D 1F 且D 1F ⊂平面AA 1D 1D , ∴P ∈平面AA 1D 1D .又P ∈EC 且CE ⊂平面ABCD , ∴P ∈平面ABCD ,即P 是平面ABCD 与平面AA 1D 1D 的公共点, 而平面ABCD ∩平面AA 1D 1D =AD , ∴P ∈AD .∴CE 、D 1F 、DA 三线共点.19.如图,在四棱锥P ABCD -中,四边形ABCD 是菱形,PB PD =,且E ,F 分别是BC , CD 的中点. 求证: (1)EF ∥平面PBD ;(2)平面PEF ⊥平面PAC .(江苏省苏北四市2020届高三第一次调研)(本小题满分14分)20.如图,在四棱锥E ABCD -中,底面ABCD 为矩形,平面ABCD ⊥平面ABE ,90AEB ∠=,BE BC =,F 为CE 的中点,求证: (1)AE ∥平面BDF ;(2)平面BDF ⊥平面ACE .(江苏省徐州市2020届高三第一次调研考试)(本小题满分14分)【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题DP(第16题图)AB C EF1.D解析::如图,当030AOC ACB ∠=∠=时,直线AC 满足条件; 同理,当030AOB ABC ∠=∠=时,直线AB 满足条件;又由图形的对称性,知在另一侧存在两条满足条件与直线l 成异面直线的直线 故选D 2.D 3.C 4.B5.C 【2020高考真题四川理6】【解析】A.两直线可能平行,相交,异面故A 不正确;B.两平面平行或相交;C.正确;D.这两个平面平行或相交. 6.③⑤ ②⑤ 7. 8. 9. 10.第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人得分二、填空题11. 12. 13. 14. 15.60 16.1或2 评卷人得分三、解答题17. 18.19.证明线面平行,要寻找线线平行;而要证明面面垂直就需要转化为线面垂直。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学专题复习 《立体几何初步空间几何与点线面》单元过关检测 经典荟萃,匠心巨制!独家原创,欢迎下载! 注意事项: 1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上
第I卷(选择题) 请点击修改第I卷的文字说明
评卷人 得分 一、选择题
1.在空间中,过点A作平面的垂线,垂足为B,记)(AfB.设,是两个不同的平面,对空间任意一点P,)]([)],([21PffQPffQ,恒有21PQPQ,则 ( )
A.平面与平面垂直 B.平面与平面所成的(锐)二面角为045
C.平面与平面平行 D.平面与平面所成的(锐)二面角为060 (2020年普通高等学校招生统一考试浙江数学(理)试题(纯WORD版))
2.关于直线,mn与平面,,有以下四个命题: ①若//,//mn且//,则//mn;②若,mn且,则mn; ③若,//mn且//,则mn;④若//,mn且,则//mn; 其中正确命题的序号是 .
3.过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为(A) (A)316 (B)916 (C)38 (D)932(2020全国2理)
4.到两互相垂直的异面的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是
(A) 直线 (B) 椭圆 (C) 抛物线 (D) 双曲线(2020重庆理)
5.已知空间三条直线.lmn、、若l与m异面,且l与n异面,则( ) A.m与n异面. B.m与n相交. C.m与n平行. D.m与n异面、相交、平行均有可能. (2020上海春)
6.α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线, 给出四个论断:① m n ②αβ ③ m β ④ n α 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:___________________.
7.如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不.
正确..的是( )(2020年高考辽宁卷理科8)
(A) AC⊥SB (B) AB∥平面SCD (C) SA与平面SBD所成的角等于SC与平面SBD所成的角 (D)AB与SC所成的角等于DC与SA所成的角
8. 1.有下列四个命题: ①过平面外一点平行于此平面的所有直线必在同一平面内;②平行于同一平面的两条直线平行;③过平面外一点作与该平面平行的平面,有且只有一个;④分别在两个平行平面内的两条直线一定平行。 其中真命题的个数是-------------------------------------------------------------------------------------( )
(A) 1 (B) 2 (C) 3 (D) 9.平面与平面平行的一个充分条件是----------------------------------------------------------( )
(A)内有两条直线与平行 (B)内有无数条直线与平行 (C)内任一直线与平行 (D)、都平行于同一直线 10.若对任意的长方体A,都存在一个与A等高的长方体B,使得B与A的侧面积之比和体积之比都等于k,则k的取值范围是( )
A.0k B.01k C.1k D.1k
第II卷(非选择题) 请点击修改第II卷的文字说明
评卷人 得分 二、填空题
11.在在四棱锥O-ABCD中,底面ABCD为菱形,OA⊥平面ABCD, E为OA的中点, F为BC的中点, 求证:EF//平面OCD.
12.如图:E,H分别是空间四边形ABCD的边AB,AD的中点,平面α过EH分别交BC,CD于F,G
求证:EH∥FG
DABCF
O 13.对于直线m,n和平面,,,有如下四个命题: (1)若//m,nm,则n(2)若m,nm,则//n
(3)若,,则//(4)若m,nm//,n,则
其中正确命题的序号是. 14.长方体1111ABCDABCD中,已知111130BABBAC,则AB和11AC所成的角是_____;1AA和1BC所成的角是___________;1AB和1AC所成的角的余弦值是_____________
15.设m、n是不同的直线,a、b、g是不同的平面,有以下四个命题:①//////abbgagüïïÞýïïþ;②//mmabbaü^ïï轣ýïïþ;③//mmaabbü^ïï轣ýïïþ;④////mnmnaaüïïÞýïÌïþ,其中假命题是_______(填序号).
16.若圆锥的高是底面半径和母线的等比中项,则称此圆锥为“黄金圆锥”.已知某黄金圆锥的侧面积为S,则这个圆锥的高为 ▲ .
评卷人 得分 三、解答题
17.如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点. (I)求证:PACPBC平面平面; (II)2.ABACPACPBA若,1,1,求证:二面角的余弦值 (2020年普通高等学校招生统一考试辽宁数学(理)试题(WORD版))
18.如图所示,在棱长为2的正方体1111ABCDABCD中,E、F分别为1DD、DB的中点. (1)求证: (1)、EF//平面
11ABCD;
(2)、求证:1EFBC; (3)、求三棱锥EFCBV1的体积.(江苏省宿豫中学2020年3月高考第二次模拟考试)
证明:(1)连结1BD,在BDD1中,E、F分别为1DD,DB的中点,则 11111111
////EFDBDBABCDEFABCDEFABCD平面平面平面 。。。4分
(2)
1111111
,BCABBCBCABBCABCDABBCB平面
111111
BCABCDBDABCD平面
平面11
1//BCBDEFBD
1
EFBC
。。。。。。。。4分
(3)11CFBDDB平面,1CFEFB平面 且 2CFBF
1132EFBD
,222211(2)26BFBFBB
222211111(22)3BEBDDE
,∴22211EFBFBE 即1
90EFB
11113BEFCCBEFBEFVVSCF=11132EFBFCF=11362132
。。。。。。6分
CDBF
E
D1C
1
B1
AA1
CDBF
E
D1C
1
B1
AA119.已知:如图,平面∥平面,直线ab、是异面直线,a与、分别交于AB、两点,b与、分别交于CD、两点,EF、分别为
ABCD、的中点,求证:EF∥平面。
20.如图2所示,图(a)为大小可变化的三棱锥P-ABC. (1)将此三棱锥沿三条侧棱剪开,假定展开图刚好是一个直角梯形P1P2P3A,如图(b)所示.求证:侧棱PB⊥AC;
图2 (2)由(1)的条件和结论,若三棱锥中PA=AC,PB=2,求侧面PAC与底面ABC所成角;
(3)将此三棱锥沿三条侧棱剪开,假定其展开图刚好是一个三角形P1P2P3,如图(c)所示.已知P1P3=P2P3,P1P2=2a,若三棱锥相对棱PB与AC间的距离为d,求此三棱锥的体积.
【参考答案】***试卷处理标记,请不要删除 评卷人 得分 一、选择题
1.A 2. ②③ 3.A 解析:设球的半径为R, 过球的一条半径的中点,作垂直于该半径的平面,由勾股
定理可得一个半径为32R的圆,所以21223()32416RSSR,故选A 本题主要考察截面的形状和球的表面积公式,难度中等 4.ABC 解析:D 解析:排除法 轨迹是轴对称图形,排除A、C,轨迹与已知直线不能有交点,排除B
5.D 6. 若②③④则① 或若①③④则② 7.ABC 解析: D 解析:对于A:因为SD⊥平面ABCD,所以DS⊥AC.因为四边形ABCD为正方形,所以AC⊥BD,故AC⊥平面ABD,因为SB平面ABD,所以AC⊥SB,正确.对于B:因为AB//CD,所以AB//平面SCD.对于C:设ACBDO.因为AC⊥平面ABD,所以SA和SC在平面SBD内的射影为SO,则∠ASO和∠CSO就是SA与平面SBD所成的角和SC与平面SBD所成的角,二者相等,正确.故选D.
8. 9. 10. 第II卷(非选择题) 请点击修改第II卷的文字说明
评卷人 得分 二、填空题
11. 12. 13. 14. 15.②④;
