哈夫曼树hufferman构成原理应用及其数学证明
哈夫曼算法详解

7 5 2 4 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
weight parent lchild rchild
a 1 b 2
weight parent lchild rchild a 1 b 2 c 3 d 4 5 6
Hale Waihona Puke c 3d 4 5 6 7
7 5 2 4 6 0 0
wn构造n棵只有根结点的二叉树令起权值为wj?在森林中选取两棵根结点权值最小的树作左右子树构造一棵新的二叉树置新二叉树根结点权值为其左右子树根结点权值之和?在森林中删除这两棵树?在森林中删除这两棵树同时将新得到的二叉树加入森林中同时将新得到的二叉树加入森?重复上述两步直到只含一棵树为止这棵树即哈夫曼树例a7b5c2d4a7b5c2d46a71118a7b5c2d4611b5c2d46例w529781423311514297823311142978231135887151429233581129148715291135819234211118819234229141415152958113581914292387151135819292314871529358711358192342291487152958100?huffman算法实现?一棵有n个叶子结点的huffman树有2n1个结点?采用顺序存储结构一维结构数组?结点类型定义typedefstructintweight
8
3
14 7
15
Huffman算法实现
一棵有n个叶子结点的Huffman树有2n-1个结点 采用顺序存储结构——一维结构数组 结点类型定义
typedef struct { int weight; int parent,lchild,rchild; }HTNode;
数据结构第六章 哈夫曼树
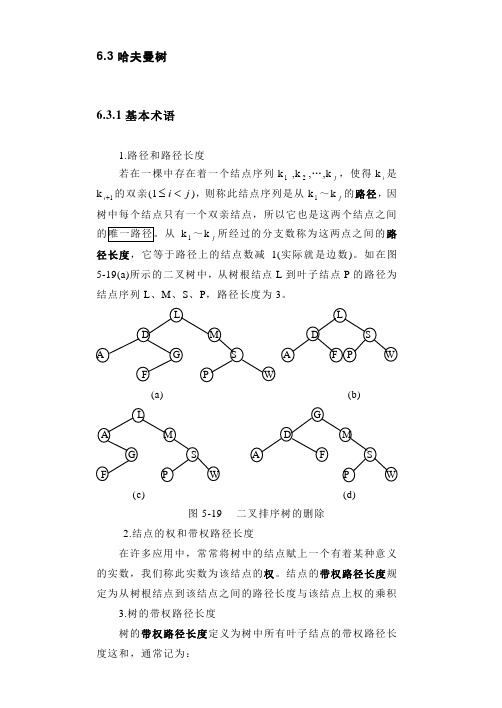
6.3哈夫曼树6.3.1基本术语1.路径和路径长度若在一棵中存在着一个结点序列k1 ,k2,…,kj,使得ki是k1+i 的双亲(1ji<≤),则称此结点序列是从k1~kj的路径,因树中每个结点只有一个双亲结点,所以它也是这两个结点之间k 1~kj所经过的分支数称为这两点之间的路径长度,它等于路径上的结点数减1(实际就是边数)。
如在图5-19(a)所示的二叉树中,从树根结点L到叶子结点P的路径为结点序列L、M、S、P,路径长度为3。
(a) (b)(c) (d)图5-19 二叉排序树的删除2.结点的权和带权路径长度在许多应用中,常常将树中的结点赋上一个有着某种意义的实数,我们称此实数为该结点的权。
结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积3.树的带权路径长度树的带权路径长度定义为树中所有叶子结点的带权路径长度这和,通常记为:2 WPL = ∑=n i i i lw 1其中n 表示叶子结点的数目,i w 和i l 分别表示叶子结点i k 的权值和根到i k 之间的路径长度 。
4.哈夫曼树哈夫曼(Huffman)树又称最优二叉树。
它是n 个带权叶子结点构成的所有二叉树中,带权路径长度 WPL 最小的二叉树。
因为构造这种树的算法是最早由哈夫曼于1952年提出的,所以被称之为哈夫曼树。
例如,有四个叶子结点a 、b 、c 、d ,分别带权为9、4、5、2,由它们构成的三棵不同的二叉树(当然还有其它许多种)分别如图5-20(a)到图5-20(c)所示。
b ac a b cd d c a b d(a) (b) (c)图5-20 由四个叶子结点构成的三棵不同的带权二叉树 每一棵二叉树的带权路径长度WPL 分别为:(a) WPL = 9×2 + 4×2 + 5×2 + 2×2 = 40(b) WPL = 4×1 + 2×2 + 5×3 + 9×3 = 50(c) WPL = 9×1 + 5×2 + 4×3 + 2×3 = 37其中图5-20(c)树的WPL 最小,稍后便知,此树就是哈夫曼树。
哈夫曼树的实际应用

哈夫曼树的实际应用
哈夫曼树(Huffman Tree)是一种重要的数据结构,它在信息编码和压缩、数据传输和存储、图像处理等领域有广泛应用。
1. 数据压缩:哈夫曼树是一种无损压缩的方法,能够有效地减小数据的存储空间。
在进行数据压缩时,可以使用哈夫曼树构建字符编码表,将出现频率较高的字符用较短的编码表示,而出现频率较低的字符用较长的编码表示,从而减小数据的存储空间。
2. 文件压缩:在文件压缩领域,哈夫曼树被广泛应用于压缩算法中。
通过构建哈夫曼树,可以根据字符出现的频率来生成不同长度的编码,从而减小文件的大小。
常见的文件压缩格式如ZIP、GZIP等都使用了哈夫曼树。
3. 图像压缩:在图像处理中,哈夫曼树被用于图像压缩算法中。
通过将图像中的像素值映射为不同长度的编码,可以减小图像的存储空间,提高图像传输和存储的效率。
常见的图像压缩格式如JPEG、PNG等都使用了哈夫曼树。
4. 文件传输:在数据传输中,哈夫曼树被用于数据压缩和传输。
通过对数据进行压缩,可以减小数据的传输时间和带宽占用。
在传输过程中,接收方可以通过哈夫曼树解码接收到的数据。
5. 数据加密:在数据加密中,哈夫曼树可以用于生成密钥,从而实现数据的加密和解密。
通过将字符映射为不同长度的编码,可以实
现对数据的加密和解密操作。
哈夫曼树在信息编码和压缩、数据传输和存储、图像处理等领域有广泛应用,能够有效地减小数据的存储空间、提高数据传输效率、实现数据加密等功能。
简单介绍哈夫曼树_华清远见

简单介绍哈夫曼树本篇文章给大家带来的内容是哈夫曼树,简单介绍一下哈夫曼树,以及解析,希望对大家的学习有所帮助。
废话不多说,马上进入正题。
给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
哈夫曼树是二叉树的一个典型应用,利用哈夫曼树,我们可以形成哈夫曼编码,进而实现对数据的压缩与解压处理。
哈夫曼树,指的是对于一组具有确定权值的叶子结点的具有最小带权路径长度的二叉树。
哈夫曼树当中的几个概念我们不得不说一下:(1)路劲(Path):从树中的一个结点到另一个结点之间的分支构成两个结点间的路径。
(2)路径长度(Path Length):路径上的分支树。
(3)树的路径长度(Path Length of Tree):从树的根结点到每个结点的路径长度之和。
在结点数目相同的二叉树中,完全二叉树的路径长度最短。
(4)结点的权(Weight of Node):在一些应用中,赋予树中结点的一个有实际意义的树。
(5)结点的带权路径长度(Weight Path Length of Node):从该结点到树的根结点的路径长度与该结点的权的乘积。
(6)树的带权路径长度(WPL):树中所有叶子结点的带权路径长度之和在下图所示的四棵二叉树,都有4个叶子结点,其权值分别1、2、3、4,他们的带权路径长度分别为:(a)WPL = 1 x 2 + 2 x 2 + 3 x 2 + 4 X 2 = 20(b)WPL = 1 x 1 + 2 x 2 + 3 x 3 + 4 x 3 = 28(c)WPL = 1 x 3 + 2 x 3 + 3 x 2 + 4 x 1 = 19(d)WPL = 2 x 1 + 1 x 2 + 3 x 3 + 4 x 3 = 29其中,(c)图所示的二叉树的带权路径长度最小,这棵树就是哈夫曼树。
哈夫曼树

字符序列:DATA TRERTER ARE AREA ART 用0、1组合进行编码,希望01串长度最短。 字符集为{A,D,T,R,E},各字母出现的次 数为{6,1,4,6,4} 高频字符,译码尽可能短
一个方案
– – – – – A:10 D:010 T:011 R:11 E:00
基本术语
结点的权
– 在许多实际应用中,常常将树中的某些结 点赋上一个具有一定意义的实数,这个实 数称为该结点的权
结点的带权路径
– 从根结点到结点的路径长度*结点的权
树的带权路径WPL
– 树中所有叶子结点的带权路径长度之和
基本术语
对所有叶子结点i计算 Wi Li
计算WPL
哈夫曼树
最优树/哈夫曼树
(1)与n个权对应的结点构成具有n棵二叉 树的森林F={T1,T2,…,Tn},其中每棵二叉 树Ti都只有一个根结点,左右子树均空 (2)从F中选出根结点权值最小的两棵树 作为一棵树的左右子树,且置新树的根 结点权值为左右子树根结点权值之和 (3)从F中删除这两棵树,将新树加入F (4)重复(2)、(3),直到F中只含一棵树
哈夫曼树
哈夫曼(haffman)树又称为最优二叉树, 它是n个带权叶子结点构成的二叉树中 WPL最小的二叉树。 ??
ቤተ መጻሕፍቲ ባይዱ
– 所有叶子结点的权值均为1(或相等),构 成的二叉树形式? – 在哈夫曼树中叶子结点的权与路径长度的关 系? – 叶子数目已知,结点总数=? – 唯一性?
哈夫曼树—构造(贪心)
ht[m].codify:=“”; for i:=m downto n+1 do begin p:=ht[i].lchild; if p<>0 then ht[p].codify:=ht[i].codify+”0” p:=ht[i].rchild; if p<>0 then ht[p].codify:=ht[i].codify+”1” end;
数据结构-哈夫曼树及其应用

15
40 a
30 b
5
c
10 d
15 e
二、哈夫曼树及其应用
2.哈夫曼树的求解过程 ③实例:已知有5个叶子结点的权值分别为:5 , 15 , 40 , 30 , 10 ;试画出一棵相应的哈夫曼树。
30
40 a
30 b
15
15 e
5
c
10 d
二、哈夫曼树及其应用
2.哈夫曼树的求解过程 ③实例:已知有5个叶子结点的权值分别为:5 , 15 , 40 , 30 , 10 ;试画出一棵相应的哈夫曼树。
WPL=∑wi*li最小的二叉树称为“最优
i=1 n
二叉树”或称为“哈夫曼树”。
二、哈夫曼树及其应用
2.哈夫曼树的值为{w1,w2,...wn},构 造一棵最优二叉树。
二、哈夫曼树及其应用
2.哈夫曼树的求解过程 ②方法:
步骤1:构造一个具有n棵二叉树的森林F={T1,T2,......,Tn}, 其中Ti是只有一个根结点且根结点的权值为wi的二叉树。 步骤2:在F中选取两棵其根结点的权值最小的二叉树,从F 中删除这两棵树,并以这两棵二叉树为左右子树构造一棵 新的二叉树添加到F中,该新的二叉树的根结点的权值为 其左右孩子二叉树的根结点的权值之和。 步骤3:判断F中是否只有唯一的一棵二叉树。若是,则求 解过程结束;否则,转步骤2。
二、哈夫曼树及其应用
3.哈夫曼编码 ②压缩编码:
例如:对于刚才的4个字符的编码问题,可以按如 下不等长编码方案进行编码: A: 0 B: 00 C: 1 D: 01 则对于电文“ABACCDA”的二进制电码为: 000011010 总长为9位 问题:译码时可能出现多意性,即译码不唯一:
二、哈夫曼树及其应用
数据结构哈夫曼树课件

总结词
优化、提升
详细描述
基于哈夫曼树的网络流量分类算法的优化策 略主要从以下几个方面进行优化和提升:一 是优化哈夫曼树的构造算法,提高树的构造 效率和准确性;二是利用多级哈夫曼编码技 术,降低编码和解码的时间复杂度;三是引 入机器学习算法,对网络流量特征进行自动
提取和分类,进一步提升分类准确率。
THANKS
基于堆排序的构造算法
总结词:堆排序是一 种基于比较的排序算 法,它利用了堆这种 数据结构的特点,能 够在O(nlogn)的时间 内完成排序。在哈夫 曼树的构造中,堆排 序可以用来找到每个 节点的父节点,从而 构建出哈夫曼树。
详细描述:基于堆排 序的构造算法步骤如 下
1. 定义一个最大堆, 并将每个节点作为一 个独立的元素插入到 堆中。每个元素包含 了一个节点及其权值 。
哈夫曼编码的基本概念
哈夫曼编码是一种用于无损数据压缩的熵编码算法,具有较高的编码效率和较低的 编码复杂度。
它利用了数据本身存在的冗余和相关性,通过构建最优的前缀编码来实现高效的数 据压缩。
哈夫曼编码是一种可变长编码,其中每个符号的编码长度取决于它在输入序列中出 现的频率。
哈夫曼编码的实现方法
构建哈夫曼树
节ቤተ መጻሕፍቲ ባይዱ。
优化编码长度
在分配码字时,通过一些策略优化 编码长度,例如给高频符号更短的 码字。
可变长度编码
为了提高压缩比,可以使用可变长 度编码,即对于高频符号赋予更短 的码字,对于低频符号赋予更长的 码字。
04
哈夫曼树在数据压 缩中的应用
基于哈夫曼编码的数据压缩算法
哈夫曼编码是一种可变长度的 编码方式,通过统计数据的出 现频率来构建哈夫曼树,实现 数据压缩。
哈夫曼树

n
(wk—第k个叶结点的权值;pk—第k个叶结点的带权路径长度)
达到最小。
2、最优二叉树的构造方法 假定给出n个结点ki(i=1‥n),其权值分别为wi(i=1‥n)。要构造以此n个 结点为叶结点的最优二叉树,其构造方法如下:
首先,将给定的n个结点构成n棵二叉树的集合F={T1,T2,……,Tn}。其 中每棵二叉树Ti中只有一个权值为wi的根结点ki,其左、右子树均为空。然后 做以下两步
}
测试数据: 输入: 5 75246 输出: 54
3、哈夫曼编码
使用频率高的采用短的的编码,则总的编码长度便可减少.
例如:在某通讯中只使用abcd四种字符,其出现频率分别 为:0.4,0.3,0.2,0.1。请进行哈夫曼编码。使通讯码尽可能 的短
并写出信息:bbdaac的编码。
1.给定一个整数集合{3,5,6,9,12},下列二叉树哪个 是该整数集合对应的霍夫曼(Huffman)树。 ( )
⑴在F中选取根结点权值最小的两棵二叉树作为左右子树,构造一棵新 的二叉树,并且置新的二叉树的根结点的权值为其左、右子树根结点的权值之 和; ⑵在F中删除这两棵二叉树,同时将新得到的二叉树加入F中;
重复⑴、⑵,直到在F中只含有一棵二叉树为止。这棵二叉树便是最优二叉树。 以上构造最优二叉树的方法称为哈夫曼(huffmann)算法。
int data;
int prt, lch, rch; };
//结点的权值
//父指针、左、右孩子指针
node ht[MAXN];
int n,m; int path[LEAF];
//ht[1]..ht[n]为叶结点,ht[n+1]..ht[2n-1]
//n 为读入的叶结点数,m 为总结点数 //叶结点到根的路径长度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈夫曼树hufferman构成原理应用及其数学证明
哈夫曼树(Huffman Tree),又称最优树,它是一种常用的编码技术,它是一种十分高效的字符编码技术, 它主要是通过对字符按照出现频率高低进行分组,从而构成一颗树;每个字符的编码由树的层次顺序确定,字符越靠近根节点,编码越短,且编码长度与概率成正比,最后得出最优(最短)编码。
哈夫曼树构成原理:
哈夫曼树构成原理是通过将信源字符重新按照概率顺序构成一棵有序树来实现的,即带有权值的叶子节点的树。
例如,某信源由四种字符A,B,C,D组成,出现的概率分别为p1,p2,p3,p4。
则可以构成一棵哈夫曼树。
首先,将四个字符依据概率从大到小重新排列,得到ABCD,依据概率大小选择A和B两个字符,以他们为叶子节点构成根节点,这样就分出了两颗子树。
接着将C和D两个字符以此作为叶子节点构成另外两棵子树,将他们与上面的根节点联接在一起,当初始树建立完毕,就得到了一棵哈夫曼树。
哈夫曼树数学证明:
证明哈夫曼树是最优树:
假设一棵信源树的叶子节点有n个,则此树的权重之和为:
w1+w2+…+wn,其中wi是叶子节点i的权重,建立该信源树的目标是将其权重之和最小化,而在没有违反信源编码原理的前提下,树的最小权重之和也就是最优树的权重之和。
假设w1~wn分别为叶子节点1~n的权重,从大到小排列为
w1,w2,…,wn,一棵以w1,w2,…,wn为叶子节点的最优树的权重之和为:
T(w1,w2,…,wn)=w1+w2+…+wn+2(w1+w2)+2
(w1+w2+w3)+……+2(w1+w2+…+wn-1)=2(w1+w2+…+wn-1)+wn =2T(w1,w2,…,wn-1)+wn
由上式可知,最优树的权重之和T(w1,w2,…,wn)是由T (w1,w2,…,wn-1)和wn组成的,也就是说,每次取出w1,
w2,…,wn中的最大者wn作为树的一个节点,其余的作为树的另一个节点,而每一次节点的选取都是满足最优化条件的,因此一棵满足最优树条件的树就是哈夫曼树,而此树的权重之和也就是最优树的权重之和.
从上述可以看出,哈夫曼树构成原理和哈夫曼树数学证明都支持哈夫曼树是最优树的观点,因此哈夫曼树是一种有效的编码技术。
