电路分析课件j14
合集下载
邱关源《电路》第九章正弦稳态电路的分析1

第九章 正弦稳态电路的分析
BUCT
9. 1 阻抗和导纳 9. 2 阻抗(导纳)的串联和并联 9. 3 电路的相量图 9. 4 正弦稳态电路的分析 9. 5 正弦稳态电路的功率 9. 6 电路的谐振
1
9. 3 电路的相量图
一、RL、RC串联电路
IR
+
U _
+
_ UR +
jL
U_L
P188
U
j
0
8—11 BUCT
1, 纯电阻 0, 纯电抗
X<0, j < 0 , 容性负载, 超前功率因数
例:cos j = 0.5 (滞后),则j =60o(电压领先电流60o)。
一般用户: 异步电机 空载 cosj =0.2~0.3 满载 cos j =0.7~0.85
日光灯
cosj =0.45~0.6
17
功率因数的提高
k
1
Qk
0
14
* 复功率守恒, 不等于视在功率守恒.
BUCT
I
+
U_
+ U 1 _
+
U_ 2
S UI* (U1 U 2 )I * U1I * U 2I* S1 S2
b
一般情况下: S Sk k 1
例:
S S2 Q2 S1 P2
Q1 P1
R2 UR2 I 33.9 1.73 19.6W
L UL2 I 72.45 1.73 41.88W
L2 41.88 314 0.133H
12
复功率
BUCT
为了用相量U和I来计算功率,引入“复功率”
I
+
BUCT
9. 1 阻抗和导纳 9. 2 阻抗(导纳)的串联和并联 9. 3 电路的相量图 9. 4 正弦稳态电路的分析 9. 5 正弦稳态电路的功率 9. 6 电路的谐振
1
9. 3 电路的相量图
一、RL、RC串联电路
IR
+
U _
+
_ UR +
jL
U_L
P188
U
j
0
8—11 BUCT
1, 纯电阻 0, 纯电抗
X<0, j < 0 , 容性负载, 超前功率因数
例:cos j = 0.5 (滞后),则j =60o(电压领先电流60o)。
一般用户: 异步电机 空载 cosj =0.2~0.3 满载 cos j =0.7~0.85
日光灯
cosj =0.45~0.6
17
功率因数的提高
k
1
Qk
0
14
* 复功率守恒, 不等于视在功率守恒.
BUCT
I
+
U_
+ U 1 _
+
U_ 2
S UI* (U1 U 2 )I * U1I * U 2I* S1 S2
b
一般情况下: S Sk k 1
例:
S S2 Q2 S1 P2
Q1 P1
R2 UR2 I 33.9 1.73 19.6W
L UL2 I 72.45 1.73 41.88W
L2 41.88 314 0.133H
12
复功率
BUCT
为了用相量U和I来计算功率,引入“复功率”
I
+
电路分析专题讲解PPT课件
§ 1 – 2 参考方向
一、参考方向----正方向 二、关联参考方向
§ 1 – 3 无源元件
一、电阻元件R 1。u – i 关系 2。伏安特性 3。电导G 4。单位
iR u
二、电容元件C
1。q – u关系 2。C的单位 3。u – i 关系 4。电场能WC
C i
u
三、电感元件L
1。 Ψ– i 关系
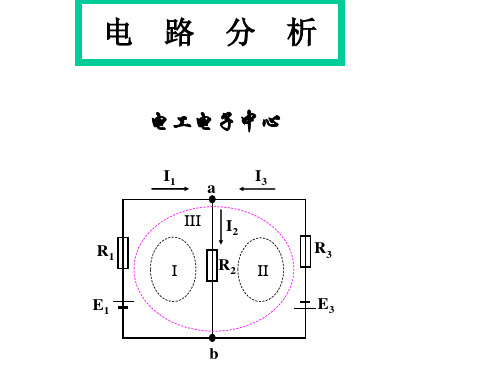
② 受∑i=0、∑u=0约束的正负号
I1= – 3A
例如:求I3= ?
显然:由
有
I1= I2 + I3
②
I3 = I1 – I2
①
= – 3A– 2A = – 5A
I2= 2A
I3= ?
例2 求输出电压
U= –E3–(R1 + R4 )I I 取决于外电路
R2 5Ω
特殊地,当输出端开路时
I=0, U= –E3
例1(恒压源)
Ius=1A
Us 10V
I=1A
R 10Ω
U=10V
U=10V
Ius
I=1A
Us 10V
R1
R
10Ω
10Ω U=10V
Ius
Us 10V
Ius Us 10V
Is=1A
I=1A
1A R1 10Ω
R 10Ω U=10V
Is=2A
I=1A
1A R1 10Ω
R 10Ω
U=10V
IUS
I=1A
I
Is 1/r g U R
(a)
(b)
Notice: 1。等效仅对外部而言,内部不等效! 2。注意变换前后方向的一致性, 3。理想电源之间不可互换。 4。受控源亦可互换,但应保持控制量不变
电路原理ppt课件

在参考方向选定后,电流(或电压) 值才有正负之分。 对任何电路分析时都应先指定各处的 i , u 的参考方向。 例:
I
a
R
b
若 I = 5A ,则实际方向与参考方向一致, 若 I =-5A ,则实际方向与参考方向相反。
16
R
5、关联参考方向: i
+
u
-
当电压的参考方向指定后,指定电流从标以电压参考 方向的“+”极性端流入,并从标“—”端流出,即电流
i +
R
i – +
R
u
u = Ri
u
u = –Ri
–
19
1.3电功率和能量
1. 电功率
单位时间内电场力所做的功。
dw p dt
dw u dq
dq i dt
dw dw dq p ui dt dq dt
w
t
t0
u ( )i ( )d
(Watt,瓦特) (Joule,焦耳)
20
的参考方向与电压的参考方向一致,也称电流和电压
为关联参考方向。反之为非关联参考方向。
17
例
i
+
A U B
电压电流参考方向如图中所标, 问:对A、两部分电路电压电流参考方向 关联否? 答: A 电压、电流参考方向非关联;
B 电压、电流参考方向关联。
-
18
小结:
(1) 分析电路前必须选定电压和电流的参考方向。 (2) 参考方向一经选定,必须在图中相应位置标注 (包括方 向和符号),在计算过程中不得任意改变。 (3) 参考方向不同时,其表达式符号也不同,但实际方向不变。
-
P4吸 U 4 I 2 (4) 1 4W(实际发出)
I
a
R
b
若 I = 5A ,则实际方向与参考方向一致, 若 I =-5A ,则实际方向与参考方向相反。
16
R
5、关联参考方向: i
+
u
-
当电压的参考方向指定后,指定电流从标以电压参考 方向的“+”极性端流入,并从标“—”端流出,即电流
i +
R
i – +
R
u
u = Ri
u
u = –Ri
–
19
1.3电功率和能量
1. 电功率
单位时间内电场力所做的功。
dw p dt
dw u dq
dq i dt
dw dw dq p ui dt dq dt
w
t
t0
u ( )i ( )d
(Watt,瓦特) (Joule,焦耳)
20
的参考方向与电压的参考方向一致,也称电流和电压
为关联参考方向。反之为非关联参考方向。
17
例
i
+
A U B
电压电流参考方向如图中所标, 问:对A、两部分电路电压电流参考方向 关联否? 答: A 电压、电流参考方向非关联;
B 电压、电流参考方向关联。
-
18
小结:
(1) 分析电路前必须选定电压和电流的参考方向。 (2) 参考方向一经选定,必须在图中相应位置标注 (包括方 向和符号),在计算过程中不得任意改变。 (3) 参考方向不同时,其表达式符号也不同,但实际方向不变。
-
P4吸 U 4 I 2 (4) 1 4W(实际发出)
电工电子学完整ppt课件

K
u k ( t ) 0 或
u降 u升 或 uR US
k 1
式中 uk(t) 为该回路中第 k 条支路电压,K 为该回路处的支路数
示例
R2 i2
+ US_1
+ u2 _ +
R1 i1
+ _u1
_u3 _ u4 +
_ US4+ R4 i4
R3 i3
① 标定各元件电压、电流参考方向 ② 选定回路绕行方向,顺时针或逆时针 顺时针
小结 · 分析电路前必须选定电压和电流的参考方向
· 参考方向一经选定,必须在图中相应位置标注 (包括方向和符号), 在计算过程中不得任意改变。
· 参考方向也称为假定正方向,以后讨论均在参考方向下进行,不考虑 实际方向。
· 电路中电位参考点可任意选择,参考点一经选定,电路中各点的电位
值就是唯一的,当选择不同的电位参考点时,电路中各点电位值将
Lumped parameter element
集总条件 实际电路的尺寸远小于使用时其最高工作频率所对应的
波长 d
注意
• 采用集总电路模型意味着不考虑电路中电场与磁场的相互作用, 不考虑电磁波的传播现象,认为电能的传送是瞬时完成的
• 集总假设为本课程的基本假设,以后所述的电路基本定律、定理 等均是以该假设为前提成立的
_
R1
+ US2
_
R2
b=3
n=2
R3
l=3
m=2
精品课件
22
2. 基尔霍夫电流定律 (KCL)
在集总参数电路中,任意时刻,对任意节点流出或流入该节点电流的代数 和等于零。
K
ik (t) 0
课件-第1章 电路分析的基本概念

(1.2)
7 式中dW是电场力所作的功,单位是焦耳(J);dq为电荷量,单 位是C);电压U 的单位是伏特,简称伏(V)。电压也有恒定电 压和和时变电压之分,分别用符号U和 u 表示(直流量有时不 分大小写)。
图1-4 电压参考方向
电压参考方向(参考极性)的选择同样具有任意性,通常在 电路图上用“+”表示参考方向的高电位端,“-”表示参考方向 的低电位端,如图1-4所示。或用双下标表示电压的参考方向, 如uab 表示电压参考方向从a点指向b点。电压实际方向的判定 与电流的类似。
例1.2 电路如图1.12所示,各支路电流参考方向已标出, 已知 I1 = 8 A ,I2 = 3 A ,I3 = -1 A ,I5 = 2 A,求I4 。
13
解: 对于结点a ,根据KCL可得 I 1–I2 –I3 + I4 –I5 = 0 所以 I4 = -I1 + I2 + I3 + I5 = -8 + 3 +(-1)+ 2 = - 4 A I4为负值,说明I4的实际方向与参考方向相反,即I4实际流出 结点a 。
U、I间关联参考方向:今后在求电压电流时,必须事 先规定好参考方向,否则求出的值无意义。而且为了 分析方便,通常将某元件上电压电流参考方向选为一 致,即电流的参考方向由电压的“+”指向“-”,这 样选定的参考方向称为关联参考方向,简称关联方向。
电位的概念及计算: 将电路中任一点作为参考点, 把a点到参考点的电压称为a点电位,用符号Va(或Ua) 表示。电路中a、b两点间的电压与该两点电位有以 下关系: Uab = Va - Vb (1.3) 今后如未说明,通常选接地点作参考点,并且参 考点电位为零。引入电位概念后,两点间电压的实 际方向即由高电位指向低电位。
第1章 电路分析基础

Conclusion:支路电流法的一般解题步骤: 1. 确定电路的支路数,选定参考方向,设待求支路电流的 数为m。 2. 选定所有的独立结点(n-1),应用kcl列写n-1 个方程。 3. 选择独立回路并指定每个回路的绕行方向,应用kvl列写m(n-1)个方程。 4.联立求解方程,得出m个结果。 5. 应用欧姆定律求出各支路的电压。 例题:书19页例1.10、1.11
i1
u R1
R2 R1 R2
iS
i2
u R2
R1 R1 R2
iS
简单电阻电路的计算:18页例1.9
第40页,共58页。
1.3.3支路电流法
电路有m条电路,以m条支路电流作为未知量,应用
基尔霍夫定律列出m个独立的方程式,联立求解方程式 即可解出各支路电流。这就是支路电流法。
I1 U1
R1
a I2
b
电感(Inductance)等 为了对实际电路进行分析,可忽略负载的次要因素,将其近 似看作理想电路元件,简称为元件(Element ) 。 元件通过端子与外电路相连,按端子的数目可将元件分为 :二端元件、三端元件、四端元件等。
第4页,共58页。
实际情况中,电路由电源(信号源)、负载和中间环结组 成。
3、联立求解3个方程即可。
R1
b
3个方程如下: Il+I2+IS3-I4=0 I1R1-US1+US2-I2R2=0 I2R2-US2+I4R4=0
解之得:
Il=-22(A)
I2=14(A) I4=10(A)
第43页,共58页。
1.3.4结点电压法 以结点电压作为未知量,将各支路电流用结点电压表示
U4
R2
R3
U5
R4 R5
i1
u R1
R2 R1 R2
iS
i2
u R2
R1 R1 R2
iS
简单电阻电路的计算:18页例1.9
第40页,共58页。
1.3.3支路电流法
电路有m条电路,以m条支路电流作为未知量,应用
基尔霍夫定律列出m个独立的方程式,联立求解方程式 即可解出各支路电流。这就是支路电流法。
I1 U1
R1
a I2
b
电感(Inductance)等 为了对实际电路进行分析,可忽略负载的次要因素,将其近 似看作理想电路元件,简称为元件(Element ) 。 元件通过端子与外电路相连,按端子的数目可将元件分为 :二端元件、三端元件、四端元件等。
第4页,共58页。
实际情况中,电路由电源(信号源)、负载和中间环结组 成。
3、联立求解3个方程即可。
R1
b
3个方程如下: Il+I2+IS3-I4=0 I1R1-US1+US2-I2R2=0 I2R2-US2+I4R4=0
解之得:
Il=-22(A)
I2=14(A) I4=10(A)
第43页,共58页。
1.3.4结点电压法 以结点电压作为未知量,将各支路电流用结点电压表示
U4
R2
R3
U5
R4 R5
电力系统三相短路故障分析PPT课件
例6-4
• 电力系统接线图如图6-11所示,其中G为发电 机,M为电动机,负载(6)为由各种电动机组合 而成的综合负荷,设在电动机附近发生三相短 路故障,试画出下列电力系统三相短路故障分 析时的等值网络图。
第29页/共67页
例6-4
第30页/共67页
6.3.2.起始次暂态电流的计算
• 得到等值电路后,起始次暂态电流
• 三相短路功率主要是用来校验断路器的切断能力,要求短路时, 断路器一方面能切断这么大的短路电流,另一方面断路器断开 时其触头还要能经受工作电压的作用。
表达式: Skt 3U N It
用标幺值表示为:Skt*
3U N It 3U B I B
It*
I*
在有名值计算中: Skt 3UN I I*SB
第27页/共67页
表6-3 短路分析时元件的近似模型
元件
发电机 (调相机)
负荷
负荷 模型
与稳态模 型相同, 近似计算 时可忽略 电阻。
计算公式
E(0 ) U 0 jI0 X
RL
U(20-), PL
第X2L8页/U共Q(260L7-)页
EM (0 ) U 0 jI0 X M
若只计电抗,则:
只求其数值
Ik E jX Uk(0) jX
第32页/共67页
Ik E X Uk(0) X
例6-5
• 化简图6-12所示的电力系统等值电路,并求出起始次暂态电流。
第33页/共67页
例6-5
求出起始次暂态电流的标幺值
I1*
E* X13* X12*
1.018 0.5571.43
工作遭到破坏。 4. 破坏电力系统中各发电厂之间并列运行的稳定性,引起系统振
《电工电子技术》(宋强)417-0课件 14
清零后 R d 接高电平,以允许数
存
码的寄存。
器
3)记忆保持
数 码
R d 接高电平,CP无下降沿,
3
寄 则各触发器保持原状态不变,
存 寄存器处在记忆保存状态。
器
第 20 页
2)并行数据输入
在 R d 接高电平的前提下,发出一
2
个存数正脉冲CP,将要存入的数
据d3d2d1d0依次加到数据输入
端D3D2D1D0,在CP脉冲下降沿
• 14.2.1 数码寄存器 • 14.2.2 移位寄存器
14.2
第14章 触发器和时序逻辑电路
寄 存 器
数 码 寄 存 器
第 19 页 图14-11 4位数码寄存器
第14章 触发器和时序逻辑电路
1)清0
14.2
开始时,在 R d 端加负脉冲,使
1 各触发器清零,即 Q0Q1Q2Q30000。
寄
电工电子技术
北京金企鹅文化发展中心
目录页
第2页
第14章 触发器和时序逻辑电路
14.1 双稳态触发器 14.2 寄存器 14.3 计数器 14.4 555定时器
过渡页
第3页
14.1 双稳态触发器
• 14.1.1 RS触发器 • 14.1.2 JK触发器 • 14.1.3 D触发器和T触发器 • 14.1.4 触发器逻辑功能的转化
计 数 器
二 进 制 计 数 器
表14-8 4位同步二进制加法计数器的状态转换表
第14章 触发器和时序逻辑电路
第 27 页
同步二进制计数器
14.3
计 数 器
二 进 制 计 数 器
由波形图可以看出,若计数脉冲的输入频率为f0,则Q0,Q1,Q2和Q3端输出
滤波器电路分析 课件
PPT课件
19
RC一阶高通滤波电路相频特性曲线,从图中可任意看 出当f=100.697KHZ时,相角超前46.497 deg。
PPT课件
20
3.3RC二阶低通滤波电路
设计RC二阶低通滤波器电路,可以通过将两个RC一阶低通滤波电路 级联等到,RC二阶低通滤波电路。
图 14-9
PPT课件
21
下面给出一个fc=200KHZ的RC二阶低通滤波电路的仿真电路图
1
? ? 0
RC PPT课件
27
图12 RC带通滤波电路幅频特性,相频特性曲 线
PPT课件
28
RC带通滤波电路仿真原理图
PPT课件
29
RC带通滤波电路,中心频率6.504KHZ
PPT课件
30
RC带通滤波电路相频特性曲线
PPT课件
31
实际应用分析:图12(a)表示工频正弦交流电经全波整流后
的波形,试设计一个RC低通滤波电路来滤除其谐波分量
图12 求解过程:全波整流波形可用傅里叶级数展开为
PPT课件
32
其中f等于工频50HZ
ω ? 2π ? 628rad/s T
设A=100V,则
u1(t) ? [63.66? 42.44cos(? t) ? 8.488cos(2? t)? 3.638cos(3? t) ? ...]V
采用图(b)所示一阶RC滤波电路,并选择电路元件参数满足以下 条件
ωC
?
1 RC
?
1
?
(3-5)
将上式改写为
(3-4) (3-6)
PPT课件
15
RC一阶高通滤波电路幅度,相角 表达式
图 14-8
《电路分析》——正弦稳态分析
0 电压超前电流角 0 电压与电流同相 0 电压滞后电流角 180 电压与电流反相
>0, u超前i 角,或i 落后u 角(u 比i先到达最大值);
u, i u i
O
t
yu yi
<0, i 超前 u 角,或u 滞后 i 角,i 比 u 先到达最大值。
Im A2
0
图解法
A1 Re
(2) 乘除运算——采用极坐标形式
若 A1=|A1| 1 ,A2=|A2| 2
则:
A1 A2
A1 e j1
A2 e j2
A1
A e j(12 ) 2
A1 A2 1 2 乘法:模相乘,角相加。
A1 A2
| A1 |θ1 | A2 |θ2
几种不同值时的旋转因子
Im
(1) ,
jI jI
I
2
j
e2
cos
j sin
j
2
2
I I
0
Re
jI
jI
(2) ,
jபைடு நூலகம்
e2
cos(
)
j sin(
)
j
2
2
2
(3) , e j cos( ) j sin( ) 1
其它非正弦的周期信号不能照搬这个关系式;
(2)工程上所说的正弦电压和电流的大小都是指有效值; (3)一般电压表和电流表的刻度都是按有效值来标定的; (4)交流电气设备铭牌上所标定的电压、电流值都是有效 值。如“220V,100W”的白炽灯,是指它的额定电压的有效 值是220V。
>0, u超前i 角,或i 落后u 角(u 比i先到达最大值);
u, i u i
O
t
yu yi
<0, i 超前 u 角,或u 滞后 i 角,i 比 u 先到达最大值。
Im A2
0
图解法
A1 Re
(2) 乘除运算——采用极坐标形式
若 A1=|A1| 1 ,A2=|A2| 2
则:
A1 A2
A1 e j1
A2 e j2
A1
A e j(12 ) 2
A1 A2 1 2 乘法:模相乘,角相加。
A1 A2
| A1 |θ1 | A2 |θ2
几种不同值时的旋转因子
Im
(1) ,
jI jI
I
2
j
e2
cos
j sin
j
2
2
I I
0
Re
jI
jI
(2) ,
jபைடு நூலகம்
e2
cos(
)
j sin(
)
j
2
2
2
(3) , e j cos( ) j sin( ) 1
其它非正弦的周期信号不能照搬这个关系式;
(2)工程上所说的正弦电压和电流的大小都是指有效值; (3)一般电压表和电流表的刻度都是按有效值来标定的; (4)交流电气设备铭牌上所标定的电压、电流值都是有效 值。如“220V,100W”的白炽灯,是指它的额定电压的有效 值是220V。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 t uC(t ) = ∫ iC(ξ )dξ + uC(0− ) C 0-
表示电感电流和电容电压的初始值。 其中 iL(0− )、uC(0− ) 表示电感电流和电容电压的初始值。
表示根据R、 、 元件时域电压电流的关系式如 图14-3表示根据 、L、C元件时域电压电流的关系式如 - 表示根据 何得到它们频域电路模型的过程。 何得到它们频域电路模型的过程。
在进行正弦稳态分析时,为了避免建立微分方程, 在进行正弦稳态分析时,为了避免建立微分方程, 我们将电路的时域模型变换为相量模型, 我们将电路的时域模型变换为相量模型,再根据相量形 式的KCL、KVL和VCR直接建立复数的代数方程来求 、 式的 和 直接建立复数的代数方程来求 所示: 解。具体分析步骤如图14-1所示: 具体分析步骤如图 - 所示
1 t iL(t ) = ∫ uL(ξ )dξ + iL(0− ) L 0-
频域关系 UR (s) = RIR (s)
1 1 IL(s) = UL(s) + iL (0− ) sL s UL(s) = sLIL(s) − LiL(0− ) UC(s) = 1 1 IC(s) + uC(0− ) sC s IC(s) = sCUC(s) − CuC(0− )
−αt
ω s2 + ω2
s s2 + ω2 n! sn+1 K K + s +α − jω s +α + jω
下面给出拉普拉斯变换的性质
性质 线性性质 微分规则 积分规则 关系式
L [a1 f1(t ) + a2 f2 (t )] = a1F (s) + a2F (s) 1 2
L[ df ] = sF(s) − f (0− ) dt
图14-5 -
的频域模型如图(b)所示 解:图(a)的频域模型如图 所示,列出网孔电流方程 的频域模型如图 所示,
1 1 12 8 1+ s I1(s) − s IL(s) = s − s − 1 I (s) + s + 1+ 1 I (s) = 4 + 8 L s 1 s s
图14-6 -
1.用矩阵形式列出个结点的KCL方程 .用矩阵形式列出个结点的 方程
支路 1 ① 结点 ② ③ 2 3 4 5
I1(s) 1 1 0 0 0 I2 (s) 0 = 0 0 −1 −1 1 0 I3 (s) 0 0 0 −1 1 I (s) 0 4 I5 (s)
简写为 其中
AI(s)=0 =
1 1 0 0 0 A= 0 - - 1 0 1 1 0 0 0 - 1 1
称为关联矩阵,它表示支路与结点的关联关系, 称为关联矩阵,它表示支路与结点的关联关系,其元素为
k i 1 如果支路 离开结点 aik = − 1 如果支路 进入结点 k i 0 如果支路 不与结点 相连 k i
第十四章 动态电路的频域分析
动态电路的基本分析方法是建立电路的微分方程, 动态电路的基本分析方法是建立电路的微分方程, 并求解微分方程得到电压电流,对于高阶动态电路而言, 并求解微分方程得到电压电流,对于高阶动态电路而言, 建立和求解微分方程都十分困难。 建立和求解微分方程都十分困难。对于单一频率正弦激 励的线性时不变电路,为避免建立和求解微分方程, 励的线性时不变电路,为避免建立和求解微分方程,常 常采用相量法。 常采用相量法。相量法是将正弦电压电流用相应的相量 电压电流表示, 电压电流表示,将电路的微分方程变换为复数代数方程 来求解,得到相量形式的电压电流后, 来求解,得到相量形式的电压电流后,再反变换为正弦 电压电流。 电压电流。
求解得到电感电流的拉普拉斯变换后, 求解得到电感电流的拉普拉斯变换后,再用部分分式 展开为
4(s2 + 3s + 3) 6 − 2s IL(s) = = + 2 2 s(s + 2s + 2) s s + 2s + 2 6 − 2s = + s (s + 1− j)( s + 1+ j) 6 −1− j −1+ j = + + s s + 1− j s + 1+ j
2.用矩阵形式列出支路电压与结点电压关系的KVL方程 用矩阵形式列出支路电压与结点电压关系的KVL方程 KVL
根据电感电流的拉普拉斯变换, 根据电感电流的拉普拉斯变换,查拉普拉斯变换表 14-1,可以得到电感电流的零输入响应、 零状态响应 - ,可以得到电感电流的零输入响应、 和全响应为
−5 9 ' −t −3t 零 入 应 输 响 + → iL(t ) = (−5e + 9e ) ε(t )A (s + 1) (s + 3) 1 −1 " −t −3t 零 态 应 状 响 + → iL(t ) = (e − e ) ε(t )A (s + 1) (s + 3) −4 8 −t −3t 全 应 响 + → iL(t ) = (−4e + 8e ) ε(t )A (s + 1) (s + 3)
(t ∑i(t) = 0 ∑u(t) = 0
对每个结点 对每一回 路
对 每个结点 对 每一回 路
频域形式的基尔霍夫电流定律和电压定律分别表示为
∑I(s) = 0 ∑U(s) = 0
对于R、 、 元件电压电流的关系式如下所示 元件电压电流的关系式如下所示: 对于 、L、C元件电压电流的关系式如下所示: 时域关系 uR (t ) = RiR (t )
图14-1 -
能不能找到一种类似的变换方法来求解一般线性时 不变电路的全响应, 不变电路的全响应,而不必列出微分方程和确定初始条 件呢?回答是肯定的,我们可以采用拉普拉斯变换, 件呢?回答是肯定的,我们可以采用拉普拉斯变换,用 类似的方法来分析任意信号激励下, 类似的方法来分析任意信号激励下,线性时不变动态电 路的完全响应,其具体分析步骤如图 - 所示 所示: 路的完全响应,其具体分析步骤如图14-2所示:
0− ∞
∞
= ∫ e−stdt
0+
1 −st =− e s 0 1 = s
∞
下面给出常用函数的拉普拉斯变换
f (t )
F(s) = ∫ f (t )e−stdt
0−
∞
δ (t ) ε (t )
e
−αt
1 1/s 1 s +α
sin(ωt ) cos(ωt ) tn 2 | K | e cos(ωt + ∠K)
查拉普拉斯变换表可以得到电感电流为
iL (t ) = [6 + 2 2e−t cos(t − 135o )]A
郁金香
§14-3 线性时不变电路的性质 - 一、频域形式的表格方程 表格方程由KCL、KVL和元件 、 和元件VCR方程组成。现在以 方程组成。 表格方程由 和元件 方程组成 电路加以说明。 图14-6电路加以说明。 - 电路加以说明
时间函数f(t)的拉普拉斯变换记为 时间函数 的拉普拉斯变换记为 L [ f (t )] ,其定义为
L [ f (t )] = ∫ f (t )e dt
−st 0−
∞
其中 s = σ + jω 称为复频率。积分的上下限是固定的, 称为复频率。积分的上下限是固定的, 无关, 积分的结果与t无关,只取决于参数s,它是复频率的函 数,即
t 0-
L [∫
f (ξ )dξ ] =
1 F(s) s
其中
L [ f (t )] = F(s) L [ f1(t )] = F1(s)
L [ f2 (t )] = F2 (s)
郁金香
§14-2 动态电路的频域分析 -
若将时域的电压u(t)和电流 的拉普拉斯变换记为 和电流i(t)的拉普拉斯变换记为 若将时域的电压 和电流 U(s)和I(s),则时域形式的基尔霍夫电流定律和电压定律 和 , 分别表示为
图14-1 -
图14-1 -
采用频域分析方法还可以得到线性时不变电路的很 多基本性质。 多基本性质。本章先介绍拉普拉斯变换和动态电路的频 域分析方法, 域分析方法,然后介绍一种采用频域分析法的动态网络 分析程序,供读者学习电路课程时使用。 分析程序,供读者学习电路课程时使用。
§14-l 拉普拉斯变换 -
图14-3 -
由此可见, 由此可见,在频域模型中电感电流和电容电压的初 始值是以一个阶跃电源或冲激电源的形式出现的。 始值是以一个阶跃电源或冲激电源的形式出现的。
二、频域法分析线性时不变电路的主要步骤 (一)画出频域的电路模型 一 画出频域的电路模型 已知时域电路模型可以画出频域的电路模型,其步骤如下: 已知时域电路模型可以画出频域的电路模型,其步骤如下: 1.将时域模型中的各电压电流用相应的拉普拉斯变换表示, .将时域模型中的各电压电流用相应的拉普拉斯变换表示, 并标明在电路图上。 并标明在电路图上。 2.将R、L、C元件用图 -3所示频域等效电路模型表示。 . 元件用图14- 所示频域等效电路模型表示 所示频域等效电路模型表示。 、 、 元件用图 其中,电感电流的初始值 是以阶跃电流源i 其中,电感电流的初始值iL(0-)是以阶跃电流源 L(0-)/s或冲激 是以阶跃电流源 或冲激 电压源LiL(0-)的形式出现。电容电压的初始值uC(0-)是以阶跃 电压源 的形式出现。电容电压的初始值 是以阶跃 的形式出现 电压源u 或冲激电流源Cu 的形式出现。 电压源 C(0-)/s或冲激电流源 C(0-)的形式出现。 或冲激电流源 的形式出现
图14-4 -
电路的频域模型, 所示, 解:图(a)电路的频域模型,如图 (b)所示,由此列出频 电路的频域模型 所示 域形式的网孔方程, 域形式的网孔方程,并求解得到电感电流的拉普拉斯变 换如下所示。 换如下所示。
