粒子群算法的基本流程
一种求解符号回归问题的粒子群优化算法

一种求解符号回归问题的粒子群优化算法全文共四篇示例,供读者参考第一篇示例:粒子群优化算法(Particle Swarm Optimization,PSO)是一种模拟鸟群等社会行为的启发式优化算法,用于解决优化问题。
在符号回归中,我们通常需要找出一组数学函数来准确拟合数据集。
在这篇文章中,我们将讨论一种基于粒子群优化的算法,用于解决符号回归问题。
1. 粒子群优化算法简介粒子群优化算法最初由Kennedy和Eberhart在1995年提出,灵感来源于鸟群和鱼群等集体行为。
PSO算法模拟了鸟群中鸟群中鸟群在搜索食物时的行为。
每个“粒子”代表一个解决方案,并根据个体最优和群体最优不断调整自身位置,以寻找全局最优解。
PSO算法的核心思想是通过计算粒子在解空间中的位置和速度,不断更新粒子的位置和速度以朝着更优解的方向移动。
在每次迭代中,粒子会根据其个体最优和群体最优调整自身位置,直到达到停止条件为止。
PSO算法简单且易于实现,同时能够在全局搜索和局部搜索之间取得平衡,具有较好的收敛性和鲁棒性。
2. PSO算法在符号回归中的应用符号回归问题是指通过给定的数据集,在已知数学表达式的情况下,求解该表达式中的未知参数。
符号回归在数据建模、函数逼近等领域广泛应用,例如在机器学习、数据挖掘和人工智能等领域中。
PSO算法在符号回归中的应用主要通过优化数学表达式的系数来拟合数据集。
通过粒子的位置和速度更新,PSO算法能够搜索适合的数学表达式和参数,以最小化拟合误差,找出最优解。
在符号回归中,通常采用多项式回归、指数回归、对数回归等形式的函数来拟合数据集。
PSO算法可以很好地适应不同类型的数学表达式,并找到最佳的函数形式和参数值,以提高模型的准确性和泛化能力。
3. 粒子群优化算法的步骤在符号回归问题中,应用PSO算法的步骤如下:(1)初始化粒子群:随机初始化一组粒子,每个粒子表示一个解决方案,即一个数学表达式及其参数值。
(2)计算适应度:根据每个粒子的数学表达式和参数值,计算适应度函数值,即拟合误差的度量。
粒子群算法

粒子群算法原理及简单案例[ python ]介绍粒子群算法(Particle swarm optimization,PSO)是模拟群体智能所建立起来的一种优化算法,主要用于解决最优化问题(optimization problems)。
1995年由 Eberhart和Kennedy 提出,是基于对鸟群觅食行为的研究和模拟而来的。
假设一群鸟在觅食,在觅食范围内,只在一个地方有食物,所有鸟儿都看不到食物(即不知道食物的具体位置。
当然不知道了,知道了就不用觅食了),但是能闻到食物的味道(即能知道食物距离自己是远是近。
鸟的嗅觉是很灵敏的)。
假设鸟与鸟之间能共享信息(即互相知道每个鸟离食物多远。
这个是人工假定,实际上鸟们肯定不会也不愿意),那么最好的策略就是结合自己离食物最近的位置和鸟群中其他鸟距离食物最近的位置这2个因素综合考虑找到最好的搜索位置。
粒子群算法与《遗传算法》等进化算法有很多相似之处。
也需要初始化种群,计算适应度值,通过进化进行迭代等。
但是与遗传算法不同,它没有交叉,变异等进化操作。
与遗传算法比较,PSO的优势在于很容易编码,需要调整的参数也很少。
一、基本概念与遗传算法类似,PSO也有几个核心概念。
粒子(particle):一只鸟。
类似于遗传算法中的个体。
1.种群(population):一群鸟。
类似于遗传算法中的种群。
2.位置(position):一个粒子(鸟)当前所在的位置。
3.经验(best):一个粒子(鸟)自身曾经离食物最近的位置。
4.速度(velocity ):一个粒子(鸟)飞行的速度。
5.适应度(fitness):一个粒子(鸟)距离食物的远近。
与遗传算法中的适应度类似。
二、粒子群算法的过程可以看出,粒子群算法的过程比遗传算法还要简单。
1)根据问题需要,随机生成粒子,粒子的数量可自行控制。
2)将粒子组成一个种群。
这前2个过程一般合并在一起。
3)计算粒子适应度值。
4)更新种群中每个粒子的位置和速度。
粒子群优化算法概述[1]
![粒子群优化算法概述[1]](https://img.taocdn.com/s3/m/020552f8c1c708a1284a4497.png)
计算机辅助工艺课程作业学生:赵华琳学号: s时间:09年6月粒子群优化算法概述0.前言优化是科学研究、工程技术和经济管理等领域的重要研究工具。
它所研究的问题是讨论在众多的方案中寻找最优方案。
例如,工程设计中怎样选择设计参数,使设计方案既满足设计要求又能降低成本;资源分配中,怎样分配有限资源,使分配方案既能满足各方面的基本要求,又能获得好的经济效益。
在人类活动的各个领域中,诸如此类,不胜枚举。
优化这一技术,正是为这些问题的解决,提供理论基础和求解方法,它是一门应用广泛、实用性很强的科学。
近十余年来,粒子群优化算法作为群体智能算法的一个重要分支得到了广泛深入的研究,在路径规划等许多领域都有应用。
本文主要结合现阶段的研究概况对粒子群优化算法进行初步介绍。
1.粒子群优化算法的基本原理1.1 粒子群优化算法的起源粒子群优化(PSO)算法是由Kennedy和Eberhart于1995年用计算机模拟鸟群觅食这一简单的社会行为时,受到启发,简化之后而提出的[1][2]。
设想这样一个场景:一群鸟随机的分布在一个区域中,在这个区域里只有一块食物。
所有的鸟都不知道食物在哪里。
但是他们知道当前的位置离食物还有多远。
那么找到食物的最优策略是什么呢。
最简单有效的方法就是追寻自己视野中目前离食物最近的鸟。
如果把食物当作最优点,而把鸟离食物的距离当作函数的适应度,那么鸟寻觅食物的过程就可以当作一个函数寻优的过程。
鱼群和鸟群的社会行为一直引起科学家的兴趣。
他们以特殊的方式移动、同步,不会相互碰撞,整体行为看上去非常优美。
生物学家CargiReynolds提出了一个非常有影响的鸟群聚集模型。
在他的模拟模型boids中,每一个个体遵循:避免与邻域个体相冲撞、匹配邻域个体的速度、试图飞向感知到的鸟群中心这三条规则形成简单的非集中控制算法驱动鸟群的聚集,在一系列模拟实验中突现出了非常接近现实鸟群聚集行为的现象。
该结果显示了在空中回旋的鸟组成轮廓清晰的群体,以及遇到障碍物时鸟群的分裂和再度汇合过程。
粒子群的基本原理

粒子群的基本原理
粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,模拟生物群体中的信息传递和合作行为。
其基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。
PSO算法的基本原理如下:
1. 初始化粒子群:随机初始化一群粒子,每个粒子代表一个解,并为每个粒子随机分配一个速度。
2. 评估粒子适应度:根据特定问题的目标函数,计算每个粒子的适应度值。
3. 更新个体最优解:对于每个粒子,记录其个体历史最优解,即该粒子达到的最好解。
4. 更新全局最优解:从所有粒子的个体历史最优解中选取适应度最好的解作为全局最优解。
5. 更新粒子速度和位置:根据粒子当前位置、速度和个体、全局最优解,通过调整速度和位置来更新粒子的状态。
6. 重复步骤2至5,直到满足停止条件(如达到预定迭代次数或找到满意解)。
在PSO算法中,粒子的速度和位置的更新是通过以下公式进行计算:
v(i+1) = w*v(i) + c1*r1*(p(i)-x(i)) + c2*r2*(g(i)-x(i))
x(i+1) = x(i) + v(i+1)
其中,v(i+1)为粒子下一时刻速度,x(i+1)为粒子下一时刻位置,w为惯性权重,c1、c2为加速因子,r1、r2为随机数,p(i)为个体历史最优解,g(i)为全局最优解。
通过迭代更新粒子的速度和位置,PSO算法可以逐渐搜索到全局最优解附近的解空间。
pso粒子群算法

onal Conference on Neural Networks.1995.1942~1948.)。源
算法介绍 算法介绍
设想这样一个场景:一群鸟在随机的搜索食物。 PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最 优解。在每一次的迭代中,粒子通过跟踪两个“极值”(pb 在这个区域里只有一块食物,所有的鸟都不知 est,gbest)来更新自己。 道食物在那。但是它们知道自己当前的位置距 在找到这两个最优值后,粒子通过下面的公式来更新自己 离食物还有多远。 的速度和位置。
的总数
算法介绍
算法介绍 算法介绍
抽象: PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最 鸟被抽象为没有质量和体积的微粒 (点),并延伸到N维 优解。在每一次的迭代中,粒子通过跟踪两个“极值”(pb 空间,粒子 I 在N维空间的位置表示为矢量Xi=(x1,x est,gbest)来更新自己。 x , ,„,xN),飞行速度表示为矢量Vi=x(v 2在找到这两个最优值后,粒子通过下面的公式来更新自己 1 V v2,„,v ).每个粒子都有一个由目标函数决定的适应值(fitne N的速度和位置。 ss value) ,并且知道自己到目前为止发现的最好位置 (1) 式 (pbest) 和现在的位置 Xi .这个可以看作是粒子自己的 V V c rand () ( pbest i i 1 i xi ) c2 rand () ( gbesti xi ) 飞行经验.除此之外,每个粒子还知道到目前为止整个 (2)式 群体中所有粒子发现的最好位置(gbest)(gbest是pbest x x V i i 中的最好值)i .这个可以看作是粒子同伴的经验.粒子 在式 (1)、(2)中,i=1,2,…,M,M是该群体中粒子 就是通过自己的经验和同伴中最好的经验来决定下一步 的总数 的运动。
优化算法-粒子群优化算法

步骤四:对于粒子的每一维,根据式(1)计算得到一个随机点 的位置。
步骤五:根据式(2)计算粒子的新的位置。
步骤六:判断是否满足终止条件。
粒子群优化算法
PSO算法在组合优化问题中的应用
典型的组合优化问题:TSP
粒子群优化算法
量子行为粒子群优化算法的基本模型
群智能中个体的差异是有限的,不是趋向于无穷大的。群体的聚 集性是由相互学习的特点决定的。
个体的学习有以下特点: 追随性:学习群体中最优的知识
记忆性:受自身经验知识的束缚
创造性:使个体远离现有知识
粒子群优化算法
聚集性在力学中,用粒子的束缚态来描述。产生束缚态的原因是 在粒子运动的中心存在某种吸引势场,为此可以建立一个量子化 的吸引势场来束缚粒子(个体)以使群体具有聚集态。
描述为: 给定n 个城市和两两城市之间的距离, 求一条访问各城市
一次且仅一次的最短路线. TSP 是著名的组合优化问题, 是NP难题, 常被用来验证智能启发式算法的有效性。
vid (t 1) wvid (t) c1r1 pid (t) xid (t) c2r2( pgd (t) xid (t))
xid (t 1) xid (t) vid (t 1)
粒子群优化算法
w 惯性权重 可以是正常数,也可以是以时间为变量的线性或非线性
正数。
粒子群优化算法
通常动态权重可以获得比固定值更好的寻优结果,动态权重可以在 pso搜索过程中呈线性变化,也可以根据pso性能的某个测度函数 而动态改变,目前采用的是shi建议的随时间线性递减权值策略。
粒子群优化算法
量子粒子群算法的公式

量子粒子群算法的公式量子粒子群算法(Quantum Particle Swarm Optimization,QPSO)是一种元启发式优化算法,它结合了粒子群优化算法和量子计算的概念。
其公式可以用以下方式表示:1. 初始化量子粒子的位置和速度:\( x_i^0 = rand(x_{\text{min}}, x_{\text{max}}) \)。
\( v_i^0 = rand(-|x_{\text{max}}-x_{\text{min}}|, |x_{\text{max}}-x_{\text{min}}|) \)。
2. 计算适应度:\( f_i^0 = f(x_i^0) \)。
3. 更新量子粒子的位置和速度:\( x_i^{t+1} = x_i^t + v_i^t \)。
\( v_i^{t+1} = \frac{1}{2} \left( \frac{1}{N}\sum_{j=1}^{N} \frac{1}{\sqrt{1 + \frac{(x_i^tx_j^t)^2}{\lambda^2}}} \right)^2 v_i^t \)。
其中,\( x_i^t \) 表示第 \( i \) 个粒子在第 \( t \) 代的位置,\( v_i^t \) 表示第 \( i \) 个粒子在第 \( t \) 代的速度,\( f(x_i^t) \) 表示第 \( i \) 个粒子在位置 \( x_i^t \) 的适应度,\( x_{\text{min}} \) 和 \( x_{\text{max}} \) 分别表示搜索空间的最小值和最大值,\( N \) 表示粒子群中粒子的数量,\( \lambda \) 是一个常数。
以上公式描述了量子粒子群算法的基本过程,通过不断迭代更新粒子的位置和速度,以及根据适应度函数进行优化,最终寻找到最优解。
这种算法结合了经典粒子群优化算法和量子力学的概念,具有较强的全局搜索能力和收敛速度。
粒子群算法粒子群算法简介
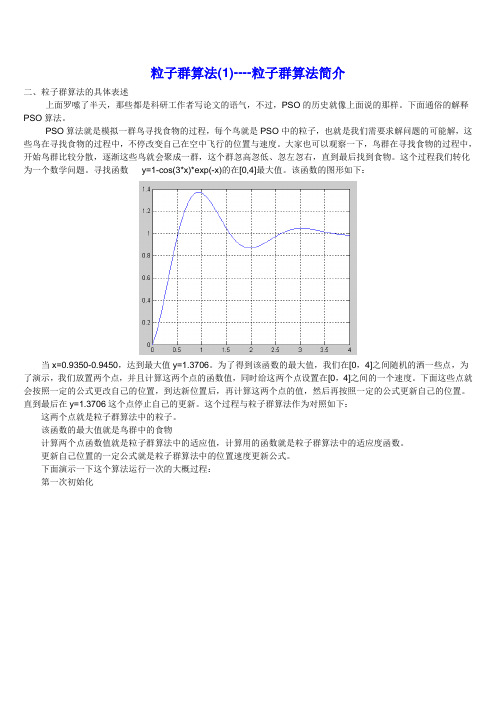
粒子群算法(1)----粒子群算法简介二、粒子群算法的具体表述上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO的历史就像上面说的那样。
下面通俗的解释PSO算法。
PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0,4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0,4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群算法(2)----标准的粒子群算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
粒子群算法的基本流程
粒子群算法(Particle Swarm Optimization,PSO)是一种模拟鸟群觅食行为的优化算法,通过模拟鸟群中个体之间的协作和信息共享,寻找最优解。
它最早由美国社会心理学家Kennedy和Eberhart于1995年提出,被广泛应用于各个领域的优化问题。
粒子群算法的基本流程可以分为初始化、迭代更新和停止准则三个步骤。
1. 初始化
在粒子群算法中,需要初始化一组粒子,每个粒子代表问题的一个解。
粒子的位置表示解的搜索空间中的一个点,粒子的速度表示解的搜索方向和速度。
初始化时,需要给每个粒子随机分配一个位置和速度,并记录每个粒子的历史最佳位置和全局最佳位置。
2. 迭代更新
在每一次迭代中,需要更新每个粒子的位置和速度,以及更新每个粒子的历史最佳位置和全局最佳位置。
2.1 更新粒子的速度
粒子的速度更新公式为:
v(t+1) = w * v(t) + c1 * rand() * (pbest - x(t)) + c2 * rand() * (gbest - x(t))
其中 v(t+1) 表示粒子在下一次迭代中的速度,v(t) 表示粒子当前的速度,w 是惯性权重,c1 和 c2 是加速因子,rand() 是一个介于0和1之间的随机数,pbest 表示粒子的历史最佳位置,gbest 表示全局最佳位置,x(t) 表示粒子当前的位置。
2.2 更新粒子的位置
粒子的位置更新公式为:
x(t+1) = x(t) + v(t+1)
其中x(t+1) 表示粒子在下一次迭代中的位置,x(t) 表示粒子当前的位置,v(t+1) 表示粒子在下一次迭代中的速度。
2.3 更新粒子的历史最佳位置和全局最佳位置
在每次迭代中,需要根据当前位置和历史最佳位置来更新粒子的历史最佳位置。
同时,需要根据所有粒子的历史最佳位置来更新全局最佳位置。
3. 停止准则
迭代更新的过程会持续进行,直到满足停止准则为止。
常见的停止准则有达到最大迭代次数、目标函数值收敛等。
粒子群算法的基本流程如上所述。
在实际应用中,可以根据具体问题的特点来调整粒子群算法的参数,如惯性权重、加速因子等,以获得更好的优化效果。
同时,粒子群算法也可以与其他优化算法相
结合,形成混合算法,提高求解能力。
粒子群算法是一种简单而有效的优化算法,具有全局搜索能力和较快的收敛速度。
它已成功应用于各个领域的优化问题,并取得了良好的效果。
未来,随着对粒子群算法的研究和改进,相信它将在更多领域发挥重要作用。
