15.2全等三角形判定SSS
全等三角形的判定sss基础题

一、引言全等三角形是初中数学中的重要概念,对其判定方法的掌握是学生学习几何的基础。
全等三角形的判定方法有很多种,其中sss判定法是最基础的一种方法。
本文将对sss判定法进行详细介绍,帮助读者加深对全等三角形判定的理解。
二、什么是全等三角形在进行全等三角形的判定之前,首先需要了解什么是全等三角形。
全等三角形是指具有相同三边长度和三个对应角度相等的三角形。
当两个三角形能够满足这两个条件时,我们称它们是全等三角形。
三、 sss判定法的原理sss判定法是指当两个三角形的三条边分别相等时,这两个三角形就是全等的。
这一判定法的原理基于边对应相等的性质,即三角形的三条边完全相等那么这两个三角形就是全等的。
四、 sss判定法的步骤为了更加具体地了解sss判定法的应用,我们可以简单总结为以下步骤:1. 首先比较两个三角形的三条边,确定它们是否分别相等;2. 如果两个三角形的三条边分别相等,则可以得出这两个三角形是全等的结论。
五、 sss判定法的应用举例为了更好地理解sss判定法的应用,我们来看一个具体的例子:已知△ABC和△XYZ,其中AB=XY,BC=YZ,AC=XZ。
我们要判定△ABC和△XYZ是否全等。
根据sss判定法,我们首先比较三条边的长度:1. AB=XY2. BC=YZ3. AC=XZ因为△ABC和△XYZ的三条边分别相等,所以根据sss判定法,我们可以得出结论:△ABC和△XYZ是全等的。
六、总结通过以上介绍,我们对sss判定法有了更深入的了解。
sss判定法是全等三角形判定中最基础的一种方法,但是在实际应用中仍然非常重要。
通过不断练习和应用,我们可以更加熟练地运用这一方法来判定三角形的全等性,提高自己的数学水平。
七、结语在学习数学知识的过程中,掌握全等三角形的判定方法是至关重要的。
希望本文的介绍能够帮助读者更好地理解和掌握sss判定法,为今后的学习和工作奠定坚实的数学基础。
八、sss判定法的应用场景sss判定法可以在很多实际问题中得到应用。
全等三角形的判定SSS
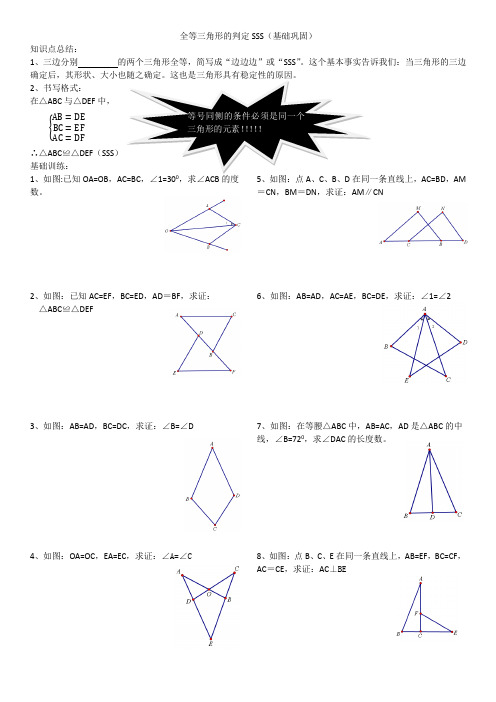
全等三角形的判定SSS (基础巩固)知识点总结:1、三边分别 的两个三角形全等,简写成“边边边”或“SSS ”。
这个基本事实告诉我们:当三角形的三边确定后,其形状、大小也随之确定。
这也是三角形具有稳定性的原因。
2、书写格式:在△ABC 与△DEF 中, {AB =DE BC =EF AC =DF∴△ABC ≌△DEF (SSS )基础训练:1、如图:已知OA=OB ,AC=BC ,∠1=300,求∠ACB 的度数。
2、如图:已知AC=EF ,BC=ED ,AD =BF ,求证: △ABC ≌△DEF3、如图:AB=AD ,BC=DC ,求证:∠B=∠D4、如图:OA=OC ,EA=EC ,求证:∠A=∠C5、如图:点A 、C 、B 、D 在同一条直线上,AC=BD ,AM =CN ,BM =DN ,求证:AM ∥CN6、如图:AB=AD ,AC=AE ,BC=DE ,求证:∠1=∠27、如图:在等腰△ABC 中,AB=AC ,AD 是△ABC 的中线,∠B=720,求∠DAC 的长度数。
8、如图:点B 、C 、E 在同一条直线上,AB=EF ,BC=CF ,AC =CE ,求证:AC ⊥BE等号同侧的条件必须是同一个三角形的元素!!!!!能力提升:1、如图:E在BC边上,AD=AB,AE=AC,DE=BC,求证:∠1=∠32、如图:已知△AOB≌△COD,△COE≌△AOF,求证:△BOF≌△DOE3、如图:AC与BD相交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF,求证:AE∥CF4、如图:AC=BD,AD=BC,AD与BC相交于点O,且CO=OD,过O点作△ABC的中线,交AB于点E,求证:DE⊥AB5、如图:已知AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠26、如图:在△ABC中,AB=AC,D是BC中点,E是AC上一点,且AE=AD,若∠EDC=180,求∠BAD的度数。
全等三角形判定条件SSS
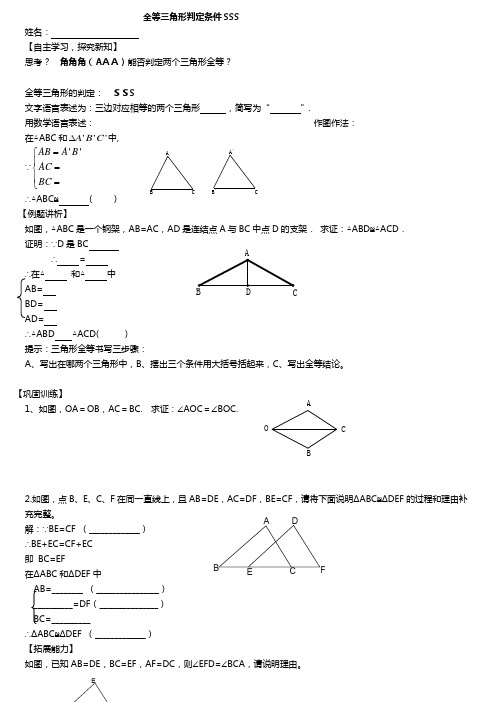
全等三角形判定条件SSS姓名:【自主学习,探究新知】思考? 角角角(A AA)能否判定两个三角形全等?全等三角形的判定: SSS文字语言表述为:三边对应相等的两个三角形 ,简写为“ ”.用数学语言表述: 作图作法:在△ABC 和'''A B C ∆中,∵''AB A B AC BC =⎧⎪=⎨⎪=⎩∴△ABC ≌ ( )【例题讲析】 如图,△ABC 是一个钢架,AB=AC ,AD 是连结点A 与BC 中点D 的支架. 求证:△ABD ≌△ACD .证明:∵D 是BC∴ = ∴在△ 和△ 中AB=BD=AD=∴△ABD △ACD( )提示:三角形全等书写三步骤:A 、写出在哪两个三角形中,B 、摆出三个条件用大括号括起来,C 、写出全等结论。
【巩固训练】1、如图,OA =OB ,AC =BC. 求证:∠AOC =∠BOC.2.如图,点B 、E 、C 、F 在同一直线上,且AB=DE ,AC=DF ,BE=CF ,请将下面说明ΔABC ≌ΔDEF 的过程和理由补充完整。
解:∵BE=CF (_____________)∴BE+EC=CF+EC即 BC=EF在ΔABC 和ΔDEF 中AB=________ (________________)__________=DF (_______________)BC=__________∴ΔABC ≌ΔDEF (_____________)【拓展能力】如图,已知AB=DE ,BC=EF ,AF=DC ,则∠EFD=∠BCA ,请说明理由。
C 'B 'A 'C B A A BDEF CO A BAB C D EF。
2全等三角形判定一SSSSAS基础知识讲解

全等三角形判定一(SSS SAS (基础)【学习目标】1 .理解和掌握全等三角形判定方法 1 ―― “边边边”,和判定方法2―― “边角边”;2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定1 ―― “边边边” 全等三角形判定1―― “边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“ SSS').要点诠释:如图,如果A'B' = AB, A'C' = AC B'C' = BC 则^ ABC^A A'B'C'.要点诠释:如图,如果AB = A'B' , / A=/ A' ,AC = A'C',则△ ABC^^ A'B'C '. 注意:这里的角,指的是两组对应边的夹角.2.有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ ABC与△ ABD中,AB= AB AO AD, / B=/ B,但△ ABC与△ ABD不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.A【典型例题】要点二、全等三角形判定2―― “边角边”1.全等三角形判定2―― “边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS).类型一、全等三角形的判定 1 ―― “边边边”••• pg QM 在^ RPMm RQM中,RP = RQ(已知),{PM =QM ,[RM = RM (公共边)•••△ RPM PA RQM SSS .••• / PRM=/ QRMT全等三角形对应角相等).即RM平分/ PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中在的两个三角形全等,举一反三:AA BC, AO BD试证明:/ CAD=/ DBC.【答案】证明:连接DC在厶ACD与△ BDC中AD =BC* AC =BDCD =DC (公共边)•••△ ACD^^ BDC( SSS•/ CAD=/ DBC(全等三角形对应角相等)类型二、全等三角形的判定2―― “边角边”2、已知:如图,AB= AD, AC= AE,/ 1 = / 2.求证:BC= DE【思路点拨】【答案与解析】证明:由中点的定义得pgQM RM为公共边,则可由SSS定理证明全等.••• M为PQ的中点(已知),.把证明一对角或线段相等的问题, 综合应用全等三角形的性质和判定.转化为证明它们所【变式】已知:如图,AC= AE需要找夹角/ BAC与/ DAE夹角可由等量代换证得相等.【答案与解析】证明:•// 1 = / 2•••/ 1 + / CAD=/ 2 +/ CAD 即/ BAG- / DAE 在^ ABC和△ ADE中r AB = AD{N BAC =N DAE[A C =AE【答案】AE= CD并且AE! CD证明:延长AE交CD于F ,•••△ ABC和△ DBE是等腰直角三角形••• AB= BC, BD= BE 在^ ABE和^ CBD中[AB =BC2ABE =N CBD =90。
全等三角形判定二(SSS)(基础)知识讲解

全等三角形判定二(SSS )(基础)撰稿:常春芳【学习目标】1.理解和掌握全等三角形判定方法4——“边边边”;2.能把证明角相等或线段相等的问题,转化为证明它们所在的两个三角形全等.3. 探索三角形全等的判定方法,能利用三角形全等进行证明,掌握综合法证明的格式; 【要点梳理】要点一、全等三角形判定4——“边边边” 全等三角形判定4——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).要点诠释:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .要点二、判定方法的选择已知条件 可选择的判定方法 一边一角对应相等 SAS AAS ASA 两角对应相等 ASA AAS 两边对应相等SAS SSS要点三、如何选择三角形证全等1.可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;2.可以从已知出发,看已知条件确定证哪两个三角形全等;3.由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;4.如果以上方法都行不通,就添加辅助线,构造全等三角形. 要点四、全等三角形证明方法全等三角形是平面几何内容的基础,这是因为全等三角形是研究特殊三角形、四边形、相似图形、圆等图形性质的有力工具,是解决与线段、角相关问题的一个出发点.运用全等三角形,可以证明线段相等、线段的和差倍分关系、角相等、两直线位置关系等常见的几何问题.可以适当总结证明方法. 1. 证明线段相等的方法:(1) 证明两条线段所在的两个三角形全等.(2) 利用角平分线的性质证明角平分线上的点到角两边的距离相等. (3) 等式性质.2. 证明角相等的方法:(1) 利用平行线的性质进行证明.(2) 证明两个角所在的两个三角形全等.(3) 利用角平分线的判定进行证明.(4) 同角(等角)的余角(补角)相等.(5) 对顶角相等.3.证明两条线段的位置关系(平行、垂直)的方法;可通过证明两个三角形全等,得到对应角相等,再利用平行线的判定或垂直定义证明. 4.辅助线的添加:(1)作公共边可构造全等三角形;(2)倍长中线法;(3)作以角平分线为对称轴的翻折变换全等三角形;(4)利用截长(或补短)法作旋转变换的全等三角形.5. 证明三角形全等的思维方法:(1)直接利用全等三角形判定和证明两条线段或两个角相等,需要我们敏捷、快速地发现两条线段和两个角所在的两个三角形及它们全等的条件.(2)如果要证明相等的两条线段或两个角所在的三角形全等的条件不充分时,则应根据图形的其它性质或先证明其他的两个三角形全等以补足条件.(3)如果现有图形中的任何两个三角形之间不存在全等关系,此时应添置辅助线,使之出现全等三角形,通过构造出全等三角形来研究平面图形的性质.要点五、三角形的稳定性三角形的三条边确定后,三角形的形状和大小就确定不变了,这个性质叫做三角形的稳定性。
八年级数学三角形全等的判定
A
A'
B
C B'
C'
活动一
按下列条件做三角形,并通过比较判断它们之间是 否全等,由此你有什么发现?
第一组:一条边为6cm;
大家要 合作哦
第二组:一个角是45°;
第三组:两条边分别为4cm和6cm;
第四组:一条边为6cm,一个角为45°;
第五组:两个? 怎么判断一个人究竟有没有他的"自我"呢?我可以提出一个检验的方
法,就是 看他能不能独处。当你自己一个人呆着时,你是感到百无聊赖,难以忍受呢,还是感到一种 宁静、充实和满足? 对于有"自我"的人来说,独处是人生中的美好时刻和美好体验,虽则有些寂寞,寂寞中却 又有一种充实。独处是灵魂生长的必要空间。在独处时,我们从别人
与一个 人的性格完全无关,爱好独处的人同样可能是一个性格活泼、喜欢朋友的人,只是无论他怎 么乐于与别人交往,独处始终是他生活中的必需。在他看来,一种缺乏交往的生活当然是一 种缺陷,一种缺乏独处的生活则简直是一种灾难了。 当然,人是一种社会性的动物,他需
要与他的同类交往,需要爱和被爱,否则就无法生存。 世上没有一个人能够忍受绝对的孤独。但是,绝对不能忍受孤独的人却是一个灵魂空虚的人 。世上正有这样的一些人,他们最怕的就是独处,让他们和自己呆一会儿,对于他们
精神的家园 ? 现代世界是商品世界,我们不能脱离这个世界求个人的生存和发展,这是一个事实。 但是,这不是全部事实。我们同时还生活在历史和宇宙中,生活在自己惟一的一次生命过程 中。所以,对于我们的行为,我们不能只用交换价值来衡量,而应有更加开阔久远的参照系 。
在投入现代潮流的同时,我们要有所坚守,坚守那些永恒的人生价值。一个不能投入的人 是一个落伍者,一个无所坚守的人是一个随波逐流者。前者令人同情,后者令人鄙视。也许 有人两者兼顾,成为一个高瞻远瞩的弄潮儿,那当然就是令人钦佩的了。 "人是要有一点精神的。"-
