(完整版)平行四边形判定,题型归纳(较难)
中考数学平行四边形的判定经典题型精编

平行四边形的判定一、【基础知识精讲】1.平行四边形的判定方法:①两组对边分别平行②两组对边分别相等③一组对边平行且相等的四边形是平行四边形④两组对角分别相等⑤对角线互相平分2.平行四边形性质的运用:①直接运用平行四边形性质解决某些问题,如求角的度数,线段的长度,证明角相等或互补,证明线段相等或倍分等.②判别一个四边形为平行四边形,从而得到两直线平行.③先判别—个四边形是平行四边形,然后再用平行四边形的特征去解决某些问题.二、【例题精讲】例1.(1)根据下列条件,不能判别四边形是平行四边形的是( )A.一组对边平行且相等的四边形B.两组对角分别相等的四边形C.对角线相等的四边形D.对角线互相平分的四边形(2)下列条件中不能确定四边形ABCD是平行四边形的是()A.AB=CD,AD∥BC B.AB=CD,AB∥CDC.AB∥CD,AD∥BC D.AB=CD,AD=BC例2.已知:如图,□ABCD中,点E、F在对角线上,且AE=CF.求证:四边形BEDF是平行四边形.例3.如图,□ABCD 的对角线AC 、BD 交于O ,EF 过点O 交AD 于E ,交BC 于F ,G 是OA 的中点,H 是OC 的中点,求证:四边形EGFH 是平行四边形.三、【同步练习】 A 组1.如图,四边形ABCD ,AC 、BD 相交于点O , 若OA=OC,OB=OD,则四边形ABCD 是______, 根据是_____________________ .2.在图中,AC=BD , AB=CD=EF ,CE=DF ,图中有哪些互相平行的线段?3.一个四边形的三个内角的度数依次如下选项,其中是平行四边形的是( ) A .88°,108°,88° B .88°,104°,108° C .88°,92°,92° D .88°,92°,88°4.如图,四边形ABCD 中,AD=BC ,DE ⊥AC ,BF ⊥AC ,垂足分别是E 、F ,AF=CE .求证:四边形ABCD 是平行四边形.OCDBA5、已知如图:在ABCD 中,延长AB 到E ,延长CD 到F ,使BE=DF , 则线段AC 与EF 是否互相平分?说明理由.6.如图,在ABCD 中,点E 、F 在对角线AC 上,并且OE=OF .(1)OA 与OC ,OB 与OD 相等吗? (2)四边形BFDE 是平行四边形吗?(3)若点E ,F 在OA ,OC 的中点上,你能解决上述问题吗?B 组1、在ABCD 中,∠ABC=750,AF ⊥BC 于F ,AF 交BD 于E ,若DE=2AB ,则∠AED 等于( ) A 、600 B 、650 C 、700 D 、7502.如图,在ABCD 的各边AB 、BC 、CD 、DA 上,分别取点K 、L 、M 、N ,使AK=CM 、BL=DN ,则四边形KLMN 为平行四边形FED CBA3.如图,在△ABC 中,D 是AC 的中点,E 是线段BC 延长线上一点,过点A 做BE 的 平行线与线段ED 的延长线交于点F ,连接AE ,CF 。
专题23 平行四边形(归纳与讲解)(原卷版)

专题23 平行四边形【专题目录】技巧1:判定平行四边形的五种常用方法技巧2:平行四边形中的折叠问题【题型】一、平行线的性质、掌握平行四边形的概念及有关性质和判定,并能进行计算和证明.用符号“▱”表示,平行四边形ABCD记作“▱ABCD”,读作“平行四边形ABCD”1、平行四边形对边平行且相等;几何描述:∵四边形ABCD是平行四边形∴AB=CD,AD=BC;AB∥CD,AD∥BC2、平行四边形对角相等、邻角互补;几何描述:∵四边形ABCD是平行四边形∴∠1=∠3,∠2=∠4,∠1+∠4=180°…3、平行四边形对角线互相平分;【类型】三、利用一组对边平行且相等判定平行四边形3.如图,点E ,F 在□ABCD 的边BC ,AD 上,BE =13BC ,FD =13AD ,连接BF ,DE . 求证:四边形BEDF 是平行四边形.几何描述:∵四边形ABCD 是平行四边形 ∴AO=OC=12AC,BO=OD=12BD【类型】四、利用两组对角分别相等判定平行四边形4.下面给出了四边形ABCD中▱A、▱B、▱C、▱D的度数之比,其中能判定四边形ABCD是平行四边形的是()A.1:2:2:1 B.2:2:1:1 C.1:2:1:2 D.1:1:2:2【类型】五、利用对角线互相平分平分判定平行四边形5.如图,将▱ABCD的对角线BD向两个方向延长,分别至点E和点F,BE=DF.求证:四边形AECF是平行四边形.技巧2:平行四边形中的折叠问题【类型】一、平行四边形中的折叠问题1.如图,E,F分别是£ABCD的边AD、BC上的点,EF=6,▱DEF=60°,将四边形EFCD沿EF 翻折,得到EFC′D′,ED′交BC于点G,则▱GEF的周长为()A.9B.12C.9√3D.18【题型讲解】【题型】一、平行线的性质例1、如图,在▱ABCD中,CE平分▱BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是()A.B.C.D.【题型】二、平行线的性质证明例2、如图,四边形ABCD 是平行四边形,点E ,B ,D ,F 在同一条直线上,请添加一个条件使得ABE CDF △≌△,下列不正确...的是( )A .AE CF =B .AEB CFD ∠=∠C .EAB FCD ∠=∠ D .BE DF =【题型】三、平行线性质与判定例3、已知ABCD ,O 为对角线AC 的中点,过O 的一条直线交AD 于点E ,交BC 于点F .(1)求证:AOE COF △≌△;(2)若:12AE AD =:,AOE △的面积为2,求ABCD 的面积. 【题型】四、平行线性质与判定证明例4、已知:如图,在梯形ABCD 中,//AD BC ,对角线BD 、AC 相交于点E ,过点A 作//AF DC ,交对角线BD 于点F .(1)求证:DF DEBD BE=; (2)如果ADB ACD ∠=∠,求证:线段CD 是线段DF 、BE 的比例中项. 【题型】五、三角形中位线有关的面积计算例5、如图,▱ABC 中,AD 、BE 是两条中线,则S ▱EDC :S ▱ABC =( )A .1:2B .2:3C .1:3D .1:4相似三角形(达标训练)一、单选题1.在四边形ABCD 中,对角线AC 和BD 交于点O ,下列条件不能判断四边形ABCD 是平行四边形的是( )A .OA OC =,OB OD = B .AB DC =,AD BC = C .AB DC ∥,AB DC =D .AB DC ∥,AD BC =2.如图,平行四边形ABCD 中,100C ∠=︒,点E 在CD 上,且AE AD =,则DAE ∠的度数是( )A .20︒B .30︒C .40︒D .80︒3.如图,▱ABC 中,AB =10,AC =7,BC =9,点D 、E 、F 分别是AB 、AC 、BC 的中点,则四边形DBFE 的周长是( )A .13B .15C .17D .194.在ABCD 中,对角线AC ,BD 相交于点O ,下列结论一定正确的是( )A .OB OD = B .AB BC =C .AC BD = D .180ABC ADC ∠+∠=︒5.已知:如图,在ABCD 中,E ,F 分别是AB ,CD 的中点.求证:四边形EBFD 是平行四边形.以下是排乱的证明过程:▱EB FD∴=;▱AB CD EB FD∴=,∥;▱▱四边形EBFD是平行四边形;▱又11,22EB AB FD CD==;▱四边形ABCD是平行四边形.证明步骤正确的顺序是()AC6只728.在四边形ABCD中,已知AD▱BC,▱B=▱D,AE▱BC于点E,AF▱CD于点F.(1)求证:四边形ABCD是平行四边形;(2)若AF=2AE,BC=6,求CD的长.相似三角形(提升测评)1点A 2ABC 中,,则下列结论错误的是(A AE BFAD ABEF DECE EA3长是( )A .28B .29C .30D .314.如图,四边形ABCD 中,AB ∥DC ,4CD =,10AB =,点M ,N 分别是边AD 和对角线BD 的中点,且MN与对角线AC交于点P,则PN的长为()A.2B.3C.5D.75A6ABC,D则______.7形三、解答题8.如图,已知矩形ABCD中,对角线AC、BD相交于点O,过点A作AE∥BD,交CB的延长线于点E.(1)求证:AE=AC;(2)9交(1)(2)。
平行四边形的性质与判定压轴题八种模型全攻略(解析版)

专题05平行四边形的性质与判定压轴题八种模型全攻略【考点导航】目录【典型例题】 (1)【考点一利用平行四边形的性质求解】 (1)【考点二利用平行四边形的性质证明】 (3)【考点三判断能否构成平行四边形】 (7)【考点四添一个条件成为平行四边形】 (10)【考点五证明四边形是平行四边形】 (12)【考点六平行四边形中的折叠问题】 (16)【考点七利用平行四边形的性质无刻度作图】 (18)【考点八利用平行四边形的性质与判定综合】 (21)【过关检测】 (27)【典型例题】【考点一利用平行四边形的性质求解】【答案】3【分析】本题考查了平行四边形的性质,平行线的性质,角平分线的定义,等角对等边;熟练掌握平行四=边形的性质,得出AF AB根据平行四边形的对边平行且相等可得AD BC ∥,6DC AB ==,9AD BC ==;根据两直线平行,内错角相等可得AFB FBC ∠=∠;根据从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线可得ABF FBC ∠=∠;推得ABF AFB ∠=∠,根据等角对等边可得6AF AB ==,6DE DC ==,即可列出等式,求解.【详解】解:∵四边形ABCD 是平行四边形,∴AD BC ∥,6DC AB ==,9AD BC ==,∵AD BC ∥,∴AFB FBC ∠=∠,∵BF 平分ABC ∠,∴ABF FBC ∠=∠,则ABF AFB ∠=∠,∴6AF AB ==,同理可证:6DE DC ==,∵2EF AF DE AD =+-=,即669EF +-=,解得:3EF =;故答案为:3.【变式训练】【答案】22【分析】本题考查平行四边形的性质以及三角形周长等知识,解题的关键是记住平行四边形的对角线互相平分.根据平行四边形对角线互相平分求出【详解】解:∵四边形ABCD 是平行四边形,【答案】16【分析】此题考查了平行四边形的性质及周长的计算,关键.根据题意,OM 垂直平分【考点二利用平行四边形的性质证明】例题:(2023下·广东广州·八年级校考期中)平行四边形ABCD 中,AE BF 、分别平分DAB ∠和ABC ∠交CD 于点E F AE BF 、,、交于点G .(1)求证:AE BF ⊥;(2)判断DE 和CF 的大小关系,并说明理由【答案】(1)证明见解析(2)DE CF =,理由见解析【分析】本题考查平行四边形的性质、角平分线的定义,等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型;(1)证明90BAE ABF ∠+∠=︒,即可推出90AGB ∠=︒即AE BF ⊥;(2)证明,DE AD CF BC ==,再利用平行四边形的性质AD BC =,即可解决问题;【详解】(1)证明:如图,∵在平行四边形ABCD 中,AD BC ∥,180DAB ABC ∴∠+∠=︒,AE、BF 分别平分DAB ∠和ABC ∠,22DAB BAE,ABC ABF ∴∠=∠∠=∠,22180BAE ABF ∴∠+∠=︒,即90BAE ABF ∠+∠=︒,90AGB ∴∠=︒,AE BF ∴⊥;(2)解:结论:线段DF 与CE 是相等关系,即DF CE =,∵在平行四边形ABCD 中,CD AB ∥,DEA EAB ∴∠=∠,又AE 平分DAB ∠,DAE EAB ∴∠=∠,DEA DAE ∴∠=∠,DE AD ∴=,同理可得,CF BC =,又∵在平行四边形ABCD 中,AD BC =,DE CF ∴=.【变式训练】1.(2023上·福建厦门·九年级校联考阶段练习)如图,四边形ABCD 是平行四边形,延长BC 到点E ,使得CE BC =,连接AE 交CD 于点F .证明:AFD EFC △≌△.【答案】证明见解析【分析】本题考查平行四边形的性质,三角形全等的证明.由平行四边形的性质可得AD BC ∥,AD BC =,从而D FCE ∠=∠,AD CE =,又AFD EFC ∠=∠,通过“AAS ”证得ADF ECF ≌△△.【详解】∵四边形ABCD 是平行四边形,∴AD BC ∥,AD BC =,∴D FCE ∠=∠,∵AD BC =,CE BC =,∴AD CE =,∴在ADF △和ECF △中,D FCE AFD EFC AD EC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ADF ECF △△≌.2.(2023下·广东佛山·八年级校联考期末)如图,在平行四边形ABCD 中,2AB BC =,点E 为AB 的中点,连接CE 并延长与DA 的延长线相交于点F .(1)求证:AEF BEC ≌△△;(2)求证:DE 是CDF ∠的平分线.【答案】(1)见解析(2)见解析【分析】(1)根据四边形ABCD 是平行四边形,连接CE 并延长与DA 的延长线相交于点F 得CB DF ∥,则BCE AFE ∠=∠,根据点E 为AB 的中点得AE BE =,利用AAS 即可证明;(2)根据四边形ABCD 是平行四边形得AB CD ∥,可得AED CDE ∠=∠,根据2AB BC =,点E 为AB 的中点,得AE AD =,则AED ADE ∠=∠,等量代换得CDE ADE ∠=∠,即可得.【详解】(1)证明:∵四边形ABCD 是平行四边形,连接CE 并延长与DA 的延长线相交于点F ,∴CB DF ∥,∴BCE AFE ∠=∠,∵点E 为AB 的中点,∴AE BE =,在AEF △和BEC 中,AFE BCE AEF BEC AE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AEF BEC AAS ≌;(2)证明:∵四边形ABCD 是平行四边形,∴AB CD ∥,∴AED CDE ∠=∠,∵2AB BC =,点E 为AB 的中点,∴AE AD =,∴AED ADE ∠=∠,∴CDE ADE ∠=∠,∴DE 是CDF ∠的平分线.【点睛】本题考查了平行四边形的性质,全等三角形的判定与性质,角平分线的判定,解题的关键是理解题意,掌握这些知识点.3.(2023上·北京海淀·九年级统考期中)如图,ABCD Y 的对角线,AC BD 交于点,O EF 过点O 且分别与,AD BC 交于点,E F .△≌△(1)求证:AOE COF(2)记四边形ABFE的面积为【答案】(1)证明见解析【考点三判断能否构成平行四边形】例题:(2023下·北京海淀·八年级北京市十一学校校考阶段练习)如图,在四边形ABCD中,对角线AC与BD 相交于点O,下列条件中不能判定四边形ABCD是平行四边形的是()A .OA OC =,OB OD=B .AB CD ∥,AD CB ∥C .AB CD =,AD CB=D .AB CD ∥,AD CB=【答案】D 【分析】由平行四边形的判定定理对边对各个选项进行判断即可.【详解】解:A 、∵OA OC =,OB OD =,∴四边形ABCD 是平行四边形,故选项A 不符合题意;B 、∵AB CD ∥,AD CB ∥,∴四边形ABCD 是平行四边形,故选项B 不符合题意;C 、∵AB CD =,AD CB =,∴四边形ABCD 是平行四边形,故选项C 不符合题意;D 、由AB CD ∥,AD CB =,不能判定四边形ABCD 是平行四边形,故选项D 符合题意.故选:D .【点睛】本题考查了平行四边形的判定定理,熟记平行四边形的判定定理是解题的关键.【变式训练】1.(2023下·江西赣州·八年级校联考期末)如图,在ABCD Y 中,点E ,F 分别在BC ,AD 上.下列条件中,不能..得出四边形AECF 一定为平行四边形的是()A .AF CE=B .AE CF =C .AE CF ∥D .BAE DCF∠=∠【答案】B 【分析】根据平行四边形的判定方法逐项判断即可.【详解】A 、∵四边形ABCD 为平行四边形,∴AD BC ∥,即AF CE ∥.又AF CE =,∴四边形AECF 为平行四边形.(一组对边平行且相等的四边形为平行四边形)该选项不符合题意.B 、无法证明四边形AECF 为平行四边形,该选项符合题意.C 、∵四边形ABCD 为平行四边形,∴AD BC ∥,即AF CE ∥.又AE CF ∥,∴四边形AECF 为平行四边形.(两组对边分别平行的四边形为平行四边形)该选项不符合题意.D 、∵四边形ABCD 为平行四边形,∴BAD BCD ∠=∠,B D ∠=∠.又BAE DCF ∠=∠,EAF BAD BAE ∠=∠-∠,FCE BCD DCF ∠=∠-∠,∴EAF FCE Ð=Ð.∵AEC B BAE ∠=∠+∠,AFC D DCF ∠=∠+∠,∴AEC AFC ∠=∠.∴四边形AECF 为平行四边形.(两组对角分别相等的四边形为平行四边形)该选项不符合题意.故选:B .【点睛】本题主要考查平行四边形的性质和判定,牢记平行四边形的判定方法是解题的关键.2.(2023下·安徽合肥·八年级校考期末)如图,AD BC ∥,AD BC =,E 、F 是线段BD 上的两点,则以下条件不能判断四边形AECF 是平行四边形的是()A .BE DF=B .AEB DFC =∠∠C .AF FE=D .AE BD ⊥,CF BD⊥【答案】C 【分析】连接AB 、CD 、AC 交BD 于点O ,根据平行四边形的对角线互相平分可得OA OC =,OB OD =,再根据对角线互相平分的四边形是平行四边形,只要证明得到OE OF =即可,然后根据各选项的条件分析判断结合平行四边形的判定即可得解.【详解】解:连接AB ,CD ,,AD BCAD BC=,∴四边形ABCD是平行四边形,连接AC交BD于O,∴=,BO ODAO OC=,=,BE DF∴=,OE OF∴四边形AECF是平行四边形,故A不符合题意;,∠=∠AEB CFD\Ð=Ð,AEO CFO∴∥,AE CF,AO OC∠=∠AOE COF=,≌,∴∆∆(AAS)AOE COF∴=,AE CF∴四边形AECF是平行四边形,故B不符合题意;=,故无法判定四边形AECF是平行四边形,故C符合题意;AF FE⊥,,CF BD⊥AE BD∴∠=∠,AEB CFD以下的证明与B相同,故D选项不符合题意;故答案为:C.【点睛】本题考查了平行四边形的判定与性质以及全等三角形的判定和性质,熟练掌握平行四边形的性质与判定是解题的关键.【考点四添一个条件成为平行四边形】【答案】BE DF =或BF DE =或BAE DCF ∠=∠.【分析】用反推法,假如四边形是平行四边形,会推出什么结果,这结果就是要添加的条件.【详解】解:使四边形AECF 是平行四边形.就要使AE CF ,AE CF =,就要使AEB CFD ≅△△,而在平行四边形中已有AB CD =,ABE CDF ∠=∠,再加一个BE DF =或BF DE =可用SAS 证AEB CFD ≅△△,或BAE DCF ∠=∠用ASA 证AEB CFD ≅△△.故答案为:BE DF =或BF DE =或BAE DCF ∠=∠.【点睛】本题考查了平行四边形的判定与性质,本题是开放题,答案不唯一,可以针对各种特殊的平行四边形的判定方法,给出条件,本题主要是通过给出证明AEB CFD ≅△△的条件来得到AE CF ,AE CF =,根据四边形中一组对边平行且相等就可证明为是平行四边形.【变式训练】【答案】AD BC=【分析】在DEBF 中可得ED BF ∥行四边形.【详解】解:添加条件AD BC =,【答案】2或3【分析】根据平行四边形的判定可知,分两种情况:可得.【考点五证明四边形是平行四边形】Y的对角线AC,BD相交于点O,例题:(2023上·山东东营·八年级校考阶段练习)已知:如图,ABCDBM AC ⊥,DN AC ⊥,垂足分别为M ,N .求证:四边形BMDN 是平行四边形.【答案】见解析【分析】本题主要考查平行四边形的判定与性质、全等三角形的判定与性质,首先根据平行四边形的性质得到AB CD =,BAM DCN ∠=∠,然后证明出()AAS ABM CDN △△≌,得到MB DN =,然后证明出MB DN ∥,即可证明四边形BMDN 是平行四边形.熟悉相关性质是解题的关键.【详解】∵四边形ABCD 是平行四边形∴AB CD =,BAM DCN∠=∠∵BM AC ⊥,DN AC⊥∴90AMB CND ∠=∠=︒∴()AAS ABM CDN △△≌∴MB DN=∵BM AC ⊥,DN AC⊥∴90OMB OND ∠=∠=︒∴MB DN∥∴四边形BMDN 是平行四边形.【变式训练】1.(2023下·天津·八年级校考期中)如图,在平行四边形ABCD 中,点G H ,分别是AB CD ,的中点,点E F 、在对角线AC 上,且AE CF =.(1)求证:AGE CHF ≌△△;(1)求证:四边形CEDF 是平行四边形;(2)若6AB =,8AD =,A ∠=【答案】(1)见解析(2)27由(1)得:四边形CEDF 是平行四边形,CE DF ∴=,四边形ABCD 是平行四边形,60BCD A ∴∠=∠=︒,CD =【考点六平行四边形中的折叠问题】【答案】40︒/40度【分析】本题考查平行四边形的性质,折叠的性质.根据平行四边形和折叠的性质,得到而求出MFA∠的度数,利用三角形的内角和定理,进行求解即可.【详解】解:∵平行四边形∥,∴CD AB故答案为:40︒.【变式训练】【答案】110︒/110度【分析】根据平行四边形的性质和外角定义证明折可得240EDB ∠=∠=︒,然后利用三角形内角和定理即可解决问题.【详解】解:设BE ,DC 交于点∵四边形ABCD 是平行四边形,∴AB CD ∥,∴ABD CDB ∠=∠,由翻折可知:ABD EBD ∠=∠,∴EBD CDB ∠=∠,E A ∠=∠,【答案】30︒/30度【分析】由平行四边形的性质得∠=由三角形外角性质求出AEF【详解】解: 四边形ABCD是平行四边形,【考点七利用平行四边形的性质无刻度作图】例题:(2023上·江苏泰州·八年级校联考阶段练习)如图,平行四边形ABCD中,只用无刻度的直尺按下列要求画图.(不写画法)(1)在图1中,点E 是BC 的中点,作边AD 上的中点F ;(2)在图2中,ABC ∠的平分线交AD 于点F ,在边BC 上的找点P ,使得连接DP 后,DP 平分ADC ∠.【答案】(1)见详解(2)见详解【分析】本题主要考查利用平行四边形性质作图,(1)利用平行四边形对角线相互平分的性质,即可确定EO AB ∥,且点E 为中点,即可求得点F 也为中点;(2)利用平行四边形对角线相互平分的性质,可判定四边形FBPD 为平行四边形,结合BF 平分ABC ∠,则DP 即为所求.【详解】(1)解:连接AC 和BD 交于点O ,连接EO ,延长EO 交AD 于点F ,如图,(2)连接AC 和BD 交于点O ,连接FO ,延长FO 交BC 于点P ,如图,【变式训练】1.(2023下·江西吉安·八年级统考期末)例在ABCD Y 中,点E 为AB 上一点,请仅用无刻度直尺按要求作图(保留作图痕迹,不写作法,题目要求画的线画实线,其他的线画虚线)(1)如图1,E 为AB 边上一点,AE AD =,画出∠D 的角平分线;(2)如图2,E 为AB 边上一点,AE AD =,画出∠B 的角平分线.【答案】(1)见解析(2)见解析【分析】(1)连接DE ,由AE AD =得AED ADE ∠=∠,结合平行线的性质可得AED CDE ∠=∠,进而可得DE 平分ADC ∠,即DE 即为所求;(2)连接AC BD ,交于点O ,连接EO 并延长交CD 点F ,连接BF ,BF 为所求.【详解】(1)解:如图:DE 即为所求.(2)解:如图:BF 即为所求.【点睛】本题考查作图一复杂作图、平行四边形的性质、等腰三角形的性质等知识点,熟练掌握平行四边形的性质是解答本题的关键.2.(2023上·湖北黄石·九年级统考期中)如图是由小正方形组成的86⨯网格,每个小正方形的顶点叫做格点.四边形ABCD 的四个顶点都是格点,仅用无刻度的直尺........在给定网格中完成画图(画图过程用虚线,画图结果用实线).(1)判断四边形ABCD 的形状;(2)在图1中,在CD 上画点E ,使=45ABE ∠︒;(3)在图2中的CD 上画点G ,使CG AD =.【答案】(1)平行四边形(2)见解析(3)解:如图2,点G即为所求;【考点八利用平行四边形的性质与判定综合】Y对角线AC上的两点.例题:(2023下·广东深圳·八年级校考期末)已知:如图,E、F是ABCD(1)若AE CF =,求证:四边形BFDE 是平行四边形;(2)若DE AC ⊥,BF AC ⊥,垂足分别为E 、F ,35EDF ∠=︒,求FBE ∠的度数.【答案】(1)见解析(2)35︒【分析】(1)连接BD 交AC 于O ,根据ABCD Y ,得OB OD =,OA OC =,继可证得OE OF =,即可由平行四边形的判定定理得出结论.(2)先由DE AC ⊥,BF AC ⊥,得出90AED BFC ∠=∠=︒,DE BF ∥,再证()AAS ADE CBF ≌△△,得DE BF =,从而证得四边形BFDE 是平行四边形,即可根据平行四边形的性质得35FBE EDF ∠=∠=︒.【详解】(1)证明:连接BD 交AC 于O ,∵ABCD Y ,∴OB OD =,OA OC =,∵AE CF =,∴AE OA CF OC -=-,即OE OF =,∴四边形BFDE 是平行四边形.(2)解:∵DE AC ⊥,BF AC ⊥,∴90AED BFC ∠=∠=︒,DE BF ∥,∵ABCD Y ,∴AD BC =,AD BC ∥,∴DAE BCF ∠=∠,在ADE V 和CBF V 中,DAE BCF AED BFC AD BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ADE CBF ≌△△,∴DE BF =,∴四边形BFDE 是平行四边形∴35FBE EDF ∠=∠=︒.【点睛】本题考查平行四边形的性质与判定,全等三角形的判定与性质.熟练掌握平行四边形的性质与判定是解题的关键.【变式训练】1.(2023下·吉林长春·八年级校考期中)如图,ABCD Y 中,E 、F 分别是AB 、CD 上的点,且BE DF =,连接EF 交BD 于O .(1)连接BF 、DE ,判断四边形DEBF 的形状并说明理由.(2)若6AE =,2BE =,BOF 的面积为2,求ABCD Y 的面积.(3)若BD AD ⊥,45A ∠=︒,EF AB ⊥,延长EF 交AD 的延长线于G ,当1FG =时,则AB 的长为______.【答案】(1)四边形DEBF 是平行四边形,理由见解析;(2)16;(3)4;【分析】(1)分别证明DF EB ∥,BE DF =,即可;(2)利用平行四边形的性质,由BOF 的面积为2,得到4EFB S = ,再利用三角形同底等高的性质,得到EDB △的面积,再求出8ADB S = ,则可知ABCD Y 的面积为216ADB S = ;(3)由ADB 是等腰直角三角形,得出45A ∠=︒,因为EF AB ⊥,得出45G ∠=︒,所以ODG 与DFG 都是等腰直角三角形,从而依次求得GF 、GE 、AE 的长,则AB 可求;【详解】(1)解:四边形DEBF 是平行四边形;(1)如图①,求证:四边形ABCD 是平行四边形;(2)如图②,BE 平分ABC ∠,交AD 于点E .若30α=︒,2AB =(3)如图③,平分ABC ∠,交AD 于点E ,作AH CD ⊥交射线DC 图①图②综上所述,线段AF ,DE ,CH 之间的数量关系为DE CH AF +=或DE CH AF-=【过关检测】一、单选题1.(2023上·吉林长春·八年级校联考期末)在ABCD Y 中,80A C ∠+∠=︒,则D ∠的度数为()A .140︒B .40︒C .70︒D .80︒【答案】A【分析】本题考查了平行四边形的性质,熟练掌握平行四边形对角相等、邻角互补是解题的关键.由平行四边形的性质得,A C AB CD ∠=∠∥,则180A D ∠+∠=︒,再求出40A ∠=︒,即可解决问题.【详解】解:∵四边形ABCD 是平行四边形,∴,A C AB CD ∠=∠∥,180,A D ∴∠+∠=︒80,A C ∠+∠=︒Q 40,A C \Ð=Ð=°180140,D A ∴∠=︒-∠=︒故选:A .2.(2023下·全国·八年级假期作业)有下列说法:①平行四边形的两组对边分别平行且相等;②平行四边形的对角线互相平分;③平行四边形的对角相等、邻角互补;④平行四边形的对角线相等.其中正确的说法有()A .4个B .2个C .3个D .4个【答案】C【解析】略3.(2023上·吉林长春·八年级校考期中)如图,点P 是ABCD Y 内的一点,过点P 作直线EF 、GH 分别平行于AB 、BC ,与ABCD Y 的边分别交于G 、F 、H 、E .则图中平行四边形的个数为()A .4个B .5个C .8个D .9个【答案】D 【分析】本题考查平行四边形的判定和性质,根据两组对边分别平行的四边形为平行四边形,进行判断即可.【详解】解:∵ABCD Y ,∴,∥∥AD BC AB CD ,∵过点P 作直线EF 、GH 分别平行于AB 、BC ,∴,EF AB CD GH AD BC ∥∥∥∥,∴四边形,,,,,,,AGPE ABFE AGHD GBCH EPHD PFCH EFCD GBFP 均为平行四边形,∴加上ABCD Y 共9个;故选D .4.(2023上·吉林长春·八年级长春外国语学校校考阶段练习)如图,点E 是ABCD Y 边AD 延长线上一点,连接BE 、CE 、BD ,BE 与CD 交于点F .添加以下条件,不能判定四边形BCED 为平行四边形的是()A .DE DA=B .ABD DCE ∠=∠C .DEB BCD ∠=∠D .EF FB=【答案】C 【分析】本题主要考查了平行四边形的判定与性质、全等三角形的判定与性质、平行线的性质等知识,理解并掌握平行四边形的判定定理是解题关键.首先根据平行四边形的性质可得AD BC ∥,CD AB ∥,AD BC =,CD AB =,若DE DA =,由“一组对边平行且相等的四边形为平行四边形”,即可判断选项A ;若ABD DCE ∠=∠,易得DCE CDB ∠=∠,即可证明BD CE ∥,由“两组对边分别平行的四边形为平行四边形”即可判断选项B ;若EF FB =,证明DEF CBF ≌△△,由全等三角形的性质可得DE CB =,由“一组对边平行且相等的四边形为平行四边形”,即可判断选项D ;由DEB BCD ∠=∠不能证明四边形BCED 为平行四边形,即可判断选项C .【详解】解:∵四边形ABCD 为平行四边形,∴AD BC ∥,CD AB ∥,AD BC =,CD AB =,即DE BC ∥,若DE DA =,则有DE BC =,∴四边形BCED 为平行四边形,故选项A 不符合题意;∵CD AB ∥,∴ABD CDB ∠=∠,若ABD DCE ∠=∠,则有DCE CDB ∠=∠,∴BD CE ∥,又∵DE BC ∥,∴四边形BCED 为平行四边形,故选项B 不符合题意;∵DE BC ∥,∴DEF CBF ∠=∠,若EF FB =,则在DEF 和CBF V 中,DEF CBF EF FB DFE CFB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴(ASA)DEF CBF ≌,∴DE CB =,又∵DE BC∥∴四边形BCED 为平行四边形,故选项D 不符合题意;由DEB BCD ∠=∠不能证明四边形BCED 为平行四边形,选项C 符合题意.故选:C .5.(2023下·浙江·八年级校联考期中)如图,E ,F 分别是平行四边形ABCD 的边AB ,CD 上的点,AF 与A .a b+B .12c a b --【答案】B 【分析】本题主要考查平行四边形的性质,据平行四边形的面积与三角形的面积公式可得三角形12DEC S DC EM =⋅ ,ABCD S DC EM c =⋅= ,12DEC S c ∴= , 四边形ABCD 是平行四边形,二、填空题【答案】24︒【分析】本题主要考查了平行四边形的性质,根据平行四边形的性质得出形两个锐角角互余即可求得答案.【答案】213【分析】本题主要考查平行四边形的性质及勾股定理的运用,长度,则BD即可求解,解答本题的关键在于表示出所需边长.【详解】解:∵四边形ABCD【答案】40【分析】本题主要考查了平行四边形的性质、垂直平分线的判定与性质、等腰三角形的判定与性质等知识点,灵活运用相关性质和判定是解题的关键.【答案】40°/40度【分析】根据平行四边形的性质可得∠=∠,然后由四边形内角和定理即可解决问题.EFD EFN【详解】解:∵四边形ABCD是平行四边形,∥,∴AB CDAD BC,∴∠=∠,DAM AMB,DAM BAM ∠=∠∴∠=∠,BAM AMB同理可证,AE EM=,可得1()2EF AD CM=-=综上所述,EF的长为故答案为:5或2.三、解答题(1)求证:CE AB=(2)连接CF,若CF DE⊥【答案】(1)见解析(2)解:过点D作DH⊥=,∵E∠=60°,CD CE是等边三角形,∴CDE∥,∵CD AB(1)求证:四边形ADFE 是平行四边形;(2)若25BD AE ==,,直接写出【答案】(1)见解析(2)13【分析】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、等腰三角形的性质、勾股定理(1)在BC 上取点M ,使四边形ABME 为平行四边形;(2)在CD 的延长线上取一点F ,使四边形BDFA 为平行四边形.【答案】(1)见详解(2)见详解【分析】(1)连接AC ,交BD 于点O ,连接EO 并延长交为平行四边形,则AE BM ∥,又因为E 为AD 的中点,以四边形ABME 为平行四边形;(2)连接BE 并延长交CD 的延长线于点F ,连接AF ,则点则FC AB ∥,所以ABE DFE ∠=∠,又因为E 为AD 的中点,所以()AAS ABE DFE ≌△△,即AB DF =,所以四边形BDFA 【详解】(1)解:点M 即为所求:(2)解:如图,点F 即为所求:【点睛】本题考查作图-复杂作图、平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解答本题的关.14.(2023下·陕西渭南·八年级统考期末)如图,在ABCD Y 中,点E 是CD 延长线上的一点,连接AE ,EAD DBC ∠=∠,BE 交AD 于点F .(1)求证:四边形ABDE 为平行四边形;(2)若4BAD EAD ∠=∠,50BDC ∠=︒,求C ∠的度数.【答案】(1)见解析(2)104度【分析】(1)平行四边形的性质,得到AD BC ∥,AB CD ,进而得到ADB DBC ∠=∠,推出EAD ADB ∠=∠,得到AE BD ,即可得证;(2)邻补角求出BDE ∠,平行四边形的性质,得到BAE BDE ∠=∠,结合4BAD EAD ∠=∠,求出EAD ∠,进而得到DBC ∠的度数,再利用外角的性质,求解即可.【详解】(1)证明:∵四边形ABCD 是平行四边形,∴AD BC ∥,AB CD ,(1)求证:四边形BEDF 是平行四边形;(2)若AB BF ⊥,8AB =,6BF =,AC 【答案】(1)证明见解析(2)192516.(2023上·辽宁沈阳·九年级东北育才双语学校校考阶段练习)将ED绕点E逆时针旋转90︒得到EF(1)当点E 在线段BC 上,=45ABC ∠︒时,如图①,求证:BEF AED ≌△△:(2)当点E 在线段BC 延长线上,=45ABC ∠︒时,如图②;当点E 在线段CB 延长线上,ABC ∠如图③,请猜想并直接写出线段AE ,EC ,BF 的数量关系;(3)在(1)、(2)的条件下,若3BE =,5DE =,则CE =______.【答案】(1)见解析∴()SAS BEF AED ≌;(2)解:当=45ABC ∠︒时,如图②:∵AE BC ⊥,=45ABC ∠︒,∴45BAE ∠=︒,90AEB ∠=︒,∴AE BE =,90BEF AEF ∠+∠=︒,∵ED 绕点E 逆时针旋转90︒得到EF ,∴,90DE EF DEF =∠=︒,∴90AEF AED ∠+∠=︒,∴AED BEF ∠=∠,在BEF △和AED △中,AE BE AED BEF DE EF =⎧⎪∠=∠⎨⎪=⎩,∴()SAS BEF AED ≌;∴BF AD =,∵四边形ABCD 是平行四边形,∴BC AD =,∴BF BC =,∵BE BC EC =+,∴AE BF EC =+;当135ABC ∠=︒时,如图③:∵135ABC ∠=︒,∴=45ABE ∠︒,∵AE BC ⊥,∴45BAE ∠=︒,90AEB ∠=︒,∴AE BE =,90BED AED ∠+∠=︒,∵ED 绕点E 逆时针旋转90︒得到EF ,∴,90DE EF DEF =∠=︒,∴90BED BEF ∠+∠=︒,【点睛】本题主要考查了平行四边形的性质,三角形的全等的判定和性质,旋转的性质,解题的关键是掌握三角形全等的判定方法,证明BEF AED ≌△△,以及掌握全等三角形对应边相等,平行四边形对边相等.。
(完整版)平行四边形知识点及典型例题,推荐文档
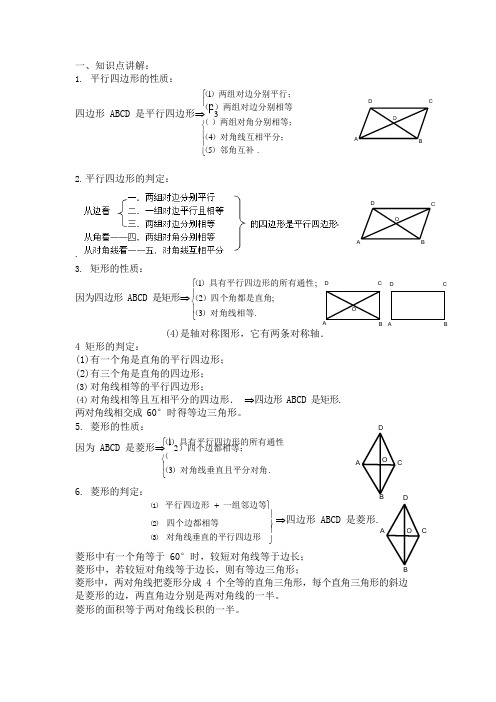
OOO ⎪ ⎨ ⎩ ⎩⎬ 一、知识点讲解:1. 平行四边形的性质:(⎧ 1)两组对边分别平行;⎪ DC(2)两组对边分别相等四边形 ABCD 是平行四边形⇒ ⎪ 3(⎨ )两组对角分别相等; (⎪ 4)对角线互相平分; AB(⎩ 5)邻角互补 .2. 平行四边形的判定:DC.3.矩形的性质: A B(⎧ 1)具有平行四边形的所有通性; DC DC因为四边形 ABCD 是矩形⇒ (⎪ 2)四个角都是直角; (⎪ 3)对角线相等.AB AB(4)是轴对称图形,它有两条对称轴.4 矩形的判定:(1)有一个角是直角的平行四边形; (2)有三个角是直角的四边形; (3) 对角线相等的平行四边形;(4) 对角线相等且互相平分的四边形. ⇒四边形 ABCD 是矩形. 两对角线相交成 60°时得等边三角形。
5. 菱形的性质:D(⎧ 1)具有平行四边形的所有通性 因为 ABCD 是菱形⇒ ⎪ 2)四个边都相等;6. 菱形的判定:(⎨(⎪ 3)对角线垂直且平分对角. ACBD(1) 平行四边形 + 一组邻边等⎫ (2) 四个边都相等(3) 对角线垂直的平行四边形 ⎪⇒四边形 ABCD 是菱形. ⎪A C⎭菱形中有一个角等于 60°时,较短对角线等于边长;菱形中,若较短对角线等于边长,则有等边三角形;B 菱形中,两对角线把菱形分成 4 个全等的直角三角形,每个直角三角形的斜边是菱形的边,两直角边分别是两对角线的一半。
菱形的面积等于两对角线长积的一半。
OOEFOAEO F C⎩ (⎨ ⇒ 7.正方形的性质:D(⎧ 1)具有平行四边形的所有通性;C DC四边形 ABCD 是正方形⇒ ⎪2)四个边都相等,四个角都是直角 (⎪ 3)对角线相等垂直且平分对角.A B A B8. 正方形的判定:(1) 平行四边形 + 一组邻边等+ 一个直角⎫ ⎪(2) 菱形 +一个直角 (3) 菱形 +对角线相等 (4) 矩形 + 一组邻边等 (5) 矩形 + 对角线互相垂直⎪ ⎪⎬ 四边形 ABCD 是正方形. ⎪ ⎪ ⎭9. 1.三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三遍的一半。
专题9.3 平行四边形的判定【九大题型】(举一反三)(苏科版)(解析版)

专题9.3 平行四边形的判定【九大题型】【苏科版】
【题型1 判断能否构成平行四边形】...................................................................................................................1【题型2 添加条件构成平行四边形】...................................................................................................................4【题型3 数图形中平行四边形的个数】...............................................................................................................7【题型4 求与已知三点组成平行四边形的点的个数】.....................................................................................10【题型5 证明四边形是平行四边形】.................................................................................................................14【题型6 全等三角形拼平行四边形问题】.........................................................................................................18【题型7 利用平行四边形的判定和性质求解】.................................................................................................22【题型8 利用平行四边形的判定和性质证明】.................................................................................................28【题型9 平行四边形的应用】.............................................................................................................................36
平行四边形的判定知识点总结及其对应题型含详解

平行四边形的判定01 基础题知识点1两组对边分别相等的四边形是平行四边形1•如图,AB=CD=EF,且厶ACE^ABDF,则图中平行四边形的个数为(C)CA・1B・2C・3D・42•若四边形ABCD的边AB=CD,BC=DA,则这个四边形是平行四边形,理由是两组对边分别相等的四边形是平行四边形.知识点2两组对角分别相等的四边形是平行四边形3•下而给出四边形ABCD中的度数之比,英中能判宦四边形ABCD 为平行四边形的是(E)2・ 1 : 2 : 3 : 4 B. 2 : 3 : 2 : 3C・2:2:3:3 D1 :2:2:34• 一个四边形的三个相邻内角的度数依次如下,那么其中是平行四边形的是(刀)A・ 88°, 108° > 88°B. 88°, 104°, 108°C- 88°,92°,92°D. 108°,72°,108°知识点3对角线互相平分的四边形是平行四边形5.如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件BO=DO(答案不唯二1(只添一个即可),使四边形ABCD是平行四边形.6・已知:如图,在四边形ABCD中,AB〃CD,对角线AC,BD相交于点O,且AO=CO. 求证:四边形ABCD是平行四边形.证明:•••AB〃CD,•••ZABO=ZCDO, ZBAO=ZDCO.••• AABO^ACDOGUS)・•••BO=DO.•••四边形ABCD是平行四边形.7 •如图,在-ABCD中,对角线AC,BD相交于点O,点E,F分别是OB,OD的中点,求证:四边形AECF是平行四边形.证明:•••四边形ABCD是平行四边形,•••OA=OC > OB=OD.•••点E,F分别是OB,OD的中点,AOE=OF.又VOA=OC,・•.四边形AECF是平行四边形.知识点4 一组对边平行且相等的四边形是平行四边形8.如图所示,四边形ABCD和AEFD都是平行四边形,则四边形BCFE是平行四边形,理由:•纠.对也atm的四边形肚丫行四边形.9• (2016新疆)如图,在四边形ABCD中,AD〃BC,AE丄AD交BD于点E,CF丄BC交BD 于点F,且AE=CF.求证:四边形ABCD是平行四边形.证明:TAE丄AD,CF丄BC,•••ZEAD=ZFCB = 90° . VAD/7BC,••• ZADE= ZCBF.在ZXAED 和Z\CFB 中,fZADE=ZCBF,< ZEAD=ZFCB,I AE=CF、:.AAED^ACFBC^S)・AAD=BC.•••四边形ABCD是平行四边形.02 中档题10•小玲的爸爸在制作平行四边形框架时,采用了一种方法:如图所示,将两根木条AC,BD 的中点重叠,并用钉子固左,则四边形ABCD就是平行四边形,这种方法的依据是(J)2・对角线互相平分的四边形是平行四边形B•两组对角分别相等的四边形是平行四边形C •两组对边分别相等的四边形是平行四边形D•两组对边分别平行的四边形是平行四边形11- (2016衢州)已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C为顶点的四边形是平行四边形,则x=4或_2.12•已知:如图,在四边形ABCD中,AB=CD,BC=AD,点E,F在AC上,且AF= CE.求证:四边形BEDF是平行四边形.VAB=CD,BC=AD,・•.四边形ABCD是平行四边形.•••AO=CO,BO=DO.VAF=CE,•••AF-AO=CE-CO,即OF=OE. 又VOB = OD,•••四边形BEDF是平行四边形・13・(2017-南京)如图,在ABCD中,点E > F分别在AD,BC上,且AE=CF,EF,BD 相交于点O,求证:OE=OF.证明:连接BE,DF.•••四边形ABCD是平行四边形,:.AD//BC > AD=BC.VAE=CF,•••DE=BF.又VDE/7BF,.•・四边形BEDF是平行四边形..-.OE=OF.14・(2016张家界)已知:如图,在四边形ABCD中,AB//CD,E是BC的中点,直线AE 交DC 的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.解:四边形ABFC是平行四边形. 证明:•••AB〃CD, AZBAE=ZCFE.TE 是BC 的中点,•••BE=CE. 在Z\ABE 和ZkFCE 中,rZBAE=ZCFE,< ZAEB=ZFEC,I BE=CE,A AABE^AFCE(AAS)・:.AB=CF. 又•:AB〃CF、:•四边形是平行四边形.03 综合题15 •如图所示,在四边形ABCD中,AD/7BC,AD=24 cm,BC = 30 cw,点P从点A向点D以1 c?n/s 的速度运动,到点D即停止.点Q从点C向点B以2 an!s的速度运动,到点B 即停止.直线PQ将四边形ABCD截成两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,英中一个四边形为平行四边形?解:设当P,Q两点同时岀发ts后,四边形ABQP或四边形PQCD是平行四边形. 根据题意> 得AP=5 > PD=(24-t)cw,CQ=25,BQ=(30-2t)c?w(0WtW15)・①若四边形ABQP是平行四边形,•••AD〃BC,•••还需满足AP=BQ./.t=30—2t.解得t=10.•••10s后四边形ABQP是平行四边形:②若四边形PQCD是平行四边形,VAD//BC,•••还需满足PD=CQ./. 24—t=2t.解得t=8.••・8 s后四边形PQCD是平行四边形.综上所述:当P,Q两点同时出发8秒或10秒后,所截得两个四边形中英中一个四边形为平行四边形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对角线取值范围问题(同三角形第三边中线取值范围)平行四边形一边长为10,一条对角线长为6,则它的另一条对角线长a的取值范围为 ( )A.4〈a〈16 B.14〈a<26 C.12<a<20 D.8〈a<32平行四边形的判定:1:定义法:两组对边分别平行的四边形是平行四边形2:一组对边平行且相等的四边形是平行四边形3:两组对边分别相等的四边形是平行四边形4:对角线相互平分的四边形是平行四边形14.平行四边形的判定(一)定义法:两组对边分别平行的四边形是平行四边形例题1:如图,四边形ABCD是平行四边形,连接AC.过点A作AE⊥BC于点E;过点C作CF∥AE,交AD于点F;求证:四边形AECF为平行四边形练习:1、已知:如图,△ABC是等边三角形,D、E分别是BA、CA的延长线上的点,且AD=AE,连接ED并延长到F,使得EF=EC,连接AF、CF、BE.(1)求证:四边形BCFD是平行四边形;证明:(1)∵△ABC为等边三角形,且AE=AD,∴由题可知∠AED=∠ADE=∠EAD=60°∴EF∥BC,又∵EC=EF,∴△ECF为等边三角形,即∠EFC=∠EDB=60°,∴CF∥BD∴四边形BCFD为平行四边形.2、如图:平行四边形ABCD中,M、N分别是AB、CD的中点,AN与DM相交于点P,BN与CM相交于点Q.试说明PQ与MN互相平分。
3、如图,在四边形ABCD中,AH、CG、BE、FD分别是∠A、∠C、∠B、∠D的角平分线,且BE∥FD,AH∥CG,证明四边形ABCD为平行四边形.15。
平行四边形的判定(二):一组对边平行且相等的四边形是平行四边形例题1:如图,在ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G。
求证:AF=DF【答案】解:(1)证明:如图1,连接BD、AE,∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD。
∵DE=CD,∴AB∥DE,AB=DE。
∴四边形ABDE是平行四边形。
∴AF=DF。
练习:1、如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE .(1)求证:四边形AECF 为平行四边形;【答案】(1)证明∵四边形ABCD 是平行四边形(已知),∴BC∥AD(平行四边形的对边相互平行)。
又∵AM 丄BC (已知),∴AM⊥AD。
∵CN 丄AD (已知),∴AM∥CN。
∴AE∥CF。
又由平行得∠ADE=∠CBD,又AD=BC(平行四边形的对边相等)。
在△ADE 和△CBF 中, ∠DAE=∠BCF=90 ,AD=CB,∠ADE=∠FBC, ∴△ADE≌△CBF(ASA ),∴AE=CF(全等三角形的对应边相等)。
∴四边形AECF 为平行四边形(对边平行且相等的四边形是平行四边形)。
2、如图:在ABCD 中,H F G E ,,,分别是四条边上的点,且,AE CF BG DH ==,试说明:EF 与GH 相互平分.例题2:如图,△ABC 和△ADE 都是等边三角形,点D 在BC 边上,AB 边上有一点F ,且BF=DC ,连接EF 、EB .(1)求证:△ABE ≌△ACD ; (2)求证:四边形EFCD 是平行四边形练习:1、如图1,在△OAB 中,∠OAB=90°,∠AOB=30°,OB=8.以OB 为一边,在△OAB 外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E。
(1)求点B的坐标。
(2)求证:四边形ABCE是平行四边形。
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.【解析】(1)∵∠AOB=30°,OB=8,∴AB=4,OA=4,∴B(4,4)。
(2)∵△OBC是等边三角形,∴OC=OB=8。
∵D点为OB的中点,∴OD=4.又∵AD是Rt△OAB斜边的中线,∴AD=OB=OD,∴∠ODA=180°-2×30°=120°,∴∠EDO=60°.又∠EOD=60°,∴△OED为等边三角形,∴OE=4,∴E(0,4),∴CE=4,CE=AB.又∵CE∥AB,∴四边形ABCE是平行四边形。
(3)∵GA=GC,∴GA2=GC2.即OG2+OA2=(OC-OG)2,OG2+(4)2=(8-OG)2,∴OG=1.16.平行四边形的判定(三):两组对边分别相等的四边形是平行四边形例题1:如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是【】A .平行四边形B .矩形C .菱形D .梯形练习:1、如图,点A 、B 、C 是坐标平面内不在同一直线上的三点,画出以A 、B 、C 三点为顶点的平行四边形..ABC xy例题2:如图所示,试证明:四边形PONM 是平行四边形.练习: 1、在ABCD 中,分别以AD,BC 为边向内作等边△ADE 和等边△BCF ,连接BE ,DF.求证:四边形BEDF 是平行四边形.2、四边形的四条边长分别是a 、b 、c 、d ,其中a 、c 为对边,且满足cd ab d c b a 222222+=+++,则这个四边形一定是( )A .平行四边形B .两组对角分别相等的四边形C .对角线互相垂直的四边形D .对角线相等的四边形3、等边△ABC中,点D在BC上,点E在AB上,且CD=BE,以AD为边作等边△ADF,如图.求证:四边形CDFE是平行四边形.4、如图所示,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF,猜想:四边形ADEF是什么四边形,试证明你的结论.证明:四边形ADEF是平行四边形.连接ED、EF,∵△ABD、△BCE、△ACF分别是等边三角形,∴AB=BD,BC=BE,∠DBA=∠EBC=60°.∴∠DBE=∠ABC.∴△ABC≌△DBE.同理可证△ABC≌△FEC,∴AB=EF,AC=DE.∵AB=AD,AC=AF,∴AD=EF,DE=AF.∴四边形ADEF是平行四边形17.平行四边形的判定(四):对角线相互平分的四边形是平行四边形例题1:已知A (2,3)B (—2,5),A 、B 点关于原点的对称点分别为C 、D,依次连接A 、B 、C 、D 点,则四边形ABCD 是什么四边形?例题2、如图,在平行四边形ABCD 中,连接对角线BD ,过A 、C 两点分别作AE BD ⊥于E 点,CF BD ⊥于F 点,求证:四边形AECF 是平行四边形练习:1、如图是某市一公园的路面示意图,其中,ABCD 是平行四边形,BE ⊥AC, DF ⊥AC ,E 、F 是垂足,G 、H 分别是BC 、AD 的中点,连接EG 、GF 、FH ,HE 为公园中小路,问小明从B 地经E 地,H 地到F 地,与小强从D 地经F 地,G 地到E 地,谁的路程远?2、如图所示,在ABCD 中,E 、F 是对角线AC 上两点,且AF =CE,求证:四边形BEDF 是平行四边形.3、如图,在ABCD 中,点M 、N 是对角线AC 上的点,且AM =CN , DE =BF ,求证:四边形MFNE 是平行四边形18。
坐标平行四边形知识点总结:若A 、B 、C 为已知点,则求一点D 与他们构成平行四边形,则有三个点1D 、2D 、3D ,则有1D =A+B-C 2D =A+C-B 3D =B+C —A (按照中点坐标公式和对角线相互平分性质)例题1、已知点A (﹣1,0),B (2,﹣1),D(0,1).请在直角坐标系中找一点C 与A 、B 、C 、D 四点构成平行四边形,则点C 的坐标为 ______________________。
练习:1、若以A (—0.5,0),B (2,0),C (0,1)三点为顶点要画平行四边形,则第 四个顶点不可能在【 】A. 第一象限 B 。
第二象限 C 。
第三象限 D 。
第四象限2、已知点D 与点A (8,0),B(0,6),C(a ,﹣a )是一平行四边形的四个顶点,则CD 长的最小值为 .例题2、如图,在平面直角坐标系中,已知Rt △AOB 的两条直角边0A 、08分别在y 轴和x 轴上,并且OA 、OB 的长分别是方程27120x x -+=的两根(OA 〈0B),动点P 从点A 开始在线段AO 上以每秒l 个单位长度的速度向点O 运动;同时,动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 运动,设点P 、Q 运动的时间为t 秒. (1)求A 、B 两点的坐标。
(2)当t=2时,在坐标平面内,是否存在点M ,使以A 、P 、Q 、M 为顶点的四边形是平行四边形?若存在,请直接写出M 点的坐标;若不存在,请说明理由练习:1、如图x C y ⊥⊥BC 轴于点,BA 轴于A 点,B(3,4),四边形ABCD 沿直线EF 折叠,点A 落在BC 边上的G 处,E 、F 分别在AD 、AB 上,且AF=2. (1)求G 点坐标;(2)求直线EF 解析式;(3)点N 在x 轴上,直线EF 上是否存在点M ,使以M 、N 、F 、G 为顶点的四边形是平行四边形?若存在,请直接写出M 点的坐标;若不存在,请说明理由19。
动点平行四边形例题1:在四边形ABCD 中,AD ∥BC ,且AD >BC,BC=6cm ,P 、Q 分别从A 、C 同时出发,P 以1cm/s 的速度由A 向D 运动,Q 以2cm/s 的速度由C 出发向B 运动,几秒后四边形ABQP 是平行四边形?练习:1、如图,在△ABC 中,AB=AC ,射线AM ∥BC ,点P 从点A 出发沿射线AM 运动,同时点Q 从点B 出发沿射线BC 运动,设运动时间为t (s ).(1)连接PQ 、AQ 、PC ,当PQ 经过AC 的中点D 时,求证:四边形AQCP 是平行四边形; (2)若BC=6cm ,点P 速度为1cm/s ,点Q 的速度为4cm/s ,填空: ①当t 为_______s 时,以A 、Q 、C 、P 为顶点的四边形是平行四边形;(1)证明:∵D 为AC 中点, ∴AD=CD , ∵AM ∥BC , ∴∠PAC=∠ACB ,QPCBA在△ADP和△CDQ中,∠PAD=∠DCQAD=CD∠ADP=∠CDQ,∴△ADP≌△CDQ(ASA),∴PD=DQ,又∵AD=CD,∴四边形AQCP是平行四边形;(2)①当Q在线段BC上,AP=QC时,以A、Q、C、P为顶点的四边形是平行四边形,由题意得:t=6-4t,解得:t=1.2,当Q在C的右边时,AP=QC时,以A、Q、C、P为顶点的四边形是平行四边形,由题意得:t=4t—6,解得:t=2,故答案为:1。
