对球面划分三角形面网格示例
3.网壳结构(上)

四角锥柱面网壳的主要形式
54
三角锥柱面网壳 抽空三角锥柱面网壳
双层柱壳的 上下弦杆可能 都受压。
55
四、椭圆抛物面网壳网格形式
试分析下列网格的划分特点
三向型
单斜杆型
联方型
56
五、双曲抛物面网壳网格形式
正交正放型
正交斜放型
57
六、局部双层网壳网格形式
单层网壳的承载力主要由稳定控制,材料的实 际工作应力仅为允许应力的1/10~1/6。
1)单层柱面网壳
单斜杆型柱面网壳
人字形柱面网壳
刚度较差,适用于中、小型网壳
49
悉尼国际水上运动中心 50
双斜杆型
联方型
三向网格型
双斜杆型连接复杂 联方型网格刚度差 三向型网格刚度最好
51
为提高刚度和稳定性,对于长柱壳应设横向肋
汉堡博物馆庭院
52
2)双层柱面网壳 主要有交叉桁架体系和四角锥、三角锥体系。
34
球面网壳的网格划分 主要有6种形式: • 肋环型 • 施威德勒型 • 联方型 • 凯威特型 • 三向网格型 • 短程线型
35
1)肋环型 (Rib-Ring System)
只有经向和纬向杆件,大部分网格呈梯形 除顶部节点外,构造简单 杆件承受弯矩,整体刚度差 适用于中、小型网壳
试分析图中有几种杆件和节点形式?
38
4)三向网格型 (Three-way System)
几何构成方法 • 在球面的水平投影面上,将跨度
n等分,作出正三角形网格,再 投影到球面上(小矢跨比) • 在球面上用三个方向、相交成60 度的大圆构成(大矢跨比)
特点 受力性能好,外形美观,适用于大、中型网壳
39
球面上取点的方法

球面上取点的方法在球面上取点的问题可以归纳为两种情况:一是球面上均匀分布的点集,二是随机分布的点集。
下面将介绍这两种情况下的取点方法。
一、球面上均匀分布的点集1. 正二十面体法(Icosahedron Method)正二十面体是一种由20个等边三角形组成的多面体。
它具有对称性,每个顶点周围的角度相等。
在球面上取点的方法是,将球面等分成20个等大的三角形,并在每个三角形的中心取一个点。
2. 高斯-勒让德法(Gauss-Legendre Method)这种方法基于数值积分的思想,通过在球面上选取一些特定的积分点,然后利用对称性生成其他点。
这些特定的积分点可以通过数值计算方法得到,其中一种常用的方法是高斯-勒让德公式。
3. 均匀分布法(Uniform Distribution Method)这种方法是将球面上的点均匀的排列在各个纬度线上。
首先,在纬度方向上选取一些离赤道等距的纬度线,并在每条纬度线上间隔相等的取点;然后,在每个纬度线上选取一些等距的经度线,同样在每个经度线上取点。
通过调整纬度线和经度线的数量和间距,可以控制点的数量和分布密度。
二、球面上随机分布的点集1. 高斯分布法(Gaussian Distribution Method)这种方法利用了高斯分布的性质,通过在球面上随机生成一个高斯分布的随机向量,然后将该向量归一化得到球面上的一个点。
由于高斯分布是各向同性的,所以随机生成的点在球面上会呈现出随机分布的趋势。
2. 渐进方位法(Progressive Azimuth Method)这种方法是通过渐进方位来定义球面上随机点的分布。
首先,在球面上随机选择一个起始点;然后,随机生成一个方位角和极角,并在起始点周围的一些范围内生成下一个点;重复上述步骤,直到生成足够数量的点。
3. 拉特斯网格法(Lattice Grid Method)这种方法是将球面划分为一个规则的网格,然后在每个网格中随机选取一个点作为球面上的一个点。
ANSYS 13.0 Workbench 网格划分及操作案例

第 3章 ANSYS 13.0 Workbench网格划分及操作案例网格是计算机辅助工程(CAE)模拟过程中不可分割的一部分。
网格直接影响到求解精 度、求解收敛性和求解速度。
此外,建立网格模型所花费的时间往往是取得 CAE 解决方案所 耗费时间中的一个重要部分。
因此,一个越好的自动化网格工具,越能得到好的解决方案。
3.1 ANSYS 13.0 Workbench 网格划分概述ANSYS 13.0 提供了强大的自动化能力,通过实用智能的默认设置简化一个新几何体的网 格初始化,从而使得网格在第一次使用时就能生成。
此外,变化参数可以得到即时更新的网 格。
ANSYS 13.0 的网格技术提供了生成网格的灵活性,可以把正确的网格用于正确的地方, 并确保在物理模型上进行精确有效的数值模拟。
网格的节点和单元参与有限元求解,ANSYS 13.0在求解开始时会自动生成默认的网格。
可以通过预览网格,检查有限元模型是否满足要求,细化网格可以使结果更精确,但是会增 加 CPU 计算时间和需要更大的存储空间,因此需要权衡计算成本和细化网格之间的矛盾。
在 理想情况下,我们所需要的网格密度是结果随着网格细化而收敛,但要注意:细化网格不能 弥补不准确的假设和错误的输入条件。
ANSYS 13.0 的网格技术通过 ANSYS Workbench的【Mesh】组件实现。
作为下一代网格 划分平台, ANSYS 13.0 的网格技术集成 ANSYS 强大的前处理功能, 集成 ICEM CFD、 TGRID、 CFXMESH、GAMBIT网格划分功能,并计划在 ANSYS 15.0 中完全整合。
【Mesh】中可以根 据不同的物理场和求解器生成网格,物理场有流场、结构场和电磁场,流场求解可采用 【Fluent】、【CFX】、【POLYFLOW】,结构场求解可以采用显式动力算法和隐式算法。
不同的 物理场对网格的要求不一样,通常流场的网格比结构场要细密得多,因此选择不同的物理场, 也会有不同的网格划分。
球面分割方案

球面分割方案球面分割方案是指将球体表面按照一定规则进行划分,以便于进行球面上的计算和分析。
在计算机图形学、物理学、化学等领域都有着广泛的应用。
本文将介绍几种常见的球面分割方案以及它们的特点和应用。
一、经纬度划分经纬度划分是最常见的球面分割方案之一。
它将球体表面划分成一系列纬度和经度线构成的网格。
经度线是垂直于球心的线,从南极到北极穿过球面;纬度线是与经线相交的水平线,从一个极点到另一个极点。
经纬度划分可以用来表示地球上的经纬度坐标。
这种划分方案的特点是简单易用,能够提供全球范围内的坐标表示。
然而,经纬度划分在极地地区存在着畸变,导致区域缩小和形变,不适用于需要高精度分析的情况。
二、正多面体划分正多面体划分是将球面划分成多个等面积的小多面体,如正四面体、正六面体、正八面体等。
这种划分方案适用于需要分析局部区域的情况,例如计算物体表面的法向量、判断点是否在物体表面等。
正多面体划分的优点是可以得到均匀分布的采样点,适用于一些数值计算和模拟问题。
然而,在全球尺度的分析中,正多面体划分会导致分割的边界不连续,不方便进行全球范围内的计算。
三、等距离划分等距离划分是将球面划分成一系列等距离的小区域。
这种划分方案适用于需要精确度高、分辨率均匀的情况,例如全球气候模拟、地质勘探等。
等距离划分的特点是能够保持距离的一致性,对于一些需要考虑地球曲率的问题尤为重要。
然而,等距离划分也存在着数据存储和计算复杂度较高的问题,需要综合考虑实际应用中的需求。
结论不同的球面分割方案适用于不同的应用场景,选择合适的分割方案是保证计算和分析结果准确性的重要一步。
经纬度划分适用于全球范围内的坐标表示,正多面体划分适用于局部区域的分析,等距离划分适用于高精度和均匀分布的需求。
在实际应用中,还可以根据具体需求进行适当的改进和组合,以提高分割方案的效果和适用性。
常用曲面的变尺寸三角形网格划分

常用曲面的变尺寸三角形网格划分
杨晓东;刘春太;申长雨
【期刊名称】《计算机应用与软件》
【年(卷),期】2000(017)004
【摘要】针对常用的旋转面(包括圆锥面、圆柱面、圆台面、球面、圆环面等)、柱状平扫面的特点,在参数平面内采用统一的数据结构表示,将曲面网格划分问题归结为对参数平面的平面网格划分问题.在对参数平面进行网格划分时,根据网格尺寸要求生成适当的内部结点,然后用Delaunay三角化方法生成变尺寸光滑过渡的高质量三角形,满足有限元高精度分析计算的需要.
【总页数】5页(P22-25,54)
【作者】杨晓东;刘春太;申长雨
【作者单位】郑州工业大学橡塑模具国家工程研究中心郑州 450002;郑州工业大学橡塑模具国家工程研究中心郑州 450002;郑州工业大学橡塑模具国家工程研究中心郑州 450002
【正文语种】中文
【中图分类】TP39
【相关文献】
1.基于曲面展开的自由曲面网格划分 [J], 潘炜;吴慧;李铁瑞;高博青
2.基于网格划分的曲面延伸方法及延伸曲面的精度控制 [J], 王俊生;幸研
3.任意曲面的三角形网格划分 [J], 陈永府;张华
4.任意平面区域的变尺寸有限元网格划分 [J], 刘春太;杨晓东;申长雨;陈静波
5.基于曲面拟合的复杂自由曲面网格划分 [J], 陈礼杰;吴慧;李铁瑞;高博青
因版权原因,仅展示原文概要,查看原文内容请购买。
短程线三角形网格网壳与双向子午线网格网壳的技术性能比较
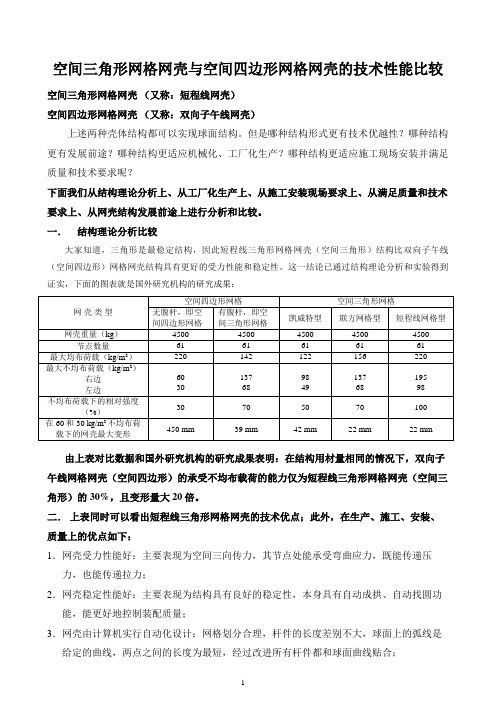
空间三角形网格网壳与空间四边形网格网壳的技术性能比较空间三角形网格网壳(又称:短程线网壳)空间四边形网格网壳(又称:双向子午线网壳)上述两种壳体结构都可以实现球面结构。
但是哪种结构形式更有技术优越性?哪种结构更有发展前途?哪种结构更适应机械化、工厂化生产?哪种结构更适应施工现场安装并满足质量和技术要求呢?下面我们从结构理论分析上、从工厂化生产上、从施工安装现场要求上、从满足质量和技术要求上、从网壳结构发展前途上进行分析和比较。
一.结构理论分析比较大家知道,三角形是最稳定结构,因此短程线三角形网格网壳(空间三角形)结构比双向子午线(空间四边形)网格网壳结构具有更好的受力性能和稳定性。
这一结论已通过结构理论分析和实验得到证实,下面的图表就是国外研究机构的研究成果:由上表对比数据和国外研究机构的研究成果表明:在结构用材量相同的情况下,双向子午线网格网壳(空间四边形)的承受不均布载荷的能力仅为短程线三角形网格网壳(空间三角形)的30%,且变形量大20倍。
二.上表同时可以看出短程线三角形网格网壳的技术优点;此外,在生产、施工、安装、质量上的优点如下:1.网壳受力性能好:主要表现为空间三向传力,其节点处能承受弯曲应力,既能传递压力,也能传递拉力;2.网壳稳定性能好:主要表现为结构具有良好的稳定性,本身具有自动成拱、自动找圆功能,能更好地控制装配质量;3.网壳由计算机实行自动化设计:网格划分合理,杆件的长度差别不大,球面上的弧线是给定的曲线,两点之间的长度为最短,经过改进所有杆件都和球面曲线贴合;4.所有零部件实现了工厂化、标准化生产,采用模具加工,质量好,效率高,成本低;5.现场施工安装方便、快捷,φ50m直径的短程线三角形网格网壳现场安装时间仅需10天,施工费用节省,现场安装时无需大型起吊设备配合,不占用施工现场地方,且现场动火量少(除边缘节点板少量动火外);6.现场安装网壳自动成拱、自动找圆,安装质量得到保证;7.网壳与罐顶不用焊接,顶板施工方便,节省工时,球面成形度好,外观圆滑美观;8.短程线三角形网格网壳的杆件防腐工作可工厂预先完成,不需现场施工,由于现场杆件安装不需动火,防腐质量得到保证;9.短程线三角形网格网壳具有可修复性,且费用低,时间短;经实验破坏后,修复实体破坏试验罐(1/4破坏面)仅用了三天时间。
足球(3dmax 网格编辑实例)
编辑网格
编辑网格:把物体转换为可编辑网格,可对其顶点和面进行编辑,从而改变它的形状。
4.3.1顶点子对象、
创建:在视图中创建一个顶点
删除:删除点、
附加:附加另外一个物体同时进行编辑
分离:分离出去,成为独立对象、
切角:可以生成切角斜面
焊接:三维顶点焊接
平面化:使顶点强制成平面
塌陷:选中的点合并到集中心位置的点上
4.3.2 边子对象
挤出:选着边拉出一个距离
切角:倒角效果
4.3.3 面和多边形子对象
拆分:细分成3个小面
挤出:选着面挤出厚度
炸开:当前选中的炸开分离成独立的对象
足球:
1,在顶视图,拓展基本体--异面体命名:足球
2,修改面板系列:十二面体系列参数:p:0.3
炸开
4,框选全部,,进入修改面板,添加网格平滑细分量:迭代次数:2
5,添加球形化
6.添加网格编辑,打开多边形子对象全选挤出
7.添加一个网格平滑细分方法:四边形输出迭代次数:2
8,指定材质
按(M)键打开材质编辑器选着一个空白材质球,选着标准材质 standard
选着多维/子对象
9.设置数量:2 单击1号材质
10,漫反射:黑色高光级别:131,光泽度为:15 转入下级同级,
11,漫反射为白色
赋予材质:得到效果。
网格划分原理与实例(最终版本)
破解影 射路径 是复杂 几何网 格处理 的不二 法则
分块要诀:
a、获得和积分路径大约一致的网格路径,提高积分精度。 b、获得高质量Hexa网格,节省计算成本,满足非线性计算
的网格变形需求。 c、 “分块” 是讲求刀法的。武士的刀法,是用来杀出一条生
路,网格技术的刀法,则是为了砍出完整的sweep路径。
暖通模具—
五、六面体 难点:影射
混合网格
关系过于复 杂,需要混
合网格减少
网格数量
建筑结构案例——广告牌CFD
约50万结构化网格
难点: 1、Hexa贴体壁面网格捕捉近壁区流场特征。 2、实体+无厚度膜双侧非连续网格技术(inner wall+split)
案例——标准四坡结构CFD 约60万混合网格,包含覆面Grid
3、网格算法是Computer Graphics和Computer Mathematics结合的产物,和力学无关。
4、网格可以连续,也可以不连续。 5、网格是艺术,不仅仅是技术。
二、网格剖分基本刀法:
1、自由网格剖分——算法复杂
a、现有的CAE软件通常自带自由网格划分功能,以自由网格方案为
六面体网格。 本质:等同于全手工网格制作。
案例1——多体组合复杂网格
约8万混合网格,含接触、预紧、非连续网格、材料非线 性和显式破坏。
KT形矩管桁架试件-反力架网格模型
案例2——屠龙刀:3D几何
几何模型
屠龙刀拓补结构
屠龙刀网格
屠龙刀网格模型(全结构化六面体方案)
好刀还需好刀法—— 屠龙也会砍缺!
(vertices)。
影射拓补
2.1基于拓扑的分块
分块拓扑的思想即是切分复杂几何的基本拓补体,展露原 始几何的本质拓扑结构。以圆形为简单例子,下图为圆面没有
python匹配最近经纬度的算法
python匹配最近经纬度的算法【原创版】目录1.算法概述2.匹配经纬度的方法3.Python 实现代码4.算法的优缺点正文1.算法概述最近经纬度算法是一种用于查找两个地点之间最短路径的算法。
在众多地理信息系统(GIS)应用中,这种算法具有广泛的应用前景。
通过使用 Python 编程语言,我们可以轻松地实现这一算法,从而在各种场景下快速找到最近经纬度。
2.匹配经纬度的方法在实现最近经纬度算法时,通常采用以下两种匹配方法:(1)哈希表法:将地球表面划分为若干个网格,用哈希表存储每个网格的经纬度信息。
在查询时,通过哈希表快速找到与给定点最近的网格,然后计算两个网格之间的最短路径。
这种方法的优点是查询速度快,但缺点是需要大量的存储空间来存储哈希表。
(2)球面三角法:球面三角法是一种基于球面几何的算法,通过将地球表面分解为若干个三角形,利用三角形的性质计算最短路径。
在Python 中,我们可以使用球面三角库(如`geopy`库)来实现这一算法。
这种方法的优点是存储空间小,但缺点是计算过程较为复杂,查询速度相对较慢。
3.Python 实现代码下面是一个使用球面三角法实现最近经纬度算法的 Python 示例代码:```pythonfrom geopy.geocoders import Nominatimfrom geopy.distance import distancedef get_lat_lng(address):geolocator = Nominatim(user_agent="myGeocoder")location = geolocator.geocode(address)return titude, location.longitudedef find_nearest_location(point, locations):lat_lngs = [(location[1], location[0]) for location in locations]distances = [distance(point, (lat, lng)) for lat, lng in lat_lngs]return min(distances, key=distances.get)if __name__ == "__main__":point_address = "40.7128, -74.0060" # 纽约nearest_location = find_nearest_location((40.7128,-74.0060), ["10175", # 北京"51.5098, -0.1181", # 伦敦"37.421999, 8.8247" # 东京])print("最近地点:", nearest_location)```在这个示例中,我们首先使用`geopy`库获取给定点和备选地点的经纬度,然后使用`find_nearest_location`函数计算最近地点。
图解球体表面积和体积正确计算方法及计算公式
图解球体外表积和体积正确计算方法及计算公式一、球体面积球体外表是可以由N个带弧形的等腰三角形拼凑而成,见图一、图二、图三。
设球体的二分之一水平中心为腰线,在球顶和球底正中各设一个顶点和底点a,然后从顶点到腰线按等分分割成N个带弧形的等腰三角形。
根据定义:线的长度不因弯曲而改变,球面可无限分割成N个等腰三角形如图二、图四、图五所示,所有分割好带弧形的等腰三角形都可以自然平展成标准的等腰三角形,亦可将等腰三角形拼凑成方形。
在理解上述图例球体外表和等腰三角形的关系后,我们可以对球体外表积的计算有比拟清晰的判断。
即,球体外表可以分割成N个相等的等腰三角形,等腰三角形亦可拼凑成方形,由此推导出球体面积可以用矩形公式计算。
即S = 长×宽,如果我们设球体1/4之一的周长为宽,设球体的周长为长,则球体外表积公式为:S=1/4周长×周长〔见图六〕例1:球体直径是1个单位,求球体外表积〔用上述最新推导公式S=1/4周长×周长〕S =〔3.14159÷4〕×3.14159 = 2.4674㎡二、球体体积设以球心作一条垂线或水平中心线,然后以垂线或水平中心向外将球体按等分无限分割成N 个半圆楔形体。
见图七、图八。
球体分割完成后,将半圆楔形体镜像排列成圆柱体,见图九、图十。
从图七、图八、图九、图十看,球体从中心按等分分割成半圆楔形体后可以排列堆砌成圆柱体,根据计算得出定义:与球体同直径同体积的圆柱体的柱高正好是球体周长的1/4。
则球体体积公式为:V =πR平方×周长的1/4 或:V = D〔直径的三次方〕×0.616849233例2:球体直径是1个单位,求球体体积〔用上述最新推导公式〕V =πR平方×周长的1/4= 3.14159×0.25×0.7853975= 0.616849233三、公知公式在球体面积、体积计算中出现的错误1、球体面积如何检验球体面积计算的正确,最好的方法就是用计算结果制成N个等腰三角形的薄膜反贴球体外表。
