中考数学专题复习课件怎样秒杀二次函数压轴题共张
中考专题08 瓜豆原理-最新中考数学二次函数压轴题核心考点突破

A
B
C
M
O
E
D
连接 AM 并延长与圆 M 交点即为所求的点 O,此时 AO 最大,根据 AB 先求 AM, 再根据 BC 与 BO 的比值可得圆 M 的半径与圆 A 半径的比值,得到 MO,相加即 得 AO.
A
B
C
M
O
E
D
此题方法也不止这一种,比如可以如下构造旋转,当 A、C、A’共线时,可得 AO 最大值.
学易同步精品课堂
中物理
瓜豆原理
在辅助圆问题中,我们了解了求关于动点最值问题的方式之一— —求出动点轨迹,即可求出关于动点的最值.
今天继续讨论另一类动点引发的最值问题,在此类题目中,题目
或许先描述的是动点P,但最终问题问的可以是另一点Q,当然P、 Q之间存在某种联系,从P点出发探讨Q点运动轨迹并求出最值,
A
D
F
G
B
E
C
【分析】同样是作等边三角形,区别于上一题求动点路径长,本题是求 CG 最小值,可以将 F 点看成是由点 B 向点 A 运动,由此作出 G 点轨迹:
考虑到 F 点轨迹是线段,故 G 点轨迹也是线段,取起点和终点即可确定线段位置,
初始时刻 G 点在 G1 位置,最终 G 点在 G2 位置( G2 不一定在 CD 边),G1G2 即为 G
A
N
α
M α
B
C
【2017 姑苏区二模】如图,在等边△ABC 中,AB=10,BD=4,BE=2,点 P 从点 E 出发沿
EA 方向运动,连结 PD,以 PD 为边,在 PD 的右侧按如图所示的方式作等边△DPF,当点
P 从点 E 运动到点 A 时,点 F 运动的路径长是________.
2021年中考一轮复习 数学热点问题《二次函数压轴题的突破与提升》六大必考模型专题练习

中考数学热点问题《二次函数压轴题的突破与提升》六大必考模型专题练习题型一:求图形面积类问题1. 如图,假设篱笆(虚线部分)的长度为16m,则所围成矩形ABCD 的最大面积是 .2. 如图,抛物线y=-x 2+2x+3与y 轴交于点C,点D(0,1),点P 是抛物线上的动点.若△PCD 是以CD 为底的等腰三角形,此时△PCD 的面积为________.3.如图,已知二次函数2y x bx c =++的图象与y 轴交于点A, 与x 轴正半轴交于B,C 两点,且BC =2,ABC S ∆ =3,则b 的值为( )A.-5B.4或-4C. 4D.-4 4.如图,抛物线经过A (-2,0),B ,C (0,2)三点. (1)求抛物线的解析式;(2)在直线AC 下方的抛物线上有一点D ,使得△DCA 的面积最大,求点D 的坐标.题型二:参数求值类问题1. 若函数y=(m-1)x |m|+1是二次函数,则m 的值为____.2. 抛物线y=x 2-2x+m 2+2(m 是常数)的顶点在 ( ) A.第一象限B.第二象限C.第三象限D.第四象限3. 已知二次函数y=-x 2+2x+m.(1)如果二次函数的图象与x 轴有两个交点,求m 的取值范围.4. 当a ≤x ≤a+1时,函数y=x 2-2x+1的最小值为1求a 的值.5. 已知二次函数263y kx x =-+的图象与x 轴有交点,求k 的取值范围.题型三:利用图像分析类问题1. 下列图象中,当ab >0时,函数y =ax 2与y =ax +b 的图象是( )2. 如图,二次函数y=ax 2+bx+c 的图象与x 轴相交于(-2,0)和(4,0)两点,当函数值y>0时,自变量x 的取值范围是 ( )A.x<-2B.-2<x<4C.x>0D.x>43.已知二次函数的图象如图所示,对称轴是,则下列结论中正确的是( ).A.0>ac B.0>b C.04ac -2<bD.4. 二次函数y=ax 2+bx+c(a ≠0)的大致图象如图所示,顶点坐标为(-2,-9a),下列结论:①4a+2b+c>0;②5a -b+c=0;③若方程a(x+5)(x-1)=-1有两个根x 1和x 2,且x 1<x 2,则-5<x 1<x 2<1;④若方程|ax 2+bx+c|=1有四个根,则这四个根的和为-4.其中正确的结论有 ( )A.1个B.2个C.3个D.4个5. 如图所示是二次函数c bx ax y ++=2图象的一部分,图象过A 点(3,0),二次函数图象对称轴为1=x ,给出四个结论:①ac b 42>;②0<bc ;③02=+b a ;④0=++c b a ,其中正确结论是( )A.②④B.①③C.②③D.①④ 题型四:动点求最值类问题2y ax bx c =++1x=20a b +=1. 若二次函数y=x2-4x+c的图象经过点(0,3),则函数y的最小值是.2. 如图是函数y=x2-2x-3(0≤x≤4)的图象,直线l∥x轴且过点(0,m),将该函数在直线l上方的图象沿直线l向下翻折,在直线l下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是 .3. 如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为________.4. 如图,抛物线y=x2-bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.(1)求抛物线的表达式.(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.5. 若二次函数y=ax2+b的最大值为4,且该函数的图象经过点A(1,3).(1)a=________,b=________,顶点D的坐标为________;(2)求这个抛物线关于x轴对称后所得的新函数表达式;(3)是否在抛物线上存在点B,使得S△DOB =2S△AOD?若存在,请求出B的坐标;若不存在,请说明理由.6. 已知m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.(1)求这个抛物线的解析式.(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,试求出点C,D 的坐标,并判断△BCD的形状.(3)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为√2个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.题型五:实际应用类问题1. 图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-1(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴.若OA=10m, 400则桥面离水面的高度AC为( )A.16940mB.174mC.16740mD.154m2. 某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品,售后经过统计得到此商品单价在第x 天(x 为正整数)销售的相关信息,如表所示:(1)请计算第几天该商品单价为25元/件?(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数表达式. (3)这30天中第几天获得的利润最大?最大利润是多少?3. 某果园有100棵橙子树,平均每棵树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了x 棵橙子树.(1)直接写出平均每棵树结的橙子个数y(个)与x 之间的关系. (2)果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?4. 河上有一座桥孔为抛物线形的拱桥,水面宽6m时,水面离桥孔顶部3m.因降暴雨水位上升1m.(1)如图①,若以桥孔的最高点为原点,建立平面直角坐标系,求抛物线的解析式;(2)一艘装满物资的小船,露出水面的高为0.5m、宽为4m(横断面如图②).暴雨后这艘船能从这座拱桥下通过吗?请说明理由.题型六:综合应用类问题1. 已知抛物线y=ax2+bx-4经过点A(2,0),B(-4,0),与y轴交于点C.(1)求这条抛物线的表达式.(2)如图1,点P是第三象限内抛物线上的一个动点,当四边形ABPC的面积最大时,求点P的坐标.(3)如图2,线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.2. 如图,抛物线y=-23x2+bx+c与x轴交于A,B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,2),直线CD:y=-x+2与x轴交于点D.动点M在抛物线上运动,过点M作MP⊥x轴,垂足为点P,交直线CD于点N.(1)求抛物线的表达式.(2)当点P在线段OD上时,△CDM的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.(3)点E是抛物线对称轴与x轴的交点,点F是x轴上一动点,点M在运动过程中,若以C,E,F,M为顶点的四边形是平行四边形时,请写出点F的坐标.3. 如图,在平面直角坐标系中,直线y=mx+3与抛物线交于点A(9,-6),与y轴交于点B,抛物线的顶点C的坐标是(4,-11).(1)分别求该直线和抛物线的函数表达式;(2)D是抛物线上位于对称轴左侧的点,若△ABD的面积为812,求点D的坐标;(3)在y轴上是否存在一点P,使∠APC=45°?若存在,求出满足条件的点P的坐标;若不存在,请说明理由.4. 如图1,抛物线y=-3[(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在5点B的左侧),与y轴交于点C,连接BC. (1)求m,n的值.(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN,BN.求△NBC 面积的最大值.(3)如图3,点M,P分别为线段BC和线段OB上的动点,连接PM,PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P 的坐标;若不存在,请说明理由.。
中考数学解答题压轴题突破 重难点突破七 二次函数综合题 类型四:二次函数与特殊四边形问题

Ⅰ)如答图①,连接AC,分别过点A,B作对边的平行线交于 点F. 在▱ ACBF中,∵C(0,-5)向右平移1个单位长度,再向上平 移5个单位长度得到A(1,0), ∴B(5,0)按照相同的平移方式得到F(6,5);
解:设点Q的坐标为(a,b),过点Q作QM∥x轴,过点B作BM∥y轴,交QM 于点M,过点F作FN∥y轴交QM于点N,过点E作EK∥x轴交BM于点K, ∴△BMQ≌△QNF≌△EKB, ∴NF=KB=MQ=|a+2|,QN=EK=BM=|b|, ∴点F的坐标为 (a-b,a+b+2), 点E的坐标为 (-2-b,a+2),
Ⅱ)如答图②,分别过点A,C作BC,AB的平行线交于点 F,在▱ ABCF中,∵B(5,0)向左平移5个单位长度,再向 下平移5个单位长度得到C(0,-5), ∴A(1,0)按照相同的平移方式得到F(-4,-5);
Ⅲ)如答图③,连接AC,分别过点B,C作对边的平行线交 于点F.在▱ ACFB中,∵A(1,0)向左平移1个单位长度,再 向下平移5个单位长度得到C(0,-5), ∴B(5,0)按照相同的平移方式得到F(4,-5); 综上所述,满足条件的点F分别为(6,5),(-4,-5)或 (4,-5).
(1)求抛物线的函数解析式; (2)把抛物线 y=x2+bx+c 平移,使得新抛物线的顶点 为点 P(2,-4).M 是新抛物线上一点,N 是新抛物线对 称轴上一点,直接写出所有使得以点 A,B,M,N 为顶点 的四边形是平行四边形的点 M 的坐标,并把求其中一个 点 M 的坐标的过程写出来.
解:(1)该抛物线的函数解析式为y=x2-72x-1. (2)满足条件的点M的坐标为 (2,-4),(6,12),(-2,12). 由题意可知,平移后抛物线的函数解析式为 y=x2-4x, 对称轴为直线x=2,如答图.
【中考数学压轴题专题突破02】二次函数中的动点问题
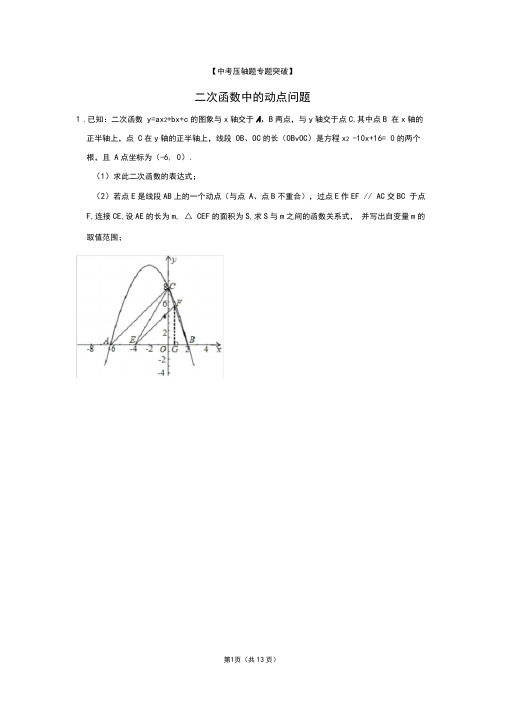
【中考压轴题专题突破】二次函数中的动点问题1.已知:二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,其中点B 在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OBvOC)是方程x2 -10x+16= 0的两个根,且A点坐标为(-6, 0).(1)求此二次函数的表达式;(2)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF // AC交BC 于点F,连接CE,设AE的长为m, △ CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;2.如图是二次函数y= ( x+m) 2+k的图象,其顶点坐标为M (1, -4).(1)求出图象与x轴的交点A, B的坐标;(2)在二次函数的图象上是否存在点P,使S APAB=—S;AMAB?若存在,求出P点的坐标,4若不存在,请说明理由;(3)点C在x轴上一动点,以BC为边作正方形BCDE ,正方形BCDE还有一个顶点(除点B外)在抛物线上,请写出满足条件的点E的坐标;(4)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b与此图象至少有三个公共点时,请直接写出b的取值范围是 .即圄2 邺3.如图,二次函数图象的顶点为坐标系原点O,且经过点A (3, 3), 一次函数的图象经过点A和点B (6, 0).(1)求二次函数与一次函数的解析式;(2)如果一次函数图象与y轴相交于点C,点D在线段AC上,与y轴平行的直线DE 与二次函数图象相交于点巳/ CDO = / OED ,求点D的坐标;(3)当点D在直线AC上的一个动点时,以点O、C、D、E为顶点的四边形能成为平行四边形吗?请说明理由.4.如图,二次函数y=ax2+bx+c (a^0)的图象与x轴交于A (- 3, 0)、B (1, 0 与y轴相交点C (0,近).(1)求该二次函数解析式;(2)连接AC、BC,点M、N分别是线段AB、BC上的动点,且始终满足BM = 接MN.①将4BMN沿MN翻折,B点能恰好落在AC边上的P处吗?若能,请判断四边形的形状并求出PN的长;若不能,请说明理由.②将^ BMN沿MN翻折,B点能恰好落在此抛物线上吗?若能,请直接写出此时于MN的对称点Q的坐标;若不能,请说明理由.两点,BN,连BMPNB点关5.如图,在平面直角坐标系中,抛物线y=』!x2-2F3x-代与x轴交于A、B两点(点3 3(1)判断△ ABC的形状,并说明理由;(2)如图(1),点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点p作Y轴的平行线交X轴于点E.当△ PBC面积的最大值时,点F为线段BC 一点(不与点BC重合),连接EF,动点G从点E出发,沿线段EF以每秒1个单位的速度运动到点F,再沿FC以每秒2工3个单位的速度运动到点C后停止,当点F的坐标| 3是多少时,点G在整个运动过程中用时最少?(3)如图2,将4ACO沿射线CB方向以每秒个单位的速度平移,记平移后的△ ACO 为AA l C l O l连接AA1,直线AA1交抛物线与点M,设平移的时间为t秒,当^ AMC 1为等腰三角形时,求t的值.6.如图,二次函数y=—x2+bx- -的图象与x轴交于点A (-3, 0)和点B,以AB为边在2 2x轴上方作正方形ABCD ,点P是x轴上一动点,连接DP ,过点P作DP的垂线与y轴交于点E.(1)b=;点D的坐标:;(2)线段AO上是否存在点P (点P不与A、。
中考数学 精讲篇 中考压轴题重难点突破七 二次函数与几何综合题 类型二

设 M(0,m),直线 BM 的解析式为 y=k2x+b2, 将点 M,B 代入,得m0==b-2,2k2+b2,解得kb22==m2m.,
m ∴直线 BM 的解析式为 y=2x+m,∵点 P为直线 BM 与抛物线的交点,
m y=2x+m, ∴联立方程组得y=-14x2+32x+4,化简得(x+2)(x-8+2m)=0,
∵S△ACD=3,∴-32t2-92t=3,解得 t1=-1,t2=-2.
当 t=-1 时,点 D 的坐标为(-1,-4), 当 t=-2 时,点 D 的坐标为(-2,-3). 综上所述,满足条件的点 D 的坐标为(-1,-4)或(-2,-3).
【思路点拨】 第一步:设点 D 的横坐标为 t, 用含 t 的式子表示△ACD 的面积; 第二步:利用面积关系 S△ACD=3,列关于 t 的方程求解,进而得出点 D 的 坐标.
(4)如图,已知点 P 是直线 AC 下方抛物线上一动点,设点 P 的横坐标为 m,求四边形 APCO 面积的最大值;
解:由(1)(3)可知点 A(-3,0),C(0,-3), lAC:y=-x-3, 设直线 x=m 与直线 AC 交于点 F, 则点 P 的坐标为(m,m2+2m-3), 点 F 的坐标为(m,-m-3). 则 PF=-m-3-(m2+2m-3)=-m2-3m.
∴S 四边形 APCO=S△ACP+S△ACO=12OA·PF+12OA·OC=12×3×(-m2-3m+3) =-32(m2+3m)+92=-32m+322+683.
由题意可知,-3<m<0,
3
63
∴当 m=-2时,S 四边形 APCO 最大值为 8 .
【思路点拨】 第一步:设直线 x=m 与直线 AC 交于点 F,用含 m 的式子表示出 PF 的长; 第二步:由 S 四边形 =S +S APCO △ACP △ACO 列出式子,即可得到最大值.
2024年山西中考数学专题讲解——专题一、二次函数压轴题——六、运动产生的角度问题

y
A
O
B
M
x
四、例题讲解
【分析】
2 2 4
(1)抛物线: y x x 2 ;
3
3
3
(2)考虑到 tan ABO ,但 tan 2ABO 并不可求,以及 A B 平分∠OBM 也并不容易转化,
2
故考虑其他思路.
思路 1:构造全等三角形.
作△AOB 关于 AB 的对称的△ANB ,BN 与抛物线的交点即为 M 点.
-3)。
(1)抛物线的解析式为
;
四、例题讲解
已知:抛物线y=a(x+1)(x-3)与x轴相交于A、B两点,与y轴的交于点C(0,
-3)。
(2)若点P是抛物线上的动点,且满足
∠PCB =45°,请求出点P的坐标;
四、例题讲解
已知:抛物线y=a(x+1)(x-3)与x轴相交于A、B两点,与y轴的交于点C(0,
设 H 点坐标为(3,m),则 A H=-m, BH
令 m
3 0
2
m 2
13
故 H 点坐标为 3, .
4
2
3 0
13
,解得: m .
4
2
m 2
2
四、例题讲解
y
A
O
B
M
x
H
5
由 B 、H 两点坐标求直线 BH 解析式: y x 2 ,
C(0,-3)。
(9)若点P在抛物线上,满足∠PCB =∠ACB,
求点P的坐标;
四、例题讲解
已知:抛物线y=a(x+1)(x-3)与x轴相交于A、B两点,与y轴的交于点
中考专题02 将军饮马(一)-最新中考数学二次函数压轴题核心考点突破共47页文档
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔,思而不学则殆。——孔子
中考专题02 将军饮马(一)-最新中考数 学二次函数压轴题核心考点突破
51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
初中数学二次函数压轴题解题技巧
初中数学二次函数压轴题解题技巧
一、关于二次函数的基本概念
1、什么是二次函数?
二次函数是一类特殊的函数,由定义域上的每一个实数组成,关于y的方程也叫二次方程或者二次曲线,其一般形式为y=ax2+bx+c,其中a≠0。
2、什么是二次函数的图形?
二次函数的图形一般是抛物线的形状,它的顶点为抛物线函数的极值点,有3种情况:
(1)若a>0,那么抛物线为上升,顶点位于抛物线与x轴的交点,记为(x0,y0),当x变化时,y处于上升状态;
(2)若a<0,那么抛物线为下降,顶点位于抛物线与x轴的交点,记为(x0,y0),当x变化时,y处于下降状态;
(3)若a=0,那么抛物线变成一条直线,且顶点映射向无穷远,无法确定。
二、关于解题技巧
1、根据题意分析求解
判断给定的方程的类型,是一元二次方程还是方程组,是一元二次方程可以用代数法解题;是方程组则可以用代数法或者几何法求解。
2、具体的求解步骤
(1)一元二次方程
(a)将二次项系数、一次项系数、常数项分别乘以同等量的系
数,使方程左边系数统一为1;
(b)将二次项提到一边,将其他因式放到另一边,使其成一般形式;
(c)对得到的一般形式求解,它的解一定是一个双根,具体求解可利用一元二次方程的完全平方根式;
(d)将求得的解代回原方程即可得出所求解。
(2)一元二次方程组
(a)求出第一个方程的一个变量的值,代入第二个方程求解;
(b)将求出的另一个变量值代入第一个方程,得出另一个变量的值,得出全部解。
17专题八 二次函数压轴题类型二 面积问题(PPT课件)
交点,即为所求Q点.
∵直线BC的解析式为y=-x+3,
PM=2, ∴过点P且与BC平行的直线
l1 为y=-x+3+2=-x+5,
例2题解图②
联立
y y
x5 x2 2
x
3
解得
x1
y2
2 3
,
x2 y2
1 4
∴Q1 (2,3),
∵M(1,2),
2
2
背景
问题
在抛物线上求一点P,
如图,平面直角坐标系中,抛物线l交 使得S△ACP=S△BCP x轴于点A、B,与y轴交于点D,点C在
x轴下方的图象上,AC交y轴于点M
方法指导
作图
求法
由AE=BE可证 过点C作AB平行线与l的交点 △AGE≌△BHE, 即为点P;取AB中点E,直线 于是高AG=BH CE与l的交点即为点P
(1)解:由题意可知点A(-1,0),点B(3,0)是抛物线与 x轴的两个交点, ∴抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3;
热身小练习
设点D的坐标为(t,①_-__t_2+__2_t_+__3_),点C的坐 标为(0,②___3___),已知点B的坐标为(3,0), 则OB=③___3___;点P的坐标为④__(1_,__4_)__, 点M的坐标为⑤__(_1_,__2_) _,PM=⑥____2____.
与AC相距h个单位的直线,此 直线与l的交点即为点P
及与l的交点坐标
方法指导
问题
求法
在抛物线上求多 一点P,使得
S ACP kSABC
(k为定值且k>0)
