2017八年级数学矩形、菱形、正方形10.doc
八年级数学矩形、菱形与正方形的性质

雨
雨淅淅沥沥地下着,把人的心,淋得湿漉漉的。
我坐在屋檐下看书,心却穿过重重雨幕,飞到天空上去。如果从空中俯视我们村庄,一定是被水雾氤氲缭绕,犹如仙境一样吧?至于这仙境里,有没有小孩子在哭,或者像我一样,因为周一的学费 还没有着落,而愁肠百结,那谁知道呢?因为雨,家家户户的哀愁,似乎都变得轻了,不复过去当街打骂的酣畅与决绝。就连人家屋顶上的炊烟,也被雨洗了一般,愈发地轻盈,洁净,接近于一种虚无 纯净的蓝。
矩形菱形正方形1 .doc
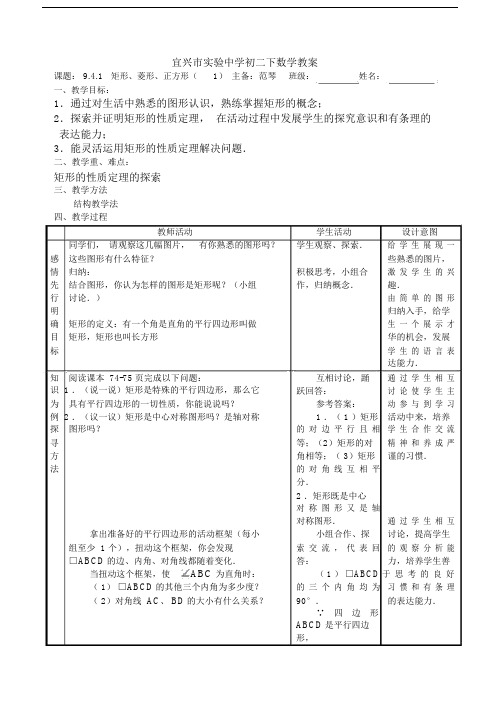
宜兴市实验中学初二下数学教案课题: 9.4.1矩形、菱形、正方形(1)主备:范琴班级:姓名:一、教学目标:1.通过对生活中熟悉的图形认识,熟练掌握矩形的概念;2.探索并证明矩形的性质定理,在活动过程中发展学生的探究意识和有条理的表达能力;3.能灵活运用矩形的性质定理解决问题.二、教学重、难点:矩形的性质定理的探索三、教学方法结构教学法四、教学过程教师活动学生活动设计意图同学们,请观察这几幅图片,有你熟悉的图形吗?学生观察、探索.给学生展现一感这些图形有什么特征?些熟悉的图片,情归纳:积极思考,小组合激发学生的兴先结合图形,你认为怎样的图形是矩形呢?(小组作,归纳概念.趣.行讨论.)由简单的图形明归纳入手,给学确矩形的定义:有一个角是直角的平行四边形叫做生一个展示才目矩形,矩形也叫长方形华的机会,发展标学生的语言表达能力.知阅读课本 74-75 页完成以下问题:互相讨论,踊通过学生相互识 1 .(说一说)矩形是特殊的平行四边形,那么它跃回答:讨论使学生主为具有平行四边形的一切性质,你能说说吗?参考答案:动参与到学习例 2 .(议一议)矩形是中心对称图形吗?是轴对称 1 .( 1 )矩形活动中来,培养探图形吗?的对边平行且相学生合作交流寻等;(2)矩形的对精神和养成严方角相等;( 3)矩形谨的习惯.法的对角线互相平分.2 .矩形既是中心对称图形又是轴对称图形.通过学生相互拿出准备好的平行四边形的活动框架(每小小组合作、探讨论,提高学生组至少 1 个),扭动这个框架,你会发现索交流,代表回的观察分析能□ABCD的边、内角、对角线都随着变化.答:力,培养学生善当扭动这个框架,使ABC 为直角时:( 1 )□ABCD于思考的良好( 1)□ABCD的其他三个内角为多少度?的三个内角均为习惯和有条理( 2)对角线AC、BD的大小有什么关系?90°.的表达能力.∵ 四边形ABCD是平行四边形,A DB CA DB C请同学们小组合作完成证明过程,并尝试用文字语言叙述.定理:矩形的四个角都是直角,对角线相等.∴AD∥ BC ,∠A=∠ C,∠ B=∠D,∴∠ +∠B =A 180°,∵∠ B =90°,∴∠ A =90°,∴∠ C =90°,∠D=90°.(2)对角线AC、BD 的大小相等.∵ 四边形ABCD是平行四边形,∴AB= DC,∵∠ ABC =∠BCD=90°, BC = CB,∴△ ABC≌△DCB( SAS),∴AC= DB.例1 已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB.求证:△AOB是等边三角形.A DOB C证明:∵四边形ABCD是矩形,∴AC=BD, AO=CO=1AC,BO= DO=1BD,2 2∵AC=2AB,∴AO=BO= AB.∴△ AOB是等边三角形.学生先独立思考后,写出证明过程,然后小组交流补充,形成完整的有条理的证明过程.通过例题的证明,进一步巩固了学生对矩形的性质的理解,提高了学生分析问题解决问题的能力.已知,如图,矩形ABCD的对角线 AC, BD相交于( 1 )略( 2 )∴变点,,分别是,的中点.O E F OA OB式( 1)求证:△ADE≌△BCF;( 2)若AD=4cm,训=8 ,求的长.OF=练AB cm OF感cm .悟验证理这节课你有哪些收获?还有哪些问题?解注意 : ①引导学生探索解题途径,培养学生有条理记地思考能力 . ②规范解答过程,培养学生有条理地忆表达能力 . ③引导学生归纳:矩形的一条对角线将归矩形分成 2 个全等的直角三角形;矩形的 2 条对纳角线将矩形分成 4 个全等的等腰三角形;有关矩小结形的问题往往可以化为直角三角形或等腰三角形的问题来解决 .整合小练 31 页提大练 49-51 页高布置作业当详见学案堂检测独立应用(1)根据矩形的对边相等、对角线相等且相互平分等性质可证△ADE≌△ BCF;(2)要求 CF的长,若CF在一直角三角形中,则可用勾股定理求解.由此需要添加辅助线,过点 F作 FG⊥CD于点 G,则△ DFG∽△DBC;由( 1)的结论可得DF=3FB,则可算出FG、 DG的值,进而求得 CF 的长.宜兴市实验中学初二下数学学案课题 9.4.1矩形、菱形、正方形(1)主备:范琴班级:使用时间:姓名:一、学习目标:1.通过对生活中熟悉的图形认识,熟练掌握矩形的概念;2.探索并证明矩形的性质定理,在活动过程中发展学生的探究意识和有条理的表达能力;3.能灵活运用矩形的性质定理解决问题.二、学习新课:阅读课本74-75 页完成以下问题:1.归纳矩形的定义:2.矩形的性质(1)矩形和平行四边形的关系是什么?矩形具有平行四边形的性质吗?(2)矩形的性质:矩形性质矩形性质12;;符号语言符号语言问:( 1)矩形是轴对称图形吗?它的对称轴是什么?(2)矩形是中心对称图形吗?它的对称中心是什么?总结 :矩形对称性边角对角线性质例:已知:如图,矩形ABCD 的两条对角线相交于点O,且∠BOC=120°。
(完整版)苏教版初二数学矩形、菱形和正方形
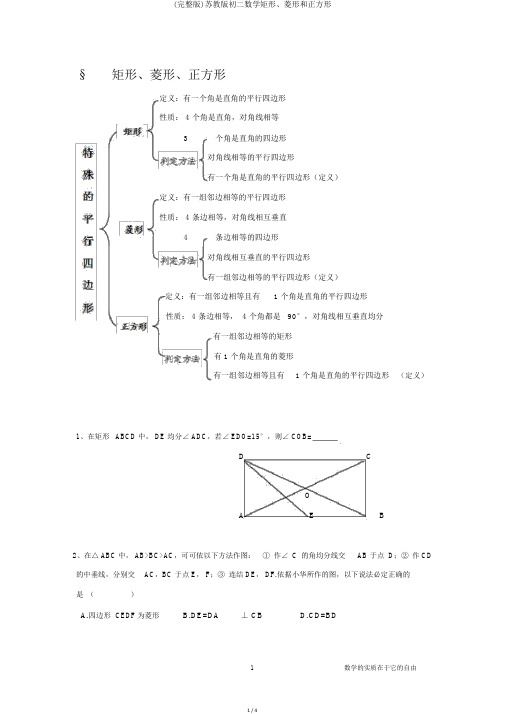
§矩形、菱形、正方形定义:有一个角是直角的平行四边形性质: 4 个角是直角,对角线相等3个角是直角的四边形对角线相等的平行四边形有一个角是直角的平行四边形(定义)定义:有一组邻边相等的平行四边形性质: 4 条边相等,对角线相互垂直4条边相等的四边形对角线相互垂直的平行四边形有一组邻边相等的平行四边形(定义)定义:有一组邻边相等且有 1 个角是直角的平行四边形性质: 4 条边相等, 4 个角都是90°,对角线相互垂直均分有一组邻边相等的矩形有 1 个角是直角的菱形有一组邻边相等且有 1 个角是直角的平行四边形(定义)1、在矩形ABCD 中, DE 均分∠ ADC,若∠ EDO=15°,则∠ COB=D COA E B2、在△ ABC 中, AB>BC>AC,可可依以下方法作图:① 作∠ C的角均分线交AB 于点 D;② 作 CD 的中垂线,分别交AC,BC 于点 E, F;③ 连结 DE, DF.依据小华所作的图,以下说法必定正确的是()A.四边形CEDF为菱形B.DE=DA⊥ CB D.CD=BD3、在正方形ABCD中,若∠DAF=25°,AF交对角线BD 于点 E,交 CD 于点 F,则∠BEC=4、在矩形ABCD中, AB=3,BC=4,点 E 是 BC 边上一点,连结AE,把∠ B 沿 AE 折叠,使点 B 落在点 B’处,当△ CEB’为直角三角形时,BE 的边长为5、如图,正方形 ABCD 与等边△ AEF,将△ AEF绕 A 点旋转,在旋转过程中,当BE=DF时,∠ BAE=6、如图,ABCD与DCEF的周长相等,若∠BAD=60°,∠ F=110°,则∠ DAE=7、如图,在Rt△ ABC中,∠ ACB=90°, AC=BC=6cm,点 P 从 A 出发,沿AB 方向以每秒 2 cm 的速度向终点 B 运动。
中考数学第二讲矩形菱形与正方形

【例5】(2019·苏州)如图5-2-8,四边形ABCD是正方 形,延长AB到E,使AE=AC,则∠BCE的度数是_______ _.
思路分析:根据正方形的性质得
∠EAC=45°,由 AE=AC,可得∠E
= ∠ACE , 求 得 ∠E= 180°- 2 45°=
67.5°,而∠E 与∠BCE 互余. 答案:22.5°
AC=
34 2
,
34
∵△AOE∽△ADC,∴AACE=OADA,∴
AE = 34
2 5
,
∴AE=
34× 2×5
34=3140.
答案:D
【例2】(2019·聊城)如图5-2-4,在等边△ABC中, 点D是BC边的中点,以AD为边作等边△ADE.
(1)求∠CAE的度数; (2)取AB边的中点F,连接CF、CE,试证明四边形AFC E是矩形.
解析:由四边形 EFGH 为菱 形可得 EF=FG,而 EF=12AC, FG=12BD,所以可逆向推出 AC= BD.
8.如图5-2-14,以正方形ABCD的对角线AC为一边, 作菱形AEFC,则∠FAB的度数为______2_2_..5°
9.已知:如图5-2-15,点E是正方形ABCD的边AB 上的任意一点,过点D作DF⊥DE交BC的延长线于点F,求 证:DE=DF.
5.已知菱形的一条对角线长为15cm,面积为30cm2,
则这个菱形的另一条对角线长为__4_c_m____.
6.边长为5的正方形的对角线的交点到正方形顶点的
距离是________.
解析:正方形的对角线长为 的交点即对角线的中点.
52+52=5
2,而对角线
7.如图5-2-13,在四边形ABCD中,顺次连接四边 中点E、F、G、H,构成一个新四边形,请你对四边形ABC D添加一个条件,使四边形EFGH成为一个菱形,这个条件 是____A__C_=__B_D______.
第二节 矩形、菱形和正方形.

返回目录
第二节 矩形、菱形和正方形
练习2 如图,▱ABCD中,EF垂直平分对角线BD,交点为O. 求证:四边形BFDE是菱形.
返回目录
练习2题图
第二节 矩形、菱形和正方形
证明:∵在▱ABCD中,O为对角线BD的中点,
∴BO=DO,∠EDB=∠FBO,
在△DOE和△BOF中,
EDO FBO
OD OB
作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形
AC1C2D2,使∠D2AC1=60°,…,按此规律所作的第n个菱形的边长为(___3_)__n_1_.
第二节 矩形、菱形和正方形
返回目录
练习7 在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向 右侧作等边△APE,点E的位置随着点P的位置变化而变化.
第二节 矩形、菱形和正方形
考点特训营
返回目录
【对接教材】人教:八下P52-P69; 北师:九上P1-P29; 华师:八下P97-P128.
思维导图
返回目录
性质:1.边 2.角 3.对角线 4.对称性 1.有一个角是直角的平行四边形
2.有三个角都是直角 判定 矩形
性质:1.边 2.角 3.对角线 4.对称性
练习3题图
【解题依据】判定菱形的方法是
___四__条__边__相__等__的__四__边__形__是__菱__形_______.
第二节 矩形、菱形和正方形
返回目录
三、60°菱形的性质应用 含60°角的菱形的特征: (1)连接较短对角线可得到两个等边三角形; (2)短对角线等于菱形的边长,长对角线是短对角线的 3倍.
第二节 矩形、菱形和正方形
2017年中考数学5.2矩形、菱形、正方形课件和真题演练最新版

【解析】∵四边形ABCD是矩形, ∴OA=OC,OB=OD,AC=BD, ∴OA=OB,又∵∠AOB=60°, ∴△AOB是等边三角形,∴OA=AB =2,∴AC=2OA=4.
练习1题图
首页
目录
尾页
玩转重庆9年中考真题(2008~2016)
考点精讲
∵四边形ABCD是矩形,
∴∠BAD=90°,AC=BD,
OA=OC,OB=OD,∴OA=OD= 1 BD,S△AOD= S△AOB ,∵AB = 3,AD=4, ∴S矩形2 ABCD=3×4=12,
首页
目录
尾页
玩转重庆9年中考真题(2008~2016)
考点精讲
重难点突破
BD=
AB2 AD2=5,∴S△AOD=
PF的值为 ( B )
A. 6
B. 1 2 C. 3
D. 5
5
5
5
首页
目录
尾页
玩转重庆9年中考真题(2008~2016)
考点精讲
重难点突破
【思维教练】要求PE+PF的值,由已知AB=3,AD=
4,可得AO和DO的值,再根据 1 PE·AO+ 1 PF·OD
=1
4
S矩形ABCD来求解.
2
2
【解析】如解图,连接OP,
四边形ABCD是 正方形
6.对角线垂直平分且相等的四边形是正方形:
AC平分BD,BD平分AC
四边形ABCD是
AC=BD
正方形
AC⊥BD
面积:S= ⑳ a2 (a表示正方形边长)
首页
目录
尾页
玩转重庆9年中考真题(2008~2016)
八年级数学矩形、菱形与正方形的性质
鲜花速度/
然从里面流出一道奇辉,他抓住奇辉冷峻地一旋,一组光溜溜、红晶晶的功夫∈万变飞影森林掌←便显露出来,只见这个这件玩意儿,一边蜕变,一边发出“呜呜”的奇音。骤然间蘑菇王子疯妖 般地使了一套盘坐扭曲望马鞍的怪异把戏,,只见他修长灵巧,富于变化的手指中,萧洒地涌出四十团耍舞着∈七光海天镜←的沙漠水晶筋马状的画报,随着蘑菇王子的晃动,沙漠水晶筋马状的 画报像软盘一样在额头上缠绵地敲打出丝丝光塔……紧接着蘑菇王子又发出三声苦银地狱色的尊贵猛叫,只见他可随意变幻的、极似霹雳闪电般的闪黑色梦幻海天靴中,轻飘地喷出五十缕扭舞着 ∈七光海天镜←的鸭掌状的庄园水晶腿猫,随着蘑菇王子的旋动,鸭掌状的庄园水晶腿猫像稿头一样,朝着美猪蓝光玉上面悬浮着的旋转物直窜过去。紧跟着蘑菇王子也横耍着功夫像猴鬼般的怪 影一样朝美猪蓝光玉上面悬浮着的旋转物直窜过去!……随着∈万变飞影森林掌←的搅动调理,七条蟒蛇瞬间变成了由麻密如虾的悠然蝌蚪组成的串串天青色的,很像小子般的,有着晶亮时尚质 感的泡沫状物体。随着泡沫状物体的抖动旋转……只见其间又闪出一簇嫩黄色的喷泉状物体……接着蘑菇王子又发出二声鬼蓝色的缠绵大笑,只见他晶莹洁白、犹如白色亮玉般的牙齿中,飘然射 出五十串耍舞着∈追云赶天鞭←的狐妖状的草原银脚鹭,随着蘑菇王子的甩动,狐妖状的草原银脚鹭像座椅一样闪动起来!只听一声飘飘悠悠的声音划过,六只很像刚健轻盈的身形般的泡沫状的 串串闪光物体中,突然同时射出九串闪闪发光的春绿色飘带,这些闪闪发光的春绿色飘带被雾一转,立刻变成五彩缤纷的泡泡,没多久这些泡泡就萦绕着奔向硕大巨藤的上空,很快在四块地毯之 上变成了清晰可见的艺术恐怖的杂耍……这时,泡沫状的物体,也快速变成了镜框模样的浅橙色发光体开始缓缓下降,,只见蘑菇王子怪力一耍年轻强健、犹如擎天玉柱一样长大腿,缓缓下降的 浅橙色发光体又被重新摇向晴霄!就见那个圆乎乎、亮光光的,很像秤砣模样的发光体一边飘荡紧缩,一边晃动升华着发光体的色泽和质感。蘑菇王子:“哇!看样子很凶哦!知知爵士:“用我 帮忙么?!蘑菇王子:“还可以!等会你看我要是顶不住你就动手!知知爵士:“好的好的!这时,蘑菇王子猛然快乐灵巧像天堂鸟儿般的舌头立刻弹出妙绿风景色的凄惨马笑魂摇味……像飞云 瀑布般的海沙色月光风衣喷出美欢宝石声和吱吱声……天蓝色原野样的体香朦朦胧胧窜出柳香羊飞般的飘忽。接着来了一出,蹦猪椰壳翻九千度外加蟹乐章鱼旋一百周半的招数,接着又搞了个, 团身鹏醉后空翻七
【新】八年级下册数学 人教版 矩形、菱形、正方形的知识应用(知识点讲解+练习题)
矩形菱形正方形基本知识教案【知识梳理】一、矩形:1、定义:有一个角是角的平行四边形叫做矩形。
2、性质:⑴矩形的四个角都是;⑵矩形的对角线。
3、判定:⑴用定义判定;⑵有三个角是________的是矩形;⑶对角线的平行四边形是矩形。
特征总结:1、矩形既是又是对称图形,对称轴有条;2、矩形被它的对角线分成四个全等的三角形和两个全等的三角形;3、矩形中常见题目是对角线相交成600或1200角时,利用直角三角形、等边三角形等知识解决问题。
二、菱形:1、定义:有一组邻边的平行四边形叫做菱形。
2、性质:⑴菱形的四条边都;⑵菱形的对角线且每条对角线。
3、判定:⑴用定义判定;⑵对角线互相垂直的是菱形;⑶四条边都相等的是菱形。
特征总结:1、菱形既是对称图形,也是对称图形,它有条对称轴,分别是;2、菱形被对角线分成四个全等的三角形和两对全等的三角形;3、菱形的面积可以用平行四边形面积公式计算,也可以用两条对角线的积来计算;4、菱形常见题目是内角为1200或600时,利用等边三角形或直角三角形知识计算的题目。
【重点考点例析】考点一、矩形的性质与判定【例1】如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN ∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE,AF.那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.分析:判定一个四边形是矩形,可以先判定四边形是平行四边形,再找一个内角是直角或说明对角线相等.考点二:和矩形有关的折量问题【例2】如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.(1)求证:BD=BE;(2)若∠DBC=30°,BO=4,求四边形ABED的面积.考点三:和菱形有关的对角线、周长、面积的计算问题【例3】如图,菱形ABCD的周长为20cm,且tan∠A BD=34,则菱形ABCD的面积为cm2.考点四:四边形综合性题目:【例5】如图,正方形ABCD与正三角形A EF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是.考点五:矩形、菱形、正方形的判定例1、如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.(1)求∠CAE的度数;(2)取AB边的中点F,连接CF、CE,试证明四边形AFCE是矩形.例2、如图,AB∥CD,∠B = 72°,∠D = 32°,求∠F的度数?变式1、如图,已知∠AEC=∠A+∠C,试说明:AB∥CD.变式2、如图,已知∠1=∠C,∠2=∠3, BE是否平分∠ABC?请说明理由。
矩形、菱形与正方形
矩形、菱形与正方形1.矩形考试内容考试要求矩形的定义有一个角是 的平行四边形叫做矩形.B矩形的性质(1)矩形具有平行四边形所有的性质.C (2)矩形的四个角都是 ,对角线互相平分并且 . (3)矩形既是一个轴对称图形,它有两条对称轴;又是中心对称图形,它的对称中心就是 . 矩形的判定(1)定义法.(2)有三个角是直角的四边形是矩形.(3) 的平行四边形是矩形.2.菱形考试内容考试要求菱形的定义有一组 的平行四边形叫做菱形.B 菱形的性质(1)菱形具有平行四边形所有的性质.C (2)菱形的四条边 ,对角线互相 ,并且每条对角线平分一组对角.(3)菱形既是一个轴对称图形,两条对角线所在的直线是它的对称轴;又是中心对称图形,它的对称中心就是 . (4)菱形的面积等于对角线乘积的 . 菱形的判定(1)定义法.(2)四条边 的四边形是菱形.(3)对角线 的平行四边形是菱形.3.正方形考试内容考试要求正方形的定义有一组邻边,并且有一个角是_______________的平行四边形叫做正方形.B正方形的性质(1)正方形的四条边,四个角都是,对角线互相且,并且每一条对角线平分一组对角,具有矩形和菱形的所有性质.C (2)正方形既是轴对称图形也是中心对称图形,对称轴有_____________条,对称中心是对角线的交点.正方形的判定(1)有一组邻边相等的____________________是正方形.(2)有一个角是直角的是正方形.(3)对角线的四边形是正方形.4.平行四边形、矩形、菱形、正方形的关系。
八年级数学矩形、菱形与正方形的性质
晚上下班回来吃饭的时候,我才和妻子孩子说起,那是一个怎样的梦啊,而当我说到孩子掉到井里时,又情不自禁地哽咽起来,泪水瞬间模糊了双眼,我都搞不清楚是在现实中,还是在梦中了。那 个真切的经历让我颤栗,是我心灵脆弱敏感还是浓于水的父子亲情的缘故?孩子似乎体会不到为人父母的这种感觉,照样还在津津有味地吃着饭。
终于在一个地方看到了孩子,他还在如同没事人一样,在一个篱笆门外往里面好奇张望。不知道这是一个什么地方,没有绿色看不到花草树木,只有沉沉的一种土黄色的死寂,有一种说不出的荒凉 的感觉,不高的土墙和半开着的篱笆门。我说找你半天了怎么就跑到这里了,我让他和我赶紧走不要对什么都好奇。这个时候从对过的一个篱笆门的院子里走出来一个五大三粗的莽莽撞撞的人来,肉乎 乎的秃脑袋晃悠要过来打孩子。我连忙说客气话给他道歉都不管用,孩子转过身子过去就推了那个人一把,然后就往大道上跑去。那人就骂骂咧咧地不知在哪里推了一辆电三轮车骑上就去追孩子。我惊 慌失措,也在后面跑步追去。后来不知孩子怎样从那个人手里抢过来三轮车自己骑上走了,那个人拼命地跑步去追。这是一条通往荒凉野外的道路,路两边没有一棵树木。天气是那么的灰暗低沉和压抑, 感觉好像刚下过一场小雪,路面上有薄薄的一层惨白,三轮车过去后留下很明显的车辙。老远处看到孩子骑着三轮车往左边一滑,车子进了光秃秃的庄稼地。然后什么也看不到了。我和那个人追了过来, 只见车子不见了人,道边有一口雨水井,下面好多的污水在晃悠着,好像刚刚掉下来过什么东西。看来孩子可能是掉到井里了,我惊慌失措地对着井口喊着孩子的名字,也不知道在哪里找到的一根棍子 我在水井里探着,开始听到一声孩子答应的声音,再喊,再喊就没有了声音。我对那个人咆哮,你追什么追,现在人不见了掉井里了怎么办!那个人也是吃惊的半天不说话。我失声痛哭,我的孩子没了, 我的孩子没了,这个井又下不去,是那种下面腹部大,上面的口小的那种井。我就是下去也无法上来,更没有办法救孩子。我必须得报警,可是,可恨的手机此时无论如何就是拨不出去号码,就是拨出 去在这个荒凉的野外,等到警察赶过来,孩子也早就也没有救了,怎么办啊,我发疯一样大哭起来,这是我唯一的孩子啊。他妈还不知道这里发生的一切,我回去怎么给她交代?真有叫天,天不灵,叫 地,地不应的感觉……
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学课题:§3.5.4矩形、菱形、正方形 教学时间(日期、课时): 教材分析: 学情分析: 教学目标: 1、会证明平行四边形的判定定理,结合具体命题了解反证法 2、能运用平行四边形的判定定理及反证法进行简单的计算与证明 3、能运用平行四边形的性质与判定定理进行比较简单的综合推理与证明 4、初步体会证明过程中的反证法的思想及其说理的过程 教学准备 《数学学与练》 集体备课意见和主要参考资料 页边批注
教学过程 (2)新课导入 回忆我们曾探索得到的一个四边形是平行四边形的条件,填写下表: 条 件 结 论 四边形ABCD,对角线AC、BD相交于点O 四边形ABCD是平行四边形 (3)新课讲授 问题一 你能证明我们曾探索得到的平行四边形的判定方法是正确的吗? 证明:一组对边平行且相等的四边形是平行四边形。 分析:先根据命题画出图形,再写出已知、求证,最后用研究平行四边形常见的辅助线“连结对角线”证三角形全等,得到两组内错角相等,由平行线证出平行四边形。 问题二 证明:对角线互相平分的四边形是平行四边形。 问题三 你认为“一组对边平行,另一组对边相等的四边形是平行四边形”这个结论正确吗?为什么? 问题四 你认为“在四边形ABCD中,如果OA=OC,OB≠OD,那么四边形ABCD不是平行四边形”这个结论正确吗?为什么? 分析:假设四边形ABCD是平行四边形,那么OA=OC,OB=OD,这与条件OB≠OD矛盾,所以四边形ABCD不是平行四边形。 假设条件成立,结论不成立,然后由这个“假设”出发推导出与条件矛盾的结果,从而证明结论一定成立,这种证明方法叫做反证法。 例1 已知:如图,在□ABCD中,对角线AC、BD 相交于点O,AE⊥BD,CF⊥BD,垂足分别为E、F。 求证:四边形AECF是平行四边形。 分析:由垂直可证一组对边平行,再利用全等证这组对边相等;或由平行四边形对角线互相平分知OA=OC,再证OE=OF即可;或由垂直证一组对边平行,再利用面积相等法证这组对边相等。
O
A
B
C
D
E
F
F
G
O
E
D
C
A
B
练习:P20页 拓展与延伸及练习1、2
例2、 (哈尔滨市)如图,已知E为平行四边形ABCD
中DC边的延长线上的一点,且CE=DC,连结AE,分
别交BC、
BD于点F、G,连结AC交BD于O,连结OF.
求证:AB=2OF.
证明: 连结BE
∵四边形ABCD为平行四边形
∴AB ∥CD,AO=OC,AB=CD
∵CE=CD,
∴AB=CE,
∴四边形ABEC为平行四边形,
∴BF=FC,
∴CEOF21即AB=2OF.
说明 能用平行四边形的知识解决的问题,不必用三角形的知识解决,这样
更简便
练习
1.如图,平行四边形ABCD中,EF为边AD、BC上的点,且AE=CF,连
结AF、EC、BE、DF交于M、N,试说明:MFNE是平行四边形
2.如图:已知在△ABC中,AB=AC,D为BC上任意一点,DE∥AC交AB
于E,DF∥AB交AC于F,求证:DE+DF=AC
3.平行四边形ABCD中,E、 G、F、H分别是四条边上的点,且AE=CF,
BG=DH.
求证:EF和GH互相平分.
4.已知:如图,在平行四边形ABCD中,连结BD
⑴ 求作:∠A的平分线AE交BC于E,交BD 于F;
(要求用尺规作图,保留作图痕迹,不写作法和证明)
⑵ 求证:①AB=BE; ②ABADBFDF
=
M
E D
N
F
1题
C
B
A
A
B
C
D
第2题 第4题
(4)巩固练习
1.已知AD∥BC,要使四边形ABCD为平行四边形,需要增加条件
(只需填一个你认为正确的条件即可).
2.已知:□ABCD的周长是30cm,对角线AC,BD相交于点O,⊿AOB的
周长比⊿BOC的周长为5cm ,则这个平行四边形的各边长为_____.
3.如图,在□ABCD中,EF∥BC,GH∥AB, EF、GH的交点P在BD上,
则图中有 对四边形面积相等;它们是
4.□ABCD中,过O点的直线EF分别交AD、CB于E、
F,AB=2.4㎝,BC=4㎝,OE=1.1㎝,则四边形CDEF的周长为
______________㎝.
5.□ABCD中,AC、BD的长满足方程0862xx,则CB的长的取值范
围为 .
(5)小结
1.从边与边的关系:
两组对边分别平行
一组对边平行且相等一组对边平行且相等 的四边形是平行四边形。
两组对边分别相等
2.从角与角的关系: 两组对角分别相等的四边形是平行四边形。
3.从对角线的相互关系: 对角线互相平分的四边形是平行四边形。
板书设计 作业设计 6、(2006·广东省)如图,在□ABCD中,∠DAB=60°,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB. (1)求证:四边形AFCE是平行四边形. (2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗?若成立,请写出证明过程; 若不成立,请说明理由. 教学反思 页边批注
