2020年中考数学压轴培优练习:一次函数图像类(附解析)
河南省2020年中考数学压轴题全揭秘专题10一次函数与反比例函数综合题含解析

专题06图形面积计算【例1】(2019·南阳模拟)如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,则整个阴影部分的面积为()A .9π﹣9 B.9π﹣6C.9π﹣18 D.9π﹣124x【答案】D.【解析】解:连接OD,由折叠的性质知:CD=CO,BD=BO,∠DBC=∠OBC,∴OB=OD=BD,即△OBD是等边三角形,∴∠DBO=60°,∴∠CBO =30°, ∴OC =12OB =2152, ∴S 阴影=S 扇形AOB ﹣S △BDC ﹣S △OBCS △BDC =S △OBC =12×OB ×OC =ky x=×6×2=612,S 扇形AOB =9π,∴S 阴影=S 扇形AOB ﹣S △BDC ﹣S △OBC=9π﹣612﹣612=9π﹣1212.所以答案为:D .【变式1-1】(2019·开封模拟)如图,把半径为2的⊙O 沿弦AB ,AC 折叠,使弧AB 和弧BC 都经过圆心O ,则阴影部分的面积为( )A .4y x=B .m xC .212OC CA =D .4【答案】C .【解析】解:过O 作OD ⊥AC 于D ,连接AO 、BO 、CO ,∴OD =2DP BP ⋅AO =1,AD =32-AC =12OC CA =,∴∠OAD =30°,∴∠AOC =2∠AOD =120°, 同理∠AOB =120°,∠BOC =120°, ∴S 阴=2S △AOC=2×36x×22=212OC CA , 所以答案为:C .【变式1-2】(2017·郑州一模)如图,半径为1的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M 与圆心O 重合,则图中阴影部分的面积是 .【答案】12. 【解析】解:设折痕为AB ,连接OM 交AB 于点C ,连接OA 、OB ,由题意知,OM ⊥AB ,且OC =MC =, 在RT △AOC 中,OA =1,OC =, ∴∠AOC =60°,AC =2k,AB =2AC =52,∴∠AOB =2∠AOC =120°,S 阴影=S 半圆﹣2S 弓形ABM=π×12﹣2(12)=12. 故答案为:154.【例2】(2019·郑州外外国语测试)如图所示,在Rt △ABC 中,∠ACB =90°,AC =BC ,将Rt △ABC 绕点A 逆时针旋转30°后得到Rt △ADE ,若图中阴影部分面积为kx,则AB =【答案】2.【解析】S 阴影=S △ADE +S 扇形BAD -S △ABC ∵S △ADE = S △ABC ∴S 阴影= S 扇形BAD =k x, ∴3x=k x, 解得:AB =2, 故答案为:2.【变式2-1】(2019·河南南阳一模)如图,在正方形ABCD 中,AB =3,点M 在CD 边上,且DM =1,△AEM 与△ADM 关于AM 所在直线对称,将△ADM 按顺时针方向绕点A 旋转90°得到△ABF ,连接EF ,则线段EF 的长为()A . 3B .3k C .12D . ()2133124k --+【分析】求线段的长度,常用方法是将所求线段放在直角三角形中借助勾股定理求解,如图作出辅助线,通过分析可知,△ADM ≌△ABF ≌△AEM ,可得DM =EM =1,AE =AD =AB =3,进而利用△AEK ∽△EMH ,求得EH ,MH 的长,再计算出EG ,FG 的长,在Rt △EFG 中,利用勾股定理求EF 的长度即可.【解析】过点E 作EG ⊥BC 于G ,作EH ⊥CD 于H ,延长HE 交AB 于K ,如图所示,由题意知,△ADM ≌△ABF ≌△AEM , ∴DM =EM =1,AE =AD =AB =3, 由△AEK ∽△EMH ,2k 34得:mx=3,∴设EH=x,则AK=3x,即DH=3x,MH=3x-1,在Rt△EMH中,由勾股定理得:mx,解得:x=0(舍)或x=,∴MH=,AK=DH=A D A C C DB E BC C E==,CH=3-DH=623C EB EC E+==,KE=BG=3MH=6x,∴FG=BF+BG=620k bk b+=⎧⎨-+=⎩,EG=CH=623C EB EC E+==,在Rt△EFG中,由勾股定理得:EF=24kb=⎧⎨=⎩,故答案为:C.【变式2-2】(2019·洛阳二模)如图,矩形ABCD中,AB=2,BC=1,将矩形ABCD绕点A旋转得到矩形AB′C′D′,点C的运动路径为弧CC′,当点B′落在CD上时,则图中阴影部分的面积为.【答案】32.【解析】解:连接AC’,AC,过点B’作B’E⊥AB于E,如图图所示,由旋转性质,得:AC=AC’,AB’=AB=2,∠CAB=∠C’AB’,∵BC=B’E=1,∴∠B’AB=30°,∴∠C’AC=30°,∴AE=,B’C=2-,在Rt△ABC中,由勾股定理得:AC=12-, ∴S阴影=S扇形C’AC-S△AB’C’-S△B’CA=k x.故答案为:8x -.【例3】(2019·河南南阳一模)如图,在△ABC中,AB=BC,∠ABC=90°,CA=4,D为AC的中点,以D 为圆心,以DB的长为半径作圆心角为90°的扇形EDF,则图中阴影部分的面积为.【分析】设DE与BC交于M,DF与AB交于N,S阴影=S扇形EDF-S四边形DMBN,根据△DBM≌△DAN,得S四边形DMBN=S△BDA,再利用扇形面积公式及三角形面积公式求解即可.【解析】解:设DE与BC交于M,DF与AB交于N,∵AB=BC,∠ABC=90°,D是AC中点,∴∠A=∠C=∠CBD=∠DBA=45°,AD=BD=2,∠BDA=90°,∵∠EDF=90°,∴∠BDM=∠ADF,∴△DBM≌△DAN,即S△DBM=S△DAN,∴S四边形DMBN=S△BDA,S阴影=S扇形EDF-S四边形DMBN=1 2=152=π-2,故答案为:π-2.【变式3-1】(2018·洛阳三模)如图,在扇形OAB中,C是OA的中点,CD⊥OA,CD与弧AB交于点D,以O为圆心,OC的长为半径作弧CE交OB于点E,若OA=6,∠AOB=120°,则图中阴影部分的面积为.【答案】12.【解析】解:连接OD,交弧CE于F,连接AD,∵OC=AC=3,CD⊥OA,∴CD是线段OA的垂直平分线,∴OD=AD,∵OD=OA,∴△OAD是等边三角形,∵∠AOB=120°,∴∠DOA=∠BOD=60°,∴CD=2x OC=332,∴S阴影=S扇形BOD-S扇形EOF+S△COD-S扇形COF=4 3=3π+13.即答案为:3π+.【变式3-2】(2018·河南第一次大联考)如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )A .3a 2 B .k xa 2C .23a 2D .a【答案】B .【解析】解:如图,过O 作OE ⊥AD 于E ,OF ⊥CD 于F ,∴OE =OF ,∠EOF =90°, ∴四边形OEDF 是正方形,OF =3k , ∵扇形的圆心角为直角, ∴△OME ≌△ONF , ∴S 阴影=S 正方形OEDF =2k, 故答案为:B .1.(2018·河南师大附中模拟)如图,菱形ABCD 和菱形ECGF 的边长分别为2和3,∠A =120°,则图中阴影部分(△BDF )的面积等于.【答案】23.【解析】解:由题意得:S △BDF =S 菱形ABCD +S 菱形ECGF -S △BGF -S △EDF -S △ABD菱形ECGF 边CG 边上的高为:GF ·sin 60°=13232k k ⎛⎫=⨯⨯- ⎪⎝⎭,菱形ECGF边CE边上的高为:EF·sin60°=13 232k k⎛⎫=⨯⨯- ⎪⎝⎭,∴S△BDF=kx=2x,故答案为:.2.(2019·济源一模)汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝,如图所示的弦图中,中间的小正方形ABCD的边长为 1,分别以A,C为圆心,1为半径作圆弧,则图中阴影部分的面积为【答案】2.【解析】解:连接BD,S阴影=2(S扇形BAD-S△ABD)=2(2)=2,故答案为:2.3.(2019·偃师一模)如图,正方形ABCD中,AB=1,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接EF,则图中阴影部分的面积是2m yx=.【解析】解:过F作FM⊥BE于M,则∠FME=∠FMB=90°,∵四边形ABCD是正方形,AB=1,∴∠DCB=90°,DC=BC=AB=1,∠DCB=45°,由勾股定理得:BD=12,由旋转性质得:∠DCE=90°,BF=BD=12,∠FBE=90°-45°=45°,∴BM=FM=1,即C点与M点重合,ME=1,∴阴影部分的面积:S=S△BCD+S△BFE+S扇形DCE-S扇形DBF=12+1+kx-3=2-m yx =,故答案为:2-m yx =.4.(2019·洛阳三模)如图,已知矩形ABCD的两条边AB=1,AD=,以B为旋转中心,将对角线BD 顺时针旋转60°得到线段BE,再以C为圆心将线段CD顺时针旋转90°得到线段CF,连接EF,则图中阴影部分面积为.【答案】33.【解析】解:连接CE,由CD=AB=1,AD3,得:BD=2,∴∠ADB=30°,∴∠DBC=30°,由旋转知∠DBE=60°,BE=BD=2,∴∠DBC=∠EBC=30°,此时D、C、E共线,∴S阴影=S扇形DCF+S△BCD+S△BEF-S扇形DBE=1 2=kx.故答案为:.5.(2019·周口二模)如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕点O逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为()A.12x B.C.12D.kx【答案】B.【解析】解:过O作OF⊥A’B’于F,由旋转性质得:OA=OA’=3,OB=OB’=6,∴F为A’E的中点,∵E为OB中点,∴OE=BE=3,在Rt△A’OB’中,由勾股定理得:A’B’=m x,∴OF=,在Rt△A’OF中,由勾股定理得:A’F=2x ,∴A’E=1 2∴B’E=A’B’-A’E=52,故答案为:B.6.(2019·周口二模)如图,等腰直角三角形ABC,绕点C顺时针旋转得到△A′B′C,AB′所在的直线经过A′C的中点时,若AB=2,则阴影部分的面积为_________.【答案】kx.【解析】解:延长AB’交A’C于E,由题意知E为A’C的中点,∵A’B’=B’C=AB=BC=2,∴B’E⊥A’C,在Rt△ABC中,由勾股定理得:AC=2k x,∴CE=A’E,∴∠CAE=30°,∠ACE=60°,∴S阴影=S扇形ACA’-S△ACE-S△A’B’E=k x=12x.故答案为:.7.(2017·新野一模)如图,在扇形OAB中,∠O=60°,OA=413,四边形OECF是扇形OAB中最大的菱形,其中点E,C,F分别在OA,弧AB,OB上,则图中阴影部分的面积为.【答案】8π﹣8kax bx+≥.【解析】解:连接EF、OC交于点H,则OH=12OC=2kax bx+≥,∠FOH=∠AOC=30°,在Rt△FOH中,FH=OH×tan30°=2,∴菱形FOEC的面积=12×4kax bx+≥×4=8kax bx+≥,扇形OAB的面积=6yx=-=8π,则阴影部分的面积为8π﹣8kax bx+≥,故答案为:8π﹣8kax bx+≥.8.(2019·开封二模)如图,在圆心角为120°的扇形OAB中,半径OA=2,C为弧AB的中点,D为OA 上任意一点(不与点O、A重合),则图中阴影部分的面积为.【答案】kxπ.【解析】解:连接OC,BC,由题意知∠BOC=∠AOC=60°,∵OB=OC,∴△BOC为等边三角形,∴∠OCB=∠COA=60°,∴BC∥OA,∴S△BOC=S△BCD,∴S阴影=S弓形BC+S△BCD=S弓形BC+S△BOC=S扇形BOC=kxπ,故答案为:kxπ.9.(2019·安阳一模)如图,在正方形ABCD中,AD=3,将线段AB绕点B逆时针旋转90°得到线段BE,将线段AC绕点C逆时针旋转90°得到线段CF,连接EF,则图中阴影部分的面积是___________.【答案】kx.【解析】解:由图知:S阴影=S扇形ABE+S△BEF-S弓形AFS弓形AF=S扇形ACF-S△ACF由题意知,AD=3,AC=CF=33x,AB=BC=BF=BE=3,∠EBA=∠ACF=90°,∴S弓形AF=S扇形ACF-S△ACF=31xy=⎧⎨=⎩-13xy=-⎧⎨=-⎩=-9,S阴影=S扇形ABE+S△BEF-S弓形AF=mx+-(-9)=mx.10.(2019·省实验一模)如图,将半径为1的半圆O,绕着其直径的一端点A顺时针旋转30°,直径的另一端点B的对应点为B',O的对应点为O',则图中阴影部分的面积是.【答案】11 5451 22⨯⨯-⨯⨯.【解析】解:连接O′D、B′D,∵∠B′AB=30°,∴∠AO′D=120°,∵AB′是直径,∴∠ADB′=90°,由∠B ′AB =30°,得B ′D =2kxAB ′=1,在Rt △ADB ’中,由勾股定理得,AD =2k x,∴S 阴影=S 扇形BAB ’-S △AO ’D -S 扇形DO ’B ’+S 扇形AO ’D -S △AO ’D=2k x=2π故答案为:12. 11.(2019·叶县一模)如图,在平行四边形ABCD 中,以点A 为圆心,AB 的长为半径的圆恰好与CD 相切于点C ,交AD 于点E ,延长BA 与⊙A 相交于点F .若弧EF 的长为6x,则图中阴影部分的面积为 .【答案】kx. 【解析】解:连接AC ,∵DC 是⊙A 的切线, ∴AC ⊥CD , ∵AB =AC =CD ,∴△ACD 是等腰直角三角形, ∴∠CAD =45°,∵四边形ABCD 是平行四边形, ∴AD ∥BC ,∴∠CAD =∠ACB =45°,∴∠ACB=∠B=45°,∴∠FAD=∠B=45°,∵弧EF的长为6x,∴2x,解得:r=2,∴S阴影=S△ACD﹣S扇形ACE=kx.故答案为:kx.12.(2019·濮阳二模)如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作弧CE交AB于点E,以点B为圆心,BC的长为半径作弧CD交AB于点D,则阴影部分的面积为.【答案】π﹣2.【解析】解:S阴影=S△ABC﹣S空白,∵∠ACB=90°,AC=BC=2,∴S△ABC=12×2×2=2,S扇形BCD=51=12π,S空白=2×(2﹣12π)=4﹣π,S阴影=S△ABC﹣S空白=2﹣4+π=π﹣2,故答案为:π﹣2.13.(2019·南阳模拟)如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为.【答案】4﹣π.【解析】解:连接AD∵⊙A与BC相切于点D,∴AD⊥BC,∵∠EPF=45°,∴∠BAC=2∠EPF=90°.∴S阴影=S△ABC﹣S扇形AEF=×4×2﹣=4﹣π.故答案是:4﹣π.14.(2019·商丘二模)如图,在扇形OAB中,∠AOB=90°,点C为OB的中点,CD⊥OB交弧AB于点D.若OA=2,则阴影部分的面积为.【答案】323.【解析】解:连接DO,则OD=OA=OB=2,∵CD∥OA,∠AOB=90°,∴∠OCD=90°,∵C为OB的中点,∴CO=kyx=OB=kyx=DO,∴∠CDO=30°,∠COD=60°,则CD=,∴S阴影=S扇形BOD-S△OCD=6 yx==32,故答案为:32.15.(2019·开封二模)如图,在▱ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙O相交于点F.若弧EF的长为π,则图中阴影部分的面积为.【答案】8﹣2π.【解析】解:连结AC,∵CD是圆A的切线,∴AC⊥CD,即∠ACD=90°,∵四边形ABCD为平行四边形,∴AB∥CD,AD∥BC,∴∠CAF=90°,∠FAE=∠B,∠EAC=∠ACB,∵AB=AC,∴∠B=∠ACB,∴∠FAE=∠EAC=45°,∵弧EF的长为π,设圆A的半径为r,,得:r=4,∴S阴影=S△ACD﹣S扇形CAE=12×4×4﹣12=8﹣2π.故答案为:8﹣2π.16.(2019·安阳二模)如图,点C为弧AB的三等分点(弧BC<弧AC),∠AOB=90°,OA=3,CD⊥OB,则图中阴影部分的面积为.【答案】kx.【解析】解:连接OC,AC,由题意知:∠COD=30°,∠AOC=60°,∵CD⊥OB,∴S△OCD=S△ACD,∵∠CDO=90°,OC=OA=3,∠COD=30°,∴CD=8x,OD=,S阴影=S△ACD+S弓形AC =S△OCD+S弓形AC=kx××8x+-6x×32=kx.故答案为:kx.17.(2019·平顶山三模)如图,长方形纸片ABCD的长AB=3,宽BC=2,以点A为圆心,以AB的长为半径作弧;以点C为圆心,以BC的长为半径作弧.则图中阴影部分的面积是.【答案】kx-6.【解析】解:由图可知:S阴影=+2-S矩形ABCD = +-6=x-6,故答案为:kx-6.18.(2019·名校模考)如图,在△ABC中,∠ABC=45°,∠ACB=30°,AB=2,将△ABC绕点C顺时针旋转60°得△CDE,则图中线段AB扫过的阴影部分的面积为.【答案】.【解析】解:过A作AF⊥BC于F,∵∠ABC=45°,∴AF=BF=AB=,在Rt△AFC中,∠ACB=30°,AC=2AF=2,FC=,由旋转的性质可知,S△ABC=S△EDC,S阴影=S扇形DCB+S△EDC﹣S△ABC﹣S扇形ACE=S扇形DCB﹣S扇形ACE==,故答案为:.19.(2019·枫杨外国语三模)如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D,连接A′B,则图中阴影部分的面积为 .【答案】.【解析】解:连接BD,B’D,由题意知:∠BDB’=90°,A’C=A’D-CD=1,由勾股定理得:BD=B’D=5,∴S阴影=S扇形DBB’-S△BCD-S△A’B’D-S△A’BC==.故答案为:.20.(2019·中原名校大联考)如图,在菱形ABCD中,AB=2,∠BAC=30°,将菱形ABCD绕点A逆时针旋转120°,点B的对应点为点B′,点C的对应点为点C′,点D的对应点为点D′,则图中阴影部分的面积为.【答案】.【解析】解:连接BD,与AC相交于点O,则BD=2BO=2,AC=AD=2,S扇形=S扇形CAC′+S△ABC+S△AC′D′﹣S菱形ABCD﹣S扇形DAD′=S扇形CAC′﹣S扇形DAD′==.故答案为:.21.(2019·三门峡一模)如图,在平行四边形ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD 的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是__________.【答案】3-.【解析】解:∵∠A=30°,AD=2,∴平行四边形AB边上的高为:AD·sin30°=,∵AB=4,∴BE=2,S阴影=S平行四边形ABCD-S扇形AED-S△BEC=4--=3-故答案为:3-.22.(2019·周口二模)如图,PA、PB是半径为1的⊙O的两条切线,点A、B分别为切点,∠APB=60°,OP与弦AB交于点C,与⊙O交于点D.阴影部分的面积是(结果保留π).【答案】.【解析】解:∵PA、PB是⊙O的切线,∴OA⊥PA,OB⊥PB,OP平分∠APB,∵∠APB=60°,∴∠APO=30°,∠POA=60°,由AP=BP,OA=OB得:OP垂直平分AB,∴AC=BC,∴S△AOC=S△BOC,∴S阴影部分=S扇形OAD.故答案为:.。
2020年中考数学专题复习训练第三章:变量和函数_3.2:一次函数(解析)
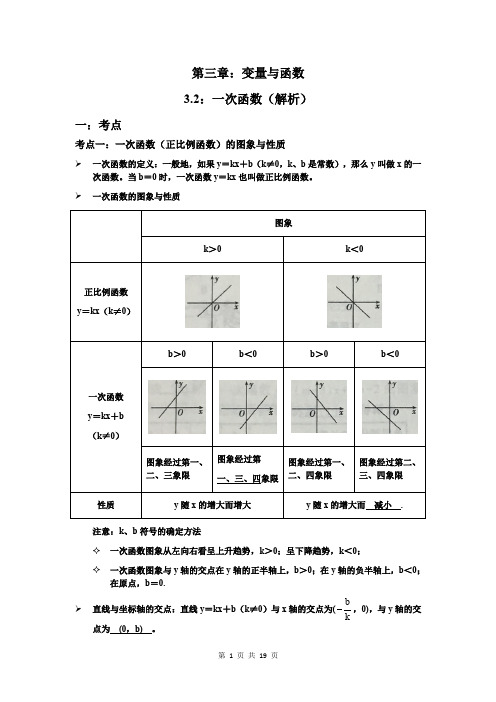
第三章:变量与函数 3.2:一次函数(解析)一:考点考点一:一次函数(正比例函数)的图象与性质一次函数的定义:一般地,如果y =kx +b (k ≠0,k 、b 是常数),那么y 叫做x 的一次函数。
当b =0时,一次函数y =kx 也叫做正比例函数。
一次函数的图象与性质注意:k 、b 符号的确定方法✧ 一次函数图象从左向右看呈上升趋势,k >0;呈下降趋势,k <0;✧ 一次函数图象与y 轴的交点在y 轴的正半轴上,b >0;在y 轴的负半轴上,b <0;在原点,b =0. 直线与坐标轴的交点:直线y =kx +b (k ≠0)与x 轴的交点为(kb,0),与y 轴的交点为 (0,b) 。
用待定系数法求函数解析式:步骤可归纳为“一设二列三解四还原”。
✧ 一设:设出一次函数解析式的一般式y =kx +b (k ≠0);✧ 二列:根据已知两点的坐标或已知的两个条件列出关于k 、b 的二元一次方程组; ✧ 三解:解这个方程组,求出k 、b 的值;✧ 四还原:将求得的k 、b 的值再代入y =kx +b (k ≠0)中,求得一次函数解析式。
一次函数图象的平移:✧ 一次函数y =kx +b 的图象可以看作是直线y =kx 向上(下)平移b 个单位长度得到的。
当b >0时,将直线y =kx 向上平移b 个单位长度;当b <0时,将直线y =kx 向下平移b 个单位长度。
✧ 当21k k =,21b b ≠时,直线11b x k y +=与直线22b x k y +=平行。
1. 在平面直角坐标系中,一次函数b kx y +=的图象如图所示,则k 和b 的取值范围是( C )A. k >0,b >0B. k >0,b <0C. k <0,b >0D. k <0,b <02. 一次函数y =kx -1的图象经过点P ,且y 的值随x 值的增大而增大,则点P 的坐标可以为( C )A. (﹣5,3)B. (1,﹣3)C. (2,2)D. (5,﹣1)3. 如图,在矩形AOBC 中,A(﹣2,0)、B(0,1)。
备考2020中考数学一轮专题复习学案:专题13一次函数的图象与性质(含答案)

备考2020中考数学一轮专题复习学案专题13 一次函数的图像与性质考试说明:1.结合具体情境体会和理解正比例函数和一次函数的意义,能根据已知条件确定它们的表达式.2.会画一次函数的图象,能结合图象讨论这些函数的增减变化.3.理解正比例函数概念、图象、性质.4.通过讨论一次函数与二元一次方程组的关系,从运动变化的角度,用函数的观点加深对已经学习过的方程等内容的认识,构建和发展相互联系的知识体系.思维导图:知识点一:一次函数的概念知识梳理:【命题点一】一次函数的定义【典例1】函数y=(2m–1)x3m–2+3是一次函数,则m的值为_________.【答案】1【解析】∵函数y=(2m–1)x3m–2+3是一次函数,∴3m–2=1,2m–1≠0.∴m=1.故答案为1.【变式训练】1.(2019•梧州)下列函数中,正比例函数是()A.y=﹣8x B.y=8xC.y=8x2D.y=8x﹣42.要使函数y=(m–2)x n–1+n是一次函数,应满足()A.m≠2,n≠2 B.m=2,n=2 C.m≠2,n=2 D.m=2,n=0知识点二:一次函数的图像知识梳理:正比例函数y=kx(常数k≠0)的图象一条经过原点与点(1,k)的直线.一次函数y=kx+b(k,b 是常数,k≠0)的图象一条与y轴交于点(0,b),与x轴交于点(–bk,0)的直线.其中b叫做直线在y 轴上的截距,截距不是距离,是直线与y 轴交点的纵坐标,截距可正,可负,也可为0.【技巧】画一次函数的图象,只需过图象上两点作直线即可,一般取(0,b),(–bk,0)两点.一次函数图象的平移直线y=kx+b(k≠0,b≠0)可由直线y=kx(k≠0)向上或向下平移得到.当b>0时,将直线y=kx向上平移b个单位长度,得到直线y=kx+b;当b<0时,将直线y=kx向上平移|b|个单位长度,得到直线y=kx+b.【命题点二】一次函数的图象【典例2】函数y=2x–2的图象大致是()A.B.C.D.【答案】C【解析】∵函数y=2x–2,∴函数y=2x–2经过点(1,0),(0,–2).故选C.【变式训练】1.(2019•包头)正比例函数y=kx的图象如图所示,则k的值为()A.–43B.43C.–34D.342.若b<0,则一次函数y=–x+b的图象大致是()A.B.C.D.【命题点三】一次函数图象上点的坐标【典例3】【2019•锦州】如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为()A.14B.12C.2 D.4【答案】A【解析】∵在一次函数y=2x+1中,当x=0时,y=1,当y=0时,x=0.5,∴OA=0.5,OB=1.∴△AOB的面积=0.5×1÷2=14.故选A.【点拨】由一次函数的解析式分别求出点A和点B的坐标,即可作答.【考试方向】主要考查一次函数与坐标轴交点坐标以及三角形的面积公式.【变式训练】3.(2019•陕西)若正比例函数y=﹣2x的图象经过点O(a﹣1,4),则a的值为()A.﹣1 B.0 C.1 D.24.(2019•天津)直线y=2x﹣1与x轴的交点坐标为_________.【命题点四】直线的平移【典例4】【2019•梧州】直线y=3x+1向下平移2个单位,所得直线的解析式是()A.y=3x+3 B.y=3x﹣2 C.y=3x+2 D.y=3x﹣1【答案】D【解析】直线y=3x+1向下平移2个单位,所得直线的解析式是:y=3x+1﹣2=3x﹣1.故选D.【点拨】直接利用一次函数平移规律进而得出答案.【考试方向】主要考查一次函数图象与几何变换,正确记忆平移规律是解题关键.【变式训练】5.(2019•陕西)在平面直角坐标系中,将函数y=3x的图象向上平移6个单位长度,则平移后的图象与x 轴的交点坐标为()A.(2,0)B.(﹣2,0)C.(6,0)D.(﹣6,0)6.(2019•邵阳)一次函数y1=k1x+b1的图象l1如图所示,将直线l1向下平移若干个单位后得直线l2,l2的函数表达式为y2=k2x+b2.下列说法中错误的是()A.k1=k2B.b1<b2C.b1>b2D.当x=5时,y1>y2知识点三:一次函数图像的性质知识梳理:函数k,b的值大致图象经过的象限函数的性质【命题点五】正比例函数图象的性质【典例5】【2019•大庆】正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是()A.B.C.D.【答案】A【解析】∵正比例函数y=kx(k≠0)的函数值y随x的增大而减小,∴k<0,∵一次函数y=x+k的一次项系数大于0,常数项小于0,∴一次函数y=x+k的图象经过第一、三、四象限,且与y轴的负半轴相交.故选A.【点拨】根据自正比例函数的性质得到k<0,然后根据一次函数的性质得到一次函数y=x+k的图象经过第一、三象限,且与y轴的负半轴相交.【考试方向】主要考查一次函数的图象:一次函数y=kx+b(k、b为常数,k≠0)是一条直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;图象与y轴的交点坐标为(0,b).【变式训练】1.设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m=()A.2 B.–2 C.4 D.–42.(2019•本溪)函数y=5x的图象经过的象限是_________.【命题点六】一次函数图象的性质【典例6】【2019•潍坊】当直线y=(2﹣2k)x+k﹣3经过第二、三、四象限时,则k的取值范围是_________.【答案】1<k<3【解析】y=(2﹣2k)x+k﹣3经过第二、三、四象限,∴2﹣2k<0,k﹣3<0.∴k>1,k<3.∴1<k<3.故答案为1<k<3.【点拨】根据一次函数y=kx+b,k<0,b<0时图象经过第二、三、四象限,可得2﹣2k<0,k﹣3<0,即可求解.【考试方向】本题考查一次函数图象与系数的关系;掌握一次函数y=kx+b,k与b对函数图象的影响是解题的关键.【变式训练】3.(2019•广安)一次函数y =2x ﹣3的图象经过的象限是( )A .一、二、三B .二、三、四C .一、三、四D .一、二、四4.(2019•成都)已知一次函数y =(k ﹣3)x +1的图象经过第一、二、四象限,则k 的取值范围是_________. 知识点四: 一次函数与方程、不等式知识梳理:【命题点七】一次函数与二元一次方程组【典例7】【2019•贵阳】在平面直角坐标系内,一次函数y =k 1x +b 1与y =k 2x +b 2的图象如图所示,则关于x ,y 的方程组{y −k 1x =b 1,y −k 2x =b 2的解是_________.【答案】{x =2,y =1【解析】∵一次函数y =k 1x +b 1与y =k 2x +b 2的图象的交点坐标为(2,1),∴关于x ,y 的方程组{y −k 1x =b 1,y −k 2x =b 2的解是{x =2,y =1.故答案为{x =2,y =1. 【变式训练】1.已知直线l 1:y =–3x +b 与直线l 2:y =–kx +m 在同一坐标系中的图象交于点(1,–2),那么方程组{3x +y =b ,kx +y =m的解是( ) A .{x =1,y =−2B .{x =1,y =2C .{x =−1,y =−2D .{x =−1,y =22.若以二元一次方程x +2y –b =0的解为坐标的点(x ,y )都在直线y =–12x +b –1上,则常数b =( ) A .12 B .2 C .–1 D .1【命题点八】一次函数与一元一次不等式【典例8】【2019•遵义】如图所示,直线l 1:y =32x +6与直线l 2:y =–52x +–2交于点P (–2,3),不等式32x +6>–52x +–2的解集是( )A .x >–2B .x ≥–2C .x <–2D .x ≤–2【答案】A【解析】由图象可知,当x >–2时, 32x +6>–52x +–2.∴不等式32x +6>–52x +–2的解集是x >–2.故选A . 【变式训练】3.(2019•黔东南州)如图所示,一次函数y =ax +b (a 、b 为常数,且a >0)的图象经过点A (4,1),则不等式ax +b <1的解集为_________.4.(2019•烟台)如图,直线y =x +2与直线y =ax +c 相交于点P (m ,3),则关于x 的不等式x +2≤ax +c的解为_________.参考答案知识点11.【答案】A【解析】A 、y =﹣8x ,是正比例函数,符合题意;B 、y =8x ,是反比例函数,不合题意;C 、y =8x 2,是二次函数,不合题意;D 、y =8x ﹣4,是一次函数,不合题意.故选A .2.【答案】C【解析】∵函数y =(m –2)x n –1+n 是一次函数,∴m –2≠0,n –1=1.∴m ≠2,n =2.故选C . 知识点21.【答案】B【解析】由图知,点(3,4)在函数y =kx 上,∴3k =4,解得k =43.故选B .2.【答案】C【解析】∵一次函数y =–x +b 中,k =–1<0,b <0,∴一次函数的图象经过二、三、四象限.故选C .3.【答案】A【解析】∵正比例函数y =﹣2x 的图象经过点O (a ﹣1,4),∴4=﹣2(a ﹣1),解得:a =﹣1.故选A .4.【答案】(12,0)【解析】根据题意知,当直线y =2x ﹣1与x 轴相交时,y =0.∴2x ﹣1=0,解得x =12. ∴直线y =2x +1与x 轴的交点坐标是(12,0).故答案为(12,0). 5.【答案】B【解析】由“上加下减”的原则可知,将函数y =3x 的图象向上平移6个单位长度所得函数的解析式为y =3x +6.∵此时与x 轴相交,则y =0,∴3x +6=0,即x =﹣2,∴点坐标为(﹣2,0),故选B .6.【答案】B【解析】∵将直线l 1向下平移若干个单位后得直线l 2,∴直线l 1∥直线l 2,∴k 1=k 2,∵直线l 1向下平移若干个单位后得直线l 2,∴b 1>b 2,∴当x =5时,y 1>y 2,故选B .知识点31.【答案】B【解析】把x =m ,y=4代入y =mx 中,可得m =±2.∵y 的值随x 值的增大而减小,∴m =–2.故选B .2.【答案】一、三【解析】函数y =5x 的图象经过第一、三象限.故答案为:一、三.3.【答案】C【解析】∵一次函数y=2x﹣3,∴该函数经过第一、三、四象限.故选C.4.【答案】k<3【解析】y=(k﹣3)x+1的图象经过第一、二、四象限,∴k﹣3<0,∴k<3.故答案为k<3.知识点41.【答案】A【解析】∵直线l1:y=–3x+b与直线l2:y=–kx+m在同一坐标系中的图象交于点(1,–2),∴方程组{3x+y=b,kx+y=m的解是{x=1,y=−2.故选A.2.【答案】B【解析】∵以二元一次方程x+2y–b=0的解为坐标的点(x,y)都在直线y=–12x+b–1上,直线解析式乘以2得2y=–x+2b–2,变形为2y+x–2b+2=0,∴–b=–2b+2,解得b=2.故选B.3.【答案】x<4【解析】∵一次函数y=ax+b(a、b为常数,且a>0)的图象如图所示,经过点A(4,1),且函数值y 随x的增大而增大,∴不等式ax+b<1的解集为x<4.故答案为x<4.4.【答案】x≤1【解析】点P(m,3)代入y=x+2,得m=1,∴P(1,3).结合图象可知x+2≤ax+c的解为x≤1.故答案为x≤1.。
2020年中考数学压轴题专练十 一次函数与反比例函数综合练(含答案解析)
专题10一次函数与反比例函数综合题【例1】(2019·偃师一模)如图,直线l:y=ax+b交x轴于点A(3,0),交y轴于点B(0,-3),交反比例函数y=kx于第一象限的点P,点P的横坐标为4.(1)求反比例函数y=kx的解析式;(2)过点P作直线l的垂线l1,交反比例函数y=kx的图象于点C,求△OPC的面积.【变式1-1】(2018·河南第一次大联考)如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=–12x+3交AB,BC于点M,N,反比例函数kyx=的图象经过点M,N.(1)求反比例函数的解析式;(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.【例2】(2019·济源一模)已知:如图,一次函数 y =kx +3 的图象与反比例函数y =mx(x >0)的图象交于点P ,P A ⊥x 轴于点A ,PB ⊥y 轴于点B ,一次函数的图象分别交x 轴、y 轴于点C ,D ,且S △DBP =27,12OC CA =. (1)求点 D 的坐标;(2)求一次函数与反比例函数的解析式;(3)根据图象写出x 取何值时,一次函数 y =kx +3 的值小于反比例函数y =mx的值.【变式2-1】(2019·洛阳三模)如图,在平面直角坐标系中,菱形 ABDC 的顶点 D ,C 在反比例函数y =k x 上(k >0,x >0),横坐标分别为12和2,对角线 BC ∥x 轴,菱形ABDC 的面积为 9. (1)求 k 的值及直线 CD 的解析式; (2)连接 OD ,OC ,求△OCD 的面积.【例3】(2019·西华县一模)如图,在矩形OABC中,OA=3,OC=2,点F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=kx的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;(2)当k为何值时,△EF A的面积最大,最大面积是多少?【变式3-1】(2019·中原名校大联考)如图,一次函数y=kx+b的图象与反比例函数y=mx的图象交于A,B两点,与x轴交于点C(﹣2,0),点A的纵坐标为6,AC=3CB.(1)求反比例函数的解析式;(2)请直接写出不等式组mx<kx+b<4的解集;(3)点P(x,y)是直线y=k+b上的一个动点,且满足(2)中的不等式组,过点P作PQ⊥y轴交y 轴于点Q,若△BPQ的面积记为S,求S的最大值.1.(2019·郑州外国语测试)如图所示,在平面直角坐标系中,直线l1:y=12-x与反比例函数y=kx的图象交于A、B两点,点A在点B左侧,已知A点的纵坐标为2.(1)求反比例函数的解析式;(2)根据图象直接写出12-x>kx的解集;(3)将直线y=12-x沿y轴向上平移后的直线l2与反比例函数y=kx在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.2.(2018·河师大附中模拟)如图,已知函数y=kx(x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥y轴,AC=1(点C在A点的下方),过点C作CD∥x轴,与函数y=kx(x>0)的图象交于点D,过点B作BE⊥CD于E,E在线段CD上,连接OC、OD.(1)求△OCD的面积;(2)当BE=12AC时,求CE的长.3.(2018·洛阳三模)如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(不与A、B重合),过点F的反比例函数y=kx(k>0)的图象与BC边交于点E.(1)当F为AB边的中点时,求该函数的解析式;(2)当k为何值时,△EF A的面积为23?4.(2019·洛阳二模)如图,A,B分别在反比例函数y=kx(x<0)和y=2x(x>0)的图象上,AB∥x轴,交y轴于点C.若△AOC的面积是△BOC面积的2倍.(1)求k的值;(2)当∠AOB=90°时,直接写出点A,B的坐标.5.(2019·周口二模)如图,点A (-2,a ),C (3a -10,1)是反比例函数my x(x <0)图象上的两点. (1)求m 的值;(2)过点A 作AP ⊥x 轴于点P ,若直线y =kx +b 经过点A ,且与x 轴交于点B ,当∠P AC =∠P AB 时,求直线AB 的解析式.6.如图,已知双曲线y =kx经过点B (33,1),点A 是双曲线第三象限上的动点,过B 作BC ⊥y 轴,垂足为C ,连接AC .(1)求k 的值;(2)若△ABC 的面积为63,求直线AB 的解析式;(3)在(2)的条件下,写出反比例函数值大于一次函数值时x 的取值范围.7.(2018·焦作一模)如图,一次函数y =﹣12x +b 与反比例函数y =kx(x >0)的图象交于点A (2,6)和B (m ,1)yxOAPC(1)填空:一次函数的解析式为,反比例函数的解析式为;(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.8.(2018·信阳一模)如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=﹣12x+3交AB,BC分别于点M,N,反比例函数y=kx的图象经过点M,N.(1)求反比例函数的解析式;(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.9.(2019·南阳毕业测试)如图,直线y=kx+b与反比例函数y=mx的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C,D.(1)求此一次函数和反比例函数的解析式;(2)求△AOB的面积.10.(2019·开封二模)如图,A(4,3)是反比例函数y=kx在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=kx的图象于点P.(1)求反比例函数y =kx的表达式;(2)求点B 的坐标; (3)求△OAP 的面积.11.(2019·安阳一模)如图,在平面直角坐标系中,反比例函数ky x=(k ≠0)与一次函数y =ax +b (a ≠0)交于第二、四象限的A ,B 两点,过点A 作AD ⊥y 轴于点D ,OD =3,S △AOD =3,点B 的坐标为(n ,-1).(1)求反比例函数和一次函数的解析式; (2)请根据图象直接写出kax b x+≥的自变量x 的取值范围.12.(2019·三门峡二模)如图,在平面直角坐标系xOy 中,直线y =x ﹣2与双曲线y =kx(k ≠0)相交于A ,B 两点,且点A 的横坐标是3.(1)求k 的值;(2)过点P (0,n )作直线,使直线与x 轴平行,直线与直线y =x ﹣2交于点M ,与双曲线y =kx(k≠0)交于点N ,若点M 在N 右边,求n 的取值范围.A BDO xy13.(2019·濮阳二模)如图,已知反比例函数y =mx(m ≠0)的图象经过点(1,4),一次函数y =﹣x +b 的图象经过反比例函数图象上的点Q (﹣4,n ).(1)求反比例函数与一次函数的表达式;(2)一次函数的图象分别与x 轴、y 轴交于A 、B 两点,与反比例函数图象的另一个交点为P 点,连结OP 、OQ ,求△OPQ 的面积.14.(2019·商丘二模)如图,一次函数y =k 1x +b 与反比例函数y =2k x的图象交于A (2,m ),B (n ,﹣2)两点.过点B 作BC ⊥x 轴,垂足为C ,且S △ABC =5.(1)求一次函数与反比例函数的解析式. (2)根据所给条件,请直接写出不等式k 1x +b >2k x的解集; (3)若P (p ,y 1),Q (﹣2,y 2)是函数y =2k x图象上的两点,且y 1≥y 2,求实数p 的取值范围.。
2020年(河南)中考数学压轴题全揭秘精品专题10 一次函数与反比例函数综合题(含答案解析)
专题10一次函数与反比例函数综合题【例1】(2019·偃师一模)如图,直线l:y=ax+b交x轴于点A(3,0),交y轴于点B(0,-3),交反比例函数y=k x于第一象限的点P,点P的横坐标为4.(1)求反比例函数y=kx的解析式;(2)过点P作直线l的垂线l1,交反比例函数y=kx的图象于点C,求△OPC的面积.【答案】见解析.【解析】解:(1)△y=ax+b交x轴于点A(3,0),交y轴于点B(0,-3),△3a+b=0,b=-3,解得:a=1,即l1的解析式为:y=x-3,当x=4时,y=1,即P(4,1),将P点坐标代入y=kx得:k=4,即反比函数的解析式为:y=4x;(2)设直线l1与x轴、y轴分别交于点E,D,△OA=OB=3,△△OAB=△OBA=45°,△l△l1,△△DPB=90°,△△ODP=45°,设直线l1的解析式为:y=-x+b,将点P(4,1)代入得:b=5,联立:y=-x+5,y=4x,解得:x=1,y=4或x=4,y=1,即C(1,4),△S△OPC=S△ODE-S△OCD-S△OPE=12×5×5-12×5×1-12×5×1=15 2.【变式1-1】(2018·河南第一次大联考)如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=–12x+3交AB,BC于点M,N,反比例函数kyx=的图象经过点M,N.(1)求反比例函数的解析式;(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.【答案】见解析.【解析】解:(1)△B(4,2),四边形OABC为矩形,△OA=BC=2,在y=–12x+3中,y=2时,x=2,即M(2,2),将M(2,2)代入kyx=得:k=4,△反比例函数的解析式为:4 yx =.(2)在4yx=中,当x=4时,y=1,即CN=1,△S四边形BMON=S矩形OABC-S△AOM-S△CON=4×2-12×2×2-12×4×1=4,△S△OPM=4,即12·OP·OA=4,△OA=2,△OP=4,△点P的坐标为(4,0)或(-4,0).【例2】(2019·济源一模)已知:如图,一次函数y=kx+3 的图象与反比例函数y=mx(x>0)的图象交于点P,P A△x轴于点A,PB△y轴于点B,一次函数的图象分别交x轴、y轴于点C,D,且S△DBP=27,12 OCCA=.(1)求点D的坐标;(2)求一次函数与反比例函数的解析式;(3)根据图象写出x 取何值时,一次函数 y =kx +3 的值小于反比例函数y =mx的值.【答案】见解析.【解析】解:(1)△一次函数y =kx +3与y 轴相交, △令x =0,解得y =3, △D 的坐标为(0,3);(2)△OD △OA ,AP △OA ,△DCO =△ACP ,△DOC =△CAP =90°, △Rt △COD △Rt △CAP , △12OD OC AP AC ==,OD =3, △AP =OB =6, △DB =OD +OB =9, △S △DBP =27, 即2DP BP⋅=27, △BP =6, △P (6,-6),把P 坐标代入y =kx +3,得到k =32-, 则一次函数的解析式为:y =32-x +3; 把P 坐标代入反比例函数解析式得:m =-36,则反比例解析式为:y =−36x; (3)联立y =−36x,y =32-x +3得:x =-4,y =9或x =6,y =-6,即直线与双曲线两个交点坐标为(-4,9),(6,-6),△当x >6或-4<x <0时,一次函数的值小于反比例函数的值.【变式2-1】(2019·洛阳三模)如图,在平面直角坐标系中,菱形 ABDC 的顶点 D ,C 在反比例函数y =kx上(k >0,x >0),横坐标分别为12和2,对角线 BC △x 轴,菱形ABDC 的面积为 9. (1)求 k 的值及直线 CD 的解析式; (2)连接 OD ,OC ,求△OCD 的面积.【答案】见解析.【解析】解:(1)连接AD ,△菱形 ABDC 的顶点D ,C 在反比例函数y =k x 上,横坐标分别为12和2, △D (12,2k ),C (2, 2k), ∵BC ∥x 轴, ∴B (-1,2k ),A (12,-k ), ∴BC =3,AD =3k , ∵S 菱形ABCD =9,∴12×3×3k=9,解得:k=2,△D(12,4),C(2, 1),设直线CD的解析式为y=mx+n,∴12m+n=4,2m+n=1,解得:m=-2,n=5,即直线CD的解析式为y=-2x+5.(2)设直线y=-2x+5交x轴、y轴于点F,E,则F(52,0),E(0,5),∴S△OCD=S△EOF-S△OED-S△OCF=12×5×52-12×5×12-12×1×52=154,即△OCD的面积为:15 4.【例3】(2019·西华县一模)如图,在矩形OABC中,OA=3,OC=2,点F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=kx的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;(2)当k为何值时,△EF A的面积最大,最大面积是多少?【答案】见解析.【解析】解:(1)∵矩形OABC中,OA=3,OC=2,∴B(3,2),∵F为AB的中点,∴F(3,1),∵点F在反比例函数y=kx的图象上,∴k=3,即函数的解析式为y =3x; (2)E ,F 两点坐标为:E (2k ,2),F (3,3k ), ∴S △EF A =12AF •BE =12×3k (3﹣2k ), =()2133124k --+, ∴当k =3时,S △EF A 有最大值,最大值34. 【变式3-1】(2019·中原名校大联考)如图,一次函数y =kx +b 的图象与反比例函数y =mx的图象交于A ,B 两点,与x 轴交于点C (﹣2,0),点A 的纵坐标为6,AC =3CB .(1)求反比例函数的解析式; (2)请直接写出不等式组mx<kx +b <4的解集; (3)点P (x ,y )是直线y =k +b 上的一个动点,且满足(2)中的不等式组,过点P 作PQ ⊥y 轴交y 轴于点Q ,若△BPQ 的面积记为S ,求S 的最大值.【答案】见解析.【解析】解:(1)过点A 作AD ⊥x 轴于D ,过B 作BE ⊥x 轴于E ,则∠ADC =∠BEC =90°, ∵∠ACD =∠BCE , ∴△ACD ∽△BCE , ∴AD AC CD BE BC CE ==,即623CE BE CE+==,解得:BE=2,CE=1,∴A(1,6),∴反比例函数解析式为y=6x;(2)将A(1,6),C(﹣2,0)代入y=kx+b,得:620k bk b+=⎧⎨-+=⎩,解得:24kb=⎧⎨=⎩,即直线解析式为:y=2x+4,由B(﹣3,﹣2),得不等式组6x<2x+4<4的解集为:﹣3<x<0;(3)设P(m,2m+4)(﹣3<m<0),则PQ=﹣m,△BPQ中PQ边上的高为2m+4﹣(﹣2)=2m+6,∴S=12•(﹣m)(2m+6)=﹣m2﹣3m=﹣(m+32)2+94,∴当m=﹣32时,S取得最大值,最大值为94.1.(2019·郑州外国语测试)如图所示,在平面直角坐标系中,直线l1:y=12-x与反比例函数y=kx的图象交于A、B两点,点A在点B左侧,已知A点的纵坐标为2.(1)求反比例函数的解析式;(2)根据图象直接写出12-x>kx的解集;(3)将直线y=12-x沿y轴向上平移后的直线l2与反比例函数y=kx在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.【答案】见解析.【解析】解:(1)在y=12-x中,y=2时,x=-4,即A(-4,2),△反比例函数y=kx的图象过点A,△k=-8,即反比例函数的解析式为:y=8x -;(2)联立y=8x-,y=12-x,解得:x=-4,y=2(点A);或x=4,y=-2,即B(4,-2),∴12-x>kx的解集为:x<-4或0<x<4;(3)设平移后的直线与x轴交于点D,连接AD、BD,△CD△AB,△△ABC的面积等于△ABD的面积,等于30,△S△AOD+S△BOD=30,△12·OD·|y A|+12·OD·|y B|=30,△OD=15,即D(15,0),设平移后直线的解析式为:y=12-x+m,将D(15,0)代入得:m=152,即平移后的直线函数表达式为:y=12-x+152.2.(2018·河师大附中模拟)如图,已知函数y=kx(x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC△y轴,AC=1(点C在A点的下方),过点C作CD△x轴,与函数y=kx(x>0)的图象交于点D,过点B作BE△CD于E,E在线段CD上,连接OC、OD.(1)求△OCD的面积;(2)当BE =12AC 时,求CE 的长.【答案】见解析.【解析】解:(1)将A (1,2)代入y =kx得:k =2, △AC △y 轴,AC =1, △C (1,1),△CD △x 轴,D 在y =2x上, △D (2,1),△S △OCD =12×1×1=12. (2)△BE =12AC ,△BE =12,△BE △CD , △点B 的纵坐标为32, △B 点在函数y =2x上, △B (43,32), △CH =43-1=13,△DH =1.5,△CD =+1.5,在Rt △CDE 中,△CED =60°,△CE =°sin60CD(米).3.(2018·洛阳三模)如图,在矩形OABC 中,OA =3,OC =2,F 是AB 上的一个动点(不与A 、B 重合),过点F 的反比例函数y =kx(k >0)的图象与BC 边交于点E . (1)当F 为AB 边的中点时,求该函数的解析式;(2)当k 为何值时,△EF A 的面积为23?【答案】见解析.【解析】解:(1)由题意知,AB =OC =2,BC =OA =3, △F 是AB 中点, △F (3,1),将F (3,1)代入y =kx得:k =3, 即反比例函数的解析式为:y =3x.(2)由图象知,点F 位于B 点下方,B (3,2), △当x =3时,y <2, 即k <6, △0<k <6,由题意知,F 点横坐标为3,即F (3, 3k ), 同理,得E 点坐标为(2k,2), △S △EF A =12AF BE ⋅⋅ 13232k k ⎛⎫=⨯⨯- ⎪⎝⎭△2313232k k ⎛⎫=⨯⨯- ⎪⎝⎭解得:k =2,或k =4,当k 为2或4时,△EF A 的面积为23.4.(2019·洛阳二模)如图,A ,B 分别在反比例函数y =kx(x <0)和y =x (x >0)的图象上,AB △x 轴,交 y 轴于点C .若△AOC 的面积是△BOC 面积的2倍.(1)求k 的值;(2)当△AOB =90°时,直接写出点A ,B 的坐标.【答案】见解析.【解析】解:(1)△AB △x 轴,△S △AOC =2k ,S △BOC ,△△AOC 的面积是△BOC 面积的2倍,△2k,△k (舍)或k =-.即k 的值为:-.(2)△△AOB =90°,△ACO =90°, △△A +△ABO =△B +△BOC =90°, △△A =△BOC , △△AOC △△OBC ,△△AOC 的面积是△BOC 面积的2倍,△OCBC=设B (a ),△aa ,解得:a a =(舍),即B (1,),△A (-2).5.(2019·周口二模)如图,点A (-2,a ),C (3a -10,1)是反比例函数my x=(x <0)图象上的两点. (1)求m 的值;(2)过点A作AP⊥x轴于点P,若直线y=kx+b经过点A,且与x轴交于点B,当∠P AC=∠P AB时,求直线AB的解析式.【答案】见解析.【解析】解:(1)∵点A(-2,a),C(3a-10,1)是反比例函数myx上,∴-2a=3a-10,解得:a=2,∴A(-2,2),C(-4,1),∴m=-4;(2)分两种情况讨论:①当点B在AP左侧时,∵∠P AC=∠P AB,∴A、C、B三点共线,将A(-2,2),C(-4,1)代入y=kx+b,并解得:k=12,b=3,即直线AB的解析式为:y=12x+3;②当点B在AP右侧时,∵∠P AC=∠P AB,∴此时直线AB与①中的直线AB关于直线AP成轴对称,此时k=-12,将(-2,2)代入y=-12x+b,得:b=1,即直线AB的解析式为:y=-12x+1;综上所述,直线AB的解析式为:y=12x+3,y=-12x+1.6.(2017·新野一模)如图,已知双曲线y =kx经过点B (1),点A 是双曲线第三象限上的动点,过B 作BC ⊥y 轴,垂足为C ,连接AC .(1)求k 的值;(2)若△ABC 的面积为,求直线AB 的解析式;(3)在(2)的条件下,写出反比例函数值大于一次函数值时x 的取值范围.【答案】见解析.【解析】解:(1)把B (1)代入y =kx中得,∴k ,(2)设△ABC 中BC 边上的高为h ,∵BC ⊥y 轴,B (1)∴BC ,∵△ABC 的面积为∴12BC •h , 解得:h =4,∴点A 的纵坐标为﹣3,把y =﹣3代入y ,得:x =,即A 3),设直线AB 的解析式为:y =mx +n ,把A 3)和B (,1)代入y =mx +n ,并解得:m,b=-2,∴直线AB的解析式为y x﹣2.(3)由图象可得:x或0<x<7.(2018·焦作一模)如图,一次函数y=﹣12x+b与反比例函数y=kx(x>0)的图象交于点A(2,6)和B(m,1)(1)填空:一次函数的解析式为,反比例函数的解析式为;(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.【答案】(1)y=﹣12x+7,y=12x;(2)见解析.【解析】解:(1)把点A(2,6)代入y=kx,得k=12,即反比函数解析式为:y=12x.∵点B(m,1)在y=12x上,∴m=12,即B(12,1).∵直线y=﹣12x+b过点A(2,6),∴b=7,∴一次函数的表达式为y=﹣12x+7.∴答案为:y=﹣12x+7,y=12x.(2)设直线AB与y轴交于点P,点E的坐标为(0,a),连接AE,BE,则点P的坐标为(0,7),∵S△AEB=S△BEP﹣S△AEP=5,∴12×|a﹣7|×(12﹣2)=5,∴|a﹣7|=1,解得:a=6或a=8,即点E的坐标为(0,6)或(0,8).8.(2018·信阳一模)如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=﹣12x+3交AB,BC分别于点M,N,反比例函数y=kx的图象经过点M,N.(1)求反比例函数的解析式;(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.【答案】见解析.【解析】解:(1)∵B(4,2),四边形OABC是矩形,∴OA=BC=2,在y=﹣12x+3中,当y=2时,x=2,∴M(2,2),将x=4代入y=﹣12x+3得:y=1,∴N(4,1),∵反比例函数y=kx的图象经过点M(2,2),∴k=4,∴反比例函数的解析式是y=4x;(2)S四边形BMON=S矩形OABC﹣S△AOM﹣S△CON=4×2﹣12×2×2﹣12×4×1=4;∵△OPM的面积与四边形BMON的面积相等,∴12OP×AM=4,而AM=2,∴OP=4,∴点P的坐标是(0,4)或(0,﹣4).9.(2019·南阳毕业测试)如图,直线y=kx+b与反比例函数y=mx的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C,D.(1)求此一次函数和反比例函数的解析式;(2)求△AOB的面积.【答案】见解析.【解析】解:(1)将点A(﹣1,2)代入y=mx,得m=﹣2,∴反比例函数解析式为:y=2x -.将B(﹣4,n)代入y=2x-中,得:n=12;B点坐标为(﹣4,12).将A(﹣1,2)、B(﹣4,12)代入y=kx+b中,得:-k+b=2,-4k+b=12,解得:k=12,b=52,∴一次函数的解析式为y=12x+52;(2)在y=12x+52中,当y=0时,x=﹣5,∴C(﹣5,0),即OC=5.S△AOC=S△AOC﹣S△BOC=12•OC•|y A|﹣12•OC•|y B|=154.10.(2019·开封二模)如图,A(4,3)是反比例函数y=kx在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=kx的图象于点P.(1)求反比例函数y=kx的表达式;(2)求点B的坐标;(3)求△OAP的面积.【答案】见解析.【解析】解:(1)∵点A(4,3)在反比例函数y=kx的图象上,∴k=12,即反比例函数解析式为:y=12x;(2)如上图,过点A作AC⊥x轴于点C,则OC=4,AC=3,在Rt△OAC中,由勾股定理得:OA=5,∵AB∥x轴,AB=OA=5,∴点B的坐标为(9,3);(3)∵B(9,3),∴可得OB所在直线解析式为y=13 x,联立:y=13x,y=12x,解得:x=6,y=2或x=-6,y=-2(舍),∴P(6,2),如上图所示,过点P作PD⊥x轴于D,∴S△OAP=S梯形PDCA=5.11.(2019·安阳一模)如图,在平面直角坐标系中,反比例函数kyx=(k≠0)与一次函数y=ax+b(a≠0)交于第二、四象限的A,B两点,过点A作AD⊥y轴于点D,OD=3,S△AOD=3,点B的坐标为(n,-1).(1)求反比例函数和一次函数的解析式;(2)请根据图象直接写出kax bx+≥的自变量x的取值范围.【答案】见解析.【解析】解:(1)∵AD⊥y轴,OD=3,∴S△AOD=12OD·AD,S△AOD=3∴AD=2,即A(-2,3),将A(-2,3)代入kyx=中,得:k=-6,即反比例函数解析式:6 yx =-.当y=-1时,x=6,即B(6,-1),将A(-2,3), B(6,-1)代入y=ax+b得:-2a+b=3,6a+b=-1,解得:a=12-,b=2,即一次函数的解析式为:y=12-x+2.(2)观察图象可知,kax bx+≥的解集为:x≤-2或0<x≤6.12.(2019·三门峡二模)如图,在平面直角坐标系xOy中,直线y=x﹣2与双曲线y=kx(k≠0)相交于A,B两点,且点A的横坐标是3.(1)求k的值;(2)过点P(0,n)作直线,使直线与x轴平行,直线与直线y=x﹣2交于点M,与双曲线y=kx(k≠0)交于点N,若点M在N右边,求n的取值范围.【答案】见解析.【解析】解:(1)在y=x﹣2中,当x=3时,y=1,∴A(3,1),∵点A(3,1)在双曲线y=kx上,∴k=3;(2)联立y=x﹣2,y=3x,解得:31xy=⎧⎨=⎩或13xy=-⎧⎨=-⎩,即B(﹣1,﹣3),如下图所示:当点M在N右边时,n的取值范围是n>1或﹣3<n<0.13.(2019·濮阳二模)如图,已知反比例函数y=mx(m≠0)的图象经过点(1,4),一次函数y=﹣x+b的图象经过反比例函数图象上的点Q(﹣4,n).(1)求反比例函数与一次函数的表达式;(2)一次函数的图象分别与x轴、y轴交于A、B两点,与反比例函数图象的另一个交点为P点,连结OP、OQ,求△OPQ的面积.【答案】见解析.【解析】解:(1)反比例函数y=mx图象经过点(1,4),∴m=4,即反比例函数的表达式为:y=4 x .∵反比例函数的图象过点Q(﹣4,n),∴n=-1,∵一次函数y=﹣x+b的图象过点Q(﹣4,-1),∴b=-5,即一次函数的表达式为:y=﹣x﹣5;(2)联立y=﹣x﹣5,y=4x,解得:x=-4,y=-1或x=-1,y=-4,∴P(﹣1,﹣4),在一次函数y=﹣x﹣5中,当y=0时,x=﹣5,∴点A (﹣5,0), ∴S △OPQ =S △OP A ﹣S △OAQ=11545122⨯⨯-⨯⨯=152. 14.(2019·商丘二模)如图,一次函数y =k 1x +b 与反比例函数y =2k x的图象交于A (2,m ),B (n ,﹣2)两点.过点B 作BC ⊥x 轴,垂足为C ,且S △ABC =5.(1)求一次函数与反比例函数的解析式. (2)根据所给条件,请直接写出不等式k 1x +b >2k x的解集; (3)若P (p ,y 1),Q (﹣2,y 2)是函数y =2k x图象上的两点,且y 1≥y 2,求实数p 的取值范围.【答案】见解析.【解析】解:(1)∵S △ABC =12•BC •(x A -x B ) =12×2×(2﹣n ), ∴12×2×(2﹣n )=5, 即n =-3,∴A (2,3),B (﹣3,﹣2), ∴k 2=6,即反比例函数的解析式是y =6x. 把A (2,3),B (﹣3,﹣2)代入y =k 1x +b 得:112332k b k b +=⎧⎨-+=-⎩,解得:k 1=1,b =1,即一次函数的解析式是y =x +1;(2)∵当﹣3<x <0或x >2时,一次函数图象在反比例函数图象上方,∴不等式k 1x +b >2k x的解集是﹣3<x <0或x >2; (3)在y =6x中,当x >0时,y 随x 增大而减小;当x >0时,y >0, 当x =-2时,y 2=-3,即Q (-2,-3)∴若y 1≥y 2,实数p 的取值范围是:p ≤﹣2或p >0.15.(2019·开封模拟)如图,在平面直角坐标系xOy 中,已知正比例函数y 1=﹣2x 的图象与反比例函数y 2=kx的图象交于A (﹣1,n ),B 两点.(1)求出反比例函数的解析式及点B 的坐标; (2)观察图象,请直接写出满足y ≤2的取值范围;(3)点P 是第四象限内反比例函数的图象上一点,若△POB 的面积为1,请直接写出点P 的横坐标.【答案】见解析. 【解析】解:解:(1)把A (﹣1,n )代入y 1=﹣2x ,得n =2, ∴A (﹣1,2),把A (﹣1,2)代入y 2=kx,可得k =﹣2, ∴反比例函数的表达式为y 2=﹣2x,由反比例函数图象性质,知点B 与点A 关于原点对称, ∴B (1,﹣2).(2)由图象可知,y ≤2时自变量x 的取值范围是:x <﹣1或x >0; (3)过B 作BM ⊥x 轴于M ,过P 作PN ⊥x 轴于N ,∵S梯形MBPN=S△POB=1,设P(m,﹣2m),则12(2+2m)|m﹣1|=1,解得:m=12或m=12,综上所述,P.16.(2019·开封二模)如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=kx(k>0,x>0)的图象上,点D的坐标为(4,3).(1)求k的值;(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=kx(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.【答案】见解析.【解析】解:(1)过点D作DE⊥y轴于E,∵点D的坐标为(4,3),∴DE=4,OE=3,由勾股定理得:OD=5,∴AD=5,∴点A坐标为(4,8),∵点A在反比例函数y=kx的图象上,∴k=32;(2)由D(4,3)知,当平移后落在y=32x的图象上,则y=3,即32x=3,即x=323,∴平移的距离为:323-4=203,即菱形ABCD沿x轴正方向平移的距离为20 3.17.(2019·郑州联考)如图,点A的坐标为(3,0),点C的坐标为(0,4),OABC为矩形,反比例函数k yx =的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.(1)求反比例函数kyx=和直线OE的函数解析式;(2)求四边形OAFC的面积?【答案】见解析.【解析】解:(1)由题意得:点B(3,4),点D(3,2),将D(3,2)代入kyx=,得k=6.即反比例函数的解析式为6yx =;在6yx=中,当y=4时,x=32,即E(32,4),设直线OE的解析式为:y=mx,将(32,4)代入得:m=83,即直线OE的解析式为y=83 x;(2)连接AC,在Rt△OAC中,OA=3,OC=4,由勾股定理得:AC=5,∵AF=12,CF=13.∴AC2+AF2=CF2,∴∠CAF=90°,∴S四边形OAFC=S△OAC+S△CAF=12×3×4+12×5×12=36.18.(2019·安阳二模)如图,直线y=12x与反比例函数y=kx(x>0)的图象交于点A,已知点A的横坐标为4.(1)求反比例函数的解析式;(2)将直线y=12x向上平移3个单位后的直线l与y=kx(x>0)的图象交于点C;①求点C的坐标;②记y=kx(x>0)的图象在点A,C之间的部分与线段OA,OC围成的区域(不含边界)为W,则区域W内的整点(横,纵坐标都是整数的点)的个数为.【答案】见解析.【解析】解:(1)将x=4代入y=12x,得:y=2,∴A(4,2),将A点代入y=kx,得:k=8,∴反比例函数的解析式y=8x;(2)①l的解析式为y=12x+3,联立:y=12x+3,y=8x得:∴x=2,y=4或x=-8,y=-1(舍),∴C(2,4);②4个;19.(2019·名校模考)在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=kx(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)(1)求一次函数和反比例函数的解析式;(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.【答案】见解析.【解析】解:(1)将(﹣2,3)代入y=﹣x+b,得:b=1,将(﹣2,3)代入y=kx,得:k=-6,即:一次函数的解析式为y=﹣x+1,反比例函数的解析式为y=6x;(2)在y=﹣x+1中,当x=0时,y=1,即C(0,1),由平移知:CF=4.联立y=﹣x+1,y=6x,解得:x=3,y=-2或x=-2,y=3,∴B(3,-2),A(-2,3),∴S△ABF=12×4×(2+3)=10.20.(2019·枫杨外国语三模)如图,一次函数y=﹣x+b与反比例函数y=kx(k≠0)的图象相交于A、B两点,其中A(﹣1,4),直线l⊥x轴于点E(﹣4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC.(1)求出b和k;(2)判定△ACD的形状,并说明理由.【答案】见解析.【解析】解:(1)将A(﹣1,4)代入一次函数y=﹣x+b,得:b=3,将A(﹣1,4)代入反比例函数y=kx,得k=﹣4;(2)△ACD是等腰直角三角形.∵直线x=﹣4与一次函数y=﹣x+3交于点D,∴D(﹣4,7),同理,可得:C(﹣4,1),∵A(﹣1,4),C(﹣4,1),D(﹣4,7)∴CD=6,∵∠AFD=∠AFC=90°,由勾股定理得:AC=AD=32,∵AD2+AC2= 36,CD2=36∴AD2+AC2=CD2∴△ACD是直角三角形,∵AD=AC∴△ACD是等腰直角三角形.。
2023年九年级数学下册中考数学综合培优测试卷:一次函数图像与几何变换【含答案】

2023年九年级数学下册中考数学综合培优测试卷:一次函数图像与几何变换一、单选题1.在平面直角坐标系中,把直线y=3x 向左平移2个单位长度,平移后的直线解析式是( )A .y=3x+2B .y=3x-2C .y=3x+6D .y=3x-62.若一次函数y=2x-3的图象平移后经过点(3,1),则下列叙述正确的是( )A .沿x 轴向右平移3个单位长度B .沿x 轴向右平移1个单位长度C .沿x 轴向左平移3个单位长度D .沿x 轴向左平移1个单位长度3.在平面直角坐标系中,将直线沿y 轴向下平移6个单位后,得到一条新的直线,该直y =−32x +3线与x 轴的交点坐标是( )A .B .C .D .(0,3)(−2,0)(4,0)(6,0)4.已知直线向下平移2个单位长度后得到直线,且直线与直线关于l 1:y =kx +3l 2l 2l 3:y =−x +1y 轴对称,则k 的值为( ).A .B .1C .2D .3−15.在平面直角坐标系中,将函数 的图象向上平移6个单位长度,则平移后的图象与x 轴的y =3x 交点坐标为( ) A .(2,0)B .(-2,0)C .(6,0)D .(-6,0)6.把直线y=-x+1向上平移3个单位长度后得到的直线的解析式为( )A .y=-x+4B .C .y=x+4D .y=x-27.将直线沿x 轴向左平移3个单位得到直线L ,则直线L 的解析式是( )y =2x +5A .y =2x +2B .y =2x +8C .y =2x -1D .y =2x +118.对于一次函数y =﹣2x+4,下列结论错误的是( )A .函数的图象不经过第三象限B .函数的图象与x 轴的交点坐标是(2,0)C .函数的图象向下平移4个单位长度得y =﹣2x 的图象D .若两点A(x 1,y 1),B(x 2,y 2)在该函数图象上,且x 1<x 2,则y 1<y 29.将一次函数y =﹣3x 的图象沿y 轴向下平移4个单位长度后,所得图象的函数表达式为( )A .y =﹣3(x ﹣4)B .y =﹣3x +4C .y =﹣3(x +4)D .y =﹣3x ﹣410.在平面直角坐标系中,将直线 先关于 轴作轴对称变换,再将所得直线关于y =−3x +4x y 轴作轴对称变换,则经两次变换后所得直线的表达式是( )A .B .C .D .y =4x−3y =−4x +3y =3x +4y =−3x−411.将直线向上平移2个单位长度,则平移后的直线所对应的函数解析式为( )y =−2x +3A .B .C .D .y =−2x +1y =−4x +5y =−2x +5y =−4x +112.将直线向上平移5个单位长度后得到直线,则下列关于直线的说y =x +1y =kx +b y =kx +b 法错误的是( )A .函数图象经过第一、二、三象限B .函数图象与轴的交点在轴的正半轴x xC .点在函数图象上(−2,4)D .随的增大而增大y x 二、填空题13.直线 +3的图像是由正比例函数 图像向 (填上或下)平移 y =3x 个单位得到或由正比例函数 图像向 (填左或右)平移 个单位得到可以得到的一条直线14.直线 沿 轴平移3个单位,则平移后直线与 轴的交点坐标为 .y =2x−1y y 15.在平面直角坐标系中,把直线y=2x 向左平移1个单位长度,平移后的直线解析式是 .16.将正比例函数y=﹣2x 的图象沿y 轴向上平移5个单位,则平移后所得图象的解析式是 .17.如图,在平面直角坐标系中,A (1,0),B (3,0),点C 在第一象限,∠ABC=90°,AC=25,直线l 的关系式为: .将△ABC 沿x 轴向左平移,当点C 落在直线l 上时,线段AC 扫y =−x−3过的面积为 平方单位.18.已知直线与直线关于y 轴对称,当时,,当y 1=ax +b(a ≠0)y 2=kx +5(k ≠0)x >−52y 1>0时,,则直线 .x >52y 2<0y 1=三、综合题19.如图,直线 与 轴、 轴交于点 、 ,直线 与 轴l 1:y =2x +1x y D A l 2:y =mx +4x y 轴分别交于点 、 ,两直线相交于点 .C B P(1,b)(1)求 , 的值; b m (2)求 的值;S △PDC −S △PAB (3)垂直于 轴的直线 与直线 , 分别交于点 , ,若线段 的长为x x =a l 1l 2M N MN 2,求 的值.a 20.如图,直线y =kx +4的图象与y 轴交于点A ,与x 轴交于点B (2,0),直线AF 交x 轴负半轴于点F ,且OF =2OA .(1)求出k 的值为 ,直线AF 的解析式为 ;(2)若将直线AB 沿y 轴向下平移,平移后的直线恰好经过C (﹣3,0),与y 轴相交于点D ,且直线CD 与直线AF 交于点E ,求点E 的坐标.21.如图,一次函数 的图象与反比例函数( 为常数且 )的图象相交于y =x +5y =kx k k ≠0 , 两点.A(−1,m)B(1)求反比例函数的表达式;(2)将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反y =x +5y b (b >0)比例函数的图象有且只有一个交点,求 的值.y =kx b 22.已知反比例函数与正比例函数 相交于 .y 1=kx y 2=x A(2,2)(1)求 值.k (2)画出反比例函数的图象.(3)当 时,直接写出 的范围?y 1>y 2x (4)根据图象,解不等式 .kx <x−323.背景知识:已知两直线 , ,若 ,则m :y 1=k 1x +b 1n :y 2=k 2x +b 2(k 1k 2≠0)m ⊥n ;若 ,则 .k 1k 2=−1m//n k 1=k 2应用:在平面直线坐标系 中,直线 交x 轴于点C ,交y 轴于点D ,若 xoy l 1:y =x−1l 2⊥l 1于点 ,交y 轴于点A ,交x 轴于点B.P(2,1)(1)求直线 的表达式; l 2(2)求 的面积;△ABC (3)若将直线 向下平移 个单位,得到新的直线 ,交y 轴于点E ,交直线 于点F ,l 1q l 3l 2使得 ,求 的值.S △AEF =16q 24.已知:如图1,在平面直角坐标系中,一次函数y = x+3交x 轴于点A ,交y 轴于点B ,点C34是点A 关于y 轴对称的点,过点C 作y 轴平行的射线CD ,交直线AB 与点D ,点P 是射线CD 上的一个动点.(1)求点A ,B 的坐标.(2)如图2,将△ACP 沿着AP 翻折,当点C 的对应点C′落在直线AB 上时,求点P 的坐标. (3)若直线OP 与直线AD 有交点,不妨设交点为Q(不与点D 重合),连接CQ ,是否存在点P ,使得S △CPQ =2S △DPQ ,若存在,请求出对应的点Q 坐标;若不存在,请说明理由.答案解析部分1.【答案】C 2.【答案】B 3.【答案】B 4.【答案】B 5.【答案】B 6.【答案】A 7.【答案】D 8.【答案】D 9.【答案】D 10.【答案】D 11.【答案】C 12.【答案】B13.【答案】y=3x ;上;3;y=3x ;左;114.【答案】(0,2)或(0, )−415.【答案】y=2x+216.【答案】y =-2x+517.【答案】4018.【答案】或2x +55+2x19.【答案】(1)解:∵点 在直线 上,∴ ,P(1,b)l 1:y =2x +1b =2×1+1=3∵ 在直线 上,∴ ,∴P(1,3)l 2:y =mx +43=m +4m =−1(2)解:∵直线 与 轴、 轴交于点 、 ,l 2:y =−x +4x y D A ∴ ,,A(0,1)D(−12,0)∵直线 与 轴、 轴分别交于点 、 ,l 2:y =−x +4x y C B ∴ , ,B(0,4)C(4,0)∴S △PDC −S △PAB =12DC ⋅y P −12AB ⋅x P =12×(12+4)×3−12×(4−1)×1=214(3)解:设直线 与直线 , 分别交于点 , , x =a l 1l 2M N 当 时, ;当 时, ,x =a y M =2a +1x =a y N =4−a ∵ ,∴ ,解得或 ,MN =2|2a +1−(4−a)|=2a =13a =53所以 的值为 或 a 135320.【答案】(1)-2;y =+412x (2)解:∵直线AB 沿y 轴向下平移,平移后的直线恰好经过C (﹣3,0), ∴设直线DC 的解析式为y =﹣2x+d ,把C (﹣3,0)代入得d =﹣6,∴直线DC 的解析式为y =﹣2x﹣6.解得,{y =−2x−6y =12x +4{x =−4y =2∴E (﹣4,2).21.【答案】(1)解:由题意,将点 代入一次函数 得: A(−1,m)y =x +5m =−1+5=4∴A(−1,4)将点 代入得: ,解得 A(−1,4)y =k x k−1=4k =−4则反比例函数的表达式为;y =−4x (2)解:将一次函数 的图象沿 轴向下平移 个单位得到的一次函数的解析式为 y =x +5y b y =x +5−b 联立{y =x +5−by =−4x 整理得: x 2+(5−b)x +4=0一次函数 的图象与反比例函数 的图象有且只有一个交点∵y =x +5−b y =−4x 关于x 的一元二次方程 只有一个实数根∴x 2+(5−b)x +4=0 此方程的根的判别式 ∴Δ=(5−b)2−4×4=0解得 b 1=1,b 2=9则b 的值为1或9.22.【答案】(1)解:∵反比例函数y 1= 与正比例函数y 2=x 相交于A (2,2).kx ∴k=2×2=4(2)解:描出点(1,4),(2,2),(4,1), 用平滑的曲线连接,画出反比例函数的图象如图,(3)解:由图象可知,当0<x<2和x<-2时,y1>y2.(4)解:观察图象,直线y=x向下平移3个单位,与反比例函数的交点为(4,1)和(-1,-4),∴不等式 <x-3的解集为:-1<x <0和x >4.kx 23.【答案】(1)解:由 ,得 ,l 1:y =x−1k 1=1 , ,∵l 2⊥l 1∴k 2⋅k 1=−1,∴k 2=−1设 ,把 代入解析式得:b=3,l 2:y =−x +b P(2,1) ;∴l 2:y =−x +3(2)解:由图象可得:, 与x 轴交于点B 、C , 令y=0,则有 ∵l 2:y =−x +3l 1:y =x−1∴B(3,0),C(1,0),又 与y 轴交于点A , 令x=0,则有 ,∵l 2:y =−x +3∴A(0,3) OA=3,BC=2, ;∴∴S △ABC =12BC ⋅OA =3(3)解: 将直线 向下平移 个单位,得到新的直线 ,∵l 1q l 3 ,令x=0则 , ,∴l 3:y =x−1−q y =−1−q ∴E(0,−1−q) ,∴AE =3−(−1−q)=4+q 交直线 于点F , 解得,∵l 3l 2∴{y =−x +3y =x−1−q {x =4+q 2y =2−q 2 , ,∵S △AEF =12AE ⋅F x =16∴12×(4+q)⋅4+q 2=16解得 (不符题意,舍去).q 1=4,q 2=−12 .∴q =424.【答案】(1)解:令x=0,则y=3,∴B (0,3),令y=0,则 x+3=0,34∴x=﹣4,∴A (﹣4,0);(2)解:∵点C 是点A 关于y 轴对称的点, ∴C (4,0),∵CD ⊥x 轴,∴x=4时,y=6,∴D (4,6),∴AC=8,CD=6,AD=10,由折叠知,AC'=AC=8,∴C'D=AD﹣AC'=2,设PC=a ,∴PC'=a ,DP=6﹣a ,在Rt △DC'P 中,a2+4=(6﹣a )2,∴a= ,83∴P (4, );83(3)解:设P (4,m ), ∴CP=m ,DP=|m﹣6|,∵S △CPQ =2S △DPQ ,∴CP=2PD ,∴2|m﹣6|=m ,∴m=4或m=12,∴P (4,4)或P (4,12),∵直线AB 的解析式为y= x+3①,34当P (4,4)时,直线OP 的解析式为y=x ②,联立①②解得,x=12,y=12,∴Q (12,12),当P (4,12)时,直线OP 解析式为y=3x ③,联立①③解得,x= ,y=4,43∴Q ( ,4),43。
2020年中考数学二轮复习一次函数压轴专题训练
2020年中考数学二轮复习:《一次函数》压轴专题训练yOA18OABC轴重合,.如图,将一张边长为放在直角坐标系中,使得的正方形纸片与BPxABAOC 重合).将正方形纸片为正方形、点与轴重合,点边上的一点(不与点OHEFOPGPCPGBCHO.处,点落在.连接处,落在,折痕为交、于折叠,使点初步探究4AP1时)当(=E;①直接写出点的坐标EF的函数表达式.②求直线深入探究2PABAPOOPH的度数总是相等,请说明理由.上移动时,∠在边()当点与∠拓展应用3PABPBH的周长是否发生变化?并证明你的结论.)当点(在边上移动时,△ByBBOy2x+bxA2逆时针旋转=轴交于点绕着点,与与.已知直线,将线段轴交于点36DOBCD90BCCCDx.°得到线段,四边形,过点轴于点作的面积为⊥AB1的解析式;)求直线(BCBHHPODCPCPBH2,过为线段上一点,连接上一点,连接(=)点,点为,且ACEtFAEACPOBHCPCDE的,连接,△于、点、作的横坐标为的垂线交、,设点tSS的函数解析式;面积为与,求PKxKPDF32OHFKOH,求点轴于点(⊥)在(=)的条件下,连接交,过点作,若P的坐标.BCC31ABA地,.如图(,甲汽车从)所示,在站匀速驶往,地出发经两地间有一车站2ABC)是两辆汽车行驶时地,两车速度相同.如图(乙汽车从站匀速驶往地出发经xCy(小时)之间的函数关系的图象.离(千米)与行驶时间站的路程kmABh km 1a b;两地的距离为()填空:=,,=2PMMNyx之间的函数表达式(自变量取值范围不用写);所表示的、与()求线段3xC的路程之和最小?满足什么条件时,甲、乙两车距离车站)求行驶时间(.CDByA4xOyABx,直线轴分别交于点.如图,在平面直角坐标系轴、中,直线、点与CD+5xCDAByxy,直线、点的解析式为轴、,直线轴分别交于分别交于点=﹣与45EmOBOCykx+bk0.的解析式为,=:((),且≠=),两直线交于点:CD1的解析式;()求直线FA2CDy,轴交于点使得平移后的直线经过(点,)将直线且与向下平移一定的距离,AEDF 的面积.求四边形/505分的速度回家,小明到米.小明从家去李宁体育馆游泳,同时,妈妈从李宁体育馆以/250分的速度回家取伞,立即米体育馆后发现要下雨,立即返回,追上妈妈后,小明以y250/(米)与小明米又以分的速度折回接妈妈,并一同回家.如图是两人离家的距离x(分)之间的函数图象.出发的时间FDAC四点在一条直、(注:小明和妈妈始终在同一条笔直的公路上行走,图象上、、线上)AFOB1的函数表达式;)求线段(及线段BC2C的函数表达式;)求点的坐标及线段(1500 x3米;时,小明与妈妈相距()当为4DD的实际意义.坐标,并说明点)求点(.x+bABykx+b61ACyxA,且分别和直线轴上一点=﹣.如图,已知直线::交于=2142OCCBOBy=、点交=轴于点.,且1k的值;()求9ACABxS21D上轴上方,当(上一点,且在)如图时,在线段,点=是直线ACD△FAMNxFCFNFCNF沿,使得分别为=,将△,点轴、轴上的动点,连接,取一点NFCNFMD+MC′的最小值;翻折至△′,求32HPACAOPHPCP,(上的动点,连接)如图,是否存在这样的点,分别为射线,,PCHPHAP为直角三角形同时成立.请直接写出满足条件的点为等腰三角形,△使得△坐标.71ACyx+bBCykx2k0),且,直线.如图﹣,已知直线的解析式为的解析式为=﹣≠=(BOC6.△的面积为1kb的值;)求(和21ACA90ADDyM轴上,若点点逆时针旋转(,点)如图°得到直线,将直线在绕xNADDM+MN+NB的值最小时,求为直线为上的一个动点,当轴上的一个动点,点MDM+MN+NB 的最小值;的坐标及此时点32AODACAODADxP,平移得到△′′轴交于点′(′与)如图,将△′,沿着直线ADDPDAPP点坐标.′′连接、是等腰三角形时,求此时,当△+xBx8BCyAx轴正交.如图,在平面直角坐标系中,直线轴于点:,点=在mABCCOC),的中线,的坐标为(半轴上,为△CO1的长;)求线段(DADADD2OCECE的横坐,点为,设点()点的中点,连接在的延长线上,连接tStCDES的函数解析式;的面积为,求标为,△与OBDDFDBBCF23FDB,=∠、)在(()的条件下,点为射线上一点,连接,且∠FCES坐标.,求此时=值及点9xOylykx+6xyABOB两点,且中,直线与:、.在平面直角坐标系=轴、轴分别交于111xyAB+bCEkOAlyx、轴、经过点分别交于点轴、=(,直线,:=直线),与22FD三点.、1l 的解析式;()求直线121CBCDABDBCD的面积;,连接时,求点)如图,当的坐标和△(⊥32DABQQCD是以)如图上运动时,在坐标轴上是否存在点,当点,使△在直线(CDQ的坐标,若不存在,请说明理为底边的等腰直角三角形?若存在,请直接写出点由.10yx+1yx2PyAB两点.=轴交于﹣和直线相交于点.如图,直线=﹣、,分别与1P的坐标;()求点2ABP的面积;)求△(3MNyx+1yx2MNyMN5,∥轴,若=()、分别是直线=﹣和=﹣上的两个动点,且MN两点的坐标.直接写出、ABB02A11lxy30为直角边.如图,直线(与),以线段轴、轴分别交于点)、点(,,a90P1ABCBAC)为坐标系中的一个°,点=,在第一象限内作等腰直角三角形,∠(动点.l1的表达式;()请直接写出直线ABC2的面积;)求出△(aABCABP3的值.)当△面积相等时,求实数(与△yxBcdTb12A a)(,,),.定义:在平面直角坐标系中,对于任意两点(),若点(,41Mx8yNTAB,满足(﹣=,,的融合点.例如:=,那么称点是点(和),y0EM12ND32T是直线,)是点(),则点和(),点的融合点.如图,已知点﹣,EDT xy+2x的融合点.(和上任意一点,点,)是点=T E16;的坐标为()若点的纵坐标是,则点2T xyyx的函数关系式:)求点)的纵坐标((,与横坐标3ETxHDTHE的坐标.()若直线交轴于点,当△为直角三角形时,求点131xOyykx+8xyAB两点,已轴于分别交.如图、,在平面直角坐标系中,直线轴,=A60CAB3Dx 轴正半轴上的一个动在直线,点知点坐标(上,横坐标为,是),点CDCD Rt CDECDE90°.△=点,连结,以,且∠为直角边在右侧构造一个等腰1ABC点坐标;()求直线的解析式以及2DmmE的坐标;,试用含(的横坐标为)设点的代数式表示点32OCOEOCEE的坐标.)如图,请直接写出使得△(,连结周长最小时,点,20B14ABA y),且与,.如图,在平面直角坐标系中,直线,经过点)和((CCOCABD的横坐标为与,且点交于点.轴交于点,直线1AB的解析式;()求直线2OAAOD的形状;)连接,试判断△(3PCCO1O运动,运动时)动点以每秒从点个单位长度的速度向终点出发沿线段(tQOyQD到达点出发沿从点间为轴的正半轴以相同的速度运动,当点秒,同时动点PQPQOAMtOPM为等腰三角形?当△为何值时,设,同时停止运动.时,与交于点,t值.求出所有满足条件的15ABxAyBOCyx=,与,与直线轴交于点.在平面直角坐标系中,直线轴交于点与:1C.交于点x+10y11AB.=﹣()当直线时,如图解析式为2C的坐标;求点①x+10xx.②根据图象求出当满足什么条件时﹣<22AOCONABONEOAC9,且,垂足为()如图的面积为,作∠的平分线,△,若⊥OA6PQOAOEAQPQAQ+PQ是否存在=.,分别为线段、上的动点,连接与,试探索最小值?若存在,求出这个最小值:若不存在,说明理由.参考答案11OEPEaAE8aAP4,,则,=.解:(=)①设:==﹣222APPEAE+Rt AEP,△=在中,由勾股定理得:22+16a8aa5,),解得:即﹣==(E05),(故点,05);,故答案为:(FFRyR,作过点轴于点⊥②OPOPEFOPEF,折叠后点关于直线落在⊥处,则点对称,则、EFR+FER90FER+AOP90AOPEFR,°,而∠°,∴∠==∠∴∠∠∠=OAPFRERFAO,,而∠==∠AOPFREAAS),≌△∴△(ERAP4,=∴=OREOOR541F81),=,故点﹣=(﹣,=b+EFykx,=、得:的坐标代入一次函数表达式:,解得:将点x+5EFy;=﹣故直线的表达式为:2PEOE,)证明:∵(=EOPEPO.∴∠=∠EPHEOC90°,又∵∠=∠=EPHEPOEOCEOP.﹣∠=∠﹣∠∴∠.POCOPH.即∠=∠ABOC,又∵∥APOPOC.∴∠=∠APOOPH;∴∠=∠3OOQPHQ.)解:如图,过⊥作,垂足为(1APOOPH,由(=∠)知∠AOPQOP中,和△在△APOOPHAOQPOPOP,=∠∠==∠,,∠AOPQOPAAS).∴△≌△(APQPAOOQ.,=∴=AOOC,又∵=OCOQ.∴=COQH90OHOH,又∵∠°,=∠==OCHOQHSAS).≌△∴△(CHQH.=∴PHBPB+BH+PHAP+PB+BH+HCAB+CB16;∴△的周长====16.故答案为:21BOB90BC,)∵将线段°得到线段.解:(绕着点逆时针旋转OBBCOBC90°,,∠==∴CDxD,⊥∵轴于点CDO90°,∴∠=BOD90°,=∵∠OBCD为正方形,∴四边形.OBCD36.∵四边形的面积为OB6,∴=B06),(,∴y2x+byB,与∵直线轴交于点=b6,∴=ABy2x+6;的解析式为=∴直线2y2x+6xA,与=轴交于点()∵直线A30),(﹣∴,1BBLCPLCDM,,垂足为如图⊥,过点于点作,交BHBC,=∵CLHL,=∴BLCPEFCP,,⊥∵⊥BMEF,∴∥CMME,∴=CBM+BMCBMC+MCL90°∠∠=∠=∵∠CBMPCD,∴∠=∠BCMPDCBCCD,∵∠==∠,BCMCDPASA),∴△(≌△CMPD,=∴PDCMME6t,=∴﹣==CE2CM26t),(==﹣∴ADOA+OD9,==∵9t+540St6);≤≤∴=(=﹣=a3PD,=)设(.2BFCDBMEF,∥,∵∥如图,BFEM是平行四边形,∴四边形BFEMPDa,===∴OFOP,∴=FPFKOHA',与连接交于,设OFP45°,∴∠=FOP+FHP180°,∠∵∠=FOPH四点共圆,∴、、、OFPOHP45°,∴∠==∠OHF45°,=∴∠FKOH,∵⊥FA'H90°,∴∠=EFK45°,∴∠=3EEREFFKR,⊥作于点如图交射线,过点EFR为等腰直角三角形,∴△EFER,∴=FFGCDGRxyQCD的延长线于点,交轴于点轴的平行线交作,过点于点⊥作过点.NKE、,连接RNEFGE90FEGERN,==∠∴∠°,∠=∠EFGRENAAS),∴△(≌△ENFGEGRNPDa,∴===,=CGBFaGEa,,∵===EDb,设=DNCE2aOQOFa+b,===∴,=PDPKaODCD2a+b,==∵==,OKb,∴=OKQR,∵∥,∴,即2b++bab3a,∴)=(()ab,=∴3a6,∴=a2,=∴P40).∴,(31300560km/h,)两车的速度为:=÷.解:(a6075120,﹣)==×(b752,﹣==AB300+120420,两地的距离是:=1202420;,故答案为:,2PMyxykx+b,(与)设线段=所表示的之间的函数表达式是,,得PMyxy60x+300;所表示的与即线段=﹣之间的函数表达式是MNyxymx+n,=与之间的函数表达式是设线段所表示的,,得MNyxy60x300;=与之间的函数表达式是﹣即线段所表示的3DEycx+d,=对应的函数解析式为)设(.,,得DEy60x+120,对应的函数解析式为即=﹣EFyex+f,对应的函数解析式为设=,,得EFy60x120,即=对应的函数解析式为﹣Cskm,设甲、乙两车距离车站的路程之和为0x2时,≤≤当s60x+300+60x+120120x+420,=(﹣))=﹣(﹣x2ss180,=取得最小值,此时时,=则当2x5时,<当≤s60x+300+60x120180,=(﹣)=(﹣)5x7时,当≤≤s60x300+60x120120x420,(﹣﹣)=)=(﹣x5ss180,则当取得最小值,此时==时,由上可得,x2x5C的路程之和最小.行驶时间满足≤≤时,甲、乙两车距离车站xy+5m41EAB,.解:(的解析式)将点()代入直线=﹣,m,解得=E),∴点的坐标为(,OBOC54OB5,:,=:=OC4,=∴C40),∴点坐标为(﹣,CE40),(,),点,(﹣将点CDykx+b中,=代入直线的解析式解得xy+2CD.所以直线=解析式为x+50x82y0,,解得(=)当时,﹣==A80),点坐标为(所以,CDAy轴交于点,向下平移一定的距离,平移后的直线经过∵直线点,且与x+ydAF,的解析式为=∴设直线A80d4,,=﹣把)代入得(x4AFy.=的解析式为所以直线﹣F04).的坐标为(所以点,﹣如图,EGxG,⊥轴于点作AEDF的面积为:所以四边形S+S+S AOFODEGAEG△梯形△+2+488+×)﹣=(×(×)×32.=32AEDF.的面积为答:四边形kx15OBy,)设的函数表达式为=.解:(100300030kk,=,得=30yOB0x100x);(=≤≤的函数表达式为即线段6050F3000,÷=的横坐标为:点0F60),,的坐标为(则点.AFykx+b,的函数表达式为:设直线=11,,得AFy50x+3000;=﹣的函数表达式为即直线2x45y5045+3000750,)当×=(=﹣时,=C45750),的坐标为(即点,BCykx+b,设线段=的函数表达式为22,,得BCy150x+750030x45);≤的函数表达式是≤=﹣即线段(31500米时,()当小明与妈妈相距50x+3000100x1500100x50x+30001500150x+7500)﹣(﹣或(﹣=﹣﹣(﹣或)=﹣50x+30001500,)=x10x30,解得:==或x10301500米.为∴当时,小明与妈妈相距或1030;或故答案为:4750250345+348,=((分钟),)∵=÷E480)的坐标为(∴点,EDy250x48250x12000,()==﹣﹣∴直线的函数表达式AFy50x+3000,对应的函数解析式为=﹣∵,∴,得D50500),∴点,的坐标为(50500米的地方将伞送到妈妈手里.分钟时离家实际意义:小明将在20C0416OB2OC4B),,﹣.解:()、=)、(=的坐标分别为:(,则点,yCACbx+=﹣的坐标代入将点:并解得:1+2ACyx=﹣,的表达式为:y0x6A60),,(,故点=,则=令.b+kxBAy,、,解得:的坐标代入将点=得:2kABy4x;,即=故直线=的表达式为:﹣6CBC2B,(的坐标得,)由点、=6BCxx6x9SSS×)==,×(()=﹣=×﹣﹣ABCDDACDBCAD△△△x9,解得:=D29y2xD4x9);=(=﹣时,,故点=当,ACFACFCF=,即=,==FFHyH,作⊥轴于点过点ACOCA60°,的表达式知,∠由直线=FCHHFCF sin60),=,则(=,=,故点°=2CDDCDxD9F三点共线作点′关于轴的对称点′、′(′,当,﹣′、),连接MCMD+′最小,时,CFFFFCDMD+MCD﹣′=′==′′最小值为﹣′﹣;﹣4CAO3AC30AC;的表达式知,∠==°,=()由直线90PHA°时,①当∠=PHC为等腰直角三角形,则△aCHHP,==设a2HPHAAP,,=则==264ACCH+HAaaa﹣=,解得:=,==412AP12a6464AP2﹣=﹣)=,=﹣,则=﹣(6P40);,(故点﹣CPH90°时,②当∠=CPHHPCP,为等腰三角形,则则=HPCPa Rt PHAHA2HP2a,△=,则在中,设===CPH90°,∵∠=HPOC,∴∥a,=则,解得:,即=a4PA,===P20);(故点,46200P).)或(,﹣综上,点,的坐标为:(71BCykx2C02),,则点.解:(﹣)直线的解析式为,﹣=(Cyx+b2bb2,=﹣==﹣将点的坐标代入,解得:得:﹣ACyx2;=﹣的表达式为:故直线﹣2OB6OBCOOBBOC6,=,解得:=△×=的面积=?0B6),,故点(k0Bykx26k2;=﹣,解得:得:=将点的坐标代入=﹣2kb;,故==﹣2A2AC90DAD0),,,则点()将直线绕点逆时针旋转(°得到直线+2xyDAAD;、的坐标得,直线=的表达式为:由点MBBADBBNADCx,则,交交′,连接关于直线过点作点的对称点′于点轴于点NM为所求点,、点.CDxMCMDNBNB′,轴的对称点,则,而关于点=是点=DM+MN+NBMC+MN+NBBC为最小,′=′=故AD45BBACABAB8,′⊥=直线,则的倾斜角为′=°,ABAD45ABABB28),,故点直线′与′⊥的夹角也为,°,故直线′(﹣BCBCy5x2,由点=﹣′、的表达式为:的坐标得,直线﹣′x0x2y05,==,即﹣令=﹣,解得:﹣0M),故点(﹣,2CB+MN+NBDM;=最小值为=′DAO3AODACmm′,′个单位,(向下平移)设△′沿着直线个单位得到△向右平移mm2A),则点﹣′(,﹣AbADyx+′的坐标代入上式得:设直线′,将点′=′的表达式为:m2mm2+bb2,﹣′==﹣﹣′,解得:mADyx+22,′的表达式为:﹣′=则直线202mDm0x2m2P220Amy),,则,﹣=(﹣),而点,故点),点(令′(=﹣﹣,,22222222+42m+8PDAP2mDA2m2+m22m;,则(﹣′﹣=﹣),)′=(=(﹣=)22+8mm2DAPA2,解得:方程无解;当时,′==′2mAPPD;时,同理可得:=当=′4m0ADPD,=(舍去)或时,同理可得:当=′02P06).)或(综上,点(,,By18BCx+x,轴于点=交.解:()∵直线:0B8),坐标(﹣∴点,mC),的坐标为(∵.+x,=∴m,∴=﹣C),坐标为(﹣∴点5CO;==∴2)如图,(OCABC的中线,∵为△BOAO8,=∴=108S,==∴××ACO△O00C),∵点坐标(),点坐标为(﹣,xCOy,解析式为:∴直线=﹣tDt),∴点(,﹣8St4t×(﹣×,=)=﹣∴AOD△10St4SS﹣=﹣=,﹣∴AOCACDAOD△△△ADE的中点,∵点为52StS;∴=﹣=﹣ACD△tA80D3tEAD中点,,(()∵点(),点,﹣是),点tE,﹣坐标(),∴点CE,∵=2213+t+,=)()﹣∴(﹣.t6t8,,∴=﹣=﹣218D68),,,(﹣)或(﹣∴点6Dt2665S7,)﹣=﹣=当×(﹣(﹣,),=﹣时,则点1DFxH,延长轴于点交Hx0)设点,(FDBOBD,∵∠=∠DHBH,∴=+8x=∴20x,∴=0H20),(∴点,b+DHykx,的解析式为:设直线=∴∴+yxDH,的解析式为:=﹣∴直线++xx,∴=﹣x,∴=F),,(∴点1158S2Dt888,)﹣),=﹣==﹣当,点(﹣,×(﹣2B8880D),,(﹣),点,(﹣∵点.DBO90°,∴∠=FDBOBD90°,=∠=∵∠DFBO,∴∥8F,∴点的纵坐标为+x8,∴=x,∴=8F).(,∴点F8坐标为(综上所述:点,).)或(,91ykx+6,.解:(=)1x0y6,==时,当OB6,=∴OAOB,=∵2OA,∴=02A),∴,(﹣2k+6A+6200ykx,,=)代入:=把中得:﹣(﹣11k,=1x+6ly;∴直线=的解析式为:121CCHxH,(⊥)如图轴于,过作1C),(∵,CHOH1,=∴,=ABABO Rt4=△,=中,AB2OA,=∴OBA30OAB60°,=°,∠=∴∠.CDAB,∵⊥ADE90°,∴∠=AED30°,∴∠=EH,∴=2EHOEOH+=,=∴20E),(∴,bx+E2Ck1y0,把((,)和=)代入中得:,2,解得:xy+2l,=﹣∴直线:2F02BF624,,﹣)即=∴=(,则,解得3D),∴(﹣,x4BFxS)=;(==∴﹣DCBCD△3)分四种情况:(Qy2DDMyMCCNyN,①当在作轴的正半轴上时,如图,过⊥作⊥轴于轴于,过QCDCD为底边的等腰直角三角形,∵△是以CQD90CQDQ,°,==∴∠DMQCNQ90°,==∠∴∠.MDQCQN,∴∠=∠DMQQNCAAS),≌△(∴△CNQNQMDM,∴===,m+6m0DmQ0m+1),),则,,﹣<设(()(OQQN+ONOM+QM,==∴+6+m+1m,即﹣=2m1,==﹣20Q);(,∴Qx3DDMxMCCNxN,⊥⊥轴于作②当作在,过轴的负半轴上时,如图,过轴于DMQQNCAAS),≌△(同理得:△DMQNQMCN1,∴==,=m+6m0QDmm+10),(,),则设)((,<OQQNONOMQM,=﹣∴﹣=m+61m,即﹣=﹣﹣45m﹣=,40Q6﹣(∴,);Qx4DDMxMCCNxN,轴于⊥作,过轴于⊥作,过轴的负半轴上时,如图在当③.DMQQNCAAS),≌△(同理得:△DMQNQMCN1,∴===,m+6m0QDmm10),(,),则,设()(<﹣OQQNONOM+QM,﹣∴==m+1m6,即﹣﹣=﹣﹣5m4,﹣=﹣046Q);﹣∴(﹣,Qy5DDMyMCCNyN,轴于⊥作,过轴于⊥作,过轴的负半轴上时,如图在当④.DMQQNCAAS),≌△同理得:△(CNQMDMQN,==,=∴m+6m0Q0m+1Dm),(),则()(,,设<OQQNONOM+QM,=∴﹣=6+m1m,=﹣即﹣﹣﹣1m2,﹣=﹣2Q0,﹣∴);(QQCDCDQ0,±为底边的等腰直角三角形,点综上,存在点的坐标是(,使△是以4640260).,)或(,﹣)或(﹣﹣101yx+1yx2P相交于点)∵直线﹣=﹣.解:(=和直线,∴,解之得:P,∴点坐标为:2yx+1yx2yAB两点轴于和直线=)∵直线=﹣、﹣分别交(A01B02),(,﹣∴(,),AB3,=∴.P1)知由(S;=∴=ABP△3Mmm+1Nmm2),,),则(,﹣)设﹣((MN5,∵=|m+1m2|5,﹣()﹣∴=﹣m1m4,解得或=﹣=M43N42M12N13).(),,,﹣)或(﹣∴(﹣(,,﹣),A1yBkx+b11,将点解得:、得:解:(.的坐标代入一次函数表达式:,=)l;故直线的表达式为:ABC Rt2中,(△)在2222213AB3OA+2+OB==由勾股定理得:=ABC为等腰直角三角形,∵△2ABS;==∴ABC△PAPO3BP,则:(,)连接,1P:在第一象限时,如图①若点aSS1S3,,∵==,=BOPABOAPO△△△SS+SS,﹣=∴=ABOBOPABPAPO△△△△.;,解得即P2:②若点在第四象限时,如图aS3S1S,,=﹣,∵==BOPAPOABO△△△SSSS+,==﹣∴ABOABPAPOBOP△△△△3a;即,解得=﹣a3ABPABC的值为.故:当△面积相等时,实数或﹣与△121Eyx+2E6,)∵点上一点,点是直线.解:(的纵坐标是=x+26,∴=x4,解得,=E46),的坐标是(,∴点T xyDE的融合点,()是点,和∵点2yx,=,∴===2T),,∴点的坐标为(2);,故答案为:(2Eaa+2),()设点,的坐标为(T xyDE的融合点,,)是点∵点和(yx,,∴==a3x3a3y2,﹣=,﹣=解得,3x33y2,﹣∴﹣=xy;=整理得,﹣3Eaa+2),)设点(的坐标为(,T),则点的坐标为(,THD90ET的横坐标相同,=与点°时,点当∠a,∴=a,解得,=E),,此时点的坐标为(TDH90TD的横坐标相同,°时,点与点当∠=3,=∴a6,解得,=E68),的坐标为(此时点,DTH90°时,该情况不存在,当∠=6E8DTH).的坐标为(,综上所述,当△,为直角三角形时,点)或(131A60ykx+8中,)把)代入(.解:(=,0+86k,=,解得:得,∴x3y4,代入,得==把C34);(∴,2CFxFEGxG,轴于点⊥,轴于点⊥)作(.CDE是等腰直角三角形,∵△CDDECDE90°,∴,∠==CDF90EDGDEGCFDDGE90°,=∠=∠,且∠∴∠==°﹣∠CDFDEGAAS)(∴△≌△CFDG4DFEG3m,=∴,=﹣==OG4+m,∴=E4+mm3);,(∴﹣3E4+mm3Elyx7上,),则点=(﹣)点在直线(﹣,:lyH07),交(设:直线轴于点,﹣OlO′,作直线过点的对称点l45HOxO77),轴,则点∵直线,﹣的倾斜角为°,则′(′∥COlEE′为所求点,于点′交直线连接′,则点OC是常数,OCEOC+CE+OEOC+OE+CEOC+CE+OEOC+CO′为最小,′′=△周长=′=′=′+COCOyx=﹣′的坐标得,直线′的表达式为:、由点,联立,解得:.故:b+Bykx141A得:的坐标代入一次函数表达式:,解得:、.解:(=)将点,x+2ABy;的表达式为:故直线=﹣x+2D022ABy),,则点)直线=﹣的表达式为:,((22243AD1AODOABD,=,的坐标得:=由点、,、=222ADDO+OA,故=AOD为直角三角形;故△1OC+2CAB3y2x,(),则)直线的表达式为:(,故点=﹣,=AB30DBO30ODA60DOA30°则直线=的倾斜角为=°,即∠=°,则∠°,则∠1OC2C,),则故点=(,CABCOBDBO30AOC30DOC60°,=则点°,则∠是的中点,故∠==∠=°,∠OQCPtOPOCPC2t,﹣==﹣==,则OPOM1,①当=时,如图180AOC75OQP45OMPMPO°,°﹣∠°,故∠则∠)==∠==(PPHyH,过点作轴于点⊥2tOPOH),﹣=则=(2tPHQH,=﹣由勾股定理得:()=+2tOH2ttOQQH+,=)﹣(=﹣)=(t;=解得:MOMP2,=时,如图②当MPOMOP30QOP60°,=∠°,而∠==则∠OQP90°,=∴∠2tOPOQt),故=(=﹣,即t;解得:=POPM时,③当=OMPMOP30MOQ30°,==∠=°,而∠则∠故这种情况不存在;t.或=综上,115,由題意,.解:(①),解得:C44).,(所以.x4ABOC的下方,>观察图象可知位于直线时,直线②x+104xx.>时,﹣即<2OCOMOPMQ,上截取,连结(=)由题意,在ONAOC,∵平分∠AOQCOQ,∴∠=∠OQOQ.又=POQMOQSAS),≌△(∴△PQMQ,∴=AQ+PQAQ+MQ,=∴AQMAMOCAQ+MQ最小,当在同一直銭上,且、吋,、⊥AQ+PQ存在最小値;即ABON,∴⊥AEOCEO,∴∠=∠AEOCEOASA),≌△∴△(OCOA6,∴==OAC9,∵△的面积为OCAM9,?∴=AM3,∴=AQ+PQ3.存在最小值,最小值为∴。
2020年中考数学压轴题专题复习:一次函数与反比例函数-答案
2020年中考数学压轴题专题复习:一次函数与反比例函数一、选择题(本大题共6道小题)1. 如图,A 、B 两点在反比例函数y =k 1x 的图象上,C 、D 两点在反比例函数y =k 2x的图象上,AC ⊥x 轴于点E ,BD ⊥x 轴于点F ,AC =2,BD =3,EF =103,则k 2-k 1=( )A. 4B.143 C. 163D. 62. 已知一次函数y =kx +b -x 的图象与x 轴的正半轴相交,且函数值y 随自变量x 的增大而增大,则k ,b 的取值情况为( )A. k >1,b <0B. k >1,b >0C. k >0,b >0D. k >0,b <03. 下列函数中,满足y 的值随x 的值增大而增大的是( )A. y =-2xB. y =3x -1C. y =1xD. y =x 24. 设函数y =kx (k ≠0,x >0)的图象如图所示,若z =1y,则z 关于x 的函数图象可能为( )5. 二次函数y =ax 2+bx +c (a ,b ,c 为常数且a ≠0)的图象如图所示,则一次函数y =ax+b 与反比例函数y =cx的图象可能是( )6. 若式子k-1+(k-1)0有意义,则一次函数y=(1-k)x+k-1的图象可能是()二、填空题(本大题共5道小题)7. 已知反比例函数y =k x的图象在每一个象限内y 随x 的增大而增大,请写一个符合条件的反比例函数解析式____________.8. 如图所示,已知点C (1,0),直线y =-x +7与两坐标轴分别交于A ,B 两点,D ,E分别是AB ,OA 上的动点,则△CDE 周长的最小值是________.9. 将函数y =2x +b (b 为常数)的图象位于x 轴下方的部分沿x 轴翻折至其上方后,所得的折线是函数y =|2x +b |(b 为常数)的图象,若该图象在直线y =2下方的点的横坐标x 满足0<x <3,则b 的取值范围为____________.10. 如图,一次函数y =kx +b 的图象分别与反比例函数y =a x的图象在第一象限交于点A (4,3),与y 轴的负半轴交于点B ,且OA =OB .(1)求函数y =kx +b 和y =ax的表达式;(2)已知点C (0,5),试在该一次函数图象上确定一点M ,使得MB =MC .求此时点M 的坐标.11. 如图,已知点A ,C 在反比例函数y =a x的图象上,点B ,D 在反比例函数y =b x的图象上,a >b >0,AB ∥CD ∥x 轴,AB ,CD 在x 轴的两侧,AB =34,CD =32,AB 与CD 间的距离为6,则a -b 的值是________.三、解答题(本大题共4道小题)12. 如图,在平面直角坐标系xOy 中,直线y =-x +3与x 轴交于点C ,与直线AD 交于点A (43,53),点D 的坐标为(0,1). (1)求直线AD 的解析式;(2)直线AD 与x 轴交于点B ,若点E 是直线AD 上一动点(不与点B 重合),当△BOD 与△BCE相似时,求点E的坐标.13. 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下,已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).(1)求出w与x的函数关系式;(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.14. 如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.(1)求m的值;(2)求A、B两点的坐标;(3)点P(a,b)(-3<a<1)是抛物线上一点,当△P AB的面积是△ABC面积的2倍时,求a、b的值.15. 如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).(1)求a,b的值;(2)点C是该二次函数图象上A、B两点之间的一动点,横坐标为x(2<x<6).写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.答案一、选择题(本大题共6道小题)1. 【答案】A 【解析】设E (x 1,0),F (x 2,0),则A (x 1,k 1x 1),D (x 2,k 2x 2),B (x 2,k 1x 2),C (x 1,k 2x 1),∴AC =k 1-k 2x 1=2,BD =k 2-k 1x 2=3,∴k 1-k 2=2x 1,k 2-k 1=3x 2,∴2x 1+3x 2=0,又∵EF =x 2-x 1=103,∴x 2=43,∴k 2-k 1=3x 2=3×43=4.2. 【答案】A 【解析】原解析式可变形为y =(k -1)x +b ,∵函数值y 随自变量x 的增大而增大,∴k -1>0,∴k >1,∵图象与x 轴正半轴相交,∴b <0,∴满足题意的k 、b 情况为k >1,b <0.3. 【答案】B 【解析】一次函数y =-2x 中,y 随x 增大而减小;一次函数y =3x -1中,y 随x 的增大而增大;反比例函数y =1x 中,在每一个分支上,y 随x 的增大而减小;二次函数y =x 2中,当x >0时,y 随x 增大而增大,当x <0时,y 随x 的增大而减小,故答案为B .4. 【答案】D 【解析】函数y =k x(k ≠0,x >0)的图象在第一象限,则k >0,x >0.由已知得z =1y =1k x=xk,所以z 关于x 的函数图象是一条射线,且在第一象限,故选D.5. 【答案】C 【解析】抛物线开口向上,所以a >0,对称轴在y 轴右侧,所以a 、b异号,所以b <0,抛物线与y 轴交于负半轴,所以c <0,所以直线y =ax +b 过第一、三、四象限,反比例函数y =cx位于第二、四象限,故答案为C.6. 【答案】C 【解析】式子k -1+(k -1)0有意义,则k >1,所以1-k <0,k -1>0,所以一次函数y =(1-k )x +k -1的图象经过第一、二、四象限.二、填空题(本大题共5道小题)7. 【答案】y =-2x(答案不唯一) 【解析】∵反比例函数的图象在每一个象限内y 随x的增大而增大,∴k <0,∴k 可取-2(答案不唯一).8. 【答案】10 【解析】作点C 关于y 轴的对称点C 1(-1,0),点C 关于直线AB 的对称点C 2,连接C 1C 2交OA 于点E ,交AB 于点D ,则此时△CDE 的周长最小,且最小值等于C 1C 2的长.∵OA =OB =7,∴CB =6,∠ABC =45°.∵AB 垂直平分CC 2,∴∠CBC 2=90°,∴C 2的坐标为(7,6).在Rt △C 1BC 2中,C 1C 2=C 1B 2+C 2B 2=82+62=10.即△CDE 周长的最小值是10.9. 【答案】-4<b<-2 【解析】先求出直线y =2与y =|2x +b|的交点的横坐标,再由已知条件列出关于b 的不等式组,便可求出结果.由⎩⎪⎨⎪⎧y =2y =|2x +b|,得⎩⎪⎨⎪⎧y =2y =2x +b或⎩⎪⎨⎪⎧y =2y =-2x -b ,解得x =2-b 2或x =-2+b2,∵0<x<3,∴⎩⎨⎧2-b2<3-b +22>0,解得-4<b<-2.10. 【答案】(1)【思路分析】由点A 的坐标和OA =OB 可得点B 的坐标,用待定系数法即可求出一次函数的解析式;将点A 的坐标代入反比例函数解析式中即可求出反比例函数的解析式.解:∵点A(4,3),∴OA =42+32=5,∴OB =OA =5, ∴B(0,-5),将点A(4, 3),点B(0, -5)代入函数y =kx +b 得,⎩⎪⎨⎪⎧4k +b =3b =-5,解得⎩⎪⎨⎪⎧k =2b =-5,(2分) ∴一次函数的解析式为y =2x -5, 将点A(4, 3)代入y =ax 得,3=a 4, ∴a =12,∴反比例函数的解析式为y =12x, ∴所求函数表达式分别为y =2x -5和y =12x.(4分) (2)【思路分析】由题意可知,使MB =MC 的点在线段BC 的垂直平分线上,故求出线段BC 的垂直平分线和一次函数的交点即可.解:如解图,∵点B 的坐标为(0, -5),点C 的坐标为(0, 5),∴x 轴是线段BC 的垂直平分线, ∵MB =MC ,∴点M 在x 轴上,又∵点M 在一次函数图象上,∴点M 为一次函数的图象与x 轴的交点,如解图所示, 令2x -5=0,解得x =52,(6分)∴此时点M 的坐标为(52, 0).(8分)11. 【答案】3 【解析】设点A 的纵坐标为y 1,点C 的纵坐标为y 2,∵AB ∥CD ∥x轴,∴点B 的纵坐标为y 1,点D 的纵坐标为y 2,∵点A 在函数y =ax 的图象上,点B 在函数y =b x 的图象上,且AB =34,∴a y 1-b y 1=34,∴y 1=4(a -b )3,同理y 2=2(b -a )3,又∵AB与CD 间的距离为6,∴y 1- y 2=4(a -b )3-2(b -a )3=6,解得a -b =3.三、解答题(本大题共4道小题)12. 【答案】解:(1)设直线AD 的解析式为y =kx +b(k≠0), 将D(0,1)、A(43,53)代入解析式得⎩⎪⎨⎪⎧b =143k +b =53, 解得⎩⎪⎨⎪⎧b =1k =12,∴直线AD 的解析式为y =12x +1.(3分) (2)直线AD 的解析式为y =12x +1,令y =0,得x =-2, ∴B(-2,0),即OB =2.∵直线AC 的解析式为y =-x +3,令y =0,得x =3,∴C(3,0),即BC =5,设E(x ,12x +1), ①当E 1C ⊥BC 时,∠BOD =∠BCE 1=90°,∠DBO =∠E 1BC ,∴△BOD ∽△BCE 1,此时点C 和点E 1的横坐标相同,将x =3代入y =12x +1, 解得:y =52, ∴E 1(3,52).(6分) ②当CE 2⊥AD 时,∠BOD =∠BE 2C =90°,∠DBO =∠CBE 2,∴△BOD ∽△BE 2C ,如解图,过点E 2作E 2F ⊥x 轴于点F ,则∠E 2FC =∠BFE 2=90°.∵∠E 2BF +∠BE 2F =90°,∠CE 2F +∠BE 2F =90°,∴∠E 2BF =∠CE 2F ,∴△E 2BF ∽△CE 2F ,则E 2F BF =CF E 2F, 即E 2F 2=CF·BF ,(12x +1)2=(3-x)(x +2),解得:x 1=2,x 2=-2(舍去),∴E 2(2,2);(9分)③当∠EBC =90°时,此情况不存在.综上所述,点E 的坐标为E 1(3,52)或E 2(2,2).(10分)13. 【答案】解:(1)当0≤x≤50时,设商品的售价y 与时间x 的函数关系式为y =kx +b(k 、b 为常数且k≠0),∵y =kx +b 经过点(0,40),(50,90),∴⎩⎪⎨⎪⎧b =4050k +b =90, 解得⎩⎪⎨⎪⎧k =1b =40, ∴y =x +40,∴y 与x 的函数关系式为:y =⎩⎨⎧x +40 (0≤x≤50,且x 为整数)90 (50<x≤90,且x 为整数),(2分) 由数据可知每天的销售量p 与时间x 成一次函数关系.设每天的销售量p 与时间x 的函数关系式为p =mx +n(m ,n 为常数,且m≠0), ∵p =mx +n 过点(60,80),(30,140),∴⎩⎪⎨⎪⎧60m +n =8030m +n =140,解得⎩⎪⎨⎪⎧m =-2n =200, ∴p =-2x +200(0≤x≤90,且x 为整数),(3分)当0≤x≤50时,w =(y -30)·p=(x +40-30)(-2x +200),=-2x 2+180x +2000,当50<x≤90时,w =(90-30)×(-2x +200)=-120x +12000,综上所述,每天的销售利润w 与时间x 的函数关系式是:w =⎩⎨⎧-2x 2+180x +2000 (0≤x≤50,且x 为整数)-120x +12000 (50<x≤90,且x 为整数).(5分) (2)当0≤x≤50时,w =-2x 2+180x +2000=-2(x -45)2+6050,∵a =-2<0且0≤x≤50,∴x =45时,w 最大=6050(元),(6分)当50<x≤90时,w =-120x +12000,∵k =-120<0,∴w 随x 增大而减小.∴x =50时,w 最大=6000(元),∵6050>6000,∴x =45时,w 最大=6050(元),即销售第45天时,当天获得的销售利润最大,最大利润是6050元.(8分)(3)24天.(10分)【解法提示】①当0≤x ≤50,若w 不低于5600元,则w =-2x 2+180x +2000≥5600,解得30≤x ≤60,∴30≤x ≤50;②当50<x ≤90时,若w 不低于5600元,则w =-120x +12000≥5600,解得x ≤1603, ∴50<x ≤1603, 综合①②可得30≤x ≤1603, ∴从第30天到第53天共有24天利润不低于5600元.14. 【答案】解:(1)∵抛物线y =x 2-(m +3)x +9的顶点在x 轴的正半轴上,∴方程x 2-(m +3)x +9=0有两个相等的实数根,∴b 2-4ac =[-(m +3)]2-4×9=0,解得m =3或m =-9,又∵抛物线对称轴大于0,即m +3>0,∴m =3.(3分)(2)由(1)可知抛物线解析式为y =x 2-6x +9,联立一次函数y =x +3,可得⎩⎪⎨⎪⎧y =x 2-6x +9y =x +3, 解得⎩⎪⎨⎪⎧x =1y =4或⎩⎪⎨⎪⎧x =6y =9, ∴A(1,4),B(6,9).(6分)(3)如解图,分别过A 、B 、P 三点作x 轴的垂线,垂足分别为R 、S 、T ,∵A(1,4),B(6,9),C(3,0),P(a ,b),∴AR =4,BS =9,RC =3-1=2,CS =6-3=3,RS =6-1=5,PT =b ,RT =1-a ,ST =6-a ,∴S △ABC =S 梯形ABSR -S △ARC -S △BCS =12×(4+9)×5-12×2×4-12×3×9=15, S △PAB =S 梯形PBST -S 梯形ARTP -S 梯形ARSB =12(9+b)(6-a)-12(b +4)(1-a)-12×(4+9)×5=12(5b -5a -15).(8分)又∵S △PAB =2S △ABC ,∴12(5b -5a -15)=30,即b -a =15, ∴b =15+a ,∵P 点在抛物线上,∴b =a 2-6a +9,∴15+a =a 2-6a +9,解得a =7±732, ∵-3<a<1,∴a =7-732, ∴b =15+7-732=37-732.(10分)15. 【答案】解:(1)∵二次函数y =ax 2+bx 的图象经过点A(2,4)与B(6,0).∴⎩⎪⎨⎪⎧4a +2b =436a +6b =0, 解得⎩⎪⎨⎪⎧a =-12b =3.(4分) (2)如解图①,过点A 作x 轴的垂线,垂足为点D(2,0),连接CD ,过点C 作CE ⊥AD ,CF ⊥x 轴,垂足分别为点E ,点F ,则S △OAD =12OD·AD =12×2×4=4, S △ACD =12AD·CE =12×4×(x -2)=2x -4, S △BCD =12BD·CF =12×4×(-12x 2+3x)=-x 2+6x , 则S =S △OAD +S △ACD +S △BCD =4+(2x -4)+(-x 2+6x)=-x 2+8x.∴S 关于x 的函数表达式为S =-x 2+8x(2<x<6).(10分)∵S =-(x -4)2+16,∴当x =4时,四边形OACB 的面积S 取最大值,最大值为16.(12分)图①【一题多解】解法一:由(1)知y =-12x 2+3x ,如解图②,连接AB ,则 S =S △AOB +S △ABC ,其中S △AOB =12×6×4=12, 设直线AB 解析式为y 1=k 1x +b 1,将点A(2,4),B(6,0)代入,易得,y 1=-x +6,过C 作直线l ⊥x 轴交AB 于点D ,∴C(x ,-12x 2+3x),D(x ,-x +6), ∴S △ABC =S △ADC +S △BDC =12·CD·(x -2)+12·CD·(6-x)=12·CD·4=2CD , 其中CD =-12x 2+3x -(-x +6)=-12x 2+4x -6, ∴S △ABC =2CD =-x 2+8x -12,∴S =S △ABC +S △AOB =-x 2+8x -12+12=-x 2+8x =-(x -4)2+16(2<x<6), 即S 关于x 的函数表达式为S =-x 2+8x(2<x<6),∴当x =4时,四边形OACB 的面积S 取最大值,最大值为16.图②解法二:∵点C 在抛物线y =-12x 2+3x 上, ∴点C(x ,-12x 2+3x), 如解图③,过点A 作AD ⊥x 轴,垂足为点D ,过点C 作CE ⊥x 轴,垂足为点E ,则 点D 的坐标为(2,0),点E 的坐标为(x ,0),∴S =S △OAD +S 梯形ADEC +S △CEB =12×2×4+12(4-12x 2+3x)(x -2)+12(6-x)(-12x 2+3x)=-x 2+8x ,∵S =-x 2+8x =-(x -4)2+16(2<x<6),∴当x =4时,四边形OACB 的面积S 取最大值,最大值为16.图③。
2020年中考数学必考经典题讲练案-一次函数的图象性质问题(解析版)【苏科版】 (2)
2020年中考数学必考经典题讲练案【苏科版】专题06一次函数的图象性质问题【方法指导】一次函数的具体知识点有:1.一次函数的相关概念(1)概念:一般来说,形如y=kx+b(k≠0)的函数叫做一次函数.特别地,当b =0时,称为正比例函数.(2)图象形状:一次函数y=kx+b是一条经过点(0,b)和(-b/k,0)的直线.特别地,正比例函数y=kx的图象是一条恒经过点(0,0)的直线.2.一次函数的性质k,b符号k>0,b>0K>0,b<0K>0,b=0k<0,b>0k<0,b<0k<0,b=0 大致图象经过象限一、二、三一、三、四一、三一、二、四二、三、四二、四图象性质y随x的增大而增大y随x的增大而减小3.一次函数与坐标轴交点坐标(1)交点坐标:求一次函数与x轴的交点,只需令y=0,解出x即可;求与y轴的交点,只需令x=0,求出y即可.故一次函数y=kx+b(k≠0)的图象与x轴的交点是⎝⎛⎭⎫-bk,0,与y轴的交点是(0,b);(2)正比例函数y=kx(k≠0)的图象恒过点(0,0).4.确定一次函数表达式的条件(1)常用方法:待定系数法,其一般步骤为:①设:设函数表达式为y=kx+b(k≠0);②代:将已知点的坐标代入函数表达式,解方程或方程组;③解:求出k与b的值,得到函数表达式.(2)常见类型:①已知两点确定表达式;②已知两对函数对应值确定表达式;③平移转化型:如已知函数是由y=2x平移所得到的,且经过点(0,1),则可设要求函数的解析式为y=2x+b,再把点(0,1)的坐标代入即可.5.一次函数图象的平移规律:①一次函数图象平移前后k不变,或两条直线可以通过平移得到,则可知它们的k值相同.②若向上平移h单位,则b值增大h;若向下平移h单位,则b值减小h.6.一次函数与方程一元一次方程kx+b=0的根就是一次函数y=kx+b(k、b是常数,k≠0)的图象与x轴交点的横坐标.7.一次函数与方程组二元一次方程组1112y k x by k x b=+⎧⎨=+⎩的解⇔两个一次函数y=k1x+b1和y=k2x+b2图象的交点坐标.8.一次函数与不等式(1)函数y=kx+b的函数值y>0时,自变量x的取值范围就是不等式kx+b>0的解集(2)函数y=kx+b的函数值y<0时,自变量x的取值范围就是不等式kx+b<0的解集【题型剖析】【类型1】一次函数的性质和性质的应用【例1】(2019春•如皋模拟)已知函数y=(2m+1)x+m﹣3.(1)若这个函数的图象经过原点,求m的值(2)若这个函数的图象不经过第二象限,求m的取值范围.【变式1-1】(2019•玄武区校级模拟)已知一次函数y=kx+b,函数值y随自变量x的增大而减小,且kb<0,则函数y=kx+b的图象大致是()【变式1-2】(2019•常州校级模拟)已知一次函数y=kx+b,函数值y随自变量x的增大而减小,且kb<0,则函数y=kx+b的图象大致是()【变式1-3】(2019•邳州市模拟)已知函数y=(2m+1)x+m﹣3(1)若函数图象经过原点,求m的值;(2)若函数的图象平行直线y=3x﹣3,求m的值;(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.【类型2】:一次函数与方程不等式【例2】(2019春•崇川区校级模拟)已知直线y=﹣3x+b与直线y=﹣kx+1在同一坐标系中交于点,则关于x的方程﹣3x+b=﹣kx+1的解为x=.【变式2-1】(2019春•京口区校级模拟)已知一次函数y=kx+b与y=mx+n的图象如图所示,若kx+b<mx+n,则x的取值范围为.【变式2-2】(2018秋•垣曲县期末)如图,已知直线y=ax+b和直线y=kx交于点P(﹣4,﹣2),则关于x,y的二元一次方程组的解是.【类型3】:一次函数图象上点的坐标特征【例3】(2019春•海陵区校级期末)如图,直线y1=3x+4交x轴、y轴于点A、C,直线y2x+4交x 轴、y轴于点B、C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为()A.B.6 C.D.【变式3-1】(2019•无锡二模)在平面直角坐标系中,已知A、B、C、D四点的坐标依次为(0,0)、(6,0),(8,6),(2,6),若一次函数y=mx﹣8m+6的图象将四边形ABCD的面积分成1:3两部分,则m的值为()A.B.或C.或D.或1【变式3-2】(2019春•海州区校级期中)如图,在平面直角坐标系中,一次函数y=2x﹣5的图象经过正方形OABC的顶点A和C,则正方形OABC的面积为()A.9 B.10 C.12 D.13【类型4】:一次函数的几何变换问题【例4】(2019春•如皋市期中)直线y=3x+2沿y轴向下平移6个单位,则平移后直线解析式为.【变式4-1】(2019•鼓楼区二模)在平面直角坐标系中,将函数y=2x﹣3的图象先向右平移2个单位长度,再沿y轴翻折,所得函数对应的表达式为.【变式4-2】(2018秋•邗江区校级期末)若直线L1经过点(0,4),L2经过点(3,2),且L1与L2关于x 轴对称,则L1与L2的交点坐标为.【变式4—3】(2019春•常州期中)如图,在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点B(6,2),C(4,0),直线y=2x+1以每秒1个单位长度的速度沿y轴向下平移,经过秒该直线可将平行四边形OABC分成面积相等的两部分.【类型5】:一次函数的几何综合性问题【例5】.(2018秋•张家港市期末)如图,一次函数y=﹣x+7的图象与正比例函数y x的图象交于点A,点P(t,0)是x正半轴上的一个动点.(1)点A的坐标为(,);(2)如图1,连接P A,若△AOP是等腰三角形,求点P的坐标:(3)如图2,过点P作x轴的垂线,分别交y x和y=﹣x+7的图象于点B,C.是否存在正实数,使得BC OA,若存在求出t的值;若不存在,请说明理由.【变式5-2】(2019春•溧阳市期中)在平面直角坐标系xOy中,点M的坐标为(x1,y1),点的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角分平行于x轴、y轴,则称该菱形为边的“坐标菱形”.(1)已知点A(2,0),B(0,3),则以AB为边的“坐标菱形”的面积为;(2)若点C(1,2),点D在直线x=5上,以CD为边的“坐标菱形”为正方形,求直线CD的函数表达式.【变式5-3】(2019•洪泽区二模)如图,直线y x+4与x轴、y轴分别交于A,B两点,C是OB的中点,D是AB上一点,四边形OEDC是菱形,(1)求A、C两点的坐标;(2)求证:△BCD为等边三角形;(3)请直接写出同时经过A、E两点的直线的函数表达式.【达标检测】1.若一次函数(y kx b k =+,b 为常数,且0)k ≠的图象经过点(0,1)A -,(1,1)B ,则不等式1kx b +>的解为()A .0x <B .0x >C .1x <D .1x >2.(2019•扬州)若点P 在一次函数4y x =-+的图象上,则点P 一定不在( ) A .第一象限B .第二象限C .第三象限D .第四象限3.(2018•徐州)若函数y kx b =+的图象如图所示,则关于x 的不等式20kx b +<的解集为( )A .3x <B .3x >C .6x <D .6x >4.(2018•常州)一个正比例函数的图象经过(2,1)-,则它的表达式为( ) A .2y x =-B .2y x =C .12y x =-D .12y x =5.(2019•秦淮区二模)在平面直角坐标系中,点A 、B 的坐标分别是(0,3)、(4,0)-,则原点到直线AB 的距离是( ) A .2B .2.4C .2.5D .36.(2019•孝义市二模)已知点1(A x ,1)y 和点2(B x ,2)y 在一次函数(1)y m x n =++的图象上,并且12x x <,12y y >,则m 的取值范围是( )A .0m >B .0m <C .1m >-D .1m <-7.(2019•姜堰区二模)已知过点(1,2)的直线(0)y ax b a =+≠不经过第四象限,设2S a b =+,则S 的取值范围为( ) A .24S <<B .24S <C .24S <D .24S8.(2019•常州一模)已知点1(x ,3),2(x ,2)是直线21y x =-+上两点,则下列正确的是( ) A .120x x ->B .120x x -<C .12x x =D .120x x +>二.填空题(共5小题)9.(2019•徐州)函数1y x =+的图象与x 轴、y 轴分别交于A 、B 两点,点C 在x 轴上.若ABC ∆为等腰三角形,则满足条件的点C 共有 个.10.(2019•无锡)已知一次函数y kx b =+的图象如图所示,则关于x 的不等式30kx b ->的解集为 .11.(2019•惠山区二模)当13x -时,不等式40mx +>始终成立,则m 的取值范围是 .12.(2019•天宁区校级二模)在平面直角坐标系中,A 点坐标为(1,0),C 点坐标为(7,0),若点P 在直线3y kx =+上运动时,只存在一个点P 使90APC ∠=︒,则k 的值是13.(2019•靖江市校级一模)平面直角坐标系中,P 为直线y x b =-+上一点,过P 作PA x ⊥轴于A ,PB y ⊥轴于B .当矩形PAOB 的面积为6时,相应的点P 有且只有3个,则b = . 三.解答题(共7小题)14.(2019•南京)已知一次函数12(y kx k =+为常数,0)k ≠和23y x =-. (1)当2k =-时,若12y y >,求x 的取值范围.(2)当1x <时,12y y >.结合图象,直接写出k 的取值范围.15.(2019•梁溪区一模)如图,已知(3,0)A ,(0B ,)(30)a a -<<,以AB 为一边在AB 上方作正方形ABCD ,点E 与点A 关于y 轴对称,直线EC 交y 轴于点F ,连接DF . (1)求直线EF 所对应的函数表达式; (2)判断CE 与DF 的数量关系并说明理由.16.(2019•滨湖区一模)如图,已知矩形OABC的顶点A在x轴的负半轴上,顶点C在y轴上,且4AB=.P 为OC上一点,将BCP∆沿PB折叠,点C落在第三象限内点Q处,BQ与x轴的交点M恰好为OA的中点,且1MQ=.(1)求点A的坐标;(2)求折痕PB所对应的函数表达式.17.(2019•鼓楼区校级模拟)如图,一次函数y kx b=+的图象经过B、C,A是此图象上一点,AM垂直于x轴,垂足为M,求:(1)一次函数y kx b=+的解析式;(2)梯形ABOM的面积S;(3)CAM∠的正弦函数的值.18.(2019•宝应模拟)如图,在平面直角坐标系xOy中,过点(2,0)A-的直线交y轴正半轴于点B,将直线AB绕着O顺时针旋转90︒后,分别与x轴y轴交于点D、C.(1)若4OB=,求直线AB的函数关系式;(2)连接BD,若ABD∆的面积是7.5,求点B的运动路径长.19.(2019•长春一模)如图,平面直角坐标系中,直线343y x =+分别交x 轴、y 轴于点A 、C ,直线BC 与直线AC 关于y 轴对称,动点D 从点A 出发,沿AC 以每秒2个单位长度的速度向终点C 运动,当点D 出发后,过点D 作//DE BC 交折线A O C --于点E ,以DE 为边作等边DEF ∆,设DEF ∆与ACO ∆重叠部分图形的面积为S ,点D 运动的时间为t 秒. (1)写出坐标:点(A ),点(B ),点(C ); (2)当点E 在线段AO 上时,求S 与t 之间的函数关系式; (3)求出以点B 、E 、F 为顶点的三角形是直角三角形时t 的值; (4)直接写出点F 运动的路程长为 .。
专题05一次函数压轴题年中考数学压轴题分类全国通用解析版
专题05 一次函数压轴题一、单选题1.如图,在平面直角坐标系中,点1234,,,,A A A A L 在x 轴正半轴上,点123,,,B B B L 在直线(0)y x ³上,若1(1,0)A ,且112223334,,,A B A A B A A B A V V V L 均为等边三角形,则线段20192020B B 的长度为( )A .2B .2C .2D .2【答案】D【分析】根据题意得出∠A n OB n =30°,从而推出A n B n =OA n ,得到B n B n+1n A n+1,算出B 1A 2=1,B 2A 3=2,B 3A 4=4,找出规律得到B n A n+1=2n-1,从而计算结果.【解析】解:设△B n A n A n+1的边长为a n ,∵点B 1,B 2,B 3,…是直线(0)y x =³上的第一象限内的点,过点A 1作x 轴的垂线,交直线(0)y x x =³于C ,∵A 1(1,0),令x=1,则∴A 1∴111tan A C A OC OA Ð==∴∠A n OB n =30°,∵112223334,,,A B A A B A A B A V V V L 均为等边三角形,∴∠B n A n A n+1=60°,∴∠OB n A n =30°,∴A n B n =OA n ,∵∠B n A n+1B n+1=60°,∴∠A n+1B n B n+1=90°,∴B n B n+1B n A n+1,∵点A 1的坐标为(1,0),∴A 1B 1=A 1A 2=B 1A 2=1,A 2B 2=OA 2=B 2A 3=2,A 3B 3=OA 3=B 3A 4=4,...,∴A n B n =OA n =B n A n+1=2n-1,∴20192020B B2019A 202020182,故选D .【点睛】本题考查了一次函数的性质、等边三角形的性质以及三角形外角的性质,本题属于基础题,难度不大,解决该题型题目时,根据等边三角形边的特征找出边的变化规律是关键.2.如图,过点0(0,1)A 作y 轴的垂线交直线:l y =于点1A ,过点1A 作直线l 的垂线,交y 轴于点2A ,过点2A 作y 轴的垂线交直线l 于点3A ,…,这样依次下去,得到012A A A D ,234A A A D ,4564A A D ,…,其面积分别记为1S ,2S ,3S ,…,则100S ( )A .100B .100C .1994D .3952【答案】D【分析】本题需先求出OA 1和OA 2的长,再根据题意得出OA n =2n ,把纵坐标代入解析式求得横坐标,然后根据三角形相似的性质即可求得S 100.【解析】∵点0A 的坐标是(0,1),∴01OA =,∵点1A 在直线y x =上,∴12OA =,01A A =∴24OA =,∴38OA =,∴416OA =,得出2n n OA =,∴12n n n A A +=∴1981982OA =,1981981992A A =∵11(41)2S =-=,∵21200199A A A A ∥,∴012198199200D D ∽A A A A A A ,∴21001S S =,∴39639522S ==故选D .【点睛】本题主要考查了如何根据一次函数的解析式和点的坐标求线段的长度,以及如何根据线段的长度求出点的坐标,解题时要注意相关知识的综合应用.3.在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线22y tx t =++(0t >)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t 的取值范围是()A .122t £<B .112t <£C .12t <£D .122t ££且1t ¹【答案】D【分析】画出函数图象,利用图象可得t 的取值范围.【解析】∵22y tx t =++,∴当y=0时,x=22t--;当x=0时,y=2t+2,∴直线22y tx t =++与x 轴的交点坐标为(22t --,0),与y 轴的交点坐标为(0,2t+2),∵t>0,∴2t+2>2,当t=12时,2t+2=3,此时22t--=-6,由图象知:直线22y tx t =++(0t >)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,如图1,当t=2时,2t+2=6,此时22t--=-3,由图象知:直线22y tx t =++(0t >)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,如图2,当t=1时,2t+2=4,22t--=-4,由图象知:直线22y tx t =++(0t >)与两坐标轴围成的三角形区域(不含边界)中有且只有三个整点,如图3,∴122t ££且1t ¹,故选:D.【点睛】此题考查一次函数的图象的性质,一次函数图象与坐标轴交点坐标,根据t 的值正确画出图象理解题意是解题的关键.4.如图,直线334y x =-+与x 轴、y 轴分别交于A 、B 两点,点P 是以C (﹣1,0)为圆心,1为半径的圆上一点,连接PA ,PB ,则△PAB 面积的最小值是( )A .5B .10C .15D .20【答案】A【分析】作CH ⊥AB 于H 交⊙O 于E 、F .当点P 与E 重合时,△PAB 的面积最小,求出EH 、AB 的长即可解决问题【解析】作CH ⊥AB 于H 交⊙O 于E 、F .连接BC .∵A(4,0),B(0,3),∴OA=4,OB=3,AB=5.∵S△ABC= 12AB•CH=12AC•OB,∴AB•CH=AC•OB,∴5CH=(4+1)×3,解得:CH=3,∴EH=3﹣1=2.当点P与E重合时,△PAB的面积最小,最小值12=´5×2=5.故选A.【点睛】本题考查了一次函数图象上的点的坐标特征、一次函数的性质、直线与圆的位置关系等知识,解题的关键是学会添加常用辅助线,利用直线与圆的位置关系解决问题,属于中考填空题中的压轴题.5.如图,平面直角坐标系xOy中,点A的坐标为(9,6),AB⊥y轴,垂足为B,点P从原点O出发向x 轴正方向运动,同时,点Q从点A出发向点B运动,当点Q到达点B时,点P、Q同时停止运动,若点P 与点Q的速度之比为1:2,则下列说法正确的是( )A.线段PQ始终经过点(2,3)B.线段PQ始终经过点(3,2)C .线段PQ 始终经过点(2,2)D .线段PQ 不可能始终经过某一定点【答案】B【分析】当OP=t 时,点P 的坐标为(t ,0),点Q 的坐标为(9﹣2t ,6).设直线PQ 的解析式为y=kx+b (k≠0),利用待定系数法求出PQ 的解析式即可判断;【解析】当OP=t 时,点P 的坐标为(t ,0),点Q 的坐标为(9﹣2t ,6).设直线PQ 的解析式为y=kx+b (k≠0),将P (t ,0)、Q (9﹣2t ,6)代入y=kx+b ,得,0(92)6kt b t k b +=ìí-+=î,解得:2323k t t b t ì=ïï-íï=ï-î,∴直线PQ 的解析式为y=23t -x+23t t -.∵x=3时,y=2,∴直线PQ 始终经过(3,2),故选B .【点睛】本题考查一次函数图象上的点的特征、待定系数法等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.6.规定:()3f x x =-,()4g y y =+,例如()4437f -=--=,()4440g -=-+=,下列结论中,正确的是( )①若()()0f x g y +=,则2318x y -=;②若4x <-,则()()12f x g x x =-;③能使()()f x g x =成立的x 的值不存在;④式子()()11f x g x -++的最小值是9.A .1个B .2个C .3个D .4个【答案】B【分析】根据非负数和为0的性质可判定①,由4x <-可以化简绝对值,进而可判断②;由两数绝对值相等得出两数相等或互为相反数可判断③;分三种情况讨论化简绝对值,利用一次函数的性质可判断④.【解析】解:①若()()0f x g y +=,即340x y -++=,解得:3,4x y ==-,则2318x y -=;故①正确;②若4x <-,则()()()()23412f x g x x x x x =-+--=+-,故错误;③若()()f x g x =,则34x x -=+,即34x x -=+或34x x -=--,解得:0.5x =-,所以能使()()f x g x =成立的x 的值存在;故错误;④式子()()1145f x g x x x -++=-++,当5x £-时,()()114521f x g x x x x -++=---=--,则()()11f x g x -++的值随x 的增大而减小,所以当x =-5时有最小值9;当54x -<<时,()()11459f x g x x x -++=-++=;当4x ³时,()()114521f x g x x x x -++=-++=+,则()()11f x g x -++的值随x 的增大而增大,所以当x =4时有最小值9;综上所述:()()11f x g x -++的最小值是9,故正确;∴正确的有①④,共2个;故选B .【点睛】本题主要考查一次函数的性质及绝对值,熟练掌握一次函数的性质及绝对值是解题的关键.7.如图,已知在平面直角坐标系xOy 中,点,A B 是函数102103103x x y x x ìæö-+ç÷ïïèø=íæöï>ç÷ïèøî…图象上的两动点,且点A 的横坐标是m ,点B 的横坐标是1m +,将点A ,点B 之间的函数图象记作图型L ,把图型L 沿直线1:32l y x =-+进行翻折,得到图型¢L ,若图型¢L 与x 轴有交点时,则m 的取值范围为( )A .2427m ££B .1727m ££C .2437m ££D .1737m ££【答案】A【分析】先由AB 关于l 对称直线和x 轴相交得到x 轴关于直线l 对称的直线也与AB 相交,作x 轴关于直线l 对称直线l 1,即其在132y x =-+中,然后再求出C 、D 点的坐标,求出OD 的长,设l 1的解析式为y =k (x -6),作DE ⊥l 1,可得OE =3,然后运用点与直线的距离求得k ,最后再代入分段函数即可求得m 的取值范围.【解析】解:∵AB 关于l 对称直线和x 轴相交∴x 轴关于直线l 对称的直线也与AB相交作x轴关于直线l对称直线l1,即其在132y x=-+中当y=0时,x=6,即C(6,0)在l中,当x=0时,y=3,即OD=3设l1的解析式为y=k(x-6),作DE⊥l1∵x轴和直线l1关于直线l对称∴OD=OE=3∴D到l1的距离3,解得k=4 3 -∴l1:y=43-x+8由题意可知:43-x+8=-2x+10103xæöç÷èø…,43-x+8=x103xæö>ç÷èø,解得x=3,x=247∴交点的横坐标为3和24 7∵交点在l上∴3≤m≤247或3≤m+1≤247,即2427m…….故选A.【点睛】本题主要考查了分段函数的应用、轴对称的性质、点到直线的距离等知识点,灵活运用相关知识成为解答本题的关键.8.如图,在平面直角坐标系中,Q是直线y=﹣12x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点Q¢,连接OQ¢,则OQ¢的最小值为( )A B C D【答案】B【分析】利用等腰直角三角形构造全等三角形,求出旋转后Q′的坐标,然后根据勾股定理并利用二次函数的性质即可解决问题.【解析】解:作QM⊥x轴于点M,Q′N⊥x轴于N,设Q(m,122m-+),则PM=1m﹣,QM=122m-+,∵∠PMQ=∠PNQ′=∠QPQ′=90°,∴∠QPM+∠NPQ′=∠PQ′N+∠NPQ′,∴∠QPM=∠PQ′N ,在△PQM 和△Q′PN 中,'90''PMQ PNQ QPM PQ N PQ Q P Ð=Ð=°ìïÐ=Ðíï=î,∴△PQM ≌△Q′PN(AAS),∴PN=QM=122m -+,Q′N=PM=1m ﹣,∴ON=1+PN=132m -,∴Q′(132m -,1m ﹣),∴OQ′2=(132m -)2+(1m ﹣)2=54m 2﹣5m+10=54(m ﹣2)2+5,当m=2时,OQ′2有最小值为5,∴OQ′故选:B .【点睛】本题考查了一次函数图象上点的坐标特征,一次函数的性质,三角形全等的判定和性质,坐标与图形的变换-旋转,二次函数的性质,勾股定理,表示出点的坐标是解题的关键.9.如图,已知△ABC 的三个顶点A (a ,0)、B (b ,0)、C (0,2a )(b >a >0),作△ABC 关于直线AC 的对称图形△AB 1C , 若点B 1恰好落在y 轴上,则a b的值为( )A.13B.49C.12D.38【答案】D【分析】由B(b,0)、C(0,2a),可得,△ABC关于直线AC的对称图形△AB1C,且点B1恰好落在y 轴上,即可确定B1的坐标,进而确定BB1的中点D的坐标;△ABC关于直线AC的对称图形△AB1C,则段BB1的中点D在直线AC上;再由A(a,0)、C(0,2a)确定直线AC的解析式,最后将D点坐标代入求解即可.【解析】解:∵B(b,0)、C(0,2a)∴∵△ABC关于直线AC的对称图形△AB1C,且点B1恰好落在y轴上∴B1的坐标为(0,∴BB1的中点D的坐标为(2b∵A(a,0)、C(0,2a)∴直线AC的解析式为:y=-2x+2a∵△ABC 关于直线AC 的对称图形△AB 1C ,∴段BB 1的中点D 在直线AC 上222b a =-´+,即22323240a b ab +-= ∴2322430a a b b æöæö-+=ç÷ç÷èøèø且a b >0解得:a b =38故答案为D .【点睛】本题考查了轴对称变换、勾股定理、线段的中点坐标、一次函数解析式等在知识点,考查知识点较多,灵活应用相关知识成为解答本题的关键.10.如图,已知正比例函数y =kx (k >0)的图象与x 轴相交所成的锐角为70°,定点A 的坐标为(0,4),P 为y 轴上的一个动点,M 、N 为函数y =kx (k >0)的图象上的两个动点,则AM +MP +PN 的最小值为( )A.2B.4sin40°C.D.4sin20°(1+cos20°+sin20°cos20°)【答案】C【分析】如图所示直线OC、y轴关于直线y=kx对称,直线OD、直线y=kx关于y轴对称,点A′是点A关于直线y =kx的对称点,作A′E⊥OD垂足为E,交y轴于点P,交直线y=kx于M,作PN⊥直线y=kx垂足为N,此时AM+PM+PN=A′M+PM+PE=A′E最小(垂线段最短),在RT△A′EO中利用勾股定理即可解决.【解析】解:如图所示,直线OC、y轴关于直线y=kx对称,直线OD、直线y=kx关于y轴对称,点A′是点A关于直线y=kx的对称点.作A′E⊥OD垂足为E,交y轴于点P,交直线y=kx于M,作PN⊥直线y=kx垂足为N,∵PN=PE,AM=A′M,∴AM+PM+PN=A′M+PM+PE=A′E最小(垂线段最短),在RT△A′EO中,∵∠A′EO=90°,OA′=4,∠A′OE=3∠AOM=60°,OA′=2,A′E=∴OE=12∴AM+MP+PN的最小值为故选:C.【点睛】本题考查轴对称﹣最短问题、垂线段最短、直角三角形30度角的性质、勾股定理、一次函数等知识,解题的关键是利用轴对称性质正确找到等P的位置,题目有点难度,是最短问题中比较难的题目.11.如图,在直角坐标系中,等腰直角△ABO的O点是坐标原点,A的坐标是(﹣4,0),直角顶点B在第二象限,等腰直角△BCD的C点在y轴上移动,我们发现直角顶点D点随之在一条直线上移动,这条直线的解析式是( )A.y=﹣2x+1B.y=﹣1x+2C.y=﹣3x﹣2D.y=﹣x+22【答案】D【分析】抓住两个特殊位置:当BC与x轴平行时,求出D的坐标;C与原点重合时,D在y轴上,求出此时D的坐标,设所求直线解析式为y=kx+b,将两位置D坐标代入得到关于k与b的方程组,求出方程组的解得到k 与b的值,即可确定出所求直线解析式.【解析】当BC与x轴平行时,过B作BE⊥x轴,过D作DF⊥x轴,交BC于点G,如图1所示.∵等腰直角△ABO的O点是坐标原点,A的坐标是(﹣4,0),∴AO=4,∴BC=BE=AE=EO=GF=12OA=2,OF=DG=BG=CG=12BC=1,DF=DG+GF=3,∴D坐标为(﹣1,3);当C与原点O重合时,D在y轴上,此时OD=BE=2,即D(0,2),设所求直线解析式为y=kx+b(k≠0),将两点坐标代入得:32k bb-+=ìí=î,解得:12kb=-ìí=î.则这条直线解析式为y=﹣x+2.故选D.【点睛】本题属于一次函数综合题,涉及的知识有:待定系数法确定一次函数解析式,等腰直角三角形的性质,坐标与图形性质,熟练运用待定系数法是解答本题的关键.12.如图,已知点A(1,4),点B(3,5),在y轴上取一点C,连接AC,将线段AC绕点C顺时针旋转90°到CD,连接AD,BD,则AD+BD的最小值是()A .B .C .D .5【答案】D【分析】首先证明点D 的运动轨迹是直线y =﹣x+3,作点A 关于直线y =﹣x+3的对称点M (﹣1,2),连接BM 交直线y =﹣x+3于D′,连接AD′,此时AD′+BD′的值最小,最小值为线段BM 的长.【解析】解:如图,过点A 作AE y ^轴于点E ,过点D 作DF y ^轴于点F ,设C (0,m ),由题意A (1,4),线段CD 是由线段CA 顺时针旋转90°得到,则AEC CFD @V V ,∴1AE CF ==,4EC FD m ==-,∴1OF m =-,∴D (4﹣m ,m ﹣1),设4﹣m =x ,m ﹣1=y ,可得y =﹣x+3,∴点D 的运动轨迹是直线y =﹣x+3,作点A 关于直线y =﹣x+3的对称点M (﹣1,2),连接BM 交直线y =﹣x+3于D′,连接AD′,此时AD′+BD′的值最小,最小值为线段BM 的长,∵B(3,5),M(﹣1,2),∴BM5,∴AD+BD的最小值为5,故选:D.【点睛】本题考查动点问题,解题的关键是分析出动点D的运动轨迹,然后利用轴对称的性质求出线段和的最小值.二、填空题13.如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为B(﹣4,6),D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF的周长最小时,点E的坐标为__________.【答案】()0.4,0-【分析】先得出D 点关于x 轴的对称点坐标为H (0,-4),再通过转化,将求四边形BDEF 的周长的最小值转化为求FG +BF 的最小值,再利用两点之间线段最短得到当F 、G 、B 三点共线时FG +BF 的值最小,用待定系数法求出直线BG 的解析式后,令y =0,即可求出点F 的坐标,最后得到点E 的坐标.【解析】解:如图所示,∵D (0,4),∴D 点关于x 轴的对称点坐标为H (0,-4),∴ED =EH ,将点H 向左平移3个单位,得到点G (-3,-4),∴EF =HG ,EF ∥HG ,∴四边形EFGH 是平行四边形,∴EH =FG ,∴FG =ED ,∵B (-4,6),∴BD又∵EF =3,∴四边形BDEF 的周长=BD +DE +EF +BF =FG +3+BF ,要使四边形BDEF 的周长最小,则应使FG +BF 的值最小,而当F 、G 、B 三点共线时FG +BF 的值最小,设直线BG 的解析式为:()0y kx b k =+¹∵B (-4,6),G (-3,-4),∴4634k b k b -+=ìí-+=-î,∴1034k b =-ìí=-î,∴1034y x =--,当y =0时, 3.4x =-,∴()3.4,0F -,∴()0.4,0E -故答案为:()0.4,0-.【点睛】本题综合考查了轴对称的性质、最短路径问题、平移的性质、用待定系数法求一次函数的解析式等知识,解决问题的关键是“转化”,即将不同的线段之间通过转化建立相等关系,将求四边形的周长的最小值问题转化为三点共线和最短的问题等,本题蕴含了数形结合与转化的思想方法等.14.如图,一次函数2y x =与反比例数()0k y k x=>的图像交于A ,B 两点,点M 在以()2,0C 为圆心,半径为1的C e 上,N 是AM 的中点,已知ON 长的最大值为32,则k 的值是_______.【答案】3225根据题意得出ON 是ABM V 的中位线,所以ON 取到最大值时,BM 也取到最大值,就转化为研究BM 也取到最大值时k 的值,根据,,B C M 三点共线时,BM 取得最大值,解出B 的坐标代入反比例函数即可求解.【解析】解:连接BM ,如下图:在ABM V 中,,O N Q 分别是,AB AM 的中点,ON \是ABM V 的中位线,12ON BM \=,已知ON 长的最大值为32,此时的3BM =,显然当,,B C M 三点共线时,取到最大值:3BM =,13BM BC CM BC =+=+=,设(,2)B t t ,由两点间的距离公式:2BC ==,22(2)44t t \-+=,解得:124,05t t ==(取舍),48(,55B \,将48(,55B 代入()0k y k x=>,解得:3225k =,故答案是:3225.【点睛】本题考查了一次函数、反比例函数、三角形的中位线、圆,研究动点问题中线段最大值问题,解题的关键是:根据中位线的性质,利用转化思想,研究BM 取最大值时k 的值.15.如图,过直线:l y =上的点1A 作11A B l ^,交x 轴于点1B ,过点1B 作12B A x ^轴.交直线l 于点2A ;过点2A 作22A B l ^,交x 轴于点2B ,过点2B 作23B A x ^轴,交直线l 于点3A ;……按照此方法继续作下去,若11OB =,则线段1n n A A -的长度为______.(结果用含正整数n 的代数式表示)【答案】2532n -´【分析】根据题意由11OB =,直线l 关系式,可以得出A 2的坐标,可判断出∠OA 2B 1=30°,∠A 2OB 1=60°,根据题意可得出∠A 1B 1O=30°,可求出OA 1的值,在Rt △OA 2B 1中,可以求出OA 2的长;再在Rt △OA 2B 2中,利用30°角所对的直角边是斜边的一半,可求出OB 2的值,同理可求出OA 3,OB 3……,然后再找规律,得出OA n 的值,用OA n -OA n-1,从而求得点A n A n-1的值.【解析】解:∵OB 1=1,根据题意,结合,得出A 2(∴在Rt △A 2OB 1中,根据勾股定理得OA 2=2∴∠OA 2B 1=30°,∠A 2OB 1=60°∵A 1B 1⊥OA 1∴∠A 1B 1O=30°,又OB 1=1∴OA 1=12由OA 2=2,得OB 2=4,∴OA 3=8,OB 3=16,按照此规律即可求出OA n =2n 32- ,OA n -1=2n 52-∴A n A n -1=2n 32--2n 52-=22n 52n 5222·--- =2n 532´-【点睛】本题考查一次函数图象上线段长度特征,勾股定理,含30°角的直角三角形的特性,在找规律时,不断求出OA 1,OA 2,...OA n 的长度即可找出规律,求出答案.16.如图,直线AM 的解析式为1y x =+与x 轴交于点M ,与y 轴交于点A ,以OA 为边作正方形ABCO ,点B 坐标为()1,1.过点B 作1EO MA ^交MA 于点E ,交x 轴于点1O ,过点1O 作x 轴的垂线交MA 于点1A 以11O A 为边作正方形1111O A B C ,点1B 的坐标为()5,3.过点1B 作12E O MA ^交MA 于1E ,交x 轴于点2O ,过点2O 作x 轴的垂线交MA 于点2A ,以22O A 为边作正方形2222O A B C ,L ,则点2020B 的坐标______.【答案】()20202020231,3´-【分析】根据题意得出三角形AMO 为等腰直角三角形,∠AMO=45°,分别求出个线段的长度,表示出B 1和B 2的坐标,发现一般规律,代入2020即可求解【解析】解:∵AM 的解析式为1y x =+,∴M (-1,0),A (0,1),即AO=MO=1,∠AMO=45°,由题意得:MO=OC=CO 1=1,O 1A 1=MO 1=3,∵四边形1111O A B C 是正方形,∴O 1C 1=C 1O 2=MO 1=3,∴OC 1=2×3-1=5,B 1C 1=O 1C 1=3,B 1(5,3),∴A 2O 2=3C 1O 2=9,B 2C 2=9,OO 2=OC 2-MO=9-1=8,综上,MC n =2×3n ,OC n =2×3n -1,B n C n =A n O n =3n ,当n=2020时,OC 2020=2×32020-1,B 2020C 2020 =32020,点B ()20202020231,3´-,故答案为:()20202020231,3´-.【点睛】本题考查规律型问题、等腰直角三角形的性质以及点的坐标,解题的关键是学会探究规律的方法,属于中考常考题型.17.如图在平面直角坐标系中,直线4y x =-+的图像分别与y 轴和x 轴交于点A ,点B .定点P 的坐标为,点Q 是y 轴上任意一点,则12PQ QB +的最小值为__________.【答案】【分析】以点P 为顶点,y 轴为一边,在y 轴右侧作30OPD Ð=°,与x 轴交于点D ,作点B 关于y 轴的对称点B ¢,过点B ¢作B E PD ¢^,交y 轴与点Q ,根据直角三角形的性质得出B E ¢即为最小值,然后利用勾股定理和直角三角形的性质求出B E ¢的长即可.【解析】如图,以点P 为顶点,y 轴为一边,在y 轴右侧作30OPD Ð=°,与x 轴交于点D ,作点B 关于y 轴的对称点B ¢,过点B ¢作B E PD ¢^,交y 轴与点Q ,∵30B E PD OPD ¢^Ð=°,,∴12QE PQ =,∵此时BQ B Q ¢=,则B E ¢即为12PQ QB +的最小值.∵3090OPD POD Ð=°Ð=°,,∴260PD OD ODP =Ð=°,,根据勾股定理可得222(2)OD OD +=,解得6OD =,∵直线4y x =-+的图象分别与y 轴和x 轴交于点A ,点B ,令x =0,得y =4;令y =0,得x =4,则点(0,4)(4,0)A B ,,∴4OB =,∴4OB ¢=,∴4610B D =+=¢,∵60B E PD ODP ¢^Ð=°,,∴30EB D ¢Ð=°,∴152DE B D ¢==,∴B E ===¢即12PQ QB +的最小值为.故答案为:.【点睛】本题考查勾股定理,最短路径问题,以及一次函数与坐标轴的交点等,正确得出最短路径是解题关键.18.甲、乙两辆冷链运输车从某公司疫苗存储库同时出发,各自将一批疫苗运往省疾控中心疫苗仓储库,他们将疫苗运到省疾控中心疫苗仓储库后,省疾控中心将按规定流程对疫苗的质量进行检查验收,检查验收及卸货的时间共为30分钟,然后甲、乙两辆冷链运输车又各自按原路原速返回公司疫苗存储库,在整个过程中,假设甲、乙两辆冷链运输车均保持各自的速度匀速行驶,且甲车的速度比乙车的速度快.甲、乙两车相距的路程y (千米)与甲车离开公司疫苗存储库的时间x (小时)之间的关系如图所示,则在甲车返回到公司疫苗存储库时,乙车距公司疫苗存储库的距离为________千米.【答案】36【分析】根据图象求出甲、乙速度和公司疫苗存储库到省疾控中心疫苗仓储库的距离,从而可得甲回到公司疫苗存储库所用时间,求出这段时间乙行驶路程,即可得到答案.【解析】解:如图:由A(1.8,18)可知,甲1.8小时达到省疾控中心疫苗仓储库,且1.8小时,甲、乙相距18千米,即甲比乙多行驶18千米,∴甲、乙速度差为:V甲-V乙=18÷1.8=10(千米/时),∵检查验收及卸货的时间共为30分钟(0.5小时),∴C(2.3,0),而xD=2.5,∴甲比乙早0.2小时返回,即甲比乙早0.2小时到省疾控中心疫苗仓储库,设甲速度为x千米/时,则乙速度是(x-10)千米/时,可得:1.8x=(1.8+0.2)(x-10),解得x=100,∴甲速度为100千米/时,乙速度是90千米/时,公司疫苗存储库到省疾控中心疫苗仓储库的距离是180千米,∵在整个过程中,甲、乙两辆冷链运输车均保持各自的速度匀速行驶,∴甲从第2.3小时返回,到公司疫苗存储库时间为2.3+1.8=4.1(小时),乙从2.5小时开始返回,到4.1小时所行路程为:(4.1-2.5)×90=144(千米),此时到公司疫苗存储库距离是180-144=36(千米),∴甲车返回到公司疫苗存储库时,乙车距公司疫苗存储库的距离是36千米.故答案为:36.【点睛】本题考查一次函数图象及应用,读懂图象,特别是理解重要点的坐标,是解题的关键.三、解答题19.已知函数2(0)(0)x x y x x -£ì=í>î的图象如图所示,点()11,A x y 在第一象限内的函数图象上.(1)若点()22,B x y 也在上述函数图象上,满足21x x <.①当214y y ==时,求12,x x 的值;②若21x x =,设12=-w y y ,求w 的最小值;(2)过A 点作y 轴的垂线AP ,垂足为P ,点P 关于x 轴的对称点为P ¢,过A 点作x 轴的线AQ ,垂足为Q ,Q 关于直线¢AP 的对称点为Q ¢,直线AQ ¢是否与y 轴交于某定点?若是,求出这个定点的坐标;若不是,请说明理由.【答案】(1)①122,4x x ==-;②14-;(2)直线AQ ¢与y 轴交于定点,定点的坐标为10,4æöç÷èø.【分析】(1)①先确定20x £,再根据214y y ==代入求解即可得;②先确定2210,x x x <-=,从而可得21122,y x y x ==-,再代入w 可得一个关于1x 的二次函数,利用二次函数的性质即可得;(2)先分别求出点,,P P Q ¢的坐标,再利用待定系数法求出直线,AP QQ ¢¢的解析式,从而可得点Q ¢的坐标,然后利用待定系数法求出直线AQ ¢的解析式,由此即可得出结论.【解析】解:(1)①对于二次函数2y x =,在0x >内,y 随x 的增大而增大,21211,40,x x x y y <>==Q ,20x \£,则当14y =时,214x =,解得12x =或120x =-<(舍去),当24y =时,24x -=,解得24x =-;②21121,0,x x x x x <>=Q ,2210,x x x \<-=,21122,y x y x \==-,则22121211()w y y x x x x =-=--=-,化成顶点式为2111()24w x =--,由二次函数的性质可知,在1>0x 内,当112x =时,w 取最小值,最小值为14-;(2)由题意,设¢AP 与QQ ¢交于点B ,画图如下,11(x ,)A y Q 在已知函数的第一象限内的图象上,211y x \=,即211(,)A x x ,AP y ^Q 轴,AQ x ^轴,点P 关于x 轴的对称点为P ¢,22111(0,),(0,),(,0)P P Q x x x ¢\-,设直线¢AP 的解析式为11y k x b =+,将点22111(,),(0,)P A x x x ¢-代入得:21111211k x b x b x ì+=í=-î,解得112112k x b x =ìí=-î,则直线¢AP 的解析式为2112y x x x =-,Q Q 关于直线¢AP 的对称点为Q ¢,QQ AP ¢¢\^,\设直线QQ ¢的解析式为2112b x y x +=-,将点1(,0)Q x 代入得:121201x b x -+=,解得212b =,则直线QQ ¢的解析式为11212x y x +=-,联立211121122y x x x y x x ì=-ïí=-+ïî,解得211212121(12)4141x x x x x y x ì+=ï+ïíï=ï+î,即22111221141(12),41x x x B x x æö+ç÷++èø,设点Q ¢的坐标为(,)Q m n ¢,则2111212121(12)2410241m x x x x x n x ì++=ï+ïí+ï=ï+î,解得121212141241x m x x n x ì=ï+ïíï=ï+î,即21122114142,1x x Q x x æö¢ç÷++èø,设直线AQ ¢的解析式为33y k x b =+,将点22111122112(,),1,414x x A x x Q x x æö¢ç÷++èø代入得:2313121133221124141k x b x x x k b x x ì+=ïí+=ï++î,解得2131314414x k x b ì-=-ïïíï=ïî,则直线AQ ¢的解析式为21144114x y x x -=-+,当0x =时,14y =,即直线AQ ¢与y 轴交于定点10,4æöç÷èø.【点睛】本题考查了二次函数与一次函数的综合、轴对称等知识点,熟练掌握待定系数法是解题关键.20.在平面直角坐标系中,点A的坐标为(,点B 在直线8:3l y x =上,过点B 作AB 的垂线,过原点O 作直线l 的垂线,两垂线相交于点C .(1)如图,点B ,C 分别在第三、二象限内,BC 与AO 相交于点D .①若BA BO =,求证:CD CO =.②若45CBO Ð=°,求四边形ABOC 的面积.(2)是否存在点B ,使得以,,A B C 为顶点的三角形与BCO V 相似?若存在,求OB 的长;若不存在,请说明理由.【答案】(1)①见解析;②552;(2)存在,444,9,1【分析】(1)①等腰三角形等角对等边,则BAD AOB Ð=Ð,根据等角的余角相等和对顶角相等,得到CDO COD Ð=Ð,根据等角对等边,即可证明CD CO =;②添加辅助线,过点A 作AH OB ^于点H ,根据直线l 的解析式和角的关系,分别求出线段AB 、BC 、OB 、OC 的长,则11+22ABC CBO ABOC S S S AB BC OB OC =+=´´V V 四边形;(2)分多钟情况进行讨论:①当点C 在第二象限内,ACB CBO Ð=Ð时;②当点C 在第二象限内,ACB BCO Ð=Ð时;③当点C 在第四象限内,ACB CBO Ð=Ð时.【解析】解:(1)①证明:如图1,∵BA BO =,∴12Ð=Ð.∴BA BC ^,∴2590Ð+Ð=°.而45Ð=Ð,∴2490Ð+Ð=°.∵OB OC ^,∴1390Ð+Ð=°.∴34Ð=Ð,∴CD CO =.②如图1,过点A 作AH OB ^于点H .由题意可知3tan 18Ð=,在Rt AHO V 中,3tan 18AH OH Ð==.设3m AH =,8m OH =.∵222AH OH OA +=,∴()()22238m m +=,解得1m =.∴38AH OH ==,.∵4590CBO ABC Ð=°Ð=°,,∴45ABH Ð=°,∴3,tan 45sin 45AH AH BH AB ====°°∴5OB OH BH =-=.∵45OB OC CBO ^Ð=°,,∴tan 455,cos 45OB OC OB BC =´°===°,∴111522ABC S AB BC =´=´=V ,112555222CBO S OB OC =´=´´=V :∴552ABC CBO ABOC S S S =+=V V 四边形.(2)过点A 作AH OB ^于点H ,则有38AH OH ==,.①如图2,当点C 在第二象限内,ACB CBO Ð=Ð时,设OB t=∵ACB CBO Ð=Ð,∴//AC OB .又∵AH OB OC OB ^^,,∴3AH OC ==.∵AH OB AB BC ^^,,∴12902390Ð+Ð=°Ð+Ð=°,,∴13Ð=Ð,∴AHB BOC V V ∽,∴AH HB BO OC=,∴383t t -=,整理得2890t t -+=,解得4t =∴4OB =②如图3,当点C 在第二象限内,ACB BCO Ð=Ð时,延长AB CO ,交于点G ,则ACB GCB V V ≌,∴A B G B =.又∵AH OB OC OB ^^,,∴90AHB GOB Ð=Ð=°,而ABH GBO Ð=Ð,∴ABH GBO V V ≌,∴142OB HB OH ===③当点C 在第四象限内,ACB CBO Ð=Ð时,AC 与OB 相交于点E ,则有BE CE =.(a )如图4,点B 在第三象限内.在Rt ABC V 中,1290,90ACB CAB Ð+Ð=°Ð+Ð=°,∴2CABÐ=Ð∴AE BE CE ==,又∵,AH OB OC OB ^^,∴90AHE COE Ð=Ð=°,而AEH CEOÐ=Ð∴AHE COE V V ≌,∴142HE OE OH ===∴5AE ==,∴5BE =,∴9OB BE OE =+=(b )如图5,点B 在第一象限内.在Rt ABC V 中90,90ACB CAB CBO ABE Ð+Ð=°Ð+Ð=°∴CAB ABE Ð=Ð,∴AE BE CE ==.又∵,AH OB OC OB ^^,∴90AHE COE Ð=Ð=°而AEH CEO Ð=Ð,∴AHE COEV V ≌∴142HE OE OH ===∴5AE ==,∴5BE =,∴1OB BE OE =-=综上所述,OB 的长为444,9,1.【点睛】本题涉及到等腰三角形、等角的余角相等、利用切割法求四边形的面积和相似三角形等知识,综合性较强.在题中已知两个三角形相似时,要分情况考虑.21.某超市从厂家购进A 、B 两种型号的水杯,两次购进水杯的情况如下表:进货批次A 型水杯(个)B 型水杯(个)总费用(元)一1002008000二20030013000(1)求A 、B 两种型号的水杯进价各是多少元?(2)在销售过程中,A 型水杯因为物美价廉而更受消费者喜欢.为了增大B 型水杯的销售量,超市决定对B 型水杯进行降价销售,当销售价为44元时,每天可以售出20个,每降价1元,每天将多售出5个,请问超市应将B 型水杯降价多少元时,每天售出B 型水杯的利润达到最大?最大利润是多少?(3)第三次进货用10000元钱购进这两种水杯,如果每销售出一个A 型水杯可获利10元,售出一个B 型水杯可获利9元,超市决定每售出一个A 型水杯就为当地“新冠疫情防控”捐b 元用于购买防控物资.若A 、B 两种型号的水杯在全部售出的情况下,捐款后所得的利润始终不变,此时b 为多少?利润为多少?【答案】(1)A 型号水杯进价为20元,B 型号水杯进价为30元;(2)超市应将B 型水杯降价5元后,每天售出B 型水杯的利润达到最大,最大利润为405元;(3)A ,B 两种杯子全部售出,捐款后利润不变,此时b 为4元,利润为3000元.【分析】(1)主要运用二元一次方程组,设A 型号水杯为x 元,B 型号水杯为y 元,根据表格即可得出方程组,解出二元一次方程组即可得A 、B 型号水杯的单价;(2)主要运用二次函数,由题意可设:超市应将B 型水杯降价z 元后,每天售出B 型水杯的利润达到最大,最大利润为w ,每个水杯的利润为()4430z --元;每降价1元,多售出5个,可得售出的数量为()205z +个,根据:利润=(售价-进价)×数量,可确定函数关系式,依据二次函数的基本性质,开口向下,在对称轴处取得最大值,即可得出答案;(3)根据(1)A 型号水杯为20元,B 型号水杯为30元.设10000元购买A 型水杯m 个,B 型水杯n 个,所得利润为W 元,可列出方程组,利用代入消元法化简得到利润W 的函数关系式,由于利润不变,所以令未知项的系数为0,即可求出b ,W .【解析】(1)解:设A 型号水杯进价为x 元,B 型号水杯进价为y 元,根据题意可得:100200800020030013000x y x y +=ìí+=î,解得:2030x y =ìí=î,∴A 型号水杯进价为20元,B 型号水杯进价为30元.(2)设:超市应将B 型水杯降价z 元后,每天售出B 型水杯的利润达到最大,最大利润为w ,根据题意可得:()()4430205w z z =--+,化简得:2550280w z z =-++,当()505225b z a =-=-=´-时,255505280405max w =-´+´+=,∴超市应将B 型水杯降价5元后,每天售出B 型水杯的利润达到最大,最大利润为405元.(3)设购买A 型水杯m 个,B 型水杯n 个,所得利润为W 元,根据题意可得:()203010000109m n W b m n +=ìí=-+î①②将①代入②可得:()100002010930m W b m -=-+´,化简得:()()106300043000W b m b m =--+=-+,使得A ,B 两种杯子全部售出后,捐款后所得利润不变,则40b -=,得4b =,当4b =时,3000W =,∴A ,B 两种杯子全部售出,捐款后利润不变,此时b 为4元,利润为3000元.【点睛】题目主要考察二元一次方程、一元二次函数的以及一次函数的应用,难点是对题意的理解及对函数和方程的综合运用.22.如图,在平面直角坐标系中,点F 的坐标是(4,2),点P 为一个动点,过点P 作x 轴的垂线PH ,垂足为H ,点P 在运动过程中始终满足PF PH =【提示:平面直角坐标系内点M 、N 的坐标分别为11(,)x y 、22(,)x y ,则2222121()()MN x x y y =-+-】(1)判断点P 在运动过程中是否经过点C (0,5)(2)设动点P 的坐标为(,)x y ,求y 关于x 的函数表达式:填写下表,并在给定坐标系中画出 函数的图象:x ...02468...y ......(3)点C 关于x 轴的对称点为C ¢,点P 在直线C F ¢的下方时,求线段PF 长度的取值范围【答案】(1)点P 在运动过程中经过点C (0,5);(2)y 与x 的函数表达式为21254y x x =-+,表格和图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学压轴培优练习:一次函数图像类一.选择题1.如图,直线y=x,点A 1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A2019的坐标为()A.(22017,0)B.(22018,0)C.(22020,0)D.(24034,0)2.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1.5小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t=或t=,其中正确的结论有()A.1个B.2个C.3个D.4个3.如图所示,在同一条道路上,甲车从A地到B地,乙车从B地到A地,甲乙同时出发,甲车先到达目的地,图中的折线段表示甲、乙两车之间的距离y(km)与行驶时间(h)的函数关系的图象,下列说法错误的是()A.出发2h后,两车相遇B.乙的速度是48km/hC.出发3h后,甲车距离B地96kmD.甲车到B地比乙车到A地早h4.八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为()A.y=x B.y=x C.y=x D.y=x5.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:会员年卡类型办卡费用(元)每次游泳收费(元)A类50 25B类200 20C类400 15例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为()A.购买A类会员卡B.购买B类会员年卡C.购买C类会员年卡D.不购买会员年卡6.如图,在平面直角坐标系xOy中,直线y=﹣x+分别与x轴、y轴交于点P、Q,在Rt△OPQ中从左向右依次作正方形A1B1C1C2、A2B2C2C3、A3B3C3C4…A n B n∁n C n+1,点A1、A2、A3…A n在x轴上,点B1在y轴上,点C1、C2、C3…C n+1在直线PQ上;再将每个正方形分割成四个全等的直角三角形和一个小正方形,其中每个小正方形的边都与坐标轴平行,从左至右的小正方形(阴影部分)的面积分别记为S1、S2、S3…S n,则S n可表示为()A..B..C..D..7.如图A、B两地相距50km.甲于某日下午1点骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地.图中折线PQR和线段MN分别表示甲和乙行驶的路程s与该日下午时间t之间的关系.下列说法正确的有()①甲、乙两人同时到达目的地;②乙出发后30分钟后追上甲;③甲的平均速度是10km/h,乙的速度是50km/h;④甲、乙相遇时距出发地25km.A.1个B.2个C.3个D.4个8.如图,在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是()A.()2019B.()2018C.()2019D.()20189.如图所示,把Rt△ABC放在平面直角坐标系中,∠CAB=90°,BC=5,点A,B的坐标分别为(2,0),(5,0),将△ABC沿与y轴平行的方向向下平移,当点C落在y =x﹣2上时,线段BC扫过的面积为()A.3 B.7.5 C.15 D.2510.如图,直线l:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,在x轴正方向上取点B3,使B2B3=B2A3;…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2017等于()A.24030B.24031C.24032D.24033二.填空题11.如图,在平面直角坐标系中,已知直线y=﹣x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点,将△ABC沿直线AC折叠,使得点B恰好落在轴x轴上,则点C的坐标为.12.小亮和妈妈从家出发到长嘉汇观看国庆灯光秀,妈妈先出发,2分钟后小亮沿同一路线出发去追妈妈,当小亮追上妈妈时发现相机落在途中了,妈妈立即返回找相机,小亮继续前往长嘉汇,当小亮到达长嘉汇时,妈妈刚好找到了相机并立即前往长嘉汇(妈妈找相机的时间不计),小亮在长嘉汇等了一会,没有等到妈妈,就沿同一路线返回接妈妈,最终与妈妈会合,小亮和妈妈的速度始终不变,如图是小亮和妈妈两人之间的距离y(米)与妈妈出发的时间x(分钟)的图象;则小亮开始返回时,妈妈离家的距离为米.13.暑假假期,小明和小亮两家相约自驾车从重庆出发前往相距172千米的景区游玩两家人同时同地出发,以各自的速度匀速行驶,出发一段时间后,小明家因故停下来休息了15分钟,为了尽快追上小亮家,小明家提高速度后仍保持匀速行驶(加速的时间忽略不计),小明家追上小亮家后以提高后的速度直到景区,小亮家保持原速,如图是小明家、小亮家两车之间的距离s(km)与出发时间t(h)之间的函数关系图象,则小明家比小亮家早到景区分钟.14.如图,正方形OABC的顶点O在坐标原点,正方形ADEF的边AD与AB在同一宜线上,AF与OA在同一直线上,且AB=AD,OA边和AB边所在直线的解析式分别为:y=x和y=﹣x+,则点E的坐标为.15.如图,正方形A1B1C1O、A2B2C2C1……按照如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),B3(7,4),则B2019的坐标是.16.一列慢车从A地驶往B地,一列快车从B地驶往A地,两车同时出发,分别驶向目的地后停止.如图,折线表示两车之间的距离y(千米)与慢车行驶时间t(小时)之间的关系,求当快车到达A地时,慢车与B地的距离为千米.17.如图所示,直线y=x+2与两坐标轴分别交于A、B两点,点C是OB的中点,D、E 分别是直线AB、y轴上的动点,当△CDE周长最小时,点D的坐标为.18.如图,直线y=x+1与直线y=mx﹣n相交于点M(1,b),则关于x,y的方程组的解为.19.已知A、B两地之间的距离为20千米,甲步行,乙骑车,两人沿着相同路线,由A地到B地匀速前行,甲、乙行进的路程s与x(小时)的函数图象如图所示.(1)乙比甲晚出发小时;(2)在整个运动过程中,甲、乙两人之间的距离随x的增大而增大时,x的取值范围是.20.直线y=x+1与x轴交于点D,与y轴交于点A1,把正方形A1B1C1O1、A2B2C2C1和A3B3C3C2按如图所示方式放置,点A2、A3在直线y=x+1上,点C1、C2、C3在x轴上,按照这样的规律,则正方形A2019B019C2019C2018中的点B2019的坐标为.三.解答题21.甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B 地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.(1)求甲、乙两车行驶的速度V甲、V乙.(2)求m的值.(3)若甲车没有故障停车,求可以提前多长时间两车相遇.22.甲、乙两位同学从学校出发沿同一条绿道到相距学校1500m的图书馆去看书,甲步行,乙骑自行车.图1中OD,AC分别表示甲、乙离开学校的路程y(m)与甲行走的时间x(min)之间的函数图象(1)求线段AC所在直线的函数表达式;(2)设d(m)表示甲、乙两人之间的路程,在图2中补全d关于x的函数图象;(标注必要的数据)(3)当x在什么范围时,甲、乙两人之间的路程至少为180m.23.已知A(2,0),直线y=(2﹣)x﹣2交x轴于点F,y轴于点B,直线l∥AB且交y轴于点C,交x轴于点D,点A关于直线l的对称点为A',连接AA',A'D.直线l从AB开始,以1个单位每秒的速度沿y轴正方向向上平移,设移动时间为t.(1)求A'点的坐标(用t的代数式表示);(2)请猜想AB与AF长度的数量关系,并说明理由;(3)过点C作直线AB的垂线交直线y=(2﹣)x﹣2于点E,以点C为圆心CE 为半径作⊙C,求当t为何值时,⊙C与△AA′D三边所在直线相切?24.已知:甲、乙两车分别从相距300km的A,B两地同时出发相向而行,甲到B地后立即返回,如图是它们离各自出发地的距离y与行驶时间x之间的函数图象.(1)求甲车离出发地的距离y与行驶时间x之间的函数关系式,并标明自变量x的取值范围;(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;(3)它们在行驶过程中有几次相遇?并求出每次相遇的时间.25.A、B两地相距60km,甲从A地去B地,乙从B地去A地,图中L1、L2分别表示甲、乙俩人离B地的距离y(km)与甲出发时间x(h)的函数关系图象.(1)根据图象,直接写出乙的行驶速度;(2)解释交点A的实际意义;(3)甲出发多少时间,两人之间的距高恰好相距5km;(4)若用y3(km)表示甲乙两人之阐的距离,请在坐标系中画出y3(km)关于时间x (h)的的数关系图象,注明关键点的数据.参考答案一.选择题1.解:由题意可得,点A 1坐标为(1,0),点B1的坐标为(1,),点A2坐标为(2,0),点B2的坐标为(2,2),点A3坐标为(4,0),点B3的坐标为(4,4),……∴点A2019的坐标为(22018,0),故选:B.2.解:由图象可知A、B两城市之间的距离为300km,故①正确;设甲车离开A城的距离y与t的关系式为y甲=kt,把(5,300)代入可求得k=60,∴y甲=60t,把y=150代入y甲=60t,可得:t=2.5,设乙车离开A城的距离y与t的关系式为y乙=mt+n,把(1,0)和(2.5,150)代入可得,解得,∴y乙=100t﹣100,令y甲=y乙可得:60t=100t﹣100,解得t=2.5,即甲、乙两直线的交点横坐标为t=2.5,乙的速度:150÷(2.5﹣1)=100,乙的时间:300÷100=3,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故②错误;甲、乙两直线的交点横坐标为t=2.5,此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故③错误;令|y甲﹣y乙|=40,可得|60t﹣100t+100|=40,即|100﹣40t|=40,当100﹣40t=40时,可解得t=,当100﹣40t=﹣40时,可解得t=,又当t=时,y甲=40,此时乙还没出发,当t=时,乙到达B城,y甲=260;综上可知当t的值为或或或t=时,两车相距40千米,故④不正确;故选:A.3.解:A、出发2h后,其距离为零,即两车相遇,正确;B、乙的速度是=48km/h,正确;C、甲的速度为:km/h,240﹣72×3=24km,错误;D、h,即甲车到B地比乙车到A地早h,正确;故选:C.4.解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC 于C,∵正方形的边长为1,∴OB=3,∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,∴两边分别是4,∴三角形ABO面积是5,∴OB•AB=5,∴AB=,∴OC=,由此可知直线l经过(,3),设直线方程为y=kx,则3=k,k=,∴直线l解析式为y=x,故选:C.5.解:设一年内在该游泳馆游泳的次数为x次,消费的钱数为y元,根据题意得:y A=50+25x,y B=200+20x,y C=400+15x,当40≤x≤50时,1050≤y A≤1300;1000≤y B≤1200;1000≤y C≤1150;由此可见,C类会员年卡消费最低,所以最省钱的方式为购买C类会员年卡.故选:C.6.解:∵P(13,0),Q(0,),∴tan∠OPQ=,∵每个小正方形的边都与坐标轴平行,∴∠OA1B1=∠OA2B2=…=∠OA n B n,∴每组小正方形的边长都是该组小长方形边长的两直角边之差,正方形A1B1C1C2中,设点C1(a1,b1),∴b1=4a1,将点C1(a1,4a1)代入直线y=﹣x+,∴a1=1,b1=3,∴正方形A1B1C1C2中阴影正方形边长为2;∴阴影部分面积4;正方形A2B2C2C3中,设点C2(a2,b2),∴a2=4a1﹣=4,b2=b1﹣a1=3,∴正方形A2B2C2C3中阴影正方形边长为×2=;∴阴影部分面积,;正方形A3B3C3C3中,设点C3(a3,b3),∴a3=4a1+3a2=,b2=b1﹣a1﹣a2=,∴正方形A3B3C3C3中阴影正方形边长××2=;∴阴影部分面积;以此推理,第n个阴影正方形的边长为2×;∴阴影部分面积;故选:A.7.解:①乙比甲早到B城,早了5﹣3=2个小时;所以甲、乙两人同时到达目的地是错误的;②由图可知:M(2,0),N(3,50),Q(2,20),R(5,50)设直线QR的函数表达式为s1=k1t+b1,直线MN的函数表达式为s2=k2t+b2,将各点坐标代入对应的表达式,得:解得:,,解得:,∴s1=10t,s2=50t﹣100,联立两式可得直线QR、MN的交点的坐标为O(2.5,25)所以乙出发半小时后追上甲,故乙出发后30分钟后追上甲是正确的;③乙的速度为=50千米/时,甲的平均速度为=12.5千米/时,故甲的平均速度是10km/h,乙的速度是50km/h,是错误的;④因为乙出发半小时后追上甲,所以甲、乙相遇时距出发地25km,是正确的;故选:B.8.解:∵A1(1,1)在直线y=∴b=∴y=x+设A2(x2,y2),A3(x3,y3),A4(x4,y4),…,A2019(x2019,y2019)则有y2=x2+,y3=x3+,…y2019=x2019+.又∵△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.∴x2=2y1+y2,x3=2y1+2y2+y3,…x2019=2y1+2y2+2y3+…+2y2018+y2019.将点坐标依次代入直线解析式得到:y2=y1+1y3=y1+y2+1=y2y4=y3…y2019=y2018又∵y1=1∴y2=y3=()2y4=()3…y2019=()2018故选:B.9.解:∵∠CAB=90°,BC=5,点A、B的坐标分别为(2,0)、(5,0),∴AC=4,当点C落在y=x﹣2上时,如图,∴四边形BB′C′C是平行四边形,把x=2代入直线y=x﹣2,解得y=﹣1,即AC′=1,∴CC′=5,∴平行四边形BB′C′C的面积=AB×A′C′=5×3=15;故选:C.10.解:∵OB1=OA1;过点B1作A2B1⊥x轴,B1B2=B1A2;A3B2⊥x轴,B2B3=B2A3;…∴△△OA1B1,△B1A2B2,△B2A3B3是等腰直角三角形,∵y=x+1交y轴于点A1,∴A1(0,1),∴B1(1,0),∴OB1=OA1=1,∴S1=×1×1=×12,同理S2=×2×2=22,S3=4×4=42;…∴S n=22n﹣2=22n﹣3,∴S2017=22×2017﹣3=24031,故选:B.二.填空题(共10小题)11.解:当x=0时,y=﹣x+3=3,∴点B的坐标为(0,3);当y=0时,有﹣x+3=0,∴x=4,∴点A的坐标为(4,0).∴AB==5.①当点B恰好落在x轴负半轴时,设该点为B′,如图1所示.根据折叠的性质可知:CB′=CB,AB′=AB,∵点C的坐标为(0,n),∴OC=n,CB′=3﹣n,OB′=1,∵CB′2=OB′2+OC2,即(3﹣n)2=1+n2,∴n=,∴点C的坐标为(0,);②当点B恰好落在x轴正半轴时,设该点为B″,如图2所示.根据折叠的性质可知:CB″=CB,AB″=AB,∵点C的坐标为(0,n),∴OC=﹣n,CB″=3﹣n,OB″=9,∵CB″2=OB″2+OC2,即(3﹣n)2=92+(﹣n)2,∴n=﹣12,∴点C的坐标为(0,﹣12).故答案为:(0,)或(0,﹣12).12.解:妈妈的速度为:100÷2=50(米/分),小亮的速度为:[100+50(12﹣2)]÷(12﹣2)=60(米/分),相遇时行走的路程为:12×50=600(米),观察图象在x=18时,小亮和妈妈的相距最大,可知是小亮到达长嘉汇所经历的时间,所以家到长嘉汇的距离为:60×(18﹣2)=960(米),由(18﹣12=6分钟)可知妈妈返回找到相机行走路程为:6×50=300(米),此时设小亮在长嘉汇等妈妈的时间为t分钟,由图象知小亮与妈妈会合所用时间为27﹣18=9分钟可建立方程如下:60×(9﹣t)+50×9═960﹣(600﹣300),解得t=5.5(分钟),∴小亮开始返回时,妈妈离家的距离为:50×(18+5.5﹣6×2)=575(米).故答案为:57513.解:设出发时小明家的速度是a千米/小时,小亮家的速度是b千米/小时,且a>b,由题意得:0.8(a﹣b)=8,a=b+10,小明家因故停下来休息了15分钟,可知A(1.05,12),小亮的速度为:=80(千米/小时),∴小明家的速度是90千米/小时,设小明加速后的速度为m千米/小时,根据题意得:×80=(﹣1.05)m+0.8×90,m=100,﹣﹣1.05,=0.1(小时),=6(分),即小明家比小亮家早到景区6分钟.故答案为:6.14.解:联立OA边和AB边所在直线的解析式成方程组,,解得:,∴点A的坐标为(4,3).过点A作AM⊥x轴于点M,过点C作CN⊥N于点N,连接CE,则点A为线段CE 的中点,如图所示.∵∠CON+∠AOC+∠AOM=180°,∠AOC=90°,∴∠CON+∠AOM=90°.∵∠AOM+∠OAM=90°,∴∠CON=∠OAM.在△AOM和△OCN中,,∴△AOM≌△OCN(AAS),∴ON=AM,CN=OM,∴点C的坐标为(﹣3,4).∵点A为线段CE的中点,∴点E的坐标为(11,2).故答案为:(11,2).15.解:∵点B1、B2的坐标分别为(1,1),(3,2),∴A1(0,1),A2(1,2),∵点A1,A2在直线y=kx+b上,∴,解得,∴y=x+1,∵点B2的坐标为(3,2),∴点A3的坐标为(3,4),∴点B3的坐标为(7,4),∴点A4的坐标为(7,8),∴点B4坐标为(15,8),…,∴Bn的横坐标是:2n﹣1,纵坐标是:2n﹣1.∴B n的坐标是(2n﹣1,2n﹣1),∴B2019的坐标是(22019﹣1,22018).故答案为(22019﹣1,22018).16.解:由图象可得,慢车的速度为:1200÷10=120(千米/小时),快车的速度为:1200÷4﹣120=180(千米/小时),则快车到达A地的所用的时间为:1200÷180=(小时),故当快车到达A地时,慢车与B地的距离为:1200﹣120×=400(千米),故答案为:400.17.解:如图,作点C关于AB的对称点F,关于AO的对称点G,连接DF,EG,∵直线y=x+2与两坐标轴分别交于A、B两点,点C是OB的中点,∴B(﹣2,0),C(﹣1,0),∴BO=2,OG=1,BG=3,易得∠ABC=45°,∴△BCF是等腰直角三角形,∴BF=BC=1,由轴对称的性质,可得DF=DC,EC=EG,当点F,D,E,G在同一直线上时,△CDE的周长=CD+DE+CE=DF+DE+EG=FG,此时△DEC周长最小,设直线FG的解析式为:y=kx+b,∵F(﹣2,1),G(1,0),∴,∴,直线FG的解析式为:y=﹣x+,解得,∴点D的坐标为(﹣,),故答案为:(﹣,).18.解:∵直线y=x+1经过点M(1,b),∴b=1+1,解得b=2,∴M(1,2),∴关于x的方程组的解为,故答案为:.19.(1)由函数图象可知,乙比甲晚出发1小时.故答案为:1.(2)在整个运动过程中,甲、乙两人之间的距离随x的增大而增大时,有两种情况:一是甲出发,乙还未出发时:此时0≤x≤1;二是乙追上甲后,直至乙到达终点时:设甲的函数解析式为:y=kx,由图象可知,(4,20)在函数图象上,代入得:20=4k,∴k=5,∴甲的函数解析式为:y=5x①设乙的函数解析式为:y=k′x+b,将坐标(1,0),(2,20)代入得:,解得,∴乙的函数解析式为:y=20x﹣20 ②由①②得,∴,故≤x≤2符合题意.故答案为:0≤x≤1或≤x≤2.20.解:由题意可得,点B1的坐标为(1,1),点B2的坐标为(3,2),点B3的坐标为(7,4),点B4的坐标为(15,8),…,则点B2019的坐标为(22019﹣1,22018),故答案为:(22019﹣1,22018).三.解答题(共5小题)21.解:(1)由图可得,,解得,,答:甲的速度是60km/h乙的速度是80km/h;(2)m=(1.5﹣1)×(60+80)=0.5×140=70,即m的值是70;(3)甲车没有故障停车,则甲乙相遇所用的时间为:180÷(60+80)=,若甲车没有故障停车,则可以提前:1.5﹣=(小时)两车相遇,即若甲车没有故障停车,可以提前小时两车相遇.22.解:(1)设AC表达式为y=kx+b,把(6,0)、(21,25)代入得解得k=100,b=﹣600,所以AC所在直线的函数表达式y=100x﹣600;(2)设甲出发x分钟后两人相遇,则解得x=15,即甲出发15分钟后两人相遇,此时d=0,21分钟后乙到图书馆,甲距图书馆1500﹣60×21=240米,因此图象如下:(3)设甲出发x分钟甲、乙两人之间的路程至少为180m.①当乙没出发时,60x≥180,解得x≥3;当甲乙相遇前,即x≤15时60x﹣(100x﹣600)≥180解得x≤10.5,即3≤x≤10.5时甲、乙两人之间的路程至少为180m;③当甲乙相遇后,即x>15时100x﹣600﹣60x≥180,解得x≥19.5,即19.5≤x≤21时甲、乙两人之间的路程至少为180m;④乙到达终点后,1500﹣60x≥180,解得≤22;综上当3<x≤10.5或19.5≤x≤22分钟时甲、乙两人之间的路程至少为180m.23.解:(1)∵l∥AB.∴∠ODC=∠OAB,∵A(2,0)B(0,﹣2),∴tan∠OAB=,∴∠ODC=∠OAB=30°.∵BC=t,∴OC=2﹣t,∴OD=(2﹣t),∴AD=t.∵点A关于直线l的对称点为A',∴A'D=AD=t∠A'DA=60°,∴△A'DA是正三角形.过点A'作A'H⊥AD于H,∴AH=tA'H=t,∴A'点的坐标为(2﹣t,t).(2)AB=AF.说明:∵F(4+2,0),∴AF=4,在Rt△OAB中,OA=2,OB=2,∴AB=4,∴AB=AF.(3)∵直线l是点A和A'的对称轴,∴直线l是∠A'DA的平分线,∴点C到直线AD和A'D的距离相等,∴当⊙C与AD相切时,也一定与A'D相切.∵∠OAB=30°且AB=AF,∴∠ABF=15°,∴∠CBF=75°.∵CE⊥AB∠OBA=60°,∴∠BCE=30°,∴∠CEB=75°,∴CB=CE.∵⊙C与AD相切,∴OC=CE=CB,∴t=1.当⊙C与AA'相切于点M时,CE=CB=CM,∴CM=t,∵CM=DM﹣CD,在Rt△OCD中,∠ODC=30°,OC=t﹣2,∴CD=2t﹣4,∴2t﹣4+t=t,∴t=.24.解:(1)当0≤x≤3时,是正比例函数,设为y=kx,x=3时,y=300,代入解得k=100,所以y=100x;当3<x≤时,是一次函数,设为y=kx+b,代入两点(3,300)、(,0),得,解得,所以y=540﹣80x.综合以上得甲车离出发地的距离y与行驶时间x之间的函数关系式为:y=;(2)设出发后a小时,两车离各自出发地的距离相等.由题意﹣80a+540=40a,解得a=s,答:出发后小时,两车离各自出发地的距离相等.(3)由题意有两次相遇.①当0≤x≤3,100x+40x=300,解得x=;②当3<x≤时,(540﹣80x)+40x=300,解得x=6.综上所述,两车第一次相遇时间为第小时,第二次相遇时间为第6小时.25.【解答】解:(1)由图象可得,乙的行驶速度为:60÷(3.5﹣0.5)=20km/h;(2)设l1对应的函数解析式为y1=k1x+b1,,解得,即l1对应的函数解析式为y1=﹣30x+60;设l2对应的函数解析式为y2=k2x+b2,,解得,即l2对应的函数解析式为y2=20x﹣10,,解得,即点A的坐标为(1.4,18),∴点A的实际意义是在甲出发1.4小时时,甲乙两车相遇,此时距离B地18km;(3)由题意可得,|(﹣30x+60)﹣(20x﹣10)|=5,解得,x1=1.3,x2=1.5,答:当甲出发1.3h或1.5h时,两人之间的距离恰好相距5km;(4)由题意可得,当0≤x≤0.5时,y3=﹣30x+60,当0.5<x≤1.4时,y3=y1﹣y2=(﹣30x+60)﹣(20x﹣10)=﹣50x+70,当1.4<x≤2时,y3=y2﹣y1=(20x﹣10)﹣(﹣30x+60)=50x﹣70,当2<x≤3.5时,y3=20x﹣10,y3(km)关于时间x(h)的函数关系图象如右图(图2)所示.。
