群蚁算法编程代码
蚁群算法
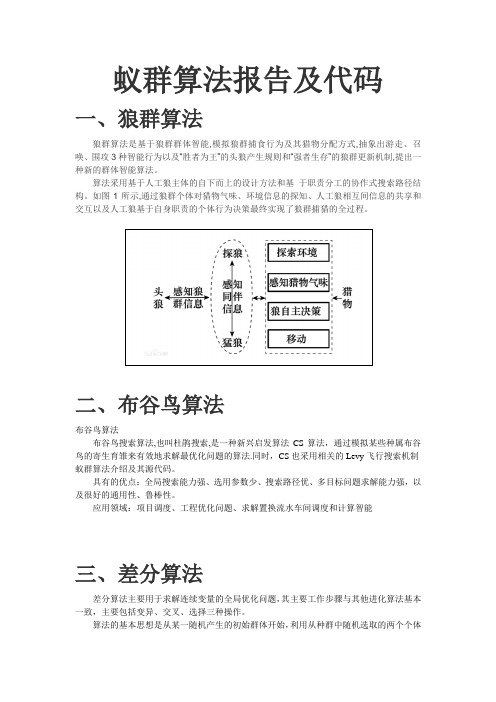
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。
算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。
如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。
二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法,通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时,CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。
具有的优点:全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强,以及很好的通用性、鲁棒性。
应用领域:项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题,其主要工作步骤与其他进化算法基本一致,主要包括变异、交叉、选择三种操作。
算法的基本思想是从某一随机产生的初始群体开始,利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源,将差向量加权后按照一定的规则与第三个个体求和而产生变异个体,该操作称为变异。
然后,变异个体与某个预先决定的目标个体进行参数混合,生成试验个体,这一过程称之为交叉。
如果试验个体的适应度值优于目标个体的适应度值,则在下一代中试验个体取代目标个体,否则目标个体仍保存下来,该操作称为选择。
在每一代的进化过程中,每一个体矢量作为目标个体一次,算法通过不断地迭代计算,保留优良个体,淘汰劣质个体,引导搜索过程向全局最优解逼近。
四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。
从理论上分析,迭代过程中,在保留上一代最佳个体的前提下,遗传算法是全局收敛的。
五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法,是集群智能思想的一个具体应用,它的主要特点是不需要了解问题的特殊信息,只需要对问题进行优劣的比较,通过各人工蜂个体的局部寻优行为,最终在群体中使全局最优值突现出来,有着较快的收敛速度。
蚁群算法程序(matlab)

蚁群算法程序(matlab)% 以下是蚁群算法MATLAB程序,请尊重原作者劳动,引用时请注明出处。
% 已经运行过,无误。
% 蚁群算法MATLAB程序function[R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ACATSP( C,NC_max,m,Alpha,Beta,Rho,Q)%%==================================== =====================================%% 主要符号说明%% C n个城市的坐标,n×2的矩阵%% NC_max 蚁群算法MATLAB程序最大迭代次数%% m 蚂蚁个数%% Alpha 表征信息素重要程度的参数%% Beta 表征启发式因子重要程度的参数%% Rho 信息素蒸发系数%% Q 表示蚁群算法MATLAB程序信息素增加强度系数%% R_best 各代最佳路线%% L_best 各代最佳路线的长度%%==================================== =====================================%% 蚁群算法MATLAB程序第一步:变量初始化n=size(C,1);%n表示问题的规模(城市个数)D=zeros(n,n);%D表示完全图的赋权邻接矩阵for i=1:nfor j=1:nif i~=jD(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;elseD(i,j)=eps; % i = j 时不计算,应该为0,但后面的启发因子要取倒数,用eps(浮点相对精度)表示endD(j,i)=D(i,j); %对称矩阵endendEta=1./D; %Eta为启发因子,这里设为距离的倒数Tau=ones(n,n); %T au为信息素矩阵Tabu=zeros(m,n); %存储并记录路径的生成NC=1; %迭代计数器,记录迭代次数R_best=zeros(NC_max,n); %各代最佳路线L_best=inf.*ones(NC_max,1); %各代最佳路线的长度L_ave=zeros(NC_max,1); %各代路线的平均长度while NC<=NC_max %停止条件之一:达到最大迭代次数,停止%% 蚁群算法MATLAB程序第二步:将m只蚂蚁放到n个城市上Randpos=[]; %随即存取for i=1:(ceil(m/n))Randpos=[Randpos,randperm(n)];endTabu(:,1)=(Randpos(1,1:m))'; %此句不太理解?%% 蚁群算法MATLAB程序第三步:m只蚂蚁按概率函数选择下一座城市,完成各自的周游for j=2:n %所在城市不计算for i=1:mvisited=Tabu(i,1:(j-1)); %记录已访问的城市,避免重复访问J=zeros(1,(n-j+1)); %待访问的城市P=J; %待访问城市的选择概率分布Jc=1;for k=1:nif length(find(visited==k))==0 %开始时置0J(Jc)=k;Jc=Jc+1; %访问的城市个数自加1endend%% 下面计算蚁群算法MATLAB程序待选城市的概率分布for k=1:length(J)P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^B eta);endP=P/(sum(P));%% 按概率原则选取下一个城市Pcum=cumsum(P); %cumsum,元素累加即求和Select=find(Pcum>=rand); %若计算的概率大于原来的就选择这条路线to_visit=J(Select(1));Tabu(i,j)=to_visit;endendif NC>=2Tabu(1,:)=R_best(NC-1,:);end%% 蚁群算法MATLAB程序第四步:记录本次迭代最佳路线L=zeros(m,1); %开始距离为0,m*1的列向量for i=1:mR=Tabu(i,:);for j=1:(n-1)L(i)=L(i)+D(R(j),R(j+1)); %原距离加上第j个城市到第j+1个城市的距离endL(i)=L(i)+D(R(1),R(n)); %一轮下来后走过的距离endL_best(NC)=min(L); %最佳距离取最小pos=find(L==L_best(NC));R_best(NC,:)=Tabu(pos(1),:); %此轮迭代后的最佳路线L_ave(NC)=mean(L); %此轮迭代后的平均距离NC=NC+1 %迭代继续%% 蚁群算法MATLAB程序第五步:更新信息素Delta_Tau=zeros(n,n); %开始时信息素为n*n的0矩阵for i=1:mfor j=1:(n-1)Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1 ))+Q/L(i);%此次循环在路径(i,j)上的信息素增量endDelta_Tau(Tabu(i,n),Tabu(i,1))=Delta_T au(Tabu(i,n),Tabu(i,1))+ Q/L(i);%此次循环在整个路径上的信息素增量endTau=(1-Rho).*Tau+Delta_Tau; %考虑信息素挥发,更新后的信息素%% 蚁群算法MATLAB程序第六步:禁忌表清零Tabu=zeros(m,n); %%直到最大迭代次数end%% 蚁群算法MATLAB程序第七步:输出结果Pos=find(L_best==min(L_best)); %找到最佳路径(非0为真)Shortest_Route=R_best(Pos(1),:) %最大迭代次数后最佳路径Shortest_Length=L_best(Pos(1)) %最大迭代次数后最短距离subplot(1,2,1) %绘制第一个子图形DrawRoute(C,Shortest_Route) %画路线图的子函数subplot(1,2,2) %绘制第二个子图形plot(L_best)hold on %保持图形plot(L_ave,'r')title('平均距离和最短距离') %标题% 蚁群算法MATLAB程序子函数function DrawRoute(C,R)%%==================================== =====================================%% DrawRoute.m%% 画路线图的子函数%%-------------------------------------------------------------------------%% C Coordinate 节点坐标,由一个N×2的矩阵存储%% R Route 路线%%==================================== =====================================N=length(R);scatter(C(:,1),C(:,2));hold onplot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)],'g')hold onfor ii=2:Nplot([C(R(ii-1),1),C(R(ii),1)],[C(R(ii-1),2),C(R(ii),2)],'g') hold onendtitle('旅行商问题优化结果 ')。
蚁群算法matlab代码讲解

蚁群算法matlab代码讲解蚁群算法(Ant Colony Algorithm)是模拟蚁群觅食行为而提出的一种优化算法。
它以蚁群觅食的方式来解决优化问题,比如旅行商问题、图着色问题等。
该算法模拟了蚂蚁在寻找食物时的行为,通过信息素的正反馈和启发式搜索来实现问题的最优解。
在蚁群算法中,首先需要初始化一组蚂蚁和问题的解空间。
每只蚂蚁沿着路径移动,通过信息素和启发式规则来选择下一步的移动方向。
当蚂蚁到达目标位置后,会根据路径的长度来更新信息素。
下面是一个用MATLAB实现蚁群算法的示例代码:```matlab% 参数设置num_ants = 50; % 蚂蚁数量num_iterations = 100; % 迭代次数alpha = 1; % 信息素重要程度因子beta = 5; % 启发式因子rho = 0.1; % 信息素蒸发率Q = 1; % 信息素增加强度因子pheromone = ones(num_cities, num_cities); % 初始化信息素矩阵% 初始化蚂蚁位置和路径ants = zeros(num_ants, num_cities);for i = 1:num_antsants(i, 1) = randi([1, num_cities]);end% 迭代计算for iter = 1:num_iterations% 更新每只蚂蚁的路径for i = 1:num_antsfor j = 2:num_cities% 根据信息素和启发式规则选择下一步移动方向next_city = choose_next_city(pheromone, ants(i, j-1), beta);ants(i, j) = next_city;endend% 计算每只蚂蚁的路径长度path_lengths = zeros(num_ants, 1);for i = 1:num_antspath_lengths(i) = calculate_path_length(ants(i, :), distances);end% 更新信息素矩阵pheromone = (1 - rho) * pheromone;for i = 1:num_antsfor j = 2:num_citiespheromone(ants(i, j-1), ants(i, j)) = pheromone(ants(i, j-1), ants(i, j)) + Q / path_lengths(i); endendend```上述代码中的参数可以根据具体问题进行调整。
基本蚁群算法程序

//基本蚁群算法程序//程序在vc++6.0下面同过,对原来的做了一点修改。
//你可以使用本代码,如果感到对你有用的话,请通知作者,作者会很高兴。
//通讯地址:[email]fashionxu@[/email]//by FashionXu#include#include#include#includeusing namespace std;const int iAntCount=34;//ant numbersconst int iCityCount=51;const int iItCount=2000;const double Q=100;const double alpha=1;const double beta=5;const double rou=0.5;int besttour[iCityCount];double rnd(int low,double uper){double p=(rand()/(double)RAND_MAX)*((uper)-(low))+(low);return (p);};int rnd(int uper){return (rand()%uper);};class GInfo{public:double m_dDeltTrial[iCityCount][iCityCount];//信息素增量double m_dTrial[iCityCount][iCityCount];//信息素痕迹double distance[iCityCount][iCityCount];//距离};GInfo Map;{private:int ChooseNextCity();double prob[iCityCount];//转移概率int m_iCityCount;int AllowedCity[iCityCount]; public:void addcity(int city);int tabu[iCityCount];//行走路径void Clear();void UpdateResult();double m_dLength;double m_dShortest;void move();ant();void move2last();};void ant::move2last(){int i;for(i=0;i if (AllowedCity[i]==1) {addcity(i);break;}}void ant::Clear(){m_dLength=0;int i;for(i=0;i {prob[i]=0;AllowedCity[i]=1;}i=tabu[iCityCount-1];m_iCityCount=0;addcity(i);}ant::ant(){m_dLength=m_dShortest=0;m_iCityCount=0;int i;AllowedCity[i]=1;prob[i]=0;}}void ant::addcity(int city){//add city to tabu;tabu[m_iCityCount]=city;m_iCityCount++;AllowedCity[city]=0;}int ant::ChooseNextCity(){//Update the probability of path selection//select a path from tabu[m_iCityCount-1] to nextint i;int j=10000;double temp=0;int curCity=tabu[m_iCityCount-1];for (i=0;i{if((AllowedCity[i]==1)){temp+=pow((1.0/Map.distance[curCity][i]),beta)*pow((Map.m_dTrial[c urCity][i]),alpha);//距离 //残留信息量}}double sel=0;for (i=0;i{if((AllowedCity[i]==1)){prob[i]=pow((1.0/Map.distance[curCity][i]),beta)*pow((Map.m_dTrial [curCity][i]),alpha)/temp;sel+=prob[i];}elseprob[i]=0;}double mRate=rnd(0,sel);double mSelect=0;for ( i=0;i{if((AllowedCity[i]==1))mSelect+=prob[i] ;if (mSelect>=mRate){j=i;break;}}if (j==10000){temp=-1;for (i=0;i{if((AllowedCity[i]==1))if (temp{temp=pow((1.0/Map.distance[curCity][i]),beta)*pow((Map.m_dTrial[ curCity][i]),alpha);j=i;}}}return j;}void ant::UpdateResult(){// Update the length of tourint i;for(i=0;i m_dLength+=Map.distance[tabu[i]][tabu[i+1]];m_dLength+=Map.distance[tabu[iCityCount-1]][tabu[0]];}void ant::move(){//the ant move to next town and add town ID to tabu.int j;j=ChooseNextCity();addcity(j);}class project{public:void UpdateTrial();double m_dLength;void initmap();ant ants[iAntCount];void GetAnt();void StartSearch();project();};void project::UpdateTrial(){//calculate the changes of trial informationint i;int j;for(i=0;i {for (j=0;j {Map.m_dDeltTrial[ants[i].tabu[j]][ants[i].tabu[j+1]]+=Q/ants[i].m_ dLength ;Map.m_dDeltTrial[ants[i].tabu[j+1]][ants[i].tabu[j]]+=Q/ants[i].m_ dLength;}Map.m_dDeltTrial[ants[i].tabu[iCityCount-1]][ants[i].tabu[0]]+=Q/an ts[i].m_dLength;Map.m_dDeltTrial[ants[i].tabu[0]][ants[i].tabu[iCityCount-1]]+=Q/an ts[i].m_dLength;}for (i=0;i {for (j=0;j {Map.m_dTrial[i][j]=(rou*Map.m_dTrial[i][j]+Map.m_dDeltTrial[i][j] );Map.m_dDeltTrial[i][j]=0;}}}void project::initmap(){int i;int j;for(i=0;i for (j=0;j {Map.m_dTrial[i][j]=1;Map.m_dDeltTrial[i][j]=0;}}project::project(){//initial map,read map infomation from file . et.initmap();m_dLength=10e9;ifstream in("eil51.tsp");struct city{int num;int x;int y;}cc[iCityCount];for (int i=0;i{in>>cc[i].num>>cc[i].x>>cc[i].y;besttour[i]=0;}int j;for(i=0;i for (j=0;j{{Map.distance[i][j]=sqrt(pow((cc[i].x-cc[j].x),2)+pow((cc[i].y-cc[ j].y),2));}}}void project::GetAnt(){//randomly put ant into mapint i=0;int city;srand( (unsigned)time( NULL ) +rand());for (i=0;i {city=rnd(iCityCount);ants[i].addcity(city);}}void project::StartSearch(){//begin to find best solutionint max=0;//every ant tours timesint i;int j;double temp;int temptour[iCityCount];while (max{for(j=0;j{for (i=0;i ants[j].move();}for(j=0;j{ants[j].move2last();ants[j].UpdateResult ();}//find out the best solution of the step and put it into temp int t;temp=ants[0].m_dLength;for (t=0;ttemptour[t]=ants[0].tabu[t];for(j=0;j{if (temp>ants[j].m_dLength){temp=ants[j].m_dLength;for ( t=0;t temptour[t]=ants[j].tabu[t];}}if(tempm_dLength=temp;for ( t=0;t{besttour[t]=temptour[t];}printf("%d : %f\n",max,m_dLength);UpdateTrial();for(j=0;j ants[j].Clear();max++;}printf("The shortest toure is : %f\n",m_dLength); for ( int t=0;t printf(" %d ",besttour[t]);}int main(){project TSP;TSP.GetAnt();TSP.StartSearch();return 0;}。
(完整版)蚁群算法matlab程序实例整理

function [y,val]=QACSticload att48 att48;MAXIT=300; % 最大循环次数NC=48; % 城市个数tao=ones(48,48);% 初始时刻各边上的信息最为1rho=0.2; % 挥发系数alpha=1;beta=2;Q=100;mant=20; % 蚂蚁数量iter=0; % 记录迭代次数for i=1:NC % 计算各城市间的距离for j=1:NCdistance(i,j)=sqrt((att48(i,2)-att48(j,2))^2+(att48(i,3)-att48(j,3))^2);endendbestroute=zeros(1,48); % 用来记录最优路径routelength=inf; % 用来记录当前找到的最优路径长度% for i=1:mant % 确定各蚂蚁初始的位置% endfor ite=1:MAXITfor ka=1:mant %考查第K只蚂蚁deltatao=zeros(48,48); % 第K只蚂蚁移动前各边上的信息增量为零[routek,lengthk]=travel(distance,tao,alpha,beta);if lengthk<routelength % 找到一条更好的路径routelength=lengthk;bestroute=routek;endfor i=1:NC-1 % 第K只蚂蚁在路径上释放的信息量deltatao(routek(i),routek(i+1))=deltatao(routek(i),routek(i+1))+Q/lengthk ;enddeltatao(routek(48),1)=deltatao(routek(48),1)+Q/lengthk;endfor i=1:NC-1for j=i+1:NCif deltatao(i,j)==0deltatao(i,j)=deltatao(j,i); y=bestroute;end val=routelength;end tocendtao=(1-rho).*tao+deltatao;endy=bestroute;val=routelength;tocfunction [y,val]=travel(distance,tao,alpha,beta) % 某只蚂蚁找到的某条路径[m,n]=size(distance);p=fix(m*rand)+1; %fix取整函数val=0; % 初始路径长度设为0tabuk=[p]; % 假设该蚂蚁都是从第p 个城市出发的for i=1:m-1np=tabuk(length(tabuk)); % 蚂蚁当前所在的城市号p_sum=0;for j=1:mif isin(j,tabuk)continue;elseada=1/distance(np,j);p_sum=p_sum+tao(np,j)^alpha*ada^beta;endendcp=zeros(1,m); % 转移概率for j=1:mif isin(j,tabuk)continue;elseada=1/distance(np,j);cp(j)=tao(np,j)^alpha*ada^beta/p_sum;endendNextCity=pchoice(cp);tabuk=[tabuk,NextCity];val=val+distance(np,NextCity);endy=tabuk;function y=isin(x,A) % 判断数x 是否在向量A 中,如在返回1 ,否则返回0 y=0;for i=1:length(A)if A(i)==xy=1;break;endendfunction y=pchoice(A)a=rand;tempA=zeros(1,length(A)+1);for i=1:length(A)tempA(i+1)=tempA(i)+A(i);endfor i=2:length(tempA)if a<=tempA(i)y=i-1;break;endend。
蚁群算法C

这里发个贴吧里面的蚁群算法代码。
// AO.cpp : 定义控制台应用程序的入口点。
#pragma once#include <iostream>#include <math.h>#include <time.h>const double ALPHA=1.0; //启发因子,信息素的重要程度const double BETA=2.0; //期望因子,城市间距离的重要程度const double ROU=0.5; //信息素残留参数const int N_ANT_COUNT=34; //蚂蚁数量const int N_IT_COUNT=1000; //迭代次数const int N_CITY_COUNT=51; //城市数量const double DBQ=100.0; //总的信息素const double DB_MAX=10e9; //一个标志数,10的9次方double g_Trial[N_CITY_COUNT][N_CITY_COUNT]; //两两城市间信息素,就是环境信息素double g_Distance[N_CITY_COUNT][N_CITY_COUNT]; //两两城市间距离//eil51.tsp城市坐标数据double x_Ary[N_CITY_COUNT]={37,49,52,20,40,21,17,31,52,51,42,31,5,12,36,52,27,17,13,57,62,42,16,8,7,27,30,43,58,58,37,38,46,61,62,63,32,45,59,5,10,21,5,30,39,32,25,25,48,56,30};double y_Ary[N_CITY_COUNT]={52,49,64,26,30,47,63,62,33,21,41,32,25,42,16,41,23,33,13,58,42,57,57,52,38,68,48,67,48,27,69,46,10,33,63,69,22,35,15,6,17,10,64,15,10,39,32,55,28,37,40};//返回指定范围内的随机整数int rnd(int nLow,int nUpper){return nLow+(nUpper-nLow)*rand()/(RAND_MAX+1);}//返回指定范围内的随机浮点数double rnd(double dbLow,double dbUpper){double dbTemp=rand()/((double)RAND_MAX+1.0);return dbLow+dbTemp*(dbUpper-dbLow);}//返回浮点数四舍五入取整后的浮点数double ROUND(double dbA){return (double)((int)(dbA+0.5));}//定义蚂蚁类class CAnt{public:CAnt(void);~CAnt(void);public:int m_nPath[N_CITY_COUNT]; //蚂蚁走的路径double m_dbPathLength; //蚂蚁走过的路径长度int m_nAllowedCity[N_CITY_COUNT]; //没去过的城市 int m_nCurCityNo; //当前所在城市编号int m_nMovedCityCount; //已经去过的城市数量public:int ChooseNextCity(); //选择下一个城市void Init(); //初始化void Move(); //蚂蚁在城市间移动void Search(); //搜索路径void CalPathLength(); //计算蚂蚁走过的路径长度};//构造函数CAnt::CAnt(void){}//析构函数CAnt::~CAnt(void){}//初始化函数,蚂蚁搜索前调用void CAnt::Init(){for (int i=0;i<N_CITY_COUNT;i++){m_nAllowedCity[i]=1; //设置全部城市为没有去过 m_nPath[i]=0; //蚂蚁走的路径全部设置为0}//蚂蚁走过的路径长度设置为0m_dbPathLength=0.0;//随机选择一个出发城市m_nCurCityNo=rnd(0,N_CITY_COUNT);//把出发城市保存入路径数组中m_nPath[0]=m_nCurCityNo;//标识出发城市为已经去过了m_nAllowedCity[m_nCurCityNo]=0;//已经去过的城市数量设置为1m_nMovedCityCount=1;}//选择下一个城市//返回值为城市编号int CAnt::ChooseNextCity(){int nSelectedCity=-1; //返回结果,先暂时把其设置为-1//============================================================================ ==//计算当前城市和没去过的城市之间的信息素总和double dbTotal=0.0;double prob[N_CITY_COUNT]; //保存各个城市被选中的概率for (int i=0;i<N_CITY_COUNT;i++){if (m_nAllowedCity[i] == 1) //城市没去过{prob[i]=pow(g_Trial[m_nCurCityNo][i],ALPHA)*pow(1.0/g_Distance[m_nCurCityNo][i],BET A); //该城市和当前城市间的信息素dbTotal=dbTotal+prob[i]; //累加信息素,得到总和}else //如果城市去过了,则其被选中的概率值为0{prob[i]=0.0;}}//============================================================================ ==//进行轮盘选择double dbTemp=0.0;if (dbTotal > 0.0) //总的信息素值大于0{dbTemp=rnd(0.0,dbTotal); //取一个随机数for (int i=0;i<N_CITY_COUNT;i++){if (m_nAllowedCity[i] == 1) //城市没去过{dbTemp=dbTemp-prob[i]; //这个操作相当于转动轮盘,如果对轮盘选择不熟悉,仔细考虑一下if (dbTemp < 0.0) //轮盘停止转动,记下城市编号,直接跳出循环{nSelectedCity=i;break;}}}}//============================================================================ ==//如果城市间的信息素非常小( 小到比double能够表示的最小的数字还要小)//那么由于浮点运算的误差原因,上面计算的概率总和可能为0//会出现经过上述操作,没有城市被选择出来//出现这种情况,就把第一个没去过的城市作为返回结果//题外话:刚开始看的时候,下面这段代码困惑了我很长时间,想不通为何要有这段代码,后来才搞清楚。
【转】蚁群算法原理及其实现(python)
【转】蚁群算法原理及其实现(python)蚁群算法(AG)是⼀种模拟蚂蚁觅⾷⾏为的模拟优化算法,它是由意⼤利学者Dorigo M等⼈于1991年⾸先提出,并⾸先使⽤在解决TSP(旅⾏商问题)上。
之后,⼜系统研究了蚁群算法的基本原理和数学模型.蚁群算法的基本思想:蚁群算法的基本原理:1、蚂蚁在路径上释放信息素。
2、碰到还没⾛过的路⼝,就随机挑选⼀条路⾛。
同时,释放与路径长度有关的信息素。
3、信息素浓度与路径长度成反⽐。
后来的蚂蚁再次碰到该路⼝时,就选择信息素浓度较⾼路径。
4、最优路径上的信息素浓度越来越⼤。
5、最终蚁群找到最优寻⾷路径。
⼈⼯蚁群与真实蚁群对⽐:基于TSP问题的基本蚁群算法:TSP求解中,假设蚁群算法中的每只蚂蚁是具有以下特征的简单智能体:每次周游,每只蚂蚁在其经过的⽀路(i,j)上都留下信息素。
‚蚂蚁选择城市的概率与城市之间的距离和当前连接⽀路上所包含的信息素余量有关。
ƒ为了强制蚂蚁进⾏合法的周游,直到⼀次周游完成后,才允许蚂蚁游⾛已访问过的城市(这可由禁忌表来控制)。
基本蚁群的两个过程:(1)状态转移(2)信息素更新(1)状态转移为了避免残留信息素过多⽽淹没启发信息,在每只蚂蚁⾛完⼀步或者完成对所有n个城市的遍历(也即⼀个循环结束)后,要对残留信息进⾏更新处理。
由此,t+n时刻在路径(i,j)上的信息量可按如下规则进⾏调整:(2)信息素更新模型蚁周模型(Ant-Cycle模型)蚁量模型(Ant-Quantity模型)蚁密模型(Ant-Density模型)区别:1.蚁周模型利⽤的是全局信息,即蚂蚁完成⼀个循环后更新所有路径上的信息素;2.蚁量和蚁密模型利⽤的是局部信息,即蚂蚁完成⼀步后更新路径上的信息素。
基本流程:蚁群算法中主要参数的选择:蚁群算法中主要参数的理想选择如下:国内外,对于离散域蚁群算法的改进研究成果很多,例如⾃适应蚁群算法、基于信息素扩散的蚁群算法等,这⾥仅介绍离散域优化问题的⾃适应蚁群算法。
蚁群算法整个程序(matlab)
蚁群算法整个程序(matlab)main:%function [bestroute,routelength]=Ant clccleartic% 读入城市间距离矩阵数据文件CooCity = load( 'CooCity.txt' ) ;% 城市网络图坐标数据文件,txt形式给出 NC=length(CooCity); % 城市个数for i=1:NC % 计算各城市间的距离for j=1:NCdistance(i,j)=sqrt((CooCity(i,2)-CooCity(j,2))^2+(CooCity(i,3)-CooCity(j,3))^2);endend% distance=xlsread('DistanceCity.xls'); % 城市间距离矩阵数据文件,excel形式给出MAXIT=10; % 最大循环次数Citystart=[]; % 起点城市编号tau=ones(NC,NC); % 初始时刻各边上的信息痕迹为1rho=0.5; % 挥发系数alpha=1; % 残留信息相对重要度beta=5; % 预见值的相对重要度Q=10; % 蚁环常数NumAnt=20; % 蚂蚁数量%bestroute=zeros(1,48); % 用来记录最优路径routelength=inf; % 用来记录当前找到的最优路径长度for n=1:MAXITfor k=1:NumAnt %考查第K只蚂蚁deltatau=zeros(NC,NC); % 第K只蚂蚁移动前各边上的信息增量为零%[routek,lengthk]=path(distance,tau,alpha,beta,[]); % 不靠率起始点[routek,lengthk]=path(distance,tau,alpha,beta,Citystart); % 指定起始点if lengthk<routelength % 找到一条更好的路径routelength=lengthk;bestroute=routek;endfor i=1:NC-1 % 第K只蚂蚁在路径上释放的信息量deltatau(routek(i),routek(i+1))=deltatau(routek(i),routek(i+1))+Q/le ngthk; % 信息素更新end%deltatau(routek(NC),1)=deltatau(routek(NC),1)+Q/lengthk; %endlength_n(n)=routelength; % 记录路径收敛tau=(1-rho).*tau; % 信息素挥发end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% costtime=toc;subplot(1,2,1),plot([CooCity(bestroute,2)],[CooCity(bestroute,3)],'-*')subplot(1,2,2),plot([1:MAXIT],length_n,'-*')[routelength,costtime]inroute:function Y=inroute(n,A)% A 为已过城市点集合,如果n在A中返回1 Y=0;for i=1:length(A)if A(i)==nY=1;break;endendnextcitychoose:% % ,为何不直接以转移概率最大值对应节点为下一转移节点 % 随机决策原则确定下步转移节点, 转移概率累积序列大于某随机值方向 functionN=nextcitychoose(Cp)a=rand;s=0;for i=1:length(Cp)s=s+Cp(i);if a<=sN=i;break;endendnextcitychoose2:% % 直接以转移概率最大值对应节点为下一转移节点% 随机决策原则确定下步转移节点function N=nextcitychoose2(Cp)I=find(Cp==max(Cp));N=I(1);nextcitychoose3% % 直接以转移概率最大值对应节点为下一转移节点% 随机决策原则确定下步转移节点function N=nextcitychoose2(Cp)I=find(Cp==max(Cp));N=I(1);path:% 某只蚂蚁找到的某条路径routek,lengthk function [routek,lengthk]=path(distance,tau,alpha,beta,Citystart) [m,n]=size(distance);if isempty(Citystart) % 如果不确定起点p=fix(m*rand)+1; % 随机方式初始化起点,均匀概率 else p=Citystart; % 外部给定确定起点endlengthk=0; % 初始路径长度设为 0routek=[p]; % 蚂蚁路径点序列,即该蚂蚁已经过的城市集合,路径初始起点for i=1:m-1np=routek(end); % 蚂蚁路径城市序号,依次经过的城市编号np_sum=0; % 路由长度初始为 0for j=1:mif inroute(j,routek) % 判断城市节点j是否属于tabuk,即是否已经过continue;else % j为还未经过的点,对ada=1/distance(np,j); % 预见度np_sum=np_sum+tau(np,j)^alpha*ada^beta; % 路由表:信息痕迹、预见度endendcp=zeros(1,m); % 转移概率,基于路径长度及路由表for j=1:mif inroute(j,routek)continue;elseada=1/distance(np,j); % 预见度cp(j)=tau(np,j)^alpha*ada^beta/np_sum; % np到j的转移概率endendNextCity=nextcitychoose3(cp); % 根据转移概率确定下一个城市,% 这里采用不同的随机决策原则所得效果也不同:% nextcitychoose3 取转移概率最大值方向% nextcitychoose和nextcitychoose2 转移概率累积序列大于某随机值方向% 直观地,取转移概率最大值方向方法,决策结果稳定且收敛快routek=[routek,NextCity]; % 更新路径lengthk=lengthk+distance(np,NextCity); % 更新路径长度 end。
蚁群算法Delphi源程序
蚁群算法Delphi源程序:{*Ant algorithm for VRP —Ant cycle, Ant density, Ant quantity*}const inf=99999999; eps=1E-8type item=integer;var FN:string; f:System. Text;procedure T_VRPANT_RUN;const maxn=500; ruo=0.7; Q=10;label loop;type item2=real;Arr1=array of array of item;Arr2=array of array of item2;Arr3=array of array of boolean;Arr4=array of array of item;Arr5=array of array of item2;var n,i,j,k,l,ii,jj,count,s,maxcount,tweight,index,model,qq,capa,m,Last,selected,tm,weight:item;tmax,tmin:item2;datatype:byte;W,route,opt,cycle:arrl;t,dt:arr2;ch:arr3;x,y:arr5;Len,tlen,nearest,series,demand,kcount,tkcount:arr4;function PValue(i,j,k:item):item2var 1:item; sum:item2;beginSum:=0;For 1:=2 to n doIf(capa>demand[1])and(ch[1]and(cycle[k,l]=0)and(1< >i)thenSum:=sum+t[i,1]/w[i,l];If(sum>eps)and(cycle[k,j]=0)and(j< >i)thenSun:t[i,j]/ w[i,l]/sumPValue:=sum;end;procedure TwoOpt(p:item);var ahead,i,i1,i2,index,j,j1,j2,last,limit,max,next,s1,s2,t1,t2,maxtemp:item;pt:arr4; beginsetLength(ph,n+1);t1:=1; t2:=1; sl:=1; s2:=1;for I:=1 to p-1 do pt[route[k,i]:=route[k,i+1];pt[route[k,p]:=route[k,l];repeatmaxtemp:=0; i1:=1;for i:=1 to p-2 dobeginif i=1 then limit:=p-1 else limit:=p;i2:=pt[i1]; j1:=pt[i2];for j:=i+2 to limit dobeginj2:=pt[j1]max:=w[i1,i2]+w[j1,j2]-(w[i1,j1]=+w[i2,j2]);if(max>maxtemp)thenbegins1:=i1; s2:=i2; t1=j1; t2=j2; maxtemp:=max;end;j1:=j2;end;i1:=i2;end;if ( maxtemp>0) thenbeginpt[s1]:=t1; next:=s2; last:= t2;repeatahead:=pt[next];pt[next]:=last;last:=next;next:=ahead;until next=t2;end;until(maxtemp=0);index:=1;for i:=1 to p dobeginroute[k,i]:=index; index:=pt[index];end;end;procedure Antmove;label lop, select, check,next;var a,j,k:item;begink:=1; capa:=qq; last:=n-1;for j:=1 to last do series[j]:=j+1;for j:=1 to last do ch[j]:=truefor j:=1 to last do kcount[j]:=0;lop:nearest[k]:=1;for j:=1 to n do cycle[k,j]:=0;select:a:=nearest[k]; j:=1;while j< =last dobeginindex:=0;selected:=random(last)+1;if (capa> =demand[series[selected]])thenbeginindex:=series[selected];if (random<PValue(a,index,k)) then goto check;index:=series[selected];end;j:=j+1;end;if index=0 then goto next;check:cycle[k,nearest[k]]:=index;nearest[k]:=cysle[k,nearest[k]];ch[index]:=false;capa:=capa-demand[index];kcount[k]:=kcountt[k]+1;last:=last-1;for j:=selected to last do series[j]:=series[j+1];if last>=1 then goto select;next:if last>=1 then;begin k:=k+1; capa:=qq; goto lop; end;m:=k;end;beginAssignFile(f,FN); Reset(f);{$I-}Readln(f,n,datatype,qq,maxcount); {$I+}If(IOResult< >0)or(n<4)or(n>maxn)or(maxcount<1)or(datatype<1) or(datatype>2)or(qq<=0) thenbegin ShowMessage(‘数据错误’); System.Close(f); exit; end; SetLength(t,n+1,n+1);SetLength(dt,n+1,n+1);SetLength(w,n+1,n+1);SetLength(opt,n+1,n+1);SetLength(route,n+1,n+1);SetLength(cycle,n+1,n+1);If datatype=1 thenbeginSetLength(x,n+1); SetLength(y,n+1);for i:=1 to n dobegin{$I-}Readln(f,ii,x[i],y[i]); {$I+}If(IOResult< >0)or(ii< >i) thenBegin Show Message(‘数据错误’); System.Close(f); exit; end;end;for i:=1 to n-1 do for j:=i+1 to n dobeginw[i,j]:=trunc(sprt(spr(x[i]-x[j])+spr(y[i]-y[j]))+0.5);w[j,i]:=w[i,j]; t[i,j]:=1; dt[i,j]:=0;t[j,i]:=t[i,j]; dt[j,i]:=dt[i,j];end;for i:=1 to n dobeginw[i,i]:=inf; t[i,i]:=1; dt[i,i]:=0;end;SetLength(x,0); SetLength(y,0);endelsebeginfor i:=1 to n-1 do for j:=i+1 to n dobegin{$I-}Readln(f,ii,jj,w[i,j]); {$I+}If(IOResult< >0)or(ii< >i) or(jj< >j)or(w[i,j]<1)thenbegin Show Message(‘数据错误’); System.Close(f); exit; end;w[j,i]:=w[i,j]; t[i,j]:=1; dt[i,j]:=0;t[j,i]:=t[i,j]; dt[j,i]:=dt[i,j];end;for i:=1 to n dobeginw[i,i]:=inf; t[i,i]:=1; dt[i,i]=0;end;end;SetLength(len,n+1);SetLength(tlen,n+1);SetLength(series,n+1);SetLength(nearest,n+1);SetLength(tkcount,n+1,n+1);SetLength(demand,n+1);SetLength(kcount,n+1);SetLength(ch,n+1);demand[1]:=0;for i:=2 to n dobegin{$I-}Readln(f,ii,demand[i];{$I+}If(IOResult< >0)or(ii< >i)or(demand[i]>qq)or(demand[i]<0)thenbegin Show Message(‘数据错误’); System.Close(f); exit; end;endSystem.Close(f);FN:=Copy(FN,1,Length(FN)-4)+’.OUT’;Show Message(’输出结果存入文件:’+FN);AssignFile(f,FN);Rewrite(f);count:=0;tweight:=inf;index:=1;tm:=inf;randomize;model:=random(3)+1;1oop:AntMove;weight:=0;for k:=1 to m do len[k]:=0;for k:=1 to m dobeginindex:=1;for i:=1 to kcount[k]+1 dobeginroute[k,i]:=index; index:=cycle[k,index];end;TwoOpt(kcount[k]+1);Len[k]:=w[route[k,kcount[k]+1],route[k,1]];for i:=1 to kcount[k] do len[k]:=len[k]+w[route[k,i],route[k,i+1]]; weight:=weight+len[k];end;if m< tm thenbegintm:=m; tweight:=weight;for k:=1 to tm dobegintkcount[k]:=kcount[k];for j:=1 to tkcount[k]+1 do opt[k,j]:=route[k,j];tlen[k]:=len[k];end;end;if m=tm then if tweight>weight thenbegintweight:=weight;for k:=1 to tm dobegintkcount[k]:=kcount[k];for j:=1 to tkcount[k]+1 do opt[k,j]:=route[k,j];tlen[k]:=len[k];end;end;for k:=1 to tm dobegincase model of1: beginfor 1:=1 to kcount[k] dobeginii:=route[k,l];jj=route[k,1+1];dt[ii,jj]:=dt[ii,jj]+q/len[k];end;ii:=route[k,kcount[k]+1]; jj=route[k,1];dt[ii,jj]:=dt[ii,jj]+q/len[k];end;2: beginfor 1:=1 to kcount[k] dobeginii:=route[k,l]; jj:=route[k,1+1];dt[ii,jj]:=dt[ii,jj]+q;end;ii:=route[k,kcount[k]+1]; jj:=route[k,1];dt[ii,jj]:=dt[ii,jj]+q;end;3: beginfor 1:=1 to kcount[k] dobeginii:=route[k,1]; jj:=route[k,l+1]dt[ii,jj]:=dt[ii,jj]+q/w[ii,jj];end;ii:=route[k,kcount[k]+1]; jj:=route[k,1];dt[ii,jj]:=dt[ii,jj]+q/w[ii,jj];endendend;for i:=1 to n do for j:=1 to n dobegint[i,j]:=ruo*t[i,j]+dt[i,j];tmax:=1/(tweight*(1-ruo); tmin=tmax/5;if (t[i,j]>tmax) then t[i,j]:=tmax;if (t[i,j]<tmin) then t[i,j]:=tmin;end;count:=count+1;for i:=1 to n do for j:= 1 to n do dt[i,j]:=0;if count<maxcount then goto loop;for k:=1 to tm dobeginwriteln(f); writeln(f,’第’,k,’条路线:’);writeln(f,’回路总长= ’,then[k]);write(f,’回路路径= ’);for j:= to tkcount[k] +1 do write(f,opt[k,j],’’);writeln(f,’1’); end;writeln(f); writeln(f,’所需车辆数= ’,tm);writeln(f); writeln(f,’车辆总行程= ’,tweight);System.Close(f);end;。
粒子群蚁群混合算法
粒子群蚁群混合算法
粒子群蚁群混合算法是一种优化算法,将粒子群算法和蚁群算法相结合,利用它们各自的优点进行优化。
该算法通常用于解决复杂的优化问题,如多目标优化、非线性优化等。
在粒子群蚁群混合算法中,粒子群算法模拟了一群鸟或昆虫在搜索环境中的行为,通过粒子的位置和速度来探索解空间。
而蚁群算法则模拟了蚂蚁在寻找食物时的行为,通过蚂蚁遗留的信息素来引导搜索过程。
粒子群蚁群混合算法中,粒子群算法的速度和位置更新公式如下: $$v_i^{t+1} = wv_i^t + c_1r_1(pbest_i - x_i^t) +
c_2r_2(gbest - x_i^t)$$
$$x_i^{t+1} = x_i^t + v_i^{t+1}$$
其中,$v_i^t$表示粒子$i$在$t$时刻的速度,$x_i$表示粒子
$i$在$t$时刻的位置,$pbest_i$表示粒子$i$的个体最优解,$gbest$表示全局最优解,$w$是惯性因子,$c_1$和$c_2$是学习因子,$r_1$和$r_2$是随机数。
蚁群算法则通过信息素的更新和挥发来实现搜索过程,信息素更新公式如下:
$$tau_{ij}^{t+1} = (1-rho)tau_{ij}^t + Deltatau_{ij}^t$$ 其中,$tau_{ij}$表示从节点$i$到节点$j$的信息素浓度,$rho$是信息素挥发系数,$Deltatau_{ij}$是信息素增量。
粒子群蚁群混合算法中,将粒子群算法和蚁群算法的更新公式相
结合,实现了更加高效的搜索过程。
该算法的应用范围广泛,可用于机器学习、神经网络等领域的优化问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MODEL: TITLE 交通流均衡; SETS:
ROAD/AB,AC,BC,BD,CD/:Y; CAR/2,3,4/; LINK(CAR,ROAD): T, X; ENDSETS DATA: ! 行驶时间(分钟) ;
T=20,52,12,52,20 30,53,13,53,30
40,54,14,54,40; ENDDATA [OBJ] MIN=@SUM(LINK: T*X); ! 目标函数; ! 四个节点的流量守恒条件; [NODE_A] Y(@INDEX(AB))+Y(@INDEX(AC)) = 6; [NODE_B] Y(@INDEX(AB))=Y(@INDEX(BC))+Y(@INDEX(BD)); [NODE_C] Y(@INDEX(AC))+Y(@INDEX(BC))=Y(@INDEX(CD)); [NODE_D] Y(@INDEX(BD))+Y(@INDEX(CD))=6; ! 每条道路上的总流量Y等于该道路上的分流量X的和; @FOR( ROAD(I): [ROAD_LIM] @SUM(CAR(J): X(J,I)) = Y(I)); ! 每条道路的分流量X的上下界设定; @FOR(LINK(I,J)|I#EQ#1: @BND(0,X(I,J),2) ); @FOR(LINK(I,J)|I#GT#1: @BND(0,X(I,J),1) ); END
clc,clear load sj.txt; x=sj(:,1); y=sj(:,2); sj=[x y]; d1=[70,40]; sj=[d1;sj;d1]; sj=sj*pi/180; d=zeros(102); for i=1:101 for j=i+1:102 temp=cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)); d(i,j)=6370*acos(temp); end end d=d+d'; S0=[];Sum=inf; rand('state',sum(clock)); for j=1:1000 S=[1 1+randperm(100),102]; temp=0; -276- for i=1:101 temp=temp+d(S(i),S(i+1)); end if tempS0=S;Sum=temp; end end e=0.1^30;L=20000;at=0.999;T=1; for k=1:L c=2+floor(100*rand(1,2)); c=sort(c); c1=c(1);c2=c(2); df=d(S0(c1-1),S0(c2))+d(S0(c1),S0(c2+1))-d(S0(c1-1),S0(c1))-d(S0(c2),S0(c2+1)); if df<0 S0=[S0(1:c1-1),S0(c2:-1:c1),S0(c2+1:102)]; Sum=Sum+df; elseif exp(-df/T)>rand(1) S0=[S0(1:c1-1),S0(c2:-1:c1),S0(c2+1:102)]; Sum=Sum+df; end T=T*at; if Tbreak; end end S0,Sum
计算结果
53.7121 15.3046 51.1758 0.0322 46.3253 28.2753 30.3313 6.9348 56.5432 21.4188 10.8198 16.2529 22.7891 23.1045 10.1584 12.4819 20.1050 15.4562 1.9451 0.2057 26.4951 22.1221 31.4847 8.9640 26.2418 18.1760 44.0356 13.5401 28.9836 25.9879 38.4722 20.1731 28.2694 29.0011 32.1910 5.8699 36.4863 29.7284 0.9718 28.1477 8.9586 24.6635 16.5618 23.6143 10.5597 15.1178 50.2111 10.2944 8.1519 9.5325 22.1075 18.5569 0.1215 18.8726 48.2077 16.8889 31.9499 17.6309 0.7732 0.4656 47.4134 23.7783 41.8671 3.5667 43.5474 3.9061 53.3524 26.7256 30.8165 13.4595 27.7133 5.0706 23.9222 7.6306 51.9612 22.8511 12.7938 15.7307 4.9568 8.3669 21.5051 24.0909 15.2548 27.2111 6.2070 5.1442 49.2430 16.7044 17.1168 20.0354 34.1688 22.7571 9.4402 3.9200 11.5812 14.5677 52.1181 0.4088 9.5559 11.4219 24.4509 6.5634 26.7213 28.5667 37.5848 16.8474 35.6619 9.9333 24.4654 3.1644 0.7775 6.9576 14.4703 13.6368 19.8660 15.1224 3.1616 4.2428 18.5245 14.3598 58.6849 27.1485 39.5168 16.9371 56.5089 13.7090 52.5211 15.7957 38.4300 8.4648 51.8181 23.0159 8.9983 23.6440 50.1156 23.7816 13.7909 1.9510 34.0574 23.3960 23.0624 8.4319 19.9857 5.7902 40.8801 14.2978 58.8289 14.5229 18.6635 6.7436 52.8423 27.2880 39.9494 29.5114 47.5099 24.0664 10.1121 27.2662 28.7812 27.6659 8.0831 27.6705 9.1556 14.1304 53.7989 0.2199 33.6490 0.3980 1.3496 16.8359 49.9816 6.0828 19.3635 17.6622 36.9545 23.0265 15.7320 19.5697 11.5118 17.3884 44.0398 16.2635 39.7139 28.4203 6.9909 23.1804 38.3392 19.9950 24.6543 19.6057 36.9980 24.3992 4.1591 3.1853 40.1400 20.3030 23.9876 9.4030 41.1084 27.7149
tic clc,clear load sj.txt x=sj(:,1); y=sj(:,2); sj=[x y]; d1=[70,40]; sj0=[d1;sj;d1]; sj=sj0*pi/180; d=zeros(102); for i=1:101 for j=i+1:102 temp=cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)); d(i,j)=6370*acos(temp); end end d=d+d';L=102;w=50;dai=100; for k=1:w c=randperm(100); c1=[1,c+1,102]; flag=1; while flag>0 flag=0; for m=1:L-3 for n=m+2:L-1 if d(c1(m),c1(n))+d(c1(m+1),c1(n+1))flag=1; c1(m+1:n)=c1(n:-1:m+1); end end end end J(k,c1)=1:102; end J=J/102; J(:,1)=0;J(:,102)=1; rand('state',sum(clock)); A=J; for k=1:dai B=A; c=randperm(w);
for i=1:2:w F=2+floor(100*rand(1)); temp=B(c(i),F:102); B(c(i),F:102)=B(c(i+1),F:102); B(c(i+1),F:102)=temp; end by=find(rand(1,w)<0.1); if length(by)==0 by=floor(w*rand(1))+1; end C=A(by,:); L3=length(by); for j=1:L3 bw=2+floor(100*rand(1,3)); bw=sort(bw); C(j,:)=C(j,[1:bw(1)-1,bw(2)+1:bw(3),bw(1):bw(2),bw(3)+1:102]); end G=[A;B;C]; TL=size(G,1);
[dd,IX]=sort(G,2);temp(1:TL)=0; for j=1:TL for i=1:101 temp(j)=temp(j)+d(IX(j,i),IX(j,i+1)); end end [DZ,IZ]=sort(temp); A=G(IZ(1:w),:); end path=IX(IZ(1),:) long=DZ(1) toc xx=sj0(path,1);yy=sj0(path,2); plot(xx,yy,'-o')
