型钢混凝土剪力墙轴压比计算及其限值研究
轴压比,剪重比的定义和介绍

1.什么是轴压比轴压比:主要为控制结构的延性,规范对墙肢和柱均有相应限值要求,见抗规6.3.7和6.4.6。
u=N/A*fc,u—轴压比,对非抗震地区,u=0.9N—柱轴力设计值A—柱截面面积fc—砼抗压强度设计值2.什么是周期比?剪重比?位移比?楼层最小剪力系数?新的建筑结构设计规范在结构可靠度、设计计算、配筋构造方面均有重大更新和补充,特别是对抗震及结构的整体性,规则性作出了更高的要求,使结构设计不可能一次完成。
如何正确运用设计软件进行结构设计计算,以满足新规范的要求,是每个设计人员都非常关心的问题。
以SATWE软件为例,进行结构设计计算步骤的讨论,对一个典型工程而言,使用结构软件进行结构计算分四步较为科学。
1.完成整体参数的正确设定计算开始以前,设计人员首先要根据新规范的具体规定和软件手册对参数意义的描述,以及工程的实际情况,对软件初始参数和特殊构件进行正确设置。
但有几个参数是关系到整体计算结果的,必须首先确定其合理取值,才能保证后续计算结果的正确性。
这些参数包括振型组合数、最大地震力作用方向和结构基本周期等,在计算前很难估计,需要经过试算才能得到。
(1)振型组合数是软件在做抗震计算时考虑振型的数量。
该值取值太小不能正确反映模型应当考虑的振型数量,使计算结果失真;取值太大,不仅浪费时间,还可能使计算结果发生畸变。
《高层建筑混凝土结构技术规程》5.1.13-2条规定,抗震计算时,宜考虑平扭藕联计算结构的扭转效应,振型数不宜小于15,对多塔结构的振型数不应小于塔楼的9倍,且计算振型数应使振型参与质量不小于总质量的90%。
一般而言,振型数的多少于结构层数及结构自由度有关,当结构层数较多或结构层刚度突变较大时,振型数应当取得多些,如有弹性节点、多塔楼、转换层等结构形式。
振型组合数是否取值合理,可以看软件计算书中的x,y向的有效质量系数是否大于0.9。
具体操作是,首先根据工程实际情况及设计经验预设一个振型数计算后考察有效质量系数是否大于0.9,若小于0.9,可逐步加大振型个数,直到x,y两个方向的有效质量系数都大于0.9为止。
不同轴压比对剪力墙抗震性能影响分析

义为无穷大,忽略其变形,泊松比设置趋于 0。
网格划分直接影响模拟计算结果的精度,网格划
(a) 边界条件设置
分过大,计算精度无法保证,若划分的过小,则可能致
使计算收敛较为困难。采用结构化网格划分技术,网
格的划分考虑到局部部件划分不均匀,根据混凝土墙
体尺寸纵向及横向尺寸,网格单元尺寸保持在 40mm~
解,剪力墙结构形式在我国高层住宅的使用率以达到
90%[1],剪力墙在房屋及构筑物中主要承受水平荷载
和竖向荷载的墙体。往往在项目设计时,设计师过渡
考虑墙体材料强度及水平抗侧刚度,导致设计出的剪
力墙具有用材多、截面大、抗侧移刚度大、延性低的特
点[3]。这也就导致此类剪力墙在地震作用下破坏严
重,究其原因是此类剪力墙有较大的抗侧刚度,在地
端部,轴压比在 0.1~0.3 时,剪力墙呈现弯曲破坏,轴压比在 0.4~0.5 时,剪力墙呈现出斜压破坏,随着轴压比的提
高,剪力墙抗剪承载力增大,而其塑性变形能力在减弱,剪力墙抗侧承载力存在阈值,且剪力墙出现损伤后,抗剪
承载力下降较快,刚度退化速率下降速率较快。
关键词:轴压比
0
剪力墙
破坏模式
抗剪承载力
压比在 0.4~0.5 之间时,可以得出墙体有竖向损伤带
形成,为典型的斜压破坏础地梁相对地面无相对滑移及
转角,即其侧面及底边设置为完全固定,U1=U2=U3=
UR1=UR2=UR3=0,在加载梁设置耦合点 RP1 耦合于
整个顶面,沿 Y 轴方向在 RP1 点上施加轴向力,该轴
伸及压缩应力应变关系见图 4。
(a) 砌体单轴受压应力应变关系 (b) 砌体单轴受拉应力应变关系
轴压比,剪重比的定义和介绍

1.什么是轴压比轴压比:主要为控制结构的延性,规范对墙肢和柱均有相应限值要求,见抗规6.3.7和6.4.6。
u=N/A*fc,u—轴压比,对非抗震地区,u=0.9N—柱轴力设计值A—柱截面面积fc—砼抗压强度设计值2.什么是周期比?剪重比?位移比?楼层最小剪力系数?新的建筑结构设计规范在结构可靠度、设计计算、配筋构造方面均有重大更新和补充,特别是对抗震及结构的整体性,规则性作出了更高的要求,使结构设计不可能一次完成。
如何正确运用设计软件进行结构设计计算,以满足新规范的要求,是每个设计人员都非常关心的问题。
以SATWE软件为例,进行结构设计计算步骤的讨论,对一个典型工程而言,使用结构软件进行结构计算分四步较为科学。
1.完成整体参数的正确设定计算开始以前,设计人员首先要根据新规范的具体规定和软件手册对参数意义的描述,以及工程的实际情况,对软件初始参数和特殊构件进行正确设置。
但有几个参数是关系到整体计算结果的,必须首先确定其合理取值,才能保证后续计算结果的正确性。
这些参数包括振型组合数、最大地震力作用方向和结构基本周期等,在计算前很难估计,需要经过试算才能得到。
(1)振型组合数是软件在做抗震计算时考虑振型的数量。
该值取值太小不能正确反映模型应当考虑的振型数量,使计算结果失真;取值太大,不仅浪费时间,还可能使计算结果发生畸变。
《高层建筑混凝土结构技术规程》5.1.13-2条规定,抗震计算时,宜考虑平扭藕联计算结构的扭转效应,振型数不宜小于15,对多塔结构的振型数不应小于塔楼的9倍,且计算振型数应使振型参与质量不小于总质量的90%。
一般而言,振型数的多少于结构层数及结构自由度有关,当结构层数较多或结构层刚度突变较大时,振型数应当取得多些,如有弹性节点、多塔楼、转换层等结构形式。
振型组合数是否取值合理,可以看软件计算书中的x,y向的有效质量系数是否大于0.9。
具体操作是,首先根据工程实际情况及设计经验预设一个振型数计算后考察有效质量系数是否大于0.9,若小于0.9,可逐步加大振型个数,直到x,y两个方向的有效质量系数都大于0.9为止。
型钢混凝土(SRC)柱、剪力墙和梁破坏形态划分及其变形指标限值
弯曲破坏的 SRC 剪力墙弹塑性位移角限值见表 F.2.2.1,剪切破坏的 SRC 剪力墙弹塑性
位移角限值见表 F.2.2.2。
表 F.2.2.1 弯曲破坏 SRC 剪力墙弹塑性位移角限值
构件参数
性能水准
≤0.1 ≤0.1 ≥0.4 ≥0.4 ≤0.1 ≤0.1 ≥0.4 ≥0.4
th
h
≥0.3 ≥0.3 ≥0.3 ≥0.3 ≤0.05 ≤0.05 ≤0.05 ≤0.05
飈h
h
≥0.2 ≤0.08 ≥0.2 ≤0.08 ≥0.2 ≤0.08 ≥0.2 ≤0.08
表 F.1.2.3 剪切破坏 SRC 柱弹塑性位移角限值 性能水准
无损坏 轻微损坏 轻度损坏 中度损坏
0.007 0.006 0.003 0.003 0.005 0.004 0.003 0.003
0.013 0.011 0.005 0.005 0.009 0.007 0.004 0.003
构件参数
≤0.1 ≥0.6 ≤0.1 ≥0.6
≥0.03 ≥0.03 ≤0.01 ≤0.01
表 F.1.2.2 弯剪破坏 SRC 柱弹塑性位移角限值
性能水准
无损坏 轻微损坏 轻度损坏 中度损坏 比较严重损坏
0.014 0.007 0.009 0.005
0.022 0.011 0.015 0.006
严重 损坏 0.075 0.062 0.034 0.030 0.046 0.035 0.020 0.018
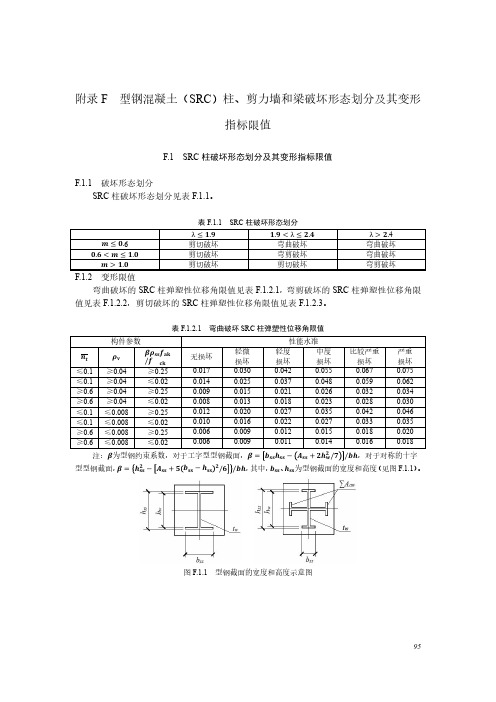
注: 为型钢约束系数,对于工字型型钢截面, =
/ / ,对于对称的十字
型型钢截面, =
쳌
/ / ,其中, 、 为型钢截面的宽度和高度(见图 F.1.1)。
图 F.1.1 型钢截面的宽度和高度示意图 95
型钢混凝土框架—混凝土筒体结构设计在超高层建筑中的应用与探讨

型钢混凝土框架—混凝土筒体结构设计在超高层建筑中的应用与探讨在高度为近190米的超高层建筑的结构设计中,采用型钢混凝土框架-钢筋混凝土筒体结构形式。
本文着重探讨了结构体系及布置、结构设计的构想、结构整体计算与分析等。
并在核心筒剪力墙极其外围墙体设计、外框架型钢混凝土梁柱节点设计、上部结构嵌固部位的分析验算、连梁超筋问题的处理以及抗震构造措施上,作进一步的探讨。
标签:超高层建筑;型钢混凝土框架-钢筋混凝土筒体;关键构件1 工程概况本工程位于上海浦东新区,包括5栋高层商办楼、1栋多层商业楼以及3层整体地下室。
地下室场地平面尺寸约为250mx190m,总建筑面积约14万平方。
(总平面图见图1)1号楼坐落在大地下室的西北角,地上41层,底层和标准层层高分别为6.4m 和4.5m,主屋面高近190m;标准层外包平面尺寸为50.4m×50.4m,地上建筑面积96600m2,采用型钢混凝土框架-钢筋混凝土筒体结构。
地下室顶板面-1.200,覆土厚1米。
地下室顶板面作为上部结构的嵌固端。
本文重点阐述1号楼的结构布置,见标准层结构平面图(图2),以及关键构件的处理措施。
2 结构设计分析1号楼地上建筑面积近10万平方,经常使用人数超过8000人,按照重点设防类(乙类设防),应按8度要求加强其抗震措施。
结构设计年限为50年,结构重要系数为1.0。
根据工程的工程性质、使用功能及业主要求,为钢组合框架-钢筋混凝土筒体结构,根据《高层建筑钢-混凝土混合结构设计规程》DG/TJ08-015-2004(上海),钢组合框架-混凝土筒体结构不超过限高190米的高度,不属于超限高层范围。
地下一层顶板作为上部结构嵌固端,三层地下室为框架结构,高层对应地下部分局部采用型钢混凝土,上部钢柱和混凝土筒体内型钢倒插入地下一层。
地下一层顶板作为上部结构嵌固端处。
高层建筑首层结构层标高高出地下室顶板600,在高低处通过构造措施保证地下室顶板的连续性。
yjk边缘构件轴压比

根据《建筑抗震设计规范》(GB50011-2010)第6.3.4条,对于剪力墙结构和部分框支剪力墙结构,应特别注意墙肢的轴压比。
对于一级和二级抗震等级的剪力墙,其轴压比不得超过以下限值:
剪力墙:0.6;
部分框支剪力墙的一、二、三级:0.8(一级)、0.9(二级)、1.0(三级)。
其中,边缘构件指的是剪力墙的端部边缘的混凝土构件,是剪力墙结构中用于传递剪力和轴力的结构部件。
轴压比指的是构件的轴压力设计值与构件的截面面积和混凝土轴心抗压强度设计值的乘积的比值。
对于一级和二级抗震等级的剪力墙,如果边缘构件为矩形截面,且其轴压比超过规范限值,可以考虑在墙肢端部设置型钢或钢筋混凝土带型边缘构件,以提高其承载能力和延性。
需要注意的是,不同的建筑和结构类型有不同的规范和标准,具体的轴压比限值和边缘构件的设计要求可能会有所不同。
因此,在进行结构设计时,应仔细阅读相关规范和标准,并咨询专业工程师或结构工程师进行设计和评估。
剪力墙轴压比
剪力墙轴压比剪力墙轴压比是一种用来衡量墙体抗剪抵抗能力的参数。
一般情况下,墙体抗剪抵抗能力越强,剪力墙轴压比越大。
剪力墙轴压比(Shear Wall Axial Pressure Ratio,简称SWAP)是指墙体上受剪荷载P对应的上拉荷载系数Au与墙体上受拉荷载Q 对应的下拉荷载系数Ad之比值,即P/Q。
由此可知,剪力墙轴压比的大小取决于墙体的型式、强度、尺寸以及墙体内部的配筋等等。
剪力墙轴压比的计算可以根据墙体的形式和尺寸和墙体内部的配筋选择相应的计算方法。
从规范中给出的,常用的计算方法有等效肋条长度法、累计力学模型法、统计值法及全体潮流流法等。
下面从这几种计算方法入手,来探讨剪力墙轴压比的计算。
一、等效肋条长度法根据此法,墙体内部受剪强度最大的肋条可以用概略条来替代,等效肋条长度可表示为leff=ba。
leff表示墙体内部受剪强度最大的肋条长度,η为受剪荷载与上拉荷载系数之比,b为墙体的宽度,a 为墙体的厚度。
根据这种方法,墙体的剪力墙轴压比可以计算如下:SWPA = * AE * b/A * leff。
在这里,AE是墙体内部受剪强度最大的肋条配筋面积,A是墙体单位面积的抗压强度。
二、累计力学模型法此法基于非线性结构力学原理,将墙体分成多个部分,使用多点拟合的方法来计算墙体的剪力墙轴压比。
累计力学模型法提供了两个计算参数,即神经筋应力Fy和神经筋受剪强度Mt。
Fy表示墙体的配筋应力,单位为MPa;Mt表示受剪强度,单位为N*m。
根据这种方法,墙体的剪力墙轴压比可以计算如下: SWPA = Fy * b/Mt 。
三、统计值法此法基于某些实验研究,提出各种边界条件下墙体的剪力墙轴压比统计值。
按照统计值法,在不同情况下,墙体的剪力墙轴压比可以近似地用它们的统计值来计算。
四、全体潮流流法此法认为,在某些条件下,墙体的抗剪抵抗能力可以用一个全体潮流模型来模拟。
全体潮流流法以满足一定条件的柔性模型为基础,将墙体的抗剪抵抗能力表示为一个全局的满足约束条件的潮流模型,用以计算墙体的剪力墙轴压比。
型钢混凝土梁柱空间节点受力性能及抗剪承载力计算研究
型钢混凝土梁柱空间节点受力性能及抗剪承载力计算研究目录1绪论 (1)1.1概述 (1)1.2型钢混凝土节点研究现状 (2)1.2.1国外研究现状 (2)1.2.2国内研究现状 (3)1.2.3存在的问题 (4)1.3本文的研究内容 (4)2型钢混凝土梁柱节点弹塑性性能有限元分析 (6)2.1概述 (6)2.2试验概况 (6)2.2.1试件设计 (6)2.2.2加载方案 (8)2.3型钢混凝土梁柱节点有限元模型 (9)2.3.1材料本构模型 (9)2.3.2网格划分和相互作用 (12)2.3.3边界条件 (13)2.4模型有效性验证 (14)2.4.1破坏形态 (14)2.4.2混凝土应力状态 (15)2.4.3型钢应力状态 (16)2.4.4滞回曲线 (17)2.4.5骨架曲线 (19)2.4.6节点区剪切变形对比 (20)2.5本章小结 (21)3单向加载型钢混凝土空间节点抗震性能研究 (23)3.1概述 (23)3.2SRC空间节点有限元方案 (23)3.2.1模型尺寸设计 (23)3.2.2有限元模型 (24)3.3SRC梁柱平面与空间节点的抗震性能 (26)I3.3.1破坏形态 (26)3.3.2滞回曲线 (27)3.3.3骨架曲线 (29)3.3.4承载能力和延性性能 (31)3.4空间中节点抗震性能影响因素分析 (33)3.4.1楼板 (33)3.4.2轴压比 (34)3.4.4混凝土强度 (35)3.4.5型钢腹板厚度 (36)3.5本章小结 (37)4不同加载路径下SRC空间中节点滞回性能和损伤评估 (38) 4.1概述 (38)4.2加载路径 (38)4.3加载路径对空间中节点受力性能的影响 (39)4.4.1滞回曲线 (39)4.4.2骨架曲线 (41)4.4.3延性性能 (43)4.4.4耗能能力 (44)4.4.5刚度退化 (45)4.4SRC梁柱空间中节点的地震损伤评估 (47)4.4.1地震损伤模型 (47)4.4.2损伤模型适用性分析 (49)4.4.3加载路径对节点损伤的影响 (50)4.4.4配钢形式对节点损伤的影响 (51)4.5本章小结 (51)5SRC梁柱空间中节点抗剪承载力计算研究 (53)5.1概述 (53)5.2SRC梁柱空间中节点受力特点 (53)5.3空间中节点单向加载承载力计算 (53)5.3.1节点受力过程 (53)5.3.2计算模拟试件的极限剪力 (54)II5.3.3受力机理 (55)5.3.4抗剪承载力计算 (57)5.3.5相关系数的确定及实用公式提出 (61)5.4SRC梁柱空间中节点双向加载承载力计算 (62) 5.4.1加载角度对试件峰值荷载的影响 (63)5.4.2SRC空间中节点极限剪力的计算 (64)5.4.3空间中节点X与Y向抗剪承载力的关系 (65) 5.4.4节点抗剪承载力计算及其验证 (65)5.5本章小结 (66)6结论与展望 (67)6.1主要结论 (67)6.2问题及展望 (68)参考文献 (69)附录 (74)致谢 (75)IIIIV。
剪力墙轴压比的名词解释是
剪力墙轴压比的名词解释是剪力墙轴压比的名词解释是,是指剪力墙在承受荷载时,墙体内各点的剪应力与压应力之比。
剪力墙是指在建筑结构中,用来抵抗横向风荷载和地震力的一种结构构件。
剪力墙轴压比的概念对于剪力墙的设计与分析非常重要,它在控制剪力墙的受力性能和稳定性方面起到了关键的作用。
剪力墙轴压比也被称为墙体的长细比或者宽厚比。
这个比值描述了剪力墙在分布荷载下的受力状态。
在剪力墙的设计过程中,合理的剪力墙轴压比能够确保墙体具有良好的承载能力和稳定性。
剪力墙轴压比的计算公式通常为:V/M。
其中,V代表墙体中的剪力,M代表墙体中的弯矩。
这一比值能够反映出剪力墙在受力状态下承载能力的大小。
一般来说,当轴压比较小时,墙体的受力能力相对较强,稳定性较好;而当轴压比较大时,墙体的受力能力会下降,容易出现失稳现象。
对于剪力墙轴压比的要求,不同标准和规范都有相应的规定。
一般来说,剪力墙的设计应在规定的轴压比范围内,并满足相应的强度和稳定性要求。
常见的剪力墙轴压比限值为0.3到0.5。
在实际设计过程中,工程师需要根据具体的工程情况和要求,选择合适的轴压比进行设计。
为了控制剪力墙轴压比,工程师可以通过调整剪力墙的几何形状、尺寸和位置,以及墙体材料的使用,来达到理想的轴压比。
在设计中,需要综合考虑剪力墙的受力性能、稳定性以及施工工艺等因素。
剪力墙轴压比的合理选择对于剪力墙的性能和安全性至关重要。
如果轴压比过小,墙体可能无法承担设计荷载,导致结构的不稳定和破坏;而如果轴压比过大,墙体可能过于脆弱,无法充分发挥其抗震和抗风的能力。
总之,剪力墙轴压比作为剪力墙设计中的重要参数,对于剪力墙的受力性能和稳定性具有重要影响。
合理选择剪力墙轴压比,并依据相关的设计规范进行设计和计算,可以确保剪力墙具有良好的承载能力和稳定性,保障建筑结构的安全性和可靠性。
因此,在剪力墙的设计和分析中,对剪力墙轴压比的理解和合理运用非常重要。
预压型钢混凝土柱轴压比推导及轴压比限值分析
其 中:11, 为混凝土轴力分配系数 ;n 为型钢轴力分配 系 数。在设计状 态下 n。和 n。基本相 同,为便 于计 算 ,将式 (3) 变形 为 :
N =n(foA。+,自A。)
(4)
式中 :Ⅳ为型钢混凝土柱 的轴压力 限值 ;n为型钢混凝土
柱的轴压力限值系数 。
在结构设计 中 ,柱轴压 比的取 值不仅对 结构 的抗 震性能 有很 大的影响 ,同时也是 确定 柱子 的截 面尺 寸 、型钢 含量及 抗震配筋构造 等的重要依据 。然而 ,业 内对 型钢混凝 土柱轴 压 比的定 义有 很大 分 歧 ,而 对其 限值 则 更是 没 有统 一 的看 法 ,我 国现行 的两部 SRC结 构的行业 标准 ,其适用 范围均 明 确规定 为适 用于实腹式配钢 的 SRC柱 ,而对于预压型钢混凝 土柱 的轴压 比限制 的研 究 尚属少 见 ,很 少有 相 关 的参 考文 献 。本文 主要是通 过对 预压 型钢混 凝 土柱轴 压 比公式 进行 推导 ,引入参数预压 比并 分析 其对轴 压 比 的影 响 ,提 出 了预 压型钢混凝土柱轴 压 比限值 ,从 而为预压 型钢混凝 土柱结构 的推广应用 提供理论基础和技术支持 。
(3)
1I_—— —
图 1 预 压 型 钢 混 凝 土 柱 截 面
预压 型钢混凝 土柱在 一期 和二期 轴力作 用下 的压应 变
[定稿 日期]2015—09—07 [作 者简介]张涛 (1983一),男 ,研 究 生,一级 注册 结构 工程 师,从事结构设计工作 ;张波(1981一),男 ,本科 ,国家注 册监理工程 师,从事工程监理工作。
对于钢筋混凝 土柱 ,轴压 比公 式为 :
n
