高中数学 第三章不等式 §3.2.2一元二次不等式(二)导学案 苏教版必修5
苏教版必修5高中数学3.2《一元二次不等式》word导学案1

班级:姓名:学号:第学习小组
【学习目标】学习目标:
1、通过函数图象了解一元二次不等式与相应函数、方程的联系。
2、会解一元二次不等式。
【课前预习】课前预习
1.一元二次不等式和相应的二次函数是否有内在的联系?
2.一元二次不等式的定义:
3. 的解集为
4. 为什么实数时,函数 的值等于0,大于0?小于0?
【课堂研讨】
例1解下列不等式:
(1) ;(2) ;
(3) ;(4) .
利用一元二次不等式与一元二次函数、一元二次方程之间的关系求解不等式。
例2.解不等式: .
例3.求下列函数的定义域.
(1). ; (2).
解决与一元二次不等式求解有关的问题。
小结:1.当 时,一元二次不等式 (或 )的解集
与二次函数 图象及一元二次方程 的解的关系:
(1) ;(2) .
2.已知集合A=
3.不等式 的解集为_________________________________________________.
4.不等式 的解集为__________________________________________.
5.不等式 的解集为________________________________________.
6.不等式 的解集为__________________________________.
7.已知一元二次方程 的解根是 , ,且 ,
那么 的解集是__________________________________________.
8.解下列不等式:
(1) ;(2) ;
(3) ;(4) .
高中数学3.2一元二次不等式(3)导学案(无答案)苏教版必修5

课题:3.2 一元二次不等式(3)班级: _ 姓名: ______________ 学号:______ 第_学习小组【学习目标】掌握一元二次不等式的解法;进一步理解一元二次不等式,一元二次方程和二次函数之间的关系;学会处理含参数的一元二次不等式恒成立问题.【课前预习】1 •解不等式:(1) X4 X2 6 0 ;(2) 2x 5、x3 0 .【课堂研讨】. 2例1.分别求实数m的取值范围,使方程x mx m 3 0的两根满足下列条件: (1) 两根都大于5; (2) 一根大于0小于1, 一根大于1小于2 .例2.已知关于x的一元二次不等式kx2 2x 6k 0.(1)若不等式的解集是{x|x 3或x 2},求实数k的值;(2) 若不等式的解集是R,求实数k的取值范围.例3.当实数a为何值时,不等式(a2 3a 2)x2 (a 1)x 2 0的解是一切实数?{x|x 2 (p 2)x 4 0}, M {x|x 0},若 A Mp 的取值范围.例4.已知A 求实数 【学后反思】课题32 —元二次不等式(3)检测案2 . kR , X 1 , X 2是方程x 2 2 2 2 2kx 1 k0的两实根,则为X 2最小值( )A. 2 B . 0 C . 1 D . 2A {X||x2}, 2x 1 1},若 A 3 . a | B {x| —— B ,则( )x 2 A .0 a 1 B 0 a 1 C .0 a 1 D . 0 a 14 . 不等式ax 2 bx c 0的解集是{x |x 1 或 x 3} ,则 a :b : c【课后巩固】2x k 2 1 0对一切实数x 恒成立,求实数k 的取值范围.1 .解不等式:(1) x 4 x 22 0 ; (2) 2x . x 1.3.设 f(x) (m 1)x 2 mx m 1,班级:姓名: 学号: 第 学习小组【课堂检测】 1 •若关于x 的不等式ax 2 bx c A. a 0且 b 2 4ac 0C. a 0 且 b 2 4ac 00 (a 0)的解集是空集,那么(2 B . a 0且 b 4ac 0 D . a 0且 b 2 4ac 02 .已知不等式x 2(1)若方程f(x) 0有实根,则实数m的取值范围是______________(2)若不等式f(x) 0的解集为,则实数m的取值范围是_______________________(3) ______________________________________________________ 若不等式f(x) 0的解集为R,则实数m的取「值范围是 ________________________。
高中数学 第三章不等式 §3.2.3一元二次不等式(三)教师版导学案 苏教版必修5

§3.2一元二次不等式(三) 第 24 课时一、学习目标(1)掌握利用二次函数图象求解一元二次不等式的方法;(2)从不等式的解集出发求不等式中参数的值或范围的问题;(3)从二次函数或是一元二次方程的角度,来解决一元二次不等式的综合题.二、学法指导从不等式的解集出发求不等式中参数的值或范围的问题,掌握一元二次不等式恒成立的解题思路.三、课前预习1.一元二次不等式20(0)ax bx c a ++>>与相应的函数2(0)y ax bx c a =++>、相应的方程20(0)ax bx c a ++=>之间有什么关系?2. 一元二次不等式恒成立情况小结:20ax bx c ++>(0a ≠)恒成立⇔ .20ax bx c ++<(0a ≠)恒成立⇔ .四、课堂探究例1.已知关于x 的不等式20x mx n -+≤的解集是{|51}x x -≤≤,求实数,m n 之值.解: 不等式20x mx n -+≤的解集是{|51}x x -≤≤ ∴125,1x x =-=是20x mx n -+=的两个实数根,∴由韦达定理知:5151m n -+=⎧⎨-⨯=⎩∴45m n =-⎧⎨=-⎩. 例2.已知不等式20ax bx c ++>的解集为{|23}x x <<求不等式20cx bx a -+>的解集. 解:由题意 23230b a c a a ⎧+=-⎪⎪⎪⨯=⎨⎪<⎪⎪⎩, 即560b a c a a =-⎧⎪=⎨⎪<⎩. 代入不等式20cx bx a -+>得: 2650(0)ax ax a a ++=<.即26510x x ++<,∴所求不等式的解集为11{|}32x x -<<-. 例3.已知一元二次不等式2(2)2(2)40m x m x -+-+>的解集为R ,求m 的取值范围.解: 2(2)2(2)4y m x m x =-+-+为二次函数,2m ∴≠二次函数的值恒大于零,即2(2)2(2)40m x m x -+-+>的解集为R .200m ->⎧∴⎨∆<⎩, 即224(2)16(2)0m m m >⎧⎨---<⎩, 解得:226m m >⎧⎨<<⎩m ∴的取值范围为{|26}m m <<(2m =适合). 拓展:1.已知二次函数2(2)2(2)4y m x m x =-+-+的值恒大于零,求m 的取值范围.2.已知一元二次不等式2(2)2(2)40m x m x -+-+≤的解集为φ,求m 的取值范围.3.若不等式2(2)2(2)40m x m x -+-+≤的解集为φ,求m 的取值范围.归纳:一元二次不等式恒成立情况小结:20ax bx c ++>(0a ≠)恒成立⇔00a >⎧⎨∆<⎩. 20ax bx c ++<(0a ≠)恒成立⇔00a <⎧⎨∆<⎩.例4.若函数y =x 的取值范围是一切实数,求k 的取值范围.解: y =中自变量x 的取值范围是R ,∴220x kx k ++≥恒成立.∴2440k k ∆=-≤ ∴01k ≤≤故k 的取值范围是{|01}k k ≤≤. 拓展:若将函数改为y =,如何求k 的取值范围? 例5.若不等式2210mx x m -+-<对满足22m -≤≤的所有m都成立,求实数x 的取值范围.解:已知不等式可化为2(1)(12)0x m x -+-<.设2()(1)(12)f m x m x =-+-,这是一个关于m 的一次函数(或常数函数),从图象上看,要使()0f m <在22m -≤≤时恒成立,其等价条件是:22(2)2(1)(12)0,(2)2(1)(12)0,f x x f x x ⎧=-+-<⎪⎨-=--+-<⎪⎩ 即222230,2210.x x x x ⎧+->⎪⎨--<⎪⎩ 解x <<所以,实数x 的取值范围是⎝⎭. 五、巩固训练关于x 的不等式223x x k k x x -+>-+对一切实数x 恒不成立,求k 的取值范围.六、回顾小结:1.从不等式的解集出发求不等式中参数的值或范围的问题;2.一元二次不等式恒成立的问题.七、课外作业:课本第71页 第5、6题; 第94页 复习题 第4、11题. 补充:1.设12,x x 是关于x 的方程22210()x kx k k R -+-=∈的两个实根,求2212x x +的最小值; 2.不等式02x a x->-的解集为{|22}x x -<<,求不等式20x x a ++>的解集;3.已知不等式2222(1)0x ax a x x a +++>++对一切实数x 都成立,求a 的取值范围.。
高二数学新教材苏教版必修5学案:第3章 3.2 第1课时 一元二次不等式的解法
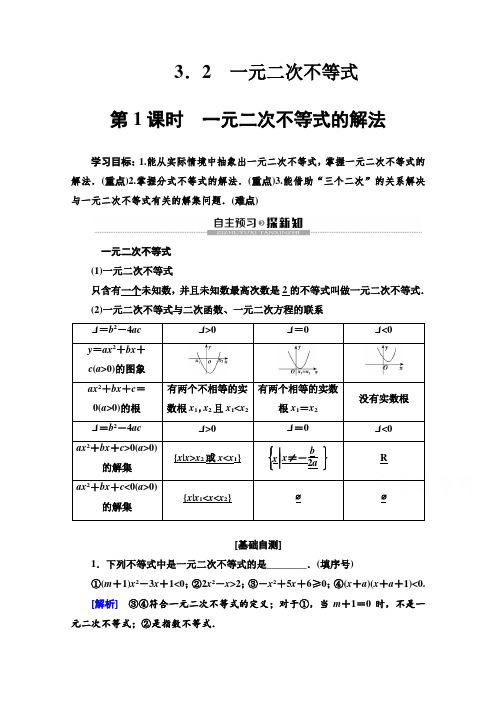
3.2一元二次不等式第1课时一元二次不等式的解法学习目标:1.能从实际情境中抽象出一元二次不等式,掌握一元二次不等式的解法.(重点)2.掌握分式不等式的解法.(重点)3.能借助“三个二次”的关系解决与一元二次不等式有关的解集问题.(难点)一元二次不等式(1)一元二次不等式只含有一个未知数,并且未知数最高次数是2的不等式叫做一元二次不等式.(2)一元二次不等式与二次函数、一元二次方程的联系Δ=b2-4ac Δ>0Δ=0Δ<0y=ax2+bx+c(a>0)的图象ax2+bx+c=0(a>0)的根有两个不相等的实数根x1,x2且x1<x2有两个相等的实数根x1=x2没有实数根Δ=b2-4ac Δ>0Δ=0Δ<0ax2+bx+c>0(a>0)的解集{x|x>x2或x<x1}⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x⎪⎪⎪x≠-b2a Rax2+bx+c<0(a>0)的解集{x|x1<x<x2}∅∅[基础自测]1.下列不等式中是一元二次不等式的是________.(填序号)①(m+1)x2-3x+1<0;②2x2-x>2;③-x2+5x+6≥0;④(x+a)(x+a+1)<0.[解析]③④符合一元二次不等式的定义;对于①,当m+1=0时,不是一元二次不等式;②是指数不等式.[答案] ③④2.不等式x 2+x -2<0的解集为________.[解析] 令f (x )=x 2+x -2=(x +2)(x -1),画出函数图象可知,当-2<x <1时,f (x )<0,从而不等式x 2+x -2<0的解集为{x |-2<x <1}.[答案] {x |-2<x <1}一元二次不等式的基本解法解下列不等式.(1)2x 2+5x -3<0;(2)-3x 2+6x ≤2; (3)-x 2+6x -10>0.[解] (1)Δ=49>0,方程2x 2+5x -3=0的两根为x 1=-3,x 2=12,作出函数y =2x 2+5x -3的图象,如图①所示.用阴影描出原不等式的解,由图可得原不等式的解集为⎩⎨⎧⎭⎬⎫x |-3<x <12.(2)原不等式等价于3x 2-6x +2≥0,Δ=12>0,解方程3x 2-6x +2=0,得x 1=3-33,x 2=3+33,作出函数y =3x 2-6x +2的图象,如图②所示,由图可得原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |x ≤3-33或x ≥3+33.(3)原不等式可化为x 2-6x +10<0,∵Δ=-4<0,∴方程x 2-6x +10=0无实根, 又∵二次项系数大于0, ∴x 2-6x +10>0恒成立. ∴原不等式的解集为∅. [规律方法]解一元二次不等式的步骤(1)通过对不等式变形,使二次项系数大于零; (2)计算对应方程的判别式;(3)求出相应的一元二次方程的根,或根据判别式说明方程没有实根; (4)根据函数图象与x 轴的相关位置写出不等式的解集.提醒:画出对应函数y =ax 2+bx +c 的图象简图,由图象得出不等式的解集更加直观清楚.[跟踪训练]1.求下列一元二次不等式的解集. (1)x 2-5x >6;(2)4x 2-4x +1≤0; (3)(5-x )(x +1)≥0. [解] (1)由x 2-5x >6, 得x 2-5x -6>0, ∴(x -6)(x +1)>0, ∴x >6或x <-1.∴不等式的解集为{x |x >6或x <-1}. (2)∵4x 2-4x +1=(2x -1)2≥0, ∴4x 2-4x +1≤0的解集为⎩⎨⎧ x ⎪⎪⎪⎭⎬⎫x =12.(3)由(5-x )(x +1)≥0, 得(x -5)(x +1)≤0, ∴-1≤x ≤5,∴原不等式的解集为{x |-1≤x ≤5}.“三个二次”间对应关系的应用已知函数f (x )=ax 2+(b -8)x -a -ab ,不等式f (x )>0的解集为{x |-3<x <2}.(1)求函数y =f (x )的解析式;(2)当关于x 的不等式ax 2+bx +c ≤0的解集为R 时,求c 的取值范围. [思路探究] (1)根据题意确定方程f (x )=0的根⇒利用根与系数关系列方程组求a ,b 得到函数解析式.(2)将不等式的解集问题转化为对应函数的图象问题⇒列不等式求出c 的取值范围.[解] (1)因为f (x )>0的解集为{x |-3<x <2},所以-3,2是方程ax 2+(b -8)x -a -ab =0的两根,所以⎩⎪⎨⎪⎧-3+2=-b -8a ,-3×2=-a -aba ,解得⎩⎨⎧a =-3,b =5,所以f (x )=-3x 2-3x +18.(2)因为a =-3<0,所以二次函数y =-3x 2+5x +c 的图象开口向下,要使-3x 2+5x +c ≤0的解集为R ,只需Δ≤0,即25+12c ≤0,所以c ≤-2512. 所以当c ≤-2512时,-3x 2+5x +c ≤0的解集为R. [规律方法]1.三个“二次”中,二次函数是主体,讨论二次函数主要是将问题转化为一元二次方程和一元二次不等式的形式来研究.2.讨论一元二次方程和一元二次不等式又要将其与相应的二次函数相联系,通过二次函数的图象及性质来解决问题,关系如下:提醒:由于忽视二次项系数的符号和不等号的开口方向易写错不等式的解集形式.[跟踪训练] 2.若不等式ax 2+bx +c ≥0的解集是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ -13≤x ≤2,求不等式cx 2+bx +a <0的解集.[解] 由ax 2+bx +c ≥0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ -13≤x ≤2知a <0,又⎝ ⎛⎭⎪⎫-13×2=c a <0,则c >0. 又-13,2为方程ax 2+bx +c =0的两个根,∴-b a =53,∴b a =-53.又c a =-23,∴b =-53a ,c =-23a ,∴不等式cx 2+bx +a <0变为⎝ ⎛⎭⎪⎫-23a x 2+⎝ ⎛⎭⎪⎫-53a x +a <0,即2ax 2+5ax -3a >0. 又∵a <0, ∴2x 2+5x -3<0,所求不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ -3<x <12.分式不等式的解法1.“2x-1 3x+1≥0”与“(2x-1)(3x+1)≥0”是同解不等式吗?为什么?[提示]不是.因为前者3x+1≠0,而后者3x+1可以为0.2.不等式“x+1x-5>1”与不等式“x+1>x-5”是同解不等式吗?为什么?[提示]不是.因为“x-5”的符号不定,故x+1x-5>1不等价于x+1>x-5.解下列不等式.(1)x-3x+2<0;(2)x+12x-3≤1;(3)2x+11-x<0.[解](1)∵x-3x+2<0,∴(x-3)(x+2)<0,∴-2<x<3,∴原不等式的解集为{x|-2<x<3}.(2)∵x+12x-3≤1,∴x+12x-3-1≤0,∴-x+42x-3≤0,即x-4x-32≥0.此不等式等价于(x-4)⎝⎛⎭⎪⎫x-32≥0且x-32≠0,解得x<32或x≥4.∴原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x⎪⎪⎪x<32或x≥4.(3)由2x+11-x<0,得x+12x-1>0,此不等式等价于⎝⎛⎭⎪⎫x+12(x-1)>0,解得x<-12或x>1,∴原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x <-12或x >1. 母题探究:1.(变条件)本例(1)变为解不等式x -3x +2≤0.[解] ∵x -3x +2≤0, ∴⎩⎨⎧(x -3)(x +2)≤0,x +2≠0, ∴-2<x ≤3.∴原不等式的解集为{x |-2<x ≤3}. 2.(变条件)本例(3)变为解不等式2x +11-x≥1. [解] 移项得2x +11-x -1≥0,整理得3x1-x≥0, 它的同解不等式为⎩⎨⎧3x (x -1)≤0,x -1≠0,∴0≤x <1,∴原不等式的解集为{x |0≤x <1}. [规律方法] 分式不等式的解题策略解分式不等式要先通过移项、通分转化为以下类型再进行求解: (1)f (x )g (x )>0型,f (x )g (x )>0⇔f (x )g (x )>0; (2)f (x )g (x )<0型,f (x )g (x )<0⇔f (x )g (x )<0; (3)f (x )g (x )≥0型,f (x )g (x )≥0⇔⎩⎨⎧f (x )g (x )≥0,g (x )≠0; (4)f (x )g (x )≤0型,f (x )g (x )≤0⇔⎩⎨⎧f (x )g (x )≤0,g (x )≠0.1.不等式2x 2-x -1>0的解集是__________. [解析] ∵(2x +1)(x -1)>0,∴x <-12或x >1.[答案] ⎝ ⎛⎭⎪⎫-∞,-12∪(1,+∞) 2.不等式-6x 2-x +2≤0的解集为__________.[解析] -6x 2-x +2≤0⇔6x 2+x -2≥0⇔(2x -1)·(3x +2)≥0⇔x ≤-23或x ≥12. [答案] ⎝ ⎛⎦⎥⎤-∞,-23∪⎣⎢⎡⎭⎪⎫12,+∞3.不等式x +1x -1≥0的解集是__________.[解析] ∵⎩⎨⎧(x +1)(x -1)≥0,x -1≠0,∴x >1或x ≤-1.[答案] (-∞,-1]∪(1,+∞)4.已知不等式ax 2+5x +b <0的解集为{x |-3<x <2},则不等式bx 2+5x +a >0的解集为________________.[解析] 因为ax 2+5x +b <0的解集为{x |-3<x <2}, 所以a >0,⎩⎪⎨⎪⎧-3+2=-5a ,-3×2=ba ,解得a =5,b =-30.则不等式bx 2+5x +a >0变为-30x 2+5x +5>0, 即6x 2-x -1<0,解得:-13<x <12.[答案] ⎝ ⎛⎭⎪⎫-13,125.求函数f (x )=2x 2+x -3+lg(3+2x -x 2)的定义域. [解] 要使函数f (x )有意义,则x 满足不等式组 ⎩⎨⎧2x 2+x -3≥0, ①3+2x -x 2>0, ②由①得x ≥1或x ≤-32,由②得-1<x <3,∴⎩⎪⎨⎪⎧x ≥1,或x ≤-32,-1<x <3,∴1≤x <3,∴函数f (x )的定义域为[1,3).由Ruize收集整理。
高中数学《3.2一元二次不等式(3)》教案 苏教版必修5

江苏省宿迁市沭阳县潼阳中学高中数学教案:《3.2一元二次不等式(3)》苏教版必修5中国书法艺术说课教案今天我要说课的题目是中国书法艺术,下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。
一、教材分析:本节课讲的是中国书法艺术主要是为了提高学生对书法基础知识的掌握,让学生开始对书法的入门学习有一定了解。
书法作为中国特有的一门线条艺术,在书写中与笔、墨、纸、砚相得益彰,是中国人民勤劳智慧的结晶,是举世公认的艺术奇葩。
早在5000年以前的甲骨文就初露端倪,书法从文字产生到形成文字的书写体系,几经变革创造了多种体式的书写艺术。
1、教学目标:使学生了解书法的发展史概况和特点及书法的总体情况,通过分析代表作品,获得如何欣赏书法作品的知识,并能作简单的书法练习。
2、教学重点与难点:(一)教学重点了解中国书法的基础知识,掌握其基本特点,进行大量的书法练习。
(二)教学难点:如何感受、认识书法作品中的线条美、结构美、气韵美。
3、教具准备:粉笔,钢笔,书写纸等。
4、课时:一课时二、教学方法:要让学生在教学过程中有所收获,并达到一定的教学目标,在本节课的教学中,我将采用欣赏法、讲授法、练习法来设计本节课。
(1)欣赏法:通过幻灯片让学生欣赏大量优秀的书法作品,使学生对书法产生浓厚的兴趣。
(2)讲授法:讲解书法文字的发展简史,和形式特征,让学生对书法作进一步的了解和认识,通过对书法理论的了解,更深刻的认识书法,从而为以后的书法练习作重要铺垫!(3)练习法:为了使学生充分了解、认识书法名家名作的书法功底和技巧,请学生进行局部临摹练习。
三、教学过程:(一)组织教学让学生准备好上课用的工具,如钢笔,书与纸等;做好上课准备,以便在以下的教学过程中有一个良好的学习气氛。
(二)引入新课,通过对上节课所学知识的总结,让学生认识到学习书法的意义和重要性!(三)讲授新课1、在讲授新课之前,通过大量幻灯片让学生欣赏一些优秀的书法作品,使学生对书法产生浓厚的兴趣。
高中数学第3章不等式2-1一元二次不等式的解法学案苏教版必修5
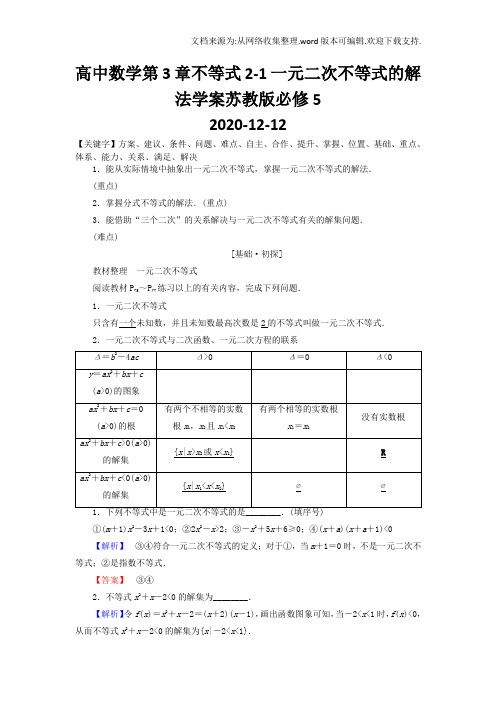
高中数学第3章不等式2-1一元二次不等式的解法学案苏教版必修52020-12-12【关键字】方案、建议、条件、问题、难点、自主、合作、提升、掌握、位置、基础、重点、体系、能力、关系、满足、解决1.能从实际情境中抽象出一元二次不等式,掌握一元二次不等式的解法.(重点)2.掌握分式不等式的解法.(重点)3.能借助“三个二次”的关系解决与一元二次不等式有关的解集问题.(难点)[基础·初探]教材整理一元二次不等式阅读教材P75~P77练习以上的有关内容,完成下列问题.1.一元二次不等式只含有一个未知数,并且未知数最高次数是2的不等式叫做一元二次不等式.2.一元二次不等式与二次函数、一元二次方程的联系①(m+1)x2-3x+1<0;②2x2-x>2;③-x2+5x+6≥0;④(x+a)(x+a+1)<0【解析】③④符合一元二次不等式的定义;对于①,当m+1=0时,不是一元二次不等式;②是指数不等式.【答案】③④2.不等式x2+x-2<0的解集为________.【解析】令f(x)=x2+x-2=(x+2)(x-1),画出函数图象可知,当-2<x<1时,f(x)<0,从而不等式x2+x-2<0的解集为{x|-2<x<1}.【答案】 {x |-2<x <1}[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流: 疑问1:_________________________________________________ 解惑:_________________________________________________ 疑问2:_________________________________________________ 解惑:_________________________________________________ 疑问3:_________________________________________________ 解惑:_________________________________________________[小组合作型]一元二次不等式的基本解法解下列不等式.(1)2x 2+5x -3<0;(2)-3x 2+6x ≤2; (3)-x 2+6x -10>0.【精彩点拨】 移项,化一边为0―→二次项系数化为正数―→ 验根是否存在―→求根―→求不等式的解集【自主解答】 (1)Δ=49>0,方程2x 2+5x -3=0的两根为x 1=-3,x 2=12,作出函数y =2x 2+5x -3的图象,如图①所示.用阴影描出原不等式的解,由图可得原不等式的解集为⎩⎨⎧⎭⎬⎫x |-3<x <12.(2)原不等式等价于3x 2-6x +2≥0,Δ=12>0,解方程3x 2-6x +2=0,得x 1=3-33,x 2=3+33,作出函数y =3x 2-6x +2的图象,如图②所示,由图可得原不等式的解集为 ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |x ≤3-33或x ≥3+33. (3)原不等式可化为x 2-6x +10<0,∵Δ=-4<0,∴方程x 2-6x +10=0无实根, 又∵二次项系数大于0,∴x 2-6x +10>0恒成立. ∴原不等式的解集为∅. 解一元二次不等式的步骤:(1)通过对不等式变形,使二次项系数大于零; (2)计算对应方程的判别式;(3)求出相应的一元二次方程的根,或根据判别式说明方程没有实根;(4)根据函数图象与x 轴的相关位置写出不等式的解集. [再练一题]1.求下列一元二次不等式的解集.(1)x 2-5x >6;(2)4x 2-4x +1≤0;(3)(5-x )(x +1)≥0. 【解】 (1)由x 2-5x >6,得x 2-5x -6>0, ∴(x -6)(x +1)>0, ∴x >6或x <-1.∴不等式的解集为{x |x >6或x <-1}. (2)∵4x 2-4x +1=(2x -1)2≥0,∴4x 2-4x +1≤0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x =12.(3)由(5-x )(x +1)≥0, 得(x -5)(x +1)≤0, ∴-1≤x ≤5,∴原不等式的解集为{x |-1≤x ≤5}.“三个二次”间对应关系的应用若不等式ax 2+5x -2>0的解集是⎩⎪⎨⎪⎭⎪⎬⎪x ⎪⎪⎪12<x <2,求不等式ax 2-5x +a 2-1>0的解集.【导学号:】【精彩点拨】 利用不等式解集的端点值为对应方程的根,求出a 的值,再解不等式即可.【自主解答】 由已知条件可知a <0,且12,2是相应方程ax 2+5x -2=0的两个根,由根与系数关系得,⎩⎪⎨⎪⎧-5a =52,-2a =1,解得a =-2.∴ax 2-5x +a 2-1>0化为2x 2+5x -3<0, 化为(2x -1)(x +3)<0, 解得-3<x <12.所以不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-3<x <12.“三个二次”之间的内在联系[再练一题]2.若不等式ax 2+bx +c ≥0的解集是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-13≤x ≤2,求不等式cx 2+bx +a <0的解集.【解】 由ax 2+bx +c ≥0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-13≤x ≤2知a <0, 又⎝ ⎛⎭⎪⎫-13×2=c a <0,则c >0.又-13,2为方程ax 2+bx +c =0的两个根,∴-b a =53,∴b a =-53. 又c a =-23, ∴b =-53a ,c =-23a ,∴不等式cx 2+bx +a <0变为⎝ ⎛⎭⎪⎫-23a x 2+⎝ ⎛⎭⎪⎫-53a x +a <0,即2ax 2+5ax -3a >0. 又∵a <0, ∴2x 2+5x -3<0,所求不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-3<x <12. [探究共研型]分式不等式的解法探究1 “2x -3x +1≥0”与“(2x -1)(3x +1)≥0”是同解不等式吗?为什么?【提示】 不是.因为前者3x +1≠0,而后者3x +1可以为0. 探究2 不等式“x +1x -5>1”与不等式“x +1>x -5”是同解不等式吗?为什么? 【提示】 不是.因为“x -5”的符号不定,故x +1x -5>1不等价于x +1>x -5. 解下列不等式.(1)x -3x +2<0; (2)x +12x -3≤1;(3)2x +11-x<0. 【精彩点拨】 移项→通分→等价变形→解一元二次不等式 【自主解答】 (1)∵x -3x +2<0, ∴(x -3)(x +2)<0,∴-2<x <3, ∴原不等式的解集为{x |-2<x <3}.(2)∵x +12x -3≤1,∴x +12x -3-1≤0,∴-x +42x -3≤0,即x -4x -32≥0. 此不等式等价于(x -4)⎝ ⎛⎭⎪⎫x -32≥0且x -32≠0, 解得x <32或x ≥4.∴原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <32,或x ≥4. (3)由2x +11-x <0,得x +12x -1>0,此不等式等价于⎝ ⎛⎭⎪⎫x +12(x -1)>0,解得x <-12或x >1,∴原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <-12,或x >1. 分式不等式的解题策略解分式不等式要先通过移项、通分转化为以下类型再进行求解: (1)f x g x >0型,f xg x >0⇔f (x )g (x )>0;(2)f xg x <0型,f xg x<0⇔f (x )g (x )<0;(3)f x g x ≥0型,f x g x ≥0⇔⎩⎪⎨⎪⎧f xg x ≥0,g x ≠0;(4)f x g x ≤0型,f xg x ≤0⇔⎩⎪⎨⎪⎧f xg x ≤0,g x ≠0.[再练一题] 3.解下列不等式.(1)x +21-x <0;(2)2x -1x +3≥1. 【解】 (1)由x +21-x <0,得x +2x -1>0,此不等式等价于(x +2)(x -1)>0,∴原不等式的解集为{x |x <-2或x >1}.(2)移项得2x -1x +3-1≥0,整理得x -4x +3≥0, 它的同解不等式为⎩⎪⎨⎪⎧x -4x +3≥0,x +3≠0,∴x ≥4或x <-3.∴原不等式的解集为{x |x <-3或x ≥4}.[构建·体系]1.不等式2x 2-x -1>0的解集是__________. 【解析】 ∵(2x +1)(x -1)>0,∴x <-12或x >1.【答案】 ⎝⎛⎭⎪⎫-∞,-12∪(1,+∞) 2.不等式-6x 2-x +2≤0的解集为__________.【解析】 -6x 2-x +2≤0⇔6x 2+x -2≥0⇔(2x -1)·(3x +2)≥0⇔x ≤-23或x ≥12.【答案】 ⎝ ⎛⎦⎥⎤-∞,-23∪⎣⎢⎡⎭⎪⎫12,+∞3.不等式x +1x -1≥0的解集是__________. 【解析】 ∵⎩⎪⎨⎪⎧x +1x -1≥0,x -1≠0,∴x >1或x ≤-1.【答案】 (-∞,-1]∪(1,+∞)4.若不等式ax 2+8ax +21<0的解集是{x |-7<x <-1},那么a 的值是________.【导学号:】【解析】 由题意可知,-7,-1是方程ax 2+8ax +21=0的两个根,∴(-7)×(-1)=21a,∴a =3.【答案】 35.求函数f (x )=2x 2+x -3+lg(3+2x -x 2)的定义域. 【解】 要使函数f (x )有意义,则x 满足不等式组 由①得x ≥1或x ≤-32,由②得-1<x <3, ∴⎩⎪⎨⎪⎧x ≥1,或x ≤-32,-1<x <3,∴1≤x <3,∴函数f (x )的定义域为[1,3). 我还有这些不足:(1)_________________________________________________ (2)_________________________________________________ 我的课下提升方案:(1)_________________________________________________ (2)_________________________________________________学业分层测评(十五) (建议用时:45分钟)[学业达标]一、填空题1.一元二次方程ax 2+bx +c =0的根为2,-1,则当a <0时,不等式ax 2+bx +c ≥0的解集为________.【解析】 由方程ax 2+bx +c =0的根为2,-1,知函数y =ax 2+bx +c 的零点为2,-1,又∵a <0,∴函数y =ax 2+bx +c 的图象是开口向下的抛物线, ∴不等式ax 2+bx +c ≥0的解集为{x |-1≤x ≤2}. 【答案】 {x |-1≤x ≤2}2.不等式组⎩⎪⎨⎪⎧x 2-1<0,x 2-3x <0的解集为________.【解析】 ∵x 2-1<0的解集为{x |-1<x <1},x 2-3x <0的解集为{x |0<x <3},∴⎩⎪⎨⎪⎧x 2-1<0,x 2-3x <0的解集为{x |0<x <1}.【答案】 {x |0<x <1}3.不等式3x -1x -2≤0的解集为________.【解析】 不等式3x -1x -2≤0等价于⎩⎪⎨⎪⎧3x -1x -2≤0,x -2≠0,解得13≤x <2.【答案】 ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪13≤x <24.下列不等式中解集为实数集R 的是__________.(填序号) ①x 2+4x +4>0;②x 2>0;③x 2-x +1≥0; ④1x -1<1x.【解析】 ①不等式可化为(x +2)2>0,∴解集为{x |x ≠-2};②不等式解集为{x |x ≠0};③由Δ=1-4<0,∴不等式解集为R ;④由定义域要求x ≠0,∴解集为{x |x ≠0}.【答案】 ③5.已知不等式ax 2-bx -1≥0的解集是⎣⎢⎡⎦⎥⎤-12,-13,则不等式x 2-bx -a <0的解集是________.【解析】 由题意知,-12,-13是方程ax 2-bx -1=0的两实根,∴⎩⎪⎨⎪⎧-12+⎝ ⎛⎭⎪⎫-13=ba ,⎝ ⎛⎭⎪⎫-12×⎝ ⎛⎭⎪⎫-13=-1a ,解得a =-6,b =5,∴x 2-bx -a <0⇔x 2-5x +6<0⇔2<x <3. 【答案】 (2,3) 6.不等式axx -1<1的解集为{x |x <1或x >2},那么a 的值为________. 【导学号:】【解析】ax x -1<1化为axx -1-1<0,即a -1x +1x -1<0,等价于[(a -1)x +1](x -1)<0, ∴(a -1)x 2-(a -2)x -1<0,∴1,2是方程(a -1)x 2-(a -2)x -1=0的两个根.∴⎩⎪⎨⎪⎧1+2=a -2a -1,1×2=-1a -1,解得a =12.【答案】 127.关于x 的不等式x 2-2ax -8a 2<0(a >0)的解集为(x 1,x 2),且x 2-x 1=15,则a 等于__________.【解析】 由题意知x 1,x 2是方程x 2-2ax -8a 2=0的两根,所以x 1+x 2=2a ,x 1x 2=-8a 2,则(x 2-x 1)2=(x 1+x 2)2-4x 1x 2=4a 2+32a 2=36a 2,又x 2-x 1=15,可得36a 2=152,又a >0,则a =52.【答案】 528.设函数f (x )=⎩⎪⎨⎪⎧x 2-4x +6,x ≥0,x +6,x <0,则不等式f (x )>f (1)的解集是__________.【解析】 f (1)=12-4×1+6=3,不等式即为f (x )>3.①当x ≥0时,不等式即为解得⎩⎪⎨⎪⎧x >3或x <1,x ≥0,即x >3或0≤x <1;②当x <0时, 不等式即为⎩⎪⎨⎪⎧x +6>3,x <0,解得-3<x <0.综上,原不等式的解集为(-3,1)∪(3,+∞). 【答案】 (-3,1)∪(3,+∞) 二、解答题9.解不等式x 2-3|x |+2≤0.【解】 x 2-3|x |+2≤0⇔|x |2-3|x |+2≤0⇔(|x |-1)·(|x |-2)≤0⇔1≤|x |≤2. 当x ≥0时,1≤x ≤2; 当x <0时,-2≤x ≤-1.∴原不等式的解集为{x |-2≤x ≤-1,或1≤x ≤2}.10.已知函数f (x ) =x 2+ax +b (a ,b ∈R )的值域为[0,+∞),若关于x 的不等式f (x )<c 的解集为(m ,m +6),求实数c 的值.【解】 由函数f (x )=x 2+ax +b (a ,b ∈R )的值域为[0,+∞),可知对于x 2+ax +b=0,有Δ=a 2-4b =0,即b =a 24,所以f (x )=x 2+ax +b =x 2+ax +a 24=⎝ ⎛⎭⎪⎫x +a 22,由f (x )=⎝ ⎛⎭⎪⎫x +a 22<c ,解得-c -a 2<x <c -a2.又不等式f (x )<c 的解集为(m ,m +6),所以⎝⎛⎭⎪⎫c -a 2-⎝ ⎛⎭⎪⎫-c -a2=2c =6,解得c =9.[能力提升]1.已知一元二次不等式f (x )<0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x <-1,或x >12,则f (10x)>0的解集为________.【解析】 由题知,一元二次不等式f (x )>0的解集为⎝ ⎛⎭⎪⎫-1,12,即-1<10x <12⇒x <-lg2.【答案】 {x |x <-lg 2}2.已知f (x )是定义在R 上的奇函数.当x >0时,f (x )=x 2-4x ,则不等式f (x )>x 的解集用区间表示为__________.【导学号:】【解析】 设x <0,则-x >0,所以f (x )=-f (-x )=-[(-x )2-4(-x )]=-x 2-4x ,又f (0)=0,所以f (x )=⎩⎪⎨⎪⎧x 2-4x ,x ≥0,-x 2-4x ,x <0,当x ≥0时,由x 2-4x >x ,解得x >5;当x <0时,由-x 2-4x >x ,解得-5<x <0,故f (x )>x 的解集为(-5,0)∪(5,+∞).【答案】 (-5,0)∪(5,+∞)3.若不等式ax 2+bx +1>0的解集是 ⎝ ⎛⎭⎪⎫-13,12,则ax +b x ≥0的解集为__________.【解析】 由题知-13,12是方程ax 2+bx +1=0的两根.∴-13×12=1a ,-13+12=-ba,∴a =-6,b =1.文档来源为:从网络收集整理.word 版本可编辑.欢迎下载支持.把a =-6,b =1代入ax +b x≥0得 -6x +1x ≥0,∴解集为⎝ ⎛⎦⎥⎤0,16. 【答案】 ⎝ ⎛⎦⎥⎤0,16 4.已知集合A ={x |x 2-2x -3≤0,x ∈R },B ={x |x 2-2mx +m 2-4≤0,x ∈R ,m ∈R }.(1)若A ∩B =[0,3],求实数m 的值;(2)若A ⊆∁R B ,求实数m 的取值范围.【解】 由已知得A ={x |-1≤x ≤3},B ={x |m -2≤x ≤m +2},(1)∵A ∩B =[0,3],∴⎩⎪⎨⎪⎧ m -2=0,m +2≥3, ∴⎩⎪⎨⎪⎧ m =2,m ≥1,∴m =2.(2)∁R B ={x |x <m -2或x >m +2}.∵A ⊆∁R B ,∴m -2>3或m +2<-1,∴m >5或m <-3.故m 的取值范围为(-∞,-3)∪(5,+∞).。
高中数学第3章不等式3.2一元二次不等式第1课时一元二次不等式及其解法课件苏教版必修5
若a1=1,即a=1,则x∈∅;
若a1>1,即0<a<1,则1<x<a1.
综上所述,当a<0时,原不等式的解集为
xx<1a或x>1
;当a=0
时,原不等式的解集为{x|x>1};当0<a<1时,原不等式的解集为
x 1<x<a1
;当a=1时,原不等式的解集为∅;当a>1时,原不等式的
2.方程 x2-2x-3=0 与不等式 x2-2x-3>0 的解集分别是什么? 观察结果你发现什么问题?这又说明什么?
[提示] 方程 x2-2x-3=0 的解集为{-1,3}. 不等式 x2-2x-3>0 的解集为{x|x<-1 或 x>3},观察发现不等式 x2-2x-3>0 解集的端点值恰好是方程 x2-2x-3=0 的根.
4.三个“二次”的关系
设f(x)=ax2+bx+c(a>0),方程ax2+bx+c=0的判别式Δ=b2-4ac
判别式
Δ>0
Δ=0
Δ<0
解不等式 求方程f(x)=0 f(x)>0或 的解
有两个不等 的实数解 x1,x2
有两个相等的实 没有实
数解x1=x2
数解
画函数y=f(x) 的示
意图 f(x)<0
由于Δ<0,方程x2-2x+3=0无解,
∴不等式-x2+2x-3<0的解集为R.
(4)原不等式可化为3x2-5x+2<0,
由于Δ>0,方程3x2-5x+2=0的两根为x1=23,x2=1,
∴不等式-3x2+5x-2>0的解集为x23<x<1
2019-2020学年高中数学 第三章《不等式》一元二次不等式教学案苏教版必修5.doc
2019-2020学年高中数学 第三章《不等式》一元二次不等式教学案苏教版必修5二、教学目标理解一元二次方程、一元二次不等式与二次函数的关系,掌握图像法解一元二次不等式的 方法,培养数形结合的能力,培养分类讨论的思想方法。
三、教学重点:一元二次不等式的解法四、教学难点:理解二次函数、一元二次方程、一元二次不等式解集的关系 五、教学过程 1、情境设置:(1(2)观察二次函数y=2x -方程260x x --= 不等式26x x -->0 不等式26x x --<0的解集是(3)我们将二次函数y=26x x --变为2(0)y ax bx c a =++>,那么图像与X 轴有几个叫点?(4)三个二次关系:思考:(1)若0a <,如何解不等式ax 2+bx+c>0和ax 2+bx+c<0?(2)不等式(1)(2)0x x -->解集是3、例题讲解例1、解下列不等式(1)22530x x -+< (2)2340x x -+>(3)22430x x ++> (4)29610x x -+≤例2、解下列不等式(1)2620x x --+< (2)21442x x ->+(3)213x x -< (4)(2)(2)1x x -+>例3、x 是什么实数时,函数2514y x x =-++的值是: (1)0 (2)正数 (3)负数4、课堂小结解一元二次不等式一元二次不等式的“四部曲”(1)把二次项系数化为正数 (2)计算判别式(3)解对应的一元二次方程(4)根据一元二次方程的根,结合图像,写出不等式的解集六、课后作业 1、解下列不等式(1)23720x x -+> (2)2260x x --+≥(3)(1)0x x -≤ (4)210x x ++>(5)2232x x -> (6)23540x x -+>(7)(2)(3)1x x x x +<-+ (8)(31)(1)4x x -+>2、已知集合{}2|3100A x x x =--≤,集合{}|121B x m x m =+≤≤-若B A ⊆求m 的取值范围3、已知集合{}2|230A x x x =--<,集合{}2|60B x x x =+->,全集U=R,求:(1)A B ⋃ (2)A B ⋂ (3)R A B ⋂ð4、写出满足条件{}{}1,21,2,3,4,5M ⊆⊆的所有集合M。
高中数学新苏教版精品教案《苏教版高中数学必修5 3.2 一元二次不等式》
《一元二次不等式的解法复习课》教学设计一、教材分析本节课内容体现在它的工具性,蕴藏重要的数形结合思想,与代数、三角、圆锥曲线以及导数等内容密切相关,许多问题的解决都会借助一元二次不等式的解法。
二、教学目标知识目标 正确理解二次方程、二次不等式和二次函数三者的关系,通过二次函数函数图象研究对应不等式解集的方法;能力目标 培养学生运用数形结合、等价转化及分类讨论等数学思想方法。
情感目标 培养学生从形到数的转换能力,从特殊到一般的归纳概括能力。
三、学习者特征分析学生基础较差,逻辑思维能力欠缺,需要及时引导学生进行归纳、总结四、教学方法与学法教师启发引导,辅以“教师讲--学生练“结合的方法五、教学资源:、实物展台六、教学过程1基础回归(1)不等式0432≤--x x 的解集为___________(2)不等式01562<+--x x 的解集为__________(3)不等式0121>+-x x 的解集是_____________ (4)已知不等式012>-+bx ax 的解集是{}43<<x x ,则________________,==b a (5)已知不等式03222>-+-k x x 对一切实数x 恒成立,则实数k 的取值范围为_________通过五道基础回归题,帮助学生回顾一元二次不等式、分式不等式的解法,一元二次不等式与一元二次方程、二次函数三者之间的关系。
2一元二次不等式解法总结若一般形式二次函数:)0(2>++=a c bx ax y 对应不等式又如何求解呢?0>∆ 0=∆ 0<∆ 二次函数 cbx ax y ++=2(0>a )的图象c bx ax y ++=2c bx ax y ++=2 c bx ax y ++=2一元二次方程 ()的根002>=++a c bx ax 有两相异实根 )(,2121x x x x < 有两相等实根 a b x x 221-== 无实根 的解集)0(02>>++a c bx ax {}21x x x x x ><或 ⎭⎬⎫⎩⎨⎧-≠a b x x 2 R 的解集)0(02><++a c bx ax {}21x x x x << ∅ ∅思考:不等式0)4)(2(>--x x 的解集是 ;如果二次项系数为负数时,先做等价转化,把二次项系数化为正数,再利用函数的图象由学生自己求解。
高一数学苏教版必修5教师用书:第3章 3.2 一元二次不等式 第2课时 一元二次不等式的应用
第2课时一元二次不等式的应用1.掌握含字母参数的一元二次不等式的解法.(重点)2.会解与一元二次不等式有关的恒成立问题.(难点)3.会以一元二次不等式为数学模型,求解相应的实际问题.(重点)[小组合作型](1)解关于x 的不等式:x 2+(1-a )x -a <0.(2)解关于x 的不等式:ax 2-(a -1)x -1<0(a ∈R ).【精彩点拨】 (1)解相应方程的根―→比较讨论两根大小―→得解集(2)【自主解答】 (1)方程x 2+(1-a )x -a =0的解为x 1=-1,x 2=a ,函数y =x 2+(1-a )x -a 的图象开口向上,则当a <-1时,原不等式解集为{x |a <x <-1};当a =-1时,原不等式解集为∅;当a >-1时,原不等式解集为{x |-1<x <a }.(2)原不等式可化为: (ax +1)(x -1)<0, 当a =0时,x <1;当a >0时,⎝ ⎛⎭⎪⎫x +1a (x -1)<0,∴-1a <x <1; 当a =-1时,x ≠1;当-1<a <0时,-1a >1,⎝ ⎛⎭⎪⎫x +1a (x -1)>0,∴x >-1a 或x <1;当a <-1时,-1a <1, ∴x >1或x <-1a .综上,原不等式的解集是: 当a =0时,{x |x <1}; 当a >0时,⎩⎨⎧⎭⎬⎫x |-1a <x <1; 当a =-1时,{x |x ≠1}; 当-1<a <0时,⎩⎨⎧⎭⎬⎫x |x <1或x >-1a ; 当a <-1时,⎩⎨⎧⎭⎬⎫x |x <-1a 或x >1.字母参数的一元二次不等式分类讨论的顺序:(1)若二次项系数含有参数,则需对二次项系数大于0与小于0进行讨论; (2)若求对应一元二次方程的根需用公式,则应对判别式Δ进行讨论; (3)若求出的根中含有参数,则应对两根的大小进行讨论.[再练一题]1.解关于x 的不等式2x 2+ax +2>0(a ∈R ). 【解】 Δ=a 2-16,下面分情况讨论:(1)当Δ<0,即-4<a <4时,方程2x 2+ax +2=0无实根,所以原不等式的解集为R .(2)当Δ≥0,即a ≥4或a ≤-4时,方程2x 2+ax +2=0的两个根为 x 1=14(-a -a 2-16), x 2=14(-a +a 2-16).当a =-4时,原不等式的解集为{x |x ∈R ,且x ≠1}; 当a >4或a <-4时,原不等式的解集为⎩⎪⎨⎪⎧x ⎪⎪⎪ x <14(-a -a 2-16),⎭⎬⎫或x >14(-a +a 2-16);当a =4时 ,原不等式的解集为 {x |x ∈R ,且x ≠-1}.某汽车厂上年度生产汽车的投入成本为10万元/辆,出厂价为12万元/辆,年销售量为10 000辆.本年度为适应市场需求,计划提高产品质量,适度增加投入成本.若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应地提高比例为0.75x,同时预计年销售量增加的比例为0.6x,已知年利润=(出厂价-投入成本)×年销售量.(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;(2)为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?【精彩点拨】(1)利用“年利润=(出厂价-投入成本)×年销售量”.(2)解“y>(12-10)×10 000”即可.【自主解答】(1)由题意得y=[12(1+0.75x)-10(1+x)]×10 000×(1+0.6x )(0<x <1),整理得y =-6 000x 2+2 000x +20 000(0<x <1). (2)要保证本年度的年利润比上年度有所增加,必须有 ⎩⎨⎧ y -(12-10)×10 000>0,0<x <1, 即⎩⎨⎧-6 000x 2+2 000x >0,0<x <1, 解得0<x <13,所以投入成本增加的比例应在⎝ ⎛⎭⎪⎫0,13范围内.解不等式应用题的一般步骤:(1)认真审题,抓住问题中的关键词,找准不等关系; (2)引入数学符号,用不等式表示不等关系,使其数学化; (3)求解不等式; (4)还原实际问题.[再练一题]2.某校园内有一块长为800 m,宽为600 m的长方形地面,现要对该地面进行绿化,规划四周种花卉(花卉带的宽度相同),中间种草坪,若要求草坪的面积不小于总面积的一半,求花卉带宽度的范围.【解】设花卉带的宽度为x m,则中间草坪的长为(800-2x)m,宽为(600-2x)m.根据题意可得(800-2x)(600-2x)≥12×800×600,整理得x2-700x+600×100≥0,即(x-600)(x-100)≥0,所以0<x≤100或x≥600,x≥600不符合题意,舍去.故所求花卉带宽度的范围为(0,100]m.[探究共研型]探究1 一元二次不等式ax 2+bx +c >0的解集是R 的等价条件是什么? 【提示】 ⎩⎨⎧a >0,Δ=b 2-4ac <0.探究2 不等式f (x )≤a 恒成立,x ∈[m ,n ]的等价条件是什么? 【提示】 f (x )≤a ,x ∈[m ,n ]恒成立⇔f (x )的最大值≤a ,x ∈[m ,n ].设函数f (x )=mx 2-mx -1.(1)若对于一切实数x ,f (x )<0恒成立,求m 的取值范围; (2)对于x ∈[1,3],f (x )<-m +5恒成立,求m 的取值范围. 【精彩点拨】 (1)分m =0和m ≠0两类,结合函数图象求解. (2)利用函数最值或分离变量m ,求范围. 【自主解答】 (1)要使mx 2-mx -1<0恒成立, 若m =0,显然-1<0.若m ≠0,⎩⎨⎧m <0,Δ=m 2+4m <0⇒-4<m <0. ∴-4<m ≤0.(2)法一 要使f (x )<-m +5在x ∈[1,3]上恒成立. 就要使m ⎝ ⎛⎭⎪⎫x -122+34m -6<0在x ∈[1,3]上恒成立.令g (x )=m ⎝ ⎛⎭⎪⎫x -122+34m -6,x ∈[1,3].当m >0时,g (x )是增函数,∴g (x )的最大值为g (3)=7m -6<0, ∴0<m <67;当m =0时,-6<0恒成立; 当m <0时,g (x )是减函数,∴g (x )的最大值为g (1)=m -6<0,得m <6, ∴m <0.综上所述,m <67.法二 当x ∈[1,3]时,f (x )<-m +5恒成立, 即当x ∈[1,3]时,m (x 2-x +1)-6<0恒成立. ∵x 2-x +1=⎝ ⎛⎭⎪⎫x -122+34>0,又m (x 2-x +1)-6<0, ∴m <6x 2-x +1=6⎝ ⎛⎭⎪⎫x -122+34.又x ∈[1,3],∴⎝ ⎛⎭⎪⎫x -122+34≥⎝ ⎛⎭⎪⎫3-122+34=7, ∴m <67.有关不等式恒成立求参数的取值范围问题,通常处理方法有两种:(1)考虑能否分离参数,若能,则构造关于变量的函数,转化为求函数的最大(小)值,从而建立参数的不等式;(2)若参数不能分离,则应构造关于变量的函数(如一次、二次函数),并结合图象建立参数的不等式求解.[再练一题]3.若(m+1)x2-(m-1)x+3(m-1)<0对任何实数x恒成立,求实数m的取值范围.【解】由题意可知当m+1=0,即m=-1时,原不等式可化为2x-6<0,不符合题意,应舍去;当m+1≠0时,由(m+1)x2-(m-1)x+3(m-1)<0对任何实数x恒成立,则有⎩⎨⎧m +1<0,Δ=(m -1)2-12(m +1)(m -1)<0,解得m <-1311.综上所述,实数m 的取值范围是⎝ ⎛⎭⎪⎫-∞,-1311.1.若a <0,则关于x 的不等式(x -5a )(x +a )>0的解集为 .【导学号:92862080】【解析】 ∵a <0,∴-a >5a , ∴(x -5a )(x +a )>0的解集为 {x |x >-a 或x <5a }.【★答案☆】 {x |x >-a 或x <5a }2.关于x 的不等式x (x +m )-2<0的解集为(-1,n ),则实数m ,n 的值分别为 .【解析】 不等式x (x +m )-2<0,即x 2+mx -2<0, 由题意得⎩⎨⎧-1+n =-m ,-1×n =-2,解得m =-1,n =2.【★答案☆】 -1,23.如果关于x 的不等式2kx 2+kx -38<0对一切实数x 都成立,则k 的取值范围是 .【解析】 当k =0时,-38<0显然成立. 当k ≠0时,由题意得⎩⎪⎨⎪⎧k <0,Δ=k 2-4×2k ⎝ ⎛⎭⎪⎫-38<0,∴⎩⎨⎧k <0,k 2+3k <0,即-3<k <0. 综上可知-3<k ≤0. 【★答案☆】 (-3,0]4.已知不等式ax 2+2x -4>0的解集为空集,则a 的取值范围是 .【导学号:92862081】【解析】 由题意知,⎩⎨⎧a <0,Δ=4+16a ≤0对x ∈R 恒成立,解得a ≤-14.【★答案☆】 ⎝ ⎛⎦⎥⎤-∞,-145.已知a >0,解关于x 的不等式(x -2)(ax -2)>0. 【解】 当a >0时,原不等式化为(x -2)·⎝ ⎛⎭⎪⎫x -2a >0. (1)当0<a <1时,两根的大小顺序为2<2a ,原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x >2a 或x <2; (2)当a =1时 ,2=2a ,原不等式的解集为{x |x ≠2};(3)当a >1时,两根的大小顺序为2>2a ,原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <2a 或x >2. 综上所述,当0<a <1时,原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x >2a或x <2; 当a =1时,原不等式的解集为{}x |x ≠2; 当a >1时,原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <2a 或x >2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3.2一元二次不等式(二) 第 23 课时
一、学习目标 (1)经历从实际情景抽象出一元二次不等式模型的过程,从中体会由实际问题建立数学模型的方法; (2)利用二次函数图象求解含字母的一元二次不等式; (3)让学生充分体会数学知识、数学思想方法在问题解决中的重要作用,进一步提高学习数学的兴趣. 二、学法指导 解一元二次不等式的一般步骤: 当0a>时,解形如20(0)axbxc>或20(0)axbxc<的一元二次不等式,一般可分为三步: (1)确定对应方程20axbxc的解; (2)画出对应函数2yaxbxc图象的简图; (3)由图象得出不等式的解集。 三、课前预习 1.一元二次不等式20(0)axbxca与相应的函数2(0)yaxbxca、相应的方程20(0)axbxca之间有什么关系? 2.解不等式: (1) 234xx; (2)0322xx; (3) 2(1)(30)0xxx; (4)2212311xxx. 3.归纳解一元二次不等式的步骤: 四、课堂探究 例1.用一根长为100m的绳子能围成一个面积大于2600m的矩形吗?当长、宽分别为多少米时,所围成的矩形的面积最大? 解: 例2.某小型服装厂生产一种风衣,日销货量x件与货价p元/件之间的关系为1602px,生产x件所需成本为50030Cx元,问:该厂日产量多大时,日获利不少于1300元? 解: 例3.汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素. 在一个限速为40km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了.事后现场勘查测得甲车的刹车距离略超过12m,乙车的刹车距离略超过10m,又知甲、乙两种车型的刹车距离()sm与车速(/)xkmh之间分别有如下关系:
22
0.10.01,0.050.005sxxsxx
乙
甲
.问:甲、乙两车有无
超速现象?
分析:根据汽车的刹车距离可以估计汽车的车速.
解:
例4.解关于x的不等式2(2)20xaxa.
例5.已知:22|320,|(1)0AxxxBxxaxa,
(1)若AB,求a的取值范围;
(2)若BA,求a的取值范围;
(3)若ABI为一元集,求a的取值范围;
(4)若ABBI,求a的取值范围;
解:
五、巩固训练
求下列不等式的解集:
(1)22120xaxa; (2)2106511xx.
六、回顾小结:
1.有关一元二次不等式的实际问题,在于理清各个量之间的关系,
建立数学模型;
2.利用二次函数图象求解含字母的一元二次不等式.
七、课外作业:课本第71页 练习 第1题;习题3.2 第4题;
第94页 复习题 第1(3)、(4),2题.
补充:
1.求不等式24318xx的整数解;
2.解不等式:(1)2223513134xxxx; (2)223()0xaaxa.
3.求不等式220xxa的解集.
