2017年北京市昌平区初三数学一模试卷及答案
昌平区2017-2018学年第一学期初三数学期末试卷

昌平区2017-2018 学年第一学期初三年级期末质量抽测数学试卷2018.1 学校:班级: 姓名:考1.本试卷共 8 页,共五道大题,28 道小题,满分 100 分.考试时间 120 分钟.生2.在试卷和答题卡上认真填写班级、姓名和考试编号.须3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.知4.考试结束,请将本试卷和答题卡一并交回.一、选择题(共8 道小题,每小题2 分,共16 分)下列各题均有四个选项,其中只有一.个.是符合题意的.1.已知∠A 为锐角,且 sin A=22,那么∠A 等于A.15°B.30°C.45°D.60°2.如图是某几何体的三视图,该几何体是A.圆锥B.圆柱C.长方体D.正方体(第 2 题图)(第 3 题图)(第 4 题图)kyx3.如图,点B 是反比例函数(k 0)在第一象限内图象上的一点,过点B 作BA⊥x 轴于点A,BC⊥y 轴于点C,矩形AOCB 的面积为 6,则k 的值为A.3 B.6 C.-3 D.-64.如图,⊙O 是△ABC 的外接圆,∠A =50,则∠BOC 的大小为A.40°B.30°C.80°D.100°5.将二次函数y x2 6x 5 用配方法化成y (x h)2 k 的形式,下列结果中正确的是A.y (x 6)2 5 B.y (x 3)2 5C.y (x 3)2 4 D.y (x 3)2 9第1 页6.如图,将ΔABC 绕点C 顺时针旋转,点B 的对应点为点E,点A 的对应点为点D,当点E 恰好落在边AC 上时,连接AD,若∠ACB=30°,则∠DAC 的度数是DAECB(第 6 题图)(第 7 题图)A.60°B.65°C.70°D.75°7.如图,AB 为⊙O 的直径,点C 为⊙O 上的一点,过点C 作⊙O 的切线,交直径AB 的延长线于点D,若∠A=25°,则∠D 的度数是A.25°B.40°C.50°D.65°8.小苏和小林在如图所示的跑道上进行 4×50 米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是A.两人从起跑线同时出发,同时到达终点.B.小苏跑全程的平均速度大于小林跑全程的平均速度.C. 小苏在跑最后 100m 的过程中,与小林相遇 2 次.D.小苏前 15s 跑过的路程小于小林前 15s 跑过的路程.二、填空题(共8 道小题,每小题2 分,共16 分)9.请写出一个图象在第二,四象限的反比例函数的表达式.10.如图,在平面直角坐标系xOy 中,点A,点B 的坐标分别为(0 ,2),(1,0 ),将线段AB 沿x 轴的正方向平移,若点B 的对应点的坐标为B ( 2 ,0 ),则点 A 的对应点A' 的坐标'为.(第 10 题图)第2 页11.如图,PA ,PB 分别与⊙O 相切于 A 、B 两点,点 C 为劣弧 AB 上任意一点,过点 C 的切线分别交 AP ,BP 于 D ,E 两点.若 AP=8,则 △PDE 的周长为 .12.抛物线 yx 2 bx c 经过点 A (0,3),B (2,3),抛物线的对称轴为.(第 11 题图)13.如图,⊙O 的半径为 3,正六边形 ABCDEF 内接于⊙O ,则劣弧 AB 的长为.14.如图,在直角三角形 ABC 中,∠C =90°,BC =6,AC =8,点 D 是 AC 边上一点,将△BCD 沿 BD 折叠,使点 C 落在 AB 边的 E 点,那么 AE 的长度是.15.如图,在平面直角坐标系 xOy 中,△CDE 可以看作是△AOB 经过若干次图形的变化(平移、轴对称、 旋转)得到的,写出一种由△AOB 得到△CDE 的过程:.A BCFOE D(第 13 题图) (第 14 题图) (第 15 题图)16.阅读以下作图过程:第一步:在数轴上,点 O 表示数 0,点 A 表示数 1,点 B 表示数 5,以 AB 为直径作半圆(如图); 第二步:以 B 点为圆心,1 为半径作弧交半圆于点 C (如图); 第三步:以 A 点为圆心,AC 为半径作弧交数轴的正半轴于点 M .请你在下面的数轴中完成第三步的画图(保留作图痕迹,不写画法),并写出点 M 表示的数为________.CO AB 015(第 16 题图)x三、解答题(共 6 道小题,每小题 5 分,共 30 分) 17.计算: 2sin 30t an 60cos 60 t an 45 .第 3 页18.二次函数图象上部分点的横坐标x,纵坐标y 的对应值如下表:x … 4 3 2 1 0 1 2 …y … 5 0 3 4 3 0 5 …(1)求这个二次函数的表达式;(2)在图中画出这个二次函数的图象.19.如图,在△ABC 中,AB=AC,BD⊥AC 于点D.AC=10,cos A= 45,求BC 的长.ADB C20.如图,AB 是⊙O 的直径,弦CD⊥AB 于点E,连接AC,BC.(1)求证: A BCD;(2)若AB=10,CD=8,求BE 的长.第4 页21.尺规作图:如图,AC 为⊙O 的直径.(1)求作:⊙O 的内接正方形ABCD.(要求:不写作法,保留作图痕迹);(2)当直径AC=4 时,求这个正方形的边长.22.某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测量某塔的高度,他们先在点D 用高1.5米的测角仪DA 测得塔顶M 的仰角为30,然后沿DF 方向前行40 m 到达点E 处,在E 处测得塔顶M 的仰角为60.请根据他们的测量数据求此塔MF 的高.(结果精确到0.1m,参考数据: 2 1.41, 3 1.73, 6 2.45)MA B CD E F四、解答题(共4 道小题,每小题6 分,共24 分)23.如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为 10m 时,桥洞与水面的最大距离是 5m.(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图),你选择的方案是_____(填方案一,方案二,或方案三),则B 点坐标是______,5m 求出你所选方案中的抛物线的表达式;(2)因为上游水库泄洪,水面宽度变为 6m,求水面上涨的高度.10myyyAOxxxA OB AO BB方案 1 方案 2 方案 3第5 页24.如图,AB 为⊙O 的直径,C、F 为⊙O 上两点,且点C 为弧BF 的中点,过点C 作AF 的垂线,交AF 的延长线于点E,交AB 的延长线于点D.(1)求证:DE 是⊙O 的切线;A(2)如果半径的长为 3,tan D= 34,求AE 的长.OB FD CE25.小明根据学习函数的经验,对函数y x 45x2 4 的图象与性质进行了探究.下面是小明的探究过程,请补充完整:(1)自变量x 的取值范围是全体实数,x 与y 的几组对应数值如下表:311 5 91 1 113 19 5 1x …-2 -1 0 1 2 …24 4 2 4 4 2 4524 5y … 4.3 3.2 0 -2.2 -1.4 0 2.8 3.7 4 3.7 2.8 0 -1.4 -2.2 m 3.2 4.3 …其中m= ;(2)如图,在平面直角坐标系xOy 中,描出了以上表中各组对应值为坐标的点,根据描出的点,画出该函数的图象;(3)观察函数图象,写出一条该函数的性质;(4)进一步探究函数图象发现:①方程x 45x2 4 0 有个互不相等的实数根;②有两个点(x1,y1)和(x2,y2)在此函数图象上,当x2 >x1>2 时,比较y1 和y2 的大小关系为:y1 y2 (填“>”、“<”或“=”) ;③若关于x 的方程x4 5x2 4 a 有 4 个互不相等的实数根,则a 的取值范围是.第6 页26.在平面直角坐标系xOy 中,抛物线y=mx2-2mx-3 (m≠0)与y 轴交于点A,其对称轴与x 轴交于点B 顶点为C 点.(1)求点A 和点B 的坐标;(2)若∠ACB=45°,求此抛物线的表达式;(3)在(2)的条件下,垂直于轴的直线与抛物线交于点P(x1,y1)和Q(x2,y2),与直线AB 交y l于点N(x3,y3),若x3<x1<x2,结合函数的图象,直接写出x1+x2+x3 的取值范围为.y54321–5 –4 –3 –2 –1 1 2 3 4 5xO–1–2–3–4–5五、解答题(共2 道小题,每小题7 分,共14 分)27.已知,△ABC 中,∠ACB=90°,AC=BC,点D 为BC 边上的一点.(1)以点C 为旋转中心,将△ACD 逆时针旋转 90°,得到△BCE,请你画出旋转后的图形;(2)延长AD 交BE 于点F,求证:AF⊥BE;(3)若AC= ,BF=1,连接CF,则CF 的长度为.5C CDDA B A B备用图第7 页28.对于平面直角坐标系xOy 中的点P,给出如下定义:记点P 到x 轴的距离为d ,到y 轴的距离为1 d ,2若 d 为点P 的最大距离;若d d ,则称1 2 1 d d ,则称1 2d 为点P 的最大距离.2例如:点P(3,4 )到到x 轴的距离为 4,到y 轴的距离为 3,因为 3 < 4,所以点P 的最大距离为4 . (1)①点A(2,5)的最大距离为;②若点B(a ,2 )的最大距离为5,则a 的值为;(2)若点C 在直线y x 2上,且点C 的最大距离为5,求点C 的坐标;(3)若⊙O 上存.在.点M,使点M 的最大距离为5,直接写出⊙O 的半径r 的取值范围.y54321–5 –4 –3 –2 –1 1 2 3 4 5O–1–2–3–4–5x第8 页昌平区 2017-2018 学年度第一学期初三年级期末质量抽测数学参考答案及评分标准2018. 1一、选择题(共 8 道小题,每小题 2 分,共 16 分)题号 1 2 3 4 5 6 7 8 答案CABDCDBD二、填空题(共 8 道小题,每小题 2 分,共 16 分) 题号 910 11 12 1314答案y2 (答案不唯一)(3,2)16直线 x =14x题号 1516答案将△AOB 绕点 O 顺时针旋转 90°,再沿 x 轴向右平移一个单位(答案不唯一)15 1(作图正确 1 分.答案正确 1 分)三、解答题(共 6 道小题,每小题 5 分,共 30 分) 17.解: 2sin 30t an 60cos 60tan 45112 3 1 ………………………………………………………… 4 分2213 . ………………………………………………………………… 5 分 218.解:(1)由题意可得二次函数的顶点坐标为( 1, 4 ).………………………………… 1 分设二次函数的解析式为: y a (x 1)24………………2 分y3把点(0,3)代入 y a (x 1)2 4 得 a121∴ y(x 1)2 4…………………………………3 分–4 –3 –2 –1 O123x(2)如图所示 ……………………………………………………… 5 分–119.解:∵AC=AB ,AB=10,–2∴AC=10.…………………………………………… 1 分–3–4在 Rt △ABD 中∵cos A = A D AB =4 5, ∴AD=8,…………………………………………………………………… 2 分 ∴DC=2.…………………………………………………………………………… 3 分∴BD AB 2AD2 6.…………………………………………………………4 分∴BC BD 2DC2 2 10 .……………………………………………………5 分第9 页20.(1)证明:∵ 直径 AB ⊥弦 CD ,A∴弧 BC =弧 BD . …………………… 1 分 ∴A BCD .…………………… 2分(2)解:连接 OCO∵ 直径 AB ⊥弦 CD ,CD =8,∴CE =ED =4. …………………… 3 分 CED∵ 直径 AB =10,B∴CO =OB =5. 在 Rt △COE 中OECO2CE23…………………… 4 分∴ BE2 .…………………… 5 分B21.(1)如图所示…………………… 2分(2)解:AC∵ 直径 AC =4,O∴OA =OB =2.……………………… 3 分D∵正方形 ABCD 为⊙O 的内接正方形, ∴∠AOB=90°,……………………… 4 分 ∴ ABOA2OB22 2 …………………… 5分.22.解:由题意:AB =40,CF =1.5,∠MAC=30°,∠MBC =60°, ∵ ∠MAC=30°,∠MBC =60°, ∴∠AMB=30° M∴∠AMB =∠MAB∴ AB =MB =40.………………………… 1 分 在 Rt △ACD 中,AB C ∵ ∠MCB=90°,∠MBC =60°,DEF∴ ∠BMC =30°.∴ BC = 1 2BM =20.………………………… 2 分 ∴ MCMB 2BC220 3 ………………………………… 3分.,∴ MC 34.6. ……………………………………………… 4分 ∴ MF = MC+CF =36.1.………………………………………………………… 5 分 ∴ 塔 MF 的高约为 36.1 米. …………………………………… 5 分第 10 页yy23.yAOxxxA OB AO BB方案1 方案2 方案3解:方案1:(1)点B 的坐标为(5,0)……………1 分设抛物线的解析式为:y a(x 5)(x 5) ……………2 分1由题意可以得到抛物线的顶点为(0,5),代入解析式可得:a5∴抛物线的解析式为:1y (x 5)(x 5) ……………3 分5(2)由题意:把x 3代入y 1 (x 5)(x 5) 解得:16y =3.2……………5 分5 5∴水面上涨的高度为3.2m……………6 分方案2:(1)点B 的坐标为(10,0)……………1 分设抛物线的解析式为:y ax(x 10) ……………2 分1由题意可以得到抛物线的顶点为(5,5),代入解析式可得:a5∴抛物线的解析式为:1y x(x 10)……………3 分5(2)由题意:把x 2 代入y 1 x(x 10)解得:16y =3.2……………5 分5 5∴水面上涨的高度为3.2m……………6 分方案3:(1)点B 的坐标为(5, 5)……………1 分由题意可以得到抛物线的顶点为(0,0)设抛物线的解析式为:y ax2 ……………2 分1把点B 的坐标(5, 5),代入解析式可得:a5∴抛物线的解析式为: 1 2y x ……………3 分5(2)由题意:把x 3代入y 1 x2 解得:9y = 1.8……………5 分5 5∴水面上涨的高度为5 1.8 3.2m……………6 分第11 页24.(1)证明:连接OC ,∵点C 为弧BF 的中点, ∴弧BC =弧CF . ∴BAC FAC .…………… 1 分∵OA OC ,∴OCA OAC .A∴OCA FAC .……………………2 分∵AE ⊥DE ,O∴CAE ACE 90 . ∴OCA ACE90 .BFDCE∴OC ⊥DE .∴DE 是⊙O 的切线. …………………… 3分(2)解:∵tan D= O C CD = 3 4,OC =3,∴CD =4.…………………………… 4分 ∴OD = OC2CD 2=5.∴AD= OD+ AO=8.…………………………… 5分OC AE 3∵sin D=== ,OD AD 524∴AE=.……………………………6分55y25. (1)m =0,…………… 1 分4(2)作图,……………2 分3(3)图像关于y 轴对称, (答案不唯一) ……………3 分2(4)19(5)a44–4–3 –2 –1 O1 2 34 –1x26.解:(1)∵抛物线y=mx 2-2mx -3 (m ≠0)与y 轴交于点A ,–2 –3 ∴点A 的坐标为(0,3);…………………… 1 分–4∵抛物线y=mx 2-2mx -3 (m ≠0)的对称轴为直线x 1,∴点B 的坐标为(1,0).…………………… 2 分 (2)∵∠ACB =45°,∴点C 的坐标为(1,4),…………………… 3 分把点C 代入抛物线y=mx 2-2mx -3 得出m1,∴抛物线的解析式为y=x2-2x-3.……………………4 分(3)53x x x 2 ……………………6 分1 2 3第12 页27.(1)补全图形……………………2 分E (2)证明:C ∵ΔCBE 由ΔCAD 旋转得到,∴ΔCBE≌ΔCAD,……………… 3 分 FD ∴∠CBE=∠CAD,∠BCE=∠ACD=90°,……………4 分∴∠CBE+∠E=∠CAD+∠E, AB ∴∠BCE=∠AFE=90°,∴AF⊥BE.……………………………………5 分(3) 2 ………………………………………………7 分28.解:(1)①5………………………1 分②5……………………… 3 分(2)∵点C 的最大距离为 5,∴当x 5 时,y 5,或者当y 5时,x 5 . ………………4 分分别把x 5 ,y 5代入得:当x 5时,y 7 ,当x 5 时,y 3 ,当y 5 时,x 7 ,当y 5时,x 3,∴点C(5,3 )或(3 ,5).………………………5 分(3)5 r 5 2 .…………………………………7分第13 页。
2017北京中考数学一模27汇总

l2017中考一模27汇编27(西城).在平面直角坐标系xOy 中,二次函数y =mx 2 -(2m + 1)x + m -5的图象与x 轴有两个公共点.(1)求m 的取值范围;(2)若m 取满足条件的最小的整数, ①写出这个二次函数的解析式;②当n ≤ x ≤ 1时,函数值y 的取值范围是-6 ≤ y ≤ 4-n ,求n 的值;③将此二次函数平移,使平移后的图象经过原点O .设平移后的图象对应的函数表达式为y =a (x -h )2 + k ,当x < 2时,y 随x 的增大而减小,求k 的取值范围.27(房山). 在平面直角坐标系xOy 中,直线32-=x y 与y 轴交于点A ,点A 与点B 关于x 轴对称,过点B 作y 轴的垂线l ,直线l 与直线32-=x y 交于点C. (1)求点C 的坐标;(2)如果抛物线n nx nx y 542+-= (n >0)与线段BC 有唯一公共点,求n 的取值范围.27(顺义).如图,已知抛物线28(0)y ax bx a =++≠与x 轴交于A (-2,0),B 两点,与y 轴交于C 点,tan ∠ABC =2.(1)求抛物线的表达式及其顶点D 的坐标;(2)过点A 、B 作x 轴的垂线,交直线CD 于点E 、F ,将抛物线沿其对称轴向上平移m 个单位,使抛物线与线段EF (含线段端点)只有1个公共点.求m 的取值范围.27(平谷).直线33y x =-+与x 轴,y 轴分别交于A ,B 两点,点A 关于直线1x =-的对称点为点C .(1)求点C 的坐标;(2)若抛物线()230y mx nx m m =+-≠经过A ,B ,C 三点,求该抛物线的表达式;(3)若抛物线()230y ax bx a =++≠ 经过A ,B 两点,且顶点在第二象限,抛物线与线段AC 有两个公共点,求a 的取值范围.27(通州).在平面直角坐标系xOy 中,抛物线2222+-+-=m m mx x y 的顶点为D.线段AB 的两个端点分别为A (-3,m ),B (1,m ). (1)求点D 的坐标(用含m 的代数式表示); (2)若该抛物线经过点B (1,m ),求m 的值;(3)若线段AB 与该抛物线只有一个公共点,结合函数的图象,求m 的取值范围.27(海淀).平面直角坐标系xOy 中,抛物线2222y mx m x =-+交y 轴于A 点,交直线x =4于B 点.(1)抛物线的对称轴为x = (用含m 的代数式表示); (2)若AB ∥x 轴,求抛物线的表达式;(3)记抛物线在A ,B 之间的部分为图象G (包含A ,B 两点),若对于图象G 上任意一点P (P x ,P y ),2P y ≤,求m 的取值范围.27(东城).二次函数2(2)2(2)5y m x m x m =+-+-+,其中20m +>. (1)求该二次函数的对称轴方程; (2)过动点C (0,n )作直线l ⊥y 轴.① 当直线l 与抛物线只有一个公共点时, 求n 与m 的函数关系;② 若抛物线与x 轴有两个交点,将抛物线在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象. 当n =7时,直线l 与新的图象恰好有三个公共点,求此时m 的值;(3)若对于每一个给定的x 的值,它所对应的函数值都不小于1,求m 的取值范围.27(丰台).在平面直角坐标系xOy 中,抛物线()01242≠-+-=m m mx mx y 与平行于x 轴的一条直线交于A ,B 两点. (1)求抛物线的对称轴;(2)如果点A 的坐标是(-1,-2),求点B 的坐标;(3)抛物线的对称轴交直线AB 于点C , 如果直线AB 与y 轴交点的纵坐标为-1,且抛物线顶点D 到点C 的距离大于2,求m 的取值范围.27(门头沟). 在平面直角坐标系xOy 中,抛物线()()13y a x x =+-与x 轴交于A ,B 两点,点A 在点B 的左侧,抛物线的顶点为P ,规定:抛物线与x 轴围成的封闭区域称为“G 区域”(不包含边界).(1)如果该抛物线经过(1, 3),求a 的值,并指出此时“G 区域”有______个整数点;(整数点就是横纵坐标均为整数的点) (2)求抛物线()()13y a x x =+-的顶点P 的坐标(用含a 的代数式表示); (3)在(2)的条件下,如果G 区域中仅有4个整数点时,直接写出a 的取值范围.27(石景山).在平面直角坐标系xOy 中,抛物线2443(0)y ax ax a a =-+-≠的顶点为A . (1)求顶点A 的坐标;(2)过点(0,5)且平行于x 轴的直线l ,与抛物线2443(0)y ax ax a a =-+-≠交于B ,C 两点.①当2a =时,求线段BC 的长;②当线段BC 的长不小于6时,直接写出a 的取值范围.。
北京市各区2017年中考数学一模试题汇编 四边形(无答案)
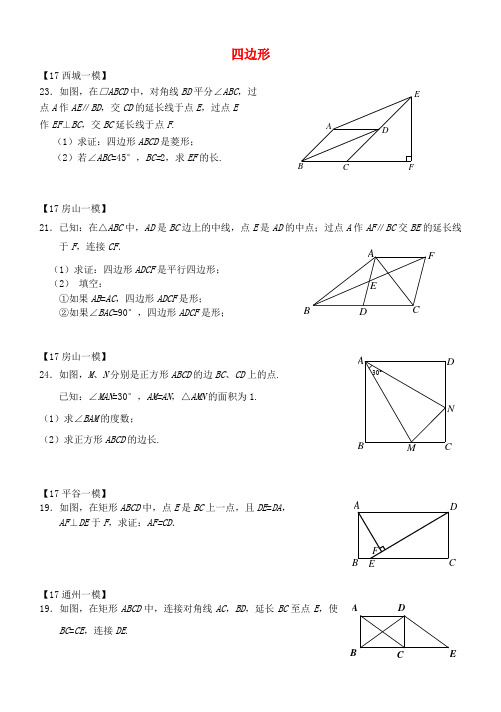
30°NM DCBA四边形【17西城一模】23.如图,在□ABCD 中,对角线BD 平分∠ABC ,过 点A 作AE ∥BD ,交CD 的延长线于点E ,过点E 作EF ⊥BC ,交BC 延长线于点F . (1)求证:四边形ABCD 是菱形; (2)若∠ABC =45°,BC=2,求EF 的长.【17房山一模】21.已知:在△ABC 中,AD 是BC 边上的中线,点E 是AD 的中点;过点A 作AF ∥BC 交BE 的延长线于F ,连接CF .(1)求证:四边形ADCF 是平行四边形; (2) 填空:①如果AB =AC ,四边形ADCF 是形;②如果∠BAC =90°,四边形ADCF 是形;【17房山一模】24.如图,M 、N 分别是正方形ABCD 的边BC 、CD 上的点.已知:∠MAN =30°,AM=AN ,△AMN 的面积为1. (1)求∠BAM 的度数; (2)求正方形ABCD 的边长.【17平谷一模】19.如图,在矩形ABCD 中,点E 是BC 上一点,且DE =DA ,AF ⊥DE 于F ,求证:AF=CD .【17通州一模】19.如图,在矩形ABCD 中,连接对角线AC ,BD ,延长BC 至点E ,使BC =CE ,连接DE .ADCFEFEDCBA求证:DE =AC .【17通州一模】23.如图,四边形ABCD 的对角线AC ⊥BD 于点E ,AB=BC ,F 为四边形ABCD外一点,且∠FCA =90°,∠CBF =∠DCB . (1)求证:四边形DBFC 是平行四边形;(2)如果BC 平分∠DBF ,∠F=45°,BD=2,求AC 的长.【17丰台一模】19.如图,四边形ABCD 中,AB ∥DC ,∠B= 90º,F 为DC 上一点,且AB =FC ,E 为AD 上一点,EC 交AF 于点G ,EA = EG .求证:ED = EC .【17丰台一模】23.如图,在四边形ABCD 中,∠ABC =90°,DE ⊥AC 于点E ,且AE =CE ,DE =5,EB =12. (1)求AD 的长;(2)若∠CAB =30°,求四边形ABCD 的周长.【17石景山一模】19.如图,在四边形ABCD 中,AB ∥DC ,E 是CB 的中点,AE 的延长线与DC 的延长线相交于点F . 求证:AB FC =.【17石景山一模】23.如图,在□ABCD 中,过点A 作AE ⊥BC 于点E ,AF ⊥DC 于点F ,AE AF =.(1)求证:四边形ABCD 是菱形;FG F ED CBAACD EF ECBAD(2)若60EAF ∠=°,2CF =,求AF 的长.【17海淀一模】 23.如图,在ABCD 中,AE ⊥BC 于点E 点,延长BC 至F 点使CF=BE ,连接AF ,DE ,DF .(1)求证:四边形AEFD 是矩形; (2)若AB =6,DE =8,BF =10,求AE 的长.【17门头沟一模】23.如图,将一张矩形纸片ABCD 沿直线MN 折叠,使点C 落在点A 处,点D 落在点E 处,直线MN 交BC 于点M ,交AD 于点N . (1)请判断△CMN 的形状,并说明理由;(2)如果3MC ND =,4CD =,求线段MN 的长.【17东城一模】23.如图,四边形ABCD 为平行四边形,∠BAD 的角平分线AF 交CD 于点E ,交BC 的延长线于点F .(1)求证:BF =CD ;(2)连接BE ,若BE ⊥AF ,∠BFA =60°,BE=求平行四边形ABCD的周长.【17顺义一模】19.如图,□ABCD 中,BE ⊥CD 于E ,CE =DE .求证:∠A=∠ABD .【17顺义一模】B EC FA DABCD E23.已知:如图,四边形ABCD 中,对角线AC ,BD 相交于点O ,AB=AC=AD ,∠DAC =∠ABC .(1)求证:BD 平分∠ABC ;(2)若∠DAC =45 ,OA =1,求OC 的长. 【17朝阳一模】8. 如图,广场中心的菱形花坛ABCD 的周长是40米,∠A =60°,则A ,C 两点之间的距离为A.5米B.C.10米D.【17朝阳一模】20.如图,四边形ABCD 中,AB ∥DC ,AE ,DF 分别是∠BAD ,∠ADC 的平分线,AE ,DF 交于点O . 求证:AE ⊥DF .【17朝阳一模】23.如图,在△ABC 中,AB =AC ,AD 是BC 边的中线,过点A 作BC的平行线,过点B 作AD 的平行线,两线交于点E . (1)求证:四边形ADBE 是矩形;(2)连接DE ,交AB 于点O ,若BC =8,AO =25, 求cos ∠AED 的值.【17怀柔一模】22.如图,已知菱形ABCD 的对角线AC,BD 相交于点O ,延长AB 至点E ,使BE=AB ,连接CE . (1)求证:四边形BECD 是平行四边形;(2)若∠E=60°,AC=求菱形ABCD 的面积.【17大兴一模】20. 如图,□ABCD 中,E 是AB 的中点,连结CE 并延长交DA 的延长ODCBA线于点F.求证:AF=AD.【17大兴一模】23.如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD交BC的延长线于点E.(1)求证:四边形ACED是平行四边形;(2)若BD=4,AC=3,求cos∠CDE的值.。
2017北京初三一模数学汇编之函数压轴题

2017北京初三一模数学汇编之函数压轴题西城27.在平面直角坐标系xOy 中,二次函数2(21)5y mx m x m =-++-的图象与x 轴有两个公共点. (1)求m 的取值范围;(2)若m 取满足条件的最小的整数,①写出这个二次函数的解析式;②当1n x ≤≤时,函数值y 的取值范围是64y n --≤≤,求n 的值;③将此二次函数图象平移,使平移后的图象经过原点O .设平移后的图象对应的函数表达式为2()y a x h k =-+,当2x <时,y 随x 的增大而减小,求k 的取值范围.海淀27.平面直角坐标系xOy 中,抛物线2222y mx m x =-+交y 轴于A 点,交直线x =4于B 点.(1)抛物线的对称轴为x = (用含m 的代数式表示); (2)若AB ∥x 轴,求抛物线的表达式;(3)记抛物线在A ,B 之间的部分为图象G (包含A ,B 两点),若对于图象G 上任意一点P (P x ,P y ),2P y ≤,求m 的取值范围.27.二次函数2(2)2(2)5y m x m x m =+-+-+,其中20m +>. (1)求该二次函数的对称轴方程; (2)过动点C (0, n )作直线l ⊥y 轴.① 当直线l 与抛物线只有一个公共点时, 求n 与m 的函数关系;② 若抛物线与x 轴有两个交点,将抛物线在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象. 当n =7时,直线l 与新的图象恰好有三个公共点,求此时m 的值; (3)若对于每一个给定的x 的值,它所对应的函数值都不小于1,求m 的取值范围.朝阳l27. 在平面直角坐标系xOy 中,直线32-=x y 与y 轴交于点A ,点A 与点B 关于x 轴对称,过点B 作y 轴的垂线l ,直线l 与直线32-=x y 交于点C. (1)求点C 的坐标;(2)如果抛物线n nx nx y 542+-= (n >0)与线段BC 有唯一公共点,求n 的取值范围.平谷27.直线33y x =-+与x 轴,y 轴分别交于A ,B 两点,点A 关于直线1x =-的对称点为点C . (1)求点C 的坐标;(2)若抛物线()230y mx nx m m =+-≠经过A ,B ,C 三点,求该抛物线的表达式;(3)若抛物线()230y ax bx a =++≠ 经过A ,B 两点,且顶点在第二象限,抛物线与线段AC 有两个公共点,求a 的取值范围.27.在平面直角坐标系xOy 中,抛物线2222+-+-=m m mx x y 的顶点为D.线段AB 的两个端点分别为A (-3,m ),B (1,m ).(1)求点D 的坐标(用含m 的代数式表示); (2)若该抛物线经过点B (1,m ),求m 的值;(3)若线段AB 与该抛物线只有一个公共点,结合函数的图象,求m 的取值范围.丰台27.在平面直角坐标系xOy 中,抛物线()01242≠-+-=m m mx mx y 与平行于x 轴的一条直线交于A ,B 两点.(1)求抛物线的对称轴;(2)如果点A 的坐标是(-1,-2),求点B 的坐标;(3)抛物线的对称轴交直线AB 于点C , 如果直线AB 与y 轴交点的纵坐标为-1,且抛物线顶点D 到点C 的距离大于2,求m 的取值范围.27.在平面直角坐标系xOy 中,抛物线2443(0)y ax ax a a =-+-≠的顶点为A . (1)求顶点A 的坐标;(2)过点(0,5)且平行于x 轴的直线l ,与抛物线2443(0)y ax ax a a =-+-≠交于,C 两点. ①当2a =时,求线段BC 的长;②当线段BC 的长不小于6时,直接写出a 的取值范围.顺义27.如图,已知抛物线28(0)y ax bx a =++≠与x 轴交于A (-2,0),B 两点,与y 轴交于C 点,tan ∠ABC =2. (1)求抛物线的表达式及其顶点D 的坐标;(2)过点A 、B 作x 轴的垂线,交直线CD 于点E 、F ,将抛物线沿其对称轴向上平移m 个单位,使抛物线与线段EF (含线段端点)只有1个公共点.求m 的取值范围.西城答案27.解:(1)∵二次函数2(21)5y mx m x m =-++-的图象与x 轴有两个公共点. ∴[]20(21)4(5)0m m m m ≠⎧⎪⎨-+--⎪⎩> 解得124m ->且0m ≠. ∴m 的取值范围是124m ->且0m ≠. (2)①m 取满足条件的最小的整数,由(1)可知1m =.∴二次函数的解析式为234y x x =--.②图象的对称轴为直线32x =.当时312n x ≤≤<,函数值y 随自变量x 的增大而减小.∵函数值y 的取值范围是64y n --≤≤, ∴当1x =时,函数值为6-. 当x n =时,函数值为4n -. ∴2346n n --=-.解得2n =-或4n =(不合题意,舍去). ∴n 的值为2-. ③由①可知,1a =, 又函数图象经过原点,∴2k h =-,∵当2x <时,y 随x 的增大而减小, ∴2h ≥, ∴4k -≤.海淀答案27.(1)m ; --------------------------------------------------------------------------------------------------- 2分 (2)∵ 抛物线2222y mx m x =-+与y 轴交于A 点,∴ A (0,2).------------------------------------------------------------------------------------- 3分 ∵ AB ∥x 轴,B 点在直线x =4上,∴ B (4,2),抛物线的对称轴为直线x =2. --------------------------------------------- 4分 ∴ m =2.∴ 抛物线的表达式为2282y x x =-+. --------------------------------------------------- 5分(3)当0m >时,如图1.∵()02A ,,∴要使04P x ≤≤时,始终满足2P y ≤,只需使抛物线2222y mx m x =-+的对称轴与直线x=2重合或在直线x=2的右侧. ∴2m ≥. -------------------------------------------- 6分当0m <时,如图2,0m <时,2P y ≤恒成立. ------------------- 7分综上所述,0m <或2m ≥.东城答案27.解:(1)对称轴方程:2(2)12(2)m x m -+=-=+. …………1分(2)①∵直线l 与抛物线只有一个公共点,∴23n m =-+. …………3分 ② 依题可知:当237m -+=-时,直线l 与新的图象恰好有三个公共点. ∴5m =. …………5分(3)抛物线2(2)2(2)5y m x m x m =+-+-+的顶点坐标是(1,23)m -+.依题可得 20,23 1.m m +>⎧⎨-+≥⎩解得2,1.m m >-⎧⎨≤⎩ ∴ m 的取值范围是21m -<≤. …………7分房山答案27.解:(1)∵直线y =2x -3与y 轴交于点A (0,-3) ------1分 ∴点A 关于x 轴的对称点为B (0,3),l 为直线y =3 ∵直线y =2x -3与直线l 交于点C ,∴点C 的坐标为(3,3) ------2分(2)∵抛物线n nx nx y 542+-= (n >0) ∴y = nx 2-4nx +4n +n = n (x -2)2+n∴抛物线的对称轴为直线x=2,顶点坐标为(2,n ) ------3分 ∵点B (0,3),点C (3,3)错误!未找到引用源。
2017各地中考及北京各区一、二模数学试题分类整理——三视图、平面展开图
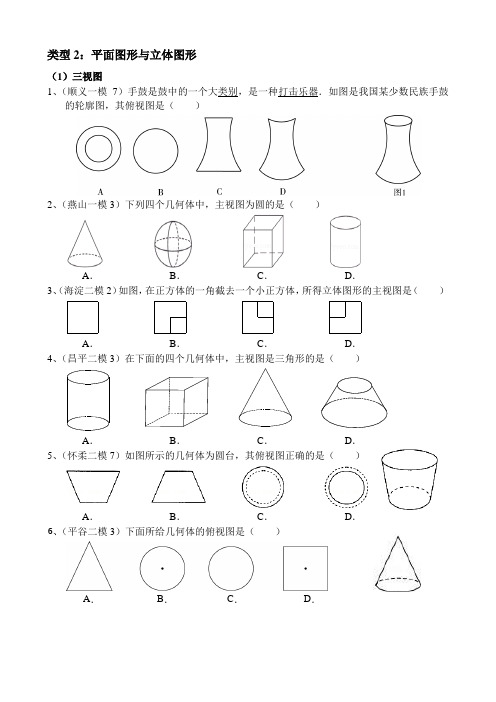
类型2:平面图形与立体图形(1)三视图1、(顺义一模7的轮廓图,其俯视图是()2、(燕山一模3)下列四个几何体中,主视图为圆的是()A.B.C.D.3、(海淀二模2)如图,在正方体的一角截去一个小正方体,所得立体图形的主视图是()A.B.C.D.4、(昌平二模3)在下面的四个几何体中,主视图是三角形的是()A.B.C.D.5、(怀柔二模7)如图所示的几何体为圆台,其俯视图正确的是()A.B.C.D.6、(平谷二模3)下面所给几何体的俯视图是()A.B.C.D.7、(房山一模5)如图,A ,B ,C ,D 是四位同学画出的一个空心圆柱的主视图和俯视图,正确的一组是( )A .B .C .D .8、(东城一模6)下列哪个几何体,它的主视图、左视图、俯视图都相同( )A .B .C .D .9、(怀柔一模6)下面几何体中,主视图、左视图和俯视图形状都相同,大小均相等的是( )A .圆柱B .圆锥C .三棱柱D .球10、(西城一模4)如图是某几何体的三视图,该几何体是( )A .三棱柱B .长方体C .圆锥D .圆柱11、(朝阳一模3)如图是某个几何体的三视图,该几何体是( )A.棱柱 B .圆锥 C .球 D .圆柱 第10题图 第11题图 第12题图 第13题图12、(通州一模4)如图是某个几何体的三视图,该几何体是( ) A .圆锥 B .四棱锥 C .圆柱D .四棱柱13、(丰台二模3)如图是几何体的三视图,该几何体是( )A .圆锥B .圆柱C .正三棱锥D .正三棱柱14、(平谷一模3、门头沟一模4)右图是某几何体从不同角度看到的图形,这个几何体是( )A .圆锥B .圆柱C .正三棱柱D .三棱锥15、(石景山一模7)若某几何体的三视图如右图所示,则该几何体是 ( )A .B .C .D .主视图俯视图俯视图左视图主视图主视图 左视图 俯视图16、(青岛中考14)已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为____。
2017各地中考及北京各区一、二模数学试题分类整理——一次函数、反比例函数

类型5:一次函数、反比例函数(1)反比例函数基础1、(房山一模9)在同一平面直角坐标系中,正确表示函数()0≠+=k k kx y 与()0≠=k xky 图象2<x <2 A .1<y <3 B .2<y <3 C .1<y<6D .3<y <6 3、(广东中考7)如图,在同一平面直角坐标系中,直线与双曲线 相交于A 、B 两点,已知点A 的坐标为(1,2),则点B 的坐标为( )A .(-1,-2)B .(-2,-1)C .(-1,-1)D .(-2,-2)4、(昌平二模10)如图,点A 是反比例函数1y x=(0)x >上的一个动点,连接OA ,过点O 作OB ⊥OA ,并且使OB=2OA 连接AB ,当点A 在反比函数图象上移动时,点B 也在某一反比例函数图象k y x=上移动,k 的值为( ) A . 2 B . -2C .4D . -45、(房山二模12)已知反比例函数的图象满足条件:在各自的象限内y 随x 的增大而增大,请你写出一个符合条件的函数表达式_________.6、(海淀一模15)如图,在平面直角坐标系xOy 中,A (1,1),B (2,2),双曲线y k x=与线段AB 有公共点,则k 的取值范围是________. 7、(平谷一模13)请写出一个在各自象限内,y 的值随x 值的增大而增大的反比例函数表达式 .8、(平谷二模14)如图,在平面直角坐标系中,等腰直角三角形△ABC 的腰长是2,写出一个函数(0)ky k x=≠,是它的图象与△ABC 有公共点,这个函数表达式为_____________.11(0)y k x k =≠22(0)k y k x=≠yyO x第14题图9、(怀柔二模15)在平面直角坐标系xOy 中,直线12y x =与双曲线22y x =的图象如图所示, 小明说:“满足12y y >的x 的取值范围是1x >.”你同意他的观点吗?答: .理由是 .10、(福建中考16)已知矩形ABCD 的四个顶点均在反比例函数1y x=的图象上,且点A 的横坐标是2,则矩形ABCD的面积为 .11、(遵义中考18)如图,点E ,F 在函数y =2x 的图象上,直线EF分别与x 轴、y 轴交于点A 、B ,且BE :BF =1:3,则△EOF 的面积是 .12、(温州中考15)如图,矩形OABC 的边OA ,OC 分别在x轴、y 轴上,点B 在第一象限,点D 在边BC 上,且∠AOD =30°,四边形OA ′B ′D 与四边形OABD 关于直线OD 对称(点A ′和A ,B ′和B 分别对应),若AB =1,反比例函数(0)ky k x=≠的图象恰好经过点 A ′,B ,则k 的值为_________.(2)一次函数基础 13、(德州中考9)公式表示当重力为P 时的物体作用在弹簧上时弹簧的长度.代表弹簧的初始长度,用厘米(cm )表示,K 表示单位重力物体作用在弹簧上时弹簧拉伸的长度,用厘米(cm )表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( )A .B .C .D . 14、(苏州中考6)若点(),m n A 在一次函数3y x b =+的图像上,且32m n ->,则b 的取值范围为( ) A .2b > B .2b >- C .2b < D .2b <- 15、(东城二模13)已知一次函数y 1=k 1x +5和y 2=k 2x +7,若k 1>0且k 2<0,则这两个一次函数的图象的交点在第 象限.16、(房山二模14)直线()0≠+=k b kx y 的图象如图所示,由图象可知当y <0时x 的取值范围是__________.0L L KP =+0L 100.5L P =+105L P =+800.5L P =+805L P =+17、(昌平二模9)如图,两个一次函数图象的交点坐标为(2,4),则关于x ,y 的方程组⎩⎨⎧+=+=2211b x k y b x k y 的解为( )A .⎩⎨⎧==42y xB .⎩⎨⎧==24y xC .⎩⎨⎧=-=04y xD .⎩⎨⎧==03y x18、(海淀二模14)某登山队从大本营出发,在向上攀登的过程中,测得所在位置的气温y ℃与向上攀登的高度x km 的几组对应值如下表:2.5 km 时,登山队所在位置的气温约为 ℃. 19、(海淀一模21)在平面直角坐标系xOy 中,直线11:l y k x b =+过A (0,3-),B (5,2),直线222:l y k x =+. (1)求直线1l 的表达式;(2)当4x ≥时,不等式122k x b k x +>+恒成立,请写出一个满足题意的2k 的值.20、(顺义一模21)如图,在平面直角坐标系xOy 中,已知直线与直线相交于点A (1,2),直线与x 轴交于点B (3,0).(1)分别求直线和的表达式;(2)过动点P (0,n )且平行于x 轴的直线与,的交点分别为C ,D ,当点C 位于点D 左方时,写出n 的取值范围.1:(0)l y mx m =≠2:(0)l y ax b a =+≠2l 1l 2l 1l 2l x 2x+b 221、(燕山一模21)如图,直线b +=kx y 与x 轴交于点A (1,0),与 y 交于点B (0,-2).(1) 求直线AB 的表达式;(2)点C 是直线AB 上的点,且CA =AB ,过动点P (m ,0)且垂直于x 轴的直线与直线AB 交于点D ,若点D 不在线段BC 上,写出m 的取值范围.22、(西城二模23)直线24y x =-+与x 轴交于点A ,与y 轴交于点B ,直线y kx b =+(k ,b是常数,k ≠0)经过点A ,与y 轴交于点C ,且OC =OA .(1)求点A 的坐标及k 的值;(2)点C 在x 轴上方,上点P 在第一象限,且在直线24y x =-+上,若PC =PB ,求点P 的坐标.(3)反比例函数综合23、(苏州中考25)如图,在C ∆AB 中,C C A =B ,x AB ⊥轴,垂足为A .反比例函数k y x=(0x >)的图像经过点C ,交AB 于点D .已知4AB =,5C 2B =.(1)若4OA =,求k 的值;(2)连接C O ,若D C B =B ,求C O 的长.24、(东城二模21)如图,在平面直角坐标系中,OA ⊥OB ,AB ⊥x 轴于点C ,点A )在反比例函数(0)ky k x=≠的图象上. (1)求反比例函数(0)ky k x=≠的解析式和点B 的坐标;(2)若将△BOA 绕点B 按逆时针方向旋转 60º 得到△BDE (点O 与点D 是对应点),补全图形,直接写出点E 的坐标,并判断点E 是否在该反比例函数的图象上,说明理由.25、(门头沟一模21)如图,在平面直角坐标系xOy 中的第一象限内,反比例函数图象过点A (2,1)和另一动点B (x , y ). (1)求此函数表达式;(2)如果1y >,写出x 的取值范围;(3)直线AB 与坐标轴交于点P ,如果PB AB =,直接写出点P 的坐标.26、(朝阳一模22)在平面直角坐标系xOy 中,直线12y x b =+与双曲线4y x=的一个交点为A(m ,2),与y 轴交于点B .(1)求m 和b 的值;(2)若点C 在y 轴上,且△ABC 的面积是2,请直接写出点C 的坐标.27、(西城一模22)在平面直角坐标系xOy ,直线y =x -1与y 轴交于点A ,与双曲线交于点B (m ,2).(1)求点B 的坐标及k 的值;(2)将直线AB 平移,使它与x 轴交于点C ,与y 轴交于点D ,若△ABC 的面积为6,求直线CD 的表达式.28、(东城一模21)如图,在平面直角坐标系xOy 中,直线()0y kx b k =+≠与双曲线6y x=相交于点A (m ,3),B (-6,n ),与x 轴交于点C .(1)求直线()0y kx b k =+≠的解析式; (2)若点P 在x 轴上,且32ACP BOC S S =△△,求点P 的坐 标(直接写出结果).=kyx29、(房山一模23)如图,在平面直角坐标系xOy 中,一次函数)0(≠+=k b kx y 的图象与反比例函数xy 12=的图象交于A 、B 两点,点A 在第一象限,点B 的坐标为(6,n ),直线AB 与x 轴交于点C , E 为x 轴正半轴上一点,且tan ∠AOE =.(1)求点A 的坐标;(2)求一次函数的表达式;(3)求△AOB 的面积.30、(丰台一模21)如图,在平面直角坐标系xOy 中,直线m x y +-=3与双曲线xky =相交于点A (m ,2). (1)求双曲线xky =的表达式; (2)过动点P (n ,0)且垂直于x 轴的直线与直线m x y +-=3及双曲线xky =的交点分别为B 和C ,当点B 位于点C 下方时,求出n 的取值范围.-3431、(怀柔一模23) 如图,在平面直角坐标系xOy 中,直线y =x +b 与双曲线ky x=相交于A ,B 两点,已知A (1,3),B (-3,m ).(1)求一次函数和反比例函数的表达式;(2)如果点P 是y 轴上一点,且ABP △的面积是4,求点P 的坐标.32、(平谷一模21)在平面直角坐标xOy 中,直线()10y kx k =+≠与双曲线()0my m x=≠的一个交点为A (﹣2,3),与x 轴交于点B .(1)求m 的值和点B 的坐标;(2)点P 在y 轴上,点P 到直线()10y kx k =+≠33、(石景山一模22)如图,在平面直角坐标系xOy 中,直线(0)y kx bk =+≠与双曲线 (0)m y m x=≠交于点(2,3)A -和点(,2)B n .(1)求直线与双曲线的表达式;(2)对于横、纵坐标都是整数的点给出名称叫整点.动点P 是双曲线 (0)m y m x=≠上的整点,过点P 作垂直于x 轴的直线,交直线AB 于点Q ,当点P 位于点Q 下方时,请直接写出整点P 的坐标.34、(通州一模20)在平面直角坐标系xOy 中,过原点O 的直线l 1与双曲线xy 2=的一个交点为A (1,m ).(1)求直线l 1的表达式;(2)过动点P (n ,0)(n >0)且垂直于x 轴的直线与直线l 1和双曲线xy 2=的交点分别为B ,C ,当点B 位于点C 上方时,直接写出n 的取值范围.35、(海淀二模21)如图,在平面直角坐标系xOy 中,过点A (2,0)的直线l :3y mx =-与y 轴交于点B .(1)求直线l 的表达式;(2)若点C 是直线l 与双曲线n y x=的一个公共点,AB =2AC ,直接写出n 的值.36、(丰台二模21)如图,在平面直角坐标系xOy 中,双曲线xmy =与直线12+-=x y 交于点A (-1,a ). (1)求a ,m 的值; (2)点P 是双曲线xmy =上一点,且OP 与直线12+-=xy 平行,求点P 的横坐标.37、(昌平二模23)一次函数1+2y x b =-(b 为常数)的图象与x 轴交于点A (2,0),与y轴交于点B ,与反比例函数xky =的图象交于点C (-2,m ).(1)求点C 的坐标及反比例函数的表达式;(2)过点C 的直线与y 轴交于点D ,且1:2:=BO C CBD S S △△,求点D 的坐标.38、(通州二模21)在平面直角坐标系xOy 中,直线12+=x y 与双曲线xky =的一个交点为A (m ,-3).(1)求双曲线的表达式;(2)过动点P (n ,0)(n <0)且垂直于x 轴的直线与直线12+=x y 和双曲线xky =的交点分别为B ,C ,当点B 位于点C 上方时,直接写出n 的取值范围.39、(石景山二模23)如图,在平面直角坐标系xOy 中,直线3(0)y kx k =+≠与x 轴交于点A ,与双曲线(0)m y m x=≠的一个交点为(1,4)B -.(1)求直线与双曲线的表达式;(2)过点B 作BC ⊥x 轴于点C ,若点P 在双曲线m y x=上,且△PAC 的面积为4,求点P的坐标.40、(顺义二模21)如图,在平面直角坐标系xOy 中,反比例函数(0)ky k x=≠与一次函数4(0)y ax a =+≠的图象只有一个公共点A (2,2),直线(0)y mx m =≠也过点A .(1)求k 、 a 及m 的值; (2)结合图象,写出4kmx ax x<+<时x 的取值范围.41、(平谷二模21)如图,一次函数()0y kx b k =+≠与反比例函数()0my m x=≠的图象在第一象限内交于A (1,6),B (3,n )两点.(1)求这两个函数的表达式;(2)根据图象直接写出0mkx b x +-<的x 的取值范围.42、(北京中考23)如图,在平面直角坐标系xOy 中,函数()0ky x x=>的图象与直线2y x =-交于点()3,A m . (1)求k m 、的值;(2)已知点()(),0P n n n >,过点P 作平行于x 轴的直线,交直线2y x =-于点M ,过点P 作平行于y 轴的直线,交函数()0ky x x=>的图象于点N . ①当1n =时,判断线段PM 与PN 的数量关系,并说明理由; ②若PN PM ≥,结合函数的图象,直接写出n 的取值范围.43、(河南中考20)如图,一次函数y=﹣x+b与反比例函数y=k(x>0)的图象交于A(m,3)x和B(3,1).(1)填空:一次函数的解析式为,反比例函数的解析式为;(2)点P是线段AB上一点,过点P作PD⊥x轴于点D,连接OP,若△POD的面积为S,求S的取值范围.。
昌平区20172018初三上期末数学试题及答案
昌平区2017-2018学年第一学期初三年级期末质量抽测数学试卷2018.1 学校:班级: 姓名:考生须知1.本试卷共8页,共五道大题,28道小题,满分100分.考试时间120分钟.2.在试卷和答题卡上认真填写班级、姓名和考试编号.3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.4.考试结束,请将本试卷和答题卡一并交回.一、选择题(共8道小题,每题2分,共16分)以下各题均有四个选项,其中只有一个..是符合题意的.1.已知∠A为锐角,且sin A=22,那么∠A等于A.15° B.30° C.45° D.60°2.如图是某几何体的三视图,该几何体是A.圆锥B.圆柱C.长方体D.正方体(第2题图)(第3题图)(第4题图)3.如图,点B是反比例函数kyx=(0k≠)在第一象限内图象上的一点,过点B作BA⊥x轴于点A,BC⊥y轴于点C,矩形AOCB的面积为6,那么k的值为A.3 B.6 C.-3 D.-64.如图,⊙O是△ABC的外接圆,∠A =50︒,那么∠BOC的大小为A.40° B.30° C.80° D.100°5.将二次函数265y x x =-+用配方式化成2()y x h k =-+的形式,以下结果中正确的选项是 A .2(6)5y x =-+B .2(3)5y x =-+C .2(3)4y x =--D .2(3)9y x =+-6.如图,将ΔABC 绕点C 顺时针旋转,点B 的对应点为点E ,点A 的对应点为点D ,当点E 恰好落在边AC 上时,连接AD ,假设∠ACB=30°,那么∠DAC 的度数是(第6 题图) (第7 题图)A .60° B.65° C. 70° D.75°7.如图,AB 为⊙O 的直径,点C 为⊙O 上的一点,过点C 作⊙O 的切线,交直径AB 的延长线于点D ,假设∠A =25°,那么∠D 的度数是A .25° B.40° C.50° D.65°8.小苏和小林在如下图的跑道上进行4×50米折返跑.在整个进程中,跑步者距起跑线的距离y (单位:m )与跑步时刻t (单位:s )的对应关系如以下图所示.以下表达正确的选项是A .两人从起跑线同时动身,同时抵达终点.B .小苏跑全程的平均速度大于小林跑全程的平均速度. C. 小苏在跑最后100m 的进程中,与小林相遇2次. D .小苏前15s 跑过的路程小于小林前15s 跑过的路程.EDCB A二、填空题(共8道小题,每题2分,共16分)9.请写出一个图象在第二,四象限的反比例函数的表达式 . 10.如图,在平面直角坐标系xOy 中,点A ,点B 的坐标别离为(0,2), (1-,0),将线段AB 沿x 轴的正方向平移,假设点B 的对应点的坐标为 'B (2,0),那么点A 的对应点'A 的坐标为 . (第10题图)11.如图,PA ,PB 别离与⊙O 相切于A 、B 两点,点C 为劣弧AB 上任意一点,过点C 的切线别离交AP ,BP 于D ,E 两点.假设AP=8,那么△PDE 的周长为 .12.抛物线2y x bx c =++通过点A (0,3),B (2,3),抛物线的对称轴为 . (第11题图) 13.如图,⊙O 的半径为3,正六边形ABCDEF 内接于⊙O ,那么劣弧AB 的长为 . 14.如图,在直角三角形ABC 中,∠C =90°,BC =6,AC =8,点D 是AC 边上一点,将△BCD 沿BD 折叠,使点C 落在AB 边的E 点,那么AE 的长度是 .15.如图,在平面直角坐标系xOy 中,△CDE 能够看做是△AOB 通过假设干次图形的转变(平移、轴对称、旋转)取得的,写出一种由△AOB 取得△CDE 的进程: .(第13题图) (第14题图) (第15题图) 16.阅读以下作图进程:第一步:在数轴上,点O 表示数0,点A 表示数1,点B 表示数5,以AB 为直径作半圆(如图); 第二步:以B 点为圆心,1为半径作弧交半圆于点C (如图); 第三步:以A 点为圆心,AC 为半径作弧交数轴的正半轴于点M .请你在下面的数轴中完成第三步的画图(保留作图痕迹,不写画法),并写出点M 表示的数为________.xA B 01C5OOFE DCBA(第16题图)三、解答题(共6道小题,每题5分,共30分) 17.计算:2sin30tan60cos60tan 45︒-︒+︒-︒.18.二次函数图象上部份点的横坐标x ,纵坐标y 的对应值如下表:x … 4-3- 2- 1-1 2… y…53- 4-3-5…(1)求那个二次函数的表达式; (2)在图中画出那个二次函数的图象.19.如图,在△ABC 中, AB=AC ,BD ⊥AC 于点D .AC =10,cos A =45,求BC 的长.20.如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,连接AC ,BC . (1)求证:A BCD ∠=∠;D CBA(2)若AB =10,CD =8,求BE 的长.21.尺规作图:如图,AC 为⊙O 的直径.(1)求作:⊙O 的内接正方形ABCD .(要求:不写作法,保留作图痕迹); (2)当直径AC=4时,求那个正方形的边长.22.某校九年级数学爱好小组的同窗进行社会实践活动时,想利用所学的解直角三角形的知识测量某塔的高度,他们先在点D 用高1.5米的测角仪DA 测得塔顶M 的仰角为30︒,然后沿DF 方向前行40m 抵达点E 处,在E 处测得塔顶M 的仰角为60︒.请依照他们的测量数据求此塔MF 的高.(结果精准到0.1m ,参考数据:41.12≈,73.13≈,45.26≈)四、解答题(共4道小题,每小题6分,共24分)23.如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m 时,桥洞与水面 的最大距离是5m .(1)通过讨论,同窗们得出三种成立平面直角坐标系的方案(如以下图), 你选择的方案是_____(填方案一,方案二,或方案三),那么B 点坐标是______,5m10mAB CDFEM求出你所选方案中的抛物线的表达式;(2)因为上游水库泄洪,水面宽度变成6m ,求水面上涨的高度.24.如图,AB 为⊙O 的直径,C 、F为⊙O 上两点,且点C 为弧BF 的中点,过点C 作AF 的垂线,交AF 的延长线于点E ,交AB 的延长线于点D . (1)求证:DE 是⊙O 的切线; (2)若是半径的长为3,tan D=34,求AE 的长.25.小明依照学习函数的体会,对函数4254y x x =-+ 下面是小明的探讨进程,请补充完整:(1)自变量x 的取值范围是全部实数,x 与y 的几组对应数值如下表: 其中m = ;(2)如图,在平面直角坐标系xOy 中,描出了以上表中各组对应值为坐标的点,依照描出的点,画出该函数的图象;(3)观看函数图象,写出一条该函数的性质 ; (4)进一步探讨函数图象发觉:①方程42540x x -+=有 个互不相等的实数根;y 方案 2方案 3方案 1②有两个点(x 1,y 1)和(x 2,y 2)在此函数图象上,当x 2 >x 1>2时,比较y 1和y 2的大小关系为:y 1 y 2 (填“>”、“<”或“=”) ;③假设关于x 的方程4254x x a -+=有4个互不相等的实数根,那么a 的取值范围是 .26.在平面直角坐标系xOy 中,抛物线y=mx 2-2mx -3 (m ≠0)与y 轴交于点A ,其对称轴与x 轴交于点B极点为C 点.(1)求点A 和点B 的坐标;(2)假设∠ACB =45°,求此抛物线的表达式;(3)在(2)的条件下,垂直于y 轴的直线l 与抛物线交于点P (x 1,y 1)和Q (x 2,y 2),与直线AB 交于点N (x 3,y 3),假设x 3<x 1<x 2,结合函数的图象,直接写出x 1+x 2+x 3的取值范围为 .五、解答题(共2道小题,每题7分,共14分)xy –1–2–3–4–512345–1–2–3–4–512345O27.已知,△ABC 中,∠ACB =90°,AC =BC ,点D 为BC 边上的一点.(1)以点C 为旋转中心,将△ACD 逆时针旋转90°,取得△BCE ,请你画出旋转后的图形; (2)延长AD 交BE 于点F ,求证:AF ⊥BE ;(3)假设AC = ,BF =1,连接CF ,那么CF 的长度为 .28.关于平面直角坐标系xOy 中的点P ,给出如下概念:记点P 到x 轴的距离为1d ,到y 轴的距离为2d ,假设12d d ≥,那么称1d 为点P 的最大距离;假设12d d <,那么称2d 为点P 的最大距离.例如:点P (3-,4)到到x 轴的距离为4,到y 轴的距离为3,因为3 < 4,因此点P 的最大距离为4. (1)①点A (2,5-)的最大距离为 ;②假设点B (a ,2)的最大距离为5,那么a 的值为 ; (2)假设点C 在直线2y x =--上,且点C 的最大距离为5,求点C 的坐标;5备用图AACDB BDC(3)假设⊙O上存在..点M,使点M的最大距离为5,直接写出⊙O的半径r的取值范围.昌平区2017-2018学年度第一学期初三年级期末质量抽测数学参考答案及评分标准2018. 1一、选择题(共8道小题,每题2分,共16分)二、填空题(共8道小题,每题2分,共16分)三、解答题(共6道小题,每题5分,共30分) 17.解: 2sin30tan60cos60tan 45︒-︒+︒-︒ 122112=⨯- ………………………………………………………… 4分 12=. ………………………………………………………………… 5分 18.解:(1)由题意可得二次函数的极点坐标为(1-,4-).………………………………… 1分设二次函数的解析式为:2(1)4y a x =+-………………2分把点(0,3)代入2(1)4y a x =+-得1a =∴2(1)4y x =+-…………………………………3分(2)如下图 ……………………………………………………… 5分19.解:∵AC=AB ,AB=10,∴AC=10.…………………………………………… 1分 在Rt △ABD 中∵cos A =AD AB = 45, ∴AD=8,…………………………………………………………………… 2分∴DC=2.…………………………………………………………………………… 3分 ∴6BD ==.………………………………………………………… 4分∴BC ==.…………………………………………………… 5分20.(1)证明:∵直径AB⊥弦CD,∴弧BC=弧BD. …………………… 1分∴A BCD∠=∠.…………………… 2分(2)解:连接OC∵直径AB⊥弦CD,CD=8,∴CE=ED=4. …………………… 3分∵直径AB =10,∴CO =OB=5.在Rt△COE中3OE=…………………… 4分∴2BE=.…………………… 5分21.(1)如下图…………………… 2分(2)解:∵直径AC =4,∴OA =OB=2. ……………………… 3分∵正方形ABCD为⊙O的内接正方形,∴∠AOB=90°,……………………… 4分∴AB== 5分. 22.解:由题意:AB=40,CF=1.5,∠MAC=30°,∠MBC =60°,∵∠MAC=30°,∠MBC =60°,∴∠AMB=30°∴∠AMB=∠MAB∴AB=MB=40.………………………… 1分在Rt△ACD中,∵∠MCB=90°,∠MBC =60°,∴∠BMC =30°.∴BC =12BM=20.………………………… 2分∴MC==………………………………… 3分.,∴MC≈34.6.……………………………………………… 4分∴MF= MC+CF=36.1.………………………………………………………… 5分AC AA B C D FEM∴ 塔MF 的高约为36.1米. …………………………………… 5分 23.解:方案1:(1)点B 的坐标为(5,0)…………… 1分 设抛物线的解析式为:(5)(5)y a x x =+-…………… 2分 由题意能够取得抛物线的极点为(0,5),代入解析式可得:15a =- ∴抛物线的解析式为:1(5)(5)5y x x =-+-…………… 3分 (2)由题意:把3x =代入1(5)(5)5y x x =-+-解得:165y ==3.2…………… 5分 ∴水面上涨的高度为3.2m …………… 6分方案2:(1)点B 的坐标为(10,0)…………… 1分 设抛物线的解析式为:(10)y ax x =-…………… 2分由题意能够取得抛物线的极点为(5,5),代入解析式可得:15a =- ∴抛物线的解析式为:1(10)5y x x =--…………… 3分 (2)由题意:把2x =代入1(10)5y x x =--解得:165y ==3.2…………… 5分 ∴水面上涨的高度为3.2m …………… 6分方案3:(1)点B 的坐标为(5, 5-)…………… 1分 由题意能够取得抛物线的极点为(0,0) 设抛物线的解析式为:2y ax =…………… 2分 把点B 的坐标(5, 5-),代入解析式可得:15a =-∴抛物线的解析式为:215y x =-…………… 3分y 方案 2方案 3方案 1(2)由题意:把3x =代入215y x =-解得:95y =-= 1.8-…………… 5分 ∴水面上涨的高度为5 1.8-=3.2m …………… 6分24.(1)证明:连接OC ,∵点C 为弧BF 的中点, ∴弧BC =弧CF .∴BAC FAC ∠=∠.…………… 1分∵OA OC =, ∴OCA OAC ∠=∠.∴OCA FAC ∠=∠.……………………2分∵AE ⊥DE ,∴90CAE ACE ︒∠+∠=.∴90OCA ACE ︒∠+∠=. ∴OC ⊥DE .∴DE 是⊙O 的切线. …………………… 3分 (2)解:∵tan D=OC CD =34,OC =3, ∴CD =4.…………………………… 4分 ∴OD.∴AD= OD+ AO=8.…………………………… 5分∵sin D=OC OD =AE AD =35, ∴AE=245.……………………………6分25. (1)m =0,…………… 1分 (2)作图,……………2分(3)图像关于y 轴对称, (答案不唯一) ……………3分 (4)<(5)944a -<< 26.解:(1)∵抛物线y=mx 2-2mx -3 (m ≠0)与y 轴交于点A , ∴点A 的坐标为,3-(0);…………………… 1分∵抛物线y=mx 2-2mx -3 (m ≠0)的对称轴为直线1x =,∴点B 的坐标为,0(1).…………………… 2分 (2)∵∠ACB =45°,∴点C 的坐标为,4-(1),…………………… 3分 把点C 代入抛物线y=mx 2-2mx -3 得出1m =,∴抛物线的解析式为y=x 2-2x -3. …………………… 4分 (3)123523x x x <++< ……………………6分 27.(1)补全图形…………………… 2分 (2)证明:∵ΔCBE 由ΔCAD 旋转取得,∴ΔCBE ≌ΔCAD ,……………… 3分∴∠CBE =∠CAD ,∠BCE =∠ACD =90°,……………4分 ∴∠CBE +∠E =∠CAD +∠E , ∴∠BCE =∠AFE =90°,∴AF ⊥BE .……………………………………5分(3………………………………………………7分 28.解:(1)①5……………………… 1分②5±……………………… 3分 (2)∵点C 的最大距离为5,∴当5x <时,5y =±,或当5y <时,5x =±. ………………4分 别离把5x =±,5y =±代入得: 当5x =时,7y =-,当5x =-时,3y =,当5y =时,7x =-,当5y =-时,3x =,∴点C (5-,3)或(3,5-).……………………… 5分 (3)5r ≤≤…………………………………7分ACBDF E。
2017年北京市昌平区中考二模数学试题及答案
昌平区初三年级第二次统一练习A6铅笔作答,其他试题一、选择题(共8道小题,每小题4分,共32分)下列各题均有四个选项,其中只有一个..是符合题意的.1.5-的相反数是A.5B.15C.15-D.5-2.植树造林可以净化空气、美化环境. 据统计一棵50年树龄的树,以累计计算,除去花、果实与木材价值,总计创值约196 000美元.将196 000用科学记数法表示应为A.319610⨯ B.419.610⨯ C.51.9610⨯D.60.19610⨯3.若右图是某几何体的三视图,则这个几何体是A.三菱锥 B.圆柱 C.球D.圆锥俯视图 主视图 左视图4.六边形的内角和为A .360︒B .540︒C .720︒D .1080︒5.如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,随机转盘停止后,指针指向蓝色区域的概率是A .16 B .13 C .12 D .236.如图,把一块直角三角板的直角顶点放在直尺的一边上,1=35°,那么∠2的度数为 A .35°B .45°C .55°D .65°7.10名同学分成A 、B 两队进行篮球比赛,他们的身高(单位:cm )如下表所示:B AODC 183设A 、B 两队队员身高的平均数分别为A x ,B x ,身高的方差分别为2A S ,2B S ,则下列关系中完全正确的是A .AB x x =,22A B S S>B .A B x x =,22A B S S<C .A B x x >,22A B S S > D .A B x x <,22A B S S<8.如图1,已知点E 、F 、G 、H 是矩形ABCD 各边的中点,AB=6,AD=8.动点M 从点E 出发,沿E →F →G →H →E 匀速运动,设点M 运动的路程为x ,点M 到矩形的某一个顶点的距离为y , 如果y 关于x 的函数图象如图2所示,则矩形的这个顶点是H GFED A图1 图2A .点A B. 点B C. 点C D. 点D二、填空题(共4道小题,每小题4分,共16分)9.函数y x 的取值范围是 .10.如图,⊙O 的直径CD ⊥弦AB ,∠AOC =50°,则∠CDB 的大小为 .11.如图,李大爷要借助院墙围成一个矩形菜园ABCD ,用篱笆围成的另外三边总长为24m ,设BC 的长为x m ,矩形的面积为y m 2,则y 与x 之间的函数表达式为 .12.如图,在平面直角坐标系中,已知点()()3,00,4A B -,,对△AOB 连续作旋转变化,依次得到三角形①、②、③、④、…,则第⑦个三角形的直角顶点的坐标是 ;第 个三角形的直角顶点的坐标是 .三、解答题(共6道小题,每小题5分,共30分) 13.计算:013sin60(-1)2π-︒+-.14. 解不等式组:34,554 2.x x x x +>⎧⎨-<-⎩菜园DC BA墙1715. 如图,AD ⊥BC 于点D ,BE ⊥AC 于点E ,AD 与BE 相交于点F ,且BF =AC .求证:DF =DC .A BCFE16.已知3=y x ,求22222()x y x y xy xy y --÷-的值.17.已知关于 x 的一元二次方程 2410x x m -+-= 有两个相等的实数根,求m 的值及方程的根.18.如图,已知□ABCD ,E ,F 是对角线BD 上的两点,且BE =DF .(1)求证:四边形AECF 是平行四边形;(2)当AE 垂直平分BC 且四边形AECF 为菱形时,直接写出AE ∶AB 的值.E BA四、解答题(共4道小题,每小题5分,共20分)19.如图,定义:若双曲线(0)k y k x=>与直线y =x 相交于A 、B 两点,则线段AB 的长度为双曲线(0)k y k x=>的对径.(1)求双曲线1y x =的对径;(2)若双曲线(0)ky k x=>的对径是,求k 的值.20.在某中学开展的“书香伴我行”读书活动中,为了解九年级300名学生读书情况,随机调查了九年级50名学生读书的册数.统计数据如下表所示:(1)这50个样本数据的众数是 ,中位数是 ;(2)根据样本数据,估计该校九年级300名学生在本次活动中读书多于2册的人数;(3)学校广播站的小记者对被调查的50名学生中读书册数最少和最多的人进行随即采访,请利用树状图或列表,求被采访的两人恰好都是读书册数最多的学生的概率.21.如图,已知BC为⊙O的直径, EC是⊙O的切线,C是切点,EP 交⊙O于点A,D,交CB延长线于点P. 连接CD,CA,AB.(1)求证:∠ECD=∠EAC;(2)若PB=OB=2,CD=3,求PA的长.22.如右图,把边长为a=2的正方形剪成四个全等的直角三角形,在下面对应的正方形网格(每个小正方形的边长均为1)中画出用这四个直角三角形按要求分别拼成的新的多边形(要求全部用上,互不重叠,互不留隙).(1)矩形(非正方形);(2)菱形(非正方形);(3)四边形(非平行四边形).(2)(1)(3)五、解答题(共3道小题,第23题7分,第24题7分,第25题8分,共22分)23.已知抛物线2(31)2(1)(0)y ax a x a a=-+++≠.(1)求证:无论a为任何非零实数,该抛物线与x轴都有交点;(2)若抛物线2(31)2(1)=-+++与x轴交于A(m,0)、B(n,0)y ax a x a两点,m、n、a均为整数,一次函数y=kx+b(k≠0)的图象经过点P(n -l,n+l)、Q(0,a),求一次函数的表达式.24.【探究】如图1,在△ABC中, D是AB边的中点,AE⊥BC于点E,BF⊥AC于点F,AE,BF相交于点M,连接DE,DF. 则DE,DF 的数量关系为 .【拓展】如图2,在△ A B C 中 ,C B = C A ,点 D 是AB 边的 中点 ,点M 在 △ A B C 的内部 ,且 ∠MBC =∠MAC . 过点M 作ME ⊥BC 于点E ,MF ⊥AC 于点F ,连接DE ,DF . 求证:DE =DF ;【推广】如图3,若将上面【拓展】中的条件“CB =CA ”变为“CB ≠CA ”,其他条件不变,试探究DE 与DF 之间的数量关系,并证明你的结论.ADBECMFAD BCMF MABCDF图3图2图125.如图,已知点A (1,0),B (0,3),C (-3,0),动点P (x ,y )在线段AB 上,CP 交y 轴于点D ,设BD 的长为t . (1)求t 关于动点P 的横坐标x 的函数表达式;(2)若S △BCD :S △AOB =2:1,求点P 的坐标,并判断线段CD 与线段AB 的数量及位置关系,说明理由;(3)在(2)的条件下,若M 为x 轴上的点,且∠BMD 最大,请直接写出点M 的坐标.昌平区2017—2017学年初三第二次统一练习数学试卷参考答案及评分标准A6一、选择题(共8个小题,每小题4分,共32分)二、填空题(共4个小题,每小题4分,共16分)三、解答题(共6道小题,每小题5分,共30分) 13.解:原式=1312- …………………………………………………………………… 4分12+. ……………………………………………………………………………… 5分14.解:34,554 2.x x x x +>⎧⎨-<-⎩①②由①得,2x >-. ………………………………………………………………………… 2分由②得,3x <. …………………………………………………………………………… 4分∴原不等式组的解集为:23x -<<. (5)分15.证明:∵AD ⊥BC 于D ,BE ⊥AC 于E , ∴90.BDF ADC BEC ∠=∠=∠=︒ 在Rt BEC ∆和Rt ADC ∆中,∠C =∠C ,∴.B A ∠=∠ (1)分在△BDF 和△ADC 中,,,.BDF ADC B A BF AC ∠=∠∠=∠=⎧⎪⎨⎪⎩………………………… 3分 ∴△BDF≌△ADC . ……………………………………………………………………4分∴DF =DC . ……………………………………………………………………………… 5分A BCFE16.解:原式=()()2()()2y x y x y x y xy x y -+-⋅- …………………………………………………………………2分=2x y x+. …………………………………………………………………………………3分 ∵ 3xy =,∴3x y =. …………………………………………………………………………………4分 ∴原式=32233y y y +=⨯. …………………………………………………………… 5分17.解:∵关于 x 的一元二次方程 2410x x m -+-= 有两个相等的实数根, ∴164(1)0m ∆=--=. ……………………………………………………………1分 ∴5m =. …………………………………………………………………………………2分 ∴方程可化为2440x x -+=. ……………………………………………………………3分∴2(2)0x -=.∴122x x ==. (5)分注:正确求出一个根,扣1分.18. (1)证明:连接对角线AC 交对角线BD 于点O . ∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD . …………………………… 2分 ∵点E ,F 是对角线BD 上的两点,且BE =DF ,∴.OB BE OD DF -=-即OE =OF . …………………………… 3分 ∴四边形AECF 是平行四边形. ………………………………………………… 4分 (2)…………………………………………………………………………………………… 5分四、解答题(共4道小题,每小题5分,共20分) 19. 解:(1) ∵1y x=与 y =x 相交于A 、B 两点,∴A (1,1),B (-1,-1). ……………………………………………………OABCDEF……………… 2分∴AB =……………………………………………………………………………3分(2) ∵双曲线(0)k y k x=>的对径是∴AB =.则OA = (4)分设(,)A m m ,OA == ∴m =5. ∴k =25. ……………………………………………………………………………5分20.解:(1)众数为3,中位数为2. …………………………………………………………………2分(2)在50名学生中,读书多于2本的学生有20名,所以,300×=120.………………………………………………………………………3分答:该校八年级300名学生在本次活动中读书多于2册的约有120名.(3)设读书最少的人为A ,读书最多的人为B 1,B 2,B 3.B 2 ……………………………………………………………………………4分被采访的两人恰好都是读书册数最多的学生的情况如下:(B 1,B 2)、(B 1,B 3)、(B 2,B 1)、(B 2,B 3)、(B 3,B 1)、(B 3,B 2),共6种,所以,被采访的两人恰好都是读书册数最多的学生的概率为P==.…………………5分 21. (1)证明:连接BD .∵BC 为⊙O 的直径, ∴90.CDB ∠=︒…………………………………………1分∵EC 与⊙O 相切, ∴90.ECP ∠=︒∵90,90,ECD DCB ECB DBC DCB ∠+∠=∠=︒∠+∠=︒ ∴.ECD CBD ∠=∠ ………………………………2分∵,EAC CBD ∠=∠ ∴∠ECD =∠EAC . ………………………………………………………………………3分(2)作DF ⊥BC 于点F . 在Rt △CDB 中,BD=CD BD DF BC ==在Rt △CDF 中,9.4CF ==∴15.4PF PC CF =-=在Rt △DFP 中,DP ==∵,,PAB PCD P P ∠=∠∠=∠∴PAB∆∽.PCD ∆.PBPD==. ∴PA = ……………………………………………………………………………5分 22.解:如图,(1) …………………………………………………………………………………… 1分(2)………………………………………………………………………………………… 3分(3)……………………………………………………………………………………… 5分(1)(2)(3)五、解答题(共3道小题,第23题7分,第24题7分,第25题8,共22分)23.解:(1)证明:∵△=[]2a a a-+-⨯+……………………………………………………(31)42(1)1分=221a a-+=2a-≥(1)0∴无论a为任何非零实数,该抛物线与x轴都有交点.……………………………… 2分(2)解:∵抛物线2(31)2(1)=-+++与x轴交于A(m,0)、y ax a x aB(n,0)两点,(3)∴1a≠.令2(31)2(1)(0)y ax a x a a =-+++≠中y =0, 有:2(31)2(1)0ax a x a -+++=.解得:x =2,11.x a=+…………………………………………………………………3分∵m 、n 、a 均为整数, ∴a =-1,m =0,n =2或m =2,n =0. ……………………………………………………… 5分∵一次函数y =kx +b (k ≠0) 的图象经过点P (n -l ,n +l )、Q (0,a ),∴当a =-1,n =2时,有P (1,3)、Q (0,-1),解得:4 1.y x =- ……………………………………………………………6分当a =-1,n =0时,有P (-1,1)、Q (0,-1),解得:2 1.y x =-- ……………………………………………………… 7分24.【探究】DE =DF . …………………………………………………………………………………1分【拓展】如图2,连接CD .∵在△ A B C 中 ,C B = C A ,图2F MCBD A∴∠CAB =∠CBA . ∵∠MBC =∠MAC ,∴∠MAB =∠MBA . …………………………… 2分 ∴AM =BM .∵点 D 是 边 AB 的 中点 ,∴点M 在CD上. ……………………………………………………………………… 3分∴CM 平分∠FCE . ∴∠FCD =∠ECD .∵ME ⊥BC 于E ,MF ⊥AC 于F , ∴MF =ME . 又∵CM =CM , ∴△CMF ≌△CME . ∴CF =CE . ∵CD =CD ,∴△CFD ≌△CED . ∴DE =DF . ……………………………………………………………………………… 4分【推广】 DE =DF .如图3,作AM 的中点G ,BM 的中点H .图3HGF M CE BD A∵点 D 是 边 AB 的 中点 , ∴1//,.2DG BM DG BM =同理可得:1//,.2DH AM DH AM =∵ME ⊥BC 于E ,H 是BM 的中点, ∴在Rt △BEM 中, 1.2HE BM BH ==∴DG =HE . ………………………………………………………………………………… 5分同理可得:.DH FG = ∵DG //BM ,DH //GM ,∴四边形DHMG 是平行四边形. ∴∠DGM =∠DH M .∵∠MGF =2∠MAC , ∠MHE =2∠MBC , 又∵∠MBC =∠MAC , ∴∠MGF =∠MHE .∴∠DGM +∠MGF =∠DHM +∠MHE . ∴∠DGF =∠DHE . ………………………………………………………………………6分∴△DHE ≌△FGD . ∴DE =DF . ………………………………………………………………………………… 7分25.解:(1)如图,∵点A (1,0),B (0,3),∴直线AB 的解析式为:3 3.y x =-+ ∵OB =3,BD =t , ∴OD =3-t .设P (x ,-3x +3), 作PE ⊥AC 于E ,则OE =x ,PE =-3x +3.∵PE //y 轴, ∴△COD ∽△CEP . ∴OD OC PE CE=∴33.333t x x -=-++∴12(01).3xt x x =≤≤+ …………………………………………………………………… 3分(2)如图,CD =AB ,CD ⊥AB .∵1313,22AOB S ∆=⨯⨯= S △BCD :S △AOB =2:1,∴ 3.BCD S ∆= ∴BD =2. ∴12 2.3xx =+解得:35x =. ∴36,.55P ⎛⎫ ⎪⎝⎭………………………………………………… 4分∵OD =OA =1,OC =OB =3,∠COD =∠BOA =90°, ∴△COD ≌△BOA .∴CD=AB. …………………………………………………………………………… 5分∵△COD≌△BOA,∴∠OCD=∠ABO.又∵∠CDO=∠BDP,∴∠BPD=∠COD=90°.∴CD⊥AB. …………………………………………………………………………………… 6分,(3)MM(. …………………………………………………………………… 8分。
2017北京初三一模数学汇编之函数压轴题
2017北京初三一模数学汇编之函数压轴题西城27.在平面直角坐标系xOy 中,二次函数2(21)5y mx m x m =-++-的图象与x 轴有两个公共点. (1)求m 的取值范围;(2)若m 取满足条件的最小的整数,①写出这个二次函数的解析式;②当1n x ≤≤时,函数值y 的取值范围是64y n --≤≤,求n 的值;③将此二次函数图象平移,使平移后的图象经过原点O .设平移后的图象对应的函数表达式为2()y a x h k =-+,当2x <时,y 随x 的增大而减小,求k 的取值范围.海淀27.平面直角坐标系xOy 中,抛物线2222y mx m x =-+交y 轴于A 点,交直线x =4于B 点.(1)抛物线的对称轴为x = (用含m 的代数式表示); (2)若AB ∥x 轴,求抛物线的表达式;(3)记抛物线在A ,B 之间的部分为图象G (包含A ,B 两点),若对于图象G 上任意一点P (P x ,P y ),2P y ≤,求m 的取值范围.27.二次函数2(2)2(2)5y m x m x m =+-+-+,其中20m +>. (1)求该二次函数的对称轴方程; (2)过动点C (0, n )作直线l ⊥y 轴.① 当直线l 与抛物线只有一个公共点时, 求n 与m 的函数关系;② 若抛物线与x 轴有两个交点,将抛物线在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象. 当n =7时,直线l 与新的图象恰好有三个公共点,求此时m 的值; (3)若对于每一个给定的x 的值,它所对应的函数值都不小于1,求m 的取值范围.朝阳l27. 在平面直角坐标系xOy 中,直线32-=x y 与y 轴交于点A ,点A 与点B 关于x 轴对称,过点B 作y 轴的垂线l ,直线l 与直线32-=x y 交于点C. (1)求点C 的坐标;(2)如果抛物线n nx nx y 542+-= (n >0)与线段BC 有唯一公共点,求n 的取值范围.平谷27.直线33y x =-+与x 轴,y 轴分别交于A ,B 两点,点A 关于直线1x =-的对称点为点C . (1)求点C 的坐标;(2)若抛物线()230y mx nx m m =+-≠经过A ,B ,C 三点,求该抛物线的表达式;(3)若抛物线()230y ax bx a =++≠ 经过A ,B 两点,且顶点在第二象限,抛物线与线段AC 有两个公共点,求a 的取值范围.27.在平面直角坐标系xOy 中,抛物线2222+-+-=m m mx x y 的顶点为D.线段AB 的两个端点分别为A (-3,m ),B (1,m ).(1)求点D 的坐标(用含m 的代数式表示); (2)若该抛物线经过点B (1,m ),求m 的值;(3)若线段AB 与该抛物线只有一个公共点,结合函数的图象,求m 的取值范围.丰台27.在平面直角坐标系xOy 中,抛物线()01242≠-+-=m m mx mx y 与平行于x 轴的一条直线交于A ,B 两点.(1)求抛物线的对称轴;(2)如果点A 的坐标是(-1,-2),求点B 的坐标;(3)抛物线的对称轴交直线AB 于点C , 如果直线AB 与y 轴交点的纵坐标为-1,且抛物线顶点D 到点C 的距离大于2,求m 的取值范围.27.在平面直角坐标系xOy 中,抛物线2443(0)y ax ax a a =-+-≠的顶点为A . (1)求顶点A 的坐标;(2)过点(0,5)且平行于x 轴的直线l ,与抛物线2443(0)y ax ax a a =-+-≠交于,C 两点. ①当2a =时,求线段BC 的长;②当线段BC 的长不小于6时,直接写出a 的取值范围.顺义27.如图,已知抛物线28(0)y ax bx a =++≠与x 轴交于A (-2,0),B 两点,与y 轴交于C 点,tan ∠ABC =2. (1)求抛物线的表达式及其顶点D 的坐标;(2)过点A 、B 作x 轴的垂线,交直线CD 于点E 、F ,将抛物线沿其对称轴向上平移m 个单位,使抛物线与线段EF (含线段端点)只有1个公共点.求m 的取值范围.西城答案27.解:(1)∵二次函数2(21)5y mx m x m =-++-的图象与x 轴有两个公共点. ∴[]20(21)4(5)0m m m m ≠⎧⎪⎨-+--⎪⎩> 解得124m ->且0m ≠. ∴m 的取值范围是124m ->且0m ≠. (2)①m 取满足条件的最小的整数,由(1)可知1m =.∴二次函数的解析式为234y x x =--.②图象的对称轴为直线32x =.当时312n x ≤≤<,函数值y 随自变量x 的增大而减小.∵函数值y 的取值范围是64y n --≤≤, ∴当1x =时,函数值为6-. 当x n =时,函数值为4n -. ∴2346n n --=-.解得2n =-或4n =(不合题意,舍去). ∴n 的值为2-. ③由①可知,1a =, 又函数图象经过原点,∴2k h =-,∵当2x <时,y 随x 的增大而减小, ∴2h ≥, ∴4k -≤.海淀答案27.(1)m ; --------------------------------------------------------------------------------------------------- 2分 (2)∵ 抛物线2222y mx m x =-+与y 轴交于A 点,∴ A (0,2).------------------------------------------------------------------------------------- 3分 ∵ AB ∥x 轴,B 点在直线x =4上,∴ B (4,2),抛物线的对称轴为直线x =2. --------------------------------------------- 4分 ∴ m =2.∴ 抛物线的表达式为2282y x x =-+. --------------------------------------------------- 5分(3)当0m >时,如图1.∵()02A ,,∴要使04P x ≤≤时,始终满足2P y ≤,只需使抛物线2222y mx m x =-+的对称轴与直线x=2重合或在直线x=2的右侧. ∴2m ≥. -------------------------------------------- 6分当0m <时,如图2,0m <时,2P y ≤恒成立. ------------------- 7分综上所述,0m <或2m ≥.东城答案27.解:(1)对称轴方程:2(2)12(2)m x m -+=-=+. …………1分(2)①∵直线l 与抛物线只有一个公共点,∴23n m =-+. …………3分 ② 依题可知:当237m -+=-时,直线l 与新的图象恰好有三个公共点. ∴5m =. …………5分(3)抛物线2(2)2(2)5y m x m x m =+-+-+的顶点坐标是(1,23)m -+.依题可得 20,23 1.m m +>⎧⎨-+≥⎩解得2,1.m m >-⎧⎨≤⎩ ∴ m 的取值范围是21m -<≤. …………7分房山答案27.解:(1)∵直线y =2x -3与y 轴交于点A (0,-3) ------1分 ∴点A 关于x 轴的对称点为B (0,3),l 为直线y =3 ∵直线y =2x -3与直线l 交于点C ,∴点C 的坐标为(3,3) ------2分(2)∵抛物线n nx nx y 542+-= (n >0) ∴y = nx 2-4nx +4n +n = n (x -2)2+n∴抛物线的对称轴为直线x=2,顶点坐标为(2,n ) ------3分 ∵点B (0,3),点C (3,3)错误!未找到引用源。
初三数学一模试题 (含答案)
昌平区—第二学期初三年级第一次统一练习数 学 试 卷 (120分钟) .4第Ⅰ卷 (机读卷 共32分)一、选择题(共8个小题,每小题4分,共32分.) 在下列各题的四个备选答案中,只有一个是正确的. 1.-3的倒数等于A .3-B .3C .13-D .132. 据4月16日在“志愿北京”网站消息:截至4月15日,已有1450000人报名成为城市志愿者.把数字1450000用科学记数法表示为A .81.4510⨯B .70.14510⨯C .61.4510⨯D .414510⨯3. 如图,AB ∥CD ,∥ECD =70°,∥E=60°,则图中∥1的大小是A .100°B .110°C .120°D .130°4.下列计算正确的是( )A.222)(b a b a -=- B.6234)2(a a =- C. 5232a a a =+ D.1)1(--=--a a 5.在函数2+=x y 中,自变量x 的取值范围是A.2x -≥B.2x ≤且0x ≠ C.0x ≥ D.2x -≤6. 已知:()2210a b -++=,则ab 的值为A.1 B.-1 C.2 D.-27. 某校体育训练队(初中组)共有7名队员,他们的年龄(单位:岁)分别为:12,13,13,14,12,13,15.则他们年龄的众数和中位数分别为A.13,14 B.13,13 C.13,13.5 D.14,138.如图1是一个小正方体的展开图,小正方体从如图2所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是A .京B .中C .奥D .运1EDCBA昌平区—学年初三年级第一次统一练习数 学 试 卷 (120分钟) .4第Ⅱ卷 (非机读卷 共88分)考 生 须 知1.考生要认真填写密封线内的学校、班级、姓名、考试编号。
3.答题时字迹要工整,画图要清晰,卷面要整洁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
昌平区2017年初三年级第二次统一练习 数学试卷(120分钟 满分120分)
2017.5
一、选择题(共10道小题,每小题3分,共30分) 下列各题均有四个选项,其中只有一个..是符合题意的. 1.2016年10月12日至15日,第二届中国―互联网+‖大学生创新创业全国总决赛上,ofo共享单车从全国约119000个创业项目中脱颖而出,最终获得金奖. 将119000用科学计数法表示应为
A.41.1910 B. 60.11910 C.51.1910 D. 411.910 2.如图,点A、B在数轴上表示的数的绝对值相等,且AB=4,那么点A表示的数是
A. 3 B. 2 C. 1 D. 3 3.在下面的四个几何体中,主视图是三角形的是
A B C D 4.钟鼎文是我国古代的一种文字,是铸刻在殷周青铜器上的铭文,下列钟鼎文中,不是轴对称图形的是
A B C D 5.如图,△ABC中,∠ACB=90°,∠B=55°,点D是斜边AB的中点,那么∠ACD的度数为 A.15° B. 25° C. 35° D.45°
BADCB
A6.若0322aa,代数式)2(1aa的值是 A.31 B.31 C.-3 D.3 7.初三(1)班体育委员统计本班30名同学体育中考成绩数据如下表所示: 成绩 25 26 27 28 29 30 人数 2 3 5 6 10 4 则这30名同学成绩的众数和中位数分别是. A.29,30 B.29,28 C.28,30 D.28,28 8.如图,将北京市地铁部分线路图置于正方形网格中,若设定崇文门站的坐标为(0,-1),雍和宫站的坐标为(0,4),则西单站的坐标为 A.(0,5) B.(5,0) C.(0,-5) D.(-5,0)
8题 9题 9.如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组2211bxkybxky的解为
A.42yx B.24yx C.04yx D.03yx 10.如图,点A是反比例函数1yx(0)x上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比函数图象上移动时,点B也在某一反比例函数图象kyx上移动,k的值为 A. 2 B. -2 C.4 D. -4
二、填空题(共6道小题,每小题3分,共18分)
x
yABO
xy24
-4
y=k1x+b1y=k2x+b
2
3O11.如图,正方形ABCD,根据图形写出一个正确的等式: _____ _ . 11题 12题 14题 12.如图,四边形 ABCD的顶点均在⊙O上,∠A=70°,则∠C=___________°. 13.《孙子算经》是中国古代重要的数学著作,《孙子算经》共有三卷.第三卷里有一题:“今有兽,六首四足;禽,四首二足,上有七十六首,下有四十六足.问:禽、兽各几何?” 译文:“现在有一种野兽,长有六头四足;有一种鸟,长有四头两足,把它们放一起,共有76头,46足.问野兽、鸟各有多少只?”设野兽x只,鸟y只,可列方程组为__________________. 14.如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=__________ 米. 15.如图,已知钝角△ABC,老师按照如下步骤尺规作图: 步骤1:以C为圆心,CA为半径画弧①; 步骤2:以B为圆心,BA为半径画弧②,交弧①于点D; 步骤3:连接AD,交BC延长线于点H . 小明说:图中的BH⊥AD且平分AD. 小丽说:图中AC平分∠BAD. 小强说:图中点C为BH的中点. 他们的说法中正确的是___________.他的依据是_____________________. 16.已知二次函数xmxy)12(2,当0x时,y随x的增大而减小,则m的取值范围是__________. 三、解答题(共6道小题,每小题5分,共30分) 17.计算: 101tan6032()(2)3
OADBCEBACDa
aabbbbaDCBA
ABCDH18. 解不等式组:xxxx23105)2(3 19. 如图,在等边△ABC中,点D为边BC的中点,以AD为边作等边△ADE,连接BE. 求证:BE=BD
20. 关于x的一元二次方程0)12(2mxmx (1)求证:方程总有两个不相等的实数根; (2)写出一个m的值,并求此时方程的根.
21. 如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F. (1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD=21时, 若CD=5,求AD长.
FE
D
CBA
BC
AED22. 2016年共享单车横空出世,更好地解决了人们“最后一公里”出行难的问题,截止到2016年底, “ofo共享单车‖的投放数量是“摩拜单车‖投放数量的1.6倍,覆盖城市也远超于“摩拜单车‖, “ofo共享单车‖注册用户量约为960万人,“摩拜单车‖的注册用户量约为750万人,据统计使用一辆“ofo共享单车‖的平均人数比使用一辆“摩拜单车‖的平均人数少3人,假设注册这两种单车的用户都在使用共享单车,求2016年“摩拜单车‖的投放数量约为多少万台?
四、解答题(共4道小题,每小题5分,共20分) 23. 一次函数1+2yxb(b为常数)的图象与x轴交于点A(2,0),与y轴交于点B,与反比
例函数xky的图象交于点C(-2,m). (1)求点C的坐标及反比例函数的表达式; (2)过点C的直线与y轴交于点D,且1:2:BOCCBDSS△△,求点D的坐标.
24. 近几年,中国在线旅游产业发展迅猛,在线旅游产业是依托互联网,以满足旅游消费者信息查询、产品预订及服务评价为核心目的,囊括了包括航空公司、酒店、景区、租车公司、海内外旅游服务供应商及搜索引擎、OTA、电信运营商、旅游资讯及社区网站等在线旅游平台的新产业. 据数据统计:2012年中国在线旅游市场交易金额约为2219亿元,2013年中国在线旅游市场交易金额约为3015亿元,2014年中国在线旅游市场交易金额相比2013年增加了1117亿元,2015年中国在线旅游市场交易金额约为5424亿元,2016年中国在线旅游市场交易金额为6622亿元,在人们对休闲旅游观念的不断加强之下,未来两年中国在线旅游市场交易规模会持续上涨. (1)请用折线统计图或条形统计图将2012—2016年中国在线旅游市场交易金额的数据描述出来,并在图中标明相应数据; (2)根据绘制的统计图中提供的信息,预估2017年中国在线旅游市场交易金额约为___________亿元,你的预估理由是_______________________________________. 25. 如图,AB为⊙O的直径,点D,E为⊙O上的两个点,延长AD至C,使∠CBD=∠BED. (1)求证:BC是⊙O的切线; (2)当点E为弧AD的中点且∠BED=30°时,⊙O半径为2,求DF的长度.
26.有这样一个问题:探究函数2)2(1xy的图象与性质,小静根据学习函数的经验,对函数2)2(1x
y的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
(1)函数2)2(1xy的自变量x的取值范围是__________; (2)下表是y与x的几组对应值. x „ -1 0 1 23 25 3 4 „
y „ 91 41 1 4 m 1 41 „
表中的m=__________; (3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
(4)结合函数图象,写出一条该函数图象的性质:______________________________.
FBO
CDE
A
xy–1–2123456–1
–2
12345O五、解答题(共3道小题,第27,28小题各7分,第29小题8分,共22分) 27. 在平面直角坐标系xOy中,抛物线)0(42mmxmxy与x轴交于A,B两点(点A在点B的左侧). (1)求点A,B的坐标及抛物线的对称轴; (2)过点B的直线l与y轴交于点C,且2tanACB,直接写出直线l的表达式; (3)如果点)(1nxP,和点)(2nxQ,在函数)0(42mmxmxy的图象上,PQ=2a且21xx, 求26221aaxx的值.
28. 如图,在正方形ABCD中,E为AB边上一点,连接DE,将△ADE绕点D逆时针旋转90°得到△CDF,作点F关于CD的对称点,记为点G,连接DG. (1)依题意在图1中补全图形; (2)连接BD,EG,判断BD与EG的位置关系并在图2中加以证明; (3)当点E为线段AB的中点时,直接写出∠EDG的正切值.
ED
CB
A图2图1A
BCD
E
