九年级数学上册第二十二章二次函数22.1二次函数的图象和性质22.1.2二次函数y=ax2的图像和性质课件新版新人
22.1.2二次函数y=ax2图像与性质
y=ax2+c (a≠0) 开口方向 顶点坐标 对称轴 增 减 性 极值
a>0 向上 (0 ,c) y轴
当x<0时, y随着x的增大而减小。 当x>0时, y随着x的增大而增大。
a<0 向下 (0 ,c) y轴
当x<0时, y随着x的增大而增大。 当x>0时, y随着x的增大而减小。
x=0时,y最小=c
x y = x2 · · · · · · -3 -2 -1 0 1 2 3 · · · · · ·
9
4
1
0
1
9
4
9
2. 根据表中x,y的数值在 坐标平面中描点(x,y) 3.连线 如图,再用平 滑曲线顺次连接各点, -3 2 就得到y = x 的图象.
y = x2
6
3 3
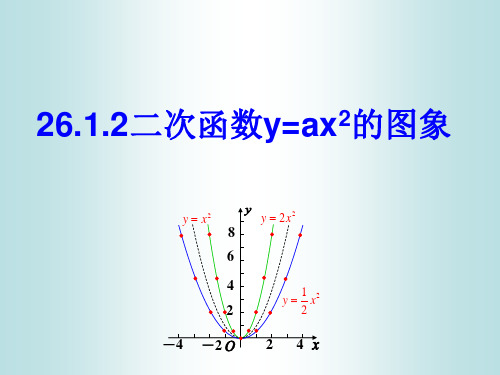
二次函数 y = x2的图象是一条曲线,它的形状类似 于投篮球时球在空中所经过的路线,只是这条曲线 开口向上,这条曲线叫做抛物线 y = x2 , 二次函数的图象都是抛物线, 它们的开口或者向 上或者向下. 一般地,二次函数 y = ax2 + bx + c (a≠0)的图象叫做抛物线y = ax2 + bx + c y = x2
m2+m
解②得:m1=-2, m2=1 由①得:m>-1 ∴ m=1 此时,二次函数为: y=2x2,
x ….. y=x2 …… y=x2+1 ……
-2 4
-1 1
0 0
y
8
1 1
2 4
…… ……
5
2
0
2
5
y=x2+1
函数y=x2+1的图象与y=x2的 图象的位置有什么关系? 函数y=x2+1的图 象与y=x2的图象 的形状相同吗?
二次函数 y=ax2的图象和性质 人教版九年级数学上册同步课堂教案

第二十二章二次函数22.1二次函数的图象和性质22.1.2 二次函数y=ax2的图象和性质一、教学目标1.正确理解抛物线的有关概念.2.会用描点法画出二次函数y=ax²的图象,概括出图象的特点.3.掌握形如y=ax²的二次函数图象的性质,并会应用.二、教学重难点重点:正确理解抛物线的有关概念.难点:会用描点法画出二次函数y=ax²的图象,概括出图象的特点,掌握形如y=ax²的二次函数图象的性质,并会应用.三、教学过程【新课导入】[复习导入]问题1:1.二次函数的定义?一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数.问题2:一次函数的图象是一条直线,二次函数的图象是什么形状?如何画一个二次函数的图象?【新知探究】(一)二次函数y=ax2的图象先画二次函数y=x2 的图象.[课件展示]1.列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:x…-3-2-10123…y=x2…9410149…2. 描点:根据表中x,y的数值在坐标平面中描点(x, y)3. 连线:如图,再用平滑曲线顺次连接各点,就得到y = x2的图象.二次函数y=x2的图象类似于投篮时或掷铅球时球在空中所经过的路线,只是这条曲线开口向上.我们把它叫做抛物线.[思考]画出函数y=-x2的图象.x…-3-2-10123…y=x2…-9-4-10-1-4-9…(二)二次函数y=ax2的性质[讨论交流]1.利用你前面学习的函数图象的性质,说说二次函数y=x2的图象有哪些性质,并与同伴交流.[归纳总结](1)y=x2是一条抛物线;(2)图象开口向上;(3)图象关于y轴对称;(4)顶点(0 ,0);(5)图象有最低点.[讨论交流]2.说说二次函数y=-x2的图象有哪些性质,与同伴交流.[归纳总结](1)y=-x2是一条抛物线;(2)图象开口向下;(3)图象关于y轴对称;(4)顶点(0 ,0 );(5)图象有最高点.[归纳总结]二次函数y=ax2 的图象性质:(1)y=ax2是一条抛物线;(2)顶点都在原点;(3)图像关于y轴对称;(4)当a>0时,开口向上;当a<0时,开口向下.[深入思考]观察下列图象,抛物线y=ax2与y=-ax2(a>0)的关系是什么?[思考]问题1:观察图形,y随x的变化如何变化?[归纳总结]对于抛物线y = ax 2 (a>0)当x>0时,y随x取值的增大而增大;当x<0时,y随x取值的增大而减小.[思考]问题2:观察图形,y随x的变化如何变化?[归纳总结]对于抛物线y = ax 2 (a<0)当x>0时,y随x取值的增大而减小;当x<0时,y随x取值的增大而增大.x2,y=2x2的图象.例1 在同一直角坐标系中,画出函数y=12解:分别列表,再画出它们的图象,如图x…-4-3-2-101234…y=1x2…8 4.520.500.52 4.58…2x…-2-1.5-1-0.500.51 1.52…y=2x2…8 4.520.500.52 4.58…x2,y=x2 , y=2x2开口大小与a的大小有什么关系?[思考]二次函数y=12当a>0时,a越大,开口越小.x2,y=−2x2的图象.[思考]在同一直角坐标系中,画出函数y=−12x…-4-3-2-101234…x2…-8-4.5-2-0.50-0.5-2-4.5-8…y=−12x…-2-1.5-1-0.500.51 1.52…y=−2x2…-8-4.5-2-0.50-0.5-2-4.5-8…x2,y=−x2 , y=−2x2开口大小与a的大小有什么关系?[思考]二次函数y=−12当a<0时,a越小(即a的绝对值越大),开口越小.[课件展示]y=ax2 (a≠0)a>0a<0图象开口方向向上向下顶点坐标(0 ,0)(0 ,0)对称轴y轴y轴增减性当x<0时,y随着x的增大而减小;当x>0时,y随着x的增大而增大.当x<0时,y随着x的增大而增大;当x>0时,y随着x的增大而减小.最值x=0时,y最小=0x=0时,y最大=0抛物线y=ax2(a≠0)的形状是由|a|来确定的,一般说来, |a|越大,抛物线的开口就越小;|a|越小,抛物线的开口就越大.例2 已知y =(m+1)x m2+m是二次函数,且其图象开口向上,求m的值和函数解析式.解: 依题意有:{m+1>0,①m2+m=2.②解②得m1=-2, m2=1;由①得m>-1.∴m=1.此时,二次函数解析式为: y=2x2.例3 已知二次函数y=x2.(1)判断点A(2,4)在二次函数图象上吗?(2)请分别写出点A关于x轴的对称点B的坐标,关于y轴的对称点C的坐标,关于原点O的对称点D的坐标.解:(1)当x=2时,y=x2=4,所以A(2,4)在二次函数图象上;(2)点A关于x轴的对称点B的坐标为(2,-4),点A关于y轴的对称点C的坐标为(-2,4),点A关于原点O的对称点D的坐标为(-2,-4);【课堂小结】二次函数y=ax2的图象及性质y=ax2 (a≠0)a>0a<0图象开口方向向上向下顶点坐标(0 ,0)(0 ,0)对称轴y轴y轴增减性当x<0时,y随着x的增大而减小;当x>0时,y随着x的增大而增大.当x<0时,y随着x的增大而增大;当x>0时,y随着x的增大而减小.最值x=0时,y最小=0x=0时,y最大=0抛物线y=ax2(a≠0)的形状是由|a|来确定的,一般说来, |a|越大,抛物线的开口就越小;|a|越小,抛物线的开口就越大.【课堂训练】1.函数y=2 x 2的图象的开口向上,对称是y轴,顶点是(0,0);在对称轴的左侧,y随x的增大而减小,在对称轴的右侧,y随x的增大而增大.2.函数y=-3x 2的图象的开口向下,对称轴是y轴,顶点(0,0);在对称轴的左侧,y 随x 的增大而 增大 ,在对称轴的右侧,y 随x 的增大而 减小 . 3.已知 y =(k +2)x k2+k−4是二次函数,且当x >0时,y 随x 增大而增大,则k = 2 .4.若抛物线 y =a x 2 (a ≠ 0),过点(-1,2).(1)a 的值是 2 ;对称轴是 y 轴 ,开口 向上 ;(2)顶点坐标是 (0,0) ,顶点是抛物线上的最 小 值 ,抛物线在x 轴的 上 方(除顶点外);(3) 若A ( x 1, y 1),B (x 2, y 2)在这条抛物线上,且x 1< x 2<0, 则y 1 > y 2. [拓广探索]5.已知:如图,直线y =3x +4与抛物线y =x 2交于A 、B 两点,求出A 、B 两点的坐标,并求出两交点与原点所围成的三角形的面积. 解:由题意得{y =3x +4,y =x 2.解得{x =4,y =16,或{x =−1,y =1,所以此两函数的交点坐标为A (4,16)和B (-1,1). ∵直线y =3x +4与y 轴相交于点C (0,4),即CO =4. ∴S △ACO =12·CO ·4=8,S △BOC = 12 ×4×1=2, ∴S △ABO =S △ACO +S △BOC =10. 【布置作业】【教学反思】教学过程中,强调学生自主探索和合作交流,在操作中探究二次函数y =ax 2的图象与性质,体会数学建模的数形结合的思想方法.。
人教版九年级上册数学课件 第二十二章 二次函数 第1课时 二次函数y=ax2+k的图象和性质 (2)

y= 3x-3, 析式为 y= 3 x-3.联立直线 DC 与抛物线的解析式可得y=13x2-3, 解得
x1=0, y1=-3,
yx22==63,3,
所以 M1(3
3 ,6);
②如图,若点 M2 在点 B 下方,设 M2C 交 x 轴于点 E,易得∠OEC=45 °-15°=30°,易得 OE=3 3 .
15.(10分)(云南中考)已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称 轴是y轴,并且与x轴有两个交点.
(1)求k的值; (2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P 的坐标. 解:(1)∵抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,∴k2+k-6=0, 解得k1=-3,k2=2,又∵抛物线y=x2+(k2+k-6)x+3k与x轴有两个交点, ∴3k<0,∴k=-3 (2)∵点P在抛物线y=x2-9上,且P到y轴的距离是2,∴点P的横坐标为2或 -2,当x=2时,y=-5,当x=-2时,y=-5.∴P(2,-5)或P(-2,-5)
(1)求m的值; (2)求函数y=ax2+b(a≠0)的解析式; (3)抛物线上是否存在点M,使得∠MCB=15°?若存在,求出点M的坐 标;若不存在,请说明理由.
解:(1)将(0,-3)代入y=x+m,可得m=-3
(2)将 y=0 代入 y=x-3 得 x=3,所以点 B 的坐标为(3,0).
将(0,-3),(3,0)代入
人教版
第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.3 二次函数y=a(x-h)2+k的图象和性质 第1课时 二次函数y=ax2+k的图象和性质
1.(3分)抛物线y=x2+1的图象大致是( C )
人教版九年级上册数学作业课件 第22章 二次函数 第1课时 二次函数y=ax2+bx+c的图象和性质

解:(1)对称轴是直线 x=-1,顶点(-1,72 ),y 最大=72
(2)对称轴是直线 x=-3,顶点(-3,-18),y 最小=-18
14.(2020·仙桃)把抛物线C1:y=x2+2x+3先向右平移4个单位长度, 再向下平移5个单位长度得到抛物线C2.
(1)直接写出抛物线C2的函数关系式; (2)动点P(a,-6)能否在抛物线C2上?请说明理由; (3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0,比较y1, y2的大小.
解:(1)y=x2+2x+3=(x+1)2+2,∵把抛物线C1:y=x2+2x+3先 向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2,∴C2: y=(x+1-4)2+2-5,即y=(x-3)2-3,∴抛物线C2的函数关系式为y =(x-3)2-3
(2)动点P(a,-6)不在抛物线C2上,理由如下:∵抛物线C2的函数关 系式为:y=(x-3)2-3,∴函数的最小值为-3,∵-6<-3,∴动点
=-12 x2+2x,∴PD+BD=-12 x2+2x+54 x=-12 (x-143 )2+13629 ,∵54 <
x<4,-12
<0,∴当 x=143
时,PD+BD 有最大值为13629
,此时,点
13 P( 4
,
-5372 )
(3)设平移后的抛物线 L′解析式为 y=12 (x-m)2-13221 ,联立方程组可得
(1)求直线 AB 的解析式及抛物线顶点的坐标; (2)如图 1,点 P 为第四象限且在对称轴右侧抛物线上一动点,过点 P 作 PC⊥x 轴,垂足为 C,PC 交 AB 于点 D,求 PD+BD 的最大值,并求出此时点 P 的坐标;
(3)如图 2,将抛物线 L:y=12 x2-54 x-3 向右平移得到抛物线 L′,直线 AB 与 抛物线 L′交于 M,N 两点,若点 A 是线段 MN 的中点,求抛物线 L′的解析式.
22.1.2二次函数y=ax的平方的图像及性质

4.小结
(1)本节课学了哪些主要内容? (2)本节课是如何研究二次函数 y = ax 2 的图象和 性质的?
5.布置作业
教科书习题 22.1 第 3,4 题.
探究二
1 2 2 y 2 x y x 1、在同一直角坐标系中,画出函数 , 2 的图象,这两个函数的图象与函数 y = x 2 的图象相比, 有什么共同点?有什么不同点?
2、当 a>0 时,二次函数y = ax 2 的图象有什么特点? 【归纳】一般的,当a>0时,抛物线 y ax 的开口向 上,对称轴是Y轴,顶点是原点,顶点是抛物线的最低 点,a越大,抛物线的开口越小。
2
探究三
类比 a>0 时的研究过程,探究当 a<0 时,二次 函数 y = ax 2 的图象特征. 1、用几何画板在同一直角坐标系中,画出a<0的几 个二次函数的图函数二次函数 y = ax 2 的图象特征.
2 y ax 【归纳】一般的,当a<0时,抛物线 的开口向
(2) y 3x ; 开口向下、y 轴、原点.
1 2 (3) y x ; 开口向上、y 轴、原点. 3 1 2 (4) y x .开口向下、y 轴、原点. 3
3.巩固练习
1 2 2、二次函数 y 2 x 的图象是一条 抛物线 ,当x<0
时,y 随 x 的增大而 减 小 ;当x>0时,y 随 x 的增大
人教版九年级
上册
22.1
二次函数的图象和性质 (第2课时)
(一)复习引入-----学习导图
图象的形状 图象的形状
图象的位置
一 次 函 数
类比
二 次 函 数
y ax 2 (a 0)
图象的位置
人教版数学九年级上册《22.1.2二次函数y=ax2的图象和性质》说课稿1

人教版数学九年级上册《22.1.2二次函数y=ax2 的图象和性质》说课稿1一. 教材分析人教版数学九年级上册《22.1.2二次函数y=ax^2 的图象和性质》这一节,是在学生已经掌握了函数的概念、一次函数的图象和性质的基础上,进一步引导学生学习二次函数的图象和性质。
通过这一节的学习,使学生能够掌握二次函数的一般形式,了解二次函数的图象特征,以及掌握二次函数的性质。
教材通过丰富的例题和练习题,帮助学生巩固所学知识,提高解决问题的能力。
二. 学情分析九年级的学生已经具备了一定的函数知识,对一次函数的图象和性质有了初步的了解。
但是,二次函数相对于一次函数来说,图象和性质更加复杂,需要学生有一定的抽象思维能力。
此外,学生可能对二次函数的图象和性质在实际问题中的应用还不够清晰,需要教师在教学中进行引导和启发。
三. 说教学目标1.知识与技能目标:让学生掌握二次函数的一般形式,了解二次函数的图象特征,掌握二次函数的性质。
2.过程与方法目标:通过观察、分析、归纳等方法,引导学生自主探究二次函数的图象和性质。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的探究精神和合作意识。
四. 说教学重难点1.教学重点:二次函数的一般形式,二次函数的图象特征,二次函数的性质。
2.教学难点:二次函数的图象和性质在实际问题中的应用。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例分析法、小组讨论法等,引导学生主动探究,提高学生的参与度和积极性。
2.教学手段:利用多媒体课件,展示二次函数的图象和性质,使抽象的知识更加直观形象。
同时,利用练习题和案例,帮助学生巩固所学知识。
六. 说教学过程1.导入:通过复习一次函数的图象和性质,引出二次函数的一般形式,激发学生的学习兴趣。
2.探究二次函数的图象特征:让学生观察二次函数的图象,引导学生发现二次函数的顶点、开口方向等特征。
3.探究二次函数的性质:通过小组讨论,让学生归纳出二次函数的增减性、对称性等性质。
九年级数学上册 22.1.2 二次函数y=ax2的图象和性质教案 (新版)新人教版-(新版)新人教版
教 学 内 容一、探索新知:画二次函数y =x 2的图象. 列表:x … -3 -2 -1 0 1 2 3y =x 2…描点,并连线由图象可得二次函数y =x 2的性质:1.二次函数y =x 2是一条曲线,把这条曲线叫做______________. 2.二次函数y =x 2中,二次函数a =_______,抛物线y =x 2的图象开口______. 3.自变量x 的取值X 围是____________.4.观察图象,当两点的横坐标互为相反数时,函数y 值相等,所描出的各对应点关于________对称,从而图象关于___________对称.5.抛物线y =x 2与它的对称轴的交点( , )叫做抛物线y =x 2的______. 因此,抛物线与对称轴的交点叫做抛物线的_____________. 6.抛物线y =x 2有____________点(填“最高”或“最低”) . 二、例题分析例1 在同一直角坐标系中,画出函数y =12x 2,y =x 2,y =2x 2的图象.解:列表并填:x…-4 -3 -2 -112341.填表:开口方向顶点 对称轴有最高或最低点最值y =23 x 2当x =____时,y 有最_______值,是_y =-8x 22.若二次函数y =ax 2的图象过点(1,-2),则a 的值是___________. 3.二次函数y =(m -1)x 2的图象开口向下,则m____________. 4.如图,① y =ax 2② y =bx 2③ y =cx 2 ④ y =dx 2比较a 、b 、c 、d 的大小,用“>”连接.___________________________________七、目标检测1.函数y =37x 2的图象开口向_______,顶点是__________,对称轴是________,当x =___________时,有最_________值是_________. 2.二次函数y =mx22 m 有最低点,则m =___________.3.二次函数y =(k +1)x 2的图象如图所示,则k 的取值 X 围为___________.4.写出一个过点(1,2)的函数表达式_________________. 六、教学效果追忆:。
二次函数y=ax2+bx+c的图象和性质 第2课时 课件(共16张PPT)人教版数学九年级上册
【例题】
【例2】已知抛物线的顶点为(-1,-3), 与y轴交点为(0,-5),求抛物线的解析式.
y
-1
ox
-3
解析:设所求的二次函数为y=a(x+1)2-3Байду номын сангаас由点( 0,-5 )在抛物线上得:
a-3=-5, 得a=-2 故所求的抛物线解析式为y=-2(x+1)2-3
【例题】 【例3】当x=1时,抛物线最高点的纵坐标为4,且与x 轴两交点之间的距离为6,求此函数解析式.
【例题】
【例1】已知一个二次函数的图象过(-1,10),
(1,4),(2,7)三点,求这个函数的解析式.
解析:设所求的二次函数为y=ax2+bx+c,
由条件得:
a-b+c=10, a+b+c=4,
4a+2b+c=7,
解方程组得:a=2, b=-3, c=5.
因此,所求二次函数的解析式是:y=2x2-3x+5
(1,1).求这个二次函数的表达式. 解:设这个二次函数的表达式为y=ax2+bx+c.
依题意得 a-b+c=-5, c=-4, 解得 a+b+c=1,
a=2,
b=3, c=-4,
∴这个二次函数的表达式为y=2x2+3x-4.
已知条件
待定系数法 求二次函数解析式
所选方法
①已知三点坐标
用一般式法:y=ax2+bx+c
解析:方法一:由题意知,抛物线的顶点为(1,4),对
称轴为x=1,又因为抛物线与x轴两交点之间的距离为6,
所以抛物线与x轴的两交点为(-2,0)和(4,0),
设函数解析式为y=a(x-1)2+4,因为当x=-2时,y=0,
九年级数学上册第22章《二次函数y=ax^2的图象和性质》名师教案(人教版)
22.1.2 二次函数2ax y =的图象和性质一、教学目标 (一)学习目标1.会用描点法画出形如y=ax 2的二次函数图象,了解抛物线的有关概念; 2.通过观察图象,能说出二次函数y=ax 2的图象特征和性质;3.在类比探究二次函数 y=ax 2的图象和性质的过程中,进一步体会研究函数图象和性质的基本方法和数形结合的思想. (二)学习重点会画二次函数y=ax²的图象,理解其图象特征和性质. (三)学习难点用描点法画二次函数y=ax 2的图象以及探索二次函数性质,体会数与形的相互联系. 二、教学设计 (一)课前设计 1.预习任务(1)二次函数y=ax 2 ,当a>0时,图象特征和性质是: ①图象是一条抛物线,开口向上;②原点(0,0)是图象的顶点,也是最低点,当x=0时,函数y 有最小值0;③图象是轴对称图形,对称轴是y 轴(直线x=0);在对称轴的左侧(即x<0时),抛物线从左到右下降,y 随x 的增大而减小;在对称轴右侧(即x>0时),抛物线从左到右上升,y 随x 的增大而增大.(2)二次函数y=ax 2 ,当a<0时,图象特征和性质是: ①图象是一条抛物线,开口向下;②原点(0,0)是图象的顶点,也是最高点,当x=0时,函数y 有最大值0;③图象是轴对称图形,对称轴是y 轴(直线x=0);在对称轴的左侧(即x<0时),抛物线从左到右上升,y 随x 的增大而增大;在对称轴右侧(即x>0时),抛物线从左到右下降,y 随x 的增大而减小. 2.预习自测1.二次函数26x y =的图象开口向________,对称轴是________,顶点坐标________,当x_______时,y 随x 的增大而增大,当x_______时,y 随x 的增大而减小, 当x=______时,y 有最______值,为 .【知识点】二次函数2ax y =的图象和性质【解题过程】由二次函数2y ax =的图象和性质可得.【思路点拨】牢记二次函数2ax y =的图象和性质是解题的关键 【答案】上,y 轴,(0,0),>0,<0,0,小,02.函数22x y -=的图象开口方向________,对称轴是_______,顶点坐标__________, 在y 轴的左侧,y 随x 的增大而______,在y 轴的右侧,y 随x 的增大而______. 当x=_______时,函数有最______值,为 . 【知识点】二次函数2ax y =的图象和性质【解题过程】由二次函数2y ax =的图象和性质可得.【思路点拨】牢记二次函数2ax y =的图象和性质是解题的关键 【答案】下,y 轴,(0,0),增大,减小,0,大,03.函数231x y =与13y x =-2的图象之间的关系是____________.【知识点】二次函数2ax y =的图象和性质与【解题过程】因函数231x y =与231x y -=的二次项系数互为相反数,其图象的形状相同,只是开口方向相反,所有它们的图象关于x 轴对称.【思路点拨】由二次函数2ax y =与2ax y -=的图象关于x 轴对称可得 【答案】关于x 轴对称 4.已知函数72-=m mxy 的图象是抛物线,且开口向下,则m 的值为_______.【知识点】二次函数2ax y =的图象和性质【解题过程】由272m -=得3m =±,又开口向下,故3m =-【思路点拨】牢记二次函数的概念和2ax y =的图象和性质是解题的关键 【答案】3m =- (二)课堂设计 1.知识回顾(1)二次函数的定义:一般地,形如c bx ax y ++=2(a≠0)的函数叫做x 的二次函数. (2)一次函数y=kx+b (k≠0)的图象与性质:图象是一条直线;当k>0时,直线通过一、三象限,y 随x 的增大而增大;当k<0时,直线通过二、四象限,y 随x 的增大而减小.(3)研究函数时,了解函数性质的主要工具是:函数的图象.(4)画函数图象的主要步骤:①列表.②描点.③连线.2.问题探究探究一画出二次函数2y=的图象重点、难点知识★▲ax●活动①合作探究1.实践操作:用描点法画2xy=的图象。
初中数学人教版九年级上册《22.1.2二次函数的图象和性质》课件
二次函数y=ax2的 图象和性质
人教版 九年级数学上
知识要点
1.二次函数y=ax2的图象 2.二次函数y=ax2的性质
看一看:观察下列运动,试着发现它们的规律。
二次函数y=ax2的图象
问题1.1:根据所学知识,试着画出二次函数y=x2的图像。
在y = x2 中自变量x可以是任意实数,列表表示几组 对应值:
x … -3 -2 -1
0
1
2
3…
y=-x2 … -9 -4 -1 0 -1 -4 -9 …
二次函数y=ax2的性质 y
顶点
-5 -4 -3 -2 -1 O 1 2 3 4 5 x
-3
对称轴
-6
根据表中x,y的数值在坐 标平面中描点(x,y)
用平滑曲线顺次连接 各点,就得到y = -x2 的图象 图象开口向下,有最高点
A.-9<y≤-1 B.-9≤y<-1 C.-9≤y≤0 D.-9<y≤0
4.如图,在同一坐标系中,作出①y=3x2,②y= 1 x2, 2
③y=x2的图象,则图象中从里到外的三条抛物线对应的
函数依次是___①__③_②______.(填序号)
5.二次函数y=ax2的图象如图所示. (1)求这个二次函数解析式; (2)若另一函数图象与该函数图象关于x轴对称,试求另一个 函数的解析式.
-9
y
y
9
-5 -4 -3 -2 -1 O 1 2 3 4 5 x
6
y = x2
-3 y =- x2
-6 3
-9 -3 -2 -1 O1 2 3 x
二次函数y=ax2的图象
练一练:如图,函数y=2x2的图象大致为( C )
