河北省武邑中学2017-2018学年高一下学期暑假作业数学试题(13) Word版含答案
河北省武邑中学2017-2018学年高一下学期暑假作业物理试题(34) Word版含答案

河北武邑中学2017-2018学年高一升高二暑假作业物理学科(第34期)完成时间: ______________ 姓名班级学号完成日期家长签字A.液体中的扩散现象是由于液体的对流形成的B.扩散现象在气体、液体中可以发生,在固体中不能发生C.扩散现象是由物质分子无规则运动产生的D.扩散现象是不同物质间的一种化学反应2.将闭合多匝线圈置于仅随时间变化的磁场中,线圈平面与磁场方向垂直,关于线圈中产生的感应电动势和感应电流,下列表述正确的是( )A.感应电动势的大小与线圈的匝数无关B.穿过线圈的磁通量越大,感应电动势越大C.穿过线圈的磁通量变化越快,感应电动势越大D.感应电流产生的磁场方向与原磁场方向始终相同3.如图甲所示,圆形线圈垂直放在匀强磁场里,第1秒内磁场方向指向纸里.若磁感应强度大小随时间变化的关系如图乙,那么,下面关于线圈中感应电流的说法正确的是( )A.在第1秒内感应电流增大,电流方向为逆时针B.在第2秒内感应电流大小不变,电流方向为顺时针C.在第3秒内感应电流减小,电流方向为顺时针D.在第4秒内感应电流大小不变,电流方向为顺时针4.假设有两个相距很远的分子,仅在分子力作用下,由静止开始逐渐接近,直到不能再接近为止,若两分子相距无穷远时分子势能为零,在这个过程中,关于分子势能大小的变化情况正确的是()A.分子势能先增大,再减小,后又增大B.分子势能先减小,后增大C.分子势能先减小,再增大,后又减小D.分子势能先增大,后减小5.如图所示,面积相同、总电阻相同的单匝闭合线圈甲、乙、丙、丁绕垂直于磁场方向的轴在匀强磁场中以角速度ω匀速转动,线圈甲、乙、丙、丁在转动过程中产生的电流的有效值分别为甲I 、乙I 、丙I 、丁I ,关于甲I 、乙I 、丙I 、丁I 的大小关系,下列说法正确的是( )A .甲I >丙IB .丙I <丁IC .甲I =丁ID . 乙I >丙I6.如图所示,一辆质量为m 的小车静止在光滑水平桌面上,一汽缸水平固定在小车上,一质量为2m ,面积为S 的活塞将一定质量的理想气体封闭在汽缸内,汽缸静止时,活塞与汽缸底部相距为0L 。
河北省武邑中学2017-2018学年高一上学期周考(12.11)数学试题 Word版含答案

2017-2018学年高一上学期数学周测第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.函数()sin f x x x =-零点的个数是( ) A .0 B .1 C .2 D .32.如图是函数()f x 的图像,它与x 轴有4个不同的公共点,给出下列四个区间之中,存在不能用二分法求出的零点,该零点所在的区间是( )A .[]2.1,1--B .[]4.1,5C .[]1.9,2.3D .[]5,6.1 3.函数()22x f x a x=--的一个零点在区间()1,2内,则实数a 的取值范围是( )A .()1,3B .()1,2C .()0,3D .()0,2 4.函数()()2ln 2f x x x=--的零点所在的大致区间是( ) A .()1,2 B .()2,3 C .()3,4 D .()4,55.已知a 是函数()122log x f x x =-的零点,若00x a <<,则()0f x 的值满足( )A .()00f x =B .()00f x <C .()00f x >D .不确定6.设1x 、2x 是方程ln 2x m -=(m 为实常数)的两根,则12x x +的值为( )A .4B .2C .4-D .与m 有关7.函数()322x f x x =+-在区间()0,2内的零点个数是( ) A .0 B .1 C .2 D .3 8.函数()ln 1y x =+与1y x=的图象交点的横坐标所在区间为( ) A .()0,1 B .()1,2 C .()2,3 D .()3,49.若a b c <<,则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间( )A .(),a b 和(),b c 内B .(),a -∞和(),a b 内C .(),b c 和(),c +∞内D .(),a -∞和(),c +∞内10.若函数()312f x ax a =+-在区间()1,1-内存在一个零点,则a 的取值范围是( )A .1,5⎛⎫+∞ ⎪⎝⎭B .()1,1,5⎛⎫-∞-⋃+∞ ⎪⎝⎭C .11,5⎛⎫- ⎪⎝⎭D .(),1-∞-11.已知函数()2x f x x =+,()ln g x x x =+,()1h x x =的零点分别为1x ,2x ,3x ,则1x ,2x ,3x 的大小关系是( )A .213x x x <<B .123x x x <<C .132x x x <<D .321x x x <<12.若函数()21f x ax x =--有且仅有一个零点,则实数a 的取值为( )A .0B .14-C .0或14- D .2第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知函数()2,01,0x x f x fx x ⎧=⎨-⎩≤>()()g x f x x a =--,若函数()g x 有两个零点,则实数a 的取值范围为 .14.定义在R 上的函数()f x 满足()()516f x f x ++=,当(]1,4x ∈-时,()22x f x x =-,则函数()f x 在[]0,2013上的零点个数是 .15.已知函数()221,0,2,0x x f x x x x ⎧-⎪=⎨--⎪⎩>≤若函数()()g x f x m =-有3个零点,则实数m 的取值范围是 .16.已知()f x 是定义在R 上且周期为3的函数,当[)0,3x ∈时,()2122f x x x =-+.若函数()y f x a =-在区间[]3,4-上有10个零点(互补相同),则实数a 的取值范围是 .三、解答题 (本大题共5小题,共60分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分12分)设函数()()()2320,,f x ax a c x c a a c R --++∈>.(1)设0a c >>.若()22f x c c a -+>对[)1,x ∈+∞恒成立,求c 得取值范围; (2)函数()f x 在区间()0,1内是否有零点,有几个零点?为什么? 18. (本小题满分12分)已知函数()22ln f x x x =-,()2h x x x a =-+. (Ⅰ)求函数()f x 的极值;(Ⅱ)设函数()()()k x f x h x =-,若函数()k x 在[]1,3上恰有两个不同零点,求实数a 的取值范围.19. (本小题满分12分) 已知函数()3221f x x x ax =+-+.(1)若函数()f x 在点()()1,1f 处的切线斜率为4,求实数a 的值; (2)若函数()()g x f x '=在区间()1,1-上存在零点,求实数a 的取值范围. 20. (本小题满分12分)已知二次函数()f x 的最小值为4-,且关于x 的不等式()0f x ≤的解集为{}13,x x x R -∈≤≤.(1)求函数()f x 的解析式; (2)求函数()()4ln f x g x x x=-的零点个数. 21. (本小题满分12分)已知函数()()22,,x x f x ae be cx a b c R -=--∈的导函数()f x '为偶函数,且曲线()y f x =在点()()0,0f 处的切线的斜率为4c -.(Ⅰ)确定a ,b 的值;(Ⅱ)若3c =,判断()f x 的单调性; (Ⅲ)若()f x 有极值,求c 得取值范围.试卷答案一、选择题1-5:BCCCB 6-10:ABBABB 11、12:BC 二、填空题13.(),1-∞ 14.604 15.()0,1 16.10,2⎛⎫ ⎪⎝⎭三、解答题17.解(1)因为二次函数()()232f x ax a c x c =-++的图象的对称轴3a cx a+=,由条件0a c >>,得2a a c +>,故221333a c a a a +=<<,即二次函数()f x 的对称轴在区间[)1,+∞的左边,且抛物线开口向上,故()f x 在[)1,+∞内是增函数. 若()22f x c c a -+>对[)1,x ∈+∞恒成立,则()()2min 12f x f c c a =-+>,即22a c c c a --+>,得20c c -<,所以01c <<.(2)①若()()()010f f c a c ⋅=⋅-<,则0c <,或a c <,二次函数()f x 在()0,1内只有一个零点.18.(Ⅱ)()()()2ln k x f x h x x x a =-=-+-()21k x x '∴=-+,若()0k x '=,则2x =当(]1,2x ∈时,()0f x '<;当(]2,3x ∈时,()0f x '>. 故()k x 在[)1,2x ∈上递减,在(]2,3x ∈上递增()()()10,20,30,k k k ⎧⎪∴⎨⎪⎩≥<≥1,22ln 2,32ln 3,a a a ⎧⎪∴-⎨⎪-⎩≤>≤22ln 232ln 3a ∴--<≤.所以实数a 的取值范围是(]22ln 2,32ln3-- 19.解由题意得()()234g x f x x x a '==+-. (1)()1344f a '=+-=,3a ∴=.(2)法一①当()110g a -=--=,1a =-时,()()g x f x '=的零点()11,13x =-∈-;②当()170g a =-=,7a =时,()f x '的零点()71,13x =-⊕-,不合题意;③当()()110g g -<时,17a -<<;④当()()()4430,211,310,10a g g ∆=⨯+⎧⎪⎪--⎪⎨⎪⎪-⎪⎩≥<<>>时,413a --≤<.综上所述,4,73a ⎡⎫∈-⎪⎢⎣⎭.法二()()g x f x '=在区间()1,1-上存在零点,等价于234x x a +=在区间()1,1-上有解,也等价于直线y a =与曲线234y x x =+在()1,1-有公共点.作图可得4,73a ⎡⎫∈-⎪⎢⎣⎭.22244343,7333a x x x ⎛⎫⎡⎫=+=+-∈- ⎪⎪⎢⎝⎭⎣⎭.20.解(1)()f x 是二次函数,且关于x 的不等式()0f x ≤的解集为{}13,x x x R -∈≤≤,()()()21323f x a x x ax ax a ∴=+-=--,且0a >. ()()min 144f x f a ∴==-=-,1a =. 故函数()f x 的解析式为()223f x x x =--. (2)()()22334ln 4ln 20x x g x x x x x x x--=-=--->,()()()2213341x x g x x x x --'∴=+-=.令()0g x '=,得11x =,23x =.当x 变化时,()g x ',()g x 的取值变化情况如下:当03x <≤时,()()140g x g =-≤<.又因为()g x 在()3,+∞上单调递增,因而()g x 在()3,+∞上只有1个零点. 21.【答案】(Ⅰ)1a =,1b =;(Ⅱ)增函数;(Ⅲ)()4,+∞. 试题解析:解:(Ⅰ)对()f x 求导得()2222x x f x ae be c -'=+-,由()f x '为偶函数,知()()f x f x ''-=,即()()2220x x a b e e --+=,因220x x e e -+>,所以a b = 又()022f a b c '=+-,故1a =,1b =. (Ⅱ)当3c =时,()223x x f x e e x -=--,那么()22223310x x f x e e -'=+-=≥>故()f x 在R 上位增函数.(Ⅲ)由(Ⅰ)知()2222x x f x e e c -'=+-,而222224x x e e -+=≥,当0x =时等号成立.下面分三种情况进行讨论.当4c <时,对任意x R ∈,()22220x f x e e c -'=+->,此时()f x 无极值; 当4c =时,对任意0x ≠,()222240x f x e e -'=+->,此时()f x 无极值;当4c >,令2xe t =,注意到方程220t c t +-=有两根,1,20t =,即()0f x '=有两个根111ln 2x t =或221ln 2x t =. 当12x x x <<时,()0f x '<;又当2x x >时,()0f x '>从而()f x 在2x x =处取得极小值.综上,若()f x 有极值,则c 的取值范围为()4,+∞.考点:1、导数的几何意义及导数在研究函数性质中的应用;2、分类讨论的思想.故()g x 在()0,+∞上只有1个零点.。
河北省武邑中学高一数学下学期暑假作业试题(27)

河北省武邑中学2015-2016学年高一数学下学期暑假作业试题(27)一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的 1. 集合{1,0,1}A =-的子集个数是A. 5B. 8C. 16D. 322. 已知54sin =θ,53cos -=θ,则θ2是( ) A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角 3. 在ABC ∆中,三边a ,b ,c 满足bc c b a ++=222,则角A 等于( ) A.ο30 B.ο60 C.ο120 D.ο1504. 一个蜂巢里有1只蜜蜂,第1天,它飞出去找回了3个伙伴;第2天,4只蜜蜂飞出去,各自找回了3个伙伴......如果这个找伙伴的过程继续下去,第6天所有的蜜蜂都归巢后,蜂巢中蜜蜂的总只数为( )A.243B.729C.1024D.4096 5. 对于非零向量、,下列命题中正确的是( )A . ⇒=0或B .∥⇒在上的投影为C .⇒2D . ⇒6. 甲、乙、丙、丁四名射击手在选拔赛中的平均环数x 及其标准差s 如下表所示,则选送决赛的最佳人选应是_________.甲 乙 丙 丁 x7 8 8 7 s2.52.52.837. 一组数据12,,18,20,27,23x ,它们的中位数是21,即x 是_______.8. 某市居民2009~2005年家庭年平均收入x (单位:万元)与年平均支出y (单位:万元)的统计资料如下表所示:年份 2005 2006 2007 2008 2009 收入x 11.5 12.1 13 13.3 15 支出y6.88.89.81012根据统计资料,居民家庭年平均收入的中位数是_____,家庭年平均收入与年平均支出有____线性相关关系.9. 某单位为了了解用电量y 度与气温C x ο之间的关系,随机统计了某4天的用电量与当天气温.气温(℃) 14 12 8 6 用电量(度)22263438由表中数据得回归直线方程∧∧∧+=a x b y 中2-=∧b ,据此预测当气温为5℃时,用电量的度数约为____.10.(本小题满分14分)已知角α为第四象限角,且其终边与单位圆交点的横坐标为13. (1)求tan α的值;(2)求22sin 2sin cos 1cos αααα-+的值.11.(本小题满分14分)如图,平行四边形ABCD 中,AB a =u u u r r,AD b =u u u r r ,13CE CB =u u ur u u u r ,23CF CD =u u u r u u u r 。
河北省武邑中学2017-2018学年高一下学期暑假作业物理试题(23) Word版含答案
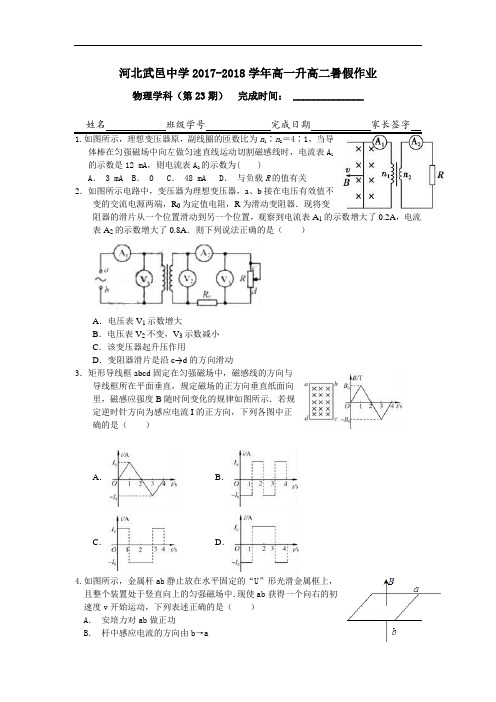
河北武邑中学2017-2018学年高一升高二暑假作业物理学科(第23期)完成时间: ______________ 姓名班级学号完成日期家长签字1.如图所示,理想变压器原,副线圈的匝数比为1∶2=4∶1,当导体棒在匀强磁场中向左做匀速直线运动切割磁感线时,电流表A1的示数是12 mA,则电流表A2的示数为( )A. 3 mA B. 0 C. 48 mA D.与负载R的值有关2.如图所示电路中,变压器为理想变压器,a、b接在电压有效值不变的交流电源两端,R0为定值电阻,R为滑动变阻器.现将变阻器的滑片从一个位置滑动到另一个位置,观察到电流表A1的示数增大了0.2A,电流表A2的示数增大了0.8A.则下列说法正确的是()A.电压表V1示数增大B.电压表V2不变,V3示数减小C.该变压器起升压作用D.变阻器滑片是沿c→d的方向滑动3.矩形导线框abcd固定在匀强磁场中,磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直纸面向里,磁感应强度B随时间变化的规律如图所示.若规定逆时针方向为感应电流I的正方向,下列各图中正确的是()A.B.C.D.4.如图所示,金属杆ab静止放在水平固定的“U”形光滑金属框上,且整个装置处于竖直向上的匀强磁场中.现使ab获得一个向右的初速度v开始运动,下列表述正确的是()A.安培力对ab做正功B.杆中感应电流的方向由b→aC.杆中感应电流逐渐减小D.杆中感应电流保持不变5.如图所示是某种汽车上的一种自动测定油箱内油面高度的装置.R是滑动变阻器.它的金属滑片是杠杆的一端,从油量表(由电流表改装而成)指针所指的刻度,就可以知道油箱内油面的高度,当滑动变阻器的金属滑片向下移动时 ( )A.电路中的电流减小,油箱油面降低B.电路中的电流减小,油箱油面升高C.电路中的电流增大,油箱油面降低D.电路中的电流增大,油箱油面升高6. 光滑曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程为y=x2,其下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属块从抛物线y=b(b>a)处以速度v沿抛物线下滑,假设抛物线足够长,则金属块在曲面上滑动的过程中产生的焦耳热总量是( )A.mgb B.mv2 C.mg(b-a) D.mg(b-a)+mv27.当远距离高压输送一定电功率时,输电线上损耗的功率与电路中的()A.输送电压的平方成正比 B.输送电压的平方成反比C.输电线中电流的平方成正比 D.导线中电流的平方成反比8. .如图所示,一个半径为r的半圆形线圈,以直径ab为轴匀速转动,转速为n,ab的左侧有垂直于纸面向里(与ab垂直)的匀强磁场,磁感应强度为B.M和N是两个集流环,负载电阻为R,线圈、电流表和连接导线的电阻不计,求:(1)从图示位置起转过转的时间内负载电阻R上产生的热量;(2)从图示位置起转过转的时间内通过负载电阻R的电荷量;(3)电流表的示数.9. 两根固定在水平面上的光滑平行金属导轨MN和PQ,一端接有阻值为R=4Ω的电阻,处于方向竖直向下的匀强磁场中.在导轨上垂直导轨跨放质量m=0.5kg的金属直杆,金属杆的电阻为r=1Ω,金属杆与导轨接触良好,导轨足够长且电阻不计.金属杆在垂直杆F=0.5N的水平恒力作用下向右匀速运动时,电阻R上的电功率是P=4W.(1)求通过电阻R的电流的大小和方向;(2)求金属杆的速度大小;(3)某时刻撤去拉力,当电阻R上的电功率为时,金属杆的加速度大小、方向.答案1.B2. D3. C4. C5. D6. D7. BC8..解:(1、3)转速为n,则ω=2πn;s=πr2最大感应电动势E m=BSω;,则因只有一半区域内有磁场,由有效值的计算公式可得:=()2××则有效值E==;则电路中电流I==;从图示位置起转过圈的时间内负载电阻R上产生的热量为I2Rt=;(2)转圈时磁通量的变化量为Φ=BS=B;所用的时间t==;则平均电动势==2nπBr2;电量Q===;答:(1)从图示位置起转过转的时间内负载电阻R上产生的热量为(2)从图示位置起转过转的时间内通过负载电阻R的电荷量为(3)电流表的示数为9.(1)通过电阻R的电流的大小是1A,方向从M到P;(2)金属杆的速度大小是10m/s;(3)当电阻R上的电功率为时,金属杆的加速度大小是0.5m/s2,方向向左【解析】试题分析:(1)根据右手定则判断出电流的方向,根据电功率的公式计算出电流的大小;(2)当到达稳定时,拉力的功率等于电流的电功率,写出表达式,即可求得结果;(3)某时刻撤去拉力,当电阻R上的电功率为时,回路中感应电流产生的安培力提供杆的加速度,写出安培力的表达式与牛顿第二定律的表达式即可.解:(1)根据电功率的公式,得:P=I2R,所以:I=A,由右手定则可得,电流的方向从M到P。
河北省武邑中学2017-2018学年高一上学期周考(12.4)数学试题 Word版含答案

2017-2018学年高一上学期数学周测第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.设()3,4=a ,b 在a 上的投影为4,在x 轴上的投影为2,则b 为( ).A .()14,2B .⎪⎭⎫ ⎝⎛-72,2C .⎪⎭⎫ ⎝⎛-72,2 D .()4,22.对任意两个非零的平面向量α和β,定义αβαβββ︒∙=∙.若平面向量a ,b 满足0a b ≥>,a 与b 的夹角⎪⎭⎫ ⎝⎛∈4,0πθ,且a b ︒和b a ︒都在集合⎭⎬⎫⎩⎨⎧∈Z n n 2中,则a b ︒=( ).A .21B .1C .23D .253.若︒=15sin 2a ,︒=15cos 4b ,a 与b 的夹角为︒30,则b a ∙的值是( ). A .23B .3C .32D .214.在ABC ∆中,︒=∠60BAC ,2=AB ,1=AC ,E ,F 为边BC 的三等分点,则AE AF ∙=( ).A .35B .45C .910D .8155.已知点O ,N ,P 在ABC ∆所在的平面内,且OA OB OC ==,0NA NB NC ++=,PA PB PB PC PC PA ∙=∙=∙,则点O ,N ,P 依次是ABC ∆的( ).A .重心、外心、垂心B .重心、外心、内心C .外心、重心、垂心D .外心、重心、内心6.已知平面上三点A 、B 、C 满足6AB =,8BC =,10CA =,则AB BC BC CA CA AB ∙+∙+∙的值等于( ).A .100B .96C .100-D .96- 7.在ABC ∆中,a ,b ,c 分别为角A ,B ,C 所对应的三角形的边长,若4230aBC bCA cAB ++=,则=B cos ( ). A .2411-B .2411C .3629D .3629-8.半圆的直径4=AB ,O 为圆心,C 是半圆上不同于A 、B 的任意一点,若P 为半径OC 的中点,则()PA PB PC +∙的值是( ).A .2-B .1-C .2D .无法确定,与C 点位置有关9.已知点()0,2-A 、()0,3B ,动点()y x P ,满足2PA PB x ∙=,则点P 的轨迹是( ).A .圆B .椭圆C .双曲线D .抛物线10.在ABC ∆中,点P 在BC 上,且2BP PC =,点Q 是AC 的中点,若()4,3PA =,()1,5PQ =,则BC 等于( ).A .()7,2-B .()21,6-C .()7,2-D .()21,6-11.若平面向量b 与向量()1,2a =-的夹角是︒180,且35b =,则b 等于( ). A .()6,3- B .()6,3- C .()3,6- D .()3,6- 12.已知()0,3-A ,()2,0B ,O 为坐标原点,点C 在AOB ∠内,22=OC ,且4π=∠AOC ,设()OC OA OB R λλ=+∈,则λ的值为( ).A .1B .31C .21D .32第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.在平面直角坐标系中,O 为原点,()0,1-A ,()3,0B ,()0,3C ,动点D 满足1CD =,则OA OB OD ++的最大值是________.14.若等边ABC ∆的边长为32,平面内一点M 满足1263CM CB CA =+,则MA MB ∙=_______.15.已知直角梯形ABCD 中,BC AD //, 90=∠ADC ,2=AD ,1=BC ,P 是腰DC 上的动点,则3PA PB +的最小值为________.16.设1e ,2e 是平面内一组基向量,且122a e e =+,12b e e =-+,则向量12e e +可以表示为另一组基向量,a b 的线性组合,即12e e +=________a +________b . 三、解答题 (本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知点()2,1-A ,()8,2B 以及13AC AB =,13DA BA =-,求点C 、D 的坐标和CD 的坐标.18.已知()1,7A 、()4,1B ,直线ax y 21=与线段AB 交于C ,且2AC CB =,求实数a 的值.19.设两个向量22(2,cos )a λλα=+-和(,sin )2mb m α=+,其中λ、m 、a 为实数,若2a b =,求mλ的取值范围. 20.平面上的两个向量OA ,OB 满足OA a =,OB b =,且O A O B⊥,422=+b a .向量(),OP xOA yOB x y R =+∈,且121212222=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y b x a .(1)如果点M 为线段AB 的中点,求证: 1122MP x OA y OB ⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭;(2)求OP 的最大值,并求此时四边形OAPB 面积的最大值.21.在直角坐标系xOy 中,已知点()1,1A ,()3,2B ,()2,3C ,点()y x P ,在ABC ∆三边围成的区域(含边界)上.(1)若0PA PB PC ++=,求OP ;(2)设(),OP mAB nAC m n R =+∈,用x ,y 表示n m -,并求n m -的最大值.高一数学答案一、选择题1.D2. C3.B4.A5.C6. C7. A8. A9. D 10. B 11. A 12.D 二、填空题13.17+ 14.2- 15. 511-=t 16.32 31- 三、解答题17.设点C ,D 的坐标分别为()11,y x 、()22,y x , 由题意得()111,2AC x y =+-,()3,6AB =,()221,2DA x y =---,()3,6BA =--.因为13AC AB =,13DA BA =-,所以有 ⎩⎨⎧=-=+,22,1111y x 和⎩⎨⎧=-=--,22,1122y x 解得⎩⎨⎧==,4,011y x 和⎩⎨⎧=-=,0,222y x所以点C ,D 的坐标分别是()4,0、()0,2-,从而()2,4CD =-- 18.解析 设()y x C ,,则()7,1AC x y =--,()1,4CB x y =--,①⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛+=-=+∴ααλλsin 22cos 2222m m ② ①代入②消去λ整理得()2941sin 22-+-=-m m α.1sin 1≤≤-α ,()41sin 02≤-≤∴α,从而429402≤-+-≤m m ,由⎪⎩⎪⎨⎧≤-+-≥-+-,4294,029422m m m m 得241≤≤m . 易证m m22-=λ在⎥⎦⎤⎢⎣⎡2,41上是增函数,16≤≤-∴m λ,即[]1,6-∈∴mλ. 19.(1)证明:因为点M 为线段AB 的中点, 所以1122OM OA OB =+. 所以()11112222MP OP OM xOA yOB OA OB x OA y OB ⎛⎫⎛⎫⎛⎫=-=+-+=-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(2)解:设点M 为线段AB 的中点, 则由OA OB ⊥,知112MA MB MO AB ====. 又由(1)及121212222=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y b x a ,得2222222222111112222MP OP OM x OA y OB x a y b ⎛⎫⎛⎫⎛⎫⎛⎫=-=-+-=-+-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭所以1MP MO MA MB ====.故P 、O 、A 、B 四点都在以M 为圆心、1为半径的圆上, 所以当且仅当OP 为圆M 的直径时,max2OP =.这时四边形OAPB 为矩形, 则2222OAPBa b S OA OB ab +=∙=≤=四边形,当且仅当2==b a 时,四边形OAPB 的面积最大,最大值为2. 21.解:(1)方法一:0PA PB PC ++=,又()()()()1,12,33,263,63PA PB PC x y x y x y x y ++=--+--+--=--,⎩⎨⎧=-=-∴,036,036y x 解得 ⎩⎨⎧==,2,2y x 即()2,2OP =,故22OP =. 方法二:0PA PB PC ++=,则()()()0OA OP OB OP OC OP -+-+-=,()()12,23OP OA OB OC ∴=++= 22OP ∴=(2)OP mAB nAC =+,()()n m n m y x ++=∴2,2,,⎩⎨⎧+=+=∴,2,2n m y n m x 两式相减得,x y n m -=-,令t x y =-,由图知,当直线t x y +=过点()3,2B 时,t 取得最大值1,故n m -的最大值为1.。
河北武邑中学2017-2018学年下学期开学考试数学(理科)试卷(附答案) (2)

河北武邑中学2017-2018学年下学期开学考试数学(理科)试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合,,则( )A. B. C. D.【答案】A【解析】由题得(注意分母不能为零),所以,故选A.2. 设常数,集合,,若,则的取值范围为()A. B. C. D.【答案】B【解析】由题得,因为,所以通过画数轴分析得到,(注意一定要取等),故选B.3. 我国古代数学算经史书之一的《九章算术》有一衰分问题:今有北乡八千一百人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,则北乡遣()A. 104人B. 108人C. 112人D. 120人【答案】B【解析】解析:由题设可知这是一个分层抽样的问题,其中北乡可抽取的人数为,则,应选答案B。
4. 在中,角,,所对的边分别为,,,若,则为()A. 等腰三角形B. 直角三角形C. 等腰直角三角形D. 等腰三角形或直角三角形【答案】D【解析】由题得或是等腰三角形或直角三角形. 故选D.5. 若,则()A. B. C. D.【答案】B【解析】由条件得,将上式两边分别平方,得,即,解得或(舍去),∴.选B.6. 已知函数,则不等式的解集为()A. B. C. D.【答案】C【解析】由题意知函数为偶函数,且在上单调递增.由可得,∴,解得.又,即.∴且.故不等式的解集为.选C.7. 设向量,满足,,且,则向量在向量方向上的投影为()A. B. C. D.【答案】D【解析】∵,∴,∴.∴.设向量和向量的夹角为,8. 四面体的各条棱长都相等,为棱的中点,过点作平面平行的平面,该平面与平面、平面的交线分别为、,则,所成角的余弦值为()A. B. C. D.【答案】B【解析】由题意,的所成角即,不妨设棱长为2,则,所以,故选B。
9. 已知函数与,设,,若存在,,使得,则实数的取值范围为()A. B. C. D.【答案】C【解析】因为, ∴f(x)是增函数,f(2)=1+2-3=0,所以.∵存在,,使得,∴.即在[1,3]上有解.设则所以当时,,h(x)是增函数;当时,,f(x)是减函数. ∵,所以,故选C.10. 已知抛物线:上一点,直线:,:,则到这两条直线的距离之和的最小值为()A. B. C. D.【答案】D【解析】由题得直线:是抛物线的准线,设P到直线的距离为PA,点P到直线的距离为PB,所以到这两条直线的距离之和为|PA|+|PB|=|PF|+|PB|,当P,B,F三点共线时,距离之和最小. 此时,最小值为,故选D.点睛:本题的关键是看到|PA|要联想到抛物线的定义,抛物线上的点到焦点的距离等于它到准线的距离,所以|PA|=|PF|,后面就迎刃而解了. 在圆锥曲线里,一般情况下,只要看到焦半径就要想到圆锥曲线的定义,这是一个一般的规律.11. 过双曲线的右支上一点,分别向圆:和圆:()作切线,切点分别为,,若的最小值为58,则()A. B. C. D.【答案】B【解析】设是双曲线的左、右焦点,也是题中圆的圆心,所以,显然其最小值为,,故选B.12. 已知函数在上的最大值为5,则实数的取值范围是()A. B. C. D.【答案】D【解析】当x≥0时,,∴是减函数,时,f(x)是增函数,由于f(0)=1,f(2)=5,所以函数f(x)在[0,2]的最大值为5,所以在[-2,0]的最大值必须小于等于5,∴,故选D.点睛:本题的关键是逻辑分析出思路,根据题意分析出在[-2,0]的最大值必须小于等于5,得到这个恒等式,再转化这个恒等式.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知,,则__________;满足的实数的取值范围是__________.【答案】(1). ;(2).【解析】(1),所以;(2),解得的取值范围是。
河北省武邑中学2017-2018学年高一上学期周考(10.9)数学试题 Word版含答案
数学试题第Ⅰ卷(共60分)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知有理数,,a b c 在数轴上的位置如图所示,化简a b c b +--的结果是( )A . a c +B . c a -C .c a --D .2a b c +-2. 如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为2280,100cm cm ,且甲容器装满水,乙容器是空的,若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了 8cm , 则甲的容积是( )A .31280cmB .32560cmC .33200cmD .3400cm 3. 观察下列算式,1234567822,24,28,216,232,264,2128,2256========,…用你所发现的规律得出20102的末位数字是( )A .2B .4C .6D .8 4. 如果2x =是方程112x a +=-的解, 那么a 的值是( )A .0B .2C .2-D .6- 5. 方程21123x x -+-=去分母得( ) A . ()()13221x x --=+ B .()()62231x x --=+ C .()()63221x x --=+ D .63622x x --=+6. 在()11,1,0,4,3,1,0842⎛⎫⎛⎫------++--- ⎪ ⎪⎝⎭⎝⎭,这几个有理数中,负数的个数是( ) A .5个 B .4个 C . 3个 D .2个7. 对于有理数,a b ,如果0,0ab a b <+<,则下列各式成立的是( )A .0,0a b <<B .0,0a b b a >><且C .0,0a b a b >><且D .0,0a b b a ><>且 8. 若()2320m n -++=,则2m n +的值为( )A . 4-B .1-C .0D .49. 一个两位数, 个位数字与十位数字的和是9,如果将个位数字与十位数字对调后所得的新数比原数大9,则原来的两位数为( )A .54B .27C .72D .4510. 解方程12110.30.7x x +--=时, 可变形为( ) A .10102010137x x +--= B .101201137x x +--= C .1012011037x x +--= D .101020101037x x +--= 11. 方程()515x -=的解是( )A . 1x =B .2x =C .3x =D .4x = 12. 如果5126x -⎛⎫-⎪⎝⎭的倒数是3,那么x 的值是( ) A .3- B . 1- C .1 D .3 13. 如图是我市十二月份某一天的天气预报,该天最高气温比最低气温高( )A .7CB . 3C C .3C -D .7C -14. 中国人民银行宣布,从2007年6月5日起,上调人民币存款利率, 一年定期存款利率上调到003.06,某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除0020的利息税). 设到期后银行应向储户支付现金x 元,则所列方程正确的是( ) A .0050005000 3.06x -=⨯ B . ()000050002050001 3.06x +⨯=⨯+C .()0000005000 3.062050001 3.06x +⨯⨯=⨯+D .0000005000 3.06205000 3.06x +⨯⨯=⨯15. 若关于x 的一元一次方程23132x k x k---=的解为1x =-,则k 的值为( ) A .27 B . 1 C . 1311- D .0第Ⅱ卷(共90分)二、填空题(将答案填在答题纸上)16. 定义一种新运算:14a b a b ⊗=-, 那么()41⊗-= .17. 若4y =,则yx= .18. 用字母表示有理数的加法运算律: (1)交换律 ; (2)结合律 .19. 若5,1a b ==,且0a b -<,则a b +的值等于 . 20. 填空:()a b c +-+= .三、解答题 (解答应写出文字说明、证明过程或演算步骤.)21.如图,E 是矩形ABCE 的边BC 上一点,,EF AE EF ⊥ 分别交,AC CD 于点,,M F BG AC ⊥,垂足为,G BG 交AE 于点H .(1)求证:;ABEECF ∆∆(2)找出与ABH ∆相似的三角形, 并证明;(2)若E 是BC 中点,2,2BC AB AB ==, 求EM 的长.22. 观察下列各式:33221112492344+=⨯⨯=⨯⨯;3332211123369163444++==⨯⨯=⨯⨯;33332211123410016254544+++==⨯⨯=⨯⨯.(1)计算:3333312345++++ 的值; (2)计算:333331234...10+++++ 的值; (3)猜想: 333331234...n +++++ 的值.23. 3201420103-⎛⎫++ ⎪⎝⎭24. 人体中成熟的红细胞的平均直径为0.0000077米,用科学记数法表示为米. 25. 计算或化简:计算()01126020112π-+-+-.河北省武邑中学2017-2018学年高一上学期周考(10.9)数学试题参考答案一、选择题(每小题5分,共60分)1-5.ACBCC 6-10.ADBDA 11-15.BDACB 二、填空题(每小题5分,共20分)16.2 17.16 18. (1)a b b a +=+;(2)()()a b c a b c ++=++ 19.4- 或6- 20.a b c -+ 三、解答题21.解:(1)证明四边形ABCD 是矩形,90ABE ECF ∴∠=∠=,,90AE EF AEB FEC ⊥∠+∠=,90,,AEB BAE BAE CEF ABEECF ∴∠+∠=∴∠=∠∴∆∆..(2)ABH ECM ∆∆,证明:,,BG AC ABH CEM ABH CEM ⊥∴∠=∠∴∆=∠, 由(1)知,ABH ECM ∴∆∆.(3)作MR BC ⊥,垂足为R ,12,::,45,45,22AB BE EC AB BC MR RC AEB MER CR MR===∴==∠=∴∠==,1122333MR ER EC ∴===⨯=,∴在Rt EMR ∆中,sin 453MR EM ==23. 解: 32014201027161443-⎛⎫++=++= ⎪⎝⎭.24. 解:67.710-⨯科学记数法的形式为10a ⨯,且a 的绝对值大于等于1小于10,0.0000077变为7.7小数点右移6位所以然6,即答案为. 25. 解: ()01126020112π-+-+-111113112222=+=-++=-.。
河北省武邑中学2017-2018学年高二下学期暑假作业数学文试题(10) Word版含答案
2017-2018学年暑假作业10姓名 班级学号完成日期 家长签字一:选择题 1已知函数,那么=A.1B.1.5C.D.42.直线20cos 20sin 3{t y t x -=+=(t 为参数)的倾斜角( )A.20 B. 70 C. 110 D. 160数,()2f a =,则()f a -的值为 . 3.已知函( )A. 1B. 0C. -1D. -24.参数方程αααα(,sin 22cos2sin ⎪⎩⎪⎨⎧+=+=y x 为参数)的普通方程为()A. 122=-x y B. 122=-y x C. )2|(|122≤=-x x y D. )2|(|122≤=-x y x5..给出下列(1)实数的共轭复数一定是实数;(2)满足2z i z i -++=的复数z 的轨迹是椭圆; (3)若2,1m Z i ∈=-,则1230;m m m m i i i i ++++++=(4)若“a ,b ,c 是不全相等的实数”,则0)()()(222≠-+-+-a c c b b a ; (5) 若“a ,b ,c 是不全相等的实数”, a c c b b a ≠≠≠,,不能同时成立 其中正确的序号是( ) A.(1)(2)(3) B.(1)(3)(4) C.(2)(3)(5) D.(3)(4)(5)二.填空题()()22ln e 11x f x x x =+-+6.从1,2,3,4,5,6,7中任取两个不同的数,事件A 为“取到的两个数的和为偶数”,事件B 为“取到的两个数均为偶数",则)(A B P =__________.7.在平面内,三角形的面积为S ,周长为C ,则它的内切圆的半径r=.在空间中,三棱锥的体积为V ,表面积为S ,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R= . 三.解答题8. 设平面直角坐标系原点与极坐标极点重合,x 轴正半轴与极轴重合,若已知曲线C 的极坐标方程为222123cos 4sin ρθθ=+,直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧=+=ty t x 22221(t 为参数,t ∈R ) (1)求曲线C 的标准方程和直线l 的普通方程(2)若点P 为曲线C 上的动点,求点P 到直线l 的最大距离.(3)9. 观察下题的解答过程:已知正实数b a ,满足1=+b a ,求1212+++b a 的最大值解:23221221222+=++≤⋅+a a a ,23221221222+=++≤⋅+b b b相加得43)1212(2212212=++≤+++=⋅++⋅+b a b a b a221212≤+++∴b b ,等号在21==b a 时取得, 即1212+++b a 的最大值为22. 请类比上题解法,使用综合法证明下题:已知正实数z y x ,,满足2=++z y x ,求证:121212+++++z y x 21≤10. 设函数()f x ,()g x 的定义域均为R ,且()f x 是奇函数,()g x 是偶函数,()()e x f x g x +=,其中e 为自然对数的底数.(1)求()f x ,()g x 的解析式,并证明:当0x >时,()0f x >,()1g x >;(2)设0a ≤,1b ≥,证明:当0x >时,()()(1)()(1)f x ag x a bg x b x+-<<+-.参考答案1. C2. C3. B4. C5. B6. 13 7.8. (I )曲线C 的极坐标方程为ρ2= ,化为直角坐标方程:3x 2+4y 2=12,即=1.(3分)直线l 的参数方程为(t 为参数,t ∈R ),化为普通方程:x ﹣1﹣y=0(6分)(II )设P (2cos θ,3sinθ),θ∈[0,2π),则点P 到直线l 的距离d==≤=,其中α=arctan.∴点P 到直线l 的最大距离是.(12分)9.:3523712371222+=++≤⋅+x x x3523712371222+=++≤⋅+y y y3523712371222+=++≤⋅+z z z相加得7537)121212(=+++≤⋅+++++z y x z y x 即21737121212=⋅≤+++++z y x ,等号在32===z y x 时取得10. (Ⅰ)由()f x , ()g x 的奇偶性及()()e x f x g x +=,得:()()e .x f x g x --+=联立①②解得1()(e e )2x x f x -=-,1()(e e )2x x g x -=+.(3分)当0x >时,e 1x >,0e 1x -<<,故()0.f x > 又由基本不等式,有1()(e e )12x x g x -=+,即() 1.g x > (5分)(Ⅱ)由(Ⅰ)得 2111e 1()(e )(e )(e e )()2e 2e 2x x x x x x x f x g x -''=-=+=+=,2111e 1()(e )(e )(e e )()2e 2e 2xx x x x x x g x f x -''=+=-=-= ,当0x >时,()()(1)f x ag x a x >+-等价于()()(1)f x axg x a x >+-,()()(1)f x bg x b x<+-等价于()()(1).f x bxg x b x <+- ④设函数 ()()()(1)h x f x cxg x c x =---,其中c 为常数且c ≤0或c ≥1 由①②,有()()()()(1)h x g x cg x cxf x c '=----(1)[()1]().c g x cxf x =--- 因为0x >,则若0c ≤,由(1)问结论易得()0h x '>,故()h x 在[0,)+∞上为增函数,从而()(0)0h x h >=,即()()(1)f x cxg x c x >+-,故③式成立.若1c ≥,由(1)问结论得()0h x '<,故()h x 在[0,)+∞上为减函数,从而()(0)0h x h <=,即()()(1)f x cxg x c x <+-,故④成立.综合③④,得 ()()(1)()(1)f x ag x a bg x b x+-<<+-.。
河北省武邑中学2017-2018学年高二下学期暑假作业数学文试题(8) Word版含答案
2017-2018学年暑假作业8 姓名 班级学号 完成日期 家长签字一 、选择题1.已知集合{}{},,,,5313,2,1==B A 则=⋂B A ( ) A.{}31, B.{}21, C.{}532,1,, D.{}531,,2.若,032,:0200≤++∈∃x x R x p 则p 的否定p ⌝是( )A.032,2>++∈∀x x R xB. 032,2≥++∈∀x x R xC.032,2>++∉∀x x R x .D. 032,2>++∈∃x x R x3.若R a ∈,则"3">a 是"09"2>-a 的( ) A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件4. 曲线2ax y =在点),1(a 处的切线与直线062=--y x 垂直,则a 等于( )A.1B.41C.41- D.1- 5. 若关于x 的不等式a a x x 3132->--+的解集不空,则实数a 的范围是( )A .()(),14,-∞-+∞B .()1,4-C .()(),41,-∞-+∞D .()4,1-二、填空题6. 已知{}{}0,21>-=≤-=a x x B x x A ,若B B A =⋃,则实数a 的取值范围是 .7.已知,,0)1()12(:,0132:22≤+++-≤+-a a x a x q x x p 若q ⌝是p ⌝的充分不必要条件,则实数a 的取值范围是 .三、解答题8. 已知下面两个::p x R ∃∈使210x ax -+=;:q x R ∀∈,都有 220x x a -+>.若p q ∧是真,求实数的取值范围.9. 在平面直角坐标系xOy 中,斜率为1的直线l 过定点)4,2(--.以O 为极点,x 轴非负半轴为极轴建立极坐标系.已知曲线C 的极坐标方程为.0cos 4sin2=-θθρ (1)求曲线C 的直角坐标方程以及直线l 的参数方程; (2)两曲线相交于N M ,两点,若),,(4-2-P 求PN PM +的值.10. 已知c b a ,,为正数,且.1=++c b a (1)求cb a 111++的最小值; (2)求111++的最小值.答案1-5:AAACB 6. 13.)1,(--∞ 7. ]21,0[ 8. 解::p x R ∃∈使210x ax -+=为真,则240a ∆=-≥解得:2a ≥或2a ≤-;:q x R ∀∈,都有220x x a -+>为真,则440a ∆=-< 解得1a >当p q ∧是真时,需p 真且q 真,所以实数a 的取值范围是2a ≥.9.(12分)(1),4:2x y C =)(224222:为参数t t y t x l ⎪⎪⎩⎪⎪⎨⎧+-=+-=(6分) (2)212(6分)10.(12分)(1)9(6分)(2)1(6分)。
河北省武邑中学2017-2018学年高一上学期周考(11.20)数学试题 Word版含答案
2017-2018学年 数学试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.设全集{}1,2,3,4,5,6U =,集合{}2A =1,,{}2,3B =,则()U A C B =( )A .{}2B .{}4,5C .{}2,3D .{}1 2.cos510︒的值为( ) A .12 B .12- C3.已知角α的终边经过点()3,4P -,则sin α的值等于( ) A .35- B .35 C .45 D .45- 4.下列四组函数中,表示同一函数的是( ) A .()2log 2xf x =,()g x =.()f x =()g x x =C. ()f x x =, ()2x g x x= D .()2ln f x x =,()2ln g x x =5.若()sin 0πθ-<,()tan 0πθ+>,则θ的终边在( )A .第一象限B .第二象限 C.第三象限 D .第四象限 6.若cos 0θ<,且cos sin θθ-=,那么θ的( )A .第一象限角B .第二象限角 C.第三象限角 D .第四象限角7.设函数()()()240,log 0,x x f x x ⎧≤⎪=⎨>⎪⎩则()()1f f -的值为( )A .2B .1 C.-1 D .28.一项实验中获得的一组相关变量,y t 之间的数据整理后得到如图所示的散点图,下列函数中可以近似刻画与之间关系的最佳选择是( )A .t y a =B .log a y t = C.3y at = D .y = 9.设()cos 80m -︒=,那么tan100︒=( )AB . D .10.函数()2sin f x x x m =++,,33x ππ⎡⎤∈-⎢⎥⎣⎦有零点,则m 的取值范围是( )A .)⎡+∞⎣B .(,-∞ C.((),23,-∞+∞D .⎡-⎣11.函数()f x 满足对定义域内的任意x ,都有()()()221f x f x f x ++<+,则函数()f x 可以是( )A .()ln f x x =B .()22f x x x =- C.()xf x e =D .()21f x x =+12.设()f x 是定义在R 上的偶函数,对任意的x R ∈,都有()()22f x f x -=+,且当[]2,0x ∈-时,()112xf x ⎛⎫=- ⎪⎝⎭,则在区间(]2,6-内关于x 的方程()()2log 20f x x -+=的根的个数为( )A .1B .2 C.3 D .4第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知tan 2α=,则2cos α= .14.一个半径为R 的扇形,周长为4R ,则这个扇形的面积是 .15.函数13xy ⎛⎫= ⎪⎝⎭的值域为 .16.如图,过原点O 的直线与函数2xy =的图像交于A B 、两点,过B 作y 轴的垂线交函数4x y =的图像于点C ,若AC 平行于y 轴,则点A 的坐标为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分12分) 已知角x 的终边经过点()1,3P -. (Ⅰ)求sin cos x x +的值;(Ⅱ)求()()sin cos 22cos cos x x x x πππ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭--的值.18. (本小题满分12分) (1)已知()1cos 2πα+=-,α为第一象限角,求1cos 22πα⎛⎫+=- ⎪⎝⎭; (2)已知1cos 63πα⎛⎫-=⎪⎝⎭,求52cos sin 63ππαα⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭的值. 19. (本小题满分12分)sin α,cos α为方程244210x mx m -+-=的两个实根,,02πα⎛⎫∈- ⎪⎝⎭,求m 及α的值.20. (本小题满分12分)已知函数()()2lg 1f x x =+和()()lg 21g x x =+(t 为常数). (1)求函数()f x 的定义域;(2)若[]0,1x ∈时,()g x 有意义,求实数t 的取值范围;(3)若存在[]0,1x ∈,使得()()f x g x ≤成立,求实数t 的取值范围. 21. (本小题满分12分)销售甲、乙两种商品所得利润与投入资金x (万元)的关系分别为()f x a =+,()g x bx =(其中,,m a b R ∈),函数()f x 、()g x 对应的曲线分别为1C 、2C ,如图所示.(Ⅰ)求函数()f x 与()g x 的解析式;(Ⅱ)若该商场一共投资4万元经销甲、乙两种商品,求该商场所获利润的最大值.试卷答案一、选择题1-5:DCCAC 6-10:CDBBD 11、12:AD 二、填空题 13.1514.2R 15.(]0,1 16.()1,2 三、解答题17.(Ⅰ)由点()1,3P -在角x的终边上,得sin x =,cos x =sin cos x x +=∴(Ⅱ)()()()sin cos cos sin 22tan cos cos cos cos x x x x x x x x x πππ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭==----18.试题解析:(1)()1cos cos 2παα+=-=-1cos 2α=∴,又α为第一象限角,则cos sin 2παα⎛⎫+=-=== ⎪⎝⎭111sin cos 326369πππαα⎡⎤⎛⎫⎛⎫=---=--=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.考点:(1)诱导公式(2)两角和与差的正余弦函数19.解:sin α,cos α为方程244210x mx m -+-=的两个实根2210m m -+≥∴且sin cos m αα+=,21sin cos 4m αα-=,代入()2sin cos 12sin cos αααα+=+,得m =又,02πα⎛⎫∈-⎪⎝⎭.21sin cos 04m αα-=<∴,sin cos m αα+==,sin α=∴,1cos 2α=, 又,02πα⎛⎫∈-⎪⎝⎭,3πα=-∴,m =∴3πα=-. 20.解:(1)由10x +>得1x >-()f x ∴的定义域为()1,-+∞(2)依题意[]0,1x ∈时,20x t +>恒成立,即2t x >-恒成立 又20x -≤故t 的取值范围是()0,+∞. (3)当[]0,1x ∈时,()()()()()222lg 1lg 2121f x g x x x t x x t x ≤⇔+≤+⇔+≤+⇔+依题意存在[]0,1x ∈使得21t x ≥+ 又2112x ≤+≤1t ≥∴,同时满足0t >使()g x 在[]0,1x ∈时有意义故t 的取值范围是[)1,+∞21.解:(1)由题意0835m a m a +=⎧⎪⎨+=⎪⎩,解得45m =,45a =-, ()()405f x x =≥∴. 又由题意885b =得15b =()()105g x x x =≥∴(2)设销售甲商品投入资金x 万元,则乙投入()4x -万元 由(1)得()41455y x =+-,()04x ≤≤t =,(1t ≤≤则有()2214121555y t t t =-+=--+,(1t ≤≤,当2t =即3x =时,y 取最大值1.∴该商场所获利润的最大值为1万元.。
