选修1-1课件:3.1.3 导数的几何意义
合集下载
人教B版选修1-1高中数学3.1.3《导数的几何意义》ppt课件

本 答案 曲线 f(x)在点(x0,f(x0))处的切线,点(x0,f(x0))一定是
专 题
切点,只要求出 k=f′(x0),利用点斜式写出切线即可;
栏 目
而曲线 f(x)过某点(x0,y0)的切线,给出的点(x0,y0)不一定
开 关
在曲线上,
即使在曲线上也不一定是切点.
填一填 研一研 练一练
研一研·问题探究、课堂更高效
∴y′|x=1=2.
∴曲线在点 P(1,1)处的切线方程为 y-1=2(x-1),即 y=2x-1.
3.1.3
填一填 研一研 练一练
研一研·问题探究、课堂更高效
3.1.3
(2)点 P(3,5)不在曲线 y=x2 上,设切点为(x0,y0)
由(1)知,y′| xx0 =2x0, ∴切线方程为 y-y0=2x0(x-x0),
从图中可以看出,直线 l1 的倾斜程度小于直线 l2 的倾斜程度,这 说明曲线 h(t)在 t1 附近比在 t2 附近下降得缓慢.
研一研·问题探究、课堂更高效
3.1.3
填一填 研一研 练一练
小结 导数与函数图象升降的关系:
若函数 y=f(x)在 x=x0处的导数存在且 f′(x0)>0(即切线的斜
本 由 P(3,5)在所求直线上得 5-y0=2x0(3-x0)
①
专
题 栏
再由 A(x0,y0)在曲线 y=x2 上得 y0=x02
②
目 开
联立①,②得,x0=1 或 x0=5.
关 从而切点 A 的坐标为(1,1)或(5,25)
当切点为(1,1)时,
切线的斜率为 k1=2x0=2, 此时切线方程为 y-1=2(x-1),
=0,则
高中数学新人教B版选修1-1第三章导数及其应用3.1.3导数的几何意义课件

第三章 §3.1 导 数
3.1.3 导数的几何意义
学习目标
XUEXIMUBIAO
1.了解导函数的概念,理解导数的几何意义. 2.会求简单函数的导函数. 3.根据导数的几何意义,会求曲线上某点处的切线方程. 4.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.
内容索引
NEIRONGSUOYIN
解析 设点 P(x0,2x20+4x0),
则 f′(x0)= lim Δx→0
fx0+Δx-fx0 Δx
= lim Δx→0
2Δx2+4Δx0x·Δx+4Δx=4x0+4,
令4x0+4=16,得x0=3,∴P(3,30).
12345
课堂小结
KETANGXIAOJIE
1.导数 f′(x0)的几何意义是曲线 y=f(x)在点(x0,f(x0))处切线的斜率,即 k=
线上,则以该点为切点的切线方程为y-f(x0)=f′(x0)(x-x0);若已知点不在 切线上,则应先设出切点(x0,f(x0)),表示出切线方程,然后求出切点.
∴x0=2,∴P(2,8+a). 将x=2,y=8+a代入到8x-y-15=0中,
得a=-7.
反思感悟 利用导数的几何意义将数与形联系起来,根据图象中切线与割线 的倾斜角的大小确定数据的大小.
f2-f1 跟踪训练 4 (1)已知函数 f(x)在 R 上可导,其部分图象如图所示,设
2-1
=a,则下列不等式正确的是
则12a-23a·|a3|=16, 解得a=±1.
核心素养之直观想象
HEXINSUYANGZHIZHIGUANXIANGXIANG
求切线倾斜角的范围
典例 已知点 P 在曲线 y=x3-x+32上,直线 l 为曲线在 P 点处的切线,求直 线 l 的倾斜角的取值范围.
3.1.3 导数的几何意义
学习目标
XUEXIMUBIAO
1.了解导函数的概念,理解导数的几何意义. 2.会求简单函数的导函数. 3.根据导数的几何意义,会求曲线上某点处的切线方程. 4.正确理解曲线“过某点”和“在某点”处的切线,并会求其方程.
内容索引
NEIRONGSUOYIN
解析 设点 P(x0,2x20+4x0),
则 f′(x0)= lim Δx→0
fx0+Δx-fx0 Δx
= lim Δx→0
2Δx2+4Δx0x·Δx+4Δx=4x0+4,
令4x0+4=16,得x0=3,∴P(3,30).
12345
课堂小结
KETANGXIAOJIE
1.导数 f′(x0)的几何意义是曲线 y=f(x)在点(x0,f(x0))处切线的斜率,即 k=
线上,则以该点为切点的切线方程为y-f(x0)=f′(x0)(x-x0);若已知点不在 切线上,则应先设出切点(x0,f(x0)),表示出切线方程,然后求出切点.
∴x0=2,∴P(2,8+a). 将x=2,y=8+a代入到8x-y-15=0中,
得a=-7.
反思感悟 利用导数的几何意义将数与形联系起来,根据图象中切线与割线 的倾斜角的大小确定数据的大小.
f2-f1 跟踪训练 4 (1)已知函数 f(x)在 R 上可导,其部分图象如图所示,设
2-1
=a,则下列不等式正确的是
则12a-23a·|a3|=16, 解得a=±1.
核心素养之直观想象
HEXINSUYANGZHIZHIGUANXIANGXIANG
求切线倾斜角的范围
典例 已知点 P 在曲线 y=x3-x+32上,直线 l 为曲线在 P 点处的切线,求直 线 l 的倾斜角的取值范围.
人教新课标A版高二数学《选修1-1》3.1.3 导数的几何意义

1-x03=3x02(1-x0),即2x03-3x02+1=0,解得x0=1或
x0=- 1 .
2 3 故所求的切线方程为y-1=3(x-1)或y-1= 4
(x-1),
即3x-y-2=0或3x-4y+1=0.
题目类型二、求切点的坐标
【技法点拨】
求切点坐标的五个步骤
(1)先设切点坐标(x0,y0); (2)求导函数f′(x); (3)求切线的斜率f′(x0); (4)由斜率间的关系列出关于x0的方程,解方程求x0; (5)点(x0,y0)在曲线f(x)上,将(x0,y0)代入求y0得切点坐标.
【典例训练】 1.曲线f(x)=x3+x-2在P0处的切线平行于直线y=4x-1, 则点P0的坐标为( ) (A)(1,0) (C)(2,8) (B)(1,0)和(-1,-4) (D)(2,8)和(-1,-4)
这个概念:(1)提供了求曲线上某点切线的斜率的
一种方法;(2)说明了切线斜率的本质——函数在
x=x0处的导数.
2.“函数f(x)在点x0处的导数”、“导函数”、 “导数”之间的区别与联系 (1)区别 ①函数在一点处的导数,就是在该点附近的函数 值的改变量与自变量的改变量之比的极限,它是 一个常数,不是变量. ②函数的导数,是对某一区间内任意点x而言的, 就是函数f(x)的导函数f′(x).
y x
y =tanβ.显然, x 是割线PQ的斜
率.我们发现,当点Q沿着曲线无限接近点P即Δx→0时,
割线PQ有一个极限位置PT.则我们把直线PT称为曲
线在点P处的切线.设切线的倾斜角为α,那么当Δx→0
时,割线PQ的斜率称为曲线在点P处ห้องสมุดไป่ตู้切线的斜率.
高中数学选修1-1.3.1.3导数的几何意义(PPT课件)人教版

ห้องสมุดไป่ตู้
例3:证明:(1)可导的偶函数的导函数为奇函数; (2)可导的奇函数的导函数为偶函数. 证:(1)设偶函数f(x),则有f(-x)=f(x).
f ( x x ) f ( x ) 函 数y f ( x )可 导, lim f ( x ). x 0 x f ( x x ) f ( x ) f ( x x ) f ( x ) f ( x ) lim lim x 0 x 0 x x f ( x x ) f ( x ) lim f ( x ). x 0 x
3
P
y |x2 22 4.
x
-2 -1
即点P处的切线的斜率等于4.
O -1 -2
1
2
(2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.
例2:设函数f(x)在点x0处可导,求下列各极限值:
(1) lim
x 0
f ( x 0 x ) f ( x 0 ) f ( x0 h) f ( x0 h) ; ( 2) lim . h 0 x 2h
导数的概念
3.1 导数的几何意义
1.曲线的切线 如图,曲线C是函数y=f(x) y 的图象,P(x0,y0)是曲线C上的 任意一点,Q(x0+Δ x,y0+Δ y) 为P邻近一点,PQ为C的割线, PM//x轴,QM//y轴,β为PQ的 倾斜角. 则 : MP x , MQ y, O y tan . x y 表明: 就是割线的斜率 . x
1
y
M
求曲线在某点处的切线方程 的基本步骤:先利用切线斜率 的定义求出切线的斜率,然后 利用点斜式求切线方程.
例3:证明:(1)可导的偶函数的导函数为奇函数; (2)可导的奇函数的导函数为偶函数. 证:(1)设偶函数f(x),则有f(-x)=f(x).
f ( x x ) f ( x ) 函 数y f ( x )可 导, lim f ( x ). x 0 x f ( x x ) f ( x ) f ( x x ) f ( x ) f ( x ) lim lim x 0 x 0 x x f ( x x ) f ( x ) lim f ( x ). x 0 x
3
P
y |x2 22 4.
x
-2 -1
即点P处的切线的斜率等于4.
O -1 -2
1
2
(2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.
例2:设函数f(x)在点x0处可导,求下列各极限值:
(1) lim
x 0
f ( x 0 x ) f ( x 0 ) f ( x0 h) f ( x0 h) ; ( 2) lim . h 0 x 2h
导数的概念
3.1 导数的几何意义
1.曲线的切线 如图,曲线C是函数y=f(x) y 的图象,P(x0,y0)是曲线C上的 任意一点,Q(x0+Δ x,y0+Δ y) 为P邻近一点,PQ为C的割线, PM//x轴,QM//y轴,β为PQ的 倾斜角. 则 : MP x , MQ y, O y tan . x y 表明: 就是割线的斜率 . x
1
y
M
求曲线在某点处的切线方程 的基本步骤:先利用切线斜率 的定义求出切线的斜率,然后 利用点斜式求切线方程.
高中数学人教版选修1-1 3.1.3导数的几何意义 课件1

(2)两者的联系:在 x=x0 处的导数 f′(x0)是导函数 f′(x) 在 x=x0 处的函数值,因此求函数在某一点处的导数.
课堂互动
1.导数几何意义的理解
例题 1 若函数 y=f(x)的导函数在区间[a,b]上是增函数,则函数 y =f(x)在区间[a,b]上的图象可能是( )
【思路探究】 (1)导数的几何意义是什么?(2)y=f(x)的导 函数在区间[a,b]上是增函数,说明 y=f(x)图象的切线有什么 特点?
重点难点
重点:导数的几何意义,求曲线上过一点处的切线方程. 难点:“以直代曲”的数学思想方法;以及切线定义的理 解——在每处“附近”变化率与瞬时变化率的近似关系的理 解.
教学设计
教学建议
为了更好的完成本节课的教学目标,帮助学生理解本节课 内容,突出重点,突破难点,宜设计了如下的教法和学法:
(1)教学设计:探讨教学法,即教师通过问题→诱导→演示 →讨论→探索结果→归纳总结.
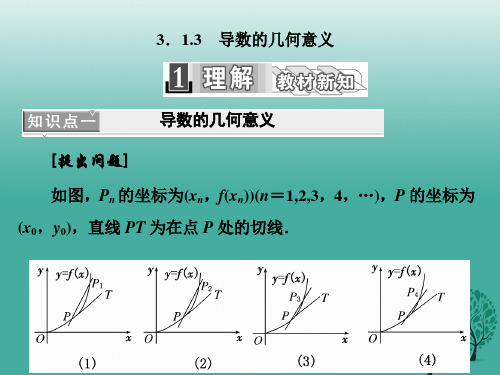
【提示】 点 Pn 趋近于点 P 时,割线 PPn 趋近于过点 P 的 切线 PT.
3.第 2 题图中割线 PPn 的斜率 kn=fxxnn--xf0x0,当点 Pn 无 限趋近于点 P 时,此斜率与切线 PT 的斜率有何大小关系?
【提示】 kn 无限趋近于切线 PT 的斜率.
1.设点 P(x0,f(x0)),Pn(xn,f(xn))是曲线 y=f(x)上不同的点, 当点 Pn(xn,f(xn))(n=1,2,3,4…)沿着曲线 f(x)趋近于点 P(x0,f(x0)) 时,割线 PPn 趋近于确定的位置,这个确定位置的直线 PT 称为 过点 P 的 切线 ,且 PT 的斜率 k=lixn→m x0 fxxnn--fxx00= f′(x0) .
课堂互动
1.导数几何意义的理解
例题 1 若函数 y=f(x)的导函数在区间[a,b]上是增函数,则函数 y =f(x)在区间[a,b]上的图象可能是( )
【思路探究】 (1)导数的几何意义是什么?(2)y=f(x)的导 函数在区间[a,b]上是增函数,说明 y=f(x)图象的切线有什么 特点?
重点难点
重点:导数的几何意义,求曲线上过一点处的切线方程. 难点:“以直代曲”的数学思想方法;以及切线定义的理 解——在每处“附近”变化率与瞬时变化率的近似关系的理 解.
教学设计
教学建议
为了更好的完成本节课的教学目标,帮助学生理解本节课 内容,突出重点,突破难点,宜设计了如下的教法和学法:
(1)教学设计:探讨教学法,即教师通过问题→诱导→演示 →讨论→探索结果→归纳总结.
【提示】 点 Pn 趋近于点 P 时,割线 PPn 趋近于过点 P 的 切线 PT.
3.第 2 题图中割线 PPn 的斜率 kn=fxxnn--xf0x0,当点 Pn 无 限趋近于点 P 时,此斜率与切线 PT 的斜率有何大小关系?
【提示】 kn 无限趋近于切线 PT 的斜率.
1.设点 P(x0,f(x0)),Pn(xn,f(xn))是曲线 y=f(x)上不同的点, 当点 Pn(xn,f(xn))(n=1,2,3,4…)沿着曲线 f(x)趋近于点 P(x0,f(x0)) 时,割线 PPn 趋近于确定的位置,这个确定位置的直线 PT 称为 过点 P 的 切线 ,且 PT 的斜率 k=lixn→m x0 fxxnn--fxx00= f′(x0) .
高中数学3.1.3导数的几何意义课件新人教A版选修1-1
∴ΔΔxy=3x02+2ax0-9+(3x0+a)Δx+(Δx)2.
lim
Δx→0
ΔΔxy=3x20+2ax0-9,
7.导数的几何意义理解的误区 [典例] 已知曲线 y=2x2-7,求曲线过点 P(3,9)的切线方程.
[随堂即时演练]
1.设 f′(x0)=0,则曲线 y=f(x)在点(x0,f(x0))处的切线 ( )
A.不存在
B.与 x 轴平行或重合
C.与 x 轴垂直
D.与 x 轴斜交
解析:f′(x0)=0,说明曲线 y=f(x)在点(x0,f(x0))处的切线斜率为 0, 所以与 x 轴平行或重合. 答案:B
导数几何意义的综合应用
[例 3] 设函数 f(x)=x3+ax2-9x-1(a<0),若曲线 y=f(x)的 斜率最小的切线与直线 12x+y=6 平行,求 a 的值.
[解] ∵Δy=f(x0+Δx)-f(x0) =(x0+Δx)3+a(x0+Δx)2-9(x0+Δx)-1-(x30+ax02-9x0-1) =(3x20+2ax0-9)Δx+(3x0+a)(Δx)2+(Δx)3,
3.1.3 导数的几何意义))(n=1,2,3,4,…),P 的坐标为 (x0,y0),直线 PT 为在点 P 处的切线.
导函数
[提出问题]
已知函数 f(x)=-x2+2.
问题 1:如何求 f′(x0)?
提示:f′(x0)=Δlixm→0
-x0+Δx2+2--x20+2 Δx
=Δlixm→0 (-2x0-Δx)=-2x0.
问题 2:若 x0 是一变量 x,f′(x)是常量吗?
提示:f′(x)=-2x,说明 f′(x)不是常量,而是关于 x 的
函数.
高中数学人教A版选修1-1课件3-1-3导数的几何意义2
点(题型三),都是导数几何意义的直接应用,即切点处的导数值就
是该切线的斜率.
3.已知曲线 C:y=x3-3x2+2x,直线 l:y=kx,且直线 l 与 曲线 C 相切于点(x0,y0)(x0≠0),求直线 l 的方程及切点坐标.
【解析】直线 l 过原点,则 k=xy00(x0≠0),由点(x0,y0)在曲线
自主探究
1.能否认为过曲线上一点 P 的切线有且只有一条并且以这点为 切点?
【答案】这种说法不正确.过曲线上一点的切线可能不止一条, 这点也不一定是切点.如图:l1 与 l2 均是曲线的切线且均过 P 点,但 l1 与曲线的切点并非点 P.
2.f′(x0)与 f′(x)的区别是什么?
【答案】f′(x)是函数 f(x)的导函数,简称导数,是对一个区间 而言的,它是一个确定的函数,依赖于函数本身,而与 x0,Δx 无 关;f′(x0)表示的是函数 f(x)在 x=x0 处的导数,是对一个点而言的, 它是一个确定的值,与给定的函数及 x0 的位置有关,而与 Δx 无关.
题型三 求切点坐标 【例 3】 已知曲线 y=x2 在点 P 处的切线分别满足下列条件, 求 P 点坐标. (1)平行于直线 y=4x-5; (2)与 x 轴成 135°的倾斜角.
思路点拨:设切点坐标,根据导数的几何意义求切线斜率,然 后利用两直线平行条件求切点坐标.
【解析】
∵f′(x)= lim Δx→0
(1)函数在一点处的导数,就是该点的函数值的改变量与相应 自变量的改变量的比值的极限.它是一个数值,不是一个变数.
(2)函数的导数,是对某一区间内任意一点 x 而言的. (3)函数 y=f(x)在 x0 处的导数,就是导函数 f′(x)在 x=x0 处的 函数值.
高中数学人教A版选修1-1课件:3.1.3 导数的几何意义
-18-
目标导航
题型一 题型二 题型三 题型四
知识梳理
重难聚焦
典例透析
导数几何意义的综合应用
【例 3】 已知曲线 C:y=x3.求: (1)曲线 C 上横坐标为 1 的点处的切线方程; (2)(1)中的切线与曲线 C 是否还有其他的公共点? 解:(1)将 x=1 代入曲线 C 的方程,得 y=1, ∴切点为 P(1,1).
0
-8-
目标导航
知识梳理
重难聚焦
典例透析
3.理解导数的几何意义 剖析:函数 y=f(x)在点 x0 处的导数的几何意义是曲线 y=f(x)在点 P(x0,f(x0))处切线的斜率.也就是说,曲线 y=f(x)在点 P(x0,f(x0))处的切 线的斜率是 f'(x0),相应地,切线的方程为 y-f(x0)=f'(x0)(x-x0). 说明:当 Δx 无限趋近于
������x →0
������
-11-
目标导航
题型一 题型二 题型三 题型四
知识梳理
重难聚焦
典例透析
即 12x-3y-16=0.
(2)在点 P 处的切线方程是 y− 3 = 4(������ − 2),
8
-12-
目标导航
题型一 题型二 题型三 题型四
知识梳理
重难聚焦
典例透析
反思解决这类题,要先求出函数y=f(x)在x0处的导数,即曲线在该点 处切线的斜率,再由直线方程的点斜式便可求出切线方程.应注意 导数的几何意义中所说的点应在曲线上,否则在该点处的导数不是 斜率.
-20-
目标导航
题型一 题型二 题型三 题型四
知识梳理
重难聚焦
典例透析
反思1.导数的几何意义是曲线的切线的斜率,已知切点可以求斜率, 已知斜率也可以求切点,从而可以与解析几何的知识相联系. 2.导数几何意义的综合应用题目的解题关键还是求函数在某点 处的导数,即切线的斜率,注意结合相关知识如函数、方程、不等 式等求解.
3.1.3导数的概念和几何意义_课件-湘教版数学选修1-1
即切线过抛物线y=x2上的点(2,4),(3,9). 所以切线方程分别为y-4=4(x-2),y-9=6(x-3). 化简得y=4x-4,y=6x-9, 此即是所求的切线方程. 点评 在求曲线过某点的切线方程时,第一要判断该点是否在曲线上,再根 据不同情况求解.
课堂总结 1.函数在某一点处的瞬时变化率即为函数在该点处的导 数. 2.导数f′(x0)的几何意义是曲线y=f(x)在点(x0,f(x0))处的切 线的斜率,即当d→0时,k=fx0+dd-fx0=f′(x0). 3.求曲线的切线方程应充分利用导数的几何意义,抓住两 点: (1)切点在曲线上,则在切点处的导数值即为切线的斜率; (2)若已知点不在曲线上时,要设出切点再利用导数几何意义和已 知条件去求.
C.f′(x0)=2x0
D.f′(x0)=d+2x0
答案 C
3.已知函数y=f(x)图象如图,则f′(xA)与f′(xB)的大小关系 是( ).
A.f′(xA)>f′(xB) B.f′(xA)<f′(xB) C.f′(xA)=f′(xB) D.不能确定
答案 A
4.在曲线f(x)=x2+x上取一点P(1,2),则在区间[1,1+d]上的 平均变化率为________,在点P(1,2)处的导数f′(1)=________.
当 d→0 时 1-xx+1 d→1-x12, ∴f′(x)=1-x12, ∴f′(1)=1-112=0.
题型四 利用导数求切线方程 【例4】 已知曲线C:y=x2. (1)求曲线C在点(1,1)处的切线方程; (2)求过点(1,0)且与曲线C相切的直线的方程;
解 (1)fx+dd-fx=x+dd2-x2=2x+d. 当d→0时,2x+d→2x, ∴f′(x)=2x,f′(1)=2 ∴曲线y=x2在(1,1)处的切线方程为 y-1=2(x-1),即y=2x-1.
人教版高中数学选修1-1课件:3.1.3 导数的几何意义
备课素材
1.导数的几何意义 (1)导数 f′(x0)的几何意义是曲线 y=f(x)在点(x0,f(x0))处的切线的斜率,即 k =lim f(x0+ΔxΔ)x-f(x0)=f′(x0),物理意义是运动物体在某一时刻的瞬时 速度. (2)导数与切线的关系:f′(x0)>0 时,切线的倾斜角为锐角;f′(x0)<0 时,切线 的倾斜角为钝角;f′(x0)=0 时,切线与 x 轴平行.f(x)在 x0 处的导数不存在, 则切线垂直于 x 轴或不存在.
∆������
(2)会利用导数的几何意义解释实际生活问题,体会“以直代曲”的数学思想方法.
三维目标
2.过程与方法 通过让学生在动手实践中探索、观察、反思、总结,发现问题,解决问题,从而达 到培养学生的学习能力、思维能力、应用能力和创新能力的目的. 3.情感、态度与价值观 通过在探究过程中渗透逼近和“以直代曲”思想,使学生了解近似与精确间的辩证 关系;通过有限来认识无限,体验数学中转化思想的意义和价值.
备课素材
(3)求曲线的切线方程,要注意已知点是否在曲线上.如果已知点在曲线上,则以 该点为由点的由线方程为y-f(x0)=f′(x0)(x-x0);若已知点不在曲线上,则设出切 点(x0,f(x0)),表示出切线方程,然后求出切点. 2.“函数f(x)在点x0处的导数”“导函数”“导数”三者之间的区别与联系 (1)“函数在一点处的导数”,就是在该点的函数的改变量与自变量的改变量的比的 极限,它是一个数值,不是变数.
备课素材
(2)“导函数”:如果函数 f(x)在开区间(a,b)内每一点都可导,就说 f(x)在开区间(a,b)内
可导,这时对于区间(a,b)内每一个确定的值 x0,都对应着一个导数 f′(x0),这样就在开
