四川省巴中市2015届高三零诊考试数学文试题Word版含答案
四川省巴中市2015届高三零诊理综试题(扫描版)

四川省巴中市2015届高三零诊2014年零诊试题答案选择题:1A 2D 3C 4B 5C 6D 7D第II卷(非选择题共48分)8. (12分,1分/空)(1)①②③ (2)能提高神经系统的兴奋性(3)神经递质高尔基体和线粒体 0 (4)组织液 (5)B 胰岛素胰岛 B (6)两次方向相反9.(11分,1分/空)I:(1)叶黄素类囊体(薄膜)(2)12小时内右侧截取部分光合作用制造的有机物总量(3)30 细胞质基质、线粒体、叶绿体黑暗II:(1)琼脂(2)稀释涂布平板(3)先调节pH,后灭菌高压蒸汽灭菌(4)基因突变10.(10分,除标注外1分/空)(1)次生(2)70 偏大(3) 11.3(2分)(4)生长、发育和繁殖热能(5)生物的种间关系(6)C (2分)11. (15分,除标注外2分/空)(1) 染色体结构的变异(倒位)(2)①雌和雄雄②6 3/8(3)截刚毛纯种刚毛刚毛截刚毛四川省巴中市2015届高三零诊模拟物理答案及评分标准一、选择题(每小题6分,共42分)题号 1 2 3 4 5 6 7答案C C D A A BD BC1选C:解析:A应为横波;均匀变化的电场一定产生恒定的磁场,则B错误;D应是法拉第;则选C.【说明】本题源于教材,主要考查学生对基本规律的记忆。
属于较易难度试题。
2选C :【说明】本题源于教材,主要考查学生对基本规律的过程的探究,对数据的处理能力。
属于较易难度试题。
3选D :【说明】本题考查整体法和隔离法,属于中等难度试题。
4选A:本题考查电场有关力和能的性质,属于中等难度试题。
5选A: 本题考查机械波及机械振动的基本知识,属于中等难度试题。
6 选BD :解析:母星与太阳密度相等,而休积约为60倍,说明母星的质量是太阳质量的60倍。
由万有引力提供向心力可知r T m r Mm G 222⎪⎭⎫ ⎝⎛=π,所以23131⎪⎪⎪⎭⎫ ⎝⎛=⨯太母太母T T M r r M ,代入数据得到B 正确,由加速度2rGM a =知识,加速度之比为3448060⨯,所以D 正确。
2015届高三第三次诊断性考试数学(文科)试卷及答案四川省雅安市

D. 既不充分也不必要条件
4.
设 a 为锐角,若
cos
a
=
4 5,则
sin
2a
的值为
A. 12 25
B. 24 25
24 C. -
25
12 D. -
25
5. 执行如图所示的程序框图 , 若输入 n 的值为 2, 则输出 s 的值是
A. 1
B. 2
C. 4
D. 7
6. 某几何体的三视图如图所示,则它的体积是
cos x
与直线 y 在 y 轴右侧的交点按横坐标从小到大依次记为
P1,
4
4
2
P2, P3,, ,则 | P2P4| = ________.
15. 以下命题,错误的是 _________ (写出全部错误命题)
①若 f (x) x3 (a 1) x2 3x 1没有极值点,则 2 a 4
A. 8 2 3
B. 8 3
C. 8 2
2
D.
3
7. 已知直线 l : x ky 5 0 与圆 O : x2 y 2 10 与交于 A, B
两点且 OA OB 0 ,则 k
A.2
B.
2 C.
2 D.
2
8.若实数 a,b 满足 a2 b 2≤ 1,则关于 x 的方程 x2 2x a b 0 有实数根的概率是
笔书写在答题卡的对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3. 考试结束后,将答题卡收回。
第Ⅰ卷 (选择题, 50 分)
一、选择题: 本大题共 10 个小题 , 每小题 5 分 , 共 50 分. 在每小题给出的四个选项中,只有一项是符
合题目要求的 .
【数学】四川省成都七中2015届高三零诊模拟考试(文)

四川省成都七中2015届高三零诊模拟考试(文) 一、选择题:本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,选出符合题目要求的一项.1.命题“0||,2≥+∈∀x x R x ”的否定是( )A.0||,2<+∈∀x x R xB. 0||,2≤+∈∀x x R xC. 0||,2000<+∈∃x x R xD. 0||,2000≥+∈∃x x R x【知识点】命题的否定.【答案解析】C 解析 :解:∵命题0||,2≥+∈∀x x R x 是全称命题, ∴命题0||,2≥+∈∀x x R x 的否定是:0||,2000<+∈∃x x R x ,故选:C .【思路点拨】根据全称命题的否定是特称命题即可得到结论.2.设集合{||1|2}A x x =-<,{|2,[0,2]}x B y y x ==∈,则AB =( )A .[0,2] B.[1,3) C. (1,3) D.(1,4)【知识点】交集及其运算.【答案解析】B 解析 :解:{||1|2}A x x =-<={x 丨﹣1<x <3}, {|2,[0,2]}x B y y x ==∈={y|1≤y ≤4},则A ∩B={x|1≤y <3},故选:B【思路点拨】求出集合A ,B 的元素,利用集合的基本运算即可得到结论.3.在极坐标系中,过点22(,)π且与极轴平行的直线方程是( ) A .2ρ= B.2θπ= C. cos 2ρθ= D.sin =2ρθ 【知识点】极坐标与直角坐标的互化,简单曲线的极坐标方程求解.【答案解析】D 解析 :解:先将极坐标化成直角坐标表示,22(,)π化为(2,0), 过(2,0)且平行于x 轴的直线为y=2,再化成极坐标表示,即ρsin θ=2. 故选:D .【思路点拨】先将极坐标化成直角坐标表示,过(2,0)且平行于x 轴的直线为y=2,再化成极坐标表示即可.4.已知实数,x y 满足(01)x ya a a <<<,则下列关系式恒成立的是( )A .33x y > B. sin sin x y > C. 22ln(1)ln(1)x y +>+ D. 221111x y >++ 【知识点】指数函数的图像与性质.【答案解析】A 解析 :解:∵实数x ,y 满足a x <a y (0<a <1),∴x >y ,A .当x >y 时,x 3>y 3,恒成立,B .当x=π,y=时,满足x >y ,但sinx >siny 不成立. C .若ln (x 2+1)>ln (y 2+1),则等价为x 2>y 2成立,当x=1,y=﹣1时,满足x >y ,但x 2>y 2不成立.D .若>,则等价为x 2+1<y 2+1,即x 2<y 2,当x=1,y=﹣1时,满足x >y ,但x 2<y 2不成立.故选:A .【思路点拨】不等式的大小比较,利用函数的单调性的性质依此判断即可.5.已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( ) A .1 B .2 C .3 D .4【知识点】由三视图还原实物图.菁优【答案解析】D 解析 :解:由题意可知,几何体是三棱锥,其放置在长方体中形状如图所示(图中红色部分),利用长方体模型可知,此三棱锥的四个面中,全部是直角三角形.故选D .【思路点拨】由题意可知,几何体为三棱锥,将其放置在长方体模型中即可得出正确答案.6. 下列函数中,对于任意x ∈R ,同时满足条件()()f x f x =-和(π)()f x f x -=的函数是( )A .()sin =f x xB .()sin cos =f x x xC .()cos =f x xD .22()cos sin =-f x x x【知识点】抽象函数及其应用;函数的奇偶性;函数的周期性.【答案解析】D 解析 :解:对于任意x ∈R ,f (x )满足()()f x f x =-, 则函数()f x 是偶函数,选项中,A ,B 显然是奇函数,C ,D 为偶函数, 俯视图侧(左)视图正(主)视图又对于任意x ∈R ,()f x 满足(π)()f x f x -=,则(π)()f x f x +=,即f (x )的最小正周期是π,选项C 的最小正周期是2π,选项D 22()cos sin =cos2f x x x x =-其最小正周期是22ππ= 故同时满足条件的是选项D .故选D . 【思路点拨】由()f x 满足()()f x f x =-,根据函数奇偶性的定义得()f x 为偶函数,将选项A ,B 排除,因为它们是奇函数,再由()f x 满足(π)()f x f x -=推出函数的最小正周期是π,由三角函数的周期公式得选项D 符合.7.执行右图程序框图,如果输入的x ,t 均为2,则输出的S= ( )A. 4B. 5C. 6D. 7【知识点】程序框图.【答案解析】D 解析 :解:若x=t=2,则第一次循环,1≤2成立,则M= 11×2=2,S=2+3=5,k=2, 第二次循环,2≤2成立,则M= 22×2=2,S=2+5=7,k=3, 此时3≤2不成立,输出S=7,故选:D .【思路点拨】根据条件,依次运行程序,即可得到结论.8.设x,y 满足约束条件70310350x y x y x y +-≤⎧⎪-+≤⎨⎪--≥⎩,则2z x y =-的最大值为( )A.10B.8C.3D.2【知识点】线性规划的简单应用【答案解析】B 解析 :解:作出不等式组对应的平面区域如图:(阴影部分ABC ).由z=2x-y 得y=2x-z ,平移直线y=2x-z ,由图象可知当直线y=2x-z 经过点C 时,直线y=2x-z 的截距最小,此时z 最大.由70310x y x y +--+⎧⎨⎩=,=解得52x y ⎧⎨⎩=,=即C (5,2) 代入目标函数z=2x-y ,得z=2×5-2=8.故选:B .【思路点拨】作出不等式组表示的平面区域,由z=2x-y 可得-z 表示直线z=2x-y 在直线上的截距,截距-z 越小,z 越大,利用数形结合可求z 的最大值9. 如图,设P 为正四面体A BCD -表面(含棱)上与顶点不重合的一点,由点P 到四个顶点的距离组成的集合记为M ,如果集合M 中有且只有2个元素,那么符合条件的点P 有( )A .4个 B.6个 C. 10个 D.14个【知识点】新定义.【答案解析】C 解析 :解:分以下两种情况讨论:(1)点P到其中两个点的的距离相等,到另外两个点的距离分别相等,且这两个距离相等,此时点P 位于正四面体各棱的中点,符合条件的有6个点;(2)点P 到其中三个点的的距离相等,到另外一个点的距离与它到其它三个点的距离不相等,此时点P 在正四面体各侧面的中心,符合条件的有4个点;综上,满足题意的点共计10个,故答案选C.【思路点拨】抓住已知条件中的关键点进行分类讨论即可.10. 抛物线24y x =的焦点为F ,点(,)P x y 为该抛物线上的动点,又点(1,0)A -,则||||PF PA 的最小值是( ) A.12【知识点】抛物线的基本性质;直线与抛物线的位置关系.【答案解析】B 解析 :解:由题意可知,抛物线的准线方程为1x =-,()1,0A -, 如图,过P 作PN 垂直直线1x =-于N ,B AD C . P由抛物线的定义可知PF PN =,连结PA ,当PA 是抛物线的切线时,||||PF PA 有最小值,则APN ∠最大,即PAF ∠最大,就是直线PA 的斜率最大, 设在PA 的方程为:1y k x =+(),所以214y k x y x =+⎧⎨=⎩(), 解得:2222240k x k x k +-+=(), 所以2242440k k ∆=--=(),解得1k =±,所以45NPA ∠=︒,||||PF PA = cos NPA ∠ =2. 故选B .【思路点拨】通过抛物线的定义,转化PF PN =,要使||||PF PA 有最小值,只需APN ∠最大即可,作出切线方程即可求出比值的最小值. 二、填空题:本大题共5小题,每小题5分,共25分.11.设向量,a b满足|a b |+=,|a b |-=,则a b ⋅=【知识点】平面向量数量积的运算.【答案解析】1 解析 :解:∵|a b |+=|a b |-=∴分别平方得2222210,26,a a b b a a b b +⋅+=-⋅+=两式相减得44a b ⋅=, 即1a b ⋅=,故答案为:1.【思路点拨】将等式进行平方,相加即可得到结论. 12.设△ABC 的内角A B C 、、 的对边分别为a b c 、、,且1cos 4a b C ==1,=2,,则sin B =【知识点】余弦定理;同角三角函数间的基本关系.【答案解析】4解析 :解:∵C 为三角形的内角,cosC=, ∴sinC==, 又a=1,b=2,∴由余弦定理c 2=a 2+b 2﹣2abcosC 得:c 2=1+4﹣1=4,解得:c=2,又sinC=,c=2,b=2, ∴由正弦定理=得:sinB===. 故答案为: 【思路点拨】由C 为三角形的内角,及cosC 的值,利用同角三角函数间的基本关系求出sinC 的值,再由a 与b 的值,利用余弦定理列出关于c 的方程,求出方程的解得到c 的值,再由sinC ,c 及b 的值,利用正弦定理即可求出sinB 的值.13. 已知抛物线)1)0(22m M p px y ,(上一点>=到其焦点的距离为5,双曲线122=-a y x 的左顶点为A ,若双曲线一条渐近线与直线AM 垂直,则实数a = 【知识点】双曲线的简单性质;抛物线的简单性质. 【答案解析】14解析 :解:根据抛物线的焦半径公式得1+=5,p=8. 取M (1,4),则AM 的斜率为2,由已知得﹣×2=﹣1,故a=. 故答案为:.【思路点拨】根据抛物线的焦半径公式得1+=5,p=8.取M (1,4),由AM 的斜率可求出a 的值.【典型总结】本题考查双曲线和性质和应用,解题时要注意抛物线性质的应用.14.随机地向半圆0y <<a 为正常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,则原点与该点的连线与x 轴的夹角小于4π的概率为 . 【知识点】几何概型. 【答案解析】112π+ 解析 :解:由已知得半圆(a >0) 则半圆的面积S=其中原点与该点的连线与x 轴夹角小于的平面区域面积为:S 1=故原点与该点的连线与x 轴夹角小于的概率P===故答案为:【思路点拨】根据已知条件,分别求出题目中半圆的面积,再求出满足条件原点与该点的连线与x 轴夹角小于的事件对应的平面区域的面积,然后代入几何概型,即可得到答案.【典型总结】几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A 的基本事件对应的“几何度量”N(A ),再求出总的基本事件对应的“几何度量”N,最后根据P=求解.15.若直线l 与曲线C 满足下列两个条件:)(i 直线l 在点()00,y x P 处与曲线C 相切;)(ii 曲线C 在P 附近位于直线l 的两侧,则称直线l 在点P 处“切过”曲线C .下列5个命题:①直线0:=y l 在点()0,0P 处“切过”曲线C :2x y =②直线1:-=x l 在点()0,1-P 处“切过”曲线C :2)1(+=x y③直线x y l =:在点()0,0P 处“切过”曲线C :x y sin =④直线x y l =:在点()0,0P 处“切过”曲线C :x y tan =⑤直线1:-=x y l 在点()0,1P 处“切过”曲线C :x y ln =其中正确的是 _(写出所有正确命题的编号)【知识点】命题的真假判断与应用;曲线与方程.【答案解析】C 解析 :解:对于①,由2x y =,得y ′=2x ,则00|x y ='=,直线y=0是在点P (0,0)的曲线C 的切线,但2x y =恒在直线y=0上方,∴命题①错误;对于②,由21y x =+(),得21y x '=+(),则10|x y =-'=,而直线l :x=-1的斜率不存在,在点P (-1,0)处不与曲线C 相切,∴命题②错误;对于③,由y=sinx ,得y ′=cosx ,则01|x y ='=,直线y=x 是过点P (0,0)的曲线的切线,又x ∈,02π⎛⎫- ⎪⎝⎭时x <sinx ,x ∈0,2π⎛⎫ ⎪⎝⎭时x >sinx ,满足曲线C 在P (0,0)附近位于直线y=x 两侧,∴命题③正确;对于④,由y=tanx ,得y ′=21cos x,则01|x y ='=,直线y=x 是过点P (0,0)的曲线的切线,又x ∈,02π⎛⎫- ⎪⎝⎭时tanx <x ,x ∈0,2π⎛⎫ ⎪⎝⎭时tanx >x ,满足曲线C 在P (0,0)附近位于直线y=x 两侧,∴命题④正确;对于⑤,由y lnx =,得y ′=1x,则11|x y ='=,曲线在P (1,0)处的切线为1y x =-, 由g (x )=x-1-lnx ,得()g x '=1−1x ,当x ∈(0,1)时,()g x '<0,当x ∈(1,+∞)时,()g x '>0.∴g (x )在(0,+∞)上有极小值也是最小值,为g (1)=0.∴1y x =-恒在y lnx =的上方,不满足曲线C 在点P 附近位于直线l 的两侧,命题⑤错误.∴正确的命题是③④.故答案为:③④.【思路点拨】分别求出每一个命题中曲线C 的导数,得到曲线在点P 出的导数值,求出曲线在点P 处的切线方程,再由曲线在点P 两侧的函数值与对应直线上点的值的大小判断是否满足(ii ),则正确的选项可求.三、解答题:(本大题共6小题,共75分.16-19题每题12分,20题13分,21题14分)16. 已知函数sin 2(sin cos )()cos x x x f x x-=. (Ⅰ)求函数f (x )的定义域及最大值;(Ⅱ)求使()f x ≥0成立的x 的取值集合.【知识点】三角函数的化简求值;二倍角的正弦;二倍角的余弦.【答案解析】(Ⅰ)定义域为{x |x ∈R ,且x ≠kπ,k ∈Z }.最大值为1x 的取值集合为{x |4πk π+≤x ≤k ππ+且2x k p p ?,k ∈Z }. 解析 :解:(Ⅰ) cos x ≠0知2x k p p ?,k ∈Z , 即函数f (x )的定义域为{x |x ∈R ,且x ≠kπ,k ∈Z }.………………………3分又∵ x x x x x x x x x x x f 2sin 22cos 12cos sin 2sin 2cos )cos (sin cos sin 2)(2--⨯=-=-= )2cos 2(sin 1x x +-=)42sin(21π+-=x ,∴ 21)(max +=x f . ……………………………………………………………8分(Ⅱ)由题意得1)04πx +≥,即sin(2)4πx +≤解得324πk π+≤24πx +≤924πk π+,k ∈Z , 整理得4πk π+≤x ≤k ππ+,k ∈Z . 结合x ≠kπ,k ∈Z 知满足f (x )≥0的x 的取值集合为 {x |4πk π+≤x ≤k ππ+且2x k p p ?,k ∈Z }.……………………………12分 【思路点拨】(1)根据函数f (x )的解析式可得cosx ≠0,求得x 的范围,从而求得函数f (x )的定义域.再利用三角函数的恒等变换化简函数f (x)的解析式为1)4πx +,从而求得函数的最大值.(2)由题意得1)04πx +≥,即sin(2)4πx +≤,解得x 的范围,再结合函数的定义域,求得满足f (x )≥0 的x 的取值集合.17. 成都市为增强市民的环保意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[)20,25,第2组[)25,30,第3组[)30,35,第4组[)35,40,第5组[40,45],得到的频率分布直方图如图所示.(Ⅰ)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?(Ⅱ)在(Ⅰ)的条件下,决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.【知识点】等可能事件的概率;频率分布直方图.【答案解析】(Ⅰ)应从第3,4,5组中分别抽取3人,2人,1人.(Ⅱ)概率为3.5 解析 :解:第3组的人数为0.3×100=30, 第4组的人数为0.2×100=20, 第5组的人数为0.1×100=10. …………3分因为第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:第3组:3060×6=3; 第4组:2060×6=2; 第5组:1060×6=1. 所以应从第3,4,5组中分别抽取3人,2人,1人. …………6分(2)记第3组的3名志愿者为A 1,A 2,A 3,第4组的2名志愿者为B 1,B 2,第5组的1名志愿者为C 1.则从6名志愿者中抽取2名志愿者有:(A 1,A 2),(A 1,A 3),(A 1,B 1),(A 1,B 2),(A 1,C 1),(A 2,A 3),(A 2,B 1),( A 2,B 2),(A 2,C 1),(A 3,B 1),(A 3,B 2), 第(17)题图(A 3,C 1),(B 1,B 2),(B 1,C 1),(B 2,C 1),共有15种. …………8分其中第4组的2名志愿者B 1,B 2至少有一名志愿者被抽中的有:(A 1,B 1), (A 1,B 2), (A 2,B 1), (A 2,B 2), (A 3,B 1), (A 3, B 2), (B 1,B 2), (B 1,C 1), (B 2,C 1),共有9种,………10分所以第4组至少有一名志愿者被抽中的概率为93.155=…………12分 【思路点拨】Ⅰ)先分别求出这3组的人数,再利用分层抽样的方法即可得出答案; (Ⅱ)从6名志愿者中抽取2名志愿者有15种情况,其中第4组的2名志愿者B 1,B 2至少有一名志愿者被抽中有9种情况,再利用古典概型的概率计算公式即可得出.【典型总结】熟练掌握频率分布直方图、分层抽样的定义、古典概型的概率计算公式、互斥事件及相互独立事件的概率计算公式是解题的关键.18 如图,矩形ABCD 中,AD ⊥平面ABE ,2===AE EB BC ,F 为CE 上的点,且BF ⊥平面ACE 。
四川省巴中市高三“零诊”(10月)考试数学(文)试题(含答案)

巴中市普通高中2016届高三“零诊”考试数学(文科)(考试时间:120分钟 满分:150分)第I 卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项 中,只有一项符合题目要求。
) 1.已知集合A {x| -1<x<2},B {x| -3<x< 1},则A B =( ) A. ( -3,2) B. (1,2) C.( -1,1) D. ( -3, -1) 2.若复数z 满足21z i=+ (i 为虚数单位),则z=( ) A. 1+i B.1-i C. -1+i D. -1-i3. 已知平面α∥平面β,若直线m,n 分别在平面α,β内,则m,n 的关系可能是( ) A.平行 B.相交 C.异面 D.平行或异面4. 已知p:x>1,p:x>1或x<-1,则p 是q 的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件 5. 为大力提倡“厉行节约,反对浪费”,巴中市通过随机询问100名性别不同的居民是否做到 “光盘”行动,得到如下联表:经计算附表:A. 在犯错误的概率不超过1%的前提下,认为“该市居民能否做到‘光盘’行动 与性别有关”B. 在犯错误的概率不超过1%的前提下,认为“该市居民能否做到‘光盘’行动 与性别无关”C. 有90%以上的把握认为“该市居民能否做到‘光盘’行动与性别有关”D. 有90%以上的把握认为“该市居民能否做到‘光盘’行动与性别无关” 6. 下列函数中,是偶函数且在区间(0, ∞)上单调递减的函数是( ) A. 1()f x x =B. 1()()3x f x = C. 2()1f x x =+ D.f (x)=lg|x|7. 若抛物线y2 =2px 的焦点与圆x 2+y 2-4x=0的圆心重合,则p 的值为( ) A. -2, B.2 C. -4 D.4 8. 若某几何体的三视图如图所示,则这几何体的直观图可能是()9. 已知g(x)=sin2x 的图像,要得到f (x)=sin(2x-4π),只需将g (x)的图像( )A. 向右平移8π个单位 B. 向左平移8π个单位 C. 向右平移4π个单位 D. 向左平移4π个单位10.若某程序框图如右图所示,则该程序运行后输出i 的值是( ) A.2 B.4 C.6 D.811.实数x,y 满足约束条件10()10 x-3y+30 x y f x x y +-≥⎧⎪=--≤⎨⎪≥⎩,则z=x+2y 的最大值为( ) A.1 B.2 C.7 D.812. 设函数32231(0)()e (x>0)ax x x x f x ⎧++≤⎪=⎨⎪⎩,在[-2,2]上的最大值为2,则实数a 的取值范围是()第II 卷(非选择题 共90 分)二、填空题(本大题共4小题,每小题5分,共20分。
四川省成都七中实验学校2015届高三零诊模拟训练数学试题 Word版
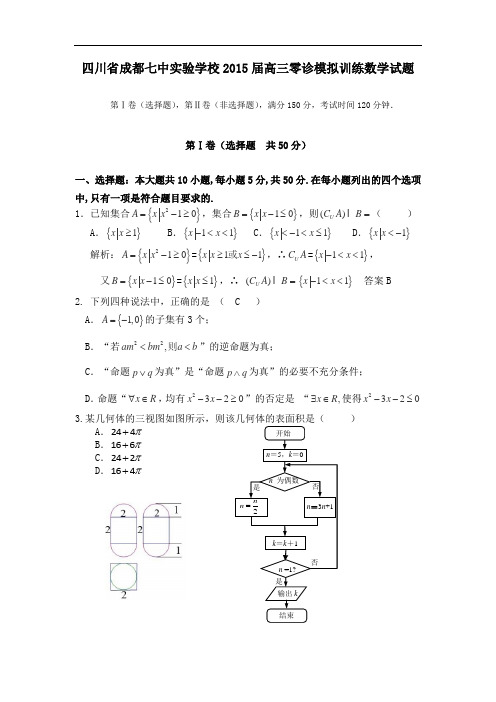
四川省成都七中实验学校2015届高三零诊模拟训练数学试题第Ⅰ卷(选择题),第Ⅱ卷(非选择题),满分150分,考试时间120分钟.第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的.1.已知集合{}210A x x =-≥,集合{}10B x x =-≤,则()U C A B =I ( ) A .{}1x x ≥ B .{}11x x -<< C .{}11x x <-<≤ D .{}1x x <- 解析:{}210A x x =-≥={}11x x x 或≥≤-,∴U C A ={}11x x -<<, 又{}10B x x =-≤={}1x x ≤,∴ ()U C A B =I {}11x x -<< 答案B 2. 下列四种说法中,正确的是 ( C ) A .}{1,0A =-的子集有3个;B .“若22,am bm a b <<则”的逆命题为真;C .“命题p q ∨为真”是“命题p q ∧为真”的必要不充分条件;D .命题“x R ∀∈,均有2320x x --≥”的否定是 “,x R ∃∈使得2320x x --≤ 3.某几何体的三视图如图所示,则该几何体的表面积是( ) A .244π+ B .166π+C .242π+D .164π+由三视图知,该几何体是由两个半径为1的半球和一个棱长为2正方体组成,表面积为42262242S πππ=+⨯⨯-=+,选C .4. 阅读如图所示的程序框图,运行相应的程序,输出的结果k =( B )A. 4B. 5C. 6D. 75.函数3,0(),0-+<⎧=⎨≥⎩x x a x f x a x (01)a a >≠且是R 上的减函数,则a 的取值范围是( B )A .()0,1B .1[,1)3C .1(0,]3D .2(0,]3解:据单调性定义,()f x 为减函数应满足:0013a a a <<⎧⎨≥⎩即113a ≤<. 答案B 6. 已知向量()()ABC BC AB ∆︒︒=︒︒=则,45sin ,30cos ,120sin ,120cos 的形状为 ( C )A .直角三角形B .等腰三角形C . 钝角三角形D .锐角三角形()()cos120,sin120cos30,sin 45=cos120cos30+sin120sin 45AB BC ⋅=︒︒⋅︒︒︒︒︒︒1=02->,所以ABC ∠为钝角 答案C7. 设,m n 为空间的两条不同的直线,,αβ为空间的两个不同的平面,给出下列命题:①若m ∥α,m ∥β,则α∥β; ②若,m m αβ⊥⊥,则α∥β; ③若m ∥α,n ∥α,则m ∥n ; ④若,m n αα⊥⊥,则m ∥n . 上述命题中,所有真命题的序号是 ( D )A. ①②B. ③④C. ①③D. ②④8.某企业拟生产甲、乙两种产品,已知每件甲产品的利润为3万元,每件乙产品的利润为2万元,且甲、乙两种产品都需要在A 、B 两种设备上加工.在每台设备A 、每台设备B 上加工1件甲产品所需工时分别为1h 和2h ,加工1件乙产品所需工时分别为2h 和1h ,A 设备每天使用时间不超过4h ,B 设备每天使用时间不超过5h ,则通过合理安排生产计划,该企业在一天内的最大利润是 ( D )A .18万元B . 12万元C . 10万元D .8万元9. 若()sin(2)f x x b ϕ=++, 对任意实数x 都有()()3f x f x π+=-,2()13f π=-,则实数b 的值为 ( A )A .2-或0B .0或1C .1±D .2±解:由()3f x f x π⎛⎫+=- ⎪⎝⎭可得()f x 关于直线6x π=对称,因为213f π⎛⎫=-⎪⎝⎭且函数周期为π,所以21163f f b ππ⎛⎫⎛⎫=-==±+ ⎪ ⎪⎝⎭⎝⎭,所以2b =-或0b =10. 我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知1F 、2F 是一对相关曲线的焦点,P 是它们在第一象限的交点,当 6021=∠PF F 时,这一对相关曲线中双曲线的离心率是( A )A .3 B.2 C.332 D.2 解:设椭圆的半长轴为1a ,椭圆的离心率为1e ,则1111,c ce a a e ==.双曲线的实半轴为a ,双曲线的离心率为e ,,c ce a a e==.12,,(0)PF x PF y x y ==>>,则由余弦定理得2222242cos 60c x y xy x y xy =+-=+-,当点P 看做是椭圆上的点时,有22214()343c x y xy a xy =+-=-,当点P 看做是双曲线上的点时,有2224()4c x y xy a xy =-+=+,两式联立消去xy 得222143c a a =+,即22214()3()c cc e e=+,所以22111()3()4e e +=,又因为11e e =,所以22134e e +=,整理得42430e e-+=,解得23e =,所以e ,,选A.第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5题,每小题5分,共25分.答案填在答题卡上. 11. 设{}n a 是公差不为零的等差数列,12a =且136,,a a a 成等比数列,则2014a =22017=n a 12. 已知a b>,且1ab =,则221a b a b++-的最小值是 . 13.有一个内接于球的四棱锥P ABCD -,若PA ABCD ⊥底面,2BCD π∠=,2ABC π∠≠,BC =3,CD =4,PA =5,则该球的表面积为________.解: 由∠BCD =90°知BD 为底面ABCD 外接圆的直径,则2r =32+42=5.又∠DAB =90°⇒PA ⊥AB ,PA ⊥AD ,BA ⊥AD .从而把PA ,AB ,AD 看作长方体的三条棱,设外接球半径为R ,则(2R )2=52+(2r )2=52+52, ∴4R 2=50,∴S 球=4πR 2=50π.14.已知函数221,(20)()3,(0)ax x x f x ax x ⎧⎪⎨⎪⎩++-<≤=->有3个零点,则实数a 的取值范围是 .解:因为二次函数最多有两个零点,所以函数必有一个零点,从而0a >,所以函数3(0)y ax x =->221(20)y ax x x =++-< 必有两个零点,故需要()()22022000440a f f a ìïï-<-<ïïïïï->íïï>ïïïï=->ïîV ,解得34a < 答案 3(,)4+∞15.下列命题正确的有___________.①已知A,B 是椭圆+=22134x y 的左右两顶点, P 是该椭圆上异于A,B 的任一点,则⋅=-34AP BP k k .②已知双曲线-=2213y x 的左顶点为1A ,右焦点为2F ,P 为双曲线右支上一点,则⋅12PA PF 的最小值为-2.③若抛物线C :=24x y 的焦点为F ,抛物线上一点(2,1)Q 和抛物线内一点(2,)R m >(1)m ,过点Q 作抛物线的切线1l ,直线2l 过点Q 且与1l 垂直,则2l 平分∠RQF ;④已知函数()f x 是定义在R 上的奇函数,'=->>(1)0,()()0(0)f xf x f x x , 则不等式>()0f x 的解集是-+∞(1,0)(1,).答案 (2) (3) (4)三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.16.(本小题满分12分)在△ABC 中,角A 、B 、C 所对的边分别是a 、b 、c ,且222823ABC b c a S ∆+-=(其中ABC S ∆为△ABC 的面积).(1)求2sin cos 22B CA ++;(2)若2b =,△ABC 的面积为3,求a .解析:(1)由已知得A bc A bc sin 21382cos 2⨯=即0sin 4cos 3>=A A 53sin =∴A 54cos =A212cos cos 22cos 2cos 12cos 2sin 22-+=++=++A A A A A C B50592152425162=-⨯+⨯=………………6分 (2)由(Ⅰ)知53sin =A 2,3sin 21===∆b A bc S ABC ,A b c a c cos 265222++==∴ 又13545222542=⨯⨯⨯-+=∴a13=∴a ……………………………………12分17.(本小题满分12分)已知数列{}n a ,其前n 项和为n S ,点(),n n S 在抛物线23122y x x =+上;各项都为正数的等比数列{}n b 满足13511,1632==b b b .(1)求数列{}n a ,{}n b 的通项公式;(2)记n n n c a b =,求数列{}n c 的前n 项和n T . 解:(1)23122n S n n =+Q 当1n =时,2a S ==∴数列n a 是首项为2,公差为3的等差数列,31n a n ∴=- 又各项都为正数的等比数列{}n b 满足13511,432b b b ==解得1,22b q ==,()2n n b ∴= ……………………5分(2)由题得1(31)()2n n c n =-①②①-②得2311111113()()()(31)()22222n n n T n +⎡⎤=++++--⎢⎥L52n n T ∴=- ………………………………………………12分18. (本小题满分12分)已知函数3221()(1)3f x x a x b x =--+,其中,a b 为常数. (1)当6,3a b ==时,求函数()f x 的单调递增区间;(2)若任取[0,4],[0,3]a b ∈∈,求函数()f x 在R 上是增函数的概率.19. (本小题满分12分)如图,已知平面ABCD ⊥平面BCEF ,且四边形ABCD 为矩形,四边形BCEF 为直角梯形, 090CBF ∠=,//BF CE ,BC CE ⊥,4DC CE ==, 2BC BF ==.(1)作出这个几何体的三视图(不要求写作法).(2)设,P DF AG Q =⋂是直线DC 上的动点,判断并证明直线PQ 与直线EF 的位置关系.(3)求直线EF 与平面ADE 所成角的余弦值.19.(1)如右图. (2)垂直.(3)220.(本小题满分13分)平面内两定点12,A A 的坐标分别为(2,0),(2,0)-,P 为平面一个动点,且P 点的横坐标()2,2x ∈-. 过点P 作PQ 垂直于直线12A A ,垂足为Q ,并满足21234PQ AQ A Q =⋅. (1)求动点P 的轨迹方程.(2)当动点P 的轨迹加上12,A A 两点构成的曲线为C . 一条直线l 与以点(1,0) 为圆心,半径为2的圆M 相交于,A B 两点. 若圆M 与x 轴的左交点为F ,且6FA FB ⋅=. 求证:直线l 与曲线C 只有一个公共点.解:(1)设(),P x y ,()2,2x ∈-则:2212,2,2PQ y AQ x A Q x ==+=- 所以:23(2)(2)4y x x =-+,即:22143x y +=,()2,2x ∈- -----4分 (2)由(1)知曲线C 的方程为22143x y +=,圆M 的方程为()2214x y -+=,则()1,0F - 设()()1122,,,A x y B x y①当直线l 斜率不存在时,设l 的方程为:0x x =,则:12012,x x x y y ===-,()()01021,,1,FA x y FB x y =+=+因为6FA FB ⋅=,所以:()201216x y y ++=,即:()220116x y +-=因为点A 在圆M 上,所以:()220114x y -+=代入上式得:02x =±所以直线l 的方程为:2=+x (经检验x=-2不合题意舍去), 与曲线C 只有一个公共点. ------5分 经检验x=-2不合题意舍去所以 x=2 -------6分②当直线l 斜率存在时,设l 的方程为:y kx m =+,联立直线与圆的方程:()2214y kx mx y =+⎧⎪⎨-+=⎪⎩,消去x 得: 222(1)2(1)30k x km x m ++-+-=所以:12221222(1)131km x x k m x x k -⎧+=⎪⎪+⎨-⎪=⎪+⎩------------8分 因为:()()11221,,1,FA x y FB x y =+=+,且6FA FB ⋅=所以:121212()5x x x x y y +++=又因为:1122y kx my kx m =+⎧⎨=+⎩,所以:()()2212121212()y y kx m kx m k x x km x x m =++=+++代入得:221212(1)(1)()5k x x km x x m +++++=, 化简得:2243m k -=--------10分 联立直线l 与曲线C 的方程:22143y kx m x y =+⎧⎪⎨+=⎪⎩,消去x 得:222(34)84120k x kmx m +++-= 22222(8)4(34)(412)48(43)km k m k m ∆=-+-=-+ ----12分 因为:2243m k -=,所以0∆=,即直线l 与曲线C 只有一个公共点21.(本小题满分14分) (文科)已知函数()1xaf x x e =-+(a R ∈,e 为自然对数的底数). (1)若曲线()y f x =在点(1,(1))f 处的切线平行于x 轴,求a 的值; (2)求函数()f x 的极值;(3)当1a =的值时,若直线:1l y kx =-与曲线()y f x =没有公共点,求k 的最大值.解:(Ⅰ)由()1x a f x x e =-+,得 ()1xaf x e '=-. 又曲线()y f x =在点()()1,1f 处的切线平行于x 轴, 得()10f '=,即10ae-=,解得a e =.(Ⅱ)()1xa f x e '=-, ①当0a ≤时,()0f x '>,()f x 为(),-∞+∞上的增函数,所以函数()f x 无极值. ②当0a >时,令()0f x '=,得x e a =,ln x a =.(),ln x a ∈-∞,()0f x '<;()ln ,x a ∈+∞,()0f x '>.所以()f x 在(),ln a -∞上单调递减,在()ln ,a +∞上单调递增,故()f x 在ln x a =处取得极小值,且极小值为()ln ln f a a =,无极大值.综上,当0a ≤时,函数()f x 无极小值;当0a >,()f x 在ln x a =处取得极小值ln a ,无极大值.(Ⅲ)当1a =时,()11x f x x e=-+令()()()()111xg x f x kx k x e =--=-+, 则直线l :1y kx =-与曲线()y f x =没有公共点,等价于方程()0g x =在R 上没有实数解. 假设1k >,此时()010g =>,1111101k g k e -⎛⎫=-+<⎪-⎝⎭, 又函数()g x 的图象连续不断,由零点存在定理,可知()0g x =在R 上至少有一解, 与“方程()0g x =在R 上没有实数解”矛盾,故1k ≤.又1k =时,()10x g x e=>,知方程()0g x =在R 上没有实数解. 所以k 的最大值为1.另解(Ⅲ)当1a =时,()11x f x x e=-+.直线l :1y kx =-与曲线()y f x =没有公共点, 等价于关于x 的方程111xkx x e -=-+在R 上没有实数解,即关于x 的方程: ()11xk x e -=(*)在R 上没有实数解.①当1k =时,方程(*)可化为10x e =,在R 上没有实数解. ②当1k ≠时,方程(*)化为11x xe k =-.令()xg x xe =,则有()()1xg x x e '=+.令()0g x '=,得1x =-,当x 变化时,()g x '的变化情况如下表:当1x =-时,()min g x e=-, 同时当x 趋于+∞时,()g x 趋于+∞, 从而()g x 的取值范围为1,e ⎡⎫-+∞⎪⎢⎣⎭.所以当11,1k e ⎛⎫∈-∞- ⎪-⎝⎭时,方程(*)无实数解, 解得k 的取值范围是()1,1e -. 综上,得k 的最大值为1.(理科)已知函数2()ln f x x x =+.(1)若函数()()g x f x ax =-在定义域内为增函数,求实数a 的取值范围;(2)在(1)的条件下,若1a >,3()3x xh x e ae =-,[0,ln 2]x ∈,求()h x 的极小值;(3)设2()2()3()F x f x x kx k R =--∈,若函数()F x 存在两个零点,m n<<(0)m n ,且满足02x m n =+,问:函数()F x 在00(,())x F x 处的切线能 否平行于x 轴?若能,求出该切线方程,若不能,请说明理由.解:(Ⅰ)21()()ln ,()2.g x f x ax x x ax g x x a x'=-=+-=+-由题意,知()0,(0,)g x x '≥∈+∞恒成立,即min 1(2)a x x≤+…… 2分又10,2x x x>+≥x =时等号成立.故min 1(2)x x+=a ≤……4分(Ⅱ)由(Ⅰ)知,1a <≤ 令x e t =,则[1,2]t ∈,则3()()3.h x H t t at ==-2()333(H t t a t t '=-=+……5分由()0H t '=,得t =或t =(舍去),34(1,2[1,2]a ∈,①若1t <≤()0,()H t H t '<单调递减;()h x在也单调递减; 2t <≤,则()0,()H t H t '>单调递增. ()h x 在2]也单调递增;故()h x的极小值为(ln 2h =-……8分(Ⅲ)设()F x 在00(,())x F x 的切线平行于x 轴,其中2()2ln .F x x x kx =-- 结合题意,有220002ln 0,2ln 0,2,220,m m km n n kn m n x x k x ⎧--=⎪--=⎪⎪+=⎨⎪⎪--=⎪⎩ ……10分①—②得2ln ()()().m m n m n k m n n -+-=-,所以02ln 2.m n k x m n =-- 由④得0022.k x x =- 所以2(1)2()ln .1m m m n n m n m n n--==++⑤ ……11分 设(0,1)m u n =∈,⑤式变为2(1)ln 0((0,1)).1u u u u --=∈+ 设2(1)ln ((0,1))1u y u u u -=-∈+, 2222212(1)2(1)(1)4(1)0,(1)(1)(1)u u u u u y u u u u u u +--+--'=-==>+++ 所以函数2(1)ln 1u y u u -=-+在(0,1)上单调递增,因此,1|0u y y =<=, 即2(1)ln 0.1u u u --<+ 也就是,2(1)ln 1m m n m n n-<+,此式与⑤矛盾. 所以()F x 在00(,())x F x 处的切线不能平行于x 轴.……14分① ② ③④。
四川省达州市2015届高三第一次诊断性测试数学(文)试题 Word版含答案

达州市普通高中2015届第一次诊断性测试数学试题(文科)本试卷分选择题和非选择题两部分,全卷共4页,第Ⅰ卷(选择题)1至2页,第Ⅱ卷(非选择题)3至4页,满分150分.考试时间120分钟.注意事项:1. 答题前,考生务必将自己的姓名、考号用0.5毫米黑色字迹的签字笔或钢笔填写在答题卡上,将条形码贴在答题卡规定的位置上.2. 选择题必须使用2B 铅笔将答案标号填涂在答题卡上对应题目标号的位置上, 非选择题用0.5毫米黑色字迹的签字笔或钢笔书写在答题卡的对应框内,超出答题区书写的答案无效;在草稿纸、试题卷上的答案无效.3. 考试结束后,将答题卡收回.第Ⅰ卷(选择题,共50分)一.选择题:本大题共10个小题;每小题5分,共50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的。
1.已知全集U ={1,2,3,4,5},集合A ={1,2,3},B ={2,4}, 则(∁U A )∪B 为( )A .{1,2,4}B .{2,3,4}C .{2,4,5}D .{2,3,4,5} 2.设()()()()⎩⎨⎧>+≤-=10,1010,2x x f x x x f 则()2015f 的值为 A .2B .3C .4D .53.如果复数()i i z +-=1,则( )A .|z |=2B .z 的实部为1 C.z 的共轭复数为1+i D .z 的虚部为-1 4. 在正项等比数列}{n a 中,3lg lg lg 963=++a a a ,则102a a 的值是 ( ) A. 100 B. 10 C. 9 D. 3 5. 定义某种运算⊙:S a =⊙b 的算原理如框图,则式子5⊙3+2⊙4= ( ) A .14 B .15C .16D .186.函数f(x)=sin(ωx +φ)(ω>0,|φ|<π2)的部分图象如图所示,如果x 1,x 2∈(-π6,π3),且f(x 1)=f(x 2),则f(x 1+x 2)=( )A.12B.22C.32D .17.某选手参加演讲比赛的一次评委打分如茎叶图所示,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为A . 86.5,1.5B .86.5,1.2C .86,1.5D .86,1.2 8 .下列说法正确..的是( ) A .命题“x ∀∈R ,0xe >”的否定是“x ∃∈R ,0<x e ”B .命题 “已知,x y ∈R ,若55,10≠≠≠+y x y x 或则”是真命题C .22x x ax +≥在[]2,0∈x 上恒成立⇔max min 2)()2(ax x x ≥+在[]2,0∈x 上恒成立”D .命题:若1a =-,则函数()221f x ax x =+-只有一个零点的逆命题为真命题。
四川省绵阳市2015届高三第三次诊断考试数学(文)试题 (Word版含答案)
绵阳市高中2015届第三次诊断性考试数学(文)本试卷分第I卷(选择题)和第B卷(非选择题)。
第I卷1至2页,第B卷2至4 页.共4页.满分150分考试时间120分钟。
考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。
考试结束后,将答题卡交回。
第I卷(选择题,共50分)注意事项:必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑。
第I卷共10小题。
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的1.已知i是虚数单位,则32ii-+等于(A)-l+i (B) 1-i (C) 1+i (D) -1-i2.已知向量为非零向量,则的(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分又不必要条件3.己知函数的图象在同一直角坐标系中对称轴相同,则ω的值为(A) 4(B) 2 (C) 1(D)1 24、已知M,N为集合I的非空真子集,且M,N不相等,若(A)M(B)N(C)I(D)∅5.一机器元件的三视图及尺寸如右图示(单位:dm),则该组合体的体积为(A) 80 dm3(B) 88 dm3(C) 96 dm}3(D) 120dm36.若,则下列不等式成立的是7.某流程图如图所示,现输入如下四个函数,则可以输出f(x)的是8、已知C是半径为1,圆心角为60°的圆弧上的动点,如图,若其中,则x+y的最大值是9.己知四梭锥P-ABCD的各条棱长均为13, M, N分别是PA, BD上的点,且PM:MA=BN:ND=5:8,则线段MN的长(A)5(B)6 (C) 7(D)810.已知点是抛物线y2=4x上相异两点,且满足=4,若AB的垂直平分线交x轴于点M,则△AMB的面积的最大值是第II卷(非选择题共100分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指的答题区域内作答.作图题可先用铂笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚。
四川省宜宾市2015届高三第一次诊断考试数学文试题 Word版含答案
文档 1 / 12 2014年秋期普通高中三年级第一次诊断测试 数 学(文史类)
本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题).第Ⅰ卷1至2页,第Ⅱ卷3至4页.考生作答时,须将答案答在答题卡上,在本试卷、草稿纸上答题无效.满分150分,考试时间120分钟. 考试结束后,将本试题卷和答题卡一并交回. 第Ⅰ卷(选择题,共50分) 注意事项: 必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑.
一、选择题:本大题共10个小题,每小题5分,共50分;在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知全集4,3,2,1,0U,集合3,2,1A,则ACU (A) 4,0(B) 3,2,1(C) 4,3,2,1,0(D) 4,3,2,0
2.抛物线24yx的焦点坐标是
(A) (0,1) (B) (0,-1) (C) (-1,0) (D) (1,0) 3. 函数)2sin(xy的图象 (A) 关于x轴对称(B) 关于y轴对称 (C) 关于原点对称(D) 关于直线2
x对称
4.给出下列三个命题: ①命题p:xR,使得012xx, 则p:xR,使得012xx
②”或“15xx是“2
450xx”的充要条件.
③若qp为真命题,则pq为真命题. 是
k=0,S=1 开始
k<3? S=S.2k k=k+1
输出S 结束 否 文档 2 / 12 其中正确..命题的个数为 (A) 0(B) 1(C) 2(D) 3 5.执行如图所示的程序框图,输出的S值是
(A) 2 (B) 4 (C) 8 (D) 16
6.已知),10(12logaaa且则a的取值范围是
(A) (2,+)(B) (0,1) (C) 12(0,)(2,+) (D) (0,1)(2,+)
7.已知单位向量m和n的夹角为60,记a=n-m , 2b=m, 则向量a与b的夹角为 (A) 30(B)60(C) 120(D) 150 8.一个三棱柱的侧视图、俯视图如图所示,则三棱柱的表面积是 (A) 2616 (B) 3616 (C) 2612 (D) 3614
四川省眉山市2015届高三第一次诊断性考试数学文试题 Word版含答案
是眉山市高中2015届第一次诊断性考试数 学(文史类) 2015.01注意事项:1. 答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.2. 答选择题时,必须使用2B 铅笔把答题卡上对应题目的答案标号涂黑. 如需改动,用橡皮擦干净后,再选涂其他答案标号.3. 答非选择题时,必须使用0.5毫米的黑色签字笔,将答案书写在答题卡规定的位置上.4. 所有题目必须在答题卡上作答,在试题卷上答题无效.5. 考试结束,将答题卡上交.一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中.只有一个是符合题目要求的.1.已知全集为R ,集合2{|0},{|680}A x x B x x x =≥=-+≤,则B C A R = A .}0|{≤x xB .}42|{≤≤x xC .}420|{><≤x x x 或D .}420|{≥≤<x x x 或2.下列说法错误的是A .两两相交且不过同一点的三条直线必在同一平面内;B .过直线外一点有且只有一个平面与已知直线垂直;C .如果共点的三条直线两两垂直,那么它们中每两条直线确定的平面也两两垂直;D .如果两条直线和一个平面所成的角相等,则这两条直线一定平行;3.若c b a ,,为实数,则下列命题中正确的是 A .若a b >,则22ac bc > B .若b a <,则c b c a +<+ C .若b a <,则bc ac < D .若b a <,则ba 11> 4.若2log 4)(2+=x x f ,则(2)(4)(8)f f f ++=A .12B .24C .30D .48 5.阅读右侧程序框图,如果输出5=i ,那么在空白 矩形框中应填入的语句为A. i S *=2B. 12-*=i SC. 22-*=i SD. 42+*=i S 6.一个棱锥的三视图如图,则该棱锥的全面积是A .4+2 6B .4+ 6C .4+2 2D .4+ 27.已知向量a 是与单位向量b 夹角为060的任意向量,则对任意的正实数t ,||ta b - 的最小值是A .0B .12 CD .1 8.下列命题正确的是①“62<<x ”是 “01242<--x x ”的必要不充分条件; ②函数x x f 2tan )(=的对称中心是)0,2(πk (k Z ∈); ③“32,10x R x x ∀∈-+≤”的否定是“01,23>+-∈∃x x R x ”;④设常数a使方程sin x x a =在闭区间[0,2π]上恰有三个解123,,x x x , 则123x x x ++=37π. A .①③ B .②③ C .②④ D .③④9.函数()f x 的零点与()422xg x x =+-的零点之差的绝对值不超过0.25, 则()f x 可以是 A.()2(1)f x x =-B.()41f x x =- C. 1()ln()2f x x =-D.()1xf x e =- 10.设函数()y f x =在区间(),a b 上的导函数为()f x ',()f x '在区间(),a b 上的导函数为()f x '',若在区间(),a b 上0)(<''x f 恒成立,则称函数()f x 在区间(),a b 上为“凸函数”;已知234236121)(x x m x x f --=在()1,3上为“凸函数”,则实数m 的取值范围是 A .31(,)9-∞ B .31[,5]9C .)2,(--∞D .),2[+∞ 二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡相应位置上. 11.若),(2)(R y x i y i i x ∈+=-,则复数=+yi x12.已知x 、y 满足约束条件5003x y x y x -+≥⎧⎪+≥⎨⎪≤⎩,则24z x y =+的最小值是13.已知幂函数)(x f y =的图象过点)22,21(,则)]2([log 2f =14.有两个等差数列2,6,10,…,190及2,8,14,…,200,由这两个等差数列的公共项按从小到大的顺序组成一个新数列,则这个新数列的各项之和为 15.下列命题中①函数1()f x x=在定义域内为单调递减函数; ②函数)0()(>+=x xax x f 的最小值为a 2;③已知定义在R 上周期为4的函数()f x 满足(2)(2)f x f x -=+,则()f x 一定为偶函数;④已知函数32()(0)f x ax bx cx d a =+++≠,则0a b c ++=是()f x 有极值的必要不充分条件;⑤已知函数()sin f x x x =-,若0a b +>,则()()0f a f b +>.其中正确命题的序号为 (写出所有正确命题的序号).三、解答题: 本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤 16.(本小题满分12分)在ABC ∆中,角,,A B C 的对边分别是,,a b c ,若(2)cos cos a c B b C -=。
四川省遂宁市2015届高三零诊考试数学(理)试题 Word版含答案
遂宁市高中2015届零诊考试数学(理科)试题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
总分150分。
考试时间120分钟。
第Ⅰ卷(选择题,满分50分)注意事项:1.答题前,考生务必将自己的姓名、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上。
并检查条形码粘贴是否正确。
2.选择题使用2B 铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3.考试结束后,将答题卡收回。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,只有一个是符合题目要求的。
1.已知集合{}{}()12,1R A x x B x x A C B =-≤≤=<⋂,则= A. {}1x x > B. {}1x x ≥C. {}2x x 1<≤ D. {}2x x 1≤≤ 2.复数512ii=- A .2i - B .2i -+ C .12i - D .12i -+ 3.设R b a ∈,,则“4>+b a ”是“2,2>>b a 且”的A .必要不充分条件 B. 充分不必要条件 C. 充分必要条件 D. 既非充分又非必要条件 4. 在等差数列{}n a 中,452,4a a ==,记n a 的前n 项和为n S ,则8S = A .12B .16C .24D .48 5. 已知,m n 表示两条不同直线,α表示平面,下列说法正确的是 A .若//m α,//n α, 则//m n B .若m α⊥,n α⊂,则m n ⊥ C .若m α⊥,m n ⊥,则//n α D .若//m α,m n ⊥,则n α⊥ 6. 执行下面的框图,若输入的N 是6,则输出p 的值是A .120B .720C .1440D .5040 7.A ,B 两点之间的距离为5,那么(1)f -= A .-1 B .1 CD8. 若函数()()()01xxf x ka a a a -=->≠-∞+∞且在,上既是奇函数又是增函数,则()()log a g x x k =-的图象是A B C D9. 某单位安排7位员工在星期一至星期日值班,每天1人,每人值班1天,若7位员工中的甲、乙排在相邻两天,丙不排在星期一,丁不排在星期日,则不同的安排方案共有 A. 504种 B. 960种 C. 1008种 D. 1108种10. 定义函数348,12,2()1(), 2.22x x f x x f x ⎧--⎪⎪=⎨⎪>⎪⎩≤≤,则函数()()6g x xf x =-在区间[]1,64(n *)∈N 内的所有零点的和为A .192B .189C .1894 D .1892第Ⅱ卷(非选择题,满分100分)注意事项:1.请用蓝黑钢笔或圆珠笔在第Ⅱ卷答题卡上作答,不能答在此试卷上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四川省巴中市2015届上学期高三年级零诊考试数学试卷(文科)本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分。
全卷满分150分,考试时间120分钟。
第I 卷(选择题50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项符合题目要求。
1. 若{}{}032|,1|22=--===x x x B x x A ,则B A ⋂=( )A. {}3B. {}1C. ∅D. {}1-2. 若b a R c b a >∈,,,,则下列不等式成立的是( )A.1122+>+c b c aB. 22b a >C. ba 11<D. ||||c b c a >3. 要得到函数()1cos +=x y 的图象,只要将函数x y cos =的图象( )A. 向左平移1个单位B. 向右平移1个单位C. 向左平移21个单位D. 向右平移21个单位 4. 某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是( )5. 阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n 后,输出的()20,10∈S ,那么n 的值为( )A. 3B. 4C. 5D. 66. 某工厂甲、乙、丙三个生产了同一种产品,数量分别为120件,80件,60件,为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n 的样本进行调查,其中从丙车间的产品中抽取了3件,则n =( )A. 9B. 10C. 12D. 137. 若b a c b a +===,2||,1||,且c ⊥a ,则向量a 与b 的夹角为( )A. 30°B. 60°C. 120°D. 150°8. 设变量y x ,满足约束条件⎪⎩⎪⎨⎧-≥-≤+≥+144222y x y x y x ,则目标函数y x z -=3的取值范围是( )A. ⎥⎦⎤⎢⎣⎡-6,23B. ⎥⎦⎤⎢⎣⎡--1,23C. []6,1-D. ⎥⎦⎤⎢⎣⎡-23,6 9. 已知双曲线()0,012222>>=-b a by a x 的左顶点与抛物线px y 22=(0>p )的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )A. 32B. 52C. 34D. 5410. 设S ,T 是R 的两个非空子集,如果存在一个从S 到T 的函数()x f y =满足:(1)(){}S x x f T ∈=|;(2)对任意S x x ∈21,,当21x x <时,恒有()()21x f x f <,那么称这两个集合“保序同构”以下集合对不是“保序同构”的是( )A. *N A =,N B =B. {}31|≤≤-=x x A ,{}1008|≤<-==x x x BC. {}R B x x A =<<=,10|D. Q B Z A ==,第II 卷(非选择题100分)二、填空题:本大题共5小题,每小题5分,共25分。
11. 在复平面内,复数ii-12对应的点的坐标为__________。
12. 在△ABC 中,已知∠BAC=60°,∠ABC=45°,BC=3,则AC=_________。
13. 已知函数()⎪⎩⎪⎨⎧<≤-<=20,tan 0,23πx x x x x f ,则⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛4πf f =_____________。
14. 已知圆O :522=+y x ,直线⎪⎭⎫⎝⎛<<=+201sin cos :πθθθy x l ,设圆O 上到直线l 的距离等于1的点的个数为k ,则=k ____________。
15. 已知数列{}n a 满足n a a a n n 2,3311=-=+,则na n的最小值为__________。
三、解答题:本大题共6小题,共75分。
解答应写出文字说明,证明过程或演算步骤。
16. (12分)已知函数()x xx x f sin 2sin 2cos 22+-=。
(1)求函数()x f 的最小正周期;(2)设⎪⎭⎫⎝⎛∈4,00πx 且()5240=x f 时,求⎪⎭⎫ ⎝⎛+60πx f 的值。
17. (12分)已知等比数列{}n a 中,311=a ,公比31=q 。
(1)n S 为{}n a 的前n 项和,证明:21nn a S -=;(2)设n n a a a b 32313log ......log log +++=,求数列{}n b 的通项公式。
18. (12分)根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3,设各车主购买保险相互独立。
(1)求该地1位车主至少购买甲、乙两种保险中的1种的概率;(2)求该地的3位车主中恰有1位车主甲、乙两种保险都不购买的概率。
19. (12分)三棱柱111C B A ABC -中,1AA AB =,∠CAB=2π。
(1)证明:1CB ⊥1BA ;(2)已知5,2==BC AB ,求三棱锥11ABA C -的体积。
20. (13分)已知椭圆()01:2222>>=+b a by a x C 的一个顶点为A (2,0),离心率为22。
直线)1(-=x k y 与椭圆C 交于不同的两点M ,N 。
(1)求椭圆C 的方程;(2)当△AMN 的面积为310时,求k 的值。
21. (14分)()()0ln ||>--=a x a x x f 。
(1)若1=a ,求()x f 的单调区间及()x f 的最小值;(2)若0>a ,求()x f 的单调区间;(3)证明:()()()12121ln ...33ln 22ln 222222++-<+++n n n nn ,*N n ∈,且2≥n 。
参考答案:一、选择题:DAADB DCABD二、11.(-1,1) 12.2 13. -214.4 15.221 三、16. 解 :由题设有f (x )=cos x +sin x =)4sin(2π+x ,(Ⅰ)函数f (x )的最小正周期是T =2π.(Ⅱ)由f (x 0)=524得54)4sin(0=+πx 因为x 0∈(0,4π),所以)2,4(40πππ∈+x从而cos()40π+x =53. 于是]6)4sin[(2)6(00πππ++=+x x f =102364+17. (1)证明:因为nn a 31=,2311n n S -=,所以21n na S -=.(2)解:2)1()21(log log log 32313+-=+++-=+++=n n n a a a b n n 所以{b n }的通项公式为2)1(+-=n n b n . 18.解:记A 表示事件:该地的1位车主购买甲种保险;B 表示事件:该地的1位车主购买乙种保险但不购买甲种保险;C 表示事件:该地的1位车主至少购买甲、乙两种保险中的1种;D 表示事件:该地的1位车主甲、乙两种保险都不购买. (1)P (A )=0.5,P (B )=0.3,C =A +B ,P (C )=P (A +B )=P (A )+P (B )=0.8.(2)D=C ,P (D )=1-P (C )=1-0.8=0.2,P (E )=3×0.2×0.82=0.384.19. 解:(1)证明:如图,连接AB 1,∵ABC -A 1B 1C 1是直三棱柱,2π=∠CAB ,∴AC ⊥平面ABB 1A 1. 故AC ⊥BA 1.又∵AB =AA 1,∴四边形ABB 1A 1是正方形. ∴BA 1⊥AB 1.又CA ∩AB 1=A , ∴BA 1⊥平面CAB 1,又∵CB 1⊥平面CBA 1,∴CB 1⊥BA 1.(2)∵AB =AA 1=2, BC=5,∴AC =A 1C 1=1.由(1)知,A 1C 1⊥平面ABA 1,∴323111111=⋅=∆-C A S V ABA ABA C . 20、解:(1)椭圆C 的方程为12422=+y x .(2)由已知及(1)得(1+2k 2)x 2-4k 2x +2k 2-4=0.设点M ,N 的坐标分别为(x 1,y 1),(x 2,y 2),则y 1=k (x 1-1),y 2=k (x 2-1),x 1+x 2=22214k k +,x 1x 2=222142k k +-.所以]4))[(1(212212x x x x k MN -++==22221)64)(1(2kk k +++.又因为点A (2,0)到直线y =k (x -1)的距离21kk d +=,所以△AMN 的面积为22216421k k k d MN S ++=⋅=.由310216422=++k k k 解得k =±1.21. 解析:,ln 1)(,1)1(x x x f a --==当1≥x 时,.011)(,ln 1)('≥-=--=xx f x x x f )(x f ∴在区间),1[+∞上是递增的当10<<x 时,.011)(,ln 1)('<--=--=xx f x x x f )(x f ∴在区间(0,1)上是递减的故1=a 时,)(x f 的递增区间为),1[+∞,递减区间为(0,1),.0)1()(min ==f x f (2)①若,1≥a当a x ≥时,.011)(,ln )('≥-=--=xx f x a x x f )(x f ∴在区间),[+∞a 上是递增的当a x <<0时,.011)(,ln )('<--=--=xx f x x a x f )(x f ∴在区间),0(a 上是递减的②若,10<<a当a x ≥时,xx x x f x a x x f 111)(,ln )('-=-=--=, 当1>x 时,,0)('>x f 当1<<x a 时,,0)('<x f则)(x f 在区间),1[+∞上是递增的,在区间)1,[a 上是递减的; 当a x <<0时,.011)(,ln )('<--=--=xx f x x a x f )(x f ∴在区间),0(a 上是递减的,而)(x f 在a x =处有意义,则)(x f 在区间),1[+∞上是递增的,在区间)1,0(上是递减的. 综上,当1≥a 时,)(x f 的递增区间为),[+∞a ,递减区间为),0(a ; 当10<<a 时,)(x f 的递增区间为),1[+∞,递减区间为)1,0(; 证明:(3)由(1)可知,当1,1>=x a 时,有0ln 1>--x x ,即xx x 11ln -<, ∴222222ln 33ln 22ln nn +++ 22211311211n -++-+-< =)13121(1222n n +++-- ])1(1431321[1+⨯++⨯+⨯--<n n n)11141313121(1+-++-+---=n n n )1(2)12)(1()1121(1++-=+---=n n n n n 故222222ln 33ln 22ln nn +++ <)1(2)12)(1(++-n n n ,2≥∈*n N n 且。
