小学一年级奥数-几何.docx
小学奥数几何专题
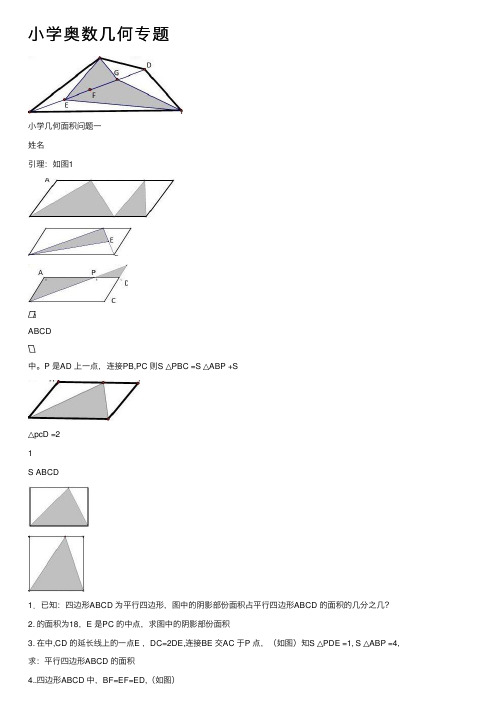
⼩学奥数⼏何专题⼩学⼏何⾯积问题⼀姓名引理:如图1ABCD中。
P 是AD 上⼀点,连接PB,PC 则S △PBC =S △ABP +S△pcD =21S ABCD1.已知:四边形ABCD 为平⾏四边形,图中的阴影部份⾯积占平⾏四边形ABCD 的⾯积的⼏分之⼏?2. 的⾯积为18,E 是PC 的中点,求图中的阴影部份⾯积3. 在中,CD 的延长线上的⼀点E ,DC=2DE,连接BE 交AC 于P 点,(如图)知S △PDE =1, S △ABP =4,求:平⾏四边形ABCD 的⾯积4..四边形ABCD 中,BF=EF=ED,(如图)(1) 若S 四边形ABCD =15则S 阴 = (2)若S △AEF + S △BFC =15 则S 四边形ABCD =(第⼀题图)(3)若S △AEF= 3 S △BFC =2 则S 四边形ABCD =5. 四边形ABCD 的对⾓线BD 被E,F ,G 三点四等份,(如图)若四边形AECG=15 则S 四边形ABCD =E P 图1ADCB(适应长⽅形、正⽅形)BGBFC AED6.四边形ABCD 的对⾓线BD 被E,F ,G 三点四等份,(如图)若阴影部份⾯积为15 则S 四边形ABCD =7.若ABCD 为正⽅形,F 是DC 的中点,已知:S △BFC = 1 (1)则S 四边形ADFB =(2) S △DFE =(3) S △AEB =8.直⾓梯形ABCD 中.AE=ED,BC=18,AD=8,CD=6,且BF=2FC,S △GED =S △GFC .求S 阴=⼩学⼏何⾯积问题⼆姓名 1.如图S △AEF= 2, AB=3AE CF=3EF 则S △ABC=2. 如图S △BDE=30 ,AB=2AE , DC=4AC 则S △ABC=3.正⽅形ABCD 中,E,F,G 为BC 边上四等份点, M,N,P 为对⾓线AC 上的四等份点(如图)若S 正⽅形ABCD=32 则S △NGP=4.已知:S △ABC=30 D 是BC 的中点 AE=2ED 则S △BDE=ACBD第1题第2题5. 已知:AD=DB DE=3EC AF=3FE 若S △ABC =160 求S △EFC =6.已知:在△ABC 中,FC=3AF EC=2BE BD=DF 若S △DFE=3则S △ABC=7.ABCD 为平⾏四边形,AG=GC,BE=EF=FC,若S △GEF =2,则S ABCD =8.ABCD 是梯形,AD // BC(如图)则S △AOB= S △AOD= (第8题)9. ABCD是梯形,AD // BC(如图)则S △DOC= S △BOC= (第9题)10.ABCD 是梯形,AD // BC(如图),且BO=3OD, S △AOB=15则S 梯ABCD=(第10题)BACACC CB CCCCBC L 2L 111. 如图BD=DE, EC=3EF AF=2FD若△DFE 的⾯积等于1 则△ABC 的⾯积为(第11题)⼩学⼏何⾯积问题三姓名1.在梯形ABCD 中,AD//BC,图中阴影部分的⾯积为4,OC=2AO, 求 S 梯ABCD = 2在梯形ABCD 中,AD//BC,S △BOC=14 OC=2AO 求 S 梯ABCD =3. 在梯形ABCD 中,AD//BC,S △AOB=14 OC=3AO 求 S 梯ABCD =4.在梯形ABCD 中,AD//BC,图中阴影部分的⾯积为30,OC=3AO,S △AOB =6求S 空=5.读⼀读:A 若直线L 1//L 2 (如图⼀)⼀.当⾼不变,底扩⼤(或缩⼩)K 倍。
小学奥数平面几何

所以
S△ ADN
1 3
S△
ABN
1 3
1 7
S△
ABC
1 21
S△
ABC
同理
S△BEQ
1 21 S△ABC
在∆ABC中,根据燕尾定理,S△ABP : S△ACP BF : CF 1: 2 S△ABP : S△CBP AI : CI 1: 2
所以 S△ABP
1 5 S△ABC
所以 S五边形DNPQE
A
A
CD E B
FG
CD E
F
G
B
【解析】连接AF,BD, 根据题意可知CF=5+7+15=27,DG=7+15+6;
所以,SBEF
15 27
SCBF
SBEC
12 27
SCBF
SAEG
21 28 SADG
SAED
7 28 SADG
于是:
21 28
SADG
15 27 SCBF
65
7
12
28 SADG 27 SCBF 38
A
B
CD
④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的 平行四边形);
⑤三角形面积等于与它等底等高的平行四边形面积的一半;
⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底 相等,面积比等于它们的高之比.
3
.
二、鸟头定理
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在∆ABC中,D,E分别AB,AC是上的点如图 ⑴(或D在BA的延长线上,E在
一年级上册数学试题-奥数几何:小棒游戏

小棒游戏知识框架用火柴棒可以拼搭成各种有趣的图形,这些图形随着火柴棒的移动、增减,会发出意想不到的变化,这类游戏非常有趣、益智,你也来试试看。
例题精讲【例1】用两根小棍,摆成一个锐角、一个直角、一个钝角。
【考点】小棒游戏【难度】1星【题型】解答题【解析】角是由从一点引出的两条射线构成的。
直角的两边互相垂直,三角板有一个角就是这样的直角。
教室里天花板上的角都是直角。
锐角比直角小,钝角比直角大。
【答案】【例2】用四根小棍摆出两条平行直线,再摆出两条相交直线。
【考点】小棒游戏【难度】1星【题型】解答题【解析】两条直线互相平行,没有交点,无论延伸多远都不相交。
两条直线相交,只有一个交点。
【答案】【例3】用小棍摆出一个三角形、一个正方形、一个菱形、一个长方形、一个平行四边形、一个等腰梯形、一个五边形、一个六边形、一个八边形。
【考点】小棒游戏【难度】1星【题型】解答题【解析】三角形最少要三根小棍,还可以用更多的方法。
正方形最少需要四根小棍,还可以是八根,十六根……等等,需要注意摆放的四个角的角度是直角。
菱形最少需要四根小棍,还可以是八根,十六根……等等。
长方形最少需要六根小棍,可以发散孩子的思维。
以及需要注意角度问题。
平行四边形最少需要四根小棍,可以与正方形、菱形、长方形比较分析。
等腰梯形最少需要5根小棍,需要注意上底下底平行。
五边形最少需要5根小棍,可以发散孩子的思维,多动手摆一摆。
六边形最少需要6根小棍,可以发散孩子的思维,多动手摆一摆。
八边形最少需要8根小棍,可以发散孩子的思维,多动手摆一摆。
【答案】答案不唯一。
【例4】用三根小棍可以摆出一个三角形,如图。
(1)再加两根火柴棍,摆出两个三角形。
(2)再加两根,摆出三个三角形来。
(3)再加两根,摆出五个三角形来。
【考点】小棒游戏【难度】2星【题型】解答题【解析】一个三角形必需三根火柴棍,这样计算,摆两个三角形就需要六根。
但是现在只给你增加两根,却要求你用五根摆出两个三角形,可见必有一根火柴棍要供两个三角形公用才行。
一年级基本立体几何通用版(奥数拓展+测试)

基本立体几何(一)基本立体图形的概括所有点不在同一平面上的图形叫立体图形。
对现实物体认识上的一种抽象,即把现实的物体在只考虑其形状和大小,而忽略其它因素的基础上在平面上的表示。
(二)基本立体图形的表示例1、在括号中写出下面立体图形的名称【练习1.1】下面立体图形名称是________。
知识本源典型例题【练习1.2】下面立体图形名称是______体。
例2、数一数,图中分别有几个,将数字填入()中。
【练习2.1】下面立体图形名称是______体。
【练习2.2】数一数有_______个正方体。
例3、如图所示的三角形旋转形成什么图形?【练习3.1】绕着正方形的一条边旋转得到体。
【练习3.2】绕着长方形的一条边旋转得到体。
例4、把立体与其展开图用线连接起来【练习4.1】下面的图形可以形成体。
【练习4.2】下面的图形可以折叠成的立体图形的名称是。
例5、如图,正方体展开图中数字1对面上是数字_________。
【练习5.1】正方体展开得到个面。
【练习5.2】圆柱体展开,其中有个圆。
例6、由正方体和四棱锥组成的立体,沿着红色虚线展开,画出展开图。
【练习6.1】对一个球体横着切一刀,切得的截面是形【练习6.2】立体图形展开变成图形。
基本立体几何-测试卷A姓名:分数:时间:分钟1、(单选题)下面立体图形名称是_______。
A、长方体B、正方体C、圆柱D、圆锥2、(单选题)下面立体图形的名称是_______。
A、长方体B、正方体C、圆柱D、圆锥3、(单选题)下面立体图形的名称是_______。
A、长方体B、正方体C、圆柱D、圆锥4、数一数,下图中有_______个正方体。
5、(单选题)绕着正方形的一条边旋转得到_________。
A、长方体B、正方体C、圆柱D、圆锥6、(单选题)绕着长方形的一条边旋转得到_________。
A、长方体B、正方体C、圆柱D、圆锥7、(单选题)下面的图形可以形成_________立体图形。
小学奥数教学方案一年级简单几何

小学奥数教学方案一年级简单几何一、引言在小学一年级的数学教学中,简单几何是一个重要的内容。
通过学习几何,学生能够提高空间思维能力,培养观察和分析问题的能力。
本文将介绍一种适合一年级学生的奥数教学方案,旨在帮助他们在简单几何方面取得更好的学习成果。
二、教学目标1.了解基本几何概念,如点、线、面;2.辨别不同形状的基本几何图形;3.运用基本几何知识解决简单问题;4.培养学生的观察和推理能力。
三、教学过程1.引入通过展示不同的几何图形图片,激发学生对几何的兴趣和好奇心。
引导学生观察图形的特点,并与日常生活中的实物进行联系,以便更好地理解几何概念。
2.学习点、线、面的概念通过实物和图片,向学生介绍点、线、面的概念。
学生可以观察周围的物体,辨别其中的点、线、面,并进行分类。
3.学习基本几何图形针对一年级学生的认知能力,教师可以教授一些基本的几何图形,如圆形、正方形、长方形和三角形。
通过展示实物示例和图片,引导学生认识这些图形的特点。
4.练习图形分类给学生一些几何图形的图片,让他们进行分类,激发他们观察和分析问题的能力。
教师可以提供一些提示,指导学生发现图形的共同特点,并将它们分组。
5.游戏与实践设计一些趣味的游戏和实践活动,帮助学生巩固所学的几何知识。
例如,让学生在教室或校园里寻找不同的几何图形,或者指导他们用纸板和颜色纸制作几何图形。
6.应用练习给学生一些简单的几何问题,让他们运用所学的几何知识解决。
例如,“在你的环境中找出一个圆形的物体”,或者“用正方形的纸板拼凑出一个长方形”。
7.总结对本节课的内容进行总结,并再次强调学生在几何学习中所取得的进步。
可以让学生分享他们在观察、分析和解决问题过程中的体验和思考。
四、教学评估教师可以通过观察学生的参与情况、回答问题的能力以及实践活动的表现,对学生的几何学习进行评估。
可以给学生一些简单的练习题,以检测他们是否掌握了基本几何概念和技能。
五、延伸活动为了进一步培养学生的几何能力,可以组织一些延伸活动。
小学奥数可以分为计算、计数、数论、几何.docx

小学奥数可以分算、数、数、几何、用、行程、合七大板,其中必掌握的三十六个知点,内容从和差倍、年到循小数,包含了小学奥数七个模的知。
以下是小学奥数知清:2、年的三个基本特征:①两个人的年差是不的;②两个人的年是同增加或者同减少的;③两个人的年的倍数是生化的;3、一基本特点:中有一个不的量,一般是那个“ 一量”,目一般用“照的速度”⋯⋯等来表示。
关:根据目中的条件确定并求出一量;5、兔同基本概念:兔同又称置、假,就是把假的那部分置出来;基本思路:①假,即假某种象存在(甲和乙一或者乙和甲一):②假后,生了和目条件不同的差,找出个差是多少;③每个事物造成的差是固定的,从而找出出个差的原因;④再根据两个差作适当的整,消去出的差。
基本公式:①把所有假成兔子:数=(兔脚数× 数-脚数)÷(兔脚数-脚数)②把所有兔子假成:兔数=(脚数一脚数× 数)÷(兔脚数一脚数)关:找出量的差与位量的差。
6、盈基本概念:一定量的对象,按照某种标准分组,产生一种结果:按照另一种标准分组,又产生一种结果,由于分组的标准不同,造成结果的差异,由它们的关系求对象分组的组数或对象的总量.基本思路:先将两种分配方案进行比较,分析由于标准的差异造成结果的变化,根据这个关系求出参加分配的总份数,然后根据题意求出对象的总量.基本题型:①一次有余数,另一次不足;基本公式:总份数=(余数+不足数)÷两次每份数的差②当两次都有余数;基本公式:总份数=(较大余数一较小余数)÷两次每份数的差③当两次都不足;基本公式:总份数=(较大不足数一较小不足数)÷两次每份数的差基本特点:对象总量和总的组数是不变的。
关键问题:确定对象总量和总的组数。
第二部分(知识点7-11 )7、牛吃草问题基本思路:假设每头牛吃草的速度为“ 1”份,根据两次不同的吃法,求出其中的总草量的差;再找出造成这种差异的原因,即可确定草的生长速度和总草量。
小学的奥数-几何五大模型(鸟头模型)

模型二鸟头模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图⑴(或D 在BA 的延长线上,E 在AC 上如图 2),则:():()ABC ADES S AB AC AD AE △△EDCBAEDCBA图⑴图⑵【例1】如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB,:4:7AE AC,16ADES △平方厘米,求ABC △的面积.EDCBAEDCB A【解析】连接BE ,::2:5(24):(54)ADE ABES S AD AB △△,::4:7(45):(75)ABE ABC S S AE AC△△,所以:(24):(75)ADE ABCS S △△,设8ADES △份,则35ABCS △份,16ADE S △平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.三角形等高模型与鸟头模型【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?E D CBA A BCD E【解析】连接BE .∵3EC AE ∴3ABCABESS又∵5AB AD ∴515ADEABEABCSSS,∴1515ABCADESS.【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ,3BE,6AE,乙部分面积是甲部分面积的几倍?乙甲E D CBAABCDE甲乙【解析】连接AD .∵3BE ,6AE ∴3AB BE ,3ABDBDES S又∵4BD DC ,∴2ABCABDSS,∴6ABCBDE SS ,5S S 乙甲.【例2】如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD,:3:2AE EC ,12ADE S △平方厘米,求ABC △的面积.EDC B A EDCB A【解析】连接BE ,::2:5(23):(53)ADE ABES S AD AB △△::3:(32)(35):(32)5ABE ABCS S AE AC△△,所以:(32):5(32)6:25ADE ABC S S △△,设6ADES △份,则25ABCS △份,12ADES △平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例3】如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AFCF ,三角形AFE(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?EFDCBA【解析】连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326()倍.因此,平行四边形的面积为8648(平方厘米).【例4】已知DEF △的面积为7平方厘米,,2,3BECE AD BD CF AF ,求ABC △的面积.FED CBA【解析】:():()(11):(23)1:6BDE ABCS S BD BE BA BC △△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA △△:():()(21):(34)1:6ADF ABC S S ADAF ABAC △△设24ABCS △份,则4BDES △份,4ADF S △份,9CEFS △份,244497DEFS △份,恰好是7平方厘米,所以24ABCS △平方厘米【例5】如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE,:3:2BC CD,三角形BDE 的面积是多少?AB EC DDC EB A【解析】由于180ABC DBE,所以可以用共角定理,设2AB 份,3BC份,则5BE 份,325BD 份,由共角定理:():()(23):(55)6:25ABC BDES S ABBC BE BD △△,设6ABCS △份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5平方厘米,三角形BDE 的面积是12.5平方厘米【例6】(2007年”走美”五年级初赛试题)如图所示,正方形ABCD 边长为6厘米,13AEAC ,13CF BC .三角形DEF 的面积为_______平方厘米.FED C BA【解析】由题意知13AEAC 、13CFBC ,可得23CEAC .根据”共角定理”可得,:():()12:(33)2:9CEF ABC S S CF CE CB AC △△;而66218ABCS △;所以4CEF S △;同理得,:2:3CDE ACD S S △△;,183212CDE S △,6CDF S △故412610DEFCEFDECDFCS S S S △△△△(平方厘米).【例7】如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB ;延长BC 至E ,使2CEBC ;延长CA 至F ,使3AF AC ,求三角形DEF 的面积.F EDCB A AB CDEF【解析】(法1)本题是性质的反复使用.连接AE 、CD .∵11ABC DBC S S ,1ABCS ,∴S1DBC.同理可得其它,最后三角形DEF 的面积18.(法2)用共角定理∵在ABC 和CFE 中,ACB 与FCE 互补,∴111428ABC FCES AC BC SFC CE .又1ABCS,所以8FCES.同理可得6ADFS ,3BDES.所以186318DEFABCFCEADFBDESS SSS.【例8】如图,平行四边形ABCD ,BE AB ,2CF CB ,3GD DC ,4HA AD ,平行四边形ABCD 的面积是2,求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CDEF【解析】连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC 与FBE 互补,∴111133ABC FBES AB BC S BE BF△△.又1ABC S △,所以3FBES △.同理可得8GCF S △,15DHGS △,8AEH S △.所以8815+3+236EFGH AEH CFG DHGBEFABCDS S S S S S △△△△.所以213618ABCD EFGHS S .【例9】如图,四边形EFGH 的面积是66平方米,EAAB ,CBBF ,DCCG ,HD DA ,求四边形ABCD 的面积.H GFED CB A A BCDEFG H 【解析】连接BD .由共角定理得:():()1:2BCD CGFS S CD CB CGCF △△,即2CGFCDBS S △△同理:1:2ABD AHE S S △△,即2AHE ABDS S △△所以2()2AHECGFCBDADB ABCDS S S S S △△△△四边形连接AC ,同理可以得到2DHGBEFABCDS S S △△四边形5AHECGFHDGBEFEFGHABCDABCDS S S S S S S △△△△四边形四边形四边形所以66513.2ABCDS 四边形平方米【例10】如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是.A B CD EF GHA B CD EFGH【解析】连接AC 、BD .由于2BE AB ,2BFBC ,于是4BEFABCS S,同理4HDGADCSS.于是444BEFHDGABC ADCABCD SS S SS .再由于3AE AB ,3AH AD ,于是9AEHABDSS,同理9CFGCBDSS.于是999AEHCFG ABDCBDABCD SS S S S .那么491260EFGHBEFHDG AEHCFGABCDABCD ABCDABCDABCDS SSSSS S S S S .【例11】如图,在ABC △中,延长AB 至D ,使BD AB ,延长BC 至E ,使12CEBC ,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【解析】∵在ABC △和CFE △中,ACB 与FCE 互补,∴224111ABC FCES AC BC S FC CE △△.又2ABCS,所以0.5FCES.同理可得2ADF S △,3BDES △.所以20.532 3.5DEFABC CEF DEB ADF S S S S S △△△△△【例12】如图,1ABCS △,5BCBD ,4AC EC ,DGGSSE ,AFFG .求FGSS.SGF E DCBA 【解析】本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGSS △.【例13】如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCDEF GABCDEF G【解析】连接AF 、EG .因为218164BCFCDES S △△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEFS,8EFGS,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFCS,32ABFE S ,24ABFS,所以12ABGS平方厘米.【例14】四个面积为1的正六边形如图摆放,求阴影三角形的面积.HGFEDCB A【解析】如图,将原图扩展成一个大正三角形DEF ,则AGF 与CEH 都是正三角形.假设正六边形的边长为为a ,则AGF 与CEH 的边长都是4a ,所以大正三角形DEF 的边长为4217,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF 的面积为496.由于4FAa ,3FBa ,所以AFB 与三角形DEF 的面积之比为43127749.同理可知BDC、AEC与三角形DEF的面积之比都为1249,所以ABC的面积占三角形DEF面积的1213134949,所以ABC的面积的面积为4913136496.【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE的面积是.BDCEA【解析】从图中可以看出,虚线AB和虚线CD外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC和虚线DE外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363,所以五边形的面积是12103633.。
最新小学奥数之立体几何问题

立体图形⑴ 立体图形的表面积和体积公式长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED BA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥【例 1】 如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?改.又是多少?【例 2】右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)练习:在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【例 3】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【例 4】一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?(锯一次增加两个面)练习.一个表面积为256cm的长方体如图切成27个小长方体,这27个小长方体表面积的和是2cm.表面积最小:互相重合的面最多时表面积最小【例 5】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?体积:例1. 如图11-6,从长为13厘米,宽为9厘米的长方形硬纸板的四角去掉边长2米的正方形,然后,沿虚线折叠成长方体容器.这个容器的体积是多少立方厘米?例2. 某工人用薄木板钉成一个长方体的邮件包装箱,并用尼龙编织条如图11-9所示在三个方向上加固.所用尼龙编织条的长分别为365厘米、405厘米、485厘米.若每个尼龙条加固时接头处都重叠5厘米,则这个长方体包装箱的体积是多少立方米?⑵不规则立体图形的表面积整体观照法例1. 如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.例2. 如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.例3.把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.例4.用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?例5.下图是由18个边长为1厘米的小正方体拼成的,求它的表面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小一奥几何1.如下图所示,小猫的照片被剪掉了4块.①处应该补的是哪块?B. C. D.2.如下图所示,小猫的照片被剪掉了4块.③处应该补的是哪块?B. C. D.3.如下图所示,小猫的照片被剪掉了4块.④处应该补的是哪块?A. B. C. D.4.哪个选项的图形,可以和图1拼成一个圆形呢?A. B. C.5.哪个选项的图形可以和图1拼成一个圆形呢?A. B. C.7.下列选项中,哪个图形可以和②图形拼成①图形呢?①8.下列选项中,哪个图形可以和②图形拼成①图形呢?10.下列选项中,可以和图2拼成仁牯的是哪个呢?11.下列选项中,可以和图2拼成《上的是哪个呢?1.下面四个立体图形中,哪个是正方体?3.下面四个立体图形中,哪个是圆柱体?4.下面三个立体图形中,最容易滚动的是哪个?5.下面三个立体图形中,最不容易滚动的是哪个?6.下面三个立体图形中,最容易滚动的是哪个?7.下面两组积木,比较牢固的是哪组呢?® ② A.① B.②8.下面两组积木,比较牢固的是哪组呢?①② A.① B.②9.下面两组积木,比较不牢固的是哪组呢?A.①B.②10.将下面的圆柱体竖着切一刀,切出来的面是什么形状呢?1.这个飞机从上面看可能是什么样子的呢?2.这个飞机从正面看可能是什么样子的呢?3.这个飞机从左面看可能是什么样子的呢?4.这个圆柱从上面看可能是什么样子的呢?5.这个圆柱从左面看可能是什么样子的呢?6.这个长方体从正面看是什么样子的呢?,则它从后面看是什么样子呢?,则它从右面看是什么样子呢?9.—个物体从右面看是,则它从左面看是什么样子呢?A.尸B.C.气]D.尸10.下面这个积木从右面看是什么样子的?12.下面这个积木从上面看是什么样子的?C.A.①④B.②③C.①③④D.①②③④2.下面图中,哪些是角?A.①③B.②④C.②③④D.①②③④3.下面图中,哪些是角?① ② ③A.①②B.②③④C.③④D.①②③④4.下图中哪个角比较大?4厂5.下图中哪个角比较大?② A.① B.② C. 一样大6.下图中哪个角比较大?A.①B.②C.—样大7.下图是哪种角?—— A.锐角B.直角C.钝角8.下图是哪种角?A.锐角B,直角C.钝角9.下图是哪种角?A.锐角B.直角C.钝角10.下面的图形共有几个角?A. 4B. 5C. 6D. 711.下面的图形共有几个角?LJ A. 4 B. 5 C. 6 D. 712.下面的图形共有几个角?1.下面这个七巧板中有几个单独的大三角形?A. 1B. 2C. 3D. 42.下面这个七巧板中有几个单独的正方形?A. 1B. 2C. 3D. 43.下面这个七巧板中有几个单独的小三角形A. 4B. 3C. 2D. 14.左图是七巧板中的2个小三角形,你能用它们拼出七巧板中的哪些图形?(两块都用上)B. 4 或7 D. 4或6或75.左图是七巧板中的2个小三角形和1个中三角形,你能用它们拼出七巧板中的哪些图形?(三块都用上)A. 1B. 1或2C. 4 或6D. 1或4 或66.左图是七巧板中的2个小三角形和1个正方形,你能用它们拼出七巧板中的哪些图形?(三块都用上)ZI、口 A. 1 B. 4 或6 C. 1 或2 D. 1 或4 或67.左图中红色部分是七巧板中的哪一块?A. 3 或5B. 4C. 7D. 1 或28.左图中红色部分是七巧板中的哪一块?A. 3 或5B. 4C. 7D. 1 或29.左图中红色部分是七巧板中的哪一块?A. 3 或5B. 4C. 6D. 1 或210.把右图七巧板中的序号填入左图对应的图形中,哪个选项是正确的?A.①B.②C.③D.④2.将下图折成正方体后,红色部分的相对面是哪个A.①B.②C.③D.④3.将下图折成正方体后,红色部分的相对面是哪个?A.①B.②C.③D.④4.将下图折成正方体后,红色部分的相对面是哪个?A.①B.②C.③D.④①③④A.①B.②C.③D.④6.将下图折成正方体后,红色部分的相对面是哪个?A.①B.②C.③D.④7.将下图折成正方体后,红色部分的相对面是哪个?A.①B.②C.③D.④8.将下图折成正方体后,红色部分的相对面是哪个?①A.①B.②C.③D.④9.将下图折成正方体后,红色部分的相对面是哪个?①④③A.①B.②C.③D.④10.将下图折成正方体后,红色部分的相对面是哪个?A.①B.②C.③D.④A.①B.②C.③D.④12.将下图折成正方体后,红色部分的相对面是哪个?A.①B.②C.③D.④13.下面哪个图形不能折成正方体?14.下面哪个图形不能折成正方体?15.下面哪个图形不能折成正方体?A. B.16.下面哪个图形不能折成正方体?A. B. ------------------17.下面哪个图形不能折成正方体?A. B.18.下面哪个图形不能折成正方体?B.19.下面哪个图形不能折成正方体?A. B.20.下面哪个图形不能折成正方体?A.21.下面哪个图形不能折成正方体?A.22.下面哪个图形不能折成正方体?23.下面哪个图形不能折成正方体?A.24.下面哪个图形不能折成正方体?1. 用两个完全相同的小正方形拼图.下列选项中,不符合图形剪拼规则的是哪个?2. 用两个完全相同的小正方形拼图.下列选项中,不符合图形剪拼规则的是哪个?3. 用两个完全相同的小正方形拼图.下列选项中,不符合图形剪拼规则的是哪个4. 用三个完全相同的小正方形拼图.下列选项中,不符合图形剪拼规则的是哪个?A LL ±J B.田 C.罟5. 用三个完全相同的小正方形拼图.下列选项中,不符合图形剪拼规则的是哪个?6. 用三个完全相同的小正方形拼图.下列选项中,不符合图形剪拼规则的是哪个?A. —|1Z|—B.C. |~|7. 用四个完全相同的小正方形拼图.下列选项中,不能拼成的是哪个?8. 用四个完全相同的小正方形拼图.下列选项中,不能拼成的是哪个?.尹C A. B,LLy DH Z H A. A. A.D.9. 用四个完全相同的小正方形拼图.下列选项中,不能拼成的是哪个?10. 如下图所示,用四个完全相同的小三角形拼图(三角形可以任意旋转).下列选项中,不能拼成的是哪个? A -NM B. /I/N C.\^\ D. ZJZ\ 11. 如下图所示,用四个完全相同的小三角形拼图(三角形可以任意旋转).下列选项中,不能12. 如下图所示,用四个完全相同的小三角形拼图(三角形可以任意旋转).下列选项中,不能 大小相等的2个图形.下列选项中,哪种分法是不正确的?15. 把下面的长方形分成形状相同、大小相等的2个图形.下列选项中,哪种分法是不正确的?DC B 14.把下面的长方形分成形状相同、 大小相等的2个图形.下列选项中,哪种分法是不正确的?A. C.A.13.把下面的正方形分成形状相同、16. 把下面的正方形分成形状相同、大小相等的4个图形.下列选项中,哪种分法是不正确的? 17. 把下面的长方形分成形状相同、大小相等的4个图形.下列选项中,哪种分法是不正确的? .下列选项中,哪种分法是不正确的?20. 把下面的正六边形分成形状相同、大小相等的4个图形.下列选项中,哪种分法是不正确的?21. 把下面的正六边形分成形状相同、大小相等的4个图形.下列选项中,哪种分法是不正确的?22. 把下面的图形分成形状相同、大小相等的4个图形.下列选项中,哪种分法是不正确的?18.把下面的长方形分成形状相同、大小相等的4个图形 19.把下面的正六边形分成形状相同、大小相等的4个图形.下列选项中,哪种分法是不正确的?23.把下面的图形分成形状相同、大小相等的4个图形.下列选项中,哪种分法是不正确的?24.把下面的图形分成形状相同、大小相等的4个图形.下列选项中,哪种分法是不正确的?25.请把下面的正方形分割成形状相同、大小相等的3个图形,使每个图形中都含有一只小青26.请把下面的正方形分割成形状相同、大小相等的3个图形,使每个图形中都含有一只小青蛙.下列选项中,哪种分割方法是不正确的?27.请把下面的正方形分割成形状相同、大小相等的3个图形,使每个图形中都含有一只小青蛙.下列选项中,哪种分割方法是正确的?29.请把下面的长方形分割成形状相同、大小相等的4个图形,使每个图形中都含有一只小青蛙.下列选项中,哪种分割方法是正确的?仰rx.30.请把下面的长方形分割成形状相同、大小相等的4个图形,使每个图形中都含有一只小青31.请把下面的正方形分割成形状相同、大小相等的4个图形,使每个图形中都含有一只小猫.下列选项中,哪种分割方法是正确的?32.请把下面的正方形分割成形状相同、大小相等的4个图形,使每个图形中都含有一只小猫.下列选项中,哪种分割方法是正确的?A. B. C.列选项中,哪种分割方法是正确的?34.请把下面的正方形分割成形状相同、大小相等的4个图形,使每个图形中都含有一只小猫.下 列选项中,哪种分割方法是正确的?列选项中,哪种分割方法是正确的?36.请把下面的正方形分割成形状相同、大小相等的4个图形,使每个图形中都含有一只小猫.下 列选项中,哪种分割方法是正确的?U'--- III&35.请把下面的正方形分割成形状相同、大小相等的4个图形,使每个图形中都含有一只小猫.下。
