20稳恒磁场二解答
高考物理稳恒电流题20套(带答案)含解析

高考物理稳恒电流题20套(带答案)含解析一、稳恒电流专项训练1. 4~1.0T 范围内,磁敏电阻的阻值随磁感应强度线性变化(或均匀变化) (4)磁场反向,磁敏电阻的阻值不变. 【解析】(1)当B =0.6T 时,磁敏电阻阻值约为6×150Ω=900Ω,当B =1.0T 时,磁敏电阻阻值约为11×150Ω=1650Ω.由于滑动变阻器全电阻20Ω比磁敏电阻的阻值小得多,故滑动变阻器选择分压式接法;由于x VA xR R R R >,所以电流表应内接.电路图如图所示.(2)方法一:根据表中数据可以求得磁敏电阻的阻值分别为:130.4515000.3010R -=Ω=Ω⨯,230.911516.70.6010R -=Ω=Ω⨯,331.5015001.0010R -=Ω=Ω⨯,431.791491.71.2010R -=Ω=Ω⨯,532.7115051.8010R -=Ω=Ω⨯, 故电阻的测量值为1234515035R R R R R R ++++=Ω=Ω(1500-1503Ω都算正确.) 由于0150010150R R ==,从图1中可以读出B =0.9T 方法二:作出表中的数据作出U -I 图象,图象的斜率即为电阻(略).(3)在0~0.2T 范围,图线为曲线,故磁敏电阻的阻值随磁感应强度非线性变化(或非均匀变化);在0.4~1.0T 范围内,图线为直线,故磁敏电阻的阻值随磁感应强度线性变化(或均匀变化);(4)从图3中可以看出,当加磁感应强度大小相等、方向相反的磁场时,磁敏电阻的阻值相等,故磁敏电阻的阻值与磁场方向无关.本题以最新的科技成果为背景,考查了电学实验的设计能力和实验数据的处理能力.从新材料、新情景中舍弃无关因素,会看到这是一个考查伏安法测电阻的电路设计问题,及如何根据测得的U 、I 值求电阻.第(3)、(4)问则考查考生思维的灵敏度和创新能力.总之本题是一道以能力立意为主,充分体现新课程标准的三维目标,考查学生的创新能力、获取新知识的能力、建模能力的一道好题.2.要描绘某电学元件(最大电流不超过6mA,最大电压不超过7V)的伏安特性曲线,设计电路如图,图中定值电阻R为1KΩ,用于限流;电流表量程为10mA,内阻约为5Ω;电压表(未画出)量程为10V,内阻约为10KΩ;电源电动势E为12V,内阻不计。
稳恒磁场练习题答案
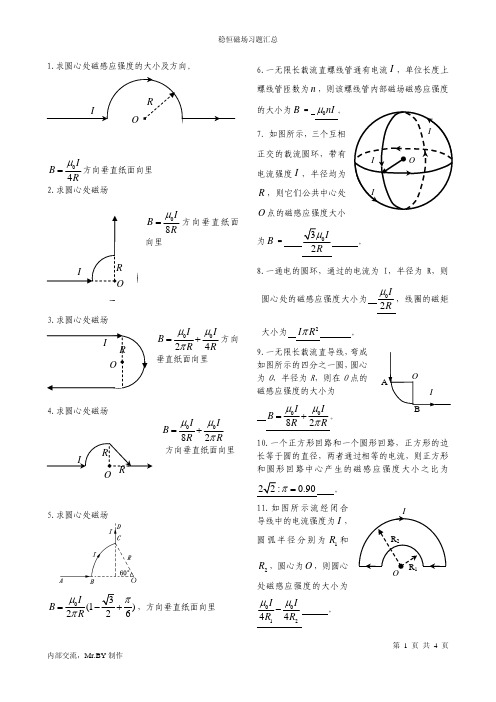
1.求圆心处磁感应强度的大小及方向。
04B R=方向垂直纸面向里2.求圆心处磁场08IB Rμ=方向垂直纸面向里3.求圆心处磁场024I IB R Rμμπ=+方向垂直纸面向里4.求圆心处磁场0082IIB RRμμπ=+方向垂直纸面向里5.求圆心处磁场(1226I B R μππ=−+,方向垂直纸面向里 6.一无限长载流直螺线管通有电流I ,单位长度上螺线管匝数为n ,则该螺线管内部磁场磁感应强度的大小为B = 0nI μ。
7.如图所示,三个互相正交的载流圆环,带有电流强度I ,半径均为R ,则它们公共中心处O 点的磁感应强度大小为B =02IR。
8.一通电的圆环,通过的电流为I,半径为R,则圆心处的磁感应强度大小为02IRμ,线圈的磁矩大小为 2I R π 。
9.一无限长载流直导线,弯成如图所示的四分之一圆,圆心为O ,半径为R ,则在O 点的磁感应强度的大小为 0082IIB RRμμπ=+。
10.一个正方形回路和一个圆形回路,正方形的边长等于圆的直径,两者通过相等的电流,则正方形和圆形回路中心产生的磁感应强度大小之比为11.如图所示流经闭合导线中的电流强度为I ,圆弧半径分别为1R 和2R ,圆心为O ,则圆心001244IIR R μμ−。
12.一载有电流强度为I 的细导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管,两螺线管单位长度上的匝数相等。
设2R r =,则两螺线管内部的磁感应强度的大小比值为:RrB B =1:1 。
13. 在同一平面上有三根等距离放置的长通电导线,如图所示,导线1、2、3分别载有1A 、2A 、3A 的电流,它们所受的安培力分别为1F 、2F 、3F ,则12F F = 7/8 ;13F F = 7/15 ;23F F = 8/15 。
(0174F d μπ=,0284F d μπ=,03154F dμπ=;故1278F F =,13715F F =,23815F F =) 14. 如图所示,长直导线中通有稳恒电流1I ,在其旁边有一导线段ab ,长为L ,距长直导线距离为d ,当它通有稳恒电流2I 时,该导线ab 所受磁力大小为012ln 2I I d Ld μπ+ 。
习题第06章(稳恒磁场)-参考答案.

第六章 稳恒磁场思考题6-1 为什么不能把磁场作用于运动电荷的力的方向,定义为磁感强度的方向?答:对于给定的电流分布来说,它所激发的磁场分布是一定的,场中任一点的B 有确定的方向和确定的大小,与该点有无运动电荷通过无关。
而运动电荷在给定的磁场中某点 P 所受的磁力F ,无论就大小或方向而言,都与运动电荷有关。
当电荷以速度v 沿不同方向通过P 点时,v 的大小一般不等,方向一般说也要改变。
可见,如果用v 的方向来定义B 的方向,则B 的方向不确定,所以我们不能把作用于运动电荷的磁力方向定义为磁感应强度B 的方向。
6-2 从毕奥-萨伐尔定律能导出无限长直电流的磁场公式aIB πμ2=。
当考察点无限接近导线(0→a )时,则∞→B ,这是没有物理意义的,如何解释?答:毕奥-萨伐尔定律是关于部分电流(电流元)产生部分电场(dB )的公式,在考察点无限接近导线(0→a )时,电流元的假设不再成立了,所以也不能应用由毕奥-萨伐尔定律推导得到的无限长直电流的磁场公式aIB πμ2=。
6-3 试比较点电荷的电场强度公式与毕奥-萨伐尔定律的类似与差别。
根据这两个公式加上场叠加原理就能解决任意的静电场和磁场的空间分布。
从这里,你能否体会到物理学中解决某些问题的基本思想与方法?答:库仑场强公式0204dqr dE rπε=,毕奥一萨伐定律0024Idl r dB r μπ⨯= 类似之处:(1)都是元场源产生场的公式。
一个是电荷元(或点电荷)的场强公式,一个是电流元的磁感应强度的公式。
(2)dE 和dB 大小都是与场源到场点的距离平方成反比。
(3)都是计算E 和B 的基本公式,与场强叠加原理联合使用,原则上可以求解任意分布的电荷的静电场与任意形状的稳恒电流的磁场。
不同之处: (1)库仑场强公式是直接从实验总结出来的。
毕奥一萨伐尔定律是从概括闭合电流磁场的实验数据间接得到的。
(2)电荷元的电场强度dE 的方向与r 方向一致或相反,而电流元的磁感应强度dB 的方向既不是Idl 方向,也不是r 的方向,而是垂直于dl 与r 组成的平面,由右手螺旋法则确定。
第十五章 稳恒磁场自测题答案

第十五章 稳恒磁场一、选择题答案: 1-10 DABAB CCBBD 11-20DCABB BBDAB 二、填空题答案 1. 0 2. 3a x = 3.BIR2 4. 2104.2-⨯ 5. 0 6. I 02μ 7. 2:1 8. απcos 2B R 9.不变10. < 11.RI 20μ 12. qB mv 13. 2:1 14. = 15 k13108.0-⨯ 16 4109-⨯ 17无源有旋18. 1.4A 19. 2 20. I a 2 B/2三、计算题1. 如右图,在一平面上,有一载流导线通有恒定电流I ,电流从左边无穷远流来,流过半径为R 的半圆后,又沿切线方向流向无穷远,求半圆圆心O 处的磁感应强度的大小和方向。
解:如右图,将电流分为ab 、bc 、cd 三段,其中,a 、d 均在无穷远。
各段在O 点产生的磁感应强度分别为:ab 段:B 1=0 (1分) bc 段:大小:RI B 402μ=(2分)方向:垂直纸面向里 (1分) cd 段:大小:RI B πμ403=(2分)方向:垂直纸面向里 (1分) 由磁场叠加原理,得总磁感应强度)1(40321+=++=ππμRI B B B B (2分)方向:垂直纸面向里 (1分)2. 一载有电流I 的长导线弯折成如图所示的形状,CD 为1/4 圆弧,半径为R ,圆心O 在AC 、EF 的延长线上。
求O 点处的磁感应强度。
解:各段电流在O 点产生的磁感应强度分别为:AC 段:B 1=0 (1分) CD 段:大小:RI B 802μ=(2分)方向:垂直纸面向外 (1分) DE 段:大小:RI RI B πμπμ2)135cos 45(cos 224003=-⋅=(2分)方向:垂直纸面向外 (1分) EF 段:B 4=0 (1分) 由磁场叠加原理,得总磁感应强度RI RI B B B B B πμμ28004321+=+++= (1分)方向:垂直纸面向外 (1分)3. 如右图所示,一匝边长为a 的正方形线圈与一无限长直导线共面,置于真空中。
(物理)物理稳恒电流练习题20含解析

(物理)物理稳恒电流练习题20含解析一、稳恒电流专项训练1.如图,ab 和cd 是两条竖直放置的长直光滑金属导轨,MN 和M′N′是两根用细线连接的金属杆,其质量分别为m 和2m.竖直向上的外力F 作用在杆MN 上,使两杆水平静止,并刚好与导轨接触;两杆的总电阻为R ,导轨间距为l.整个装置处在磁感应强度为B 的匀强磁场中,磁场方向与导轨所在平面垂直.导轨电阻可忽略,重力加速度为g.在t =0时刻将细线烧断,保持F 不变,金属杆和导轨始终接触良好.求:(1)细线烧断后,任意时刻两杆运动的速度之比; (2)两杆分别达到的最大速度. 【答案】(1)1221v v = (2)12243mgR v B l = ;22223mgR v B l= 【解析】 【分析】细线烧断前对MN 和M'N'受力分析,得出竖直向上的外力F=3mg ,细线烧断后对MN 和M'N'受力分析,根据动量守恒求出任意时刻两杆运动的速度之比.分析MN 和M'N'的运动过程,找出两杆分别达到最大速度的特点,并求出. 【详解】解:(1)细线烧断前对MN 和M'N'受力分析,由于两杆水平静止,得出竖直向上的外力F=3mg .设某时刻MN 和M'N'速度分别为v 1、v 2. 根据MN 和M'N'动量守恒得出:mv 1﹣2mv 2=0 解得:122v v =: ① (2)细线烧断后,MN 向上做加速运动,M'N'向下做加速运动,由于速度增加,感应电动势增加,MN 和M'N'所受安培力增加,所以加速度在减小.当MN 和M'N'的加速度减为零时,速度最大.对M'N'受力平衡:BIl=2mg②,EI R=③,E=Blv 1+Blv 2 ④ 由①﹣﹣④得:12243mgR v B l =、22223mgRv B l = 【点睛】能够分析物体的受力情况,运用动量守恒求出两个物体速度关系.在直线运动中,速度最大值一般出现在加速度为0的时刻.2.对于同一物理问题,常常可以从宏观与微观两个不同角度进行研究,找出其内在联系,从而更加深刻地理解其物理本质。
物理学第3版习题解答_第6章稳恒磁场

I 2 dr
FBC 方向垂直 BC 向上,大小
FBc
d
0 I1 0 I1 I 2 d a ln 2r 2 d
d a
I 2 dl
0 I1 2r
∵
dl FBC
d a
dr cos 45
∴
a
0 I 2 I1dr II d a 0 1 2 ln 2r cos 45 d 2
B dl 8
a
0
ba
B dl 8 0
B dl 0
c
(1)在各条闭合曲线上,各点 B 的大小不相等. (2)在闭合曲线 C 上各点 B 不为零.只是 B 的环路积分为零而非每点 B 为零
图 6-25 思考题
6-4 图
1
6-5 安培定律 dF Idl B 有任意角度?
线,试指出哪一条是表示顺磁质?哪一条是表示抗磁质?哪一条是表示铁磁质? 答: 曲线Ⅱ是顺磁质,曲线Ⅲ是抗磁质,曲线Ⅰ是铁磁质.
图 6-27
思考题-6-8
2
习题
6-1 如图 6-28 所示的正方形线圈 ABCD,每边长为 a,通有电流 I.求正方形中心 O 处 的磁感应强度。 I A D 解 正方形每一边到 O 点的距离都是 a/2,在 O 点产生的磁场 大小相等、方向相同.以 AD 边为例,利用直线电流的磁场公式:
I1 电阻R2 . I 2 பைடு நூலகம்阻R1 2
I 1 产生 B1 方向 纸面向外
B1
0 I 1 (2 ) , 2R 2
I 2 产生 B2 方向 纸面向里
第5章稳恒磁场答案.
第5章 稳恒磁场5.1 在定义磁感应强度B 的方向时,为什么不将运动电荷受力的方向规定为磁感应强度B 的方向?答:由于运动电荷在磁场中的受力方向与电荷运动方向有关,则不能用来描述磁场的性质,故不能规定该方向为磁感应强度的方向。
5.2 一无限长载流导线所载电流为I ,当它形成如图5.27所示的三种形状时,则o Q P B B B ,,之间的关系为(1) o Q P B B B >> ; (2) o P Q B B B >>; (3) P o Q B B B >> ; (4) P Q o B B B ≥>。
解:aIB P πμ=20 )(22120+πμ=a I B Q )(21200π+πμ=a I BP Q B B B >>∴0,故选(4)。
5.3 在同一根磁感应线上的各点,磁感应强度B 的大小是否处处相同?答:同一磁感应线上的各点,磁感应强度B的大小不一定处处相等。
5.4 磁场的高斯定理⎰⎰=⋅0s d B表示的重要性质是什么?答: ⎰⎰=⋅0s d B表示的重要性质是磁场是无源场,磁感应线是无头无尾的闭合线。
5.5 如图5.28所示 ,两导线中的电流21I I ,均为5A ,对图中所示的三条闭合曲线a ,b ,c 分别写出安培环路定理式等号右边电流的代数和,并说明:(1) 在各条闭合曲线上,各点的磁感应强度B 的大小是否相等? (2) 在闭合曲线 c 上各点的磁感应强度B 是否为零?为什么? 答:电流代数和依次为1212I I I I --,, (1)不相等。
(2)不为零,这是因为与曲线C 环绕的电流代数和IPa图 5.27 题5.2图图5.28 题5.5图为零,只能给出B沿C 的环量为零,C 上各点的磁感应强度是所有电流在相应点产生的,一般不为零。
5.6 在安培定律的数学表示B l Id F d⨯=中,哪两个矢量始终是正交的?哪两个矢量之间可以有任意角?答:BF d l Id F d⊥⊥,l Id 与B之间可以有任意的夹角。
(完整版)稳恒磁场作业习题及参考答案.doc
赵近芳编大学物理学 ch9. 稳恒磁场 作业习题及参考答案9-6 已知磁感应强度B 2.0 Wb ·m -2 的均匀磁场,方向沿x 轴正方向,如题 9-6 图所示.试求:(1) 通过图中 abcd 面的磁通量; (2) 通过图中 befc 面的磁通量; (3)通过图中 aefd 面的磁通量.解: 如题 9-6 图所示(1) 通过 abcd 面积 S 1 的磁通是 : 1B S 1 2.0i (0.3 0.4)i 0.24 ( Wb )(2) 通过 befc 面积 S 2 的磁通量 :2B S 22.0i (0.3 0.3)k(3) 设 aefd 面积 S 3 的法线正方向如图,则通过aefd 面积 S 3 的磁通量:3 B S 32 (0.30.5)cos20.15 4 0.24 ( Wb )题 9-6 图59-7 如题 9-7图所示, AB 、 CD 为长直导线, BC 为圆心在 O 点的一段圆弧形导线,其半径为R .若通以电流 I ,求 O 点的磁感应强度.解:如题9-7 图所示, O 点磁场由 AB 、 BC 、 CD 三部分电流产生.其中AB 段产生: B 1BC 段产生:B 2 0I60I(即垂直纸面向里)2R 360,方向题 9-7 图12 RCD 段产生: B 3I (sin 90 sin 60 ) 0I (13) ,方向4 R2 R 22【或: B 3I(cos120cos180 )I(13) ,方向 】4 R2 R22∴B 0B 1B 2B 30 I(13 ) , 方向 .2 R2 69-8 在真空中,有两根互相平行的无限长直导线L 1 和 L 2 ,相距 0.1m ,通有方向相反的电流, I 1 =20A,I 2 =10A ,如题 9-8图所示. A , B 两点与导线在同一平面内.这两点与导线L 2 的距离均为 5.0cm .试求 A , B 两点处的磁感应强度,以及磁感应强度为零的点的位置.解:如题 9-8 图所示, B A 方向垂直纸面向里,大小为:B A0 I120 I21.2 10 4 T2 (0.1 0.05)0.05B B 方向垂直纸面向外,大小为:0 I10 I21.33 10 5 T题 9-8 图B B22 (0.1 0.05) 0.05设 B0在 L 2 外侧距离 L 2 为 r 处,则II 20 , 解得: r 0.1 m9-12 两平行长直导线相距d =40cm ,每根导线载有电流 I 1 = I 2 =20A ,如题 9-12图所示.求:(1) 两导线所在平面内与该两导线等距的一点A 处的磁感应强度;(2) 通过图中斜线所示面积的磁通量. ( r 1 = r 3 =10cm, l =25cm) .解: (1) B A0 I10 I24 105 (T) 方向纸面向外2 ( d) 2 ( d)22题 9-12 图(2)dS ldr ,则: dB dS Bldr取面元d r 1 r 2 0 I 1 0 I 2]ldr0 I 1lln 30 I 2 lln1I 1lln 3 2.2 106( Wb )r 1 [S2 r2 (d r )2239-13 一根很长的铜导线载有电流 10A ,设电流均匀分布。
稳恒磁场(习题课)-精品文档
L
L
L
B 0I 2r
2. 无限长直均匀载流圆柱面的磁场分布
R
I
r
dl
B
0rR
lB d l lB d B l ld B l 2 r 0B0
r R
lB d l lB d B l ld B l 2 r 0 I
04π10 7NA2
任意载流导线在点 P 处的磁感强度
磁感强度 叠加原理
B dB
0I
dl
r
4π r3
Idl
dB
r
I
dB
P* r Idl
dB0
4π
Idlr r3
毕奥—萨伐尔定律
例 判断下列各点磁感强度的方向和大小.
1
8
2
X+
磁感应强度。
A
B
1
1
I O
D
C
I
Bo440Ia(co4sco34s)22a0I
2
例、如图所示,有一无限长通电流的偏平铜 片,宽度为a,厚度不计,电流I在铜片上均 匀地自下而上流过,在铜片外与铜片共面、 离铜片右边缘为b的P点的磁感应强度的大小 为多少?
I
P
b
a
x dx
O
P
x
I Tq 2qq2
B 0IR2
2(R2 x2)3/2
0qR2 4(R2 x2)3/2
q R x
P
B
例 求绕轴旋转的带电圆盘轴线上的磁场( P430 9.5)
解 dq2 rdr
I
dq dt
大学物理稳恒磁场习题及答案之欧阳理创编
衡水学院理工科专业《大学物理B 》稳恒磁场习题解答时间:2021.03.05创作:欧阳理一、填空题(每空1分)1、电流密度矢量的定义式为:dIj n dS ⊥=,单位是:安培每平方米(A/m2)。
2、真空中有一载有稳恒电流I 的细线圈,则通过包围该线圈的封闭曲面S 的磁通量=0 .若通过S 面上某面元d S 的元磁通为d,而线圈中的电流增加为2I 时,通过同一面元的元磁通为d',则d ∶d'=1:2 。
3、一弯曲的载流导线在同一平面内,形状如图1(O 点是半径为R1和R2的两个半圆弧的共同圆心,电流自无穷远来到无穷远去),则O 点磁感强度的大小是2020100444R IR IR IB πμμμ-+=。
4、一磁场的磁感强度为k c j b i a B++= (SI),则通过一半径为R ,开口向z轴正方向的半球壳表面的磁通量的大小为πR2cWb 。
5、如图2所示通有电流I 的两根长直导线旁绕有三种环路;在每种情况下,等于:对环路a :d B l ⋅⎰=____μ0I__; 对环路b :d B l ⋅⎰=___0____; 对环路c :d B l ⋅⎰=__2μ0I__。
6、两个带电粒子,以相同的速度垂直磁感线飞入匀强磁场,它们的质量之比是1∶4,电荷之比是1∶2,它们所受的磁场力之比是___1∶2__,运动轨迹半径之比是_____1∶2_____。
二、单项选择题(每小题2分)( B )1、均匀磁场的磁感强度B 垂直于半径为r 的圆面.今以该圆周为边线,作一半球面S ,则通过S 面的磁通量的大小为 A. 2r2BB.r2BC. 0D.无法确定的量O I R 1 R 2 图1 b ⊗ ⊙c I I c a图2( C )2、有一个圆形回路1及一个正方形回路2,圆直径和正方形的边长相等,二者中通有大小相等的电流,它们在各自中心产生的磁感强度的大小之比B1 / B2为A. 0.90B. 1.00C. 1.11D.1.22(D )3、如图3所示,电流从a 点分两路通过对称的圆环形分路,汇合于b 点.若ca 、bd 都沿环的径向,则在环形分路的环心处的磁感强度A. 方向垂直环形分路所在平面且指向纸内B. 方向垂直环形分路所在平面且指向纸外C .方向在环形分路所在平面内,且指向aD .为零( D )4、在真空中有一根半径为R 的半圆形细导线,流过的电流为I ,则圆心处的磁感强度为A.R 140πμ B. R 120πμ C .0D .R140μ ( C )5、如图4,边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷.此正方形以角速度绕AC 轴旋转时,在中心O 点产生的磁感强度大小为B1;此正方形同样以角速度绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感强度的大小为B2,则B1与B2间的关系为A. B1= B2B. B1= 2B2C .B1= 21B2D .B1= B2 /4(B )6、有一半径为R 的单匝圆线圈,通以电流I ,若将该导线弯成匝数N = 2的平面圆线圈,导线长度不变,并通以同样的电流,则线圈中心的磁感强度和线圈的磁矩分别是原来的(A) 4倍和1/8. (B) 4倍和1/2. (C) 2倍和1/4.(D) 2倍和1/2.三、判断题(每小题1分,请在括号里打上√或×)( × )1、电源的电动势是将负电荷从电源的负极通过电源内部移到电源正极时,非静电力作的功。
