【中考复习】2018届中考数学复习第八章第一节随堂演练1166
2018届中考英语复习随堂演练八下第8课时试题及答案

第8课时随堂演练一、用所给词的适当形式填空1.Mr. Liu (raise) his voice, but I still couldn't hear him clearly.2.My brother's (tooth) are white and good. He brushes them twice a day.3.There are many (passenger) waiting at ZhengZhou train station when it is near the Spring Festival.4.The strong rain this week caused 78 people's (die) in these cities.5.The smile on the mother's face showed her (satisfy) with her daughter when her daughter rushed across the finishing line.6.The good teacher should (control) his class and attract the students' attentions. 7.Some people won't realize the (importa nt) of their health until they lose it. 8.Sometimes (feel) are difficult to put into words.9.She was famous in our neighborhood for her (kind) to the neighbors.10.As a good school, we should care for the full (develop) of our students.二、从方框中选择合适的词并用其适当形式填空The man doesn't mind risks. He walked to the highest mountain.2.—Didn't you see the on the wall “No Photos”?—Sorry, I won't do that.3.Mr. White a basketball team last year in our school, and they played ver y well now. 4.The boy sang a song the sick girl up.5.I was very about going to the zoo tomorrow. I can't sleep now.6.It was v ery hard for me to make a , but I decided to leave this job.7.Please put away the glass away, or it may hurt the c hildren.8.My grandparents have understanding the meaning of the online words, but they try their best to learn from me and the Internet.9.These are very kind to the patients. We call them white angel.10.My brother hurt by accident. We must send him to the hospital at once.三、词语运用阅读短文,从方框中选择适当的词并用其正确形式填空,使短文通顺,意思完整。
2018年中考数学试卷

.2018 年中考数学试卷一、选择题(本大题共10 小题,每题 3 分,满分 30 分. 在每题给出的四个选项中,有一项为哪一项切合题目要求的)1.(3 分)四个数 0, 1,,中,无理数的是()A.B.1C.D.02.(3 分)以下图的五角星是轴对称图形,它的对称轴共有()A.1 条 B.3 条 C.5 条 D.无数条3.(3 分)以下图的几何体是由 4 个同样的小正方体搭成的,它的主视图是()A.B.C.D.4.(3 分)以下计算正确的选项是()A.(a+b)2=a2+b2B. a2 +2a2=3a4C.x2y÷=x2(y≠0)D.(﹣ 2x2)3=﹣8x6 5.(3 分)如图,直线 AD,BE被直线 BF和 AC所截,则∠ 1 的同位角和∠ 5 的内错角分别是()A.∠ 4,∠ 2B.∠ 2,∠ 6C.∠ 5,∠ 4D.∠ 2,∠ 4.6.(3 分)甲袋中装有 2 个同样的小球,分别写有数字 1 和 2:乙袋中装有 2 个同样的小球,分别写有数字 1 和 2.从两个口袋中各随机拿出 1 个小球,拿出的两个小球上都写有数字 2 的概率是()A.B.C.D.7.(3 分)如图, AB是⊙ O的弦, OC⊥AB,交⊙ O于点 C,连结 OA,OB, BC,若∠ABC=20°,则∠ AOB的度数是()A.40°B.50°C.70°D.80°8.(3 分)《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9 枚(每枚黄金重量同样),乙袋中装有白银 11 枚(每枚白银重量同样),称重两袋相等.两袋相互互换 1 枚后,甲袋比乙袋轻了 13 两(袋子重量忽视不计).问黄金、白银每枚各重多少两?设每枚黄金重 x 两,每枚白银重 y 两,依据题意得()A.B.C.D.9.(3 分)一次函数 y=ax+b 和反比率函数y=在同向来角坐标系中的大概图象是()A.B.C.D.10.( 3 分)在平面直角坐标系中,一个智能机器人接到以下指令:从原点O 出发,按向右,向上,向右,向下的方向挨次不停挪动,每次挪动1m.其行走路线以下图,第 1 次挪动到 A1,第 2 次挪动到 A2,,第 n 次挪动到 A n.则△ OA2A2018的面积是()2222A.504m B.m C.m D.1009m二、填空题(本大题共 6 小题,每题 3 分,满分 18 分 . )11.(3 分)已知二次函数 y=x2,当 x>0 时,y 随 x 的增大而(填“增大”或“减小”).12.(3 分)如图,旗杆高 AB=8m,某一时辰,旗杆影子长 BC=16m,则 tanC=.13.( 3分)方程 =的解是.14.( 3分)如图,若菱形 ABCD的极点 A, B 的坐标分别为( 3, 0),(﹣ 2,0),点 D 在 y 轴上,则点 C 的坐标是.15.( 3 分)如图,数轴上点 A 表示的数为 a,化简: a+=.16.( 3 分)如图, CE是? ABCD的边 AB的垂直均分线,垂足为点O,CE与 DA的延伸线交于点 E.连结 AC,BE, DO,DO与 AC交于点 F,则以下结论:①四边形 ACBE是菱形;②∠ ACD=∠BAE;③AF:BE=2:3;④S 四边形AFOE:S△COD=2:3.此中正确的结论有.(填写全部正确结论的序号)三、解答题(本大题共 9 小题,满分 102 分. 解答应写出文字说明、证明过程或演算步骤 . )17.( 9 分)解不等式组:.18.( 9 分)如图, AB与 CD订交于点 E, AE=CE,DE=BE.求证:∠ A=∠ C.19.( 10 分)已知 T=+..(1)化简 T;(2)若正方形 ABCD的边长为 a,且它的面积为 9,求 T 的值.20.( 10 分)跟着挪动互联网的迅速发展,鉴于互联网的共享单车应运而生.为认识某小区居民使用共享单车的状况,某研究小组随机采访该小区的10 位居民,获得这 10 位居民一周内使用共享单车的次数分别为:17, 12,15,20, 17,0,7,26,17, 9.( 1)这组数据的中位数是,众数是;(2)计算这 10 位居民一周内使用共享单车的均匀次数;(3)若该小区有 200 名居民,试预计该小区居民一周内使用共享单车的总次数.21.( 12 分)友情商铺 A 型号笔录本电脑的售价是 a 元/ 台.近来,该商铺对 A 型号笔录本电脑举行促销活动,有两种优惠方案.方案一:每台按售价的九折销售;方案二:若购置不超出 5 台,每台按售价销售;若超出 5 台,超出的部分每台按售价的八折销售.某企业一次性从友情商铺购置 A 型号笔录本电脑 x 台.(1)当 x=8 时,应选择哪一种方案,该企业购置花费最少?最少花费是多少元?(2)若该企业采纳方案二购置更合算,求 x 的取值范围.22.( 12 分)设 P(x,0)是 x 轴上的一个动点,它与原点的距离为y1.(1)求 y1对于 x 的函数分析式,并画出这个函数的图象;(2)若反比率函数 y2 = 的图象与函数 y1的图象订交于点 A,且点 A 的纵坐标为2.①求 k 的值;②联合图象,当y1>y2时,写出 x 的取值范围.23.( 12 分)如图,在四边形ABCD中,∠ B=∠C=90°, AB> CD,AD=AB+CD.(1)利用尺规作∠ ADC的均分线 DE,交 BC于点 E,连结 AE(保存作图印迹,不写作法);(2)在( 1)的条件下,①证明: AE⊥DE;②若 CD=2,AB=4,点 M, N分别是 AE, AB上的动点,求 BM+MN的最小值.24.( 14 分)已知抛物线y=x2+mx﹣2m﹣4(m>0).(1)证明:该抛物线与 x 轴总有两个不一样的交点;(2)设该抛物线与 x 轴的两个交点分别为 A,B(点 A 在点 B 的右边),与 y 轴交于点 C, A,B,C 三点都在⊙ P 上.①试判断:无论 m取任何正数,⊙ P 能否经过 y 轴上某个定点?假如,求出该定点的坐标;若不是,说明原因;②若点 C 对于直线 x=﹣的对称点为点 E,点 D(0,1),连结 BE,BD, DE,△BDE的周长记为 l ,⊙ P 的半径记为 r ,求的值.25.( 14 分)如图,在四边形ABCD中,∠ B=60°,∠ D=30°, AB=BC.(1)求∠ A+∠C的度数;(2)连结 BD,研究 AD, BD,CD三者之间的数目关系,并说明原因;( 3)若 AB=1,点 E 在四边形 ABCD内部运动,且知足222AE=BE+CE,求点 E 运动路径的长度.2018 年广东省广州市中考数学试卷参照答案与试题分析一、选择题(本大题共10 小题,每题 3 分,满分 30 分. 在每题给出的四个选项中,有一项为哪一项切合题目要求的)1.【解答】解: 0,1,是有理数,是无理数,应选: A.2.【解答】解:五角星的对称轴共有 5 条,应选: C.3.【解答】解:从正面看第一层是三个小正方形,第二层右边一个小正方形,应选: B.4.【解答】解:(A)原式 =a2+2ab+b2,故 A 错误;(B)原式 =3a2,故 B 错误;(C)原式 =x2y2,故 C 错误;应选: D.5.【解答】解:∠1 的同位角是∠2,∠5 的内错角是∠6,应选: B..6.【解答】解:以下图:,一共有 4 种可能,拿出的两个小球上都写有数字 2 的有 1 种状况,故拿出的两个小球上都写有数字 2 的概率是:.应选: C.7.【解答】解:∵∠ ABC=20°,∴∠ AOC=40°,∵AB是⊙O的弦,OC⊥AB,∴∠ AOC=∠BOC=40°,∴∠ AOB=80°,应选: D.8.【解答】解:设每枚黄金重x 两,每枚白银重y 两,由题意得:,应选: D.9.【解答】解:当y=ax+b 经过第一、二、三象限时,a>0、b>0,由直线和 x 轴的交点知:﹣>﹣ 1,即 b<a,∴ a﹣ b> 0,因此双曲线在第一、三象限.应选项 B 不建立,选项 A 正确.当 y=ax+b 经过第二、一、四象限时,a<0,b>0,此时 a﹣b<0,双曲线位于第二、四象限,应选项 C、D均不建立;应选: A..10.【解答】解:由题意知 OA4n=2n,∵2018÷ 4=504÷2,∴ OA2018= +1=1009,∴A2A2018=1009﹣1=1008,2则△ OA2A2018的面积是×1×1008=504m,应选: A.二、填空题(本大题共 6 小题,每题 3 分,满分 18 分 . )11.2【解答】解:∵二次函数 y=x ,张口向上,对称轴为y 轴,故答案为:增大.12.【解答】解:∵旗杆高 AB=8m,旗杆影子长 BC=16m,∴ tanC=,故答案为:13.【解答】解:去分母得: x+6=4x,解得: x=2,经查验 x=2 是分式方程的解,故答案为: x=214.【解答】解:∵菱形 ABCD的极点 A,B 的坐标分别为( 3,0),(﹣ 2, 0),点 D.在 y 轴上,∴ AB=5,∴ AD=5,∴由勾股定理知: OD===4,∴点 C 的坐标是:(﹣ 5, 4).故答案为:(﹣ 5,4).15.【解答】解:由数轴可得:0<a<2,则 a+=a+=a+( 2﹣ a)=2.故答案为: 2.16.【解答】解:∵四边形 ABCD是平行四边形,∴AB∥CD,AB=CD,∵ EC垂直均分 AB,∴OA=OB=AB= DC,CD⊥CE,∵OA∥DC,∴===,∴AE=AD,OE=OC,.∵OA=OB,OE=OC,∴四边形 ACBE是平行四边形,∵AB⊥EC,∴四边形 ACBE是菱形,故①正确,∵∠ DCE=90°, DA=AE,∴AC=AD=AE,∴∠ ACD=∠ADC=∠BAE,故②正确,∵OA∥CD,∴==,∴ = = ,故③错误,设△ AOF的面积为 a,则△ OFC的面积为 2a,△ CDF的面积为 4a,△ AOC的面积 =△AOE的面积 =3a,∴四边形 AFOE的面积为 4a,△ ODC的面积为 6a∴S 四边形AFOE:S△COD=2:3.故④正确,故答案为①②④.三、解答题(本大题共 9 小题,满分 102 分. 解答应写出文字说明、证明过程或演算步骤 . )17.【解答】解:,解不等式①,得x>﹣ 1,解不等式②,得x< 2,不等式①,不等式②的解集在数轴上表示,如图.,原不等式组的解集为﹣ 1<x<2.18.【解答】证明:在△ AED和△ CEB中,,∴△ AED≌△ CEB(SAS),∴∠ A=∠ C(全等三角形对应角相等).19.【解答】解:(1)T=+==;(2)由正方形的面积为 9,获得 a=3,则T= .20.【解答】解:(1)依据大小次序从头摆列后,第5、第 6 个数分别是15 和 17,因此中位数是( 15+17)÷ 2=16,17 出现 3 次最多,因此众数是17,故答案是 16,17;( 2)=14,答:这 10 位居民一周内使用共享单车的均匀次数是14 次;(3) 200×14=2800答:该小区居民一周内使用共享单车的总次数为2800 次.21.【解答】解:设购置 A 型号笔录本电脑x 台时的花费为 w 元,(1)当 x=8 时,方案一: w=90%a×8=7.2a ,方案二: w=5a+(8﹣5)a×,∴当 x=8 时,应选择方案一,该企业购置花费最少,最少花费是7.2a 元;(2)∵若该企业采纳方案二购置更合算,∴ x> 5,方案一:,方案二:当 x>5 时, w=5a+(x﹣5)a×﹣4a=a+0.8ax ,则 0.9ax >a+0.8ax ,x>10,∴ x 的取值范围是 x> 10.22.【解答】解:(1)由题意 y1=x.函数图象以下图:(2)①由题意A(2,2),∴2= ,∴k=4.②察看图象可知: x> 2 时, y1> y2.23.【解答】解:(1)如图,∠ ADC的均分线 DE以下图.(2)①延伸 DE交 AB的延伸线于 F.∵ CD∥AF,∴∠ CDE=∠F,∵∠CDE=∠ADE,∴∠ ADF=∠F,∴ AD=AF,∵ AD=AB+CD=AB+BF,∴ CD=BF,∵∠ DEC=∠BEF,∴△ DEC≌△ FEB,∴DE=EF,∵ AD=AF,∴AE⊥DE.②作点 B 对于 AE的对称点 K,连结 EK,作 KH⊥AB于 H, DG⊥AB于 G.连结 MK.∵AD=AF,DE=EF,∴AE均分∠ DAF,则△ AEK≌△ AEB,∴AK=AB=4,在 Rt△ ADG中, DG==4 ,∵KH∥DG,∴ = ,∴= ,∴KH=,∵MB=MK,∴MB+MN=KM+MN,∴当 K、M、N 共线,且与 KH重合时, KM+MN的值最小,最小值为GH的长,∴ BM+MN的最小值为.24.【解答】解:(1)令 y=0,∴x2+mx﹣2m﹣4=0,22∴△ =m﹣4[ ﹣2m﹣4]=m +8m+16,∵m> 0,∴△> 0,∴该抛物线与 x 轴总有两个不一样的交点;(2)令 y=0,∴x2+mx﹣2m﹣4=0,∴( x﹣2)[x+ (m+2)]=0 ,∴x=2 或 x=﹣( m+2),∴A( 2, 0),B(﹣( m+2), 0),∴OA=2, OB=m+2,令 x=0,∴y=﹣2(m+2),∴C( 0,﹣ 2(m+2)),∴OC=2( m+2),①经过定点( 0,1)原因:如图,∵点 A,B,C在⊙ P上,∴∠ OCB=∠OAF,在 Rt△ BOC中, tan ∠ OCB= ==,在 Rt△ AOF中, tan ∠ OAF= = = ,∴OF=1,∴点 F 的坐标为( 0, 1);②如图 1,在 Rt △BOD中,依据勾股定理得, BD= ,由①知,点 F(0,1),∵D(0,1),∴点D在⊙ P上,∵点 E 是点 C 对于抛物线的对称轴的对称点,∴∠ DCE=90°,∴DE是⊙P 的直径,∴∠ DBE=90°,∵∠ BED=∠OCB,∴tan ∠BED= ,在 Rt△ BDE中, tan ∠ BED= =,∴BE=2 ,依据勾股定理得, DE==5,∴l=BD+BE+DE=5+3 , r= DE= ,∴=..25.【解答】解:(1)如图 1 中,在四边形 ABCD中,∵∠ A+∠ B+∠C+∠D=180°,∠ B=60°,∠ C=30°,∴∠ A+∠C=360°﹣ 60°﹣ 30°=270°.222( 2)如图 2 中,结论: DB=DA+DC.原因:连结 BD.以 BD为边向下作等边三角形△BDQ.∵∠ ABC=∠DBQ=60°,∴∠ ABD=∠CBQ,∵AB=BC,DB=BQ,∴△ ABD≌△ CBQ,∴ AD=CQ,∠ A=∠BCQ,∵∠ A+∠ BCD=∠ BCQ+∠BCD=270°,∴∠ BCQ=90°,222∴ DQ=DC+CQ,∵CQ=DA,DQ=DB,222∴ DB=DA+DC.( 3)如图 3 中,连结 AC,将△ ACE绕点 A 顺时针旋转 60°获得△ ABR,连结 RE.222则△ AER是等边三角形,∵ EA=EB+EC,EA=RE,EC=RB,222∴ RE=RB+EB,∴∠ EBR=90°,∴∠ RAE+∠RBE=150°,∴∠ ARB+∠AEB=∠AEC+∠AEB=210°,∴∠ BEC=150°,∴点 E 的运动轨迹在 O为圆心的圆上,在⊙ O上取一点 K,连结 KB,KC,OB,OC,∵∠ K+∠BEC=180°,∴∠ K=30°,∠ BOC=60°,∵OB=OC,∴△ OBC是等边三角形,∴点 E的运动路径 ==.。
2018年中考数学预测试卷8 精品
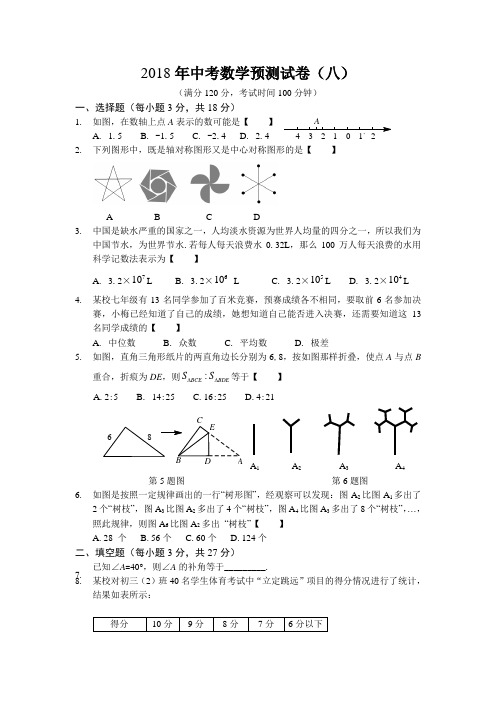
2018年中考数学预测试卷(八)(满分120分,考试时间100分钟)一、选择题(每小题3分,共18分)1. 如图,在数轴上点A 表示的数可能是【 】A . 1.5B . -1.5C . -2.4D . 2.42. 下列图形中,既是轴对称图形又是中心对称图形的是【 】A B C D3. 中国是缺水严重的国家之一,人均淡水资源为世界人均量的四分之一,所以我们为中国节水,为世界节水.若每人每天浪费水0.32L ,那么100万人每天浪费的水用科学记数法表示为【 】A . 3.2×710L B . 3.2×610 L C . 3.2×510L D . 3.2×410L 4. 某校七年级有13名同学参加了百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的【 】A . 中位数B . 众数C . 平均数D . 极差5. 如图,直角三角形纸片的两直角边长分别为6,8,按如图那样折叠,使点A 与点B重合,折痕为DE ,则:BCE BDE S S ∆∆等于【 】 A .2:5 B . 14:25 C .16:25 D .4:21A 1 A 2 A 3 A 4 第5题图 第6题图6. 如图是按照一定规律画出的一行“树形图”,经观察可以发现:图A 2比图A 1多出了2个“树枝”, 图A 3比图A 2多出了4个“树枝”, 图A 4比图A 3多出了8个“树枝”,…,照此规律,则图A 6比图A 2多出 “树枝”【 】 A .28 个 B .56个 C .60个 D .124个二、填空题(每小题3分,共27分)7. 已知∠A =40°,则∠A 的补角等于_________.8. 某校对初三(2)班40名学生体育考试中“立定跳远”项目的得分情况进行了统计,结果如表所示:图③图②图①A根据表中数据,可以知道这次“立定跳远”成绩的中位数是___________. 9. 已知m =1n =1_________.10. 如图,一个圆形转盘被等分成八个扇形区域,上面分别标有数字1、2、3、4,转盘指针的位置固定,转动转盘后任其自由停止,转动转盘一次,当转盘停止转动时,记指针指向标有“3”所在区域的概率为P (3),指针指向标有“4”所在的区域的概率为P (4),则P (3) P (4)(填“>”“=”或“<”).NME DCB ACBDOAE第10题图 第12题图 第13题图11. 母亲节那天,很多同学给妈妈准备了鲜花和礼盒,购买一束鲜花和两个礼盒需要143元,购买两束鲜花和一个礼盒需要121元,则买5束鲜花和5个礼盒的总价为 元.12. 如图,在五边形ABCDE 中,∠BAE =125°,∠B =∠E =90°,AB =BC ,AE =DE ,在BC 、DE 上分别找一点M 、N ,使得△AMN 周长最小时,∠AMN +∠ANM 的度数为_______. 13. 如图,已知AB 是圆O 的直径,C 是AB 延长线上一点,BC =OB ,CE 是圆O 的切线,切点为D ,过点A 作AE ⊥CE ,垂足为E .则CD :DE 的值是__________. 14. 定义新运算“☉”如下:当a ≥b 时,a ☉b =b ²;当a <b 时,a ☉b =a .则当x =2时,(1☉x )-(3☉x )的值为___________.15. 如图,图①中的圆与正方形各边都相切,设这个圆的周长为1C ,图②中的四个圆的半径相等,并依次外切,且与正方形的边相切,设这四个圆的周长之和为2C;图③中的九个圆的半径相等,并依次外切,且与正方形的各边相切,设这九个圆的周长之和为3C,…,以此规律,当正方形边长为2时,则123C C C +++…99100C C ++= .三、解答题(本大题共8个小题,满分75分)16. (8分)(1)计算:1O 01()3tan30(12---+ ;(2)解不等式组:40320x x ->⎧⎨+>⎩,并把它的解集在数轴上表示出来.17. (9分)如图,在边长为1的小正方形组成的网格中,△ABC 的三个顶点均在格点上,请按要求完成下列各题:BFEAP(1)画线段AD ∥BC 且使AD =BC ,连接CD ;(2)线段AC 的长为 ,CD 的长为 ,AD 的长 为 ;(3)△ACD 为 三角形,四边形ABCD 的面积为 ; (4)若E 为BC 中点,求tan ∠CAE 的值.18. (9分)某生态示范园要对1号、2号、3号、4号四个新品种共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广.通过实验得知:3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出).500株幼苗中各品种幼苗所占百分比统计图 各品种幼苗成活数统计图图2图1品种各品种幼苗成活率统计图2号3号25%4号25%1号30%500株幼苗中各品种幼苗所占百分比统计图(1)实验所用的2号果树幼苗的数量是___株;(2)求出3号果树幼苗的成活数,并把图2的统计图补充完整; (3)你认为应选哪一种果树幼苗进行推广?请通过计算说明理由.19. (9分) 某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.(1)符合题意的组建方案有几种?请你帮学校设计出来;(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?20. (9分)如图,大海中有A 和B 两个岛屿,为测量它们之间的距离,在海岸线PQ上点E 处测得∠AEP =74°,∠BEQ =30°;在点F 处测得∠AFP =60°,∠BFQ =60°,EF =1km . (1)判断AB ,AE 的数量关系,并说明理由;(2)求两个岛屿A 和B 之间的距离(结果精确到0.1km ). (参考数据:≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)21. (10分)如图,线段AD =5,⊙A 的半径为1,C 为⊙A 上一动点,CD 的垂直平分线分别交CD ,AD 于点E ,B ,连接BC ,AC ,构成△ABC ,设AB =x . (1)求x 的取值范围;CFGB N MEDA N M EDC FG BA P ED CQBA (2)若△ABC 为直角三角形,则x =_________; (3)设△ABC 的面积的平方为W ,求W 的最大值.22. (10分)(1)如图1,在△ABC 中,点D ,E ,Q 分别在AB ,AC ,BC上,且DE ∥BC ,AQ 交DE 于点P .求证:DP PEBQ QC=. (2) 如图,在△ABC 中,∠BAC =90°,正方形DEFG 的四个顶点在△ABC 的边上,连接AG ,AF 分别交DE 于M ,N 两点. ①如图2,若AB =AC =1,直接写出MN 的长; ②如图3,求证MN 2=DM ·EN .图1 图2 图3 23. (11分)如图,已知抛物线2y x bx c =++与x 轴交于点A (1,0)和点B ,与y 轴交于点 C (0,-3).(1)求抛物线的解析式;(2)如图1,已知点H (0,-1).问在抛物线上是否存在点G (点G 在y 轴的左侧),使得GHC GHA S S ∆∆=?若存在,求出G 点坐标,若不存在,请说明理由; (3)如图2,抛物线上点D 在x 轴上的正投影为点E (-2,0),F 是OC 的中点,连接DF ,P 为线段BD 上一点,若∠EPF =∠BDF ,求线段PE 的长.。
2018中考模拟试卷数学

2018年中考模拟试题九年级数学满分120分 时间90分钟一、选择题:本大题共10小题,每小题3分,共30分.每小题给出的四个选项中,只有一项是符合题目要求的,将此选项的代号填入题后的括号内.1.9的平方根是( ) A .±3 B.C .3 D.2.如图所示,该几何体的俯视图是( )A. B. C. D.3.截至去年底,国家开发银行对“一带一路”沿线国家累计贷款超过1600亿美元,其中1600亿用科学记数法表示为( )A .16×1010B .1.6×1010C .1.6×1011D .0.16×10124.下列运算正确的是( )A .3a +2b =5abB .(m 2)3=m 5C .a 2•a 3=a 5D .(x +y )2=x 2+y 2 5.下列命题中的假命题是( ) A .一组邻边相等的平行四边形是菱形 B .一组邻边相等的矩形是正方形C .一组对边平行且相等的四边形是平行四边形D .一组对边相等且有一个角是直角的四边形是矩形 6.不等式组的解在数轴上表示为( ) A.B.C. D.7..如图,⊙O 是△ABC 的外接圆,已知∠ABO =40°,则∠ACB 的大小为( )A .60°B .50°C .40°D .30°8.在正方形网格中,△ABC 在网格中的位置如图,则cosB 的值为( )A. B. C. D .29.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm ,到屏幕的距离为60cm ,且幻灯片中的图形的高度为6cm ,则屏幕上图形的高度为( )A .24cmB .18cmC .12cmD .6cm10.(3分)如图,正方形ABCD 的边长为3cm ,动点P 从B 点出发以3cm/s 的速度沿着边BC ﹣CD ﹣DA 运动,到达A 点停止运动;另一动点Q 同时从B 点出发,以1cm/s 的速度沿着边BA 向A 点运动,到达A 点停止运动.设P 点运动时间为x (s ),△BPQ 的面积为y (cm 2),则y 关于x 的函数图象是( )A.B.C. D.二、填空题:本大题共8小题,每小题3分,共24分.把答案写在题中的横线上.11.分解因式:x 3﹣4x= . 12.在函数xx y 4+=中,自变量x 的取值范围是____________. 13.分式方程的解是 .14.若关于x 的方程2230kx x -+=有两个不相等的实数根,则k 的取值范围是 . 15.把函数的图象向左平移1个单位,再向上平移6个单位,所得的抛物线的函数关系式为 .16.如图,在底边BC 为2,腰AB 为2的等腰三角形ABC 中,DE 垂直平分AB 于点D ,交BC于点E ,则△ACE 的周长为.17.如图,AB 为⊙O 的直径,点C 在⊙O 上,若∠OCA=50°,AB=4,则扇形BOC 的面积为 .18.对于实数a ,b ,我们定义符号max{a ,b}的意义为:当a ≥b 时,max{a ,b}=a ;当a <b 时,max{a ,b]=b ;如:max{4,﹣2}=4,max{3,3}=3,若关于x 的函数为y=max{x+3,﹣x+1},则该函数的最小值是 .三、解答题:本大题共10小题,共66分.解答应写出必要的文字说明、证明过程或演算步骤. 19.(4分)计算:|﹣2|﹣(π﹣2015)0+(﹣)﹣2﹣2sin60°+.20.(4分)已知x=1是关于x 的一元二次方程x 2﹣4mx +m 2=0的根,求代数式的值.21.(6分)如图所示,在边长为1的正方形组成的网格中,△AOB 的顶点均在格点上,点A ,B 的坐标分别是A (3,3)、B (1,2),△AOB 绕点O 逆时针旋转90°后得到△A 1OB 1.(1)画出△A 1OB 1,直接写出点A 1,B 1的坐标; (2)在旋转过程中,点B 经过的路径的长.22.(6分)如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE ,在小楼的顶端D 处测得障碍物边缘点C 的俯角为30°,测得大楼顶端A 的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果保留根号)23.(6分)现有4张卡片(形状、大小和质地都相同),正面分别写有A、B、C、D和一个算式,将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.(1)用列表法或画树状图表示抽取两张卡片可能出现的所有情况(卡片可用A、B、C、D表示).(2)求出抽取的两张卡片上的算式都错误的概率.24.(7分)“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,某食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽(以下分别用A,B,C,D表示这四种不同的口味粽子)的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅不完整的统计图.请根据以上信息回答下列问题:(1)本次参加抽样调查的居民有多少人?(2)将两幅不完整的统计图补充完整;(3)若居民区有8000人,请估计爱吃D粽的人数?25.(7分)如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数的图象交于C、D两点,DE⊥x轴于点E,已知C 点的坐标是(6,﹣1),DE=3.(1)求反比例函数与一次函数的解析式;(2)求△CDE的面积.26.(8分)如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.(1)求证:四边形ADCE是菱形;(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)27.(8分)如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.(1)求证:PA是⊙O的切线;(2)若tan∠BAD=,且OC=4,求BD的长.28.(10分)27.(本题16分)如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(12,52)和B(4,m),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.。
2018年河北省中考《2.2一元二次方程》复习课件+随堂演练含真题分类汇编解析

应用根的判别式时,当一元二次方程不是一般形式时, 要先化成一般形式.
知识点四 一元二次方程的应用 1.列一元二次方程解应用题的一般步骤:(1)审,即审 清题意,找出题中的已知量、未知量;(2)设,即设出关 键未知数;(3)列,即找出等量关系,列方程;(4)解, 即解方程;(5)验,即检验结果是否正确或是否有实际 意义;(6)答,回归题中,规范作答.
讲:应用根与系数关系的前提 (1)二次项系数a≠0;(2)判别式Δ≥0.因此利用一元二 次方程根与系数的关系求方程中所含字母的值或范围时, 必须要考虑这两个条件. 练:链接变式训练7
7.(2017·烟台)若x1,x2是方程x2-2mx+m2-m-1=0
的两个根,且x1+x2=1-x1x2,则m的值为( D )
列一元二次方程解决实际问题的关键是找出“等量关系”, 在得到方程的解之后,要记得检验它是否符合实际意义.
10.(2017·杭州)某景点的参观人数逐年增加,据统
计,2014年为10.8万人次,2016年为16.8万人次.
设参观人次的平均年增长率为x,则(
)
C
A.10.8(1+x)=16.8
B.16.8(1-x)=10.8
(2)由于生产工序不同,蛋糕产品每提高一个档次,一天 产量会减少4件.若生产的某档次产品一天的总利润为 1 080元,该烘焙店生产的是第几档次的产品?
解:(1)(14-10)÷2+1=3(档次). 答:此批次蛋糕属第3档次产品. (2)设烘焙店生产的是第x档次的产品, 根据题意得(2x+8)×(76+4-4x)=1 080, 解得x1=5,x2=11(舍去). 答:该烘焙店生产的是第5档次的产品.
1.(2017·嘉兴)用配方法解方程x2+2x-1=0时,
中考数学试题-2018年中考数学考点专题跟踪突破复习试

考点跟踪突破4 分式及其运算一、选择题(每小题6分,共30分)1.(2018·凉山州)分式|x|-3x +3的值为零,则x 的值为( A )A .3B .-3C .±3D .任意实数2.(2018·无锡)分式22-x可变形为( D )A .22+xB .-22+xC .2x -2D .-2x -2 3.(2018·金华)下列计算错误的是( A ) A .0.2a +b 0.7a -b =2a +b 7a -b B .x 3y 2x 2y 3=x y C .a -b b -a=-1 D .1c +2c =3c 4.设m >n >0,m 2+n 2=4mn ,则m 2-n2mn =( A ) A .2 3 B . 3 C .- 3 D .35.(2018·杭州)若(4a 2-4+12-a)·w =1,则w =( D )A .a +2(a ≠-2)B .-a +2(a ≠2)C .a -2(a ≠2)D .-a -2(a ≠-2) 二、填空题(每小题6分,共30分) 6.(2018·济宁)如果从一卷粗细均匀的电线上截取1米长的电线,称得它的质量为a 克,再称得剩余电线的质量为b 克,那么原来这卷电线的总长度是__ba +1__米.7.(2018·襄阳)计算:a 2-1a 2+2a ÷a -1a =__a +1a +2__.8.(2018·宜宾)分式方程x x -2-1x 2-4=1的解是__x =-32__.9.(2018·成都)已知关于x 的分式方程x +k x +1-kx -1=1的解为负数,则k 的取值范围是__k >12且k ≠1__.10.(2018·内江)已知三个数x ,y ,z 满足xy x +y =-2,yz y +z =43,zx z +x =-43,则xyz xy +xz +yz=__-4__. 解析:由xy x +y=-2得x +y xy =-12,裂项得1y +1x =-12,同理1z +1y=34,1x +1z =-34,所以1y +1x +1z +1y +1x +1z =-12+34-34=-12,1z +1x +1y =-14,于是xy +yz +zx xyz =1z +1x +1y =-14,所以xyzxy +yz +zx =-4 三、解答题(共40分) 11.(6分)计算:(1)(2018·宜宾)(3a a -3-a a +3)·a 2-9a ;解:原式=3a (a +3)-a (a -3)(a -3)(a +3)·(a +3)(a -3)a =3a 2+9a -a 2+3a (a -3)(a +3)·(a +3)(a -3)a =2a (a +6)(a -3)(a +3)·(a +3)(a -3)a =2a +12 (2)(x +x x 2-1)÷(2+1x -1-1x +1).解:原式=x 3-x +x x 2-1÷2x 2-2+x +1-x +1x 2-1=x 3x 2-1·x 2-12x 2=x212.(8分)解分式方程:(1)(2018·宁波)31-x =xx -1-5;解:去分母得-3=x -5(x -1),去括号得:-3=x -5x +5,移项合并同类项得:4x =8,x =2,经检验x =2是原分式方程的解(2)(2018·呼和浩特)3x 2+2x -1x 2-2x=0.解:x =413.(8分)已知1x -1y =3,求分式2x -14xy -2y x -2xy -y 的值.解:解法一:∵1x -1y =3,∴y -x xy =3,y -x =3xy ,x -y =-3xy.原式=2x -2y -14xy x -y -2xy =2(x -y )-14xy (x -y )-2xy =-6xy -14xy -3xy -2xy =-20xy -5xy=4解法二:∵1x -1y =3,∴xy ≠0,∴原式=(2x -14xy -2y )÷xy (x -2xy -y )÷xy=2y -14-2x 1y -2-1x=-2(1x -1y )-14-(1x -1y )-2=-6-14-3-2=-20-5=414.(8分)(2018·凉山州)先化简,再求值:a -33a 2-6a ÷(a +2-5a -2),其中a 2+3a -1=0.解:原式=a -33a (a -2)÷a 2-4-5a -2=a -33a (a -2)·a -2(a +3)(a -3)=13a 2+9a,当a 2+3a -1=0,即a 2+3a =1时,原式=1315.(10分)若abc =1,求a ab +a +1+b bc +b +1+cca +c +1的值.分析:本题可将分式通分后,再进行化简求值,但较复杂,下面介绍两种简单的解法.解法一:因为abc =1,所以a ,b ,c 都不为零.原式=a ab +a +1+a a ·b bc +b +1+ab ab ·c ca +c +1=aab +a +1+ab abc +ab +a +abc abca +abc +ab =a ab +a +1+ab 1+ab +a +1a +1+ab =a +ab +1ab +a +1=1解法二:由abc =1,得a =1bc ,将之代入原式.原式=1bc 1bc ·b +1bc +1+b bc +b +1+c c·1bc +c +1=1b +1+bc+b bc +b +1+bc1+bc +b =1+b +bc 1+b +bc =1。
2018年中考英语复习第一部分随堂演练八上第9课时试题
第9课时随堂演练一、根据句意和所给的中文提示,写出句子中的单词1.Could you help me buy some _______ (点心)?2._______ (既然) everyone is here, let's start our party.3._______ (两者都不) of them went to the park last Sunday.4.Mr. Green always _______ (提供) his help when I'm in trouble.5.Peter isn't friendly because he often _______ (争吵) with other people.6.You must _______ (归还) my dictionary tomorrow.7.My parents always ask me to _______ (竞争) with my classmates.8.Many students have too much _______ (压力) now.9.With the __________ (发展) of science, we can enjoy our life better.10.Driving a car too fast may _______ (引起) car accident.二、根据句意用所给词的适当形式填空1.Can you tell me the _______ (true) why Mary gave up the new job?2.Our English teacher asks us _______ (read) more English every day.3.Neither of the pens ____ (be) hers.4.Don't let children _______ (play) on the street. It's dangerous.5.China is one of the _______ (develop) countries in the world.6.Our English teacher is a man of _______ (fair).7.Do you think it's necessary for us _______ (learn) English well?8.Thirty years ___ (be) a long time.9.I think young people today need to be _______ (independence).10.Mrs. White often offers _______ (do) the housework at home.11.Mary is always _______ (help) other people.12.His _______ (old) brother is three years older than him.13.These vegetables are good for the healthy _______ (develop) of children.14.Being deaf makes _____________ (communicate) very difficult.15.Do you get on well with your family _______ (member)?三、短文填空根据短文内容及首字母提示填空,使短文意思完整、连贯When you apologize to someone, you're telling him that you're (1) s_______ for what you did or said, like you did something (2) w_______ at home, or you said something terrible to your friends.Something you say sorry (3) b_______ you feel ashamed of yourself and nervous about what you did. In these causes, you shouldn't (4) p_______ yourself so hard. You can (5) a_______ yourself to make mistakes sometimes. If you still feel ashamed, you can (6) d_______ with it by (7) e_______ to others. And also you can find out what has (8) c_______ the problem and make sure not to make the same mistake again.Sometimes you don't think you are wrong when you say sorry. You may just want to get on well with others. Sometimes someone may not (9) a_______ your apology. But you should (10) c_______ talking to him. If you give it up now, you may make the problem worse.参考答案一、1.snacks 2.Since 3.Neither 4.offers 5.argues 6.return pete 8.pressure 9.development 10.cause二、1.truth 2.to read 3.is 4.play 5.developing 6.fairness 7.to learn 8.is 9.independent 10.to do 11.helping12.elder 13.development munication 15.members三、1.sorry 2.wrong 3.because4.push 5.allow 6.deal 7.explaining8.caused 9.accept 10.continue。
2018届中考数学复习第三章函数第一节平面直角坐标系与函数随堂演练20180503216
平面直角坐标系与函数随堂演练1.若点A(m,n)在第二象限,那么点B(-m,|n|)在( )A.第一象限B.第二象限C.第三象限D.第四象限x+22.(2016·威海)函数y=的自变量x的取值范围是( )xA.x≥-2 B.x≥-2且x≠0C.x≠0D.x>0且x≠-23.(2017·淄博)小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部.则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是()4.(2017·潍坊)小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )A.(-2,1) B.(-1,1)C.(1,-2) D.(-1,-2)5.如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1 cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )1A.AE=6 cm4B.sin∠EBC=52C.当0<t≤10时,y=t25D.当t=12 s时,△PBQ是等腰三角形x-16.(2017·营口)函数y=中,自变量x的取值范围是_________.x+17.如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合,试写出重叠部分面积y(cm2) 与MA长度x(cm)之间的函数关系式(指出自变量取值范围)是________________________.参考答案1.A 2.B 3.D 4.B 5.D16.x≥17.y=x2(0<x≤10)22。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8章 第一节
随堂演练
1.(2017·德州)某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
尺码 39 40 41 42 43
平均每天销售数量/件 10 12 20 12 12
该店主决定本周进货时,增加了一些41码的衬衫,影响该店主决策的统计量是
( )
A.平均数 B.方差
C.众数 D.中位数
2.(2017·威海)某校排球队10名队员的身高(厘米)如下:
195,186,182,188,188,182,186,188,186,188.
这组数据的众数和中位数分别是( )
A.186,188 B.188,187
C.187,188 D.188,186
3.(2017·泰安)某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 5 10 20 50 100
人数 4 16 15 9 6
则他们捐款金额的中位数和平均数分别是( )
A.10,20.6 B.20,20.6 C.10,30.6 D.20,30.6
4.(2017·枣庄)下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
方差 3.6 3.6 7.4 8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙
C.丙 D.丁
5.(2017·青岛)小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法中错误的是(
)
A.众数是6吨 B.平均数是5吨
C.中位数是5吨 D.方差是43
6.(2017·潍坊)甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表
所示,丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数和方差两个因素分析,应选( )
甲 乙
平均数 9 8
方差 1 1
A.甲 B.乙 C.丙 D.丁
7.(2017·日照)为了解某初级中学附近路口的汽车流量,交通管理部门调查了某周一至周五下午放学时
间段通过该路口的汽车数量(单位:辆),结果如下:
183 191 169 190 177
则在该时间段中,通过这个路口的汽车数量的平均数是______.
8.七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下
表(部分):
月均用水量x/m3 0<x≤5 5<x≤10 10<x≤15 15<x≤20 x>20
频数/户 12 20 3
频率 0.12 0.07
若该小区有800户家庭,据此估计该小区月均用水量不超过10 m3的家庭约有______户.
9.(2017·青岛)某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“使用手机的
目的”和“每周使用手机的时间”的问卷调查,并绘制成如图所示的统计图.已知“查资料”的人数是
40人.
请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是_____度;
(2)补全条形统计图;
(3)该校共有学生1 200人,估计每周使用手机时间在2小时以上(不含2小时)的人数.
参考答案
1.C 2.B 3.D 4.A 5.C 6.C 7.182 8.560
9.解:(1)126
(2)一共抽取的人数为40÷40%=100,
所以每周使用手机3小时以上的人数为100-2-16-18-32=32.补全条形统计图如图:
(3)1 200×32+32100=768.
答:估计每周使用手机时间在2小时以上(不含2小时)的人数为768人.
