《二元一次方程》基础训练(含答案)
初一下册二元一次方程练习题含答案)

二元一次方程组解法练习题精选〔含答案〕一.解答题〔共16小题〕1.求适合的x,y的值.2.解以下方程组〔1〕〔2〕〔3〕〔4〕.3.解方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和.〔1〕求k,b的值.〔2〕当x=2时,y的值.〔3〕当x为何值时,y=3?7.解方程组:〔1〕;〔2〕.8.解方程组:9.解方程组:10.解以下方程组:〔1〕〔2〕11.解方程组:〔1〕〔2〕12.解二元一次方程组:〔1〕;〔2〕.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.〔1〕甲把a看成了什么,乙把b看成了什么?〔2〕求出原方程组的正确解.14.15.解以下方程组:〔1〕;〔2〕.16.解以下方程组:〔1〕〔2〕二元一次方程组解法练习题精选〔含答案〕参考答案与试题解析一.解答题〔共16小题〕1.求适合的x,y的值.解二元一次方程组.考点:分析:先把两方程变形〔去分母〕,得到一组新的方程,然后在用加减消元法消去未知数x,求出y的值,继而求出x的值.解答:解:由题意得:,由〔1〕×2得:3x﹣2y=2〔3〕,由〔2〕×3得:6x+y=3〔4〕,〔3〕×2得:6x﹣4y=4〔5〕,〔5〕﹣〔4〕得:y=﹣,把y的值代入〔3〕得:x=,∴.点此题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.评:2.解以下方程组〔1〕〔2〕〔3〕〔4〕.考点:解二元一次方程组.分析:〔1〕〔2〕用代入消元法或加减消元法均可;〔3〕〔4〕应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解解:〔1〕①﹣②得,﹣x=﹣2,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考点:解二元一次方程组.专题:计算题.分析:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:注意:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:析:解答:解:〔1〕原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.此题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:此题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.〔1〕求k,b的值.〔2〕当x=2时,y的值.〔3〕当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.分析:〔1〕将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k、b的值.〔2〕将〔1〕中的k、b代入,再把x=2代入化简即可得出y的值.〔3〕将〔1〕中的k、b和y=3代入方程化简即可得出x的值.解答:解:〔1〕依题意得:①﹣②得:2=4k,所以k=,所以b=.〔2〕由y=x+,把x=2代入,得y=.〔3〕由y=x+把y=3代入,得x=1.点评:此题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:〔1〕;〔2〕.考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:〔1〕先去分母再用加减法,〔2〕先去括号,再转化为整式方程解答.答:解:〔1〕原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;〔2〕原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:此题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:此题为了计算方便,可先把〔2〕去分母,然后运用加减消元法解此题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:此题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解以下方程组:〔1〕〔2〕考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:〔1〕运用代入法,把①代入②,可得出x,y的值;〔2〕先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:〔1〕,由①,得x=4+y③,代入②,得4〔4+y〕+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.〔2〕原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练到达对知识的强化和运用.11.解方程组:〔1〕〔2〕解答:解:〔1〕原方程组可化简为,解得.〔2〕设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:〔1〕;〔2〕.考点:解二元一次方程组.专题:计算题.分析:〔1〕运用加减消元的方法,可求出x、y的值;〔2〕先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:〔1〕将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;〔2〕此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练到达对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.〔1〕甲把a看成了什么,乙把b看成了什么?〔2〕求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:〔1〕把甲乙求得方程组的解分别代入原方程组即可;〔2〕把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由〔1〕+〔2〕,并解得x=〔3〕,把〔3〕代入〔1〕,解得y=,∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解以下方程组:〔1〕;〔2〕.解二元一次方程组.考点:将两个方程先化简,再选择正确的方法进行消元.分析:解解:〔1〕化简整理为,答:①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.〔2〕化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.点评:16.解以下方程组:〔1〕〔2〕解二元一次方程组.考点:分观察方程组中各方程的特点,用相应的方法求解.析:解解:〔1〕①×2﹣②得:x=1,。
(完整版)二元一次方程组练习题(含答案),推荐文档
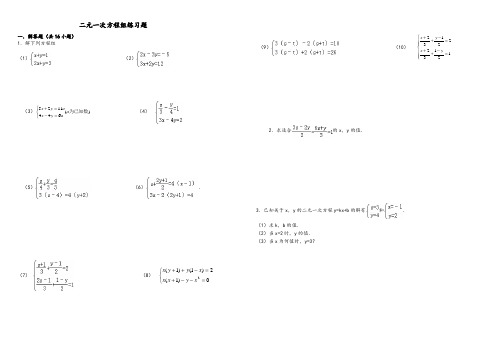
二元一次方程组练习题一.解答题(共16小题) 1.解下列方程组 (1)(2)(3))(6441125为已知数a a y x a y x ⎩⎨⎧=-=+ (4)(5)(6).(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x(9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2.求适合的x ,y 的值.3.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值. (3)当x 为何值时,y=3?1.解下列方程组(1)(2);(3);(4)(5).(6)(7)(8)(9)(10);2.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.二元一次方程组解法练习题精选参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x ﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考解二元一次方程组.点:专题:计算题. 分析: 先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法. 解答:解:原方程组可化为, ①×4﹣②×3,得 7x=42, 解得x=6.把x=6代入①,得y=4. 所以方程组的解为.点评: ;二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点: 解二元一次方程组. 专题: 计算题. 分析: 把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单. 解答:解:(1)原方程组化为,①+②得:6x=18, ∴x=3.代入①得:y=.所以原方程组的解为. 点评: 要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点: 解二元一次方程组. 专题: 计算题;换元法. 分析: 本题用加减消元法即可或运用换元法求解. 解答:解:,①﹣②,得s+t=4, ①+②,得s ﹣t=6, 即, 解得.所以方程组的解为.点评: 此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值. (3)当x 为何值时,y=3?考点: 解二元一次方程组. 专题: 计算题. 分析:(1)将两组x ,y 的值代入方程得出关于k 、b 的二元一次方程组,再运用加减消元法求出k 、b 的值.(2)将(1)中的k 、b 代入,再把x=2代入化简即可得出y 的值. (3)将(1)中的k 、b 和y=3代入方程化简即可得出x 的值.解答: 解:(1)依题意得:①﹣②得:2=4k , 所以k=, 所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x ﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b ,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a 、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.点评:解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.。
(完整)二元一次方程组练习题含答案,推荐文档

x y 90 (A) x y 15
x y 90 (C) x 15 2 y
x y 90
(B)
x
2
y
15
2x 90
(D)
x
2
y
15
A
(C) m<0,n>0
(D)m<0,n<0
二、D填空题(每小题 4 分,共 20 分)
x° y°
B
2x y 3k -1
11.若关于
C
x,y
的二元一次方程组
A.
x y 246 x y 246 x y 216 x y 246
2 y x 2
B.2x y 2
C.
y
2
x
2
D.2 y x 2
二、填空题 9.已知方程 2x+3y-4=0,用含 x 的代数式表示 y 为:y=_______;用含
y 的代数式表示 x 为:x=________.
的解
x
y
m n
中(
)
(A) m>0,n>0
o (B)m>0,n<0
x 4
ax y 1
17.已知
y
3
是关于
x,y
的二元一次方程组
x
by
2
的解,
求出 a+b 的值.
(1) x 、 y 的值;
(2) x2013 y2012 的值.
18.(8 分)为了净化空气,美化环境,我市青羊区计划投资 1.8 万元种银杏和芙蓉树共 80 棵,已知某苗圃负责种活以上两种树 苗的价格分别为:300 元/棵,200 元/棵,问可种银杏树和芙蓉树 各多少棵?
16.已知
x y
2 1
代代代代
(完整版)二元一次方程组练习题(含答案)

二元一次方程组练习题一.解答题(共16小题) 1.解下列方程组(1)(2)(3)(4))(6441125为已知数a a y x ay x ⎩⎨⎧=-=+(5)(6).(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x (9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x 2.求适合的x ,y 的值.3.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值.(3)当x 为何值时,y=3?1.解下列方程组(1)(2);(3);(4)(5).(6)(7)(8)(9)(10);2.在解方程组时,由于粗心,甲看错了方程组中的a ,而得解为,乙看错了方程组中的b ,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解. a t a nd Al l th i ng si nh ei r be i ng a 二元一次方程组解法练习题精选参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:t h i n gt a t i mA l lt h in gs inh ei r be i ng ar ef o rs om et h②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考点:解二元一次方程组.专题:计算题.分析:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:;二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点:解二元一次方程组.专题:计算题.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.h i ng at h i n ga ta ti m分析:(1)将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k、b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.t h i n ga ta ti n gs inh ei r be i ng ar eg oo df o rs om e点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.t h i n ga ta ti me an dA lh ei ro od fo rs om e解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;i n g a ta ti me an dA l lt h in gs inh ei r be i ng ar eg oo df o rs om et h in g(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程. 16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.点评:解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解. 。
(完整版)二元一次方程组练习题(含答案)(最新整理)

x 4
1
21.解:经验算
y
1
是方程
2Hale Waihona Puke x+3y=5的解,再写一个方程,如
x-y=3.
x y 13 22.(1)解:设 0.8 元的邮票买了 x 枚,2 元的邮票买了 y 枚,根据题意得 0.8x 2 y 20
.
4y 1 x (2)解:设有 x 只鸡,y 个笼,根据题意得 5( y 1) x .
二、填空题
9.已知方程 2x+3y-4=0,用含 x 的代数式表示 y 为:y=_______;用含 y 的代数式表示 x 为:x=________.
1
10.在二元一次方程- x+3y=2 中,当 x=4 时,y=_______;当 y=-1 时,x=______.
2
11.若 x3m-3-2yn-1=5 是二元一次方程,则 m=_____,n=______.
20.解:由(│x│-1)2+(2y+1)2=0,可得│x│-1=0 且 2y+1=0,∴x=±1,y=-
1
.
2
1
13
当 x=1,y=- 时,x-y=1+ = ;
2
22
1
11
当 x=-1,y=- 时,x-y=-1+ =- .
2
22
解析:任何有理数的平方都是非负数,且题中两非负数之和为 0,
则这两非负数(│x│-1)2 与(2y+1)2 都等于 0,从而得到│x│-1=0,2y+1=0.
x y
1
1 2
代入方程
2x-ky=4
中,2+
1 2
k=4,∴k=1.
最新人教版七年级数学下册第八章 二元一次方程组 8.4 三元一次方程组的解法 基础训练题(含答案)

最新人教版七年级数学下册第八章 二元一次方程组 基础训练题(含答案)8.4 三元一次方程组的解法1.下列是三元一次方程组的是( )A.⎩⎨⎧2x =5x 2+y =7x +y +z =6 B.⎩⎪⎨⎪⎧3x -y +z =-2x -2y +z =9y =-3 C.⎩⎨⎧x +y -z =7xyz =1x -3y =4 D.⎩⎨⎧x +y =2y +z =1x +z =9 2.观察方程组⎩⎨⎧3x -y +2z =3,2x +y -4z =11,7x +y -5z =1的系数特点,若要使求解简便,消元的方法应选取( )A .先消去xB .先消去yC .先消去zD .以上说法都不对3.将三元一次方程组⎩⎨⎧5x +4y +z =0, ①3x +y -4z =11, ①x +y +z =-2 ①经过步骤①-①和①×4+①消去未知数z 后,得到的二元一次方程组是( )A.⎩⎨⎧4x +3y =27x +5y =3B.⎩⎨⎧4x +3y =223x +17y =11C.⎩⎨⎧3x +4y =27x +5y =3D.⎩⎨⎧3x +4y =223x +17y =11 4.已知方程组⎩⎨⎧x +2y =k ,2x +y =1的解满足x +y =3,则k 的值为( ) A .10 B .8 C .2 D .-85.由方程组⎩⎨⎧2x +y =7,2y +z =8,2z +x =9,可以得到x +y +z 的值等于( )A .8B .9C .10D .116.解下列三元一次方程组:(1)⎩⎨⎧2x +y =4,①x +3z =1,①x +y +z =7;①(2)⎩⎨⎧x +z -3=0,①2x -y +2z =2,①x -y -z =-3.①7.一个三位数,个位、百位上的数字的和等于十位上的数字,百位上的数字的7倍比个位、十位上的数字的和大2,个位、十位、百位上的数字的和是14.则这个三位数是____________.8.已知-a x +y -z b 5c x +z -y 与a 11b y +z -x c 是同类项,则x =_______,y =_______,z =_______.9.已知y =ax 2+bx +c ,当x =1时,y =3;当x =-1时,y =1;当x =0时,y =1.求a ,b ,c 的值.10.2016里约奥运会,中国运动员获得金、银、铜牌共70枚,位列奖牌榜第三.其中金牌比银牌多8枚,铜牌比银牌的总数的2倍少10枚.问金、银、铜牌各多少枚?参考答案:1-5 DBABA6.(1)解:由①,得y =4-2x.①由①得z =1-x 3.①把①,①代入①,得x +4-2x +1-x 3=7.解得x =-2.①y =8,z =1.①原方程组的解为⎩⎨⎧x =-2,y =8,z =1.(2)解:①-①,得x +3z =5.①解由①,①组成的方程组,得⎩⎨⎧x =2,z =1. 将⎩⎨⎧x =2,z =1代入①,得y =4. ①原方程组的解为⎩⎨⎧x =2,y =4,z =1.7.2758.6 8 39.解:①y =ax 2+bx +c ,当x =1时,y =3;当x =-1时,y =1;当x =0时,y =1,①代入,得⎩⎨⎧a +b +c =3,①a -b +c =1,①c =1,①把①代入①和①,得⎩⎨⎧a +b =2,a -b =0.解得a =1,b =1, 即a =1,b =1,c =1.10.解:设金牌x 枚,银牌y 枚,铜牌z 枚,则⎩⎨⎧x +y +z =70,x -y =8,2y -z =10,解得⎩⎨⎧x =26,y =18,z =26.答:金牌26枚,银牌18枚,铜牌26枚.。
二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选(含答案)一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).3.解方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).8.解方程组:9.解方程组:10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2).13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1);(2).16.解下列方程组:(1)(2)二元一次方程组解法练习题精选(含答案)参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.解二元一次方程组.考点:分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.评:2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考点:解二元一次方程组.专题:计算题.分析:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:注意:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点:解二元一次方程组.专题:计算题.分把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.析:解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.分析:(1)将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=,∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.点评:。
二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选(含答案)一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).解方程组:4.解方程组:5.解方程组:3.6.已知关于x,y的二元一次方程y=kx+b 的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?.7.解方程组:(1);(2).解方程组:9.解方程组:8.10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2).13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1);(2).解下列方程组:(1)(2)16..二元一次方程组解法练习题精选(含答案)参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.,然后在用加减消元法消去未知数,,2.解下列方程组(1)(2)(3)(4).故原方程组的解为故原方程组的解为)原方程组可化为.所以原方程组的解为,x=,代入×﹣.所以原方程组的解为3.解方程组:解:原方程组可化为所以方程组的解为4.解方程组:)原方程组化为,.所以原方程组的解为5.解方程组:,.所以方程组的解为6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?的二元一次方程组)依题意得:,.y=x+y=y=x+7.解方程组:(1);(2).)原方程组可化为,;)原方程可化为.8.解方程组:解:原方程组可化为则原方程组的解为9.解方程组:解:原方程变形为:10.解下列方程组:(1)(2))﹣代入﹣=所以原方程组的解为)原方程组整理为所以原方程组的解为11.解方程组:(1)(2),∴原方程组可化为,∴原方程组的解为12.解二元一次方程组:(1);(2).;)此方程组通过化简可得:.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.)把代入方程组.代入方程组.∴方程组为则原方程组的解是14.∴原方程组的解为15.解下列方程组:(1);(2).)化简整理为故原方程组的解为)化简整理为故原方程组的解为16.解下列方程组:(1)(2)∴原方程组的解为)原方程组可化为∴原方程组的解为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《二元一次方程》基础训练一、填空题(每空2分,共26分): 1.已知二元一次方程1213-+y x =0,用含y 的代数式表示x ,则x =_________; 当y =-2时,x =___ ____.2.在:(1)⎩⎨⎧-==23y x 、(2)453x y =⎧⎪⎨=-⎪⎩、(3)1472x y ⎧=⎪⎪⎨⎪=-⎪⎩这三组数值中,_________是方程组x -3y =9的解,______是方程2 x +y =4的解,______是方程组3924x y x y -=⎧⎨+=⎩的解.3.已知⎩⎨⎧=-=54y x 是方程41x +2 my +7=0的解,则m =_______.4.若方程组⎩⎨⎧=-=+137by ax by ax 的解是⎩⎨⎧-=-=12y x ,则a =__,b =_. 5.已知等式y =kx +b ,当x =2时,y =-2;当x =-21时,y =3,则k =____,b =____. 6.若|3a +4b -c |+41(c -2 b )2=0,则a ∶b ∶c =_________. 7.当m =_______时,方程x +2y =2,2x +y =7,mx -y =0有公共解.8.一个三位数,若百位上的数为x ,十位上的数为y ,个位上的数是百位与十位上的数的差的2倍,则这个三位数是_______________. 二、选择题(每小题2分,共16分):9.已知下列方程组:(1)⎩⎨⎧-==23y y x ,(2)324x y y z +=⎧⎨-=⎩,(3)1310x y x y ⎧+=⎪⎪⎨⎪-=⎪⎩,(4)1310x y x y ⎧+=⎪⎪⎨⎪-=⎪⎩, 其中属于二元一次方程组的个数为( )(A )1 (B )2 (C )3 (D )4 10.已知2 x b +5y 3a 与-4 x 2a y 2-4b是同类项,则b a 的值为( )(A )2 (B )-2 (C )1 (D )-111.已知方程组⎩⎨⎧-=-=+1242m ny x n y mx 的解是⎩⎨⎧-==11y x ,那么m 、n 的值为( ) (A )⎩⎨⎧-==11n m (B )⎩⎨⎧==12n m (C )⎩⎨⎧==23n m (D )⎩⎨⎧==13n m 12.三元一次方程组156x y y z z x +=⎧⎪+=⎨⎪+=⎩的解是( )(A )105x y z =⎧⎪=⎨⎪=⎩ (B )124x y z =⎧⎪=⎨⎪=⎩ (C )104x y z =⎧⎪=⎨⎪=⎩ (D )410x y z =⎧⎪=⎨⎪=⎩13.若方程组⎩⎨⎧=+=-+14346)1(y x y a ax 的解x 、y 的值相等,则a 的值为( )(A )-4 (B )4 (C )2 (D )1 14.若关于x 、y 的方程组⎩⎨⎧=-=+ky x ky x 73的解满足方程2x +3y =6,那么k 的值为( )(A )-23 (B )23 (C )-32 (D )-23 15.若方程y =kx +b 当x 与y 互为相反数时,b 比k 少1,且x =21,则k 、b 的值分别是( )(A )2,1 (B )32,35 (C )-2,1 (D )31,-32 16.某班学生分组搞活动,若每组7人,则余下4人;若每组8人,则有一组少3人.设全班有学生x 人,分成y 个小组,则可得方程组( ) (A )7483x y x y +=⎧⎨-=⎩ (B )7483y x y x =+⎧⎨+=⎩ (C )7483y x y x =-⎧⎨=+⎩ (D )7483y x y x =+⎧⎨=+⎩三、解下列方程组(每小题4分,共20分):17.⎩⎨⎧-=-=-.557832y x y x 18.230.5344575615x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩.19.⎪⎩⎪⎨⎧=+=4.1%40%2552y x yx 20.⎩⎨⎧-=++=+.b a y x b a y x 2127521257(a 、b 为非零常数)21.⎪⎩⎪⎨⎧=++=-+=+-.10076702302z y x z y x z y x四、解答题(每小题6分,共18分)22.已知方程组⎩⎨⎧+=+=+25332n y x n y x 的解x 、y 的和为12,求n 的值.23.已知方程组⎩⎨⎧-=+=-1332by ax y x 与⎩⎨⎧=+=+3321123by ax y x 的解相同,求a 2+2ab +b 2 的值.24.已知代数式x2+ax+b当x=1和x=-3时的值分别为0和14,求当x=3时代数式的值.五、列方程组解应用问题(每1小题10分,共20分)25.某校去年一年级男生比女生多80人,今年女生增加20%,男生减少25%,结果女生又比男生多30人,求去年一年级男生、女生各多少人.26.A、B两地相距20千米,甲、乙两人分别从A、B 两地同时相向而行,两小时后在途中相遇.然后甲返回A地,乙继续前进,当甲回到A地时,乙离A地还有2千米,求甲、乙两人的速度.参考答案1.【提示】把y 作为已知数,求解x .【答案】x =62y -;x =32. 2.【提示】将三组数值分别代入方程、方程组进行检验.【答案】(1),(2);(1),(3);(1). 【点评】方程组的解一定是方程组中各个方程共同的解. 3.【提示】把⎩⎨⎧=-=54y x 代入方程,求m .【答案】-53.4.【提示】将⎩⎨⎧-=-=12y x 代入713ax by ax by +=⎧⎨-=⎩中,原方程组转化为关于a 、b 的二元一次方程组,再解之.【答案】a =-5,b =3.5.【提示】把x 、y 的对应值代入,得关于k 、b 的二元一次方程组.【答案】k =-2,b =2.【点评】通过建立方程组求解待定系数,是常用的方法. 6.【提示】由非负数的性质,得3 a +4 b -c =0,且c -2b =0.再用含b 的代数式表示a 、c ,从而求出a 、b 、c 的值.【答案】a =-32b ,c =2b ;a ∶b ∶c =-2∶3∶6. 【点评】用一个未知数的代数式表示其余的未知数,是一种常用的有效方法. 7.【提示】先解方程组2227x y x y +=⎧⎨+=⎩,将求得的x 、y 的值代入方程mx -y =0,或解方程组22270x y x y mx y +=⎧⎪+=⎨⎪-=⎩.【答案】⎩⎨⎧-==14y x ,m =-41.【点评】“公共解”是建立方程组的依据. 8.【提示】将各数位上的数乘相应的位数,再求和. 【答案】100 x +10 y +2(x -y ).9.【提示】方程组(2)中含有三个未知数,方程组(3)中y 的次数都不是1, 故(2)、(3)都不是二元一次方程组.【答案】B . 10.【提示】由同类项定义,得⎩⎨⎧-==+b a a b 42325,解得⎩⎨⎧=-=21b a ,所以b a =(-1)2=1.【答案】C . 11.【提示】将⎩⎨⎧-==11n m 代入方程组,得关于m 、n 的二元一次方程组解之.【答案】D .12.【提示】把三个方程的两边分别相加,得x +y +z =6或将选项逐一代入方程组验证,由x +y =1知(B )、(D )均错误;再由y +z =5,排除(C ),故(A )正确,前一种解法称之直接法...;后一种解法称之逆推验证法......【答案】A . 【点评】由于数学选择题多为单选题——有且只有一个正确答案,因而它比一般题多一个已知条件:选择题中有且只有一个是正确的.故解选择题除了直接法以外,还有很多特殊的解法,随着学习的深入,我们将逐一向同学们介绍.13.【提示】把x =y 代入4x +3y =14,解得x =y =2,再代入含a 的方程.【答案】C . 14.【提示】把k 看作已知常数,求出x 、y 的值,再把x 、y 的值代入2 x +3 y =6,求出k .【答案】B . 15.【提示】由已知x =21,y =-21,可得⎪⎩⎪⎨⎧=-+=-.12121b k b k 【答案】D .16【提示】由题意可得相等关系:(1)7组的学生数=总人数-4;(2)8组的人数=总人数+3.【答案】C .17.【提示】用加减消元法先消去x .【答案】⎩⎨⎧-=-=.65y x 18.【提示】先整理各方程,化为整数系数的方程组,用加减法消去x .【答案】⎪⎩⎪⎨⎧=-=.223y x19.【提示】由第一个方程得x =52y ,代入整理后的第二个方程;或由第一个方程,设x =2 k ,y =5 k ,代入另一个方程求k 值.【答案】⎪⎪⎩⎪⎪⎨⎧==.15142528y x 20.【提示】将两个方程左、右两边分别相加,得x +y =2a ①,把①分别与两个方程联立求解.【答案】⎩⎨⎧-=+=.b a y b a x【点评】迭加消元,是未知数系轮换方程组的常用解法. 21.【提示】将第一个方程分别与另外两个方程联立,用加法消去y .【答案】357x y z =⎧⎪=⎨⎪=⎩.【点评】分析组成方程组的每个方程中各未知项系数的构成特点,是选择恰当解题方法的关键所在,因而解题前要仔细观察,才能找出解题的捷径. 22.【提示】解已知方程组,用n 的代数式表示x 、y ,再代入 x +y =12.【答案】n =14. 23.【提示】先解方程组⎩⎨⎧=+=-1123332y x y x 求得x 、y ,再代入方程组⎩⎨⎧=+-=+3321by ax by ax 求a 、b . 【答案】⎩⎨⎧=-=52b a . 【点评】当n 个方程组的解相同,可将方程组中的任意两个方程联立成新的方程组. 24.【提示】由题意得关于a 、b 的方程组.求出a 、b 写出这个代数式,再求当x =3时它的值.【答案】5.【点评】本例在用待定系数法求出a 、b 的值后,应写出这个代数式,因为它是求值的关键步骤.25.【提示】设去年一年级男生、女生分别有x 人、y 人,可得方程组⎪⎩⎪⎨⎧=--+=-.30)100251()100201(80x y y x【答案】x =280,y =200.26.【提示】由题意,相遇前甲走了2小时,及“当甲回到A 地时,乙离A 地还有2千米”,可得列方程组的另一个相等关系:甲、乙同向行2小时,相差2千米.设甲、乙两人的速度分别为x 千米/时,y 千米/时,则⎩⎨⎧=-=+.2)(220)(2y x y x 【答案】甲的速度为5.5千米/时,乙的速度为4.5千米/时。
