noip复赛模拟卷一
NOIP复赛模拟题

NOIP2006复赛模拟题(普及组水平)(时间:3小时)注意事项:1. 严格按照题目所要求的格式进行输入、输出。
2. 题目测试数据有严格的时间,超时不得分。
所有题目的时限均为1秒。
3. 输入文件格式不用判错。
程序文件名、输入输出文件名等请严格按照要求。
4. 本次比赛共4题。
5. 同时提交pas、exe文件,请使用freepascal编译。
编译后的exe请留意是否能正确运行。
为方便测试,所有pas、exe均存在一个文件夹中,该文件夹用你的中文名字命名,然后把整个文件夹压缩为一个rar文件(该文件也是用你的中文名字命名)提交到老师邮箱:*************。
第一题位置(posi.pas)求数A在数组B中的位置.输入及格式:第一行是数A ,一维数组B的元素个数N(N<=105),中间用空格隔开。
第二行是已按升序排列的一维数组B (-32768<B[i],A<32767),数间用空格隔开。
输出及格式:数A在B中的下标。
B中如果存在多个A,则输出下标最小的一个。
如果B 中不存在A,则输出“-1”输入样例1:3 61 3 3 4 5 10输出样例1:2输入样例2:1 33 4 5输出样例2:-1第二题面积(area.pas)一幅图由0和*组成,编程计算由“*”号所围成的图形的面积。
面积是指*号所围成的闭合曲线中0的数目。
输入:由0,*组成的图输出:面积数输入样例:0000000000000**000000*00*0000*000*00000***000000000000输出样例:5输入样例2:000000000000*000*0*0输出样例2:第三题阶乘位数(jc.pas)问题描述:在很多软件中需要用到较大的整数。
比如一些软件将大数用于数据安全传送的密匙或者密码编译等等。
在这个问题中,你要根据给你的整数,算出这个数的阶乘的位数。
输入格式:输入文件包含若干行整数。
第一行为n,表示有n组数据,接下来是n行,每行一个整数m(1≤m≤107)。
小学生信息学奥林匹克复赛模拟试题一

小学生信息学奥林匹克复赛模拟试题一说明:1.严格按题目要求的输入、输出格式读写数据,否则不得分。
2.请在D盘根目录下建立以自己考号命名的文件夹,并把需要提交的文件(即每一题的源文件和编译后的可执行文件)保存在此文件夹内。
3.竞赛结束后速离开考场,不要关机。
第一题:开灯游戏(xj1.pas)【问题描述】有n盏灯,放在一排,从1到n依次顺序编号。
有m个人也从1到m依次顺序编号。
第1个人(1号)将灯全部关闭;第2个人(2号)将凡是2的倍数的灯打开;第3个人(3号)将凡是3的倍数的灯作相反处理(该灯如是打开的,则将它关闭;如是关闭的,则将它打开)。
以后的人都和3号一样,将凡是自己编号倍数的灯作相反处理。
试计算当第m个人操作后,哪几盏灯是亮的?【输入格式】从键盘输入n,m的值。
(n,m均为小于32768的自然数,且n>=m)【输出格式】在同一行输出亮着的灯的编号。
(没有灯亮则输出“NO”)【样例输入】5 3【样例输出】2 3 4第二题:数列求和(xj2.pas)【问题描述】简单数列是有规律排列的一些数,例如1,2,3,4,5,6,7就是这样的数列,这种数列中的后一个数总是前一个数多或少一个相同的数,其实只要知道这种数列中的前三个数和最后一个数就可以写出数列中的所有的数。
你的任务是根据给出的数列求出这个数列所有数的和。
每个数列的前三个数和最后一个数从键盘输入。
【输入格式】输入只有一行,分别为数列的前三个数和最后一个数。
所有输入均为不大于32767的自然数。
【输出格式】以等式的形式输出这个数列的和。
【样例输入1】项数=(末项-首项) div 公差+11 2 3 7【样例输出2】1+2+3+…+7=28【样例输入2】-3 -1 1 5【样例输出2】(-3)+(-1)+1+…+5=5(说明:算式中只要求输出前三个数和最后一个数,中间的数用…代表,等式左边的负数要加上小括号)第三题:算式求解(xj3.pas)【问题描述】输入一个算式,输出算式的结果。
noip2015普及组复赛试题

noip2015普及组复赛试题题目一:矩阵运算给定一个n阶方阵A(1 ≤ n ≤ 100),求A的所有指定行指定列删除后得到的新矩阵的行列式。
输入格式:输入第一行包含一个整数n,表示方阵的阶数。
接下来n行,每行包含n个整数,表示方阵A的元素。
接下来一行包含两个整数,表示要删除的行和列的序号。
输出格式:输出一个整数,表示新矩阵的行列式的值。
题目要求:首先,我们需要编写一个能够计算矩阵行列式的函数,然后根据题意进行修改,使其能够处理删除指定行列后的新矩阵,并返回新矩阵的行列式的值。
算法思路:我们可以使用拉普拉斯展开定理来计算矩阵行列式的值。
首先定义一个变量result,初始化为0。
然后遍历矩阵的第一行元素,对于第i 个元素,根据其正负性,计算其余元素组成的(n-1)阶子矩阵的行列式的值,并递归调用自身。
最后将每个元素计算得到的行列式值乘以其对应的元素,累加到result上。
然后根据题目要求,在计算每个元素对应的子矩阵时,判断是否需要删除指定的行列。
如果需要删除,则直接跳过该行列,否则继续计算。
代码如下:```pythondef determinant(matrix):n = len(matrix)if n == 1:return matrix[0][0]result = 0for i in range(n):if n > 2:sub_matrix = [row[:i] + row[i+1:] for row in matrix[1:]]else:sub_matrix = matrix[1:]det = determinant(sub_matrix)result += (-1) ** i * matrix[0][i] * detreturn resultn = int(input())matrix = []for _ in range(n):row = list(map(int, input().split()))matrix.append(row)row, col = map(int, input().split())matrix = [matrix[i][:col] + matrix[i][col+1:] for i in range(row)] # 删除指定列matrix = matrix[:row] + matrix[row+1:] # 删除指定行result = determinant(matrix)print(result)```题目二:水果分配小明和他的朋友们买了n个水果,其中有x个苹果和y个香蕉。
历届noip提高组复赛试题

NOI’ 95“同创杯”全国青少年信息学(计算机)奥林匹克竞赛分区联赛复赛试题(高中组)(上机编程,完成时间:210 分钟)<1>编码问题:设有一个数组A:ARRAY[0..N-1] OF INTEGER;数组中存放的元素为0~N-1 之间的整数,且A[i]≠ A[j](当i≠ j时)。
例如: N=6 时,有:此时,数组 A 的编码定义如下:A[0] 的编码为0;A[i] 的编码为:在A[0] ,A[1]∴上面数组 A 的编码为:A= ( 4,3, 0, 5,1, 2),, A[i-1] 中比 A[i] 的值小的个数(B= (0, 0,0,3,1, 2)i=1 ,2,, N-1 )程序要求解决以下问题:①给出数组 A 后,求出其编码。
②给出数组 A 的编码后,求出 A 中的原数据。
<2> 灯的排列问题:设在一排上有 N 个格子( N≤ 20),若在格子中放置有不同颜色的灯,每种灯的个数记为 N 1, N2, N k( k 表示不同颜色灯的个数)。
放灯时要遵守下列规则:①同一种颜色的灯不能分开;②不同颜色的灯之间至少要有一个空位置。
例如: N=8 (格子数)R=2 (红灯数)B=3 (蓝灯数)放置的方法有:R-B 顺序R R B B BR R B B BR R B B BR R B B BR R B B BR R B B BB-R顺序B B B BBBBBBBBBBBBBBR RRRBRRRRRRRR放置的总数为12 种。
数据输入的方式为:NP1(颜色,为一个字母)P2N1(灯的数量)N2Q(结束标记, Q 本身不是灯的颜色)程序要求:求出一种顺序的排列方案及排列总数。
<3> 设有一个四层的积木块,1~ 4 层积木块的数量依次为:5, 6,7, 8如下图所示放置:815851691423414326其中,给出第三层与第四层所标示的数字,并已知第三层的数据是由第四层的数据计算出来的。
NOIP2014普及组复赛试题

1. 珠心算测验【问题描述】 珠心算是一种通过在脑中模拟算盘变化来完成快速运算的一种计算技术。
珠心算训练,既能够开发智力,又能够为日常生活带来很多便利,因而在很多学校得到普及。
某学校的珠心算老师采用一种快速考察珠心算加法能力的测验方法。
他随机生成一个正整数集合,集合中的数各不相同,然后要求学生回答:其中有多少个数,恰好等于集合中另外两个(不同的)数之和? 最近老师出了一些测验题,请你帮忙求出答案。
【输入】输入文件名为count.in 。
输入共两行,第一行包含一个整数n ,表示测试题中给出的正整数个数。
第二行有n 个正整数,每两个正整数之间用一个空格隔开,表示测试题中给出的正整数。
【输出】输出文件名为count.out 。
输出共一行,包含一个整数,表示测验题答案。
【输入输出样例】 count.in count.out 4 1 2 3 42【样例说明】由1+2=3,1+3=4,故满足测试要求的答案为2。
注意,加数和被加数必须是集合中的两个不同的数。
【数据说明】对于100%的数据,3 ≤ n ≤ 100,测验题给出的正整数大小不超过10,000。
2.比例简化【问题描述】在社交媒体上,经常会看到针对某一个观点同意与否的民意调查以及结果。
例如,对某一观点表示支持的有1498人,反对的有902人,那么赞同与反对的比例可以简单的记为1498:902。
不过,如果把调查结果就以这种方式呈现出来,大多数人肯定不会满意。
因为这个比例的数值太大,难以一眼看出它们的关系。
对于上面这个例子,如果把比例记为5:3,虽然与真实结果有一定的误差,但依然能够较为准确地反映调查结果,同时也显得比较直观。
现给出支持人数A,反对人数B,以及一个上限L,请你将A比B化简为A’比B’,要求在A’和B’均不大于L且A’和B’互质(两个整数的最大公约数是1)的前提下,A’/B’≥A/B 且A’/B’ - A/B的值尽可能小。
【输入】输入文件名为ratio.in。
noip普及组复赛入门训练1答案

noip普及组复赛入门训练1答案PASCAL复习21. 字符统计(文件名ZFTJ.PAS)读入一组字符,以“?”作为结束标志,统计其中元音字母、辅音字母、数字和其它符号个数(“?”作为结束标志,不计算个数)。
如输入字符为SouA56#s?,则输出YY=3,FY=2,SZ=2,QT=1。
输入输出样例:输入:SouA56#sEenTk3&?输出:YY=5,FY=5,SZ=3,QT=2var s1,S2,S3,S4,t:longint;c:char;begin S1:=0;S2:=0;S3:=0;S4:=0;while c<>'?' dobegin read(c);if ((c>='a') and (c<='z')) or ((c>='A') AND (C<='Z')) THENif (c='a') or (c='e') or (c='i') OR (c='o') or (c='u') or(c='A') OR (c='E') OR (c='I') OR (c='O') OR (c='U')THEN S1:=S1+1 ELSE S2:=S2+1ELSEIF (c>='0') and (c<='9') then s3:=s3+1ELSE S4:=S4+1;end;writeln('YY=',S1,'FY=',S2,'SZ=',S3,'QT=',S4-1);END.2.取数(QS.PAS)问题描述:我们来玩一个游戏:自然数1到N,按顺序列成一排,你可以从中取走任意个数,但是相邻的两个不可以同时被取走。
(NOIP2009)复赛模拟试题
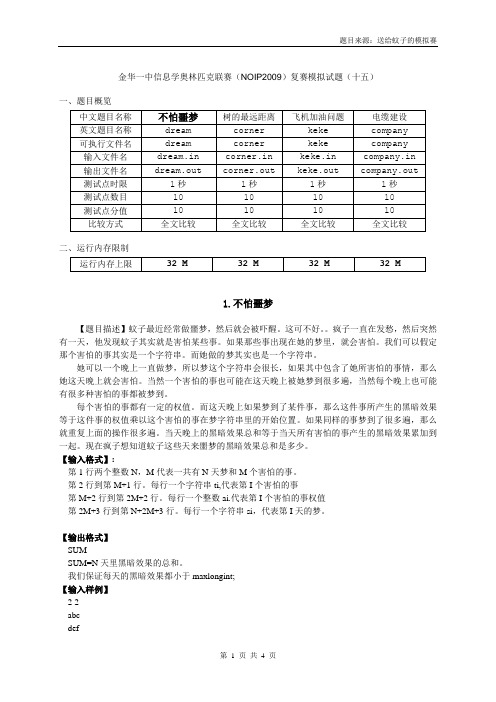
金华一中信息学奥林匹克联赛(NOIP2009)复赛模拟试题(十五)一、题目概览二、运行内存限制1.不怕噩梦【题目描述】蚊子最近经常做噩梦,然后就会被吓醒。
这可不好。
疯子一直在发愁,然后突然有一天,他发现蚊子其实就是害怕某些事。
如果那些事出现在她的梦里,就会害怕。
我们可以假定那个害怕的事其实是一个字符串。
而她做的梦其实也是一个字符串。
她可以一个晚上一直做梦,所以梦这个字符串会很长,如果其中包含了她所害怕的事情,那么她这天晚上就会害怕。
当然一个害怕的事也可能在这天晚上被她梦到很多遍,当然每个晚上也可能有很多种害怕的事都被梦到。
每个害怕的事都有一定的权值。
而这天晚上如果梦到了某件事,那么这件事所产生的黑暗效果等于这件事的权值乘以这个害怕的事在梦字符串里的开始位置。
如果同样的事梦到了很多遍,那么就重复上面的操作很多遍。
当天晚上的黑暗效果总和等于当天所有害怕的事产生的黑暗效果累加到一起。
现在疯子想知道蚊子这些天来噩梦的黑暗效果总和是多少。
【输入格式】:第1行两个整数N,M代表一共有N天梦和M个害怕的事。
第2行到第M+1行。
每行一个字符串ti,代表第I个害怕的事第M+2行到第2M+2行。
每行一个整数ai.代表第I个害怕的事权值第2M+3行到第N+2M+3行。
每行一个字符串si,代表第I天的梦。
【输出格式】SUMSUM=N天里黑暗效果的总和。
我们保证每天的黑暗效果都小于maxlongint;【输入样例】2 2abcdef12abcdefdefabc【输出样例】15【友情提示】1*1+2*4+1*4+2*1=15对于数据的把握和时间复杂度的估计是成败的关键。
如果出现一个梦是:ab而害怕的事有a,b,ab,那么a,b,ab都需要参与计算..【数据规模】对于30%的数据N,M<=50对于所有的数据N<=200.M<=200. length(si)<=200.length(ti)<=200.ai<=10.2.那23个路口【题目描述】故事的起源不加赘述,那23个路口。
noip复赛普及组试题

CCF 全国信息学奥林匹克联赛〔NOIP2021 〕复赛普及组〔请选手务必仔细阅读本页内容〕一.题目大要中文题目名称金币扫雷游戏求和销售员英文题目与子目录名coin mine sum salesman 可执行文件名coin mine sum salesman 输入文件名输出文件名每个测试点时限 1 秒 1 秒 1 秒 1 秒测试点数量10101010每个测试点分值10101010附加样例文件有有有有结果比较方式全文比较〔过滤行末空格及文末回车〕题目种类传统传统传统传统运行内存上限128M128M128M128M 二.提交源程前言件名对于 C++语言对于C语言对于 pascal语言三.编译命令〔不包括任何优化开关〕对于 C++语言g++ -o coin -g++ -o mine -g++ -o sum -g++ -o salesmanlm lm lm-lm 对于C语言gcc -o coin gcc -o mine gcc -o sum gcc -o salesman-lm-lm-lm-lm对于 pascal语言fpc fpc fpc fpc 本卷须知:1、文件名〔程序名和输入输出文件名〕必定使用英文小写。
2、 C/C++中函数 main()的返回值种类必定是int,程序正常结束时的返回值必定是3、全国一致评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor4G,上述时限以此配置为准。
0 。
,,内存4、只供应 Linux格式附加样例文件。
5、特别提示:评测在当前最新宣告的NOI Linux下进行,各语言的编译器版本以其为准。
1.金币c/pas)国王将金作工,放忠的士。
第一天,士收到一枚金;此后两天〔第二天和第三天〕,每天收到两枚金;此后三天〔第四、五、六天〕,每天收到三枚金;此后四天〔第七、八、九、十天〕,每天收到四枚金⋯⋯;种工放模式会素来延下去:当 N 天每天收到 N 枚金后,士会在此后的 N+1 天里,每天收到 N+1 枚金。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NOIP 2011复赛练习卷(一) 1、最优贸易 (trade.pas/c/cpp) 【问题描述】 C 国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市。任意两个 城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路,一部分 为双向通行的道路,双向通行的道路在统计条数时也计为 1 条。
C 国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价 格不一定相同。但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后,便决定在旅游的同时,利用商品在不同城市中的差价赚回一点旅费。设C国n个城 市的标号从1~ n,阿龙决定从1号城市出发,并最终在n号城市结束自己的旅行。在旅游的过程中,任何城市可以重复经过多次,但不要求经过所有n个城市。阿龙通过这样的贸易方式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品——水晶球,并在之后经过的另一个城市卖出这个水晶球,用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游,他决定这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。
假设C国有5个大城市,城市的编号和道路连接情况如下图,单向箭头表示这条道路为单向通行,双向箭头表示这条道路为双向通行。
假设 1~n 号城市的水晶球价格分别为 4,3,5,6,1。 阿龙可以选择如下一条线路:1->2->3->5,并在 2 号城市以 3 的价格买入水晶球,在 3号城市以 5 的价格卖出水晶球,赚取的旅费数为 2。
阿龙也可以选择如下一条线路 1->4->5->4->5,并在第 1 次到达 5 号城市时以 1 的价格买入水晶球,在第 2 次到达 4 号城市时,以 6 的价格卖出水晶球,赚取的旅费数为 5。
现在给出 n 个城市的水晶球价格、m 条道路的信息(每条道路所连接的两个城市的编号以及该条道路的通行情况)),请你告诉阿龙,他最多能赚取多少旅费。
【输入】(trade.in) 第1行:包含 2 个正整数 n 和 m,中间用一个空格隔开,分别表示城市的数目和道路的数目。
第2行:n 个正整数,每两个整数之间用一个空格隔开,按标号顺序分别表示这 n 个城市的商品价格。
接下来 m 行:每行有 3 个正整数x、y、z,每两个整数之间用一个空格隔开。如果z=1, 表示这条道路是城市x到城市y之间的单向道路;如果 z=2,表示这条道路为城市 x 和城市 y 之间的双向道路。
【输出】(trade.out) 1 行:包含 1 个整数,表示最多能赚取的旅费。如果没有进行贸易,则输出 0。 【输入输出样例】 trade.in trade.out 5 5 4 3 5 6 1 1 2 1 1 4 1 2 3 2 5 3 5 1 4 5 2 【数据范围】 输入数据保证 1 号城市可以到达 n 号城市。 10%的数据: 1≤n≤6。 30%的数据: 1≤n≤100。 50%的数据: 不存在一条旅游路线,可以从一个城市出发,再回到这个城市。 100%的数据: 1≤n≤100000,1≤m≤500000,1≤x,y≤n,1≤z≤2,1≤各城市水晶球价格≤100。
2、Elaxia的路线 (travel.pas/c/cpp)
【问题描述】 最近,Elaxia和Warren的关系特别好,他们很想整天在一起,但是,大学的学习太紧张了,他们必须合理地安排两个人在一起的时间。Elaxia和Warren每天都要奔波于宿舍和实验室之间,他们希望在节约时间的前提下,一起走的时间尽可能长。
现在,已知的是Elaxia和Warren所在的宿舍和实验室的编号以及学校的地图,地图上有N个路口、M条路,经过每条路都需要一定的时间。
具体地说,就是要求无向图中,两对点之间最短路的最长公共路径。 【输入】(travel.in) 第1行:两个整数N和M(含义如题中所述)。 第2行:4个整数x1、y1、x2、y2 (1<=x1<=N, 1<=y1<=N, 1<=x2<=N, 1<=y2<=N),分别表示Elaxia的宿舍和实验室及Warren的宿舍和实验室的标号(两对点分别为x1,y1,x2,y2)。
接下来的M行:每行3个整数u、v、L(1<=u<=N, 1<=v<=N, 1<=L<=10000),表示u和v之间有一条路,经过这条路所需的时间为L。
【输出】(travel.out) 1行:一个整数,表示每天两人在一起的时间(即最长公共路径的长度)。 【输入输出样例】 travel.in travel.out 9 10 1 6 7 8 1 2 1 2 5 2 2 3 3 3 4 2 3 9 5 3 4 5 3 4 6 4 4 7 2 5 8 1 7 9 1 【数据规模】 30%的数据: N<=100; 60%的数据: N<=1000; 100%的数据: N<=1500,输入数据保证没有重边和自环。 3、间谍网络 (age.pas/c/cpp) 【问题描述】 由于外国间谍的大量渗入,国家安全正处于高度的危机之中。如果A间谍手中掌握着关于B间谍的犯罪证据,则称A可以揭发B。有些间谍收受贿赂,只要给他们一定数量的美元,他们就愿意交出手中掌握的全部情报。所以,如果我们能够收买一些间谍的话,我们就可能控制间谍网中的每一分子。因为一旦我们逮捕了一个间谍,他手中掌握的情报都将归我们所有,这样,就有可能逮捕新的间谍,掌握新的情报。
我们的反间谍机关提供了一份资料,包括所有已知的受贿的间谍,以及他们愿意收受的具体数额。同时,我们还知道哪些间谍手中具体掌握了哪些间谍的资料。假设总共有n个间谍(n不超过3000),每个间谍分别用1到3000的整数来标识。
请根据这份资料,判断我们是否有可能控制全部的间谍。如果可以,求出我们所需要支付的最少资金;否则,输出不能被控制的一个间谍。
【输入】(age.in) 输入文件的第一行只有一个整数n。 第二行是整数p,表示愿意被收买的人数,1<=p<=n。 接下来的p行,每行有两个整数,第一个数是一个愿意被收买的间谍的编号,第二个数表示他将会被收买的数额。这个数额不超过20000。
紧跟着一行只有一个整数r,1<=r<=8000。接下来有r行,每行有两个正整数,表示数对(A,B),即A间谍掌握了B间谍的证据。
【输出】(age.out) 如果可以控制所有的间谍,第一行输出YES,并在第二行中输出所需支付的贿金最小值;否则,输出NO,并在第二行输出不能控制的间谍中,编号最小的的间谍编号。
【样例输入1】 3 2 1 10 2 100 2 1 3 2 3 【样例输出1】 YES 110 【样例输入2】 4 2 1 100 4 200 2 1 2 3 4 【样例输出2】 NO 3 4、feast (feast.pas/c/cpp) 【问题描述 】 满汉全席是中国最丰盛的宴客菜肴,有许多种不同的材料通过满族或是汉族的料理方式,呈现在数量繁多的菜色之中。由于菜色众多而繁杂,只有极少数博学多闻、技艺高超的厨师能够做出满汉全席,而能够烹饪出经过专家认证的满汉全席,也是中国厨师最大的荣誉之一。
世界满汉全席协会是由能够料理满汉全席的专家厨师们所组成,而他们之间还细分为许多不同等级的厨师。为了招收新进的厨师进入世界满汉全席协会,将于近日举办满汉全席大赛,协会派出许多会员当作评委,为的就是要在参赛的厨师之中,找到满汉料理界的明日之星。
每位参赛的选手可以得到 n 种材料,选手可以自由选择用满式或是汉式料理将材料做成菜肴。
大赛共有 m 位评委把关。每一位评委对于满汉全席有各自独特的见解,但基本的见解是:要有两样菜色作为满汉全席的标志。如某评委认为,如果没有汉式东坡肉及满式的涮羊肉锅,就不能算是满汉全席。 为了避免过于有主见的评审意见,大会规定,对每一位参赛者来说,一个评委除非是在认为必备的两样菜色都没有做出来的状况下,才能淘汰他,否则就不能淘汰他。换句话说,参赛者在这两种材料的做法中,只要其中一个能符合评委的喜好,即可通过该评委的审查。例如,当材料中有猪肉、羊肉和牛肉时,有四位评委的喜好如下表所示:
评委一 评委二 评委三 评委四 满式牛肉 满式猪肉 汉式牛肉 汉式牛肉 汉式猪肉 满式羊肉 汉式猪肉 满式羊肉 如参赛者甲做出满式猪肉、满式羊肉和满式牛肉料理,他将无法满足评委三的要求,无法通过评审。而参赛者乙做出汉式猪肉、满式羊肉和满式牛肉料理,就可以满足所有评委的要求。
但是,大会后来发现,在这样的制度下,如果材料选择跟派出的评委没有特别安排好的话,所有的参赛者最多只能通过部分(而不是全部)评委的审查,所以可能会发生没有一个人通过考核的情形。例如,当有四位评委的喜好如下表所示时,则不论参赛者采取什么样的做法,都不可能通过所有评委的考核:
评委一 评委二 评委三 评委四 满式羊肉 满式猪肉 汉式羊肉 汉式羊肉 汉式猪肉 满式羊肉 汉式猪肉 满式猪肉 所以,大会希望你写一个程序来判断:对所选出的 m 位评委,会不会发生没有人能通过考核的窘境,以便帮助组织合适的评审团。
【输入】(feast.in) 测试文件的第一行包含一个数字 K,代表测试文件包含了K 组测试数据。 每一组测试数据的第一行包含两个数字n 和m(n≤100,m≤1000),代表有n 种材料,m 位评委。为方便起见,材料舍弃中文名称而给予编号,编号分别从1 到n。
接下来的m 行,每行都代表对应的评委所拥有的两个喜好,每个喜好由一个英文字母和一个数字代表,如m1 代表这个评委喜欢第1 个材料通过满式料理做出来的菜,而h2 代表这个评委喜欢第 2 个材料通过汉式料理做出来的菜。
每个测试文件不会有超过50 组的测试数据。 【输出】(feast.out) 对每一组测试数据,输出一行对应的答案:如果不会发生没有人能通过考核的窘境,输出 GOOD,否则输出 BAD(大写字母)。
【样例输入1】 2 3 4
