高中数学概率大题(经典二)
高中数学 概率经典例题和巩固练习及答案

高中数学:概率总复习(例题、巩固练习、例题和巩固练习详解)【典型例题】要点一:随机事件与概率例1.某射手在相同条件下进行射击,结果如下:(1)问该射手射击一次,击中靶心的概率约是多少? (2)假设该射手射击了300次,估计击中靶心的次数是多少?举一反三:【变式1】若在同等条件下进行n 次重复试验得到某个事件A 发生的频率()n f ,则随着n 的逐渐增大,有( )A .()n f 与某个常数相等B .()n f 与某个常数的差逐渐减小C .()n f 与某个常数的差的绝对值逐渐减小D .()n f 与某个常数的附近摆动并趋于稳定要点二:互斥事件与对立事件例2.经统计,在某储蓄所一个营业窗口等候的人数及相应概率如下:(1)至多2人排队等候的概率是多少? (2)至少3人排队等候的概率是多少?举一反三:【变式1】某地区的年降水量在下列范围内的概率如下表所示:.要点三:古典概型例3.5张奖券中有2张是中奖的,首先由甲抽一张,然后由乙抽一张,求:(1)甲中奖的概率P(A);(2)甲、乙都中奖的概率P(B);(3)只有乙中奖的概率P(C);(4)乙中奖的概率P(D).举一反三:【变式1】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.(Ⅰ)求取出的两个球上标号为相邻整数的概率;(Ⅱ)求取出的两个球上标号之和能被3整除的概率.【变式2】从含有两件正品a1,a2和一件次品b1的三件产品中,每次任取一件,每次取出后不放回,连续取两次,求取出的两件产品中恰有一件次品的概率.要点四:几何概型例4、从甲地到乙地有一班车在9:30到10:00到达,若某人从甲地坐该班车到乙地转乘9:45到10:15出发的汽车到丙地去,问他能赶上车的概率是多少?举一反三:【变式1】在0~1之间随机选择两个数,这两个数对应的点把长度为1的线段分成了三条线段,试求这三条线段能构成三角形的概率.【变式2】已知关于x 的二次函数2()41f x ax bx =-+.(1)设集合P ={-1,1,2,3,4,5}和Q ={-2,-1,1,2,3,4},分别从集合P 和Q 中随机取一个数作为a 和b ,求函数()y f x =在区间[1,+∞)上是增函数的概率:(2)设点(a ,b)是区域8000x y x y +-≤⎧⎪>⎨⎪>⎩内的随机点,求函数()f x 在区间[1,+∞)上是增函数的概率.【巩固练习】1.一个射手进行射击,记事件E 1:“脱靶”,E 2:“中靶”,E 3:“中靶环数大于4”,E 4:“中靶环数不小于5”,则在上述事件中,互斥而不对立的事件共有( ) A .1对 B .2对 C .3对 D .4对2.某校学生毕业后有回家待业,上大学和补习的三种方式,现取一个样本调查结果如图所示,若该校每一个学生上大学的概率为45,则每个学生补习的概率为( )A .110 B .225 C .325D .153.从一批羽毛球产品中任取一个,其质量小于4.8 g 的概率为0.3,质量小于4.85g 的概率为0.32,那么质量在[4.8,4.85)(g)范围内的概率是( ) A .0.62 B .0.38 C .0.02 D .0.684.先后抛掷骰子三次,则至少一次正面朝上的概率是( ) A .81 B . 83 C . 85 D . 87 5.有五条线段长度分别为1,3,5,7,9,从这5条线段中任取3条,则所取3条线段能构成一个三角形的概率为( )。
高中数学概率统计练习题

y 2015年12月31日期末复习题(二)一.选择题(共12小题)1.某工厂生产A,B,C三种不同型号的产品,产品数量之比依次为2:3:5.现用分层抽样方法抽出一个容量为n的样本,样本中A型号产品有16件,则此样本的容量为()A.40B.80C.160D.3202.某县教育局为了解本县今年参加一次大联考的学生的成绩,从5000名参加今年大联考的学生中抽取了250名学生的成绩进行统计,在这个问题中,下列表述正确的是()A.5000名学生是总体B.250名学生是总体的一个样本C.样本容量是250D.每一名学生是个体3.(2015?抚顺模拟)某校三个年级共有24个班,学校为了了解同学们的心理状况,将每个班编号,依次为1到24,现用系统抽样方法.抽取4个班进行调查,若抽到的最小编号为3,则抽取最大编号为()A.15B.18C.21D.224.一个频率分布表(样本容量为30)不小心倍损坏了一部分,只记得样本中数据在[20,60)上的频率为0.8,则估计样本在[40,50),[50,60)内的数据个数共为()A.15B.16C.17D.195.如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本重量的中位数为()A.11B.11.5C.12D.12.56.某公司在2014年上半年的收入x(单位:万元)与月支出(单位:万元)的统计资料如下表所示:月份1月份2月份3月份4月份5月份6月份收入x12.314.515.017.019.820.6支出Y5.63 5.75 5.82 5.89 6.11 6.18根据统计资料,则()A.月收入的中位数是15,x与y有正线性相关关系B.月收入的中位数是17,x与y有负线性相关关系C.月收入的中位数是16,x与y有正线性相关关系D.月收入的中位数是16,x与y有负线性相关关系7.下列事件是随机事件的是()(1)连续两次掷一枚硬币,两次都出现正面向上.(2)异性电荷相互吸引(3)在标准大气压下,水在1℃时结冰(4)任意掷一枚骰子朝上的点数是偶数.A.(1)(2)B.(2)(3)C.(3)(4)D.(1)(4)8.从装有除颜色外完全相同的2个红球和2个白球的口袋内任取2个球,那么对立的两个事件是()A.至少有1个白球,至少有1个红球B.至少有1个白球,都是红球C.恰有1个白球,恰有2个白球D.至少有1个白球,都是白球9.抛掷一枚质地均匀的硬币,如果连续抛掷2011次,那么第2010次出现正面朝上的概率是()A.B.C.D.10.口袋内装有一些大小相同的红球、白球和黒球,从中摸出1个球,摸出红球的概率是0.42,摸出白球的概率是0.28,那么摸出黒球的概率是()A.0.42B.0.28C.0.3D.0.711.已知5件产品中有2件次品,其余为合格品.现从这5件产品中任取2件,恰有一件次品的概率为()A.0.4B.0.6C.0.8D.112.函数f(x)=x2﹣x﹣2,x∈[﹣5,5],在定义域内任取一点x0,使f(x0)≤0的概率是()A.B.C.D.二.填空题(共4小题)13.在棱长为2的正方体内随机取一点,取到的点到正方体中心的距离大于1的概率.14.从甲、乙、丙、丁四人中任选两名代表,甲被选中的概率为。
2022年秋高中数学第四章概率与统计测评试题二新人教B版选择性必修第二册
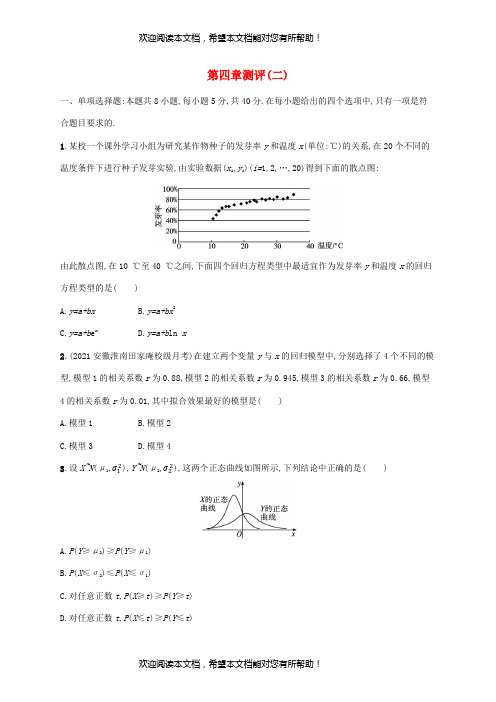
第四章测评(二)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(x i,y i)(i=1,2,…,20)得到下面的散点图:由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是()A.y=a+bxB.y=a+bx2C.y=a+b e xD.y=a+b ln x2.(2021安徽淮南田家庵校级月考)在建立两个变量y与x的回归模型中,分别选择了4个不同的模型,模型1的相关系数r为0.88,模型2的相关系数r为0.945,模型3的相关系数r为0.66,模型4的相关系数r为0.01,其中拟合效果最好的模型是()A.模型1B.模型2C.模型3D.模型43.设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态曲线如图所示,下列结论中正确的是()A.P(Y≥μ2)≥P(Y≥μ1)B.P(X≤σ2)≤P(X≤σ1)C.对任意正数t,P(X≥t)≥P(Y≥t)D.对任意正数t,P(X≤t)≥P(Y≤t)4.(2021安徽宣城郎溪校级月考)甲、乙两人各进行1次射击,如果两人击中目标的概率都是0.7,则其中恰有1人击中目标的概率是( ) A.0.49B.0.42C.0.7D.0.915.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠面积增加值分别为0.2万公顷、0.39万公顷和0.78万公顷,则沙漠面积增加数y (单位: 万公顷)关于年数x (单位:年)的函数关系较为接近的是( ) A.y=0.2x B.y=0.1x 2+0.1x C.y=0.2+log 4xD.y=2x106.(2021江西抚州南城校级期中)设离散型随机变量X 的分布列为若随机变量Y=X-2,则P (Y=2)等于( ) A.0.3B.0.4C.0.6D.0.77.(2021北京西城校级期中)在一段时间内,甲去博物馆的概率为0.8,乙去博物馆的概率为0.7,且甲乙两人各自行动,则在这段时间内,甲乙两人至少有一个去博物馆的概率是( ) A.0.56B.0.24C.0.94D.0.848.(2021陕西榆林一模)设0<a<12,0<b<12,随机变量ξ的分布列为当a 在0,12内增大时,( ) A.E (ξ)增大,D (ξ)增大 B.E (ξ)增大,D (ξ)减小 C.E (ξ)减小,D (ξ)增大 D.E (ξ)减小,D (ξ)减小二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.对某中学的高中女生体重y(单位:kg)与身高x(单位:cm)进行线性回归分析,根据样本数据(x i,y i)(i=1,2,3,…,12),计算得到相关系数r=0.996 2,用最小二乘法近似得到回归直线方程为y^=0.85x-85.71,则以下结论正确的是()A.y与x正相关B.x与y具有较强的线性相关关系,得到的回归直线方程有价值C.若该中学某高中女生身高增加1 cm,则其体重约增加0.85 kgD.若该中学某高中女生身高为160 cm,则可断定其体重为50.29 kg10.(2021福建福州一模)“一粥一饭,当思来之不易”,道理虽简单,但每年我国还是有2 000多亿元的餐桌浪费,被倒掉的食物相当于2亿多人一年的口粮.为营造“节约光荣,浪费可耻”的氛围,某市发起了“光盘行动”.某机构为调研民众对“光盘行动”的认可情况,在某大型餐厅中随机调查了90位来店就餐的客人,制成如下列联表,通过计算得到χ2的值为9.已知P(χ2≥6.635)=0.010,P(χ2≥10.828)=0.001,则下列判断正确的是()A.在该餐厅用餐的客人中大约有66.7%的客人认可“光盘行动”B.在该餐厅用餐的客人中大约有99%的客人认可“光盘行动”C.有99%的把握认为“光盘行动”的认可情况与年龄有关D.在犯错误的概率不超过0.1%的前提下,认为“光盘行动”的认可情况与年龄有关11.(2021新高考Ⅰ)有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则下列说法错误的是( ) A.甲与丙相互独立 B.甲与丁相互独立 C.乙与丙相互独立 D.丙与丁相互独立12.小张从家到公司开车有两条线路,所需时间(单位:分钟)随交通堵塞状况有所变化,其概率分布如表所示,则下列说法正确的是( )A.任选一条线路,“所需时间小于50分钟”与“所需时间为60分钟”是对立事件B.从所需的平均时间看,线路一比线路二更节省时间C.如果要求在45分钟以内从家赶到公司,小张应该走线路一D.若小张上、下班走不同线路,则所需时间之和大于100分钟的概率为0.04 三、填空题:本题共4小题,每小题5分,共20分.13.(2021四川成都武侯校级模拟)已知某产品的销售额y (单位:万元)与广告费用x (单位:万元)之间的关系如表所示,若销售额与广告费用之间的回归直线方程为y ^=6.5x+a ^,预计当广告费用为6万元时的销售额约为 万元.14.一个袋子内装有除颜色不同外其余完全相同的3个白球和2个黑球,从中不放回地任取两次,每次取一球,在第一次取到的是白球的条件下,第二次也取到白球的概率是 .15.(2021福建福州期中)已知随机变量ξ服从二项分布,即ξ~B6,12,则E (2ξ+3)= ,D (2ξ+3)= .16.(2021浙江杭州期中)已知随机变量ξ的分布列如表所示,若P (ξ≤x )=34,则实数x 的取值范围是 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)(2021山东模拟)短视频已成为很多人生活中娱乐不可或缺的一部分,很多人喜欢将自己身边的事情拍成短视频发布到网上,某人统计了发布短视频后1~8天的点击量(单位:万次)的数据并进行了初步处理,得到下面的散点图及一些统计量的值.其中t i =x i 2.某位同学分别用两种模型:①y ^=b ^x 2+a ^,②y ^=d ^x+c ^进行拟合. (1)根据散点图,比较模型①,②的拟合效果,应该选择哪个模型?(2)根据(1)的判断结果及表中数据建立y 关于x 的回归方程;(在计算回归系数时精确到0.01) (3)预测该短视频发布后第10天的点击量是多少.附:b ^=∑i=1n(x i -x)(y i -y)∑i=1n (x i -x)2,a ^=y −b ^x .18.(12分)(2021陕西模拟)为了调查某校学生对学校食堂的某种食品的喜爱是否与性别有关,随机对该校100名性别不同的学生进行了调查,得到如下列联表.(1)请将上述列联表补充完整;(2)判断是否有99.9%的把握认为是否喜爱某种食品与性别有关?(3)用分层抽样的方法在喜爱某种食品的学生中抽6人,现从这6名学生中随机抽取2人,求恰好有1名男生喜爱某种食品的概率.附:χ2=n(ad -bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d.19.(12分)从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图频率分布直方图:(1)求这500件产品质量指标值的样本平均数x和样本方差s2(同一组中的数据用该组区间的中点值为代表);(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数x,σ2近似为样本方差s2.①利用该正态分布,求P(187.8≤Z≤212.2);②某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间[187.8,212.2]的产品件数,利用①的结果,求E(X).附:√150≈12.2.若Z~N(μ,σ2),则P(μ-σ≤Z≤μ+σ)≈0.683,P(μ-2σ≤Z≤μ+2σ)≈0.954.20.(12分)(2021四川自贡模拟)在一次产品质量抽查中,发现某箱5件产品中有2件次品.(1)从该箱产品中随机抽取1件产品,求抽到次品的概率;(2)从该箱产品中依次不放回随机抽取2件产品,求抽出的2件产品中有次品的概率P;(3)若重复进行(2)的试验10次,则出现次品次数的期望是10P,请问上述结论是否正确?请简要说明理由.21.(12分)(2021新高考Ⅰ)某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B类问题中的每个问题回答正确得80分,否则得0分.已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.22.(12分)小明在某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前54单没有奖励,超过54单的部分每单奖励20元.(1)请分别求出甲、乙两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式.(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的频率分布直方图,其中当某天的派送量指标在m-15,m 5(m=1,2,3,4,5)时,日平均派送量为50+2m单,若将频率视为概率,回答下列问题:①估计这100天中的派送量指标的平均数(同一组中的数据用该组区间的中点值为代表);②根据以上数据,设每名派送员的日薪为X(单位:元),试分别求出甲、乙两种方案的日薪X的分布列及数学期望.请利用数学期望帮助小明分析他选择哪种薪酬方案比较合适?并说明你的理由.参考答案第四章测评(二)1.D 结合题中散点图,由图象的大致走向判断,此函数应该是对数函数模型,故应该选用的函数模型为y=a+b ln x.2.B 在4个不同的回归模型中,模型2的相关系数r=0.945最大,所以拟合效果最好.故选B.3.D 由图象知,μ1<μ2,σ1<σ2,P (Y ≥μ2)=12, P (Y ≥μ1)>12,故P (Y ≥μ2)<P (Y ≥μ1),故A 错误;因为σ1<σ2,所以P (X ≤σ2)>P (X ≤σ1),故B 错误;对任意正数t ,P (X ≥t )<P (Y ≥t ),故C 错误;对任意正数t ,P (X ≤t )≥P (Y ≤t ),故D 正确.故选D.4.B 甲、乙两人各进行1次射击,两人击中目标的概率都是0.7,则其中恰有1人击中目标的概率是C 21×0.7×0.3=0.42. 故选B.5.D 将(1,0.2),(2,0.39),(3,0.78)代入y=0.2x ,当x=3时,y=0.6,和0.78相差较大;将(1,0.2),(2,0.39),(3,0.78)代入y=0.1x 2+0.1x ,当x=2时,y=0.6,和0.39相差较大;将(1,0.2),(2,0.39),(3,0.78)代入y=0.2+log 4x ,当x=2时,y=0.7,和0.39相差较大;将(1,0.2),(2,0.39),(3,0.78)代入y=2x 10,当x=1时,y=0.2,当x=2时,y=0.4,与0.39相差0.01,当x=3时,y=0.8,和0.78相差0.02.综合以上分析,选用函数关系y=2x 10较为接近. 故选D.6.A 由离散型随机变量X 的分布列得0.2+0.1+0.1+0.3+m=1,解得m=0.3,因为随机变量Y=X-2,所以P (Y=2)=P (X=4)=0.3.故选A.7.C 根据题意,设甲去博物馆为事件A ,乙去博物馆为事件B ,则P (A )=0.8,P (B )=0.7,则P (A )=0.2,P (B )=0.3,两人都不去博物馆的概率P (AB )=0.2×0.3=0.06,则甲乙两人至少有一个去博物馆的概率P=1-P (AB )=0.94.故选C.8.D 由题意可得E (ξ)=-12+b=-a ,D (ξ)=(-1+a )2×12+(0+a )2×a+(1+a )2×b=-a+122+54.当a 在0,12内增大时,E (ξ)减小,D (ξ)减小.故选D.9.ABC 由于回归直线方程中x 的系数为0.85>0,因此y 与x 正相关,故A 正确;根据相关系数r=0.9962接近1,故B 正确;由回归直线方程中系数的意义可得身高x 每增加1cm,其体重约增加0.85kg,故C 正确;当某女生的身高为160cm 时,其体重估计值是50.29kg,而不是确定值,故D 错误.故选ABC. 10.AC 因为χ2的值为9,且P (χ2≥6.635)=0.010,P (χ2≥10.828)=0.001,因为9>6.635,但9<10.828,所以有99%的把握认为“光盘行动”的认可情况与年龄有关,或者说,在犯错误的概率不超过1%的前提下,认为“光盘行动”的认可情况与年龄有关,所以选项C 正确,选项D 错误;由表可知认可“光盘行动”的人数为60人,所以在该餐厅用餐的客人中认可“光盘行动”的比例约为6090×100%≈66.7%,故选项A 正确,选项B 错误.故选AC.11.ACD 由已知得P (甲)=16,P (乙)=16, P (丙)=56×6=536,P (丁)=66×6=16,P (甲丙)=0≠P (甲)P (丙),P (甲丁)=16×6=136,P (乙丙)=16×6=136≠P (乙)P (丙),P (丙丁)=0≠P (丙)P (丁).由于P (甲丁)=P (甲)·P (丁)=136,根据相互独立事件的性质,知事件甲与丁相互独立,故B 正确,A,C,D 错误.12.BD “所需时间小于50分钟”与“所需时间为60分钟”是互斥而不对立事件,A 错误; 线路一所需的平均时间为30×0.5+40×0.2+50×0.2+60×0.1=39分钟,线路二所需的平均时间为30×0.3+40×0.5+50×0.1+60×0.1=40分钟,所以线路一比线路二更节省时间,B 正确;线路一所需时间小于45分钟的概率为0.7,线路二所需时间小于45分钟的概率为0.8,小张应该选线路二,故C 错误;所需时间之和大于100分钟,则线路一、线路二的时间可以为(50,60),(60,50)和(60,60)三种情况, 概率为0.2×0.1+0.1×0.1+0.1×0.1=0.04,故D 正确.故选BD.13.48 ∵x =15×(0+1+2+3+4)=2,y =15×(10+15+20+30+35)=22, ∴a ^=22-6.5×2=9,则y ^=6.5x+9,取x=6,得y ^=6.5×6+9=48.14.12 记事件A :第一次取得白球, 事件B :第二次取得白球.则P (B|A )=P(AB)P(A)=3×25×435=12.15.9 6 ∵随机变量ξ~B 6,12,∴E (ξ)=6×12=3,D (ξ)=6×12×12=32.则E (2ξ+3)=2E (ξ)+3=9,D (2ξ+3)=22D (ξ)=6.16.[2,3) 由随机变量ξ的分布列,结合P (ξ≤x )=34,得P (ξ≤x )=P (ξ=-2)+P (ξ=0)+P (ξ=2)=14+14+14=34,故实数x 的取值范围是[2,3). 17.解(1)由散点图可知,模型①效果更好.(2)∵t i =x i 2,∴y ^=b ^t+a ^,∵b ^=∑i=18(t i -t)(y i -y)∑i=18(t i-t)2=686.83570≈0.19,∴a ^=y −b ^t =5-0.19×25.5≈0.16,∴y ^=0.19x 2+0.16.(3)由(2)可知,令x=10,则y ^=0.19×100+0.16=19.16.预测该短视频发布后第10天的点击量是19.16万次.18.解(1)完成列联表如下:(2)由(1)得χ2=100×(20×10-30×40)250×50×60×40=503≈16.667>10.828,所以有99.9%的把握认为是否喜爱某种食品与性别有关.(3)用分层抽样的方法在喜爱某种食品的学生中抽6人,则其中男生有20×660=2(人),女生有4人.则从这6名学生中随机抽取2人有C 62=15(种)结果,其中恰好有1名男生喜爱某种食品有C 21C 41=8(种)结果,故所求的概率P=815.19.解(1)这500件产品质量指标值的样本平均数x 和样本方差s 2分别为 x =170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200, s 2=(-30)2×0.02+(-20)2×0.09+(-10)2×0.22+0×0.33+102×0.24+202×0.08+302×0.02=150.(2)①由(1)知,Z~N (200,150),因为σ=√150≈12.2,从而P (187.8≤Z ≤212.2)=P (200-12.2≤Z ≤200+12.2)≈0.683.②由①知,一件产品的质量指标值位于区间[187.8,212.2]的概率约为0.683,依题意知X~B (100,0.683),所以E (X )=100×0.683=68.3.20.解(1)从该箱产品中随机抽取1件产品,抽到次品的概率为25.(2)从该箱产品中依次不放回随机抽取2件产品,抽出的2件产品中有次品的概率P=1-35×24=710.(3)正确.若重复进行(2)的试验10次,则出现次品的次数X~B 10,710,所以出现次品的次数E (X )=10×710=7=10P.21.解(1)X=0,20,100. P (X=0)=1-0.8=0.2=15,P (X=20)=0.8×(1-0.6)=45×25=825,P (X=100)=0.8×0.6=45×35=1225.所以X 的分布列为(2)若小明先回答A 类问题,期望为E (X ).则E (X )=0×15+20×825+100×1225=2725.若小明先回答B类问题,Y为小明的累计得分, Y=0,80,100,P(Y=0)=1-0.6=0.4=25,P(Y=80)=0.6×(1-0.8)=35×15=325,P(Y=100)=0.6×0.8=35×45=1225.E(Y)=0×25+80×325+100×1225=2885.因为E(X)<E(Y),所以小明应选择先回答B类问题.22.解(1)甲方案中派送员日薪y与送单数n的函数关系式为y=100+n,n∈N,乙方案中派送员日薪y与送单数n的函数关系式为y={140,n≤54,n∈N,20n-940,n≥55,n∈N.(2)①(0.1×1+0.3×1.5+0.5×1+0.7×1+0.9×0.5)×0.2=0.44.②X甲的分布列为所以E(X甲)=152×0.2+154×0.3+156×0.2+158×0.2+160×0.1=155.4. X乙的分布列为所以E(X乙)=140×0.5+180×0.2+220×0.2+260×0.1=176.由以上的计算结果可以看出,E(X甲)<E(X乙),即甲方案日工资期望小于乙方案日工资期望,所以小明应选择乙方案.。
高中数学第三章概率2

(整数值)随机数(random numbers)的产生课时目标 1.了解随机数的意义.2.会用模拟方法(包括计算器产生随机数进行模拟)估计概率.3.理解用模拟方法估计概率的实质.1.随机数要产生1~n(n∈N*)之间的随机整数,把n个____________相同的小球分别标上1,2,3,…,n,放入一个袋中,把它们__________,然后从中摸出一个,这个球上的数就称为随机数.2.伪随机数计算机或计算器产生的随机数是依照__________产生的数,具有________(________很长),它们具有类似________的性质.因此,计算机或计算器产生的并不是______,我们称它们为伪随机数.3.利用计算器产生随机数的操作方法:用计算器的随机函数RANDI(a,b)或计算机的随机函数RANDBETWEEN(a,b)可以产生从整数a到整数b的取整数值的随机数.4.利用计算机产生随机数的操作程序每个具有统计功能的软件都有随机函数,以Excel软件为例,打开Excel软件,执行下面的步骤:(1)选定A1格,键入“=RANDBETWEEN(0,1)”,按Enter键,则在此格中的数是随机产生的0或1.(2)选定A1格,按Ctrl+C快捷键,然后选定要随机产生0,1的格,比如A2至A100,按Ctrl+V快捷键,则在A2至A100的数均为随机产生的0或1,这样相当于做了100次随机试验.(3)选定C1格,键入频数函数“=FREQUENCY(A1∶A100,0.5)”,按Enter键,则此格中的数是统计A1至A100中,比0.5小的数的个数,即0出现的频数.(4)选定D1格,键入“=1-C1/100”按Enter键,在此格中的数是这100次试验中出现1的频率.一、选择题1.从含有3个元素的集合的所有子集中任取一个,所取的子集是含有2个元素的集合的概率是( )A.310B.112C.4564D.382.用计算机随机模拟掷骰子的试验,估计出现2点的概率,下列步骤中不正确的是( ) A .用计算器的随机函数RANDI(1,7)或计算机的随机函数RANDBETWEEN(1,7)产生6个不同的1到6之间的取整数值的随机数x ,如果x =2,我们认为出现2点B .我们通常用计算器n 记录做了多少次掷骰子试验,用计数器m 记录其中有多少次出现2点,置n =0,m =0C .出现2点,则m 的值加1,即m =m +1;否则m 的值保持不变D .程序结束,出现2点的频率m n作为概率的近似值3.假定某运动员每次投掷飞镖正中靶心的概率为40%,现采用随机模拟的方法估计该运动员两次投掷飞镖恰有一次命中靶心的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中靶心,5,6,7,8,9,0表示未命中靶心;再以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数: 93 28 12 45 85 69 68 34 31 25 73 93 02 75 56 48 87 30 11 35据此估计,该运动员两次掷镖恰有一次正中靶心的概率为( ) A .0.50 B .0.45 C .0.40 D .0.354.从{1,2,3,4,5}中随机选取一个数为a ,从{1,2,3}中随机选取一个数为b ,则b >a 的概率是( ) A.45B.35 C.25 D.155.从1,2,3,…,30这30个数中任意选一个数,则事件“是偶数或能被5整除的数”的概率是( ) A.710B.35C.45D.1106.任取一个三位正整数N ,对数log 2N 是一个正整数的概率为( ) A.1225B.3899 C.1300D.1450二、填空题7.对一部四卷文集,按任意顺序排放在书架的同一层上,则各卷自左到右或由右到左卷号恰为1,2,3,4顺序的概率等于________.8.盒子里共有大小相同的3只白球,1只黑球,若从中随机地摸出两只球,则它们颜色不同的概率是________.9.通过模拟试验,产生了20组随机数:6830 3013 7055 7430 7740 4422 7884 2604 3346 09526807 9706 5774 5725 6576 5929 9768 6071 9138 6754如果恰有三个数在1,2,3,4,5,6中,则表示恰有三次击中目标,问四次射击中恰有三次击中目标的概率约为________.三、解答题10.掷三枚骰子,利用Excel软件进行随机模拟,试验20次,计算出现点数之和是9的概率.11.某篮球爱好者做投篮练习,假设其每次投篮命中的概率是60%,那么在连续三次投篮中,三次都投中的概率是多少?能力提升12.从4名同学中选出3人参加物理竞赛,其中甲被选中的概率为( )A.14 B.12C.34D.以上都不对13.甲、乙两支篮球队进行一局比赛,甲获胜的概率为0.6,若采用三局两胜制举行一次比赛,试用随机模拟的方法求乙获胜的概率.1.(1)常用的随机数的产生方法主要有抽签法,利用计算器或计算机.(2)利用摸球或抽签得到的数是真正意义上的随机数,用计算器或计算机得到的是伪随机数.2.用整数随机模拟试验时,首先要确定随机数的范围,利用哪个数字代表哪个试验结果: (1)试验的基本结果等可能时,基本事件总数即为产生随机数的范围,每个随机数代表一个基本事件;(2)研究等可能事件的概率时,用按比例分配的方法确定表示各个结果的数字个数及范围. 答案:3.2.2 (整数值)随机数(randomnumbers )的产生知识梳理1.大小、形状 充分搅拌 2.确定算法 周期性 周期 随机数 真正的随机数 作业设计1.D [所有子集共8个,∅,{a},{b},{c},{a ,b},{a ,c},{b ,c},{a ,b ,c},含两个元素的子集共3个,故所求概率为38.]2.A [计算器的随机函数RANDI(1,7)或计算机的随机函数RANDBETWEEN(1,7)产生的是1到7之间的整数,包括7,共7个整数.]3.A [两次掷镖恰有一次正中靶心表示随机数中有且只有一个数为1,2,3,4中的之一.它们分别是93,28,45,25,73,93,02,48,30,35共10个,因此所求的概率为1020=0.5.]4.D [由题意知基本事件为从两个集合中各取一个数,因此基本事件总数为5×3=15. 满足b>a 的基本事件有(1,2),(1,3),(2,3)共3个, ∴所求概率P =315=15.]5.B6.C [N 取[100,999]中任意一个共900种可能,当N =27,28,29时,log 2N 为正整数,∴P =1300.] 7.112解析 用树形图可以列举基本事件的总数. ①②③④ ②①③④ ③①②④ ④①②③ ①②④③ ②①④③ ③①④② ④①③② ①③②④ ②③①④ ③②①④ ④②③① ①③④② ②③④① ③②④① ④②①③ ①④②③ ②④①③ ③④①② ④③①②①④③② ②④③① ③④②① ④③②① 总共有24种基本事件,故其概率为P =224=112.8.12解析 给3只白球分别编号为a ,b ,c,1只黑球编号为d ,基本事件为ab ,ac ,ad ,bc ,bd ,cd 共6个,颜色不同包括事件ad ,bd ,cd 共3个,因此所求概率为36=12.9.14解析 由题意四次射击中恰有三次击中对应的随机数有3个数字在1,2,3,4,5,6中,这样的随机数有3013,2604,5725,6576,6754共5个,所求的概率约为520=14.10.解 操作步骤:(1)打开Excel 软件,在表格中选择一格比如A 1,在菜单下的“=”后键入“=RANDBETWEEN(1,6)”,按Enter 键,则在此格中的数是随机产生的1~6中的数. (2)选定A 1这个格,按Ctrl +C 快捷键,然后选定要随机产生1~6的格,如A 1∶T 3,按Ctrl +V 快捷键,则在A 1∶T 3的数均为随机产生的1~6的数.(3)对产生随机数的各列求和,填入A 4∶T 4中. (4)统计和为9的个数S ;最后,计算概率S /20.11.解 我们通过设计模拟试验的方法来解决问题,利用计算机或计算器可以产生0到9之间的取整数值的随机数.我们用1,2,3,4,5,6表示投中,用7,8,9,0表示未投中,这样可以体现投中的概率是60%.因为是投篮三次,所以每三个随机数作为一组. 例如,产生20组随机数:812 932 569 683 271 989 730 537 925 834 907 113 966 191 432 256 393 027 556 755这就相当于做了20次试验,在这组数中,如果3个数均在1,2,3,4,5,6中,则表示三次都投中,它们分别是113,432,256,556,即共有4个数,我们得到了三次投篮都投中的概率近似为420=20%.12.C [4名同学选3名的事件数等价于4名同学淘汰1名的事件数,即4种情况, 甲被选中的情况共3种,∴P=34.]13.解 利用计算器或计算机生成0到9之间取整数值的随机数,用0,1,2,3,4,5表示甲获胜;6,7,8,9表示乙获胜,这样能体现甲获胜的概率为0.6.因为采用三局两胜制,所以每3个随机数作为一组.例如,产生30组随机数(可借助教材103页的随机数表). 034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959774 246 762 428 114 572 042 533 237 322 707 360 751就相当于做了30次试验.如果恰有2个或3个数在6,7,8,9中,就表示乙获胜,它们分别是738,636,964,736,698,637,616,959,774,762,707.共11个.所以采用三局两胜制,乙获胜的概率约为1130≈0.367.。
人教B版(2019)高中数学必修第二册 第五章统计与概率5.3.4频率与概率同步习题(含答案)

5.3.4 频率与概率知识点一频率与概率1.在n次重复进行的试验中,事件A发生的频率为mn,当n很大时,P(A)与mn的关系是( )A.P(A)≈mnB.P(A)<mnC.P(A)>mnD.P(A)=mn2.某企业生产的乒乓球被某乒乓球训练基地指定为训练专用球.日前有关部门对某批产品进行了抽样检测,检测结果如下表所示:抽取球数n 5010020050010002000 优等品数m 45921944709541902优等品频率m n(2)从这批乒乓球产品中任取一个,估计其为优等品的概率是多少?(结果保留到小数点后三位)3.某市统计近几年新生儿出生数及其中男婴数(单位:人)如下:时间2016年2017年2018年2019年出生婴儿数21840230702009419982 出生男婴数11453120311029710242(2)该市男婴出生的概率约为多少?知识点二对概率的正确理解4.下列说法正确的是( )A.甲、乙二人比赛,甲胜的概率为35,则比赛5场,甲胜3场B.某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈C.随机试验的频率与概率相等D.天气预报中,预报明天降水概率为90%,是指降水的可能性是90%5.围棋盒里放有同样大小的9枚白棋子和1枚黑棋子,每次从中随机摸出1枚棋子后再放回,一共摸10次,你认为一定有一次会摸到黑棋子吗?说明你的理由.知识点三用频率估计概率6.从某校高二年级的所有学生中,随机抽取20人,测得他们的身高(单位:cm)分别为:162,153,148,154,165,168,172,171,173,150,151,152,160,165,164,179,149,158,159,175.根据样本频率分布估计总体分布的原理,在该校高二年级的所有学生中任抽一人,估计该生的身高在155.5~170.5 cm之间的概率约为( )A.25B.12C.23D.137.在检测一批相同规格共500 kg航空用耐热垫片的品质时,随机抽取了280片,检测到有5片非优质品,则这批垫片中非优质品约为( ) A.8.834 kg B.8.929 kgC.10 kg D.9.835 kg8.随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4500名网上购物消费者进行了调查(每名消费者限选一种情况回答),统计结果如下表:“满意”的概率是( )A.715B.25C.1115D.13159.某人捡到不规则形状的五面体石块,他在每个面上用数字1~5进行了标记,投掷100次,记录下落在桌面上的数字,得到如下频数表:10.某工厂为了节约用电,规定每天的用电量指标为1000度,按照上个月的用电记录,在30天中有12天的用电量超过指标,若这个月(按30天计)仍没有具体的节电措施,则该月的第一天用电量超过指标的概率约是________.11.对某批产品进行抽样检查,数据如下:抽查________件产品.12.某教授为了测试贫困地区和发达地区的同龄儿童的智力出了10个智力题,每个题10分,然后做了统计,统计结果如表:贫困地区到0.001);(2)求两个地区参加测试的儿童得60分以上的概率.13.某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如表:赔付金额(元)01000200030004000 车辆数500130100150120(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.14.假设甲、乙两种品牌的同类产品在某地区市场上销售量相等,为了解它们的使用寿命,现从这两种品牌的产品中分别随机抽取100个进行测试,结果统计如图所示:(1)估计甲品牌产品寿命小于200 h的概率;(2)这两种品牌产品中,某个产品已使用了200 h,试估计该产品是甲品牌的概率.15.近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨):“厨余垃圾”箱“可回收物”箱“其他垃圾”箱厨余垃圾400100100可回收物3024030其他垃圾202060(1)试估计厨余垃圾投放正确的概率;(2)试估计生活垃圾投放错误的概率;(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.:易错点一混淆概率与频率的概念把一枚质地均匀的硬币连续掷了1000次,其中有496次正面朝上,504次反面朝上,则可认为掷一次硬币正面朝上的概率为________.易错点二对用频率估计概率的方法理解不透致误已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989据此估计,该运动员三次投篮恰有两次命中的概率为________.一、单项选择题1.从一批电视机中随机抽出10台进行质检,其中有一台次品,下列说法正确的是( )A.次品率小于10% B.次品率大于10%C.次品率等于10% D.次品率接近10%2.某人将一枚硬币连抛10次,正面朝上的情形出现了6次,若用A表示正面朝上这一事件,则A的( )A.概率为35B.频率为35C.频率为6 D.概率接近0.63.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如表:卡片号码12345678910 取到的次数101188610189119A.0.53 B.0.5C.0.47 D.0.374.若在同等条件下进行n次重复试验得到某个事件A发生的频率f(n),则随着n的逐渐增大,有( )A.f(n)与某个常数相等B.f(n)与某个常数的差逐渐减小C.f(n)与某个常数的差的绝对值逐渐减小D.f(n)在某个常数的附近摆动并趋于稳定5.对一批产品的长度(单位:毫米)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)上为二等品,在区间[10,15)和[30,35]上为三等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( )A.0.09 B.0.20C.0.25 D.0.456.某厂生产的电器是家电下乡政府补贴的指定品牌,其产品是优等品的概率为90%,现从该厂生产的产品中任意地抽取10件进行检验,结果前9件产品中有8件是优等品,1件是非优等品,那么第10件产品是优等品的概率为( ) A.90% B.小于90%C.大于90% D.无法确定7.有下列说法:①抛掷硬币出现正面向上的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上;②如果某种彩票的中奖概率为110,那么买10张这种彩票一定能中奖;③在乒乓球、排球等比赛中,裁判通过上抛均匀塑料圆板并让运动员猜着地时是正面还是反面来决定哪一方先发球,这样做不公平;④一个骰子掷一次得到点数2的概率是16,这说明一个骰子掷6次会出现一次点数2.其中不正确的说法是( )A.①②③④ B.①②④C.③④ D.③8.某市交警部门在调查一起车祸过程中,所有的目击证人都指证肇事车是一辆普通桑塔纳出租车,但由于天黑,均未看清该车的车牌号码及颜色,而该市有两家出租车公司,其中甲公司有100辆桑塔纳出租车,3000辆帕萨特出租车,乙公司有3000辆桑塔纳出租车,100辆帕萨特出租车.交警部门应先调查哪家公司的车辆较合理?( )A.甲公司B.乙公司C.甲与乙公司D.以上都对二、多项选择题9.下列说法中,正确的有( )A.频率是反映事件发生的频繁程度,概率是反映事件发生的可能性大小B.百分率是频率,但不是概率C.频率是不能脱离试验次数n的实验值,而概率是具有确定性的不依赖于试验次数的理论值D.频率是概率的近似值,概率是频率的稳定值10.下列说法正确的是( )A.事件A的概率为P(A),必有0≤P(A)≤1B.事件A的概率P(A)=0.999,则事件A是必然事件C.用某种药物对患有胃溃疡的500名病人进行治疗,结果有380人有明显的疗效.现有胃溃疡的病人服用此药,则估计有明显疗效的概率约为76% D.某奖券的中奖率为50%,则某人购买此奖券10张,一定有5张中奖11.李老师在某大学连续3年主讲经济学院的高等数学,下表是李老师这门课3年来学生的考试成绩(取整数)分布:法正确的是( )A.估计她得90分以上(含90分)的概率约为0.067B.估计她得60~69分的概率约为0.150C.估计她得60分以上(含60分)的概率约为0.982D.估计她得59分以下(含59分)的概率约为0.10812.某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买,则下列说法正确的是( )B.估计顾客同时购买乙和丙的概率为0.2C.估计顾客在甲、乙、丙、丁中同时购买3种商品的概率为0.4D.如果顾客购买了甲,则该顾客同时购买乙、丙、丁中的丙的可能性最大三、填空题13.一家保险公司想了解汽车的挡风玻璃破碎的概率,公司收集了20000辆汽车的数据,时间是从某年的5月1日到下一年的4月30日,共发现有600辆汽车的挡风玻璃破碎,则一辆汽车在一年内挡风玻璃破碎的概率的近似值是________.14.一个容量为20的样本,数据的分组及各组的频数如下:[10,20)2个;[20,30)3个;[30,40)x个;[40,50)5个;[50,60)4个;[60,70]2个.则x等于________;根据样本的频率估计概率,数据落在[10,50)的概率约为________.15.玲玲和倩倩是一对好朋友,她俩都想去观看某明星的演唱会,可手里只有一张票,怎么办呢?玲玲对倩倩说:“我向空中抛2枚同样的一元硬币,如果落地后一正一反,就我去;如果落地后两面一样,就你去!”你认为这个游戏公平吗?答:________.16.某公司有5万元资金用于投资开发项目,如果成功,一年后可获收益12%;一旦失败,一年后将丧失全部资金的50%.下表是去年200例类似项目开发的实施结果.四、解答题17.电影公司随机收集了电影的有关数据,经分类整理得到下表:(1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;(2)随机选取1部电影,估计这部电影没有获得好评的概率;(3)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化,假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加0.1,哪类电影的好评率减少0.1,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)18.某中学从参加高一年级上学期期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图所示的频率分布直方图.观察图形的信息,回答下列问题:(1)估计这次考试的及格率(60分及以上为及格);(2)从该校高一年级随机选取一名学生,估计这名学生该次期末考试成绩在70分以上(包括70分)的概率.19.某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40) 天数21636257 4(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.20.甲、乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台机床生产的零件各100件进行检测,检测结果统计如下:测试指标[85,90)[90,95)[95,100)[100,105)[105,110)甲机床81240328 乙机床7184029 6(2)甲机床生产1件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20,假设甲机床某天生产50零件,请估计甲机床该天的日利润(单位:元);(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层随机抽样的方法抽取5件,从这5件中任意抽取2件进行质量分析,求这2件都是乙机床生产的概率.5.3.4 频率与概率知识点一频率与概率1.在n次重复进行的试验中,事件A发生的频率为mn,当n很大时,P(A)与mn的关系是( )A.P(A)≈mnB.P(A)<mnC.P(A)>mnD.P(A)=mn答案 A解析根据概率的定义,当n很大时,频率是概率的近似值.2.某企业生产的乒乓球被某乒乓球训练基地指定为训练专用球.日前有关部门对某批产品进行了抽样检测,检测结果如下表所示:抽取球数n 5010020050010002000 优等品数m 45921944709541902优等品频率m n(2)从这批乒乓球产品中任取一个,估计其为优等品的概率是多少?(结果保留到小数点后三位)解(1)表中乒乓球为优等品的频率依次是0.900,0.920,0.970,0.940,0.954,0.951.(2)由(1)知,随着抽取的球数n的增加,计算得到的频率值虽然不同,但都在常数0.950的附近摆动,所以任意抽取一个乒乓球检测时,其为优等品的概率约为0.950.3.某市统计近几年新生儿出生数及其中男婴数(单位:人)如下:(2)该市男婴出生的概率约为多少?解(1)2016年男婴出生的频率为1145321840≈0.524.同理可求得2017年、2018年和2019年男婴出生的频率分别为0.521,0.512,0.513.(2)该市男婴出生的概率约为0.52.知识点二对概率的正确理解4.下列说法正确的是( )A.甲、乙二人比赛,甲胜的概率为35,则比赛5场,甲胜3场B.某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈C.随机试验的频率与概率相等D.天气预报中,预报明天降水概率为90%,是指降水的可能性是90%答案 D解析A中,此概率只说明发生的可能性大小,具有随机性,并非一定是比赛5场甲胜3场;B中,此治愈率只说明发生的可能性大小,具有随机性,并非10个病人一定有1人治愈;C中,随机试验的频率可以估计概率,并不等于概率;D中,概率为90%,即可能性是90%.故选D.5.围棋盒里放有同样大小的9枚白棋子和1枚黑棋子,每次从中随机摸出1枚棋子后再放回,一共摸10次,你认为一定有一次会摸到黑棋子吗?说明你的理由.解不一定.有放回地摸10次棋子相当于做10次重复试验,因为每次试验的结果都是随机的,所以摸10次棋子的结果也是随机的.可能有两次或两次以上摸到黑棋子,也可能没有一次摸到黑棋子.知识点三用频率估计概率6.从某校高二年级的所有学生中,随机抽取20人,测得他们的身高(单位:cm)分别为:162,153,148,154,165,168,172,171,173,150,151,152,160,165,164,179,149,158,159,175.根据样本频率分布估计总体分布的原理,在该校高二年级的所有学生中任抽一人,估计该生的身高在155.5~170.5 cm之间的概率约为( )A.25B.12C.23D.13答案 A解析从已知数据可以看出,在随机抽取的这20名学生中,身高在155.5~170.5 cm之间的学生有8人,频率为25,故可估计在该校高二年级的所有学生中任抽一人,其身高在155.5~170.5 cm之间的概率约为2 5 .7.在检测一批相同规格共500 kg航空用耐热垫片的品质时,随机抽取了280片,检测到有5片非优质品,则这批垫片中非优质品约为( ) A.8.834 kg B.8.929 kgC.10 kg D.9.835 kg答案 B解析由题意可得,该批垫片中非优质品约为5280×500≈8.929 kg.8.随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4500名网上购物消费者进行了调查(每名消费者限选一种情况回答),统计结果如下表:满意情况不满意比较满意满意非常满意人数200n 21001000 “满意”的概率是( )A.715B.25C.1115D.1315答案 C解析由题意,得n=4500-200-2100-1000=1200,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的总人数为1200+2100=3300,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的频率为33004500=1115.由此估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率为1115.故选C.9.某人捡到不规则形状的五面体石块,他在每个面上用数字1~5进行了标记,投掷100次,记录下落在桌面上的数字,得到如下频数表:落在桌面的数字1234 5 频数3218151322答案0.35解析落在桌面的数字不小于4,即4,5的频数共13+22=35,所以频率为35100=0.35,所以估计落在桌面的数字不小于4的概率约为0.35.10.某工厂为了节约用电,规定每天的用电量指标为1000度,按照上个月的用电记录,在30天中有12天的用电量超过指标,若这个月(按30天计)仍没有具体的节电措施,则该月的第一天用电量超过指标的概率约是________.答案0.4解析由频率的定义可知用电量超过指标的频率为1230=0.4,由频率估计概率,知第一天用电量超过指标的概率约是0.4.11.对某批产品进行抽样检查,数据如下:抽查________件产品.答案1000解析根据题表中数据可知合格品出现的频率依次为0.94,0.92,0.96,0.95,0.95,故合格品出现的概率约为0.95,因此要从该批产品中抽到950件合格品大约需要抽查1000件产品.12.某教授为了测试贫困地区和发达地区的同龄儿童的智力出了10个智力题,每个题10分,然后做了统计,统计结果如表:贫困地区到0.001);(2)求两个地区参加测试的儿童得60分以上的概率.解(1)贫困地区的频率分别逐渐趋近于0.5和0.55.故所求概率分别为0.5和0.55.13.某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如表:(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.解(1)设A表示事件“赔付金额为3000元”,B表示事件“赔付金额为4000元”,样本车辆总数n=500+130+100+150+120=1000,以频率估计概率得P(A)=1501000=0.15,P(B)=1201000=0.12.由于投保金额为2800元,赔付金额大于投保金额对应的情形是赔付金额为3000元或4000元,所以其概率为P(A)+P(B)=0.15+0.12=0.27.(2)设C表示事件“投保车辆中新司机获赔4000元”,由已知,样本车辆中车主为新司机的有0.1×1000=100辆,而赔付金额为4000元的车辆中,车主为新司机的有0.2×120=24辆.所以样本车辆中新司机车主获赔金额为4000元的频率为24100=0.24,由频率估计概率,得P(C)=0.24.14.假设甲、乙两种品牌的同类产品在某地区市场上销售量相等,为了解它们的使用寿命,现从这两种品牌的产品中分别随机抽取100个进行测试,结果统计如图所示:(1)估计甲品牌产品寿命小于200 h的概率;(2)这两种品牌产品中,某个产品已使用了200 h,试估计该产品是甲品牌的概率.解(1)甲品牌产品寿命小于200 h的频率为5+20100=14,用频率估计概率,所以甲品牌产品寿命小于200 h的概率为1 4 .(2)根据抽样结果,寿命大于200 h的产品共有75+70=145个,其中甲品牌产品有75个,所以在样本中,寿命大于200 h的产品是甲品牌的频率是75145=1529,用频率估计概率,所以已使用了200 h的该产品是甲品牌的概率为15 29.15.近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨):“厨余垃圾”箱“可回收物”箱“其他垃圾”箱厨余垃圾400100100可回收物3024030其他垃圾202060(2)试估计生活垃圾投放错误的概率;(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,写出a,b,c的值(结论不要求证明),并求此时s2的值.求:错误!解(1)由题意可知,厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故厨余垃圾投放正确的概率为400600=23.(2)由题意可知,生活垃圾投放错误有200+60+20+20=300,故生活垃圾投放错误的概率为3001000=3 10.(3)由题意可知,∵a+b+c=600,∴a,b,c的平均数为200,∴s2=13[(a-200)2+(b-200)2+(c-200)2]=13(a2+b2+c2-120000),∵(a+b+c)2=a2+b2+c2+2ab+2bc+2ac≥a2+b2+c2,因此有当a=600,b=0,c =0时,有s2=80000.易错点一混淆概率与频率的概念把一枚质地均匀的硬币连续掷了1000次,其中有496次正面朝上,504次反面朝上,则可认为掷一次硬币正面朝上的概率为________.易错分析由于混淆了概率与频率的概念而致误,事实上频率是随机的,而概率是一个确定的常数,与每次试验无关.答案0.5正解通过做大量的试验可以发现,正面朝上的频率都在0.5附近摆动,故掷一次硬币,正面朝上的概率是0.5,故填0.5.易错点二对用频率估计概率的方法理解不透致误已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989据此估计,该运动员三次投篮恰有两次命中的概率为________.易错分析(1)对随机数表认识不到位,不能准确找出恰有两次命中的组数;(2)对用频率估计概率的方法理解不到位,不能求出“运动员三次投篮恰有两次命中”的概率.答案1 4正解20组随机数中,恰有两次命中的有5组,用频率估计概率,因此,该运动员三次投篮恰有两次命中的概率为P=520=14.一、单项选择题1.从一批电视机中随机抽出10台进行质检,其中有一台次品,下列说法正确的是( )A.次品率小于10% B.次品率大于10%C.次品率等于10% D.次品率接近10%答案 D解析抽出的样本中次品率为110,即10%,所以总体中次品率大约为10%.2.某人将一枚硬币连抛10次,正面朝上的情形出现了6次,若用A表示正面朝上这一事件,则A的( )A.概率为35B.频率为35C.频率为6 D.概率接近0.6 答案 B解析因为抛了10次硬币,正面朝上的情形出现了6次,我们说频率为3 5,而不能说概率为35.3.从存放号码分别为1,2,…,10的卡片的盒子中,有放回地取100次,每次取一张卡片并记下号码,统计结果如表:卡片号码 1 2 3 4 5 6 7 8 9 10 取到的次数101188610189119A .0.53B .0.5C .0.47D .0.37答案 A解析 取到号码为奇数的次数为10+8+6+18+11=53,所以f =53100=0.53,所以估计取到号码为奇数的概率约为0.53.4.若在同等条件下进行n 次重复试验得到某个事件A 发生的频率f (n ),则随着n 的逐渐增大,有( )A .f (n )与某个常数相等B .f (n )与某个常数的差逐渐减小C .f (n )与某个常数的差的绝对值逐渐减小D .f (n )在某个常数的附近摆动并趋于稳定 答案 D解析 由频率和概率的关系知,在同等条件下进行n 次重复试验得到某个事件A 发生的频率f (n ),随着n 的逐渐增加,频率f (n )逐渐趋近于概率.5.对一批产品的长度(单位:毫米)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)上为二等品,在区间[10,15)和[30,35]上为三等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( )A.0.09 B.0.20C.0.25 D.0.45答案 D解析由频率分布直方图的性质可知,样本数据在区间[25,30)上的频率为1-5×(0.02+0.04+0.06+0.03)=0.25,则二等品的频率为0.25+0.04×5=0.45,故任取1件产品为二等品的概率为0.45.6.某厂生产的电器是家电下乡政府补贴的指定品牌,其产品是优等品的概率为90%,现从该厂生产的产品中任意地抽取10件进行检验,结果前9件产品中有8件是优等品,1件是非优等品,那么第10件产品是优等品的概率为( ) A.90% B.小于90%C.大于90% D.无法确定答案 A解析概率是一个确定的常数,在试验前已经确定,与试验次数无关.故选A.7.有下列说法:①抛掷硬币出现正面向上的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上;②如果某种彩票的中奖概率为110,那么买10张这种彩票一定能中奖;③在乒乓球、排球等比赛中,裁判通过上抛均匀塑料圆板并让运动员猜着地时是正面还是反面来决定哪一方先发球,这样做不公平;④一个骰子掷一次得到点数2的概率是16,这说明一个骰子掷6次会出现一次点数2.其中不正确的说法是( )A.①②③④ B.①②④C.③④ D.③答案 A解析概率反映的是随机性的规律,但每次试验出现的结果具有不确定性,因此①②④错误;③中抛掷均匀塑料圆板出现正面与反面的概率相等,是公平的,因此③错误.8.某市交警部门在调查一起车祸过程中,所有的目击证人都指证肇事车是一辆普通桑塔纳出租车,但由于天黑,均未看清该车的车牌号码及颜色,而该市有。
2019年高中数学《条件概率》经典题及答案详解

2019年高中数学《条件概率》经典题及答案详解一.选择题(共25小题)1.先后掷子(子的六个面上分别标有1,2,3,4,5,6个点)两次,落在水平桌面后,记正面朝上的点数分别为x,y,设事件A为“x y+为偶数”,事件B为“x,y中有偶数且x y≠”,则概率(|)(P B A=)A.13B.14C.12D.252.抛掷甲、乙两颗骰子,若事件A:“甲骰子的点数大于4”;事件B:“甲、乙两骰子的点数之和等于7”,则(|)P B A的值等于()A.13B.118C.16D.193.一个家庭有两个小孩,假设生男生女是等可能的,已知这个家庭有一个是女孩的条件下,这时另一个也是女孩的概率是()A.14B.23C.12D.134.盒中有红球5个,蓝球11个,其中红球中有2个玻璃球,3个木质球;蓝球中有4个玻璃球,7个木质球,现从中任取一球,假设每个球被摸到的可能性相同.若已知取到的球是玻璃球,则它是蓝球的概率为()A.23B.13C.1116D.5165.投掷一枚骰子,若事件{A=点数小于6},事件{B=点数大于2},则(|)P B A等于( )A.25B.12C.35D.346.书架上有三本数学书和两本语文书,某同学两次分别从书架各取一本书,取后不放回,若第一次从书架取出一本数学书记为事件A,第二次从书架取出一本数学书记为事件B,则(|)(P B A=)A.12B.110C.310D.357.已知某同学在高二期末考试中,A和B两道选择题同时答对的概率为23,在A题答对的情况下,B题也答对的概率为89,则A题答对的概率为()A.14B.12C.34D.798.甲、乙二人参加一项抽奖活动,每人抽奖中奖的概率均为0.6,两人都中奖的概率为0.4,则已知甲中奖的前提下乙也中奖的概率为()A.625B.35C.25D.239.某校自主招生面试共有7道题,其中4道理科题,3道文科题,要求不放回地依次任取3道题作答,则某考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率为()A.17B.15C.37D.4510.篮子里装有3个红球,4个白球和5个黑球,球除颜色外,形状大小一致.某人从篮子中随机取出两个球,记事件A=“取出的两个球颜色不同”,事件B=“取出一个红球,一个白球”,则(|)(P B A=)A.211B.1247C.1219D.1611.春天是鼻炎和感冒的高发期,某人在春季里鼻炎发作的概率为0.8,鼻炎发作且感冒的概率为0.6,则此人鼻炎发作的条件下,他感冒的概率为()A.0.48B.0.40C.0.64D.0.7512.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹进行一场比赛,则在齐王的马获胜的条件下,齐王的上等马获胜的概率为()A.23B.12C.13D.113.某校从学生会文艺部6名成员(其中男生4人,女生2人)中,任选3人参加学校举办的“庆元旦迎新春”文艺汇演活动.设“男生甲被选中”为事件A,“女生乙被选中”为事件B,则(|)P B A为()A.15B.25C.35D.31014.一种灯泡使用一年的概率为0.8,使用两年的概率为0.4,现有已经使用一年的灯泡,它还能使用一年的概率是()A.0.4B.0.5C.0.6D.0.815.将3颗骰子各掷一次,记事件A为“三个点数都不同”,事件B为“至少出现一个1点”,则条件概率(|)P A B和(|)P B A分别为()A.160,291B.560,1891C.601,912D.911,216216.甲乙二人争夺一场围棋比赛的冠军,若比赛为“三局两胜”制,甲在每局比赛中获胜的概率均为23,且各局比赛结果相互独立,则在甲获得冠军的情况下,比赛进行了三局的概率为()A.13B.25C.23D.4517.小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件A=“4个人去的景点不相同”,事件B=“小赵独自去一个景点”,则(|)(P A B=)A.29B.13C.49D.5918.九江气象台统计,5月1日浔阳区下雨的概率为415,刮风的概率为215,既刮风又下雨的概率为110,设A为下雨,B为刮风,那么(|)(P A B=)A.12B.34C.25D.3819.某校组织高一、高二年级书法比赛,高一、高二年级参赛人数分别占60%、40%;并且高一年级获奖人数占本年级参赛人数的16,高二年级获奖人数占本年级参赛人数的18.现从所有参赛学生中任意抽取一人,记事件A表示该学生来自高一,事件B表示该学生获奖,则(|)P B A的值为()A.18B.215C.536D.32020.甲、乙两人独立地对同一目标各射击一次,命中率分别为0.6和0.7,在目标被击中的情况下,甲、乙同时击中目标的概率为()A.2144B.1522C.2150D.92521.2016年6月9日是“端午节”,小明的妈妈为小明煮了6个粽子,其中腊肉馅2个,豆沙馅4个,小明随机取出两个,事件A=“取到的两个为同一种馅”,事件B=“取到的两个都是豆沙馅”,则(|)(P B A=)A.34B.67C.310D.121322.某同学投篮第一次命中的概率是0.75,连续两次投篮命中的概率是0.6,已知该同学第一次投篮命中,则其随后第二次投篮命中的概率是()A .0.45B .0.6C .0.75D .0.823.甲、乙两地都位于长江下游,根据天气预报的记录知,一年中下雨天甲市占20%,乙市占18%,两市同时下雨占12%.则甲市为雨天,乙市也为雨天的概率为( )A .0.6B .0.7C .0.8D .0.6624.某射击手射击一次命中的概率是0.7,连续两次均射中的概率是0.4,已知某次射中,则随后一次射中的概率是( )A .710B .67C .47D .2725.根据历年气象统计资料知,某地区某日吹东风的概率为13,下雨的概率为25,既吹东风又下雨的概率为15.现已知该日吹东风,则该日下雨的概率为( ) A .15 B .25 C .35 D .45二.填空题(共5小题)26.某一批花生种子,如果每1粒种子发芽的概率均为23,那么播下4粒种子,恰有2粒发芽的概率是 (用数字作答).27.设某种动物由出生算起活到20岁的概率为0.8,活到25岁的概率为0.4,现有一个20岁的这种动物,它能活到25岁的概率是 .28.从标有1,2,3,4,5的五张卡片中,依次抽出2张,则在第一次抽到偶数的条件下,第二次抽到奇数的概率为 .29.甲袋中有5个红球,2个白球和3个黑球,乙袋中有4个红球,3个白球和3个黑球.先从甲袋中随机取出一球放入乙袋,分别以1A ,2A 和3A 表示由甲袋取出的球是红球,白球和黑球的事件;再从乙袋中随机取出一球,以B 表示由乙袋取出的球是红球的事件.则下列结论①P (B )922=;②12(|)5P B A =;③事件B 与事件1A 相互独立;④1A ,2A ,3A 是两两互斥的事件.其中正确的是 (写出所有正确结论的编号).30.彩票公司每天开奖一次,从1,2,3,4四个号码中随机开出一个作为中奖号码,开奖时如果开出的号码与前一天相同,就要重开,直到开出与前一天不同的号码为止.如果第一天开出的号码是4,则第五天开出的号码也同样是4的概率为 .2019年高中数学《条件概率》经典题及答案详解一.选择题(共25小题)1.先后掷子(子的六个面上分别标有1,2,3,4,5,6个点)两次,落在水平桌面后,记正面朝上的点数分别为x ,y ,设事件A 为“x y +为偶数”,事件B 为“x ,y 中有偶数且x y ≠”,则概率(|)(P B A = )A .13B .14C .12D .25【解答】解:根据题意,若事件A 为“x y +为偶数”发生,则x 、y 两个数均为奇数或均为偶数.共有23318⨯⨯=个基本事件,∴事件A 的概率为P (A )2331662⨯⨯==⨯ 而A 、B 同时发生,基本事件有“24+”、“ 26+”、“ 42+”、“ 46+”、“ 62+”、“ 64+”, 一共有6个基本事件,因此事件A 、B 同时发生的概率为61()666P AB ==⨯ 因此,在事件A 发生的情况下,B 发生的概率为1()16(|)1()32P AB P B A P A ===. 故选:A .2.抛掷甲、乙两颗骰子,若事件A :“甲骰子的点数大于4”;事件B :“甲、乙两骰子的点数之和等于7”,则(|)P B A 的值等于( )A .13B .118C .16D .19【解答】解:由题意,(|)P B A 为抛掷甲、乙两颗骰子,甲骰子的点数大于4时甲、乙两骰子的点数之和等于7的概率.抛掷甲、乙两颗骰子,甲骰子的点数大于4,基本事件有2612⨯=个,甲骰子的点数大于4时甲、乙两骰子的点数之和等于7,基本事件有2个,21(|)126P B A ∴==. 故选:C .3.一个家庭有两个小孩,假设生男生女是等可能的,已知这个家庭有一个是女孩的条件下,这时另一个也是女孩的概率是( )A .14B .23C .12D .13【解答】解:一个家庭中有两个小孩只有4种可能:{男,男},{男,女},{女,男},{女,女}.记事件A 为“其中一个是女孩”,事件B 为“另一个也是女孩”,则{A =(男,女),(女,男),(女,女)},{B =(男,女),(女,男),(女,女)},{AB =(女,女)}. 于是可知3()4P A =,1()4P AB =. 问题是求在事件A 发生的情况下,事件B 发生的概率,即求(|)P B A ,由条件概率公式,得114(|)334P B A ==. 故选:D .4.盒中有红球5个,蓝球11个,其中红球中有2个玻璃球,3个木质球;蓝球中有4个玻璃球,7个木质球,现从中任取一球,假设每个球被摸到的可能性相同.若已知取到的球是玻璃球,则它是蓝球的概率为( )A .23B .13C .1116D .516【解答】解:记“取到蓝球”为事件A ,“取到玻璃球”为事件B ,则已知取到的球为玻璃球,它是蓝球的概率就是B 发生的条件下A 发生的条件概率,记作(|)P A B .41()164P AB ==,P (B )63168==, ∴已知取到的球是玻璃球,则它是蓝球的概率为1()24(|)3()38P AB P A B P B ===. 故选:A .5.投掷一枚骰子,若事件{A =点数小于6},事件{B =点数大于2},则(|)P B A 等于()A .25B .12C .35D .34【解答】解:投掷一枚骰子,事件{A =点数小于6},事件{B =点数大于2},则P (A )56=,1()2P AB =,1()32(|)5()56P AB P B A P A ∴===. 故选:C .6.书架上有三本数学书和两本语文书,某同学两次分别从书架各取一本书,取后不放回,若第一次从书架取出一本数学书记为事件A ,第二次从书架取出一本数学书记为事件B ,则(|)(P B A = )A .12B .110C .310D .35【解答】解:事件发生的概率P (A )35=, 事件B 发生的概率为P (B )12=, 事件AB 同时发生的概率3()10P AB =, 3()110(|)3()25P AB P B A P A ∴===, 故选:A .7.已知某同学在高二期末考试中,A 和B 两道选择题同时答对的概率为23,在A 题答对的情况下,B 题也答对的概率为89,则A 题答对的概率为( ) A .14 B .12 C .34 D .79【解答】解:设事件A :答对A 题,事件B :答对B 题,则()P AB P =(A )P (B )23=, ()8(|)()9P AB P B A P A ==, P ∴(A )34=. 故选:C .8.甲、乙二人参加一项抽奖活动,每人抽奖中奖的概率均为0.6,两人都中奖的概率为0.4,则已知甲中奖的前提下乙也中奖的概率为( )A .625B .35C .25D .23【解答】解:每人抽奖中奖的概率均为0.6,两人都中奖的概率为0.4,设甲中奖概率为P (A ),乙中奖的概率为P (B ),两人都中奖的概率为()P AB , 则P (A )0.6=,P (B )0.6=,两人都中奖的概率为()0.4P AB =, 则已知甲中奖的前提下乙也中奖的概率为()0.42(/)()0.63P AB P B A P A ===, 故选:D .9.某校自主招生面试共有7道题,其中4道理科题,3道文科题,要求不放回地依次任取3道题作答,则某考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率为( )A .17B .15C .37D .45【解答】解:设事件A 表示“第一次抽到理科题”,事件B 表示“第二次抽到文科题”,事件C 表示“第三次抽到文科题”,则P (A )47=,4324()76535P ABC =⨯⨯=, ∴某考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率为:4()135(|)4()57P ABC P BC A P A ===. 故选:B .10.篮子里装有3个红球,4个白球和5个黑球,球除颜色外,形状大小一致.某人从篮子中随机取出两个球,记事件A = “取出的两个球颜色不同”,事件B = “取出一个红球,一个白球”,则(|)(P B A = )A .211B .1247C .1219D .16【解答】解:篮子里装有3个红球,4个白球和5个黑球,球除颜色外,形状大小一致. 某人从篮子中随机取出两个球,记事件A = “取出的两个球颜色不同”,事件B = “取出一个红球,一个白球”,则P (A )22234521247166C C C C ++=-=, 11342122()11C C P AB C ==,2()1211(|)47()4766P AB P B A P A ∴===. 故选:B .11.春天是鼻炎和感冒的高发期,某人在春季里鼻炎发作的概率为0.8,鼻炎发作且感冒的概率为0.6,则此人鼻炎发作的条件下,他感冒的概率为( )A .0.48B .0.40C .0.64D .0.75【解答】解:设某人鼻炎发作为事件A ,某人感冒为事件B ,则P (A )0.8=,()0.6P AB =,()0.6(|)0.75()0.8P AB P B A P A ∴===. 故选:D .12.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹进行一场比赛,则在齐王的马获胜的条件下,齐王的上等马获胜的概率为( )A .23B .12C .13D .1【解答】解:设齐王的上,中,下三个等次的马分别为a ,b ,c ,田忌的上,中,下三个等次的马分别为记为A ,B ,C ,从双方的马匹中随机选一匹进行一场比赛的所有的可能为Aa ,Ab ,Ac ,Ba ,Bb ,Bc ,Ca ,Cb ,Cc ,根据题设其中Ab ,Ac ,Bc 是田忌胜共三种可能,则在齐王的马获胜有6种情况,其中齐王的上等马获胜的有3种情况, 故在齐王的马获胜的条件下,齐王的上等马获胜的概率为3162=. 故选:B .13.某校从学生会文艺部6名成员(其中男生4人,女生2人)中,任选3人参加学校举办的“庆元旦迎新春”文艺汇演活动.设“男生甲被选中”为事件A ,“女生乙被选中”为事件B ,则(|)P B A 为( )A .15B .25C .35D .310【解答】解:142542 (|)105ABAn CP B An C====,故选:B.14.一种灯泡使用一年的概率为0.8,使用两年的概率为0.4,现有已经使用一年的灯泡,它还能使用一年的概率是()A.0.4B.0.5C.0.6D.0.8【解答】解:记“灯泡使用一年”为事件A,记“灯泡使用两年”为事件B,根据题意,易得P(A)0.8=,()0.4P AB=,由条件概率的计算方法0.40.50.8P==,故选:B.15.将3颗骰子各掷一次,记事件A为“三个点数都不同”,事件B为“至少出现一个1点”,则条件概率(|)P A B和(|)P B A分别为()A.160,291B.560,1891C.601,912D.911,2162【解答】解:根据条件概率的含义,(|)P A B其含义为在B发生的情况下,A发生的概率,即在“至少出现一个1点”的情况下,“三个点数都不相同”的概率,“至少出现一个1点”的情况数目为66655591⨯⨯-⨯⨯=,“三个点数都不相同”则只有一个1点,共135460C⨯⨯=种,60(|)91P A B∴=;(|)P B A其含义为在A发生的情况下,B发生的概率,即在“三个点数都不相同”的情况下,“至少出现一个1点”的概率,1(|)2P B A∴=,故选:C.16.甲乙二人争夺一场围棋比赛的冠军,若比赛为“三局两胜”制,甲在每局比赛中获胜的概率均为23,且各局比赛结果相互独立,则在甲获得冠军的情况下,比赛进行了三局的概率为()A.13B.25C.23D.45【解答】解:由题意,甲获得冠军的概率为22212122203333333327⨯+⨯⨯+⨯⨯=,其中比赛进行了3局的概率为212122833333327⨯⨯+⨯⨯=,∴所求概率为820227275÷=, 故选:B .17.小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件A = “4个人去的景点不相同”,事件B = “小赵独自去一个景点”,则(|)(P A B = ) A .29B .13C .49 D .59【解答】解:小赵独自去一个景点,则有4个景点可选,其余3人只能在小赵剩下的3个景点中选择,可能性为33327⨯⨯=种所以小赵独自去一个景点的可能性为427108⨯=种 因为4 个人去的景点不相同的可能性为432124⨯⨯⨯=种, 所以242(|)1089P A B ==. 故选:A .18.九江气象台统计,5月1日浔阳区下雨的概率为415,刮风的概率为215,既刮风又下雨的概率为110,设A 为下雨,B 为刮风,那么(|)(P A B = ) A .12B .34C .25 D .38【解答】解:由题意P (A )415=,P (B )215=,1()10P AB =, 1()310(|)2()415P AB P A B P B ∴===,故选:B .19.某校组织高一、高二年级书法比赛,高一、高二年级参赛人数分别占60%、40%;并且高一年级获奖人数占本年级参赛人数的16,高二年级获奖人数占本年级参赛人数的18.现从所有参赛学生中任意抽取一人,记事件A 表示该学生来自高一,事件B 表示该学生获奖,则(|)P B A 的值为( ) A .18B .215C .536D .320【解答】解:事件A 表示该学生来自高一,事件B 表示该学生获奖,(|)P B A 表示来自高二的条件下,获奖的概率.由题意,设参赛人数为x ,则高一、高二年级参赛人数分别为0.6.0.4x x ,高一年级获奖人数0.1x ,高二年级获奖人数0.05x . 0.051(|)0.48x P B A x ∴==, 故选:A .20.甲、乙两人独立地对同一目标各射击一次,命中率分别为0.6和0.7,在目标被击中的情况下,甲、乙同时击中目标的概率为( ) A .2144B .1522C .2150D .925【解答】解:根据题意,记甲击中目标为事件A ,乙击中目标为事件B ,目标被击中为事件C ,则P (C )1()()1(10.6)(10.7)0.88P A P B =-=---=; 则在目标被击中的情况下,甲、乙同时击中目标的概率为0.60.7210.8844P ⨯==; 故选:A .21.2016年6月9日是“端午节”,小明的妈妈为小明煮了6个粽子,其中腊肉馅2个,豆沙馅4个,小明随机取出两个,事件A = “取到的两个为同一种馅”,事件B = “取到的两个都是豆沙馅”,则(|)(P B A = ) A .34B .67C .310D .1213【解答】解:由题意,P (A )222426715C C C +==,62()155P AB ==, ()6(|)()7P AB P B A P A ∴==, 故选:B .22.某同学投篮第一次命中的概率是0.75,连续两次投篮命中的概率是0.6,已知该同学第一次投篮命中,则其随后第二次投篮命中的概率是( ) A .0.45B .0.6C .0.75D .0.8【解答】解:设随后第二次投篮命中的概率为p ,则有题意可得0.750.6p ⨯=, 解得0.8p =, 故选:D .23.甲、乙两地都位于长江下游,根据天气预报的记录知,一年中下雨天甲市占20%,乙市占18%,两市同时下雨占12%.则甲市为雨天,乙市也为雨天的概率为( ) A .0.6B .0.7C .0.8D .0.66【解答】解:记甲市下雨为事件A ,乙市下雨为事件B , 根据题意有P (A )0.2=,P (B )0.18=,()0.12P AB =; 则在甲市下雨的条件下,乙市下雨的概率为()0.120.6()0.20p AB P A ==; 故选:A .24.某射击手射击一次命中的概率是0.7,连续两次均射中的概率是0.4,已知某次射中,则随后一次射中的概率是( ) A .710B .67C .47D .27【解答】解:设“某次射中”为事件A ,“随后一次的射中”为事件B , 则()0.4P AB =,P (A )0.7=, ()4(|)()7P AB P B A P A ∴==, 故选:C .25.根据历年气象统计资料知,某地区某日吹东风的概率为13,下雨的概率为25,既吹东风又下雨的概率为15.现已知该日吹东风,则该日下雨的概率为( )A .15B .25 C .35D .45【解答】解:设事件A 表示“某地区某日吹东风”,事件B 表示“某地区某日下雨”, 则P (A )13=,P (B )25=,1()5P AB =,∴已知该日吹东风,则该日下雨的概率:1()35(|)1()53P AB P B A P A ===.故选:C .二.填空题(共5小题)26.某一批花生种子,如果每1粒种子发芽的概率均为23,那么播下4粒种子,恰有2粒发芽的概率是427(用数字作答).【解答】解:如果每1粒发芽的概率为23,那么播下4粒种子恰有2粒发芽的概率是:2224214()()3327C =. 故答案为:427. 27.设某种动物由出生算起活到20岁的概率为0.8,活到25岁的概率为0.4,现有一个20岁的这种动物,它能活到25岁的概率是 0.5 .【解答】解:设A = “能活到20岁”, B = “能活到25岁”,则P (A )0.8=,P (B )0.4=,而所求概率为(|)P B A ,由于B A ⊆,故AB B =,于是()()0.4(|)0.5()()0.8P AB P B P B A P A P A ====, 所以这个动物能活到25岁的概率是0.5. 故答案为:0.5.28.从标有1,2,3,4,5的五张卡片中,依次抽出2张,则在第一次抽到偶数的条件下,第二次抽到奇数的概率为34. 【解答】解:在第一次抽到偶数时,还剩下1个偶数,3个奇数,∴在第一次抽到偶数的条件下,第二次抽到奇数的概率为34. 故答案为:34. 29.甲袋中有5个红球,2个白球和3个黑球,乙袋中有4个红球,3个白球和3个黑球.先从甲袋中随机取出一球放入乙袋,分别以1A ,2A 和3A 表示由甲袋取出的球是红球,白球和黑球的事件;再从乙袋中随机取出一球,以B 表示由乙袋取出的球是红球的事件.则下列结论①P (B )922=;②12(|)5P B A =;③事件B 与事件1A 相互独立;④1A ,2A ,3A 是两两互斥的事件.其中正确的是 ①④ (写出所有正确结论的编号).【解答】解:由题意1A ,2A ,3A 是两两互斥的事件,151()102P A ==,221()105P A ==,33()10P A =,11151()5112(|)1()112P BA P B A P A ⨯===,由此知,②错误; 24(|)11P B A =,34(|)11P B A =; 而P (B )123()()()P A B P A B P A B =++112233()(|)()(|)()(|)P A P B A P A P B A P A P B A =++=1514343492115111011101122⨯+⨯+⨯+⨯=, 由此知①正确,③错误.1A ,2A ,3A 是两两互斥的事件,由此知④正确;对照四个命题知①④正确; 故答案为:①④.30.彩票公司每天开奖一次,从1,2,3,4四个号码中随机开出一个作为中奖号码,开奖时如果开出的号码与前一天相同,就要重开,直到开出与前一天不同的号码为止.如果第一天开出的号码是4,则第五天开出的号码也同样是4的概率为 727. 【解答】解:第一天开出4,则后4天开出的中奖号码的种数有43种, 第五天同样开出4,则中间三天开出的号码种数:第二天有3种,第三天如果是4,则第4天有3种,第三天如果不是4,则第4天有2种, 满足条件的种数有32231321⨯⨯+⨯⨯=种, 故所求概率2178127p ==. 故答案为:727。
高中数学《随机事件的概率》典型例题

高中数学《随机事件的概率》典型例题例1、指出下列事件是必然事件,不可能事件,还是随机事件。
(1)某体操运动员将在某次运动会上获得全能冠军;(2)一个三角形的大边对的角小,小边对的角大;(3)如果,那么;(4)某人购买福利彩票中奖。
答案:(1)(4)是随机事件,(2)是不可能事件,(3)是必然事件例2、在下列试验中,哪些试验给出的随机事件是等可能的?(1)投掷一枚均匀的硬币,“出现正面”与“出现反面”;(2)一个盘子中有三个大小完全相同的球,其中红球、黄球、黑球各一个,从中任取一球,“取出的是红球”“取出的是黄球”“取出的是黑球”;(3)一个盒子中有四个大小完全相同的球,其中红球、黄球各一个,黑球两个,从中任取一球,“取出的是红球”“取出的是黄球”“取出的是黑球”。
解:(1)中给出的随机事件“出现正面”与“出现反面”是等可能的。
(2)中给出的三个随机事件:“取出的是红球”“取出的是黄球”“取出的是黑球”,由于球的大小、个数相同,因此这三个事件是等可能的。
(3)中给出的随机事件:“取出的是红球”“取出的是黄球”“取出的是黑球”,由于三种球的数量不同,因此这三个事件不是等可能的。
例3、有5副不同的手套,甲先任取一只,乙再任取一只,然后甲又任取一只,最后乙再取一只,求下列事件的概率:(1)A={甲正好取到2只配对手套};(2)B={乙正好取到2只配对手套}。
解:(1)A含基本事件数:① 先取一双,方法数为;② 将取到的一双放到第一、三位,分法数为2;③ 在余下的8只手套中,任取2只放到二、四位,分法数为,由分步计数原理,A含基本事件数为,故;(2)B含基本事件数:① 先取一双,放到二、四位,分法数为;② 在余下的8只手套中任取2只放到一、三位,分法数为。
由分步计数原理,B含基本事件数为,故。
例4、从1,2,3,4,5五个数字中,任意有放回地连续抽取三个数字,求下列事件的概率。
(1)三个数字完全不同;(2)三个数字中不含1和5;(3)三个数字中5恰好出现两次。
高中数学 7.1.2 全概率公式 课后练习、课时练习

一、单选题1. 已知甲、乙盒子各装有形状大小完全相同的小球,其中甲盒子内有2个红球,1个白球;乙盒子内有3个红球,2个白球.若第一次先从甲盒子内随机抽取1个球放入乙盒子中,则第二次从乙盒子中抽1个球是红球的概率为()A.B.C.D.2. 某高校有智能餐厅、人工餐厅,甲第一天随机地选择一餐厅用餐,如果第一天去餐厅,那么第二天去餐厅的概率为0.6;如果第一天去餐厅,那么第二天去餐厅的概率为0.8.则甲第二天去餐厅用餐的概率为()A.0.75 B.0.7 C.0.56 D.0.383. 某射击小组共有25名射手,其中一级射手5人,二级射手10人,三级射手10人,若一、二、三级射手能通过选拔进入比赛的概率分别是0.9,0.8,0.4,则任选一名射手能通过选拔进入比赛的概率为()A.0.48 B.0.66 C.0.70 D.0.754. 排球比赛实行“每球得分制”,即每次发球后,谁取胜谁就得1分,得分的队有发球权,最后先得25分的队获得本局比赛胜利,若出现比分,要继续比赛至某队领先2分才能取胜,该局比赛结束.甲、乙两队进行一局排球比赛,已知甲队发球时甲队获胜的概率为,乙队发球时甲队获胜的概率为,且各次发球的胜负结果相互独立.若此时甲、乙两队双方比分为平,且甲队拥有发球权,则甲队得25分且取得该局比赛胜利的概率为()A.B.C.D.5. 长时间玩手机可能影响视力,据调查,某校学生大约30%的人近视,而该校大约有40%的学生每天玩手机超过2h,这些人的近视率约为60%.现从每天玩手机不超过2h的学生中任意调查一名学生,则他近视的概率为()A.B.C.D.6. 3月15日是国际消费者权益日.中央电视台特地推出3.15公益晚会,曝光了食品、医美、直播等多领域乱象,在很大程度上震慑了一些不良商家,也增强了消费者的维权意识.一名市民在某商店买了一只灯泡,结果用了两个月就坏了,他拨打了12315投诉电话.通过调查,发现该商店将一些不合格灯泡混入一批合格灯泡中以次充好卖给顾客.假设合格灯泡在使用1000小时后损坏的概率为0.004,不合格灯泡在使用1000小时后损坏的概率为0.4,若混入的不合格灯泡数占灯泡总数的25%,现一顾客在该商店买一只灯泡,则该灯泡在使用1000小时后不会损坏的概率为()A.0.103 B.0.301 C.0.897 D.0.699二、多选题7. 甲箱中有5个红球,2个白球和3个黑球,乙箱中有3个红球,3个白球和3个黑球,先从甲箱中随机取出一球放入乙箱,分别以和表示由甲箱取出的球是红球,白球和黑球的事件;再从乙箱中随机取出一球,以表示由乙箱取出的球是红球的事件,则下列结论正确的是()A.事件与事件相互独立B.C.D.8. 如图,已知正方体顶点处有一质点Q,点Q每次会随机地沿一条棱向相邻的某个顶点移动,且向每个顶点移动的概率相同,从一个顶点沿一条棱移动到相邻顶点称为移动一次,若质点Q的初始位置位于点A处,记点Q移动n 次后仍在底面ABCD上的概率为,则下列说法正确的是()A.B.C.D.点Q移动4次后恰好位于点的概率为0三、填空题9. 盒中有个红球,个黑球,今随机地从中取出一个,观察其颜色后放回,并加上同色球个,再从盒中抽取一球,则第二次抽出的是黑球的概率是_________.10. 一学生接连参加同一课程的两次考试,第一次及格的概率为p,若第一次及格则第二次及格的概率也为p;若第一次不及格则第二次及格的概率为.若已知他第二次已经及格,则他第一次及格的概率为 __.11. 一道单项选择题有4个答案,要求学生将正确答案选择出来.某考生知道正确答案的概率为,在乱猜时,4个答案都有机会被他选择,若他答对了,则他确实知道正确答案的概率是___________.12. 某厂用甲、乙两台机器生产相同的零件,它们的产量各占,而各自的产品中废品率分别为,则该厂这种零件的废品率为__________.四、解答题13. 设某工厂有两个车间生产同型号家用电器,第1车间的次品率为0.15,第2车间的次品率为0.12,两个车间的成品都混合堆放在一个仓库,假设第1,2车间生产的成品比例为2:3.今有一客户从成品仓库中随机提一台产品,求该产品合格的概率.14. 鲜花饼是以云南特有的食用玫瑰花入料的酥饼,是具有云南特色的云南经典点心代表,鲜花饼的保质期一般在三至四天.据统计,某超市一天鲜花饼卖出3箱的概率为,卖出箱的概率为,卖出箱的概率为,没有卖出的概率为,为了保证顾客能够买到新鲜的鲜花饼,该超市规定当天结束营业后检查货架上存货,若卖出箱及以上,则需补货至箱,否则不补货.假设第一天该超市开始营业时货架上有箱鲜花饼.(1)在第一天结束营业后货架上有箱鲜花饼的条件下,求第二天结束营业时货架上有箱存货的概率;(2)求第二天结束营业时货架上有箱存货的概率.15. (1)已知与独立,且,求;(2)已知,,,求,.16. 现有甲、乙两个袋子,其中甲袋中有6个红球和2个白球,乙袋中有3个红球和5个白球,两袋子中小球形状和大小完全相同.从这两个袋子中选择一个袋子,再从该袋子中一次摸出两个球,称为一次试验.已知选择甲袋子的概率为,选择乙袋子的概率为.拟进行多次重复试验,直到摸出的两个球均为红球,不再试验.(1)求第一次试验摸出两个红球的概率;(2)已知需进行第二次试验,计算第一次试验摸出的两个球来自甲袋的概率.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
. .. . s ..
高中数学概率大题(经典二) 一.解答题(共10小题) 1.某会议室用5盏灯照明,每盏灯各使用灯泡一只,且型号相同.假定每盏灯能否正常照明只与灯泡的寿命有关,该型号的灯泡寿命为1年以上的概率为p1,寿命为2年以上的概率为p2.从使用之日起每满1年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换. (Ⅰ)在第一次灯泡更换工作中,求不需要换灯泡的概率和更换2只灯泡的概率; (Ⅱ)在第二次灯泡更换工作中,对其中的某一盏灯来说,求该盏灯需要更换灯泡的概率; (Ⅲ)当p1=0.8,p2=0.3时,求在第二次灯泡更换工作,至少需要更换4只灯泡的概率(结果保留两个有效数字). 2.已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止.设ξ为取出的次数,求ξ的分布列及Eξ. 3.某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有n位学生,每次活动均需该系k位学生参加(n和k都是固定的正整数),假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系k位学生,且所发信息都能收到,记该系收到李老师或张老师所发活动通知信息的学生人数为X. (I)求该系学生甲收到李老师或张老师所发活动通知信息的概率; (II)求使P(X=m)取得最大值的整数m. 4.在医学生物学试验中,经常以果蝇作为试验对象,一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.以ξ表示笼内还剩下的果蝇的只数. (Ⅰ)写出ξ的分布列(不要求写出计算过程)和数学期望Eξ; (Ⅱ)求概率P(ξ≥Eξ). 5.A,B,C三个班共有100名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如表(单位:小时): A班 6 6.5 7 7.5 8 B班 6 7 8 9 10 11 12 C班 3 4.5 6 7.5 9 10.5 12 13.5 (Ⅰ)试估计C班的学生人数; (Ⅱ)从A班和C班抽出的学生中,各随机选取一个人,A班选出的人记为甲,C班选出的人记为乙.假设所有学生的锻炼时间相对独立,求该周甲的锻炼时间比乙的锻炼时间长的概率; (Ⅲ)再从A,B,C三班中各随机抽取一名学生,他们该周锻炼时间分别是7,9,8.25(单位:小时),这3个新数据与表格中的数据构成的新样本的平均数记为μ1,表格中数据的平均数记为μ0,试判断μ0和μ1的大小.(结论不要求证明) 6.某商场经销某商品,根据以往资料统计,顾客采用的付款期数ξ的分布列为 ξ 1 2 3 4 5
P 0.4 0.2 0.2 0.1 0.1 商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元,η表示经销一件该商品的利润. (Ⅰ)求事件A:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率P(A); . .. . s ..
(Ⅱ)求η的分布列及期望Eη. 7.甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”得1分;如果两人
都没猜对,则“星队”得0分.已知甲每轮猜对的概率是,乙每轮猜对的概率是;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求: (I)“星队”至少猜对3个成语的概率; (II)“星队”两轮得分之和为X的分布列和数学期望EX. 8.某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4,现从这10人中随机选出2人作为该组代表参加座谈会. (1)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率; (2)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列和数学期望. 9.购买某种保险,每个投保人每年度向保险公司交纳保费a元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为1﹣0.999104. (Ⅰ)求一投保人在一年度内出险的概率p; (Ⅱ)设保险公司开办该项险种业务除赔偿金外的成本为50 000元,为保证盈利的期望不小于0,求每位投保人应交纳的最低保费(单位:元). 10.某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下: A地区:62 73 81 92 95 85 74 64 53 76 78 86 95 66 97 78 88 82 76 89 B地区:73 83 62 51 91 46 53 73 64 82 93 48 65 81 74 56 54 76 65 79 (1)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可); (2)根据用户满意度评分,将用户的满意度从低到高分为三个等级: 满意度评分 低于70分 70分到89分 不低于90分 满意度等级 不满意 满意 非常满意 记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的频率,求C的概率.
11.某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出 . .. . s ..
的2个球中,若都是红球,则获一等奖,若只有1个红球,则获二等奖;若没有红球,则不获奖. (1)求顾客抽奖1次能获奖的概率; (2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X,求X的分布列和数学期望. 12.端午节吃粽子是我国的传统习俗,设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同,从中任意选取3个. (Ⅰ)求三种粽子各取到1个的概率; (Ⅱ)设X表示取到的豆沙粽个数,求X的分布列与数学期望. 13.为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加,现有来自甲协会的运动员3名,其中种子选手2名,乙协会的运动员5名,其中种子选手3名,从这8名运动员中随机选择4人参加比赛. (Ⅰ)设A为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”,求事件A发生的概率; (Ⅱ)设X为选出的4人中种子选手的人数,求随机变量X的分布列和数学期望. 14.已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束. (Ⅰ)求第一次检测出的是次品且第二次检测出的是正品的概率; (Ⅱ)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求X的分布列和均值(数学期望) 15.某银行规定,一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定,小王到银行取钱时,发现自己忘记了银行卡的密码,但是可以确定该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定. (1)求当天小王的该银行卡被锁定的概率; (2)设当天小王用该银行卡尝试密码次数为X,求X的分布列和数学期望. 16.若n是一个三位正整数,且n的个位数字大于十位数字,十位数字大于百位数字,则称n为“三位递增数”(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次,得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分,若能被5整除,但不能被10整除,得﹣1分,若能被10整除,得1分. (Ⅰ)写出所有个位数字是5的“三位递增数”; (Ⅱ)若甲参加活动,求甲得分X的分布列和数学期望EX. 17.设每个工作日甲,乙,丙,丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4,各人是否需使用设备相互独立. (Ⅰ)求同一工作日至少3人需使用设备的概率; (Ⅱ)实验室计划购买k台设备供甲,乙,丙,丁使用,若要求“同一工作日需使用设备的人数大于k”的概率小于0.1,求k的最小值. 18.20名学生某次数学考试成绩(单位:分)的频率分布直方图如图: (Ⅰ)求频率分布直方图中a的值; (Ⅱ)分别求出成绩落在[50,60)与[60,70)中的学生人数; (Ⅲ)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率. . .. . s ..
19.某大学志愿者协会有6名男同学,4名女同学,在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院,现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同). (Ⅰ)求选出的3名同学是来自互不相同学院的概率; (Ⅱ)设X为选出的3名同学中女同学的人数,求随机变量X的分布列和数学期望. 20.一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立. (Ⅰ)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率; (Ⅱ)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望E(X)及方差D(X).
