山东省威海市乳山一中2013届高三12月月考综合能力测试试卷
山东省威海市乳山一中高三物理上学期12月月考试题(含解析)

威海市乳山一中2015届高三上学期12月月考物理试题一,选择题(40分,每题至少有一个正确选项,全部选出得4分,漏选得2分,错选或多选不得分)1.在物理学发展的过程中,有许多伟大的科学家做出了突出贡献。
关于科学家和他们的贡献,下列说法正确的是()A.首先提出场的概念并引入了场线的科学家是麦克斯韦B.德国天文学家开普勒对他导师第谷观测的行星数据进行多年研究,得出了万有引力定律C.英国物理学家卡文迪许利用卡文迪许扭秤首先较准确的测定了静电力常量D.古希腊学者亚里士多德认为物体下落快慢由它们的重量决定,伽利略在他的《两种新科学的对话》中利用逻辑推断使亚里士多德的理论陷入了困境【答案】D【命题立意】本题旨在考查物理学史。
【解析】A、法拉第提出可以用电场线描绘电场的分布,极大地促进了人们对电磁现象的研究,故A错误;B、德国天文学家开普勒对他导师第谷观测的行星数据进行多年研究,得出了行星运动规律,故B错误;C、英国物理学家卡文迪许利用卡文迪许扭秤首先较准确的测定了万有引力常量,故C错误;D、古希腊学者亚里士多德认为物体下落快慢由它们的重量决定,伽利略利用逻辑推断使亚里士多德的理论陷入了困境,故D正确;故选:AD2.电场中等势面如图所示,下列关于该电场描述正确的是()A.A点的电场强度比C点的小B.负电荷在A点电势能比C点电势能小C.电荷沿等势面AB移动过程中,电场力始终不做功D.正电荷由A移到C,电场力做负功【答案】BC【命题立意】本题旨在考查等势面、电势能。
【解析】A、点A周围的等势面比C点周围的等势面密,则A点的场强比C点的大,故A错误;B、负电荷在高电势点电势能小,在低电势点电势能高,故负电荷在A点电势能比在C点电势能小,故B正确;C 沿着等势面移动点电荷,电势能不变,电场力不做功.故C正确;D 正电荷由A到C,为沿电场力方向运动,则电场力做正功.故D错误。
故选:BC3.关于磁感应强度下列说法正确的是:()A、放在磁场中的通电导线,电流越大,受到的磁场力也越大,表示该处的磁感应强度越大B、磁感线的指向就是磁感应强度的方向C、垂直磁场放置的通电导线的受力方向就是磁感应强度的方向D、磁感应强度的大小、方向与放入磁场的通电导线的电流大小、导线长度、导线取向等均无关【答案】D【命题立意】本题旨在考查磁感应强度。
山东省威海市乳山市乳山一中2014届高三12月份限时训练全科政治及答案

高三政治综合训练(三)说明:本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共30小题计l00分。
考试时间为90分钟。
请将第1卷答案涂在答题卡上,第II卷答案写在答题纸上.只交答题卡和第II卷答题纸。
第I卷(选择题共50分)一、本卷共25小题,每小题2分,共计50分。
在每题给出的四个选项中,只有一项是最符合题目要求的。
1、甲、乙是某国生产A商品的两家企业,2012年它们24小时分别生产A商品4件、5件,乙企业的劳动生产率刚好等于该行业的平均劳动生产率,乙企业每24小时创造的价值总量为1100元,2013年甲企业劳动生产率提高50%,乙企业提高劳动生产率20%,整个行业提高劳动生产率10%,其他条件不变,甲、乙企业24小时生产的A商品的价值总量分别为A.1320元1320元B.1320元1200元C.1200元1200元D.1452元1320元21、某年大自然对农业格外恩惠,寒冷的冬季冻死了害虫,适于播种的春天早早到来,夏季丰沛的雨水使禾苗茁壮成长,阳光灿烂的秋季又使农作物易于收割和运输。
年终,农民琼斯一家高高兴兴围坐在火炉旁计算一年的收入。
结果使他们大吃一惊:少见的好年景和大丰收却使这个农家的收入比往年减少!他的邻居以及其他地方的农民也遭遇相同的命运。
这个故事就是经济学上著名的“丰收悖论”。
丰收悖论的主要成因在于A.市场调节不是万能的,有些领域不能由市场调节B.充分的市场竞争中劳动效率与劳动收益成反比C.大丰收使社会劳动生产率提高从而减少单位商品价值量D.小麦等基本粮食作物需求弹性小3、2013年4月11日,渣打银行(中国)有限公司宣布,已经获得银监会和中国人民银行批准,在全国银行间债券市场成功发行总额为人民币50亿元的金融债券。
本次债券所募集的资金将全部用于支持小微企业贷款,这也是外资银行第一次在华发行小微企业金融债券。
小微企业金融债券①以小微企业的经营利润作为还本付息的保证②其利率通常高于大中型企业债券③其利率一般高于同期银行存款利率④风险和收益一般高于国债A.①②B.①④C.②③D.③④4.有评论针对欧盟对我国光伏产品实行的“双反”措施指出:双反既不利人也不利己,制裁的是中国企业,但也无异于判了欧盟光伏产业死刑。
山东省潍坊一中2013届高三12月月考测试 基本能力

潍坊一中2013届高三12月月考测试基本能力试题第一部分(共70题,在每题给出的四个选项中,只有一个选项最符合题目要求,每小题1分,共70分)1.2012年,全国普通高校毕业生规模680余万人,比去年增加20万人,高校毕业生就业形势依然严峻,够大学生都要“抢”工作。
一个“抢”字启示求职者必须树立()A.自主择业观B.职业平等观C.竞争就业观D.多种方式就业观2.团圆是农历新年永恒的主题。
2012年年根将至,如潮的人群依然奔向大小车站,拥挤着要赶在大年三十前回家。
老一辈人依然有着浓厚的年的情结,一年年地坚守着过年的习俗,鞭炮、春联、福字、年画、祭祖、拜年、压岁钱等年的专有事物在他们心中分量依然很重。
材料显示出()A.《文化对人的影响是深远持久的B.文化对人的影响是潜移默化的C.春节的习俗不会改变D.人们摆脱不了旧传统的束缚3.“我爱我的国,我爱我的家。
”这句话体现了爱国与爱家是统一的,下列名言与这句话主旨一致的是()A.一片丹心图报国,两行清泪为思亲B.国家将兴有祯祥,国家将亡有妖孽C.历览前贤国与家,成由勤俭败由奢D.千龄人事一朝空,四海为家此路穷4.通常所说的水资源是指目前人类可以大量利用的()A.冰川水、河流水、湖泊水B.河流水、淡水湖泊水、浅层地下水C.冰川水、大气水、土壤水D.大气水、淡水湖泊水、沼泽水5.下列地点与诗句“坐地日行八万里,巡天遥看一千河,最吻合的是()A.90°E,89°N B.80°W,40°SC.10°E,1°S D.180°W,7l°S6.平时我们日常生活中所指的—天是()A.太阳日B.恒星日C.23小时56分4秒D.回归日7.下图所示的几种情况中,昼夜温差最小的是()8.某河流右岸侵蚀严重,且所在地区一年中有两次太阳直射现象,则该河流位于()A.赤道B.赤道与南回归线之间C.北回归线D.赤道与北回归线之间9.一位学者在他的著作里说:在20世纪的大幕拉开的时候,当时的世界大国们在东方进行了一次很不光彩的集体亮相。
山东省威海市乳山市乳山一中2014届高三12月份限时训练全科化学及答案

高三化学阶段检测三第I卷(选择题共48分)可能用到的相对原子质量:H 1 S 32 O 16 Na 23 Cu 64一、选择题(每题3分,共48分。
每小题只有一个....选项符合题意)1、下列说法不.正确的是A.空气中的NO2等氮氧化合物是造成光化学烟雾的主要原因B.NO、CO有剧毒都是因为它们易与血液中的血红蛋白结合C.减少使用氟利昂(氟氯代烷)的目的是为了减少酸雨D.大量使用含磷洗涤剂会造成水体富营养化2、下列装置中,都伴随有能量变化,其中是由化学能转变为电能的是( )。
3、设N A为阿佛加德罗常数,下列叙述中正确的是A.标准状况下,22.4LCO2和O2混合气体中含有的氧原子数为N AB.0.1mol Fe在0.1mol C12中充分燃烧,转移的电子数为0.3N AC.2mol SO2和1mol O2在密闭容器中加热(V2O5催化)充分反应后,容器内分子总数为2N A D.将0.1mol Cl2与足量NaOH溶液在常温下充分反应,转移的电子数为0.1N A4、一定量的锌粉和2mol/L的过量的盐酸反应,若向其中加入少量下列物质:①石墨②CuO ③铜粉④铁粉⑤浓盐酸⑥CuSO4。
其中能够加快反应速率,但又不影响产生H2的总量的是A.①②③⑤⑥B.①③⑤C.③④⑤D.①③⑥5、下列离子方程式正确的是A.硫酸铝溶液中加入过量氨水: Al3++3OH-==Al(OH)3↓B.明矾净水:Al3++3H 2O Al(OH)3(胶体)+3H+C.向FeI2中通入少量Cl2:2Fe2++Cl2==2Fe3++2Cl-D.洗涤试管内壁的银镜:Ag+2H++NO-3==Ag++NO2↑+H2O6、电子层数相同的短周期元素X、Y、Z、W,其中X的最外层电子数比K层少1,Y的最外层电子数比K层多l,Z的单质常用于制造太阳能电池,W的原子半径是同周期中最小的。
下列推断中正确的是A.Z的氢化物的热稳定性强于W的氢化物B.Z元素在自然界中的存在形态,既有游离态又有化合态C.X、Y、W的原子半径依次减小,对应单核的离子半径依次增大D.X、Y、W的最高价氧化物对应水化物之间互相都能发生反应7、强酸与强碱的稀溶液发生中和反应:H+(aq)+OH-(aq)=H2O(l) △H=-57.3 kJ·mol-1。
2022-2023学年山东省威海市乳山市高二年级上册学期12月月考数学试题【含答案】

2022-2023学年山东省威海市乳山市第一中学高二上学期12月月考数学试题一、单选题1.过与的交点,且平行于向量的直线方程为( )2x y +=0x y -=(3,2)v = A .B .3210x y --=3250x y +-=C .D .2310x y -+=2310x y --=【答案】C【分析】首先求出两直线的交点坐标,然后再根据所求直线平行于向量,从而可求出答案.(3,2)v =【详解】由,得,所以交点坐标为,2x y x y -=⎧⎨+=⎩1,1x y ==()1,1又因为直线平行于向量,所以所求直线方程为,(3,2)v = ()2113y x -=-即.2310x y -+=故选:C.2.已知数列是等比数列,满足,数列是等差数列,且,则等于{}n a 51184a a a ={}n b 88b a =79b b +( )A .24B .16C .8D .4【答案】C【解析】利用等比数列和等差数列的性质计算.【详解】∵数列是等比数列,∴,又,∴,{}n a 2511884a a a a ==80a ¹84a =又是等差数列,∴.{}n b 7988228b b b a +===故选:C .【点睛】关键点点睛:本题考查等差数列与等比数列的性质,掌握等差数列与等比数列的性质是解题关键.对正整数,若,是等差数列,则,若是等比,,,m n p l m n p l +=+{}n a m n p la a a a +=+{}n a 数列,则,特别地若,是等差数列,则,若是等比数列,m n p la a a a =2m n p +={}n a 2m n pa a a +={}n a 则.2m n pa a a =3.设B 是椭圆的上顶点,点P 在C 上,则的最大值为( )22:15x C y +=PBA .BCD .252【答案】A【分析】设点,由依题意可知,,,再根据两点间的距离公式得到()00,P x y ()0,1B 220015x y +=,然后消元,即可利用二次函数的性质求出最大值.2PB【详解】设点,因为,,所以()00,P x y ()0,1B 220015x y +=,()()()22222220000001251511426444PB x y yy y y y ⎛⎫=+-=-+-=--+=-++⎪⎝⎭而,所以当时,的最大值为.011y -≤≤014y =-PB 52故选:A .【点睛】本题解题关键是熟悉椭圆的简单几何性质,由两点间的距离公式,并利用消元思想以及二次函数的性质即可解出.易错点是容易误认为短轴的相对端点是椭圆上到上定点B 最远的点,或者认为是椭圆的长轴的端点到短轴的端点距离最大,这些认识是错误的,要注意将距离的平方表示为二次函数后,自变量的取值范围是一个闭区间,而不是全体实数上求最值..4.在平面直角坐标系中,,,点满足,,点为xOy ()3,0A ()0,3B -M OM xOA yOB =+1x y +=N曲线上的动点,则的最小值为( ).y =MNA .B .CD 11【答案】C【分析】首先确定点和的轨迹方程,以及画出两个轨迹图象,根据数形结合分析的最小M N MN值.【详解】,所以直线的方程是30103AB k --==-AB 3y x =-点满足,,点在直线上,M OM xOA yOB =+ 1x y +=∴M :3AB y x =-点在曲线上,N ()()22110x y y ++=≥如图,的最小值是点到直线的距离.MNO 3y x =-minMN=故选:C【点睛】关键点点睛:本题的关键是能观察,变形出点的轨迹方程是以为圆心,半径为1N ()1,0-的半圆,才能数形结合分析两点间距离的最小值.5.已知直三棱柱中,,,,则异面直线与111ABC A B C -120ABC ∠=︒2AB =11BC CC ==1AB 所成角的余弦值为( ).1BC A .BCD12【答案】B【分析】建立空间直角坐标系,利用向量方法求解即可.【详解】如图,以为空间直角坐标系原点建立如图空间直角坐标系,B 因为,,120ABC ∠=2AB =故,.1(AB = 1(0,1,1)BC = 设与所成角为,1AB 1BC θ则cosθ=故选:B 6.已知数列的前项和满足,则( ){}n a n n S 23n n S a =-6a =A .72B .96C .108D .126【答案】B【分析】利用与的关系,结合题意可得数列是以3为首项,公比为的等比数列,利n a n S {}n a 2q =用等比数列的通项公式即可得解.【详解】当时,,解得,1n =11123a S a ==-13a =当时,即,2n ≥1122n n n n n a S S a a --=-=-12n n a a -=所以数列是以3为首项,公比为的等比数列,{}n a 2q =所以.56196a a q ==故选:B.7.已知F 1、F 2分别为双曲线C :(a >0,b >0)的左、右焦点,点A 在双曲线上,且22221x y a b -=∠F 1AF 2=60°,若∠F 1AF 2的角平分线经过线段OF 2(O 为坐标原点)的中点,则双曲线的离心率为()A BCD【答案】B【解析】首先根据角平分线定理和双曲线的定义求得和的值,再结合余弦定理计算离心1AF 2AF 率.【详解】不妨设点在第一象限,的角平分线交轴于点,因为点是线段的中点,A 12F AF ∠x M M 2OF 所以,根据角平分线定理可知,又因为,所以,12:3:1F M MF =1231AF AF =122AF AF a-=13AF a=,由余弦定理可得,所以,所以2AF a =22221492372c a a a a a =+-⨯⨯⨯=2274c a=c e a ==故选:B【点睛】本题考查双曲线的离心率,双曲线的定义,三角形角平分线定理,重点考查转化思想,计算能力,属于中档题型.8.过抛物线焦点F 的直线交抛物线于A ,B 两点,交x 轴于C 点,,则24x y =2BF CB = ( )||||AF BF =A .B .C .3D .5383103【答案】C【分析】设,由求得,再设出直线方程,代入抛物线方1122(,),(,),(,0)A x y B x y C m 2BF CB =2y AB 程后应用韦达定理得,求得,由焦半径公式求得焦半径比值.12y y 1y 【详解】由题意,设,(0,1)F 1122(,),(,),(,0)A x y B x y C m 由,得,所以,,2BF CB = 2222(,1)2(,)x y x m y --=-2212y y -=213y =设直线方程为,由得,AB (1)x t y =-2(1)4x t y x y =-⎧⎨=⎩2222(24)0t y t y t -++=所以,所以,121y y =13y =.1213131113AF y BF y ++===++故选:C .【点睛】结论点睛:本题考查直线与抛物线相交,考查焦点弦性质.设是抛物线1122(,),(,)A x y B x y 的焦点弦的端点,则,,如果抛物线方程是,则有,22y px =212y y p =-2124p x x =22x py =212x x p =-.2124p y y =二、多选题9.已知为虚数单位,则下列选项中正确的是( )i A .复数的模为5;34i z =+B .复数,则在复平面上的点在第四象限34i z =+z C .复数是纯虚数,则或()()2341imm m +-+-1m =4m =-D .若,则的最大值为1z =1iz ++1【答案】ABD【分析】对于A ,直接求复数的模判断;对于B ,先求出再判断;对于C ,由实部为零虚部不为z 零求解;对于D ,利用复数的几何意义求解【详解】解:对于A ,因为,所以A 正确;34i z =+5=对于B ,由,得,则在复平面上的点在第四象限,所以B 正确;34i z =+34i z =-z 对于C ,因为复数是纯虚数,所以,解得,所以C 错()()2341i m m m +-+-234010m m m ⎧+-=⎨-≠⎩4m =-误;对于D ,由,可知在复平面上表示的点在单位圆上,表示在复平面上单位圆上的点1z =z 1iz ++到点的距离,所以的最大值为,所以D 正确,(1,1)--1i z ++11=故选:ABD10.(多选)如图,在棱长为的正方体中,分别为的中点,则11111ABCD A B C D -E F ,1BB CD ,( )A .直线与的夹角为B .平面平面1AD BD 60AED ⊥11A FDC .点到平面D .若正方体每条棱所在直线与平面所成的角相等,1C 11AB D α则截此正方体所得截面只能是三角形和六边形α【答案】ABD【分析】作平行直线求出异面直线夹角判断A ;利用线面垂直、面面垂直的判定推理判断B ;利用等体积法计算判断C ;分析截面形状判断D 作答.【详解】在棱长为的正方体中,连接,如图,11111ABCD A B C D -111,AB BD 对角面是矩形,有,即为直线与所成角或其补角,11BDD B 11//BD B D 11AD B ∠1AD BD 而,则,即直线与的夹角为,A正确;1111AB B D AD ===1160AD B ∠= 1AD BD 60 在正方体中,取AB 中点G ,连接,如图,1111ABCD A B C D -,1A GFG 因F 为CD 中点,有,又平面,平面,则,11////FG AD A D 11A D ⊥11ABB A AE ⊂11ABB A 11A D AE ⊥在正方形中,,即,11ABB A 111tan tan 2AG BE AA G BAE AA AB ∠====∠1AA G BAE ∠=∠则,即有,而平面11190BAE AGA AA G AGA ∠+∠=∠+∠=1A G AE ⊥1111111,,A D A G A A D A G =⊂ ,11A D FG 于是得平面,又平面,因此平面平面,B 正确;⊥AE 11A D FG AE ⊂AED AED ⊥11A FD 在棱长为的正方体中,连接,如图,11111ABCD A B C D -11111A C B D O ⋂=显然是中点,于是得点到平面的距离等于点到平面的距离h ,1O 11A C 1C 11AB D 1A 11AB D由得:,解得C 不正确;111111A AB D A A B D V V --=1111111133AB D A B D S h S AA ⋅=⋅ 221112h =⨯⨯h 在正方体中,,,1111ABCD A B C D -1111//////AD BC B C A D 1111//////AB DC D C A B ,1111//////BB CC DD AA 三棱锥为正三棱锥,有与平面所成角都相等,则平面与正方体111A AB D -11111,,A A A B A D 11AB D 11AB D 的每条棱所成角都相等,由正方体的结构特征不妨令平面与直线垂直,而平面与垂直,依题意平面与平α1A C 11AB D 1A C α面平行或重合,11AB D 如图,连接,,平面,平面,有平面,11,,BC BD C D 11//BD B D 11B D ⊂11AB D BD ⊄11AB D //BD 11AB D同理平面,而平面,则有平面平面,1//BC 11AB D 11,,BD BC B BD BC ⋂=⊂1BC D 1//BC D 11AB D 当平面从点向移动(含不含)或从点D 向C 移动(含D 不含C )过程中,平面截此α1A 1B 1B 1A α正方体所得截面是三角形,当平面在平面与平面之间时,平面与正方体的六个面都相交,截面为六边形,Dα11AB D 1BC D α正确.故选:ABD 11.已知数列的前n 项和为,,则( ){}n a n S 21n S n an =++A .是等差数列{}n a B .不是等差数列{}n a C .若是递增数列,则a 的取值范围是{}n S [2,)-+∞D .若是递增数列,则a 的取值范围是{}n S (3,)-+∞【答案】BD【分析】利用等差数列的前n 项和为一元二次函数且没有常数项,可判断不是等差数列; 利用{}n a 是递增数列对于恒成立,可解出的取值范围.{}n S 10n n S S +->*n ∈N a 【详解】对于AB:等差数列的前n 项和为对应的函数为211(1)()222n n n d d dS na n a n -=+=+-为一元二次函数且没有常数项,因为,有常数项.所以不是等2(),(0)f x ax bx a =+≠21n S n an =++{}n a 差数列.故B 正确.对于CD: 因为,所以.若是递增数列,则21n S n an =++21(1)(1)1n S n a n +=++++{}n S 221(1)(1)1(1)210n n S S n a n n an a n +=++++-++=++>-*21,a n n N ⇒>--∈则.故D 正确.3a >-故选:BD.【点睛】本题考查等差数列的前n 项和公式性质与递增数列的性质.属于基础题.12.如图,,是双曲线:与椭圆的公共焦点,点是,在第一象限内的1F 2F 1C 2213y x -=2C A 1C 2C 公共点,设方程为,则下列说法正确的是( )2C ()222210,0x y a b a b +=>>A .224a b +=B .的内切圆与轴相切于点12AF F △x ()1,0C .若,则的离心率为121F F AF =2C 23D .若,则的方程为12AF AF ⊥2C 22173x y +=【答案】BCD【分析】对于A ,根据题意可得,从而可进行判断,对于B ,根据双曲线的性质和内切圆124F F =的性质分析计算,对于C ,由已知结合双曲线的定义可求出,再利用椭圆的定义可求出,12,AF AF a 从而可求出离心率,对于D ,利用勾股定理和双曲线的性质列方程可求出,从而可12212AF AF ⋅=求出,进而可求出椭圆方程.12AF AF +【详解】由双曲线的方程,可知,所以,故A 不正确;124F F =224a b -=由双曲线的定义,可知,设切点为,由内切圆的性质,可得122AF AF -=B ,又,所以,故的内切圆与轴相12122AF AF F B BF -=-=12124F F F B BF =+=13F B =12AF F △x 切于点,(双曲线的焦点三角形的内切圆与轴相切于点).故B ()1,0()222210,0x y a b a b -=>>x (),0a 正确;因为,,所以,所以,即,所以的121F F AF =122AF AF -=22AF =1226AF AF a +==3a =2C 离心率为,故C 正确.23因为,所以,又,所以12AF AF ⊥221216AF AF +=122AF AF -=,即,()22212121224AFAF AF AF AF AF -=+-=12212AF AF ⋅=所以,所以()222121212228AF AF AF AF AF AF +=++=122AF AF a +==所以,所以,椭圆的方程为.故D 正确.a =2c =2223b a c =-=2C 22173x y +=故选:BCD三、填空题13.在如图所示实验装置中,正方形框架的边长都是1,且平面平面,活动弹子ABCD ⊥ABEF 分别在正方形对角线,上移动,则长度的最小值是___________.,M N AC BF MN【分析】将问题转化为异面直线与之间距离的求解问题,以为原点建立空间直角坐标系,AC BF B 根据异面直线间距离的空间向量求法可求得结果.【详解】是异面直线,上两点,的最小值即为两条异面直线间距离.,M N AC BF MN ∴d 平面平面,,平面平面,ABCD ⊥ABEF AB BC ⊥ABCD ⋂ABEF AB =平面,又,则以为坐标原点可建立如图所示的空间直角坐标系,BC ∴⊥ABEF AB BE ⊥B 则,,,,()1,0,0A ()0,0,0B ()1,1,0F ()0,0,1C ,,,()1,0,1AC →∴=-()1,1,0BF →=()1,0,0AB →=设异面直线,的公垂向量,AC BF (),,n x y z →=则,令,则,,,0AC n x z BF n x y ⎧⋅=-+=⎪⎨⋅=+=⎪⎩ 1x =1y =-1z =()1,1,1n →∴=-,即.AB nd n →→→⋅===MN 【点睛】本题考查空间向量法求解异面直线间距离的问题,关键是能够将两异面直线上点的连线的最小值问题转化为异面直线间距离的求解问题.14.已知等比数列满足,,则使得取得最小值的为______.{}n a 13827a a -=-2489a a -=-12n a a a n 【答案】3或4【分析】根据等比数列的通项公式求出,从而求出,再利用等比数列的通项公式即可求3q =1127a =解.【详解】设公比为,则,q 24133a a q a a -==-∴,1318827a a a -=-=-∴,,,,…,1127a =219a =313a =41a =∴或4时,取得最小值.3n =12n a a a 故答案为:3或415.在公差为的等差数列中, ,且成等比数列, 则______________() 0d d ≠{}n a 11a =-2412,,a a a d =【答案】3【解析】根据等差数列的通项公式,用表示出,再根据成等比数列,列式即可d 2412,,a a a 2412,,a a a 求解.【详解】因为,所以,1(1)1(1)n a a n d n d =+-=-+-24121,13,111a d a d a d =-+=-+=-+而成等比数列,所以,解得或(舍去).2412,,a a a 13111113d d dd -+-+=-+-+3d =0d =故答案为:3.【点睛】本题主要考查等差数列的性质以及等比数列的定义的应用,属于基础题.四、双空题16.已知椭圆,焦点,,若过的直线和圆22221(0)x y a b a b +=>>1(,0)F c -2(,0)F c (0)c >1F 相切,与椭圆在第一象限交于点P ,且轴,则该直线的斜率是22212x c y c ⎛⎫-+=⎪⎝⎭2PF x ⊥___________,椭圆的离心率是___________.【答案】【分析】不妨假设,根据图形可知,,再根据同角三角函数基本关系即可求出2c =122sin 3PF F ∠=;再根据椭圆的定义求出,即可求得离心率.12tan k PF F =∠=a【详解】如图所示:不妨假设,设切点为,2c =B ,12112sin sin 3ABPF F BF A F A ∠=∠==12tan PF F ∠==所以, 由,所以,k =21212,24PF k F F c F F ===2PF=21121=sin PF PF PF F ⨯=∠于是,所以.122PF a PF +==a =c e a ===五、解答题17.已知是等差数列,是等比数列,且.{}n a {}n b 23111443,9,,b b a b a b ====(1)求的通项公式;{}n a (2)设,求数列的前n 项和.n n n c a b =+{}n c 【答案】(1)21n a n =-(2)2312n n -+【分析】(1)设等差数列的公差为,等比数列的公比为,列方程组求得,{}n a d {}n b q 11,3b q ==得到,根据,求得,,得到.13n n b -=11144,a b a b ==11a =2d =21n a n =-(2)由(1)得到,结合等差、等比数列的求和公式,即可求解.1(21)3n n c n -=-+【详解】(1)解:设等差数列的公差为,等比数列的公比为,{}n a d {}n b q由,解得,所以,2123139b b q b b q ==⎧⎨==⎩11,3b q ==1113n n n b b q --=⋅=又由,可得,所以,11144,a b a b ==141(141)27a d =+-⋅=11a =2d =所以.1(1)1(1)221n a a n d n n =+-⋅=+-⋅=-(2)解:由(1)知,,所以,21n a n =-13n n b -=1(21)3n n n n c a b n -=+=-+设数列的前n 项和为,{}n c n S 可得.()()21212(121)13312132n n n n n n n S a a a b b b n +---=+++++++=+=+- 18.已知正方形的边长为,沿将三角形折起到位置(如图),为三角形ABCD 2AC ACD PAC G 的重心,点在边上,平面.PAC E BC //GEPAB (1)若,求的值;CE EB λ=λ(2)若,求平面与平面所成锐二面角的余弦值.GE PA ⊥GEC PAC 【答案】(1)2;【分析】(1)连接CG 并延长交PA 于F ,连BF ,证得EG//BF 再借助三角形重心即可得解;(2)取AC 中点O ,连接OP ,OB ,证得OB ,OC ,OP 两两垂直,再建立空间直角坐标系,利用空间向量即可作答.【详解】(1)连接CG 并延长交PA 于F ,连BF ,如图:因平面,且平面,平面平面,则EG//BF ,//GE PAB GE ÌCBF CBF ⋂PAB BF =而为的重心,于是有,G PAC △2CE CG EB GF λ===所以的值为2;λ(2)由(1)知EG//BF ,而,则,又F 是PA 中点,于是得,GE PA ⊥BF PA ⊥2PB PA ==取AC 中点O ,连接OP ,OB ,因都是以AC 为斜边的等腰直角三角形,,PAC BAC,2224OB OP OB OP PB ==+==即是直角三角形,,而,,BOP △OB OP ⊥OC OP ⊥OC OB ^分别以射线OB ,OC ,OP 为x ,y ,z轴非负半轴建立空间直角坐标系,如图:点,则,(0,B C A P(0,F,((BC BF == 设平面CBF 的法向量,(,,)m x y z =,0000m BC m BF y z ⎧=⎧⋅=⎪⇒⎨⎨⋅==⎩⎪⎩ 令,则,即,1x =1,3y z ==(1,1,3)m = 而平面,即平面的法向量为,GE ÌCBF GEC (1,1,3)m = 又OB ⊥平面PAC ,即平面的法向量,PAC n OB == 平面与平面所成锐二面角为,GEC PAC θ则cos |cos ,|||||||m n m n m n θ⋅=〈〉===⋅ 所以平面与平面GEC PAC 19.已知圆,动点,线段与圆交于点,轴,垂()22:11F x y +-=(),M x y ()0y ≥FM F N MH x ⊥足为,.H MN MH =(1)求动点的轨迹的方程;M C (2)设为曲线上的一点,过点作圆的两条切线,分别为两切线的斜率,()()000,2P x y y >C P F 12,k k 若,求点的坐标.12311k k =P 【答案】(1)(2)24x y =()±【分析】利用抛物线的概念及标准方程直接得结论()1;设过点P 的切线方程为,即,()2()00y y k x x -=-000kx y y kx -+-=则圆心到切线的距离为,化简后利用根与系数的关系即可求解.()0,1F 1d 【详解】圆F 的圆心为,半径为1,()1 ()0,1F ,1MF MN ∴=+又轴,垂足为H ,,MH x ⊥MN MH =动点到点等于到直线的距离.∴()(),0M x y y ≥()0,1F 1y =-故动点的轨迹是以为焦点的抛物线,()(),0M x y y ≥()0,1F 则,12p =,2p ∴=则动点M 的轨迹C 的方程是;24x y =设过点P 的切线方程为,即,()2()00y y k x x -=-000kx y y kx -+-=则圆心到切线的距离为,()0,1F 1d 化简得,,()()2220000012120x k x y k y y ---+-=两切线斜率分别为,,1k 2k ,200122021y y k k x -∴=-由题设知,,又为曲线C 上的一点,2002023111y y x -=-()00,P x y由知,,()12004x y =,即,2000234111y y y -∴=-200113430y y -+=解得,或,0111y =03y =,02y > ,则03y ∴=0x =±点P 的坐标为.∴()±【点睛】本题考查了抛物线的概念及标准方程和定点与定值问题.属于中档题.20.已知椭圆的右顶点为A ,上顶点为B ,O 为坐标原点,点O 到直线AB 的22221(0)x y a b a b +=>>,的面积为1.OAB (1)求椭圆的标准方程;(2)直线l 与椭圆交于C ,D 两点,若直线l ∥直线AB ,设直线AC ,BD 的斜率分别为,证明:12,k k 为定值.12k k ⋅【答案】(1)2214x y +=(2)证明见解析【分析】(1)用a ,b 表示出直线AB 的方程,根据点O 到直线AB 的距离及的面积,求得OAB a ,b ,即可得解;(2)设直线l 的方程为,C (x 1,y 1),D (x 2,y 2),与椭圆方程联立,利用根与系数的关12y x t =-+系,得利用斜率公式得,化简可得定值.1212,y y y y +121121222-=-y y y k k x x x 【详解】(1)解:直线AB 的方程为,1x y a b +=即bx +ay -ab =0,因为的面积为1,所以,即ab =2.OAB 112ab =解得a =2,b =1,所以椭圆的标准方程为.2214x y +=(2)证明:直线AB 的斜率为,设直线l 的方程为,C (x 1,y 1),D (x 2,y 2),12-12y x t =-+代入,得2y 2-2ty +t 2-1=0,2214x y +=依题意得,Δ>0,则,212121,2t y y t y y -+==所以,1212112121221·22y y y y y k k x x x x x --==--因为12212224()()4()-=----x x x t y t y t y 2121224()⎡⎤=-++-+⎣⎦t t y y y y t y 2121212121221214()()(()()4().⎡⎤=+-+++-++=-⎣⎦y y y y y y y v y y y y y y 所以为定值.1214k k =【点睛】求定值问题常见的方法有两种:(1)从特殊入手,求出定值,再证明这个值与变量无关.(2)直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.21.已知数列的前项和为,且,,.{}n a n n S 15a =-22a =-()25n n S n a =-(1)求,的值;3a 4a (2)求数列的通项公式;{}n a (3)若数列为单调递增数列,求实数的取值范围.2n n n b S λ=-λ【答案】(1);;(2);(3).31a =44a =38n a n =-12⎛⎫+∞ ⎪⎝⎭【分析】(1)令代入已知等式计算;3,4=n (2)在中由得的递推关系,在此关系中用替换后两式()25n n S n a =-1(2)n n n a S S n -=-≥n a 1n +n 相减(消去常数项),得数列是等差数列,从而可得通项公式;{}n a (3)求出,由恒成立,得参数范围.n b 1n n b b +>【详解】解:(1)令得,故;3n =()()332735a a -+=-31a =令得,故.4n =()()442645a a -+=-44a =(2),()25n n S n a =-当时,,2n ≥()()11215n n S n a --=--相减得,()()1215n n n a n a --=-+将用代入得,n 1n +()115n n n a na +-=+相减得,,112n n n a a a -+=+2n ≥故数列为等差数列,.{}n a ()51338n a n n =-+-⨯=-(3)由数列为单调递增数列得:2n n n b S λ=-恒成立,,()12350n n n b b n λ+-=-->352n n λ->令,,352n n n C -=111323583222n n n n n n n n C C +++----=-=…,12345C C C C C <<>>的最大值为,n C 312C =故实数的取值范围为.λ12⎛⎫+∞ ⎪⎝⎭22.如图,在三棱柱中,,,,111ABC A B C -AB AC ⊥1AC BB ⊥12AB A B AC ===1BB =(Ⅰ)求证:平面;1A B ⊥ABC (Ⅱ)若是棱的中点,求直线与平面所成角的正弦值.P 11B C 1BB PAB【答案】(Ⅰ)见解析(Ⅱ【分析】(Ⅰ)根据题中的条件,利用线面垂直的判定定理,可证得平面,进而证得AC ⊥11ABB A ,利用勾股定理,可证得,利用线面垂直的判定定理,可证得平面,1AC A B ⊥1A B AB ⊥1A B ⊥ABC证得结果;(Ⅱ)利用(Ⅰ)的结论,建立空间直角坐标系,利用空间向量,求得线面角的正弦值,得到结果.【详解】(Ⅰ)证明:∵在三棱柱中,,,又,111ABC A B C -AB AC ⊥1AC BB ⊥1AB BB B ⋂=∴平面,又平面,∴,AC ⊥11ABB A 1A B ⊂11ABB A 1AC A B ⊥∵∴1BB =1AA =∵,∴,∴,12AB A B ==22211AB A B AA +=1A B AB ⊥又,∴平面.AC AB A ⋂=1A B ⊥ABC (Ⅱ)解法一:由(Ⅰ)知,直线,,两两互相垂直,如图,以为原点,分别以11A C 11A B 1BA 1A ,,所在直线为,,轴,建立空间直角坐标系,11A C 11A B 1BA x y z 1A xyz -则,,,()10,0,0A ()1,1,0P ()0,0,2B -()10,2,0B ,,()110,2,0AB A B == ()1,1,2PB =--- 设平面的法向量,PAB (),,n x y z = 则,所以,,00n AB n PB ⎧⋅=⎨⋅=⎩ 020y x y z =⎧⎨---=⎩取,则,1z =()2,0,1n =-又,设直线与平面所成角为,()10,2,2BB = 1BB PAB θ则111sin cos ,n BB n BB n BB θ⋅==⋅==∴直线平面.1BB PAB 解法二:由(Ⅰ)知,直线,,两两互相垂直,以为原点,分别以、、11A C 11A B 1BA A AC AB所在直线为,,轴,建立如图所示空间直角坐标系,Az x y z A xyz-则,,,,,()0,0,0A ()10,2,2A ()1,3,2P ()0,2,0B ()10,4,2B ()12,2,2C ,,()110,2,0AB A B == ()1,1,2PB =--- 设平面的法向量,PAB (),,n x y z = 则,所以,,00n AB n PB ⎧⋅=⎨⋅=⎩ 020y x y z =⎧⎨---=⎩取,则,1z =()2,0,1n =-又,设直线与平面所成角为,()10,2,2BB = 1BB PAB θ则111sin cos ,n BB n BB n BB θ⋅==⋅==∴直线平面.1BB PAB 【点睛】该题考查的是有关立体几何的问题,涉及到的知识点有线面垂直的判定,应用向量法求线面角的正弦值,在解题的过程中,需要对定理的条件和结论要熟记,再者就是正确建立空间坐标系.。
山东省威海市乳山一中2015届高三上学期12月月考理科数学试题 Word版含答案
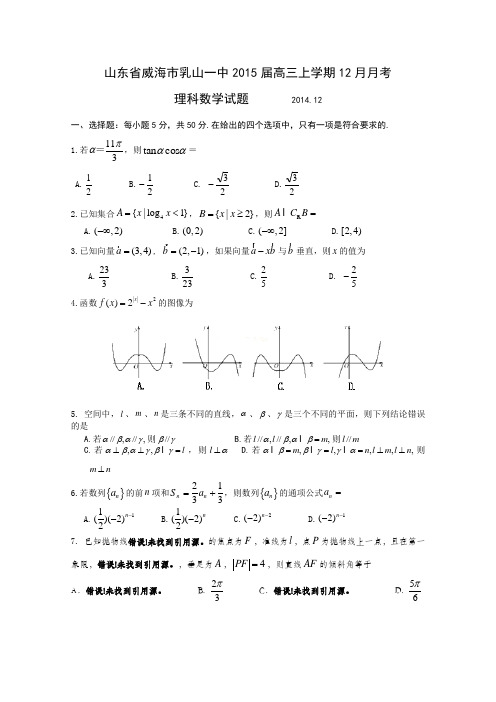
山东省威海市乳山一中2015届高三上学期12月月考理科数学试题 2014.12一、选择题:每小题5分,共50分.在给出的四个选项中,只有一项是符合要求的. 1.若113πα=,则ααcos tan = A.21 B.21- C. 23- D.232.已知集合4{|log 1}A x x =<,{|2}B x x =≥,则R A C B =A.(,2)-∞B.(0,2)C.(,2]-∞D.[2,4) 3.已知向量(3,4)a =, (2,1)b =-,如果向量a xb -与b 垂直,则x 的值为A.233B.323C.25D. 25-4.函数||2()2x f x x =-的图像为5. 空间中,l 、m 、n 是三条不同的直线,α、β、γ是三个不同的平面,则下列结论错误的是A.若//,//,αβαγ则//βγB.若//,//,,l l m αβαβ=则//l mC.若,,l αβαγβγ⊥⊥=,则l α⊥D.若,,,,,m l n l m l n αββγγα===⊥⊥则m n ⊥6.若数列{}n a 的前n 项和2133n n S a =+,则数列{}n a 的通项公式n a = A.11()(2)2n -- B.1()(2)2n- C.2(2)n -- D.1(2)n --7. 已知抛物线错误!未找到引用源。
的焦点为F ,准线为l ,点P 为抛物线上一点,且在第一象限,错误!未找到引用源。
,垂足为A ,4PF =,则直线AF 的倾斜角等于 A .错误!未找到引用源。
B.23π C .错误!未找到引用源。
D.56π8.已知0a >,,x y 满足约束条件13(3)x x y y a x ≥⎧⎪+≤⎨⎪≥-⎩,若2z x y =+的最小值为32,则a =A.14B.12C.1D.29.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且22coscos sin()sin 2A BB A B B --- 4cos()5A C ++=-.则cos A = A .45-B .45C .35D .35-10. 已知双曲线2222:1x y C a b-=的左、右焦点分别是12,F F ,正三角形12AF F 的一边1AF与双曲线左支交于点B ,且114AF BF =,则双曲线C 的离心率的值是( ) A .123+ B.13 C .1313+ D.12 二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡中相应题的横线上.11.321221(2)x dx x+⎰= . 12.已知圆锥的母线长为5cm ,侧面积为15πcm 2,则此圆锥的体积为 cm 3.13.在ABC ∆中,3BC BD =,AD AB ⊥,1AD =,则AC AD ⋅= . 14.已知命题p :x 2+2x -3>0;命题q1,若“非q 且p ”为真,则x 的取值范围是____________________.15.如图,在直三棱柱ABC-A 1B 1C 1中,底面为直角三角形。
2022-2023学年山东省威海乳山市第一中学高一上学期12月月考数学试题(解析版)
2022-2023学年山东省威海乳山市第一中学高一上学期12月月考数学试题一、单选题1.已知集合{}15A x N x =∈<<,那么下列关系正确的是( )A AB .3A ∈C .A ⊆D .{}3A ∈【答案】B【分析】根据元素与集合、集合与集合的关系进行判断即可. 【详解】集合{}{}152,3,4A x x =∈<<=N ,对选项A A ,故A 错误; 对选项B ,3A ∈,故B 正确;对选项C A ,故C 错误;对选项D ,{}3表示集合,{}3A ∈表示错误,故D 错误. 故选:B.2.设20.6a =,0.62b =,2log 0.6c =,则a ,b ,c 的大小关系为( ) A .a b c >> B .a c b >> C .b a c >> D .c a b >>【答案】C【分析】利用对数函数和指数函数的性质求解. 【详解】解:∵200.61<<,∴01a <<, ∵0.60221>=,∴1b >, ∵22log 0.6log 10<=,∴0c <, ∴b a c >>, 故选:C.3.若正数a 、b 满足4a b +≤,则下列各式中恒正确的是( )A .112ab ≥; B .111a b+≥;C 2≥;D .221162ab a b ≥-+.【答案】B【分析】由条件可得4ab ≤,可判断AC ,由11111()()14a b a b a b+≥++≥,可判断C ,由22162a a b b+≤-可判断D.【详解】∵0,0,4a b a b >>+≤,∴202a b ab +⎛⎫<≤ ⎪⎝⎭,当且仅当2a b ==时等号成立,∴2042a b ab +⎛⎫<≤≤ ⎪⎝⎭,∴114ab ≥,可取到14,故A 错误; ∵4a b +≤,∴1111111()()(2)(21444b a a b a b a b a b +≥++=++≥+=, 当且仅当2a b ==时取等号,故B 正确;2,故C 错误; 由222()2162a b ab ab a b =+-≤-+,∴2211612a b ab+≥-,取1a b ==,2211121426a b ab <-==+,221162ab a b ≥-+不成立,故D 错误.故选:B .4.某市工业生产总值2018年和2019年连续两年持续增加,其中2018年的年增长率为p ,2019年的年增长率为q ,则该市这两年工业生产总值的年平均增长率为( )A .2p q+; B .()()1112p q ++-; C D 1.【答案】D【分析】设出平均增长率,并根据题意列出方程,进行求解【详解】设该市2018、2019这两年工业生产总值的年平均增长率为x ,则由题意得:()()()2111x p q +=++,解得11x =,21x =,因为20x <不合题意,舍去故选D .5.已知某地区中小学生人数和近视情况分别如图1和如图2所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )A .100,20B .200,20C .100,10D .200,10【答案】B【详解】试题分析:由题意知,样本容量为()3500450020002%200++⨯=,其中高中生人数为20002%40⨯=,高中生的近视人数为4050%20⨯=,故选B.【考点定位】本题考查分层抽样与统计图,属于中等题.6.下列函数中,函数图象关于y 轴对称,且在()0,∞+上单调递增的是( ) A .2x y = B .21y x =- C .12y x = D .12log y x =【答案】B【分析】根据题意函数为偶函数且在()0,∞+上单调递增,对选项进行逐一验证. 【详解】函数图象关于y 轴对称,则函数为偶函数, 选项A. 2x y =不是偶函数,故排除.选项B. 21y x =-是偶函数,且在()0,∞+上单调递增,满足条件. 选项C. 12y x =不是偶函数,故排除.选项D. 12log y x =是偶函数,当0x >时,12log y x=是减函数,不满足.故选:B7.已知函数()242,1,,1,x x ax x f x a x ⎧-+<=⎨⎩对于任意两个不相等实数12,x x ,都有()()12120f x f x x x -<-成立,则实数a 的取值范围是( )A .10,2⎛⎤ ⎥⎝⎦B .13,25⎡⎤⎢⎥⎣⎦C .30,5⎛⎤ ⎥⎝⎦D .1,12⎡⎫⎪⎢⎣⎭【答案】B【分析】由题可得函数为减函数,根据单调性可求解参数的范围. 【详解】由题可得,函数()f x 为单调递减函数, 当1x <时,若()f x 单减,则对称轴21x a =≥,得:12a ≥, 当1x ≥时,若()f x 单减,则01a <<, 在分界点处,应满足142a a -+≥,即35a ≤,综上:1325a ≤≤ 故选:B8.Logistic 模型是常用数学模型之一,可用于流行病学领域.有学者根据所公布的数据建立了某地区新冠肺炎累计确诊病例()I t (t 的单位:天)的Logistic 模型:()1241etK I t -=+,其中K 为最大确诊病例数.当()00.05I t K =时,标志着已初步遏制疫情,则0t 约为()ln193≈( ) A .35 B .36 C .60 D .40【答案】B【分析】根据题意列出等式,整理化简可得0ln19124t =-,解出0t 即可. 【详解】由题意知,0()0.05I t K =,得01240.051t K K e-=+,整理,得012419t e -=,即0ln19124t =-, 解得036t ≈. 故选:B二、多选题9.已知p :[]2,3x ∃∈,220x a -+≤成立,则下列选项是p 的充分不必要条件的是( ) A .6a > B .6a < C .10a ≥ D .10a ≤【答案】AC【分析】依题意由存在量词命题为真求出参数的取值范围,再根据充分条件、必要条件的定义判断即可;【详解】解:由p :[]2,3x ∃∈,220x a -+≤成立,得当[]2,3x ∈时,()2min26a x ≥+=,即6a ≥.对于A ,“6a >”是“6a ≥”的充分不必要条件; 对于B ,“6a <”是“6a ≥”的既不充分也不必要条件; 对于C ,“10a ≥”是“6a ≥”的充分不必要条件; 对于D ,“10a ≤”是“6a ≥”的既不充分也不必要条件. 故选:AC.10.下列对各事件发生的概率判断正确的是()A .某学生在上学的路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是13,那么该生在上学路上到第3个路口首次遇到红灯的概率为427B .三人独立地破译一份密码,他们能单独译出的概率分别为15,13,14,假设他们破译密码是彼此独立的,则此密码被破译的概率为25C .甲袋中有8个白球,4个红球,乙袋中有6个白球,6个红球,从每袋中各任取一个球,则取到同色球的概率为12D .设两个独立事件A 和B 都不发生的概率为19,A 发生B 不发生的概率与B 发生A 不发生的概率相同,则事件A 发生的概率是29【答案】AC【分析】根据每个选项由题意进行计算,从而进行判断即可【详解】对于A,该生在第3个路口首次遇到红灯的情况为前2个路口不是红灯,第3个路口是红灯,所以概率为211413327⎛⎫-⨯= ⎪⎝⎭,故A正确;对于B,用A 、B 、C 分别表示甲、乙、丙三人能破译出密码,则1()5P A =,1()3P B =,1()4P C =,“三个人都不能破译出密码”发生的概率为42325345⨯⨯=,所以此密码被破译的概率为23155-=,故B 不正确;对于C,设“从甲袋中取到白球”为事件A,则82()123P A ==,设“从乙袋中取到白球”为事件B,则61()122P B ==,故取到同色球的概率为2111132322⨯+⨯=,故C 正确;对于D,易得()()P A B P BA =,即()()()()P A PB P B P A ⋅=,即()[1()]()[1()]P A P B P B P A -=-,∴()()P A P B =,又1()9P AB =,∴1()()3P A P B ==,∴2()3P A =,故D 错误故选AC【点睛】本题考查古典概型,考查事件的积,考查独立事件,熟练掌握概率的求解公式是解题关键 11.设()ln 26f x x x =+-,则下列区间中不存在零点的是( ) A .[1,2] B .[2,3] C .[3,4] D .[4,5]【答案】ACD【分析】判断(2)f 、(3)f 的符号,根据零点存在定理即可判断函数零点所在区间. 【详解】(2)ln 220f =-<,(3)ln30f =>,(2)(3)0f f ∴<,函数()ln 26f x x x =+-的零点位于[2,3].故选:ACD12.已知函数()21xf x =-,实数a ,b 满足()()f a f b =()a b <,则( )A .222a b +>B .a ∃,b ∈R ,使得01a b <+<C .222a b +=D .0a b +<【答案】CD【分析】根据函数解析式,作函数的图象,根据图象的特征,可得选项A 、C 的正误,根据基本不等式,可得选项B 、D 的正误.【详解】画出函数()21xf x =-的图象,如图所示.由图知1221a b -=-,则222a b +=,故A 错,C 对.由基本不等式可得22222222a b a b a b +=+>⋅=,所以21a b +<,则0a b +<,故B 错,D 对.故选:CD .三、填空题13.已知函数()2f x ax bx c =++,满足不等式()0f x <的解集为()(),2,t -∞-⋃+∞,且()1f x -为偶函数,则实数t =________. 【答案】0【分析】根据偶函数定义,可得20b a -=,然后根据二次不等式的解集得到二次函数的两个零点为2,t -,然后结合韦达定理,即可解出0=t【详解】根据解集易知:a<0 ,()1f x -为偶函数,可得:()()()()221112f x a x b x c ax b a x a b -=-+-+=+-+-则有:20b a -=易知20ax bx c ++=的两根为,2t -,则根据韦达定理可得:2bt a-=-解得:0=t 故答案为:0 14.若函数()221x x f x a -+=在()1,3上递减,则函数2log (2)a y x x =-增区间________.【答案】(),0∞- 【分析】函数()221xx f x a -+=在()1,3上递减,利用复合函数的单调性可得a 的取值范围,进而可判断函数2log (2)a y x x =-增区间.【详解】设t y a =,则221t x x =-+,在()1,3上递增, 函数()221xx f x a -+=在()1,3上递减,t y a ∴=在()1,3上递减,可得01a <<∴函数2log (2)a y x x =-增区间,即22u x x =-的单调递减区间令220x x ->,解得2x >或0x < ∴函数2log (2)a y x x =-增区间为,0故答案为:,0【点睛】本题考查复合函数的单调性,考查指对函数的性质,属于中档题.15.将一枚质地均匀的骰子先后抛掷两次,若第一次朝上一面的点数为a ,第二次朝上一面的点数为b ,则函数221y ax bx =-+在(],2∞-上为减函数的概率是_______.【答案】14【解析】由函数221y ax bx =-+在(],2∞-上为减函数,得到2a b ≤,再结合古典概型及其概率的计算方法,即可求解.【详解】由题意,将一枚质地均匀的骰子先后抛掷两次,可得{}1,2,3,4,5,6a ∈,{}1,2,3,4,5,6b ∈ 又由函数221y ax bx =-+在(],2∞-上为减函数,则2ba≥,即2a b ≤, 当a 取1时,b 可取2,3,4,5,6; 当a 取2时,b 可取4,5,6; 当a 取3时,b 可取6,共9种, 又因为(),a b 的取值共36种情况, 所以所求概率为91364=. 故答案为:14.【点睛】本题主要考查了古典概型及其概率的计算公式的应用,其中解答中认真审题,合理利用古典概型及其概率的计算公式求解是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.16.已知函数131()31x x f x ++=+在20211[]202-,上的最大值与最小值分别为M ,m ,则M m +=________.【答案】4【分析】构造()()2g x f x =-是奇函数,由奇函数的对称性求解. 【详解】设()()2g x f x =-,[2021,2021]x ∈-, 13131()()223131x x x x g x f x ++-=-=-=++,()()2g x f x -=--=131331322()311313x x xx x xg x -+-++--=-==-+++, 所以()g x 是奇函数,又max max ()()2g x f x M ==-,min min ()()22g x f x m =-=-, 所以max min ()()40g x g x M m +=+-=,4M m +=. 故答案为:4.四、解答题17.一元二次不等式23208kx kx +-<对一切实数x 都成立的k 的取值集合为A ,函数()()2lg 56f x x x =-++的定义域为B .(1)求集合A ,B ;(2)记C A B =,{}5D x m x m =<<+,x C ∈是x D ∈的充分不必要条件,求m 的取值范围. 【答案】(1)(3,0]A =-,()1,6B =-; (2)(5,1]--.【分析】(1)讨论0k =和0k ≠两种情况,结合判别式法求出A ,由真数大于0求出B ; (2)根据题意C 是D 的真子集,进而求得答案.【详解】(1)对A ,若0k =,则308-<,满足题意;若0k ≠,则230Δ30k k k k <⎧⇒-<<⎨=+<⎩. 综上:30k -<≤,即(3,0]A =-.对B ,()225605601,6x x x x x -++>⇒--<⇒∈-,即()1,6B =-.(2)由(1),(1,0]C A B =-⋂=,因为x C ∈是x D ∈的充分不必要条件,所以C 是D 的真子集,于是15150m m m ≤-⎧⇒-<≤-⎨+>⎩,即(5,1]m ∈--. 18.函数()()22log 25f x x ax a =--在(],2-∞-上单调递减,()1425x x g x a a +=--.(1)求a 的取值范围; (2)当2,2x时,求()g x 的最小值.【答案】(1)[)24-,(2)答案见解析 .【分析】(1)二次函数与对数函数复合的单调性讨论;(2)二次函数与指数函数复合的最小值,由x 的取值范围得到指数函数的取值范围,再求二次函数的最小值.【详解】(1)设()225t x x ax a =-- ,则()()()222log 25log f x x ax a t x =--=⎡⎤⎣⎦由题意可得,()202t a ->⎧⎪⎨-≤⎪⎩,所以24a -≤<, 所以,a 的取值范围为[)24-,. (2)因为[]22x ∈-, ,所以22122244x -⎡⎤⎡⎤∈=⎣⎦⎢⎥⎣⎦,, . 又因为()()21242525x x x g x a a a a a +=--=--- ,若 1424xa a ⎡⎫∈=⎪⎢⎣⎭,,时,()g x 有最小值25a a --; 若112244x a ⎡⎫∈-=⎪⎢⎣⎭,,时,()g x 有最小值18816a -, 19.某中学有学生500人,学校为了解学生课外阅读时间,从中随机抽取了50名学生,收集了他们2018年10月课外阅读时间(单位:小时)的数据,并将数据进行整理,分为5组:[10,12),[12,14),[14,16),[16,18),[18,20],得到如图所示的频率分布直方图.(Ⅰ)试估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数;(Ⅱ)已知这50名学生中恰有2名女生的课外阅读时间在[18,20],现从课外阅读时间在[18,20]的样本对应的学生中随机抽取2人,求至少抽到1名女生的概率;(Ⅲ)假设同组中的每个数据用该组区间的中点值代替,试估计该校学生2018年10月课外阅读时间的平均数.【答案】(Ⅰ)150(Ⅱ)710(Ⅲ)14.68 【分析】(Ⅰ)由频率分布直方图求出课外阅读时间不小于16小时的样本的频率为0.30,由此能估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数;(Ⅱ)阅读时间在[18,20]的样本的频率为0.10.从而课外阅读时间在[18,20]的样本对应的学生人数为5.这5名学生中有2名女生,3名男生,设女生为A ,B ,男生为C ,D ,E ,从中抽取2人,利用列举法能求出至少抽到1名女生的概率;(Ⅲ)由频率分布直方图能估计该校学生2018年10月课外阅读时间的平均数.【详解】(Ⅰ)0.10×2+0.05×2=0.30,即课外阅读时间不小于16小时的样本的频率为0.30.因为500×0.30=150,所以估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数为150. (Ⅱ)阅读时间在[18,20]的样本的频率为0.05×2=0.10.因为50×0.10=5,即课外阅读时间在[18,20]的样本对应的学生人数为5.这5名学生中有2名女生,3名男生,设女生为A ,B ,男生为C ,D ,E ,从中抽取2人的所有可能结果是:(A ,B ),(A ,C ),(A ,D ),(A ,E ),(B ,C ),(B ,D ),(B ,E ),(C ,D ),(C ,E ),(D ,E ).其中至少抽到1名女生的结果有7个,所以从课外阅读时间在[18,20]的样本对应的学生中随机抽取2人,至少抽到1名女生的概率为p =710(Ⅲ)根据题意,0.08×2×11+0.12×2×13+0.15×2×15+0.10×2×17+0.05×2×19=14.68(小时). 由此估计该校学生2018年10月课外阅读时间的平均数为14.68小时.【点睛】本题考查频数、概率、平均数的求法,考查频率分布直方图、列举法等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.20.已知函数()2log 1a x f x x -=+为奇函数. (1)求实数a 的值;(2)若()()22log 430m x f x x -+++≤恒成立,求实数m 的取值范围. 【答案】(1)1a =(2)[)2,+∞【分析】(1)利用奇函数定义求出实数a 的值;(2)先求解定义域,然后参变分离后求出()()22log 23g x x x =--+的取值范围,进而求出实数m 的取值范围.【详解】(1)由题意得:()()f x f x -=-,即22log log 11a x a x x x+-=--+,解得:1a =±, 当1a =-时,101a x x -=-<+,不合题意,舍去, 所以1a =,经检验符合题意;(2)由101x x->+,解得:11x -<<,由2430x x ++>得:1x >-或3x <-, 综上:不等式中()1,1x ∈-,()()22log 430m x f x x -+++≤变形为()()2log 13m x x ⎡⎤≥-+⎣⎦,即()()2log 13m x x ⎡⎤≥-+⎣⎦恒成立,令()()()2222log 23log 14g x x x x ⎡⎤=--+=-++⎣⎦,当()1,1x ∈-时,()(),2g x ∈-∞, 所以2m ≥,实数m 的取值范围为[)2,+∞.21.习近平总书记在十九大报告中指出,“要着力解决突出环境问题,持续实施大气污染防治行动”.为落实好这一精神,市环保局规定某工厂产生的废气必须过滤后才能排放.已知在过滤过程中,废气中的污染物含量P (单位:毫克/升)与过滤时间t (单位:小时)之间的函数关系式为:0()ktP t P e -=(e 为自然对数的底数,0P 为污染物的初始含量).过滤1小时后检测,发现污染物的含量为原来的45. (1)求函数()P t 的关系式;(2)要使污染物的含量不超过初始值的11000,至少还需过滤几小时?(参考数据:lg 20.3≈) 【答案】(1)04()()5t P t P =(2)30【分析】(1)由题意代入点(1,45P 0),求得函数P (t )的解析式; (2)根据函数P (t )的解析式,列不等式求出t 的取值范围即可.【详解】解:(1)根据题设,得0045k P P e -=,45k e -∴= 所以,()045t P t P ⎛⎫= ⎪⎝⎭(2)由()004151000t P t P P ⎛⎫=≤ ⎪⎝⎭,得4151000t ⎛⎫≤ ⎪⎝⎭, 两边取以10为底的对数,并整理,得t (1﹣3lg2)≥3,∴t≥30因此,至少还需过滤30小时【点睛】本题考查了指数函数模型的应用问题,求指数型函数的解析式,指数型不等式的解法,是中档题.22.对于函数()f x ,若其定义域内存在实数x 满足()()f x f x -=-,则称()f x 为“伪奇函数”. (1)已知函数()21x f x x -=+,试问()f x 是否为“伪奇函数”?说明理由; (2)若幂函数()()()31n g x n xn -=-∈R 使得()()2g x f x m =+为定义在[]1,1-上的“伪奇函数”,试求实数m 的取值范围;(3)是否存在实数m ,使得()12423x x f x m m +=-⋅+-是定义在R 上的“伪奇函数”,若存在,试求实数m 的取值范围;若不存在,请说明理由.【答案】(1)不是;(2)5,14⎡⎤--⎢⎥⎣⎦;(3)1⎡⎣. 【分析】(1)先假设()f x 为“伪奇函数”,然后推出矛盾即可说明;(2)先根据幂函数确定出()g x 的解析式,然后将问题转化为“()222x x m -=-+在[]1,1-上有解”,根据指数函数的值域以及对勾函数的单调性求解出m 的取值范围;(3)将问题转化为“()()22644222x x x x m m ---=-+++在R 上有解”,通过换元法结合二次函数的零点分布求解出m 的取值范围.【详解】(1)假设()f x 为“伪奇函数”,∴存在x 满足()()f x f x -=-,2211x x x x ---∴=--++有解,化为220x +=,无解, f x 不是“伪奇函数”;(2)()()()31n g x n x n -=-∈R 为幂函数,2n ∴=,()g x x ∴=,()2x f x m ∴=+,()2x f x m =+为定义在[]1,1-的“伪奇函数”,∴22x x m m -+=--在[]1,1-上有解,∴()222x x m -=-+在[]1,1-上有解, 令12,22x t ⎡⎤=∈⎢⎥⎣⎦,∴12m t t ⎛⎫=-+ ⎪⎝⎭在1,22t ⎡⎤∈⎢⎥⎣⎦上有解, 又对勾函数1y t t =+在1,12⎡⎫⎪⎢⎣⎭上单调递减,在(]1,2上单调递增, 且12t =时,52y =,2t =时,52y =, min max 5112,2y y ∴=+==,1y t t ∴=+的值域为52,2⎡⎤⎢⎥⎣⎦, 52,22m ⎡⎤∴∈--⎢⎥⎣⎦,5,14m ⎡⎤∴∈--⎢⎥⎣⎦; (3)设存在m 满足,即()()f x f x -=-在R 上有解,()1212423423x x x x m m m m --++∴-⋅+-=--⋅+-在R 上有解,()()22644222x x x x m m --∴-=-+++在R 上有解,令[)222,x x t -+=∈+∞,取等号时0x =,()222622m t mt ∴-=--+在[)2,∞+上有解,222280t mt m ∴-+-=在[)2,∞+上有解(*), ()2244280m m ∆=--≥,解得m ⎡∈-⎣,记()22228h t t mt m =-+-,且对称轴t m =,当m ⎡⎤∈-⎣⎦时,()h t 在[)2,∞+上递增,若(*)有解,则()22222280h mt m =-+-≤,12m ⎡⎤∴∈⎣⎦,当(m ∈时,()h t 在[)2,m 上递减,在(),m +∞上递增,若(*)有解,则()222222880h m m m m m =-+-=-≤,即280m -≤,此式恒成立,(2,m ∴∈,综上可知,1m ⎡∈⎣.【点睛】关键点点睛:解答本题(2)(3)问题的关键在于转化思想的运用,通过理解“伪奇函数”的定义,将问题转化为方程有解的问题,利用换元的思想简化运算并完成计算.。
2020-2021学年山东省威海市乳山一中高三(上)第二次月考数学试卷(A卷)
2020-2021学年山东省威海市乳山一中高三(上)第二次月考数学试卷(A卷)试题数:22,总分:1501.(单选题,5分)若集合A={x|y= √8−4x },B={x|(3x+5)(2x-7)≤0},则A∩B=()A.[ 53,2]B.(-∞,- 53]C.[2,72]D.[- 53,2]2.(单选题,5分)△ABC的内角A,B,C所对的边分别为a,b,c,若acosB=bcosA,则△ABC形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等边三角形3.(单选题,5分)已知cos(π2−α)−3cosαsinα−cos(π+α)=2,则tanα=()A.-5B.- 23C. 12D. 154.(单选题,5分)已知向量a⃗ =(2,1),b⃗⃗ =(m,-1),且b⃗⃗⊥(2 a⃗−b⃗⃗),则m的值为()A.1B.3C.1或3D.45.(单选题,5分)已知函数f(x)是定义域为R的奇函数,且当x≥0时,f(x)=log2(x+1)+2x−a,则满足f(x2-3x-1)+2<0的实数x的取值范围是()A.(-3,0)B.(-1,0)C.(0,3)D.(1,2)6.(单选题,5分)设函数f(x)=mx2-mx-1,若对于x∈[1,3],f(x)>-m恒成立,则实数m的取值范围是())A. (−∞,17B.(1,+∞)C.(-∞,1)D. (1,+∞)77.(单选题,5分)若函数f(x)=x(x-c)2在x=2处有极大值,则常数c为()A.2B.6C.2或6D.-2或-68.(单选题,5分)中国古代数学名著《张丘建算经》中记载:“今有马行转迟,次日减半,疾七日,行七百里,问日行几何”.意思是:“现有一匹马行走的速度逐渐变慢,每天走的里程数是前一天的一半,连续走了7天,共走了700里,问每天走的里数各是多少?”根据以上叙述,该匹马第四天走的里数是()A. 700127B. 2800127C. 5600127D. 448001279.(多选题,5分)已知等差数列{a n}的前n项和为S n(n∈N*),公差d≠0,S6=90,a7是a3与a9的等比中项,则下列选项正确的是()A.a1=22B.d=-2C.当n=10或n=11时,S n取得最大值D.当S n>0时,n的最大值为2010.(多选题,5分)设向量 a ⃗ , b ⃗⃗ 满足| a ⃗ |=| b ⃗⃗ |=1,且| b ⃗⃗ -2 a ⃗ |= √5 ,则以下结论正确的是( ) A. a ⃗ ⊥ b ⃗⃗ B.| a ⃗ + b⃗⃗ |=2 C.| a ⃗ - b⃗⃗ |= √2 D.< a ⃗ , b ⃗⃗ >=60°11.(多选题,5分)下列命题正确的是( )A.“a >1”是“ 1a <1 ”的必要不充分条件B.命题“∃x 0∈(0,+∞),lnx 0=x 0-1”的否定是“∀x∈(0,+∞),lnx≠x -1”C.若a ,b∈R ,则 b a +a b ≥2√b a •a b =2D.设a∈R ,“a=1”,是“函数 f (x )=a−e x 1+ae x 在定义域上是奇函数”的充分不必要条件 12.(多选题,5分)设函数 f (x )=√3cos2x −sin2x ,则下列选项正确的是( )A.f (x )的最小正周期是πB.f (x )在[a ,b]上单调递减,那么b-a 的最大值是 π2C.f (x )满足 f (π6+x)=f (π6−x)D.y=f (x )的图象可以由y=2cos2x 的图象向右平移 11π12 个单位得到13.(填空题,5分)计算:log 2 √2− log 3 19 +( 827 ) −13 =___ . 14.(填空题,5分)已知函数y=Msin (ωx+φ)(M >0,0<φ<π)的图象关于直线 x =13 对称.该函数的部分图象如图所示,AC=BC= √22 ,C=90°,则f ( 12 )的值为___ . 15.(填空题,5分)记S n 为数列{a n }的前n 项和.若S n =2a n +1,则S 6=___ .16.(填空题,5分)已知△AOB 为等腰直角三角形,OA=1,OC 为斜边的高.(Ⅰ)若P 为线段OC 的中点,则 AP⃗⃗⃗⃗⃗⃗ • OP ⃗⃗⃗⃗⃗⃗ =___ . (Ⅱ)若P 为线段OC 上的动点,则 AP⃗⃗⃗⃗⃗⃗ • OP ⃗⃗⃗⃗⃗⃗ 的取值范围为___ .17.(问答题,10分)如图,在平面直角坐标系xOy 中,点A (1,0),点B 在单位圆上,∠AOB=θ(0<θ<π).(Ⅰ)若点B (- 35 , 45 ),求tan (θ+ π4 )的值;(Ⅱ)若( OA ⃗⃗⃗⃗⃗⃗ + OB ⃗⃗⃗⃗⃗⃗ )• OB ⃗⃗⃗⃗⃗⃗ = 95 ,求cos ( 2π3 -2θ).18.(问答题,12分)已知等差数列{a n }的前n 项和为S n ,公差为2,且a 1,S 2,S 4成等比数列.(1)求a 1,a 2,a 3;(2)设 b n =a n +2n ,求数列{b n }的前9项和.19.(问答题,12分)f (x )=2lnx+ 1x -mx (m∈R ). (1)当m=-1时,求曲线y=f (x )在点(1,f (1))处的切线方程;(2)若f (x )在(0,+∞)上为单调递减,求m 的取值范围.20.(问答题,12分)设函数 f (x )=sinx(√3cosx +sinx)−12 .(Ⅰ)求函数f (x )的递增区间;(Ⅱ)在△ABC中,a,b,c分别为内角A,B,C的对边,若f(B)=1,b=2,且b(2-cosA)=a(cosB+1),求△ABC的面积.21.(问答题,12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足条件:cosA a +cosCc=1b.(1)求证:sin2B=sinAsinC;(2)在数列{a n}中,a n=2n-1,且数列{1a n a n+1}的前n项和为2ncosB2n+1,求角B.22.(问答题,12分)已知函数f(x)=12x2−x+alnx(a>0).(1)讨论f(x)的单调性;(2)若f(x)存在两个极值点x1,x2,求证:f(x1)+f(x2)>−3−2ln24.2020-2021学年山东省威海市乳山一中高三(上)第二次月考数学试卷(A卷)参考答案与试题解析试题数:22,总分:1501.(单选题,5分)若集合A={x|y= √8−4x },B={x|(3x+5)(2x-7)≤0},则A∩B=()A.[ 53,2]B.(-∞,- 53]C.[2,72]D.[- 53,2]【正确答案】:D【解析】:可以求出集合A,B,然后进行交集的运算即可.【解答】:解:∵A={x|8-4x≥0}={x|x≤2},B={x|−53≤x≤72},A∩B=[−53,2].故选:D.【点评】:本题考查了描述法、区间的定义,一元二次不等式的解法,交集的运算,考查了计算能力,属于基础题.2.(单选题,5分)△ABC的内角A,B,C所对的边分别为a,b,c,若acosB=bcosA,则△ABC形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等边三角形【正确答案】:A【解析】:利用正弦定理化简已知的等式,移项后再利用两角和与差的正弦函数公式化简,得到sin(A-B)的值为0,由A和B都为三角形的内角,得出A-B的范围,进而利用特殊角的三角函数值得出A-B=0,即A=B,利用等角对等边可得a=b,即三角形为等腰三角形.【解答】:解:∵acosB=bcosA,由正弦定理可得:sinAcosB=sinBcosA,即sinAcosB-cosAsinB=sin(A-B)=0,又-π<A-B<π,∴A-B=0,即A=B,∴a=b,则△ABC的形状是等腰三角形,故选:A.【点评】:本题考查了三角形的形状判断,涉及的知识有正弦定理,两角和与差的正弦函数公式,以及正弦函数的图象与性质,根据三角函数值求角的大小,推出sin(A-B)=0 是解题的关键.3.(单选题,5分)已知cos(π2−α)−3cosαsinα−cos(π+α)=2,则tanα=()A.-5B.- 23C. 12D. 15【正确答案】:A【解析】:直接利用诱导公式的应用和同角三角函数的关系式的变换的应用求出结果.【解答】:解:cos(π2−α)−3cosαsinα−cos(π+α)=sinα−3cosαsinα+cosα=2,所以tanα−3tanα+1=2,解得tanα=-5.故选:A.【点评】:本题考查的知识要点:三角函数关系式的恒等变换,诱导公式的应用,同角三角函数关系式的变换,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.4.(单选题,5分)已知向量a⃗ =(2,1),b⃗⃗ =(m,-1),且b⃗⃗⊥(2 a⃗−b⃗⃗),则m的值为()A.1B.3C.1或3D.4【正确答案】:C【解析】:可求出2a⃗−b⃗⃗=(4−m,3),根据b⃗⃗⊥(2a⃗−b⃗⃗)即可得出b⃗⃗•(2a⃗−b⃗⃗)=0,进行数量积的坐标运算即可求出m的值.【解答】:解:2a⃗−b⃗⃗=(4−m,3);∵ b⃗⃗⊥(2a⃗−b⃗⃗);∴ b⃗⃗•(2a⃗−b⃗⃗)=m(4−m)−3=0;解得m=1或m=3.故选:C.【点评】:考查向量垂直的充要条件,向量减法、数乘和数量积的坐标运算.5.(单选题,5分)已知函数f(x)是定义域为R的奇函数,且当x≥0时,f(x)=log2(x+1)+2x−a,则满足f(x2-3x-1)+2<0的实数x的取值范围是()A.(-3,0)B.(-1,0)C.(0,3)D.(1,2)【正确答案】:C【解析】:根据题意,利用奇函数的性质可得f(0)=log2(1)+20-a=0,可得a=1,即可得函数f(x)的解析式,结合指数函数与对数函数的性质分析可得函数f(x)在[0,+∞)上为增函数,结合函数的奇偶性可得函数f(x)在R上为增函数,由此可以将f(x2-3x-1)+2<0转化为x2-3x<0,即可求解.【解答】:解:函数f(x)是定义域为R的奇函数,则有f(0)=0,即f(0)=log21+20-a=0,解得a=1,则当x≥0时,f(x)=log2(x+1)+2x-1,则有f(1)=log22+21-1=2,而函数y=log2(x+1)和函数y=2x-1都是增函数,则函数f(x)=log2(x+1)+2x-1在[0,+∞)上为增函数,又由函数f(x)是定义域为R的奇函数,则在区间(-∞,0]上也是增函数,故函数f(x)在R上为增函数,f(x2-3x-1)+2<0⇒f(x2-3x-1)+f(1)<0⇒f(x2-3x-1)<-f(1)⇒f(x2-3x-1)<f(-1)⇒x2-3x-1<-1⇒x2-3x<0,解得0<x<3,即x的取值范围为(0,3);故选:C.【点评】:本题考查函数奇偶性与单调性的综合应用,关键是利用函数的奇偶性求出a的值.6.(单选题,5分)设函数f(x)=mx2-mx-1,若对于x∈[1,3],f(x)>-m恒成立,则实数m的取值范围是())A. (−∞,17B.(1,+∞)C.(-∞,1)D. (1,+∞)7【正确答案】:B【解析】:函数在区间上恒成立问题,可转化为函数在给定区间上的最值问题,通过求解函数的最值,列出关于实数m的不等式,达到求解该题的目的.【解答】:解:(1)当m=0时,f(x)=-1>-m恒成立,解得m>1,不合题意;,f(x)在x∈[1,3]上是单调函数.(2)当m≠0时,该函数的对称轴是x= 12① 当m>0时,由于f(x)在[1,3]上单调递增,要使f(x)>-m在x∈[1,3]上恒成立,只要f(1)=-1>-m即可.解得m>1,故m>1;② 当m<0时,由于函数f(x)在[1,3]上是单调递减,要使f(x)>-m在x∈[1,3]上恒成立,只要f(3)=9m-3m-1>-m即可,,不合题意.解得m>17综上可知:实数m 的取值范围是(1,+∞).故选:B.【点评】:本题考查函数恒成立问题的解决思路和方法,考查函数与不等式的综合问题,考查学生的转化与化归的思想和方法,考查学生分析问题解决问题的能力.7.(单选题,5分)若函数f(x)=x(x-c)2在x=2处有极大值,则常数c为()A.2B.6C.2或6D.-2或-6【正确答案】:B【解析】:求出函数的导数,再令导数等于0,求出c 值,再检验函数的导数是否满足在x=2处左侧为正数,右侧为负数,把不满足条件的 c值舍去.【解答】:解:∵函数f(x)=x(x-c)2=x3-2cx2+c2x,它的导数为f′(x)=3x2-4cx+c2,由题意知,在x=2处的导数值为 12-8c+c2=0,∴c=6,或 c=2,又函数f(x)=x(x-c)2在x=2处有极大值,故导数值在x=2处左侧为正数,右侧为负数.)(x-2),不满足导数值在x=2处左侧为正数,右侧当c=2时,f′(x)=3x2-8x+4=3(x- 23为负数.当c=6时,f′(x)=3x2-24x+36=3(x2-8x+12)=3(x-2)(x-6),满足导数值在x=2处左侧为正数,右侧为负数.故 c=6.故选:B.【点评】:本题考查函数在某点取得极大值的条件:导数值等于0,且导数在该点左侧为正数,右侧为负数.8.(单选题,5分)中国古代数学名著《张丘建算经》中记载:“今有马行转迟,次日减半,疾七日,行七百里,问日行几何”.意思是:“现有一匹马行走的速度逐渐变慢,每天走的里程数是前一天的一半,连续走了7天,共走了700里,问每天走的里数各是多少?”根据以上叙述,该匹马第四天走的里数是()A. 700127B. 2800127C. 5600127D. 44800127【正确答案】:C【解析】:由题意可知,每天走的里数是以 12 为公比的等比数列,S 7=700,结合等比数列的求和公式及通项公式可求.【解答】:解:由题意可知,每天走的里数是以 12 为公比的等比数列, 由题意可得,S 7= a 1(1−127)1−12=700,故a 1=350×128127, ∴ a 4=a 1×q 3 = 350×128127 × 18 = 5600127 . 故选:C .【点评】:本题主要考查了等比数列的求和公式及通项公式在实际问题中的应用,属于基础试题.9.(多选题,5分)已知等差数列{a n }的前n 项和为S n (n∈N *),公差d≠0,S 6=90,a 7是a 3与a 9的等比中项,则下列选项正确的是( ) A.a 1=22 B.d=-2C.当n=10或n=11时,S n 取得最大值D.当S n >0时,n 的最大值为20 【正确答案】:BCD【解析】:由等差数列的求和公式和通项公式,结合等比数列的中项性质,解方程可得首项和公差,求得等差数列的通项a n 和S n ,由二次函数的最值求法和二次不等式的解法可得所求值.【解答】:解:等差数列{a n }的前n 项和为S n ,公差d≠0, 由S 6=90,可得6a 1+15d=90,即2a 1+5d=30, ①由a 7是a 3与a 9的等比中项,可得a 72=a 3a 9,即(a 1+6d )2=(a 1+2d )(a 1+8d ), 化为a 1+10d=0, ② 由 ① ② 解得a 1=20,d=-2,则a n =20-2(n-1)=22-2n ,S n = 12 n (20+22-2n )=21n-n 2, 由S n =-(n- 212 )2+4414,可得n=10或11时,S n 取得最大值110;由S n >0,可得0<n <21,即n 的最大值为20. 故选:BCD .【点评】:本题考查等差数列的通项公式和求和公式,以及等比数列的中项性质,考查方程思想和运算能力,属于中档题.10.(多选题,5分)设向量 a ⃗ , b ⃗⃗ 满足| a ⃗ |=| b ⃗⃗ |=1,且| b ⃗⃗ -2 a ⃗ |= √5 ,则以下结论正确的是( ) A. a ⃗ ⊥ b ⃗⃗ B.| a ⃗ + b ⃗⃗ |=2 C.| a ⃗ - b ⃗⃗ |= √2 D.< a ⃗ , b ⃗⃗ >=60° 【正确答案】:AC【解析】:由已知结合向量数量积的性质对各选项进行检验即可.【解答】:解:因为| a ⃗ |=| b ⃗⃗ |=1,且| b ⃗⃗ -2 a ⃗ |= √5 , 所以 b ⃗⃗2−4a ⃗•b ⃗⃗+4a ⃗2 =5,所以 a ⃗•b ⃗⃗ =0,故 a ⃗⊥b ⃗⃗ ,选项A 正确; 因为 (a ⃗+b ⃗⃗)2= a ⃗2+2a ⃗•b ⃗⃗+b ⃗⃗2 =2, 所以| a ⃗+b⃗⃗ |= √2 ,B 错误; 因为( a ⃗−b ⃗⃗ )2= a ⃗2−2a ⃗•b ⃗⃗+b ⃗⃗2 =2, 所以| a ⃗−b ⃗⃗ |= √2 ,C 正确; 因为 a ⃗⊥b⃗⃗ , 所以 <a ⃗,b⃗⃗> = π2 ,D 错误; 故选:AC .【点评】:本题主要考查了向量数量积的性质的简单应用,属于基础试题. 11.(多选题,5分)下列命题正确的是( ) A.“a >1”是“ 1a<1 ”的必要不充分条件B.命题“∃x 0∈(0,+∞),lnx 0=x 0-1”的否定是“∀x∈(0,+∞),lnx≠x -1”C.若a ,b∈R ,则 ba +ab ≥2√ba •ab =2D.设a∈R ,“a=1”,是“函数 f (x )=a−e x1+ae x 在定义域上是奇函数”的充分不必要条件 【正确答案】:BD【解析】:对于A:直接利用不等式的解法求出解集,进一步利用充分条件和必要条件的应用求出结果.对于B:直接利用命题的否定的应用判定结果;对于C:直接利用基本不等式的应用和不等式的成立的条件的应用判定结果;对于D:直接利用奇函数的性质的应用判定结果.【解答】:解:对于选项A:1a <1,整理得1−aa<0,即a(a-1)>0,解得a>1或a<0,所以“a>1”是“ 1a<1”的充分不必要条件,故A错误;对于B:命题“∃x0∈(0,+∞),lnx0=x0-1”的否定是“∀x∈(0,+∞),lnx≠x-1”故B正确;对于C:当ab>0时,ba +ab≥2√ba•ab=2,故C错误.对于D:设a∈R,“a=1”时“函数f(x)=a−e x1+ae x =1−e x1+e x在定义域上是奇函数”,当函数f(x)=a−e x1+ae x在定义域上是奇函数,利用f(-x)=-f(x),则a=±1,故“a=1”,是“函数f(x)=a−e x1+ae x在定义域上是奇函数”的充分不必要条件,故D正确.故选:BD.【点评】:本题考查的知识要点:不等式的解法和应用,命题的否定,基本不等式,函数的奇偶性,主要考查学生的运算能力和转换能力及思维能力,属于基础题.12.(多选题,5分)设函数f(x)=√3cos2x−sin2x,则下列选项正确的是()A.f(x)的最小正周期是πB.f(x)在[a,b]上单调递减,那么b-a的最大值是π2C.f(x)满足f(π6+x)=f(π6−x)D.y=f(x)的图象可以由y=2cos2x的图象向右平移11π12个单位得到【正确答案】:ABD【解析】:首先利用关系式的变换,把函数的关系式变形成余弦型函数,进一步求出函数的周期,函数的对称轴方程,确定ABC选项,最后利用函数的图象的平移变换的应用确定选项D.【解答】:解:函数f(x)=√3cos2x−sin2x =2cos(2x+ π6),对于选项A:函数的最小正周期为T=2π2=π.故选项A正确.对于选项B:f(x)在[a,b]上单调递减,所以b-a的最大值为T2=π2,故选项B正确.对于选项C:函数f(x)满足f(π6+x)=f(π6−x),即函数的对称轴方程为x=π6+x+π6−x2=π6,当x= π6时,函数f(π6)=2cos π2=0,故选项C错误.对于选项D:函数y=2cos2x的图象向右平移11π12个单位,得到f(x)=2cos(2x- 11π6)=2cos(2x+ π6),故选项D正确.故选:ABD.【点评】:本题考查的知识要点:三角函数关系式的变换,余弦型函数的性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题.13.(填空题,5分)计算:log2√2− log319 +(827)−13 =___ .【正确答案】:[1]4【解析】:利用指数与对数运算性质即可得出.【解答】:解:原式= 12 log22- log33−2 + (32)−3×(−13)= 12 -(-2)+ 32=4.故答案为:4.【点评】:本题考查了指数与对数运算性质,考查了推理能力与计算能力,属于基础题.14.(填空题,5分)已知函数y=Msin(ωx+φ)(M>0,0<φ<π)的图象关于直线x=13对称.该函数的部分图象如图所示,AC=BC= √22,C=90°,则f(12)的值为___ .【正确答案】:[1] √34【解析】:AC=BC= √22,C=90°,故AB=1,所以T=2,ω= 2πT= 2π2=π,M=|AC|sin π4=√2 2×√22= 12,又图象关干直线x=13对称,所以π×13+φ= π2+kπ,即φ= π6+kπ,(k∈Z),又0<φ<π,所以φ= π6 ,进而可以求f ( 12 )的值.【解答】:解:依题意,AC=BC= √22 ,C=90°,故AB=1,所以T=2,ω= 2πT = 2π2 =π, M=|AC|sin π4=√22×√22 = 12 , 又图象关干直线 x =13 对称,所以 π×13+ φ= π2+kπ ,即φ= π6+kπ ,(k∈Z ),又0<φ<π,所以φ= π6 ,所以f (x )= 12sin (πx +π6) ,所以f ( 12 )= 12sin (π×12+π6) = 12 sin 2π3 = √34 . 故答案为: √34 .【点评】:本题考查的知识要点:利用函数的图象求函数的解析式,及利用函数的解析式求函数的值,主要考查学生的应用能力.15.(填空题,5分)记S n 为数列{a n }的前n 项和.若S n =2a n +1,则S 6=___ . 【正确答案】:[1]-63【解析】:先根据数列的递推公式可得{a n }是以-1为首项,以2为公比的等比数列,再根据求和公式计算即可.【解答】:解:S n 为数列{a n }的前n 项和,S n =2a n +1, ① 当n=1时,a 1=2a 1+1,解得a 1=-1, 当n≥2时,S n-1=2a n-1+1, ② , 由 ① - ② 可得a n =2a n -2a n-1, ∴a n =2a n-1,∴{a n }是以-1为首项,以2为公比的等比数列, ∴S 6=−1×(1−26)1−2=-63,故答案为:-63【点评】:本题考查了数列的递推公式和等比数列的求和公式,属于基础题. 16.(填空题,5分)已知△AOB 为等腰直角三角形,OA=1,OC 为斜边的高. (Ⅰ)若P 为线段OC 的中点,则 AP⃗⃗⃗⃗⃗⃗ • OP ⃗⃗⃗⃗⃗⃗ =___ . (Ⅱ)若P 为线段OC 上的动点,则 AP⃗⃗⃗⃗⃗⃗ • OP ⃗⃗⃗⃗⃗⃗ 的取值范围为___ .【正确答案】:[1] −18; [2] [−18,0]【解析】:(Ⅰ)可以点O 为原点,直线OB ,OA 分别为x ,y 轴,建立平面直角坐标系,从而可求出向量 AP ⃗⃗⃗⃗⃗⃗ , OP ⃗⃗⃗⃗⃗⃗ 的坐标,然后进行向量数量积的坐标运算即可;(Ⅱ)可设P (x ,x ),并得出 x ∈[0,12] ,然后可得出 AP ⃗⃗⃗⃗⃗⃗=(x ,x −1),OP ⃗⃗⃗⃗⃗⃗=(x ,x) ,从而可得出 AP ⃗⃗⃗⃗⃗⃗•OP ⃗⃗⃗⃗⃗⃗=2x 2−x ,然后配方即可求出 AP ⃗⃗⃗⃗⃗⃗•OP ⃗⃗⃗⃗⃗⃗ 的值域,进而得出 AP ⃗⃗⃗⃗⃗⃗•OP ⃗⃗⃗⃗⃗⃗ 的取值范围.【解答】:解:(Ⅰ)如图,以O 为原点,边OB ,OA 所在的直线分别为x ,y 轴,建立平面直角坐标系,则:O (0,0),A (0,1),B (1,0),C ( 12,12 ), P (14,14) ,∴ AP ⃗⃗⃗⃗⃗⃗=(14,−34),OP ⃗⃗⃗⃗⃗⃗=(14,14) , ∴ AP ⃗⃗⃗⃗⃗⃗•OP ⃗⃗⃗⃗⃗⃗=116−316=−18;(Ⅱ)∵P 是OC 上的动点,∴设P (x ,x ),x∈ [0,12] , AP ⃗⃗⃗⃗⃗⃗=(x ,x −1),OP ⃗⃗⃗⃗⃗⃗=(x ,x) , ∴ AP ⃗⃗⃗⃗⃗⃗•OP ⃗⃗⃗⃗⃗⃗ = 2x 2−x =2(x −14)2−18 ,∴ x =14时, AP ⃗⃗⃗⃗⃗⃗•OP ⃗⃗⃗⃗⃗⃗ 取最小值 −18 ;x=0时, AP ⃗⃗⃗⃗⃗⃗•OP ⃗⃗⃗⃗⃗⃗ 取最大值0,∴ AP ⃗⃗⃗⃗⃗⃗•OP ⃗⃗⃗⃗⃗⃗ 的取值范围为 [−18,0] . 故答案为:(Ⅰ) −18 ;(Ⅱ) [−18,0] .【点评】:本题考查了通过建立平面直角坐标系,利用坐标解决向量问题的方法,中点坐标公式,向量坐标的数量积的运算,配方求二次函数值域的方法,考查了计算能力,属于基础题. 17.(问答题,10分)如图,在平面直角坐标系xOy 中,点A (1,0),点B 在单位圆上,∠AOB=θ(0<θ<π).(Ⅰ)若点B (- 35, 45),求tan (θ+ π4)的值; (Ⅱ)若( OA ⃗⃗⃗⃗⃗⃗ + OB ⃗⃗⃗⃗⃗⃗ )• OB⃗⃗⃗⃗⃗⃗ = 95,求cos ( 2π3-2θ).【正确答案】:【解析】:(Ⅰ)由题意利用任意角的三角函数的定义,求得tanθ的值,再利用两角和的正切公式求得tan (θ+ π4)的值;(Ⅱ)由题意利用两个向量的数量积的运算,以及二倍角的正弦公式、两角差的余弦公式求得cos ( 2π3 -2θ)的值.【解答】:解:(Ⅰ)由题意利用任意角的三角函数的定义可得tanθ= 45−35=- 43 ,∴tan (θ+ π4 )= tanθ+11−tanθ =- 17 .(Ⅱ)∵( OA ⃗⃗⃗⃗⃗⃗ + OB ⃗⃗⃗⃗⃗⃗ )• OB ⃗⃗⃗⃗⃗⃗ = OA ⃗⃗⃗⃗⃗⃗ • OB ⃗⃗⃗⃗⃗⃗ + OB ⃗⃗⃗⃗⃗⃗2 =cosθ+1= 95 ,∴cosθ= 45,∴sinθ= √1−cos 2θ = 35, ∴sin2θ=2sinθcosθ= 2425 ,cos2θ=2cos 2θ-1= 725,∴cos ( 2π3 -2θ)=cos 2π3 cos2θ+sin 2π3 sin2θ=- 12 • 725 + √32 • 2425 = 24√3−750.【点评】:本题主要考查任意角的三角函数的定义,两角和差的三角公式,两个向量的数量积的运算,以及二倍角的正弦公式的应用,属于中档题.18.(问答题,12分)已知等差数列{a n }的前n 项和为S n ,公差为2,且a 1,S 2,S 4成等比数列.(1)求a 1,a 2,a 3;(2)设 b n =a n +2n ,求数列{b n }的前9项和.【正确答案】:【解析】:(1)先由题设求出等差数列{a n }的首项a 1,进而求得a 2,a 3;(2)先利用(1)求得a n ,进而求得b n ,再利用分组求和的办法求得数列{b n }的前9项和.【解答】:解:(1)由a 1,S 2,S 4成等比数列得 S 22=a 1S 4 ,化简得 (2a 1+d )2=a 1(4a 1+6d ) ,又d=2,解得a 1=1,所以a 2=3,a 3=5;(2)由(1)可知数列{a n }的通项公式a n =1+2(n-1)=2n-1, 所以 b n =2n −1+2n , 设{2n }的前n 项和为T n ,则 T n =2×(1−2n )1−2=2n+1−2 ,又 S n =n (1+2n−1)2=n 2 ,所以{b n }的前9项和为S 9+T 9=81+1024-2=1103.【点评】:本题主要考查等差、等比数列基本量的计算及分组求和法在数列求和中的应用,属于中档题.19.(问答题,12分)f(x)=2lnx+ 1x-mx(m∈R).(1)当m=-1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)若f(x)在(0,+∞)上为单调递减,求m的取值范围.【正确答案】:【解析】:(1)求得m=-1时,f(x)的导数,可得切线的斜率和切点,由点斜式方程可得切线的方程;(2)由题意可得f′(x)=2x −1x2−m≤0在x∈(0,+∞)恒成立,由参数分离和二次函数的最值求法,可得所求范围.【解答】:解:(1)当m=-1时,f(x)=2lnx+1x+x,∴ f′(x)=2x −1x2+1,∴f(1)=2,f'(1)=2,故曲线y=f(x)在点(1,f(1))处的切线方程是:y-2=2(x-1),即2x-y=0;(2)若f(x)在(0,+∞)上单调递减,则f′(x)=2x −1x2−m≤0在x∈(0,+∞)恒成立,即m≥2x −1x2在(0,+∞)恒成立,令g(x)=2x −1x2,(x>0),则m≥g(x)max,∵ g(x)=−(1x −1)2+1,∴当1x=1,即x=1时,有g(x)max=1,故m≥1.【点评】:本题考查导数的运用:求切线的方程和单调性,考查转化思想和方程思想、运算能力和推理能力,属于中档题.20.(问答题,12分)设函数f(x)=sinx(√3cosx+sinx)−12.(Ⅰ)求函数f(x)的递增区间;(Ⅱ)在△ABC中,a,b,c分别为内角A,B,C的对边,若f(B)=1,b=2,且b(2-cosA)=a(cosB+1),求△ABC的面积.【正确答案】:【解析】:(Ⅰ)利用三角函数恒等变换的应用化简函数解析式为f(x)=sin(2x- π6),利用正弦函数的单调性即可求解.(Ⅱ)由f(B)=1,可得sin(2B−π6)=1,进而解得B的值,由正弦定理,两角和的正弦函数公式可求2b=a+c,由余弦定理可得ac=b2=4,根据三角形的面积公式即可求解.【解答】:解:(Ⅰ)函数的解析式可化为:f(x)=√32sin2x+1−cos2x2−12= √32sin2x−1 2cos2x=sin(2x−π6).由2kπ−π2≤2x−π6≤2kπ+π2⇒kπ−π6≤x≤kπ+π3,得函数f(x)的递增区间为[kπ−π6,kπ+π3](k∈Z).(Ⅱ)因为f(B)=1,即sin(2B−π6)=1,所以2B−π6=2kπ+π2⇒B=kπ+π3,因为B是三角形的内角,所以B=π3,又因为b(2-cosA)=a(cosB+1),由正弦定理得sinB(2-cosA)=sinA(cosB+1),所以2sinB=sinA+sinAcosB+cosAsinB=sinA+sin(A+B)=sinA+sinC,所以2b=a+c,因为b=2,B=π3,由余弦定理得b2=a2+c2-ac⇒b2=(a+c)2-3ac⇒ac=b2=4.所以,S=12acsinB=12•4•sinπ3=2•√32=√3,故△ABC的面积为√3.【点评】:本题主要考查了三角函数恒等变换的应用,正弦函数的单调性,正弦定理,两角和的正弦函数公式,余弦定理,三角形的面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.21.(问答题,12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足条件:cosA a +cosCc=1b.(1)求证:sin2B=sinAsinC;(2)在数列{a n}中,a n=2n-1,且数列{1a n a n+1}的前n项和为2ncosB2n+1,求角B.【正确答案】:【解析】:(1)在已知等式中利用正弦定理化边为角得答案;(2)利用裂项相消法求出数列{1a n a n+1}的前n项和,再由其前n项和等于2ncosB2n+1求角B.【解答】:(1)证明:在等式cosAa +cosCc=1b中,由正弦定理得cosAsinA +cosCsinC=1sinB,即sinCcosA+sinAcosCsinAsinC =1sinB,∴ sin(A+C) sinAsinC =1sinB,得sin2B=sinAsinC;(2)解:由a n=2n-1,则1a1a2+1a2a3+1a4a3+ (1)a n a n+1= 11×3+13×5+… +1(2n−1)(2n+1)= 12(11−13+13−15+… +12n−1−12n+1) = 12(1−12n+1)=n2n+1.由已知得n(2n+1)=2ncosB2n+1⇒cosB=12,在△ABC中,∵0<B<π,∴ B=π3.【点评】:本题考查数列递推式,考查了裂项相消法求数列的前n项和,训练了正弦定理在解三角形中的应用,是中档题.22.(问答题,12分)已知函数f(x)=12x2−x+alnx(a>0).(1)讨论f(x)的单调性;(2)若f(x)存在两个极值点x1,x2,求证:f(x1)+f(x2)>−3−2ln24.【正确答案】:【解析】:(1)求导得f′(x),由f′(x)>0分别对a进行的讨论,从而得到f(x)的单调区间;(2)由极点的概念得到x1,x2是方程x2-x+a=0的两根,故由根与系数的关系,得到f(x1)+f(x2)关系式,最后利用单调性求得其最小值【解答】:解:(1)f′(x)=x−1+ax =x2−x+ax(a>0),① 若a≥14,x2−x+a≥0,f′(x)≥0,所以f(x)在(0,+∞)上单调递增;② 若0<a<14,解x2-x+a>0,得0<x<1−√1−4a2,或x>1+√1−4a2,解x2-x+a<0,得1−√1−4a2<x<1+√1−4a2,此时f(x)在(1−√1−4a2,1+√1−4a2)上单调递减.在(0,1−√1−4a2)上单调递增,在(1+√1−4a2,+∞)上单调递增.综上,当a≥14时,f(x)在(0,+∞)上单调递增,当0<a<14时,f(x)在(1−√1−4a2,1+√1−4a2)上单调递减,在(0,1−√1−4a2)上单调递增,在(1+√1−4a2,+∞)上单调递增.(2)由(1)知0<a<14时,f(x)存在两个极值点x1,x2,且x1,x2是方程x2-x+a=0的两根,所以x1+x2=1,x1•x2=a,所以f(x1)+f(x2)=12x12−x1+alnx1+12x22−x2+alnx2=12(x1+x2)2−x1x2−(x1+x2)+aln(x1x2) = 12−a−1+alna=alna−a−12,令g(x)=xlnx−x−12(0<x<14),g′(x)=lnx<0,所以g(x)在(0,14)上单调递减,所以g(x)>g(14)=−3−2ln24,所以f(x1)+f(x2)>−3−2ln24【点评】:本题主要考查导数研究函数单调性,导数研究函数极值的知识点,运用了求导法,参数讨论法,根与系数关系,及转化的数学思想。
山东省乳山市2013届高三数学上学期期中考试试题新人教A版.doc
高三数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷(选择题 共60分)一. 选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合{}{}(,)46,(,)327A x y x y B x y x y =+==+=,则满足()C A B ⊆I 的集合C 的个数是A .0B .1C .2D .32. 命题“设a 、b 、b a bc ac c >>∈则若,,22R ”的逆命题、否命题、逆否命题中真命题共有A .0个B .1个C .2个D .3个3. 若函数()(0,1)xf x a a a -=>≠是定义域为R 的减函数,则函数()log (1)a f x x =+的图象大致是4. 已知函数()y f x =的图象与函数112log x y +=的图象关于y x =对称,则()1f 的值为A .1B .1-C .12-D .125.已知p:α为第二象限角,q:sin cos αα>,则p 是q 成立的 A .充分非必要条件 B .必要非充分条件C .充分必要条件D .既非充分又非必要条件6. 若()f x 是R 上周期为5的奇函数,且满足(1)1f =,(2)3f =,则(8)(4)f f -的值为A .-1B .1C .-2D .27. 为得到函数)32cos(π+=x y 的图象,只需将函数x y 2sin =的图象A .向左平移125π个长度单位 B .向右平移125π个长度单位C .向左平移65π个长度单位D .向右平移65π个长度单位 8. 已知(cos 2,sin ),(1,2sin 1),(,)2a b πααααπ==-∈r r 若)4tan(,52πα+=⋅则的值为A .31 B .71 C . 72 D .329. 设,A B 是非空集合,定义:{|}A B x x A B x A B ⊗=∈∉U I 且.已知{|A x y ==,1{|2(0)}xB y y x ==>则A B ⊗为A. (2,)+∞B. (0,1)C.[0,1)(2,)⋃+∞ D. [0,1](2,)⋃+∞10. (理科)若实数x y 、满足22111x y+=,则222x y +有A .最大值3+B .最小值3+C .最大值6D .最小值610.(文科) 在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若ac B b c a 3tan )(222=-+,则角B 的值是A .6π B .3π或23π C .656ππ或 D .3π11.(理科)已知函数3211()2(,,R)32f x x ax bx c a b c =+++∈在区间(0,1)内取得极大值,在区间(1,2A .,22⎛⎫ ⎪ ⎪⎝⎭B .1,42⎛⎫⎪⎝⎭ C .(1,2) D .(1,4) 11.(文科)已知函数3211()(,,R)32f x x ax x b a b =+++∈在区间(0,1)内取得极大值,在区间(1,2)内取得极小值,则a 的取值范围为 A. 522a -<<- B. 522a << C. 522a -<< D. 522a -<<12.方程3210x bx -+=有且仅有两个不同零点,则b 的值为B.D. 不确定第Ⅱ卷(非选择题 共90分)二. 填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.13. 设a 、b 、c 是单位向量,且a b c +=r r r ,则a r 与c r的夹角为 。
山东省威海市乳山市重点中学2023-2024学年高一上学期12月月考数学试题
高一十二月份月考数学试题一、单选题1.下列四组函数中,()f x 与()g x 表示同一函数是( )A .()1f x x =-,()211x g x x -=+B .()1f x x =+,()1,11,1x x g x x x +≥-⎧=⎨--<-⎩C .()1f x =,()()01g x x =+D .()f x =()2g x =2.把物体放在冷空气中冷却,如果物体原来的温度是θ1°C ,空气的温度是θ0°C ,那么t min 后物体的温度θ(单位:°C ),可由公式()010e kt θθθθ-=+-求得,其中k 是一个随着物体与空气的接触情况而定的常数.现有60°C的物体,放在15°C 的空气中冷却,3分钟以后物体的温度是42°C .则k 的值为(精确到0.01) ( ) (参考数据:ln3 1.0986≈,ln5 1.6094≈)A .0.51B .0.28C .0.17D .0.073.已知函数()f x 是R 上的减函数,点(2,3),(3,3)A B --是其图像上的两点,则不等式(1)3f x +<的解集的补集是( ) A .(3,2)- B .(1,2)-C .(][)32,-∞-+∞D .(][),12,-∞-+∞4.已知130.20.0121.5, 1.3,,3ab c -⎛⎫=== ⎪⎝⎭则( )A .b c a <<B .a b c <<C .c a b <<D .a c b <<5.已知区间(,)a b 是关于x 的一元二次不等式2210mx x -+<的解集,则32a b +的最小值是( )A .32+B .5+C .52D .36.满足1133(1)(32)m m --+<-的实数m 的取值范围是( ).A .23,32⎛⎫ ⎪⎝⎭B .23,1,32⎛⎫⎛⎫-∞⋃⎪ ⎪⎝⎭⎝⎭ C .2,3⎛⎫+∞ ⎪⎝⎭ D .23(,1),32⎛⎫-∞-⋃ ⎪⎝⎭ 7.函数13y ⎛= ⎪⎝⎭的单调递增区间是( )A .[)1,+∞B .(],1-∞C .[]12, D .[]0,18.设奇函数()f x 在[]1,1-上是增函数,且()11f -=-,若对所有的[]1,1x ∈-及任意的[]1,1a ∈-都满足()221f x t at ≤-+,则t 的取值范围是( )A .[]22-,B .11,22⎡⎤--⎢⎥⎣⎦ C .{},20(][2,)∞-⋃⋃+∞ D .{}11,0(][,22)∞-⋃⋃+∞二、多选题 9.已知函数3()2bx f x ax +=+在区间(2,)-+∞上单调递增,则,a b 的取值可以是( )A .1a =,32b >B . 012a b <≤=,C .=-12a b =,D .1=12a b =,10.函数2()xf x x a=+的图像可能是( ) A . B .C . D .11.已知正数a ,b 满足21a b +=,则( ) A. ab 的最大值为18B. 224a b +的最小值为12 C.12a b+最小值为4D. 1ab ab+的最小值为2 12.下列说法正确的是( )A .若幂函数的图象经过点1(,2)8,则解析式为3y x -= B .若函数()45f x x-=,则()f x 在区间(),0-∞上单调递减C .幂函数y x α=(0α>)始终经过点()0,0和()1,1D .若函数()f x x =,则对于任意的1x ,2[0,)x ∈+∞有()()121222f x f x x x f ++⎛⎫≤ ⎪⎝⎭三、填空题13.已知()2212f x x x +=-,则()f x 的解析式为______________.14.若函数的定义域是1,12⎛⎫⎪⎝⎭,则函数(2)x f 的定义域是______. 15.函数()222,11,1x ax a x f x ax x ⎧-+-≥=⎨+<⎩是(),-∞+∞上的减函数,则实数a 的取值范围是______.16.定义域为R 的函数()f x 满足以下条件:①()21121212[()()]()0,(,0,,)f x f x x x x x x x -->∈+∞≠; ②()()0f x f x --=()x R ∈; ③(3)0f -=则不等式()0xf x <的解集是___________.四、解答题17.计算:(1)222333(2020)()(3)(12)28--+⋅+-(2)321lg5lg8000lg2lg lg0.066⋅+++()18.已知集合{}221216,430,08x A xB x x ax a a ⎧⎫=≤≤=-+≤>⎨⎬⎩⎭. (1)若2a =,求A B ⋃;(2)若A B ⋂=∅,求实数a 的取值范围.19.已知函数()(01x f x a a a =>≠,)的图象经过点1(2,)9.(1)求a ,并比较2(1)f b b ++与3()4f 的大小;(2)求函数223()x x g x a--=的值域.20. 已知函数()()()2log 424,x x f x b g x x =+⋅+=.(1)当=5b -时,求()f x 的定义域;(2)若()()f x g x >恒成立,求实数b 的取值范围.21.已知函数2()(1)1(0)x g x a a -=++>的图像恒过定点A ,且点A 又在函数())f x x a =+的图像上.(1)求实数a 的值; (2)解不等式()f x a <;(3)(2)22g x b +-=有两个不等实根时,求b 的取值范围.22.新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业A 公司扩大生产提供([0,10])∈x x (万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A 公司在收到政府x (万元)补贴后,防护服产量将增加到1264t k x ⎛⎫=⋅-⎪+⎝⎭(万件),其中k 为工厂工人的复工率([0.5,1]k ∈).A 公司生产t 万件防护服还需投入成本(20950)x t ++(万元).(1)将A 公司生产防护服的利润y (万元)表示为补贴x (万元)的函数(政府补贴x 万元计入公司收入); (2)在复工率为k 时,政府补贴多少万元才能使A 公司的防护服利润达到最大?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三基本能力试题 本试卷分第I卷和第II卷两部分,共7页,满分100分。考试用时100分钟。答题前,考生务必将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置。
第I卷(共70分)
注意事项: 1. 第一部分共70小题,全部为单项选择题,每小题1分,共70分。 2. 每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。不涂在答题卡上,只答在试卷上不得分。 1.从科学的角度看,下列说法正确的是( ) A.由于地球温室效应,南极的冰山正在融化,导致海平面正在上升 B.夏天天热时,可以把房间内的冰箱门打开来降低房间温度 C.在寒冷的冬季用手直接触摸双杠会感觉很冷,这是因为冷气传递给手掌 D.冬天由于天气比较干燥,人们穿在身上的化纤服装经过摩擦可以产生静电,因此晚上脱衣服时可以看到火花放电 2.一天之中,阳光随时间推移不仅有亮度的变化,色彩也随之变化。一般规律是 ①早晨光线有红色的倾向 ②中午光线最强,色彩感觉最弱 ③夕阳光线最冷 ④夜晚色调最暖 A.②③ B. ②④ C.①③ D.①② 3. 冰是水在低温条件下的一种形态,然而生活中发现,在我国北方的冬季,河流往往是表面结冰而深层依然是流动的水.对于此种现象,原因是 A.水固化成冰时会释放出热量 B.表面冰层具有隔热保温作用 C.水在O℃左右具有热缩冷涨的性质 D.气温尚未低到使河流整体冰冻的程度 4.随着科技进步,太空技术的迅速发展,太空垃圾也越来越多。目前,一种用于催毁太空垃圾的激光武器正在研制中。如图所示,某空间站看上去位于地平线上方,由于光在空气中发生了折射,所以空间站的实际位置应在图中的下方,现准备用一束激光射向该空间站,则应把激光器 A.沿视线对着空间站瞄高一些 B.沿视线对着空间站瞄低一些 C.沿视线对准空间站直接瞄准 D.条件不足,无法判别 5.历史上许多文人墨客对月亮情有独钟,创作了大量富有想象的诗歌。古诗句“钓罢归来不系船,江村月落正堪眠”“海上生明月,天涯共此时”“大漠沙如雪,燕山月似钩”“月黑雁飞高,单于夜遁逃”所描述的月相依次是 ①上弦月 ②满月 ③残月 ④新月 A.①②③④ B.②①③④ C.①④③② D.④②①③ 6.在夏天经常出现雷电交加的现象,而且是闪电过后几秒至十几秒才听到雷声。造成这种情况的主要原因是 A.雷声产生较晚 B.光的速度快 C.人的错觉 D.云层或建筑物的遮挡 7. 、高二某班的同学用木条、乳胶等做了一个长方形的奖状框用来放置他们获得的荣誉奖状(如图)。他们发现这个结构容易变形,便提出了如下四种改进方案(如图二)。你认为不合适的方案是( )。
8. 某兴趣小组想举办一期“浩瀚的星空”知识讲座,需要用多个软件整理材料。Microsoft offices是我们经常使用的办公软件,其中不同的组件也具有不同的功能。下列操作中,错误的一项是 A.在Word中,可以通过“格式”→“段落”来设置段落缩进、行距等格式 B.在Excel中,求和是通过“工具”→“常用函数”→“SUM”求得 C.在PowerPoint中,通过“幻灯片放映”→“自定义放映”可以改变幻灯片的播放顺序 D.对于文字,我们可以通过“复制”后把它“粘贴”到写字板、Word、Excel、PowerPoint中的任一软件中 9.进行户外运动时,为了减少紫外线伤害,正确的做法是 ①夏半年晴朗天气的正午前后尽量避免户外运动 ②夏半年晴天做户外运动时,要佩带必要的遮阳物品 ③冬半年由于太阳辐射较弱,可不采取防护措施 ④多云或阳光不强烈时,可不采取防护借施 A.①② B.②③ C.①④ D.②④ 10.随着航天技术的飞速发展,我国已成功实现两次载人航天飞行。当飞船的轨道舱和返回舱一起进入预定圆形轨道绕地球飞行时,下列说法错误的是 A.因为飞船离地面高度的始终相同,故飞船相对地面是静止的 B.以轨道舱为参照物,返回舱是静止的 C.在大气层外宇航员透过舷窗看星星没有闪烁的感觉 D.通过无线电波,地面技术人员可以对飞船进行控制及与宇航员通话 11.中国地域辽阔,民族众多,不同的地理环境、生活习俗、语言特点、文化传统、审美观念等因素,造就了民间音乐的民族风格或地方特色。下列说法不正确的是 A.“信天游”是西北民歌中有代表性的类型之一 B.南方民歌歌词比较含蓄,善用比兴,旋律多婉转、流畅、细腻、抒情 C.“广东音乐”的主奏乐器是唢呐和扬琴 D.“长调”和“短调”是蒙古族民歌的代表性体裁 12.雪花,被人们称为“冬之精灵”。科学研究发现,世界上没有两片雪花的形状是完全相同的。不同雪花中,水分子 A.数目都是巨大的 B.数目都是相同的 C.化学性质不相同 D.空间排列方式相同 13.中国园林,名之为“文人园”,是因其往往散发着书卷气。书法艺术便是苏州园林的景观特色之一。其中,留园“五峰仙馆”厅内楹联写道:
第7题图一 A B C D
细绳 木条 小角板
第7题图二 下列对这幅对联的理解和赏析有错误的一项是 A.上联说读书,下联谈赏花,读书、赏花皆为消闲的好方式,借以养生健身,尽可为之 B.上联的“书”则指“四书五经”中的“四书”,“易”“骚”分别是指《易经》、《离骚》 C.“书”“易”“骚”“庄”“汉文”都各有其特点,宜用不同的方法读之,从中吸取不同的营养 D.菊、梅、莲、兰、海棠,因各有其品格,故要仔细观察玩味,从而赏出不同的妙处来
14在下列作品中,找出罗丹的作品
15.很多动物是“应用物理高手”,它们为了适应生存环境,进化出了符合一定物理规律的身体部位。下列说法从物理学的角度看,正确的是 A.骆驼的脚掌很大,可以减小压强 B.泥鳅的体表有层黏液,可以增大摩擦 C.啄木鸟有尖硬的喙,可以减小压强 D.蚯蚓腹部有许多刚毛,可以减小摩擦 16.山东有丰富的旅游资源,各地组织开发了文体、民俗等30多项专项旅游活动,深受游客欢迎。4月20日潍坊、8月20日青岛、9月2日泰安、9月26日曲阜每年都定期开展国际专项旅游节庆活动。我省举办以体育文体活动为主题的节庆活动的城市,下列城市合适的是 A.潍坊、曲阜 B.泰安、曲阜 C.潍坊、泰安 D.青岛、曲阜 17.生活中有这么三个现象(如下列三幅图):第一、早晨和傍晚,在日出和日落前后的天边,时常会出现五彩缤纷的彩霞;第二、夏天的雨后,天空常常出现半圆形的彩虹;第三、插在水杯中的饮料管,似乎在水面处断了。造成这些现象的主要原因分别是
A.都是光的散射 B.都是光的折射
C.光的散射、光的反射、光的折射 D.光的散射、光的折射、光的折射 18.自古以来,很多文人墨客感慨大自然的魅力,用美妙的诗句描述一幅幅美丽的自然景观。下列诗词与所描述的地点对应正确的是 A.江作青罗带,山如碧玉簪。——桂林 B.天苍苍,野茫茫,风吹草低见牛羊。——新疆 C.两岸猿声啼不住,轻舟已过万重山。——金沙江 D.早穿棉袄午穿纱,围着火炉吃西瓜。——内蒙古 19.保护环境是每个公民的责任。下列做法不利于保护环境的是 ①大量使用化石能源 ②城市生活垃圾分类处理 ③过量使用化肥、农药 ④推广使用太阳能产品 ⑤大量使用塑料方便袋 ⑥推广使用一次性筷子 A.①②③④ B.①③⑤⑥ C.②③⑤⑥ D.①③④⑥ 20.生活中的设计无处不在,艺术作品的创作也遵循一定的设计法则,观察下图,根据你的理解和感受,下列法则与作品排序对应正确的是 ①对比与调和 ②节奏与韵律 ③疏可走马,密不透风 ④对称与均衡
A.①③②④ B. ②①④③ C. ③④②① D. ④①②③ 21.亚当·斯密说过:“如果一个社会的经济发展成果不能真正分流到大众手中,那么它在道义上将是不得人心的,并且有风险的,因为它注定会威胁到社会的稳定。”这句话强调的是 A.在收入分配中要防止出现两极分化 B.公平的收入分配有助于协调人们的利益关系 C.提高经济效率是增加社会财富根本途径 D.收入分配要坚持“效率优先、兼顾公平”原则 22.温总理南下指挥抗灾工作时说:“民安了国才能安,国安了领导人的心才能安。”此语,体现了我国古代的民本思想。在我国古代先哲中,第一次将民的地位、作用提到高于君主的程度的是 A.孔子 B.孟子 C.庄子 D.韩非子 23.正确地防范传染病应做到控制传染源、切断传播途径和保护易感人群,下列措施属于切断传播途径的是 A.接种安全有效的疫苗 B.饭前便后要洗手 C.定时进行体检 D.经常打太极拳锻炼身体 24.随着生活水平的提高,各种电器、电子产品进入了普通家庭。彩色电视机、电脑、冰箱、空调、高级音响……给人们带来了许许多多的欢乐,但同时也给人们的健康带来了无形的隐患。电器在使用和操作过程中,会产生一种所谓的“电子雾”,这个“电子雾”其实就是 A.大量自由电子形成的雾 B.线路发热使水蒸气遇冷形成的雾气 C.产生的各种不同波长和频率的电磁波 D.电器元件烧毁时形成的烟气 25.“热情”奏鸣曲是一首规模宏大、气势磅礴的作品,激烈的矛盾冲突、顽强的斗争精神等典型的作曲家风格在此一览无余,评论家们将这首乐曲比作“火山的爆发”、“花岗石河床中的熔岩”。如果请你用《热情》为文章配乐,下列文章中你会选择的一篇是 A.朱自清 《荷塘月色》 B.徐志摩 《再别康桥》
