统计学课后第四章习题答案
统计学习题答案 第4章 抽样与抽样分布

统计学习题答案第4章抽样与抽样分布第4章抽样与抽样分布——练习题(全免)1. 一个具有64n个观察值的随机样本抽自于均=值等于20、标准差等于16的总体。
⑴给出x的抽样分布(重复抽样)的均值和标准差⑵描述x的抽样分布的形状。
你的回答依赖于样本容量吗?⑶计算标准正态z统计量对应于5.15=x的值。
⑷计算标准正态z统计量对应于23x的值。
=解: 已知n=64,为大样本,μ=20,σ=16,⑴在重复抽样情况下,x的抽样分布的均值为a. 20, 2b. 近似正态c. -2.25d. 1.502 . 参考练习4.1求概率。
⑴x<16;⑵x>23;⑶x>25;⑷.x落在16和22之间;⑸x<14。
解: a. 0.0228 b. 0.0668 c. 0.0062 d.0.8185 e. 0.00133. 一个具有100n个观察值的随机样本选自于=μ、16=σ的总体。
试求下列概率的近似值:30=解: a. 0.8944 b. 0.0228 c. 0.1292 d. 0.96994. 一个具有900=n 个观察值的随机样本选自于100=μ和10=σ的总体。
⑴ 你预计x 的最大值和最小值是什么? ⑵ 你认为x 至多偏离μ多么远?⑶ 为了回答b 你必须要知道μ吗?请解释。
解:a. 101, 99 b. 1 c. 不必5. 考虑一个包含x 的值等于0,1,2,…,97,98,99的总体。
假设x 的取值的可能性是相同的。
则运用计算机对下面的每一个n 值产生500个随机样本,并对于每一个样本计算x 。
对于每一个样本容量,构造x 的500个值的相对频率直方图。
当n 值增加时在直方图上会发生什么变化?存在什么相似性?这里30,10,5,2====n n n n 和50=n 。
解:趋向正态6. 美国汽车联合会(AAA )是一个拥有90个俱乐部的非营利联盟,它对其成员提供旅行、金融、保险以及与汽车相关的各项服务。
统计学第四章答案及习题
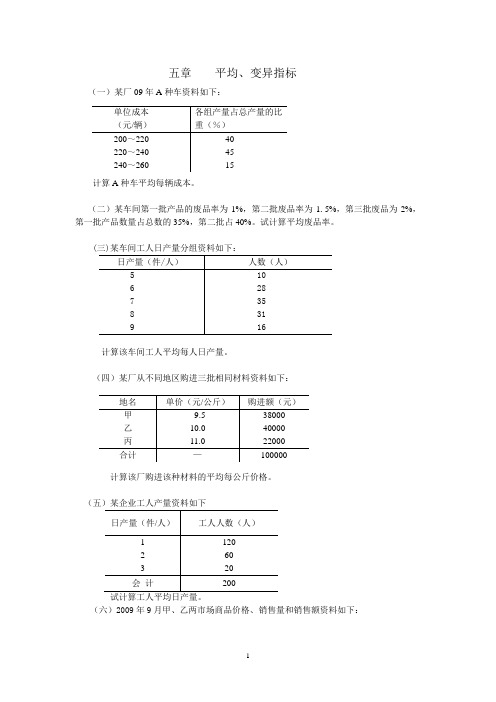
五章平均、变异指标(一)某厂09年A种车资料如下:计算A种车平均每辆成本。
(二)某车间第一批产品的废品率为1%,第二批废品率为1.5%,第三批废品为2%,第一批产品数量占总数的35%,第二批占40%。
试计算平均废品率。
计算该车间工人平均每人日产量。
(四)某厂从不同地区购进三批相同材料资料如下:计算该厂购进该种材料的平均每公斤价格。
试计算工人平均日产量。
(六)2009年9月甲、乙两市场商品价格、销售量和销售额资料如下:试分别计算商品在两个市场平均每件的销售价格。
(七)某厂某车间工人产量分组资料如下:要求:计算该车间工人平均每人日产量、标准差。
答案(一)=fX xf∑∑=210×0.4+230×0.45+250×0.15=225(元/辆) (二)χ = ∑x∑ff=1%×35%+1.5%×40%+2%×25%= 1.45%(三)χ=∑∑ff χ=(5×10+6×28+7×35+8×31+9×16)÷(10+28+35+31+16) =855/120=7.125(件)(四)380004000022000=10()3800040000220009.51011m X m x ∑++==∑++元/公斤(10分) (五)2002036021201⨯+⨯+⨯=⎰∑⎰⨯∑=X =)/(5.1200/300人件=(六)日产量(公斤) 工人数(人)20~30 1030~40 7040~50 90 50~60 30 合计 200(元/件)(元/件)(七)=(25×10﹢35×70﹢45×90﹢55×30)/(10﹢70﹢90﹢30)=42(公斤)日产量 (公斤) 组中值 (x ) 人 数 (f) 20-30 30-40 40-50 50-60 25 35 45 55 10 70 90 30 -17 -7 3 13 2890 3430 810 5070 合计—200—12200标准差σ=(公斤)81.76120012200)(2===-∑∑ffx x六章 动态数列(一) 某企业09年二季度商品库存如下:计算该企业二季度平均库存额。
统计学第四章课后题及答案解析

第四章一、单项选择题1.由反映总体单位某一数量特征的标志值汇总得到的指标是()A.总体单位总量B.质量指标C.总体标志总量D.相对指标2.各部分所占比重之和等于1或100%的相对数()A.比例相对数B.比较相对数C.结构相对数D.动态相对数3.某企业工人劳动生产率计划提高5%,实际提高了10%,则提高劳动生产率的计划完成程度为()A.104.76%B.95.45%C.200%D.4.76%4.某企业计划规定产品成本比上年度降低10%实际产品成本比上年降低了14.5%,则产品成本计划完成程度()A.14.5%B.95%C.5%D.114.5%5.在一个特定总体内,下列说法正确的是( )A.只存在一个单位总量,但可以同时存在多个标志总量B.可以存在多个单位总量,但必须只有一个标志总量C.只能存在一个单位总量和一个标志总量D.可以存在多个单位总量和多个标志总量6.计算平均指标的基本要求是所要计算的平均指标的总体单位应是()A.大量的B.同质的C.有差异的D.不同总体的7.几何平均数的计算适用于求()A.平均速度和平均比率B.平均增长水平C.平均发展水平D.序时平均数8.一组样本数据为3、3、1、5、13、12、11、9、7这组数据的中位数是()A.3B.13C.7.1D.79.某班学生的统计学平均成绩是70分,最高分是96分,最低分是62分,根据这些信息,可以计算的测度离散程度的统计量是()A.方差B.极差C.标准差D.变异系数10.用标准差比较分析两个同类总体平均指标的代表性大小时,其基本的前提条件是( )A.两个总体的标准差应相等B.两个总体的平均数应相等C.两个总体的单位数应相等D.两个总体的离差之和应相等11.已知4个水果商店苹果的单价和销售额,要求计算4个商店苹果的平均单价,应采用()A.简单算术平均数B.加权算术平均数C.加权调和平均数D.几何平均数12.算术平均数、众数和中位数之间的数量关系决定于总体次数的分布状况。
概率论与数理统计课后习题答案 第四章

(2) ρxy.
(1)
(2)(X,Y)的分布律为
Y X
0
1
-1
0
1
习题 4.1 1. 设随机变量 X 的概率密度为
(1) 求 E(X)
其他
(2)
解: (1)
(2) 2. 设连续型随机变量 X 的分布函数为
试确定常数 a,b,并求 E(X). 解:
(1)
其他
又因当
时
(2) 3. 设轮船横向摇摆的随机振幅 X 的概率密度为
的导数为 的导数为
即 即
求 E(X). 解:
4. 设 X1, X2,….. Xn 独立同分布,均值为 ,且设
D. (X,Y)~N(
)
解: 与 不相关 ρ
5. 设二维随机变量(X,Y)~N(
A.
B. 3
C. 18
解: ρ
),则 Cov(X,Y)= B . D. 36
6. 已知随机变量 X 与 Y 相互独立,且它们分别在区间[-1,3]和[2,4]上服从均匀分布,则 E(XY)= A .
A. 3
B. 6
C. 10
解: Cov(X,Y)=0
2. 设随机变量 X 的分布律为 3 .
X
-1
0
1
2
P
0.1 0.2 0.3 0.4
令 Y=2X+1,则 E(Y)=
3
.
解: E(2X+1)=(2*-1+1)*0.1+(2*0+1)*0.2+(2*1+1)*0.3+(2*2+1)*0.4=3
3. 已知随机变量 X 服从泊松分布,且 D(X)=1,则 P{X=1}=
《统计学原理》第四章习题

《统计学原理》第四章习题及答案一.判断题部分题目1:同一个总体,时期指标值的大小与时期长短成正比,时点指标值的大小与时点间隔成反比。
()题目2:全国粮食总产量与全国人口对比计算的人均粮食产量是平均指标。
()题目3:根据分组资料计算算术平均数,当各组单位数出现的次数均相等时,按加权算数平均数计算的结果与按简单算数平均数计算的结果相同。
()题目4:同一总体的一部分数值与另一部分数值对比得到的相对指标是比较相对指标。
()题目5:某年甲、乙两地社会商品零售额之比为1:3,这是一个比例相对指标。
()题目6:某企业生产某种产品的单位成本,计划在上年的基础上降低2%,实际降低了3%,则该企业差一个百分点,没有完成计划任务。
()题目7:标准差系数是标准差与平均数之比,它说明了单位标准差下的平均水平。
()题目8:1999年与1998年相比,甲企业工人劳动生产率是乙企业的一倍,这是比较相对指标。
()题目9:中位数与众数都是位置平均数,因此用这两个指标反映现象的一般水平缺乏代表性。
()题目10:对两个性质相同的变量数列比较其平均数的代表性,都可以采用标准差指标。
()题目11:利用变异指标比较两总体平均数的代表性时,标准差越小,说明平均数的代表性越大;标准差系数越小,则说明平均数的代表性越小。
()题目12:标志变异指标数值越大,说明总体中各单位标志值的变异程度越大,则平均指标的代表性越小。
()题目13:权数对算数平均数的影响作用只表现为各组出现次数的多少,与各组次数占总次数的比重无关。
()题目14;能计算总量指标的总体必须是有限总体。
()二.单项选择题题目1:反映社会经济现象发展总规模、总水平的综合指标是()。
A、质量指标B、总量指标C、相对指标D、平均指标题目2:总量指标按反映时间状况的不同,分为()。
A、数量指标和质量指标B、时期指标和时点指标C、总体单位总量和总体标志总量D、实物指标和价值指标题目3:总量指标是用()表示的。
统计学第五版课后练答案(4-6章)

第四章统计数据的概括性度量4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics汽车销售数量10Missing 0Mean 9.60Median 10.00Mode 10Std. Deviation 4.169Percentiles 25 6.2550 10.0075 12.50单位:周岁19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求;(1)计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25和27都只有一个,因此Q3也可等于25+0.75×2=26.5。
(3)计算平均数和标准差;Mean=24.00;Std. Deviation=6.652(4)计算偏态系数和峰态系数:Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
1、确定组数:()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 - 最小值)÷ 组数=(41-15)÷6=4.3,取53、分组频数表网络用户的年龄 (Binned)分组后的直方图:客都进入一个等待队列:另—种是顾客在三千业务窗口处列队3排等待。
第四章 教育统计学课后练习题参考答案

2
X X
3.12
MD
M
d
X
n
2 .8
4. 答:
分数 组中值 频数
10 15 1
20 25 0
30 35 0
40 45 3
50 55 4
60 65 5
70 75 4
80 85 2
90 95 1
总和 20
由于已知 Md=64 因此,平均差为
2
MD
n 1 15 64 0 0 3 45 64 4 55 64 5 65 64 4 75 64 2 85 64 1 95 64 20
教育统计学(第四版),王孝玲著,华东师范大学出版社 课后题参考答案
第四章. 练习题参考答案
1.
答:
1 全距 R=Xmax-Xmin=36-20=16
四分位距 20,23,25,27,29,31,33,36 由于,Q1=24,Q3=32
2
QD
2.
Q3 Q1 32 24 4 2 2
答:
f
X Md
13.2
5. 答:
1
定义公式
由于平均数为 X
41 39 37 35 38 38 5
因此, 方差为
2 x
X X 41 - 38 39 - 38 37 - 38 35 - 38 38 - 38
2 2 2 2 2
男生 CV 因此,离散程度女生比男生大 9. 答:
平均数小于中位数,因此分布呈负偏态
偏态量 SK
3( X M d )
X
《统计学》课后练习题答案

A.透视表B.合并计算C.单变量求解D.分类汇总
5.小张收集了1957-2007年中国GDP的数据,如果要反映这50年我国生产发展的趋势,用什么图形最为合适?()(知识点3.5答案:D)
A.直方图B.散点图C.饼图D.折线图
37
பைடு நூலகம்33.6
130-140
12
10.9
103
93.6
19
17.3
140-150
5
4.5
108
98.2
7
6.4
150-160
2
1.8
110
100.0
2
1.8
合计
110
100
—
—
—
—
A.树苗高度低于110厘米的占总数的39.1%B.树苗高度低于110厘米的占总数的84.5%
C.树苗高度高于130厘米的有19棵D.树苗高度高于130厘米的有103棵
第二章数据的收集与整理
2.1数据的来源
2.2统计调查方案设计
2.3调查方法
2.4调查的组织方式:普查、抽样调查、重点调查、典型调查
2.5抽样的组织方式:简单随机抽样、系统抽样、分层抽样、整群抽样
2.6数据的审定:误差
2.7数据的分组
2.8.编制次数分布表:频数(次数)、频率
习题
一、单项选择题
1.小吴为写毕业论文去收集数据资料,()是次级数据。(知识点:2.1答案:C)
A.指标B.标志C.变量D.标志值
8.以一、二、三等品来衡量产品质地的优劣,那么该产品等级是()。(知识点:1.7答案:A)
A.品质标志B.数量标志C.质量指标D.数量指标
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章练习题
1、一组数据中出现频数最多的变量值称为()
A.众数
B.中位数 C。
四分位数 D.平均数
2、下列关于众数的叙述,不正确的是()
A。
一组数据可能存在多个众数 B。
众数主要适用于分类数据
C。
一组数据的众数是唯一的 D。
众数不受极端值的影响
3、一组数据排序后处于中间位置上的变量值称为()
A.众数 B。
中位数 C。
四分位数 D.平均数
4、一组数据排序后处于25%和75%位置上的值称为()
A.众数 B。
中位数 C.四分位数 D.平均数
5、非众数组的频数占总频数的比例称为()
A。
异众比率 B。
离散系数 C.平均差 D.标准差
6、四分位差是()
A.上四分位数减下四分位数的结果 B。
下四分位数减上四分位数的结果
C。
下四分位数加上四分位数 D。
下四分位数与上四分位数的中间值
7、一组数据的最大值与最小值之差称为()
A.平均差
B.标准差 C。
极差 D.四分位差
8、各变量值与其平均数离差平方的平均数称为()
A。
极差 B。
平均差 C.方差 D.标准差
9、变量值与其平均数的离差除以标准差后的值称为()
A.标准分数
B.离散系数 C。
方差 D。
标准差
10、如果一个数据的标准分数—2,表明该数据()
A。
比平均数高出2个标准差 B.比平均数低2个标准差
C.等于2倍的平均数 D。
等于2倍的标准差
11、经验法则表明,当一组数据对称分布时,在平均数加减2个标准差的范围之内大约有()
A。
68%的数据 B.95%的数据 C。
99%的数据D。
100%的数据
12、如果一组数据不是对称分布的,根据切比雪夫不等式,对于k=4,其意义是()
A。
至少有75%的数据落在平均数加减4个标准差的范围之内
B. 至少有89%的数据落在平均数加减4个标准差的范围之内
C。
至少有94%的数据落在平均数加减4个标准差的范围之内
D. 至少有99%的数据落在平均数加减4个标准差的范围之内
13、离散系数的主要用途是()
A。
反映一组数据的离散程度 B。
反映一组数据的平均水平
C。
比较多组数据的离散程度 D。
比较多组数据的平均水平
14、比较两组数据离散程度最适合的统计量是()
A.极差
B.平均差 C。
标准差 D。
离散系数
15、偏态系数测度了数据分布的非对称性程度。
如果一组数据的分布是对称的,则偏态系数()
A.等于0 B。
等于1 C.大于0 D.大于1
16、如果一组数据分布的偏态系数在0。
5~1或—1~-0.5之间,则表明该组数据属于()
A。
对称分布 B.中等偏态分布 C。
高度偏态分布 D。
轻微偏态分布
17、峰态通常是与标准正态分布相比较而言的。
如果一组数据服从标准正态分布,则峰态系数的值是()
A。
等于0 B。
大于0 C。
小于0 D.等于1
18、如果峰态系数k>0,表明该组数据是()
A。
尖峰分布 B.扁平分布 C.左偏分布 D.右偏分布
19、某大学经济管理学院有1200名学生,法学院有800名学生,医学院有320名学生,理学院有200名学生。
在上面的描述中,众数是 ()A。
1200 B.经济管理学院 C.200 D.理学院
20、某居民小区准备采取一项新的物业管理措施,为此,随机抽取了100户居民进行调查,其中表示赞成的有69户,表示中立的有22户,表示反对的有9户。
描述该组数据的集中趋势宜采用()
A.众数 B。
中位数 C.四分位数 D。
平均数
21、某居民小区准备采取一项新的物业管理措施,为此,随机抽取了100户居民进行调查,其中表示赞成的有69户,表示中立的有22户,
表示反对的有9户。
该组数据的中位数是()
A。
赞成 B。
69 C。
中立 D.22
22、某班共有25名学生,期末统计学课程的考试分数分别为:68,73,66,76,86,74,61,89,65,90,69,67,76,62,81,63,68,81,70,73,60,87,75,64,56,该班考试分数的下四分位数和上四分位数分别是()
A.64.5和78。
5
B.67。
5和71。
5 C。
64.5和71。
5 D.64.5和67。
5
23、假定一个样本由5个数据构成:3,7,8,9,13。
该样本的方差为()
A。
8 B.13 C。
9.7 D。
10.4
24、对于右偏分布,平均数、中位数和众数之间的关系是()
A。
平均数>中位数〉众数 B。
中位数>平均数〉众数
C。
众数〉中位数>平均数 D.众数〉平均数〉中位数
25、在某行业种随机抽取10家企业,第一季度的利润额(单位:万元)分别是:72,63。
1,54。
7,54。
3,29,26.9,25,23.9,23,20。
该组数据的中位数为()
A.28.46 B。
30.2 C。
27.95 D.28。
12
26、在某行业种随机抽取10家企业,第一季度的利润额(单位:万元)分别是:72,63。
1,54。
7,54。
3,29,26。
9,25,23。
9,23,20。
该组数据的平均数和标准差分别为()
A。
28。
46;19.54 B。
39.19;19.54 C.27。
95;381。
94 D.39。
19;381.94
26、某班学生的统计学平均成绩是70分,最高分是96分,最低分是62分,根据这些信息,可以计算的侧度离散程度的统计量是
A。
方差 B.极差 C.标准差 D。
变异系数
27、某班学生的平均成绩是80分,标准差是10分。
如果已知该班学生的考试分数为对称分布,可以判断成绩在60~100分之间的学生大约占()
A。
95% B。
89% C.68% D.99%
28、某班学生的平均成绩是80分,标准差是10分。
如果已知该班学生的考试分数为对称分布,可以判断成绩在70~90分之间的学生大约占()
A.95%
B.89% C。
68% D.99%
29、某班学生的平均成绩是80分,标准差是5分.如果已知该班学生的考试分数为非对称分布,可以判断成绩在70~90分之间的学生至少占()
A.95%
B.89%
C.68%
D.75%
30、在某公司进行的计算机水平测试中,新员工的平均得分是80分,标准差是5分。
假定新员工得分的分布是未知的,则得分在65~95分的新员工至少占()
A.75%
B.89% C。
94% D.95%
31、在某公司进行的计算机水平测试中,新员工的平均得分是80分,标准差是5分,中位数是86分,则新员工得分的分布形状是()
A.对称的 B。
左偏的 C.右偏的 D.无法确定
32、对某个告诉路段行驶过的120辆汽车的车速进行测量后发现,平均车速是85公里/小时,标准差是4公里/小时,下列哪个车速可以看作是异常值()
A.78公里/小时
B. 82公里/小时
C.91公里/小时
D.98公里/小时
33、一组样本数据为:3,3,1,5,13,12,11,9,7。
这组数据的中位数是()
A.3
B.13 C。
7。
1 D.7
34、在离散程度的测度中,最容易受极端值影响的是()
A。
极差 B。
四分位差 C。
标准差 D。
平均差
35、测度数据离散程度的相对统计量是()
A。
极差 B。
平均差 C。
标准差 D。
离散系数
36、一组数据的离散系数为0。
4,平均数为20,则标准差为()
A。
80 B。
0。
02 C。
4 D.8
37、在比较两组数据的离散程度时,不能直接比较它们的标准差,因为两组数据的()
A。
标准差不同 B。
方差不同 C。
数据个数不同 D。
计量单位不同
38、两组数据的平均数不等,但标准差相等,则()
A。
平均数小的,离散程度大 B。
平均数大的,离散程度大
C.平均数小的,离散程度小 D。
两组数据的离散程度相同。
