单代号网络图计算公式
工程网络图

工程网络图工程网络图主要用于工程项目计划管理,它首先将施工项目整个建造过程分解成若干项工作,以规定的网络符号表达各项工作之间的相互制约和相互依赖关系,并根据它们的开展顺序和相互关系,从左至右排列起来,最后形成一个网状图形,这种网状图形就是工程网络图。
其表示方法主要有双代号表示法和单代号表示法。
1.双代号网络图。
采用两个带编号的圆圈和一个中间箭线表示一项工作,工作的名称写在箭线的上面,完成工作所需要的持续时间写在箭线的下面,箭尾圆圈表示工作的开始,箭头圆圈表示工作的结束;把一项工程(或计划)的所有工作,根据其开展的先后顺序和相互制约、相互依赖的关系,用这种方法从左向右排列起来,形成的网状图形。
双代号网络图主要由工作、节点和线路三个基本要素组成。
在双代号网络图中,可将工作分为:需要消耗时间和资源的工作,如砌筑安装类、运输类和制备类施工过程;只消耗时间而不消耗资源的工作,如抹灰和粉刷等的干燥过程;不消耗时间和资源的工作三种。
而第三种为仅仅表示工作之间相互制约、相互依赖关系的逻辑关系箭线,它又称为虚工作。
在建筑工程流水施工时,虚工作使用十分频繁;如果不使用虚工作就不能正确地表达流水施工的组织方式,绘制出正确的双代号网络图。
但应注意必须严格按工作之间的逻辑关系正确使用,避免将工作之间的关系搞乱,造成网络图计算发生错误。
虚工作也是双代号网络图所特有的工作。
在一个网络图中,表示整个网络开始的节点称为网络图的起点节点;表示整个网络最终完成的节点称为网络图的终点节点;其余称中间节点。
而网络图中又将线路分为:关键线路和非关键线路两类;由此可确定出网络计划工期,关键工作和非关键工作,利用非关键工作的机动时间,科学地、合理地调配资源和对网络计划进行优化。
2.单代号网络图。
用一个大圆圈或方框表示一项工作,工作的编号写在圆圈和方框的中部,完成工作所需要的持续时间写在圆圈或方框的下部,箭线仅表示各项工作之间相互制约和依赖关系;用这种方法将一项工程(或计划)的所有工作,根据其开展的先后顺序和相互制约、相互依赖的逻辑关系,从左向右排列起来所形成的网状图形。
单代号网络图和双代号网络图(习题)

13.4 双代号网络图时间参数的计算
13.4.1 概述 1.网络图时间参数计算的目的:
目的在于确定网络图上各项工作和节点的时间参数,为网络计 划的优化、调整和执行提供明确的时间概念。 2.时间参数计算的内容:
工作持续时间、节点时间参数、工作时间参数 3.计算方法:
图上计算法、分析计算法、表上计算法、矩阵计算法、 电算法。
②形成条件:
ESi j ETi
h
i
FБайду номын сангаас i j
D i j
ES jk ETj
j
k
③计算公式:
FFij ETj ETi Dij ETj (ETi Dij ) ETj EFij
FF i j
27
13.4.4 关键工作和关键线路的确定 在网络计划中,总时差最小的工作称为关键工作。
【示例】计算下图各项时间参数。
序号 工作之间的逻辑关系 1 A、B两项工作依次施工
2
A、B、C三项工作同时 开始施工
3
A、B、C三项工作同时 结束
网络图中的表示方法
A
B
A B C A B C
说明 A制约B的开始,B 依赖A的结束
A、B、C三项工作 为平行施工方式
A、B、C三项工作 为平行施工方式
A、B、C三项工作,A 4 结束后,B、C才能开始
⑶计划工期: 根据计算工期和要求工期确定的工期。用 Tp 表示。
2.三种工期的关系:
Tc ≤ Tp≤ Tr
◆无要求工期时,计算工期等于计划工期。
29
【示例】某网络计划的有关资料如图所示,试绘制双代号网络图, 并计算各项工作的时间参数,判定关键线路。
工 作A B C D E F G H
(完整版) 单代号网络图和双代号网络图

工序 A
B
C
D
E
F
G
紧前 工序
A BC BC DE E
27
精选课件
三、 双代号网络图时间参数的计算
(一) 概述 1.网络图时间参数计算的目的:
目的在于确定网络图上各项工作和节点的时间参数,为网络计划的优化、调整和 执行提供明确的时间概念。 2.时间参数计算的内容:
节点时间参数、工作时间参数
3.计算方法:
36
精选课件
利用标号法确定关键线路
B
E
8
3
6
7
G 5
1
A 5
2
5
D 10
6
9
I 4
10
C 6
4
F
4
8
H 7
37
精选课件
(三)工期的确定 工期:泛指完成任务所需的时间。
计算工期、要求工期、计划工期
1.三种工期的概念:
⑴计算工期: ⑵要求工期:
由时间参数计算确定的工期,即关键线路的各项工作总持续时间。 用 Tc 表示。
D
4
9
F
1
5
精选课件
H 3
6
I 7
4.节点与工作的关系:
i
前导工作 (紧前工作)
后续工作 (紧后工作)
5.节点编号:
⑴目的: ①便于网络图时间参数的计算; ②便于检查或识别各项工作。
⑵原则: ①编号从小到大,可不连续但不允许重复编号;
②箭尾编号必须小于箭头编号,即:i<j。
9
精选课件
(三) 线路
3
精选课件
四、 网络计划技术的优点
1.能全面而明确地反映出各项工作之间开展的先后顺序和它们之间的相 互制约、相互依赖的关系; 2.可以进行各种时间参数的计算;
网络计划图常用时间参数和浮时计算方法

网络计划图常用时间参数和浮时计算方法首先弄清楚这两个概念:所谓总时差,就是不影响总工期的前提条件下,本工作可以利用的机动时间。
自由时差就是不影响紧后工作最早开始时间进行的前提下,本工作可以利用的机动时间。
自由时差总是小于等于总时差。
本工作的自由时差FF={紧后工作最早开始时间- 本工作最早完成时间}min。
本工作的总时差TF ={紧后工作的总时差+ 本工作与紧后工作自由时差}min。
主要是记住六个符号。
即ES EF LS LF TF FF在双代号网络图里:某工作的总时差=该工作最迟完工时间-该工作最早完工时间或该工作的总时差也可以=该工作最迟开工时间-该工作最早开工时间该工作的自由时差=该工作的紧后工作最早开工时间-该工作最早完工时间若该工作有多个紧后工作的话取其中最早开工的工作的最早开工时间。
在单代号网络图里比较麻烦该工作的自由时差=该工作紧后工作最早开始时间与该工作最早完成时间差的最小值。
本工作的总时差=该工作紧后工作的总时差与该工作与该工作紧后工作自由时差所得之和的最小值双代号网络图里TF=LS-ES or TF=LF-EFFFi,n=Tp-EFi,nFFi,j=ESj,k-EFi,j单代号网络图里TFn=0TFi=min(TFj+LAGi,j)FFi,n=Tp-EFi,nFFi=min(LAGi,j)总时差是不影响总工期的情况下该工作可以利用的机动时间自由时差是在不影响后续工作的情况下该工作可以利用的机动时间自由时差=紧后工作最早开始时间-本工作最早完工时间打个比方有个工程分为2部分完成(后面称为A部分和B部分),总工期为4天。
A部分需1天完成,其后续B部分要2天完成。
若A拖延一天从第二天开始开工,项目全部完成正好4天,不影响总工期,所以总时差为1天。
若A不拖延那么A部分最早第一天就可完成,而B部分最早第二天就可以开工,则A部分自由时差也是1天。
只要A拖延,后续工作B的最早开始时间一定受影响,当A部分拖延一天以上不仅影响后续工作B最早开始时间而且影响总工期。
(完整版) 单代号网络图和双代号网络图

双代号网络图表示法:
i
工作名称 持续时间
j
三、 网络计划技术的基本原理 1.利用网络图的形式表达一项工程中各项工作的先后顺序及逻辑关系;
2.通过对网络图时间参数的计算,找出关键工作、关键线路;
3.利用优化原理,改善网络计划的初始方案,以选择最优方案;
4.在网络计划的执行过程中进行有效的控制和监督,保证合理地利用资源, 力求以最少的消耗获取最佳的经济效益和社会效益。
A A B
说明 A制约B的开始,B依赖A 的结束 A、B、C三项工作为平 行施工方式
2
B C A
3
A、B、C三项工作同时结束
B C
A、B、C三项工作为平 行施工方式
4
A、B、C三项工作,A结束后, B、C才能开始
B A C
A制约B、C的开始,B、 C依赖A的结束,B、C为 平行施工
序号 5
工作之间的逻辑关系 A、B、C三项工作,A、B结束后, C才能开始
2.3 网络计划
2.3.1 概述
一、网络计划技术
二、网络图
三、网络计划技术的基本原理 四、网络计划技术的优缺点
2.3.1 概述
一、 网络计划技术 它是一种以网络图形来表达计划中各项工作之间相互依赖、相互制约的关系;分 析其内在规律,寻求其最优方案的计划管理技术。 二、 网络图 由箭线和节点组成的,用来表示工作的开展顺序及其相互依赖、相互制约关系的 有向、有序的网状图形。 单代号网络图表示法:
四、 网络计划技术的优点 1.能全面而明确地反映出各项工作之间开展的先后顺序和它们之间的相 互制约、相互依赖的关系;
2.可以进行各种时间参数的计算;
3.能在工作繁多、错综复杂的计划中找出影响工程进度的关键工作和关键
单代号网络图和双代号网络图详讲

工作
紧前 工作
A
-
B
A
C
A
D
B G
E
B、C G
F
C H
G
H
I
D、E E、F H、G I I -
紧后 B、C D、E E、F 工作
工作 紧前 工作
A -
B A
C A
D B G
E B、C G
F C H
G
H
I
D、E E、F H、G I I -
紧后 B、C D、E E、F 工作
B
3
D
7
G
1
A
2 C
5
E
6 H
4.在网络图中,只允许有一个终点节点,不允许出现没 有后续工作的“尽头”节点;
5.在网络图中,不允许出现重复编号的工作;
6.在网络图中,不允许出现没有开始节点的工作;
单代号网络计划时间参数的标注形式
ESi TFi EFi
工作名称
ES j TF j EFj
i
j
工作名称
Di
LS i FFi LFi
Dj
3
11 14
4
3
砌墙2
4 1 5
8 0 9
5
抹灰2
9 0 9
14 0 14
8
门窗2
14 17 1 0 15 18
10 17 21
涂料2
1
1
4
5
3
4
18 22
6
砌墙3
8
2
12
2
9
抹灰3
14 19 0 0 14 19
11 19 22
门窗3
12 22 26
网络计划计算简易方法及技巧速成

还是以上面的网络图为例,计算E工作的总时差: 以E工作为起点工作,通过E工作的线路有EH和EJ,两条线路的波形线的和都是2,所以此时E的总时差就是2。再比如,计算C工作的总时差:通过C工作的线路有三条,CEH,波形线的和为4;CEJ,波形线的和为4;CGJ,波形线的和为1,那么C的总时差就是1。
双代号时标网络图时间参数计算技巧
1双代号时标网络计划的概念
绘制规则 按最早时间绘制; 各工作的时间参数由其在时标表上的水平位置表示; 各工作持续时间由其水平投影长度表示; 自由时差由波形线表示。
1
2
注意:
2.2 时标网络计划的时间参数计算
没有紧后工作的工序 总时差=自由时差 关键路线:没有波形线的路线 时间参数的确定 计算工期 工作最早时间 工作自由时差 工作总时差* 工作最迟时间
1.1双代号网络计划概述
3)时差:一段时间 总时差 =工序推迟开工而不会影响总工期的最大时间=LS-ES=LF-EF 自由时差 =不影响紧后工作的最早开始时间的最大时间=min{紧后工作的ES}-EF
01
03
02
[例题]
在工程网络计划执行过程中,发现某工作的实际进度比其计划进度拖后5天,影响总工期2天,则该工作原来的总时差为 天
01
10
02
ቤተ መጻሕፍቲ ባይዱ
解:总时差=min{紧后工作的总时差+两者的工作间隔 对I工作:3+8=11 对J工作:4+6=10
03
[例题]
1单代号搭接网络计划概述
1
2单代号搭接网络计划的计算
2
4 单代号搭接网络计划
4.1单代号搭接网络计划概述
搭接关系的种类和表达方式 两种关系,四种时距
项目管理-单-双代号网络图
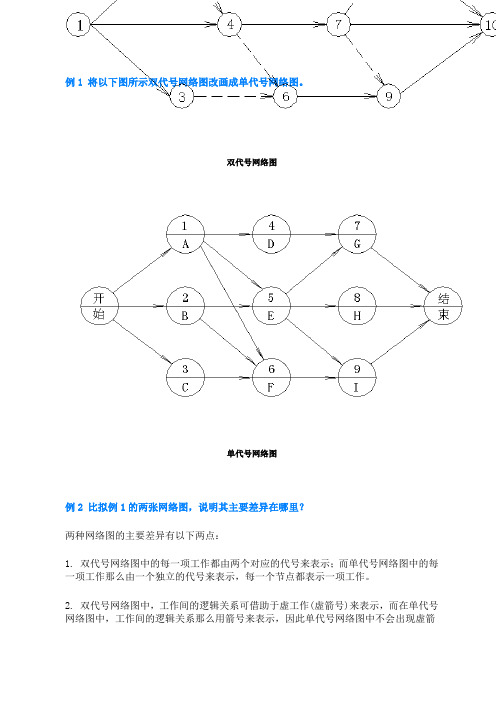
例1 将以下图所示双代号网络图改画成单代号网络图。
双代号网络图单代号网络图例2 比拟例1的两张网络图,说明其主要差异在哪里?两种网络图的主要差异有以下两点:1. 双代号网络图中的每一项工作都由两个对应的代号来表示;而单代号网络图中的每一项工作那么由一个独立的代号来表示,每一个节点都表示一项工作。
2. 双代号网络图中,工作间的逻辑关系可借助于虚工作(虚箭号)来表示,而在单代号网络图中,工作间的逻辑关系那么用箭号来表示,因此单代号网络图中不会出现虚箭号。
一幅单代号网络图中,只会出现两个虚设的工作节点,那就是表示方案开场的虚工作节点和表示方案完毕的虚工作节点。
例3 以下图为一单号网络图,网络图各圆圈中横线上边的数字是工作代号,横线下边的数字是工作持续时间。
试用图上计算法计算各工作的最早可能开场时间ES i、最迟必须开场时间LS i、总时差TF i和部分时差FF i,标记出关键线路并确定总工期。
解:根据题意用图算法推算出的各工作时间参数,见上图,关键线路用粗箭号表示。
该网络图的方案总工期为11天。
例4 某工程的单代号网络如以下图所示。
试用表上计算法求出网络图中各工作的ES i、EF、LS i、LF i、TF i、和FF i;确定关键工作并在图上说明关键线路;确定方案总工期(注:i以下图中圆圈内横线上边为工作代号,横线下边为工作持续时间)。
解:用表算法推算了各工作的时间参数见下表。
该网络图的关键线路共有3条,它们分别为:方案总工期为19天。
一、网络方案技术根本概念二、网络图的绘制:知识点总结与归纳三、网络方案时间参数的计算〔一〕、网络方案时间参数的概念〔二〕、双代号网络方案时间参数的计算双代号网络方案的时间参数既可以按工作计算,也可以按节点计算。
A.按工作计算法所谓按工作计算法,就是以网络方案中的工作为对象,直接计算各项工作的时间参数。
这些时间参数包括:工作的最早开场时间和最早完成时间、工作的最迟开场时间和最迟完成时间、工作的总时差和自由时差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在计算中常用下列符号来表示工作的各种时间参数:
——工作i 的持续时间;——工作i 的最早开始时间;
——工作i 的最早结束时间;——工作i 的最迟开始时间;
——工作i 的最迟结束时间;——工作i 的总时差;
——工作i 的自由时差。
单代号网络图的计算也可采用图上计算法或表上计算法,其计算步骤如下:
1 .计算工作最早时间
(1 )计算工作最早开始
工作i 的最早开始时间ES i 应从网络图的起点节点开始,顺着箭线方向依次逐项计算。
a. 起点节点i 的最早开始时间ES i 无规定时,其值应等于零,即:ES i =0 (i =1 )(12-27 )
b. 其他工作的最早开始时间ES i
ES i =max{ EF h } (12-28 )
或ES i =max{ ES h + D h } (12-29 )
式中EF h ——工作i 的各项紧前工作h 的最早结束时间;
ES h ——工作i 的各项紧前工作h 的最早开始时间;
D h ——工作i 的各项紧前工作h 的持续时间。
•工作i 的最早完成时间EF i
EF i =ES i + D i (12-30 )
2 .工期
单代号网络计划计算工期T c 应按下式计算:T c =EF n (12-31 )
式中EF n ——终点节点n 的最早完成时间。
类似的,单代号网络计划计算工期得到后,可以确定的计划工期T p ,计划工期也应满式(12-4 )的要求。
3 .计算前后工作时间间隔
相邻两项工作i 和j 之间的时间间隔LAG i ,j 的计算应符合下列规定:
(1 )当终点节点为虚拟节点时,其时间间隔应为:
LAG i ,n = T p – EF i (12-32 )
(2 )其他节点之间的时间间隔应为:LAG i ,j =ES j – EF i (12-33 )
4 .时差
(1 )总时差
工作i 的总时差TF i 应从网络计划的终点节点开始,逆着箭线方向依次逐项计算。
当部分工作分期完成时,有关工作的总时差必须从分期完成的节点开始逆向逐项计算。
a. 终点节点所代表工作n 的总时差TF n 值应为:
TF n =T p – EF n (12-34 )
b. 其他工作i 的总时差TF i 应为:
TF i =min{ TF j + LAG i ,j } (12-35 )
(2 )自由时差
a. 终点节点所代表工作n 的自由时差FF n 应为:
FF n =T p – EF n (12-36 )
b. 其他工作i 的自由时差FF i 应为:
FF i =min{ LAG i ,j } (12-37 )
5 .工作最迟时间
(1 )工作最迟完成时间
工作i 的最迟完成时间LF i 应从网络计划的终点节点开始,逆着箭线方向依次逐项计算。
当部分工作分期完成时,有关工作的最迟完成时间应从分期完成的节点开始逆向逐项计算。
a. 终点节点所代表的工作n 的最迟完成时间LF n ,应按网络计划的计划工期T p 确定,即:
LF n = T p (12-38 )
b. 他工作i 的最迟完成时间LF i 应为:
LF i = min{ LS j } (12-39 )
或LF i = EF i + TF i (12-40 )
式中LS j ——工作i 的各项紧后工作j 的最迟开始时间。
(2 )工作最迟开始时间
工作i 的最迟开始时间LS i 应按下式计算:
LS i = LF i – D i (12-41 )
或LS i = ES i + TF i (12-42 )
在单代号网络图中关键线路是从起点节点开始到终点节点均为关键工作,且所有工作的时间间隔均为零的线路。
