基于最小二乘法的永磁同步电机参数辨识综述
永磁同步电动机转动惯量辨识与参数自整定

Key words: permanent magnet synchronous motor; rotary inertia; observer; parameter self-tuning
0 引言
永磁同步电动机是一个多变量、 强耦合、 非线 性的控制对象, 而且其模型参数时变, 这就要求对 电机参数进行实时采样, 使得伺服系统的控制器 结构和控制器参数能够随电机参数的变化而做适
(1)
将式(1)转化为如下最小二乘格式:
[1-3] 当的调整, 以改善控制效果。
响很大, 直接关系到伺服系统的运行性能。由于 永磁同步电动机的转动惯量直接测得比较难, 所 以目前对转动惯量的测量都是间接辨识得到的, 常用的转动惯量辨识方法有状态观测器法、 扩展 卡尔曼滤波法、 高频电压注入法 [4]、 模型参考自适 应法[5] 等。 本文介绍了一种新的转动惯量辨识算法, 通 过全阶速度观测器观测到的电磁转矩和电机电角 速度, 然后利用最小二乘法实时地在线辨识电机
( 1. School of Mechanical and Electrical Engineering, Putian University, Putian Fujian 351100, China; 2. Fujian Laser Precision Machining Engineering Technology Research Center, Putian Fujian 351100, China )
56
莆 田 学 院 学 报
2017 年 4 月
ห้องสมุดไป่ตู้
的转动惯量。将辨识得到的转动惯量用于在线修 正速度控制器的参数, 最后通过仿真验证了算法 的可行性。
代下去。当系统的准则函数为最小值时, 则便可 近似认为模型的输出量 ŷ ( ∞ ) 等于输出量 y ( ∞ ), 其 中辨识得到的参数 θ̂ ( ∞ ) 就是实际系统的参数 θ。
基于扩展卡尔曼滤波器的交流永磁同步电机参数辨识的开题报告

基于扩展卡尔曼滤波器的交流永磁同步电机参数辨识的开题报告一、选题背景及意义交流永磁同步电机(PMSM)具有结构简单、质量轻、体积小、效率高、起动与调速性能优越等特点,已被广泛应用于电力、工业、交通等领域。
PMSM的参数辨识问题一直是电机控制领域研究的热点问题之一。
精确的参数辨识可以大大提高PMSM控制系统的性能和效率。
传统的基于最小二乘法的PMSM参数辨识方法依赖于直流和交流侧测量的电量,当输入电流和速度有较大偏差时,容易出现辨识精度较低的情况。
因此,使用基于扩展卡尔曼滤波器(EKF)的PMSM参数辨识方法来获得更准确的参数估计值,已成为一种热门研究方向。
二、研究目标本课题旨在设计一种基于EKF的PMSM参数辨识方法,以获得准确的参数估计值。
研究内容包括以下几个方面:1.建立PMSM的数学模型,包括电压、电流、转速等物理量的方程。
2.设计EKF算法,用于提高参数辨识的准确性。
3.编写MATLAB程序,实现样本数据的采集、处理及EKF算法的实现。
4.通过仿真实验和实际实验验证所设计的基于EKF的PMSM参数辨识方法的有效性和准确性。
三、研究内容1. PMSM的研究与数学模型建立本课题将研究PMSM的结构、特性、运行原理及数学模型。
对PMSM进行建模,通过建立电压、电流、转速等物理量的方程,为后续的参数辨识提供数学基础。
2. EKF算法的设计与实现将EKF算法应用于PMSM参数辨识过程中,可提高参数估计的准确性。
本课题将研究EKF算法的基本原理、实现过程及其在PMSM参数辨识中的应用,实现算法的设计与实现。
3. 样本数据采集和处理本课题将进行样本数据的采集和处理。
采集到的数据将作为基于EKF的PMSM参数辨识的输入,包括电机电流、电压、转速等实时信号。
4. 基于EKF的PMSM参数辨识仿真及实验根据所设计的基于EKF的PMSM参数辨识方法,开展仿真及实验验证。
通过对仿真结果和实验结果的分析,验证研究成果的有效性和准确性。
相关_最小二乘两步法在辨识中的应用与改进
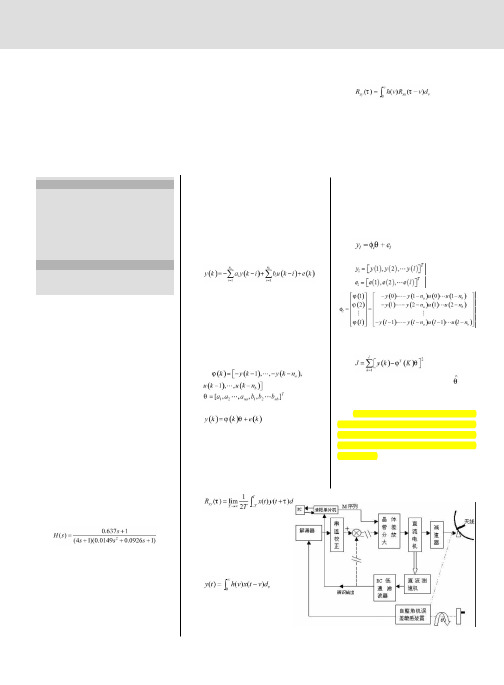
图 2 Figure.2 the comparison of R 梯 and R矩
(11)
这种形式便于计算机求解,是目前普 遍使用的求解方法。式中N △ t 要大于系统 的调整时间。同样,自相关函数 Rxx(τ) 和互相关函数 R xv(τ)都是用有限和来 近似计算积分的,引起的截断误差正比于 △ t 2。这样,在辨识中存在的误差源主要 有随机干扰,量化误差,有限和代替积分产 生的误差。其中人为误差只有有限和代替 积分产生的截断误差,结合仿真结果,我们 得出:截断误差仅仅影响到对传递函数零 点的估计,对极点估计没有影响。这样我们 可以快速,高精度地估计出系统传递函数
Байду номын сангаас
的极点,从而判定系统的稳定性。
6 互相关函数计算的梯形法改进
在前面提到,数字计算机中积分是化 为有限和近似计算的。由分析可以得知, 这种有限和计算实际上是积分的矩形近 似,引起的截断误差正比于△ t 2。我们可 以用梯形法作一改进,以减小截断误差。
将梯形近似公式
(12) 运用在互相关函数中,可得:
(2) 则(1 )式可以表示为:
(3) 所以只要能正确的利用输入、输出序 列估计出θ就能得到被辨识系统的传递函 数, 最小二乘法是一种估计θ值的方法。 3.2 辨识方法 3.2.1 互相关函数法 相关性可用互相关函数来表示:
(4) τ是时间间隔。 当 x(t)=y(t)时,互相关
函数就变成了自相关函数。 设 t=0 时,x(t)=0,而且 t
若想得到系统的精确模型可以采取减小截断误差的方法如梯形近似法甚至四阶龙10可以把r看作是系统在rxvxx入下的响应这样要获得该系统的参数模型只需把分别看作xxxv系统的输入和输出然后按最小二乘法估计参数
第五章 最小二乘法辨识

服从正态分
❖ 4)有效性
❖ 定理4:假设 (k) 是均值为零,方差为 2I 的正态
白噪声,则最小二乘参数估计量
^
是有效估计
量,即参数估计误差的协方差达到Cramer-Rao不
等式的下界
E (^
^
)(
)T
2E
(
T N
N
) 1
M 1
❖ 其中M为Fisher信息矩阵。
4、适应算法
❖ 随着更多观测数据的处理,递推最小二乘法对线性 定常系统的参数估计并非越来越精确,有时会发现
❖ 现举例说明最小二乘法的估计精度 ❖ 例5.1:设单输入-单输出系统的差分方程为
y(k) a1y(k 1) a2 y(k 2) b1u(k 1) b2u(k 2) (k)
❖ 设 u(k)是幅值为1的伪随机二位式序列,噪声 (k)是 一个方差 2可调的正态分布 N(0, 2 )随机序列。
❖ 为了克服数据饱和现象,可以用降低旧数据影响的 办法来修正算法。而对于时变系统,估计k时刻的 参数最好用k时刻附近的数据估计较准确。否则新 数据所带来的信息将被就数据所淹没。
❖ 几种算法:渐消记忆法,限定记忆法与振荡记忆法
❖ 矩阵求逆引理:设A为 n n 矩阵,B和C为 n m 矩阵,
并且A, A和 BCT I CT都A是1B 非奇异矩阵,则有矩
阵恒等式
A BCT 1 A1 A1B(I CT A1B)1CT A1
❖
令
A
PN1
,B
N 1
,C
T N 1
,根据引理有
PN1
T N 1 N 1
1
❖ 算法中,^ N 为2n+1个存贮单元(ai ,bi ,i 1,2, , n), 而 PN 是 (2n 1) (2n 1)维矩阵,显然,将 N 换成 PN 后,存贮量大为减少(因为n为模型的阶数,一般 远远小于N)
最小二乘参数辨识方法及原理

' ' ' f cy ( x, y) , f cy ( x, y) x , f cy ( x, y) y ] T ;
Y ( x, y ) = f r ( x, y) f c ( x, y) ;
i 1 i 1 n n
如果定义
h(k ) [ y(k 1), y(k 2),, y(k n),u(k 1),u(k 2),, u(k n)]
[a1 , a2 ,, an , b1 , b2 ,, bn ]
T
z (k ) h(k ) v(k )
z ( k ) y ( k ) v( k )
z
1、问题的提出
v(k )
t (k )
G (k )
y (k )
z (k )
m次独立试验的数据
f (t )
(t1 , y1 ) (t2 , y2 )
t
(tm , ym )
z(k ) a0 a1h1 (k ) a2h2 (k ) an hn (k ) v(k )
2.1 利用最小二乘法求模型参数
例:表 1 中是在不同温度下测量同一热敏电阻的阻值,根 据测量值确定该电阻的数学模型, 并求出当温度在 70 C 时
的电阻值。
表 1 热敏电阻的测量值
t (C ) R ()
20.5 765
26 790
32.7 826
40 850
51 873
61 910
73 942
零偏 标度因数 输出轴灵敏 度误差系数 二阶非线性 误差系数 摆轴灵敏度 误差系数
小二乘参数辨识方法及原理

目录
• 引言 • 小二乘参数辨识方法 • 小二乘参数辨识原理 • 小二乘参数辨识的应用 • 小二乘参数辨识的优缺点 • 小二乘参数辨识的未来发展
01
引言
目的和背景
目的
小二乘参数辨识方法是一种数学优化技术,旨在通过最小化预测值与实际观测值之间的平方误差和,来估计模 型参数。这种方法广泛应用于各种领域,如系统辨识、回归分析、机器学习等。
易于理解和实现
最小二乘法的原理直观易懂,且易于通过编程实现。
缺点
对异常值敏感
最小二乘法对数据中的异常值非常敏感,异常值可能会对参数估计 产生显著影响。
假设限制
最小二乘法要求误差项是随机的且服从正态分布,这在某些情况下 可能无法满足。
无法处理非线性问题
最小二乘法主要用于线性回归问题,对于非线性问题,可能需要其他 方法。
将小二乘参数辨识方法应用于机器学习中,提高模型 的训练效率和精度。
控制系统
将小二乘参数辨识方法应用于控制系统中,实现系统 的优化和自适应控制。
生物医学工程
将小二乘参数辨识方法应用于生物医学工程中,实现 对生理信号的准确分析和处理。
感谢您的观看
THANKS
背景
随着现代科技和工程领域的快速发展,越来越多的复杂系统需要建立数学模型进行描述和预测。小二乘参数辨 识方法作为一种有效的参数估计方法,能够为这些复杂系统的建模提供重要的技术支持。
小二乘参数辨识的定义
定义
小二乘参数辨识,也称为最小二乘法,是一种通过最小化观测数据与模型预测数据之间的平方误差和来估计模型 参数的方法。这种方法的基本思想是通过最小化误差的平方和来找到最佳的参数值,使得模型的预测结果与实际 观测结果之间的差异最小。
一种永磁同步电机离线参数辨识方法与流程

一种永磁同步电机离线参数辨识方法与流程摘要:本报告深入分析了永磁同步电机(PMSM)的离线参数辨识方法和流程,这是确保电机性能和控制最优化的关键环节。
报告详细描述了识别关键参数如定子电阻、定子电感和永磁体磁链的步骤,这些步骤包括了对电机模型的构建、参数的初步估计以及最终的参数调整。
报告强调了这些过程中所需的精确度以及准确参数辨识对电机效率和控制精度的影响,指出精确的参数辨识能够显著提升电机的运行性能和响应速度。
同时,报告还讨论了参数辨识中面临的挑战,例如环境噪声、电机老化等因素对参数辨识准确性的影响。
此外,报告还探讨了先进算法和设备在克服这些挑战中的作用,例如使用遗传算法、粒子群优化等智能算法来提高参数辨识的准确性和效率,以及采用高精度测量设备来减少测量误差。
关键词:永磁同步电机;离线参数辨识;电机控制;效率;精度Abstract: This report provides an in-depth analysis of the offline parameter identification methods and processes for Permanent Magnet Synchronous Motors (PMSM), which are crucial for ensuring optimal motor performance and control. The report details the steps involved in identifying key parameters such as stator resistance, stator inductance, and permanent magnet flux linkage. These steps include the construction of the motor model, preliminary estimation of parameters, and final parameter tuning. The report emphasizes the precision required during these processes and the impact of accurate parameter identification on motor efficiency and control accuracy, noting that precise parameter identification can significantly enhance motor operational performance and response speed. Additionally, the report discusses the challenges faced during parameter identification, such as the effects of environmental noise and motor aging on the accuracy of parameter identification. Furthermore, the report explores the role of advanced algorithms and equipment in overcoming these challenges, such as using intelligent algorithms like genetic algorithms and particle swarm optimization to improve the accuracy and efficiency of parameter identification, and employing high-precision measurement devices to reduce measurement errors.Keywords: Permanent Magnet Synchronous Motor; Offline Parameter Identification; Motor Control; Efficiency; Precision一、引言1.1研究背景在现代工业与电力系统领域,永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)因其高效、高功率密度和良好的控制性能等优点而得到广泛应用。
基于转速扰动的表贴式永磁同步电机参数辨识

电气传动2017年第47卷第8期基金项目:荆楚理工学院校级科研基金(QN201604)作者简介:邓鹏(1981-),男,硕士研究生,讲师,Email :dp12356@基于转速扰动的表贴式永磁同步电机参数辨识邓鹏(荆楚理工学院电子信息工程学院,湖北荆门448000)摘要:为解决表贴式永磁同步电机参数在线辨识时参数辨识耦合造成的辨识误差,从电机数学模型角度分析了参数辨识时的耦合关系,并通过仿真验证了表贴式永磁同步电机参数辨识时的定子电阻和转子磁链的耦合关系,同时提出了一种基于转速扰动的递推最小二乘法永磁同步电机在线解耦参数辨识方法。
该方法通过加入转速扰动结合递推最小二乘辨识方法实现了交直轴电感、定子电阻、转子磁链的在线解耦辨识。
实验和仿真验证了转速扰动的注入可以有效实现解耦辨识。
关键词:表贴式;解耦辨识;递推最小二乘;转速扰动中图分类号:TM341文献标识码:ADOI :10.19457/j.1001-2095.20170803Parameter Identification of Surface Mount Permanent Magnet SynchronousMotor Based on Rotational Speed DisturbanceDENG Peng(College of Electronic and Information Engineering ,Jingchu University of Technology ,Jingmen 448000,Hubei ,China )Abstract:In order to solve the identification error caused by parameter identification coupling in the on ⁃lineidentification of surface⁃mount permanent magnet synchronous motor ,the coupling relation of parameter identification from the view of motor mathematical model was analyzed.The coupling relation between the stator resistance and the rotor flux linkage of the surface⁃mount permanent magnet synchronous motor was verified by simulation.A method of on⁃line decoupling parameter identification based on recursive least square method for speed⁃perturbation was also proposed.In this method ,on⁃line decoupling identification of q ⁃axis and d ⁃axis inductance ,stator resistance and rotor flux linkage were realized by adding rotational speed perturbation method and recursive least square identification method.Experiments and simulations show that the injection of rotational perturbation can effectively realize decoupling identification.Key words:surface mount type ;decoupled identification ;recursive least square ;speed disturbance永磁同步电机(PMSM )由于转子侧无需励磁线圈,具有结构简单、效率高、控制方便等优点,在当前工业控制领域很受青睐[1-3]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于最小二乘法的永磁同步电机参数辨识综述 姓名:张清路 学号:S201102222 专业:控制工程 摘要:与传统电机相比,永磁同步电机具有诸多优点,因而应用非常广泛,而电机的
参数是否准确在电机的控制中具有重要意义,因此对于电机参数辨识的研究既是一个理论课题,也是一个实际应用课题。有关这方面的研究,很多科研人员做了大量工作,有参数的离线辨识和在线辨识,有在假定理想的线性状态下的辨识,也有考虑到实际情况的非线性因素下的参数辨识等等。其中频域响应法,Kalman滤波等方法都是应用比较广泛的电机参数辨识方法,但这些方法在实际应用中有不少限制条件和实现的困难。本文以系统辨识理论为基础,介绍了基于最小二乘的电机参数辨识方法。
1引言 系统辨识是研究如何利用系统试验或运行的、含有噪声的输入输出数据来建立被研究对象数学模型的一种理论和方法。系统辨识与控制理论有着密切的关系,随着计算机技术的发展和对系统控制技术要求的提高,控制理论得到了广泛的应用。在控制理论的应用中,要想获得理想的使用效果,则与能获得被控对象精确的数学模型是分不开的。但是,在很多情况下,被控对象的数学模型是不知道的,有时,系统的正常运行期间的数学模型的参数也会发生变化,这就使得依赖这个模型运行的系统控制效果大打折扣,甚至能使系统失控。因此,在应用控制理论进行控制时,建立控制对象的数学模型是基础,这是控制理论能否应用成功的关键所在。所谓通过系统辨识建立对象数学模型的依据是:研究表明,从外部对系统的认识,是通过其输入输出数据来实现的,而数学模型是表述系统动态特性的一种描述方式,系统的动态特性的表现必然蕴含在它变化的输入输出数据中。所以,通过记录系统在正常运行时的输入输出数据,或通过测量系统在人为输入作用下的输出响应,然后对这些数据进行适当的系统处理、数学计算和归纳整理,提取数据中包含的系统信息,从而建立被控对象的数学描述,这就是系统辨识。即系统辨识就是利用数学的方法从输入输出数据中提取对象数学模型的方法。
2 系统辨识 2.1定义 系统辨识是在已知和测得系统输入和输出的基础上,从一组给定的模型类中,确定一个与所测系统等价的模型。要素为:数据:指系统过程的输入数据和输出数据,塔是辨识的基础。模型类:指各种已知的系统过程模型集合,它是辨识时寻找模型的范围。等价准则:指系统行为相似性、系统效用等同性的识别标准,它是辨识优化的目标。辨识的实质就是按某种准则,从一组已知模型类中选择一个模型,使之能最好地拟合实际过程的动态特性。观测数据含有噪声,因此辨识建模实际上是一种实验统计的方法,所获得的模型只是与实际过程的外特性等价的一种近似描述。 2.2 系统辨识的误差准则 误差准则是辨识问题中不可缺少的三大要素之一,它是用来衡量模型接近实际过程的准则,它通常被表示为一个误差的泛函。因此误差准则也称为等价准则、损失函数、准则函数、误差准则函数等。这里的误差函数应该广义地理解为模型与实际过程之间的“误差”,也可以是输出误差、输入误差和广义误差。当扰动是作用在系统输出端的白噪声时,一般选择输出误差形式。但是,输出误差通常是模型参数的非线性函数,因而在这种误差准则意义下,辨识问题将归结为复杂的非线性优化问题。由于在确定这种情况的最优解时,需要用梯度法、牛顿法、共轭梯度法等迭代的最优算法,因而使得辨识算法比较复杂。如果扰动是作用在输入端的白噪声,则选用输入误差准则。这种误差准则也是模型参数的非线性函数,也是比较复杂的。因而这种误差一般仅具有理论意义,实际应用种几乎用不到。在广义误差中,最常用的是方程式误差。这种误差准则是模型参数的线性函数,求它的最优解是比较简单的,因而许多辨识算法都采用了这种误差准则[1]。 2.3系统辨识的内容和步骤 辨识问题分为模型结构辨识和参数辨识(或估计)。当系统模型结构根据工程经验或采用模型结构的辨识确定后,主要的问题是模型的参数估计。从以上的分析可见,系统辨识的内容主要包括四个方面:实验设计、模型结构辨识、模型参数辨识以及模型检验[2]。 系统辨识的一般步骤如图3-1所示:
辨识目的
实验设计输入输出信号检测存储
先验知识模型结构设定辨识方法应用非参数模型辨识模型结构
辨识
模型检验
参数模型辨识
图3-1 系统辨识的一般步骤 2.4 闭环辨识方法及可辨识条件 由于电机的参数辨识是在闭环的电机控制系统下进行的,因此有必要对闭环辨识问题进行一定的讨论。 一般在讨论辨识方法时,都是假定辨识对象在开环条件下工作的。但在许多实际问题中,辨识不一定都是在开环状态下进行的。有的系统只能在闭环条件下工作,如果断开反馈通道,系统就不稳定。有的系统可能是大系统的一部分,而在这个大系统中不允许或不可能断开反馈通道,如经济系统和生物系统等。因为它们内部存在的反馈是客观的,不可消除的,它们的辨识只能在有反馈作用的状态下进行。所以闭环系统辨识是在实际应用中经常会碰到的问题。在研究闭环系统辨识时要注意两个方面的问题:一是当系统的反馈作用不明显或隐含时,必须首先判断系统是否存在反馈,如果将存在反馈作用的系统作为开环系统进行辨识,会带来很大的辨识误差,也可能会导致不可辨识;二是开环辨识方法需要附加什么条件才能用于闭环辨识[3]。 设辨识对象如图3-2所示: 图3-2 闭环辨识对象 在图3-2中,G(q-1)是前向通道上的过程函数;R(q-1)是反馈通道上的控制器传递函数;Nv(q-1)、Nω(q-1)分别是前向通道噪声v(k)和反馈通道噪声ω(k)的滤波器,Np(q-1)是摄动信号p(k)的滤波器;v(k)和ω(k)都是零均值,方差为σv2和σω2的互不相关的平稳随机噪声;p(k)是可测的;定值信号r(k)通常设为0。 闭环辨识方法可大概分为时域法和频域法,时域法又可分为直接辨识法、间接辨识法和联合输入输出过程法,频域法是在联合输入输出过程法的基础上发展起来的一种对输入输出联合功率谱密度进行分解的方法。其中直接辨识法是利用前向通道的输入输出数据,直接建立前向通道的数学模型,而无需反馈控制器的验前信息。间接辨识法是先获得闭环系统模型,再利用反馈控制器的模型,导出前向通道模型。 决定闭环可辨识性的因素很多,在工程实践中有人总结了如下几个结论: (1) 当反馈通道是线性非时变时,无扰动信号,且给定值恒定时,闭环可辨识条件为,反馈通道模型阶次不能低于前向通道的模型阶次,闭环传递函数也不可以有零极点相消的现象。若前向通道或反馈通道存在纯延迟环节,则对辨识更有利。 (2) 若反馈通道上有足够阶次的持续激励信号,且与前向通道上的噪声不相关,则闭环系统是结构性可辨识的。 (3) 若反馈控制器能在几种调节规律之间切换,或者反馈控制器是非线性或时变的,则闭环系统也是结构性可辨识的[4,5]。
3 最小二乘辨识方法 3.1基于RLS算法的PMSM转动惯量辨识器的实现 对于永磁同步电机控制系统,其性能受到永磁同步电机的转动惯量的影响较大,转动惯量的变化会对系统的机械特性造成明显的影响。 因此,当转动惯量变化时,需要对控制系统的运行参数进行相应的调整才能获得优良的控制性能。在实际的系统中PMSM的转动惯量很难直接测量,通常需要采用参数辨识的方法获得。曾经有一些学者针对PMSM控制系统中的转动惯量的辨识方法进行了不少的研究,提出了一系列的辨识策略,如加减速法、模型参考自适应法、最小二乘法等,其中最小二乘法原理简单,便于理解和掌握,并且在一定条件下具有良好的统计特性,能较好的实现对系统参数的离线辨识[20],因此具有较广泛的实际应用价值。在对系统的时变参数进行在线辨识时,可以在最小二乘算法中加入遗忘因子,即带遗忘因子的最小二乘算法。此方法的重点在于确定遗忘因子的大小,遗忘因子过大,则算法跟踪时变参数的能力就会变差,遗忘因子太小,则参数估计值的波动又太大,从而辨识的结果就会受到影响。因此,要使带遗忘因子的最小二乘算法具有较好的辨识效果,就必须通过大量的实验来确定合适的遗忘因子,这是在运用此方法时存在的难点。为解决该问题,本节在遗忘因子最小二乘算法的基础上,通过对辨识结果进行反馈,在参数变化的时候对辨识器重新初始化,从而丢掉原来老的数据,重新对变化后的系统参数进行辨识,这样就能够最大程度减小甚至避免了带遗忘因子最小二乘算法在辨识时造成的参数的波动性,改善辨识效果。下面通过算法设计并进行仿真来进行分析。 3.2 算法设计 针对递推最小二乘算法公式
)()1()1()()1()()1(mPmXmXmPmKmPmPT (1) 随着辨识次数的不断增加,所用到的数据越来越多,对于系统的时变参数,新数据产生的辨识结果会受到老数据的影响而精度降低。为了能够对时变参数具有跟踪能力,提高辨识精度,在递推最小二乘算法的基础上引入遗忘因子λ,即遗忘因子最小二乘法。则此算法公式在式(1)基础上变为:
)](ˆ)1()1()[1()()1()(ˆ)1(ˆmmXmymXmPmKmmT
)()1()1()()1()()1(mPmXmXmPmKmPmPT )]1()()1(/[1)1(mXmPmXmKT
由公式可知,当λ=1时,遗忘因子最小二乘法就变成递推最小二乘法,λ越大,算法跟踪时变参数的能力就越弱,λ越小,算法跟踪能力越强。 由上述分析可知,当要辨识参数发生变化时,为去除老数据对辨识结果的不利影响,解决参数的波动问题,可以对老数据完全去除,重新对数据进行初始化,读入新数据进行辨识,从而提高参数的辨识精度和速度。为实现上述解决问题的思路,引入一个开关控制器,当系统参数变化时,能适时的检测到,并对变化了的参数进行初始化,利用新采集到的数据对系统参数进行辨识,从而达到改善辨识效果的作用。最小二乘辨识器的原理图如图3-3所示:
待辨识系统
开关控制器辨识器
辨识结果
控制信号 Y X
图3-3 最小二乘辨识器原理图 图3-3中的辨识器对系统的运行数据进行采集,然后通过递推最小二乘算法对待辨识系统参数进行辨识,将辨识结果反馈到开关控制器,开关控制器根据辨识的结果对辨识器进行控制。最小二乘辨识器的输出为: T
iˆˆˆˆ21
定义误差E为当前时刻各个参数的辨识结果和前一时刻辨识结果的差的绝对值之和,
