(完整word版)江苏高考数学填空题压轴题精选1
【压轴题】高考数学试题(带答案)

【压轴题】高考数学试题(带答案) 一、选择题 1.通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:
男 女 总计
爱好 40 20 60
不爱好 20 30 50
总计 60 50 110
由2222()110(40302030),7.8()()()()60506050nadbcKKabcdacbd
算得
附表: 2()PKk 0.050 0.010 0.001
k 3.841 6.635 10.828
参照附表,得到的正确结论是( ) A.有99%以上的把握认为“爱好该项运动与性别有关
”
B.有99%以上的把握认为“爱好该项运动与性别无关
”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关
”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关
”
2.一个频率分布表(样本容量为30)不小心被损坏了一部分,只记得样本中数据在
2060,上的频率为0.8,则估计样本在40,50、50,60内的数据个数共有( )
A.14 B.15 C.16 D.
17 3.在ABC中,60A,45B,32BC,则AC( ) A.32 B.3 C.23 D.43
4.抛掷一枚质地均匀的硬币两次,在第一次正面向上的条件下,第二次反面向上的概率为( ) A.14 B.13 C.12 D.
2
3 5.下列各组函数是同一函数的是( )
①32fxx与2fxxx;3fx2xyx2x与②fxx与2gxx;
③0fxx与01gxx;④221fxxx与221gttt. A.① ② B.① ③ C.③ ④ D.① ④
6.在△ABC中,a=5,b=3,则sin A:sin B的值是( )
A.53 B.35 C.37 D.
5
7 7.甲、乙、丙,丁四位同学一起去问老师询问成语竞赛的成绩。老师说:你们四人中有两位优秀,两位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩,根据以上信息,则( ) A.乙、丁可以知道自己的成绩 B.乙可以知道四人的成绩
2023年新高考数学选填压轴题汇编(一)(学生版)

2023年新高考数学选填压轴题好题汇编(一)一、单选题1.(2022·广东·广州市真光中学高三开学考试)端午佳节,人们有包粽子和吃粽子的习俗,粽子主要分为南北两大派系,地方细分特色鲜明,且形状各异,裹蒸粽是广东肇庆地区最为出名的粽子,是用当地特有的冬叶、水草包裹糯米、绿豆、猪肉、咸蛋黄等蒸制而成的金字塔形的粽子,现将裹蒸粽看作一个正四面体,其内部的咸蛋黄看作一个球体,那么,当咸蛋黄的体积为4π3时,该裹蒸粽的高的最小值为( )A.4B.6C.8D.102.(2022·广东惠州·高三阶段练习)甲罐中有5个红球,3个白球,乙罐中有4个红球,2个白球.整个取球过程分两步,先从甲罐中随机取出一球放入乙罐,分别用A1、A2表示由甲罐取出的球是红球、白球的事件;再从乙罐中随机取出两球,分别用B、C表示第二步由乙罐取出的球是“两球都为红球”、“两球为一红一白”的事件,则下列结论中不正确的是( )A.P B A1=1021 B.P C A2=47 C.P B =1942 D.P C =43843.(2022·广东·鹤山市鹤华中学高三开学考试)已知直线ax-2by+14=0平分圆C:x2+y2-4x-2y-11= 0的面积,过圆外一点P a,b向圆做切线,切点为Q,则PQ的最小值为( )A.4B.5C.6D.74.(2022·广东广州·高三开学考试)设a=ln1.1,b=e0.1-1,c=tan0.1,d=0.4π,则( )A.a<b<c<dB.a<c<b<dC.a<b<d<cD.a<c<d<b5.(2022·广东广州·高三开学考试)若空间中经过定点O的三个平面α,β,γ两两垂直,过另一定点A作直线l与这三个平面的夹角都相等,过定点A作平面δ和这三个平面所夹的锐二面角都相等.记所作直线l的条数为m,所作平面δ的个数为n,则m+n=( )A.4B.8C.12D.166.(2022·广东·深圳外国语学校高三阶段练习)已知a =e 0.05,b =ln1.12+1,c = 1.1,则( )A.a >b >cB.c >b >aC.b >a >cD.a >c >b7.(2022·广东·深圳外国语学校高三阶段练习)已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左右焦点分别为F 1,F 2,O 为坐标原点,点P 为双曲线C 中第一象限上的一点,∠F 1PF 2的平分线与x 轴交于Q ,若OQ=14OF 2 ,则双曲线的离心率范围为( )A.1,2B.1,4C.2,2D.2,48.(2022·广东·高三阶段练习)设a =4-ln4e2,b =ln22,c =1e ,则( )A.a <c <bB.a <b <cC.b <a <cD.b <c <a9.(2022·广东·高三阶段练习)定义在R 上的函数f x 满足f (-x )+f (x )=0,f (x )=f (2-x );且当x ∈[0,1]时,f (x )=x 3-x 2+x .则方程7f (x )-x +2=0所有的根之和为( )A.14B.12C.10D.810.(2022·广东·高三开学考试)设a =12e,b =ln 2,c =4-ln4e 2,则( )A.a <b <cB.c <b <aC.a <c <bD.b <c <a11.(2022·广东·高三开学考试)已知f (x )=2x 2,数列a n 满足a 1=2,且对一切n ∈N *,有a n +1=f a n ,则( )A.a n 是等差数列 B.a n 是等比数列C.log 2a n 是等比数列D.log 2a n +1 是等比数列12.(2022·广东·中山一中高三阶段练习)已知a =log 1.10.9,b =0.91.1,c =1.10.9,则a ,b ,c 的大小关系为( )A.a <b <cB.a <c <bC.b <a <cD.b <c <a13.(2022·广东·中山一中高三阶段练习)已知函数f (x )=x 2-2x +a (e x -1+e -x +1)有唯一零点,则a =()A.-12B.13C.12D.114.(2022·广东·高三阶段练习)已知平面向量a ,b ,c 满足a =b =a ⋅b=2,且b -c ⋅3b -c =0,则c -a最小值为( )A.22+1B.33-3C.7-1D.23-215.(2022·湖南·邵阳市第二中学高三阶段练习)已知f (x )是定义在R 上的函数,且对任意x ∈R 都有f (x +2)=f (2-x )+4f (2),若函数y =f (x +1)的图象关于点(-1,0)对称,且f (1)=3,则f (2021)=( )A.6B.3C.0D.-316.(2022·湖南·邵阳市第二中学高三阶段练习)对于定义在R 上的函数f x ,若存在正常数a 、b ,使得f x +a≤f x +b 对一切x ∈R 均成立,则称f x 是“控制增长函数”.在以下四个函数中:①f x =e x ;②f x试卷第1页,共50页=x ;③f x =sin x 2;④f x =x ⋅sin x .是“控制增长函数”的有( )个A.1 B.2 C.3 D.417.(2022·湖南·麻阳苗族自治县第一中学高三开学考试)《九章算术》是我国古代著名的数学著作,书中记载有几何体“刍甍”.现有一个刍甍如图所示,底面ABCD 为正方形,EF ⎳底面ABCD ,四边形ABFE ,CDEF 为两个全等的等腰梯形,EF =12AB =2,AE =23,则该刍甍的外接球的体积为( )A.642π3 B.32πC.643π3 D.642π18.(2022·湖南·麻阳苗族自治县第一中学高三开学考试)若3x -3y >5-x -5-y ,则( )A.1x >1yB.x 3>y 3C.x >yD.ln x 2+1 >ln y 2+1二、多选题19.(2022·广东·广州市真光中学高三开学考试)已知抛物线C :y 2=2px p >0 的焦点为F ,抛物线C 上的点M 1,m 到点F 的距离是2,P 是抛物线C 的准线与x 轴的交点,A ,B 是抛物线C 上两个不同的动点,O 为坐标原点,则( )A.m =±2B.若直线AB 过点F ,则OA ⋅OB=-3C.若直线AB 过点F ,则PA PB =FAFB D.若直线AB 过点P ,则AF +BF >2PF20.(2022·广东·广州市真光中学高三开学考试)若函数f 2x +2 为偶函数,f x +1 为奇函数,且当x ∈(0,1]时,f x =ln x ,则( )A.f x 为偶函数B.f e =1C.f 4-1e=-1D.当x ∈[1,2)时,f (x )=-ln (2-x )21.(2022·广东惠州·高三阶段练习)如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,M ,N ,P 分别是C 1D 1,C 1C ,A 1A 的中点,则( )A.M ,N ,B ,D 1四点共面B.异面直线PD 1与MN 所成角的余弦值为1010C.平面BMN 截正方体所得截面为等腰梯形D.三棱锥P -MNB 的体积为1322.(2022·广东·鹤山市鹤华中学高三开学考试)已知椭圆C :x 216+y 29=1的左,右焦点为F 1,F 2,点P 为椭圆C上的动点(P 不在x 轴上),则( )A.椭圆C 的焦点在x 轴上B.△PF 1F 2的周长为8+27C.|PF 1|的取值范围为94,4 D.tan ∠F 1PF 2的最大值为3723.(2022·广东广州·高三开学考试)若f x =sin x +cos x ,则下列说法正确的有( )A.f x 的最小正周期是πB.方程x =-π2是f x 的一条对称轴C.f x 的值域为1,2D.∃a ,b >0,对∀x ∈R 都满足f x +a +f a -x =2b ,(a ,b 是实常数)24.(2022·广东广州·高三开学考试)已知抛物线y 2=2px 上的四点A 2,2 ,B ,C ,P ,直线AB ,AC 是圆M :x -22+y 2=1的两条切线,直线PQ 、PR 与圆M 分别切于点Q 、R ,则下列说法正确的有( )A.当劣弧QR 的弧长最短时,cos ∠QPR =-13B.当劣弧QR 的弧长最短时,cos ∠QPR =13C.直线BC 的方程为x +2y +1=0D.直线BC 的方程为3x +6y +4=025.(2022·广东广州·高三开学考试)已知函数f x 及其导函数f x 的定义域均为R ,对任意的x ,y ∈R ,恒有f x +y +f x -y =2f x ⋅f y ,则下列说法正确的有( )A.f 0 =1 B.f x 必为奇函数C.f x +f 0 ≥0D.若f 1 =12,则2023n =1f n =12 26.(2022·广东·深圳外国语学校高三阶段练习)已知函数f (x )=cos2πxx 2-2x +3,则下列说法正确的是( )A.f (x )是周期函数B.f (x )满足f (2-x )=f (x )C.f (x )>-12D.f (x )≥k 在R 上有解,则k 的最大值是1227.(2022·广东·深圳外国语学校高三阶段练习)如图,梯形ABCD 中,AB ∥CD ,AB =2DC =23,BC =2,AB ⊥BC ,M ,P ,N ,Q 分别是边AB ,BC ,CD ,DA 的中点,将△ACD 以AC 为轴旋转一周,则在此旋转过程中,下列说法正确的是( )A.MN 和BC 不可能平行B.AB 和CD 有可能垂直C.若AB 和CD 所成角是60∘,则PQ =32D.若面ACD ⊥面ABC ,则三棱锥D -ABC 的外接球的表面积是28π试卷第1页,共50页28.(2022·广东·高三阶段练习)已知双曲线C :x 2a 2-y 2b2=1a >b >0 的左,右顶点分别为A 1,A 2,点P ,Q 是双曲线C 上关于原点对称的两点(异于顶点),直线PA 1,PA 2,QA 1的斜率分别为k PA 1,k PA 2,k QA 1,若k PA 1⋅k PA 2=34,则下列说法正确的是( )A.双曲线C 的渐近线方程为y =±34xB.双曲线C 的离心率为72C.k PA 1⋅k QA 1为定值D.tan ∠A 1PA 2的取值范围为0,+∞ 29.(2022·广东·高三阶段练习)如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为2,点M 为CC 1的中点,点P 为正方形A1B 1C 1D 1上的动点,则( )A.满足MP ⎳平面BDA 1的点P 的轨迹长度为2B.满足MP ⊥AM 的点P 的轨迹长度为223C.不存在点P ,使得平面AMP 经过点BD.存在点P 满足PA +PM =530.(2022·广东·高三开学考试)直六棱柱ABCDEF -A 1B 1C 1D 1E 1F 1中,底面是边长为2的正六边形,侧棱AA 1=2,点O 是底面ABCDEF 的中心,则( )A.OF 1⎳平面A 1CD 1B.OF 1与BC 所成角的余弦值为24C.BO ⊥平面AA 1D 1DD.B 1F 与平面CC 1F 1F 所成角的正弦值为3431.(2022·广东·高三开学考试)已知直线l :y =ax -1,曲线C 1:f (x )=e x +1+1,曲线C 1关于直线y =x +1对称的曲线C 2所对应的函数为y =g (x ),则以下说法正确的是( )A.不论a 为何值,直线l 恒过定点(0,-1);B.g (x )=ln x -1;C.若直线l 与曲线C 2相切,则a =1;D.若直线l 上有两个关于直线y =x +1对称的点在曲线C 1上,则0<a <1.32.(2022·广东·中山一中高三阶段练习)下列命题中正确的是( )A.双曲线x 2-y 2=1与直线x +y -2=0有且只有一个公共点B.平面内满足PA -PB =2a a >0 的动点P 的轨迹为双曲线C.若方程x 24-t +y 2t -1=1表示焦点在y 轴上的双曲线,则t >4D.过给定圆上一定点A 作圆的动弦AB ,则弦AB 的中点P 的轨迹为椭圆33.(2022·广东·中山一中高三阶段练习)达·芬奇的画作《抱银貂的女人》中,女士脖颈上悬挂的黑色珍珠链与主人相互映衬,显现出不一样的美与光泽,达·芬奇提出固定项链的两端,使其在重力的作用下自然下垂项链所形成的曲线称为悬链线.建立适当的平面直角坐标系后,得到悬链线的函数解析式为f (x )=a cosh xa(a >0),双曲余弦函数cosh (x )=e x +e-x 2则以下正确的是( )A.f x 是奇函数B.f x 在-∞,0 上单调递减C.∀x ∈R ,f x ≥aD.∃a ∈0,+∞ ,f x ≥x 234.(2022·广东·高三阶段练习)设a 与b 是两个不共线向量,关于向量a +λb ,λ-1 a +2λb ,-b -2a ,则下列结论中正确的是( )A.当λ>1时,向量a +λb ,λ-1 a+2λb 不可能共线B.当λ>-3时,向量a +λb ,-b -2a可能出现共线情况C.若a ⋅b =0,且a ,b 为单位向量,则当λ>-3时,向量λ-1 a +2λb ,-b -2a可能出现垂直情况D.当λ=2时,向量a-λb 与-22b -a 平行35.(2022·广东·高三阶段练习)已知函数f x =x -2 +1,g x =kx ,若方程f x =g x 有两个不相等的实根,则实数k 的取值可以是( )A.43B.34C.45D.136.(2022·湖南·邵阳市第二中学高三阶段练习)已知函数f x =sin cos x +cos sin x ,下列关于该函数结论正确的是( )A.f x 的图象关于直线x =π2对称B.f x 的一个周期是2πC.f x 的最大值为2D.f x 是区间0,π2上的减函数37.(2022·湖南·邵阳市第二中学高三阶段练习)在现代社会中,信号处理是非常关键的技术,我们通过每天都在使用的电话或者互联网就能感受到.而信号处理背后的“功臣”就是正弦型函数.函数f (x )=4i =1sin [(2i -1)x ]2i -1的图象就可以近似的模拟某种信号的波形,则( )A.函数f (x )为周期函数,且最小正周期为πB.函数f (x )的图象关于点(2π,0)对称C.函数f (x )的图象关于直线x =π2对称D.函数f (x )的导函数f (x )的最大值为438.(2022·湖南·麻阳苗族自治县第一中学高三开学考试)已知函数f (x )是定义在R 上的奇函数,当x >0时,f(x )=e -x (x -1).则下列结论正确的是( )A.当x <0时,f (x )=e x (x +1)试卷第1页,共50页B.函数f(x)有两个零点C.若方程f(x)=m有三个解,则实数m的取值范围是f(-2)<m<f(2)D.∀x1,x2∈R,f x1-f x2max=239.(2022·湖南·麻阳苗族自治县第一中学高三开学考试)2022年北京冬奥会开幕式精彩纷呈,其中雪花造型惊艳全球.有一个同学为了画出漂亮的雪花,将一个边长为1的正六边形进行线性分形.如图,图(n)中每个正六边形的边长是图n-1中每个正六边形的边长的12.记图(n)中所有正六边形的边长之和为a n,则下列说法正确的是( )A.图(4)中共有294个正六边形B.a4=10294C.a n是一个递增的等比数列D.记S n为数列a n的前n项和,则对任意的n∈N*且n≥2,都有a n>S n-1三、填空题40.(2022·广东·广州市真光中学高三开学考试)已知椭圆x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,若椭圆上存在一点P使得∠F1PF2=23π,则该椭圆离心率的取值范围是________.41.(2022·广东广州·高三开学考试)折纸是我国民间的一种传统手工艺术,明德小学在课后延时服务中聘请了民间艺术传人给同学们教授折纸.课堂上,老师给每位同学发了一张长为10cm,宽为8cm的矩形纸片,要求大家将纸片沿一条直线折叠.若折痕(线段)将纸片分为面积比为1:3的两部分,则折痕长度的取值范围是___________cm.42.(2022·广东·深圳外国语学校高三阶段练习)已知函数f(x)的导函数f (x)满足:f (x)-f(x)=e2x,且f(0)=1,当x∈0,+∞时,x(f(x)-a)≥1+ln x恒成立,则实数a的取值范围是______________.43.(2022·广东·高三阶段练习)若不等式a x+1e x-x<0有且仅有一个正整数解,则实数a的取值范围是______.44.(2022·广东·高三阶段练习)已知⊙C:x2+y2-2x-2y-2=0,直线l:x+2y+2=0,M为直线l上的动点,过点M作⊙C的切线MA,MB,切点为A,B,当四边形MACB的面积取最小值时,直线AB的方程为____.45.(2022·广东·高三开学考试)已知双曲线C:x24-y23=1,F1、F2是双曲线C的左、右焦点,M是双曲线C右支上一点,l是∠F1MF2的平分线,过F2作l的垂线,垂足为P,则点P的轨迹方程为_______.46.(2022·广东·中山一中高三阶段练习)在△ABC中,角A,B,C的对边分别为a,B,C,已知sin2A+sin2C=sin2B+sin A sin C,若△ABC的面积为334,则a+c的最小值为__________.47.(2022·广东·高三阶段练习)已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为_____.48.(2022·湖南·邵阳市第二中学高三阶段练习)设f x =ln x,0<x≤2f4-x,2<x<4,若方程f x =m有四个不相等的实根x i i =1,2,3,4 ,则x 1+x 2 2+x 23+x 24的取值范围为___________.49.(2022·湖南·麻阳苗族自治县第一中学高三开学考试)已知F 是双曲线C :x 2a 2-y 2b2=1a >0,b >0 的右焦点,过点F 的直线l 与双曲线C 的一条渐近线垂直,垂足为A ,且直线l 与双曲线C 的左支交于点B ,若3FA =AB ,则双曲线C 的渐近线的方程为______.四、双空题50.(2022·广东惠州·高三阶段练习)已知抛物线方程y 2=8x ,F 为焦点,P 为抛物线准线上一点,Q 为线段PF与抛物线的交点,定义:d P =PFFQ.已知点P -2,82 ,则d P =___________;设点P -2,t t >0 ,若4d P -PF-k >0恒成立,则k 的取值范围为___________.51.(2022·广东·鹤山市鹤华中学高三开学考试)甲射击一次,中靶概率是P 1,乙射击一次,中靶概率是P 2,已知1P 1,1P 2是方程x 2-5x +6=0的根,且P 1满足方程x 2-x +14=0.则甲射击一次,不中靶概率为_____;乙射击一次,不中靶概率为_____.52.(2022·湖南·邵阳市第二中学高三阶段练习)若f x =ln a +11-x+b 是奇函数,则a =_____,b =______.试卷第1页,共50页。
高考数学选填压轴题真题(含答案)

2016年高考数学选填压轴题真题(含答案)一.选择题(共23小题)1.以抛物线C的顶点为圆心的圆交C于A、B两点,交C的准线于D、E两点.已知|AB|=4,|DE|=2,则C的焦点到准线的距离为()A.2 B.4 C.6 D.82.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.20πD.28π3.平面α过正方体ABCD﹣A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m、n所成角的正弦值为()A.B.C.D.4.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤),x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,且f(x)在(,)上单调,则ω的最大值为()A.11 B.9 C.7 D.55.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()A.20πB.24πC.28πD.32π6.已知F1,F2是双曲线E:﹣=1的左,右焦点,点M在E上,MF1与x 轴垂直,sin∠MF2F1=,则E的离心率为()A.B.C.D.27.已知函数f(x)(x∈R)满足f(﹣x)=2﹣f(x),若函数y=与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(x m,y m),则(x i+y i)=()A.0 B.m C.2m D.4m8.若函数f(x)=x﹣sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是()A.[﹣1,1]B.[﹣1,]C.[﹣,]D.[﹣1,﹣]9.定义“规范01数列”{a n}如下:{a n}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,a k中0的个数不少于1的个数,若m=4,则不同的“规范01数列”共有()A.18个B.16个C.14个D.12个10.已知O为坐标原点,F是椭圆C:+=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF 交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为()A.B.C.D.11.在封闭的直三棱柱ABC﹣A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是()A.4πB. C.6πD.12.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18+36B.54+18C.90 D.8113.下列函数中,其定义域和值域分别与函数y=10lgx的定义域和值域相同的是()A.y=x B.y=lgx C.y=2x D.y=14.函数f(x)=cos2x+6cos(﹣x)的最大值为()A.4 B.5 C.6 D.715.已知函数f(x)(x∈R)满足f(x)=f(2﹣x),若函数y=|x2﹣2x﹣3|与y=f (x)图象的交点为(x1,y1),(x2,y2),…,(x m,y m),则x i=()A.0 B.m C.2m D.4m16.袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则()A.乙盒中黑球不多于丙盒中黑球B.乙盒中红球与丙盒中黑球一样多C.乙盒中红球不多于丙盒中红球D.乙盒中黑球与丙盒中红球一样多17.某三棱锥的三视图如图所示,则该三棱锥的体积为()A.B.C.D.118.一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为()A.+πB.+πC.+πD.1+π19.已知非零向量,满足4||=3||,cos<,>=.若⊥(t+),则实数t的值为()A.4 B.﹣4 C.D.﹣20.若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是()A.y=sinx B.y=lnx C.y=e x D.y=x321.已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x>时,f(x+)=f(x﹣).则f(6)=()A.﹣2 B.1 C.0 D.222.如图,点列{A n}、{B n}分别在某锐角的两边上,且|A n A n+1|=|A n+1A n+2|,A n≠A n+1,n∈N*,|B n B n+1|=|B n+1B n+2|,B n≠B n+1,n∈N*,(P≠Q表示点P与Q不重合)若d n=|A n B n|,S n为△A n B n B n+1的面积,则()A.{S n}是等差数列B.{S n2}是等差数列C.{d n}是等差数列 D.{d n2}是等差数列23.已知实数a,b,c.()A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100B.若|a2+b+c|+|a2+b﹣c|≤1,则a2+b2+c2<100C.若|a+b+c2|+|a+b﹣c2|≤1,则a2+b2+c2<100D.若|a2+b+c|+|a+b2﹣c|≤1,则a2+b2+c2<100二.填空题(共17小题)24.某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为元.25.α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题是(填序号)26.若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b=.27.设直线y=x+2a与圆C:x2+y2﹣2ay﹣2=0相交于A,B两点,若|AB|=2,则圆C的面积为.28.已知直线l:mx+y+3m﹣=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,若|AB|=2,则|CD|=.29.有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是.30.△ABC的内角A,B,C的对边分别为a,b,c,若cosA=,cosC=,a=1,则b=.31.双曲线﹣=1(a>0,b>0)的渐近线为正方形OABC的边OA,OC所在的直线,点B为该双曲线的焦点.若正方形OABC的边长为2,则a=.32.设函数f(x)=.①若a=0,则f(x)的最大值为;②若f(x)无最大值,则实数a的取值范围是.33.已知双曲线E:﹣=1(a>0,b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2|AB|=3|BC|,则E的离心率是.34.在[﹣1,1]上随机地取一个数k,则事件“直线y=kx与圆(x﹣5)2+y2=9相交”发生的概率为.35.已知函数f(x)=,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是.36.已知2cos2x+sin2x=Asin(ωx+φ)+b(A>0),则A=,b=.37.某几何体的三视图如图所示(单位:cm),则该几何体的表面积是cm2,体积是cm3.38.已知a>b>1,若log a b+log b a=,a b=b a,则a=,b=.39.设数列{a n}的前n项和为S n,若S2=4,a n+1=2S n+1,n∈N*,则a1=,S5=.40.如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是.2016年高考数学选填压轴题真题(含答案)参考答案与试题解析一.选择题(共23小题)1.(2016•新课标Ⅰ)以抛物线C的顶点为圆心的圆交C于A、B两点,交C的准线于D、E两点.已知|AB|=4,|DE|=2,则C的焦点到准线的距离为()A.2 B.4 C.6 D.8【解答】解:设抛物线为y2=2px,如图:|AB|=4,|AM|=2,|DE|=2,|DN|=,|ON|=,x A==,|OD|=|OA|,=+5,解得:p=4.C的焦点到准线的距离为:4.故选:B.2.(2016•新课标Ⅰ)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.20πD.28π【解答】解:由题意可知三视图复原的几何体是一个球去掉后的几何体,如图:可得:=,R=2.它的表面积是:×4π•22+=17π.故选:A.3.(2016•新课标Ⅰ)平面α过正方体ABCD﹣A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m、n所成角的正弦值为()A.B.C.D.【解答】解:如图:α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABA1B1=n,可知:n∥CD1,m∥B1D1,∵△CB1D1是正三角形.m、n所成角就是∠CD1B1=60°.则m、n所成角的正弦值为:.故选:A.4.(2016•新课标Ⅰ)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤),x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,且f(x)在(,)上单调,则ω的最大值为()A.11 B.9 C.7 D.5【解答】解:∵x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,∴,即,(n∈N)即ω=2n+1,(n∈N)即ω为正奇数,∵f(x)在(,)上单调,则﹣=≤,即T=≥,解得:ω≤12,当ω=11时,﹣+φ=kπ,k∈Z,∵|φ|≤,∴φ=﹣,此时f(x)在(,)不单调,不满足题意;当ω=9时,﹣+φ=kπ,k∈Z,∵|φ|≤,∴φ=,此时f(x)在(,)单调,满足题意;故ω的最大值为9,故选:B5.(2016•新课标Ⅱ)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()A.20πB.24πC.28πD.32π【解答】解:由三视图知,空间几何体是一个组合体,上面是一个圆锥,圆锥的底面直径是4,圆锥的高是2,∴在轴截面中圆锥的母线长是=4,∴圆锥的侧面积是π×2×4=8π,下面是一个圆柱,圆柱的底面直径是4,圆柱的高是4,∴圆柱表现出来的表面积是π×22+2π×2×4=20π∴空间组合体的表面积是28π,故选:C.6.(2016•新课标Ⅱ)已知F1,F2是双曲线E:﹣=1的左,右焦点,点M 在E上,MF1与x轴垂直,sin∠MF2F1=,则E的离心率为()A.B.C.D.2【解答】解:由题意,M为双曲线左支上的点,则丨MF1丨=,丨MF2丨=,∴sin∠MF2F1=,∴=,可得:2b4=a2c2,即b2=ac,又c2=a2+b2,可得e2﹣e﹣=0,e>1,解得e=.故选A.7.(2016•新课标Ⅱ)已知函数f(x)(x∈R)满足f(﹣x)=2﹣f(x),若函数y=与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(x m,y m),则(x i+y i)=()A.0 B.m C.2m D.4m【解答】解:函数f(x)(x∈R)满足f(﹣x)=2﹣f(x),即为f(x)+f(﹣x)=2,可得f(x)关于点(0,1)对称,函数y=,即y=1+的图象关于点(0,1)对称,即有(x1,y1)为交点,即有(﹣x1,2﹣y1)也为交点,(x2,y2)为交点,即有(﹣x2,2﹣y2)也为交点,…则有(x i+y i)=(x1+y1)+(x2+y2)+…+(x m+y m)=[(x1+y1)+(﹣x1+2﹣y1)+(x2+y2)+(﹣x2+2﹣y2)+…+(x m+y m)+(﹣x m+2﹣y m)]=m.故选B.8.(2016•新课标Ⅰ)若函数f(x)=x﹣sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是()A.[﹣1,1]B.[﹣1,]C.[﹣,]D.[﹣1,﹣]【解答】解:函数f(x)=x﹣sin2x+asinx的导数为f′(x)=1﹣cos2x+acosx,由题意可得f′(x)≥0恒成立,即为1﹣cos2x+acosx≥0,即有﹣cos2x+acosx≥0,设t=cosx(﹣1≤t≤1),即有5﹣4t2+3at≥0,当t=0时,不等式显然成立;当0<t≤1时,3a≥4t﹣,由4t﹣在(0,1]递增,可得t=1时,取得最大值﹣1,可得3a≥﹣1,即a≥﹣;当﹣1≤t<0时,3a≤4t﹣,由4t﹣在[﹣1,0)递增,可得t=﹣1时,取得最小值1,可得3a≤1,即a≤.综上可得a的范围是[﹣,].另解:设t=cosx(﹣1≤t≤1),即有5﹣4t2+3at≥0,由题意可得5﹣4+3a≥0,且5﹣4﹣3a≥0,解得a的范围是[﹣,].故选:C.9.(2016•新课标Ⅲ)定义“规范01数列”{a n}如下:{a n}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,a k中0的个数不少于1的个数,若m=4,则不同的“规范01数列”共有()A.18个B.16个C.14个D.12个【解答】解:由题意可知,“规范01数列”有偶数项2m项,且所含0与1的个数相等,首项为0,末项为1,若m=4,说明数列有8项,满足条件的数列有:0,0,0,0,1,1,1,1;0,0,0,1,0,1,1,1;0,0,0,1,1,0,1,1;0,0,0,1,1,1,0,1;0,0,1,0,0,1,1,1;0,0,1,0,1,0,1,1;0,0,1,0,1,1,0,1;0,0,1,1,0,1,0,1;0,0,1,1,0,0,1,1;0,1,0,0,0,1,1,1;0,1,0,0,1,0,1,1;0,1,0,0,1,1,0,1;0,1,0,1,0,0,1,1;0,1,0,1,0,1,0,1.共14个.故选:C.10.(2016•新课标Ⅲ)已知O为坐标原点,F是椭圆C:+=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A 的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为()A.B.C.D.【解答】解:由题意可设F(﹣c,0),A(﹣a,0),B(a,0),令x=﹣c,代入椭圆方程可得y=±b=±,可得P(﹣c,±),设直线AE的方程为y=k(x+a),令x=﹣c,可得M(﹣c,k(a﹣c)),令x=0,可得E(0,ka),设OE的中点为H,可得H(0,),由B,H,M三点共线,可得k BH=k BM,即为=,化简可得=,即为a=3c,可得e==.故选:A.11.(2016•新课标Ⅲ)在封闭的直三棱柱ABC﹣A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是()A.4πB. C.6πD.【解答】解:∵AB⊥BC,AB=6,BC=8,∴AC=10.故三角形ABC的内切圆半径r==2,又由AA1=3,故直三棱柱ABC﹣A1B1C1的内切球半径为,此时V的最大值=,故选:B12.(2016•新课标Ⅲ)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18+36B.54+18C.90 D.81【解答】解:由已知中的三视图可得:该几何体是一个以俯视图为底面的斜四棱柱,其底面面积为:3×6=18,前后侧面的面积为:3×6×2=36,左右侧面的面积为:3××2=18,故棱柱的表面积为:18+36+9=54+18.故选:B.13.(2016•新课标Ⅱ)下列函数中,其定义域和值域分别与函数y=10lgx的定义域和值域相同的是()A.y=x B.y=lgx C.y=2x D.y=【解答】解:函数y=10lgx的定义域和值域均为(0,+∞),函数y=x的定义域和值域均为R,不满足要求;函数y=lgx的定义域为(0,+∞),值域为R,不满足要求;函数y=2x的定义域为R,值域为(0,+∞),不满足要求;函数y=的定义域和值域均为(0,+∞),满足要求;故选:D14.(2016•新课标Ⅱ)函数f(x)=cos2x+6cos(﹣x)的最大值为()A.4 B.5 C.6 D.7【解答】解:函数f(x)=cos2x+6cos(﹣x)=1﹣2sin2x+6sinx,令t=sinx(﹣1≤t≤1),可得函数y=﹣2t2+6t+1=﹣2(t﹣)2+,由∉[﹣1,1],可得函数在[﹣1,1]递增,即有t=1即x=2kπ+,k∈Z时,函数取得最大值5.故选:B.15.(2016•新课标Ⅱ)已知函数f(x)(x∈R)满足f(x)=f(2﹣x),若函数y=|x2﹣2x﹣3|与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(x m,y m),则x i=()A.0 B.m C.2m D.4m【解答】解:∵函数f(x)(x∈R)满足f(x)=f(2﹣x),故函数f(x)的图象关于直线x=1对称,函数y=|x2﹣2x﹣3|的图象也关于直线x=1对称,故函数y=|x2﹣2x﹣3|与y=f(x)图象的交点也关于直线x=1对称,故x i=×2=m,故选:B16.(2016•北京)袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则()A.乙盒中黑球不多于丙盒中黑球B.乙盒中红球与丙盒中黑球一样多C.乙盒中红球不多于丙盒中红球D.乙盒中黑球与丙盒中红球一样多【解答】解:取两个球共有4种情况:①红+红,则乙盒中红球数加1个;②黑+黑,则丙盒中黑球数加1个;③红+黑(红球放入甲盒中),则乙盒中黑球数加1个;④黑+红(黑球放入甲盒中),则丙盒中红球数加1个.设一共有球2a个,则a个红球,a个黑球,甲中球的总个数为a,其中红球x个,黑球y个,x+y=a.则乙中有x个球,其中k个红球,j个黑球,k+j=x;丙中有y个球,其中l个红球,i个黑球,i+l=y;黑球总数a=y+i+j,又x+y=a,故x=i+j由于x=k+j,所以可得i=k,即乙中的红球等于丙中的黑球.故选B.17.(2016•北京)某三棱锥的三视图如图所示,则该三棱锥的体积为()A.B.C.D.1【解答】解:由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱锥,棱锥的底面面积S=×1×1=,高为1,故棱锥的体积V==,故选:A18.(2016•山东)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为()A.+πB.+πC.+πD.1+π【解答】解:由已知中的三视图可得:该几何体上部是一个半球,下部是一个四棱锥,半球的直径为棱锥的底面对角线,由棱锥的底底面棱长为1,可得2R=.故R=,故半球的体积为:=π,棱锥的底面面积为:1,高为1,故棱锥的体积V=,故组合体的体积为:+π,故选:C19.(2016•山东)已知非零向量,满足4||=3||,cos<,>=.若⊥(t+),则实数t的值为()A.4 B.﹣4 C.D.﹣【解答】解:∵4||=3||,cos<,>=,⊥(t+),∴•(t+)=t•+2=t||•||•+||2=()||2=0,解得:t=﹣4,故选:B.20.(2016•山东)若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是()A.y=sinx B.y=lnx C.y=e x D.y=x3【解答】解:函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则函数y=f(x)的导函数上存在两点,使这点的导函数值乘积为﹣1,当y=sinx时,y′=cosx,满足条件;当y=lnx时,y′=>0恒成立,不满足条件;当y=e x时,y′=e x>0恒成立,不满足条件;当y=x3时,y′=3x2>0恒成立,不满足条件;故选:A21.(2016•山东)已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x>时,f(x+)=f(x﹣).则f(6)=()A.﹣2 B.1 C.0 D.2【解答】解:∵当x>时,f(x+)=f(x﹣),∴当x>时,f(x+1)=f(x),即周期为1.∴f(6)=f(1),∵当﹣1≤x≤1时,f(﹣x)=﹣f(x),∴f(1)=﹣f(﹣1),∵当x<0时,f(x)=x3﹣1,∴f(﹣1)=﹣2,∴f(1)=﹣f(﹣1)=2,∴f(6)=2.故选:D.22.(2016•浙江)如图,点列{A n}、{B n}分别在某锐角的两边上,且|A n A n+1|=|A n+1A n+2|,A n≠A n+1,n∈N*,|B n B n+1|=|B n+1B n+2|,B n≠B n+1,n∈N*,(P ≠Q表示点P与Q不重合)若d n=|A n B n|,S n为△A n B n B n+1的面积,则()A.{S n}是等差数列B.{S n2}是等差数列C.{d n}是等差数列 D.{d n2}是等差数列【解答】解:设锐角的顶点为O,|OA1|=a,|OB1|=c,|A n A n+1|=|A n+1A n+2|=b,|B n B n+1|=|B n+1B n+2|=d,由于a,c不确定,则{d n}不一定是等差数列,{d n2}不一定是等差数列,设△A n B n B n+1的底边B n B n+1上的高为h n,由三角形的相似可得==,==,两式相加可得,==2,即有h n+h n+2=2h n+1,由S n=d•h n,可得S n+S n+2=2S n+1,﹣S n+1=S n+1﹣S n,即为S n+2则数列{S n}为等差数列.故选:A.23.(2016•浙江)已知实数a,b,c.()A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100B.若|a2+b+c|+|a2+b﹣c|≤1,则a2+b2+c2<100C.若|a+b+c2|+|a+b﹣c2|≤1,则a2+b2+c2<100D.若|a2+b+c|+|a+b2﹣c|≤1,则a2+b2+c2<100【解答】解:A.设a=b=10,c=﹣110,则|a2+b+c|+|a+b2+c|=0≤1,a2+b2+c2>100;B.设a=10,b=﹣100,c=0,则|a2+b+c|+|a2+b﹣c|=0≤1,a2+b2+c2>100;C.设a=100,b=﹣100,c=0,则|a+b+c2|+|a+b﹣c2|=0≤1,a2+b2+c2>100;故选:D.二.填空题(共17小题)24.(2016•新课标Ⅰ)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为216000元.【解答】解:(1)设A、B两种产品分别是x件和y件,获利为z元.由题意,得,z=2100x+900y.不等式组表示的可行域如图:由题意可得,解得:,A(60,100),目标函数z=2100x+900y.经过A时,直线的截距最大,目标函数取得最大值:2100×60+900×100=216000元.故答案为:216000.25.(2016•新课标Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题是②③④(填序号)【解答】解:①如果m⊥n,m⊥α,n∥β,不能得出α⊥β,故错误;②如果n∥α,则存在直线l⊂α,使n∥l,由m⊥α,可得m⊥l,那么m⊥n.故正确;③如果α∥β,m⊂α,那么m与β无公共点,则m∥β.故正确④如果m∥n,α∥β,那么m,n与α所成的角和m,n与β所成的角均相等.故正确;故答案为:②③④26.(2016•新课标Ⅱ)若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b=1﹣ln2.【解答】解:设y=kx+b与y=lnx+2和y=ln(x+1)的切点分别为(x1,kx1+b)、(x2,kx2+b);由导数的几何意义可得k==,得x1=x2+1再由切点也在各自的曲线上,可得联立上述式子解得;从而kx1+b=lnx1+2得出b=1﹣ln2.27.(2016•新课标Ⅰ)设直线y=x+2a与圆C:x2+y2﹣2ay﹣2=0相交于A,B两点,若|AB|=2,则圆C的面积为4π.【解答】解:圆C:x2+y2﹣2ay﹣2=0的圆心坐标为(0,a),半径为,∵直线y=x+2a与圆C:x2+y2﹣2ay﹣2=0相交于A,B两点,且|AB|=2,∴圆心(0,a)到直线y=x+2a的距离d=,即+3=a2+2,解得:a2=2,故圆的半径r=2.故圆的面积S=4π,故答案为:4π28.(2016•新课标Ⅲ)已知直线l:mx+y+3m﹣=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,若|AB|=2,则|CD|=4.【解答】解:由题意,|AB|=2,∴圆心到直线的距离d=3,∴=3,∴m=﹣∴直线l的倾斜角为30°,∵过A,B分别作l的垂线与x轴交于C,D两点,∴|CD|==4.故答案为:4.29.(2016•新课标Ⅱ)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是1和3.【解答】解:根据丙的说法知,丙的卡片上写着1和2,或1和3;(1)若丙的卡片上写着1和2,根据乙的说法知,乙的卡片上写着2和3;∴根据甲的说法知,甲的卡片上写着1和3;(2)若丙的卡片上写着1和3,根据乙的说法知,乙的卡片上写着2和3;又甲说,“我与乙的卡片上相同的数字不是2”;∴甲的卡片上写的数字不是1和2,这与已知矛盾;∴甲的卡片上的数字是1和3.故答案为:1和3.30.(2016•新课标Ⅱ)△ABC的内角A,B,C的对边分别为a,b,c,若cosA=,cosC=,a=1,则b=.【解答】解:由cosA=,cosC=,可得sinA===,sinC===,sinB=sin(A+C)=sinAcosC+cosAsinC=×+×=,由正弦定理可得b===.故答案为:.31.(2016•北京)双曲线﹣=1(a>0,b>0)的渐近线为正方形OABC的边OA,OC所在的直线,点B为该双曲线的焦点.若正方形OABC的边长为2,则a=2.【解答】解:∵双曲线的渐近线为正方形OABC的边OA,OC所在的直线,∴渐近线互相垂直,则双曲线为等轴双曲线,即渐近线方程为y=±x,即a=b,∵正方形OABC的边长为2,∴OB=2,即c=2,则a2+b2=c2=8,即2a2=8,则a2=4,a=2,故答案为:232.(2016•北京)设函数f(x)=.①若a=0,则f(x)的最大值为2;②若f(x)无最大值,则实数a的取值范围是(﹣∞,﹣1).【解答】解:①若a=0,则f(x)=,则f′(x)=,当x<﹣1时,f′(x)>0,此时函数为增函数,当x>﹣1时,f′(x)<0,此时函数为减函数,故当x=﹣1时,f(x)的最大值为2;②f′(x)=,令f′(x)=0,则x=±1,若f(x)无最大值,则,或,解得:a∈(﹣∞,﹣1).故答案为:2,(﹣∞,﹣1)33.(2016•山东)已知双曲线E:﹣=1(a>0,b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2|AB|=3|BC|,则E的离心率是2.【解答】解:令x=c,代入双曲线的方程可得y=±b=±,由题意可设A(﹣c,),B(﹣c,﹣),C(c,﹣),D(c,),由2|AB|=3|BC|,可得2•=3•2c,即为2b2=3ac,由b2=c2﹣a2,e=,可得2e2﹣3e﹣2=0,解得e=2(负的舍去).故答案为:2.34.(2016•山东)在[﹣1,1]上随机地取一个数k,则事件“直线y=kx与圆(x ﹣5)2+y2=9相交”发生的概率为.【解答】解:圆(x﹣5)2+y2=9的圆心为(5,0),半径为3.圆心到直线y=kx的距离为,要使直线y=kx与圆(x﹣5)2+y2=9相交,则<3,解得﹣<k<.∴在区间[﹣1,1]上随机取一个数k,使直线y=kx与圆(x﹣5)2+y2=9相交相交的概率为=.故答案为:.35.(2016•山东)已知函数f(x)=,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是(3,+∞).【解答】解:当m>0时,函数f(x)=的图象如下:∵x>m时,f(x)=x2﹣2mx+4m=(x﹣m)2+4m﹣m2>4m﹣m2,∴y要使得关于x的方程f(x)=b有三个不同的根,必须4m﹣m2<m(m>0),即m2>3m(m>0),解得m>3,∴m的取值范围是(3,+∞),故答案为:(3,+∞).36.(2016•浙江)已知2cos2x+sin2x=Asin(ωx+φ)+b(A>0),则A=,b=1.【解答】解:∵2cos2x+sin2x=1+cos2x+sin2x=1+(cos2x+sin2x)=sin(2x+)+1,∴A=,b=1,故答案为:;1.37.(2016•浙江)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是72cm2,体积是32cm3.【解答】解:由三视图可得,原几何体为由四个棱长为2cm的小正方体所构成的,则其表面积为22×(24﹣6)=72cm2,其体积为4×23=32,故答案为:72,3238.(2016•浙江)已知a>b>1,若log a b+log b a=,a b=b a,则a=4,b=2.【解答】解:设t=log b a,由a>b>1知t>1,代入log a b+log b a=得,即2t2﹣5t+2=0,解得t=2或t=(舍去),所以log b a=2,即a=b2,因为a b=b a,所以b2b=b a,则a=2b=b2,解得b=2,a=4,故答案为:4;2.39.(2016•浙江)设数列{a n}的前n项和为S n,若S2=4,a n+1=2S n+1,n∈N*,则a1=1,S5=121.【解答】解:由n=1时,a1=S1,可得a2=2S1+1=2a1+1,又S2=4,即a1+a2=4,即有3a1+1=4,解得a1=1;=S n+1﹣S n,可得由a n+1S n+1=3S n+1,由S2=4,可得S3=3×4+1=13,S4=3×13+1=40,S5=3×40+1=121.故答案为:1,121.40.(2016•浙江)如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是.【解答】解:如图,M是AC的中点.①当AD=t<AM=时,如图,此时高为P到BD的距离,也就是A到BD的距离,即图中AE,DM=﹣t,由△ADE∽△BDM,可得,∴h=,V==,t∈(0,)②当AD=t>AM=时,如图,此时高为P到BD的距离,也就是A到BD的距离,即图中AH,DM=t﹣,由等面积,可得,∴,∴h=,∴V==,t∈(,2)综上所述,V=,t∈(0,2)令m=∈[1,2),则V=,∴m=1时,V max=.故答案为:.。
江苏高考数学填空题压轴题精选3

高考压轴题精选1.如图为函数()1)f x x =<<的图象,其在点(())M t f t ,l l y 处的切线为,与轴和直线1=y 分别交于点P 、Q ,点N (0,1),若△PQN 的面积为b 时的点M 恰好有两个,则b 的取值围为 ▲ . 解:2. 已知⊙A :221x y +=,⊙B : 22(3)(4)4x y -+-=,P 是平面一动点,过P 作⊙A 、⊙B 的切线,切点分别为D 、E ,若PE PD =,则P 到坐标原点距离的最小值为 ▲ .解:设)(y x P ,,因为PE PD =,所以22PD PE =,即14)4()3(2222-+=--+-y x y x ,整理得:01143=-+y x ,这说明符合题意的点P 在直线01143=-+y x 上,所以点)(y x P ,到坐标原点距离的最小值即为坐标原点到直线01143=-+y x 的距离,为5113. 等差数列{}n a 各项均为正整数,13a =,前n 项和为n S ,等比数列{}n b 中,11b =,且2264b S =,{}n b 是公比为64的等比数列.求n a 与n b ;解:设{}n a 的公差为d ,{}n b 的公比为q ,则d 为正整数,3(1)n a n d =+-,1n n b q -=依题意有1363(1)22642(6)64n n nda d n d ab q q b q S b d q +++-⎧====⎪⎨⎪=+=⎩①由(6)64d q +=知q 为正有理数,故d 为6的因子1,2,3,6之一,解①得2,8d q == 故132(1)21,8n n n a n n b -=+-=+=4. 在ABC ∆中,2==⋅AC AB (1)求22+(2)求ABC ∆面积的最大值.||||2BC AC AB =-=4222又因为 2AB AC ⋅=,所以228AB AC +=;(2)设||||||AB c AC b BC a ===,,,由(1)知822=+c b ,2=a , 又因为bcbc bc a c b A 22282cos 222=-=-+=,所以A bc A bc S ABC2cos 121sin 21-==∆=222222421cb c b c b ⋅-≤34)2(21222=-+c b , 当且仅当c b a ==时取“=”,所以ABC ∆的面积最大值为3.5. 设等差数列{}n a 的公差为d ,0d >,数列{}n b 是公比为q 等比数列,且110b a =>. (1)若33a b =,75a b =,探究使得n m a b =成立时n m 与的关系; (2)若22a b =,求证:当2>n 时,n n b a <.解:记a b a ==11,则1,)1(-=-+=m m n aq b d n a a ,……………1分(1)由已知得2426a d aq a d aq ⎧+=⎨+=⎩,,消去d 得4232aq aq a -=, 又因为0≠a ,所以02324=+-q q ,所以2122==q q 或,……………5分若12=q ,则0=d ,舍去;……………6分 若22=q ,则2a d =,因此12)1(-=-+⇔=m m n aq a n a b a 1211-=-+⇔m q n , 所以1221-=+m n (m 是正奇数)时,m n b a =;……………8分(2)证明:因为0,0>>a d ,所以111212>+=+===ada d a a ab b q , …………11分2>n 时,1)1(---+=-n n n aq d n a b a =d n q a n )1()1(1-+--=d n q q q q a n )1()1)(1(22-+++++--d n n q a )1()1)(1(-+--<=[]0))(1()1()1(22=--=+--b a n d q a n所以,当n n b a n <>时,2. …………………………16分6. 已知圆O :221x y +=,O 为坐标原点.(1的正方形ABCD 的顶点A 、B 均在圆O 上,C 、D 在圆O 外,当点A 在圆O 上运动时,C 点的轨迹为E . (ⅰ)求轨迹E 的方程;(ⅱ)过轨迹E 上一定点00(,)P x y 作相互垂直的两条直线12,l l ,并且使它们分别与圆O 、轨迹E 相交,设1l 被圆O 截得的弦长为a ,设2l 被轨迹E 截得的弦长为b ,求a b +的最大值.(2)正方形ABCD 的一边AB 为圆O 的一条弦,求线段OC长度的最值.解:(1)(ⅰ)连结OB ,OA ,因为OA =OB =1,AB =2,所以222AB OB OA =+,所以4OBA π∠=,所以34OBC π∠=,在OBC ∆中,52222=⋅-+=BC OB BC OB OC ,所以轨迹E 是以O 为圆心,5为半径的圆,所以轨迹E 的方程为522=+y x ; (ⅱ)设点O 到直线12l l ,的距离分别为12d d ,,因为21l l ⊥,所以2222212005d d OP x y +==+=, 则22215212d d b a -+-=+,则[])5)(1(2)(64)(222122212d d d d b a --++-=+≤4⎥⎥⎦⎤⎢⎢⎣⎡--⋅++-262)(622212221d d d d =22124[122(d d -+=4(1210)8-=,当且仅当221222125,15,d d d d ⎧+=⎨-=-⎩,即22219,21,2d d ⎧=⎪⎪⎨⎪=⎪⎩时取“=”,所以b a +的最大值为 (2)设正方形边长为a ,OBA θ∠=,则cos 2a θ=,0,2θπ⎡⎫∈⎪⎢⎣⎭.当A 、B 、C 、D 按顺时针方向时,如图所示,在OBC ∆中,2212cos 2a a OC θπ⎛⎫+-+= ⎪⎝⎭,即OC == ==由2,444θππ5π⎡⎫+∈⎪⎢⎣⎭,此时(1,1]OC ∈; 当A 、B 、C 、D 按逆时针方向时,在OBC ∆中,2212cos 2a a OC θπ⎛⎫+--= ⎪⎝⎭,即OC ====,由2,444θππ3π⎡⎫-∈-⎪⎢⎣⎭,此时1,OC ∈, 综上所述,线段OC 11.7. 已知函数()1ln ()f x x a x a R =--∈.(1)若曲线()y f x =在1x =处的切线的方程为330x y --=,数a 的值; (2)求证:0)(≥x f 恒成立的充要条件是1a =;(3)若0a <,且对任意(]1,0,21∈x x ,都有121211|()()|4||f x f x x x -≤-,数a 的取值围.另解:042≤--ax x 在(]1,0∈x 上恒成立,设4)(2--=ax x x g ,只需[)0,30041)1(04)0(-∈⇒⎪⎩⎪⎨⎧<≤--=<-=a a a g g .8. 已知函数2()3,()2f x mx g x x x m =+=++. (1)求证:函数()()f x g x -必有零点; (2)设函数()G x =()()1f x g x --(ⅰ)若|()|G x 在[]1,0-上是减函数,数m 的取值围;(ⅱ)是否存在整数,a b ,使得()a G x b ≤≤的解集恰好是[],a b ,若存在,求出,a b 的值;若不存在,说明理由.9. 已知函数()1ax x ϕ=+,a 为正常数. (1)若()ln ()f x x x ϕ=+,且92a =,求函数()f x 的单调增区间;(2)若()|ln |()g x x x ϕ=+,且对任意12,(0,2]x x ∈,12x x ≠,都有2121()()1g x g x x x -<--,求a 的的取值围.解:(1) 2221(2)1'()(1)(1)a x a x f x x x x x +-+=-=++, ∵92a =,令'()0f x >,得2x >,或12x <, ∴函数()f x 的单调增区间为1(0,)2, (2,)+∞.(2)∵2121()()1g x g x x x -<--,∴2121()()10g x g x x x -+<-,∴221121()[()]0g x x g x x x x +-+<-,设()()h x g x x =+,依题意,()h x 在(]0,2上是减函数.当12x ≤≤时, ()ln 1ah x x x x =+++,21'()1(1)a h x x x =-++, 令'()0h x ≤,得:222(1)1(1)33x a x x x x x+≥++=+++对[1,2]x ∈恒成立, 设21()33m x x x x =+++,则21'()23m x x x =+-,∵12x ≤≤,∴21'()230m x x x=+->, ∴()m x 在[1,2]上是增函数,则当2x =时,()m x 有最大值为272,∴272a ≥.当01x <<时, ()ln 1ah x x x x =-+++,21'()1(1)a h x x x =--++, 令'()0h x ≤,得: 222(1)1(1)1x a x x x x x+≥-++=+--, 设21()1t x x x x =+--,则21'()210t x x x=++>, ∴()t x 在(0,1)上是增函数,∴()(1)0t x t <=, ∴0a ≥,综上所述,272a ≥10. (1)设10+<<a b ,若对于x 的不等式()()22ax b x >-的解集中的整数恰有3个,则实数a 的取值围是 ▲ .(2)若关于x 的不等式()2221x ax -<的解集中的整数恰有3个,则实数a 的取值围是▲ .解:(1)()3,1(2)⎪⎭⎫ ⎝⎛1649,92511. 已知{}n a 是公差不为0的等差数列,{}n b 是等比数列,其中1122432,1,,2a b a b a b ====,且存在常数α、β,使得n a =log n b αβ+对每一个正整数n 都成立,则βα= ▲ .12. 在直角坐标系平面两点Q P ,满足条件:①Q P ,都在函数)(x f 的图象上;②Q P ,关于原点对称,则称点对),(Q P 是函数)(x f 的一个“友好点对”(点对),(Q P 与),(P Q 看作同一个“有好点对”).已知函数⎪⎩⎪⎨⎧≥<++=,0,2,0,142)(2x ex x x x f x 则函数)(x f 的“友好点对”有 ▲ 个.13. 已知ABC ∆的三边长c b a ,,满足b a c a c b 22≤+≤+,,则ab的取值围是 ▲ . 解:⎪⎭⎫ ⎝⎛23,32xyO已知ABC ∆的三边长c b a ,,满足b a c a c b 3232≤+≤+,,则ab的取值围是 ▲ . 解:⎪⎭⎫ ⎝⎛35,4314. 已知分别以21,d d 为公差的等差数列{}n a ,{}n b ,满足120091,409a b ==. (1)若11=d ,且存在正整数m ,使得200920092-=+m m b a ,求2d 的最小值;(2)若0k a =,1600k b =且数列200921121,,,,,,b b b b a a a k k k k ++-,的前项n 和n S 满足200920129045k S S =+,求 {}n a 的通项公式.解:(1)证明:220092009m m a b +=-,21120092[(1)]2009a m d b md ∴+-=+-,即200940922-+=md m , ……4分2160080d m m ∴=+≥=. 等号当且仅当"1600"mm =即"40"=m 时成立,故40m =时,2min []80d = . ……7分(2)0a =,1600b =,1,409a b ==200912112009()()k k k k S a a a a b b b -+∴=++++++++=++2)(1k a a k 2)12009)((2009+-+k b b k 2009(2010)22k k -=+,…10分 200920129045k S S =+1()201290452k a a k +=+=904522012+k201290452k ∴⋅+2009(2010)22k k -=+40202009201018090k ∴=⨯-,220099k ∴=-,1000k ∴= ……13分故得1,011000==a a 又,11999d ∴=-,1210001(1)999999n a a n d n ∴=+-=-,因此{}n a 的通项公式为n a n 99919991000-=. ……15分15. 已知函数)(3ln )(R a ax x a x f ∈--=. (1)当1a =时,求函数)(x f 的单调区间;(2)若函数)(x f y =的图像在点))2(,2(f 处的切线的倾斜角为︒45,问:m 在什么围取值时,对于任意的[]2,1∈t ,函数⎥⎦⎤⎢⎣⎡++=)('2)(23x f m x x x g 在区间)3,(t 上总存在极值?(3)当2=a 时,设函数32)2()(-+--=xep x p x h ,若在区间[]e ,1上至少存在一个0x ,使得)()(00x f x h >成立,试数p 的取值围. 24,1e e ⎛⎫+∞ ⎪-⎝⎭16. 如图,在△ABC 中,已知3=AB ,6=AC ,7BC =,AD 是BAC ∠平分线. (1)求证:2DC BD =; (2)求AB DC ⋅的值.(1)在ABD ∆中,由正弦定理得sin sin AB BDADB BAD=∠∠①, 在ACD ∆中,由正弦定理得sin sin AC DCADC CAD=∠∠②, 所以BAD CAD ∠=∠,sin sin BAD CAD ∠=∠, sin sin()sin ADB ADC ADC π∠=-∠=∠,由①②得36BD AB DC AC ==,所以2DC BD =(2)因为2DC BD =,所以BC DC 32=. 在△ABC 中,因为22222237611cos 223721AB BC AC B AB BC +-+-===⋅⨯⨯, 所以22()||||cos()AB DC AB BC AB BC B π⋅=⋅=⋅- AD2112237()3213=⨯⨯⨯-=- 17. 已知数列{}n a 的前n 项和为n S ,数列{}1n S +是公比为2的等比数列.(1)证明:数列{}n a 成等比数列的充要条件是13a =;(2)设n n n n a b )1(5--=(*∈N n ),若1+<n n b b 对任意*∈N n 成立,求1a 的取值围.18. 已知分别以1d 和2d 为公差的等差数列{}n a 和{}n b 满足181=a ,3614=b .(1)若181=d ,且存在正整数m ,使得45142-=+m mb a ,求证:1082>d ; (2)若0==k k b a ,且数列142121b b b a a a k k k ,,,,,,, ++的前n 项和n S 满足k S S 214=,求数列{}n a 和{}n b 的通项公式;(3)在(2)的条件下,令0>==a a d a c n n b n a n ,,,且1≠a ,问不等式n n n n d c d c +≤+1是否对一切正整数n 都成立?请说明理由.19. 若椭圆)0(12222>>=+b a by a x 过点(-3,2),离心率为33,⊙O 的圆心为原点,直径为椭圆的短轴,⊙M 的方程为4)6()8(22=-+-y x ,过⊙M 上任一点P 作⊙O 的切线PA 、PB ,切点为A 、B .(1)求椭圆的方程;(2)若直线PA 与⊙M 的另一交点为Q ,当弦PQ 最大时,求直线PA 的直线方程; (3)求OB OA ⋅的最大值与最小值.(1)1101522=+y x ;(2)直线PA 的方程为:0509130103=--=+-y x y x 或 (3)20. 已知集合{}k x x x x x x D =+>>=212121,0,0),(,其中k 为正常数. (1)设21x x u =,求u 的取值围;(2)求证:当1≥k 时,不等式⎪⎭⎫⎝⎛-≤⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-k k x x x x 22112211对任意D x x ∈),(21恒成立; (3)求使不等式⎪⎭⎫⎝⎛-≥⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-k k x x x x 22112211对任意D x x ∈),(21恒成立的k 取值围.21. 设函数x m mx x x f )4(31)(223-+-=,R x ∈,且函数)(x f 有三个互不相同的零点βα,,0,且βα<,若对任意的[]βα,∈x ,都有)1()(f x f ≥成立,数m 的取值围. 解:。
高考数学压轴题精编精解精选100题详细解答(1)

高考数学压轴题精编精解精选100题1.设函数()1,121,23x f x x x ≤≤⎧=⎨-<≤⎩,()()[],1,3g x f x ax x =-∈,其中a R ∈,记函数()g x 的最大值与最小值的差为()h a 。
(I )求函数()h a 的解析式;(II )画出函数()y h x =的图象并指出()h x 的最小值。
2.已知函数()()ln 1f x x x =-+,数列{}n a 满足101a <<,()1n n a f a +=; 数列{}n b 满足1111,(1)22n n b b n b +=≥+, *n N ∈.求证:(Ⅰ)101;n n a a +<<<(Ⅱ)21;2n n a a +<(Ⅲ)若1a =则当n ≥2时,!n n b a n >⋅.3.已知定义在R 上的函数f (x ) 同时满足:(1)21212122()()2()cos24sin f x x f x x f x x a x ++-=+(12,x x ∈R ,a 为常数); (2)(0)()14f f π==;(3)当0,4x π∈[]时,()f x ≤2 求:(Ⅰ)函数()f x 的解析式;(Ⅱ)常数a 的取值范围.个 个 4.设)0(1),(),,(22222211>>=+b a bx x y y x B y x A 是椭圆上的两点,满足0),(),(2211=⋅a y b x a y b x ,椭圆的离心率,23=e 短轴长为2,0为坐标原点. (1)求椭圆的方程;(2)若直线AB 过椭圆的焦点F (0,c ),(c 为半焦距),求直线AB 的斜率k 的值;(3)试问:△AOB 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由. 5.已知数列{}n a 中各项为:12、1122、111222、 (111)⋅⋅⋅⋅⋅⋅222n⋅⋅⋅⋅⋅⋅ ……(1)证明这个数列中的每一项都是两个相邻整数的积. (2)求这个数列前n 项之和S n .6、设1F 、2F 分别是椭圆22154x y +=的左、右焦点. (Ⅰ)若P 是该椭圆上的一个动点,求21PF PF ⋅的最大值和最小值;(Ⅱ)是否存在过点A (5,0)的直线l 与椭圆交于不同的两点C 、D ,使得|F 2C|=|F 2D|?若存在,求直线l 的方程;若不存在,请说明理由.7、已知动圆过定点P (1,0),且与定直线L:x=-1相切,点C 在l 上. (1)求动圆圆心的轨迹M 的方程;.B ,A M 3,P )2(两点相交于的直线与曲线且斜率为设过点-(i )问:△ABC 能否为正三角形?若能,求点C 的坐标;若不能,说明理由 (ii )当△ABC 为钝角三角形时,求这种点C 的纵坐标的取值范围.8、定义在R 上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,且对任意的a 、b ∈R ,有f(a+b)=f(a)f(b), (1)求证:f(0)=1;(2)求证:对任意的x ∈R ,恒有f(x)>0;(3)证明:f(x)是R 上的增函数;(4)若f(x)·f(2x-x 2)>1,求x 的取值范围。
【压轴题】高考数学试题含答案
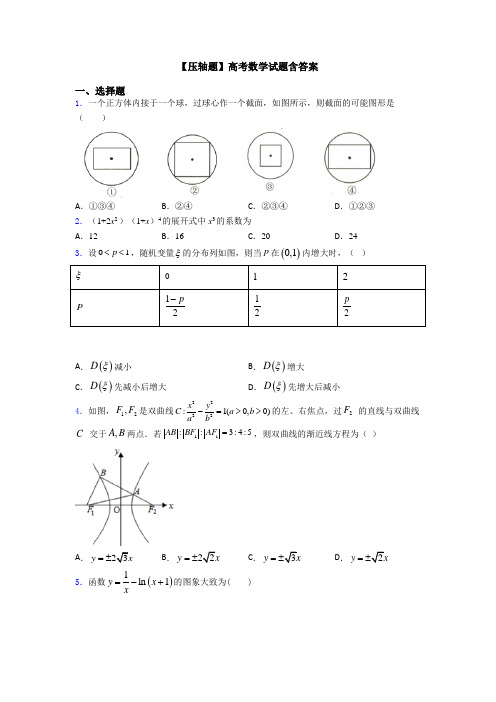
【压轴题】高考数学试题含答案 一、选择题 1.一个正方体内接于一个球,过球心作一个截面,如图所示,则截面的可能图形是( )
A.①③④ B.②④ C.②③④ D.①②③
2.(1+2x2 )(1+x)4的展开式中x3的系数为 A.12 B.16 C.20 D.
24
3.设01p,随机变量的分布列如图,则当p在0,1内增大时,( ) 0 1 2
P 12p 12 2p
A.D减小 B.D增大
C.D先减小后增大 D.D先增大后减小
4.如图,12,FF是双曲线2222:1(0,0)xyCabab的左、右焦点,过2F 的直线与双曲线C 交于,AB两点.若11::3:4:5ABBFAF,则双曲线的渐近线方程为( )
A.23yx B.22yx C.3yx D.
2yx
5.函数1ln1yxx的图象大致为( ) A. B.
C. D.
6.已知非零向量ab,满足2ab=,且bab(–),则a与b的夹角为 A.π6 B.π3 C.2π3 D.
5π
6
7.设i为虚数单位,复数z满足21iiz,则复数z的共轭复数等于( ) A.1-i B.-1-i C.1+i D.
-1+i
8.函数()lnfxxx的大致图像为 ( )
A. B.
C. D.
9.下列函数中,最小正周期为,且图象关于直线3x对称的函数是( ) A.2sin23yx B.
2sin26yx
C.2sin23xy D.
2sin23yx
10.已知复数 ,则复数在复平面内对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.一个样本a,3,4,5,6的平均数是b,且不等式x2-6x+c<0的解集为(a,b),则这个样本的标准差是( ) A.1 B.
2
C.3 D.2
上册数学压轴题练习(Word版 含答案) 汇编经典
上册数学压轴题练习(Word版含答案)汇编经典一、压轴题1.[ 问题提出 ]一个边长为 ncm(n⩾3)的正方体木块,在它的表面涂上颜色,然后切成边长为1cm的小正方体木块,没有涂上颜色的有多少块?只有一面涂上颜色的有多少块?有两面涂上颜色的有多少块?有三面涂上颜色的多少块?[ 问题探究 ]我们先从特殊的情况入手(1)当n=3时,如图(1)没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有1×1×1=1个小正方体;一面涂色的:在面上,每个面上有1个,共有6个;两面涂色的:在棱上,每个棱上有1个,共有12个;三面涂色的:在顶点处,每个顶点处有1个,共有8个.(2)当n=4时,如图(2)没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有2×2×2=8个小正方体:一面涂色的:在面上,每个面上有4个,正方体共有个面,因此一面涂色的共有个;两面涂色的:在棱上,每个棱上有2个,正方体共有条棱,因此两面涂色的共有个;三面涂色的:在顶点处,每个顶点处有1个,正方体共有个顶点,因此三面涂色的共有个…[ 问题解决 ]一个边长为ncm(n⩾3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有______个小正方体;一面涂色的:在面上,共有______个;两面涂色的:在棱上,共有______个;三面涂色的:在顶点处,共______个。
[ 问题应用 ]一个大的正方体,在它的表面涂上颜色,然后把它切成棱长1cm的小正方体,发现有两面涂色的小正方体有96个,请你求出这个大正方体的体积.2.如图,已知数轴上两点A,B表示的数分别为﹣2,6,用符号“AB”来表示点A和点B 之间的距离.(1)求AB的值;(2)若在数轴上存在一点C,使AC=3BC,求点C表示的数;(3)在(2)的条件下,点C位于A、B两点之间.点A以1个单位/秒的速度沿着数轴的正方向运动,2秒后点C以2个单位/秒的速度也沿着数轴的正方向运动,到达B点处立刻返回沿着数轴的负方向运动,直到点A到达点B,两个点同时停止运动.设点A运动的时间为t ,在此过程中存在t 使得AC =3BC 仍成立,求t 的值.3.阅读下列材料:根据绝对值的定义,|x| 表示数轴上表示数x 的点与原点的距离,那么,如果数轴上两点P 、Q 表示的数为x 1,x 2时,点P 与点Q 之间的距离为PQ=|x 1-x 2|.根据上述材料,解决下列问题:如图,在数轴上,点A 、B 表示的数分别是-4, 8(A 、B 两点的距离用AB 表示),点M 、N 是数轴上两个动点,分别表示数m 、n.(1)AB=_____个单位长度;若点M 在A 、B 之间,则|m+4|+|m-8|=______;(2)若|m+4|+|m-8|=20,求m 的值;(3)若点M 、点N 既满足|m+4|+n=6,也满足|n-8|+m=28,则m= ____ ;n=______.4.(1)如图,已知点C 在线段AB 上,且6AC cm =,4BC cm =,点M 、N 分别是AC 、BC 的中点,求线段MN 的长度;(2)若点C 是线段AB 上任意一点,且AC a =,BC b =,点M 、N 分别是AC 、BC 的中点,请直接写出线段MN 的长度;(结果用含a 、b 的代数式表示)(3)在(2)中,把点C 是线段AB 上任意一点改为:点C 是直线AB 上任意一点,其他条件不变,则线段MN 的长度会变化吗?若有变化,求出结果.5.如图,在三角形ABC 中,8AB =,16BC =,12AC =.点P 从点A 出发以2个单位长度/秒的速度沿A B C A →→→的方向运动,点Q 从点B 沿B C A →→的方向与点P 同时出发;当点P 第一次回到A 点时,点P ,Q 同时停止运动;用t (秒)表示运动时间.(1)当t 为多少时,P 是AB 的中点;(2)若点Q 的运动速度是23个单位长度/秒,是否存在t 的值,使得2BP BQ =; (3)若点Q 的运动速度是a 个单位长度/秒,当点P ,Q 是AC 边上的三等分点时,求a 的值.6.已知线段AD =80,点B 、点C 都是线段AD 上的点.(1)如图1,若点M 为AB 的中点,点N 为BD 的中点,求线段MN 的长;(2)如图2,若BC =10,点E 是线段AC 的中点,点F 是线段BD 的中点,求EF 的长; (3)如图3,若AB =5,BC =10,点P 、Q 分别从B 、C 出发向点D 运动,运动速度分别为每秒移动1个单位和每秒移动4个单位,运动时间为t 秒,点E 为AQ 的中点,点F 为PD 的中点,若PE =QF ,求t 的值.7.对于数轴上的,,A B C 三点,给出如下定义:若其中一个点与其他两个点的距离恰好满足2倍的数量关系,则称该点是其他两点的“倍联点”. 例如数轴上点,,A B C 所表示的数分别为1,3,4,满足2AB BC =,此时点B 是点,A C 的“倍联点”.若数轴上点M 表示3-,点N 表示6,回答下列问题:(1)数轴上点123,,D D D 分別对应0,3. 5和11,则点_________是点,M N 的“倍联点”,点N 是________这两点的“倍联点”;(2)已知动点P 在点N 的右侧,若点N 是点,P M 的倍联点,求此时点P 表示的数.8.如图①,已知线段30cm AB =,4cm CD =,线段CD 在线段AB 上运动,E 、F 分别是AC 、BD 的中点.(1)若8cm AC ,则EF =______cm ;(2)当线段CD 在线段AB 上运动时,试判断EF 的长度是否发生变化?如果不变请求出EF 的长度,如果变化,请说明理由;(3)我们发现角的很多规律和线段一样,如图②已知COD ∠在AOB ∠内部转动,OE 、OF 分别平分AOC ∠和BOD ∠,则EOF ∠、AOB ∠和COD ∠有何数量关系,请直接写出结果不需证明.9.小刚运用本学期的知识,设计了一个数学探究活动.如图1,数轴上的点M ,N 所表示的数分别为0,12.将一枚棋子放置在点M 处,让这枚棋子沿数轴在线段MN 上往复运动(即棋子从点M 出发沿数轴向右运动,当运动到点N 处,随即沿数轴向左运动,当运动到点M 处,随即沿数轴向右运动,如此反复⋯).并且规定棋子按照如下的步骤运动:第1步,从点M 开始运动t 个单位长度至点1Q 处;第2步,从点1Q 继续运动2t 单位长度至点2Q 处;第3步,从点2Q 继续运动3t 个单位长度至点3Q 处…例如:当3t =时,点1Q 、2Q 、3Q 的位置如图2所示.解决如下问题:(1)如果4t =,那么线段13Q Q =______;(2)如果4t <,且点3Q 表示的数为3,那么t =______;(3)如果2t ≤,且线段242Q Q =,那么请你求出t 的值.10.已知∠AOB =110°,∠COD =40°,OE 平分∠AOC ,OF 平分∠BOD .(1)如图1,当OB 、OC 重合时,求∠AOE ﹣∠BOF 的值;(2)如图2,当∠COD 从图1所示位置绕点O 以每秒3°的速度顺时针旋转t 秒(0<t <10),在旋转过程中∠AOE ﹣∠BOF 的值是否会因t 的变化而变化?若不发生变化,请求出该定值;若发生变化,请说明理由.(3)在(2)的条件下,当∠COF =14°时,t = 秒.11.(1)探究:哪些特殊的角可以用一副三角板画出?在①135︒,②120︒,③75︒,④25︒中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)(2)在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种.如图,他先用三角板画出了直线EF ,然后将一副三角板拼接在一起,其中45角(AOB ∠)的顶点与60角(COD ∠)的顶点互相重合,且边OA 、OC 都在直线EF 上.固定三角板COD 不动,将三角板AOB 绕点O 按顺时针方向旋转一个角度α,当边OB 与射线OF 第一次重合时停止.①当OB 平分EOD ∠时,求旋转角度α;②是否存在2BOC AOD ∠=∠?若存在,求旋转角度α;若不存在,请说明理由.12.设A 、B 、C 是数轴上的三个点,且点C 在A 、B 之间,它们对应的数分别为x A 、x B 、x C .(1)若AC =CB ,则点C 叫做线段AB 的中点,已知C 是AB 的中点.①若x A =1,x B =5,则x c = ;②若x A =﹣1,x B =﹣5,则x C = ;③一般的,将x C 用x A 和x B 表示出来为x C = ;④若x C =1,将点A 向右平移5个单位,恰好与点B 重合,则x A = ;(2)若AC =λCB (其中λ>0).①当x A =﹣2,x B =4,λ=13时,x C = . ②一般的,将x C 用x A 、x B 和λ表示出来为x C = .【参考答案】***试卷处理标记,请不要删除一、压轴题1.[ 问题探究 ] (2)6,24;12,24;8,8;[ 问题解决](n-2)3,(n-2)2,12(n-2),8;[ 问题解决 ] 1000cm 3.【解析】【分析】[ 问题探究 ] (2)根据(1)即可填写;[ 问题解决 ] 可根据(1)、(2)的规律填写;[ 问题应用 ] 根据[ 问题解决 ]知两面涂色的为n-12(2),由此得到方程n-12(2)=96, 解得n 的值即可得到边长及面积.【详解】[ 问题探究 ](2)没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有2×2×2=8个小正方体:一面涂色的:在面上,每个面上有4个,正方体共有 6个面,因此一面涂色的共有24个;两面涂色的:在棱上,每个棱上有2个,正方体共有12 条棱,因此两面涂色的共有24个;三面涂色的:在顶点处,每个顶点处有1个,正方体共有8 个顶点,因此三面涂色的共有8 个…[ 问题解决 ]一个边长为ncm(n ⩾3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有_32n -() _____个小正方体;一面涂色的:在面上,共有__22n -()____个; 两面涂色的:在棱上,共有__122n -()____个; 三面涂色的:在顶点处,共_8____个。
2024年新高考数学选填压轴题汇编(一)(解析版)
2024年新高考数学选填压轴题汇编(一)一、多选题1(2023·广东深圳·高三红岭中学校考阶段练习)已知长方体的表面积为10,十二条棱长度之和为16,则该长方体()A.一定不是正方体B.外接球的表面积为6πC.长、宽、高的值均属于区间1,2D.体积的取值范围为5027,2【答案】ABD【解析】设长方体的长宽高分别为a ,b ,c ,则可得2ab +ac +bc =104a +b +c =16,即ab +ac +bc =5a +b +c =4 ,又因为a +b +c 2=a 2+b 2+c 2 +2ab +ac +bc =16,所以a 2+b 2+c 2=6,由不等式可得,a 2+b 2+c 2≥ab +ac +bc ,当且仅当a =b =c 时,等号成立,而a 2+b 2+c 2>ab +ac +bc ,取不到等号,所以得不到a =b =c ,即该长方体一定不是正方体,故A 正确;设长方体外接球的半径为R ,则2R =a 2+b 2+c 2=6,即R =62,则外接球的表面积为4π622=6π,故B 正确;由a +b +c =4可得,c =4-a +b ,代入ab +ac +bc =5可得,ab +4-a +b a +b =5,即ab =5-4-a +b a +b ,因为a ,b >0,由基本不等式可得ab ≤a +b24,即5-4-a +b a +b ≤a +b24,设a +b =t ,则t >0,则5-4-t t ≤t 24,化简可得3t 2-16t +20≤0,即3t -10 t -2 ≤0,所以2≤t ≤103,即2≤a +b ≤103,又因为a +b =4-c ,则23≤c ≤2,同理可得a ,b ∈23,2 ,故C 错误;设长方体的体积为V ,则V =abc =5-4-a +b a +b 4-a +b ,且a +b =t ,2≤t ≤103,即V =5-4-t t 4-t ,其中t ∈2,103,化简可得,V =4-t 5-4t +t 2 ,t ∈2,103,且V =-5-4t +t 2 +4-t -4+2t =-3t -7 t -3 ,t ∈2,103,令V =0,则t =73或3,当t ∈2,73时,V <0,即V 单调递减,当t ∈73,3时,V >0,即V 单调递增,当t ∈3,103时,V <0,即V 单调递减,所以,当t =73时,V 有极小值,且V 73 =4-73 5-4×73+499 =5027,当t =3时,V 有极大值,且V 3 =4-3 5-4×3+9 =2,又因为V 2 =4-2 5-4×2+4 =2,V 103 =4-103 5-4×103+1009 =5027,所以V ∈5027,2 ,故D 正确;故选:ABD2(2023·广东·高三校联考阶段练习)对于数列a n ,若存在正数M ,使得对一切正整数n ,都有a n ≤M ,则称数列a n 是有界的.若这样的正数M 不存在,则称数列a n 是无界的.记数列a n 的前n 项和为S n ,下列结论正确的是()A.若a n =1n,则数列a n 是无界的 B.若a n =12nsin n ,则数列S n 是有界的C.若a n =-1 n ,则数列S n 是有界的 D.若a n =2+1n2,则数列S n 是有界的【答案】BC【解析】对于A ,∵a n =1n=1n≤1恒成立,∴存在正数M =1,使得a n ≤M 恒成立,∴数列a n 是有界的,A 错误;对于B ,∵-1≤sin n ≤1,∴-12n≤a n =12n⋅sin n ≤12n,∴S n =a 1+a 2+⋯+a n <12+122+⋯+12n=121-12 n1-12=1-12n<1,S n =a 1+a 2+⋯+a n >-12+12 2+⋯+12 n=-1+12 n>-1,所以存在正数M =1,使得S n ≤M 恒成立,∴则数列S n 是有界的,B 正确;对于C ,因为a n =-1 n ,所以当n 为偶数时,S n =0;当n 为奇数时,S n =-1;∴S n ≤1,∴存在正数M =1,使得S n ≤M 恒成立,∴数列S n 是有界的,C 正确;对于D ,1n 2=44n 2<42n -1 2n +1=412n -1-12n +1 ,∴S n =2n +1+122+132+⋅⋅⋅1n2≤2n +41-13+13-15+⋅⋅⋅+12n -1-12n +1 =2n +41-12n +1 =2n +8n 2n +1=2n -22n +1+2 ;∵y =x -22x +1在0,+∞ 上单调递增,∴n -22n +1∈13,+∞,∴不存在正数M ,使得S n ≤M 恒成立,∴数列S n 是无界的,D 错误.故选:BC .3(2023·广东·高三校联考阶段练习)如图,正方体ABCD -A 1B 1C 1D 1中,E 为A 1B 1的中点,P 为棱BC 上的动点,则下列结论正确的是()A.存在点P ,使AC 1⊥平面D 1EPB.存在点P ,使PE =PD 1C.四面体EPC 1D 1的体积为定值D.二面角P -D 1E -C 1的余弦值取值范围是55,23【答案】BC【解析】(向量法)为简化运算,建立空间直角坐标系如图,设正方体棱长为2,CP =20≤a ≤2 ,则P a ,2,2 ,E 2,1,0 ,A 2,0,0 ,C 10,2,2 ,AC 1 =-2,2,-2 ,D 1E ⋅AC 1 =-2≠0,故AC 1与D 1E 不垂直,故A 错误.由PE =PD 1知a 2+22+22=a -2 2+12+22,a =14∈0,2 ,故B 正确.V E -PC 1D 1=V P -C 1D 1E =13⋅2⋅S △C 1D 1E =13⋅2⋅12⋅2⋅2=43,为定值.故C 正确.又D 1E =2,1,0 ,D 1P =a ,2,2 ,设平面D 1EP 的法向量n 1 =x ,y ,z ,由D 1E ⋅n 1=0D 1P ⋅n 1 =0,2x +y =0ax +2y +2z =0 ,令x =2则y =-4,z =4-a ,∴n 1=2,-4,4-a ,又平面D 1EC 1的法向量n 2=0,0,1 ,∴cos n 1 ,n 2 =4-a 22+-4 2+4-a 2=11+204-a2,又0≤a ≤2,∴4≤4-a 2≤16,∴cos n 1 ,n 2 ∈66,23.故D 错误.(几何法)记棱A 1D 1,D 1D ,DC ,CB ,BB 1中点分别为F ,G ,J ,I ,H ,易知AC 1⊥平面EFGJIH ,而EF ⊂平面EFGJIH则AC 1⊥EF ,若AC 1⊥平面D 1EP ,D 1E ⊂平面D 1EP ,则AC 1⊥D 1E ,由EF ∩D 1E =E ,EF ,D 1E ⊂平面D 1EF ,所以AC 1⊥平面D 1EF ,与已知矛盾,故AC 1不垂直于平面D 1EP .故A 错误.连接EB ,D 1C ,易知BC ⊥EB ,BC ⊥D 1C ,设正方体棱长为2,知EB =5,D 1C =22,记BP =m 0≤m ≤2 ,则EP =m 2+5,D 1P =2-m2+8,由m 2+5=2-m 2+8,得m =74∈0,2 .故B 正确.V E -PC 1D 1=V P -C 1D 1E =13⋅2⋅S △C 1D 1E =13⋅2⋅12⋅2⋅2=43,为定值.故C 正确.过点P 作PM ⊥B 1C 1于点M ,易知PM ⊥D 1E ,过点M 作MN ⊥D 1E 于点N ,知D 1E ⊥平面PMN ,所以PN ⊥D 1E ,则二面角P -D 1E -C 1的平面角为∠PNM ,现在△PNM 中求解cos ∠PNM .设正方体棱长为2,NM =x ,则NP =x 2+4,∴cos ∠PNM =NMNP=xx 2+4,只需求x 取值范围即可:记BP =m 0≤m ≤2 ,则B 1M =BP =m ,分析易知M 在C 1时x 取到最大值,此时x =C 1N 1,M 在B 1时x 取到最小值,此时x =B 1N 2,又C 1N 1C 1D 1=D 1A 1D 1E 即C 1N 1=2⋅25=455,B 1N 2D 1A 1=B 1E D 1E 即B 1N 2=2⋅15=255,所以255≤x ≤455即45≤x 2≤165,∴cos ∠PNM =x x 2+4=1-4x 2+4∈66,23 .故D 错误.故选:BC4(2023·广东·高三校联考阶段练习)已知f x =xe x ,g x =x ln x .若存在x 1∈R ,x 2∈0,+∞ ,使得f x 1 =g x 2 =t 成立,则下列结论中正确的是()A.当t >0时,x 1x 2=tB.当t >0时,e ln t ≤x 1x 2C.不存在t ,使得f x 1 =g x 2 成立D.f x >g x +mx 恒成立,则m ≤2【答案】AB【解析】选项A ,∵f x 1 =g x 2 =t ∴t =x 1e x 1=x 2ln x 2=ln x 2e ln x 2>0,则x 1>0,x 2>0,ln x 2>0,且t =f (x 1)=f (ln x 2)>0,由f x =xe x ,得f x =e x x +1 ,当x >0时,f x >0,则f x 在0,+∞ 上递增,所以当t >0时,f x =t 有唯一解,故x 1=ln x 2,∴x 1x 2=x 2ln x 2=t ,故A 正确;选项B ,由A 正确,得ln t x 1x 2=ln tt(t >0),设φt =ln t t ,则φ t =1-ln tt 2,令φ t =0,解得t =e易知φt 在0,e 上单调递增,在e ,+∞ 上单调递减,∴φt ≤φe =1e ,∴ln t x 1x 2≤1e ,∴e ln t ≤x 1x 2,故B 正确;选项C ,由f x =e x x +1 ,g x =ln x +1=0,得f -1 =g 1e=0,又验证知f -1 =g 1e =-1e ,故存在t =-1e ,使得f -1 =g 1e=0,C 错误;选项D ,由x >0,f x >g x +mx 恒成立,即e x -ln x >m 恒成立,令r x =e x -ln x ,则r x =e x -1x ,由r x 在0,+∞ 上递增,又r 12=e -2<0,r 1 =e -1>0,∴存在x 0∈12,1 ,使r x 0 =0,∴r x 在0,x 0 上递减,在x 0,+∞ 上递增(其中x 0满足e x 0=1x 0,即x 0=-ln x 0).∴r x ≥r x 0 =e x 0-ln x 0=1x 0+x 0>2,要使m <e x -ln x 恒成立,∴m <r (x 0),存在2<m <r (x 0)满足题意,故D 错误.故选:AB .5(2023·广东梅州·高三大埔县虎山中学校考开学考试)已知f x 是定义在R 上的偶函数,且对任意x ∈R ,有f 1+x =-f 1-x ,当x ∈0,1 时,f x =x 2+x -2,则()A.f x 是以4为周期的周期函数B.f 2021 +f 2022 =-2C.函数y =f x -log 2x +1 有3个零点D.当x ∈3,4 时,f x =x 2-9x +18【答案】ACD【解析】依题意,f x 为偶函数,且f 1+x =-f 1-x ⇒f x 关于1,0 对称,则f x +4 =f 1+x +3 =-f 1-x +3 =-f -2-x=-f -2+x =-f 2+x =-f 1+1+x =f 1-1+x =f -x =f x ,所以f x 是周期为4的周期函数,A 正确.因为f x 的周期为4,则f 2021 =f 1 =0,f 2022 =f 2 =-f 0 =2,所以f 2021 +f 2022 =2,B 错误;作函数y =log 2x +1 和y =f x 的图象如下图所示,由图可知,两个函数图象有3个交点,C 正确;当x ∈3,4 时,4-x ∈0,1 ,则f x =f -x =f 4-x =4-x 2+4-x -2=x 2-9x +18,D 正确.故选:ACD6(2023·广东梅州·高三大埔县虎山中学校考开学考试)如图,正方形ABCD 中,E 、F 分别是AB 、BC的中点将△ADE,ΔCDF,△BEF分别沿DE、DF、EF折起,使A、B、C重合于点P.则下列结论正确的是A.PD⊥EFB.平面PDE⊥平面PDFC.二面角P-EF-D的余弦值为13D.点P在平面DEF上的投影是ΔDEF的外心【答案】ABC【解析】对于A选项,作出图形,取EF中点H,连接PH,DH,又原图知ΔBEF和ΔDEF为等腰三角形,故PH⊥EF,DH⊥EF,所以EF⊥平面PDH,所以PD⊥EF,故A正确;根据折起前后,可知PE,PF,PD 三线两两垂直,于是可证平面PDE⊥平面PDF,故B正确;根据A选项可知∠PHD为二面角P-EF-D的平面角,设正方形边长为2,因此PE=PF=1,PH=22,DH=22-22=322,PD=DF2-PF2=2,由余弦定理得:cos∠PHD=PH2+HD2-PD22PH⋅HD =13,故C正确;由于PE=PF≠PD,故点P在平面DEF上的投影不是ΔDEF的外心,即D错误;故答案为ABC.7(2023·广东·高三校联考阶段练习)在正方体ABCD-A1B1C1D1中,E,F,G分别为BC,CC1,BB1的中点,则()A.直线D1D与EF所成的角为30°B.直线A1G与平面AEF平行C.若正方体棱长为1,三棱锥A1-AEF的体积是112D.点B 1和B 到平面AEF 的距离之比是3:1【答案】BCD【解析】对于选项A ,由图可知CC 1与DD 1显然平行,所以∠EFC =45°即为所求,故选项A 不正确;对于选项B ,取B 1C 1的中点M ,连接A 1M 、GM ,如图所示,易知A 1M ⎳AE ,且A 1M ⊄平面AEF ,AE ⊂平面AEF ,所以A 1M ⎳平面AEF .又易知GM ⎳EF ,GM ⊄平面AEF ,EF ⊂平面AEF ,所以GM ⎳平面AEF .又A 1M ∩GM =M ,A 1M 、GM ⊂面A 1MG ,所以平面A 1MG ⎳平面AEF .又A 1G ⊂平面A 1MG ,所以A 1G ⎳平面AEF ,故选项B 正确;对于选项C ,由选项B 知,A 1G ⎳平面AEF ,所以A 1和G 到平面AEF 的距离相等,所以V A 1-AEF =V G -AEF =V A -FEG =13×12×12×1×1=112.故选项C 正确;对于选项D ,平面AEF 过BC 的中点E ,即平面AEF 将线段BC 平分,所以C 与B 到平面AEF 的距离相等,连接B 1C 交EF 于点H ,如图所示,显然B 1H :HC =3:1,所以B 1与B 到平面AEF 的距离之比为3:1,故选项D 正确.故选:BCD .8(2023·广东·高三校联考阶段练习)已知数列a n 满足a 1=1,a 2=3,S n 是前n 项和,若n S n +1-S n -1=n +1 S n -S n -1 ,(n ∈N *且n ≥2),若不等式a n <n -2t 2-a +1 t +a 2-a +2 对于任意的n ∈N *,t ∈1,2 恒成立,则实数a 的值可能为()A.-4 B.0C.2D.5【答案】AD【解析】由n S n +1-S n -1=n +1 S n -S n -1 ,n ≥2,则na n +1-1=n +1 a n ,n ≥2,得a n +1-1n =n +1n a n ,n ≥2;a 2-11=2=21a 1,所以a n +1n +1-a n n =1n n +1=1n -1n +1,n ≥1,则a n n -a n -1n -1=1n -1-1n ,a n -1n -1-a n -2n -2=1n -2-1n -1,⋯,a 22-a 11=1-12,上述式子累加可得a n n -a 1=1-1n ,所以a n n =2-1n<2.所以-2t 2-a +1 t +a 2-a +2≥2对于任意的t ∈1,2 恒成立,整理得2t -a -1 t +a ≤0对于任意的t ∈1,2 恒成立.方法一:对选项A ,当a =-4时,不等式为2t +5 t -4 ≤0,其解集-52,4包含1,2 ,故选项A 正确;对选项B ,当a =0时,不等式为2t +1 t ≤0,其解集-12,0不包含1,2 ,故选项B 错误;对选项C ,当a =2时,不等式为2t -1 t +2 ≤0,其解集-2,12不包含1,2 ,故选项C 错误;对选项D ,当a =5时,不等式为2t -4 t +5 ≤0,其解集-5,2 包含1,2 ,故选项D 正确.方法二:令f t =2t -a -1 t +a ,若2t -a -1 t +a ≤0对于任意的t ∈1,2 恒成立,只需f 1 ≤0f 2 ≤0,即3-a 1+a ≤05-a 2+a ≤0 ,解得a ≥5或a ≤-2.故选:AD .9(2023·广东·高三统考阶段练习)已知函数f x =sin n x +cos n x x ∈N * ,则()A.对任意正奇数n ,f x 为奇函数B.对任意正整数n ,f x 的图像都关于直线x =π4对称C.当n =3时,f x 在0,π2上的最小值22D.当n =4时,f x 的单调递增区间是-π4+k π,k π k ∈Z 【答案】BC【解析】取n =1,则f x =sin x +cos x ,从而f 0 =1≠0,此时f x 不是奇函数,则A 错误;因为f π2-x =sin n π2-x +cos n π2-x =cos n x +sin n x =f x ,所以f x 的图象关于直线x =π4对称,则B 正确;当n =3时,f x =3sin 2x cos x -3cos 2x sin x =3sin x cos x sin x -cos x ,当x ∈0,π4时,fx <0;当x ∈π4,π2 时,f x >0.所以f x 在0,π4 上单调递减,在π4,π2 上单调递增,所以f x 的最小值为f π4 =22 3+22 3=22,故C 正确;当n =4时,f x =sin 4x +cos 4x =sin 2x +cos 2x 2-2sin 2x cos 2x =1-12sin 22x=1-1-cos4x 4=14cos4x +34,则f x 的递增区间为-π4+k π2,k π2k ∈Z ,则D 错误.故选:BC .10(2023·广东·高三统考阶段练习)若实数a ,b 满足2a +3a =3b +2b ,则下列关系式中可能成立的是()A.0<a<b<1B.b<a<0C.1<a<bD.a=b【答案】ABD【解析】设f(x)=2x+3x,g(x)=3x+2x,则f(x)=2x+3x,g(x)=3x+2x都为增函数,作出两函数的图象,两个函数图象有2个交点,分别为(0,1),(1,5),对于A,作直线y=m(1<m<5)分别与f(x),g(x)图象相交,交点横坐标为a,b,且0<a<b<1,此时f(a)=g(b)=m,即2a+3a=3b+2b能成立,故A正确;对于B,作直线y=n(n<0)分别与f(x),g(x)图象相交,交点横坐标为b,a,且b<a<0,此时f(a)=g(b) =n,即2a+3a=3b+2b能成立,故B正确;对于C,a=2,f(a)=f(2)=10,因为2=a<b,所以f(b)=3b+2b>32+4=13,所以此时2a+3a=3b+2b 不可能成立,故C不正确;对于D,a=b=0或a=b=1,2a+3a=3b+2b成立,所以D正确.故选:ABD.11(2023·广东·高三统考阶段练习)已知正方体ABCD -A 1B 1C 1D 1的棱长为4,M 为DD 1的中点,N 为ABCD 所在平面上一动点,N 1为A 1B 1C 1D 1所在平面上一动点,且NN 1⊥平面ABCD ,则下列命题正确的是()A.若MN 与平面ABCD 所成的角为π4,则点N 的轨迹为圆B.若三棱柱NAD -N 1A 1D 1的表面积为定值,则点N 的轨迹为椭圆C.若点N 到直线BB 1与直线DC 的距离相等,则点N 的轨迹为抛物线D.若D 1N 与AB 所成的角为π3,则点N 的轨迹为双曲线【答案】ACD【解析】A :连接DN ,因为MD ⊥平面ABCD ,所以∠MND 是MN 与平面ABCD 所成的角,即∠MND =π4,因为M 为DD 1的中点,所以MD =12DD 1=2,在直角三角形MND 中,tan ∠MND =MD DN ⇒1=2DN⇒DN =2,因此点N 的轨迹为以D 为圆心半径为2的圆,所以本选项命题是真命题;B :过N 做EN ⊥AD ,设三棱柱NAD -N 1A 1D 1的表面积为S ,所以S =2×12×4⋅NE +(AD +DN +AN )⋅4=4(4+DN +AN +NE )=定值,显然有N 到A 、D 、直线AD 的距离之和为定值,这与椭圆的定义不符合,故本选项命题是假命题;C :连接BN ,因为BB 1⊥平面ABCD ,BN ⊂平面ABCD ,所以BB 1⊥BN ,即点N 到直线BB 1与NB 相等,所以点N 的轨迹为点N 到点B 与直线DC 的距离相等的轨迹,即抛物线,所以本选项命题是真命题;D :以D 为空间坐标系的原点,DA 、DC 、DD 1所在的直线分别为x 、y 、z ,D (0,0,0)、A (4,0,0)、B (4,4,0)、N (x ,y ,0)、D 1(0,0,4),则有AB =(0,4,0)、D 1N =(x ,y ,-4),因为D 1N 与AB 所成的角为π3,所以cos π3=AB ⋅D 1N AB ⋅D 1N ⇒12=4y 4⋅x 2+y 2+16⇒3y 2-x 2=16,所以点N 的轨迹为双曲线,故本选项命题是真命题,故选:ACD12(2023·广东江门·高三台山市第一中学校考阶段练习)已知函数f (x )=e x -1+e 1-x +x 2-2x ,若不等式f (2-ax )<f x 2+3 对任意x ∈R 恒成立,则实数a 的取值可能是()A.-4B.-12C.2D.32【答案】BC【解析】由函数f (x )=e x -1+e 1-x +x 2-2x ,令t =x -1,则x =t +1,可得g (t )=e t +e -t +t 2-1,可得g (-t )=e -t +e t +(-t )2-1=e t +e -t +t 2-1=g (t ),所以g t 为偶函数,即函数f x 的图象关于x =1对称,又由g (t )=e t -e -t +2t ,令φ(t )=g (t )=e t -e -t +2t ,可得φ (t )=e t +e -t +2>0,所以φ(t )为单调递增函数,且φ(0)=0,当t >0时,g (t )>0,g t 单调递增,即x >1时,f x 单调递增;当t <0时,g (t )<0,g t 单调递减,即x <1时,f x 单调递减,由不等式f (2-ax )<f x 2+3 ,可得2-ax -1 <x 2+3-1 ,即1-ax <x 2+2所以不等式1-ax <x 2+2恒成立,即-x 2-2<ax -1<x 2+2恒成立,所以x 2+ax +1>0x 2-ax +3>0 的解集为R ,所以a 2-4<0且(-a )2-12<0,解得-2<a <2,结合选项,可得BC 适合.故选:BC .13(2023·广东·高三河源市河源中学校联考阶段练习)已知三次函数f x =x 3+bx 2+cx +d 有三个不同的零点x 1,x 2,x 3x 1<x 2<x 3 ,若函数g x =f x -1也有三个不同的零点t 1,t 2,t 3t 1<t 2<t 3 ,则下列等式或不等式一定成立的有()A.b 2<3cB.t 3>x 3C.x 1+x 2+x 3=t 1+t 2+t 3D.x 1x 2x 3-t 1t 2t 3=1【答案】BC【解析】f x =3x 2+2bx +c ,因为原函数有三个不同的零点,则f x =0有两个不同的实根,即3x 2+2bx +c =0,则Δ=4b 2-12c >0,即b 2>3c ,所以A 错误;因为三次函数f x =x 3+bx 2+cx +d 有三个不同的零点x 1,x 2,x 3x 1<x 2<x 3 ,所以x 3+bx 2+cx +d =x -x 1 x -x 2 x -x 3 =x 3-x 1+x 2+x 3 x 2+x 1x 2+x 2x 3+x 1x 3 x -x 1x 2x 3=0,所以x 1+x 2+x 3=-b ,x 1x 2x 3=-d ,同理t 1+t 2+t 3=-b ,t 1t 2t 3=1-d ,所以x 1+x 2+x 3=t 1+t 2+t 3,x 1x 2x 3-t 1t 2t 3=-1,故C 正确,D 错误;由f x 的图象与直线y =1的交点可知t 3>x 3,B 正确.故选:BC .14(2023·广东·高三河源市河源中学校联考阶段练习)已知直线l 过抛物线E :y 2=4x 的焦点F ,与抛物线相交于A x 1,y 1 、B x 2,y 2 两点,分别过A ,B 作抛物线的准线l 1的垂线,垂足分别为A 1,B 1,以线段A 1B 1为直径作圆M ,O 为坐标原点,下列正确的判断有()A.x 1+x 2≥2B.△AOB 为钝角三角形C.点F 在圆M 外部D.直线A 1F 平分∠OFA【答案】ABD 【解析】如图所示:对选项A ,由抛物线的焦半径公式可知AB =x 1+x 2+2≥2p =4,所以x 1+x 2≥2,故A 正确;对于选项B ,OA ⋅OB =x 1x 2+y 1y 2=y 1y 2216+y 1y 2,令直线l 的方程为x =my +1,代入y 2=4x 得y 2-4my -4=0,所以y 1y 2=-4,所以OA ⋅OB=-3<0,所以△AOB 是钝角三角形,故B 正确;对选项C ,D ,由AA 1 =AF 可知∠AA 1F =∠AFA 1,又AA 1∥OF ,所以∠AA 1F =∠OFA 1=∠AFA 1,所以直线FA 1平分角∠AFO ,同理可得FB 平分角∠BFO ,所以A 1F ⊥B 1F ,即∠A 1FB 1=90°,所以圆M 经过点F ,故C 错误,D 正确.故选:ABD15(2023·广东·高三河源市河源中学校联考阶段练习)已知圆O :x 2+y 2=4和圆C :(x -3)2+(y -3)2=4,P ,Q 分别是圆O ,圆C 上的动点,则下列说法错误的是()A.圆O 与圆C 相交B.PQ 的取值范围是32-4,32+4C.x -y =2是圆O 与圆C 的一条公切线D.过点Q 作圆O 的两条切线,切点分别为M ,N ,则存在点Q ,使得∠MQN =90°【答案】AC【解析】对于A 选项,由题意可得,圆O 的圆心为O 0,0 ,半径r 1=2,圆C 的圆心C 3,3 ,半径r 2=2,因为两圆圆心距OC =32>2+2=r 1+r 2,所以两圆外离,故A 错误;对于B 选项,PQ 的最大值等于OC +r 1+r 2=32+4,最小值为OC -r 1-r 2=32-4,故B 正确;对于C 选项,显然直线x -y =2与直线OC 平行,因为两圆的半径相等,则外公切线与圆心连线平行,由直线OC :y =x ,设外公切线为y =x +t ,则两平行线间的距离为2,即t2=2,故y =x ±22,故C 错误;对于D 选项,易知当∠MQN =90°时,四边形OMQN 为正方形,故当QO =22时,∠MQN =90°,故D 正确.故选:AC .16(2023·广东佛山·高三校考阶段练习)已知函数f x =3sin ωx +cos ωx (0<ω<3)满足f x +π2 =-f x ,其图象向右平移s s ∈N * 个单位后得到函数y =g x 的图象,且y =g x 在-π6,π6上单调递减,则()A.ω=1 B.函数f x 的图象关于5π12,0 对称C.s 可以等于5D.s 的最小值为2【答案】BCD【解析】对于A ,因为f x +π2 =-f x ,f x =3sin ωx +cos ωx =2sin ωx +π6,所以2sin ωx +π2ω+π6 =-2sin ωx +π6 ,π2ω=2k +1 π,k ∈Z ,则ω=4k +2,k ∈Z ,又0<ω<3,故ω=2,故A 错误;对于B ,由选项A 得f x =2sin 2x +π6,所以f 5π12=2sin 5π6+π6 =2sinπ=0,故5π12,0 是f x 的一个对称中心,故B 正确;对于C ,f x 的图象向右平移s s ∈N * 个单位后得到函数g x =2sin 2x -s +π6的图象,则g x =2sin 2x +π6-2s ,因为g x 在-π6,π6上单调递减,所以2×-π6 +π6-2s ≥2k π+π22×π6+π6-2s ≤2k π+3π2k ∈Z ,解得-k π-π2≤s ≤-k π-π3k ∈Z ,当k =-2时,3π2≤s ≤5π3,因为s ∈N *,所以s =5,故C 正确;对于D ,因为s ∈N *,所以-k π-π3>0,则k <-13,又k ∈Z ,故k ≤-1,当k =-1时,π2≤s ≤2π3,可知s min =2,故D 正确.故选:BCD .17(2023·广东佛山·高三校考阶段练习)已知函数f x 的定义域为0,+∞ ,其导函数为f x ,且f x +f x =x ln x ,f 1e =-1e,则()A.f 1e⋅e 1e-1>f 1B.f e ⋅e e -1>f 1C.f x 在0,+∞ 上是增函数D.f x 存在最小值【答案】ABC【解析】设F x =e x -1f x ,则F x =e x -1f x +f x =e x -1x ln x ,当x >1时,F x >0,当0<x <1时,F x <0,F x =e x -1f x 在1,+∞ 上单调递增,在0,1 上单调递减,A 选项,因为1e <1,所以F 1e >F 1 ,即e 1e-1f 1e>f 1 ,A 正确;B 选项,因为e >1,所以F e >F 1 ,即e e -1f e >f 1 ,B 正确;C 选项,f x =F x e x -1,则fx =F x -F x e x -1,令g x =F x -F x ,则g x =e x -1x ln x -e x -1x ln x =e x -11+ln x ,当x >1e 时,g x >0,当0<x <1e时,g x <0,故g x =F x -F x 在0,1e 上单调递减,在1e ,+∞ 单调递增,又g 1e =F 1e -F 1e =e 1e -1⋅1e ln 1e -e 1e -1f 1e =-e 1e -1⋅1e +e 1e-1⋅1e =0,故g x =F x -F x ≥0恒成立,所以fx =F x -F x ex -1≥0在0,+∞ 上恒成立,故f x 在0,+∞ 上是增函数,C 正确;D 选项,由C 选项可知,函数f x 在0,+∞ 上单调递增,故无最小值.故选:ABC18(2023·广东惠州·高三统考阶段练习)已知定义域为R 的函数f x 满足f -x -2 =-f x +2 ,f x 在0,+∞ 解析式为f x =3x 2-2x +1,0<x ≤1log 13x 2-718 ,x >1 ,则下列说法正确的是()A.函数f x 在-13,13上单调递减B.若函数f x 在0,p 内f x <1恒成立,则p ∈0,23C.对任意实数k ,y =f x 的图象与直线y =kx 最多有6个交点D.方程f x =m m >0 有4个解,分别为x 1,x 2,x 3,x 4,则x 1+x 2+x 3+x 4>-143【答案】BD【解析】因为定义域为R 的函数f x 满足f -x -2 =-f x +2 ,即f -x -2 +f x +2 =0,所以函数为奇函数,因为f x 在0,+∞ 解析式为f x =3x 2-2x +1,0<x ≤1log 13x 2-718,x >1 ,故作出函数的图象,如图所示.选项A :由图可知,当x ∈-13,0 时,函数单调递减,当x ∈0,13时,函数单调递减,但当x ∈-13,13,并不是随着x 增加而减少,故选项A 错误;选项B :因为函数f x 在0,p 内f x <1恒成立,所以由图象可知,0<p <1由3x 2-2x +1=1解得,x 1=0,x 2=23,所以0<p ≤23,故选项B 正确;选项C :取k =74时,如图所示,1°当x ∈0,1 时,联立方程组y =74x y =3x 2-2x +1 ,化简得3x 2-154x +1=0,设函数h (x )=3x 2-154x +1,因为Δ>0h (0)=1>0h (1)=14>0且对称轴为x =58∈0,1 ,所以方程3x 2-154x +1=0在0,1 上有两个不相等的实数根,2°设m (x )=74x -log 13x 2-718 ,x ∈1,+∞ ,因为函数m (x )=74x -log 13x 2-718 在x ∈1,+∞ 上单调递增,且m (1)=74-2<0,m (2)=72-log 131118 >0,所以m (x )=74x -log 13x 2-718 在x ∈1,+∞ 在只有一个零点,所以直线y =74x 与函数y =f (x )图象在x ∈1,+∞ 有1个交点,所以当x ∈0,+∞ 时,直线y =74x 与函数y =f (x )图象有3个交点,因为函数y =74x 与函数y =f (x )均为奇函数,所以当x ∈-∞,0 时,直线y =74x 与函数y =f (x )图象有3个交点,又当x =0时,直线y =74x 与函数y =f (x )图象有1个交点,所以此时直线y =74x 与函数y =f (x )图象有7个交点,故选项C 错误;选项D :当m >0时,则根据图象可得f (x )=m 的4个解所在大致范围为x 1<0,0<x 2<13,13<x 3<1,x 4>1,因为f (x )=m 有4个解,所以23<m <1,所以23<log 13x 42-718 <1,解得139<x 4<21323+79,所以6<9x 4-7<181323,由二次函数的对称性可知,3x 2-2x +1=m 的解x 2、x 3满足x 2+x 3=23,因为函数y =f (x )为奇函数,且当x >1时解析式为y =log 13x 2-718,所以当x <-1时解析式为y =-log 13-x 2-718,所以log 13x 42-718=-log 13-x 12-718 ,所以有-x 12-718 x 42-718 =1,即x 1=-369x 4-7-79,所以x 1+x 4=x 4+-369x 4-7-79=9x 4-79-369x 4-7,设9x 4-7=t ,6<t <181323,又因为函数y =t 9-36t 在6,1813 23单调递增,所以x 1+x 4=t 9-36t >69-366=23-6=-163,所以x 1+x 2+x 3+x 4>-163+23=-143,所以选项D 正确,故选:BD .19(2023·广东揭阳·高三校考阶段练习)若定义在-1,1 上的函数f x 满足f x +f y =f x +y 1+xy,且当x >0时,f x <0,则下列结论正确的是( ).A.若x 1,x 2∈-1,1 ,x 2>x 1 ,则f x 1 +f x 2 >0B.若f 12 =-12,则f 4041 =-2C.若f 2-x +g x =4,则g x 的图像关于点2,4 对称D.若α∈0,π4,则f sin2α >2f sin α 【答案】BC【解析】令y =-x ,则f x +f -x =f 0 =0,∴f x 为奇函数,把y 用-y 代替,得到f x -f y =f x -y1-xy,设-1<y <x <1,1-x 1+y >0,∴0<x -y1-xy<1.又∵当x >0时,f x <0,∴f x <f y ,∴f x 在-1,1 上单调递减.∵x 1,x 2∈-1,1 ,x 2>x 1 ,当x >0时,f x <0,则当x 1>0时,则x 2>x 1>0,f x 1 +f x 2 <0,当x 1<0时,则x 2>-x 1>0,f x 1 +f x 2 =f x 2 -f -x 1 <0.综上,f x 1 +f x 2 <0,∴A 错误.令x =y =12,得2f 12 =f 45 ,∴f 45 =-1,令x =y =45,得2f 45 =f 4041 ,∴f 4041 =-2,∴B 正确.由f 2-x +g x =4,得f 2-x =4-g x ,得f x =4-g 2-x ,又∵f -x =4-g 2+x ,f x 为奇函数,∴f x +f -x =0,则g 2-x +g 2+x =8,则g x 的图像关于点2,4 对称,∴C 正确.f sin2α =f 2sin α⋅cos α =f2tan α1+tan 2α=2f tan α ,假设f sin2α >2f sin α ,可得f tan α >f sin α ,即tan α<sin α,当α∈0,π4时,不成立得出矛盾假设不成立,∴D 错误.故选:BC .20(2023·广东东莞·高三校联考阶段练习)已知函数f x =3sin2ωx +cos2ωx ω>0 的零点构成一个公差为π2的等差数列,把f x 的图象沿x 轴向右平移π3个单位得到函数g x 的图象,则()A.g x 在π4,π2上单调递增 B.π4,0 是g x 的一个对称中心C.g x 是奇函数 D.g x 在区间π6,2π3上的值域为0,2 【答案】AB【解析】因为f x =3sin2ωx +cos2ωx ω>0 ,所以f x =232sin2ωx +12cos2ωx =2sin 2ωx +π6 ,因为函数f x =3sin2ωx +cos2ωx ω>0 的零点依次构成一个公差为π2的等差数列,∴12⋅2π2ω=π2,∴ω=1,所以f (x )=2sin 2x +π6 ,把函数f (x )的图象沿x 轴向右平移π3个单位,得到g (x )=2sin 2x -π3 +π6 =2sin 2x -π2 =-2cos2x ,即g (x )=-2cos2x ,所以g (x )为偶函数,故C 错误;对于A :当x ∈π4,π2 时2x ∈π2,π ,因为y =cos x 在π2,π 上单调递减,所以g x 在π4,π2上单调递增,故A正确;对于B:gπ4=-2cos2×π4=-2cosπ2=0,故π4,0是g x 的一个对称中心,故B正确;对于D:因为x∈π6,2π3,所以2x∈π3,4π3,所以cos2x∈-1,12,所以g x ∈-1,2,故D错误;故选:AB21(2023·广东东莞·高三校联考阶段练习)对于函数f(x)=xln x,下列说法正确的是()A.f(x)在(1,e)上单调递增,在(e,+∞)上单调递减B.若方程f(|x|)=k有4个不等的实根,则k>eC.当0<x1<x2<1时,x1ln x2<x2ln x1D.设g(x)=x2+a,若对∀x1∈R,∃x2∈(1,+∞),使得g(x1)=f(x2)成立,则a≥e 【答案】BD【解析】函数f(x)=xln x的定义域为(0,1)∪(1,+∞),f(x)=ln x-1(ln x)2,当0<x<1或1<x<e时,f (x)<0,当x>e时,f (x)>0,f(x)在(0,1),(1,e)上都单调递减,在(e,+∞)上单调递增,A不正确;当x∈(1,+∞)时,f(x)的图象在x轴上方,且在x=e时,f(x)min=e,f(x)在(0,1)上的图象在x轴下方,显然f(|x|)是偶函数,在方程f(|x|)=k中,k<0或k=e时,方程有两个不等实根,0≤k<e时,方程无实根,k>e时,方程有4个不等的实根,B正确;因0<x1<x2<1,则有f(x2)<f(x1)<0,即x2ln x2<x1ln x1<0,于是得x2ln x1<x1ln x2,C不正确;当x∈R时,g(x)的值域为[a,+∞),当x∈(1,+∞)时,f(x)的值域为[e,+∞),因对∀x1∈R,∃x2∈(1,+∞),使得g(x1)=f(x2)成立,从而得[a,+∞)⊆[e,+∞),即得a≥e,D正确.故选:BD二、单选题22(2023·广东深圳·高三红岭中学校考阶段练习)过直线y=x上的一点作圆(x-5)2+(y-1)2=2的两条切线l1,l2,当直线l1,l2关于y=x对称时,它们之间的夹角为()A.30°B.45°C.60°D.90°【答案】C【解析】圆(x-5)2+(y-1)2=2的圆心(5,1),过(5,1)与y=x垂直的直线方程为x+y-6=0,它与y=x的交点N(3,3),N到(5,1)距离是22,圆的半径为2,两条切线l1,l2,它们之间的夹角为2×30°=60°.故选C.23(2023·广东·高三校联考阶段练习)如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△AED,△BEF,△DCF分别沿DE,EF,DF折起,使得A,B,C三点重合于点A ,若三棱锥A -EFD的所有顶点均在球O的球面上,则球O的表面积为()A.2πB.3πC.6πD.8π【答案】C【解析】根据题意可得A D ⊥A E ,A D ⊥A F ,A E ⊥A F ,且A E =1,A F =1,A D =2,所以三棱锥D -A EF 可补成一个长方体,则三棱锥D -A EF 的外接球即为长方体的外接球,如图所示,设长方体的外接球的半径为R ,可得2R =12+12+22=6,所以R =62,所以外接球的表面积为S =4πR 2=4π⋅622=6π,故选:C24(2023·广东·高三校联考阶段练习)已知f x =2sin ωx +π3+a -1 sin ωx (a >0,ω>0)在0,π 上存在唯一实数x 0使f x 0 =-3,又φx =f x -23,且有φx max =0,则实数ω的取值范围是()A.1<ω≤53B.1≤ω<53C.56<ω<32D.56<ω≤32【答案】A【解析】由题意可得f x =sin ωx +3cos ωx +a -1 sin ωx ,=a sin ωx +3cos ωx =a 2+3sin ωx +φ ,其中φ满足tan φ=3a,又φx max =0,即f x max =23,所以a 2+3=23,又a >0,解得a =3,所以f x =23sin ωx +π6,又0<x <π,所以π6<ωx +π6<ωπ+π6,因为f x 在上存在唯一实数x 0使f x 0 =-3,即sin ωx 0+π6 =-12,所以7π6<ωx +π6≤11π6,解得1<ω≤53,故选:A 25(2023·广东梅州·高三大埔县虎山中学校考开学考试)在△ABC 中,角B ,C 的边长分别为b ,c ,点O 为△ABC 的外心,若b 2+c 2=2b ,则BC ⋅AO的取值范围是()A.-14,0 B.0,2C.-14,+∞ D.-14,2【答案】D【解析】取BC 的中点D ,则OD ⊥BC ,所以BC ·AO =BC ·AD +DO =BC ·AD +BC ·DO =BC ·AD=AC -AB ⋅12AC +AB =12AC 2-AB 2=12b 2-c 2 =12b 2-2b -b 2 =b 2-b =b -122-14.因为c 2=2b -b 2>0,则b b -2 <0,即0<b <2.所以-14≤BC ⋅AO <2,故选:D .26(2023·广东·高三校联考阶段练习)已知等腰直角△ABC 中,∠C 为直角,边AC =6,P ,Q 分别为AC ,AB 上的动点(P 与C 不重合),将△APQ 沿PQ 折起,使点A 到达点A 的位置,且平面A PQ ⊥平面BCPQ .若点A ,B ,C ,P ,Q 均在球O 的球面上,则球O 体积的最小值为()A.8π3B.4π3C.82π3D.42π3【答案】C【解析】显然P 不与A 重合,由点A ,B ,C ,P ,Q 均在球D 的球面上,得B ,C ,P ,Q 共圆,则∠C +∠PQB =π,又△ABC 为等腰直角三角形,AB 为斜边,即有PQ ⊥AB ,将△APQ 翻折后,PQ ⊥A Q ,PQ ⊥BQ ,又平面A PQ ⊥平面BCPQ ,平面A PQ ∩平面BCPQ =PQ ,A Q ⊂平面A PQ ,BQ ⊂平面BCPQ ,于是A Q ⊥平面BCPQ ,BQ ⊥平面A PQ ,显然A P ,BP 的中点D ,E 分别为△A PQ ,四边形BCPQ 外接圆圆心,则DO ⊥平面A PQ ,EO ⊥平面BCPQ ,因此DO ⎳BQ ,EO ⎳A Q ,取PQ 的中点F ,连接DF ,EF ,则有EF ⎳BQ ⎳DO ,DF ⎳A Q ⎳EO ,四边形EFDO 为矩形,设A Q =x 且0<x <23,DO =EF =12BQ =23-x 2,A P =2x ,设球O 的半径R ,有R 2=DO 2+A P 2 2=34x 2-3x +3=34x -2332+2,当x =233时,R 3min=22,所以球O 体积的最小值为4πR 33=82π3.故选:C .27(2023·广东·高三校联考阶段练习)已知正项等比数列a n 的前n 项和为S n ,且满足a n S n =22n -1-2n -1,设b n =log 2S n +1 ,将数列b n 中的整数项组成新的数列c n ,则c 2023=()A.4048B.2023C.2022D.4046【答案】B【解析】令数列a n 的公比为q ,∵a n >0,∴a 1>0,q >0,因为a n S n =22n -1-2n -1,所以当n =1时,a 21=21-20=1,即a 1=1或a 1=-1(舍去),当n =2时,a 2S 2=23-21=6,即q 1+q =6,解得q =2或q =-3(舍去),所以a n =2n -1,S n =1×1-2n 1-2=2n -1,即b n =log 2S n +1 =n ,因为数列b n 中的整数项组成新的数列c n ,所以n =k 2,k ∈N *,此时b k 2=k 2=k ,即c n =n ,∴c 2023=2023.故选:B28(2023·广东·高三统考阶段练习)已知AB ⊥AC ,|AB |=t ,|AC |=1t.若点P 是△ABC 所在平面内一点,且AP =AB |AB |+2AC|AC |,则PB ⋅PC 的最大值为()A.13 B.5-22C.5-26D.10+22【答案】B【解析】以A 为坐标原点,建立如图所示的直角坐标系,设P (x ,y )则B (t ,0),C 0,1t (t >0),可得AB AB=(1,0),2AC |AC |=(0,2),所以AP =(1,2),即P (1,2),故PB =(t -1,-2),PC =-1,1t-2 ,所以PB ⋅PC =1-t +4-2t =5-t +2t ≤5-22,当且仅当t =2t即t =2时等号成立.故选:B .29(2023·广东·高三统考阶段练习)已知-π2<α-β<π2,sin α+2cos β=1,cos α-2sin β=2,则sin β+π3=A.33B.63C.36D.66【答案】A【解析】由sin α+2cos β=1,cos α-2sin β=2,将两个等式两边平方相加,得5+4sin α-β =3,sin α-β =-12,∵-π2<α-β<π2,∴α-β=-π6,即α=β-π6,代入sin α+2cos β=1,得3sin β+π3 =1,即sin β+π3 =33.故选A30(2023·广东江门·高三台山市第一中学校考阶段练习)设函数f (x )=log 2(1-x ),-1≤x <k ,x 3-3x +1,k ≤x ≤3 的值域为A ,若A ⊆[-1,1],则f (x )的零点个数最多是()A.1B.2C.3D.4【答案】C【解析】令g (x )=log 2(1-x ),则g (x )=log 2(1-x )在(-∞,1)上单调递减;令h (x )=x 3-3x +1,则h (x )=3x 2-3.由h (x )>0,得x >1或x <-1;由h (x )<0,得-1<x <1,所以h (x )在(-∞,-1)和(1,+∞)上单调递增,在(-1,1)上单调递减,于是,h (x )的极大值为h (-1)=3,极小值为h (1)=-1.在同一坐标系中作出函数g (x )和h (x )的图象,如下图:显然f (-1)=g (-1)=1;由g (x )=-1,得x =12;由f (x )的解析式,得-1<k ≤1.(1)若-1<k <0,当k ≤x <0时,f (x )>f (0)=1,不符合题意;(2)若12<k ≤1,当12<x <k 时,f (x )<f 12=-1,不符合题意;(3)若0≤k ≤12,①当-1≤x <k 时,-1<f (x )≤1;②当k ≤x ≤3时,f (1)≤f (x )≤max {f (k ),f (3)}≤1,即-1≤f (x )≤1.由①②,0≤k ≤12时符合题意.此时,结合图象可知,当k =0时,f (x )在[-1,k )上没有零点,在[k ,3]上有2个零点;当0<k ≤12时,f (x )在[-1,k )上有1个零点,在[k ,3]上有1个或2个零点,综上,f (x )最多有3个零点.故选:C .31(2023·广东江门·高三台山市第一中学校考阶段练习)设a =511,b =ln 2111,c =sin 511,则()A.c <a <bB.c <b <aC.a <b <cD.b <c <a【答案】A 【解析】当x ∈0,π2 时,记f x =x -sin x ,则f x =1-cos x ≥0,故f (x )在x ∈0,π2单调递增,故f (x )>f 0 =0,因此得当x ∈0,π2 时,x >sin x ,故511>sin 511,即a >c ;b -a =ln 2111-511=ln 1+2×511 -511,设g (x )=ln (1+2x )-x 0<x <12 ,则b -a =g 511,因为g (x )=21+2x -1=1-2x1+2x,当0<x <12时,g (x )>0.所以g (x )在0,12 上单调递增,所以g 511>g (0)=0,即b >a ,所以b >a>c .故选:A32(2023·广东·高三河源市河源中学校联考阶段练习)设椭圆x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别为F 1、F 2,P 是椭圆上一点,PF 1 =λPF 2 ,12≤λ≤2 ,∠F 1PF 2=π2,则椭圆离心率的取值范围为()A.0,22B.22,53C.23,53D.53,1 【答案】B【解析】设F 1(-c ,0),F 2(c ,0),运用椭圆的定义和勾股定理,求得e 2=λ2+1(λ+1)2,令m =λ+1,可得λ=m -1,即有λ2+1(λ+1)2=21m -12 2+12,运用二次函数的最值的求法,解不等式可得所求范围.设F 1(-c ,0),F 2(c ,0),由椭圆的定义可得,|PF 1|+|PF 2|=2a ,可设|PF 2|=t ,可得|PF 1|=λt ,即有(λ+1)t =2a ,①由∠F 1PF 2=π2,可得|PF 1|2+|PF 2|2=4c 2,即为(λ2+1)t 2=4c 2,②由②÷①2,可得e 2=λ2+1(λ+1)2,令m =λ+1,可得λ=m -1,即有λ2+1(λ+1)2=m 2-2m +2m 2=21m -12 2+12,由12≤λ≤2,可得32≤m ≤3,即13≤1m ≤23,则当m =2时,取得最小值12;当m =32或3时,取得最大值59,即有12≤e 2≤59,解得:22≤e ≤53,所以椭圆离心率的取值范围为22,53.故选:B .33(2023·广东·高三河源市河源中学校联考阶段练习)设a =ln1.1,b =e 0.1-1,c =tan0.1,则()A.a <b <cB.c <a <bC.a <c <bD.b <a <c【答案】C【解析】令f x =e x -x +1 ,所以f x =e x -1,当x >0时f x >0,当x <0时f x <0,即函数f x 在-∞,0 上单调递减,在0,+∞ 上单调递增,所以f x min =f 0 =0,即e x ≥x +1,当且仅当x =0时取等号,令x =0.1,可得b =e 0.1-1>0.1,令h (x )=tan x -x ,x ∈0,π2 ,则在x ∈0,π2 时,h (x )=1cos 2x -1>0,∴h (x )=tan x -x 在x ∈0,π2 上单调递增,∴h (x )>h (0)=0,∴x ∈0,π2时,tan x >x .∴c =tan0.1>0.1,令g x =ln x -x +1,则g x =1x -1=1-xx,所以当0<x <1时g x >0,当x >1时g x <0,即函数g x 在0,1 上单调递增,在1,+∞ 上单调递减,所以g x max =g 1 =0,即ln x ≤x -1,当且仅当x =1时取等号,所以当x =1.1,可得a =ln1.1<1.1-1=0.1,所以a 最小,设t x =e x -1-tan x x ∈0,0.1 ,则t (x )=e x -1cos 2x>0,∴t (x )在0,0.1 上单调递增,∴t (0)<t (0.1),∴t (0.1)=e 0.1-1-tan0.1>e 0-1-tan0=0,∴b =e 0.1-1>tan0.1=c ,综上可得b >c >a ;故选:C34(2023·广东佛山·高三校考阶段练习)符号x 表示不超过实数x 的最大整数,如 2.3 =2,-1.9 =-2.已知数列a n 满足a 1=1,a 2=5,a n +2+4a n =5a n +1.若b n =log 2a n +1 ,S n 为数列8100b n b n +1的前n 项和,则S 2025 =()A.2023B.2024C.2025D.2026【答案】B【解析】因为a n +2+4a n =5a n +1,则a n +2-a n +1=4a n +1-a n ,且a 2-a 1=4,所以,数列a n +1-a n 是首项为4,公比也为4的等比数列,所以,a n +1-a n =4×4n -1=4n ,①由a n +2+4a n =5a n +1可得a n +2-4a n +1=a n +1-4a n ,且a 2-4a 1=1,所以,数列a n +1-4a n 为常数列,且a n +1-4a n =1,②由①②可得a n =4n -13,因为4n +1-13-4n=4⋅4n -1-3⋅4n 3=4n -13>0,4n +1-13-2⋅4n =4⋅4n -1-6⋅4n 3=-2⋅4n +13<0,则4n <a n +1=4n +1-13<2⋅4n ,。
上册数学压轴题练习(Word版 含答案)
5.如图,数轴上点A、B表示的点分别为-6和3
(1)若数轴上有一点P,它到A和点B的距离相等,则点P对应的数字是________(直接写出答案)
(2)在上问的情况下,动点Q从点P出发,以3个单位长度/秒的速度在数轴上向左移动,是否存在某一个时刻,Q点与B点的距离等于Q点与A点的距离的2倍?若存在,求出点Q运动的时间,若不存在,说明理由.
上册数学压轴题练习(Word版 含答案)
一、压轴题
1.如图,已知数轴上两点A,B表示的数分别为﹣2,6,用符号“AB”来表示点A和点B之间的距离.
(1)求AB的值;
(2)若在数轴上存在一点C,使AC=3BC,求点C表示的数;
(3)在(2)的条件下,点C位于A、B两点之间.点A以1个单位/秒的速度沿着数轴的正方向运动,2秒后点C以2个单位/秒的速度也沿着数轴的正方向运动,到达B点处立刻返回沿着数轴的负方向运动,直到点A到达点B,两个点同时停止运动.设点A运动的时间为t,在此过程中存在t使得AC=3BC仍成立,求t的值.
2.概念学习:
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方.
如: , 等,类比有理数的乘方,我们把 记作 ,读作“2的3次商”, 记作 ,读作“ 的4次商”.一般地,我们把 个 相除记作 ,读作“ 的 次商”.
(1)直接写出结果: ______, ______.
(2)关于除方,下列说法错误的是()
A.任何非零数的2次商都等于1
B.对于任何正整数 ,
C.除零外的互为相反数的两个数的偶数次商都相等ቤተ መጻሕፍቲ ባይዱ奇数次商互为相反数
D.负数的奇数次商结果是负数,负数的偶数次商结果是正数.
历届高考数学压轴题汇总及答案
历届高考数学压轴题汇总及答案1.2019年高考数学上海卷:已知等差数列$\{a_n\}$的公差$d\in(0,\pi]$,数列$\{b_n\}$满足$b_n=\sin(a_n)$,集合$S=\{x|x=b_n,n\in N^*\}$。
1) 若$a_1=0,d=\frac{\pi}{6}$,求集合$S$的元素个数;2) 若$a_1=\frac{2\pi}{3}$,求集合$S$;3) 若集合$S$有三个元素$b_{n+T}=b_n$,其中$T$是不超过$7$的正整数,求$T$的所有可能值。
2.2019年高考数学浙江卷:已知实数$a\neq0$,函数$f(x)=a\ln x+x+1$,$x>0$。
1) 当$a=-1$时,求函数$f(x)$的单调区间;2) 对任意$x\in[\frac{3}{4},+\infty)$,有$f(x)\leq\frac{1}{2}e^{2a}$,求$a$的取值范围。
3.2019年高考数学江苏卷:设$(1+x)=a+a_1x+a_2x^2+\cdots+a_nx^n$,$n^2,n\in N^*$,已知$a_3=2a_2a_4$。
1) 求$n$的值;2) 设$(1+3x)=a+b\sqrt{3}$,其中$a,b\in N^*$,求$a^2-3b^2$的值。
4.2018年高考数学上海卷:给定无穷数列$\{a_n\}$,若无穷数列$\{b_n\}$满足对任意$n\in N^*$,都有$b_n-a_n\leq1$,则称$\{b_n\}$与$\{a_n\}$“接近”。
1) 设$\{a_n\}$是首项为$1$,公比为$\frac{1}{2}$的等比数列,构造一个与$\{a_n\}$接近的数列$\{b_n\}$,并说明理由;2) 设数列$\{a_n\}$的前四项为:$a_1=1,a_2=2,a_3=4,a_4=8$,$\{b_n\}$是一个与$\{a_n\}$接近的数列,记集合$M=\{x|x=b_i,i=1,2,3,4\}$,求$M$中元素的个数$m$;3) 已知$\{a_n\}$是公差为$d$的等差数列,若存在数列$\{b_n\}$满足:$\{b_n\}$与$\{a_n\}$接近,且在$1$的等比数列,$b_n=a_{n+1}+1$,$n\in N^*$,判断数列$\{b_n\}$是否满足$b_2-b_1,b_3-b_2,\cdots,b_{201}-b_{200}$中至少有$100$个为正数,求$d$的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏高考数学填空题压轴题精选
1.已知存在实数a 满足 2ab a ab >> ,则实数b 的取值范围为__________.
2.在△ABC 中,π6A ∠=,D 是BC 边上任意一点(D 与B 、C 不重合),且22||||AB AD BD DC =+⋅u u u r u u u r u u u r u u u r ,则B ∠等于__________.
3.设{}n a 是正项数列,其前n 项和n S 满足:4(1)(3)n n n S a a =-+,则n a =__________.
4.在直角坐标系中, 如果两点(,),(,)A a b B a b --在函数)(x f y =的图象上,那么称[],A B 为函数()f x 的一组关于原点的中心对称点([],A B 与[],B A 看作一组).函数
4sin ,0()2log (1),0
x x g x x x π⎧≤⎪=⎨⎪+>⎩,
关于原点的中心对称点的组数为__________. 5.下列说法:①当101ln 2ln x x x x
>≠+≥且时,有;②函数x y a =的图象可以由函数2x y a =(其中01a a >≠且)平移得到;③ABC ∆中,A B >是sin A sin B >成立的充要条件;④已知n S 是等差数列{}n a 的前n 项和,若75S S >,则93S S >;⑤函数(1)y f x =+与函数(1)y f x =-的图象关于直线1x =对称.其中正确的命题的序号为__________.
6.偶函数()f x 在[0,)+∞上是增函数,若(1)(3)f ax f x +>-在[1,2]x ∈上恒成立,则实数a 的取值范围是_________.
7.已知数列}{n a 满足*112311111,(2,)231
n n a a a a a a n n N n -==+++⋅⋅⋅∈-≥,若 100=k a ,则k =_________.
8、已知函数()5sin(2)f x x ϕ=+,若对任意x ∈R ,都有()()f x f x αα+=-, 则()4f π
α+=__________.
9. 在等
式tan95tan35tan35-=o o o o 中,根号下的W 表示的正整数是__________.
10. 已知函数()ln 2x f x x =+,若2(2)(3)f x f x +<,则实数x 的取值范围是__________.
11. 矩形ABCD 中,AB x ⊥轴,且矩形ABCD 恰好能完全覆盖函数()sin ,0y a ax a R a =∈≠的
一个完整周期图象,则当a 变化时,矩形ABCD 周长的最小值为__________.
12.直角三角形ABC 中,斜边BC 长为2,O 是平面ABC 内一点,点P 满足 1()2OP OA AB AC =++u u u r u u u r u u u r u u u r ,则AP u u u r =__________.
13. 不等式223()a b b a b λ+≥+对任意,a b R ∈恒成立,则实数λ的最大值为__________.
14. 已知等差数列{}n a 首项为a ,公差为b ,等比数列{}n b 首项为b ,公比为a ,其中,a b
都是大于1的正整数,且1123,a b b a <<,对于任意的*n N ∈,总存在*m N ∈,使得
3m n a b +=成立,则n a =__________.
简明参考答案(11):
1、(),1-∞-
2、5π12
3、21n +
4、2
5、②③④
6、1,3a a ><-;
7、200
8、0;
9、3;10、(1,2);11
、12 、1、13、2;14、53n -。
