2009-2010(2)线代A卷答案
2009-2010-2离散数学期中考试卷-A
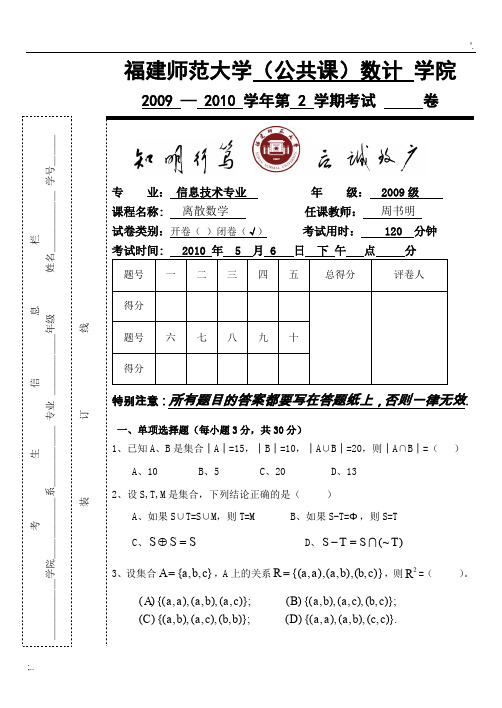
福建师范大学(公共课)数计 学院 2009 — 2010 学年第 2 学期考试 卷 考 生 信 息 栏 ______学院______系______ 专业 ______年级姓名______学号___ 装订线专 业: 信息技术专业 年 级: 2009级 课程名称: 离散数学 任课教师: 周书明 试卷类别:开卷( )闭卷(√) 考试用时: 120 分钟 考试时间: 2010 年 5 月 6 日 下 午 点 分 题号 一 二 三 四 五 总得分 评卷人 得分 题号 六 七 八 九 十 得分 特别注意:所有题目的答案都要写在答题纸上,否则一律无效. 一、单项选择题(每小题3分,共30分) 1、已知A 、B 是集合│A │=15,│B │=10,│A ∪B │=20,则│A ∩B │=( ) A 、10 B 、5 C 、20 D 、13 2、设S,T,M 是集合,下列结论正确的是( ) A 、如果S ∪T=S ∪M ,则T=M B 、如果S-T=Φ,则S=T C 、S S S =⊕ D 、)(~T S T S =- 3、设集合},,{c b a A =,A 上的关系)},(),,(),,{(c b b a a a R =,则2R =( )。
)}.,(),,(),,{()()};,(),,(),,{()()};,(),,(),,{()()};,(),,(),,{()(c c b a a a D b b c a b a C c b c a b a B c a b a a a A、、、、={∅},B=(A)),以下不正确的式子是( ) {{∅},{{∅,{∅,{∅}}}包含于B;B、{{{}}}包含于B。
09-10第一学期3学分(A卷)参考答案

⎛2 5 4 5 5⎞ 解方程组 ( A − E ) x = 0 求得 λ = 1 的一个特征向量为 ξ1 = ( 2, 4,5 ) ,单位化得 p1 = ⎜ ⎜ 15 , 15 , 3 ⎟ ⎟ ⎝ ⎠
T
T
⎛ 2 ⎞ ⎛ 3 ⎞ ⎛ −1 ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ 2 0 2 ξ1 = p1 − p3 = ( p1 + p2 ) − ( p2 + p3 ) = ⎜ ⎟ − ⎜ ⎟ = ⎜ ⎟ , ⎜ 0 ⎟ ⎜ 1 ⎟ ⎜ −1 ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ 4⎠ ⎝ 2⎠ ⎝ 2 ⎠ ⎛ 3⎞ ⎛ 2⎞ ⎛ 1 ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ −1 0 1 ξ 2 = p2 − p4 = ( p2 + p3 ) − ( p3 + p4 ) = ⎜ ⎟ − ⎜ ⎟ = ⎜ ⎟ ⎜1⎟ ⎜0⎟ ⎜ 1 ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ 2⎠ ⎝1⎠ ⎝ 1 ⎠
T T
为 A 相应于 λ2 的两个线性无关的特征向量,证明向量组 α1 , α 2 , α 3 , α 4 线性无关。 (1)解:由 b1 , b2 ," , bn 由 a1 , a2 ," , an 的线性表出关系式可知 B = AK ,其中
T (kB) = A(kB) − ( kB)T A = kAB − kBT A = kT ( B) 故 T 是 V 上的一个线性变换。
(2). T ( E11 ) = ⎜
⎛ 0 −2 ⎞ ⎛0 1⎞ ⎟ = −2 E12 − 2 E21 , T ( E12 ) = ⎜ ⎟ = E12 − E21 − 4 E22 ⎝ −2 0 ⎠ ⎝ −1 − 4 ⎠
A = ( a1
a2
a3 " an ) , B = ( b1
北京理工大学2009-2010学年第二学期工科数学分析期末试题(A卷)答案

2009-2010第二学期工科数学分析期末试题解答(A 卷)一.1.11,65arccos(2分,2分)2.(1,2,7),4(2分,2分)3.25-,}52,51{-(2分,2分)4.∑∞=+--01)1(4)1(n nn n x ,∑∞=---+11)1(4)1(4ln n nn n x n (2分,2分)5.dy dx 2-,}2,1{-(2分,2分)6.x x y ln ,34ln(2分,2分)7.0,ππ324+,0,12+π(1分,1分,1分,1分)二.⎰=Ly dlx I μ2…………………….(2分)⎰+=15322)1(1dxx x μ……………………(6分)μμ35611532=+=⎰dx x x ……………………(9分)三.设V 在第一卦限部分为1V ⎰⎰⎰⎰⎰⎰==122486V VdVx dV x I ……………(3分)⎰⎰⎰---=yx xdzdy dx x 101010248……………..(6分)⎰⎰---=xdyy x dx x 10102)1(48………………..(7分)⎰-=1022)1(24dx x x …………………(8分)54=…………………(9分)四.令02==∂∂x xz,014=-=∂∂y yz………………(2分)解得0=x ,41=y ,得驻点)41,0(,………………..(3分)由122=+y x ,得221y x -=,代入目标函数得62+-=y y z )11(≤≤-y ………………..(4分)令012=-=y dydz,得21=y ,此时23±=x ,得两点)21,23(±………..(6分)当1±=y 时,0=x ,得两点)1,0(±………………..(7分)83941,0(=z ,42321,23(=±z ,8)1,0(=-z ,6)1,0(=z 8max =z ,839min =z ……………..(9分)五.由题意,有yXx Y ∂∂=∂∂……………………….(1分)λλλλλλλλ2121)()()33()(3)()()3()(3y x y x y y x y x y x x y y x ++--+=++--+---…….(3分)即033=--+y x y x λλ,3=λ…………………….(4分)1),()1,1(33)(3)(3),(C dy y x xy dx y x x y y x u y x ++-++-=⎰…………………….(6分)11313)(3)(3C dy y x x y dx y x xy x++-++-=⎰⎰……………………(8分)C y x yx ++-=2)(……………………(10分)注:没有加C 不扣分。
江西农业大学2009—2010第一学期《线性代数》试卷_(A) - 副本

线
= (−2, 4, b)T 线性相关,则 a = − 2
b=
6
.
二.单项选择题(2 分×6=12 分)
1. 设 A, B 均为 n 阶可逆矩阵,则下列各式不 正确 的是( B ). . .. A. ( A + B ) =A + B
T T T
B. ( A + B )
T
−1
=A−1 + B −1
T T
·
a13 a23 = ( D ). a33
D. −16
C. 16
永远支持软件 097
——第 1 页 本试卷共 4 页
3. 设 α1 , α 2 是非齐次线性方程组 Ax = b 的解, β 是对应的齐次方程组 Ax = 0 的解,则
Ax = b 必有一个解是( D ).
A. α1 + α 2 B. α1 − α 2 C. β + α1 + α 2 D. β + α1 +
2 2
姓名:
AB = BA
.
不
5. 已知 3 阶方阵 A 的特征值分别为 1 ﹑ −2 ﹑ 3 ,则 A =
− 6 , A−1 = − 1 , A∗ = 36 ,
6
A − 2E = 4 .
软 件 097
订
6. 方程组 内
λ x1 + x2 = 0
x1 + λ x2 = 0
有非零解,则 λ = 1 或 − 1 .
订
C. ( AB )
−1
= B −1 A−1 a12 a22 a32
D. ( AB ) = B A
院系:
装
装
全
南京工业大学线性代数江浦A答案
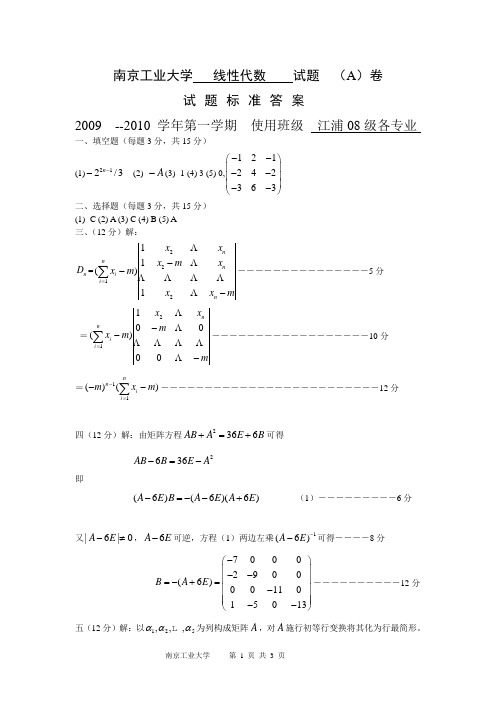
南京工业大学 线性代数 试题 (A )卷试题标准答案2009 --2010 学年第一学期 使用班级 江浦08级各专业一、填空题(每题3分,共15分)(1)3/212--n (2) A -(3) -1 (4) 3 (5) 0,121242363--⎛⎫ ⎪-- ⎪ ⎪--⎝⎭二、选择题(每题3分,共15分)(1) C (2) A (3) C (4) B (5) A 三、(12分)解:n D =mx x x m x x x m x n n n ni i ---∑=2221111)(―――――――――――――――5分=mm x x m x nn i i ---∑= 00001)(21――――――――――――――――――10分=)()(11m x m ni i n --∑=-―――――――――――――――――――――――――12分四(12分)解:由矩阵方程2366AB A E B +=+可得 2636AB B E A -=- 即(6)(6)(6)A E B A E A E -=--+ (1)―――――――――6分又|6|0A E -≠,6A E -可逆,方程(1)两边左乘1(6)A E --可得――――8分70002900(6)0011015013B A E -⎛⎫ ⎪--⎪=-+= ⎪- ⎪ ⎪--⎝⎭――――――――――12分 五(12分)解:以125,,,ααα 为列构成矩阵A ,对A 施行初等行变换将其化为行最简形。
A =103211301121752421460⎛⎫ ⎪--⎪⎪⎪⎝⎭21314124r r r r r r +--10321033300111002224⎛⎫ ⎪ ⎪ ⎪ ⎪--⎝⎭ 234332r r r r --1032100000011100044⎛⎫⎪ ⎪⎪ ⎪--⎝⎭233413r r r r r ↔↔-1032101110000110000⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭23132r r r r -- 10301011010001100-⎛⎫ ⎪- ⎪ ⎪ ⎪⎝⎭――――――――――――――――――――――――――――――――――――6分 故15(,,)3,R αα= ―――――――――――――――――――――――――――8分 其一个极大线性无关组为124,,ααα且31254123,ααααααα=+=--――――――12分六、(13分)解:系数行列式)4)(1(2111111k k k k-+=--由克莱姆法则得,当,1-≠k 且4≠k 时,方程组有唯一解。
2010级高等数学II(2)试卷A评分标准

f x ( x, y ) 2 x 0 解: 解方程组 , 得驻点 ( 0 , 1 ) , f y ( x, y ) 2 y 2 0 y2 令 L ( x, y ) x 2 y 2 2 y ( x 2 1) 2 Lx ( x, y ) 2 x 2 x 0 , 解方程组 Ly ( x, y ) 2 y 2 y 0 , 2 2 x y 2 1 , 得所有可能极值点 ( 0 , 2 ) , (0 , 2 ) , 因为 f ( 0 , 1 ) 1 , f ( 0 , 2 ) 2 2 2 , f (0 , 2 ) 2 2 2 , 所以 最大值为 f (0 , 2 ) 2 2 2 , 最小值为 f ( 0 , 1 ) 1.
若级数 bn 收敛 , 则级数 an 也收敛 .
(2) (3)
n 1 n 1
证: 由题设得 相乘得
a b a b a2 b2 , 3 3 , , n n , a1 b1 a2 b2 an 1 bn 1 an
(2) (4) (6)
a1 bn , b1
( n 1 , 2 ,3 , )
本题 得分
四、 (本题 10 分)求旋转抛物面 z x 2 y 2 含在圆柱面 x 2 y 2 1内部的那部分面积. (1) (4) (8) (9) (10)
闭区域 . 解: 投影区域 D : x 2 y 2 1 (1)
1 1 2 0 0
解: 投影区域 Dxy : x 2 y 2 1 , A 1 4 x 2 4 y 2 dxdy
(4) 将函数 f ( x)
1 展开成 ( x 1) 的幂级数, 并指出展开式成立的区间 . x2 x 6 1 1 1 1 解:f ( x) ( ) (2) ( x 3)( x 2) 5 x 3 x 2 1 1 1 1 [ ] (4) 5 4 1 x 1 1 (( x 1)) 4 1 1 ( x 1) n [ (1)n ( x 1) n ] (6) 5 4 n 0 4n n0 1 1 [ n 1 (1)n ] ( x 1) n (7) (2 x 0) (8) 5 n0 4
《线性代数》国际09-10A期末试卷
云南财经大学20020099至20201010学年第二学期《线性代数》课程期末考试试卷(A )(试)得分一二三四五六七八总分复核人阅卷人6小题,每小题2分,共12分,对的打√,错的打×).若≠A O ,则||0≠A ;().设A 为n 阶矩阵,则T ||||=A A ;().当向量组中向量的维数大于向量的个数时向量组必线性相关;().设A 为n 阶矩阵,且||0=A ,则A 中必有一列向量可由其它列向量线性表示;).设A 为m n ×矩阵,r()r =A ,则当r n =时非齐次方程组=Ax b 有唯一解;().设1λ,2λ是矩阵A 的特征值,1α,2α分别是A 的对应于1λ,2λ的特征向量,12≠λλ,则1α,2α必不成比例.()6小题,每小题2分,共12分).若排列38i 7j 625为奇排列,则i =;.已知1P AP B −=,且||0B ≠,则||||A B =;.设A 为三阶矩阵,且||2A =,*A 为A 的伴随矩阵,则行列式1*32|A A −−=;.已知四阶行列式D 中第三列元素依次为-1,2,0,1,它们的余子式依次为5,3,-7,4,则D =;5.若向量组T 1(1,11)α=,,T 2(1,2,3)=α,T 3(1,3)=,αt 线性相关,则t 的取值满足;6.设A 为n 阶方阵,且齐次线性方程组AX =O 有非零解,则A 必有一个特征值为.三、单项选择题(本大题共6小题,每小题2分,共12分)1.设D 为n 阶行列式,则D 为零的充分必要条件是();(A )D 中有两行(列)的对应元素成比例;(B )D 中有一行(列)的所有元素均为零;(C )D 中有一行(列)的所有元素均为可化零;(D )D 中有一行(列)的所有元素的代数余子式均为零.2.若n 阶矩阵A 满足2230A A I −−=,则矩阵A 可逆,且1A −=();(A )2A I −;(B )2I A −;(C )1(2)3A I −−;(D )1(2)3A I −.3.设矩阵111213212223313233A ⎛⎞⎜⎟=⎜⎟⎜⎟⎝⎠a a a a a a a a a ,313233312122232111121311333B −⎛⎞⎜⎟=−⎜⎟⎜⎟−⎝⎠a a a a a a a a a a a a ,1103010001P −⎛⎞⎜⎟=⎜⎟⎜⎟⎝⎠,2001010100P ⎛⎞⎜⎟=⎜⎟⎜⎟⎝⎠,则B =();(A )21P AP ;(B )12AP P ;(C )12P AP ;(D )12P P A .4.设n 元齐次线性方程组Ax O =,r()3A =−n ,且1α,2α,3α是其3个线性无关的解,则方程组的基础解系是();(A )1α,2α,12+αα;(B )12−αα,23−αα,31−αα;(C )1α,12+αα,123++ααα;(D )123++ααα,12−αα.5.设n 阶方阵A ,B 满足AB O =,则必有();(A )A O =或B O =;(B )A B O +=;(C )|A |+|B |=0;(D )|A |=0或|B |=0.6.三阶矩阵A 的特征值为2−,1,3,I 为三阶单位矩阵,则||A I −=().(A )6−;(B )0;(C )2;(D )1−.四、(10分)已知行列式1040211206002412−−=−−D ,4j A (1,2,3,4=j )为D 的第四行第j 列元素的代数余子式,求41424344+++A A A A .五、(12分)设矩阵A ,B 为n 阶矩阵,且满足2A B I AB −=+,其中100031062A ⎛⎞⎜⎟=−⎜⎟⎜⎟−⎝⎠,I 为n 阶单位矩阵,求矩阵B .六、(16分)已知向量组T 1(2,1,3,0)α=,T 2(1,0,0,1)α=,T 3(0,1,0,1)α=,T 4(0,0,1,1)α=−.求此向量组的秩和一个极大无关组,并将其余向量用此极大无关组线性表示.七、(16分)用基础解系表示下列线性方程组的全部解12341234123412342122233224+−+=⎧⎪++−=⎪⎨+++=⎪⎪+++=⎩x x x x x x x x x x x x x x x x .八、(10分)设λ是n 阶矩阵A 的一个特征值,求证:2λ是2A 的一个特征值.。
成都信息工程学院 09-10学年线性代数试题A答案[1][1]
2009——2010学年第一学期课程名称:线性代数与空间解析几何 使用班级:08级全校理工各专业 一.解: 12111111111110111101111101111011(1)1110111101111101111nir r n n n An n n +--∑-==-----(6分)1111110100000100(1)(1)(1)0001001n n n ---=-=------(4分)二.(10分)解:由2,AX A X =+得 (2)A I X A -=而101211010012A I -=-=-≠,所以2A I -可逆,1(2)X A I A -=- ---(4分) 101301101301(2)1101100112110121401214A I A ⎛⎫⎛⎫⎪ ⎪-=-→---- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭100522010432001223--⎛⎫ ⎪-- ⎪ ⎪-⎝⎭ 故522432223X --⎛⎫⎪=--⎪ ⎪-⎝⎭——(6分) 三、(10分) 解: 所求平面过点1M ,可设它的方程为(4)(1)(2)0A x B y C z -+-+-= -----(3分)因为该平面与已知平面垂直且与12M M平行,所以有62307430A B C A B C -+=⎧⎨-+-=⎩ 求得33,510A CB C=-=-, -----(5分)故,所求平面方程为631070x y z +--= ————(2分) 四.(10分) 解:1234132013201043(,,,)1441012101211210121000A αααα--⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪==→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭(4分) 1.()2R A =,向量组1234,,,αααα线性相关. --------(3分) 2. 12,αα为极大无关组, 31241242,3αααααα=-+=-+ ————(3分) 五.(10分)解: 1. 设ξ是属于特征值0λ的特征向量,即02121153111211a bλ-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪----⎝⎭⎝⎭⎝⎭-----(2分) 即0001,2,.1a b λλλ-=⎧⎪+=⎨⎪+=-⎩解得 01,3,0.a b λ=-=-= -----(3分) 2. 3212533(1)12I Aλλλλλ---=-+-=++ -----(3分)因此特征值为1231,λλλ===-又因为312()5232101R I A R --⎛⎫⎪--=--= ⎪ ⎪⎝⎭因此属于1的特征向量只有1个,因此,A 不能对角化 . -----(2 分)六.(10分)解: 331024113137()313401241598000B A b ⎛⎫---⎛⎫ ⎪⎪⎪==--→-- ⎪ ⎪ ⎪-- ⎪⎝⎭ ⎪⎝⎭ -----(4分) 由于()()2R A R B ==,方程组有解,对应方程组为;132333243724x x x x ⎧=+⎪⎪⎨⎪=-⎪⎩ 令30x =,得特解102334740x x x η⎛⎫⎛⎫ ⎪ ⎪ ⎪==- ⎪ ⎪⎪ ⎪⎝⎭ ⎪⎝⎭ -(2分)对应齐次方程组为;12223232x x x x⎧=⎪⎪⎨⎪=⎪⎩ 令31x =,得基础解系12332321x x x ξ⎛⎫-⎛⎫ ⎪ ⎪ ⎪==- ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭(2分)故,方程组的通解为:3342734201k η⎛⎫⎛⎫⎪ ⎪⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭k R ∀∈ ————(2分)七.(10分)解: 240031(4)(2)013I A λλλλλλ--=--=----故得特征值1232,4λλλ=== -----(3分)当12λ=时,由 123200001100110x x x -⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪--= ⎪ ⎪ ⎪⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭求得基础解系 1011ξ⎛⎫⎪= ⎪ ⎪-⎝⎭,单位化得10e ⎛⎫ ⎪ ⎪= ⎪ - ⎝-----(2分)当234λλ==时,由 123000001100110x x x ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-= ⎪ ⎪ ⎪⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭求得基础解系 23100,101ξξ⎛⎫⎛⎫ ⎪⎪== ⎪ ⎪⎪ ⎪⎝⎭⎝⎭,23,ξξ刚好正交, 单位化得23010,0e e ⎛⎫ ⎪⎛⎫⎪== ⎪ ⎪⎝⎭ ⎝ , -----(2分)于是得正交阵01000C ⎛⎫⎪=⎝有 1244T C AC C AC -⎛⎫⎪==⎪ ⎪⎝⎭-----(3分) 八.(10分)解: 作变换:11221233x y y x y y x y=+⎧⎪=-⎨⎪=⎩ -----(3分)则 2212312123123(,,)()()f x x x y y y y y y y y =-+-++22222121313232()y y y y y y y y =-+=+-- -----(3分)令 1122233z y y z y z y=+⎧⎪=⎨⎪=⎩ 故标准形为222123123(,,)f x x x z z z =-- -----(4分)九.(10分)解: 由方程组消去y ,得到曲线Γ在xoz 面上的投影曲线方程为:2240z x y ⎧+=⎨=⎩曲线Γ在母线平行于z 轴的柱面上,故曲线Γ在xo y 面上的投影曲线方程为: 2220x y x z ⎧+-=⎨=⎩十.(8分)解: 由于 1223312,2,32a αααααα+++ 线性相关,所以有不全为零的123,,x x x ,使 112223331(2)(2)(32)0x x a x αααααα+++++=即 131122233(2)(22)(3)0x x x x ax x ααα+++++= -----(4分) 因为 123,,ααα线性无关,故有1312232022030x x x x ax x +=⎧⎪+=⎨⎪+=⎩ 由于不全为零,从而齐次方程组有非零解,系数行列式必为零.即 1023220640,23a a a=+==------(6分)。
2009-2010高数(A)II期末A 2
XXXX 学院(本科)试卷(A 卷)2009 -2010学年第二学期《 高等数学(A)II 》试卷一. 填空题(共70分,1-21题每空3分,最后一空1分)1.微分方程y x y +='10的通解是2.微分方程032=-'-''y y y 的通解是3. 微分方程x e y y y =-'+''32的特解形式是x bxe y =*,则微分方程xe y y y =-'+''32通解是 4. 向量)1,2,1(=a 与向量)1,1,2(-=b 的夹角为:5. 过点)3,2,1(,且与平面0432=-++z y x 平行的平面方程为_______.6.直线⎩⎨⎧=-+=--0306:z y y x L 的单位方向向量为_______. 7. yoz 坐标面上的曲线1322222=-z y 绕z 轴旋转一周生成的旋转曲面方程为_____. 8. 曲线⎪⎩⎪⎨⎧===t z t y t x 23在点(1,1,1)点处的切线方程为_____.9. 球面1222=++z y x 在点)33,33,33(处的法线方程为_______. 10.11. 设y x z =,则=z d _________. 12. 设,1345=+-yz xz z 则=∂∂)0,0(x z _____________. 13. =+⎰L s y )d 1(_________,=+⎰L x y )d 1(_________, 其中L 为正向圆周线.12222=+ay a x14.设闭区域}1|),{(22≤+=y x y x D ,则二重积分=+⎰⎰D y x y x d )d (22_________.15. 将三重积分⎰⎰⎰Ωz y x z y x f d d )d ,,(在化为直角坐标系下的三次积分为____________,其中闭区域Ω是由平面0,0,0===z y x 与平面1=++z y x 所围成部分.16. 闭区域Ω由曲面222y x z +=及平面1=z 所围成,利用柱面坐标系计算三重积分=+⎰⎰⎰Ωv y x )d (22_________.17. 已知数项级数∑∞=+-11)1(n nn n ,则该级数是_______(绝对收敛、条件收敛、发散). 18. 已知正项级数n n 21sin 1∑∞=,则该级数是________(收敛、发散). 19. 已知正项级数∑∞=⎪⎭⎫ ⎝⎛+1232n n n n ,则该级数是________(收敛、发散).20. 级数∑∞=-2ln 1)1(n n n是________(绝对收敛、条件收敛、发散) 21. 幂级数∑∞=1n n nx 的收敛域是_______ 22. 设周期函数在一个周期内的表达式为⎩⎨⎧≤<≤<-=,0,0,6)(ππx x x x f 则它 的傅里叶级数在0=x 处收敛于___________.(此题得分为1分)二.计算题(共30分,每题5分)1. 求微分方程x y y =-'满足初始条件10-==x y 的特解.2. 计算曲线积分⎰-++L y y y y xe x x e d )2(d )(,其中L 是由下半圆周0,222≤=+y x y x 逆时针方向的弧段.3. 设∑是上半球面}0,1|),,{(222≥=++z z y x z y x 的整个边界曲面的上侧,则⎰⎰∑++++-+y x y y x x z z y x z y xz d z)d 122(d d )(d d 2322.4.求幂级数∑∞=1n n nx 的收敛域及其和函数.5.求函数设x y x y x y x f 933),(2233-++-=的极值.。
重庆理工大学线性代数理工类_A卷_2010年5月
10、二次型 f ( x1 , x2 , x3 ) = 2 x12 − x22 + x32 的正惯性指数是 ( A. 0 B. 1 C.2
重庆理工大学考试试题卷
2009~2010 学年第二学期
班级 学号 姓名 考试科目 线性代数(理工类) A卷 闭卷 共 2 页
·················· 密············ ·················· ············封············ ············线················ ················ 学生答题不得超过此线
重庆理工大学考试答题卷
2009~2010 学年第二学期
班级 学号 姓名 考试科目 线性代数(理工类) A卷 闭卷 共 2 页
·················· 密············ ·················· ············封············ ············线················ ················ 学生答题不得超过此线
二、填空题(本大题共 10 小题,每小题 2 分,共 20 分)
⎛ 0 0 1 ⎞⎛ 1 2 ⎞ ⎟⎛ 1 2 ⎞ ⎟⎜ ⎜ ⎟ =_______。 11、 ⎜ 0 1 0 ⎟⎜ − 1 1 ⎟⎜ ⎜ ⎟ ⎜ 1 0 0 ⎟⎜ 2 3 ⎟⎝ 0 1 ⎠ ⎠ ⎠⎝ ⎝
0⎞ ⎛1 0 ⎟ ⎜ 12、设矩阵 A = ⎜ 0 − 2 0 ⎟ ,则 A−1 = ⎜ 0 0 − 1⎟ ⎠ ⎝
12、 17、 18、
13、 19、 20、
三.、计算题。 (每小题 8 分,共 48 分)
21、 22、
23、
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
拟题学院(系): 数理学院 适用专业: 全校 2009-2010 学年 2 学期 线性代数(必修)A卷 试题标准答案 (答案要注明各个要点的评分标准) 一. 填空题(每小题3分,共15分) 1. 1 2. 12312212343 3. 0 4. 0,1xy 5. 1a 二. 选择题(每小题3分,共15分) 1. (B) 2. (C) 3. (C) 4. (D) 5. (D) 三. 计算题 (本题26分) 1.解:3112513420111533121312153402115133cc2141131208465021101627rrrr2313120211084601627rr……. (4分) 324243131240211840008105500042rrrrrr………………………………….. (8分) 2. (8分) 解: 因为矩阵A与B相似,故知A的特征值为1,2,-1,且A是可逆矩阵..……… (2分) *1AAA,而1232A, ………….. ………………….. (4分) *132232AAEAAE,记作A().有2()32,.(1)3,(2)7,(1)1 (6分) *3237121AAE (8分) 拟 题 人: 曹红妍
书写标准答案人: 曹红妍
2
3. 解:原方程变形为2AEXA
1101102,011011101101AEA~r100011010101001110
…(7分)
1011(2)101110XAEA
………………………… (10分)
四、(本题23分)
1. 解:对增广矩阵,BAb进行初等行变换,有
2121
2131011032100121rB
(6分)
(1) 当1,0,1时,RR3AB,方程组有唯一解;
(2) 当01或时,有R2,R3AB,方程组无解;
(3) 当1时,RR23AB,方程组有无穷多解. ……(10分)
当1时,
11211101
1131001011410000rB
方程组通解为12311110000xcxxccx 其中c为任意常数。 ……(13分)
2. 解:对矩阵12345A() 进行初等行变换把A化成行阶梯形,
3205012103323610433520153000241641400000~rA
(7分)
则向量组的秩为3, 124,,为向量组的一个最大无关组。 (10分)
五、(本题15分)
解: 222254245AE)10()1(2,
故得特征值为10,1321 (5分)
3
当121时,由000442442221321xxx 解得
10201221321kkxxx
,此二个向量正交,单位化后,得两个单位正交的特征向量
012
5
1
1
P
15452012540122P单位化得
15452352P
(8分)
当103时,由000542452228321xxx
解得2213321kxxx 单位化221313P,
得正交阵123(,,)PPPP323503215545131155252 (12分)
10001000101APP
. (15分)
六、证明:
设存在1m个常数12,,,,mkkkk,使
4
1122120mm
kkkkl
, (1)
则必有0k, ( 2分)
否则122121mmkkklkkk, (2)
又11122mm代入(2)式得
12
21122mmm
k
kk
lllkkk
( 4分)
与假设2不能由12,,,m线性表出矛盾,故0k
于是(1)式变为11220mmkkk.由12,,,m线性无关,
所以120mkkkk.由式(1)可知1212,,,,m线性无关. ( 6分)
