使用示波器进行信号的频谱分析(FFT分析)
示波器的频率计算和傅里叶变换

示波器的频率计算和傅里叶变换示波器是一种用于测量和显示电压波形的仪器,广泛应用于电子、通信、无线电等领域。
在使用示波器时,频率计算和傅里叶变换是两个重要的功能。
本文将介绍示波器中频率计算和傅里叶变换的原理和应用。
一、示波器的频率计算示波器的频率计算是指通过示波器测量得到的电压波形,计算出该波形的频率。
示波器中常用的频率计算方法包括周期测量法、计数法和相位比较法。
1. 周期测量法周期测量法是通过测量波形的一个完整周期所用的时间来计算频率。
示波器会自动测量出波形的周期,并根据周期计算出频率。
该方法适用于稳定且周期性的波形。
2. 计数法计数法是通过计算波形在固定时间内的周期数来计算频率。
示波器会在固定时间内对波形进行计数,并根据计数结果计算出频率。
该方法适用于任意类型的波形。
3. 相位比较法相位比较法是通过比较波形上升沿或下降沿的时间间隔来计算频率。
示波器会选择一个基准波形作为参考,然后测量其他波形与基准波形之间的时间差,再通过时间差计算频率。
该方法适用于不规则的波形。
二、示波器的傅里叶变换傅里叶变换是一种数学工具,可以将时域中的信号转换为频域中的频谱。
示波器中的傅里叶变换功能可以帮助我们了解波形的频率分量和幅度分布,以及波形的谐波情况。
傅里叶变换基本原理是将时域中的任意连续周期信号分解成多个简单的正弦和余弦信号,每个正弦和余弦信号的频率和幅度决定了原始信号的频谱特征。
示波器通过对波形进行傅里叶变换,将信号从时域转换为频域,以便更好地分析信号特性。
示波器中进行傅里叶变换主要有两种方式:快速傅里叶变换(FFT)和实时傅里叶变换(RTF)。
FFT是一种离散傅里叶变换的算法,在计算机中可以高效地对信号进行频谱分析。
RTF则是一种实时计算傅里叶变换的方法,可以实时显示波形的频谱。
傅里叶变换结果通常以频率和振幅为横纵坐标在频谱图中显示。
频谱图能够清晰地展示信号的频率分布情况,帮助我们分析信号的频率成分和谐波情况。
频谱扫描应用实验报告(3篇)

第1篇一、实验背景频谱扫描技术在信号处理、通信系统、雷达等领域有着广泛的应用。
本实验旨在通过搭建频谱扫描系统,对信号进行频谱分析,验证频谱扫描技术的实际应用效果,并分析影响频谱扫描结果的因素。
二、实验目的1. 理解频谱扫描的基本原理和过程。
2. 掌握频谱扫描仪的使用方法。
3. 分析不同参数对频谱扫描结果的影响。
4. 验证频谱扫描技术在实际应用中的有效性。
三、实验原理频谱扫描技术基于傅里叶变换(FFT)原理,将时域信号转换为频域信号,从而分析信号的频率成分。
频谱扫描过程中,信号通过频谱分析仪进行扫描,分析仪输出信号的频谱图,便于分析。
四、实验设备1. 频谱分析仪2. 信号发生器3. 信号线4. 计算机及数据采集软件五、实验步骤1. 搭建实验系统:将信号发生器输出的信号通过信号线连接至频谱分析仪,分析仪输出信号频谱。
2. 设置频谱分析仪参数:选择合适的扫描范围、分辨率、带宽等参数。
3. 进行频谱扫描:启动频谱分析仪,进行信号频谱扫描。
4. 分析频谱扫描结果:观察频谱图,分析信号的频率成分、幅度等参数。
5. 改变参数进行对比实验:改变扫描范围、分辨率、带宽等参数,观察对频谱扫描结果的影响。
六、实验结果与分析1. 基本频谱扫描:在扫描范围内,观察到信号存在多个频率成分,其中主要频率成分与信号发生器输出频率一致。
2. 改变扫描范围:当扫描范围增大时,信号频谱中出现了更多频率成分,说明扫描范围对频谱扫描结果有显著影响。
3. 改变分辨率:提高分辨率后,频谱图中频率成分更加清晰,但扫描时间变长。
4. 改变带宽:带宽变窄时,频谱图中信号成分更加集中,但可能丢失部分频率成分。
七、实验结论1. 频谱扫描技术在信号处理、通信系统、雷达等领域具有广泛的应用。
2. 频谱分析仪是频谱扫描的重要设备,其参数设置对扫描结果有显著影响。
3. 通过改变扫描范围、分辨率、带宽等参数,可以优化频谱扫描结果。
4. 频谱扫描技术在实际应用中具有很高的有效性。
示波器CSV波形数据导入Matlab进行FFT分析
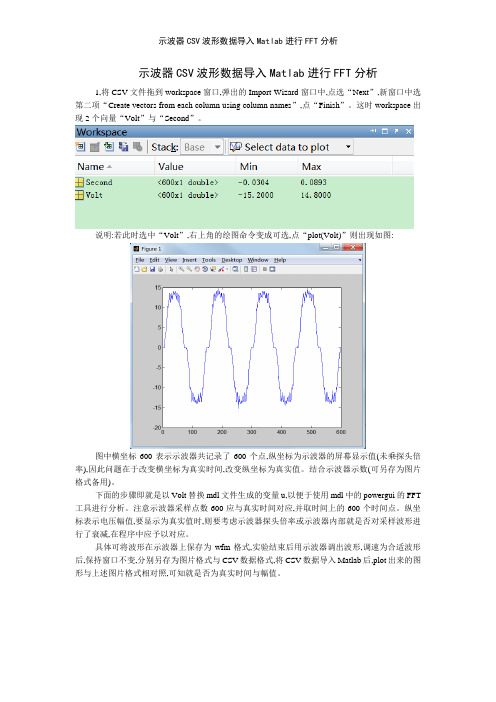
示波器CSV波形数据导入Matlab进行FFT分析1,将CSV文件拖到workspace窗口,弹出的Import Wizard窗口中,点选“Next”,新窗口中选第二项“Create vectors from each column using column names”,点“Finish”。
这时workspace出现2个向量“Volt”与“Second”。
说明:若此时选中“Volt”,右上角的绘图命令变成可选,点“plot(Volt)”则出现如图:图中横坐标600表示示波器共记录了600个点,纵坐标为示波器的屏幕显示值(未乘探头倍率),因此问题在于改变横坐标为真实时间,改变纵坐标为真实值。
结合示波器示数(可另存为图片格式备用)。
下面的步骤即就是以Volt替换mdl文件生成的变量u,以便于使用mdl中的powergui的FFT 工具进行分析。
注意示波器采样点数600应与真实时间对应,并取时间上的600个时间点。
纵坐标表示电压幅值,要显示为真实值时,则要考虑示波器探头倍率或示波器内部就是否对采样波形进行了衰减,在程序中应予以对应。
具体可将波形在示波器上保存为wfm格式,实验结束后用示波器调出波形,调速为合适波形后,保持窗口不变,分别另存为图片格式与CSV数据格式,将CSV数据导入Matlab后,plot出来的图形与上述图片格式相对照,可知就是否为真实时间与幅值。
可见,横坐标为120ms,纵坐标为10倍衰减后的值,在编程中应有相应体现。
2,打开forFFT、mdl,并运行仿真,完成后wordspace出现新的变量“u”与“tout”;Mdl文件中scope的设置已设置为保存波形名称为u,Structure with time格式,不限制最后5000个点。
由于powergui自带的FFT功能只能对该mdl文件中的scope保存的变量u进行分析,以下考虑将u中的数据替换为示波器保存的数据,注意横坐标真实时间点数0~0、1198s,(间隔0、0002s 包含两端共计600个点)与采样点数600相对应。
第26章ARM官方DSP库 FFT的示波器应用

安富莱S T M32-V5开发板数字信号处理教程文档版本:V1.0安富莱电子W W W.A R M F L Y.C O M声明本文档的版权归武汉安富莱电子有限公司所有。
任何公司或者个人未经许可,不得将本文档用于商业目的。
⏹本文档由安富莱电子原创,非我们原创的资料已经在章节的开头进行申明(特别是F F T部分)。
⏹教程中使用的D S P库是来自A R M公司。
⏹教程参考资料如下:◆C o r t e x-M4权威指南。
◆数字信号处理理论、算法与实现第二版(作者:胡广书)。
◆信号与系统第二版(作者:奥本海姆)。
◆M a t l a b的h e l p文档。
◆力科示波器基础应用系列文档。
◆百度百科,w i k i百科。
◆网络资源。
◆S T官方相关文档。
第26章F F T的示波器应用特别声明:本章节内容整理自力科示波器基础应用系列文档,原名《FFT的前世今生》。
FFT(Fast Fourier Transform,快速傅立叶变换)是离散傅立叶变换的快速算法,也是我们在数字信号处理技术中经常会提到的一个概念。
在大学的理工科课程中,在完成高等数学的课程后,数字信号处理一般会作为通信电子类专业的专业基础课程进行学习, 原因是其中涉及了大量的高等数学的理论推导,同时又是各类应用技术的理论基础。
关于傅立叶变换的经典著作和文章非常多,但是看到满篇的复杂公式推导和罗列,我们还是很难从直观上去理解这一复杂的概念,我想对于普通的测试工程师来说,掌握 FFT 的概念首先应该搞清楚这样几个问题(在这篇文章中我尝试用更加浅显的讲解,尽量不使用公式推导来说一说 FFT 的那些事儿):26.1 为什么需要 FFT26.2 变换究竟是如何进行的26.3 变换前后信号有何种对应关系26.4 在使用测试工具(示波器或者其它软件平台)进行 FFT 的方法和需要注意的问题26.5 力科示波器与泰克示波器的 FFT 计算方法的比较26.6 珊栏现象26.7 窗函数对于FFT结果的影响26.8 窗函数选择指南26.1为什么需要F F T首先 FFT(快速傅立叶变换)是离散傅立叶变换的快速算法,那么说到 FFT,我们自然要先讲清楚傅立叶变换。
实验三用FFT频谱分析

实验三用FFT频谱分析FFT(快速傅里叶变换)是一种常用的信号处理技术,可用于频谱分析。
频谱分析是分析信号中各频率成分的强度和相位的过程。
在本实验中,我们将使用FFT技术来进行频谱分析。
首先,我们需要了解一些基本概念。
任何信号都可以看作是不同频率的正弦波的叠加。
通过对信号进行傅里叶变换,我们可以将其表示为频率和幅度的函数,这就是频谱。
FFT是一种快速计算傅里叶变换的算法,大大提高了计算效率。
接下来,我们将使用Python的NumPy库来进行FFT频谱分析。
首先,我们需要导入NumPy库以及Matplotlib库用于绘图。
```pythonimport numpy as npimport matplotlib.pyplot as plt```然后,我们可以生成一个示例信号用于频谱分析。
在此实验中,我们将使用包含两个频率成分的正弦波。
```python#生成时间序列t = np.linspace(0, 1, 1000)#生成频率为10Hz和20Hz的信号f1=10f2=20signal = np.sin(2*np.pi*f1*t) + np.sin(2*np.pi*f2*t)```接下来,我们可以进行FFT频谱分析。
```python#对信号进行FFTfft = np.fft.fft(signal)#计算频率轴freqs = np.fft.fftfreq(len(signal))#绘制功率谱密度图plt.plot(freqs, np.abs(fft)**2)plt.xlabel('Frequency')plt.ylabel('Power')plt.show```这样就完成了FFT频谱分析。
我们可以通过查看功率谱密度图来了解信号的频率成分。
在图中,横轴表示频率,纵轴表示功率。
功率谱密度图可以帮助我们确定信号中存在的频率成分的强度。
在本实验中,我们使用了两个频率为10Hz和20Hz的正弦波信号进行了示例分析。
实用的几种示波器的使用技巧

实用的几种示波器的使用技巧示波器是电子工程师和科研人员在电路测试和信号分析中常用的仪器,具有测量和显示电压信号的能力。
下面是一些实用的示波器使用技巧,以帮助你更好地利用示波器进行电路测试和信号分析。
1.确定测量信号的频率范围:示波器可以测量不同频率范围的信号,但精度有所不同。
在测量信号之前,先确认信号的频率范围,然后选择相应的测量设置和示波器的带宽。
2.设置合适的时间和幅度基准:示波器的时间和幅度基准对信号的显示和分析非常重要。
通过调整时间和幅度基准,可以确保信号在屏幕上显示得清晰且易于观察。
3.使用多个通道同时测量信号:许多示波器具有多个通道,可以同时显示和测量多个信号。
利用这些通道,可以更全面地分析电路中的信号互动和相关性。
4.利用示波器的触发功能:示波器的触发功能可以帮助稳定显示不稳定或非周期性信号,并对信号进行更精确的分析。
通过设置适当的触发电平和触发类型,可以确保示波器在采样过程中始终处于稳定状态。
5.使用自动测量功能快速分析信号:示波器通常具有自动测量功能,可以快速分析信号的频率、幅度、周期等参数。
该功能可帮助用户快速获取关键信号参数,提高工作效率。
6.调整示波器的时间基准和水平控制:示波器的时间基准和水平控制对于观察和分析信号的波形非常重要。
通过调整时间基准和水平控制,可以对信号波形进行放大、缩小、平移等操作,以便更清晰地观察和分析信号特征。
7.使用示波器的延时功能:示波器的延时功能可以帮助用户观察非周期性信号或信号的特定时间段。
通过设置合适的延时时间,可以准确地捕获信号的特定瞬态或故障,并进行详细的分析。
8.选择合适的探头:示波器的探头对于测量和分析结果具有重要影响。
选择合适的探头可以确保测量结果的精度和可靠性。
在使用示波器时,根据需要选择相应的探头,并确保探头与示波器的匹配性。
9.使用示波器的FFT功能进行频谱分析:许多示波器具有FFT(快速傅里叶变换)功能,用于进行频谱分析。
示波器波形参数测量和FFT分析
示波器波形参数测量和FFT分析示波器波形参数测量和FFT分析当示波器正确捕获波形后,示波器可以对波形参数进行自动测量。
这些波形参数主要包括下面几个类别:1)电压参数/幅度参数:幅度,峰峰值,最大值,最小值,过冲,有效值等2)时间参数:上升时间/下降时间,周期/频率,脉冲宽度,占空比,时间差,建立时间/保持时间等3)眼图参数:交叉百分比,占空比失真,眼高,眼宽,抖动等4)如果示波器带有抖动分析软件,还可以测量抖动参数,如:时间间隔误差,周期到周期抖动,抖动成分分解(RJ,DJ,ISI,DCD,PJ)等。
下面介绍典型的电压参数和时间参数测量。
电压参数和时间参数测量,都需要参考点,这是测量的关键点之一。
在示波器里,一般称为:Vtop 和Vbase。
Vtop 和Vbase 的测量计算是:采用幅度统计方法。
示波器的工作过程是:先对整个屏幕进行幅度统计分析,可以得出最大电压的位置和最小电压的位置,然后对最大最小幅度的上面40%部分进行统计分析,得到的平均值,此为Vtop 值;对最大最小幅度的下面40%部分进行统计分析,得到的平均值,此为Vbase 值。
不用统计分析中间的20%部分,防止被测波形是3 态信号,而得出错误的结论。
如图1 所示。
图1 示波器Vtop 和Vbase 参数的测量一旦测试出Vtop 和Vbase,基于我们设置的测量门限(示波器的测量门限默认是10%,50%,90%),示波器可以对电压和时间参数进行自动测量。
图2 幅度/最大值/最小值/峰峰值的测量图3 过冲的测量图4 上升时间/下降时间的测量图5 周期/频率/脉宽/占空比的测量。
示波器练习题
示波器练习题一、选择题1. 示波器的核心部件是()。
A. 显示器B. 示波管C. 电源D. 探头A. 模拟示波器B. 数字示波器C. 混合信号示波器D. 数字存储示波器3. 示波器的时间基准(扫描频率)是指()。
A. 水平扫描速度B. 垂直扫描速度C. 信号频率D. 示波器屏幕刷新率4. 示波器探头上的衰减系数通常表示为()。
A. X1B. X10C. X100二、填空题1. 示波器主要由____、____、____和____等部分组成。
2. 示波器的垂直灵敏度是指____。
3. 示波器的水平灵敏度是指____。
4. 在使用示波器测量信号时,探头上的____必须与被测信号匹配。
三、判断题1. 示波器可以测量交流信号和直流信号。
()2. 示波器的探头可以直接接触被测电路,无需接地。
()3. 示波器的扫描频率越高,屏幕上显示的波形越稳定。
()4. 示波器的时间基准(扫描频率)与被测信号的频率无关。
()四、简答题1. 简述示波器的基本原理。
2. 请列举三种常见的示波器探头类型,并说明它们的特点。
3. 如何使用示波器测量交流信号的频率和幅度?4. 在使用示波器进行测量时,为什么要进行探头补偿?五、综合题1. 某模拟示波器的水平扫描速度为1ms/div,垂直灵敏度为1V/div,已知探头衰减系数为X10。
当观察到屏幕上的波形为10个周期,占据4个格子时,求被测信号的频率和峰峰值。
(1)频率:10kHz,峰峰值:5V(2)频率:1MHz,峰峰值:200mV(3)频率:100MHz,峰峰值:1V3. 使用示波器观察一个方波信号,发现波形出现顶部和底部失真,请分析可能的原因,并提出解决方法。
六、案例分析题1. 某工程师使用示波器测量一个未知频率的信号,设置水平扫描速度为5μs/div,观察到波形在屏幕上重复了4次。
请根据这些信息计算未知信号的频率。
2. 在一个电路调试过程中,工程师使用示波器观察到一个正弦波信号,垂直灵敏度为2V/div,波形峰峰值占据了3个格子。
示波器CSV波形数据导入Matlab进行FFT分析
精心整理
示波器CSV波形数据导入Matlab进行FFT分析
1,将CSV文件拖到workspace窗口,弹出的ImportWizard窗口中,点选“Next”,新窗口中选第二项“Createvectorsfromeachcolumnusingcolumnnames”,点“Finish”。
这时workspace 出现2个向量“Volt”和“Second”。
说明:若此时选中“Volt”,右上角的绘图命令变成可选,点“plot(Volt)”则出现如图:图中横坐标600表示示波器共记录了600个点,纵坐标为示波器的屏幕显示值(未乘探头倍率),因此问题在于改变横坐标为真实时间,改变纵坐标为真实值。
结合示波器示数(可另存为图片格式备用)。
下面的步骤即是以Volt替换mdl文件生成的变量u,以便于使用mdl中的powergui的FFT工
2
Mdl
5000个点。
由于
虑将u0.0002s
3
4
则应减小
准确。
其中,
5,如改变
6,菜单栏中,点Edit->CopyFigure后,即可在word中进行粘贴。
最后,分析出来的柱形图中,141.5为以33.3Hz为基波进行分析时的基波幅值;THD为波形总的谐波含量,即13.71%谐波含量;理论上THD越小,则原波形越接近正弦波。
ZDS2022示波器实操视频之67:调频信号的FFT分析
ZDS2022示波器实操视频之67:调频信号的FFT分析
摘要
大家好,如今多个领域用到了信号调制技术,与客户交流而知,他们需要对调频信号进行频率分析,那我们用ZDS2022应如何对其进行频率分析呢?
大家好,如今多个领域用到了信号调制技术,与客户交流而知,他们需要对调频信号进行频率分析,那我们用ZDS2022应如何对其进行频率分析呢?
按下【MATH】键,运算模式选择FFT,信源选择通道1,此时可在屏幕上看到FFT频谱图与频率表,ZDS2022示波器最高4Mpts的FFT分析样本点数,频率分析非常精准。
图1 调频信号FFT分析图
我们可以通过按下M旋钮模式软键切换M旋钮的模式为水平或垂直,还可以通过短按旋钮M1实现,在旋钮处于水平模式下旋转M2旋钮,调整频谱图的水平偏移,旋转旋钮M1,可调整频谱图的水平档位。
由调频信号的频谱图分析知,载波中心频率约为100KHz,且偏移频率为20KHz。
ZDS2022示波器FFT分析能力就是这么强,让您屡试不爽!
腾讯视频:/page/i/u/q/i0147qr1guq.html。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
检查波形的频率成分能够揭示出在普通的示波器图形中难以察觉的重要信息。
例如,在标准的波形图上(图1)可能看不出波形的失真或对称性方面的问题。
但是只要看一下波形的频率成分(图2)那些问题就很明显了。
在过去,观察波形的频率成分需要有频谱分析仪,还要掌握仪器的使用技能。
现在,对于深入的频率分析依然需要这样。
但是,很多基本的频率分析可以用泰克公司TDS3000这样的数字荧光示波器(DPO)来做。
为了能够观察波形的频率成分,泰克TDS3000系列具有模块化的FFT(傅立叶变换)能力。
FFT实际上显示的是波形的频率成分。
这本应用笔记将介绍TDS3000系列FFT频率图的基本知识,频率图的含义和使用方法。
波形的基本构成要了解FFT频率图,就要首先了解波形及其基本构成。
波形又区分为周期性波形和非周期性波形。
为了简单起见,我们先从周期性波形开始。
周期性波形基础。
周期性波形是按照一定的时间间隔或周期多次重复出现的波形。
正弦波、方波和三角波都是常见的周期性波形。
按照傅立叶的理论,所有的周期性波形都是由一组特定的正弦波组成的。
其中的基本正弦波也叫基波,其频率与该波形的频率相同。
例如,1千赫兹方波的基本正弦波的频率也是1千赫兹。
同样,1千赫兹三角波的基本正弦波的频率也是1千赫兹。
从本质上说,基波是波形中最重要的频率成分,它决定了波形的频率或重复周期。
在所有的非正弦周期性波形中,与基本成分同时存在的还有谐波。
谐波是频率为基波频率整倍数的正弦波。
例如,1千赫兹方波的三次谐波是3千赫兹的正弦波,而五次谐波为5千赫兹的正弦波,依此类推直至无限。
除了具有特定的频率之外,周期性波形的基波和谐波还具有特定的振幅和相位关系。
通过这些关系将基波和谐波叠加在一起,就形成了特定的波形。
这一点在图3中有进一步的说明,图中显示了一个方波的前五个频率成分相加在一起。
注意图3中合成的波形并不是一个准确的方波。
这是由于所加入的谐波还不够多。
若再加入更高次的谐波,所得波形的过渡会更陡峭波角更直,波顶和波底则更平坦。
从理论上说,需要所有的谐波(直到无限次)才能形成一个理想的方波或者任何其他的非正弦波形。
但实际上一切波形的带宽都是有限的,也就是说,高频成分的衰减非常明显。
通常,波形的主要频率成分是用频谱线来描述的。
图4描绘的是一个方波的频谱图。
图中的频率成分用垂直线条来表示,每个成分都位于频率轴上各自的频率坐标处。
每条频谱线的长度代表了该频率成分与其他成分的相对振幅。
大多数频率分析方法的基本目的都是为了得到如图4那样的频谱图。
为此可以使用各种各样的方法。
频谱分析仪是用扫频滤波器检测波形中的各个频率成分。
如果使用数字存储示波器,如泰克的TDS300系列,通过其内置的快速富利叶变换(FF有程序对波形进行数字分析,即可得到频谱图。
非周期性波形基础。
非周期性波形不重复自身。
与周期性波形不同的是,它们没有一定的重复间隔(周期)。
图5所示的单脉冲就是非周期性波形的一个例子。
由于它仅只是一个脉冲,故没有重复自身。
所以,单脉冲没有周期,属于非周期性波形。
图5下面的图形是单脉冲的FFT圈。
请注意,该图并不是一些单个的频谱线条,而是频率振幅的一个连续体,或者称之为包迹。
这种连续的频谱和单事件(瞬态)波形的特点完全不同。
瞬态信号含有全部的频率而不仅仅是谐波,频谱振幅也有规律性的变化。
对于方波,频率振幅是按照(Sin x)/x的包迹而变化的。
其他的脉冲波形具有另外的频谱形状。
静电放电、接触弧和开关瞬态都是瞬态波形的例子。
这些富含频率的波形的出现常常会造成对其他系统的干扰。
一个常见的例子是,远方的雷雨可以对收音机和电视机产生天电干扰。
另一个例子是,当给机器(如空调机)加电或断电时,在电源线上会出现尖脉冲和其他干扰。
瞬态虽然是非周期性波形的常见例子,但不是唯一的例子。
与单个的短暂的瞬态脉冲相反韭圄期性波形也可以是连续的。
数据流、机械振动波和随机噪音都是非周期性波形的典型例子。
像单事件瞬态一样,这样的波形是用单触发来获取和存储的。
单触发获取可以为待测波形提供稳定的瞬态视图。
如果用泰克TDS300系列的仪器,在分析时就可以用FFT图来检查波形的频率成分。
如何得到FFT图泰克TDS3000系列数字存储示波器用混合基FFT程序分析波形的频率成分。
混合基FFT的好处是能给出以10为底的记录长度作为结果。
这样,频率标度就能与以10为底的DSO时标控制的1-2-5序列直接匹配。
与比较常见的二进制FFT记录长度相比,这种方法更容易对频率结果作出解释。
用TDS3000系列获得FFT图的步骤如下:步骤1:用标准的TDS3000系列获取并显示波形步骤3:Math菜单上选择FFT函数和所用的通道完成上述步骤即可得到所需波形的FFT图。
FFT图的标度位于屏幕底部和MATH图标的右面。
水平标度(频率)为赫兹/分度,图的左边缘处为0赫兹。
垂直标度(相对振幅)为dBVRMS,即相对于1VRMS 的分贝值(0dB=1VRMS)。
TDS300系列的测量游标系统能够方便快捷地对波形进行精密的测量,这是在FFT图中能够采用如此精密的分度的先决条件。
下面的几个条目是对于TDS3000系列FFT及其频谱图的进一步的阐述信号获取:FFT功能适用于以单触发方式(非周期性信号)或反复触发方式(周期性信号)所获取的信号。
在获取周期性信号时,应使用Signal Averaging功能以降低信号噪音。
建议平均数不小于16。
汉宁窗(余弦平方窗):对获取的信号进行FFT分析之前,要用汉宁窗将其放大。
有关汉宁窗及其应用的详情,可参见TDS3000系列用户手册。
为了在脉冲型波形上得到最佳结果,在获取脉冲时要使用触发定位,这样其峰值就可以位于TDS3000系列显示器的水平中心位置,如图5所示。
频率分辨率:在显示出的FFT结果中有1000个频率点。
这些点在0赫兹与频谱图右侧的奈奎斯特频率(FN)之间均匀分布。
奈奎斯特频率等于捕获该波形时所用的采样率的一半。
即,若Fit to Screen 设为off,则FN=1/2*100/(时间标度设置)确定波形的频率成分TDS 300系列FFT图最基本的用途就是给出周期性波形的频率成分。
这项工作有时也叫谐波分析,因为周期性波形的频率成分与谐波密切相关。
获取任何一个周期性波形并对其施以FFT分析,即可得到该波形的频率成分。
用TDS300系列的测量游标功能则可对频率成分作进一步的分析。
只要把游标置于感兴趣的频率成分上,即可读出相应的频率和振幅的数值。
可以用同样的方法分析非周期性波形。
但要记住,瞬态脉冲具有连续的频谱而非分立的谐波。
对这样的连续频谱,通常要集中分析3分贝宽的主波瓣和旁瓣的相对振幅(见图6)。
确定波形失真TDS 300系列FFT分析的另一个基本用途就是确定波形失真。
这在图1和图2中已有描述。
图中给出了“看似正常”的正弦波及相应的频率图。
请注意图1中的正弦波看似正常。
但图2的TDS3000系列FFT分析则在正弦波的频率构成中显示出一些低电平的频率成分。
这些低电平成分的出现表明这个正弦波并不纯净.而是有谐波失真。
如果正弦波纯净的话,它的频谱就应只有一条频率等于该正弦波频率的频谱线。
真实的正弦波大多数都有一些谐波失真。
失真的程度常用某些谐波与正弦波的基波的相对电平来描述。
例如,可以说三次谐波失真比基波小50分贝。
为了识别和测量不同的谐波及其电平,可以使用TDS300系列的FFT功能和测量游标功能(见图2)。
也可以用TDS3000系列的FFT功能检查波形的对称性。
例如,一个顶部和底部都对称的方波应当只含有基波和奇次谐波。
如果方波不对称,则会在FFT图中出现偶次谐波。
当方波的不对称性增加时,这些偶次谐波的电平也增加。
在用FFT确定谐波时应该多加小心。
因为有时显现的谐波成分实际上是高频成分的假信号。
图7给出的是一个方波及其FFT图。
初看起来,在高频奇次谐波之间好象存在偶次谐波。
但实际上并非如此。
实际情况是,高频奇次谐波在圈中发生了折返,使之貌似偶次谐波。
这样解释的理由是,在频谱图的右端(奈奎斯特频率处)谐波并没有减弱到可以忽略不计。
结果,那些应从屏幕右侧逸出的高频谐波又折返到屏幕的右边缘,看起来就成了低频的假信号。
为了尽量消除这种现象,应当在时间显示中设定较少的周期,然后重新获取这个方波。
(有关假信号和其他FFT特性的详情,请参考FFT:基本原理和概念,Robert W. Ramirez, Simon & Schuster, 1985。
)其他应用前面的例子所涉及的主要是谐波分析。
检查波形的谐波还可以得到该波形的其他信息。
在很多其他的应用中也能用频率图检查周期性和非周期性波形,仅举几例如下:调幅(AM)。
调幅信号的FFT图给出载频和调制边带的相对电平。
当用单频测试音调制载波时,这是最明显的。
振动分析。
在TDS 300系列示波器上可以借助传感器将机械振动作为振动波显示出来。
这个总的振动信号波是由机械系统内各个零件发出的振动分量组成的。
可以用FFT图观察和分析各个振动分量。
例如,信号分析可用于确定系统内滚柱轴承的超量振动。
这种分析方法的好处是,在性能不佳的轴承造成更严重的机械损害和停工之前将其检测出来并替换掉。
频率响应。
可以用FFT对电路的频率响应特性迅速地做出评估。
方法是,在电路的输入端加入一个窄脉冲(冲激),在电路的输出端获取该;中激的响应波形。
用这个响应波形的FFT图即可评估电路的频率响应特性。
还可以用测量游标对频率响应做进一步的分析,例如分析其带宽滚降特性和带外响应特性等。
提高频谐图质量的技巧频谱图的质量取决于很多因素。
当然最关键的因素是FFT所要分析的那个波形。
其他的因素包括对波形的各种人为影响,如加在波形上的直流成分或偏移,以及噪音等。
获取波形的方法也会对频谱图产生影响。
下面介绍的方法可以解决提高频谱质量方面的-些主要问题:去除直流成分。
有些波形含有直流成分或偏移。
在频率图中,较大的直流成分可以掩盖其他频率成分。
为了使直流成分减至最小,应当通过交流捐合来获取波形。
即便采用了交流捐合,波形仍可能含高残留的少量直流成分。
这是由于捕获的波形周期数不是整数(例如45个周期,而非4个周期)。
最简单的办法就是将少量的残余直流成分忽略不计。
另一个办法是获取更多的波形周期以威少在边缘处的不完整周期所占的百分比。
获取更多的波形。
对于周期性波形来说,在时间图上获取较多的周期可导致在频率图上更大的频率分辨率(见图2)。
一般来说,如果在时间图上最少出现4到8个波形周期,则全频率图是最好用的。
在处理脉冲或瞬态波形时,要保证整个脉冲(包括脉冲前后的一些基线)都出现在屏幕上。
为了使频率图有最佳效果,整个脉冲应覆盖时间轴的1/8到1/4,而且应位于画面中心。
应当小心的是,如果在靠近频率图的右边缘出现了一些高频成分,则可能产生假信号(见图7)。
