全等三角形证明题专练(培优)

合集下载

三角形全等培优练习

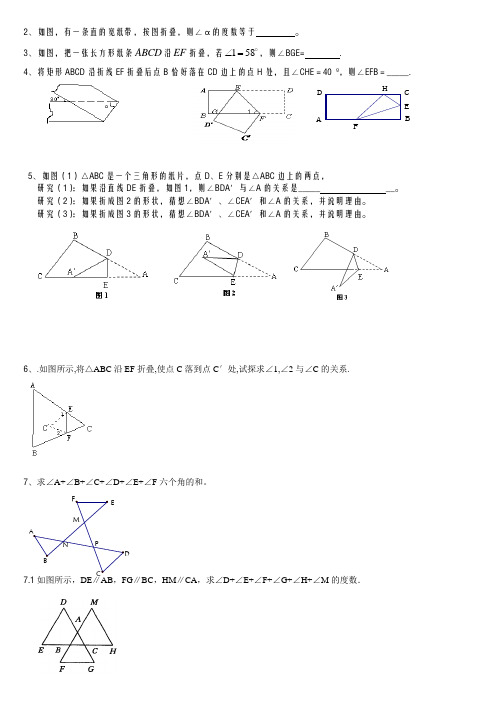
2、如图，有一条直的宽纸带，按图折叠，则∠α的度数等于。

3、如图，把一张长方形纸条ABCD 沿EF 折叠，若158∠=，则∠BGE= ． 4、将矩形ABCD 沿折线EF 折叠后点B 恰好落在CD 边上的点H 处，且∠CHE ＝40 º，则∠EFB ＝_____.5、如图（1）△ABC 是一个三角形的纸片，点D 、E 分别是△ABC 边上的两点，研究（1）：如果沿直线DE 折叠，如图1，则∠BDA ′与∠A 的关系是_____ __。

研究（2）：如果折成图2的形状，猜想∠BDA ′、∠CEA ′和∠A 的关系，并说明理由。

研究（3）：如果折成图3的形状，猜想∠BDA ′、∠CEA ′和∠A 的关系，并说明理由。

6、.如图所示,将△ABC 沿EF 折叠,使点C 落到点C ′处,试探求∠1,∠2与∠C 的关系.7、求∠A+∠B+∠C+∠D+∠E+∠F 六个角的和。

7.1如图所示，DE ∥AB ，FG ∥BC，HM ∥CA ，求∠D+∠E+∠F+∠G+∠H+∠M 的度数．H FE D C B A8、如图所示．（1）图甲是一个五角形ABCDE ，你能计算出∠A+∠B+∠C+∠D+∠E 的大小吗？（2）如图乙，如果点B 向右移动到AC 上时，还能算出∠A+∠EBD+∠C+∠D+∠E •的大小吗？（3）如图丙，点B 向右移动到AC 的另一侧时，（1）的结论成立吗？为什么？（4）如图丁，点B ，E 移动到∠CAD 的内部时，结论又如何？9、．数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．90AEF ∠=，且EF 交正方形外角DCG ∠的平行线CF 于点F ，求证：AE =EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．A D F C G EB 图1 A D FC G E B 图2 AD F GE B 图310、已知，如图3，D是的内角与外角的平分线BD与CD的交点，过D作DE//BC，交AB 于E，交AC于F。

北师大版七年级数学下全等三角形的判定小题精炼培优版(包含答案)

北师大七下全等三角形的判定小题精炼培优版一、单选题1．如图，AD =BC ，要得到△ABD 和△CDB 全等，可以添加的条件是（）A ．AB //CD B ．△ABC =△CDA C ．△A =△CD ．AD //BC2．如图，PD △AB ，PE △AC ，垂足分别为D 、E ，且P A 平分△BAC ，则△APD 与△APE 全等的理由是（）A ．SASB ．AASC ．SSSD ．ASA3．如图1，D ､E ､F 分别为△ABC 边AC ､AB ､BC 上的点，△A=△1=△C ，DE=DF ，下面的结论一定成立的是（）A ．AE=FCB ．AE=DEC ．AE+FC=ACD ．AD+FC=AB 4．如图，AB CD ，//AB CD ，判定ABC △CDA 的依据是( )A．SSS B．SAS C．ASA D．HL5．如图，AD△CD，AE△BE，垂足分别为D，E，且AB=AC，AD=AE,则下列结论△△ABE△△ACD△AM=AN：△△ABN△△ACM；△BO=EO;其中正确的有（）A．4个B．3个C．2个D．1个6．如图，点B、F、C、E在一条直线上，AB△ED，AC△FD，那么添加下列一个条件后，仍无法判定△ABC△△DEF的是（）A．AB=DE B．AC=DF C．△A=△D D．BF=EC7．如图，已知△ABC为等边三角形，点D、E分别在边BC、AC上，且AE=CD，AD与BE相交于点F，则△BFD的度数为（）A．45°B．90°C．60°D．30°8．如图所示，AB＝AC，AD＝AE，△BAC＝△DAE，△1＝25°，△2＝30°，则△3＝()A．60°B．55°C．50°D．无法计算9．如图，AB//DE，AC//DF，AC＝DF，下列条件中，不能判定△ABC△△DEF的是A．AB＝DE B．△B＝△E C．EF＝BC D．EF//BC10．如图所示，Rt△ABE△Rt△ECD，点B、E、C在同一直线上，则结论：△AE=ED；△AE△DE；△BC=AB+CD；△AB△DC中成立的是（）A．仅△B．仅△△C．仅△△△D．仅△△△△11．如图，AC=AD，BC=BD，则下列结果正确的是（）A．AB△CD B．OA=OB C．△ACD=△BDC D．△ABC=△CAB12．如图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（）A．△ACE△△BCD B．△BGC△△AFC C．△DCG△△ECF D．△ADB△△CEA13．下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（）A．甲和乙B．乙和丙C．甲和丙D．只有丙14．正三角形ABC中，BD=CE，AD与BE交于点P，△APE的度数为（）.A．45B．55C．60D．7515．如图，在等边△ABC中，D，E分别是BC，AC上的点，且BD=CE，AD与BE相交于点P，则△1+△2的度数是（）A．45°B．55°C．60°D．75°16．如图，在下列条件中，不能证明△ABD△△ACD的是（）.A ．BD =DC ，AB =ACB ．△ADB =△ADC ，BD =DC C ．△B =△C ，△BAD =△CAD D ．△B =△C ，BD =DC17．如图，已知12AC AD ∠=∠=，，从下列条件：△AB AE =；△BC ED =；△C D ∠=∠；△B E ∠=∠中添加一个条件，能使ABC △△AED 的有（）A ．1个B ．2个C ．3个D ．4个18．如图，在Rt△AEB 和Rt△AFC 中，BE 与AC 相交于点M ，与CF 相交于点D ，AB 与CF 相交于N ，△E ＝△F ＝90°，△EAC ＝△FAB ，AE ＝AF,给出下列结论：△△B ＝△C ；△CD ＝DN ；△BE ＝CF ；△△ACN△△ABM;其中正确的结论是( )A ．△△△B ．△△△C ．△△△D ．△△△19．如图是由4个相同的小正方形组成的网格图，其中△1+△2等于（）A．150°B．180°C．210°D．225°20．如图，已知△DCE=90°，△DAC=90°，BE△AC于B，且DC=EC．若BE=7，AB=3，则AD的长为（）A．3B．5C．4D．不确定21．如图，在△ABC中，AB=AC，△BAC=90°，直角△EPF的顶点P是BC中点，PE，PF分别交AB，AC于点E，F，给出下列四个结论：△△APE△△CPF；△AE=CF；△△EAF是等腰直角三角形；△S△ABC=2S四边形AEPF，上述结论正确的有（）A．1个B．2个C．3个D．4个22．如图，△ABC中，AB△BC，BE△AC，△1=△2，AD=AB，则下列结论不正确的是A．BF=DF B．△1=△EFD C．BF>EF D．FD△BC23．如图，已知AB ＝AC ，AF ＝AE ，△EAF ＝△BAC ，点C 、D 、E 、F 共线．则下列结论，其中正确的是（）△△AFB△△AEC ；△BF ＝CE ；△△BFC ＝△EAF ；△AB ＝BC ．A ．△△△B ．△△△C ．△△D ．△△△△二、填空题 24．如图，某同学把三角形玻璃打碎三块，现在他要去配一块完全一样的，你帮他想一想，带________片去，应用的原理是________（用字母表示）．25．如图，矩形ABCD 中，E 在AD 上，且EF EC ⊥，EF EC =，2DE =，矩形的周长为16，则AE 的长是______ ．26．如图所示，直线a 经过正方形ABCD 的顶点A ，分别过此正方形的顶点B ，D 作BF△a 于点F ，DE△a 于点E ，若DE ＝8，BF ＝5，则EF 的长为____．27．如图，△ACB=90°，AC=BC，AD△CE于D，BE△CD于E，AD=2.5cm，DE=1.6cm，则BE的长度为________．28．如图,已知△ABC中,AB=AC=20 cm,BC=16 cm,△B=△C,点D是AB的中点,点P在线段BC上以2 cm/s的速度由B点向C点运动,同时点Q在线段CA上由A点向C点运动,当△BPD与△CQP全等时,点Q的运动速度为______.29．如图所示，AB=AC，AD=AE，△BAC=△DAE，△1=25°，△2=30°，则△3=__________．30．在Rt△ABC中，△ACB=90°，BC=2cm，CD△AB，在AC上取一点E，使EC=BC，过点E作EF△AC交CD的延长线于点F，若EF=5cm，则AE= cm．31．如图，CA=CB，CD=CE，△ACB=△DCE=40°，AD、BE交于点H，连接CH，则△CHE=__________．32．如图，△ACB＝90°，AC＝BC，BE△CE，AD△CE，垂足分别为E，D，AD＝25，DE＝17，则BE＝______．33．如图，在△ABC中，AD△BC于D，BE△AC于E，AD与BE相交于点F，若BF＝AC，则△ABC ＝_____度．34．如图，AC△BC，AD△DB，要使△ABC△△BAD，还需添加条件_____．（只需写出符合条件一种情况）35．如图AB＝AC，AD＝AE，△BAC＝△DAE，△BAD＝25°，△ACE＝30°，则△ADE＝_____．36．如图，等边△ABC 边长为10，P 在AB 上，Q 在BC 延长线，CQ ＝P A ，过点P 作PE △AC 点E ，过点P 作PF △BQ ，交AC 边于点F ，连接PQ 交AC 于点D ，则DE 的长为_____．37．如图，△ABC 是等边三角形，AE ＝CD ，AD 、BE 相交于点P ，BQ△DA 于Q ，PQ ＝3，EP ＝1，则DA 的长是________.38．如图，90C ∠=︒，10AC =，5BC =，AM AC ⊥，点P 和点Q 从A 点出发，分别在射线AC 和射线AM 上运动，且Q 点运动的速度是P 点运动的速度的2倍，当点P 运动至__________时，ABC △与APQ 全等．39．如图，AB ＝BC 且AB △BC ，点P 为线段BC 上一点，P A △PD 且P A ＝PD ，若△A ＝22°，则△D 的度数为_________．40．如图，在△ABC中，△A=58°，AB=AC，BD=CF，BE=CD，则△EDF=____________度。

第4讲.全等三角形的经典模型(二).培优

等等…腰漫画释义满分晋级阶梯4全等三角形的经典模型（二）三角形11级特殊三角形之直角三角形三角形10级勾股定理与逆定理三角形9级全等三角形的经典模型（二）OFEC BA A F COBEDHABCDO EO GFE CB A“手拉手”数学模型：⑴ ⑵ ⑶【引例】如图，等边三角形ABE 与等边三角形AFC 共点于A ，连接BF 、CE ，求证：BF =CE 并求出∠EOB 的度数.【解析】 ∵△ABE 、△AFC 是等边三角形∴AE =AB ，AC =AF ，60∠=∠=︒EAB FAC知识互联网思路导航例题精讲题型一：“手拉手”模型3NM C B A B N CABCMN∴∠+∠=∠+∠EAB BAC FAC BAC 即∠=∠EAC BAF ∴AEC ABF △≌△ ∴BF =EC ∠=∠AEC ABF又∵AGE BGO ∠=∠ ∴60∠=∠=︒BOE EAB ∴60∠=︒EOB【例1】如图，正方形BAFE 与正方形ACGD 共点于A ，连接BD 、CF ，求证：BD =CF 并求出∠DOH 的度数.【解析】同引例，先证明ABD AFC △≌△∴BD =FC ，∠=∠BDA FCA ∵∠=∠DHO CHA ∴90∠=∠=︒DOH CAD【例2】如图，已知点C 为线段AB 上一点，ACM △、BCN △是等边三角形．⑴ 求证：AN BM =.⑵ 将ACM △绕点C 按逆时针方向旋转180°，使点A 落在CB 上，请你对照原题图在图中画出符合要求的图形；⑶ 在⑵得到的图形中，结论“AN BM =”是否还成立，若成立，请证明；若不成立，请说明理由；⑷ 在⑵所得的图形中，设MA 的延长线交BN 于D ，试判断ABD △的形状，并证明你的结论．【分析】这是一个固定后运动变化的探索题，且在一定的条件下，探究原结论的存在性（不变性）；需要画图分析、判断、猜想、推理论证．【解析】 ⑴ ∵ACM △、BCN △是等边三角形∴AC CM =，BC CN = 60ACM BCN ∠=∠=° ∴∠=∠ACN MCB在ACN △和MCB △中典题精练OHG DFECB ADNMCBA=⎧⎪∠=∠⎨⎪=⎩AC MC ACN MCB CN CB ∴ACN MCB △≌△（SAS ） ∴AN BM =⑵ 将ACM △绕点C 旋转如图：⑶ 在⑵的情况，结论AN BM =仍然成立．证明：∵60BCM NCA ∠=∠=°，CA CM =，CN CB =． ∴CAN CMB △≌△（SAS ），∴AN MB =．⑷ 如图，延长MA 交BN 于D ，则ABD △为等边三角形．证明：∵60CAM BAD ABD ∠=∠=∠=°． ∴ABD △是等边三角形．【例3】在ABC △中，90∠=BAC °，⊥AD BC 于D ，BF 平分∠ABC 交AD 于E ，交AC 于F .求证：AE=AF .54321A BCDE F【解析】 90∠=BAC °，390∴∠+∠=DAC °90⊥∴∠=︒AD BC ADC 90∴∠+∠=︒C DAC 3∴∠=∠C43152∠=∠+∠∠=∠+∠C ，BF 是ABC ∠的角平分线 12∴∠=∠ 45∴∠=∠ ∴=AE AF【例4】如图，已知ABC △中，90ACB ∠=°，CD AB ⊥于D ，ABC ∠的角平分线BE 交CD 于G ，交AC 于E ，GF AB ∥交AC 于F ．典题精练题型二：双垂+角平分线模型5ENMD CBA NMD CBA 求证：AF CG =．【分析】要证AF CG =，一般想到证明这两条线段所在的三角形全等，由图形可知，不存在直接全等三角形，因此要想到添加辅助线构造全等三角形．【解析】作EH AB ⊥于H∵12∠=∠，90ACB ∠=°∴EC EH =（角平分线定理）又∵CD AB ⊥ ∴3A ∠=∠∵431∠=∠+∠，52A ∠=∠+∠ ∴45∠=∠ ∴CE CG = ∴CG EH =又∵GF AB ∥，90∠=∠=AHE FGC ° ∴A CFG ∠=∠∴CFG EAH △≌△（AAS ） ∴=CF EA ，∴-=-CF EF EA EF ， ∴CE AF = ∴AF CG =【例5】已知：正方形ABCD 中，45MAN ∠=︒，MAN ∠绕点A 顺时针旋转，它的两边分别交线段CB DC 、于点M N 、.求证BM DN MN +=.【解析】延长ND 到E 使DE BM =∵四边形ABCD 是正方形 ∴AD =AB在ADE △和ABM △ =⎧⎪∠=∠⎨⎪=⎩AD AB ADE B DE BM ∴ADE ABM △≌△∴AM =AE ∠=∠BAM DAE典题精练题型三：半角模型54321HG FE DCBA54321G FE DCBADHFECBA∵45MAN ∠=︒ ∴45∠+∠=︒BAM NAD ∴45∠=∠=︒MAN EAN在AMN △和AEN △中 =⎧⎪∠=∠⎨⎪=⎩MA EA MAN EAN AN AN ∴AMN AEN △≌△ ∴MN =EN∴DE +DN =BM +DN=MN【例6】如图，在四边形ABCD 中，180∠+∠=︒=B D AB AD ，，E 、F 分别是线段BC 、CD 上的点，且BE +FD =EF . 求证：12∠=∠EAF BAD .ABCDEF【解析】延长FD 到H ，使DH =BE ，易证ABE ADH △≌△，再证AEF AHF △≌△1122∴∠=∠=∠=∠EAF FAH EAH BAD【例7】在等边三角形ABC 的两边AB 、AC 所在直线上分别有两点M 、N ，D 为三角形ABC 外一点，且︒=∠60MDN ,︒=∠120BDC ,BD=DC . 探究：当M 、N 分别在直线AB 、AC 上移动时，BM 、NC 、MN 之间的数量关系．AM N BCDCBN M A图1 图2⑴如图1，当点M 、N 在边AB 、AC 上，且DM=DN 时，BM 、NC 、MN 之间的数量关系是； ⑵如图2，点M 、N 在边AB 、AC 上，且当DM ≠DN 时，猜想⑴问的结论还成立吗写7出你的猜想并加以证明.【解析】 ⑴如图1， BM 、NC 、MN 之间的数量关系BM +NC=MN ．⑵猜想：结论仍然成立．证明：如图，延长AC 至E ，使CE=BM ，连接DE ． BD=CD 且120BDC ∠=．∴ 30=∠=∠DCB DBC ．又△ABC 是等边三角形，∴90MBD NCD ECD ∠=∠=∠=．在MBD △与ECD △中：BM CE MBD ECD BD CD =⎧⎪∠=∠⎨⎪=⎩∴MBD △≌ECD △(SAS ) ． ∴DM=DE , BDM CDE ∠=∠ ∴60EDN BDC MDN ∠=∠-∠= 在△MDN 与△EDN 中：⎪⎩⎪⎨⎧=∠=∠=DN DN EDN MDN DE DM ∴MDN EDN △≌△(SAS) ∴MN NE NC BM ==+第04讲精讲：典型的旋转全等构图：“手拉手”全等模型探究；【探究一】“手拉手”模型基本构图；如图1，若ABC ∆与ADE ∆旋转全等，则必有ABD ∆与ACE ∆为两个顶角相等的等腰三角形（即相似的等腰三角形）；反之，如图2，若有两个顶角相等的等腰三角形ABD ∆与ACE ∆共顶角顶点，则必有ABC ∆与ADE ∆旋转全等；而图2正是“手拉手”模型的基本构图；图1EDBA图2EDBA【探究二】将探究一中的普通等腰三角形换成特殊的图形，例如等边三角形、等腰直角三角形、正方形，然后再探究结论如何变化；ENM DC BA图3EDCBA 图4E D CB A FG 图5ED CB A如图3、图4、图5，当两个等边三角形、等腰直角三角形、正方形共顶点时，ABC ∆与ADE ∆仍然旋转全等，并且有两个共同的结论；结论1：ABC ∆≌ADE ∆；DE BC =；结论2：BC 与DE 所夹锐角等于两个等腰三角形的顶角；（倒角方法如下图6、图7、图8的八字模型）图6图7图8【探究三】将探究二中的特殊图形旋转后结论是否仍然成立；如下图9、图10、图11易得探究二中的两个结论仍然成立；图9E图10图11【探究四】深化探究二中图3的结论；如图12，可得结论1：ABC ∆≌ADE ∆；DE BC =；结论2：︒=∠=∠=∠=∠60CAE BAD COE BOD ；结论3：如图12、图13、图14，可得三对三角形全等（ABC ∆≌ADE ∆；AHD ∆≌AGB ∆；AGC ∆≌AHE ∆）9图12图13图14结论4：如图15，连接GH ，可得AGH ∆为等边三角形；（由结论3可得AH AG =）图15NM O 图16EDC BA 结论5：BE GH ∥；（由结论4可得︒=∠=∠60BAD AGH ）结论6：连接AO ，可得AO 平分BOE ∠；（如图16，分别作BC AM ⊥、DE AN ⊥，AM 与AN 分别是全等三角形ABC ∆与ADE ∆对应边BC 和DE 上的高，故相等）SFEDCBA MP N MH GFE DCBA N M DCBA题型一手拉手模型巩固练习【练习1】如图，DA ⊥AB ，EA ⊥AC ，AD=AB ，AE=AC ，则下列正确的是（）A. ABD ACE △≌△B. ADF AES △≌△C. BMF CMS △≌△D. ADC ABE △≌△【解析】 D【练习2】如图，正五边形ABDEF 与正五边形ACMHG 共点于A ，连接BG 、CF ，则线段BG 、CF具有什么样的数量关系并求出∠GNC 的度数．【解析】先证ABG AFC △≌△ 可得BG =CF ，∠=∠ACF AGB∵∠=∠NPG APC∴108∠=∠=︒GNC GAC题型二双垂+角平分线模型巩固练习【练习3】已知AD 平分∠BAC ，⊥DE AB ，垂足为E ，⊥DF AC , 垂足为F ，且DB =DC ，则EB 与FC 的关系（） A. 相等 B. EB <FC C. EB >FC D.以上都不对【解析】 A题型三半角模型巩固练习【练习4】如图，△ABC 是边长为3的等边三角形，△BDC 是等腰三角形，且∠BDC ＝120°．以D 为顶点作一个60°角，使其两边分别交AB 于点M ，交AC 于点N ，连接MN ，则△AMN 的周长为．【解析】 6【练习5】如图，在四边形ABCD 中，180∠+∠=︒B ADC ，AB AD =，E 、F 分别是边BC 、CD 延长线上的点，且复习巩固F E DCBA FEDCBA11E H GD CBA FDEGCB A12EAF BAD =∠∠，求证：EF BE FD =-【解析】证明：在BE 上截取BG ，使BG DF =，连接AG ．∵180B ADC +=︒∠∠，180ADF ADC +=︒∠∠， ∴B ADF =∠∠． ∵AB AD =，∴ABG ADF △≌△．∴BAG DAF =∠∠，AG AF =．∴12BAG EAD DAF EAD EAF BAD +=+==∠∠∠∠∠∠．∴GAE EAF =∠∠． ∵AE AE =，∴AEG AEF △≌△． ∴EG EF =∵EG BE BG =-，∴EF BE FD =-．训练1. 如图，C 为线段AB 上一点，分别以AC 、CB 为边在AB 同侧作等边ACD △和等边BCE △，AE 交DC 于G 点，DB 交CE 于H 点，求证：GH AB ∥．【分析】本题中，ACD △与BCE △是等边三角形，因此AC CD =，BC CE =，60ACD ECB ∠=∠=°，因为A 、C 、B 在同一条直线上，故60DCE ∠=°．这样可以得到ACE DCB △≌△，AEC DBC ∠=∠，故可以得到CEG CBH △≌△，则GC HC =，60CGH CHG ∠=∠=°，所以60ACG CGH ∠=∠=°，故GH AB ∥．【解析】 ∵ACD △和BCE △是等边三角形（已知）∴AC CD =，BC CE =（等边三角形的各边都相等）思维拓展训练(选讲)A B C DH QNM60ACD BCE ∠=∠=°（等边三角形的每个角都等于60°） ∵180ACD DCE BCE ∠+∠+∠=°∴60DCE ∠=°，120ACE DCB ∠=∠=°．在ACE △和DCB △中，=⎧⎪∠=∠⎨⎪=⎩AC DC ACE DCB CE CB∴ACE DCB △≌△（SAS ）∴AEC DBC ∠=∠（全等三角形的对应角相等）在BCH △和ECG △中，60∠=∠=⎧⎪=⎨⎪∠=∠⎩BCH ECG BC CE CBH CEG °∴BCH ECG △≌△（ASA ）∴CH CG =（全等三角形的对应边相等） ∴CGH CHG ∠=∠（等边对等角）∵180GCH GHC CGH ∠+∠+∠=°（三角形内角和定理） ∴60GHC CGH ∠=∠=°．∴60ACG CGH ∠=∠=°（等量代换） ∴GH AB ∥（内错角相等，两直线平行）训练2. 条件：正方形ABCD ，M 在CB 延长线上，N 在DC 延长线上，45MAN ∠=︒．结论：⑴ MN DN BM =-；⑵ AH AB =.【解析】 ⑴在CD 上取一点Q ，使DQ =BM先证AMB AQD △≌△可得AM =AQ再证AMN AQN △≌△ ∴MN =NQ∴DN DQ DN BM NQ MN -=-==⑵可证△ANH ≌△AND ，∴AH=AD=AB训练3. 如图，在Rt ABC △中，锐角ACB ∠的平分线交对边于E ，又交斜边的高AD 于O ，过O引OF BC ∥，交AB 于F ，请问AE 与BF 相等吗理由是什么A B M C H ND13ABCDO EOO 12ABCD E F FEDCBA21543G O54321G FE DC BA【解析】相等．理由如下：如图，过E 作EG BC ⊥于G ∵EC 平分ACB ∠，∴12∠=∠ ∵90EAC ∠=°，AD BC ⊥∴1490∠+∠=°，2390∠+∠=° ∴34∠=∠ ∵35∠=∠， ∴45∠=∠ ∴AE AO =∵EC 平分ACB ∠，EA AC ⊥，EG BC ⊥ ∴EA EG =，∴AO EG =，∵FO BC ∥∴AFO B ∠=∠，90BDA FOA ∠=∠=° ∴BEG FAO ∠=∠∴AFO EBG △≌△（AAS ） ∴AF BE =∴AF EF BE EF -=- ∴AE BF =．训练4. 如图，△ABD 为等腰直角三角形，45∠=︒MAN ，求证：以BM 、MN 、DN 为边的三角形是直角三角形.【解析】过B 作BD 的垂线并取BQ =ND ，连接AQ 、QM先证∴=AQB AND AQ AN △≌△，再证∴=AQM ANM MN QM △≌△∴以BM 、MN 、DN 为边的三角形是直角三角形.测试1. 如图，等腰直角△ADB 与等腰直角△AEC 共点于A ，连接BE 、CD ，则线段BE 、CD 具有什么样的数量关系和位置关系【解析】先证明ABE ADC △≌△∴BE =CD ，再类似例1倒角即可得到BE ⊥CD课后测N M DBA测试2. 如图，△ABD 为等腰直角三角形，45∠=︒MAN ，求证：以BM 、MN 、DN 为边的三角形是直角三角形.【解析】过B 作BD 的垂线并取BQ =ND ，连接AQ 、QM先证∴=AQB AND AQ AN △≌△，再证∴=AQM ANM MN QM △≌△∴以BM 、MN 、DN 为边的三角形是直角三角形.N M DBA第十五种品格：创新学会变通，变则通一天早上，一位贫困的牧师，为了转移哭闹不止的儿子的注意力，将一幅色彩缤纷的世界地图，撕成许多细小的碎片，丢在地上，许诺说：“小约翰，你如果能拼起这些碎片，我就给你二角五分钱。

人教版八年级数学第12章全等三角形培优训练 (含答案)

人教版八年级数学第12章全等三角形培优训练一、选择题1. 下列各组的两个图形属于全等图形的是()2. 如图，点E，F在线段BC上，△ABF与△DCE全等，点A与点D，点B与点C是对应顶点，AF与DE相交于点M，则∠DCE等于()A．∠B B．∠A C．∠EMF D．∠AFB3. 如图所示，P是∠BAC内一点，且点P到AB，AC的距离PE，PF相等，则△PEA≌△PF A的依据是()A．HL B．ASA C．SSS D．SAS4. 根据下列条件，能画出唯一的△ABC的是()A．AB＝3，BC＝4，AC＝8 B．AB＝4，BC＝3，∠A＝30°C．AB＝5，AC＝6，∠A＝50°D．∠A＝30°，∠B＝70°，∠C＝80°5. 如图,点A在点O的北偏西30°的方向上,AB⊥OA,垂足为A.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是()A.点O在点A的南偏东60°方向上B.点B在点A的北偏东30°方向上C.点B在点O的北偏东60°方向上D.点B在点O的北偏东30°方向上6. 如图，有一张三角形纸片ABC，已知∠B=∠C=x°，按下列方案用剪刀沿着箭头方向剪开，可能得不到全等三角形纸片的是()7. 现已知线段a，b(a<b)，∠MON=90°，求作Rt△ABO，使得∠O=90°，OA=a，AB=b.小惠和小雷的作法分别如下:小惠:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点A为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.小雷:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点O为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.则下列说法中正确的是()A.小惠的作法正确，小雷的作法错误B.小雷的作法正确，小惠的作法错误C.两人的作法都正确D.两人的作法都错误8. 如图，点G在AB的延长线上，∠GBC，∠BAC的平分线相交于点F，BE⊥CF 于点H.若∠AFB＝40°，则∠BCF的度数为()A．40°B．50°C．55°D．60°二、填空题9. 如图，在Rt△ABC中，∠C=90°，∠B=20°，以点A为圆心，小于AC的长为半径画弧与AB，AC分别交于点M，N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧相交于点P，连接AP并延长交BC于点D，则∠ADB=°.10. 如图，在△ABC中，AD⊥BC于点D，要使△ABD≌△ACD，若根据“HL”判定，还需要添加条件：____________．11. 如图，若AB＝AC，BD＝CD，∠A＝80°，∠BDC＝120°，则∠B＝________°.12. 在△ABC中，AB＝4，AC＝3，AD是△ABC的角平分线，则△ABD与△ACD 的面积之比是________．13. (2019•南通)如图，△ABC中，AB=BC，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF，若∠BAE=25°，则∠ACF=__________度．14. 如图所示，已知AD∥BC，则∠1＝∠2，理由是________________；又知AD ＝CB，AC为公共边，则△ADC≌△CBA，理由是______，则∠DCA＝∠BAC，理由是__________________，则AB∥DC，理由是________________________________．15. 如图，在△ABC中，∠C＝90°，AC＝BC，AD是∠BAC的平分线，DE⊥AB，垂足为E.若△DBE的周长为20，则AB＝________．16. 如图，△ABC的两条外角平分线BP，CP相交于点P，PE⊥AC交AC的延长线于点E.若△ABC的周长为11，PE=2，S△BPC =2，则S△ABC=.三、解答题17. 育新中学校园内有一块直角三角形(Rt△ABC)空地，如图所示，园艺师傅以角平分线AD为界，在其两侧分别种上了不同的花草，在△ABD区域内种植了一串红，在△ACD区域内种植了鸡冠花，并量得两直角边AB＝20 m，AC＝10 m，分别求一串红与鸡冠花两种花草的种植面积．18. 如图，已知△ACF≌△DBE，且点A，B，C，D在同一条直线上.若AD=16，BC=10，求AB的长.19. 我们把两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD是筝形，其中AB＝AD，CB＝CD，P是对角线AC上除A，C外的任意一点．求证：∠ABP ＝∠ADP.20. 如图，已知AP∥BC，∠P AB的平分线与∠CBA的平分线相交于点E，过点E 的直线分别交AP，BC于点D，C.求证：AD＋BC＝AB.21. (1)如图①，在△ABC中，∠BAC＝90°，AB＝CA，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为D，E.求证：DE＝BD＋CE.(2)如图②，将(1)中的条件改为：在△ABC中，AB＝CA，D，A，E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角，则结论DE＝BD＋CE是否成立？若成立，请你给出证明；若不成立，请说明理由．人教版八年级数学第12章全等三角形培优训练-答案一、选择题1. 【答案】A2. 【答案】A[解析] ∵△ABF与△DCE全等，点A与点D，点B与点C是对应顶点，∴∠DCE＝∠B.故选A.3. 【答案】A4. 【答案】C[解析] 对于选项A来说，AB＋BC<AC，不能画出△ABC；对于选项B来说，可画出△ABC为锐角三角形或者钝角三角形；对于选项C来说，已知两边及其夹角，△ABC是唯一的；对于选项D来说，△ABC的形状可确定，但大小不确定．5. 【答案】D[解析] 如图,由题意知∠AOD=30°,∠COD=90°,∴∠AOC=120°.由作图可知,OB平分∠AOC,∴∠AOB=∠AOC=60°.∴∠DOB=30°.∴点B在点O的北偏东30°方向上.6. 【答案】C[解析] 选项A中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.选项B中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.选项C中，如图①，∵∠DEC=∠B+∠BDE，∴x°+∠FEC=x°+∠BDE.∴∠FEC=∠BDE.这两个角所对的边是BE和CF，而已知条件给的是BD=CF=3，故不能判定两个小三角形全等.选项D中，如图②，∵∠DEC=∠B+∠BDE，∴x°+∠FEC=x°+∠BDE.∴∠FEC=∠BDE.又∵BD=CE=2，∠B=∠C，∴△BDE≌△CEF.故能判定两个小三角形全等.7. 【答案】A[解析] AB=b，AB是斜边，小惠作的斜边长是b符合条件，而小雷作的是一条直角边长是b.故小惠的作法正确，小雷的作法错误.8. 【答案】B[解析] 如图，过点F分别作FZ⊥AE于点Z，FY⊥CB于点Y，FW⊥AB于点W.∵AF平分∠BAC，FZ⊥AE，FW⊥AB，∴FZ＝FW.同理FW＝FY.∴FZ＝FY.又∵FZ⊥AE，FY⊥CB，∴∠FCZ＝∠FCY.由∠AFB＝40°，易得∠ACB＝80°.∴∠ZCY＝100°.∴∠BCF＝50°.二、填空题9. 【答案】125[解析] 由题意可得AD平分∠CAB.∵∠C=90°，∠B=20°，∴∠CAB=70°.∴∠CAD=∠BAD=35°.∴∠ADB=180°-20°-35°=125°.10. 【答案】AB ＝AC11. 【答案】20[解析] 如图，过点D 作射线AF.在△BAD 和△CAD 中，⎩⎨⎧AB ＝AC ，AD ＝AD ，BD ＝CD ，∴△BAD ≌△CAD(SSS)． ∴∠BAD ＝∠CAD ，∠B ＝∠C.∵∠BDF ＝∠B ＋∠BAD ，∠CDF ＝∠C ＋∠CAD ， ∴∠BDF ＋∠CDF ＝∠B ＋∠BAD ＋∠C ＋∠CAD ，即∠BDC ＝∠B ＋∠C ＋∠BAC. ∵∠BAC ＝80°，∠BDC ＝120°， ∴∠B ＝∠C ＝20°.12. 【答案】4∶3【解析】如解图，过D 作DE ⊥AB ，DF ⊥AC ，垂足分别为E 、F ，∵AD 是∠BAC 的平分线，∴DE ＝DF(角平分线上的点到角两边的距离相等)，设DE＝DF＝h，则S△ABDS△ACD ＝12AB·h12AC·h＝43.13. 【答案】70【解析】∵∠ABC=90°，AB=AC，∴∠CBF=180°–∠ABC=90°，∠ACB=45°，在Rt△ABE和Rt△CBF中，AB CBAE CF=⎧⎨=⎩，∴Rt△ABE≌Rt△CBF，∴∠BCF=∠BAE=25°，∴∠ACF=∠ACB+∠BCF=45°+25°=70°，故答案为：70．14. 【答案】两直线平行，内错角相等SAS全等三角形的对应角相等内错角相等，两直线平行15. 【答案】20[解析] 由角平分线的性质可得CD＝DE.易证Rt△ACD≌Rt△AED，则AC＝AE，DE＋DB＝CD＋DB＝BC＝AC＝AE，故DE＋DB＋EB ＝AE＋EB＝AB.16. 【答案】7[解析] 过点P作PF⊥BC于点F，PG⊥AB于点G ，连接AP.∵△ABC的两条外角平分线BP，CP相交于点P，∴PF=PG=PE=2.∵S△BPC=2，∴BC·2=2，解得BC=2.∵△ABC的周长为11，∴AC+AB=11-2=9.∴S △ABC =S △ACP +S △ABP -S △BPC =AC ·PE+AB ·PG-S △BPC =×9×2-2=7.三、解答题17. 【答案】解：如图，过点D 作DE ⊥AB 于点E ，DF ⊥AC 于点F. ∵AD 是∠BAC 的平分线，∴DE ＝DF. ∵AB ＝20 m ，AC ＝10 m ，∴S △ABC ＝12×20×10＝12×20·DE ＋12×10·DF ，解得DE ＝203(m)．∴△ACD 的面积＝12×10×203＝1003(m 2)，△ABD 的面积＝12×20×203＝2003(m 2)．故一串红的种植面积为2003 m 2，鸡冠花的种植面积为1003 m 2.18. 【答案】解:∵△ACF ≌△DBE ，∴AC=DB.∴AC-BC=DB-BC ，即AB=CD.∵AD=16，BC=10，∴AB=CD=(AD-BC )=3.19. 【答案】证明：在△ABC 和△ADC 中，⎩⎨⎧AB ＝AD ，AC ＝AC ，CB ＝CD ， ∴△ABC ≌△ADC.∴∠BAP ＝∠DAP.在△BAP 和△DAP 中，⎩⎨⎧AB ＝AD ，∠BAP ＝∠DAP ，AP ＝AP ， ∴△BAP ≌△DAP.∴∠ABP ＝∠ADP.20. 【答案】证明：如图，在AB 上截取AF ＝AD ，连接EF.∵AE 平分∠PAB ，∴∠DAE ＝∠FAE.在△DAE 和△FAE 中，⎩⎨⎧AD ＝AF ，∠DAE ＝∠FAE ，AE ＝AE ，∴△DAE ≌△FAE(SAS)．∴∠AFE ＝∠ADE.∵AD ∥BC ，∴∠ADE ＋∠C ＝180°.又∵∠AFE ＋∠EFB ＝180°，∴∠EFB ＝∠C.∵BE 平分∠ABC ，∴∠EBF ＝∠EBC.在△BEF 和△BEC 中，⎩⎨⎧∠EFB ＝∠C ，∠EBF ＝∠EBC ，BE ＝BE ，∴△BEF ≌△BEC(AAS)．∴BF ＝BC.∴AD ＋BC ＝AF ＋BF ＝AB.21. 【答案】解：(1)证明：∵BD ⊥直线m ，CE ⊥直线m ， ∴∠BDA ＝∠AEC ＝90°.∴∠BAD ＋∠ABD ＝90°.∵∠BAC ＝90°，∴∠BAD ＋∠CAE ＝90°. ∴∠CAE ＝∠ABD.在△ADB 和△CEA 中，⎩⎨⎧∠ABD ＝∠CAE ，∠BDA ＝∠AEC ，AB ＝CA ，∴△ADB ≌△CEA(AAS)．∴BD ＝AE ，AD ＝CE.∴DE ＝AE ＋AD ＝BD ＋CE.(2)成立．证明：∵∠BDA ＝∠BAC ＝α，∴∠DBA ＋∠BAD ＝∠BAD ＋∠EAC ＝180°－α. ∴∠DBA ＝∠EAC.在△ADB 和△CEA 中，⎩⎨⎧∠DBA ＝∠EAC ，∠BDA ＝∠AEC ，AB ＝CA ，∴△ADB ≌△CEA(AAS)．∴BD ＝AE ，AD ＝CE.∴DE ＝AE ＋AD ＝BD ＋CE.。

初二上数学培优专题(3)三角形全等

三角形全等例1：已知，OA=2，OB=4，以A点为顶点、AB为腰在第三象限作等腰Rt△ABC，（1）如图1，求C点的坐标；（2）如图2，P为y轴负半轴上一个动点，当P点向y轴负半轴向下运动时，以P为顶点，PA为腰作等腰Rt△APD，过D作DE⊥x轴于E点，求OP﹣DE的值；（3）如图3，已知点F坐标为（﹣2，﹣2），当G在y轴的负半轴上沿负方向运动时，作Rt△FGH，始终保持∠GFH=90°，FG与y轴负半轴交于点G（0，m），FH与x轴正半轴交于点H（n，0），当G点在y 轴的负半轴上沿负方向运动时，以下两个结论：①m﹣n为定值；②m+n为定值，其中只有一个结论是正确的，请找出正确的结论，并求出其值．例2：已知△ABC中、∠ABC=∠ACB=40°,BD是∠ABC的平分线，延长BD至点E，使得DE=AD，求∠ECA的度数。

例3．已知∠GOH=90°，A、C分别是OG、OH上的点，且OA=OC=4，以OA为边长作正方形OABC．（1）E是边OC上一点，作∠AEF=90°使EF交正方形的外角平分线CF于点F（如图1），求证：EF=AE．（2）现将正方形OABC绕O点顺时针旋转，当A点第一次落在∠GOH的角平分线OP上时停止旋转；旋转过程中，AB边交OP于点M，BC边交OH于点N（如图2），①旋转过程中，当MN和AC平行时，求正方形OABC旋转的度数；②设△MBN的周长为p，在正方形OABC的旋转过程中，p值是否有变化？请证明你的结论．例4：如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点．如果点P在线段BC上由点B出发向C点运动，同时，点Q在线段CA上由点C出发向A点运动．设运动时间为t（s）.(1)若点P的运动速度为3cm/s,则t(s)时，BP= cm,CP= cm,(用含t的代数式表示).若点Q的运动速度与点P的运动速度相等，经过几秒后，△BPD与△CQP是否全等？请说明理由．(2)若点Q的运动速度与点P的运动速度不相等，且点P的速度比点Q的速度慢1cm/s,则点Q的速度为多少时，能够使△BPD与△CQP全等？（3）若点Q以（2）中的速度从点C出发，点P以（2）中的运动速度从点B同时出发，都逆时针沿△ABC 三边运动，求经过多长时间点P与点Q第一次相遇，相遇点在△ABC的哪条边上？1.∆ABC中，高AD和BE交于点H，且BH=AC，则∠ABC=_____2.如图∠E=∠F=90°，∠B=∠C，AE=AF，给出下列结论：①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN ⑤EM=FN.其中正确的结论有（）A. 1个B. 2个C. 3个D. 4个 2题3.下列条件中能作出唯一的三角形的是（）A.已知两边及一边的对角B.已知两边及第三边上的中线C.已知两角D.已知两边及第三边上的高线4.下列判断正确的是（）A.有两边及其中一边的对角对应相等的两个三角形全等.B.有两边对应相等，且有一个角为30°的两个等腰三角形全等.C.有一个角和一边对应相等的两个直角三角形全等 .D.有两角和一边对应相等的两个三角形全等. 5题5.两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③AO=CO=AC④四边形ABCD的面积=AC•BD，其中正确的结论有 .6.如图，在△ABC中，AB=AC，∠ABC、∠ACB的平分线BD，CE相交于O点，且BD交AC于点D，CE交AB于点E．某同学分析图形后得出以下结论：①△BCD≌△CBE；②△BAD≌△BCD；③△BDA≌△CEA；④△BOE≌△COD；⑤△ACE≌△BCE；上述结论一定正确的是（）A．①②③ B．②③④ C．①③⑤ D．①③④7.下列叙述：①任意一个三角形的三条高至少有一条在三角形内部；②以a，b，c为边（a，b，c都大于0，且a+b＞c)一定可以构成一个三角形；③一个三角形内角之比为3：2：1，此三角形为直角三角形；④两个角和其中一角的对边对应相等的两个三角形全等；⑤两条边和其中一边的对角对应相等的两个三角形全等；⑥三个角对应相等的两个三角形全等；⑦两边和其中一边上的高分别相等的两个三角形全等。

专题12.18 三角形全等作辅助线模型(三)-倍长中线(专项练习)(培优篇)

专题12.18 三角形全等作辅助线模型（三）-倍长中线（专项练习）（培优篇）一、解答题1．已知，在Rt ABC △中，90BAC ∠=︒，点D 为边AB 的中点，AE CD ⊥分别交CD ，BC 于点F ，E ．（1）如图1，①若AB AC =，请直接写出EAC BCD ∠-∠=______；①连接DE ，若2AE DE =，求证：DEB AEC ∠=∠；（2）如图2，连接FB ，若FB AC =，试探究线段CF 和DF 之间的数量关系，并说明理由．2．（1）阅读理解：如图1，在ABC 中，若10AB =，6AC =．求BC 边上的中线AD 的取值范围．解决此问题可以用如下方法：延长AD 到点E ，使DE AD =，再连接BE （或将ACD △绕着点D 逆时针旋转180︒得到EBD △），把AB ，AC ，2AD 集中在ABE △中，利用三角形三边的关系即可判断中线AD 的取值范围是______；（2）问题解决：如图2，在ABC 中，D 是BC 边上的中点，DE DF ⊥于点D ，DE 交AB 于点E ，DF 交AC 于点F ，连接EF ，求证：BE CF EF +>（3）问题拓展：如图3，在四边形ABCD 中，180B D ∠+∠=︒，CB CD =，140BCD ∠=︒，以C 为顶点作一个70︒角，角的两边分别交AB ，AD 于E ，F 两点，连接EF ，探索线段BE ，DF ，EF 之间的数量关系，并加以证明．3．阅读下列材料，完成相应任务．数学活动课上，老师提出了如下问题：如图1，已知ABC ∆中，AD 是BC 边上的中线．求证：2AB AC AD +>．智慧小组的证法如下：证明：如图2，延长AD 至E ，使DE AD =，①AD 是BC 边上的中线①BD CD =在BDE ∆和CDA ∆中BD CD BDE CDA DE DA =⎧⎪∠=∠⎨⎪=⎩①BDE CDA ∆∆≌（依据一）①BE CA =在ABE ∆中，AB BE AE +>（依据二）①2AB AC AD +>．任务一：上述证明过程中的“依据1”和“依据2”分别是指：依据1：______________________________________________；依据2：______________________________________________．归纳总结：上述方法是通过延长中线AD ，使DE AD =，构造了一对全等三角形，将AB ，AC ，AD 转化到一个三角形中，进而解决问题，这种方法叫做“倍长中线法”．“倍长中线法”多用于构造全等三角形和证明边之间的关系．任务二：如图3，3AB =，4AC =，则AD 的取值范围是_____________；任务三：如图4，在图3的基础上，分别以AB 和AC 为边作等腰直角三角形，在Rt ABE ∆中，90BAE ∠=︒，AB AE =；Rt ACF ∆中，90CAF =︒∠，AC AF =．连接EF ．试探究EF 与AD 的数量关系，并说明理由．4．已知：①ABC 和①ADE 都是等腰直角三角形，①ACB=①ADE=90°，点M 是BE 的中点，连接CM 、DM ．（1）当点D 在AB 上，点E 在AC 上时（如图一），求证：DM=CM ，DM①CM ；（2）当点D 在CA 延长线上时（如图二）（1）中结论仍然成立，请补全图形（不用证明）；（3）当ED①AB 时（如图三），上述结论仍然成立，请加以证明．5．（1）如图1，AD 是ABC ∆的中线，8,6AB AC ==，求AD 的取值范围，我们可以延长AD 到点M ，使DM AD =，连接BM （如图2所示），这样就可以求出2AD 的取值范围，从而得解，请写出解题过程；（2）在（1）问的启发下，解决下列问题：如图3，AD 是ABC ∆的中线，BE 交AC 于点E ，交AD 于点F ，且AE EF =，求证：AC BF =．6．（阅读理解）课外兴趣小组活动时，老师提出了如下问题：如图1，①ABC 中，若AB ＝8，AC ＝6，求BC 边上的中线AD 的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD 到点E ，使DE ＝AD ，请根据小明的方法思考：(1)由已知和作图能得到①ADC①①EDB 的理由是_____.A ．SSSB ．SASC ．AASD ．HL(2)求得AD 的取值范围是______.A ．6＜AD ＜8B ．6≤AD≤8C ．1＜AD ＜7 D ．1≤AD≤7（感悟）解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.（问题解决）(3)如图2，AD 是①ABC 的中线，BE 交AC 于E ，交AD 于F ，且AE ＝EF.求证：AC ＝BF. 7．已知AE AB ⊥，DA AC ⊥，AE AB =，AD AC =．直线MN 过点A ，交DE 、BC于点M 、N ．（1）若AM 是EAD 中线，求证：AN BC ⊥；（2）若AN BC ⊥，求证：EM DM =．8．已知：如图，D 是①ABC 边BC 上一点，且CD ＝AB ，①BDA ＝①BAD ，AE 是①ABD 的中线．求证：AC ＝2AE ．9．如图, AB=CB, BD=BE, ①ABC=①DBE=α.(1)当α=60°, 如图则，①DPE 的度数______________(2)若①BDE 绕点B 旋转一定角度，如图所示，求①DPE （用α表示）(3)当α=90°，其他条件不变，F 为AD 的中点，求证：EC ① BF10．已知：在ABC ∆中，90ABC ACB ∠-∠=︒，点D 在BC 上，连接AD ，45ADB ∠=︒. （1）如图1，求证：BAD CAD ∠=∠；（2）如图2，点E 为BC 的中点，过点E 作AD 的垂线分别交AD 的延长线，AB 的延长线，AC 于点F G H ，，，求证：BG CH =；（3）如图3，在（2）的条件下，过点E 分别作EM AG ⊥于点M EN AC ⊥，于点N ，若26AB AC +=，1203EM EN +=，求AFG ∆的面积.11．如图，在ABC △中，D 、E 分别是BC 上两点，且BD CE =，求证：AB AC AD AE +>+.12．如图，AB AE =，AD AC =，180BAE DAC ∠+∠=︒，点F 为DE 的中点，求证：2BC AF =.参考答案1．（1）①45°；①见解析；（2）2CF DF =，理由见解析【分析】（1）①利用直角三角形两个锐角相加得90︒和三角形的外角等于不相邻的两个内角和的性质结合题干已知即可解题．①延长ED 至点G ，使得DG DE =，连接AG ，从而可证明ADG ①BDE （SAS ），再利用全等的性质，可知DGA DEB ∠=∠，即可知道//AG BC ，所以GAE AEC ∠=∠，根据题干又可得到AE EG =，所以DGA GAE ∠=∠，从而得出结论．（2）延长CD 至点H ，使得DH DF =，连接BH ，从而可证明HDB ①FDA △（SAS ），再利用全等的性质，可知BH AF =，90H AFD AFC ∠=∠=∠=︒，根据题干即可证明Rt HBF △①Rt FAC △（HL ），即得出结论．【详解】（1）①①90EAC ACD ∠+∠=︒，90AEC BCD ∠+∠=︒①EAC BCD AEC ACD ∠-∠=∠-∠①90EAC BAE ∠+∠=︒①ACD BAE ∠=∠又①AEC B BAE ∠=∠+∠①EAC BCD B BAE ACD ∠-∠=∠+∠-∠①45EAC BCD B ∠-∠=∠=︒故答案为45︒．①如图，延长ED 至点G ，使得DG DE =，连接AG ，①点D 为AB 的中点，①BD AD =，又①ADG BDE ∠=∠，①ADG ①BDE ，①DGA DEB ∠=∠，①//AG BC ，①GAE AEC ∠=∠，又①2AE DE =，①AE EG =，①DGA GAE ∠=∠，①DEB AEC ∠=∠．（2）2CF DF =．如图，延长CD 至点H ，使得DH DF =，连接BH ，①AD BD =，ADF BDH ∠=∠，①HDB ①FDA △，①BH AF =，90H AFD AFC ∠=∠=∠=︒，①BF AC =．①Rt HBF △①Rt FAC △，①2CF HF DF ==．【点拨】本题主要考查直角三角形的角的性质，三角形外角的性质，全等三角形的判定和性质以及平行线的性质．综合性较强，作出辅助线是解答本题的关键．2．（1）28AD <<；（2）见解析；（3）BE DF EF +=，见解析【分析】（1）延长AD 至E ，使DE=AD ，由SAS 证明①ACD①①EBD ，得出BE=AC=6，在①ABE 中，由三角形的三边关系求出AE 的取值范围，即可得出AD 的取值范围；（2）延长FD 至点M ，使DM=DF ，连接BM 、EM ，同（1）得①BMD①①CFD ，得出BM=CF ，由线段垂直平分线的性质得出EM=EF ，在①BME 中，由三角形的三边关系得出BE+BM ＞EM 即可得出结论；（3）延长AB 至点N ，使BN=DF ，连接CN ，证出①NBC=①D ，由SAS 证明①NBC①①FDC ，得出CN=CF ，①NCB=①FCD ，证出①ECN=70°=①ECF ，再由SAS 证明①NCE①①FCE ，得出EN=EF ，即可得出结论．【详解】（1）解：延长AD 至E ，使DE=AD ，连接BE ，如图①所示：①AD 是BC 边上的中线，①BD=CD ，在①BDE 和①CDA 中，BD CD BDE CDA DE AD =⎧⎪∠=∠⎨⎪=⎩①①BDE①①CDA （SAS ），①BE=AC=6，在①ABE 中，由三角形的三边关系得：AB -BE ＜AE ＜AB+BE ，①10-6＜AE ＜10+6，即4＜AE ＜16，①2＜AD ＜8；故答案为：2＜AD ＜8；（2）证明：延长FD 至点M ，使DM DF =，连接BM ，EM ，如图所示同（1）得，()BMD CFD SAS ∆≅∆，BM CF ∴=DE DF ⊥，DM DF =，DE DE =()EDM EDF SAS ∴∆≅∆，EM EF ∴=在BME ∆中，由三角形的三边关系得BE BM EM +>，BE CF EF ∴+>（3）BE DF EF +=证明如下：延长AB 至点N ，使BN DF =，连接CN ，如图所示180ABC D ∠+∠=︒，180NBC ABC ∠+∠=︒NBC D ∴∠=∠在NBC ∆和FDC ∆中，BN DF NBC D BC DC =⎧⎪∠=∠⎨⎪=⎩，()NBC FDC SAS ∴∆≅∆CN CF ∴=，NCB FCD ∠=∠140BCD ∠=︒，70ECF ∠=︒70BCE FCD ∴∠+∠=︒，70ECN ECF ∴∠=︒=∠在NCE ∆和FCE ∆中，CM CF ECN ECF BC DC =⎧⎪∠=∠⎨⎪=⎩()NCE FCE SAS ∴∆≅∆，EN EF ∴=．BE BN EN +=，BE DF EF ∴+=【点拨】本题考查了三角形的三边关系、全等三角形的判定与性质、角的关系等知识；本题综合性强，有一定难度，通过作辅助线证明三角形全等是解决问题的关键．3．任务一：依据1：两边和它们的夹角分别相等的两个三角形全等（或“边角边”或“SAS”）；依据2：三角形两边的和大于第三边；任务二：1722AD ＜＜；任务三：EF=2AD ，见解析【分析】任务一：依据1：根据全等的判定方法判断即可；依据2：根据三角形三边关系判断；任务二：可根据任务一的方法直接证明即可；任务三：根据任务一的方法，延长中线构造全等三角形证明线段关系即可．【详解】解：任务一：依据1：两边和它们的夹角分别相等的两个三角形全等（或“边角边”或“SAS”）；依据2：三角形两边的和大于第三边．任务二：1722AD ＜＜任务三：EF=2AD ．理由如下：如图延长AD 至G ，使DG=AD ，①AD 是BC 边上的中线①BD=CD在①ABD 和①CGD 中BD CD BDA CDG AD DG =⎧⎪∠=∠⎨⎪=⎩①①ABD①①CGD①AB=CG ，①ABD=①GCD又①AB=AE①AE=CG在①ABC 中，①ABC+①BAC+①ACB=180°，①①GCD+①BAC+①ACB=180°又①①BAE=90°，①CAF=90°①①EAF+①BAC=360°-（①BAE+①CAF ）=180°①①EAF=①GCD在①EAF 和①GCA 中AE CG EAF GCA AF AC =⎧⎪∠=∠⎨⎪=⎩①①EAF①①GCA①EF=AG①EF=2AD ．【点拨】此题是三角形综合题，主要考查了全等三角形的判定和性质，倍长中线法，构造全等三角形是解本题的关键．4．（1）证明见解析；（2）见解析；（3）见解析．【分析】（1）如图一中，延长DM 使得MN DM =，连接BN 、CN ，先证明DME NMB ∆≅∆，再证明ACD BCN ∆≅∆即可解决问题．（2）补充图形如图二所示，延长DM 交CB 的延长线于N ，只要证明DME NMB ∆≅∆，再证明CDN ∆是等腰直角三角形即可．（3）如图三中，如图一中，延长DM 使得MN DM =，连接BN 、CN ，CD ，先证明DME NMB ∆≅∆，再证明ACD BCN ∆≅∆即可．【详解】（1）证明：如图一中，延长DM 使得MN=DM ，连接BN 、CN ．在①DME 和①NMB 中，DM MN DME NMB ME MB =⎧⎪∠=∠⎨⎪=⎩，①①DME①①NMB ，①DE=BN ，①MDE=①MNB ，①DE①NB ，①①ADE=①ABN=90°，①①ABC 和①ADE 都是等腰直角三角形，①ACB=①ADE=90°，①AD=DE=BN ，AC=BC ，①A=①ABC=45°，①①CBN=45°=①A ，在①ACD 和①BCN 中，AC BC A CBN AD BN =⎧⎪∠=∠⎨⎪=⎩，①①ACD①①BCN ，①DC=CN，①ACD=①BCN，①①DCN=①ACB=90°，①①DCN是等腰直角三角形，①DM=MN，①DM=CM．DM①CM（2）解：如图二所示延长DM交CB的延长线于N，①①ABC和①ADE都是等腰直角三角形，①ACB=①ADE=90°，①AD=DE=BN，AC=BC，①A=①ABC=45°，①①EDC+①DCN=180°，①DE①CN，①①EDM=①N在①DME和①NMB中，EDM NEMD NMB EM BM∠=∠⎧⎪∠=∠⎨⎪=⎩，①①DME①①NMB，①DE=BN=AD，DM=MN，①CD=CN，①①CDN=①N=45°，CM=DM=MN，CM①DN，①DM=CM．DM①CM．（3）证明：如图三中，如图一中，延长DM交AB于N连接CN．①DE①AB ，①①MBN=①MED ，在①DME 和①NMB 中，MBN MED BM EM BMN EMD ∠=∠⎧⎪=⎨⎪∠=∠⎩，①①DME①①NMB ，①DE=BN=AD ，DM=MN ，①①ABC 和①ADE 都是等腰直角三角形，①ACB=①ADE=90°，①AD=DE=BN ，AC=BC ，①BAC=①ABC=45°，①①AED+①BAE=180°，①①BAE=135°，①①BAC=①EAD=45°，①①DAC=①CBN=45°在①ACD 和①BCN 中，AC BC DAC NBC AD BN =⎧⎪∠=∠⎨⎪=⎩，①①ACD①①BCN ，①DC=CN ，①ACD=①BCN ，①①DCN=①ACB=90°，①①DCN 是等腰直角三角形，①DM=MN ，①DM=CM ．DM①CM【点拨】本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识，解题的关键是添加辅助线构造全等三角形，记住中线延长一倍是常用辅助线，属于中考常考题型． 5．（1）17AD <<；（2）见解析．【分析】（1）延长AD 到点M ，使DM AD =，连接BM ，易证ADC MDB ∆≅∆，从而得BM AC =，根据三角形三边关系，可得214AM <<，进而即可求解；（2）先证ADC MDB ∆≅∆，结合AE EF =，可得BM BF =，结合BM AC =，即可得到结论．【详解】（1）AD DM BD CD ADC MDB ==∠=∠，，，ADC MDB ∴∆≅∆（SAS ）， ①BM AC =，①在ABM ∆中， 214AM <<，即：2214AD <<，①AD 的范围是：17AD <<；（2）延长AD 到点M ，使DM AD =，连接BM ，由（1）知：ADC MDB ∆≅∆，M CAD BM AC ∴∠=∠=，，AE EF =，CAD AFE ∴=∠，MFB AFE ∠=∠，BMF BFM ∴∠=∠，BM BF ∴=，AC BF ∴=．【点拨】本题主要考查三角形全等的判定和性质定理，三角形三边的关系，等腰三角形的性质和判定定理，添加辅助线，构造全等三角形，是解题的关键．6．(1)B ；(2)C ；(3)证明见解析.【分析】(1)根据AD ＝DE ，①ADC ＝①BDE ，BD ＝DC 推出①ADC 和①EDB 全等即可；(2)根据全等得出BE ＝AC ＝6，AE ＝2AD ，由三角形三边关系定理得出8﹣6＜2AD ＜8+6，求出即可；(3)延长AD 到M ，使AD ＝DM ，连接BM ，根据SAS 证①ADC①①MDB ，推出BM ＝AC ，①CAD ＝①M ，根据AE ＝EF ，推出①CAD ＝①AFE ＝①BFD ，求出①BFD ＝①M ，根据等腰三角形的性质求出即可.【详解】（1）解：在①ADC 和①EDB 中AD DE ADC BDE BD CD =⎧⎪∠=∠⎨⎪=⎩，①①ADC①①EDB(SAS)，故选B ；（2）解：如图：①由(1)知：①ADC①①EDB ，①BE ＝AC ＝6，AE ＝2AD ，①在①ABE 中，AB ＝8，由三角形三边关系定理得：8﹣6＜2AD ＜8+6，①1＜AD ＜7，故选C.（3）延长AD 到M ，使AD ＝DM ，连接BM ，①AD 是①ABC 中线，①CD ＝BD ，①在①ADC 和①MDB 中DC DB ADC MDB DA DM =⎧⎪∠=∠⎨⎪=⎩①①ADC①①MDB ，①BM ＝AC ，①CAD ＝①M ，①AE ＝EF ，①①CAD ＝①AFE ，①①AFE ＝①BFD ，①①BFD ＝①CAD ＝①M ，①BF ＝BM ＝AC ，即AC ＝BF.【点拨】本题考查了三角形的中线，三角形的三边关系定理，等腰三角形性质和判定，全等三角形的性质和判定等知识点，主要考查学生运用定理进行推理的能力．7．（1）详见解析；（2）详见解析.【分析】（1）延长AM 至F ，使MF AM =，易证EMF △①DMA △，可得DAM F ∠=∠，EF AD =，再根据AD AC =可得EF AC =，再利用①BAC 、①BAE 、①EAD 和①DAC 四个角和为360°，可得180BAC DAE ∠=︒-∠，利用①AEF 的内角和可得180AEF DAE ∠=︒-，可得BAC AEF ∠=∠，即可证明ABC △①EAF △，最后利用等角的余角相等的等量代换以及①ABN 的内角和为180°可得出结论.（2）过点E 作EF AD ∥交AM 的延长线于F ，则F DAM ∠=∠，根据DA AC ⊥，可得90DAM CAN ∠+∠=︒；AN BC ⊥，可得90CAN C ∠+∠=︒，等量代换得出F DAM C ∠=∠=∠．根据周角等于360°，可得180BAC DAE ∠=︒-∠；根据三角形内角和可得180∠=︒-∠AEF DAE ，可得BAC AEF ∠=∠，则可证明ABC △①EAF △（AAS ），得到EF AC =；易证EFM △①DAM △，即可得到EM DM =．【详解】解：（1）如图，延长AM 至F ，使MF AM =，①AM 是EAD 中线，①EM DM =．在EMF △和DMA △中，EM DM EMF AMD MF AM =⎧⎪∠=∠⎨⎪=⎩，①EMF △①DMA △（SAS ）．①DAM F ∠=∠，EF AD =．①AD AC =，①EF AC =．①AE AB ⊥，DA AC ⊥，①360902180BAC DAE DAE ∠=︒-︒⨯-∠=︒-∠． ①180180180AEF F EAM DAM EAM DAE ∠=︒-∠-∠=︒-∠-∠=︒-，①BAC AEF ∠=∠．在ABC △和EAF △中，EF AC BAC AEF AB AE =⎧⎪∠=∠⎨⎪=⎩，①ABC △①EAF △（SAS ）．①EAF B ∠=∠．①AE AB ⊥，①90EAF BAN ∠+∠=︒．①90B BAN ∠+∠=︒．在ABN 中，()1801809090ANB B BAN ∠=︒-∠+∠=︒-︒=︒，①AN BC ⊥．（2）如图，过点E 作EF AD ∥交AM 的延长线于F ，则F DAM ∠=∠，①DA AC ⊥，①90DAM CAN ∠+∠=︒．①AN BC ⊥，①90CAN C ∠+∠=︒．①F DAM C ∠=∠=∠．①AE AB ⊥，DA AC ⊥，①360902180BAC DAE DAE ∠=︒-︒⨯-∠=︒-∠． ①180180180AEF F EAM DAM EAM DAE ∠=︒-∠-∠=︒-∠-∠=︒-∠， ①BAC AEF ∠=∠．在ABC △和EAF △中，BAC AEF F C AB AE ∠=∠⎧⎪∠=∠⎨⎪=⎩，①ABC △①EAF △（AAS ）．①EF AC =．①AD AC =，①EF AD =．在EFM △和DAM △中，F DAM EMF DMA EF AD ∠=∠⎧⎪∠=∠⎨⎪=⎩，①EFM △①DAM △（AAS ）．①EM DM =．【点拨】本题考查三角形全等以及角度之间的等量代换，第（1）题通过“倍长中线”这一辅助线做法，构造全等三角形，从而得出角相等，在遇到有中线的题目，并且题中没有全等三角形，那么我们就可以通过延长中线，或者经过中点的线段，构造全等三角形；第（2）题是通过构造平行线，进而得到角相等，构造全等三角形，然后再根据角之间的等量代换，常见的就是等角的余角相等、等角的补角相等，当直角比较多的地方都可以想到这种方法.8．见解析.【分析】延长AE 到F ，使EF=AE ，连接DF,，可证明①ABE①①FDE ，则①BAE=①EFD ，再由外角的性质得出①ADF=①ADC ，则①ADF①①ADC ，则AF=AC ，从而得出AC=2AE.【详解】证明：延长AE 到F ，使EF=AE ，连接DF①AE 是①ABD 的中线．①BE=ED在①ABE 和①FDE 中，BE DE AEB DEF AE EF =⎧⎪∠=∠⎨⎪=⎩①①ABE①①FDE （SAS ）①AB=DF ，①BAE=①EFD①①ADB 是①ADC 的外角①①DAC+①ACD=①ADB=①BAD①①BAE+①EAD=①BAD①BAE=①EFD①①EFD+①EAD=①DAC+①ACD①①ADF=①ADC①AB=DC①DF=DC在①ADF 和①ADC 中，AD AD ADF ADC FD DC =⎧⎪∠=∠⎨⎪=⎩①①ADF①①ADC （SAS ）①AF=AC①AF=AE+EF，AE=ED①AC=2AE【点拨】本题主要考查三角形全等的判定与性质，还涉及三角形中线定义、三角形外角定理等知识点，作出辅助线以及熟练掌握三角形全等的性质定理是解题关键.9．（1）60°；（2）α；（3）证明见解析．【分析】（1）由SAS证明①ABE①①CBD，得到①AEB=①CDB，再由对顶角相等及三角形内角和公式可得①EPD=①EBD即可；（2）与（1）同理可求①DPE=①DBE，即可得出结论；（3）延长BF到K，使FK=BF，连接KD，延长EC交BK于M．由SAS证明①AFB①①DFK，得到AB=KD，①ABF=①DKF，进而得到BC=KD，KD①AB，再证明①BDK=①4，得到①EBC①①BDK，由全等三角形对应角相等得到①1=①2，即可得出结论．【详解】（1）如图1，设BE和CD相交于M．①①ABC=①DBE，①①ABE=①CBD．在①ABE和①CBD中，①AB BCABE CBDBE BD=⎧⎪∠=∠⎨⎪=⎩，①①ABE①①CBD（SAS），①①AEB=①CDB．在①PME和①BMD中，①①PME=①BMD，①AEB=①CDB，①①EPD=180°－①AEB－①PME=180°－①CDB－①BMD=①MBD=60°；（2）如图2，同理可求①DPE=①DBE=α；（3）如图3，延长BF 到K ，使FK =BF ，连接KD ，延长EC 交BK 于M ．①AF =DF ，①AFB =①DFK ，BF =KF ，①①AFB ①①DFK ，①AB =KD ，①ABF =①DKF ，①BC =KD ，KD ①AB ，①①BDK +①ABD =180°，①①BDK =180°－①ABD =180°－（①2+①3+①4+①5）=180°－[（90°－①4）+90°]=①4．在①EBC 和①BDK 中，①EB =BD ，①4=①BDK ，BC =DK ，①①EBC ①①BDK ，①①1=①2． ①①2+①EBK =90°，①①1+①EBK =90°，①①EMB =90°，①EC ①BF ．【点拨】本题考查了全等三角形的判定与性质，等腰直角三角形的性质，此类题目往往求解思路相同，证明三角形全等是解题的关键．10．(1)见解析；（2）见解析；（3）30【解析】【分析】（1）设ACB α∠=，根据条件90ABC ACB ∠-∠=︒以及外角性质可得①ADB=①C+①CAD=45°，所以9090ABC ACB a ∠=∠+︒=+︒，45CAD ADB C α∠=∠-∠=︒-，由三角形内角和定理可得()18090902BAC ααα∠=︒-+︒-=︒-，从而求解；（2）过点B 作BT GH ⊥于点T ，过点C 作CR GH ⊥的延长线于点R ，可证G AHG CHR ==∠∠∠，利用AAS 证明BET CER ∆∆≌，得出BT CR =，再利用AAS证明BGT CHR ∆∆≌即可证明；（3）连接AE ，由ASA 易证AFG AFH ∆∆≌ ，所以AG AH =，26AB AC += ，因为()()26AG BG AH CH -++= ，所以13AG AH ==，又因为AGH AEG AEH S S S ∆∆∆=+ 所以()111313120131360222213AGH S EM EN EM EN ∆=⨯⨯+⨯⨯=⨯+=⨯=，因为111222AGH AFG FG GH S GH AF S FG AF ∆∆==⨯⨯=⨯⨯，所以1302AFG AGH S S ∆∆== 【详解】（1）证明：如图1 令ACB α∠=，①90ABC ACB ∠-∠=︒，①ADB=①C+①CAD=45°，①9090ABC ACB a ∠=∠+︒=+︒，45CAD ADB C α∠=∠-∠=︒-在ABC ∆中 ①180BAC ABC ACB ∠+∠+∠=︒①()18090902BAC ααα∠=︒-+︒-=︒-=2（45°-α ）①45BAD BAC CAD CAD α∠=∠-∠=︒-=∠（2）如图2 过点B 作BT GH ⊥于点T ，过点C 作CR GH ⊥的延长线于点R ①AF GH ⊥①90AFG AFH ∠=∠=︒①9090G FAG AHF FAH ∠+∠=∠+∠=︒︒①G AHG CHR ==∠∠∠在BET ∆和CER ∆中 90BET CER BTE CRE BE CE ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩①BET CER ∆∆≌①BT CR =由（1）得BAD CAD ∠=∠，①HG①AF ，①①BGT=①AHG=①CHR ，在BGT ∆和CHR ∆中 90BGT CHR BTG CRH BT CR ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩①BGT CHR ∆∆≌①BG CH =（3）如图3 连接AE在AFG ∆和AFH ∆中 FAG FAH AF AFAFG AFH ∠=∠⎧⎪=⎨⎪∠=∠⎩①AFG AFH ∆∆≌①AG AH =①26AB AC +=①()()26AG BG AH CH -++=①13AG AH ==①AGH AEG AEH S S S ∆∆∆=+ ①()111313120131360222213AGH S EM EN EM EN ∆=⨯⨯+⨯⨯=⨯+=⨯= ①111222AGH AFG FG GH S GH AF S FG AF ∆∆==⨯⨯=⨯⨯ ①1302AFG AGH S S ∆∆==【点拨】本题考查角平分线的判定、全等三角形的证明与性质，三角形面积的计算，解题关键是恰当做出辅助线.11．详见解析【解析】【分析】如图，取DE 的中点O ，连结AO 并延长至点F ，使OF OA =，连结EF 、CF ，证明AOD FOE ∆∆≌，从而可得AD=EF ，同理可得AB=CF ，延长AE 交CF 于点G ，在ACG ∆中，根据三角形三边关系可得到AC CG AE EG +>+，在EFG ∆中，EG FG EF +>，继而通过推导即可得出答案.【详解】如图，取DE 的中点O ，连结AO 并延长至点F ，使OF OA =，连结EF 、CF ， AO FO =，DO EO =，AOD FOE ∠=∠，AOD FOE ∴∆∆≌，AD EF ∴=，同理可证：AB CF =，延长AE 交CF 于点G ，在ACG ∆中，AC CG AG +>，即AC CG AE EG +>+，①在EFG ∆中，EG FG EF +>，①①+①得，AC CG EG FG AE EG EF +++>++，即AC CF AE EF +>+，AB AC AD AE ∴+>+.【点拨】本题考查了全等三角形的判定与性质，三角形三边关系，正确添加辅助线，熟练掌握三角形三边关系是解题的关键.12．详见解析【分析】如图，延长AF 至G ，使AF FG =，连结EG ，证明ADF GEF ∆∆≌，从而可得AD GE =，ADF GEF ∠=∠，继而得GEA BAC ∠=∠，再证明AEG ACB ∆∆≌，可得AG=BC ，继而可得结论.【详解】如图，延长AF 至G ，使AF FG =，连结EG ，又DF EF =，AFD GFE ∠=∠，ADF GEF ∴∆∆≌，AD GE ∴=，ADF GEF ∠=∠.AD GE ∴，180GEA DAE ∴∠+∠=︒，180BAE DAC ∴∠+∠=︒，180DAE BAC ∴∠+∠=︒，GEA BAC ∴∠=∠，又AB AE =，AC AD =，AC GE ∴=，AEG ACB ∴∆∆≌，AG BC ∴=，即2BC AF =.【点拨】本题考查了全等三角形的判定与性质，根据倍长中线正确添加辅助线是解题的关键.。

全等三角形的性质与判定大题专练

【讲练课堂】2022-2023学年八年级数学上册尖子生同步培优题典【苏科版】专题1.7全等三角形的性质与判定大题专练（重难点培优）【名师点睛】1.全等三角形的性质与判定综合应用用全等寻找下一个全等三角形的条件，全等的性质和判定往往是综合在一起应用的，这需要认真分析题目的已知和求证，分清问题中已知的线段和角与所证明的线段或角之间的联系．2.作辅助线构造全等三角形常见的辅助线做法：①把三角形一边的中线延长，把分散条件集中到同一个三角形中是解决中线问题的基本规律．②证明一条线段等于两条线段的和，可采用“截长法”或“补短法”，这些问题经常用到全等三角形来证明．【典例剖析】【例1】（2019秋•东海县期中）如图，AB＝AC，E、D分别是AB、AC的中点，AF⊥BD，垂足为点F，AG ⊥CE，垂足为点G，试判断AF与AG的数量关系，并说明理由．【分析】结论：AF＝AG．先证明△ABD≌△ACE（SAS），推出∠ABD＝∠ACE，再证明△ABF≌△ACG （AAS）即可解决问题．【解析】结论：AF＝AG．理由：∵AB＝AC，E、D分别是AB、AC的中点，∴AD＝AC＝AB＝AE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴∠ABD＝∠ACE，∵AF⊥BD，AG⊥CE，∴∠AFB＝∠AGC＝90°．在△ABF和△ACG中，，∴△ABF≌△ACG（AAS），∴AF＝AG．【变式1】（2021秋•锡山区校级期中）如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD，BE＝CF．（1）求证：△ADE≌△ADF；（2）已知AC＝18，AB＝12，求BE的长．【分析】（1）先用（HL）证明Rt△EBD≌Rt△EBD，推DE＝DF，再用（HL）证明Rt△AED≌Rt△AFD；（2）由全等推AE＝AF，把AC长转化为AC＝AB+BE+FC，代入数值求解即可．【解答】（1）证明：∵DE⊥AB于E，DF⊥AC于F，∴∠E＝∠DFC＝∠DFA＝90°，在Rt△EBD与Rt△EBD中，∴Rt△EBD≌Rt△EBD（HL）；∴DE＝DF，在Rt△AED与Rt△AFD中，∴Rt△AED≌Rt△AFD（HL）；（2）解：∵Rt△AED≌Rt△AFD，∴AE＝AF，∴AF＝12+BE，∵AC＝AF+FC∴AC＝AB+BE+FC，∴18＝12+BE+CF，∵BE＝CF．∴18＝12+2BE，∴BE＝3．【例2】（2020春•江阴市期中）如图，AB＝AC，AD＝AE，∠BAC＝∠DAE．（1）求证：△ABD≌△ACE；（2）若∠1＝25°，∠2＝30°，求∠3的度数．【分析】（1）利用已知得出∠1＝∠EAC，进而借助SAS得出即可；（2）利用全等三角形的性质得出∠ABD＝∠2＝30°，再利用三角形的外角得出得出即可．【解答】（1）证明：∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠1＝∠EAC，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）；（2）解：∵△ABD≌△ACE，∴∠ABD＝∠2＝30°，∵∠1＝25°，∴∠3＝∠1+∠ABD＝25°+30°＝55°．【变式2】（2021秋•盐都区期中）如图，已知在四边形ABCD中，点E在AD上，∠BCE＝∠ACD，∠BAC ＝∠D，BC＝CE．（1）求证：AC＝CD．（2）若AC＝AE，∠ACD＝80°，求∠DEC的度数．【分析】（1）根据同角的余角相等可得到∠3＝∠5，结合条件可得到∠1＝∠D，再加上BC＝CE，可证得结论；（2）根据∠ACD＝80°，AC＝CD，得到∠2＝∠D＝50°，根据等腰三角形的性质得到∠4＝∠6＝65°，由平角的定义得到∠DEC＝180°﹣∠6＝115°．【解析】（1）∵∠BCE＝∠ACD，∴∠3+∠4＝∠4+∠5，∴∠3＝∠5，在△ABC和△DEC中，，∴△ABC≌△DEC（AAS），∴AC＝CD；（2）∵∠ACD＝80°，AC＝CD，∴∠2＝∠D＝50°，∵AE＝AC，∴∠4＝∠6＝65°，∴∠DEC＝180°﹣∠6＝115°．【满分训练】一．解答题（共20小题）1．（2022•丰县二模）如图，点F是△ABC的边AC的中点，点D在AB上，连接DF并延长至点E，DF＝EF，连接CE．（1）求证：△ADF≌△CEF；（2）若DE∥BC，DE＝4，求BC的长．【分析】（1）根据线段中点求出AF＝CF，再根据全等三角形的判定定理SAS推出即可；（2）根据全等三角形的性质得出∠A＝∠ACE，根据平行线的判定得出AB∥CE，根据平行四边形的判定定理得出四边形BCED是平行四边形，再根据平行四边形的性质得出即可．【解答】（1）证明：∵F为AC的中点，∴AF＝CF，在△ADF和△CEF中，，∴△ADF≌△CEF（SAS）；（2）解：∵△ADF≌△CEF，∴∠A＝∠ACE，∴AB∥CE，∵DE∥BC，∴四边形BCED是平行四边形，∴BC＝DE，∵DE＝4，∴BC＝4．2．（2022•姑苏区一模）如图，点D在射线AE上，BD＝CD，DE平分∠BDC．求证：AB＝AC．【分析】由“SAS”判定△ADC≌△ADB，得出AB＝AC即可．【解答】证明：∵DE平分∠BDC，∴∠BDE＝∠CDE，∴∠ADB＝∠ADC，在△ADC和△ADB中，，∴△ADC≌△ADB（SAS），∴AB＝AC．3．（2022•工业园区模拟）已知：如图，AB＝AC，AD＝AE，∠BAE＝∠CAD．求证：∠D＝∠E．【分析】先证∠BAD＝∠CAE，再证△BAD≌△CAE（SAS），即可得出结论．【解答】证明：∵∠BAE＝∠CAD，∴∠BAE+∠DAE＝∠CAD+∠DAE，即∠BAD＝∠CAE，在△BAD与△CAE中，，∴△BAD≌△CAE（SAS），∴∠D＝∠E．4．（2022•江阴市模拟）如图，在△ABC中，O为BC中点，BD∥AC，直线OD交AC于点E．（1）求证：△BDO≌△CEO；（2）若AC＝6，BD＝4，求AE的长．【分析】（1）根据已知条件，可证△BDO≌△CEO（AAS）；（2）根据全等三角形的性质可得BD＝CE，进一步可得AE的长．【解答】（1）证明：∵O为BC的中点，∴BO＝CO，∵BD ∥AC ，∴∠C ＝∠OBD ，∠CEO ＝∠BDO ，在△BDO 和△CEO 中，，∴△BDO ≌△CEO （AAS ）；（2）解：∵△BDO ≌△CEO ，∴BD ＝CE ，∵BD ＝4，∴CE ＝4，∵AC ＝6，∴AE ＝6﹣4＝2．5．（2022•宜兴市校级二模）已知：如图，在△ABC 中，D 是BC 边中点，CE ⊥AD 于点E ，BF ⊥AD 于点F ．（1）求证：△BDF ≌△CDE ；（2）若AD ＝5，CE ＝2，求△ABC 的面积．【分析】（1）易证BD ＝CD ，∠BFD ＝∠CED ＝90°，再由AAS 即可证得△BDF ≌△CDE ；（2）由S △ABC ＝S △ABD +S △ACD ，即可得出结果．【解答】（1）证明：∵D 是BC 边中点，∴BD ＝CD ，∵CE ⊥AD ，BF ⊥AD ，∴∠BFD ＝∠CED ＝90°，在△BDF 和△CDE 中，，∴△BDF ≌△CDE （AAS ）；（2）解：由（1）得：△BDF ≌△CDE ，∴CE ＝BF ，∴S △ABC ＝S △ABD +S △ACD ＝AD •BF +AD •CE ＝AD •CE ＝5×2＝10．6．（2022•太仓市模拟）如图，AB ＝AC ，BE ⊥AC ，CD ⊥AB 垂足分别为点E ，点D ．（1）求证：△ABE ≌△ACD ；（2）若AB ＝13，AE ＝5，求CD 的长度．【分析】（1）利用AAS 即可证明结论；（2）根据勾股定理可得BE ＝12，再根据全等三角形对应边相等即可解决问题．【解答】（1）证明：∵BE ⊥AC ，CD ⊥AB ，∴∠ADC ＝∠AEB ＝90°，在△ABE 和△ACD 中，，∴△ABE ≌△ACD （AAS ）；（2）在Rt △ABE 中，AB ＝13，AE ＝5，∴BE＝＝12，∵△ABE≌△ACD，∴CD＝BE＝12．7．（2022•金坛区一模）如图，D是△ABC的边AB上一点，CF∥AB，DF交AC于点E，DE＝EF．（1）求证：AE＝EC；（2）若AB＝5，CF＝4，求BD的长．【分析】（1）证明△ADE≌△CFE（AAS），即可得出结论；（2）由全等三角形的性质得AD＝CF＝4，即可得出答案．【解答】（1）证明：∵CF∥AB，∴∠A＝∠ECF，在△ADE和△CFE中，∴△ADE≌△CFE（AAS），∴AE＝EC；（2）解：由（1）可知，△ADE≌△CFE，∴AD＝CF＝4，∴BD＝AB﹣AD＝5﹣4＝1，即BD的长为1．8．（2021秋•鼓楼区校级期末）如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAD＝∠CAE．求证：∠ABD＝∠ACE．【分析】由“SAS”可证△ABD≌△ACE，可得结论．【解答】证明：在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴∠ABD＝∠ACE．9．（2021秋•淮安区期末）如图，已知AB＝CB，AD＝CD．求证：∠A＝∠C．【分析】连接BD，利用边边边证明△ABD≌△CBD，由全等三角形的性质即可求解．【解答】证明：连接BD，在△ABD与△CBD中，，∴△ABD≌△CBD（SSS），∴∠A＝∠C．10．（2021秋•沭阳县校级期末）如图，已知AD＝AE，AB＝AC．求证：BE＝CD．【分析】已知两边和它们的夹角对应相等，由SAS即可判定两三角形全等，进而利用全等三角形的性质解答．【解答】证明：在△AEB与△ADC中，，∴△AEB≌△ADC（SAS），∴BE＝CD．11．（2020秋•常州期末）已知：如图，AB＝AE，AB∥DE，∠ECB+∠D＝180°．求证：△ABC≌△EAD．【分析】根据全等三角形的判定方法解答即可．【解答】证明：∵AB∥DE，∴∠CAB＝∠E，∵∠ECB+∠D＝180°，∠ECB+∠ACB＝180°，∴∠D＝∠ACB，在△ABC与△EAD中，，∴△ABC≌△EAD（AAS）．12．（2020秋•苏州期末）如图，点E、F在AB上，且AE＝BF，∠C＝∠D，AC∥BD．求证：CF∥DE．【分析】根据已知条件证明△ACF≌△BDE可得∠AFC＝∠BED，进而可得CF∥DE．【解答】证明：∵AE＝BF，∴AE+EF＝BF+EF，即AF＝BE，∵AC∥BD，∴∠A＝∠B，在△ACF和△BDE中，，∴△ACF≌△BDE（AAS），∴∠AFC＝∠BED，∴CF∥DE．13．（2020秋•建邺区期末）如图，在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，点A、E、B、D在同一直线上，BC、EF交于点M，AC＝DF，AB＝DE．求证：（1）∠CBA＝∠FED；（2）AM＝DM．【分析】（1）利用HL证明Rt△ABC≌Rt△DEF可证明结论；（2）利用SAS证明△AEM≌△DBM可证明结论．【解答】证明：（1）在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，，∴Rt△ABC≌Rt△DEF（HL），∴∠CBA＝∠FED；（2）∵∠CBA＝∠FED，∴ME＝MB，且∠AEM＝∠DBM，∵AB＝DE，∴AB﹣EB＝DE﹣EB，即AE＝DB，在△AEM和△DBM中，，∴△AEM≌△DBM（SAS），∴AM＝DM．14．（2021•苏州模拟）如图，点B，F，C，E在一条直线上，AB＝DE，∠B＝∠E，BF＝CE．求证：CG＝FG．【分析】由“SAS”可证△ABC≌△DEF，可得∠ACB＝∠DFE，可得结论．【解答】证明：∵BF＝CE∴BF+CF＝CE+CF∴BC＝EF在△ABC和△DEF中∴△ABC≌△DEF（SAS）∴∠ACB＝∠DFE∴CG＝FG15．（2021•苏州模拟）如图，在△ABC中，AB＝AC，AD⊥BC于点D，BE⊥AC于点E，AD、BE相交于点H，AE＝BE．试说明：（1）△AEH≌△BEC．（2）AH＝2BD．【分析】（1）由“ASA”可证△AEH≌△BEC；（2）由全等三角形的性质可得AH＝BC，由等腰三角形的性质可得结论．【解析】（1）∵AD⊥BC，∴∠DAC+∠C＝90°，∵BE⊥AC，∴∠EBC+∠C＝90°，∴∠DAC＝∠EBC，在△AEH与△BEC中，，∴△AEH≌△BEC（ASA）；（2）∵△AEH≌△BEC，∴AH＝BC，∵AB＝AC，AD⊥BC，∴BC＝2BD，∴AH＝2BD．16．（2021•洪泽区二模）如图，线段AC交BD于O，点E，F在线段AC上，△DFO≌△BEO，且AF＝CE，连接AB、CD，求证：AB＝CD．【分析】先由△BEO≌△DFO，即可得出OF＝OE，DO＝BO，进而得到AO＝CO，再证明△ABO≌△CDO，即可得到AB＝CD．【解答】证明：∵△BEO≌△DFO，∴OF＝OE，DO＝BO，又∵AF＝CE，∴AO＝CO，在△ABO和△CDO中，，∴△ABO≌△CDO（SAS），∴AB＝CD．17．（2020秋•盐池县期末）如图，点E在CD上，BC与AE交于点F，AB＝CB，BE＝BD，∠1＝∠2．（1）求证：△ABE≌△CBD；（2）证明：∠1＝∠3．【分析】（1）由已知角相等，利用等式的性质得到夹角相等，利用SAS即可得证；（2）利用全等三角形对应角相等得到一对角相等，再由对顶角相等及内角和定理即可得证．【解答】证明：（1）∵∠1＝∠2，∴∠1+∠CBE＝∠2+∠CBE，即∠ABE＝∠CBD，在△ABE和△CBD中，，∴△ABE≌△CBD（SAS）；（2）∵△ABE≌△CBD，∴∠A＝∠C，∵∠AFB＝∠CFE，∴∠1＝∠3．18．（2020秋•泰兴市期末）如图，AC⊥BC，DC⊥EC，AC＝BC，DC＝EC，图中AE、BD有怎样的大小和位置关系？试证明你的结论．【分析】根据SAS即可求得△DCB≌△ECA，求得∠B＝∠A．因为∠AND＝∠BNC，根据三角形的内角和定理就可求得∠A+∠AND＝90°，从而证得BD⊥AE．【解析】AE＝BD，AE⊥BD，如图，∵∠ACB＝∠DCE＝90°，∠ACD＝∠ACD，∴∠DCB＝∠ECA，在△DCB和△ECA中，，∴△DCB≌△ECA（SAS），∴∠A＝∠B，BD＝AE∵∠AND＝∠BNC，∠B+∠BNC＝90°∴∠A+∠AND＝90°，∴BD⊥AE．19．（2021秋•台安县期中）如图，在四边形ABCD中，AB∥CD，∠1＝∠2，AD＝EC．（1）求证：△ABD≌△EDC；（2）若AB＝2，BE＝3，求CD的长．【分析】（1）由“AAS”即可证△ABD≌△EDC；（2）结合（1）可得AB＝DE，BD＝CD，可得结论．【解答】（1）证明：∵AB∥CD，∴∠ABD＝∠EDC．在△ABD和△EDC中，，∴△ABD≌△EDC（AAS），（2）∵△ABD≌△EDC，∴AB＝DE＝2，BD＝CD，∴CD＝BD＝DE+BE＝2+3＝5．20．（2021•姑苏区一模）如图，已知AB＝DC，AB∥CD，E、F是AC上两点，且AF＝CE．（1）求证：△ABE≌△CDF；（2）连接BC，若∠CFD＝100°，∠BCE＝30°，求∠CBE的度数．【分析】（1）根据SAS证明即可．（2）利用全等三角形的性质以及三角形内角和定理解决问题即可．【解答】（1）证明：∵AB∥CD，∴∠A＝∠DCF，∵AF＝CE，∴AE＝CF，在△ABE和△CDF中，，∴△ABE≌△CDF（SAS）．（2）∵△ABE≌△CDF，∴∠AEB＝∠CFD＝100°，∴∠BEC＝180°﹣100°＝80°，∴∠CBE＝180°﹣80°﹣30°＝70°．。

全等三角形判定的方法(培优)

全等三角形判定（考试重点）姓名：班级：分数： 1．已知AC =BD ，AE =CF ，BE =DF ，证明：AE ∥CF 。

2、已知在四边形ABCD 中，AB =CD ，AD =CB ，证明：AB ∥CD 。

3、已知CD ∥AB ，DF ∥EB ，DF =EB ，证明：AF =CE 。

4、已知ED ⊥AB ，EF ⊥BC ，BD =EF ，证明：BM =ME 。

ACBDEFBADC EF BAC M EFBD5、点C 是AB 的中点，CD ∥BE ，且CD =BE ，证明：∠D =∠E 。

6、在⊿ABC 中，高AD 与BE 相交于点H ，且AD =BD ，证明：⊿BHD ≌⊿ACD 。

7已知AD =AE ，∠B =∠C ，证明：AC =AB 。

8、已知CE ⊥AB ，DF ⊥AB ，CE =DF ，AE =BF ，证明：⊿CEB ≌⊿DF A 。

ABCE HD ADEBCBACDEFD A ECB 129、如图：在△ABC 中，∠C=90°，AC=BC ，过点C 在△ABC 外作直线MN ，AM ⊥MN 于M ，BN ⊥MN 于N 。

求证：MN=AM+BN 。

10、已知，AC ⊥CE ，AC =CE ， ∠ABC =∠DEC =900，求证：BD =AB +ED 。

11、已知AD 是⊿ABC 的中线，BE ⊥AD ，CF ⊥AD ，求证：BE =CF 。

12、已知∠BAC =∠DAE ，∠1=∠2，BD =CE ，求证：ABD ≌⊿ACE 。

NMCBAABCDEABCD FEADEBC12【知识点梳理】知识点一：全等三角形的概念——能够完全重合的两个三角形叫全等三角形.知识点二：全等三角形的性质.（1）全等三角形的对应边相等. （2）全等三角形的对应角相等.知识点三：判定两个三角形全等的方法.（1）SSS （2）SAS （3）ASA （4）AAS （5）HL（只对直角三形来说）知识点四：寻找全等三形对应边、对应角的规律.①全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边.②全等三角形对应边所对的角是对应角，两个对应边所夹的角是对应角.③有公共边的，公共边一定是对应边. ④有公共角的，公共角一定是对应角.⑤有对顶角的，对顶角是对应角.⑥全等三角形中的最大边（角）是对应边（角），最小边（角）是对应边（角）.知识点五：找全等三角形的方法.（1）一般来说，要证明相等的两条线段（或两个角），可以从结论出发，看它们分别落在哪两具可能的全等三角形中.（常用的办法）（2）可以从已知条件出发，看已知条件可以确定哪两个三角形相等.（3）可以从已知条件和结论综合考虑，看它们能否一同确定哪两个三角形全等.（4）如无法证证明全等时，可考虑作辅助线的方法，构造成全等三角形.知识点六：角平分线的性质及判定.（1）角平分线的性质：角平分线上的点到角两边的距离相等.（2）角平分线的判定：在角的内部到角的两边距离相等的点在角平分线上.（3）三角形三个内角平分线性质：三角形三条角平分线交于一点，且到三角形三边距离相等.知识点七：证明线段相等的方法.（重点）（1）中点性质（中位线、中线、垂直平分线）（2）证明两个三角形全等，则对应边相等（3）借助中间线段相等.知识点八：证明角相等的方法.（重点）（1）对顶角相等；（2）同角或等角的余角（或补角）相等；（3）两直线平行，内错角相等、同位角相等；（4）角平分线的定义；（5）垂直的定义；（6）全等三角形的对应角相等；（7）三角形的外角等于与它不相邻的两内角和.。

全等三角形专题培优(带答案)

全等三角形专题培优测验总分： 110 分测验时光： 120 分钟卷I（选择题）一.选择题（共 10 小题,每小题2 分,共 20 分）1.如图为个边长相等的正方形的组合图形,则A. B.C. D.2.下列定理中逆定理不消失的是（）B.在一个三角形中,假如双方相等,那么它们所对的角也相等C.同位角相等,两直线平行3.已知：如图,,,,则不准确的结论是（）B.C.D.4.如图,是的中位线,延伸至使,衔接,则的值为（）A. B. C. D.5.如图,在平面直角坐标系中,在轴.轴的正半轴上分离截取.,使;再分离以点.为圆心,以大于长为半径作弧,两弧交于点．若点的坐标为,则与的关系为（）A. B.C. D.6.如图,是等边三角形,,于点,于点,,则下列结论：①点在的角等分线上; ②;③;④．准确的有（）7.如图,直线..″暗示三条互订交叉的公路,现筹划建一个加油站,请求它到三条公路的距离相等,则可供选择的地址有（）8.如图,是的角等分线,则等于（）A. B.C. D.9.已知是的中线,且比的周长大,则与的差为（）A. B.C. D.10.若一个三角形的两条边与高重合,那么它的三个内角中（）卷II（非选择题）二.填空题（共 10 小题,每小题2 分,共 20 分）11.问题情境：在中,,,点为边上一点（不与点,重合）,交直线于点,衔接,将线段绕点顺时针偏向扭转得到线段（扭转角为）,衔接．特例剖析：如图．若,则图中与全等的一个三角形是________,的度数为________．类比探讨：请从下列,两题中任选一题作答,我选择________题．：如图,当时,求的度数;：如图,当时,①猜测的度数与的关系,用含的式子暗示猜测的成果,并证实猜测;②在图中将“点为边上的一点”改为“点在线段的延伸线上”,其余前提不变,请直接写出的度数（用含的式子暗示,不必证实）12.如图,正方形纸片的边长为,点.分离在边.上,将.分离沿.折叠,点.正好都落在点处,已知,则的长为________．13.在中,为的等分线,于,于,面积是,,,则的长为________．14.在中,,的垂直等分线与地点的直线订交所得到锐角为,则等于________．15.如图,等分,于,于,,则图中有________对全等三角形．16.如图,在中,,点从点动身沿射线偏向,在射线上活动．在点活动的进程中,贯穿连接,并认为边在射线上方,作等边,贯穿连接．当________时,;请添加一个前提：________,使得为等边三角形;①如图,当为等边三角形时,求证：;②如图,当点活动到线段之外时,其它前提不变,①中结论还成立吗？请解释来由．17.如图,从圆外一点引圆的两条切线,,切点分离为,．假如,,那么弦的长是________．18.如图,在中,,,是的等分线,等分交于,则________．19.浏览下面材料：小聪碰到如许一个有关角等分线的问题：如图,在中,,等分,,求的长．小聪思虑：因为等分,所以可在边上取点,使,衔接．如许很轻易得到,经由推理能使问题得到解决（如图）．请答复：是________三角形．的长为________．参考小聪思虑问题的办法,解决问题：如图,已知中,,,等分,,．求的长．20.如图,在和中,,,若要用“斜边直角边．．”直接证实,则还需填补前提：________．三.解答题（共 7 小题,每小题10 分,共 70 分）21.如图,已知为等边三角形,为延伸线上的一点,等分,,求证：为等边三角形．22.尺规作图（不请求写作法,保存作图陈迹）如图,作①的等分线; ②边上的中线;22.一块三角形外形的玻璃决裂成如图所示的三块,请你用尺规作图作一个三角形,使所得的三角形和本来的三角形全等．（不请求写作法,保存作图陈迹．不克不及在原图上作三角形）22.如图：在正方形网格中有一个,按请求进行下列绘图（只能借助于网格）：①画出中边上的高（需写出结论）．②画出先将向右平移格,再向上平移格后的．23.平行四边形中,,点为边上一点,贯穿连接,点在边地点直线上,过点作交于点．如图,若为边中点,交延伸线于点,,,,求;如图,若点在边上,为中点,且等分,求证：;如图,若点在延伸线上,为中点,且,问中结论还成立吗？若不成立,那么线段..知足如何的数目关系,请直接写出结论．24.如图,直线与轴.轴分离交于.两点,直线与直线关于轴对称,已知直线的解析式为,求直线的解析式;过点在的外部作一条直线,过点作于,过点作于,请画出图形并求证：;沿轴向下平移,边交轴于点,过点的直线与边的延伸线订交于点,与轴订交于点,且,在平移的进程中,①为定值;②为定值．在这两个结论中,有且只有一个是准确的,请找出准确的结论,并求出其值．25.如图：,,过点,于,于,．求证：．26.如图,点,在上,,,,与交于点．求证：;试断定的外形,并解释来由．27.如图,已知点是等分线上一点,,,垂足为.吗？为什么？是的垂直等分线吗？为什么？答案11.[“”,“”][“”]12.[“”]13.[“”]14.[“或”]15.[“”]16.[“;”][ "添加一个前提,可得为等边三角形;故答案为：;①∵与是等边三角形,∴,,,∴,即,在与中,,∴,∴;②成立,来由如下;∵与是等边三角形,∴,,,∴,即,在与中,,∴,∴．" ]17.[“”]18.[“”]19.[ "解：是等腰三角形,在与中,,∴,∴,,∵,∴,∴,∴是等腰三角形;" ][ "的长为,∵中,,,∴,∵等分,∴,在边上取点,使,衔接,则,∴,∴,∴,在边上取点,使,衔接,则,∴,,∵,∴,∴,∵,∴．" ]\"go题库\"20.[“”]21.证实：∵为等边三角形,∴,,即,∵等分,∴,在和中,,∴,∴,,又,∴,∴为等边三角形．22.解：如图所示：;如图所示：即为所求;;①如图所示：即为所求;②如图所示：即为所求;．．23.解：如图,在平行四边形中,,∴,∵在中,为的中点,,∴,又∵,∴,故可设,,则中,,解得,∴,又∵,,∴为的中点,∴;如图,延伸交的延伸线于点,则,∵,∴,又∵等分,∴,∴是等腰直角三角形,∴,又∵,∴,∴,,又∵为的中点,∴,∴,∴,∵,∴;若点在延伸线上,为中点,且,则中的结论不成立,准确结论为：．证实：如图,延伸交的延伸线于点,则,∵,∴,∴,又∵,∴,∴,,又∵为的中点,∴,∴,∴,∵,∴．24.解：∵直线与轴.轴分离交于.两点,∴,,∵直线与直线关于轴对称,∴∴直线的解析式为：;如图．．∵直线与直线关于轴对称,∴,∵与为象限等分线的平行线,∴与为等腰直角三角形,∴,∵,∴∴∴,,∴;①对,过点作轴于,直线与直线关于轴对称∵,,又∵,∴,则,∴∴∴∴∴．25.证实：衔接,∵,∴,∵,∴,∴,∵,,∴,在和中,∴．26.证实：∵,∴,即．又∵,,∴,∴．解：为等腰三角形来由如下：∵,∴,∴,∴为等腰三角形．27.解：．来由：∵是的等分线,且,,∴,∴;是的垂直等分线．来由：∵,在和中,,∴,∴,由,,可知点.都是线段的垂直等分线上的点,从而是线段的垂直等分线．。

武汉市七一中学八年级数学上册第十二章《全等三角形》经典练习题(培优)

一、选择题1．如图，在ABC 中，AB AC =，点D ，E 在BC 上，连接AD ，AE ，若只添加一个条件使DAB EAC ∠=∠，则添加的条件不能为（）A ．BD CE =B ．AD AE =C ．BE CD = D ．DA DE = D解析：D【分析】根据全等三角形的判定与性质，等边对等角的性质对各选项分析判断后利用排除法求解．【详解】解：A 、添加BD ＝CE ，可以利用“边角边”证明△ABD 和△ACE 全等，再根据全等三角形对应角相等得到∠DAB ＝∠EAC ，故本选项不符合题意；B 、添加AD ＝AE ，根据等边对等角可得∠ADE ＝∠AED ，然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠DAB ＝∠EAC ，故本选项不符合题意；C 、添加BE ＝CD 可以利用“边角边”证明△ABE 和△ACD 全等，再根据全等三角形对应角相等得到∠BAE=∠CAD ，可得∠DAB ＝∠EAC ，故本选项不符合题意；D 、添加DA ＝DE 无法求出∠DAB ＝∠EAC ，故本选项符合题意．故选：D ．【点睛】本题考查了等腰三角形等边对等角的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解题的关键．2．如图所示，下面甲、乙、丙三个三角形和ABC 全等的图形是（）A ．甲和乙B ．乙和丙C ．只有丙D ．只有乙B解析：B【分析】甲只有2个已知条件，缺少判定依据；乙可根据SAS 判定与△ABC 全等；丙可根据AAS 判定与△ABC 全等，可得答案．【详解】解：甲三角形只知道两条边长无法判断是否与△ABC 全等；乙三角形夹50°内角的两边分别与已知三角形对应相等，故乙与△ABC 全等；丙三角形72°内角及所对边与△ABC 对应相等且均有50°内角，可根据AAS 判定乙与△ABC 全等；则与△ABC 全等的有乙和丙，故选：B ．【点睛】本题主要考查全等三角形的判定定理，熟练掌握并充分理解三角形全等的判定定理，注意对应二字的理解很重要．3．如图所示的正方形ABCD 中，点E 在边CD 上，把ADE 绕点A 顺时针旋转得到ABF ，20FAB ∠=︒．旋转角的度数是（）A ．110°B ．90°C ．70°D ．20°B解析：B【分析】根据正方形的性质得到AB=AD ，∠BAD=90︒，由旋转的性质推出ADE ≌ABF ，求出∠FAE=∠BAD=90︒，即可得到答案．【详解】∵四边形ABCD 是正方形，∴AB=AD ，∠BAD=90︒，由旋转得ADE ≌ABF ，∴∠FAB=∠EAD ，∴∠FAB+∠∠BAE=∠EAD+∠BAE ，∴∠FAE=∠BAD=90︒，∴旋转角的度数是90︒，故选：B ．【点睛】此题考查旋转的性质，全等三角形的性质，熟记全等三角形的性质是解题的关键． 4．下列说法正确的是（）A ．两个长方形是全等图形B ．形状相同的两个三角形全等C ．两个全等图形面积一定相等D ．所有的等边三角形都是全等三角形C解析：C【分析】性质、大小完全相同的两个图形是全等形，根据定义解答．【详解】A 、两个长方形的长或宽不一定相等，故不是全等图形；B 、由于大小不一定相同，故形状相同的两个三角形不一定全等；C 、两个全等图形面积一定相等，故正确；D 、所有的等边三角形大小不一定相同，故不一定是全等三角形；故选：C ．【点睛】此题考查全等图形的概念及性质，熟记概念是解题的关键．5．如图，AD 是ABC 的角平分线，:4:3AB AC ，则ABD △与ACD △的面积比为（）．A ．4:3B ．16:9C ．3:4D ．9:16A解析：A【分析】过点D 作DE 垂直于AB ，DF 垂直于AC ，由AD 为角BAC 的平分线，根据角平分线定理得到DE=DF ，再根据三角形的面积公式表示出△ABD 与△ACD 的面积之比，把DE=DF 以及AB ：AC 的比值代入即可求出面积之比．【详解】解：过点D 作DE ⊥AB 于E ，DF ⊥AC 于F ．∵AD 为∠BAC 的平分线，∴DE=DF ，又AB ：AC=4：3，∴S △ABD ：S △ACD =（12AB•DE ）：（12AC•DF ）=AB ：AC=4：3．故选：A ．【点睛】本题考查了角平分线的性质定理：角平分线上的点到角两边的距离相等．此类题经常过角平分线上作角两边的垂线，这样可以得到线段的相等，再结合其他的条件探寻结论解决问题．6．下列命题中，假命题是（）A ．在同一平面内，垂直于同一条直线的两直线平行B ．到线段两端点距离相等的点在这条线段的垂直平分线上C ．一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等D．一边长相等的两个等腰直角三角形全等D解析：D【分析】根据垂线的性质，线段垂直平分线的判定，全等三角形的判定对各选项分析判断后利用排除法求解．【详解】A、同一平面内，垂直于同一条直线的两直线互相平行，真命题，本选项不符合题意；B、到线段两端点距离相等的点在这条线段的垂直平分线上，真命题，本选项不符合题意；C、一条直角边和另一条直角边上的中线对应相等的两个直角三角形，首先根据“HL”定理，可判断两个小直角三角形全等，可得另一条直角边相等，然后，根据“SAS”，可判断两个直角三角形全等，真命题，本选项不符合题意；D、有一边相等的两个等腰直角三角形不一定全等，如：一个等腰直角三角形的直角边与另一个等腰直角三角形的斜边相等，这两个等腰直角三角形并不全等，假命题，本选项符合题意．故选：D．【点睛】本题考查了命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．7．如图，已知AC⊥BC，DE⊥AB，AD平分∠BAC，下面结论错误的是（）A．BD＋ED＝BC B．∠B＝2∠DACC．AD平分∠EDC D．ED＋AC>AD B解析：B【分析】利用角平分线的性质定理判断A；利用直角三角形两锐角互余判断B；证明△AED≌△ACD，由此判断C；利用三角形三边关系得到AC+CD>AD，由此判断D．【详解】∵AC⊥BC，DE⊥AB，AD平分∠BAC，∴DE=DC，∠BAD=∠DAC，∵BD+DC=BC，∴BD+ED=BC，故A正确；∵∠C=90︒，∴∠B+∠BAC=90︒，∴∠B+2∠DAC=90︒，故B错误；∵DE ⊥AB ，∴∠AED=∠C=90︒,又∵∠BAD=∠DAC ，DE=CD ，∴△AED ≌△ACD ，∴∠ADE=∠ADC ，∴AD 平分∠EDC ，故C 正确；在△ACD 中，AC+CD>AD ，∴ED ＋AC >AD ，故D 正确；故选：B ．【点睛】此题考查三角形的三边关系，角平分线的性质定理，全等三角形的判定及性质，直角三角形两锐角互余的性质，熟记各知识点并应用解决问题是解题的关键．8．已知：如图，BD 为△ABC 的角平分线，且BD=BC ，E 为BD 延长线上的一点，BE=BA ，过E 作EF ⊥AB ，F 为垂足，下列结论：①△ABD ≌△EBC②∠BCE+∠BCD=180°③AD=AE=EC ④ BA+BC=2BF 其中正确的是（）A ．①②③B ．①③④C ．①②④D ．①②③④D解析：D【分析】易证ABD EBC ∆∆≌，可得BCE BDA ∠=∠，AD=EC 可得①②正确；再根据角平分线的性质可求得DAE DCE ∠=∠ ，即③正确，根据③可判断④正确；【详解】∵ BD 为∠ABC 的角平分线，∴ ∠ABD=∠CBD ，∴在△ABD 和△EBD 中，BD=BC ，∠ABD=∠CDB ，BE=BA ，∴△ABD EBC ∆∆≌(SAS)，故①正确；∵ BD 平分∠ABC ，BD=BC ，BE=BA ，∴ ∠BCD=∠BDC=∠BAE=∠BEA ，∵△ABD ≌△EBC ，∴∠BCE=∠BDA ，∴∠BCE+∠BCD=∠BDA+∠BDC=180°，故②正确；∵∠BCE=∠BDA ，∠BCE=∠BCD+∠DCE ，∠BDA=∠DAE+∠BEA，∠BCD=∠BEA，∴∠DCE=∠DAE，∴△ACE是等腰三角形，∴AE=EC，∵△ABD≌△EBC，∴AD=EC，∴AD=AE=EC，故③正确；作EG⊥BC，垂足为G，如图所示：∵ E是BD上的点，∴EF=EG，在△BEG和△BEF中BE BE EF EG=⎧⎨=⎩∴△BEG≌△BEF，∴BG=BF，在△CEG和△AFE中EF EG AE CE=⎧⎨=⎩∴△CEG≌△AFE，∴ AF=CG，∴BA+BC=BF+FA+BG-CG=BF+BG=2BF，故④正确；故选：D．【点睛】本题考查了全等三角形的判定，全等三角形对应边、对应角相等的性质，本题中熟练求证三角形全等和熟练运用全等三角形对应边、对应角相等的性质是解题的关键；9．如图，在ABC中，B C∠=∠，E、D、F分别是AB、BC、AC上的点，且BE CD=，BD CF=，若104A∠=︒，则EDF∠的度数为（）A ．24°B ．32°C ．38°D ．52°C解析：C【分析】根据题意可证明BDE CFD ≌，以及求解∠B 的度数，再由三角形的外角性质和全等三角形的性质推出∠EDF=∠B ，从而得出结果．【详解】在BDE 与CFD 中，BE CD B C BD CF =⎧⎪∠=∠⎨⎪=⎩∴()BDE CFD SAS ≌∴∠BED=∠CDF ，又∵∠B+∠BED=∠EDC=∠EDF+∠CDF ，∴∠B=∠EDF ，∵在BAC 中，∠A=104°，∠B=∠C ，∴∠B=（180°-104°）÷2=38°，∴∠EDF=38°，故选：C ．【点睛】本题考查全等三角形的判定与性质，三角形的内角和定理与外角性质，熟练证明全等并利用其性质进行推理演算是解题关键．10．如图，在△ABC 中，点E 和F 分别是AC ，BC 上一点，EF ∥AB ，∠BCA 的平分线交AB 于点D ，∠MAC 是△ABC 的外角，若∠MAC ＝α，∠EFC ＝β，∠ADC ＝γ，则α、β、γ三者间的数量关系是（）A ．β＝α+γB ．β＝2γ﹣αC ．β＝α+2γD ．β＝2α﹣2γB解析：B【分析】根据平行线的性质得到∠B=∠EFC=β，由角平分线的定义得到∠ACB=2∠BCD ，根据∠ADC 是△BDC 的外角，得到∠ADC=∠B+∠BCD ，由三角形外角的性质得到∠MAC=∠B+∠ACB ，于是得到结果．【详解】解：∵EF ∥AB ，∠EFC=β，∴∠B=∠EFC=β，∵CD平分∠BCA，∴∠ACB=2∠BCD，∵∠ADC是△BDC的外角，∴∠ADC=∠B+∠BCD，∵∠ADC=γ，∴∠BCD=γ-β，∵∠MAC是△ABC的外角，∴∠MAC=∠B+∠ACB，∵∠MAC=α，∴α=β+2（γ-β），∴β=2γ-α，故选：B．【点睛】本题考查了三角形外角的性质，角平分线的定义，平行线的性质，正确的识别图形是解题的关键．二、填空题11．如图所示，在ABC中，D是BC的中点，点A、F、D、E在同一直线上．请添加一个条件，使BDE CDF≌（不再添其他线段，不再标注或使用其他字母），并给出证明．你添加的条件是______ED=FD（答案不唯一∠E=∠CFD或∠DBE=∠DCF）【分析】根据三角形全等的判定方法SAS或AAS或ASA定理添加条件然后证明即可【详解】解：∵D是的中点∴BD=DC①若添加ED=FD在△BD解析：ED=FD（答案不唯一，∠E=∠CFD或∠DBE=∠DCF）【分析】根据三角形全等的判定方法SAS或AAS或ASA定理添加条件，然后证明即可．【详解】解：∵D是BC的中点，∴BD=DC①若添加ED=FD在△BDE和△CDF中，BD CDBDE CDF ED FD=⎧⎪∠=∠⎨⎪=⎩，∴△BDE≌△CDF（SAS）；②若添加∠E=∠CFD在△BDE 和△CDF 中，BDE CDF E CFD BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BDE ≌△CDF （AAS ）；③若添加∠DBE=∠DCF在△BDE 和△CDF 中，BDE CDF BD CD DBE DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△BDE ≌△CDF （ASA ）；故答案为：ED=FD （答案不唯一，∠E=∠CFD 或∠DBE=∠DCF ）．【点睛】本题考查了全等三角形的判定，熟练掌握三角形全等的判定方法是解题的关键． 12．如图，在Rt ABC △中，90C ∠=︒，10AC =，5BC =，线段PQ AB =，P ，Q 两点分别在线段AC 和过点A 且垂直于AC 的射线AD 上运动，当AQ =______时，ABC 和PQA △全等．5或10【分析】分两种情况：当AQ=5时当AQ=10时利用全等三角形的判定及性质定理得到结论【详解】分两种情况：当AQ=5时∵∴AQ=BC ∵AD ⊥AC ∴∠QAP=∠ACB=∵AB=PQ ∴≌△PQA （解析：5或10【分析】分两种情况：当AQ=5时，当AQ=10时，利用全等三角形的判定及性质定理得到结论．【详解】分两种情况：当AQ=5时，∵5BC =，∴AQ=BC ，∵AD ⊥AC ，∴∠QAP=∠ACB=90︒，∵AB=PQ ，∴ABC ≌△PQA （HL ）；当AQ=10时，∵10AC =，∴AQ=AC ，∵AD ⊥AC ，∴∠QAP=∠ACB=90︒，∵AB=PQ ，∴△ABC ≌△QPA ，故答案为：5或10．【点睛】此题考查全等三角形的判定及性质定理，运用分类思想，动点问题，熟记三角形的判定定理及性质定理是解题的关键．13．如图，AB 与CD 相交于点O ，OC ＝OD ．若要得到△AOC ≌△BOD ，则应添加的条件是__________．（写出一种情况即可）OA=OB （答案不唯一）【分析】全等三角形的判定方法有SASASAAASSSS 只要添加一个符合的条件即可【详解】解：OA=OB 理由是：在△AOC 和△BOD 中∴△AOC ≌△BOD （SAS ）故答案为：O解析：OA=OB ．（答案不唯一）【分析】全等三角形的判定方法有SAS ，ASA ，AAS ，SSS ，只要添加一个符合的条件即可．【详解】解：OA=OB ，理由是：在△AOC 和△BOD 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，∴△AOC ≌△BOD （SAS ）．故答案为：OA=OB ．（答案不唯一）【点睛】本题考查了全等三角形的判定的应用，通过做此题培养了学生的发散思维能力和对全等三角形的判定方法的灵活运用能力，题目答案不唯一，是一道比较好的题目．14．如图，AB ，CD 交于点O ，AD ∥BC ．请你添加一个条件_____，使得△AOD ≌△BOC ．OA ＝OB （答案不唯一）【分析】由AD ∥BC 可得∠A ＝∠B ∠C ＝∠D 然后根据全等三角形的判定方法添加条件即可【详解】解：添加的条件是OA ＝OB 理由如下：∵AD ∥BC ∴∠A ＝∠B ∠C ＝∠D 在△AOD 和解析：OA ＝OB （答案不唯一）【分析】由AD ∥BC 可得∠A ＝∠B ，∠C ＝∠D ,然后根据全等三角形的判定方法添加条件即可．【详解】解：添加的条件是OA ＝OB ，理由如下：∵AD ∥BC ，∴∠A ＝∠B ，∠C ＝∠D在△AOD 和△BOC 中A B AO BO AOD BOC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AOD ≌△BOC （ASA ）．故答案为：OA ＝OB （答案不唯一）．【点睛】本题主要考查了全等三角形的判定定理和平行线的性质，掌握全等三角形的判定定理的内容是解答本题的关键．15．如图，在ABC 中，90C ∠=︒，AD 平分BAC ∠，交BC 边于点D ，若12AB =，4CD =，则ABD △ 的面积为__________．24【分析】过D 作DE ⊥AB 垂足为E 根据角平分线定理可得DE=CD=4然后根据三角形的面积公式计算即可【详解】解：如图：过D 作DE ⊥AB 垂足为E ∵AD 平分交BC 边于点D ∴DE=CD=4∴的面积为AB解析：24【分析】过D 作DE ⊥AB 垂足为E ，根据角平分线定理可得DE=CD=4,然后根据三角形的面积公式计算即可．【详解】解：如图：过D 作DE ⊥AB 垂足为E ，∵90C ∠=︒，AD 平分BAC ∠，交BC 边于点D ，∴DE=CD=4，∴ABD △ 的面积为12AB·DE=12×12×4=24．故答案为：24．【点睛】本题主要考查了角平分线的性质定理，正确作出辅助线、构造角平分线定理所需条件成为解答本题的关键．16．如图，在ABC 中，AD 平分BAC ∠，P 为线段AD 上的一个动点，PE AD ⊥交直线BC 于点E ．若35B ∠=︒，85ACB ∠=︒，则E ∠的度数为______． 25°【分析】利用三角形内角和定理得出∠BAC 的度数进而得出∠ADC 的度数再利用三角形内角和定理和外角性质得出即可【详解】解：∵∠B=35°∠ACB=85°∴∠BAC=60°∵AD 平分∠BAC ∴∠B解析：25°【分析】利用三角形内角和定理得出∠BAC 的度数，进而得出∠ADC 的度数，再利用三角形内角和定理和外角性质得出即可．【详解】解：∵∠B=35°，∠ACB=85°，∴∠BAC=60°，∵AD 平分∠BAC ，∴∠BAD=30°，∴∠ADC=35°+30°=65°，∵∠EPD=90°，∴∠E 的度数为：90°-65°=25°．故答案为：25°．【点睛】此题主要考查了三角形内角和定理以及角平分线的性质和三角形外角的性质，根据已知得出∠BAD 度数是解题关键．17．如图，△ACB 和△DCE 中，AC ＝BC ，∠ACB ＝∠DCE ＝90°，∠ADC ＝∠BEC ，若AB ＝17，BD ＝5，则S △BDE ＝_______．30【分析】根据∠ACB ＝∠DCE ＝90°可得∠ACD ＝∠BCE 利用三角形全等判定可得△ACD ≌△BCE 则BE ＝AD ∠DAC ＝∠EBC 再证明∠DBE ＝90°根据三角形面积计算公式便可求得结果【详解】解析：30【分析】根据∠ACB ＝∠DCE ＝90°，可得∠ACD ＝∠BCE ，利用三角形全等判定可得△ACD ≌△BCE ，则BE ＝AD ，∠DAC ＝∠EBC ，再证明∠DBE ＝90°，根据三角形面积计算公式便可求得结果．【详解】解：∵∠ACB ＝∠DCE ＝90°，∴∠ACB －∠DCB ＝∠DCE －∠DCB ．即∠ACD ＝∠BCE ．∵AC ＝BC ，∠ADC ＝∠BEC ，∴△ACD ≌△BCE ．∴BE ＝AD ，∠DAC ＝∠EBC ．∵∠DAC ＋∠ABC ＝90°，∴∠EBC ＋∠ABC ＝90°．∴△BDE 为直角三角形．∵AB ＝17，BD ＝5，∴AD ＝AB －BD ＝12．∴S △BDE ＝12BD ⋅BE ＝30．故答案为：30．【点睛】本题考查了全等三角形的判定与性质，通过分析题意找出三角形全等的条件并能结合全等性质解决相应的计算问题是解题的关键．18．如图，12∠=∠，要用“SAS ”判定ADC BDC ≌△△，则可加上条件__________．AD=BD 【分析】要判定△BCD ≌△ACD 已知∠1=∠2CD是公共边具备了一边一角对应相等注意SAS 的条件；两边及夹角对相等只能选AD=BD 【详解】解：由图可知只能是AD=BD 才能组成SAS 故答案为解析：AD=BD【分析】要判定△BCD ≌△ACD ，已知∠1=∠2，CD 是公共边，具备了一边一角对应相等，注意“SAS”的条件；两边及夹角对相等，只能选AD=BD.【详解】解：由图可知，只能是AD=BD ，才能组成“SAS”，故答案为：AD=BD.【点睛】本题考查了全等的判定，掌握“SAS”的条件是两边及夹角对相等是解题的关键. 19．如图，ABC ∆中，90,6,8ACB AC cm BC cm ∠=︒==，点P 从点A 出发沿A C -路径向终点C 运动.点Q 从B 点出发沿B C A --路径向终点A 运动．点P 和Q 分别以每秒1cm 和3cm 的运动速度同时开始运动，其中一点到达终点时另一点也停止运动，在某时刻，分别过P 和Q 作PE l ⊥于,E QF l ⊥于F ．则点P 运动时间为_______________时，PEC ∆与QFC ∆全等．或【分析】对点P 和点Q 是否重合进行分类讨论通过证明全等即可得到结果；【详解】如图1所示：与全等解得:；如图2所示：点与点重合与全等解得:；故答案为:或【点睛】本题主要考查了全等三角形的判定与性质准确解析：1或72【分析】对点P 和点Q 是否重合进行分类讨论，通过证明全等即可得到结果；【详解】如图1所示：PEC ∆与QFC ∆全等，PC QC ，683∴-=-t t ，解得:1t =；如图2所示：点P 与点Q 重合， PEC 与QFC ∆全等，638∴-=-t t ，解得:72t =；故答案为:1或72．【点睛】本题主要考查了全等三角形的判定与性质，准确分析计算是解题的关键．20．如图，在△ABC 中，∠C =90°，∠A 的平分线交BC 于D ，若20ABD S ∆=cm 2，AB =10cm ，则CD 为__________cm ．4【分析】由角平分线的性质可知D 到AB 的距离等于DC 可得出答案【详解】解：作DE ⊥AB 于E ∵AD 平分∠CAB 且DC ⊥ACDE ⊥AB ∴DE=DC ∵S △ABD=20cm2AB=10cm ∴•AB•DE=2解析：4【分析】由角平分线的性质可知D 到AB 的距离等于DC ，可得出答案．【详解】解：作DE ⊥AB 于E ．∵AD 平分∠CAB ，且DC ⊥AC ，DE ⊥AB ，∴DE=DC ，∵S △ABD =20cm 2，AB=10cm ， ∴12•AB•DE=20， ∴DE=4cm ，∴DC=DE=4cm故答案为：4．【点睛】本题主要考查角平分线的性质，掌握角平分线上的点到角两边的距离相等是解题的关键．三、解答题21．如图，在Rt ABC △和Rt DEF △中，90C F ∠=∠=︒，点A 、E 、B 、D 在同一直线上，BC 、EF 交于点M ，AC DF =，AB DE =．求证：（1）CBA FED ∠=∠；（2）AM DM =．解析：（1）见解析；（2）见解析【分析】（1）根据HL 定理可得Rt △ABC ≌ Rt △DEF ，从而得到∠CBA=∠FED ；（2）由（1）所得结论和已知条件可以证得△AEM ≌△DBM ，从而可得AM=DM ．【详解】证明：（1）在Rt ABC △和Rt DEF △中，90C F ∠=∠=︒AC DF AB DE =⎧⎨=⎩∴()Rt Rt HL ABC DEF ≌△△∴CBA FED ∠=∠．（2）∵CBA FED ∠=∠∴ME MB =，且AEMDBM ∠=∠ 又∵AB DE =∴AB EB DE EB -=-即AE DB =在AEM △和DBM △中AE DB AEM DBM ME MB =⎧⎪∠=∠⎨⎪=⎩∴()AEM DBM SAS △≌△∴AM DM =．【点睛】本题考查三角形全等的判定和性质，熟练掌握三角形全等的判定定理HL 、SAS 及三角形全等的性质是解题关键．22．如图，在ABC 和BCD △中，90BAC BCD ︒∠=∠=，AB AC =，CB CD =；延长CA 至点E ，使AE AC =；延长CB 至点F ，使BF BC =．连接AD ，AF ，DF ，EF ．延长DB 交EF 于点N ．（1）求证：AD AF =；（2）求证：BD EF =．解析：（1）证明见解析；（2）证明见解析【分析】（1）结合题意得：ABF BAC ACB ∠=∠+∠，ACD ACB BCD ∠=∠+∠，推导得ABF ACD ∠=∠；通过证明ABF ACD △≌△，即可完成证明；（2）根据（1）的结论ABF ACD △≌△得：BAF CAD ∠=∠；根据题意得90BAE ∠=；再通过证明AEF ABD △≌△，即可完成证明．【详解】（1） ∵ABF BAC ACB ∠=∠+∠，ACD ACB BCD ∠=∠+∠，90BAC BCD ︒∠=∠=∴ABF ACD ∠=∠∵BF BC =，CB CD =∴BF BC CD ==即AB AC ABF ACD BF CD =⎧⎪∠=∠⎨⎪=⎩∴ABF ACD △≌△∴AF AD =；（2）∵90BAC ︒∠=∴18090BAE BAC ∠=-∠=结合（1）的结论ABF ACD △≌△∴BAF CAD ∠=∠∵90EAF BAE BAF BAF ∠=∠-∠=-∠，90BAD BAC CAD CAD ∠=∠-∠=-∠ ∴EAF BAD ∠=∠∵AE AC =，AB AC =∴AE AC AB ==即AF AD EAF BAD AE AB =⎧⎪∠=∠⎨⎪=⎩∴AEF ABD △≌△∴BD EF =．【点睛】本题考查了三角形外角、全等三角形的知识；解题的关键是熟练掌握三角形外角、全等三角形的性质，从而完成求解．23．已知：如图，BAD CAE ∠=∠，AB AD =，AC AE =．（1）求证：ABC ADE △≌△．（2）若42,86B C ∠=︒∠=︒，求DAE ∠的度数．解析：（1）详见解析；（2）52︒【分析】（1）先证明∠BAC=∠DAE ，即可根据SAS 证得结论；（2）根据三角形内角和定理求出∠BAC 的度数，再根据全等三角形的性质得到答案．【详解】（1）∵∠BAD=∠CAE ，∴∠BAD+∠DAC=∠CAE+∠DAC ．即∠BAC=∠DAE ．在△ABC 和△ADE 中AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩, ∴ABC ADE △≌△；（2）∵42,86B C ∠=︒∠=︒，∴18052BAC B C ∠=︒-∠-∠=︒．∵ABC ADE △≌△，∴52DAE BAC ∠=∠=︒．【点睛】此题考查全等三角形的判定及性质，三角形内角和定理，熟记三角形全等的判定定理是解题的关键．24．如图，Rt △ABC 中，∠ACB=90°，D 是AB 上的一点，过D 作DE ⊥AB 交AC 于点E ，CE=DE ．连接CD 交BE 于点F ．（1）求证：BC=BD ；（2）若点D 为AB 的中点，求∠AED 的度数．解析：（1）见详解；（2）60°．【分析】（1）利用HL 直接证明Rt △DEB ≌Rt △CEB ，即可解决问题．（2）首先证明△ADE ≌△BDE ，进而证明∠AED=∠DEB=∠CEB ，即可解决问题．【详解】证明：（1）∵DE ⊥AB ，∠ACB=90°，∴△DEB 与△CEB 都是直角三角形，在△DEB 与△CEB 中，EB EB DE CE =⎧⎨=⎩， ∴Rt △DEB ≌Rt △CEB （HL ），∴BC=BD ．（2）∵DE ⊥AB ，∴∠ADE=∠BDE=90°；∵点D 为AB 的中点，∴AD=BD ；在△ADE 与△BDE 中，AD BD ADE BDE DE DE =⎧⎪∠=∠⎨⎪=⎩，∴△ADE ≌△BDE （SAS ），∴∠AED=∠DEB ；∵△DEB ≌△CEB ，∴∠CEB=∠DEB ，∴∠AED=∠DEB=∠CEB ；∵∠AED+∠DEB+∠CEB=180°，∴∠AED=60°．【点睛】该命题以三角形为载体，以考查全等三角形的判定及其应用为核心构造而成；解题的关键是灵活运用全等三角形的判定及其性质，来分析、判断或推理．25．已知矩形ABCD 中，点E 是AD 中点，连接CE ，经过点A ，B ，E 三点作O ，交BC 于点F ，过点F 作FH CE ⊥于H ．（1）求证：直线FH 是O 的切线；（2）若42AD =，且点H 恰好为CE 中点时，判断此时CE 与O 的位置关系？说明理由，并求出弧EF ，线段EH ，FH 围成的图形的面积．解析：（1）见解析；（2）EC 与O 相切，理由见解析，4π-【分析】（1）连接BE ，OF ，易得出BE 是圆的直径，根据全等三角形的判定证得△EAB ≌△EDC ，继而根据平行线的性质和切线的判定即可求证结论；（2）连接EF ，易求得四边形OFHE 的边长，再利用面积的和差即可求解．【详解】（1）连接BE ，OF∵四边形ABCD 是矩形，∴90A D ∠=∠=︒，AB CD =，∵90A ∠=︒，∴BE 是O 的直径，∵点E 是AD 中点，∴EA EC =，∴△EAB ≌△EDC ，∴EB EC =，∴EBC ECB ∠=∠，∵OB OF =，∴ECB OFB ∠=∠，∴ECB OFB ∠=∠，∴//OF EC ，∴OFH FHC ∠=∠，∵FH CE ⊥，∴90FHC OFH ∠=∠=︒，又∵OF 是O 的半径，∴直线FH 是O 的切线．（2）EC 与O 相切．理由如下：连接EF ，由（1）知，BE 是O 直径，∴90EFB EFC ∠=∠=︒，∵点H 是CE 中点，∴FH EH HC ==，∵FH CE ⊥，∴90FHC ∠=︒，∴45ECF HFC ∠=∠=︒，∴90BEC ∠=︒，又∵OE 是O 的半径，∴直线EC 与圆O 相切．由上可知四边形ABFE 和四边形OFHE 都是正方形，∴11422222AE AB AD ===⨯=， ∴224BE AB AE =+=，∴2OE OF ==，∴2290π224π360OFHE OEFS S S ⨯=-=-=-正方形扇形．【点睛】本题考查直线与圆的位置关系，矩形的性质，全等三角形的判定和性质、切线的判定、勾股定理，解题的关键是综合运用所学知识．26．OAB 和ODE 均为等腰三角形，且AOB DOE β∠=∠=，OA OB =，OD OE =，连接AD 、BE ，它们所在的直线交于点F ．（1）观察发现：如图1，当60β︒=时，线段AD 与BE 的数量关系是______，AFB ∠的度数是______；（2）探究证明：如图2，当90β︒=时，线段AD 与BE 的数量关系是______，AFB ∠的度数是______，根据图2证明你的猜想；（3）拓展推广：当β为任意角时，线段AD 与BE 的数量关系是______，AFB ∠的度数是______．（用含β的式子表示）解析：（1）AD BE =，60°；（2）AD BE =，90°，理由见解析；（3）AD BE =，β【分析】（1）设AF 交BD 于G ，证明AOD BOE ≌△△，推出AD BE =，OAD OBE ∠=∠，得到60AFB AOB ∠=∠=︒；（2）证明AOD BOE ≌△△，推出AD BE =，OAD OBE ∠=∠，根据OFA DFB ∠=∠及三角形内角和定理即可证得90AFB AOB ∠=∠=︒；（3）根据（1）与（2）直接得到结论．【详解】（1）证明：设AF 交BO 于G ，∵60AOB DOE ∠=∠=︒，∴AOB BOD DOE BOD ∠-∠=∠-∠，即AOD BOE ∠=∠，∵OA OB =，OD OE =，∴AOD BOE ≌△△，∴AD BE =，OAD OBE ∠=∠，∵OGA FGB ∠=∠，∴180180OGA OAD FGB OBE ∠-∠=∠--∠︒-︒，∴60AFB AOB ∠=∠=︒，故答案为：AD BE =，60°；（2）AD BE =，90°证明：设AF 交BO 于G ，∵90AOB DOE ︒∠=∠=，∴AOB BOD DOE BOD ∠+∠=∠+∠，即AOD BOE ∠=∠，∵OA OB =，OD OE =，∴AOD BOE ≌△△，∴AD BE =，OAD OBE ∠=∠，∵OGA DGB ∠=∠，∴90AFB AOB ∠=∠=︒；故答案为：AD BE =，90°；（3）证明：由（1）与（2）可得AD BE =，AFB AOB β∠=∠=故答案为：AD BE =，β．【点睛】此题考查全等三角形的判定及性质，等腰三角形的性质，熟练掌握全等三角形的判定及性质是解题的关键．27．已知：如图，AC ＝BD ，BD ⊥AD 于点D ，AC ⊥BC 于点C ．求证：∠ABC ＝∠BAD ．解析：详见解析【分析】利用HL 证明Rt △ABD ≌Rt △BAC ，即可得到结论．【详解】∵BD ⊥AD ，AC ⊥BC ，∴∠D=∠C=90︒，在Rt △ABD 和Rt △BAC 中，AB BA BD AC=⎧⎨=⎩， ∴Rt △ABD ≌Rt △BAC （HL ），∴∠ABC ＝∠BAD ．【点睛】此题考查全等三角形的判定及性质，根据题中的已知条件确定两个三角形的对应相等的条件，根据全等的判定定理证得这两个三角形全等是解题的关键．28．如图，在平面直角坐标系中，已知点()1,A a a b -+，(),0B a ，且()2320a b a b +-+-=，C 为x 轴上点B 右侧的动点，以AC 为腰作等腰三角形ACD ，使AD AC =，CAD OAB ∠=∠，直线DB 交y 轴于点P ．（1）求证：AO AB =；（2）求证：AOC ABD ∆∆≌；（3）当点C 运动时，点P 在y 轴上的位置是否发生改变，为什么？解析：（1）证明见解析；（2）证明见解析；（3）不变，理由见解析．【分析】（1）先根据非负数的性质求出a 、b 的值，作AE ⊥OB 于点E ，由SAS 定理得出△AEO ≌△AEB ，根据全等三角形的性质即可得出结论；（2）先根据∠CAD=∠OAB ，得出∠OAC=∠BAD ，再由SAS 定理即可得出结论；（3）设∠AOB=∠ABO=α，由全等三角形的性质可得出∠ABD=∠AOB=α，故∠OBP=180°-∠ABO-∠ABD=180°-2α为定值，再由OB=2，∠POB=90°可知OP 的长度不变，故可得出结论．【详解】（1）证明：∵()2320a b a b +-+-=，∴30,20,a b a b +-=⎧⎨-=⎩解得2,1.a b =⎧⎨=⎩∴()1,3A ，()2,0B ．作AE OB ⊥于点E ，∵()1,3A ，()2,0B ，∴1OE =，211BE =-=，在AEO ∆与AEB ∆中，∵,90,,AE AE AEO AEB OE BE =⎧⎪∠=∠=︒⎨⎪=⎩∴AEO AEB ∆∆≌，∴OA AB =．（2）证明：∵CAD OAB ∠=∠，∴CAD BAC OAB BAC ∠+=∠+∠∠，即OAC BAD ∠=∠．在AOC ∆与ABD ∆中，∵,,,OA AB OAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩∴AOC ABD ∆∆≌．（3）解：点P 在y 轴上的位置不发生改变．理由：设AOB α∠=． ∵OA AB =，∴AOB ABO α∠=∠=．由（2）知，AOC ABD ∆∆≌，∴ABD AOB α∠=∠=．∵2OB =，1801802OBP ABO ABD α∠=︒-∠-∠=︒-为定值，90POB ∠=︒，易知POB ∆形状、大小确定，∴OP 长度不变，∴点P 在y 轴上的位置不发生改变．【点睛】本题考查了全等三角形的判定与性质，熟知全等三角形的判定定理是解题的关键．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.（★★★）已知：BD CE 、是ABC ∆的高，点P 在BD 的延长线上，BP AC =，点Q 在CE 上，CQ AB =，求证：⑴AP AQ =；⑵AP AQ ⊥．
P
D
Q
C
B
E
A
2.（★★★）如图，已知在ABC ∆中，AD 是BC 边上的中线，E 是AD 上一点，延长BE 交AC 于F ，AF EF =，求证：AC BE =．
F
E
D
C B
A
3.（★★★★）已知AD 为ABC ∆的中线，ADB ∠，ADC ∠的平分线分别交AB 于E 、交AC 于F ．求证：BE CF EF +>．
F
E A
B D C
4.（★★）如图，已知AB =DC ，AD =BC ，O 是BD 中点，过O 点的直线分别交DA 、BC 的延长线于E ，F ．求证：∠E =∠F
5.（★★）如图，ABC ∆中，AB AC =，90BAC ∠=︒，D 是BC 中点，ED FD ⊥，ED 与AB 交于E ，FD 与AC 交于F ．求证：BE AF =，AE CF =．
A
B
C
D
E F
6.（★★★）如图所示，已知ABC ∆中，AD 平分BAC ∠，E 、F 分别在BD 、AD 上．DE CD =，EF AC =．求证：EF ∥AB
F
A C
D E B
7.（★★★）如图所示，在ABC ∆中，AD 平分BAC ∠，AD AB =，CM AD ⊥于M ，求证2AB AC AM +=．
M
D C
B
A
8.（★★★）如图，已知在ABC ∆中，3ABC C ∠=∠，12∠=∠，BE AE ⊥．求证：2AC AB BE -=．
21E
C
B
A
9.（★★★）已知：如图，点C为线段AB上一点，ACM
∆、CBN
∆是等边三角形．
（1）求证：AN BM
=．（2）求证：CD=CE (3) 求证：CF平分∠MCN （4）求证：DE∥AB
10.（★★★）等边ABD
∆和等边CBD
∆的边长均为1，
E是BE AD
⊥上异于A D
、的任意一点，F是CD上一
点，满足1
AE CF
+=，当E F
、移动时，试判断BEF
∆的
形状．
D
F
E
C
B
A
11．（★★★★）如图，在ABC
∆中，BE是∠ABC的平
分线，AD BE
⊥，垂足为D。

求证：21C
∠=∠+∠。

N
M
A
E
D
N
M
A C
F
E
D
N
M
A C
F
E
D
N
M
A C
12．（★★）如图，Rt △ABC 中，∠BAC=90°，AC=2AB ，AD ⊥BC 于点D ，E 为AC 边的中点，连接BE 交AD 于点F ，过点E 作BE 的第一线交BC 于点G ，求证：AF=CG.
B
C
D
A
E
F G
13.（★★★）已知：如图，△ABC 中，∠ABC =45°，CD ⊥AB 于D ，BE 平分∠ABC ，且BE ⊥AC 于E ，与CD 相交于点F ，H 是BC 边的中点，连结DH 与BE 相交于点G 。

(!)求证：BF =AC ； (2)求证：CE =
1
2
BF ； (3)CE 与BC 的大小关系如何？试证明你的结论。

14．（★★）如图，已知，AB=AC ，AD=AE ，BD=CE ，延长BD 交CE 于点P ，求证：∠BAC=∠DAE ；
15.（★）如图，已知，AB=AD ，AC=AE ，∠1=∠2. （1）求证：BC=DE ；（2）若AF 平分∠BAC ，求证：AF=AC.
16.（★★★★）在△OAB 和△OCD 中，OA=OB ，OC=OD ，∠AOB=∠COD ，AC 、BD 交于点P. （1）①如图1，∠AOB=∠COD=60°，则∠APD= ，AC 与BD 的数量关系是；
②如图2，∠AOB=∠COD=90°，则∠APD= ，
AC 与BD 的数量关系是；
（2）如图3，∠AOB=∠COD=α°，则∠APD 的度数
为（用含α的式子表示），AC 与BD 之间的等量关系是；填写你的结论，并给出你的证明；
图1 图2
图3
17：（★★★★）点C 为线段AB 上一点，分别以AC 、BC 为腰在直线AB 的同侧作等腰△ACD 和等腰△BCE ，且CA=CD ，CB=CE ，∠ACD=∠BCE ，直线AE 、BD 交于点F. （1）如图1，若∠ACD=60°，则∠AFB= ；（2）如图2，若∠ACD=α°，则∠AFB= ；（用α的代数式表示）
（3）如图3，将图2中的△ACD 绕点C 顺时针旋转一个角度，延长BD 交线段AE 于点F ，试探究∠AFB 与α之间的数量关系，并给出你的证明.
O
P
D
C
B A
O
P D
C B
A
α
αO P D
C
B
A
18.（★★）已知：如图，△ABC 中，∠BAC=∠BCA ，延长BC 边的中线AD 到E 点，使AD=DE ，F 为BC 延长线上一点，且CE=CF ，求证：AF=2AD.
19.（★★）如图，等腰Rt △ABC 中，AB=AC ，过A 任作直线l ，BD ⊥l 于点D ，CE ⊥l 于点E.
(1) 若l 与BC 不相交，求证：BD+CE=DE ；
(2) 当直线l 绕A 点旋转到与BC 相交时，其它条件不变，试猜想BD 、CE 和DE 的关系？画图并给出证明.
20．（★）如图，在△ABC 中，AD 是中线，分别过点B 、C 作AD 及其延长线的垂线BE 、CF ，垂足分别为点E 、F ，求证：BE=CF ．
21.（★★）如图，在△ABC 中，D 为BC 上一点，过C
作AD 的垂线交AB 于E 点，O 为垂足，AE=AC ，EF ∥BC ，
A
B
C
E F
D
A C
D
E
A B C
E
A
O
F D
C
B
求证：CE 平分∠DEF.。