数学人教版八年级上册十字相乘
人教版数学八年级上册 十字相乘法及分组分解法复习与巩固提高

十字相乘法及分组分解法(基础)【学习目标】1. 熟练掌握首项系数为1的形如型的二次三项式的因式分解.2. 基础较好的同学可进一步掌握首项系数非1的简单的整系数二次三项式的因式分解.3. 对于再学有余力的学生可进一步掌握分数系数;实数系数;字母系数的二次三项式的因式分解.(但应控制好难度)4. 掌握好简单的分组分解法. 【要点梳理】【高清课堂 400150 十字相乘法及分组分解法 知识要点】 要点一、十字相乘法利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法.对于二次三项式,若存在 ,则要点诠释:(1)在对分解因式时,要先从常数项的正、负入手,若,则同号(若,则异号),然后依据一次项系数的正负再确定的符号(2)若中的为整数时,要先将分解成两个整数的积(要考虑到分解的各种可能),然后看这两个整数之和能否等于,直到凑对为止.要点二、首项系数不为1的十字相乘法在二次三项式(≠0)中,如果二次项系数可以分解成两个因数之积,即,常数项可以分解成两个因数之积,即,把排列如下:按斜线交叉相乘,再相加,得到,若它正好等于二次三项式的一次项系数,即,那么二次三项式就可以分解为两个因式与之积,即.要点诠释:(1)分解思路为“看两端,凑中间”(2)二次项系数一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项式,最后结果不要忘记把提出的负号添上.要点三、分组分解法pq x q p x +++)(22x bx c ++pq c p q b=⎧⎨+=⎩()()2x bx c x p x q ++=++2x bx c ++c 0c >p q 、0c <p q 、b p q 、2x bx c ++b c 、c b 2ax bx c ++a a 12a a a =c 12c c c =1212a a c c ,,,1221a c a c +2ax bx c ++b 1221a c a c b +=11a x c +22a x c +()()21122ax bx c a x c a x c ++=++a对于一个多项式的整体,若不能直接运用提公因式法和公式法进行因式分解时,可考虑分步处理的方法,即把这个多项式分成几组,先对各组分别分解因式,然后再对整体作因式分解——分组分解法.即先对题目进行分组,然后再分解因式.要点四:添、拆项法把多项式的某一项拆开或填补上互为相反数的两项(或几项),使原式适合于提公因式法、公式法或分组分解法进行分解.要注意,必须在与原多项式相等的原则下进行变形.添、拆项法分解因式需要一定的技巧性,在仔细观察题目后可先尝试进行添、拆项,在反复尝试中熟练掌握技巧和方法. 【典型例题】 类型一、十字相乘法1、将下列各式分解因式: (1); (2); (3)【答案与解析】解:(1)因为所以:原式= (2)因为所以:原式=(3)【总结升华】常数项为正,分解的两个数同号;常数项为负,分解的两个数异号. 二次项系21016x x -+2310x x --78x x x -=-()()78x x +-2810x x x --=-()()28x x --()()()2210331052x x x x x x --=-+-=-+-数一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项式,最后结果不要忘记把提出的负号添上. 举一反三:【高清课堂400150 十字相乘法及分组分解法 例1】【变式1】分解因式:(1); (2); (3) 【答案】解:(1)(2)(3)【变式2】(2016秋·闵行区期末)因式分解:()()222812x x x x +-++.【答案】解:()()222812x xx x +-++=()()2226x x xx +-+-=()()()()1223x x x x -+-+.【高清课堂400150 十字相乘法及分组分解法 例1】2、将下列各式分解因式: (1); (2) (3); (4).【思路点拨】(3)题可看成常数项,.(4)题可将看成一个整体来分解因式. 【答案与解析】解:(1);(2). (3);1072++x x 822--x x 2718x x --+()()271025x x x x ++=++()()22842x x x x --=-+()()22718(718)29x x x x x x --+=-+-=--+22355x x +-25166x x ++22616x xy y --216y -21682,826y y y y y y -=-⨯-+=-()2x +22355x x +-=()315x x ⎛⎫+- ⎪⎝⎭251116623x x x x ⎛⎫⎛⎫++=++ ⎪⎪⎝⎭⎝⎭()()2261682x xy y x y x y --=-+(4)因为所以:原式【总结升华】十字相乘法的方法简单点来讲就是:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数.注意观察式子结构,能够看作整体的看作整体.举一反三:【变式】将下列各式分解因式:(1); (2); (3); (4). 【答案】 解: (1); (2); (3);(4).3、将下列各式分解因式: (1);(2)【答案与解析】 解:(1)因为所以:原式=()()()25242292x x x -+-+=-+()()225522x x =+-+-⎡⎤⎡⎤⎣⎦⎣⎦()()2158x x =-+21136x x -+251124a a --10722+-xy y x ()()342++-+b a b a 22111121366332x x x x x x ⎛⎫⎛⎫-+=+-=+- ⎪⎪⎝⎭⎝⎭2513112443a a a a ⎛⎫⎛⎫--=-+ ⎪⎪⎝⎭⎝⎭()()2271025x y xy xy xy -+=--()()()()24313a b a b a b a b +-++=+-+-91019y y y +=()()2335y y ++(2)因为所以:原式=【总结升华】十字相乘法的方法简单点来讲就是:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数. 举一反三:【变式】分解因式:(1);(2);(3); 【答案】解:(1);(2);(3).类型二、分组分解法4、(2015春•重庆校级期中)先阅读下列材料,然后回答后面问题:将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.能分组分解的多项式通常有四项或六项,一般的分组分解有四种形式,即“2+2”分法、“3+1”分法、“3+2”分法及“3+3”分法等. 如“2+2”分法: ax+ay+bx+by=(ax+ay )+(bx+by ) =a (x+y )+b (x+y ) =(x+y )(a+b ) 如“3+1”分法:2xy+y 2﹣1+x 2=x 2+2xy+y 2﹣1=(x+y )2﹣1 =(x+y+1)(x+y ﹣1)请你仿照以上方法,探索并解决下列问题:(1)分解因式:x 2﹣y 2﹣x ﹣y ;(2)分解因式:45am 2﹣20ax 2+20axy ﹣5ay 2;(3)分解因式:4a 2+4a ﹣4a 2b ﹣b ﹣4ab+1. 【思路点拨】(1)首先利用平方差公式因式分解因式,进而提取公因式得出即可; (2)将后三项运用完全平方公式分解因式进而利用平方差公式分解因式即可; (3)重新分组利用完全平方公式分解因式得出即可. 【答案与解析】21183x x x -=()()2379x x +-2314x x +-2344x x --+2631105x x +-()()22314341311x x x x x x +-=-+=--()()223444432123x x x x x x --+=--=+-()()263110521537x x x x +-=+-解:(1)x 2﹣y 2﹣x ﹣y =(x+y )(x ﹣y )﹣(x+y ) =(x+y )(x ﹣y ﹣1); (2)45am 2﹣20ax 2+20axy ﹣5ay 2=45am 2﹣5a (4x 2﹣4xy+y 2)=5a[9m 2﹣(2x ﹣y )2] =5a (3m ﹣2x+y )(3m+2x ﹣y );(3)4a 2+4a ﹣4a 2b ﹣b ﹣4ab+1=(4a 2+4a+1)﹣b (4a 2+4a+1)=(2a+1)2(1﹣b ). 【总结升华】此题主要考查了提取公因式法分解因式以及分组分解法分解因式,正确分组是解题关键. 举一反三:【变式】分解因式: 【答案】解:原式.十字相乘法及分组分解法(提高)【学习目标】1. 熟练掌握首项系数为1的形如型的二次三项式的因式分解.2. 基础较好的同学可进一步掌握首项系数非1的简单的整系数二次三项式的因式分解.3. 对于再学有余力的学生可进一步掌握分数系数;实数系数;字母系数的二次三项式的因式分解.(但应控制好难度)4. 掌握好简单的分组分解法. 【要点梳理】【高清课堂400150 十字相乘法及分组分解法 知识要点】 要点一、十字相乘法利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法.对于二次三项式,若存在 ,则要点诠释:(1)在对分解因式时,要先从常数项的正、负入手,若,则同号(若,则异号),然后依据一次项系数的正负再确定的符号(2)若中的为整数时,要先将分解成两个整数的积(要考虑到分解的各种可能),然后看这两个整数之和能否等于,直到凑对为止.要点二、首项系数不为1的十字相乘法22244a b ab c +--()()()22222(44)222a ab b c a b c a b c a b c =-+-=--=-+--pq x q p x +++)(22x bx c ++pq c p q b=⎧⎨+=⎩()()2x bx c x p x q ++=++2x bx c ++c 0c >p q 、0c <p q 、b p q 、2x bx c ++b c 、c b在二次三项式(≠0)中,如果二次项系数可以分解成两个因数之积,即,常数项可以分解成两个因数之积,即,把排列如下:按斜线交叉相乘,再相加,得到,若它正好等于二次三项式的一次项系数,即,那么二次三项式就可以分解为两个因式与之积,即.要点诠释:(1)分解思路为“看两端,凑中间”(2)二次项系数一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项式,最后结果不要忘记把提出的负号添上.要点三、分组分解法对于一个多项式的整体,若不能直接运用提公因式法和公式法进行因式分解时,可考虑分步处理的方法,即把这个多项式分成几组,先对各组分别分解因式,然后再对整体作因式分解——分组分解法.即先对题目进行分组,然后再分解因式.要点诠释:分组分解法分解因式常用的思路有:要点四、添、拆项法把多项式的某一项拆开或填补上互为相反数的两项(或几项),使原式适合于提公因式法、公式法或分组分解法进行分解.要注意,必须在与原多项式相等的原则下进行变形.添、拆项法分解因式需要一定的技巧性,在仔细观察题目后可先尝试进行添、拆项,在反复尝试中熟练掌握技巧和方法. 【典型例题】类型一、十字相乘法1、分解因式:2ax bx c ++a a 12a a a =c 12c c c =1212a a c c ,,,1221a c a c +2ax bx c ++b 1221a c a c b +=11a x c +22a x c +()()21122ax bx c a x c a x c ++=++a 22(1)(6136)x a x a a ++--+【答案与解析】解:原式=【总结升华】将视作常数,就以为主元十字相乘可解决.举一反三:【变式】分解因式:【答案】解:原式2、分解因式:【思路点拨】该题可以先将看作一个整体进行十字相乘法分解,接着再套用一次十字相乘.【答案与解析】 解: 因为所以:原式=[-2][-12]==【总结升华】十字相乘法对于二次三项式的分解因式十分方便,大家一定要熟练掌握. 举一反三:【变式】分解因式:;【答案】解:原式3、分解下列因式()()()212332x a x a a ++---()()()()23322332x a x a x a x a =--+-⎡⎤⎡⎤⎣⎦⎣⎦=-++-a x 23345xy y x y ++--2(34)35(35)(1)y x y x y x y =+-+-=+-+()2a a -()()()22221214a a a a a a ----=--22(2)(12)a a a a ----()()()()1234a a a a +-+-222(3)2(3)8x x x x ----()()223432x x xx =---+()()()()4112x x x x =-+--(1) (2)【答案与解析】解:(1)令,则原式(2)令,原式【总结升华】此两道小题结构都非常有特点,欲分解都必须先拆开,再仔细观察每个式子中都存在大量相同的因式→整体性想法.整体性思路又称换元法,这与我们生活中搬家有些类似,要先将一些碎东西找包,会省许多事.类型二、分组分解法4、分解因式:【思路点拨】对完全平方公式熟悉的同学,一看见该式,首先想到的肯定是式子中前三项恰好构成,第4、5项→. 【答案与解析】解:原式【总结升华】①熟记公式在复杂背景下识别公式架构很重要;②我们前面练习中无论公式、配方、十字相乘一般都只涉及单一字母,其实代数式学习是一个结构的学习,其中任一个字母均可被一个复杂代数式来替代,故有时要有一些整体性认识的想法. 举一反三:【高清课堂400150 十字相乘法及分组分解法 例4】 【变式1】分解因式:(1)(2)(3) 【答案】解:(1)原式; (2)原式;22(1)(2)12x x x x ++++-22(33)(34)8x x x x +-++-21x x t ++=222(1)1212(4)(3)(5)(2)t t t t t t x x x x =+-=+-=+-=+++-2(2)(1)(5)x x x x =+-++23x x m +=2(3)(4)820(5)(4)m m m m m m =-+-=+-=+-222(35)(34)(4)(1)(35)x x x x x x x x =+++-=+-++222332x xy y x y -++-+2()x y -3()x y -2()3()2x y x y =-+-+(1)(2)x y x y =-+-+22a b ac bc -++225533a b a b --+23345xy y x y ++--()()()()()a b a b c a b a b a b c =+-++=+-+()()()()()()()225353553a ba b a b a b a b a b a b =---=+---=-+-(3)原式.【变式2】(2016秋•昌江区校级期末)分解因式:2242244241a b c ab ac bc ++--+-.【答案】解:2242244241a b c ab ac bc ++--+- =()()()2222444241a b ab ac bc c +-+-++- =()()()()222222211b a cb ac c -+-++-=()()222121b a c b a c -++-+-.类型三、拆项或添项分解因式5、(2015春•吉州区期末)阅读理解:对于二次三项式x 2+2ax+a 2可以直接用公式法分解为(x+a )2的形式,但对于二次三项式x 2+2ax ﹣8a 2,就不能直接用公式法了.我们可以在二次三项式x 2+2ax ﹣8a 2中先加上一项a 2,使其成为完全平方式,再减去a 2这项,使整个式子的值不变,于是又:x 2+2ax ﹣8a 2 =x 2+2ax ﹣8a 2+a 2﹣a 2=(x 2+2ax+a 2)﹣8a 2﹣a 2=(x+a )2﹣9a 2=[(x+a )+3a][(x+a )﹣3] =(x+4a )(x ﹣2a )像这样把二次三项式分解因式的方法叫做添(拆)项法.(1)请认真阅读以上的添(拆)项法,并用上述方法将二次三项式:x 2+2ax ﹣3a 2分解因式.(2)直接填空:请用上述的添项法将方程的x 2﹣4xy+3y 2=0化为(x ﹣ )•(x ﹣ )=0并直接写出y 与x 的关系式.(满足xy≠0,且x≠y) (3)先化简﹣﹣,再利用(2)中y 与x 的关系式求值.【答案与解析】解:(1)x 2+2ax ﹣3a2=x 2+2ax+a 2﹣4a2 =(x+a )2﹣4a 2=(x+a+2a )(x+a ﹣2a ) =(x+3a )(x ﹣a ); (2)x 2﹣4xy+3y2=x 2﹣4xy+4y 2﹣y2 =(x ﹣2y )2﹣y2233453(1)(1)(5)(1)(35)xy x y y x y y y y x y =++--=+++-=++-=(x ﹣2y+y )(x ﹣2y ﹣y )=(x ﹣y )(x ﹣3y );x=y 或x=3y ;故答案为:y ;3y(3)原式===﹣,若x=y ,原式=﹣2;若x=3y ,原式=﹣. 【总结升华】此题考查了因式分解﹣添(拆)项法,正确地添(拆)项是解本题的关键.【巩固练习1】一.选择题1. 将因式分解,结果是( )A. B. C. D.2.(2016秋•西城区校级期中)下列因式分解结果正确的是( )A .()3221510532a a a a a +=+B . ()()2943434x x x -=+-C . ()2210255a a a --=-D . ()()231025a a a a --=+-3. 如果,那么等于( )A. B. C. D.4. 若,则的值为( )A.-9B.15C.-15D.95. 如果,则为 ( )A .5B .-6C .-5D .66.把进行分组,其结果正确的是( )A. B. C. D.二.填空题7. 若,则= .2321016a a ++()()28a a -+()()28a a +-()()28a a ++()()28a a --()()2x px q x a x b -+=++p ab a b +ab -a b --()()236123x kx x x +-=-+k b 2222a b c bc --+222()(2)a c b bc ---222()2a b c bc --+222()(2)a b c bc ---222(2)a b bc c --+()()21336m m m a m b -+=++a b -8. 因式分解___________.9.(2016·潍坊三模)分解因式:3231215x x x --= .10. 因式分解:=_______________;11. 因式分解= .12.分解因式:=________.三.解答题13.若多项式可以分解成两个一次因式的积,其中、均为整数,请你至少写出2个的值.14.(宣武区校级期末)因式分解:2x 2+x ﹣3.15.分解因式:(1); (2);(3); (4); (5). 【答案与解析】一.选择题1. 【答案】C ;2. 【答案】D ;【解析】A 、()3221510532a a a a +=+,故此选项错误;B 、()()2943232x x x -=+-,故此选项错误;C 、21025a a --无法因式分解,故此选项错误;D 、()()231025a a a a --=+-,正确.3. 【答案】D ;【解析】,所以.4. 【答案】A ;【解析】.5. 【答案】B ;【解析】由题意.6. 【答案】D ;【解析】原式=.二.填空题7. 【答案】±5;【解析】,所以或者.8. 【答案】;22a b ac bc -++ax bx cx ay by cy +++++()2064x x -+321a a a +--236x px ++()()x a x b ++a b p 268x x -+21024x x +-215238a a -+22568x xy y -++225533a b a b --+()()()2x a x b x a b x ab ++=+++a b p +=-()()2123936x x x x -+=--5306b b =-=-,()()222(2)a b bc c a b c a b c --+=+--+()()2133649m m m m -+=--9,4a b =-=-4,9a b =-=-()()a b a b c +-+【解析】. 9. 【答案】()()315x x x +-;【解析】()32231215345x x x x x x --=-+=()()315x x x +-.10.【答案】;【解析】原式 .11.【答案】;【解析】. 12.【答案】; 【解析】. 三.解答题13.【解析】 解: 由题意得,则,由、均为整数,可写出满足要求的、,进而求得,36=1×36=(-1)×(-36)=2×18=(-2)×(-18)=3×12=(-3)×(-12)=4×9=(-4)×(-9)=6×6=(-6)×(-6),所以可以取±37,±20,±15,±13,±12.取上述的两个值即可.14.【解析】解:原式=(2x+3)(x ﹣1).15.【解析】解:(1);(2);(3)(4)(5)原式. 【巩固练习2】一.选择题1. (2016秋·惠民县期末)如果多项式22mx nx --能因式分解为()()32x x p ++,那么22a b ac bc -++()()()()()a b a b c a b a b a b c =+-++=+-+()()a b c x y +++()()ax bx cx ay by cy =+++++()()x a b c y a b c =+++++()()a b c x y =+++()()164x x --()()()220642064164x x x x x x -+=-+=--()()211a a +-321a a a +--()()()()221111aa a a a =+-+=+-236()()x px x a xb ++=++2236()x px x a b x ab ++=+++36a b p ab +==,a b a b p p p ()()26824x x x x -+=--()()21024122x x x x +-=+-()()2152381581a a a a -+=--()()()2222568568542x xy y x xy y x y x y -++=---=-+-()()()()()()()225353553a b a b a b a b a b a b a b =---=+---=-+-下列结论正确的是 ( ).A.m =6B.n =1C.p =-2D.mnp =32. 若()2230x a b x ab x x +++=--,且b a <,则b 的值为( ). A.5 B.-6 C.-5 D.63. 将()()256x y x y +-+-因式分解的结果是( ).A.()()23x y x y +++-B. ()()23x y x y +-++C.()()61x y x y +-++D. ()()61x y x y +++-4.(滨湖区校级期中)把多项式1+a+b+ab 分解因式的结果是( )A .(a ﹣1)(b ﹣1)B .(a+1)(b+1)C .(a+1)(b ﹣1)D .(a ﹣1)(b+1)5. 对224293x x y y +--运用分组分解法分解因式,分组正确的是( )A. 22(42)(93)x x y y ++--B. 22(49)(23)x y x y -+-C. 22(43)(29)x y x y -+-D. 22(423)9x x y y +--6.如果3233x x x m +-+有一个因式为()3x +,那么m 的值是( )A. -9B.9C.-1D.1二.填空题7.(2016•黄冈模拟)分解因式:2242y xy x --+= .8. 分解因式:224202536a ab b -+-= .9.5321x x x -+-分解因式的结果是__________.10. 如果代数式有一因式,则a 的值为_________. 11.若3223a a b ab b --+有因式()a b -,则另外的因式是_________.12. 分解因式:(1)3)32(2-+-+k x k kx ;(2)mn m x m n x -+-+22)2(三.解答题13. 已知0x y +=,31x y +=, 求2231213x xy y ++的值.14. 分解下列因式:(1)()()128222+---a a a a(2)32344xy xy x y x y -++(3)42222459x y x y y --(4)43226a a a +-15.(2015•巴南区一模)先阅读下列材料:我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等.(1)分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法. 如:ax+by+bx+ay=(ax+bx )+(ay+by )=x (a+b )+y (a+b )=(a+b )(x+y )2xy+y 2﹣1+x 2=x 2+2xy+y 2﹣1=(x+y )2﹣1=(x+y+1)(x+y ﹣1)(2)拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法.如:x 2+2x ﹣3=x 2+2x+1﹣4=(x+1)2﹣22=(x+1+2)(x+1﹣2)=(x+3)(x ﹣1)请你仿照以上方法,探索并解决下列问题:(1)分解因式:a 2﹣b 2+a ﹣b ;(2)分解因式:x 2﹣6x ﹣7;(3)分解因式:a 2+4ab ﹣5b 2. 【答案与解析】一.选择题1. 【答案】B ;【解析】()()()223233222x x p x p x p mx nx ++=+++=--, ∴22,32p p n =-+=-,解得1n =.2. 【答案】B ;【解析】()()23065x x x x --=-+,由b a <,所以6b =-. 3. 【答案】C ;【解析】把()x y +看成一个整体,分解()()()()25661x y x y x y x y +-+-=+-++. 4. 【答案】B ;【解析】解:1+a+b+ab=(1+a )+b (1+a )=(1+a )(1+b ).故选:B .5. 【答案】B ;【解析】A 各组经过提取公因式后,组与组之间无公因式可提取,所以分组不合理.B 第一组可用平方差公式分解得()()2323x y x y +-,与第二组有公因式23x y -可提取,所以分组合理,C 与D 各组均无公因式,也不符合公式,所以无法继续进行下去,分组不合理.6. 【答案】A ;【解析】由题意当3x =-时,代数式为零,解得9m =-.二.填空题7. 【答案】()()22x y x y -+--.【解析】解:2242y xy x --+=()2224y xy x -+-=()24x y --=()()22x y x y -+--.8. 【答案】()()256256a b a b -+--;【解析】原式()224202536a ab b =-+- ()()()22256256256a b a b a b =--=-+-- 9. 【答案】()()()22111x x x x +--+;【解析】原式()()()()()()()23222321111111xx x x x x x x x =-+-=-+=+--+. 10.【答案】16; 【解析】由题意当4x =时,代数式等于0,解得16a =.11.【答案】()()a b a b -+;【解析】()()322322a a b ab b a a b b a b --+=---()()2a b a b =-+.12.【答案】()()31kx k x +-+;()()x m x m n --+;【解析】()()2(23)331kx k x k kx k x +-+-=+-+; ()()()()22(2)x n m x m mn x m x m n x m x m n +-+-=---=--+⎡⎤⎣⎦.三.解答题13.【解析】解: ()()22231213334x xy y x y x y y ++=+++由0x y +=,31x y +=解得12y =所以,原式21301412⎛⎫=⨯⨯+⨯= ⎪⎝⎭. 14.【解析】解:(1)原式()()()()()()22261223a a a a a a a a =----=+-+-; (2)原式()()()()222244222xy y x x xy x y xy x y x y ⎡⎤=-++=+-=++-+⎣⎦; (3)原式()()()()()()2422222245949123231y x x y x x y x x x =--=-+=+-+; (4).15.【解析】解:(1)原式=(a+b )(a ﹣b )+(a ﹣b )=(a ﹣b )(a+b+1);(2)原式= x 2﹣6x+9-16=(x-3)2﹣16=(x-3+4)(x-3-4)=(x+1)(x ﹣7);(3)原式= a 2+4ab ﹣5b2 = a 2+4ab+4b 2﹣9b2 = (a+2b )2﹣9b2 =(a +2b ﹣3b )(a+2b +3b )=(a ﹣b )(a+5b ).()()()4322222626232a a a a a a a a a +-=+-=-+。
八年级数学十字相乘法因式分解

实际在使用此公式时,需要把 一次项系数和常数项进行分拆,在 试算时,会带来一些困难。
下面介绍的方法,正好解决了 这个困难。
即:x 2+(p+q)x+pq=(x+p)(x+q)
解因式
解:2(6x 2+x)2-11(6x 2+x) +5 = [(6x2+x) -5][2(6x 2+x)-1]
= (6x 2+x-5) (12x 2+2x-1 )
= (6x -5)(x +1) (12x 2+2x-1 )
1
-5
6
-5
2
-1
-1-10=-11
1
1
-5+6=1
练习:将下列各式分解因式 1、 7x 2-13x+6 答案(7x+6)(x+1)
2、 -y 2-4y+12 答案- (y+6)(y-2)
3、 15x2+7xy-4y 2 答案 (3x-y)(5x+4y)
4、 10(x +2)2-29(x+2) +10
答案 (2x-1)(5x+8)
5、 x 2-(a+1) x+a 答案 (x-1)(x-a)
例5 将 2x 2-3xy-2y2+3x+4y-2 分 解因式
;宁波象山包船捕鱼 宁波象山包船捕鱼
;
的事。 ? 她不属于我们,因为她是天使。 是“国家”错了 ? 在民法的慈母般的眼里,每一个人就是整个国家。——孟德斯鸠 1 ? 一百年前的法兰西。正义的一天—— ? 1898年1月13日,著名作家左拉在《震旦报》上发表致共和国总统的公开信,题为《我控诉》,将一宗为当局所讳的 冤案公曝天下,愤然以公民的名义指控“国家犯罪”,替一位素昧平生的小人物鸣不平…… ? 该举震撼了法兰西,也惊动了整个欧洲。许多年后,史家甚至视之为现代舆论和现代知识分子诞生的标志。 ? 事件源于法兰西第三共和时期,1894年,35岁的陆军上尉、犹太人德雷福斯受诬向 德国人出卖情报,被军事法庭判终身监禁。一年后,与此案有关的间谍被擒,实德雷福斯清白。然而,荒谬登场了,受自大心理和排犹意识的怂恿,军方无意纠错,理由是:国家尊严和军队荣誉高于一切,国家不能向一个“个人”低头。这个坚持得到了民族主义情绪的响应,结果,间谍 获释,而德雷福斯“为了国家利益”——继续当替罪羊。 ? 面对如此不义,左拉怒不可遏,连续发表《告青年书》《告法国书》,披露军方的弥天大谎,痛斥司法机器滥用权力,称之“最黑暗的国家犯罪”,称法兰西的共和荣誉与人权精神正经历恶梦。尤其《我控诉》一文,如重磅炸 弹令朝野震动,所有法国报刊都卷入了争论,左拉更被裹至旋涡中心:一面是良知人士的声援;一面是军方、民族主义者的谩骂,甚至有暗杀恐吓。 ? 左拉没退缩,他坚信自己的立场:这绝非德雷福斯的一己遭遇,而是法兰西公民的安全受到了国家权力的伤害;拯救一个普通人的命运 就是拯救法兰西的未来,就是维护整个社会的道德荣誉和正义精神。在左拉眼里,他这样做,完全是履践一个公民对祖国和同胞的义务,再正常再应该不过了。 ? 然而,令人悲愤的一幕又出现了:一个真正的爱国者总是为他的国家所误解。同年7月,军方以“诬陷罪”起诉左拉。作家在 友人的陪伴下出庭,他说:“上下两院、文武两制、无数报刊都可能反对我。帮助我的,只有思想,只有真实和正义的理想……然而将来,法国将会因为我挽救了她的名誉而感谢我!” ? 结果,左拉被判罪名成立,流亡海外。 ? 左拉远去了,但这个英勇的“叛国者”形象,却像一颗尖 锐的沙子折磨着法国人的神经,这毕竟是有着反强权传统、签署过《人权宣言》的民族……终于,敏感的法兰西被沙粒硌疼了,渐渐从“国家至上”的恍惚中醒来:是啊,不正是“个人正义”守护着“国家正义”吗?不正是“个体尊严”组建了“国家尊严”吗?国家唯一让国人感到骄傲 和安全的,不正是它对每个公民作出的承诺与保障吗?假如连这点都做不到,国家还有什么权威与荣誉可言?还有什么拥戴它的理由? ? 愈来愈多的民意开始倒戈,向曾背弃的一方聚集。在舆论压力下,1906年7月,即左拉去世后第4年,法国最高法院重新宣判:德雷福斯无罪。 ? 军方 败诉。法院和政府承认了自己的过失。 ? 法兰西历史上,这是国家首次向一个“个人”低下了它高傲的头颅。 ? 德雷福斯案画上了公正的句号。正像九泉之下的左拉曾高高预言的那样:法兰西将因自己的荣誉被拯救而感激那个人——那个率先控诉母邦的人。 ? 作为一桩精神事件,德 雷福斯案之所以影响至深、且像爱国课本一样传颂,并不因为它“蚍蜉撼大树”的奇迹,而在于它紧咬不舍的人权理念,在于它揭呈了现代文明的一个要义:生命正义高于国家利益;人的价值胜过一切权威;任何蔑视、践踏个体尊严和利益的行为都是犯罪,都是对法之精神的背叛、对生 命的背叛。 ? 可以说,这是世界人权史上的一次重要战役,在对“人”的理解和维护上,它矗起了一座里程碑。 2 ? 国家是有尊严的,但尊严不是趾高气扬的“面子”,它要建立在维护个体尊严和保障个体权益的承诺上,要通过为公众服务的决心、能力和付诸来兑现,它不能预支,更 不能摊派。在价值观上,国家权威与公民权益不存在大小之分,个体永远不能沦为集体羽翼下的雏鸟或孵卵,否则,就会给权力滥用国家名义谋集团之私或迫害异己提供依据。孟德斯鸠早就说过:“在民法慈母般的眼里,每一个人就是整个国家。”法国《人权宣言》、美国《权利法案》 及联合国的《公民权利与政治权利公约》,都开宗明义地宣扬了该常识。 ? 如果为了国家利益可任意贬低个体尊严,如果牺牲个体自由与权利的做法得到了宣传机器的大肆鼓吹,那么,不管该国家利益被冠以怎样的“崇高”或“伟大”,其本质都是可疑的。任何政府和部门之“权威”, 惟有在代表公意时才具合法性,才配得上民间的服从。在一个靠常识维护的国家里,每一个“个人”都是唯一性资源,都拥有平等的社会席位,每个人的福祉都是国家重要的责任目标……正是基于这些同构、互动和彼此确认的关系,个人才可能成为国家的支持者,才会滋生真正的爱国者 和“人民”概念。 ? 权力会出错,领袖会出错,政府会出错,躲闪抵赖本来就可耻,而将错就错、封杀质疑就更为人不齿了,也丢尽了权力的颜面。 ? 有无忏悔的勇气,最能检验一个团体、政府或民族的素养与质量。 ? 1992年11月,教皇约翰?保罗二世为17世纪被教廷审判的伽利略正 式平反,不久又致函教皇科学院,为达尔文摘掉了“异端”罪名。连素以“万能”著称的上帝代言人都承认“寡人有疾”,更何况凡夫俗子?同时也说明,这不失为一位胸襟辽阔、值得信赖的“上帝”。 ? 1997年,美国总统克林顿正式为士兵艾迪?卡特平反,并向其遗属颁发了一枚迟到 的勋章。艾迪是一位非洲裔美军士兵,曾在反法西斯战争中立下战功,后被误控有变节行为,停止服役。1963年,艾迪抑郁而终,年仅47岁。事隔半个世纪,美国政府终于良知醒来,并向亡魂道歉。 ? 曾炒得沸沸扬扬的《抓间谍者》禁书案,经过3年审理,于1988年10月,由英国最高法 院作出终审判决:驳回政府起诉。这部被视为泄露国家机密的书,拥有自由印刷、发行和报刊转载的权利。 ? 不得不承认,当今世上,让政府向个体认错、大人物向小人物认错、大国向小国认错……确属不易,关键能否有一种良好的理性制度、一套健正的社会价值观和文化心理——既 要有周严的法律保障,又要有公正的民心资源和舆论环境。要坚信:错了的人只有说“我错了”时——才不会在精神上惨败,才不会在道德和尊严上输光。今天,在美国前总统尼克松的私人图书馆里,最常听到的便是他的录音资料:“犯下错误不可怕,可怕的是掩盖错误……”谁也没过 多责备这位自责的老人,在他去世一周年之际,美国仍发行了印有其头像的纪念邮票。 3 ? 德雷福斯案,至少有两点让一百年后的我尤为感慨,也是让我吃惊和敬羡的地方。 首先,舆论的“讨论空间”如此之大。 ? 它包含“此类政事竟允许舆论参与”(即民众的知情范围和讨论范围) 和“舆情的规模、幅度、持续性竟如此强劲”(民众对公共事件的积极性)两层意思。一个世纪前,一个冒犯国家威严、对政府不恭的声音竟能顺利出笼,竟有报刊敢“别有用心”地发表——且不受指控,确乎不可思议。而在一场对手是国家机器的较量中,竟有那么多的民间力量汹涌而 入,不仅不避嫌、不为尊者讳,反而敢于大声对政府说“不”,就更令人惊叹了。试想,在另一些国度,即使有左拉般的斗士站出来,谁又保会有《震旦报》那样不惧烧身的媒体呢?《我控诉》能公开问世并迅速传播,至少说明一点:在当时法国,此类政治问题的讨论空间是存在的,或 者说,言论自由有较可靠的社会根基和法律依据,连政府都没想要去背叛它——这确令人鼓舞。否则,若话题一开始就被封杀,“德雷福斯”连成为街头巷议的机会都没了。而在别的地方和时代,让这类事胎死腹中、秘密流产后偷偷埋掉,是最容易想到和做到的。 ? 其次,事件的理性 结局。 ? 表面上,迎合了一个再朴素不过的公式:邪不压正!真理必胜!但实际生活中,要维持此公式的有效却极难。“正义”“真理”,从主观的精神优势到客观的力量优势,中间有很长的崎岖和险势。个人挑战权威的例子不罕见,但能迅速赢得社会同情、升至一场全民性精神运动 并获胜,即不简单了。其中,既有先驱者的孤独付出和后援力量的锲而不舍,又有来自权力的某种程度的精神合作与妥协,否则,法兰西又徒添几条为真理殉葬的嗓子或烈士而已。该案的结局是令人欣慰的,它不仅实现了左拉的控诉企图,且让“真理”用短短8年就显示了它神圣的逻辑 力量。 ? 政府最终选择了真相,选择了理性,即使它是被迫的“不得不”,这个让步也值得嘉许和为后世所纪念。它需要勇气,需要文化和理性的支持,或许还受到了某种古老榜样的注视与鼓励……这与法兰西深入人心的自由传统和民主渊源有关,与制度自身的空间和弹性有关。左拉 的胜利,乃欧洲现代民主精神的胜利。在无数人组成的“个人”面前,任何国家和政府都是渺小的;知耻近乎勇,承认过失乃维护荣誉的唯一方法……想到并做到这些,对一个诞生过狄得罗、伏尔泰、卢梭的民族来说,固然在信仰资源和精神背景上不是难事,但它所费周折和成本也令人 反思,比如曾将左拉逼入绝境的“国家主义”和“民族主义”。 ? 德雷福斯案距法国大革命已有一个世纪,在由拉斐德起草的号称“旧制度死亡书”的《人权宣言》里,早就宣告了社会对“人”的种种义务—— ? “在权利方面,人们生来是而且始终是自由平等的。”“任何政治结合的 目的都在于保存人之自然的和不可动摇的权利。这些权利就是自由、财产、安全和反抗压迫。”“凡权利无保障和分权未确立的社会,就没有宪法可言。”“自由传达思想和意见是人类最宝贵的权利之一;因此,各个公民都有言论、著述和出版的自由。” ? 可最初的德雷福斯和左拉, 不仅没享受到以上保护,反而遭及同部宣言中其它条款的迫害:“意见的发表不得扰乱法律所规定的公共秩序”“法律有权禁止有害社会的行为”……可见,再伟大的法律和政治文书,都难免给权力留出“利己性司法解释”和“选择性依法”的机会。而这类舞弊,在今天的很多国家仍司 空见惯。 ? 英国学者戴雪说过一句寓意深远的话:“不是宪法赋予个人权利与自由,而是个人权利产生宪法。”是啊,真正的法不是刻在大理石或纪念碑上,而是栖息于人的日常生活和社会细节中。唯一让制度和政党具有“合法”性的,是每个社会成员的权利和福祉,
十字相乘法(八年级数学精品课件)
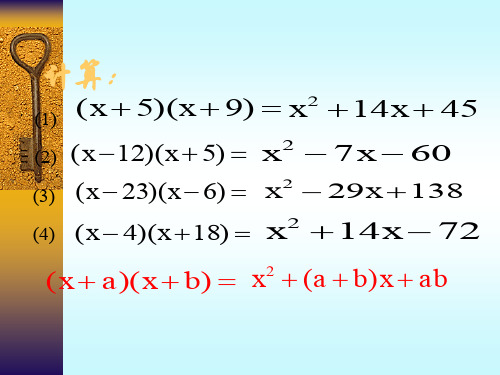
例2、把 y4-7y2-18 分 解因式
例3、把 x2-9xy+14y2 分解因式
用十字相乘法分解下列因式
1、x4-13x2+36 2、x2+3xy-4y2 3、x2y2+16xy+48 4、(2+a)2+5(2+a)-36
5、x4-2x3-48x2
例4、把 6x2-23x+10 分解因式 十字相乘法的要领是:“头尾
十字相乘法
“十字相乘法”是乘法公式: (x+a)(x+b)=x2+(a+b)x+ab的反 向运算,它适用于分解二次三 项式。
例1、把 x2+6x-7分解因式
十字相乘法(借助十字交叉线分解因式的方法)
例一:
x2 6x 7 (x 7)(x 1)
x
7
x 1
x7x 6x
因式分解:
(1) x2 14x 45= (x 5)(x 9) (2) x2 7 x 60= (x 12)(x 5)
(3) x2 29x 138= (x 23)(x 6)
(4) x2 14x 72= (x 4)(x 18) x2 (a b)x ab = (x a)(x b)
分解,交叉相乘,求和凑中,观 察试验”。
1、8x2-22x+15
2、14a2-29a-15 3、4m2+7mn-36n2
4、10(y+1)2-29(y+1)+10
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
八年级数学十字相乘法因式分解

2
5、 x -(a+1) x+a 答案 (x-1)(x-a)
2
例5 将 2x -3xy-2y +3x+4y-2 分 解因式 2 2 解: 2x -3xy-2y +3x+4y-2 2 2 =(2x -3xy-2y )+3x+4y-2
2
2
=(2x +y)(x-2y)+3x+4y-2 =(2x +y-1)(x-2y+2)
2
(x-2y)
-1
2
-4+1=-3
2(2x+y) - (x- 2 y)=3x+4y
;
/ 凤凰
stz31qus
月饼啊!”耿英自己,则会感到很对不起心爱的大壮。因为,那一轮中秋的圆月,只看到了坐在故乡小河边上那块儿大坐台上 的大壮,而大壮是在等着月儿爷爷给他传递相思之情的啊!耿正也会想起来他的秀儿。他知道,秀儿那天肯定会很想念他,而 他却给忙得忘记了八月十五节!愧疚之余,耿正会在心里告诉秀儿:“秀儿,对不起,我没有忘记了你,我只是太忙了啊!” 当然,他们还都会思念一会儿娘和小妹妹,还有已经不在人世的爹爹,以及年迈的姥娘和姥爷„„他们太想赶快回家去了,但 赚的银子还远远不够实现爹爹的那个梦想啊!好在还不到返家的最后期限呢。于是,他们暗下决心:再咬牙干几年吧!即使脱 皮掉肉,我们也一定要为爹爹实现梦想!就这样,耿正兄妹三人坚持着为了实现爹爹的美好梦想而夜以继日地辛苦忙碌着„„ 尽管开这个小饭庄确实非常辛苦,但其利润还是相当不错的。如此,兄妹三人似乎找到了能够充分施展他们自己身手的地方, 所以也就不再考虑改做其他的生意了。如果不是在那个和煦春日里的上午,那位叔叔辈儿的稷山李老乡的不期造访,耿正兄妹 三人很可能会继续干下去,一直干到他们必须返家回归故乡的最后期限„„72第七十回 换牌“南北小饭庄”|(“百日”祭奠 做完后,换牌“南北小饭庄”;招牌响亮创意好,北方饭菜超火爆。)那天,在为梁爷爷和梁奶奶做完“百日”祭奠后返回来 的路上,耿正和弟弟妹妹商议:“咱们应该给小饭店换个招牌了。这样一来,或许可以使它焕发新的生机呢!”听了哥哥的话, 耿英点点头说:“是啊,梁爷爷和梁奶奶刚刚去世的时候,咱们不忍心摘了他们亲自挂上去的那个招牌。如今‘百日’也过了, 是该换一换了。肯定得啊,本来想着来咱们饭店吃饭买饼的人,一看到这个招牌,也大多会望而却步的呢!”耿直说:“换个 招牌当然对了,可给咱们的饭店起个什么样的名字呢?我想啊,一定要起一个让人们一看了,就很想进去品尝一番的好名字!” 耿正说:“我初步考虑了一个,叫‘南北小饭庄’怎么样?”耿英想一想,说:“咱们从北方来,在南方开了个小饭店,北南 合璧!我看这个名字挺不错的,很有创意呢!”耿直说:“可这个字号里边,没有把我们的姓氏加进去啊,应该叫‘耿记南北 小饭庄’才完整!”耿正说:“这景德镇上只有咱们这一家‘南北小饭庄’,我看就没有必要把我们的姓氏加进去了吧。”耿 英也说:“我看也没有必要加了,咱这个名字主要体现的是‘南北’两个字;倘若再加上姓氏,不但掩盖了主题,而且还显得 累赘呢!”耿直仔细琢磨一番之后,说:“可不是耶,还是不加得好,那就叫‘南北小饭庄’吧,挺响亮的名字呢!”耿英补 充说:“主要是人们一看招牌,就知道咱们的小饭店里
八年级数学十字相乘法

1.十字相乘法分解因式的公式:x2+(a+b)x+ab=(x+a)(x+b)
2.能用十字相乘法来分解因式的二次三项式的系数的 特点:常数项能分解成两个数的积,且这两个数的和 恰好等于一次项的系数。
3.在用十字相乘法分解因式时,因为常数项的分解因 数有多种情况,所以通常要经过多次的尝试才能确定 采用哪组分解来进行分解因式。
1、计算 (1)(x+3)(x+4)
(2)(x+3)(x-4)
整式乘法中,有 (x+a)(x+b)=x2+(a+b)x+ab
(3) (x-3)(x+4)
(4) (x-3)(x-4) 2、有什么快速计算的方法?
整式的乘法
(x+a)(x+b)=x2+(a+b)x+ab x2+(a+b)x+ab=(x+a)(x+b)
因式分解
如果二次三项式x2+px+q中的常数项系数q能分解 成两个因数a、b的积,而且一次项系数p又恰好是a+b, 那么x2+px+q就可以进行如上的因式分解。
试一试:把x2+3x+2分解因式
∵ (+1) ×(+2)=+2 常数项
(+1)+(+2)=+3 一次项系数
x ∴x
1
2
十字交叉线
解:原式 ( x 1)( x 2)
(4)x2-11x-12 (5)x2+13x+12 (6)x2-x-12
对于x2+px+q
(1)当q>0时,a、b﹍同﹍号,且a、b的符号与p的符号
八年级数学十字相乘法因式分解-P

实际在使用此公式时,需要把 一次项系数和常数项进行分拆,在 试算时,会带来一些困难。
下面介绍的方法,正好解决了 这个困难。
即:x 2+(p+q)x+pq=(x+p)(x+q)
解因式
解:2(6x 2+x)2-11(6x 2+x) +5 = [(6x 2+x) -5][2(6x 2+x)-1] = (6x 2+x-5) (12x 2+2x-1 ) = (6x -5)(x +1) (12x 2+2x-1 )
1
-5
6-52来自-1-1-10=-11
1
1
-5+6=1
练习:将下列各式分解因式 1、 7x 2-13x+6 答案(7x+6)(x+1)
例2 分解因式 3x 2-10x+3
解:3x 2-10x+3
x
-3
=(x-3)(3x-1) 3x
-1
-9x-x=-10x
例3 分解因式 5x 2-17x-12
解:5x 2-17x-12 5x
+3
=(5x+3)(x-4) x
-4
-20x+3x=-17x
例4 将 2(6x 2+x) 2-11(6x 2+x) +5 分
=(2x 2-3xy-2y 2)+3x+4y-2
=(2x +y)(x-2y)+3x+4y-2
=(2x +y-1)(x-2y+2)
2
1
(2x+y)
-1
1
-2 (x-2y)
2
-4+1=-3
2(2x+y) - (x- 2 y)=3x+4y
x
p
x
人教版八上数学之十字相乘法及分组分解法(基础)知识讲解
十字相乘法及分组分解法(基础)【学习目标】1. 熟练掌握首项系数为1的形如pq x q p x +++)(2型的二次三项式的因式分解.2. 基础较好的同学可进一步掌握首项系数非1的简单的整系数二次三项式的因式分解.3. 对于再学有余力的学生可进一步掌握分数系数;实数系数;字母系数的二次三项式的因式分解.(但应控制好难度)4. 掌握好简单的分组分解法. 【要点梳理】要点一、十字相乘法利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法.对于二次三项式2x bx c ++,若存在pq cp q b=⎧⎨+=⎩ ,则()()2x bx c x p x q ++=++要点诠释:(1)在对2x bx c ++分解因式时,要先从常数项c 的正、负入手,若0c >,则p q 、同号(若0c <,则p q 、异号),然后依据一次项系数b 的正负再确定p q 、的符号(2)若2x b x c ++中的b c 、为整数时,要先将c 分解成两个整数的积(要考虑到分解的各种可能),然后看这两个整数之和能否等于b ,直到凑对为止.要点二、首项系数不为1的十字相乘法在二次三项式2ax bx c ++(a ≠0)中,如果二次项系数a 可以分解成两个因数之积,即12a a a =,常数项c 可以分解成两个因数之积,即12c c c =,把1212a a c c ,,,排列如下:按斜线交叉相乘,再相加,得到1221a c a c +,若它正好等于二次三项式2ax bx c ++的一次项系数b ,即1221a c a c b +=,那么二次三项式就可以分解为两个因式11a x c +与22a x c +之积,即()()21122ax bx c a x c a x c ++=++.要点诠释:(1)分解思路为“看两端,凑中间”(2)二次项系数a 一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项式,最后结果不要忘记把提出的负号添上.要点三、分组分解法对于一个多项式的整体,若不能直接运用提公因式法和公式法进行因式分解时,可考虑分步处理的方法,即把这个多项式分成几组,先对各组分别分解因式,然后再对整体作因式分解——分组分解法.即先对题目进行分组,然后再分解因式.要点四:添、拆项法把多项式的某一项拆开或填补上互为相反数的两项(或几项),使原式适合于提公因式法、公式法或分组分解法进行分解.要注意,必须在与原多项式相等的原则下进行变形.添、拆项法分解因式需要一定的技巧性,在仔细观察题目后可先尝试进行添、拆项,在反复尝试中熟练掌握技巧和方法. 【典型例题】 类型一、十字相乘法1、将下列各式分解因式: (1); (2)21016x x -+; (3)2310x x --【答案与解析】解:(1)因为78x x x -=-所以:原式=()()78x x +-(2)因为2810x x x --=-所以:原式=()()28x x --(3)()()()2210331052x x x x x x --=-+-=-+-【总结升华】常数项为正,分解的两个数同号;常数项为负,分解的两个数异号. 二次项系数一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项式,最后结果不要忘记把提出的负号添上.举一反三:【高清课堂400150 十字相乘法及分组分解法 例1】【变式1】分解因式:(1)1072++x x ; (2)822--x x ; (3)2718x x --+ 【答案】解:(1)()()271025x x x x ++=++(2) ()()22842x x x x --=-+(3) ()()22718(718)29x x x x x x --+=-+-=--+【变式2】(2016秋·闵行区期末)因式分解:()()222812x x x x +-++.【答案】解:()()222812x xx x +-++=()()2226x x xx +-+-=()()()()1223x x x x -+-+.【高清课堂400150 十字相乘法及分组分解法 例1】2、将下列各式分解因式: (1)22355x x +-; (2)25166x x ++ (3)22616x xy y --; (4).【思路点拨】(3)题216y -可看成常数项,21682,826y y y y y y -=-⨯-+=-.(4)题可将()2x +看成一个整体来分解因式. 【答案与解析】 解:(1)22355x x +-=()315x x ⎛⎫+- ⎪⎝⎭; (2)251116623x x x x ⎛⎫⎛⎫++=++ ⎪⎪⎝⎭⎝⎭. (3)()()2261682x xy y x y x y --=-+;(4)因为()()()25242292x x x -+-+=-+所以:原式()()225522x x =+-+-⎡⎤⎡⎤⎣⎦⎣⎦ ()()2158x x =-+【总结升华】十字相乘法的方法简单点来讲就是:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数.注意观察式子结构,能够看作整体的看作整体.举一反三:【变式】将下列各式分解因式:(1)21136x x -+; (2)251124a a --; (3)10722+-xy y x ; (4)()()342++-+b a b a . 【答案】 解: (1)22111121366332x x x x x x ⎛⎫⎛⎫-+=+-=+- ⎪⎪⎝⎭⎝⎭; (2)2513112443a a a a ⎛⎫⎛⎫--=-+ ⎪⎪⎝⎭⎝⎭; (3)()()2271025x y xy xy xy -+=--;(4)()()()()24313a b a b a b a b +-++=+-+-.3、将下列各式分解因式: (1);(2)【答案与解析】 解:(1)因为91019y y y +=所以:原式=()()2335y y ++(2)因为21183x x x -=所以:原式=()()2379x x +-【总结升华】十字相乘法的方法简单点来讲就是:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数. 举一反三:【变式】分解因式:(1)2314x x +-;(2)2344x x --+;(3)2631105x x +-; 【答案】解:(1)()()22314341311x x x x x x +-=-+=--; (2)()()223444432123x x x x x x --+=--=+-; (3)()()263110521537x x x x +-=+-. 类型二、分组分解法4、(2015春•重庆校级期中)先阅读下列材料,然后回答后面问题: 将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.能分组分解的多项式通常有四项或六项,一般的分组分解有四种形式,即“2+2”分法、“3+1”分法、“3+2”分法及“3+3”分法等. 如“2+2”分法: ax+ay+bx+by=(ax+ay )+(bx+by ) =a (x+y )+b (x+y ) =(x+y )(a+b ) 如“3+1”分法:2xy+y 2﹣1+x 2=x 2+2xy+y 2﹣1=(x+y )2﹣1 =(x+y+1)(x+y ﹣1)请你仿照以上方法,探索并解决下列问题:(1)分解因式:x 2﹣y 2﹣x ﹣y ;(2)分解因式:45am 2﹣20ax 2+20axy ﹣5ay 2;(3)分解因式:4a 2+4a ﹣4a 2b ﹣b ﹣4ab+1. 【思路点拨】(1)首先利用平方差公式因式分解因式,进而提取公因式得出即可; (2)将后三项运用完全平方公式分解因式进而利用平方差公式分解因式即可; (3)重新分组利用完全平方公式分解因式得出即可. 【答案与解析】解:(1)x 2﹣y 2﹣x ﹣y =(x+y )(x ﹣y )﹣(x+y ) =(x+y )(x ﹣y ﹣1); (2)45am 2﹣20ax 2+20axy ﹣5ay 2=45am 2﹣5a (4x 2﹣4xy+y 2)=5a[9m 2﹣(2x ﹣y )2] =5a (3m ﹣2x+y )(3m+2x ﹣y );(3)4a 2+4a ﹣4a 2b ﹣b ﹣4ab+1=(4a 2+4a+1)﹣b (4a 2+4a+1)=(2a+1)2(1﹣b ). 【总结升华】此题主要考查了提取公因式法分解因式以及分组分解法分解因式,正确分组是解题关键. 举一反三:【变式】分解因式:22244a b ab c +-- 【答案】解:原式()()()22222(44)222a ab b c a b c a b c a b c =-+-=--=-+--.。
八年级初二数学上册人教版 十字相乘法 名师教学PPT课件
25
思考题:把下列各式分解因式
(1) 2(x y)2 (x y)( x y) 6(x y)2
(2)(x y)(2x 2 y 3) 2
(1)(-x+5y)(3x-y) (2)(2x-2y+1)(x-y-2)
好好学习 天天向上
26
(3)(x+y)2-4(x+y)-5 =(x+y+1)(x+y-5)
对于x2+px+q
(1)当q>0时,a、b﹍﹍同号,且a、b的符号与p的符号﹍﹍相。同
(2)当q<0时,a、b﹍﹍异号,且 ﹍﹍a、﹍b中﹍绝﹍对﹍值﹍较大﹍的﹍因与数p的符号相同。
好好学习 天天向上
13
例2:试将 x2 6x 16 分解因式
解: x2 6x 16
x2 6x 16
x 8x 2
一个二三项式
两个一次二项式相乘的积
因式分解
如果二次三项式x2+px+q中的常数项系数q能 分解成两个因数a、b的积,即q=ab而且一次项 系数p又恰好是a、b的和,即p=a+b,那么 x2+px+q就可以好好进学习行天如天上向上的因式分解9。
试一试:把x2+3x+2分解因式
分析∵ (+1) ×(+2)=+2
8.(x-2)(x-3)= x2-5x+6
好好学习 天天向上
7
(x+a)(x+b) = x2+(a+b)x+ab
1. (x+2)(x+1) =x2+3x+2 2. (x+2)(x-1) =x2+x-2
3. (x-2)(x+1) =x2-x-2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
十字相乘法分解因式
一、教学目标:
1、进一步理解因式分解的定义;
2、会用十字相乘法进行二次三项式(q px x ++2)的因式分解;
3、通过学生的不断尝试,培养学生的耐心和信心,同时在尝试中提高学生的观察能力。
二、教学的重点、难点
教学重点:能熟练应用十字相乘法进行二次三项式(q px x ++2)的因式分解。
教学难点:在q px x ++2分解因式时,准确地找出a 、b ,使p ab =,q b a =+。
三、导学过程:
(一)知识回顾,创设情境,导入新课:
1、什么叫分解因式?分解因式的方法有那些?(1,提取公因式法;2,公式法)
2、你知道2ax 2+6ax+4a=2a(x 2+3x+2) 分解因式吗?
(二)自主学习
我们知道()()22356x x x x ++=++,反过来,就得到二次三项式256x x ++的因式分解形式,即()()25623x x x x ++=++,其中常数项6分解成2,3两个因数的积,而且这两个因数的和等于一次项的系数5,即6=2×3,且2+3=5。
一般地,由多项式乘法,()()()2x a x b x a b x ab ++=+++,反过来,就得到
请直接口答计算结果
内容见课件:
(三)合作探索
这就是说,对于二次三项式2x px q ++,如果能够把常数项q 分解成两个因数a 、b 的积,并且a+b 等于一次项的系数p ,那么它就可以分解因式,即()()()22x px q x a b x ab x a x b ++=+++=++。
可以用交叉线来表示:
十字相乘法的定义:利用十字交叉来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
x x +a +b
(四)、展示交流:
例1 把232x x ++分解因式。
分析:这里,常数项2是正数,所以分解成的两个因数必是同号,而2=1×2=(-1)(-2),要使它们的代数和等于3,只需取1,2即可。
例2 把342
++x x 分解因式。
例3 把
322--x x 分解因式。
(1)对于二次项系数为1方法的特征是“拆常数项,凑一次项”
当常数项为正数时,把它分解为两个同号因数的积,因式的符号与一次项系数的符号相同;
当常数项为负数时,把它分解为两个异号因数的积,其中绝对值较大的因数的符号与一次项系数的符号相同.
x 2-5x+6 x 2
-5x-6
X 2+5x-6 X 2+5x+6 练一练:
(1)x 2-7x+12 (2)x 2-4x-12
(3)x 2+8x+12 (4)x 2-11x-12
例4 2x 2-3x-2
对于二次项系数不是1的二次三项式
它的特征是“拆两头,凑中间”
当二次项系数为负数时,先提出负号,使二次项系数为正数,然后再看常数项; 常数项为正数时,应分解为两同号因数,它们的符号与一次项系数的符号相同; 常数项为负数时,应将它分解为两异号因数,使十字连线上两数之积绝对值较大的一组与一次项系数的符号相同
注意:用十字相乘法分解因式,还要注意避免以下两种错误出现:一是没有认真地验证交叉相乘的两个积的和是否等于一次项系数;二是由十字相乘写出的因式漏写字母.
例5:
16162+--x x 例6 分解因式 3x 2 -10x +3
例7 分解因式 5x 2 -17x -12
独立练习:把下列各式分解因式
作业:
(1)x 2-6x+8 (2)y 2+7y+12
(3)x 2-5x+4 (4)x 2+2x -8
3
52)5(2--x x 383)6(2-+x x 10235)7(22-+ab b a 3
84)8(2
++m m
(五)拓展提高
483715222+-++a a x x 675101162
2-+--x x y y
把下列各式分解因式
六、自主小结,达成共识
1、这堂课中你学到什么?你有什么感受?
2、你还有什么问题需要解决。
教学反思:
187)1(24-+x x 910)2(24+-x x 6552)3(2
2-+-+-y x y xy x。
