不等式约束的最优化问题
不等式约束拉格朗日乘子法

不等式约束拉格朗日乘子法摘要:一、引言二、不等式约束的拉格朗日乘数法简述三、例1:极值点在可行域内四、例2:极值点在可行域外五、总结正文:一、引言拉格朗日乘数法是一种用于解决优化问题的数学方法,特别是在处理带有约束条件的优化问题时,具有很高的实用价值。
在不等式约束条件下,拉格朗日乘数法同样具有很好的应用效果。
本文将介绍不等式约束的拉格朗日乘数法的基本原理和应用实例。
二、不等式约束的拉格朗日乘数法简述不等式约束的拉格朗日乘数法基于拉格朗日乘数法的基本思想,通过引入拉格朗日乘数,将原优化问题转化为求解一个新的优化问题,从而实现对原问题的求解。
在不等式约束条件下,拉格朗日乘数法可以有效地处理约束条件的影响,得到可行解甚至最优解。
三、例1:极值点在可行域内假设我们要求解一个带有不等式约束的最小化问题:min f(x)s.t.g(x) < 0其中,f(x) 和g(x) 是已知函数,x 是决策变量。
我们可以通过构建拉格朗日函数L(x, λ) = f(x) + λg(x),其中λ 是拉格朗日乘数,来引入约束条件。
然后求解L(x, λ) 的极小值点,即可得到原问题的最优解。
如果极值点在可行域内,我们可以通过求解梯度方程得到最优解。
四、例2:极值点在可行域外如果极值点在可行域外,此时最值可能出现在边界条件上。
我们可以通过构建拉格朗日函数L(x, λ) = f(x) + λg(x),然后分情况讨论求解梯度方程,得到最优解。
五、总结不等式约束的拉格朗日乘数法是一种有效的求解优化问题的方法,在处理带有不等式约束条件的优化问题时,具有很高的实用价值。
通过引入拉格朗日乘数,将原优化问题转化为求解一个新的优化问题,从而实现对原问题的求解。
最优化问题的建模与解法

最优化问题的建模与解法最优化问题(optimization problem)是指在一组可能的解中寻找最优解的问题。
最优化问题在实际生活中有广泛的应用,例如在工程、经济学、物流等领域中,我们经常需要通过数学模型来描述问题,并利用优化算法来求解最优解。
本文将介绍最优化问题的建模和解法,并通过几个实例来说明具体的应用。
一、最优化问题的数学建模最优化问题的数学建模包括目标函数的定义、约束条件的确定以及变量范围的设定。
1. 目标函数的定义目标函数是一个表达式,用来衡量问题的解的优劣。
例如,对于一个最大化问题,我们可以定义目标函数为:max f(x)其中,f(x)是一个关于变量x的函数,表示问题的解与x的关系。
类似地,对于最小化问题,我们可以定义目标函数为:min f(x)2. 约束条件的确定约束条件是对变量x的一组限制条件,用来定义问题的可行解集合。
约束条件可以是等式或不等式,通常表示为:g(x) ≤ 0h(x) = 0其中,g(x)和h(x)分别表示不等式约束和等式约束。
最优化问题的解必须满足所有的约束条件,即:g(x) ≤ 0, h(x) = 03. 变量范围的设定对于某些变量,可能需要限定其取值的范围。
例如,对于一个实数变量x,可能需要设定其上下界限。
变量范围的设定可以通过添加额外的不等式约束来实现。
二、最优化问题的解法最优化问题的解法包括数学方法和计算方法两种,常见的数学方法有最优性条件、拉格朗日乘子法等,而计算方法主要是通过计算机来求解。
1. 数学方法数学方法是通过数学分析来求解最优化问题。
其中,常见的数学方法包括:(1)最优性条件:例如,对于一些特殊的最优化问题,可以通过最优性条件来判断最优解的存在性和性质。
最优性条件包括可导条件、凸性条件等。
(2)拉格朗日乘子法:对于带有约束条件的最优化问题,可以通过拉格朗日乘子法将原问题转化为无约束最优化问题,从而求解最优解。
2. 计算方法计算方法是通过计算机来求解最优化问题。
最优化问题数学模型

• 进入该区域的飞机在到达区域边缘时,与区域内 飞机的距离应在60km以上;
根据当年竞赛题目给出的数据,可以验证 新进入的飞机与区域内的飞机的距离超过 60公里。
• 最多需考虑六架飞机;
cij xij 表示该队员的成 目标函数:当队员i入选泳姿j时, 绩,否则 cij xij 0 。于是接力队的成绩可表示为
f cij xij .
j 1 i 1
4
5
约束条件:根据接力队要求, xij 满足约束条件
a. 每人最多只能入选4种泳姿之一,即
x
j 1
4
ij
1.
b. 每种泳姿必须有1人而且只能有一人入选,即
分析,对实际问题进行合理的假设、简化,首先考虑用
线性规划模型,若线性近似误差较大时,则考虑用非线 性规划.
例题讲解
例1 1995年全国数学建模A题:飞行管理问题 在约1万米的高空的某边长为160km的正方 形区域内,经常有若干架飞机作水平飞行,区 域内每架飞机的位置和速度向量均由计算机记 录其数据,以便进行飞行管理。当一架欲进入 该区域的飞机到达区域边缘时,计算机记录其 数据后,要立即计算并判断是否会发生碰撞。 若会发生碰撞,则应计算如何调整各架飞机 (包括新进入的飞机)飞行的方向角,以避免 碰撞,且使飞机的调整的幅度尽量小,
目标:求函数极值或最值,求取得极值时变量的取值。
x
1.线性规划
问题:某工厂在计划期内要安排生产I、II两种产品,已 知生产单位产品所需的设备台时及A、B两种原材料的消 耗,如下表所示
I 设备 1 II 2 8台时
约束优化算法:拉格朗日乘子法

拉格朗日乘子法约束优化问题的标准形式为:min (),..()0,1,2,...,()0,1,2,...,ni j f x x R s t g x i m h x j l∈≤===,,:n i j f g h R R →其中约束优化算法的基本思想是:通过引入效用函数的方法将约束优化问题转换为无约束问题,再利用优化迭代过程不断地更新效用函数,以使得算法收敛。
1. 罚函数法罚函数法(内点法)的主思想是:在可行域的边界上筑起一道很高的“围墙”,当迭代点靠近边界时,目标函数陡然增大,以示惩罚,阻止迭代点穿越边界,这样就可以将最优解“挡”在可行域之内了。
它只适用于不等式约束:min (),..0,1,2,...,ni f x x R s tg i m ∈≤=它的可行域为: {|()0,1,2,...,}n i D x R g x i m =∈≤=对上述约束问题,其其可行域的内点可行集0D ≠∅的情况下,引入效用函数:min (,)()()B x r f x rB x =+、 其中11()()mi i B x g x ==-∑或1()|ln(())|m i i B x g x ==-∑ 算法的具体步骤如下:给定控制误差0ε>,惩罚因子的缩小系数01c <<。
步骤1:令1k =,选定初始点(0)0x D ∈,给定10r >(一般取10)。
步骤2:以()k x 为初始点,求解无约束min (,)()()k B x r f x r B x =+ 其中11()()mi i B x g x ==-∑或1()|ln(())|m i i B x g x ==-∑,得最优解()()k k x x r = 步骤3:若()()k k r B xε<,则()k x 为其近似最优解,停;否则,令,1k k r cr k k ==+,转步骤2.2. 拉格朗日乘子法(1)PH 算法:(约数为等式的情况引入)效用函数为()()min (,,)()()()()k k T T k k M x u f x u h x h x h x σσ=++判断函数为()()k k h x φ=当()()k k x φφε=<时迭代停止。
约束问题的优化方法

XR
变形的复合形
可行的新点,用新点代替最坏点, 构成新的复合形,复合形的形状 每改变一次,就向最优点移动一
XC
XL
初始复合形
步,直至逼近最优点。从复合形
法工作原理可看出,实现复合形 法最关键的是:构造复合形和复 合形变换等问题。
XH
0
x1
图4-4复合形法的算法原理
《车辆优化设计与实践》教学课件
4.3.2 方法实现的关键技术
初始点更优的新点,至此完成一
轮迭代。然后,以新点为新的初
始点,即令 X 0 X 。重复以
0
上过程,经过若干次迭代计算后,
最终取得约束最优解。
X X
X1 X0
x1 图4-1 随机方向法的原理
《车辆优化设计与实践》教学课件
4.2.2 方法实现的关键技术
实现随机方向法的关键包括初始点的选择,可行搜方 向的产生和搜索步长的选择等问题。 (1)初始点形成 随机方向法的初始点 X 0必须是一个可行点,即满足全 部不等式约束条件:g j (X 0 ) 0 ( j 1, 2, , m)。当约束条件 较为复杂,用人工不易选择可行初始点时,可用随机 选择的方法来产生。计算随机点的步骤如下: 1)输入设计变量的下限值和上限值,即
式计算随机单位向量 e j
ej
1
rr12jj
1
n
i 1
rij
22
rnj
( j 1, 2, , k)
(4-3)
《车辆优化设计与实践》教学课件
2)取一X 试j 验X步0 长0e0,j 按(4下-4式)计算K个随机点 显然,K个随机点分布在以初始点X 0为中心,以试验 步长 0为半径的超球面上。 3)检验K个随机点X j( j 1, 2, , k)是否为可行点,除 去非可行点,计算余下的可行随机点的目标函数值, 比较其大小,选出目标函数值最小的点 X L。 4)比较X L 和 X 0两点的目标函数值,若 f (X L ) f (X 0 ),则 取X L 和X 0的连线方向 f ( X L ) f ( X 0 ) 作为可行搜索方向 为止。如果缩小到很小(例如 0 106),仍然找不到 一个X L 使 f (X L ) f (X 0 )则说明 X 0 是一个局部极小点,此 时可更换初始点,转步骤1)。
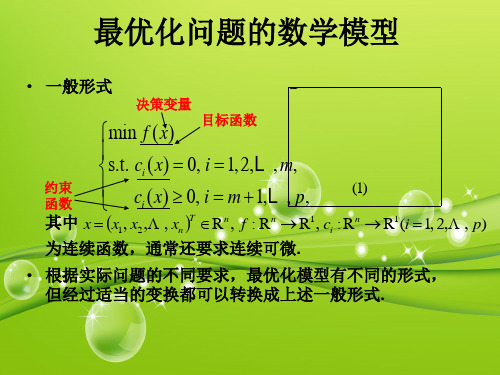
最优化问题的数学模型
为凸集.
1,
0 证明: x , y 为超球中的任意两点, 设
则有:
x 1 y
r ???
x 1 y
r r r 1
即点 x 1 y 属于超球
所以超球为凸集.
注: 常见的凸集:空集,整个欧氏空间 超平面: H
T
aR
n
和实数
,
使得: T x a
a y , x D ,
xR a x
n T
即存在超平面 H y 与凸集 D .
严格分离点
注: 点与闭凸集的分离定理。
y.
D
定理
(点与凸集的分离定理)
是非空凸集,x D, 则存在 非零向量 a R n 使成立
DR
n
目标函数
R ( i 1, 2 , , p )
1
• 根据实际问题的不同要求,最优化模型有不同的形式, 但经过适当的变换都可以转换成上述一般形式.
最优化问题的分类
最优化问题
根据约束条件 分类
m in f ( x ), x R .
n
无约束最优化问题 约束最优化问题 等式约束最优化问题 不等式约束最优化问题 混合约束优化问题
设
a xa x
T T
x D . ( D代 表 D 的 闭 包 )
_ _
定理
(两个凸集的分离定理)
n
x
x
设 D1 , D2 是
且 R 的两个非空凸集, D1 D2 ,
则存在超平面分离 D1 和 D2 , 即存在非零向量 n a R 使得 aT x aT y , x D , y D . 1 2
最优化课后习题答案
最优化课后习题答案最优化课后习题答案最优化是一门重要的数学学科,它研究如何在给定的约束条件下,找到一个最优的解决方案。
在学习最优化课程时,我们通常会遇到一些习题,这些习题旨在帮助我们理解和应用最优化的原理和方法。
本文将为大家提供一些最优化课后习题的答案,以帮助大家更好地掌握这门学科。
1. 线性规划问题线性规划是最优化中的一个重要分支,它主要研究线性约束条件下的最优解。
下面是一个线性规划问题的示例:Maximize Z = 3x + 5ySubject to:x + y ≤ 62x + y ≤ 8x, y ≥ 0首先,我们需要将目标函数和约束条件转化为标准形式。
将不等式约束转化为等式约束,引入松弛变量,得到以下标准形式:Maximize Z = 3x + 5ySubject to:x + y + s1 = 62x + y + s2 = 8x, y, s1, s2 ≥ 0接下来,我们可以使用单纯形法求解该线性规划问题。
根据单纯形法的步骤,我们可以得到最优解为 Z = 22,x = 2,y = 4,s1 = 0,s2 = 0。
2. 非线性规划问题除了线性规划,最优化还涉及到非线性规划问题。
非线性规划是指目标函数或约束条件中存在非线性项的最优化问题。
下面是一个非线性规划问题的示例:Minimize f(x) = x^2 + 3x + 5Subject to:x ≥ 0对于这个问题,我们可以使用求导的方法来找到最优解。
首先,求目标函数的导数:f'(x) = 2x + 3将导数等于零,解得 x = -1.5。
由于约束条件x ≥ 0,所以最优解为 x = 0。
3. 整数规划问题整数规划是指在最优化问题中,决策变量必须取整数值的情况。
下面是一个整数规划问题的示例:Maximize Z = 2x + 3ySubject to:x + 2y ≤ 10x, y ≥ 0x, y 为整数对于这个问题,我们可以使用分支定界法来求解。
不等式简单的线性规划问题利用简单的线性规划求最值
线性规划问题的应用
生产计划
如何安排各种资源(如人力、原材 料、设备等)以生产出最大利润或 最小成本的产品。
货物运输
如何安排车辆或船只运输货物,使 得运输成本最低或运输时间最短。
资源分配
如何将有限的资源分配给不同的项 目或任务,以获得最大的效益。
配料问题
如何在满足一定质量要求的条件下 ,使用最少的原料或以最小的成本 配制出所需的产品。
引入人工变量
对于不等式约束条件,可以引入人工变量来扩展变量的维度,将不等式约束条件 转换为等式约束条件。
不等式约束条件下线性规划问题的求解方法
将不等式约束条件加入目标函数中
将不等式约束条件加入目标函数中,并求解目标函数的最小值或最大值。
利用线性规划求解
对于不等式约束条件下线性规划问题,可以利用线性规划的求解方法,如单 纯形法、椭球法等来求解目标函数的最小值或最大值。
数据科学
1. 研究大数据分析中的优化问题;2. 探索高效的数据处理和特征提取方法;3. 提高数据 分析和处理的精度和效率。
THANKS
谢谢您的观看
迭代法
通过不断迭代,逼近最优解。
优化问题的实际应用
资源分配问题
如何分配有限资源,使得产出最大化或成本最小 化。
运输问题
如何制定最优运输计划,使得运输成本最低且满 足需求。
选址问题
如何在多个候选地点中选择最优地点,使得某项 业务运营成本最低或收益最大。
06
总结与展望
不等式简单的线性规问题求解方法的优缺点
05
利用简单的线性规划解决优化问题
优化问题的定义与分类
定义
优化问题是在一定约束条件下,寻求一个或多个自变量取何值时,使得目标 函数取得极值(极大值或极小值)。
约束优化方法的讲解
2)按经验公式
r0 f x0 1 0 g x j 1 j
m
计算r0 值。这样选取的r0 ,可以是惩罚函数中的障 碍项和原目标函数的值大致相等,不会因障碍项的值 太大则其支配作用,也不会因障碍项的值太小而被忽 略掉。 3.惩罚因子的缩减系数c的选取 在构造序列惩罚函数时,惩罚因子r是一个逐次递 减到0的数列,相邻两次迭代的惩罚因子的关系为:
(k=0,1,2,…)
逐步趋向最优解,直到满足终止准则才停止迭代。
直接解法的原理简单,方法实用,其特点是:
1)由于整个过程在可行域内进行,因此,迭代计算不论 何时终止,都可以获得比初始点好的设计点。 2)若目标函数为凸函数,可行域为凸集,则可获得全域 最优解,否则,可能存在多个局部最优解,当选择的初始 点不同,而搜索到不同的局部最优解。 3)要求可行域有界的非空集。
a) 可行域是凸集;b)可行域是非凸集
间接解法的求解思路:
将约束函数进行特殊的加权处理后,和目标函数结合起来, 构成一个新的目标函数,即将原约束优化问题转化为一个 或一系列的无约束优化问题。
x, 1 , 2 f x 1G hk x g j x 2 H
当迭代点离约束边界越远时,惩罚项愈大,这可看 成是对迭代点不满足约束条件的一种惩罚。
例6-6 用外点法求问题
hk x 0
第四章 非线性规划2-SUMT方法(罚函数法)
第二节 SUMT 方法(罚函数法)一、SUMT 方法的原理SUMT (sequential unconstrained minimization technique )法,序列无约束极小化方法,亦称为罚函数法。
它是一种不等式约束最优化问题的间接解法它的基本思想是将原来的目标函数和约束函数按一定的方式构成一个新的函数,在这个新函数中,既包括目标函数,又包括全部约束函数和一个可以变化的乘子。
当这个乘子按一定的方式改变时,就得到一个新函数序列,求每一个新函数的最优解都是一个无约束最优化问题,这样就把一个约束最优化问题转化为一系列无约束最优化问题进行求解。
所得到的最优解序列将逐步逼近原问题的最优解。
引例一:min ()f X ax = s.t ()0g X b x =-≤ 显然f (X )的最优点为x*=b ,对应的最小值为f (X*)=ab用SUMT 求解函数的最优解 构造函数11(,)()()k k kX r f X r ax r g X b xΦ=-=--0k r >—可变化乘子,它是一个很小的正数。
其最优解为:*()kX r b =+此时对应的(,)k X r Φ的最小值为***1(,)k k X r ax r b x ab Φ=--=+最优点*()k X r 和最小值*(,)k X r Φ均是kr 的函数。
当kr 取不同值时,它们有不同的值,而当0kr →时,**()k X r X b →=,*(,)*k X r f X ab Φ→=(),即最后收敛于约束最优点。
minlim[min (,)]() {|()0}kki r X r f X R X g X X R→Φ==≤∈ 以上分析从理论上说明了无约束最优化问题min (,)kX r Φ与约束优化问题min() {|()0}i f X R X g X X R=≤∈之间的联系:约束非线性规划问题可以通过构造新目标函数序列,用无约束优化方法求其极小点,并逐次逼近原问题的最优点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不等式约束的最优化问题
在实际生产和生活中,我们常常会遇到需要确定某种目标的最优解
决方案的情况,例如,最小成本、最大利润、最长飞行时间等等。
这
种针对某种优化目标的问题就是最优化问题。
当我们考虑最优化问题的时候,通常需要考虑约束条件。
约束条件即
限制性条件,它将问题的解空间控制在一定范围之内,使得问题更贴
近实际情况。
在最优化问题中,不等式约束是最常见的一种约束条件。
本文将从不
等式约束的特点、最小二乘法和KKT条件三个方面进行阐述。
不等式约束的特点
在一个包含n个变量的最优化问题中,不等式约束可以表示为:
G(x) ≤ 0
其中,G(x)是一个n维函数向量,称为约束函数。
它是一组由不等式构成的系统,它将限制x取值范围的空间控制在G(x)≤0的区域中。
而且,不等式约束通常在解的边界上成立。
对于不等式约束的优化问题,我们通常需要利用各种算法求解。
最小二乘法
最小二乘法是一种常用的数学方法,用于寻找某一函数的最佳拟合曲线。
它通常被用于估计数据中存在误差的线性回归模型中。
同时,它也被广泛地用于优化问题中。
在解决最小二乘法问题时,我们可以使用拉格朗日乘子法,显式地添加一个不等式约束。
通过这种方式,我们可以得到方程组的解,从而得到最优解。
KKT条件
在解不等式约束的最优化问题时,KKT条件是一个非常关键的思想。
KKT条件是Karush-Kuhn-Tucker条件的缩写,它是用来描述一类非线性规划问题的必要条件。
这些条件是可行性、拉格朗日对偶、互补松弛和非负性约束等方面的约束。
在不等式约束的最优化问题中,KKT条件是非常重要的,因为它们可以帮助我们建立一个完整的解题框架,并确保我们能够得到正确的结果。
它可以帮助我们确定合理的约束条件,并确保我们的优化方案具有最优性。
结论
在实际生产和生活中,不等式约束的最优化问题是非常常见的。
通过使用最小二乘法和KKT条件,我们可以解决这些问题,从而得到具有最优性的解决方案。
同时,了解不等式约束的特点也是非常重要的,它可以帮助我们设计出可行的优化方案,并确保我们的方案具有最优性和可行性。
