2018北京各区初三数学一模试题分类——二次函数(含代数综合题)
2018年北京市初三数学一模试题分类汇编-作图判定

2018年北京市初三数学一模试题分类汇编作图判定2018西城一模16.阅读下面材料:在复习课上,围绕一道作图题,老师让同学们尝试应用学过的知识设计多种不同的作图方法,并交流其中蕴含的数学原理.已知:直线和直线外的一点P.求作:过点P且与直线l垂直的直线PQ,垂足为点Q P某同学的作图步骤如下:步骤第一步作法以点P为圆心,适当长度为半径作推断P A=PB 弧,交直线l于A,B两点.第二步连接P A,PB,作∠APB的平分线,∠APQ=∠__________交直线l于点Q.直线PQ即为所求作.请你根据该同学的作图方法完成以下推理:∵P A=PB,∠APQ=∠__________,∴PQ⊥l.(依据:__________).PQ⊥l2018石景山一模16.小林在没有量角器和圆规的情况下,利用刻度尺和一副三角板画出了一个角的平分线,他的做法是这样的:如图,(1)利用刻度尺在∠AOB的两边OA,OB上分别取OM=ON;(2)利用两个三角板,分别过点M,N画OM,ON的垂线,交点为P;(3)画射线OP.OAAB则射线OP为∠AOB的平分线.请写出小林的画法的依据.MPO N B(3)分别以点 A ,B 为圆心,大于 AB 的长为半径作弧,两弧相交于点 P ;2018 平谷一模16.下面是“作已知角的角平分线”的尺规作图过程.已知:如图 1,∠MON .MMAO图 1NOP图 2BN求作:射线 OP ,使它平分∠MON . 作法:如图 2,(1)以点 O 为圆心,任意长为半径作弧,交 OM 于点 A ,交 ON 于点 B ; (2)连结 AB ;12(4)作射线 OP .所以,射线 OP 即为所求作的射线.请回答:该尺规作图的依据是 .2018 怀柔一模16. 阅读下面材料:在数学课上,老师提出利用尺规作图完成下面问题:已知:△ABC.求作:△ABC 的内切圆.AB C小明的作法如下:如图,(1)作∠ABC ,∠ACB 的平分线 BE 和 CF ,两线相交于点 O; (2)过点 O 作 OD ⊥BC ,垂足为点 D; (3)点 O 为圆心,OD 长为半径作⊙O. 所以,⊙O 即为所求作的圆. F OAEBDC.请回答:该尺规作图的依据是____________________________.2018 海淀一模16.下面是“过圆上一点作圆的切线”的尺规作图过程.已知:⊙O 和⊙O 上一点 P .求作:⊙O 的切线 MN ,使 MN 经过点 P .O作法:如图,(1)作射线 OP ;(2)以点 P 为圆心,小于 OP 的长为半径作弧交射线 OP 于 A ,B 两点;(3)分别以点 A ,B 为圆心,以大于 1AB 长为2半径作弧,两弧交于 M ,N 两点;P(4)作直线 MN .则 MN 就是所求作的⊙O 的切线.OAM PNB请回答:该尺规作图的依据是.2018 东城一模16.已知正方形 ABCD .求作:正方形ABCD 的外接圆 作法:如图,(1)分别连接AC ,BD ,交于点O ;(2)以点 O 为圆心,OA 长为半径作⊙O .⊙ O 即为所求作的圆.请回答:该作图的依据是_____________________________________.2018朝阳一模16.下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程.已知:直线a和直线外一点P.求作:直线a的垂线,使它经过P.作法:如图,(1)在直线a上取一点A,连接PA;(2)分别以点A和点P为圆心,大于AP的长为半径作弧,两弧相交于B,C两点,连接BC交PA于点D;(3)以点D为圆心,DP为半径作圆,交直线a于点E,作直线PE.所以直线PE就是所求作的垂线.请回答:该尺规作图的依据是.2018丰台一模16.下面是“作一个角等于已知角”的尺规作图过程.已知:∠A.求作:一个角,使它等于∠A.作法:如图,AB(1)以点A为圆心,任意长为半径作⊙A,交∠A的两边于B,C两点;(2)以点C为圆心,BC长为半径作弧,A C与⊙A交于点D,作射线AD.D所以∠CAD就是所求作的角.请回答:该尺规作图的依据是.2018 大兴一模16.下面是“求作∠AOB 的角平分线”的尺规作图过程.已知:如图,钝角∠AOB. 求作:∠AOB 的角平分线.作法:①在 OA 和 OB 上,分别截取 OD 、OE ,使 OD =OE ;②分别以 D 、E 为圆心,大于 1 2DE的长为半径作弧, 在∠AOB 内,两弧交于点 C ; ③作射线 OC.所以射线 OC 就是所求作的∠AOB 的角平分线.请回答:该尺规作图的依据是.2018 顺义一模16.在数学课上,老师提出一个问题“用直尺和圆规作一个矩形”小华的做法如下:(1)如图 1,任取一点 O ,过点 O 作直线 l 1,l 2;(2)如图 2,以 O 为圆心,任意长为半径作圆,与直线 l 1,l 2 分别相交于点 A 、C ,B 、D ;(3)如图 3,连接 AB 、BC 、CD 、DA .四边形 ABCD 即为所求作的矩形.l 2AD l 2A D l 2Ol 1 BOCl 1BOCl 1图1老师说:“小华的作法正确” .图2图3请回答: PM 平行与 l 的依据是.请回答:小华的作图依据是.2018 通州一模16. 尺规作图:过直线外一点作已知直线的平行线.已知:如图,直线 l 与直线 l 外一点 P . 求作:过点 P 与直线 l 平行的直线.作法如下:(1) 在直线 l 上任取两点 A , B ,连接 AP , BP ;(2) 以点 B 为圆心, AP 长为半径作弧;以点 P 为圆心, AB 长为半径作弧;如图所示,两弧交于点 M .(3) 过点 P , M 作直线. (4) 直线 PM 即为所求.PM2018 房山一模16.如图,在平面直角坐标系 xOy 中,点 A (-3,0) ,B (-1,2) .以原点 O 为旋转中心,将 △AOB 顺时针旋转 90°,再沿 x 轴向右平移两个单位,得到△A’O’B’,其中点 A’与点 A 对应,点 B’与点 B 对应. 则点 A’的坐标为__________,点 B’的坐标为__________.y5 43 B2 1-5 -4A -3 -2 -1 O-1 -2-31 2 3 4 5x2018燕山一模16.在数学课上,老师提出如下问题:︵尺规作图:确定图中CD所在圆的圆心.︵已知:CD.︵求作:CD所在圆的圆心O.曈曈的作法如下:如图,︵(1)在CD上任意取一点M,分别连接CM,DM;(2)分别作弦CM,DM的垂直平分线,C DO两条垂直平分线交于点O.C DM︵点O就是CD所在圆的圆心.老师说:“曈曈的作法正确.”请你回答:曈曈的作图依据是________________________.2018门头沟一模16.下图是“已知一条直角边和斜边做直角三角形”的尺规作图过程.已知:线段a、b,求作:Rt∆ABC.使得斜边AB=b,AC=aa作法:如图.(1)作射线AP,截取线段AB=b;Cb(2)以AB为直径,作⊙O;(3)以点A为圆心,a的长为半径作弧交⊙O于点C;A OB P (4)连接AC、CB.∆ABC即为所求作的直角三角形.请回答:该尺规作图的依据是______________________________________________.。
北京2018年中考数学复习考题训练(13)二次函数与方程、不等式

考题训练(十三)二次函数与方程、不等式A组·真题演练[2017·北京]在平面直角坐标系xOy中,抛物线y=x2-4x+3与x轴交于点A、B(点A在点B的左侧),与y轴交于点C.(1)求直线BC的表达式;(2)垂直于y轴的直线l与抛物线交于点P(x1,y1),Q(x2,y2),与直线BC交于点N(x3,y3),若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.B组·模拟训练[2016·顺义一模]在平面直角坐标系xOy中,抛物线y=ax2-2x的对称轴为直线x=-1.(1)求a的值及抛物线y=ax2-2x与x轴的交点坐标;(2)若抛物线y=ax2-2x+m与x轴有交点,且交点都在点A(-4,0),B(1,0)之间,求m的取值范围.图J13-1C组·自测训练一、选择题1.如图J13-2是二次函数y=-x2+2x+4的图象,则使y≤1成立的x的取值范围是()A.-1≤x≤3 B.x≤-1C.x≥1 D.x≤-1或x≥3J13-2J13-32.二次函数y =ax 2+bx 的图象如图J13-3,若一元二次方程ax 2+bx +m =0有实数根,则m 的最大值为( ) A .-3 B .3 C .-6 D .93.已知二次函数y =x 2-3x +m(m 为常数)的图象与x 轴的一个交点为(1,0),则关于x 的一元二次方程x 2-3x +m =0的两个实数根是( )A .x 1=1,x 2=-1B .x 1=1,x 2=2C .x 1=1,x 2=0D .x 1=1,x 2=34.若函数y =mx 2+(m +2)x +12m +1的图象与x 轴只有一个交点,那么m 的值为( )A .0B .0或2C .2或-2D .0,2或-25.已知二次函数y =ax 2+bx +c(a ≠0)的图象如图J13-4,且关于x 的一元二次方程ax 2+bx +c -m =0没有实数根,有下列结论:①b 2-4ac >0;②abc <0;③m >2.其中,正确结论的个数是( )图J13-4A .0B .1C .2D .3二、填空题6.如图J13-5,已知二次函数y =x 2+bx +c 的图象经过点A(-1,0),B(1,-2),该图象与x 轴的另一个交点为C ,则AC 的长为________.图J13-57.已知直线y =-2x +3与抛物线y =x 2相交于A ,B 两点,O 为坐标原点,那么△OAB 的面积等于________. 8.已知二次函数y =ax 2+bx +c 中,函数y 与自变量x 的部分对应值如下表:则当y<5时,x三、解答题9.已知二次函数y=x2+bx+c的图象过点A(2,5),C(0,-3).(1)求此二次函数的解析式;(2)求该抛物线与x轴的交点坐标;(3)直接写出当-3≤x≤1时,y的取值范围.10.[2015·昌平期末]已知抛物线y=x2-(2m-1)x+m2-m.(1)求证:此抛物线与x轴必有两个不同的交点;(2)若此抛物线与直线y=x-3m+3的一个交点在y轴上,求m的值.11.[2017·门头沟二模]在平面直角坐标系xOy中,抛物线y=-x2+2mx-3+4m-m2的对称轴是直线x=1.(1)求抛物线的表达式;(2)点D(n,y1),E(3,y2)在抛物线上,若y1>y2,请直接写出n的取值范围;(3)设点M(p,q)为抛物线上的一个动点,当-1<p<2时,点M关于y轴的对称点形成的图象与直线y=kx-4(k≠0)有交点,求k的取值范围.12.[2016·怀柔一模]在平面直角坐标系中,二次函数y =x 2+mx +2m -7的图象经过点(1,0).(1)求抛物线的解析式;(2)把-4<x<1时的函数图象记为H ,求此时函数y 的取值范围;(3)在(2)的条件下,将图象H 在x 轴下方的部分沿x 轴翻折,图象H 的其余部分保持不变,得到一个新图象M.若直线y =x +b 与图象M 有三个公共点,求b 的取值范围.参考答案|真题演练|解:(1)由抛物线y =x 2-4x +3与x 轴交于点A ,B(点A 在点B 的左侧),令y =0,解得x 1=1,x 2=3, ∴点A ,B 的坐标分别为(1,0),(3,0),∵抛物线y =x 2-4x +3与y 轴交于点C ,令x =0, 得y =3,∴点C 的坐标为(0,3).设直线BC 的解析式为y =kx +b ,∴⎩⎨⎧3k +b =0,b =3,解得⎩⎨⎧k =-1,b =3,∴直线BC 的解析式为y =-x +3. (2)由y =x 2-4x +3=(x -2)2-1,∴抛物线的顶点坐标为(2,-1),对称轴为直线x =2, ∵y 1=y 2,∴x 1+x 2=4.把y =-1代入y =-x +3,得x =4.∵x 1<x 2<x 3,∴3<x 3<4,即7<x 1+x 2+x 3<8, ∴x 1+x 2+x 3的取值范围为:7<x 1+x 2+x 3<8.|模拟训练|解:(1)∵抛物线y =ax 2-2x 的对称轴为直线x =-1, ∴--22a=-1,解得a =-1,∴y =-x 2-2x.令y =0,则-x 2-2x =0,解得x 1=0,x 2=-2. ∴抛物线与x 轴的交点坐标为(0,0),(-2,0).(2)∵抛物线y =ax 2-2x 与抛物线y =ax 2-2x +m 的一次项系数、二次项系数相同,∴抛物线y =ax 2-2x +m 可以由抛物线y =ax 2-2x 上下平移得到. ∵抛物线y =-x 2-2x 的对称轴与x 轴的交点为(-1,0),抛物线y =-x 2-2x 与x 轴的交点(0,0),(-2,0)都在点A ,B 之间,且点B(1,0)比点A(-4,0)离对称轴x =-1近.∴把B(1,0)代入y =-x 2-2x +m 中,得m =3, 抛物线在x 轴负半轴的交点坐标为(-3,0).把(-1,0)代入y =-x 2-2x +m 中,得m =-1, 此时抛物线与x 轴只有一个交点为(-1,0).∴-1≤m<3. |自测训练| 1.D2.B [解析] ∵抛物线的开口向上,顶点的纵坐标为-3,∴a >0, -b 24a =-3,即b 2=12a.∵一元二次方程ax 2+bx +m =0有实数根,∴Δ=b 2-4am ≥0,即12a -4am ≥0,即12-4m ≥0,解得m ≤3,∴m 的最大值为3.故选B.3.B 4.D5.D [解析] ①∵二次函数y =ax 2+bx +c 的图象与x 轴有两个交点,∴b 2-4ac>0,故①正确;②∵抛物线的开口向下,∴a<0.∵抛物线与y 轴交于正半轴,∴c>0.∵对称轴方程x =-b2a >0,∴ab<0.∵a<0,∴b>0,∴abc<0,故②正确;③∵一元二次方程ax 2+bx +c -m =0没有实数根,∴抛物线y =ax 2+bx +c 和直线y =m 没有交点,由图可得m>2,故③正确.故选D.6.3 [解析] 由二次函数y =x 2+bx +c 的图象过点(-1,0),(1,-2),得⎩⎨⎧1-b +c =0,1+b +c =-2,解得⎩⎨⎧b =-1,c =-2,所以y =x 2-x -2.令x 2-x -2=0,解得x 1=-1,x 2=2,所以AC 的长为3.7.68.0<x <4 [解析] 由表可知,抛物线的对称轴为直线x =2,所以x =4时,y =5,所以y<5时,x 的取值范围为0<x<4.9.解:(1)∵函数y =x 2+bx +c 的图象过点A(2,5),C(0,-3),∴⎩⎨⎧5=4+2b +c ,-3=c ,解得⎩⎪⎨⎪⎧b =2,c =-3.∴二次函数的解析式为y =x 2+2x -3.(2)令y =0,则x 2+2x -3=0.∴(x +3)(x -1)=0. ∴x 1=-3,x 2=1.∴抛物线与x 轴的交点坐标为(-3,0),(1,0). (3)当x =-3或x =1时,y 最大值=0; 当x =-1时,y 最小值=-4.∴-4≤y ≤0.10.解:(1)证明:∵Δ=[-(2m -1)]2-4(m 2-m)=4m 2-4m +1-4m 2+4m =1>0, ∴此抛物线与x 轴必有两个不同的交点.(2)∵此抛物线与直线y =x -3m +3的一个交点在y 轴上, ∴m 2-m =-3m +3, ∴m 2+2m -3=0, ∴m 1=-3,m 2=1,∴m 的值为-3或1.11.解:(1)∵y =-x 2+2mx -m 2-3+4m =-(x -m)2+4m -3,抛物线的对称轴是直线x =1, ∴m =1,∴y =-x 2+2x.(2)-1<n <3.(3)设点M 关于y 轴的对称点为M′,由题意可得M′(-p ,q), ∴结合-1<p <2,确定动点M 及M′, 当x =-1时,y =-3;当x =2时,y =0.因为动点M 与M′关于y 轴对称,所以翻折后的函数表达式为y =-x 2-2x(-2<x<0),图象确定如图.当直线过点(1,-3)时,由-3=k·1-4得k =1;当直线过点(-2,0)时,由0=-2k -4得k =-2.综上所述:k>1或k<-2.12.解:(1)将(1,0)代入,得m =2.∴抛物线的解析式为y =x 2+2x -3.(2)抛物线y =x 2+2x -3开口向上,且在-4<x<1范围内有最低点, ∴当x =-1时,y 有最小值为-4. 当x =-4时,y =5.∴y 的取值范围是-4≤y<5.(3)当直线y =x +b 经过(-3,0)时,b =3. 变换后抛物线的解析式为y =-x 2-2x +3. 联立可得:-x 2-2x +3=x +b , 令判别式为零可得b =214.由图象可知,b 的取值范围是3<b<214.。
2018年北京东城区初三一模数学试题答案 精品

北京市东城区2018--2018学年第二学期初三综合练习(一)数学试卷参考答案一、选择题(本题共32分,每小题4分)题 号1 2 3 45 6 7 8 答 案A C A CB DB B二、填空题(本题共16分,每小题4分)题 号9 10 1112答 案x ≠5b (a -1)2(1,0),(3,0)或 (0,3),(4,3)等938,0 1)332(-n ,0三、解答题:(本题共30分,每小题5分) 13.(本小题满分5分)解:084sin 45(3)4-︒+-π+-=22422⨯-+1+4 ………………………………………4分 =5. …………………………………… 5分14.(本小题满分5分) 解:由①得:x ≤2. --------1分 由②得:x-3>-4,x >-1. --------2分∴原不等式组的解集为 -1<x ≤2. --------3分 ∴原不等式组的整数解为 0,1,2. --------5分 15.(本小题满分5分)1)1213(22-÷-+-x x xx x x=x x x x x x x 1]12)1)(1(3[2-⨯--+---------2分 =213-+x x=12+-x x . --------3分 当13-=x 时,3133312-=-=+-x x .--------5分 16.(本小题满分5分)证明:∵AC 是∠DAE 的平分线, ∴∠1=∠2. -------1分 -121CD E231又∵AD ∥EC ,∴∠2=∠3. ------2分 ∴∠1=∠3.∴AE=CE. --------3分 在△ABE 和△CBE 中, AE=CE , ∠AEB=∠CEB , BE=BE ,∴△ABE ≌△CBE. --------4分 ∴AB=CB. ------5分17.(本小题满分5分)解:设小明家2月份用气x 立方米,则去年12月份用气(x +10) 立方米.-------1分 根据题意,得%251096109690⨯+=+-x x x . ----------------3分 解这个方程,得x =30. ---------------4分 经检验,x =30是所列方程的根.答:小明家2月份用气30立方米. -----------------5分 18.(本小题满分5分) 证明:(1)∵四边形ABCD 是平行四边形, ∴∠B=∠D. 又AE ⊥BC ,AF ⊥CD ,∴∠AEB=∠AFD.∴∠BAE=∠DAF.---------2分 (2)在Rt △ABE 中,sin ∠BAE=53,AE=4,可求 AB=5. ---------3分 又∵∠BAE=∠DAF , ∴ sin ∠DAF=sin ∠BAE=53. 在Rt △ADF 中,AF=524, sin ∠DAF =53,可求DF=518-------4分∵ CD=AB=5. ∴CF=5-518=57. …………………………………………5分 四、解答题(本题共20分,每小题5分)ABCDEF19.(本小题满分5分)解:(1)0.6;36;------------2分 (2)72°;补全图如下:60%比较了解20%非常了解基本了解不太了解2%18%------------4分(3)1500×0.6=900.答:学生中“比较了解”的人数约为900人 ------------5分 20.(本小题满分5分)(1)证明:在⊙O 中,OD ⊥AB ,CB ⊥AB ,∴AM =MB ,OD ∥BC . …………………1分 ∴AD =DC . ……………2分 (2)∵DE 为⊙O 切线, ∴OD ⊥DE ……………3分 ∴四边形MBED 为矩形.∴DE ∥AB. ……………4分 ∴MB=DE =2,M D=BE =EC =1. 连接OB.在R t △OBM 中,OB 2=OM 2+BM 2.解得 OB=25. …………………5分 21.(本小题满分5分)解:(1)∵点A (1,6),B (a ,3)在反比例函数y =xk 2的图象上, ∴ k 2=1×6=6. --------1分 ∴ a ×3=6,a =2. ∴B (2,3).由点A (1,6),B (2,3)也在直线y=k 1x+b 上, 得⎩⎨⎧=+=+,32,611b k b k解得k 1=-3.∴k 1=-3, k 2=6. -----------------2分 (2) 设点P 的坐标为(m,n ). 依题意,得21×3(m +2+m -2)=18,m =6. -----------------3分 ∴ C (6,3),E (6,0).C DxyOEPA BMOA BCDE∵ 点P 在反比例函数y =x6的图象上, ∴ n =1. ------------------4分 ∴PE :PC =1:2 . ------------------5分22.(本小题满分5分)解: (1)设AD =x ,由题意得,BG=x -2,CG=x-3. 在Rt △BCG 中,由勾股定理可得 222(2)(3)5x x -+-=. 解得 6x =. --------------2分(2)参考小萍的做法得到四边形AEGF ,∠EAF=60°,∠EGF=120°,∠AEG=∠AFG= 90°,AE=AF=AD=4. 连结EF ,可得 △AEF 为等边三角形. ∴ EF=4.∴ ∠FEG=∠EFG= 30°. ∴ EG=FG.在△EFG 中,可求,433EG =. ∴△EFG 的周长=BG+CG+BC=BG+CG+EB+FC=2EG=833. --------------5分五、解答题:(本题共22分,第23题7分,第24题7分,第25题8分) 23.(本小题满分7分)解: 由方程(m -1)x 2-(2m -1)x +2+xm =0可得)1(22)1(4)12()12(2-⨯-⨯--±--=m m m m x=)1(2)32(12)1(2)32()12(2-+±-=--±-m m m m m m111-=m x ,.22=x ∵21,x x 均为正整数,m 也是整数, ∴m =2. ----------3分 (2)由(1)知x 2-3x +2+x2=0. ∴x 2-3x +2= -x2. 画出函数y = x 2-3x +2,y = -x2的图象,---------6分 由图象可知,两个函数图象的交点个数是1. ---------7分 Oxy GF ED CBA24. (本小题满分7分)(1)△EPF 为等边三角形. --------------1分 (2)设BP=x ,则CP =6-x.由题意可 △BEP 的面积为238x . △CFP 的面积为23(6)2x -. △ABC 的面积为93.设四边形AEPF 的面积为y. ∴ 93y =-238x 23(6)2x --=25363938x x -+-. 自变量x 的取值范围为3<x <6. --------------4分(3)可证△EBP ∽△PCF.∴BP BECF CP=. 设BP=x ,则 (6)8x x -=. 解得 124,2x x ==.∴ PE 的长为4或23. --------------7分25.(本小题满分8分)解:(1)依题意,可知 C(0,8),则B(4,0) 将A(-2,0),B(4,0)代入 y=ax 2+bx +8,⎩⎨⎧=++=+-.08416,0824b a b a 解得⎩⎨⎧=-=.2,1b a 228y x x ∴=-++配方得y2(1)9x =--+,顶点D (1,9). ---------3分 (2)假设满足条件的点P 存在,依题意设(2)P t ,,由(08)(19)C D ,,,求得直线CD 的解析式为8y x =+, 它与x 轴的夹角为45. 过点P 作PN ⊥y 轴于点N.依题意知,∠NPO=30°或∠NPO=60°. ∵PN=2,∴ON=332或23. FP 2M 2N 2P 1N 1M 1Hy C D1∴存在满足条件的点P ,P 的坐标为(2,332 )和(2,23).-----------6分 (3)由上求得(80)(412)E F -,,,.当抛物线向上平移时,可设解析式为228(0)y x x m m =-+++>. 当8x =-时,72y m =-+. 当4x =时,y m =.720m ∴-+≤或12m ≤.由题意可得m 的范围为072m ∴<≤.∴ 抛物线最多可向上平移72个单位. -----------8分。
2018-2019北京四中 初三数学一模 几何综合 ,代数综合汇编

1(2019+++延庆+++一模)(1)对称轴:x =2,B (5,2) (2)12a ≥或2a ≤-2(2019+++房山+++一模)(1)∵抛物线2y x mx n =++过点A (−1,a ),B (3,a ) ∴抛物线的对称轴x =1 ∵抛物线最低点的纵坐标为−4 ∴抛物线的顶点是(1,−4) ∴抛物线的表达式是2(1)4y x =--即223y x x =-- m =−2,n =−3………… 2分 把 A (−1,a ) 代入抛物线表达式 223y x x =-- 求得a =0……………………… 3分 (2)如图当y =kx +2经过点B (3,0)时, 0=3k +2,k =−23……………………… 4分 当y =kx +2经过点A (−1,0)时,0=−k +2,k =2……………………… 5分 综上所述,当k ≤−23或k ≥2时,直线y =kx +2与G 有公共点…………… 6分3(2019+++通州+++一模)(1)∵二次函数2y x ax b =-+在0x =和4x =时的函数值相等 ∴对称轴为直线2x =………………1分(2)① 不妨设点M 在点N 的左侧 ∵对称轴为直线2x =,2MN = ∴点M 的坐标为(1,1),点N 的坐标为(3,1)………………2分 ∴22ax -=-=,11a b =-+ ∴4a =,4b =………………4分 ② 15b <≤………………6分4(2019+++平谷+++一模) (1)m(2)∵3222-+-=m mx x y ()23x m =--∴抛物线顶点坐标为(m ,-3) ∵抛物线经过点A ,B 时,且AB ∥x 轴 ∴抛物线对称轴为x=m =2 ∴抛物线的表达式为241y x x =-+ (3)01m <≤5(2019+++门头沟+++一模)(1)∵直线4y x =+与x 轴交于点A ∴点A 坐标为(-4,0) ∵直线4y x =+与与过点(0,5)且平行于x 轴的直线l 交于点B ∴点B 坐标为(1,5)………… 1分∵点A 关于直线l 的对称点为点C ∴点C 坐标为(-4,10)…………… 2分 (2)① ∵抛物线的表达式为222y x mx m m =-+-∴顶点坐标为(m ,-m )…………… 3分 ∵抛物线顶点在直线4y x =+上 ∴4m m -=+ ∴m = - 2…………… 4分 ② 6 4.m ≤≤-…………… 6分6(2019++石景山+++一模)(1)∵1(0)y kx k =+≠经过点A 23(,) ∴1k =∵直线1y x =+与抛物线2y ax bx a =++的对称轴交于点C ()m,2∴1m = (2)∵抛物线2y ax bx a =++的对称轴为1x = ∴12ba-=,即2b a =-. ∴22y ax ax a =-+2(1)a x =- ∴抛物线的顶点坐标为()1,0(3)当0a >时,如图 若抛物线过点B 01(,),则1a = 结合函数图象可得01a << 当0a <时,不符合题意综上所述,a 的取值范围是01a <<7(2019+++西城+++一模)(1)∵223y ax ax a =--=2(23)a x x --=(1)(3)a x x +- 令0=y ,得1-=x ,或3=x∴A (-1,0),B (3,0)………………2分当1a =时,抛物线化为223y x x =--=2(1)4x --∴D (1,-4)……………3分 (2) 如图,当0a >时当1a =时,抛物线在点A ,B 之间的部分与线段AB 所围成的区域 内恰有7个整点 当34a =时,抛物线在点A ,B 之间的部分与线段AB 所围成的区域 内有6个整点 结合函数图象可得,314a <≤ 当0a <时,同理可得314a<-≤- ∴a 的取值范围是314a<-≤-,或314a <≤…………6分9(2019+++丰台+++一模)(1) ()42--=m x y ()4-∴,m P 即顶点P 的纵坐标为-4 (2)①AB 长为定值 令y=0,则22240x mx m -+-= 则2()4x m -=解得22x m x m =+=-或 AB 长为2(2)4m m +--= ②当MA=5时,可求A 点坐标为(-3,0)或(3,0)∵AB=4 ∴MA=5时,m=-1或m=1 ∵214x x m m -+=+结合图象可知,21x x m -+的取值范围为212115x x m x x m -+≤--+≥或 1在平面直角坐标系xOy 中,抛物线2432y ax ax a =-+-(0a ≠)的对称轴与x 轴交于点A ,将点A 向右平移3个单位长度,向上平移2个单位长度,得到点B (1)求抛物线的对称轴及点B 的坐标(2)若抛物线与线段AB 有公共点,结合函数图象, 求a 的取值范围 2在平面直角坐标系xOy 中,二次函数2y x mx n =++的图象经过点A (−1,a )B (3,a ),且顶点的纵坐标为-4(1)求m ,n 和a 的值(2)记二次函数图象在点A ,B 间的部分为G (含点A 和点B ),若直线2y kx =+与图象G 有公共点,结合函数图象,求k 的取值范围 3已知二次函数2y x ax b =-+在0x =和4x =时的函数值相等 (1)求二次函数2y x ax b =-+的对称轴(2)过P (0,1)作x 轴的平行线与二次函数2y x ax b =-+ 的图象交于不同的两点M 、N ①当2MN =时,求b 的值②当=4PM PN +时,请结合函数图象,直接写出b 的取值范围4平面直角坐标系xOy 中,抛物线3222-+-=m mx x y 与y 轴交于点A ,过A 作AB ∥x 轴与直线x =4交于B 点 (1)抛物线的对称轴为x = (用含m 的代数式表示) (2)当抛物线经过点A ,B 时,求此时抛物线的表达式(3)记抛物线在线段AB 下方的部分图象为G (包含A ,B 两点),点P (m ,0)是x 轴上一动点,过P 作PD ⊥x 轴于P ,交图象G 于点D ,交AB 于点C ,若CD ≤1,求m 的取值范围5在平面直角坐标系xOy 中,一次函数4y x =+的图象与x 轴交于点A ,与过点(0,5)平行于x 轴的直线l 交于点B ,点A 关于直线l 的对称点为点C(1)求点B 和点C 坐标(2)已知某抛物线的表达式为222y x mx m m =-+- ① 如果该抛物线顶点在直线4y x =+上,求m 的值 ② 如果该抛物线与线段BC 有公共点,结合函数图象, 直接写出m 的取值范围6在平面直角坐标系xOy 中,直线1y kx =+(0)k ≠经过点(2,3)A ,与y 轴交于点B ,与抛物线2y ax bx a =++的对称轴交于点(,2)C m (1)求m 的值(2)求抛物线的顶点坐标(3)11(,)N x y 是线段AB 上一动点,过点N 作垂直 于y 轴的直线与抛物线交于点22(,)P x y ,33(,)Q x y (点P 在点Q 的左侧).若213x x x <<恒成立,结合 函数的图象,求a 的取值范围 7在平面直角坐标系xOy 中,已知抛物线2y x mx n =-+(1)当2m =时,①求抛物线的对称轴,并用含n 的式子表示顶点的纵坐标 ②若点1(2,)A y -,22(,)B x y 都在抛物线上,且21y y >,则2x 的取值范围是_______(1)已知点(1,2)P -,将点P 向右平移4个单位长度,得到点Q . 当3n =时,若抛物线与线段PQ 恰有一个公共点,结合函数图像,求m 的取值范围 8在平面直角坐标系xOy 中,抛物线223(0)y ax ax a a =--≠的顶点为D ,与x 轴交于A ,B 两点(A 在B 的左侧)(1) 当1a =时,求点A ,B ,D 的坐标(2) 横,纵坐标都是整数的点叫做整点.若抛物线在点A ,B 之间的部分与线段AB 所围成的区域内(不含边界)恰有7个整点,结合函数图象,求a 的取值范围 9在平面直角坐标系xoy 中,抛物线c bx ax y ++=2过原点和点A (-2,0)(1)求抛物线的对称轴(2)横纵坐标都是整数的点叫做整点,已知点⎪⎭⎫ ⎝⎛230,B ,记抛物线与直线AB 围成的封闭区域(不含边界)为 W ①当a=1时,求出区域W 内的整点个数②若区域W 内恰有3个整点,结合函数图像,直接写 出a 的取值范围 10已知抛物线2224y x mx m =-+-,抛物线的顶点为P(1)求点P 的纵坐标(2)设抛物线x 轴交于A 、B 两点,1122(,),(,)A x y B x y ,21x x >①判断AB 长是否为定值,并证明②已知点M (0,-4),且MA ≥5,求21-x x m +的取值范围 1(2019+++延庆+++一模)(1)∵∠ADC =60°,DA=DC ∴△ADC 是等边三角形 ∴∠DAC =60°,AD=AC .∵∠ABC=120°,BD 平分∠ABC ∴∠ABD=∠DBC =60° ∴∠DAC =∠DBC =60° ∵∠AOD =∠BOC∠ADB=180°-∠DAC-∠AOD ∠ACB=180°-∠DBC-∠BOC ∴∠ADB=∠ACB(2)结论:DH=BH+BC 在HD 上截取HE=HB∵AH ⊥BD ∴∠AHB=∠AHE =90° ∵AH =AH ∴△ABH ≌△AEH ∴AB=AE, ∠AEH=∠ABH =60° ∴∠AED=180°-∠AEH=120° ∴∠ABC=∠AED=120° ∵AD=AC, ∠ADB=∠ACB ∴△ABC ≌△AED ∴DE=BC ∵DH=HE+ED ∴DH=BH+BC2(2019+++房山+++一模)(1)解: 依题意,∠CAB =45° ∵∠BAD =α ∴∠CAD =45α︒-∵∠ACB =90°,BE ⊥AD ,∠ADC =∠BDE ∴∠DBE =∠CAD =45α︒-……………………………… 2分 (2)解:①补全图形如图……………………… 4分 ②猜想:当D 在BC 边的延长线上时,EB -EAEC ……………… 5分 证明:过点C 作CF ⊥CE ,交AD 的延长线于点F . ∵∠ACB =90° ∴∠ACF =∠BCE∵CA =CB ,∠CAF =∠CBE ∴△ACF ≌△BCE ………… 6分∴AF =BE ,CF =CE ∵∠ECF =90° ∴EFEC即AF -EA EC ∴EB -EA …………………… 7分3(2019+++通州+++一模)(1)连接AE∵点B 关于射线AD 的对称点为E ∴AE =AB ,BAF EAF α∠=∠=∵ABC △是等边三角形 ∴AB AC =,60BAC ACB ∠=∠=︒∴602EAC α∠=︒-,AE AC =………1分∴()1180602602ACE αα∠=︒-︒-=︒+⎡⎤⎣⎦ ∴6060BCF ACE ACB αα∠=∠-∠=︒+-︒=……………2分另解:借助圆 (2)AF EF CF -=证明:如图,作60FCG ∠=︒交AD 于点G ,连接BF ……………3分 ∵BAF BCF α∠=∠=,ADB CDF ∠=∠ ∴60ABC AFC ∠=∠=︒ ∴△FCG 是等边三角形 ∴GF =FC ……………… 4分 ∵ABC △是等边三角形 ∴BC AC =,60ACB ∠=︒∴ACG BCF α∠=∠= 在△ACG 和△BCF 中CA CB ACG BCF CG CF =⎧⎪∠=∠⎨⎪=⎩,,, ∴△ACG ≌△BCF∴AG BF =……………5分 ∵点B 关于射线AD 的对称点为E ∴BF EF =……………6分 ∴AF AG GF -= ∴AF EF CF -=………………7分 另一种证法:作60FAH ∠=︒交FC 的延长线于点H ,连接BF4(2019+++平谷+++一模) (1)∠BCD =120°-α (2)解:方法一:延长BA 使AE=BC ,连接DE 由(1)知△ADC 是等边三角形 ∴AD=CD∵∠DAB+∠DCB=∠DAB+∠DAE=180°∴∠DAB=∠DAE ∴△ADE≌△CDB ∴BD=BE ∴BD=AB+BC 方法二:延长AB使AF=BC,连接CF∠BDC=∠ADE ∵∠ABC=120°∴∠CBF=60°∴△BCF是等边三角形∴BC=CF ∵∠DCA=∠BCF=60°∴∠DCA+∠ACB=∠BCF+∠ACB 即∠DCB=∠ACF ∵CA=CD∴△ACF≌△DCB ∴BD=AF ∴BD=AB+BC(3)AC,BD的数量关系是:AC BD位置关系是:AC⊥BD于点P5(2019+++门头沟+++一模)(1)补全图形(如图1)…………… 1分证明:略………… 3分(2)线段OE,OP和OF之间的数量关系是OF+OEOP …… 4分证明:如图2,作PQ⊥PO交OB于Q∴∠2+∠3=90°,∠1+∠2=90°∴∠1=∠3又∵OC平分∠AOB,∠AOB=90°∴∠4=∠5=45°又∵∠5+∠6=90°∴∠6=45°∴∠4=∠6 ∴PO=PQ ∴△EPO≌△FPQ…………… 5分∴PE=PF,OE=FQ又∵OQ=OF+FQ =OF+OE 又∵OQ∴OF+OE…………… 6分(3)线段OE,OP和OF之间的数量关系是OF - OE…………… 7分6(2019++石景山+++一模) (1)补全的图形如图1所示 (2)△ABC 是等边三角形∴AB BC CA ==,60ABC BCA CAB ∠=∠=∠=︒由平移可知ED ∥BC ,ED =BC ……… 2分60ADE ACB ∴∠=∠=︒ 90GMD ∠=︒ 2DG DM DE ∴==…… 3分DE BC AC == DG AC ∴= AG CD ∴=……… 4分(3)线段AH 与CG 的数量关系:AH = CG ……… 5分 如图2,连接BE ,EF,ED BC =ED ∥BC BEDC ∴四边形是平行四边形 BE CD CBE ADE ABC ∴=∠=∠=∠, GM ED 垂直平分EF DF ∴= DEF EDF ∴∠=∠ED ∥BCBFE DEF BFH EDF ∴∠=∠∠=∠, BFE BFH ∴∠=∠BF BF = BEF BHF ∴△≌△………… 6分BE BH CD AG ∴===AB AC = AH CG ∴=……… 7分7(2019+++西城+++一模)D8(2019+++燕山+++一模)(1)①补全的图形如图的所示………1分 ②证明:∵∠ADE =∠B =90°∴∠EDC +∠ADB =∠BAD +∠ADB =90° ∴∠EDC =∠BAD ……………3分 (2) ①CEBD ……………4分 ②想法1:如图,过点E 作EF ⊥BC ,交BC 延长线于点F ∴∠F =90° 在△ADB 和△DEF 中,∠B =∠F =90°,∠EDC =∠BAD ,AD =DE ∴△ADB ≌△DEF ∴AB =DF ,BD =EF ∵AB =BC ∴DF =BC 即DC +CF =BD +DC ∴CF =BD =EF ∴△CEF 是等腰直角三角形 ∴CECFBD ……………7分 想法2:证明:在线段AB 上取一点F ,使得BF =BD ,连接DF∵∠B =90°,AB =BC ∴DFBD ∵AB =BC ,BF =BD ∴AB -BF =BC -BD 即AF =DC 在△ADF 和△DEC 中AF =DC ,∠BAD =∠EDC ,AD =DE ∴△ADF ≌△DECFABECD∴CE=DF BD……………7分想法3:证明:延长AB到F,使得BF=BD,连接DF,CF∵∠B=90°∴DF在Rt△ABD和Rt△CBF中∠ABD=∠CBF=90°,AB=BC,BD=BF ∴△ABD≌△CBF∴AD=CF,∠BAD=∠BCF ∵AD=DE ∴DE=CF∵∠EDC=∠BAD ∴∠EDC=∠BCF ∴DE∥CF∴四边形DFCE为平行四边形∴CE=DF BD……………7分9(2019+++丰台+++一模)10(2019+++密云+++零模) (1)补全图形AD 与BE 的数量关系为AD=BE(2)∵∠ACB=∠DCE= 60° ∴∠ACD=∠BCE 又∵AC=BC,CD=CE ∴△ACD ≌△BCE ∴AD=BE, ∠CBE=∠CAD=60°∴∠ABF=180°-∠ABC-∠CBE=60° 在Rt AFB ∆中,AF AB=∴ABDBAH O DBA1已知:四边形ABCD 中,120ABC ∠=︒,60ADC ∠=︒,AD =CD ,对角线AC ,BD 相交于点O ,且BD 平分∠ABC ,过点A 作AH BD ⊥,垂足为H (1)求证:ADB ACB ∠=∠(2)判断线段BH ,DH ,BC 之间的数量关系;并证明 2已知:Rt △ABC 中,∠ACB =90°,AC =BC(1) 如图1,点D 是BC 边上一点(不与点B ,C 重合),连接AD ,过点B 作BE ⊥AD ,交AD 的延长线于点E ,连接CE . 若∠BAD =α,求∠DBE 的大小 (用含α的式子表示)(2) 如图2,点D 在线段BC 的延长线上时,连接AD ,过点B 作BE ⊥AD ,垂足E 在线段AD 上,连接CE . ①依题意补全图2 ②用等式表示线段EA ,EB 和EC 之间的数量关系,并证明AA3如图,在等边ABC △中,点D 是线段BC 上一点.作射 线AD ,点B 关于射线AD 的对称点为E .连接CE 并 延长,交射线AD 于点F(1)设BAF α∠=,用α表示BCF ∠的度数(2)用等式表示线段AF 、CF 、EF 之间的数量关系, 并证明 4在△ABC 中,∠ABC =120°,线段AC 绕点A 逆时针旋转60°得到线段AD ,连接CD ,BD 交AC 于P (1)若∠BAC =α,直接写出∠BCD 的度数 (用含α的代数式表示) (2)求AB ,BC ,BD 之间的数量关系 (3)当α=30°时,直接写出AC ,BD 的关系5如图,∠AOB = 90°,OC 为∠AOB 的平分线,点P 为OC 上一个动点,过点P 作射线PE 交OA 于点E .以点P 为旋转 中心,将射线PE 沿逆时针方向旋转90°,交OB 于点F (1)根据题意补全图1,并证明PE = PF(2)如图1,如果点E 在OA 边上,用等式表示线段OE ,OP 和OF 之间的数量关系,并证明 (3)如图2,如果点E 在OA 边的反向延长线上,直接写出线段OE ,OP 和OF 之间的数量关系6如图,在等边△ABC 中,D 为边AC 的延长线上一点()CD AC ,平移线段BC ,使点C 移动到点D ,得到线段ED ,M 为ED 的中点,过点M 作ED 的垂线,交BC 于点F ,交AC 于点G (1)依题意补全图形 (2)求证:AG = CD(3)连接DF 并延长交AB 于点H ,用等 式表示线段AH 与CG 的数量关系,并证明PPEECCBBOOAADB A7如图,在△ABC 中,∠ABC =90°,BA=BC .将线段AB 绕点A 逆时针旋转90°得到线段AD ,E 是边BC 上的一动点,连接DE 交AC 于点F ,连接BF (1) 求证:FB=FD(2) 点H 在边BC 上,且BH=CE ,连接AH 交BF 于点N ①判断AH 与BF 的位置关系,并证明你的结论 ②连接CN .若AB =2,请直接写出线段CN 长度的最小值8如图,在△ABC 中,AB =BC ,∠B =90°,点D 为线段BC 上一个动点(不与点B ,C 重合),连接AD ,将线段AD 绕点D 顺时针旋转90°得到线段DE ,连接EC(1) ① 依题意补全图1 ② 求证:∠EDC =∠BAD(2) ① 小方通过观察、实验,提出猜想:在点D 运动的过程中,线段CE 与BD 的数量关系始终不变,用等式表示为② 小方把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法想法1:过点E 作EF ⊥BC ,交BC 延长线于点F ,只需证△ADB ≌△DEF . 想法2:在线段AB 上取一点F ,使得BF =BD ,连接DF ,只需证△ADF ≌△DEC . 想法3:延长AB 到F ,使得BF =BD ,连接DF ,CF ,只需证四边形DFCE 为平行四边形. ……请你参考上面的想法,帮助小方证明①中的猜想(一种方法即可)备用图AB CD 图1 DCBA9在ABC ∆中,090=∠ACB ,AC=BC ,D 为AB 的中点,点E 为AC 延长线上一点,连接DE ,过点D 作DF ⊥DE交CB 的延长线于点F(1)求证:BF=CE(2)若CE=AC ,用等式表示线段DF 与AB 的数量关系,并证明10已知ABC ∆为等边三角形,点D 是线段AB 上一点(不与A 、B 重合).将线段CD 绕点C 逆时针旋转60︒得到线段CE.连结DE 、BE(1)依题意补全图1并判断AD 与BE 的数量关系(2)过点A 作AF EB ⊥交EB 延长线于点F ,用等式表示线段EB 、DB 与AF 之间的数量关系并证明图2D C B A 图1A B CD。
北京市各区2018届中考数学一模试卷精选汇编函数操作专题201901281123

函数操作专题东城区25. 如图,在等腰△ABC 中,AB =AC ,点D ,E 分别为BC ,AB 的中点,连接AD .在线段AD 上任取一点P ,连接PB ,PE .若BC =4,AD =6,设PD =x (当点P 与点D 重合时,x 的值为0),PB +PE =y .小明根据学习函数的经验,对函数y 随自变量x 的变换而变化的规律进行了探究. 下面是小明的探究过程,请补充完整:(1)通过取点、画图、计算,得到了x 与y 的几组值,如下表: (说明:补全表格时,相关数值保留一位小数). (参考数据:1.414≈1.732≈2.236≈)(2) 建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)函数y 的最小值为______________(保留一位小数),此时点P 在图1中的位置为________________________.25.解:(1)4.5 . --------------------2分 (2)--------------------4分(3) 4.2,点P 是AD 与CE 的交点. --------------------6分 西城区25.如图,P 为⊙O 的直径AB 上的一个动点,点C 在»AB 上,连接PC ,过点A 作PC 的垂线交⊙O 于点Q .已知5cm AB =,3cm AC =.设A 、P 两点间的距离为cm x ,A 、Q 两点间的距离为cm y .BA某同学根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行探究. 下面是该同学的探究过程,请补充完整:(1)通过取点、画图、测量及分析,得到了x 与y 的几组值,如下表:(说明:补全表格对的相关数值保留一位小数)(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.(3)结合画出的函数图象,解决问题:当2AQ AP =时,AP 的长度均为__________cm .【解析】(1)(2)如图5图5(3)2.42. 海淀区25.在研究反比例函数1y x=的图象与性质时,我们对函数解析式进行了深入分析. 首先,确定自变量x 的取值范围是全体非零实数,因此函数图象会被y 轴分成两部分;其次,分析解析式,得到y 随x 的变化趋势:当0x >时,随着x 值的增大,1x的值减小,且逐渐接近于零,随着x 值的减小,1x的值会越来越大,由此,可以大致画出1y x=在0x >时的部分图象,如图1所示:利用同样的方法,我们可以研究函数y=的图象与性质. 通过分析解析式画出部分函数图象如图2所示.(1)请沿此思路在图2中完善函数图象的草图并标出此函数图象上横坐标为0的点A;(画出网格区域内的部分即可)(2)观察图象,写出该函数的一条性质:____________________;(3)若关于x(1)a x=-有两个不相等的实数根,结合图象,直接写出实数a的取值范围:__________.25.(1)如图:………………2分x>时,y随着x的增大而减小;(答案不唯一)………………4分(2)当1a≥. ………………6分(3)1丰台区25.如图,Rt△ABC中,∠ACB = 90°,点D为AB边上的动点(点D不与点A,点B重合),过点D作ED⊥CD交直线AC于点E.已知∠A = 30°,AB = 4cm,在点D由点A到点B运动的过程中,设AD = x cm,AE = y cm.CED小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(说明:补全表格时相关数值保留一位小数)(2)在下面的平面直角坐标系xOy 中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当AE =12AD 时,AD 的长度约为 cm . 25.解:(1)1.2; ………………………2分 (2)如右图; ………………………4分 (3)2.4或3.3 ………………………6分 石景山区25.如图,半圆O 的直径5cm AB =,点M 在AB 上且1cm AM =,点P 是半圆O 上的动点,过点B 作BQ PM ⊥交PM (或PM 的延长线)于点Q .设cm PM x =,cm BQ y =.(当点P与点A或点B重合时,y的值为0)小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当BQ与直径AB所夹的锐角为60 时,PM的长度约为cm.25.解:(1)4; 0. ………………2分(2)………………4分(3)1.1或3.7 . ………………6分朝阳区25.如图,AB是⊙O的直径,AB=4cm,C为AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=60°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=x cm,DE=y cm (当x的值为0或3时,y的值为2),探究函数y随自变量x的变化而变化的规律.(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:点F与点O重合时,DE长度约为 cm (结果保留一位小数).25. 解:本题答案不唯一,如:(1)………………………………………………1分(2)…………………………………………4分(3)3.5.……………………… 6分燕山区26.已知y是x的函数,自变量x的取值范围是x≠0的全体实数,下表是y与x的几组对应值.小华根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:(1)从表格中读出,当自变量是-2时,函数值是;(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(3)在画出的函数图象上标出x=2时所对应的点,并写出m = (4)结合函数的图象,写出该函数的一条性质:____________ .26.解:(1)当自变量是-2时,函数值是 32…………………………………1′(2)如图,该函数的图象; (略) …………………………………3′(3)标出x=2时所对应的点 …………………………………4′ 且m= …………………………………5′(4)写出该函数的性质(一条即可):_____ . …………………………………7′ 门头沟区25.在正方形ABCD 中,4AB cm = AC 为对角线,AC 上有一动点P ,M 是AB 边的中点,连接PM 、PB , 设A 、P 两点间的距离为xcm ,PM PB +长度为ycm .D A小东根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究. 下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x 与y 的几组值,如下表:(说明:补全表格时相关数值保留一位小数)(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.(3)结合画出的函数图象,解决问题:PM PB 的长度最小值约为__________cm .25.(本小题满分6分)(1)5 ……………………………………………………………………1分(2)坐标系正确……………………………………………………3分描点正确……………………………………………………4分连线正确……………………………………………………5分(3)4.5 ……………………………………………………………………6分大兴区25.如图,在△ABC中,AB=4.41cm,BC=8.83cm,P是BC上一动点,连接AP,设P,C两点间的距离为x cm,P,A两点间的距离为y cm.(当点P与点C重合时,x的值为0)小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(说明:补全表格时相关数值保留一位小数)(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当PA=PC时,PC的长度约为cm.(结果保留一位小数)25.(1)4.6 ………………………………………………………………1分(答案不唯一)(2)………………………………………………………………4分(3) 4.4 ………………………………………………………………6分(答案不唯一)平谷区25.如图,在△ABC中,∠C=60°,BC=3厘米,AC=4厘米,点P从点B出发,沿B→C→A 以每秒1厘米的速度匀速运动到点A.设点P的运动时间为x秒,B、P两点间的距离为y 厘米.B小新根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小新的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:经测量m的值是(保留一位小数).(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:在曲线部分的最低点时,在△ABC中画出点P所在的位置.25.解:(1)3.0; (1)(2)如图所示;··························4(3)如图 (5)怀柔区25、如图,在等边△ABC中, BC=5cm,点D是线段BC上的一动点,连接AD,过点D作DE⊥AD,垂足为D,交射线AC与点E.设BD为x cm,CE为y cm.小聪根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小聪的探究过程,请补充完整:(1)通过取点、画图、测量,得到了与y的几组值,如下表:(说明:补全表格上相关数值保留一位小数)(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当线段BD是线段CE长的2倍时,BD的长度约为________cm.25.(1)约 1.1; (1)分(2)如图:xy –1123456–1123456O ……………………………………………………………4分(3)约 1.7. ………………………………………………………………………………………5分 延庆区25.如图,点P 是以O 为圆心,AB 为直径的半圆上的动点,AB =6cm ,设弦AP 的长为x cm ,△APO 的面积为y cm 2,(当点P 与点A 或点B 重合时,y 的值为0).A B小明根据学习函数的经验,对函数y 随 自变量x 的变化而变化的规律进行了探究. 下面是小明的探究过程,请补充完整;(1)通过取点、画图、测量、计算,得到了x 与y 的几组值,如下表:那么m = ;(保留一位小数)(2)建立平面直角坐标系,描出以表中各组对应值为坐标的点,画出该函数图象.(3)结合函数图象说明,当△APO 的面积是4时,则AP 的值约为 .(保留一位小数)25.(1)m = 约4.3 ; ……1分(2)(画此函数图象时要体现出x 约为4.2时,y 有最大值,为4.5) ……4分 (3) 3.1或是5.1 ……6分-16123454321O顺义区25.如图,P是半圆弧AB上一动点,连接PA、PB,过圆心O作OC∥BP交PA于点C,连接CB.已知AB=6cm,设O,C两点间的距离为x cm,B,C两点间的距离为y cm.A小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:(说明:补全表格时相关数据保留一位小数)(2)建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:直接写出△OBC周长C的取值范围是.25.(1)4.6.……………………………………………………………………… 1分12(2)…………………………………………………………………………… 3分(3)6<C <12. …………………………………………………………… 5分。
北京市朝阳区2018年中考一模数学试卷(含答案)
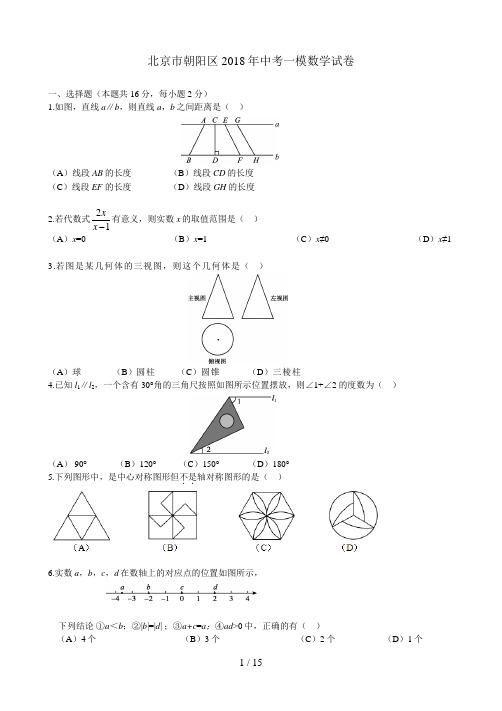
北京市朝阳区2018年中考一模数学试卷一、选择题(本题共16分,每小题2分)1.如图,直线a ∥b ,则直线a ,b 之间距离是( )(A )线段AB 的长度 (B )线段CD 的长度 (C )线段EF 的长度 (D )线段GH 的长度2.若代数式12 x x有意义,则实数x 的取值范围是( ) (A )x =0 (B )x =1 (C )x ≠0(D )x ≠13.若图是某几何体的三视图,则这个几何体是( )(A )球 (B )圆柱 (C )圆锥 (D )三棱柱 4.已知 l 1∥l 2,一个含有30°角的三角尺按照如图所示位置摆放,则∠1+∠2的度数为( )(A ) 90° (B )120° (C )150° (D )180° 5.下列图形中,是中心对称图形但不是..轴对称图形的是( )6.实数a ,b ,c ,d 在数轴上的对应点的位置如图所示,下列结论 ①a <b ;②|b |=|d | ;③a+c =a ;④ad >0中,正确的有( ) (A )4个 (B )3个 (C )2个(D )1个7. “享受光影文化,感受城市魅力”,2018年4月15-22日第八届北京国际电影节顺利举办.下面的统计图反映了北京国际电影节﹒电影市场的有关情况.根据统计图提供的信息,下列推断合理..的是( ) (A )两届相比较,所占比例最稳定的是动作冒险(含战争)类 (B )两届相比较,所占比例增长最多的是剧情类(C )第八届悬疑惊悚犯罪类申报数量比第六届2倍还多(D )在第六届中,所占比例居前三位的类型是悬疑惊悚犯罪类、剧情类和爱情类8. 如图,△ABC 是等腰直角三角形,∠A =90°,AB =6,点P 是AB 边上一动点(点P 与点A 不重合),以AP 为边作正方形APDE ,设AP =x ,正方形APDE 与△ABC 重合部分(阴影部分)的面积为y ,则下列能大致反映y 与x 的函数关系的图象是( )二、填空题(本题共16分,每小题2分) 9. 赋予式子“ab ”一个实际意义: . 10.如果023≠=n m ,那么代数式)2(4322n m nm n m +⋅--的值是 . 11.足球、篮球、排球已经成为北京体育的三张名片,越来越受到广大市民的关注. 下表是北京两支篮球队在2017-2018赛季CBA 常规赛的比赛成绩:设胜一场积x 分,负一场积y 分,依题意,可列二元一次方程组为 . 12. 如图,AB ∥CD ,AB=21CD ,S △ABO :S △CDO = .13. 如图,点A,B,C在⊙O上,四边形OABC是平行四边形,OD⊥AB于点E,交⊙O于点D,则∠BAD= 度.14. 如图,在平面直角坐标系xOy中,△O'A'B'可以看作是△OAB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OAB得到△O'A'B'的过程: .15.下列随机事件的概率:①投掷一枚均匀的骰子,朝上一面为偶数的概率;②同时抛掷两枚质地均匀的硬币,两枚硬币全部正面朝上的概率;③抛一枚图钉,“钉尖向下”的概率;④某作物的种子在一定条件下的发芽率.既可以用列举法求得又可以用频率估计获得的是(只填写序号).16.下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程.三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26-27题,每小题7分,第28题8分)17. 计算:2sin30°+ .8)4()31(01+-+-π18. 解不等式组 :⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x19. 如图,在△ACB 中,AC =BC ,AD 为△ACB 的高线,CE 为△ACB 的中线.求证:∠DAB =∠ACE.20. 已知关于x 的一元二次方程0)1(2=+++k x k x . (1)求证:方程总有两个实数根;(2)若该方程有一个根是正数,求k 的取值范围.21. 如图,在△ABC 中,D 是AB 边上任意一点,E 是BC 边中点,过点C 作AB 的平行线,交DE 的延长线于点F ,连接BF ,CD .(1)求证:四边形CDBF 是平行四边形; (2)若∠FDB =30°,∠ABC =45°,BC =,求DF 的长.22. 如图,在平面直角坐标系xOy 中,直线AB 与x 轴、y 轴分别交于点A 、B ,与反比例函数xky 的图象在第四象限交于点C ,CD ⊥x 轴于点D ,tan ∠OAB =2,OA =2,OD =1. (1)求该反比例函数的表达式;(2)点M 是这个反比例函数图象上的点,过点M 作MN ⊥y 轴,垂足为点N ,连接OM 、AN , 如果S △ABN =2S △OMN ,直接写出点M 的坐标.23. 如图,在⊙O 中,C ,D 分别为半径OB ,弦AB 的中点,连接CD 并延长,交过点A 的切线于点E . (1)求证:AE ⊥CE . (2)若AE =,sin ∠ADE =31,求⊙O 半径的长.24. 水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性,进行了抽样调查,过程如下,请补充完整.收集数据 从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:整理、描述数据 按如下分组整理、描述这两组样本数据(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀)分析数据 两组样本数据的平均数、众数和方差如下表所示:a.估计乙大棚产量优秀的秧苗数为株;b.可以推断出大棚的小西红柿秧苗品种更适应市场需求,理由为.(至少从两个不同的角度说明推断的合理性)25.如图,AB是⊙O的直径,AB=4cm,C为AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=60°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=x cm,DE=y cm(当x 的值为0或3时,y的值为2),探究函数y随自变量x的变化而变化的规律.(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:点F与点O重合时,DE长度约为cm(结果保留一位小数).26. 在平面直角坐标系xOy 中,抛物线()2440y ax ax a =--≠与y 轴交于点A ,其对称轴与x 轴交于点B .(1)求点A ,B 的坐标;(2)若方程()244=00ax ax a --≠有两个不相等的实数根,且两根都在1,3之间(包括1,3),结合函数的图象,求a 的取值范围.27. 如图,在菱形ABCD 中,∠DAB =60°,点E 为AB 边上一动点(与点A ,B 不重合),连接CE ,将∠ACE 的两边所在射线CE ,CA 以点C 为中心,顺时针旋转120°,分别交射线AD 于点F ,G. (1)依题意补全图形;(2)若∠ACE=α,求∠AFC 的大小(用含α的式子表示); (3)用等式表示线段AE 、AF 与CG 之间的数量关系,并证明.28. 对于平面直角坐标系xOy中的点P和线段AB,其中A(t,0)、B(t+2,0)两点,给出如下定义:若在线段AB上存在一点Q,使得P,Q两点间的距离小于或等于1,则称P为线段AB的伴随点.(1)当t=-3时,①在点P1(1,1),P2(0,0),P3(-2,-1)中,线段AB的伴随点是;②在直线y=2x+b上存在线段AB的伴随点M、N,且MN=b的取值范围;(2)线段AB的中点关于点(2,0)的对称点是C,将射线CO以点C为中心,顺时针旋转30°得到射线l,若射线l上存在线段AB的伴随点,直接写出t的取值范围.北京市朝阳区2018年中考一模数学试卷参考答案及评分标准一、选择题(本题共16分,每小题2分)二、填空题 (本题共16分,每小题2分)9. 答案不惟一,如:边长分别为a ,b 的矩形面积 10.4711. ⎩⎨⎧=+=+.562018,631325y x y x 12. 1:4 13. 1514. 答案不唯一,如:以x 轴为对称轴,作△OAB 的轴对称图形,再将得到三角形沿向右平移4个单位长度 15. ①②16. 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上;直径所对的圆周角是直角三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26-27题,每小题7分,第28题8分) 17. 解:原式 2213212+++⨯= …………………………………………………………………4分 225+=. ……………………………………………………………………………5分18. 解:原不等式组为⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x解不等式①,得 5<x . ………………………………………………………………………2分解不等式②,得 21>x .………………………………………………………………………4分 ∴ 原不等式组的解集为521<<x . …………………………………………………………5分19. 证明:∵AC =BC ,CE 为△ACB 的中线,∴∠CAB =∠B ,CE ⊥AB . ………………………………………………………………2分 ∴∠CAB +∠ACE =90°. …………………………………………………………………3分 ∵AD 为△ACB 的高线, ∴∠D =90°.∴∠DAB +∠B =90°. ……………………………………………………………………4分∴∠DAB =∠ACE . ………………………………………………………………………5分20. (1)证明:依题意,得k k 4)1(2-+=∆ ……………………………………………………1分 .)1(2-=k ……………………………………………………………2分∵0)1(2≥-k ,∴方程总有两个实数根. ……………………………………………………………3分(2)解:由求根公式,得11-=x ,k x -=2. …………………………………………………4分∵方程有一个根是正数, ∴0>-k .∴0<k .…………………………………………………………………………………5分21.(1)证明:∵CF ∥AB ,∴∠ECF =∠EBD . ∵E 是BC 中点, ∴CE =BE .∵∠CEF =∠BED , ∴△CEF ≌△BED . ∴CF =BD .∴四边形CDBF 是平行四边形. ……………………………………………………2分(2)解:如图,作EM ⊥DB 于点M ,∵四边形CDBF 是平行四边形,BC =24, ∴2221==BC BE ,DE DF 2=.在Rt △EMB 中,2sin =∠⋅=ABC BE EM . …………………………………………3分在Rt △EMD 中,42==EM DE . ……………………………………………………4分∴DF =8. ……………………………………………………………………………………5分22. 解:(1)∵AO =2,OD =1,∴AD =AO+ OD =3. ……………………………………………………………………1分 ∵CD ⊥x 轴于点D , ∴∠ADC =90°.在Rt △ADC 中,6tan =∠⋅=OAB AD CD ..∴C (1,-6). ……………………………………………………………………………2分∴该反比例函数的表达式是xy 6-=. …………………………………………………3分A(2)点M 的坐标为(-3,2)或(53,-10). ……………………………………………5分23. (1)证明:连接OA ,∵OA 是⊙O 的切线, ∴∠OAE =90º. ………………………………1分 ∵ C ,D 分别为半径OB ,弦AB 的中点,∴CD 为△AOB 的中位线.∴CD ∥OA . ∴∠E =90º. ∴AE ⊥CE . …………………………………2分(2)解:连接OD ,∴∠ODB =90º. ………………………………………………………………………3分∵AE =,sin ∠ADE =31, 在Rt △AED 中,23sin =∠=ADEAEAD .∵CD ∥OA , ∴∠1=∠ADE .在Rt △OAD 中,311sin ==∠OA OD .………………………………………………4分 设OD =x ,则OA =3x , ∵222OA AD OD =+, ∴()()222323x x =+.解得 231=x ,232-=x (舍). ∴293==x OA . ……………………………………………………………………5分即⊙O 的半径长为29.24. 解:整理、描述数据 按如下分组整理、描述这两组样本数据…………………………………………………………………………………………………2分25≤x <35 35≤x <45 45≤x <55 55≤x <65 65≤x <75 75≤x <85甲 5 5 5 5 4 1 乙24665212E CB O D x 大棚个数株数得出结论 a .估计乙大棚产量优秀的秧苗数为 84 株; …………………………3分b .答案不唯一,理由须支撑推断的合理性. ………………………………5分25. 解:本题答案不唯一,如:x /cm 0 0.400.55 1.00 1.80 2.29 2.61 3 y /cm23.683.844.003.653.132.702…………………………………………………………………………………………………1分(2)…………………………………………………………………………………………………4分(3)3.5.…………………………………………………………………………………………6分26.解:(1)44)2(4422---=--=a x a ax ax y .∴A (0,-4),B (2,0).…………………………………………………………2分 (2)当抛物线经过点(1,0)时,34-=a .……………………………………………4分 当抛物线经过点(2,0)时,1-=a . ……………………………………………6分 结合函数图象可知,a 的取值范围为134<≤-a .…………………………………7分27.(1)补全的图形如图所示.…………………………………………………………………………………………………1分(2)解:由题意可知,∠ECF=∠ACG=120°.∴∠FCG=∠ACE=α.∵四边形ABCD 是菱形,∠DAB=60°, ∴∠DAC=∠BAC= 30°. ………………………………………………………………2分 ∴∠AGC=30°. ∴∠AFC =α+30°. ………………………………………………………………………3分(3)用等式表示线段AE 、AF 与CG 之间的数量关系为CG AF AE 3=+.证明:作CH ⊥AG 于点H.由(2)可知∠BAC=∠DAC=∠AGC=30°.∴CA=CG. ………………………………………………………………………………………5分 ∴HG =21AG. ∵∠ACE =∠GCF ,∠CAE =∠CGF ,∴△ACE ≌△GCF. ……………………………………………………………………………6分 ∴AE =FG .在Rt △HCG 中, .23cos CG CGH CG HG =∠⋅= ∴AG =3CG . …………………………………………………………………………………7分 即AF+AE =3CG .28. 解:(1)①线段AB 的伴随点是: 23,P P . ………………………………………………2分②如图1,当直线y =2x +b 经过点(-3,-1)时,b =5,此时b 取得最大值.………………………………………………………………………………4分 如图2,当直线y =2x +b 经过点(-1,1)时,b =3,此时b 取得最小值. ………………………………………………………………………………5分 ∴ b 的取值范围是3≤b ≤5. ……………………………………………………6分(2)t 的取值范围是-12.2t ≤≤………………………………………………………………8分图1 图2。
第10讲 2018北京九年级数学一模分类---代几综合新定义(答案版)
第10讲 代几综合(新定义) 1.(海淀)在平面直角坐标系xOy 中,对于点P 和C ,给出如下定义:若C 上存在一点T 不与O 重合,使点P 关于直线OT 的对称点'P 在C 上,则称P 为C 的反射点.下图为C 的反射点P 的示意图.(1)已知点A 的坐标为(1,0),A 的半径为2,①在点(0,0)O ,(1,2)M ,(0,3)N -中,A 的反射点是____________;②点P 在直线y x =-上,若P 为A 的反射点,求点P 的横坐标的取值范围;(2)C 的圆心在x 轴上,半径为2,y 轴上存在点P 是C的反射点,直接写出圆心C 的横坐标x 的取值范围.1.解(1)①A 的反射点是M ,N . ②设直线y x =-与以原点为圆心,半径为1和3的两个圆的交点从左至右依次为D ,E ,F ,G ,过点D 作⊥DH x 轴于点H ,如图.可求得点D 的横坐标为322-. 同理可求得点E ,F ,G 的横坐标分别为22-,22,322. 点P 是A 的反射点,则A 上存在一点T ,使点P 关于直线OT 的对称点'P 在A 上,则'OP OP =.∵1'3≤≤OP ,∴13≤≤OP . 反之,若13≤≤OP ,A 上存在点Q ,使得OP OQ =,故线段PQ 的垂直平分线经过原点,且与A 相交.因此点P 是A 的反射点.∴点P 的横坐标x 的取值范围是32222≤≤x --,或23222≤≤x . (2)圆心C 的横坐标x 的取值范围是44≤≤x -.2.(西城)对于平面内的⊙C 和⊙C 外一点Q ,给出如下定义:若过点Q 的直线与⊙C 存在公共点,记为点A ,B ,设AQ BQk CQ+=,则称点A (或点B )是⊙C 的“k 相关依附点”,特别地,当点A 和点B 重合时,规定AQ BQ =,2AQ k CQ =(或2BQCQ). 已知在平面直角坐标系xOy 中,(1,0)Q -,(1,0)C ,⊙C 的半径为r .yxPO C TP’(1)如图1,当r =①若1(0,1)A 是⊙C 的“k 相关依附点”,则k 的值为__________.②2(1A +是否为⊙C 的“2相关依附点”.答:__________(填“是”或“否”). (2)若⊙C 上存在“k 相关依附点”点M , ①当1r =,直线QM 与⊙C 相切时,求k 的值.②当k =r 的取值范围.(3)若存在r的值使得直线y b =+与⊙C 有公共点,且公共点时⊙C 的附点”,直接写出b 的取值范围.2.(1(2)①如图,当1r =时,不妨设直线QM 与⊙C 相切的切点M 在x 轴上方(切点M 在x 轴下方时同理),连接CM ,则QM CM ⊥,∵(1,0)Q -,(1,0)C ,1r =, ∴2CQ =,1CM =,xx∴MQ =此时2MQk CQ== ②如图,若直线QM 与⊙C 不相切,设直线QM 与⊙C 的另一个交点为N (不妨设QN QM <,点N ,M 在x 轴下方时同理),作CD QM ⊥于点D ,则MD ND =,∴()222MQ NQ MN NQ NQ ND NQ DQ +=++=+=, ∵2CQ =, ∴2MQ NQ DQk DQ CQ CQ+===,∴当k =DQ =此时1CD =, 假设⊙C 经过点Q ,此时2r =, ∵点Q 早⊙C 外,∴r 的取值范围是12r <≤. (3)b <<.x3(东城)给出如下定义:对于⊙O的弦MN和⊙O外一点P(M,O,N三点不共线,且P,O在直线MN的异侧),当∠MPN+∠MON=180°时,则称点P是线段MN关于点O 的关联点.图1是点P为线段MN关于点O的关联点的示意图.在平面直角坐标系xOy中,⊙O的半径为1.(1)如图2,22,22M⎛⎫⎪⎪⎝⎭,22,22N⎛⎫-⎪⎪⎝⎭.在A(1,0),B(1,1),()2,0C三点中, 是线段MN关于点O的关联点的是;(2)如图3,M(0,1),N31,22⎛⎫-⎪⎪⎝⎭,点D是线段MN关于点O的关联点.①∠MDN的大小为°;②在第一象限内有一点E()3,m m,点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;③点F在直线323y x=-+上,当∠MFN≥∠MDN时,求点F的横坐标Fx的取值范围.3. 解:(1)C;(2)①60°;②△MNE是等边三角形,点E的坐标为()31,;③直线323y x=-+交y轴于点K(0,2),交x轴于点()23T,0.∴2OK=,23OT=. ∴60OKT∠=︒.作OG ⊥KT 于点G ,连接MG . ∵()M 0,1, ∴OM =1.∴M 为OK 中点 . ∴ MG =MK =OM =1.∴∠MGO =∠MOG =30°,OG =3. ∴33.22G ⎛⎫ ⎪ ⎪⎝⎭, ∵120MON ∠=︒, ∴ 90GON ∠=︒. 又3OG =,1ON =,∴30OGN ∠=︒. ∴60MGN ∠=︒.∴G 是线段MN 关于点O 的关联点.经验证,点()31E,在直线323y x =-+上. 结合图象可知, 当点F 在线段GE 上时 ,符合题意.∵G F E x x x ≤≤, ∴332F x ≤≤. 4. (朝阳) 对于平面直角坐标系xOy 中的点P 和线段AB ,其中A (t ,0)、B (t +2,0)两点,给出如下定义:若在线段AB 上存在一点Q ,使得P ,Q 两点间的距离小于或等于1,则称P 为线段AB 的伴随点. (1)当t =-3时,①在点P 1(1,1),P 2(0,0),P 3(-2,-1)中,线段AB 的伴随点是 ; ②在直线y =2x +b 上存在线段AB 的伴随点M 、N , 且MN 5=,求b 的取值范围;(2)线段AB 的中点关于点(2,0)的对称点是C ,将射线CO 以点C 为中心,顺时针 旋转30°得到射线l ,若射线l 上存在线段AB 的伴随点,直接写出t 的取值范围.4. 解:(1)①线段AB 的伴随点是: 23,P P .②如图1,当直线y =2x +b 经过点(-3,-1)时,b =5,此时b 取得最大值.如图2,当直线y =2x +b 经过点(-1,1)时,b =3,此时b 取得最小值.∴ b 的取值范围是3≤b ≤5.(2)t 的取值范围是-12.2t ≤≤ 5.(石景山)对于平面上两点A ,B ,给出如下定义:以点A 或B为圆心,AB 长为半径的圆称为点A ,B 的“确定圆”.如图为点A ,B 的“确定圆”的示意图.... (1)已知点A 的坐标为(1,0)-,点B 的坐标为(3,3), 则点A ,B 的“确定圆”的面积为_________;(2)已知点A 的坐标为(0,0),若直线y x b =+上只存在一个点B ,使得点A ,B 的“确定圆”的面积为9π,求点B 的坐标;(3)已知点A 在以(0)P m ,为圆心,以1为半径的圆上,点B 在直线33y =+ 若要使所有点A ,B 的“确定圆”的面积都不小于9π,直接写出m 的取值范围.28.解:(1)25π; ………………… 2分 (2)∵直线y x b =+上只存在一个点B ,使得点,A B 的“确定圆”的面积图1 图2AB为9π,∴⊙A 的半径3AB =且直线y x b =+与⊙A 相切于点B ,如图, ∴AB CD ⊥,45DCA ∠=°.①当0b >时,则点B 在第二象限. 过点B 作BE x ⊥轴于点E ,∵在Rt BEA ∆中,45BAE ∠=°,3AB =, ∴2BE AE ==.∴22B(. ②当0b <时,则点'B 在第四象限.同理可得'22B -(.综上所述,点B 的坐标为22-(,)或22-(. ………………… 6分(3)5m -≤或11m ≥. ………………… 8分6.(丰台)对于平面直角坐标系xOy 中的点M 和图形1W ,2W 给出如下定义:点P 为图形1W 上一点,点Q 为图形2W 上一点,当点M 是线段PQ 的中点时,称点M 是图形1W ,2W 的“中立点”.如果点P (x 1,y 1),Q (x 2,y 2),那么“中立点”M 的坐标为⎪⎭⎫⎝⎛++2,22121y y x x .已知,点A (-3,0),B (0,4),C (4,0). (1)连接BC ,在点D (12,0),E (0,1),F (0,12)中,可以成为点A 和线段BC 的“中立点”的是____________;(2)已知点G (3,0),⊙G 的半径为2.如果直线y = - x + 1上存在点K 可以成为点A 和⊙G 的“中立点”,求点K 的坐标;(3)以点C 为圆心,半径为2作圆.点N 为直线y = 2x + 4上的一点,如果存在点N ,使得y 轴上的一点可以成为点N 与⊙C 的“中立点”,直接写出点N 的横坐标的取值范围.6.解:(1)点和线段的“中立点”的是点D ,点F ; (2)点A 和⊙G 的“中立点”在以点O 为圆心、半径为1的圆上运动.因为点K 在直线y =- x +1上, 设点K 的坐标为(x ,- x +1),则x 2+(- x +1)2=12,解得x 1=0,x 2=1. 所以点K 的坐标为(0,1)或(1,0). (3)(说明:点与⊙C 的“中立点”在以线段NC 的中点P 为圆心、半径为1的圆上运动.圆P 与y 轴相切时,符合题意.) 所以点N 的横坐标的取值范围为-6≤x N ≤-2.7.(顺义)如图1,对于平面内的点P 和两条曲线1L 、2L 给出如下定义:若从点P 任意引出一条射线分别与1L 、2L 交于1Q 、2Q ,总有12PQ PQ 是定值,我们称曲线1L 与2L “曲似”,定值12PQ PQ 为“曲似比”,点P 为“曲心”.例如:如图2,以点O'为圆心,半径分别为1r 、2r (都是常数)的两个同心圆1C 、2C ,从点O'任意引出一条射线分别与两圆交于点M 、N ,因为总有12''r O M O N r 是定值,所以同心圆1C 与2C 曲似,曲似比为12r r ,“曲心”为O'. A BC N xy x y 图1Q 2Q 1L 2L 1P图2C 2C 1NMO'86422468105510D CBAO(1)在平面直角坐标系xOy 中,直线y kx =与抛物线2y x =、212y x =分别交于点A 、B ,如图3所示,试判断两抛物线是否曲似,并说明理由;(2)在(1)的条件下,以O 为圆心,OA 为半径作圆,过点B 作x 轴的垂线,垂足为C ,是否存在k 值,使⊙O 与直线BC 相切?若存在,求出k 的值;若不存在,说明理由; (3)在(1)、(2)的条件下,若将“212y x =”改为“21y x m=”,其他条件不变,当存在⊙O 与直线BC 相切时,直接写出m 的取值范围及k 与m 之间的关系式.7.(1)是.过点A ,B 作x 轴的垂线,垂足分别为D ,C .依题意可得A (k ,k 2),B (2k ,2k 2).……………………………………………… 2分 因此D (k ,0),C (2k ,0). ∵AD ⊥x 轴,BC ⊥x 轴,∴AD ∥BC .∴122===OA OD k OB OC k . ∴两抛物线曲似,曲似比是12. ………… 3分 (2)假设存在k 值,使⊙O 与直线BC 相切.则OA=OC=2k ,又∵OD=k ,AD=k 2,并且OD 2+AD 2= OA 2, ∴k 2+(k 2)2=(2k )2.∴3k =±.(舍负) 由对称性可取3k =-.综上,3k =±. ………………………… 6分(3)m 的取值范围是m >1,k 与m 之间的关系式为k 2=m 2-1 . ……… 8分 8.(延庆)平面直角坐标系xOy 中,点1(A x ,1)y 与2(B x ,2)y ,如果满足120x x +=,120y y -=,其中12x x ≠,则称点A 与点B 互为反等点.已知:点C (3,4)(1)下列各点中, 与点C 互为反等点;D (-3,-4),E (3,4),F (-3,4) (2)已知点G (-5,4),连接线段CG ,若在线段CG 上存在两点P ,Q 互为反等点,求点P 的横坐标p x 的取值范围; (3)已知⊙O 的半径为r ,若⊙O 与(2)中线段CG 的两个交点互为反等点, 求r 的取值范围.8.(1)F ……1分(2) -3≤p x ≤3 且p x ≠0 ……4分(3)4 < r≤5 ……7分9. (怀柔) P 是⊙C 外一点,若射线..PC 交⊙C 于点A ,B 两点,则给出如下定义:若0<PA ⋅PB ≤3,则点P 为⊙C 的“特征点”. (1)当⊙O 的半径为1时.①在点P 1(2,0)、P 2(0,2)、P 3(4,0)中,⊙O 的“特征点”是 ; ②点P 在直线y=x+b 上,若点P 为⊙O 的“特征点”.求b 的取值范围;(2)⊙C 的圆心在x 轴上,半径为1,直线y=x+1与x 轴,y 轴分别交于点M ,N ,若线段MN 上的所有点都不是...⊙C 的“特征点”,直接写出点C 的横坐标的取值范围.9. (1)①P 1(2,0)、P 2(0,2)…………………………………………………………………2分 ②如图, 在y=x+b 上,若存在⊙O 的“特征点”点P ,点O 到直线y=x+b 的距离m ≤2. 直线y=x+b 1交y 轴于点E ,过O 作OH ⊥直线y=x+b 1于点H. 因为OH=2,在Rt △DOE 中,可知OE=22. 可得b 1=22.同理可得b 2=-22.∴b 的取值范围是:22-≤b ≤22. …………………………………………………6分 (2)x>3或 3-<x . …………………………………………………………………………8分10(平谷)在平面直角坐标系xOy 中,点M 的坐标为()11,x y ,点N 的坐标为()22,x y ,且12x x ≠,12y y ≠,以MN 为边构造菱形,若该菱形的两条对角线分别平行于x 轴,y 轴,则称该菱形为边的“坐标菱形”.(1)已知点A (2,0),B (),则以AB 为边的“坐标菱形”的最小内角为_______; (2)若点C (1,2),点D 在直线y =5上,以CD 为边的“坐标菱形”为正方形,求直线CD 表达式;(3)⊙OP 的坐标为(3,m ) .若在⊙O 上存在一点Q ,使得以QP 为边的“坐标菱形”为正方形,求m 的取值范围.10.解:(1)60;·························································································· 1 (2)∵以CD 为边的“坐标菱形”为正方形, ∴直线CD 与直线y =5的夹角是45°. 过点C 作CE ⊥DE 于E .∴D (4,5)或()2,5-. ........................................ 3 ∴直线CD 的表达式为1y x =+或3y x =-+. (5)(3)15m ≤≤或51m -≤≤-. (7)11(门头沟)在平面直角坐标系xOy 中,点M 的坐标为11(,)x y ,点N 的坐标为22(,)x y ,且12x x ≠,12y y =,我们规定:如果存在点P ,使MNP ∆是以线段MN 为直角边的等腰直角三角形,那么称点P 为点M 、N 的 “和谐点”. (1)已知点A 的坐标为)3,1(,①若点B 的坐标为)3,3(,在直线AB 的上方,存在点A ,B 的“和谐点”C ,直接写出点C 的坐标;②点C 在直线x =5上,且点C 为点A ,B 的“和谐点”,求直线AC 的表达式. (2)⊙O 的半径为r ,点D (1,4)为点E (1,2)、F ),(n m 的“和谐点”,若使得△DEF 与⊙O 有交点,画出示意图直接.....写出半径r 的取值范围.xy OxyO备用图1 备用图211.解: (1)①)5,3()5,1(21C C 或. ……………………………………………2分②由图可知,B )3,5( ∵A (1,3) ∴AB =4∵ABC ∆为等腰直角三角形 ∴BC =4∴)1,5()7,5(21-C C 或设直线AC 的表达式为(0)y kx b k =+≠ 当)7,5(1C 时,⎩⎨⎧=+=+753b k b k ⎩⎨⎧==∴21b k2+=∴x y …………………………………3分 当)1,5(2-C 时,⎩⎨⎧-=+=+153b k b k ⎩⎨⎧=-=∴41b k4+-=∴x y …………………………………4分 ∴综上所述,直线AC 的表达式是2+=x y 或4+-=x y (2)当点F 在点E 左侧时:2r ∴≤当点F 在点E 右侧时:r…………………………………7分 综上所述:2r ∴≤ …………………………………8分12(大兴)在平面直角坐标系xOy 中,过y 轴上一点A 作平行于x 轴的直线交某函数图象于点D ,点P 是x 轴上一动点,连接D P ,过点P 作DP 的垂线交y 轴于点E (E 在线段OA 上,E 不与点O 重合),则称∠DPE 为点D ,P ,E 的“平横纵直角”.图1为点D ,P ,E 的“平横纵直角”的示意图.如图2,在平面直角坐标系xOy 中,已知二次函数图象与y 轴交于点(0,)F m ,与x 轴分别交于点B (3-,0),C (12,0). 若过点F 作平行于x 轴的直线交抛物线于点N .(1)点N 的横坐标为 ;图2 (2)已知一直角为点,,N M K 的“平横纵直角”, 若在线段OC 上存在不同的两点1M 、2M ,使相应的点1K 、2K 都与点F 重合,试求m 的取值范围;(3)设抛物线的顶点为点Q ,连接BQ 与FN 交于点H ,当4560QHN ︒≤∠≤︒时,求m 的取值范围.12.(1)9 ………………………………………………………………… 1分 (2)方法一:MK ⊥MN ,∴要使线段OC 上存在不同的两点M 1、M 2,使相应的点K 1、K 2都与点F 重合,也就是使以FN 为直径的圆与OC 有两个交点,即m r >.29=r ,29<∴m .又0>m ,290<<∴m . ………………………………………………4分方法二:0>m ,∴点K 在x 轴的上方.过N 作NW ⊥OC 于点W ,设OM x =,OK y =, 则 CW =OC -OW =3,WM =9x -. 由△MOK ∽△NWM , 得,∴9y x x m=-. ∴x mx m y 912+-=.当m y =时,219m x x m m=-+, 化为0922=+-m x x . 当△=0,即22940m -=, 解得92m =时, 线段OC 上有且只有一点M ,使相应的点K 与点F 重合.0>m ,∴ 线段OC 上存在不同的两点M 1、M 2,使相应的点K 1、K 2都与点F 重合时,m 的取值范围为290<<m . ………………………………………………………………………………4分(3)设抛物线的表达式为:)12)(3(-+=x x a y (a ≠0),又 抛物线过点F (0,m ), a m 36-=∴.m a 361-=∴.mx m x x m y 1625)29(361)12)(3(3612+--=-+-=∴. …………………………………5分过点Q 做QG ⊥x 轴与FN 交于点RFN ∥x 轴 ∴∠QRH =90°tan BG BQG QG∠=,2516QG m =,152BG =∴,又4560QHN ︒≤∠≤︒,∴3045BQG ︒≤∠≤︒∴当30BQG ∠=︒时,可求出3524=m , 当45BQG ∠=︒时,可求出524=m .m ∴的取值范围为2424355m ≤≤.13.(房山)在平面直角坐标系xOy 中,当图形W 上的点P 的横坐标和纵坐标相等时,则称点P 为图形W 的“梦之点”. (1)已知⊙O 的半径为1.①在点E (1,1),F (-22 ,-22),M (-2,-2)中,⊙O 的“梦之点”为 ;②若点P 位于⊙O 内部,且为双曲线ky x=(k ≠0)的“梦之点”,求k 的取值范围.(2)已知点C 的坐标为(1,t ),⊙C 的半径为 2 ,若在⊙C 上存在“梦之点”P ,直接写出t 的取值范围.(3)若二次函数21y ax ax =-+的图象上存在两个“梦之点”()11A x ,y ,()22B x ,y ,且122x x -=,求二次函数图象的顶点坐标.13. (1)① F ; ………………………………………………………………………1分 ② ∵⊙O 的半径为1.∴⊙O 的“梦之点”坐标为(-22 ,-22 )和(22 ,22).………………2分 又∵双曲线ky x=(k ≠0)与直线y =x 的交点均为双曲线的“梦之点”, ∴将(-22 ,-22)代入双曲线表达式中,得, 1=2k xy =……………………………………………………………………3分 ∵点P 位于⊙O 内部. ∴102k <<……………………………………………………………………4分 (2) -1≤t ≤3……………………………………………………………………………6分 (3)由“梦之点”定义可得: ()11A x ,x ,()22B x ,x . 则21x ax ax =-+.整理得,()2110ax a x -++=解得,11x =,21x a=. 把两个根代入122x x -=中,即112a-=解得,11a =-,213a =. 当1a =-时,21y x x =-++ ,其顶点坐标为(12 , 54 )………………………7分当13a =时,211133y x x =-+,其顶点坐标为(12 , 1112 )……………………8分。
北京市八区2018届初三二模数学分类汇编二模函数综合试题
北京市八区2018届初三二模数学分类汇编二模函数综合试题1东城.在平面直角坐标系xOy 中,抛物线()230y ax bx a =+-≠经过点()1,0A -和点()45B ,.(1)求该抛物线的表达式;(2)求直线AB 关于x 轴的对称直线的表达式;(3)点P 是x 轴上的动点,过点P 作垂直于x 轴的直线l ,直线l 与该抛物线交于点M ,与直线AB 交于点N .当PM PN <时,求点P 的横坐标P x 的取值范围.2西城. 抛物线M :241y ax ax a =-+- (a ≠0)与x 轴交于A ,B 两点(点A 在点B 左侧),抛物线的顶点为D .(1)抛物线M 的对称轴是直线____________; (2)当AB =2时,求抛物线M 的函数表达式;(3)在(2)的条件下,直线l :y kx b =+(k ≠0)经过抛物线的顶点D ,直线y n =与抛物线M 有两个公共点,它们的横坐标分别记为1x ,2x ,直线y n =与直线l 的交点的横坐标记为3x (30x >),若当2-≤n ≤1-时,总有13320x x x x ->->,请结合函数的图象,直接写出k 的取值范围.3海淀.在平面直角坐标系xOy 中,已知点(3,1)A -,(1,1)B -,(,)C m n ,其中1n >,以点,,A B C 为顶点的平行四边形有三个,记第四个顶点分别为123,,D D D ,如图所示.(1)若1,3m n =-=,则点123,,D D D 的坐标分别是( ),( ),( ); (2)是否存在点C ,使得点123,,,,A B D D D 在同一条抛物线上?若存在,求出点C 的坐标;若不存在,说明理由.4朝阳.已知二次函数)0(222≠--=a ax ax y .(1)该二次函数图象的对称轴是直线 ;(2)若该二次函数的图象开口向上,当-1≤x ≤5时,函数图象的最高点为M ,最低点为N ,点M 的纵坐标为211,求点M 和点N 的坐标;(3)对于该二次函数图象上的两点A (x 1,y 1),B (x 2,y 2),设t ≤ x 1 ≤ t +1,当x 2≥3时,均有y 1 ≥ y 2,请结合图象,直接写出t 的取值范围.5丰台.在平面直角坐标系xOy 中,二次函数22y x hx h =-+的图象的顶点为点D .(1)当1h =-时,求点D 的坐标;(2)当1x -≤≤≤11x -≤≤≤1时,求函数的最小值m . (用含h 的代数式表示m )6石景山.在平面直角坐标系xOy 中,抛物线()240y ax x c a =++≠经过点()34,A -和()02,B .(1)求抛物线的表达式和顶点坐标;(2)将抛物线在A 、B 之间的部分记为图象M (含A 、B 两点).将图象M 沿直线3x =翻折,得到图象N .若过点()94,C 的直线y kx b =+与图象M 、图象N 都相交,且只有两个交点,求b 的取值范围.7昌平.在平面直角坐标系xOy 中,抛物线223(0)y ax ax a a =--≠,与x 轴交于A 、B 两点(点A 在点B 的左侧).(1)求点A 和点B 的坐标;(2)若点P (m ,n )是抛物线上的一点,过点P 作x 轴的垂线,垂足为点D .①在0a >的条件下,当22m -≤≤时,n 的取值范围是45n -≤≤,求抛物线的表达式;②若D 点坐标(4,0),当PD AD >时,求a 的取值范围.8房山. 在平面直角坐标系x O y 中,二次函数2y ax bx c =++(0a ≠)的图象经过A (0,4),B (2,0),C (-2,0)三点. (1)求二次函数的表达式;(2)在x 轴上有一点D (-4,0),将二次函数的图象沿射线DA 方向平移,使图象再次经过点B .①求平移后图象顶点E 的坐标;②直接写出此二次函数的图象在A ,B 两点之间(含A ,B 两点)的曲线部分在平移过程中所扫过的面积.9清华附中26.已知如图,直线y=kx+2与x 轴正半轴相交于点A (t,0),与y 轴相交于点B ,抛物线y=-x ²+bx+c ,经过点A 和点B ,点C 在第三象限内,且AC ⊥AB,tan∠ACB=21,(1)当t 等于1时,求抛物线的表达式。
2018年中考数学真题汇编二次函数(含答案)
中考数学真题演练2 2018年中考数学真题汇编----二次函数
一、选择题
1.给出下列函数:①y=-3x+2;②y= ;③y=2x2;④y=3x,上述函数中符合条作“当x>1时,函数值y随自变量x增大而增大“的是()
A. ①③
B. ③④
C. ②④
D. ②③
【答案】B
2.如图,函数和 ( 是常数,且 )在同一平面直角坐标系的图象可能是()
A. B.
C. D.
【答案】B
3.关于二次函数,下列说法正确的是()
A. 图像与轴的交点坐标为
B. 图像的对称轴在轴的右侧
C. 当时,的值随值的增大而减小
D. 的最小值为-3
【答案】D
4.二次函数的图像如图所示,下列结论正确是( )
A. B.
C. D. 有两个不相等的实数根
【答案】C
5.若抛物线与轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. B.
C. D.
【答案】B
6.若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线。
已知某定弦抛物线的对称轴为直线x=1,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点()
A. (-3,-6)
B. (-3,0)
C. (-3,-5)
D. (-3,-1)
【答案】B
7.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=-t2+24t+1.则下列说法中正确的是()。
2018年全国中考数学真题分类 二次函数概念、性质和图象解析版(精品文档)
2018年全国中考数学真题分类 二次函数概念、性质和图象(一)一、选择题1.(2018山东滨州,10,3分)如图,若二次函数(a ≠0)图象的对称轴为x =1,与y 轴交于点C ,与x 轴交于点A 、点B (-1,0)则①二次函数的最大值为a +b +c ;②a -b +c <0;③b ²-4ac <0;④当y >0时,-1<x <3.其中正确的个数是( ) A .1 B .2 C .3 D .4第10题图【答案】B【解析】由图像可知,当x =1时,函数值取到最大值,最大值为:a +b +c ,故①正确;因为抛物线经过点B (-1,0),所以当x =-1时,y =a -b +c =0,故②错误;因为该函数图象与x 轴有两个交点A 、B ,所以b ²-4ac >0,故③错误;因为点A 与点B 关于直线x =1对称,所以A (3,0),根据图像可知,当y >0时,-1<x <3,故④正确;故选B . 【知识点】数形结合、二次函数的图像和性质2. (2018四川泸州,10题,3分)已知二次函数22233y ax ax a =+++(其中x 是自变量),当2x ≥时,y 随x 的增大而增大,且21x -≤≤时,y 的最大值为9,则a 的值为( ) A.1或2- B.2-或2 C.2 D.1【答案】D【解析】原函数可化为y=a(x+1)2+3a 2-a+3,对称轴为x=-1,当2x ≥时,y 随x 的增大而增大,所以a>0,抛物线开口向上,因为21x -≤≤时,y 的最大值为9,结合对称轴及增减性可得,当x=12y ax bx c =++xy -1BOCAx =1时,y=9,带入可得,a 1=1,a 2=-2,又因为a>0,所以a=1 【知识点】二次函数,增减性3. (2018甘肃白银,10,3)如图是二次函数2(,,y ax bx c a b c =++是常数,0)a ≠图像的一部分,与x 轴的交点A 在点(2,0)和(3,0)之间,对称轴是x =1,对于下列说法:①0ab <,②20a b +=,③30a c +>,④()(a b m am b m +≥+为常数),⑤当13-<x <时,0y >,其中正确的是( )A.①②④B.①②⑤C.②③④D.③④⑤【答案】A【思路分析】由抛物线的图像结合对称轴、与x 轴的交点逐一判断即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数(含代数综合题)
(1)二次函数图像与性质基础
1.(18朝阳毕业9)在平面直角坐标系xOy 中,二次函数172
++=x x y 的
图象如图所示,则方程0172=++x x 的根的情况是
A.有两个相等的实数根
B.有两个不相等的实数根
C.没有实数根
D.无法判断
2.(18朝阳毕业13)抛物线y =x 2-6x +5的顶点坐标为 .
3.(18大兴一模11)请写出一个开口向下,并且对称轴为直线x =1的抛物线的表达式y =
4.(18东城一模2) 当函数()2
12y x =--的函数值y 随着x 的增大而减小时,x 的取值范围是
A .x >0
B .x <1
C .1x >
D .x 为任意实数
5. (18燕山一模12)写出经过点(0,0),(-2,0)的一个二次函数的解析式
(写一个即可) 6.(18顺义一模15)如图,在边长为6cm 的正方形ABCD 中,点E 、F 、G 、
H 分别从点A 、B 、C 、D 同时出发,均以1cm/s 的速度向点B 、C 、D 、A 匀速运动,当点E 到达点B 时,四个点同时停止运动,在运动过程中,当运动时间为 s 时,四边形EFGH 的面积最小,其最小值是 cm 2.
(2)二次函数综合
1.(18平谷一模26)在平面直角坐标系xOy 中,抛物线2
23y x bx =-+-的对称轴为直线x =2.
(1)求b 的值;
(2)在y 轴上有一动点P (0,m ),过点P 作垂直y 轴的直线交抛物线于点A (x 1,y 1),B (x 2 ,y 2),
其中 12x x <.
①当213x x -=时,结合函数图象,求出m 的值;
②把直线PB 下方的函数图象,沿直线PB 向上翻折,图象的其余部分保持不变,得到一个新的图象W ,新图象W 在0≤x ≤5 时,44y -≤≤,求m 的取值范围.
H
G F
E D C
B A
2.(18延庆一模26)在平面直角坐标系xOy 中,抛物线y =ax 2-4ax +3a (a >0)与x 轴交于A ,B 两点(A 在B
的左侧).
(1)求抛物线的对称轴及点A ,B 的坐标;
(2)点C (t ,3)是抛物线243(0)y ax ax a a =-+>上一点,(点C 在对称轴的右侧),过点C 作x
轴的垂线,垂足为点D .
①当CD AD =时,求此时抛物线的表达式; ②当CD AD >时,求t 的取值范围.
3. (18石景山一模26)在平面直角坐标系xOy 中,
将抛物线2
1G y mx =+:0m ≠)
单位长度后得到抛物线2G ,点A 是抛物线2G 的顶点. (1)直接写出点A 的坐标;
(2
)过点0(且平行于x 轴的直线l 与抛物线2G 交于B ,C 两点. ①当=90BAC ∠°时,求抛物线2G 的表达式;
②若60120BAC <∠<°°,直接写出m 的取值范围.
4.(18房山一模26
)抛物线2
y ax bx =+-
x 轴于点A (-1,0)
,C (3,0),交y 轴于点B ,抛物线的对称轴与x 轴相交于点D . 点P 为线段OB 上的点,点E 为线段AB 上的点,且PE ⊥AB.
(1)求抛物线的表达式;
(2)计算PE
PB
的值;
(3)请直接写出1
2PB +PD 的最小值为 .
5. (18西城一模26)在平面直角坐标系xOy 中,抛物线G :221(0)y mx mx m m =++-≠与y 轴交于点C ,
抛物线G 的顶点为D ,直线l :1(0)y mx m m =+-≠.
(1)当1m =时,画出直线l 和抛物线G ,并直接写出直线l 被抛物线G 截得的线段长. (2)随着m 取值的变化,判断点C ,D 是否都在直线l 上并说明理由.
(3)若直线l 被抛物线G 截得的线段长不小于2,结合函数的图象,直接写出m 的取值范围.
x
6.(18朝阳毕业26)抛物线c bx x y ++=2的对称轴为直线x =1,该抛物线与x 轴的两个交点分别为A 和B ,
与 y 轴的交点为C ,其中A (-1,0).
(1)写出B 点的坐标 ;
(2)若抛物线上存在一点P ,使得△POC 的面积是△BOC 的面积的2倍,求点P 的坐标;
(3)点M 是线段BC 上一点,过点M 作x 轴的垂线交抛物线于点D ,求线段MD 长度的最大值.
7.(18怀柔一模26)在平面直角坐标系xOy 中,抛物线y=nx 2-4nx+4n-1(n ≠0),与x 轴交于点C ,D(点C
在点D 的左侧),与y 轴交于点A . (1)求抛物线顶点M 的坐标; (2)若点A 的坐标为(0,3),AB ∥x 轴,交抛物线于点B ,求点B 的坐标;
(3)在(2)的条件下,将抛物线在B ,C 两点之间的部分沿y 轴翻折,翻折后的图象记为G ,若直
线与图象G 有一个交点,结合函数的图象,求m 的取值范围.
m x y +=2
1
8.(18海淀一模26)在平面直角坐标系xOy 中,已知抛物线22y x ax b =-+的顶点在 x 轴上,1(,)P x m ,
2(,)Q x m (12x x <)是此抛物线上的两点.
(1)若1a =,
①当m b =时,求1x ,2x 的值;
②将抛物线沿y 轴平移,使得它与x 轴的两个交点间的距离为4,试描述出这一变化过程; (2)若存在实数c ,使得11x c ≤-,且27x c ≥+成立,则m 的取值范围是 .
9.(18朝阳一模26)在平面直角坐标系xOy 中,抛物线()2
440y ax ax a =--≠与y 轴交于点A ,其对
称轴与x 轴交于点B .
(1)求点A ,B 的坐标;
(2)若方程有两个不相等的实数根,且两根都在1,3之间(包括1,3),
结合函数的图象,求a 的取值范围.
()2
44=00ax ax a --≠
10.(18东城一模26)在平面直角坐标系xOy 中,抛物线()02342
≠-+-=a a ax ax y 与x 轴交于A ,B
两点(点A 在点B 左侧).
(1)当抛物线过原点时,求实数a 的值; (2)①求抛物线的对称轴;
②求抛物线的顶点的纵坐标(用含a 的代数式表示); (3)当AB ≤4时,求实数a 的取值范围.
11.(18丰台一模26)在平面直角坐标系xOy 中,抛物线243y ax ax a =-+的最高点的纵坐标是2.
(1)求抛物线的对称轴及抛物线的表达式; (2)将抛物线在1≤x ≤4之间的部分记为图象G 1,将图象G 1沿直线x = 1翻折,翻折后的图象记为G 2,图象G 1和G 2组成图象G .过(0,b )作与y 轴垂直的直线l ,当直线l 和图象G 只有两个公共点时,将这两个公共点分别记为P 1(x 1,y 1),P 2(x 2,y 2),求b 的取值范围和x 1 + x 2的值.
12.(18门头沟一模26)有一个二次函数满足以下条件:
①函数图象与x 轴的交点坐标分别为(1,0)A ,22(,)B x y (点B 在点A 的右侧);
②对称轴是3x =; ③该函数有最小值是-2.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象2x x >的部分图象向下翻折与原图象未翻折的部分组成图象“G ”,平行于x 轴的直线与图象“G ”相交于点33(,)C x y 、44(,)D x y 、55(,)E x y (345x x x <<),结合画出的函数图象求345x x x ++的取值范围.
13.(18大兴一模26)在平面直角坐标系xOy 中,抛物线22
(31)2(0)y x m x m m m =-+++>,与y 轴交
于点C ,与x 轴交于点A 1(,0)x ,B 2(,0)x ,且12x x <. (1)求1223-+x x 的值;
(2)当m=1223-+x x 时,将此抛物线沿对称轴向上平移n 个单位,使平移后得到的抛物线顶点落在△ABC 的内部(不包括△ABC 的边),求n 的取值范围(直接写出答案即可).
14.(18顺义一模26)在平面直角坐标系xOy 中,若抛物线2
y x bx c =++顶点A 的横坐标是-1,且与y
轴交于点B (0,-1),点P 为抛物线上一点. (1)求抛物线的表达式;
(2)若将抛物线2
y x bx c =++向下平移4个单位,点P 平移后的对应点为Q .如果OP =OQ ,求点Q 的坐标.
15.(18通州一模26)在平面直角坐标系xOy 中,点C 是二次函数2
441y mx mx m =+++的图象的顶点,
一次函数4+=x y 的图象与x 轴、y 轴分别交于点A ,B . (1)请你求出点A ,B ,C 的坐标;
(2)若二次函数2
441y mx mx m =+++与线段AB 恰有一个公共点,求m 的取值范围.。
