河北省迁西县上营乡上营学校九年级数学上册课件:等腰三角形(复习第一课时)(共15张PPT)
全国中学教师《初中数学》说课教学比赛---主题:《等腰三角形的性质》说课--一等奖课件

1 2
D
C
教学过程
教学过程
例1 如图,在△ABC中, AB=AC ,点D在AC边上,且BD= BC=AD,求△ABC各角的度数.
新知应用
等腰三角形的性质
1 等腰三角形的两 分析:此题利用等腰三角形的性质1来解决 个底角相等(等边 ,难度稍大一点。 可预设几个小问题,帮助学生化解难点。 对等角)
教学过程教学过程
Company Logo
布置作业
作业: 必做:教材 P56 4、7题 选做: 在等腰△ABC中,∠ A=40°, 求 ∠B 度数。
带着问题前行
小组讨论
总结
抢答
学生讲述
教师点拨
教学过程
新课导入 小组讨论 启发探究 作品点评 知识总结
小组讨论,探究新知
首先出示等腰三角形的定义、腰、底边、顶角、
底角等概念,要求学生通过自学掌握这些概念。
引导学生用纸做一个等腰三角形模型,观察重合
部分,发现等腰三角形的所有的性质。对于有困难 的学生,教师又给以动画演示。
学法指导
让教师如何教?引领学生如何学?
自主探究
学 生
注重培养 三种能力
合作学习
分析归纳
学法指导
让教师如何教?引领学生如何学?
学法设计:本节课我将采用学生小组合作,实 验操作,观察发现,师生互动,学生互动的学习 方式。学生通过小组合作学会“主动探究— 主动总结—主动提高”。突出学生是学习的 主体,他们在感受知识的过程中,提高他们 “探究—发现—联想—概括”的能力!
质 1、 2 。
教学过程
动手实践,探究新知
性质1:
A
等腰三角形的两个底角相 等.简写为“等边对等角” 符号语言: 在△ ABC中, B C
冀教版八年级数学上册 17.1《等腰三角形》 课件 (共40张PPT)PPT文档42页

56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
拉
60、生活的道路一旦选定,就要勇敢地 走到》 课件 (共40张PPT)
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
初三数学等腰三角形知识精讲
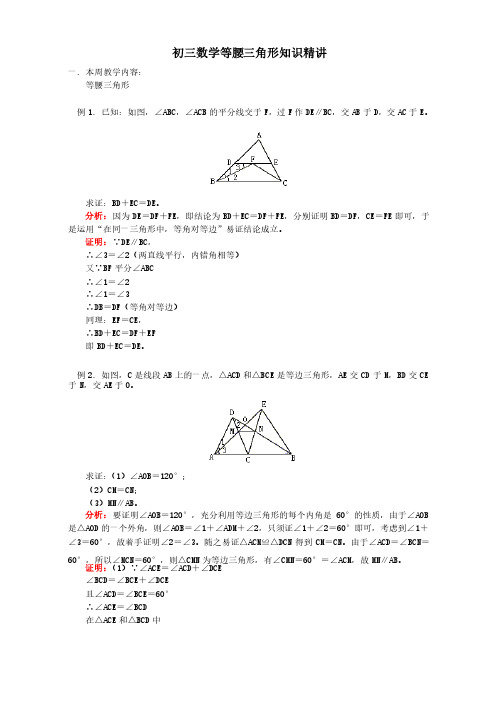
初三数学等腰三角形知识精讲一. . 本周教学内容:本周教学内容:等腰三角形等腰三角形例例1. 1. 已知:如图,∠已知:如图,∠已知:如图,∠ABC ABC ABC,∠,∠,∠ACB ACB 的平分线交于F ,过F 作DE DE∥∥BC BC,交,交AB 于D ,交AC 于E 。
求证:求证:求证:BD BD BD++EC EC==DE DE。
分析:因为DE DE==DF DF++FE FE,即结论为,即结论为BD BD++EC EC==DF DF++FE FE,分别证明,分别证明BD BD==DF DF,,CE CE==FE 即可,于是运用“在同一三角形中,等角对等边”易证结论成立。
证明:∵DE DE∥∥BC BC,, ∴∠∴∠∴∠33=∠=∠22(两直线平行,内错角相等) 又∵又∵又∵BF BF 平分∠平分∠ABC ABC ∴∠∴∠∴∠11=∠=∠2 2 ∴∠∴∠∴∠11=∠=∠3 3 ∴∴DB DB==DF DF(等角对等边)(等角对等边) 同理:同理:同理:EF EF EF==CE CE,, ∴∴BD BD++EC EC==DF DF++EF 即即BD BD++EC EC==DE DE。
例例2. 2. 如图,如图,如图,C C 是线段AB 上的一点,△上的一点,△ACD ACD 和△和△BCE BCE 是等边三角形,是等边三角形,AE AE 交CD 于M ,BD 交CE 于N ,交AE 于O 。
求证:求证:(1)∠)∠AOB AOB AOB==120120°;°;((2)CM CM==CN CN;; ((3)MN MN∥∥AB AB。
分析:要证明∠要证明∠AOB AOB AOB==120120°,充分利用等边三角形的每个内角是°,充分利用等边三角形的每个内角是6060°的性质,由于∠°的性质,由于∠°的性质,由于∠AOB AOB 是△是△AOD AOD 的一个外角,则∠的一个外角,则∠AOB AOB AOB=∠=∠=∠11+∠+∠ADM ADM ADM+∠+∠+∠22,只须证∠,只须证∠11+∠+∠22=6060°即可,考虑到∠°即可,考虑到∠°即可,考虑到∠11+∠3=6060°,故着手证明∠°,故着手证明∠°,故着手证明∠22=∠=∠33。
等腰三角形和等边三角形(整理)PPT课件

说一说 填一填
3. ( 两条边相等 )的三角形是等腰三角形,
两个底角(相等)。
(
)的三角形是等边三角形,每个
角都是( )度,它又是一个
(
)。
说一说 填一填
3. ( 两条边相等 )的三角形是等腰三角形, 两个底角(相等)。
(三条边都相等)的三角形是等边三角形, 每个角都是( 60 )度,它又是一个( 锐 角三角形 )。
说一说 填一填
• 1. ( 由三条线段围成 )的图形叫做三 角形,三角形具有( 稳定 )性。三角 形有( 3 )个顶点,( 3 )条边, ( 3 )个角,( )条高。
说一说 填一填
• 1. ( 由三条线段围成 )的图形叫做三 角形,三角形具有( 稳定 )性。三角 形有( 3 )个顶点,( 3 )条边, ( 3 )个角,( 3 )条高。
条路最近?途中那两条路一样长?为什么?
40米
20米
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
43
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
说一说 填一填
• 4.(1)一个三角形的内角和是(180)度。 • (2)用两块完全一样的三角形拼成一
个三角形,这个三角形的内角和是(180) 度。 • (3)把一个大三角形剪成两个小三角 形,每个小三角形的内角和是(180)度。
等腰三角形的“三线合一”性质 ppt课件

ppt课件
(来自《点拨》)
11
解: 如图所示,△ABC就是所求作的三角形.
知2-讲
ppt课件
12
总结
知2-讲
利用尺规作等腰三角形时,要考虑等腰三角形的隐含 条件:有两条边相等;两个角相等.pLeabharlann t课件13知2-练
1 已知∠ α和线段a (如图),用直尺和圆规作等腰三 角形ABC,使顶 角∠ BAC= ∠ α ,角平分线AD=a.
∴ ∠ BAD = ∠ CAD (角平分线的定义).
而AD=AD (公共边),
∠ ADB = ∠ADC (已知),
∴ △ABD≌△ACD(ASA).
∴ AB=AC (全等三角形的对应边相等).
∴ △ ABC是等腰三角形(等腰三角形的定义).
∵ AE是等腰三角形ABC顶角的平分线,
∴ AE丄BC.(等腰三角形三线合一),
第2章 特殊三角形
2.3 等腰三角形的性质定理
第2课时 等腰三角形的 “三线合一”性质
ppt课件
1
等腰三角形的“三线合一”
1 课堂讲解 用尺规作等腰三角形
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
ppt课件
2
如图,在△ABC中,AB=AC,AD是角平分 线.在图中找 出所有相等的线段和相等的角.由此你 发现了等腰三角 形还有哪些性质?
ppt课件
4
结论
知1-讲
等腰三角形的顶角平分线、底边上的中线 和高线 互相重合,简称等腰三角形三线合一 .
ppt课件
5
知1-讲
【例1】已知:如图 ,AD平分∠ BAC, ∠ ADB= ∠ ADC. 求证:AD丄BC.
等腰三角形三线合一ppt优秀课件

有两条边相等的三角形叫做等腰三角形。
?A
B
C
复习
等腰三角形的两底角相等。(简写为“等边对等角”)
A
∵AB=AC (已知)
∴∠B=∠C(等边对等角)
B
C
【注意】“等边对等角”的前提是在同一个三角形中。
实践验证
做一做
剪一张等腰三角形的纸片,每人所剪的等腰三角形的大
小和形状可以不一样,如图,把纸片对折,让两腰AB、AC重
A DC
学以致用
例 1 如图,在△ABC中,AB = AC,D是BC边上的中点,∠B=30°,
求∠1和∠ADC的度数。
A
你是怎 样考虑 的?
12
B
D
C
证明:∵AB=AC,BD=CD
∴AD⊥BC
∴∠BDA=∠ADC=90°
∴∠B+∠1=90°
又∵∠B=30°
∴∠1=60°
∴∠1=60°∠ADC=90°
C
例3.
综合探究
在△ABC中,已知∠A=900,AB=AC,D为BC的中点,E,F分别 是AB,AC边上的点,且BE=AF,求证:△DEF为等腰直角三角形。
证明:连接AD
∵AB=AC,∠A=90°,D为BC中点, ∴AD⊥BC, ∠BAD=∠CAD=∠B=45° ∴AD=BD=CD, 在△BDE和△ADF中,
.
推理验证
已知:△ABC中AB=AC,BD=DC。 求证:AD⊥BC,∠BAD=∠CAD
证明:在△ABD和△ACD中: ∵ BD=DC
AB=AC AD=AD ∴△ADB≌△ADC(S.S.S) ∴∠BAD=∠CAD,∠ADB=∠ADC ∵∠ADB+∠ADC=180° ∴∠ADB=∠ADC=90° ∴AD⊥BC, ∠BAD=∠CAD
冀教版八年级上册数学《等腰三角形》说课教学复习课件

★ 练一练
2、 如图,△ABC是等边三角形,E是AC上一点,D是BC延 长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求 ∠CED的度数.
解:∵△ABC是等边三角形, ∴∠ABC=∠ACB=60°. ∵∠ABE=40°, ∴∠EBC=∠ABC-∠ABE=60°-40°=20°. ∵BE=DE, ∴∠D=∠EBC=20°, ∴∠CED=∠ACB-∠D=40°.
等腰三角形
等腰三角形的两个底角相等.
等边三角形
等边三角形的三个角都相等,并且 每一 个角都等于60°.
知识讲解
问题 运用所学知识,证明你的结论. 已知:AB=AC=BC , 求证:∠A= ∠B=∠C= 60°.
证明: ∵AB=AC,
∴∠B=∠C(等边对等角) .同理 ∠A=∠C , ∴∠A=∠B=∠C. ∵ ∠A+∠B+∠C=180°, ∴ ∠A= ∠B= ∠C=60 °.
A
顶
角
腰
腰
底角
B
底角
C
底边
知识讲解
等腰三角形的性质
剪一剪:把一张长方形的纸按图中的红线对折,并剪去阴影部分(一个直 角三角形),再把得到的直角三角形展开,得到的三角形ABC有什么特点?
合作探究
B
A
AB=AC
等腰三角形
C
合作探究
折一折:△ABC 是轴对称图形吗?它的对称轴是什么?
等腰三角形是轴对称图形. 折痕所在的直线是它的对称轴.
当堂检测
1.等腰三角形的一个内角是50°,则这个三角形的底角的大小是( A )
A.65°或50°
B.80°或40°
C.65°或80°
D.50°或80°
冀教版八年级数学上册《等腰三角形》-课件-(共33张PPT)

A
B
C
D
(1)把△ABC沿BC边上的高AD所在的直线折叠, △ABC被直线 AD分成的两部分能够重合吗?如果重合,请指出重合的部分?
A
B
C
D
(1)把△ABC沿BC边上的高AD所在的直线折叠, △ABC被直线 AD分成的两部分能够重合吗?如果重合,请指出重合的部分?
M
A
O
N
B
C
1 72° 72°
B
C
5.在等腰直角三角形ABC中, ∠ACB =90°,CD 是底边上的高,那么图中有 3 个等腰直角三 角形,分别是 △ACB、 △ADC、 △BDC 。
C
45° 45°
45°
45°
A
D
B
6.如图,AD是△ABC的外角∠EAC的平分线,
且AD∥BC,试判断△ABC的形状,并说明理由
冀教版八年级数学上册 《等腰三角形》 课件 (
共33张PPT)
2023/5/28
学习目标
• 1、探索并证明等腰三角形的判定定理。 • 2、等腰三角形判定定理的运用。
学习重点:等腰三角形判定定理的运用。
复习引入
等腰三角形有哪些特征呢?
1.等腰三角形的两腰 相等 ;
A
2.等腰三角形的两个底角 相等 ,( 简称“ 等边对等角”);
选作:P146 -B组1题
八.检测
1.下列四个说法中,不正确的有( B)
①三个角都相等的三角形是等边三角形。 ➢ ②有两个角等于60°的三角形是等边三角形。 ➢ ③有一个是60°的等腰三角形是等边三角形。 ➢ ④有两个角相等的等腰三角形是等边三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
A
B
CB
C
复习目标
1、掌握等腰三角形的概念、性质、 推论及判定。并能够根据性质解 决有关问题。
2、知道等边三角形是特殊的等腰 三角形。掌握等边三角形的概念、 性质、推论及判定。并能够根据 性质解决有关问题。
重点难点
1、等腰三角形的性质和判定。 2、等腰三角形性质的应用,等
边三角形性质的应用。
C
B
D
C
C
能力提升
1、如图:已知 ABCD中,AB=7,BC=4,∠A=30°
(1)点P从点A沿边AB向点B运动,速度为1cm/s,时间为t(s).
当t为何值时,△PBC为等腰三角形?
D
A 30° P
7
若△PBC为等腰三角形
C
则PB=BC
4 B
∴7-t=4
∴t=3
同类变式
如图:已知 ABCD中,AB=7,BC=4,∠A=30°
A
知识再现(一)
等腰三角形:性质
∟
如图:等腰三角形ABC中, ∠A为顶 C
角且∠A=40°则
D
B
1、∠B=
∠C=
知识点:
2、若 AB=5,则AC=
知识点:
3、若过点A作BC的垂线BC于点D, 则∠CAD=∠ = °,CD=
知识点:
4、对称轴有
条,位置是过点
的直线。
知识点:
等腰三角形:推论
如图①:等腰三角形 ABC, AB=AC,BD⊥AC,CE⊥AB,则BD CE
B
当BP=BC时
D(钝角)
C
4
A
7
B
P
当BP=BC时
(锐角)
D
C
4
∟
30°
A
7
B 23 E
P
E4
A
7
B
P
当CB=CP时
当PB=PC时
∴t=3或11或7+ 4 3或 4 3/3 +7 时 △PBC为等腰三角形
探究动点关键:化动为静,分类讨论,关注全过程
课堂小结
说出你的收获?
布置作业
完成中考金钥匙《等腰三角形 》
A
A
A
E
⑤
D
B
C
③
B
④
B C
D
C
同类变式
(6)如图⑥,过BC边一点D作DF⊥BC,交CA延长线于点F,交 AB于点E,若AE=3,BE=7,求CF的长。
(7)如图⑦,过BC边上一点D作DE∥AC交AB于点E,DF∥AB 交AC于点F,若AB=4,求四边形AEDF的周长。
F
A ⑤
A ⑥
A
F
E
⑦
B
D
CB D
(2)若点P从点A沿射线AB运动,速度仍是1cm/s。
当t为何值时,△PBC为等腰三角形?
D
C
4 P
A
7
B
小组合作交流讨论
各个击破
1、如图:已知 ABCD中,AB=7,BC=4,∠A=30°
(2)若点P从点A沿射线AB运动,速度仍是1cm/s。
当t为何值时,△PBC为等腰三角形?
D
C
D
C
4 P
A
7
如图②:等腰三角形 ABC, AB=AC,D为AC的中点,E为AB的 中点,则BD CE
如图③:等腰三角形 ABC, AB=AC,BD平分∠ABC,CE平分 ∠ACB,则BD CE
A
D
E
C①
B
A
D
E②
C
A
B
D
E③
C
B
等腰三角形:判定
已知:三角形ABC,AB=6,AC=6, 则三角形ABC为 三角形。
知识点:
已知:三角形ABC,∠B=∠C, 则三角形ABC为 三角形。
知识点:
A
C
B
A
A
典型例题:
B
已知△ABC中,AB=AC
①C
DB
C②
D
(1)若△ABC一边长为3,周长为12,则AB=
(2)若△ABC一个角为30°,则三个角的度数为
跟踪练习
(1)如图①,若点D在BC的延长线上,∠ACD=110 °,则 ∠BAC=
(2)如图②,若点D在BC的延长线上,AC=DC,∠BAC=40°, 则∠D=
(3)如图③,若D是AC上的一点,且AD=BD=BC,求∠A的度 数。
(4)如图④,若E是AC上的一点,且BE是△ABC的中线, BE把三角形的周长分为12和15两部分,求△ABC的三边长。
(5)如图⑤,若AD是△ABC的角平分线,且△ABC的周长 为20,AD=6,求△ACD的周长。
