2018届高考数学(文)专题复习课件:第1部分 专题五 立体几何 1-5-2
2018届高三高考数学复习课件:高考专题突破四高考中的立体几何问题
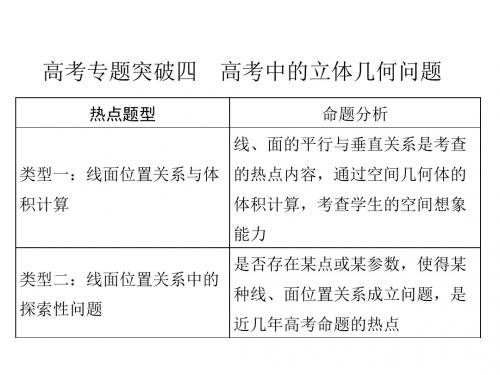
体的表面积是(
)
A.20+3π
B.24+3π
C.20+4π
D.24+4π
【解析】 根据几何体的三视图可知, 该几何体是一个正方体 和一个半圆柱的组合体,其中正方体的棱长为 2,半圆柱的底面 半径为 1,母线长为 2,故该几何体的表面积为 4×5+2×π+2 1 ×2π=20+3π. 【答案】 A
分别在AD,CD上,AE=CF,EF交BD于点
H,将△DEF沿EF折到△D′EF的位置.
(1)证明:AC⊥HD′; 5 (2)若 AB=5,AC=6,AE=4,OD′=2 2,求五棱锥 D′ABCFE 的体积.
【解析】 (1)证明 由已知得 AC⊥BD,AD=CD,又由 AE= AE CF CF 得AD=CD,故 AC∥EF,由此得 EF⊥HD,折后 EF 与 HD 保持垂直关系,即 EF⊥HD′,所以 AC⊥HD′. OH AE 1 (2)由 EF∥AC 得DO=AD=4. 由 AB=5,AC=6 得 DO=BO= AB2-AO2=4, 所以 OH=1,D′H=DH=3, 于是 OD′2+OH2=(2 2)2+12=9=D′H2,
【证明】 (1)取B1D1的中点O1,连接CO1 ,A1O1, 由于ABCDA1B1C1D1是四棱柱, 所以A1O1∥OC,A1O1=OC,
因此四边形A1OCO1为平行四边形,所以
A1O∥O1C. 又O1C⊂平面B1CD1,A1O⊄平面B1CD1, 所以A1O∥平面B1CD1.
【例2】 (2017· 山东高考)由四棱柱 ABCDA1B1C1D1截去三棱锥C1B1CD1后得到 的几何体如图所示.四边形ABCD为正方形 ,O为AC与BD的交点,E为AD的中点,
A1E⊥平面ABCD.
2018届高三数学理高考二轮复习书讲解课件第一部分 专题四 第一讲 空间几何体 精品

考点三
考点一 考点二 考点三
试题 解析
[巩固题组·增分练]
1.(2016·重庆模拟)已知三棱锥 P-ABC 的所有顶点都在半径为 1
的球 O 的球面上,△ABC 是边长为 1 的正三角形,PC 为球 O 的
直径,则该三棱锥的底面 ABC 上的高为( D )
考点一
考点一 考点二
[自主突破·提速练]
试题 解析
1.(2016·广州模拟)已知某几何体的正视图和侧视图均如图所示,
给出下列 5 个图形:
考点三
其中可以作为该几何体的俯视图的图形个数是( B )
A.5
B.4
C.3
D.2
考点一
试题 解析
考点一 考点二 考点三
由题知可以作为该几何体的俯视图的图形有①②③⑤.故选 B.
考点二
考点一 考点二 考点三
1.求三棱锥的体积时要注意三棱锥的每个面都可以作为底面; 2.在求几何体的表面积和体积时,注意等价转化思想的运用,如 用“割补法”把不规则几何体转化为规则几何体、立体几何问 题转化为平面几何问题等.
考点三 空间几何体与球的切、接问题
考点一 考点二 考点三
[经典结论·全通关] S 球=4πR2. V 球=4π3R3(R 为球半径).
考点一
试题 解析
考点一 考点二 考点三
根据直观图以及图中的辅助四边形分析可知,当正视图和侧视图 完全相同时,俯视图为 B,故选 B.
考点一
考点一 考点二 考点三
要熟悉各种基本几何体的三视图.同时要注意画三视图时,能 看到的轮廓线画成实线,看不到的轮廓线画成虚线.
【高考数学】2018届高三数学(文)二轮复习课件:攻略4.3(高频考点汇总PPT课件)

谢谢观看!
评分细则
同上
[名师秘籍] 1.写全得分步骤:在立体几何类解答题中,对于证明与计算过程中的得分点 的步骤,有则给分,无则没分,所以对于得分点步骤一定要写,如第(1)问中的 AC AE CF OH AE ⊥BD,AD=CD,AD=CD;第(2)问中DO=AD,OD′2+OH2=D′H2,AC∩OH =O 等. 2.注意利用第(1)问的结果:在题设条件下,如果第(1)问的结果对第(2)问的 证明或计算用得上,可以直接用,有些题目不用第(1)问的结果甚至无法解决,如 本题就是在第(1)问的基础上证明 OD′⊥平面 ABC.
3.牢记空间几何体的结构特征.用准线面平行、垂直的判定、性质定理及体 积公式:在立体几何类解答题中,通常都以常见的空间几何体为载体去证明空间 的垂直或平行关系,及求几何体体积,因此要牢记空间几何体的结构特征,正确 运用相关的判定定理、 性质定理、 体积公式, 如本题第(2)问中, AC⊥OD′及 OD′ ⊥平面 ABC 的证明,及五棱锥 D′ABCFE 体积 V
破解 6 大解答题
三、立体几何 典型例题 (12 分)如图,菱形 ABCD 的对角 线 AC 与 BD 交于点 O,点 E,F 分别在 AD,CD 上,AE=CF, EF 交 BD 于点 H,将△DEF 沿 EF 折到△D′EF 的位置. (1)证明:AC⊥HD′; 5 (2)若 AB=5,AC=6,AE=4,OD′=2 2,求五棱 锥 D′ABCFE 的体积. 题目拆解
本题可拆解成以下几个小问 题: (1)①AC∥EF;②EF⊥HD′. (2)①OD′⊥平面 ABC; ②求五边形 ABCFE 的面积.
标准答案
评分细则
第(1)问踩点说明(针对得分点①②③): (1)由已知得 AC⊥BD, AD=CD.1 分 得分点① ①由菱形的性质得到 AC⊥BD,AD=CD 得 1 分; AE CF ②由 AE=CF⇒AC∥EF 得 1 分; 又由 AE=CF 得AD=CD,故 AC∥EF.1 分 ③由①②得 AC⊥HD′得 2 分. 得分点② 第(2)问踩点说明(针对得分点④⑤⑥⑦⑧⑨): 由此得 EF⊥HD,故 EF⊥HD′, ④由 EF∥AC 及 AB=5,AC=6 得出 OH=1,D′H =3 得 2 分; 又 AC∥EF,所以 AC⊥HD′.2 分 得分点③ ⑤由勾股定理逆定理得到 OD′⊥OH 得 1 分; OH AE 1 (2)由 EF∥AC 得DO=AD=4. ⑥由线面垂直的性质得到 AC⊥OD′得 1 分; 由 AB=5,AC=6 得 DO=BO= AB2-AO2=4. ⑦由线面垂直的判定定理得 OD′⊥平面 ABC 得 1 分; 所以 OH=1,D′H=DH=3.2 分 得分点④ ⑧正确求出五边形 ABCFE 的面积得 2 分; (参见下页) ⑨正确求出五棱锥的体积得 1 分.
2018届高考数学文二轮复习全国通用课件:专题四 立体几何 第1讲 精品
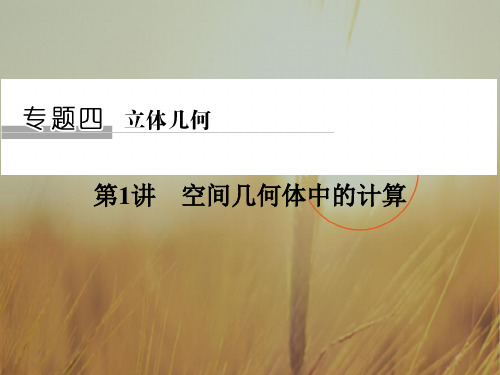
2.(2016·全国Ⅱ卷)如图是由圆柱与圆锥组合而成的几何体的 三视图,则该几何体的表面积为( )
A.20π
B.24π
C.28π
D.32π
解析 由三视图可知,组合体的底面圆的面积和周长均 为 4π,圆锥的母线长 l= (2 3)2+22=4,所以圆锥 的侧面积为 S 锥侧=12×4π×4=8π,圆柱的侧面积 S = 柱侧 4π×4=16π,所以组合体的表面积 S=8π+16π+4π= 28π,故选 C. 答案 C
解析 (1)由几何体的三视图可知空间几何体的直
观 图 如 图 所 示 .∴ 其 表 面 积
S
表
=
2×
1 2
×2×1
+
2× 43×( 2)2=2+ 3,故选 C.
(2)由三视图可知该几何体由一个正方体和一 个长方体组合而成,上面正方体的边长为2 cm, 下面长方体是底面边长为4 cm,高为2 cm,其 直观图如右图:其表面积S=6×22+2×42+ 4×2×4-2×22=80(cm2).体积V=2×2×2+ 4×4×2=40(cm3). 答案 (1)C (2)80 40
ቤተ መጻሕፍቲ ባይዱ
(2)解 因为 ABC-A1B1C1 是直三棱柱, 所以 AA1⊥CD.由已知 AC=CB,D 为 AB 的中点, 所以 CD⊥AB.又 AA1∩AB=A,于是 CD⊥平面 ABB1A1. 由 AA1=AC=CB=2,AB=2 2得 ∠ACB=90°,CD= 2,A1D= 6,DE= 3,A1E=3, 故 A1D2+DE2=A1E2,即 DE⊥A1D. 所以 VC-A1DE=13×12× 6× 3× 2=1. 探究提高 有关多面体的体积计算首先要熟悉几 何体的特征,其次运用好公式,作好辅助线等.
高三数学-2018《立体几何》高考题解析(文科) 精品

18-18《立体几何》高考题解析(文科)一选择题1把正方形ABCD 沿对角线AC 折起,当A 、B C 、D 四点为顶点的三棱锥体积最大时,直线BD 与平面ABC 所成的角的大小为 ( 5.C )A .90°B .60°C .45°D .30°(18湖南5)2四面体ABCD 四个面的重心分别为E 、F 、G 、H ,则四面体EFGH 的表面积与四面体ABCD 的表面积的比值是 (C )A .271 B .161 C .91 D .81(18湖北6) 3已知m 、n 是不重合的直线,α、β是不重合的平面,有下列命题:①若m ⊂α,n ∥α,则m ∥n ; ②若m ∥α,m ∥β,则α∥β;③若α∩β=n ,m ∥n ,则m ∥α且m ∥β; ④若m ⊥α,m ⊥β,则α∥β.其中真命题的个数是 ( 6.B ) A .0 B .1 C .2 D .3(18福建6)4如图,A 、B 、C 是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60º,O 为球心,则直线 OA 与截面ABC 所成的角是( 10.D ) A .arcsin 63B .arccos 63C .arcsin33 D .arccos 33(18福建10)5在下列关于直线l 、m 与平面α、β的命题中,真命题是 ( 13.B )A .若l ⊂β且α⊥β,则l ⊥α.B .若l ⊥β且α∥β,则l ⊥α.C .若l ⊥β且α⊥β,则l ∥α.D .若α∩β=m 且l ∥m,则l ∥α. (18上海13) 6不同直线,m n 和不同平面,αβ,给出下列命题( ) ①////m m αββα⎫⇒⎬⊂⎭ ② //////m n n m ββ⎫⇒⎬⎭③ ,m m n n αβ⊂⎫⇒⎬⊂⎭异面 ④ //m m αββα⊥⎫⇒⊥⎬⎭ 其中假命题有:( 8.D )A .0个B .1个C .2个D .3个(18重庆8)7 如图,棱长为5的正方体无论从哪一个面看,都有两个直通的边长为1的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( 12.C ) A .258 B .234 C .222 D .210(18重庆12)8. 91DA2 V 为A. 104B. 38C. 134D. 16(18天津11) (10)如图,在正三棱柱ABC —A 1B 1C 1中已知AB=1,D 在棱BB 1上,且BD=1,若AD 与平面AA 1C 1C 所成的角为α,则α= 10.D(A)3π (B)4π(C)410arcsin(D)46arcsin(18浙江10) 11正三棱柱侧面的一条对角线长为2,且与底面成45°角,则此三棱柱的体积为 ( A )A .26 B .6C .66 D .36(18甘肃3) 12已知球的表面积为20π,球面上有A 、B 、C 三点.如果AB=AC=BC=23,则球心到平面ABC 的距离为 ( A )A .1B .2C .3D .2(18甘肃11)13 正三棱锥的底面边长为2,侧面均为直角三角形,则此三棱锥的体积为(C )A .B .C .3D .18广西10) 14已知正四面体ABCD 的表面积为S ,其四个面的中心分别为E 、F 、G 、H ,设四面体EFGH 的表面积为T ,则ST等于( A )A .91B .94C .41 D .31(18河北10) 15设 m, n 是两条不同的直线,r ,,βα是三个不同的平面.给出下列四个命题: ①若m ⊥α,n ∥α,则m ⊥n;② 若α∥β, β∥r, m ⊥α,则m ⊥r; ③ 若m ∥α,n ∥α,则m ∥n;④ 若α⊥r, β⊥r,则α∥β. 其中正确命题的序号是3.A(A)①和② (B)②和③ (C)③和④ (D)①和④(18北京3) 16如图,在正方体ABCD -A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若P 到直线BC 与直线C 1D 1的距离相等,则动点P 的轨迹所在的曲线是6.D(A) 直线 (B) 圆 (C) 双曲线 (D) 抛物线(18北京6) 17正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为(C ) A .75° B .60° C .45° D .30°(18四川6)18已知球O 的半径为1,A 、B 、C 三点都在球面上,且每两点间的球面距离均为2π,则球心O 到平面ABC 的距离为( B ) A .31 B .33 C .32 D .36(18四川10) 19一个与球心距离为1的平面截球所得的圆面面积为π,则球的表面积为2.C(A )π28 (B )π8(C )π24 (D )π4 (18河北2)20如图,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且BCF ADE ∆∆、均为正三角形,EF ∥AB ,EF=2,则该多面体的体积为4.D(A )32(B )33 (C )34(D )23(18河北4) 21设三棱柱ABC-A 1B 1C 1的体积为V ,P 、Q 分别是侧棱AA 1、CC 1上的点,且PA=QC 1,则四棱锥B-APQC 的体积为C(A )16V (B )14V (C )13V (D )12V (18四川4) 22不共面的四个定点到平面α的距离都相等,这样的平面α共有D(A )3个 (B )4个 (C )6个 (D )7个(18四川11)23在正四面体P -ABC 中,D ,E ,F 分别是AB ,BC ,CA 的中点,下面四个结论中不成..立.的是(7)C (A )BC //平面PDF (B )DF ⊥平面P A E(C )平面PDF ⊥平面ABC (D )平面P AE ⊥平面 ABC (18北京7) 24对于不重合的两个平面βα与,给定下列条件:①存在平面γ,使得α、β都垂直于γ; ②存在平面γ,使得α、β都平等于γ; ③存在直线α⊂l ,直线β⊂m ,使得m l //; ④存在异面直线l 、m ,使得.//,//,//,//βαβαm m l l其中,可以判定α与β平行的条件有( 7.B )A .1个B .2个C 3个D .4个(18重庆7)25有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面 各连接中点,已知最底层正方体的棱长为2,且该塔形 的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是 ( 10.C ) A .4 B .5 C .6 D .7(18重庆10) 26如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E 是A 1B 1的中点,则E 到平面AB C1D 1的距离为( B ) A .23B .22C .21 D .33(18湖南4)27木星的体积约是地球体积的30240倍,则它的表面积约是地球表面积的(5.C )A .60倍B .6030倍C .120倍D .12030倍(18湖北5)28已知a 、b 、c 是直线,β是平面,给出下列命题:①若c a c b b a //,,则⊥⊥; ②若c a c b b a ⊥⊥则,,//;③若b a b a //,,//则ββ⊂;④若a 与b 异面,且ββ与则b a ,//相交;⑤若a 与b 异面,则至多有一条直线与a ,b 都垂直. 其中真命题的个数是 ( 8.A ) A .1 B .2 C .3D .4(18湖北8)29设地球半径为R ,若甲地位于北纬045东经0120,乙地位于南纬度075东经0120,则图1 甲、乙两地球面距离为(D ) (A(B)6R π(C)56R π (D) 23R π(18山东9) 30矩形ABCD 中,AB=4,BC=3,沿AC 将矩形ABCD 折成一个直二面角B —AC —D ,则四面体ABCD 的外接球的体积为( 9.C )A .π12125 B .π9125 C .π6125 D .π3125(18江西9) 31设α、β 为两个不同的平面,l 、m 为两条不同的直线,且l ⊂α,m ⊂β,有如下的两个命题:①若α∥β,则l ∥m ;②若l ⊥m ,则α⊥β.那么(D )(A) ①是真命题,②是假命题 (B) ①是假命题,②是真命题(C) ①②都是真命题 (D) ①②都是假命题(18浙江7) 二填空题1图1,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器(图2).当这个正六棱柱容器的底面边长为 2/3 时,其容积最大. (18福建16)2毛泽东在《送瘟神》中写到:“坐地日行八万里”。
【700分考法】2018年高考数学(理)一轮课件:专题8-立体几何(106页)

【注意】若相邻两个物体的表面相交,表面 的交线是它们的分界线;对于简单组合体, 要注意它们的组合方式,特别是它们的交线 的位置.
3.求原几何体 (或其他视图) 的基本量
17
考法2 空间几何体的三视图
1.识别三视 图的步骤
确定其是一个平面的投影,还是面与 面的交线,或者是旋转体的轮廓线的 投影.
专题8 立体几何
第1节 空间几何体的三视图、表面积和体积 第2节 空间直线、平面平行与垂直的判定及其性质 第3节 空间中的计算问题
1
第1节 空间几何体的三视图、表面积和体积
目录
600分基础
考点42
考点&考法
空间几何体的结构、三视图
考点43 考点44
几何体表面积的计算 几何体体积的计算
考法3 几何体表面积的计算
24
考点43
几何体表面积的计算
常见几何体的侧面积与表面积的计算公式
考法3 几何体表面积的计算
常用方法:
1.由三视图求相关 几何体的表面积
还原空间几何体, 确定点、线、面的位置关系及线段的长度, 利用公式进行计算.
2.根据几何体的 特征求表面积
26
考法3 几何体表面积的计算
2.外接球、内切 球的计算问题
Rt△OO′M中,OM2=OO′2+O′M2,即R2=d2+r2.
10
11
12
13
14
15
16
考法2 空间几何体的三视图
1.识别三视 图的步骤
(1)弄清结构,明确位置 (2)先画正视图,再画俯视图,最后画侧视图 (3)被遮住的轮廓线要画成虚线
2.判断余下视图
1.计算有关 线段的长
2018届高三数学文二轮复习课件:第2部分 专题四 立体几何2-4 精品
∴PO⊥BO, ∵PO⊥EF,EF∩BO=O,EF⊂平面 BFED, BO⊂平面 BFED, ∴PO⊥平面 BFED, 又梯形 BFED 的面积为 S=12(EF+BD)·HO=3 3, ∴四棱锥 P-BFED 的体积 V=13S·PO=13×3 3× 3=3.
类型二 学会审题 [例 2] (2016·高考全国乙卷)如图,已知正三棱锥 P-ABC 的侧面是 直角三角形,PA=6,顶点 P 在平面 ABC 内的正投影为点 D,D 在平面 PAB 内的正投影为点 E,连接 PE 并延长交 AB 于点 G.
(2)在平面 PAB 内,过点 E 作 PB 的平行线交 PA 于点 F,F 即为 E 在平面 PAC 内的正投影. 理由如下:由已知可得 PB⊥PA,PB⊥PC,又 EF∥PB,所以 EF ⊥PA,EF⊥PC.又 PA∩PC=P,因此 EF⊥平面 PAC,即点 F 为 E 在平面 PAC 内的正投影. 连接 CG,因为 P 在平面 ABC 内的正投影为 D,所以 D 是正三角 形 ABC 的中心.由(1)知,G 是 AB 的中点,所以 D 在 CG 上,故 CD=23CG.
1.如图①,在边长为 4 的菱形 ABCD 中,∠DAB=60°,点 E,F 分别是边 CD,CB 的中点,AC∩EF=O.沿 EF 将△CEF 翻折到△ PEF,连接 PA,PB,PD,得到如图②的五棱锥 P-ABFED,且 PB = 10.
图① (1)求证:BD⊥平面 POA; (2)求四棱锥 P-BFED 的体积.
∴四面体 N-BCM 的体积 VN-BCM=13×S△BCM×P2A=13×2 5×12×4
=4
3
5 .(12
分)
[终极提升]——登高博见 (1)利用线面平行的判定定理进行证明, 即通过线线平行证明线面平行; (2)先求出点 N 到平面 BCM 的距离及△ BCM 的面积,然后代入锥体的体积公式 求解.
2018年高考数学文课标Ⅰ专用一轮复习专题测试课件:第
答案 36π
解析 由题意作出图形,如图.
设球O的半径为R,由题意知SB⊥BC,SA⊥AC,又SB=BC,SA=AC,则SB=BC=SA=AC= 2R.连接OA, OB,
则OA⊥SC,OB⊥SC,因为平面SCA⊥平面SCB,平面SCA∩平面SCB=SC,所以OA⊥平面SCB,所以 OA⊥OB,则AB= 2R,
A.18+36 5 C.90 D.81 B.54+18 5 答案 B 由三视图可知,该几何体是底面为正方形(边长为3),高为6,侧棱长为3 5 的斜四棱柱. 其表面积S=2×32+2×3×3 5 +2×3×6=54+18 5 .故选B. 易错警示 学生易因空间想象能力较差而误认为侧棱长为6,或漏算了两底面的面积而致错..
1 6
3
=36得R=6.从而球O的表面积S=4πR2=144π.故选C.
思路分析 VO-ABC=VC-AOB.当OC垂直于面AOB时,三棱锥O-AOB,即三棱锥O-ABC的体积最大,此时
可求出半径,从而求出球O的表面积.
6.(2014大纲全国,10,5分)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该 球的表面积为 (
A.20π C.28π 答案 C
2
B.24π D.32π
3 ,底面半径为2,则圆锥的母线长为4,所以圆锥的侧面积为 由三视图知圆锥的高为2
1 ×4π×4=8π.圆柱的底面积为4π,圆柱的侧面积为4×4π=16π,从而该几何体的表面积为8π+16π+
4π=28π,故选C.
3.(2016课标全国Ⅲ,10,5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视 图,则该多面体的表面积为 ( )
2018高三大一轮复习数学(文)课件:第八章 立体几何 8-5
A.8+2 2 C.14+2 2
B.11+2 2 D.15
解析:选 B.由三视图知,该几何体是一个直四棱柱,上、下 底面为直角梯形,如图所示.
2 解析:选 C.由三视图知,该几何体上部是半径为 2 的半球, 1 下部是底面边长为 1,高为 1 的正四棱锥.故该几何体的体积为2
2 4 2 1 3 1 ×3π× +3×1×1×1= 6 π+3. 2
3.(教材改编)一个棱长为 2 cm 的正方体的顶点都在球面上, 则球的体积为________cm3.
球
4πR2 S=______
4 3 V=____ 3R
4.常用结论 (1)与体积有关的几个结论 ①一个组合体的体积等于它的各部分体积的和或差. ②底面面积及高都相等的两个同类几何体的体积相等. (2)几个与球有关的切、接常用结论 a.正方体的棱长为 a,球的半径为 R, ①若球为正方体的外接球,则 2R= 3a; ②若球为正方体的内切球,则 2R=a; ③若球与正方体的各棱相切,则 2R= 2a.
类型一
求空间几何体的表面积
[例 1] (1)(2016· 高考全国丙卷)如图所示,网格纸上小正方形 的边长为 1,粗实线画出的是某多面体的三视图,则该多面体的表 面积为( )
A.18+36 5 C.90
B.54+18 5 D.81
解析
先通过三视图还原出几何体,再求几何体的表面积.
由几何体的三视图可知,该几何体是底面为正方形的斜平行 六面体. 由题意可知该几何体底面边长为 3,高为 6,所以侧棱长为 32+62 = 3 5 . 故 该 几 何 体 的 表 面 积 S = 32×2 + (3×6)×2 + (3×3 5)×2=54+18 5.
解析:由题意知正方体的体对角线为其外接球的直径, 1 所以其外接球的半径 r=2×2 3= 3(cm), 4 4 3 所以 V 球=3π×r =3π×3 3=4 3π(cm3).
2018年高考题和高考模拟题数学(理)——专题05立体几何分类汇编(解析版)
- 让每一个人同等地提高自我5.立体几何1.【 2018 年浙江卷】已知四棱锥S- ABCD 的底面是正方形,侧棱长均相等, E 是线段 AB 上的点(不含端点),设 SE 与 BC 所成的角为θS- AB- C 的平面角为θ,则1,SE与平面ABCD所成的角为θ,二面角23A. θ1≤θ2≤θ3B. θ3≤θ2≤θ1C. θ1≤θ3≤θ2D. θ2≤θ3≤θ1【答案】 D从而由于,所以即,选 D.点睛:线线角找平行,线面角找垂直,面面角找垂面.2.【 2018 年浙江卷】某几何体的三视图以下图(单位:cm),则该几何体的体积(单位:cm3)是【答案】 C【分析】剖析:先复原几何体为向来四棱柱,再依据柱体体积公式求结果.详解:依据三视图可得几何体为一个直四棱柱,高为2,底面为直角梯形,上下底分别为1, 2,梯形的高为 2,所以几何体的体积为选 C.点睛:先由几何体的三视图复原几何体的形状,再在详细几何体中求体积或表面积等.3.【 2018 年理新课标 I 卷】已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为A. B. C. D.【答案】 A详解:依据相互平行的直线与平面所成的角是相等的,所以在正方体中,平面与线所成的角是相等的,所以平面与正方体的每条棱所在的直线所成角都是相等的,同理平面也知足与正方体的每条棱所在的直线所成角都是相等,要求截面面积最大,则截面的地点为夹在两个面与中间的,且过棱的中点的正六边形,且边长为,所以其面积为,应选 A.点睛:该题考察的是有关平面被正方体所截得的截面多边形的面积问题,首要任务是需要先确立截面的位置,以后需要从题的条件中搜寻有关的字眼,从而获得其为过六条棱的中点的正六边形,利用六边形的面积的求法,应用有关的公式求得结果.学/科 -网+4.【 2018 年理新课标 I 卷】某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,从到的路径中,最短路径的长度为A. B.C. D. 2【答案】 B【分析】剖析:第一依据题中所给的三视图,获得点M 和点 N 在圆柱上所处的地点,点M 在上底面上,点 N 在下底面上,而且将圆柱的侧面睁开图平铺,点M 、 N 在其四分之一的矩形的对角线的端点处,依据平面上两点间直线段最短,利用勾股定理,求得结果.详解:依据圆柱的三视图以及其自己的特点,能够确立点M 和点 N 分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处,所以所求的最短路径的长度为,故点睛:该题考察的是有关几何体的表面上两点之间的最短距离的求解问题,在解题的过程中,需要明确两个点在几何体上所处的地点,再利用平面上两点间直线段最短,所以办理方法就是将面切开平铺,利用平面图形的有关特点求得结果.5.【 2018 年全国卷Ⅲ理】设是同一个半径为 4 的球的球面上四点,为等边三角形且其面积为,则三棱锥体积的最大值为A. B. C. D.【答案】 B详解:以下图,点M 为三角形ABC 的重心, E 为 AC 中点,当平面时,三棱锥体积最大,此时,,,,点M为三角形ABC的重心,,中,有,,,应选 B.点睛:此题主要考察三棱锥的外接球,考察了勾股定理,三角形的面积公式和三棱锥的体积公式,判断出当平面时,三棱锥体积最大很要点,由M 为三角形ABC 的重心,计算获得,再由勾股定理获得OM ,从而获得结果,属于较难题型。
