第四章不可压缩流体的有旋流动和二维无旋流动
流体力学第四章

• 在每一个微元流束的有效截面上,各点的速度可认为是相同的 总流:无数微元流束的总和。
38
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
均匀流与非均匀流·渐变流和急变流
均匀流——同一条流线上各空间点上的流速相 同的流动,流线是平行直线,各有效截面上的 流速分布沿程不变 非均匀流——同一条流线上各空间点上的流速不 同的流动,流线不是平行直线,即沿流程方向速 度分布不均
迹线· 流线 1、迹线 1)定义:某一质点在某一时段内的运动轨迹 线。 2)迹线的微分方程
dx dy dz dt ux u y uz
烟火的轨迹为迹线
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
25
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
一维、二维和三维流动
三维流动:流动参数是x、y、z三个坐标的函数
的流动。
二维流动:流动参数是x、y两个坐标的函数的
流动。
一维流动:是一个坐标的函数的流动。
26
2016/12/26
流体运动学和动力学基础(Fluid Kinematics and Dynamics)
x= x (t)
dux ux ux dx ux dy ux dz ax dt t x dt y dt z dt
(1)当地加速度(时变加速度):流动过程中流体 由于速度随时间变化而引起的加速度; (2)迁移加速度(位变加速度):流动过程中流体 由于速度随位置变化而引起的加速度。
工程流体力学习题及答案

第1章绪论选择题【】按连续介质的概念,流体质点是指:()流体的分子;(b)流体内的固体颗粒;(c)几何的点;(d)几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
解:流体质点是指体积小到可以看作一个几何点,但它又含有大量的分子,且具有诸如速度、密度及压强等物理量的流体微团。
()【】与牛顿内摩擦定律直接相关的因素是:()切应力和压强;(b)切应力和剪切变形速度;(c)切应力和剪切变形;(d)切应力和流速。
解:牛顿内摩擦定律是,而且速度梯度是流体微团的剪切变形速度,故。
()【】流体运动黏度υ的国际单位是:()m2/s;(b)N/m2;(c)kg/m;(d)N·s/m2。
解:流体的运动黏度υ的国际单位是。
()【】理想流体的特征是:()黏度是常数;(b)不可压缩;(c)无黏性;(d)符合。
解:不考虑黏性的流体称为理想流体。
()【】当水的压强增加一个大气压时,水的密度增大约为:()1/20 000;(b)1/1 000;(c)1/4 000;(d)1/2 000。
解:当水的压强增加一个大气压时,其密度增大约。
()【】从力学的角度分析,一般流体和固体的区别在于流体:()能承受拉力,平衡时不能承受切应力;(b)不能承受拉力,平衡时能承受切应力;(c)不能承受拉力,平衡时不能承受切应力;(d)能承受拉力,平衡时也能承受切应力。
解:流体的特性是既不能承受拉力,同时具有很大的流动性,即平衡时不能承受切应力。
()【】下列流体哪个属牛顿流体:()汽油;(b)纸浆;(c)血液;(d)沥青。
解:满足牛顿内摩擦定律的流体称为牛顿流体。
()【】时空气和水的运动黏度,,这说明:在运动中()空气比水的黏性力大;(b)空气比水的黏性力小;(c)空气与水的黏性力接近;(d)不能直接比较。
解:空气的运动黏度比水大近10倍,但由于水的密度是空气的近800倍,因此水的黏度反而比空气大近50倍,而黏性力除了同流体的黏度有关,还和速度梯度有关,因此它们不能直接比较。
化工传递过程原理4-1

z
0
对于无旋流动,流体的旋度为:
rotu
uy ux
x y
k 0
0 uy ux x y
该式表明两 个速度分量 之间存在某 种关联关系
速度势函数
令: 则有:
ux
( x,
x
y)
速度势函 数
ux 2 (x, y) u y
ux y y
ux ux z z
p
2ux 2ux 2ux
x
x2 y2 z2
u ux
u
x x
L
代表惯性力
u ux
u
x x
L2
代表粘性力
雷偌数的物理意义
根据雷偌数的定义及适度变换后有:
Re
uL
u 2
L
u
L2
惯性力 粘性力
雷偌数的物理意义在于;它实质上是两种力的 比值,雷偌数的大小实质放映的是两种力在流 动中所起的主导地位不同。
u z y y
uz uz z z
p
2uz
2uz
2uz
y
x2
y 2
z 2
如果将代表粘性力项目从方程中略去运动方程变为:
势流运动方程
不可压缩流体的奈维-斯托克斯方程为:
u u u X ux x x
ux y y
ux ux z z
普兰德边界层方程
对于不可压缩流体在一无限平辟面上的二维稳态流动:
ux uy 0
y x
u
y
0
引入流函数的目的 在于将两个速度变
量用一个变量 (流函数)来代替, 从而使方程求解简化
工程流体力学42有旋流动和无旋流动
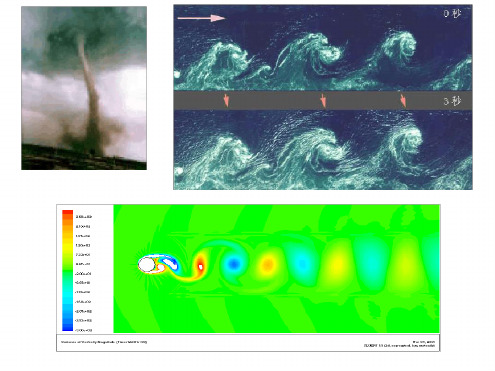
旋流动还是无旋流动。
【解】 由于
?
x
?
1 2
??? ?
?w ?y
?
?v ?z
??? ?
?
0
?
y
?
1 ?? ? u 2 ? ?z
?
ቤተ መጻሕፍቲ ባይዱ
? w ?? ? ?x ?
0
?
z
?
1 2
????
?v ?x
?
?u ?y
???? ?
?
1 a
2
?
0
所以该流动是有旋运动。
第二节 有旋流动和无旋流动
? ?v ?u ?
dΓ
?
?? ?
?
x
?
?y
??d ?
xdy
?
2?
zdA
dA
Ωz
?
dΓ dA
?
?v ?x
?
?u ?y
?
2?
z
涡量——以Ω 表示之。它定义为单位面积上的速度环量,
是一个矢量。
Ωx ?
?w ?y
?
?v ?z
?
2?
? x?
?
Ωy ?
?u ?
?z
?w ?x
?
2?
? y?
第二节 有旋流动和无旋流动
二、速度环量和旋涡强度
① 速度环量 为了进一步了解流场的运动性质,引入流体力
? 定义:
学中重要的基本概念之一——速度环量。
?
在流场中任取封闭曲线k,如图4-5所示。速度V 沿该封闭
曲线的线积分称为速度沿封闭曲线 k 的环量,简称速度环
流体力学——导论-PPT课件

2019/2/16
开复课件网 verykj
14
第二节 流体的特征和连续介质假设
一 流体的定义和特征
物质常见的存在状态是固态、液态和气态,处在 这三种状态下的物质分别称为固体、液体和气体。通 常说能流动的物质为流体,液体和气体易流动,我们 把液体和气体称之为流体。但这样说是不严格的,严 格地说应该用力学的语言来叙述:在任何微小剪切力 的持续作用下能够连续不断变形的物质,称为流体。 根据上述定义,流体显然不能保持一定的形状,即具 有流动性。但流体在静止时不能承受切向力,这显然 与固体不同。固体在静止时也能承受切向力,发生微
2019/2/16 开复课件网 verykj 7
间,何梦瑶在《算迪》一书中提出了流量为过水断面上平 均流速乘以过水断面面积的计算方法。我国在防止水患、 兴修水利方面也有着悠久的历史。相传4000多年前的大禹 治水,就表明我国古代进行过大规模的防洪工作。在公元 前256年至前210年间修建的都江堰、郑国渠和灵渠三大 水利工程,两千多年来效益卓著。以上都说明了我国劳动 人民的聪明智慧,当时对流体流动规律的认识已达到相当 高的水平。14世纪以前,我国的科学技术在世界上是处于 领先地位的。但是,近几百年来由于闭关锁国使我国的科 学得不到应有的发展,以致在流体力学方面由古代的领先 地位而落在后面。
待测液体在给定温度下的恩氏度为112cm113例11一平板距另一固定平板05mm二板水平放置其间充满流体上板在单位面积上为2nm解由牛顿内摩擦定律110由于两平板间隙很小速度分布可认为是线性分布49可用增量来表示微分pas例12长度l1m直径d200mm水平放置的圆柱体置于内径d206mm的圆管中以u1ms的速度移动已知间隙中油液的相对密度为d092运动黏度56104间隙中油的密度为kgm动力黏度为pas由牛顿内摩擦定律199209250图14恩格勒黏度计水箱电加热器长颈瓶202012151由于间隙很小速度可认为是线性分布液体的表面张力和毛细现象1表面张力当液体与其它流体或固体接触时在分界面上都产生表面张力出现一些特殊现象例如空气中的雨滴呈球状液体的自由表面好像一个被拉紧了的弹性薄膜等
第七章 理想不可压缩流体的有旋流动和无旋流动 §7-1 流体流动的连续性方程

理想正压性流体在有势的质量力作用下,任一涡管强 度不随时间变化。
作业:7-2(1)、(3), 7-5
x
vx
y
v y
z
vz
dxdydz
微元体内总质量的变化率为 :
t
CV
dV
t
CV
dxdydz
t
dxdydz
取极限:CV→0,控制体收缩为质点,得:
t
x
vx
y
vy
z
vz
0
写为矢量形式 :
(v) 0
t
讨论:1. 定常流动 (v) 0
2. 不可压缩流体流动
v 0
divv 0
vx x
dx
vx y
dy
y
vy
v y y
dy
C
C’
vy
B
v y x
dx
v y y
dy
dβ
dy
vx vy
o
dα
dx
A
A’
vx vy
vx x v y x
dx dx
d(dx) vx dxt dx vx t
x
x
x
d(dy) vy dyt dy vy t
y
y
1. 平移运动
y
C
B
dy
vx
o
dx
A vy
x
v2 2
PF
2
yvz
zvy
dx
y
v2 2
PF
2zvx
xvz
dy
z
v2 2
PF
2
xvy
yvx
dz
流体力学第4章(涡旋动力学基础)PPT文档
u ,v yx
引用流函数,并考虑:
BBB
QVndlVdyidxjdldlVdyidxj
dl nkdyidxjdl
dl
()/
AAA
BBB
AAA udyvdyxxdydxd)
表明:经过以为端点的任何曲线的流体通量,决定于该两 点的流函数差,而与曲线的长度和形状无关。
用流函数可以来方便地表征无辐散场的流体通量。
23
习题
习题4-2-2是否存在既满足无幅散条件又满足无旋条 件的流动?如果存在,举例说明。
20
u=x+y v=x-y
15
10
5
5
10
15
20
无旋:流点自传
24
三、二维流动
一般二维流动,既不满足无旋条件,也不满足无辐 散条件,流动是有旋有辐散的。此时,其涡度和散度均 不为零,即满足:
vu
0
xy
D D xy
2VVVVD()()()
dV
1
FpDV ()
dt
3
39
dV
1
FpDV ()
dt
3
dV
1
FpDD ()
dt
3
dV
14 FpD
dt
3
对上式沿闭合曲线积分,即可得到反映环流变化的方程:
d dV l
dt
dt
14
FlpllDl
3
40
ddV dtdt
3 (1)
(2)
lFlpllDl14 (3)
(4)
化为全微分=0
对于粘性流体运动,纳维——斯托可斯方程为:
dVV 12 dtt 3
VVpgVV
方程的平流项变换: VVVV
04第4章绕翼型不可压缩流动
c
环量 d cV 1cosdcV 升力 L / V c V 2
0
0
升力系数
cl
L/
qS
cV2 12V2c
2
升力线斜率
a0
dcl d
2
力矩
距前缘处面涡微元
dddL M / Vd Ldd/cM m,L/LE EqM S L/E V c0c 2dc4l qc22
翼梢处流体高压低压
3D效应 展向流动
翼梢处流体接触
p相等 L或=0 上表面流体向翼梢汇聚
升力线c/4处
翼梢翼根L L/y Vy
型马蹄涡
无穷远处与 启动涡相连
直匀流+附着涡+自由尾涡 直匀流+型马蹄涡
海姆霍兹旋涡定理/旋涡不能中断且=const; 展向涡系非均匀分布即L、展向变化; 展向两剖面间附着涡之差=自由尾涡; 定义展向非均匀分布附着涡系为展向变强度 附着涡线/升力升力线。
无穷多无穷小的点涡
面涡
ds对P点的诱导速度
dV
ds 2 r
d ds
除面涡外所有点处诱导速度满足矢量叠加原理且具有连续性 除面涡外所有点满足无旋条件
包围面涡的封闭曲线上
b
ds
a
速度势
2
1
b
ds
2 a
可以证明
面涡两侧涡切线方向速度分量不连续而法线速度分量相同; 穿过面涡切线速度的改变量与当地的涡线强度有关;
有弯度翼型
完全由弯度产生解析增量/对面涡强度分布调整
假设()=与中弧线形状及有关/类似对称翼型+与中弧线形状有关且解析的/Fourier级数表达
第四章 流体动力学(无旋运动)
d
ux dx u y dy u cos ds cos u sin ds sin
uds(cos sin ) uds
2 2
d u ds
d dq udn
d u dn
ds d dn d s n
水力学
2、流网的性质 3 对于曲边正方形网格,任意两条流线间的单宽流 量为常量。
第 五 章 液 体 三 元 流 动 基 本 原 理
s n
q C
水力学
第 五 章 液 体 三 元 流 动 基 本 原 理
3、求流网的方法 解析法 实验法(水电比拟法)
手描法
水力学
4.4.4 基本平面势流及势流叠加原理
ux u y K1 K 2 1 u y ux
水力学
2、速度势函数的性质
第 五 章 液 体 三 元 流 动 基 本 原 理
(2) 无旋不可压,速度势函数满足拉氏方程
代入不可压连续性方程得
2 2 2 0 2 2 2 x y z
2
为调和函数
lab
2
1
的单位为m2 / s.
水力学
4.4.2 速度势函数
第 1、速度势函数定义 五 章 流动无旋 u y ux 液 体 三 元 流 动 基 本 原 理
z
x
y
=0
若令
ux ,uy . x y
( ) ( ) 0 x y y x
水力学
例3
第 五 章 试求:
平面速度场 ux x 4 y
(2). 求流函数
u y y 4x
(1). 是否为可能存在的流动
五章理想不可压流体二维流动(精品)
第五章理想不可压流体的二维无旋和有旋流动1.二维流动流函数定义、性质;2.二维流动流函数方程、定解条件、应用;3.复势、复速度求解无界二维流动、应用——定常圆柱绕流;4.奇点镜像法——平壁面和圆柱干扰下二维流动.流函数基本知识理想流体流动求解——叠加原理应用第五章理想不可压流体的二维无旋和有旋流动解不可压理想流体的平面和轴对称流动思路:运动学和动力学分解(位流理论)第四章确定不可压理想流体无旋流动时,直接利用连续方程()和无旋()条件求解速度场(拉普拉斯方程:),利用柯西——拉格朗日积分求压力场(将运动学问题和动力学问题分解)。
0=⋅∇V 0=⨯∇V 0=∆ϕ利用平面流动连续方程定义一个流函数,不可压平面无旋流动流函数和势函数均满足拉普拉斯方程(运动学方程),进而可以进行基本解叠加。
ψ不可压平面无旋流动流函数和势函数满足柯西---黎曼条件,因而可以利用复变函数工具。
均匀来流垂直于长柱体绕流,机翼中部流动近似为平面流动第五章理想不可压流体的二维无旋和有旋流动5.1 不可压平面流动和轴对称流动的流函数及性质5.1.1 平面流动和轴对称流动的定义平面流动:任一时刻,流场中各点的流动速度都平行于某一固定平面,且各物理量在此平面的垂直方向上没有变化。
若流动平行于xy平面,则平面流动速度及任一物理量B表示为:),,(,0),,,(),,,(t y x B B w t v x v v t y x u u ====轴对称流动:任一时刻,流场中各物理量在以某轴线为中心的同一圆周上没有变化。
若取z轴为对称轴,则各物理量满足:,0==∂∂εεV 第五章理想不可压流体的二维无旋和有旋流动5.1 不可压平面流动和轴对称流动的流函数及性质5.1.2 平面流动和轴对称流动的流函数流函数定义:对不可压流动,连续方程:,展开为:0=⋅∇V 0)(122311132321=∂∂+∂∂q V h h q V h h h h h 对定常可压缩流动,连续方程:,展开为:0)(=⋅∇V ρ0)(122311132321=∂∂+∂∂q V h h q V h h h h h ρρ定义流函数ψ流函数的概念是1781年Lagrange 首先引进的第五章理想不可压流体的二维无旋和有旋流动或者:通常把不可压平面流动的流函数称作拉格朗日流函数不可压平面流动(直角坐标中)的流函数(q 1=x, q 2=y, q 3=z )(h 1=h 2=h 3=1):不可压平面流动(极坐标)的流函数:(q 1=r,q 2=θ,q 3=z )23111322,V h h q V h h q -=∂∂=∂∂ψψ23111322,V h h q V h h q ρψρψ-=∂∂=∂∂v xu y -=∂∂=∂∂ψψ,(h 1=1,h 2=r ,h 3=1):θψθψV rrV r -=∂∂=∂∂,第五章理想不可压流体的二维无旋和有旋流动# 柱坐标z, r, ε不可压轴对称流动(柱坐标及球坐标中)的流函数:# 球坐标R,θ,ε23111322,V h h q V h h q -=∂∂=∂∂ψψ(h 1=1,h 2=1,h 3=r):(h 1=1,h 2=R,h 3=Rsinθ):r z rV z rV r-=∂∂=∂∂ψψ,θθψθθψV R RV R R sin ,sin 2-=∂∂=∂∂2 r第五章理想不可压流体的二维无旋和有旋流动)()(4)()(42122222=+---++++-∞r d x d x Qr d x d x Q r U ππr=0 满足流线方程,即ψ=0的流线通过x 轴,另解方程)2(,0)()()()(22222222∞==+--++++-U Qb rd x d x b rd x d x b r π求速度场:V复势:复速度:共轭复速度:复速度的模:共轭复速度的表示方法:(2)复速度:以平面无旋流场的速度分量组成的复数U=u+ivψφi z W +=)(V iv u xi x dz dW =-=∂∂+∂∂=ψφiv u dzdW+=V v u dzdW=+=22αi Ve iv u dzdW -=-=dzWd artg u v tg i V dz dW ==-=-1),sin (cos ααα复速度:ivu V +=,x qφ=∂若平面点源在(x 0, y 0)θππψ'=--=-2)(2001q x x y y tg q 20202)()(,In 2y y x x q-+-==σσπφ)(2),(20202y y q v x x qu -=-=πσπσ)(22)(2)(0z z In qz In q i In q z W -='='+=ππθσπm(3)平面偶极子两无限长直线点源相距δl ,线源强度分别为q (位于z=-δl )和-q (位于z=0),当δl →0时,称这一对直线点源为平面偶极子。
