模型预测控制工具箱及应用1
预测控制

g11=poly2tfd(12.8,[16.7,1],0,1);%POL Y2TFD Create transfer functions in 3 row representation将通用的传递函数模型转换为MPC传递函数模型% g = poly2tfd(num,den,delt,delay)% POL Y2TFD creates a MPC toolbox transfer function in following format:%g为对象MPC传递函数模型% g = [ b0 b1 b2 ... ] (numerator coefficients)% | a0 a1 a2 ... | (denominator coefficients)% [ delt delay 0 ... ] (only first 2 elements used in this row)%% Inputs:% num : Coefficients of the transfer function numerator.% den : Coefficients of the transfer function denominator.% delt : Sampling time. Can be 0 (for continuous-time system)% or > 0 (for discrete-time system). Default is 0.% delay : Pure time delay (dead time). Can be >= 0.% If omitted or empty, set to zero.% For discrete-time systems, enter as PERIODS of pure% delay (an integer). Otherwise enter in time units.g21=poly2tfd(6.6,[10.9,1],0,7);g12=poly2tfd(-18.9,[21.0,1],0,3);g22=poly2tfd(-19.4,[14.4,1],0,3);delt=3;ny=2;tfinal=90;model=tfd2step(tfinal,delt,ny,g11,g21,g12,g22)%对于这个例子,N=90/3=30figure(3)plot(model)%TFD2STEP Determines the step response model of a transfer function model.传递函数模型转换成阶跃响应模型% plant = tfd2step(tfinal, delt2, nout, g1)% plant = tfd2step(tfinal, delt2, nout, g1, ..., g25)% The transfer function model can be continuous or discrete.%% Inputs:% tfinal: truncation time for step response model.% delt2: desired sampling interval for step response model.% nout: output stability indicator. For stable systems, this% argument is set equal to number of outputs, ny.% For systems with one or more integrating outputs,% this argument is a column vector of length ny with% nout(i)=0 indicating an integrating output and% nout(i)=1 indicating a stable output.% g1, g2,...: SISO transfer function described above ordered% to be read in columnwise (by input). The number of % transfer functions required is ny*nu. (nu=number of % inputs). Limited to ny*nu <= 25.%% Output:% plant: step response coefficient matrix in MPC step format. plant=model;P=6;M=2;ywt=[];uwt=[1 1];Kmpc=mpccon(model,ywt,uwt,M,P)%ywt,uwt : 相当于Q,R%MPCCON Calculate MPC controller gains for unconstrained case.% Kmpc = mpccon(model,ywt,uwt,M,P)% MPCCON uses a step-response model of the process.% Inputs:% model : Step response coefficient matrix of model.% ywt,uwt : matrices of constant or time-varying weights.相当于Q,R% If the trajectory is too short, they are kept constant% for the remaining time steps.% M : number of input moves and blocking specification. If% M contains only one element it is the input horizon% length. If M contains more than one element% then each element specifies blocking intervals.% P : output (prediction) horizon length. P = Inf indicates the% infinite horizon.%% Output:% Kmpc : Controller gain matrixtend=30;r=[0 1];[y,u]=mpcsim(plant,model,Kmpc,tend,r);%plan为开环对象的实际阶跃响应模型%model为辨识得到的开环阶跃响应模型%Kmpc相当于D阵%Tend仿真的结束时间.%R输出设定值和参考轨迹%r=[r1(1) r2(1)...rny(1);r1(2) r2(2)....rny(2);... r1(N) r2(N) ...rny(N)]%y:控制输出%u:控制变量%ym:模型预测输出%MPCSIM Simulation of the unconstrained Model Predictive Controller.% [y,u,ym] = mpcsim(plant, model, Kmpc, tend, r,usat, tfilter,% dplant, dmodel, dstep)% REQUIRED INPUTS:% plant(model): the step response coefficient matrix of the plant (model)% generated by the function tfd2step% Kmpc: the constant control law matrix computed by the function mpccon% (closed-loop simulations).For open-loop simulation, controller=[].% tend: final time of simulation.% r: for the closed-loop simulation, it is a constant or time-varying% reference trajectory. For the open-loop simulation, it is the% trajectory of the manipulated variable u.% OPTIONAL INPUTS:% usat: the matrix of manipulated variable constraints.It is a constant% or time-varying trajectory of the lower limits (Ulow), upper limits% (Uhigh) and rate of change limits (DelU) on the manipulated % variables. Default=[].% tfilter: time constants for noise filter and unmeasured disturbance lags.% Default is no filtering and step disturbance.% dplant: step response coefficient matrix for the disturbance effect on the% plant output generated by the function tfd2step. If distplant is% provided, dstep is also required. Default = [].% dmodel: step response coefficient matrix for the measured disturbance% effect on the model output generated by the function tfd2step.% If distmodel is provided, dstep is also required. Default=[].% dstep: matrix of disturbances to the plant. For output step disturbances% it is a constant or time-varying trajectory of disturbance values% For disturbances through step response models,it is a constant or% time-varying trajectory of disturbance model inputs.Default=[].% OUTPUT ARGUMENTS: y (system response), u (manipulated variable) and% ym (model response)plotall(y,u,delt)figure(2)plot(y,'*')南通大学毕业设计(论文)任务书题目锅炉液位系统的DMC-PID控制学生姓名朱养兵学院电气工程学院专业自动化班级自051学号0512012010起讫日期2009.2 -2009.6指导教师李俊红职称讲师发任务书日期2009 年2 月18 日●MATLAB 软件●JX-300X组态监控软件●浙大中控DCS●上海齐鑫公司过程控制对象●PC机。
matlab各种应用工具箱参考

2021/3/10
讲解:XX
11
二、通用工具箱
• Matlab主工具箱
• 前面课程所介绍的数值计算、符号运算、 绘图以及句柄绘图都是matlab主工具箱 的内容,是matlab的基本部分,也是我 们课程的重点。
• Matlab主工具箱位于:
c:\matlab\toolbox\matlab
• matlab主工具箱是任何版本的matlab都
simulink 的一般结构:
输入
系统
输出
2021/3/10
讲解:XX
27
仿真原理
• 当在框图视窗中进行仿真的同时,matlab 实际上是运行保存于simulink内存中s函数 的映象文件,而不是解释运行该m文件。
• s函数并不是标准m文件,它m文件的一种 特殊形式。
结构图创建方法
• 一个动态系统的创建过程,就是一个方框 图的绘制过程
rose - Angle histogram plot.
compass - Compass plot.
feather - Feather plot.
fplot - Plot function.
comet - Comet-like trajectory.
2021/3/10
讲解:XX
17
Graph annotation. title - Graph title. xlabel - X-axis label. ylabel - Y-axis label. text - Text annotation. gtext - Mouse placement of text. grid - Grid lines.
高阶谱分析工具箱
2021/3/10
Matlab中的自适应控制设计方法

Matlab中的自适应控制设计方法自适应控制是一种广泛应用于工程领域的控制策略,它通过实时地调整控制器参数,以适应系统动态特性的变化。
Matlab是一个功能强大的工具,提供了丰富的工具箱和函数,使得自适应控制的设计和实现变得更加便捷。
本文将介绍几种常见的自适应控制设计方法,并说明在Matlab中的实现。
1. 最小均方(LMS)算法最小均方算法是一种基于误差信号的单参数自适应调整方法。
通过最小化误差信号的均方值,实时更新参数以使系统逐渐趋于稳定。
Matlab中可使用函数"lms"来实现LMS算法的设计。
该函数可以根据输入信号和期望输出信号的数据进行参数的自适应调整。
2. 递归最小二乘(RLS)算法递归最小二乘算法是一种多参数自适应调整方法,它通过将参数更新与误差信号相关联,实现对参数的在线更新。
相较于LMS算法,RLS算法具有更好的收敛性能和稳定性。
Matlab中的函数"rls"可以实现递归最小二乘算法的设计,用户可以根据系统的要求自定义相关参数。
3. 自适应模型预测控制(MPC)算法自适应模型预测控制算法中,控制器利用系统的模型对未来的输出进行预测,并根据预测结果进行参数调整。
通过不断更新模型中的参数和系统输出的观测值,实现了对动态特性的自适应调整。
Matlab提供了函数"mpc"用于实现自适应模型预测控制的设计。
用户可以通过设定模型和目标函数等参数,实现对系统的自适应控制。
4. 遗传算法(GA)优化方法遗传算法是一种基于自然进化原理的优化方法,通过模拟自然选择、交叉和变异等过程,寻找最优的参数组合。
Matlab中的函数"ga"可以实现遗传算法的设计,用户可以根据系统的需求和约束,设定适应度函数以及参数的取值范围,实现对系统参数的自适应优化。
自适应控制在实际的工程中有着广泛的应用,例如航空、汽车、机器人等领域。
通过Matlab中提供的强大工具和函数,工程师可以轻松地实现自适应控制的设计和实现。
Matlab常用工具箱

Matlab常用工具箱MATLAB包括拥有数百个内部函数的主包和三十几种工具包。
工具包又可以分为功能性工具包和学科工具包。
功能工具包用来扩充MATLAB的符号计算,可视化建模仿真,文字处理及实时控制等功能。
学科工具包是专业性比较强的工具包,控制工具包,信号处理工具包,通信工具包等都属于此类。
开放性使MATLAB广受用户欢迎。
除内部函数外,所有MATLAB主包文件和各种工具包都是可读可修改的文件,用户通过对源程序的修改或加入自己编写程序构造新的专用工具包。
Matlab Main Toolbox——matlab主工具箱Control System Toolbox——控制系统工具箱Communication Toolbox——通讯工具箱Financial Toolbox——财政金融工具箱System Identification Toolbox——系统辨识工具箱Fuzzy Logic Toolbox——模糊逻辑工具箱Higher-Order Spectral Analysis Toolbox——高阶谱分析工具箱Image Processing Toolbox——图象处理工具箱LMI Control Toolbox——线性矩阵不等式工具箱Model predictive Control Toolbox——模型预测控制工具箱μ-Analysis and Synthesis Toolbox——μ分析工具箱Neural Network Toolbox——神经网络工具箱Optimization Toolbox——优化工具箱Partial Differential Toolbox——偏微分方程工具箱Robust Control Toolbox——鲁棒控制工具箱Signal Processing Toolbox——信号处理工具箱Spline Toolbox——样条工具箱Statistics Toolbox——统计工具箱Symbolic Math Toolbox——符号数学工具箱Simulink Toolbox——动态仿真工具箱Wavele Toolbox——小波工具箱[编辑本段]常用函数Matlab内部常数[3]eps:浮点相对精度exp:自然对数的底数ei 或j:基本虚数单位inf 或Inf:无限大,例如1/0nan或NaN:非数值(Not a number),例如0/0pi:圆周率p(= 3.1415926...)realmax:系统所能表示的最大数值realmin:系统所能表示的最小数值nargin: 函数的输入引数个数nargout: 函数的输出引数个数lasterr:存放最新的错误信息lastwarn:存放最新的警告信息MATLAB常用基本数学函数abs(x):纯量的绝对值或向量的长度angle(z):复数z的相角(Phase angle)sqrt(x):开平方real(z):复数z的实部imag(z):复数z的虚部conj(z):复数z的共轭复数round(x):四舍五入至最近整数fix(x):无论正负,舍去小数至最近整数floor(x):地板函数,即舍去正小数至最近整数ceil(x):天花板函数,即加入正小数至最近整数rat(x):将实数x化为分数表示rats(x):将实数x化为多项分数展开sign(x):符号函数(Signum function)。
利用Matlab进行电机控制和驱动系统设计

利用Matlab进行电机控制和驱动系统设计电机控制和驱动是现代工业中非常重要的一环。
对于电机的控制和驱动系统设计,好的方法和工具可以提高控制系统的性能和效率。
在这方面,Matlab是一种被广泛使用且功能强大的工具。
本文将探讨如何利用Matlab进行电机控制和驱动系统设计。
1. 电机控制基础知识在开始讨论Matlab的应用之前,我们先来简要介绍一些电机控制的基础知识。
电机控制系统的目标是控制电机的速度、位置或者转矩等参数,以满足特定的要求。
最常见的电机控制方法包括电阻性、矢量控制、磁场定向控制等。
此外,电机控制还需要考虑诸如速度和位置传感器、控制器硬件等外部环境因素。
2. Matlab在电机控制中的应用Matlab作为一种功能强大的数学计算工具和编程环境,可以帮助工程师完成电机控制和驱动系统的设计和仿真。
在电机控制中,Matlab的应用主要分为以下几个方面:2.1 仿真建模Matlab提供了丰富的仿真工具和函数,可以对不同类型的电机进行仿真建模。
用户可以根据电机的参数和特性,利用Matlab构建电机控制系统的模型,并进行仿真分析。
仿真结果可以帮助工程师评估不同控制策略的性能,并优化系统设计。
2.2 控制算法设计Matlab中的控制系统工具箱提供了多种控制算法的设计和调试功能。
用户可以利用这些工具箱设计电机控制系统的控制算法,包括传统的PID控制、模型预测控制、自适应控制等。
Matlab还提供了控制系统分析的函数和工具,以评估设计算法的稳定性和鲁棒性。
2.3 码中断和实时控制对于一些实时控制应用,例如电机控制系统中的编码器中断等,Matlab提供了相应的函数和工具箱来处理这些实时数据。
用户可以通过Matlab编写程序,实现电机控制系统的实时数据采集和处理,并实时调整控制参数。
2.4 驱动系统设计除了控制系统的设计,Matlab还可用于电机驱动系统的设计。
通过Matlab的仿真和建模功能,用户可以评估不同的驱动系统设计方案,包括不同的功放电路、驱动器拓扑结构等。
【系统仿真学报】_模型预测控制_期刊发文热词逐年推荐_20140723
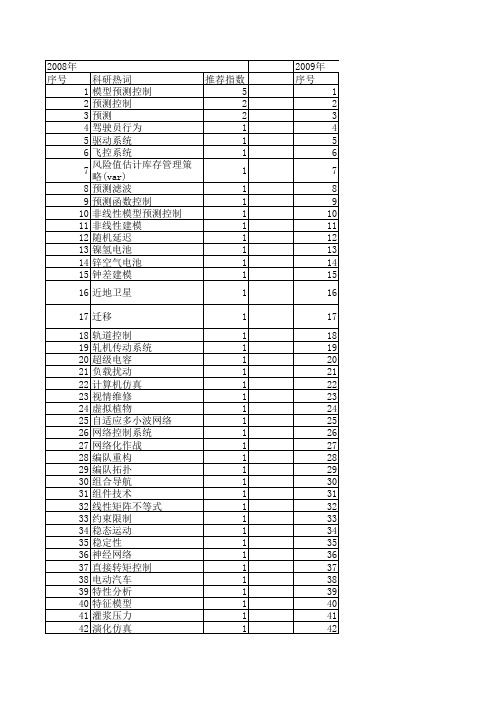
灰色系统 灰色模型 混沌粒子群优化 混沌优化 混凝投药 浊度 永磁无轴承同步电机 气化过程建模 比率检测 模糊预测控制 模型 有限记忆模型 最小方差控制 最小二乘支持向量机 智能优化算法 时变时滞 无传感器控制 无人机 数值模拟 描述函数法 指挥控制系统 悬架系统 快速性 广义预测控制 姿态运动 太阳帆板 多刚体动力学 备件供应保障 基于案例的推理 地空导弹 在线自适应 在线参数辨识 四维 双率系统 参数估计 单纯形法 单兵火力系统 协同仿真 动态路径规划 动态仿真 分块式主镜 全氢罩式炉 仿真平台 任务时间特性 任务/路径规划仿真平台 主动悬架 rbf网络
水相 模糊预测控制 模糊逻辑 模糊自适应控制 模型预测控制(mpc) 模型参考自适应控制 最优控制 智能运输系统(its) 智能模型 智能优化 无陀螺微惯性测量单元 无人机 数值仿真 故障诊断 控制策略 指挥控制 弹道解算 弹道修正 异步电机 建模 广义预测控制 平流层飞艇 大规模系统 复杂网络 填埋气体 在线仿真 变风量系统(vav) 双星定位 参数灵敏性 动态贝叶斯网络 动态矩阵控制 加速度 加权矩阵 分类规则 分布式控制 决策树 决策机制 全球定位系统 健康管理 信息融合 信息熵 信息协同 供应链管理 作动器 仿真 交通流 不确定性
93 94 95 96 97 98
truetime工具箱 l系统 hill方程 gams dsapce bp神经网络
1 1 1 1 1 1
93 94 95 96 97 98 99 100
2009年 科研热词 预测控制 模型预测控制 遗传算法 虚拟样机 电动助力转向 动力学仿真 驾驶员模型 飞行安全 预测 面形控制 非线性pid控制 集成灰模糊控制 集成控制 陀螺稳定平台 遭遇点 速率限制 递推辨识 轻武器 转向系统 转向感觉 赤潮 资源预留 资源预测 质量预测 质子交换膜燃料电池 计算机应用 航天器 自适应灰色预测控制 自校正控制 缺货量 综合评价 综合控制 线性化 纺纱 约束矩阵 累加生成操作 系统动力学 精确化供应 粒子群优化 突发任务 空中目标 神经网络逆控制 生物质 烟台四十里湾 灰色预测 推荐指数 3 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Matlab技术在嵌入式系统开发中的应用指南

Matlab技术在嵌入式系统开发中的应用指南一、引言随着科技的不断发展,嵌入式系统(Embedded System)在各个领域的应用越来越广泛。
而在嵌入式系统的开发过程中,Matlab技术的应用不可忽视。
Matlab作为一款强大的数学分析和计算软件,其在嵌入式系统开发中具有广泛应用的潜力。
本文将探讨Matlab技术在嵌入式系统开发中的应用指南,旨在帮助开发者更好地利用Matlab技术提高开发效率和系统性能。
二、Matlab在嵌入式系统开发中的基础应用1. 数据分析与处理在嵌入式系统开发过程中,数据的分析与处理是一项重要的任务。
Matlab提供了丰富的数学分析函数和工具箱,可以方便地对采集到的嵌入式系统产生的数据进行处理。
例如,可以利用Matlab提供的信号处理工具箱对嵌入式系统采集到的传感器数据进行滤波处理,以消除噪声的干扰。
此外,利用Matlab的统计分析工具箱,还可以进行数据的统计分析和建模,从而为嵌入式系统的优化提供依据。
2. 控制算法设计与仿真在嵌入式系统开发的过程中,设计合适的控制算法是至关重要的。
Matlab提供了丰富的工具和函数,可以用于控制系统的建模、设计和仿真。
例如,可以利用Matlab的控制系统工具箱进行PID控制器的设计与调试,以实现嵌入式控制系统的精确控制。
此外,Matlab还提供了Simulink工具,可以方便地进行嵌入式系统的图形化建模和仿真,从而加快系统的开发与测试速度。
三、Matlab在嵌入式系统开发中的高级应用1. 代码自动生成与优化在嵌入式系统开发中,需要将Matlab代码转换为可在目标嵌入式平台上运行的代码。
Matlab提供了Embedded Coder工具箱,可以实现自动化的代码生成。
利用Embedded Coder,开发者可以将Matlab的模型和算法直接生成C或C++代码,从而大大简化了系统的开发流程。
此外,Embedded Coder还提供了优化选项,可以对生成的代码进行优化,提高系统的运行效率和响应速度。
MATLAB常用工具箱

MATLAB常用工具箱常用工具箱MATLAB包括拥有数百个内部函数的主包和三十几种工具包。
工具包又可以分为功能性工具包和学科工具包。
功能工具包用来扩充MATLAB的符号计算,可视化建模仿真,文字处理及实时控制等功能。
学科工具包是专业性比较强的工具包,控制工具包,信号处理工具包,通信工具包等都属于此类。
开放性使MATLAB广受用户欢迎。
除内部函数外,所有MATLAB主包文件和各种工具包都是可读可修改的文件,用户通过对源程序的修改或加入自己编写程序构造新的专用工具包。
Matlab Main Toolbox——matlab主工具箱Control System Toolbox——控制系统工具箱Communication Toolbox——通讯工具箱Financial Toolbox——财政金融工具箱System Identification Toolbox——系统辨识工具箱Fuzzy Logic Toolbox——模糊逻辑工具箱Higher-Order Spectral Analysis Toolbox——高阶谱分析工具箱Image Processing Toolbox——图象处理工具箱LMI Control Toolbox——线性矩阵不等式工具箱Model predictive Control Toolbox——模型预测控制工具箱μ-Analysis and Synthesis Toolbox——μ分析工具箱Neural Network Toolbox——神经网络工具箱Optimization Toolbox——优化工具箱Partial Differential Toolbox——偏微分方程工具箱Robust Control Toolbox——鲁棒控制工具箱Signal Processing Toolbox——信号处理工具箱Spline Toolbox——样条工具箱Statistics Toolbox——统计工具箱Symbolic Math Toolbox——符号数学工具箱Simulink Toolbox——动态仿真工具箱Wavele Toolbox——小波工具箱常用函数Matlab内部常数[3]eps:浮点相对精度exp:自然对数的底数ei 或 j:基本虚数单位inf 或 Inf:无限大,例如1/0nan或NaN:非数值(Not a number),例如0/0 pi:圆周率 p(= 3.1415926...)realmax:系统所能表示的最大数值realmin:系统所能表示的最小数值nargin: 函数的输入引数个数nargout: 函数的输出引数个数lasterr:存放最新的错误信息lastwarn:存放最新的警告信息MATLAB常用基本数学函数abs(x):纯量的绝对值或向量的长度angle(z):复数z的相角(Phase angle)sqrt(x):开平方real(z):复数z的实部imag(z):复数z的虚部conj(z):复数z的共轭复数round(x):四舍五入至最近整数fix(x):无论正负,舍去小数至最近整数floor(x):下取整,即舍去正小数至最近整数ceil(x):上取整,即加入正小数至最近整数rat(x):将实数x化为多项分数展开rats(x):将实数x化为分数表示sign(x):符号函数 (Signum function)。
