2014届浙江省宁波市高三第二次模拟考试数学理试题及答案
高中理科数学复习试题选编31:双曲线(教师版)

理科数学复习试题选编31:双曲线一、选择题1 .(六校联盟高三回头联考理科数学试题)已知F 1和F 2分别是双曲线22221(0,0)x y a b a b-=>>的左、右焦点,P 是双曲线左支的一点,1PF ⊥2PF ,1PF =C ,则该双曲线的离心率为( )A 1B .12C 1D .12【答案】C2 .(绍兴市高三教学质量调测数学(理)试题(word 版) )已知双曲线22221x y a b-=(0,0)a b >>的右焦点为F ,O 为坐标原点,以OF为直径的圆与双曲线的一条渐近线相交于O ,A 两点.若△AOF 的面积为b ,则双曲线的离心率等于 ( )A .3B .5C .D .【答案】D3 .(高考模拟冲刺(提优)测试二数学(理)试题)直线过点(2,1)P 与曲线1422=-y x 恰有一个公共点,则满足条件的直线的条数为 ( )A .1B .2C .3D .4【答案】B 解:因为点(2,1)P 在渐近线上,故旋转直线一周只有2条符合条件.4 .(杭州高中高三第六次月考数学(理)试题)设双曲线C :22221x y a b -=(a >0,b >0)的右焦点为F ,左,右顶点分别为A 1,A 2.过F 且与双曲线C 的一条渐近线平行的直线l 与另一条渐近线相交于P ,若P 恰好在以A 1A 2为直径的圆上,则双曲线C 的离心率为 ( )AB .2C D .3【答案】A5 .(高考模拟冲刺(提优)测试一数学(理)试题)已知1F ,2F 分别是双曲线)0,0(12222>>=-b a by ax 的左、右焦点,过点2F 与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M ,若点M 在以线段21F F 为直径的圆外,则双曲线离心率的取值范围是 ( )A .)2,1(B .)3,2(C .)2,3(D .),2(∞+【答案】D6 .(嘉兴市高三上学期基础测试数学(理)试题)已知焦点在y 轴上的双曲线的渐近线过椭圆221416x x +=和椭圆2231164x y +=的交点,则双曲线的离心率是( )A .233B .2C .5D .52【答案】B7 .(杭州市第一次高考科目教学质量检测理科数学试题)设双曲线22143x y -=的左,右焦点分别为12,F F ,过1F 的直线交双曲线左支于,A B 两点,则22BF AF +的最小值为 ( )A .192B .11C .12D .16【答案】B 解:由题意,得:21221121248824AF AF a BF AF AF BF AB BF BF a ⎧-==⎪⇒+=++=+⎨-==⎪⎩ 显然,AB 最短即通径,2min23b AB a=⋅=,故()22min11BF AF +=8 .(温岭中学高三高考提优冲刺考试(三)数学(理)试题 )已知21F F 、分别是双曲线:C 12222=-by a x 的左、右焦点,若2F 关于渐近线的对称点恰落在以1F 为圆心,||1OF 为半径的圆上,则C 的离心率为: ( )A .3B .3C .2D .2【答案】D解析:方法一:设),(y x P 为2F 关于渐近线x aby l =:的对称点,则有: ⎪⎩⎪⎨⎧+⋅=-=-2)2c x a b y b a c x y (,解得:⎪⎪⎩⎪⎪⎨⎧+=+-=2222222)(b a abc y b a b a c x , 由⋅1=0可得:0222=++y cx x ,将上式代入化简可得:0))((2)(2222222=+-++b a b a b a ,即223a b =,即224a c =,即2==ace ,故选 D .方法二:如图:设2F 关于其渐近线的对称点为P ,连接PO ﹑1PF ,由于点P 恰落在以1F 为圆心,||1OF 为半径的圆上,故有11PF PO OF c ===,易得02160PF =∠F ,01230PF =∠F 故12PF PF ⊥,又2OH PF ⊥,故0260OHF ∠=,即3600==tan a b ,即2==ace .故选 D .9 .(嘉兴市高三第二次模拟考试理科数学试卷)设m 是平面α内的一条定直线,P 是平面α外的一个定点,动直线n 经过点P 且与m 成︒30角,则直线n 与平面α的交点Q 的轨迹是 ( )A .圆B .椭圆C .双曲线D .抛物线【答案】C :动直线n 的轨迹是以点P 为顶点、以平行于m 的直线为轴的两个圆锥面,而点Q 的轨迹就是这两个圆锥面与平面α的交线.10.(【解析】镇海中学高三5月模拟数学(理)试题)已知双曲线方程为22221(0,0)x y a b a b-=>>,离心率为2,12,F F 分别是它的左、右焦点,A 是它的右顶点,过1F 作一条斜率为(0)k k ≠的直线与双曲线交于两个点,M N ,则MAN ∠为 ( )A .锐角B .直角C .钝角D .锐角、直角、钝角都有可能【答案】答案:B 解析:由离心率为2,可得2c a =,223b a =,则双曲线方程为22233xy a -=.设1122(,),(,)M x y N x y ,因直线MN 的斜率不为零,则可设其方程为2x my a =-,与双曲线方程联立得222(31)1290m y amy a --+=,从而有2310m -≠,1221231amy y m +=-,且11.(温岭中学高三高考提优冲刺考试(五)数学(理)试题)已知F 1、F 2是双曲线C :)0(12222>>=-b a by a x的两个焦点,过曲线C 的左焦点F 1(-c ,0)和虚轴端点B(0,b )作直线l 交曲线C 左支于A 点,右支与D 点,连接AO 、DF 2,AO∥DF 2 ,则双曲线的离心率为 ( ) A .3B .6C .36+D .25+【答案】C 提示 联立方程组⎪⎪⎩⎪⎪⎨⎧=-+=1)(2222b y ax c x c b y 削去x 得02322=+-b y c by 221221,2b y y b c y y =⋅=+(*),由题意的2212y y =代入(*)中,得到⎪⎩⎪⎨⎧==2222223by b c y ,削去y 得4489c b =,可以解得2692+=e .12.(考试院高三上学期测试数学(理)试题)如图,F 1,F 2是双曲线C :22221x y a b-=(a >0,b >0)的左、右焦A ,B 两点.若 | AB | : | BF 2 | : | AF 2 |=3:4 : 5,( ).13.15 C .2D .3【答案】A13.(“六市六校”联盟高三下学期第一次联考数学(理)试题)设F 1,F 2 是双曲线)0,(1x 2222>=-b a by a 的左、右焦点,若双曲线右支上存在一点P 满足212F F PF =,且54cos 21=∠F PF ,则双曲线的渐近线方程为( )A .043=±y xB .053=±y xC .034=±y xD .045=±y x 【答案】C14.(海宁市高三2月期初测试数学(理)试题)已知点P 是双曲线C :)0,0(12222>>=-b a b y a x 左支上一点,F 1,F 2是双曲线的左、右两个焦点,且PF 1⊥PF 2,PF 2与两条渐近线相交于M ,N 两点(如图),点N 恰好xy OA B F 1F 2平分线段PF 2,则双曲线的离心率是( )5B .2C .3D .215.(普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))如图,21,F F 是椭圆14:221=+y x C 与双曲线2C 的公共焦点,B A ,分别是1C ,2C 在第二、四象限的公共点.若四边形21BF AF 为矩形,则2C 的离心率是( )A .2B .3C .23D .26 【答案】D16.(宁波市高三第一学期期末考试理科数学试卷)设圆锥曲线C 的两个焦点分别为F 1,F 2,若曲线C 上存在点P 满足|PF 1|:|F 1F 2|:|PF 2|=4:3:2, 则曲线C 的离心率等于 ( )A .2332或B .23或2 C .12或2 D .1322或【答案】D17.(嘉兴市第一中学高三一模数学(理)试题)已知双曲线c : )0(12222>>=-b a b y a x ,以右焦点F为圆心,|OF |为半径的圆交双曲线两渐近线于点M 、N (异于原点O),若|MN|=a 32,则双曲线C的离心率 是( )A 2B .3C .2D .13+【答案】COxyA BF 1F 2xyOM NP 1F 2F18.(黄岩中学高三5月适应性考试数学(理)试卷 )已知A ,B ,P 是双曲线12222=-by a x (0>a ,0>b )上不同的三点,且A ,B 连线经过坐标原点O ,若直线PA ,PB 的斜率乘积3=⋅PB PA k k ,则双曲线的离心率为 ( )A .2B .3C .2D .5【答案】C19.(温州中学高三第三次模拟考试数学(理)试题)已知双曲线22221(0,0)x y a b a b-=>>,12A A 、是实轴顶点,F 是右焦点,()0,B b 是虚轴端点,若在线段BF 上(不含端点)存在不同的两点(1,2)i p i =,使得12(1,2)i P A A i ∆=构成以12A A 为斜边的直角三角形,则双曲线离心率e 的取值范围是 ( )A .)+∞B .1,)2+∞C .1(1,)2D .1)2【答案】D .20.(湖州市高三第二次教学质量检测数学(理)试题(word 版) )已知A B P ,,是双曲线()2222100y x a b a b -=>>,上不同的三点,且A B ,连线经过坐标原点O ,若直线PA PB ,的斜率乘积3PA PB k k ⋅=,则双曲线的离心率为 ( )AB C .2D【答案】C21.(温州市高三第三次适应性测试数学(理)试题(word 版) )已知是双曲线14222=-y ax 的左焦点,双曲线右支上一动点P ,且x PD ⊥轴,D 为垂足,若线段PD FP -的最小值为52,则双曲线的离心率为 ( )A .53B .52C .25D .5【答案】A22.(杭州市高三第二次教学质检检测数学(理)试题)已知双曲线2222:1(0,0)y x C a b a b ,A ,B 是双曲线的两个顶点.P 是双曲线上的一点,且与点B 在双曲线的同一支上.P 关于y 轴的对称点是Q 若直线AP ,BQ 的斜率分别是k 1,k 2,且k 1·k 2=45,则双曲线的离心率是 ( )A .355 B .94C .32D .95【答案】C23.(温州市十校联合体高三上学期期末联考理科数学试卷)已知抛物线()022>=p px y 与双曲线()0,012222>>=-b a by a x 有相同的焦点F ,点A 是两曲线的交点,且x AF ⊥轴,则双曲线的离心率为 ( )A .12+B .13+C .215+ D .2122+【答案】A24.(名校新高考研究联盟高三第一次联考数学(理)试题)已知P 为双曲线C :221916x y -=上的点,点M满足1OM =,且0OM PM ⋅=,则当PM 取得最小值时的点P 到双曲线C 的渐近线的距离为 ( )A .95B .125C .4D .5【答案】B 二、填空题25.(永康市高考适应性考试数学理试题 )已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ,过F 的直线l 交双曲线的渐近线于A ,B 两点,且与其中一条渐近线垂直,若FB AF 4=,则该双曲线的离心率为____;【答案】210526.(乐清市普通高中高三上学期期末教学质量检测数学(理)试题)设O 为坐标原点,B A ,是双曲线1322=-y x 的渐近线上异于O 的两点,且2||||==OB OA ,则→→⋅OB OA =_______.【答案】2±,-4 27.(金丽衢十二校高三第二次联合考试理科数学试卷)我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“黄金搭档”.已知1F 、2F 是一对“黄金搭档”的焦点,P 是它们在第一象限的交点,当6021=∠PF F 时,这一对“黄金搭档”中双曲线的离心率是_______【答案】328.(温州市高三第二次模拟考试数学(理)试题)己知F 1,F 2分别是双曲线1222=-b y x 的左、右焦点,A 是双曲线上在第一象限内的点,若 |AF 2|=2且∠F 1AF 2=450.廷长AF 2交双曲线右支于点B ,则ΔF 1AB 及的面积等于___【答案】429.(建人高复高三第五次月考数学(理)试题)已知A 、B 分别是双曲线22:4C x y -=的左、右顶点,则P 是双曲线上在第一象限内的任一点,则PBA PAB ∠-∠=__________.【答案】略30.(五校联盟高三下学期第一次联考数学(理)试题)设双曲线2222:1(0)x y C a b a b-=>>的右焦点为F ,左右顶点分别为12,A A ,过F 且与双曲线C 的一条渐近线平行的直线l 与另一条渐近线相交于P ,若P 恰好在以12A A 为直径的圆上,则双曲线的离心率为______________.【答案】231.(宁波市高三第一学期期末考试理科数学试卷)如果双曲我的两个焦点分别为12(0,3)(0,3)F F 和,其中一条渐近线的方程是22y x =,则双曲线的实轴长为______. 【答案】2332.(诸暨中学高三上学期期中考试数学(理)试题)设双曲线22221(0,0)x y a b a b-=>>的右顶点A ,x 轴上有一点(2,0)Q a ,若双曲线上存在点P ,使AP PQ ⊥,则双曲线的离心率的取值范围是____________【答案】33.(温州市高三第一次适应性测试理科数学试题)已知双曲线22221x ya b-=的一条渐近线方程为2y x=,则其离心率为____【答案】34.(五校联盟高三下学期第二次联考数学(理)试题)已知双曲线22221(0,0)x ya ba b-=>>的渐近线与圆22420x y x+-+=有交点,则该双曲线的离心率的取值范围是___________.【答案】。
浙江省宁波市五校2014年5月高三适应性考试语文试题及答案

浙江省宁波市五校2014年5月高三适应性考试语文试题本试题卷全卷共8页。
满分150分,考试时间150分钟。
注意事项:1.答题前,考生务必将将自己的座位号、姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸相应的位置上。
2.请考生按规定用笔将所有试题的答案涂、写在答题纸上。
不能答在试题卷上。
一、语言文字运用(共24分,其中选择题每小题3分)1.下列词语中,加点的字注音全部无误的一项是()A.叱咤(zhà)风云骠(biào)勇城垣(yuán )力能扛(gāng)鼎B.怙恶不悛(quān)豆豉(chǐ)偌(ruò)大亘(gân)古不变C.臧否(pǐ)人物埋怨(mán )氛围(fēn)退避三舍(shě)D.舐(shì)犊情深订(dīng)正唆(suō)使年高德劭(shào)2.下列各项中,没有错别字的一项是()A.我们常常忍不住和别人比,孰不知和别人比较是没有意义的,只有和自己比较才是最有价值的。
B.马尔克斯与日本名导黑泽明熟识,两人曾在1990年的新拉美电影节会悟。
马尔克斯曾说,《百年孤独》只有黑泽明能拍成电影。
C.当地时间29日,韩国总统朴槿惠前往位于安山的集体焚香所,向“岁月”号客轮沉没事故死难者献花。
遇难乘客家属围住她倾诉报怨,朴槿惠向家属道歉。
D.现在各色“大家”依据讲坛而一夜成名,其中不乏掉书袋之人。
3.下列各句中,加点的成语运用正确的一项是()A.以前,这里是无人的北大荒,曾几何时,这里变得人烟阜盛,热闹非凡。
B.这个案件牵涉的人非常多,他们也把我的名字报到联邦调查局去考察了,可是直到今天为止,还没有接到回音。
C.东谷湖路一公交站,一辆烧得只剩骨架的电动车倒在路边。
目击者称,车主为一男子,车辆不知为何自燃,随后男子径直离开。
D.保定“油条哥”刘洪安大学毕业后开起了早点摊,他坚持用一级黄豆油炸油条,被誉为“一级油条哥”,人们信任他的油条,一锤子买卖使他的生意越做越红火。
南京市2014届高三年级第二次模拟考试数学(详解稿)

南京市2014届高三年级第二次模拟考试数 学2014.03注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.2.答题前,请务必将自己的姓名、学校、班级、学号写在答题纸的密封线内.试题的答案写在答题纸上对应题目的答案空格内.考试结束后,交回答题纸.参考公式:柱体的体积公式:V =Sh ,其中S 为柱体的底面积,h 为柱体的高.圆柱的侧面积公式:S 侧=2πRh ,其中R 为圆柱的底面半径,h 为圆柱的高.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上)1.函数f (x )=ln x +的定义域为 ▲ .1-x 2.已知复数z 1=-2+i ,z 2=a +2i(i 为虚数单位,a R ).若z 1z 2为实数,则a 的值为 ▲ . ∈3.某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有 ▲ .4.盒中有3张分别标有1,2,3的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为 ▲ .5.已知等差数列{a n }的公差d 不为0,且a 1,a 3,a 7成等比数列,则a 1d 6.执行如图所示的流程图,则输出的k 的值为 ▲ .a(第3题图)(第6题图)7.函数f (x )=A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0,0<φ<π)的图象如下图所示,则f ()的值为π3▲ .8.在平面直角坐标系xOy 中,双曲线-=1(a >0,b >0)的两条渐近线与抛物线y 2=4x 的准线相交x 2a 2y 2b 2于A ,B 两点.若△AOB 的面积为2,则双曲线的离心率为 ▲ .9.表面积为12π的圆柱,当其体积最大时,该圆柱的底面半径与高的比为 ▲ .10.已知||=1,||=2,∠AOB =,=+,则与的夹角大小为 ▲ .OA → O B → 2π3OC → 12OA → 14O B → OA →OC→ 11.在平面直角坐标系xOy 中,过点P (5,3)作直线l 与圆x 2+y 2=4相交于A ,B 两点,若OA ⊥OB ,则直线l 的斜率为 ▲ .12.已知f (x )是定义在R 上的奇函数,当0≤x ≤1时,f (x )=x 2,当x >1时,f (x +1)=f (x )+f (1),且.若直线y =kx 与函数y =f (x )的图象恰有5个不同的公共点,则实数k 的值为 ▲ .13.在△ABC 中,点D 在边BC 上,且DC =2BD ,AB ∶AD ∶AC =3∶k ∶1,则实数k 的取值范围为▲ .14.设函数f (x )=ax +sin x +cos x .若函数f (x )的图象上存在不同的两点A ,B ,使得曲线y =f (x )在点A ,B处的切线互相垂直,则实数a 的取值范围为 ▲ .一、填空题:本大题共14小题,每小题5分,计70分.1.(0,1]2.4 3.3004.5.26.4 7.1598. 9.10.60°11.1或12.2-2 13.(,) 14.[-1,1]51272325373(第7题图)二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)15.(本小题满分14分)如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,平面PAB ⊥平面ABCD ,PA ⊥PB ,BP =BC ,E 为PC 的中点.(1)求证:AP ∥平面BDE ;(2)求证:BE ⊥平面PAC .15.证:(1)设AC ∩BD =O ,连结OE .因为ABCD 为矩形,所以O 是AC 的中点.因为E 是PC 中点,所以OE ∥AP .…………………………………………4分因为AP平面BDE ,OE 平面BDE ,⊂所以AP ∥平面BDE .…………………………………………6分(2)因为平面PAB ⊥平面ABCD ,BC ⊥AB ,平面PAB ∩平面ABCD =AB ,所以BC ⊥平面PAB .………………………………………8分因为AP 平面PAB ,所以BC ⊥PA .⊂因为PB ⊥PA ,BC ∩PB =B ,BC ,PB 平面PBC ,⊂所以PA ⊥平面PBC .…………………………………………12分因为BE 平面PBC ,所以PA ⊥BE .⊂因为BP =PC ,且E 为PC 中点,所以BE ⊥PC .因为PA ∩PC =P ,PA ,PC 平面PAC ,⊂所以BE ⊥平面PAC .…………………………………………14分PBCDE A(第15题图)16.(本小题满分14分)在平面直角坐标系xOy 中,角α的顶点是坐标原点,始边为x 轴的正半轴,终边与单位圆O 交于点A (x 1 ,y 1 ),α∈(,).将角α终边绕原点按逆时针方向旋转,交单位圆于点B (x 2,y 2).π4π2π4(1)若x 1=,求x 2;35(2)过A ,B 作x 轴的垂线,垂足分别为C ,D ,记△AOC 及 △BOD 的面积分别为S 1,S 2,且S 1=S 2,求tan α的值.4316.解:(1)解法一:因为x 1=,y 1>0,所以y 1==.3545 所以sin α=,cos α=. ………………………2分4535所以x 2=cos(α+)=cos αcos -sin αsin =-. …………………………………6分π4π4π4 解法二:因为x 1=,y 1>0,所以y 1==.A (,),则=(,),…………2分35453545OA→ 3545 =(x 2,y 2), 因为·=||||cos ∠AOB ,所以x 2+y 2= ……4分O B → O A → O B → O A → O B→3545 又x 22+y 22=1,联立消去y 2得50 x 22-30x 2-7=02解得x 2=-或,又x 2<0,所以x 2=-.………………………6分解法三:因为x 1=,y 1>0,所以y 1==. 因此A (,),所以tan α=.………2分3545354543 所以tan(α+)==-7,所以直线OB 的方程为y =-7x ……………4分π41+tan α1-tan α由得x =±,又x 2<0,所以x 2=-. …………………6分{y =-7x ,x 2+y 2=1.)(2)S 1=sin αcos α=-sin2α.…………………………………………8分1214因为α(,),所以α+(,). ∈π4π2π4 ∈π23π4 所以S 2=-sin(α+)cos(α+)=-sin(2α+)=-cos2α.……………………………10分12π4π414π214 因为S 1=S 2,所以sin2α=-cos2α,即tan2α=-. …………………………………12分434343 所以=-,解得tan α=2或tan α=-. 因为α(,),所以tan α=2.………14分2tan α1-tan2α4312 ∈π4π2(第16题图)17.(本小题满分14分)如图,经过村庄A 有两条夹角为60°的公路AB ,AC ,根据规划拟在两条公路之间的区域内建一工厂P ,分别在两条公路边上建两个仓库M 、N (异于村庄A ),要求PM =PN =MN =2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).解法一:设∠AMN =θ,在△AMN 中,=.MNsin60°AMsin(120°-θ)因为MN =2,所以AM =sin(120°-θ) .………………………………………2分433在△APM 中,cos ∠AMP =cos(60°+θ).…………………………………………6分AP 2=AM 2+MP 2-2 AM ·MP ·cos ∠AMP=sin 2(120°-θ)+4-2×2× sin(120°-θ) cos(60°+θ)………………………………8分163433=sin 2(θ+60°)- sin(θ+60°) cos(θ+60°)+41631633=[1-cos (2θ+120°)]- sin(2θ+120°)+483833=-[sin(2θ+120°)+cos (2θ+120°)]+833203=-sin(2θ+150°),θ∈(0,120°). (12)203163分当且仅当2θ+150°=270°,即θ=60°时,AP 2取得最大值12,即AP 取得最大值2.3答:设计∠AMN 为60 时,工厂产生的噪声对居民的影响最小. (14)分解法二(构造直角三角形):设∠PMD =θ,在△PMD 中,∵PM =2,∴PD =2sin θ,MD =2cos θ.……………2分在△AMN 中,∠ANM =∠PMD =θ,∴=,MNsin60°AMsin θAM =sin θ,∴AD =sin θ+2cos θ,(θ≥时,结论也正确).……………6分433433π2APMNBC第17题图D AP MNBC (第17题图)AP 2=AD 2+PD 2=(sin θ+2cos θ)2+(2sin θ)23=sin 2θ+sin θcos θ+4cos 2θ+4sin 2θ…………………………8分163833=·+sin2θ+4=sin2θ-cos2θ+1631-cos2θ243343383203=+sin(2θ-),θ∈(0,).…………………………12分203163π62π3当且仅当2θ-=,即θ=时,AP 2取得最大值12,即AP 取得最大值2.π6π2π3 3 此时AM =AN =2,∠PAB =30° …………………………14分解法三:设AM =x ,AN =y ,∠AMN =α.在△AMN 中,因为MN =2,∠MAN =60°,所以MN 2=AM 2+AN 2-2 AM ·AN ·cos ∠MAN ,即x 2+y 2-2xy cos60°=x 2+y 2-xy =4.…………………………………………2分因为=,即=,MN sin60°AN sin α2sin60°ysin α所以sin α=y ,cosα===. 34x 2+4-y 22×2×x x 2+(x 2-xy )4x 2x -y 4…………………………………………6分cos ∠AMP =cos(α+60°)=cos α-sin α=·-·y =.……………………………8分1232122x -y 43234x -2y4在△AMP 中,AP 2=AM 2+PM 2-2 AM ·PM ·cos ∠AMP ,即AP 2=x 2+4-2×2×x ×=x 2+4-x (x -2y )=4+2xy . (12)x -2y4分因为x 2+y 2-xy =4,4+xy =x 2+y 2≥2xy ,即xy ≤4.所以AP 2≤12,即AP ≤2.3当且仅当x =y =2时,AP 取得最大值2.3答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.………………………………14分解法四(坐标法):以AB 所在的直线为x 轴,A 为坐标原点,建立直角坐标系.设M (x 1,0),N (x 2,x 2),P (x 0,y 0).∵MN =2,3∴(x 1-x 2)2+3x =4. …………………………………………2分22MN 的中点K (,x 2).x 1+x 2232∵△MNP 为正三角形,且MN =2.∴PK =,PK ⊥MN .3∴PK 2=(x 0-)2+(y 0-x 2)2=3,x 1+x 2232k MN ·k PK =-1,即·=-1,…………………………………………6分x 2-x 1 ∴y 0-x 2=(x 0-),∴(y 0-x 2)2=(x 0-)232x 1-x 23x 2x 1+x 2232x 1+x 22∴(1+)(x 0-)2=3,即(x 0-)2=3,∴(x 0-)2=x .x 1+x 22x 1+x 22x 1+x 229422∵x 0->0 ∴x 0-=x 2,x 1+x 22x 1+x 2232∴x 0=x 1+2x 2,∴y 0=x 1.…………………………………………8分1232∴AP 2=x +y =(2x 2+x 1)2+x =x +4x +2x 1x 22201234212122=4+4x 1x 2≤4+4×2=12, …………………………………………12分即AP ≤2.3 答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.…………………………14分解法五(变换法):以AB 所在的直线为x 轴,A 为坐标原点,建立直角坐标系.设M (x 1,0),N (x 2,x 2),P (x 0,y 0).3∵MN =2,∴(x 1-x 2)2+3x =4.即x +4x =4+2x 1x 2222122∴4+2x 1x 2≥4x 1x 2,即x 1x 2≤2.…………………4分∵△MNP 为正三角形,且MN =2.∴PK =,PK ⊥MN . 3顺时针方向旋转60°后得到.MN → MP →=(x 0-x 1,y 0),=(x 2-x 1,x 2).MP → MN→ 3 ∴=,即[x 0-x 1y 0]x 0-x 1=(x 2-x 1)+x 2,y 0=-(x 2-x 1)+x 2.12323232∴x 0=2x 2+x 1,y 0=x 1. …………………………………………8分1232∴AP 2=x +y =(2x 2+x 1)2+x =x +4x +2x 1x 2 2 02 012342 12 12 2=4+4x 1x 2≤4+4×2=12, …………………………………………12分即AP ≤2.3答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.…………………………14分解法六(几何法):由运动的相对性,可使△PMN 不动,点A 在运动.由于∠MAN =60°,∴点A 在以MN 为弦的一段圆弧(优弧)上,…………4分设圆弧所在的圆的圆心为F ,半径为R ,由图形的几何性质知:AP 的最大值为PF +R .…………8分PNCE在△AMN 中,由正弦定理知:=2R ,MNsin60°∴R =,…………10分23∴FM =FN =R =,又PM =PN ,∴PF 是线段MN 的垂直平分线.23设PF 与MN 交于E ,则FE 2=FM 2-ME 2=R 2-12=.13即FE =,又PE =. (12)33 3∴PF =,∴AP 的最大值为PF +R =2.43 3答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.…………………………14分18. (本小题满分16分)在平面直角坐标系xOy 中,已知椭圆C ∶+=1(a >b >0)的左、右焦点分别为F 1,F 2,焦距为x 2a 2y 2b 22,一条准线方程为x =2.P 为椭圆C 上一点,直线PF 1交椭圆C 于另一点Q .(1)求椭圆C 的方程;(2)若点P 的坐标为(0,b ),求过P ,Q ,F 2三点的圆的方程;(3)若=λ,且λ∈[,2],求·的最大值.F 1P → QF 1→ 12OP → OQ→(1)解:由题意得 解得c =1,a 2=2,所以b 2=a 2-c 2=1.所以椭圆的方程为+y 2=1.…………………………………………2分x 22 (2)因为P (0,1),F 1(-1,0),所以PF 1的方程为x -y +1=0.由 解得或所以点Q 的坐标为(-,-). ……………………4分{x =0,y =1,)4313解法一:因为k PF ·k PF =-1,所以△PQF 2为直角三角形. ……………………6分12因为QF 2的中点为(-,-),QF 2=,1616所以圆的方程为(x +)2+(y +)2=. ……………………8分16162518解法二:设过P ,Q ,F 2三点的圆为x 2+y 2+Dx +Ey +F =0,则 解得所以圆的方程为x 2+y 2+x +y -=0. (8)131343分(3)解法一:设P (x 1,y 1),Q (x 2,y 2),则=(x 1+1,y 1),=(-1-x 2,-y 2).F 1P→ QF 1→因为=λ,所以即F 1P→ QF 1→ {x 1+1=λ(-1-x 2),y 1=-λy 2,){x 1=-1-λ-λx 2,y 1=-λy 2,)所以解得x 2=.…………………………………………12分1-3λ2λ所以·=x 1x 2+y 1y 2=x 2(-1-λ-λx 2)-λy =-x 22-(1+λ)x 2-λOP → OQ →22λ2=-()2-(1+λ)·-λ=-(λ+) . …………………………………………14分λ21-3λ2λ1-3λ2λ74581λ因为λ∈[,2],所以λ+≥2=2,当且仅当λ=,即λ=1时,取等号.121λ 1λ所以·≤,即·最大值为. …………………………………………16分OP → OQ→ 12OP → OQ→12解法二:当PQ 斜率不存在时,在+y 2=1中,令x =-1得y =±.x 22所以,此时…………………………211(1)(2OP OQ ⋅=-⨯-= 11,22λ⎡⎤=∈⎢⎥⎣⎦当PQ 斜率存在时,设为k ,则PQ 的方程是y =k (x +1),由得(1+2k 2)x 2+4k 2x +2k 2-2=0,韦达定理 (422121222)422==1212k k x x x x k k--+++,设P (x 1,y 1),Q (x 2,y 2) ,则212121212(1)(1)OP OQ x x y y x x k x x ⋅=+=+++ 22212122222222222(1)()224(1)12122 61215122(12)2k x x k x x k k k k k k k k k k k =++++--=+++++-=⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯+=-<+分。
浙江省宁波市2015届高三一轮复习阶段性考试(月考)数学理试题 Word版含答案

浙江省宁波市2015届高三一轮复习阶段性考试数学理试题本试题卷分选择题和非选择题两部分.全卷共4页, 选择题部分1至2页, 非选择题部分3至4页.满分150分, 考试时间120分钟.请考生按规定用笔将所有试题的答案涂、写在答题纸上.第Ⅰ卷(选择题部分 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合M ={x |1122x -<<},N ={x | x 2 ≤ x },则M ∩N = (A )1[1,)2- (B )1(,1]2-(C )1[0,)2 (D )1(,0]2-2.设a >1>b >0,则下列不等式中正确的是 (A )(-a )7<(-a )9 (B )b - 9<b - 7(C )11lg lg a b > (D )11ln ln a b>3.已知R α∈,cos 3sin αα+,则tan 2α=(A )43 (B )34 (C )34- (D )43-4.若某程序框图如图所示,则输出的n 的值是(A )3 (B )4 (C )5 (D )6(第4题图)5.设,m n 是两条不同的直线,,αβ是两个不同的平面,则下列命题中正确..的是 (A )若//,m n αβ⊥且αβ⊥,则m n ⊥ (B )若,m n αβ⊥⊥且m n ⊥,则αβ⊥ (C )若/,/n m αβ⊥且n β⊥,则//m α (D )若,m n αβ⊂⊂且//m n ,则//αβ6.已知某锥体的三视图(单位:cm )如图所示,则该锥体的体积为 (A )23cm (B )43cm (C )63cm (D )83cm 7.251(1)(2)x x--的展开式的常数项是(A )48 (B )﹣48 (C )112 (D )﹣1128.袋子里有3颗白球,4颗黑球,5颗红球.由甲、乙、丙三人依次各抽取一个球,抽取后不放回.若每颗球被抽到的机会均等,则甲、乙、丙三人所得之球颜色互异的概率是 (A )14 (B )13 (C )27 (D )3119.已知实系数二次函数()f x 和()g x 的图像均是开口向上的抛物线,且()f x 和()g x 均有两个不同的零点.则“()f x 和()g x 恰有一个共同的零点”是“()()f x g x +有两个不同的零点”的(A )充分不必要条件 (B )必要不充分条件 (C )充分必要条件(D )既不充分也不必要条件10.设F 1、F 2是椭圆Γ的两个焦点,S 是以F 1为中心的正方形,则S 的四个顶点中能落在椭圆Γ上的个数最多有(S 的各边可以不与Γ的对称轴平行)(A )1个 (B )2个 (C )3个 (D )4个(第6题图)正视图侧视图俯视图第Ⅱ卷(非选择题部分 共100分)二、填空题:本大题共7小题, 每小题4分, 共28分. 11.已知复数z 满足22z z +-= i (其中i 是虚数单位),则z = ▲ . 12.设25z x y =+,其中实数,x y 满足68x y ≤+≤且20x y -≤-≤,则z 的取值范围是▲ .13.已知抛物线23x y =上两点,A B 的横坐标恰是方程2510x x ++=的两个实根,则直线AB 的方程是 ▲ .14.口袋中装有大小质地都相同、编号为1,2,3,4,5,6的球各一只.现从中一次性随机地取出两个球,设取出的两球中较小的编号为X ,则随机变量X 的数学期望是 ▲ .15.已知直线10x y --=及直线50x y --=截圆C 所得的弦长均为10,则圆C 的面积是 ▲ .16.在△ABC 中,∠C=90︒,点M 满足3BM MC =,则sin ∠BAM 的最大值是 ▲ . 17.已知点O 是△ABC 的外接圆圆心,且AB=3,AC=4.若存在非零实数....x 、y ,使得AO x AB y AC =+,且21x y +=,则cos ∠BAC = ▲ .三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. 18.(本题满分14分) 在ABC ∆中,内角,,A B C 的对边分别为,,a b c ,且sin 5B c =,11cos 14B =.(I )求角A 的大小;(II )设BC 边的中点为D ,AD =ABC ∆的面积. 19.(本小题满分14分)设等差数列{}n a 的前n 项和为n S ,且248,40a S ==错误!未找到引用源。
山东省济宁市2014届高三第二次模拟考试数学(理)试题Word版含答案

2014年山东省济宁市高考数学二模试卷(理科)
一、选择题(共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数z为纯虚数,若(2﹣i)z=a+i(i为虚数单位),则实数a的值为()A.﹣B.2C.﹣2 D.
2.已知集合A={x∈R||x﹣1|≤2},B={x∈R|x 2
≤4},则A∩B=()
A.(﹣1,2)B.[﹣1,2] C.(0,2] D.[﹣2,3]
3.已知具有线性相关的两个变量x、y之间的一组数据如下表:
且回归方程=x+3.6,则当x=6时,y的预测值为()
A.8.46 B. 6.8 C. 6.3 D. 5.76
4.设变量x、y满足约束条件:,则目标函数z=5x+3y的最大值为()A.18 B 、17 C. 27 D.
5.已知函数f(x)=cos(2x+φ)的图象沿x轴向左平移个单位后,得到函数g(x)的图象,则“φ=﹣”是“g(x)为偶函数”的()
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分又不必要条件
6.若某空间几何体的三视图如图所示,则该几何体的体积是()
A. 16 B. 32C. 48 D. 144
7.函数f(x)=1﹣x+lgx的图象大致是()。
2021届浙江省宁波市高三下学期第二次模拟考试理科数学试卷
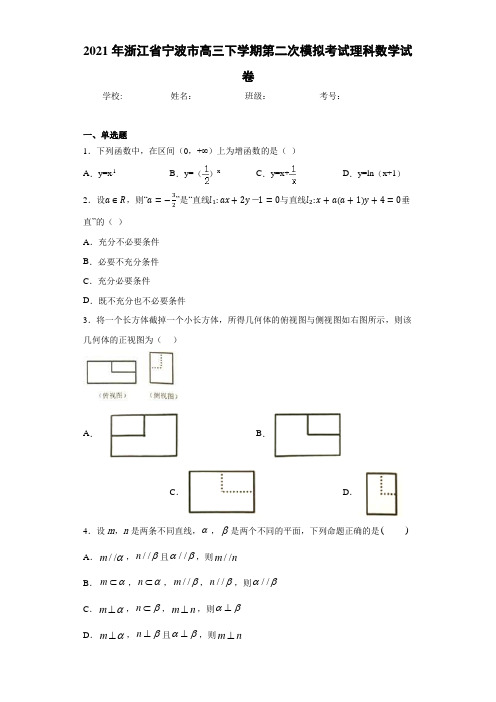
(Ⅰ)求证:数列 为等比数列,并求出公比 ;
(Ⅱ)若 对任意正整数 成立,求证:当 取到最小整数时,对于 都有 .
20.设函数 .
(Ⅰ)当 时,讨论函数 的零点个数;
(Ⅱ)若对于给定的实数 ,存在实数 ,使不等式 对于任意 恒成立.试将最大实数 表示为关于 的函数 ,并求 的取值范围.
因为图像关于直线 对称
所以
代入 化简得 ,k∈Z
所以当k=0时, 取得最小值为
所以选D
【点睛】
本题考查了三角函数图像的平移变换,三角函数对称轴的应用,属于中档题.
7.C
【解析】
试题分析:作出半圆 的图形,如下图,
设点 ,由于点C在线段OA的延长线上,所以 与 的方向相同,故 ,且 ,当点 在点 时, ,解得 .当点 在点 时, ,解得 .综上可得,则点C的纵坐标的取值范围是 ,故点C的轨迹是一条线段,其两个端点的坐标分别为 .
也可能α⊥β,故C不正确;
对于D,由m⊥α,n⊥β且α⊥β,则m与n一定不平行,否则有α∥β,与已知α⊥β矛盾,
通过平移使得m与n相交,且设m与n确定的平面为γ,则γ与α和β的交线所成的角即
为α与β所成的角,因为α⊥β,所以m与n所成的角为90°,故命题D正确.
故答案为D
【点睛】
本题考查直线与平面平行与垂直,面面垂直的性质和判断的应用,考查逻辑推理能力和空间
7.在平面直角坐标系xOy中,已知点A是半圆 上的一个动点,点C在线段OA的延长线上,当 =20时,点C的轨迹为()
A.椭圆一部分B.抛物线一段C.线段D.圆弧
8.已知点(x,y)的坐标满足条件 ,且x,y均为正整数.若4x-y取到最大值8,则整数a的最大值为()
浙江省宁波市九校(余姚中学2024学年高三数学试题学生分层训练题
浙江省宁波市九校(余姚中学2024学年高三数学试题学生分层训练题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={y |y 21x =-},B ={x |y =lg (x ﹣2x 2)},则∁R (A ∩B )=( ) A .[0,12) B .(﹣∞,0)∪[12,+∞) C .(0,12) D .(﹣∞,0]∪[12,+∞) 2.一个几何体的三视图如图所示,则该几何体的表面积为( )A .48122+B .60122+C .72122+D .843.已知数列{}n a 的前n 项和为n S ,且()()()212*111N ()n n n S S S n ++++=+∈,121,2a a ==,则n S =( ) A .()12n n + B .12n + C .21n - D .121n ++4.设n S 为等差数列{}n a 的前n 项和,若33a =-,77S =-,则n S 的最小值为( )A .12-B .15-C .16-D .18-5.已知平面向量,,a b c ,满足||2,||1,b a b c a b λμ=+==+且21λμ+=,若对每一个确定的向量a ,记||c 的最小值为m ,则当a 变化时,m 的最大值为( )A .14B .13C .12D .16.函数()2sin()f x x ωϕ=+(0,0)ωϕπ><<的部分图像如图所示,若5AB =,点A 的坐标为(1,2)-,若将函数()f x 向右平移(0)m m >个单位后函数图像关于y 轴对称,则m 的最小值为( )A .12B .1C .3πD .2π 7.抛物线的焦点是双曲线的右焦点,点是曲线的交点,点在抛物线的准线上,是以点为直角顶点的等腰直角三角形,则双曲线的离心率为( ) A . B . C .D . 8.等腰直角三角形ABE 的斜边AB 为正四面体ABCD 侧棱,直角边AE 绕斜边AB 旋转,则在旋转的过程中,有下列说法:(1)四面体E -BCD 的体积有最大值和最小值;(2)存在某个位置,使得AE BD ⊥;(3)设二面角D AB E --的平面角为θ,则DAE θ≥∠;(4)AE 的中点M 与AB 的中点N 连线交平面BCD 于点P ,则点P 的轨迹为椭圆.其中,正确说法的个数是( )A .1B .2C .3D .49.在直角ABC ∆中,2C π∠=,4AB =,2AC =,若32AD AB =,则CD CB ⋅=( ) A .18- B .63-C .18 D .6310.设集合{}2560A x x x =--<,{}20B x x =-<,则AB =( ) A .{}32x x -<<B .{}22x x -<<C .{}62x x -<<D .{}12x x -<<11.下列说法正确的是( )A .“若1a >,则1a >”的否命题是“若1a >,则21a <”B .在ABC 中,“A B >”是“sin sin A B >”成立的必要不充分条件C .“若tan 1α≠,则4πα≠”是真命题D .存在0(,0)x ∈-∞,使得0023x x <成立12.过点6(26)2P ,的直线l 与曲线213y x =-交于A B ,两点,若25PA AB =,则直线l 的斜率为( ) A .23-B .23+C .23+或23-D .23-或31-二、填空题:本题共4小题,每小题5分,共20分。
人教A版数学高二弧度制精选试卷练习(含答案)2
人教A 版数学高二弧度制精选试卷练习(含答案)学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知扇形的周长是5cm ,面积是322cm ,则扇形的中心角的弧度数是( ) A .3B .43C .433或 D .2【来源】江西省九江第一中学2016-2017学年高一下学期期中考试数学(文)试题 【答案】C2.已知扇形的周长为8cm ,圆心角为2,则扇形的面积为( ) A .1B .2C .4D .5【来源】四川省双流中学2017-2018学年高一1月月考数学试题 【答案】C3.《掷铁饼者》 取材于希腊的现实生活中的体育竞技活动,刻画的是一名强健的男子在掷铁饼过程中最具有表现力的瞬间.现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”,掷铁饼者的手臂长约为4π米,肩宽约为8π米,“弓”所在圆的半径约为1.25米,你估测一下掷铁饼者双手之间的距离约为( )1.732≈≈)A .1.012米B .1.768米C .2.043米D .2.945米【来源】安徽省五校(怀远一中、蒙城一中、淮南一中、颍上一中、淮南一中、涡阳一中)2019-2020学年高三联考数学(理)试题 【答案】B4.已知扇形的周长为4,圆心角所对的弧长为2,则这个扇形的面积是( ) A .2B .1C .sin 2D .sin1【来源】福建省泉州市南安侨光中学2019-2020学年高一上学期第二次阶段考试数学试题 【答案】B5.已知α是第三象限角,且cos cos22αα=-,则2α是( ) A .第一象限角B .第二象限角C .第三象限角D .第四象限角【来源】2012人教A 版高中数学必修四1.2任意角的三角函数练习题 【答案】B6.如图,2弧度的圆心角所对的弦长为2,这个圆心角所对应的扇形面积是( )A .1sin1B .21sin 1C .21cos 1D .tan1【来源】广西河池市高级中学2017-2018学年高一下学期第二次月考数学试题 【答案】B7.半径为10cm ,面积为2100cm 的扇形中,弧所对的圆心角为( ) A .2 radB .2︒C .2π radD .10 rad【来源】第一章滚动习题(一) 【答案】A8.若一扇形的圆心角为72︒,半径为20cm ,则扇形的面积为( ). A .240πcmB .280πcmC .240cmD .280cm【来源】陕西省西安市长安区第一中学2016-2017学年高一下学期第一次月考数学试题 【答案】D9.如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为1S ,正八边形外侧八个扇形(阴影部分)面积之和为2S ,则12S S =( )A .34B .35C .23D .1【来源】广西省南宁市马山县金伦中学、武鸣县华侨中学等四校2017-2018学年高一10月月考数学试题. 【答案】B10.在-360°到0°内与角1250°终边相同的角是( ) . A .170° B .190° C .-190°D .-170°【来源】2012人教A 版高中数学必修四1.1任意角和弧度制练习题(一)(带解析) 【答案】C11.下列各角中,终边相同的角是 ( ) A .23π和240o B .5π-和314oC .79π-和299π D .3和3o【来源】新疆伊西哈拉镇中学2018-2019学年高一上学期第二次月考数学试题 【答案】C12.已知2弧度的圆心角所对的弧长为2,则这个圆心角所对的弦长是( ) A .sin 2B .2sin 2C .sin1D .2sin1【来源】广东省东莞市2018-2019学年高一第二学期期末教学质量检查数学试题 【答案】D13,弧长是半径的3π倍,则扇形的面积等于( ) A .223cm πB .26cm πC .243cm πD .23cm π【来源】河北省隆华存瑞中学(存瑞部)2018-2019学年高一上学期第二次数学试题 【答案】D14.如图所示,用两种方案将一块顶角为120︒,腰长为2的等腰三角形钢板OAB 裁剪成扇形,设方案一、二扇形的面积分别为12S , S ,周长分别为12,l l ,则( )A .12S S =,12l l >B .12S S =,12l l <C .12S S >,12l l =D .12S S <,12l l =【来源】浙江省省丽水市2018-2019学年高一下学期期末数学试题 【答案】A15.已知sin sin αβ>,那么下列命题成立的是( ) A .若,αβ是第一象限角,则cos cos αβ> B .若,αβ是第二象限角,则tan tan αβ> C .若,αβ是第三象限角,则cos cos αβ> D .若,αβ是第四象限角,则tan tan αβ>【来源】正定中学2010高三下学期第一次考试(数学文) 【答案】D16.半径为1cm ,中心角为150°的角所对的弧长为( )cm . A .23B .23π C .56D .56π 【来源】宁夏石嘴山市第三中学2018-2019学年高一5月月考数学试题 【答案】D 17.设5sin 7a π=,2cos 7b π=,2tan 7c π=,则( ) A .a b c <<B .a c b <<C .b c a <<D .b a c <<【来源】2008年高考天津卷文科数学试题 【答案】D18.扇形的中心角为120o )A .πB .45πC D 2【来源】辽宁省大连市第八中学2016-2017学年高一下学期期中考试数学试题【答案】A19.若扇形的周长为8,圆心角为2rad ,则该扇形的面积为( ) A .2B .4C .8D .16【来源】河南省洛阳市2018-2019学年高一下学期期中考试数学试卷 【答案】B20.-300° 化为弧度是( ) A .-43πB .-53πC .-54πD .-76π【来源】2014-2015学年山东省宁阳四中高一下学期期中学分认定考试数学试卷(带解析) 【答案】B21.一个扇形的面积为3π,弧长为2π,则这个扇形的圆心角为( ) A .3π B .4π C .6π D .23π 【来源】湖北省荆门市2017-2018学年高一(上)期末数学试题 【答案】D22.《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=12(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为23π,弦长为的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中3π≈,1.73≈)A .15B .16C .17D .18【来源】湖北省2018届高三5月冲刺数学(理)试题 【答案】B23.下列各式不正确的是( ) A .-210°=76π-B .405°=49πC .335°=2312πD .705°=4712π【来源】河南信阳市息县第一高级中学、第二高级中学、息县高中2018-2019学年高一下学期期中联考数学(文)试题 【答案】C24.下列函数中,最小正周期为π2的是( )A .y =sin (2x −π3)B .y =tan (2x −π3)C .y =cos (2x +π6) D .y =tan (4x +π6)【来源】20102011年山西省汾阳中学高一3月月考数学试卷 【答案】B25.已知扇形的周长为12cm ,圆心角为4rad ,则此扇形的弧长为 ( ) A .4cmB .6cmC .8cmD .10cm【来源】江西省玉山县一中2018-2019学年高一(重点班)下学期第一次月考数学(理)试卷 【答案】C二、填空题26.已知扇形的圆心角18πα=,扇形的面积为π,则该扇形的弧长的值是______.【来源】上海市黄浦区2018-2019学年高一下学期期末数学试题 【答案】3π 27.若一个圆锥的侧面展开图是面积为2π的半圆面,则该圆锥的底面半径为_______ . 【来源】上海市浦东新区川沙中学2018-2019学年高二下学期期末数学试题 【答案】128.一个扇形的弧长与面积的数值都是5,则这个扇形中心角的弧度数为__________. 【来源】河南省灵宝市实验高中2017-2018学年高一下学期第一次月考考数学试题 【答案】5229.已知圆锥的侧面展开图是一个扇形,若此扇形的圆心角为65π、面积为15π,则该圆锥的体积为________.【来源】上海市杨浦区2019-2020学年高三上学期期中质量调研数学试题 【答案】12π30.圆O 的半径为1,P 为圆周上一点,现将如图放置的边长为1的正方形(实线所示 ,正方形的顶点A 和点P 重合)沿着圆周顺时针滚动,经过若干次滚动,点A 第一次回到点P 的位置,则点A 走过的路径的长度为 .【来源】2015届山东省日照市高三3月模拟考试理科数学试卷(带解析)31.已知扇形的圆心角为1弧度,扇形半径为2,则此扇形的面积为______. 【来源】上海市复兴高级中学2018-2019学年高一下学期3月份质量检测数学试题 【答案】232.一个球夹在120°的二面角内,且与二面角的两个面都相切,两切点在球面上的最短距离为π,则这个球的半径为_______ .【来源】上海市七宝中学2017-2018学年高二下学期期中数学试题 【答案】333.用半径为,面积为cm 2的扇形铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计), 则该容器盛满水时的体积是 .【来源】2012届江苏省泗阳中学高三上学期第一次调研考试数学试卷(实验班) 【答案】31000cm 3π34.《九章算术》是体现我国古代数学成就的杰出著作,其中(方田)章给出的计算弧田面积的经验公式为:弧田面积12=(弦⨯矢+矢2),弧田(如图阴影部分)由圆弧及其所对的弦围成,公式中“弦”指圆弧所对弦的长,“矢”等于半径长与圆心到弦的距离之差,现有弧长为43π米,半径等于2米的弧田,则弧所对的弦AB 的长是_____米,按照上述经验公式计算得到的弧田面积是___________平方米.【来源】山东省济南市2018-2019学年高一下学期期末学习质量评估数学试题【答案】1235.设扇形的半径长为2cm ,面积为24cm ,则扇形的圆心角的弧度数是 【来源】2013-2014学年山东济南商河弘德中学高一下学期第二次月考数学试卷(带解析) 【答案】236.已知一个圆锥的展开图如图所示,其中扇形的圆心角为120o ,弧长为2π,底面圆的半径为1,则该圆锥的体积为__________.【来源】2018年春高考数学(文)二轮专题复习训练:专题三 立体几何【答案】337.现用一半径为10cm ,面积为280cm π的扇形铁皮制作一个无盖的圆锥形容器(假定衔接部分及铁皮厚度忽略不计,且无损耗),则该容器的容积为__________3cm . 【来源】江苏省苏州市2018届高三调研测试(三)数学试题 【答案】128π38.已知扇形的周长为6,圆心角为1,则扇形的半径为___;扇形的面积为____. 【来源】浙江省宁波市镇海区镇海中学2018-2019学年高一上学期期中数学试题 【答案】2 2 39.给出下列命题:①第二象限角大于第一象限角;②三角形的内角是第一象限角或第二象限角;③不论用角度制还是用弧度制度量一个角,它们与扇形所在半径的大小无关; ④若sin sin αβ=,则α与β的终边相同;⑤若cos 0θ<,则θ是第二或第三象限的角. 其中正确的命题是______.(填序号)【来源】江苏省南通市启东中学2018-2019学年高二5月月考数学(文)试题 【答案】③40.设扇形的周长为4cm ,面积为21cm ,则扇形的圆心角的弧度数是________. 【来源】广东省中山市第一中学2016-2017学年高一下学期第一次段考(3月)数学(理)试题 【答案】2三、解答题41.已知扇形AOB 的周长为8.(1)若这个扇形的面积为3,求其圆心角的大小.(2)求该扇形的面积取得最大时,圆心角的大小和弦长AB .【来源】2015-2016学年四川省雅安市天全中学高一11月月考数学试卷(带解析) 【答案】(1)或;(2);.42.已知一扇形的中心角是120︒,所在圆的半径是10cm ,求: (1)扇形的弧长; (2)该弧所在的弓形的面积【来源】福建省福州市平潭县新世纪学校2019-2020学年高一上学期第二次月考数学试题【答案】(1)203π;(2)1003π-43.某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O 为圆心的两个同心圆弧和延长后通过点AD 的两条线段围成.设圆弧AB 、CD 所在圆的半径分别为()f x 、R 米,圆心角为θ(弧度).(1)若3πθ=,13r =,26=r ,求花坛的面积;(2)设计时需要考虑花坛边缘(实线部分)的装饰问题,已知直线部分的装饰费用为60元/米,弧线部分的装饰费用为90元/米,预算费用总计1200元,问线段AD 的长度为多少时,花坛的面积最大?【来源】江苏省泰州市泰州中学2019~2020学年高一上学期期中数学试题 【答案】(1)292m π(2)当线段AD 的长为5米时,花坛的面积最大44.已知一个扇形的周长为30厘米,求扇形面积S 的最大值,并求此时扇形的半径和圆心角的弧度数.【来源】上海市华东师范大学第二附属中学2018-2019学年高一上学期期末数学试题 【答案】()2rad α= 152r =45.如图所示为圆柱形大型储油罐固定在U 型槽上的横截面图,已知图中ABCD 为等腰梯形(AB ∥DC ),支点A 与B 相距8m ,罐底最低点到地面CD 距离为1m ,设油罐横截面圆心为O ,半径为5m ,56D ∠=︒,求:U 型槽的横截面(阴影部分)的面积.(参考数据:sin530.8︒≈,tan56 1.5︒≈,3π≈,结果保留整数)【来源】上海市闵行区七宝中学2019-2020学年高一上学期9月月考数学试题 【答案】202m46.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…”某教师根据这首词的思想设计如下图形,已知CE l ⊥,DF l ⊥,CB CD =,AD BC ⊥,5DF =,2BE =,AD =则在扇形BCD 中随机取一点求此点取自阴影部分的概率.【来源】山西省阳泉市2018-2019学年高一第一学期期末考试试题数学试题【答案】1)4(P A π=-47.某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由试卷第11页,总11页 扇形OAD 挖去扇形OBC 后构成的).已知10, (0<<10)OA=OB =x x ,线段BA 、CD与弧BC 、弧AD 的长度之和为30米,圆心角为θ弧度.(1)求θ关于x 的函数解析式;(2)记铭牌的截面面积为y ,试问x 取何值时,y 的值最大?并求出最大值.【来源】上海市黄浦区2018届高三4月模拟(二模)数学试题【答案】(1)210(010)10x x x θ+=<<+;(2)当52x =米时铭牌的面积最大,且最大面积为2254平方米. 48.已知一扇形的圆心角为()0αα>,所在圆的半径为R .(1)若90,10R cm α==o ,求扇形的弧长及该弧所在的弓形的面积;(2)若扇形的周长是一定值()0C C >,当α为多少弧度时,该扇形有最大面积?【来源】2019高考备考一轮复习精品资料 专题十五 任意角和弧度制及任意角的三角函数 教学案【答案】(1)2550π-;(2)见解析49.已知在半径为10的圆O 中,弦AB 的长为10.(1)求弦AB 所对的圆心角α(0<α<π)的大小;(2)求圆心角α所在的扇形弧长l 及弧所在的弓形的面积S .【来源】(人教A 版必修四)1.1.2弧度制(第一课时)同步练习02【答案】(1)π3(2)10π3;50(π3−√32) 50.已知在半径为6的圆O 中,弦AB 的长为6,(1)求弦AB 所对圆心角α的大小;(2)求α所在的扇形的弧长l 以及扇形的面积S.【来源】江西省玉山县一中2018-2019学年高一(重点班)下学期第一次月考数学(文)试卷【答案】(1)3π ;(2)2l π= ,6S π=。
浙江省宁波市北仑中学2021届高三下学期5月适应性考试(最后一模)数学试题 Word版含答案
北仑中学2020学年高三适应性考试 数学试卷本科考试分试题卷和答题卷,考生须在答题卷上作答.本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页.全卷满分150分,考试时间120分钟. 考生注意:1.答题前,考生务必将自己的姓名、准考证号用黑色的字迹的签字笔或钢笔填写在试题卷和答题纸规定的位置上.2.答题时,请按照答题纸上“注意事项”的要求.在答题纸相应的位置上规范作答,在本试卷上的作答一律无效.参考公式:若事件,A B 互斥,则 柱体的体积公式 ()()()P A B P A P B +=+ V Sh =若事件,A B 相互独立,则 其中S 表示柱体的底面积,h 表示柱体的高()()()P AB P A P B = 锥体的体积公式若事件A 在一次试验中发生的概率是p ,则n 次 13V Sh =独立重复试验中事件A 恰好发生k 次的概率 其中S 表示锥体的底面积,h 表示锥体的高()(1)(0,1,2,,)k kn k n n P k C p p k n -=-= 球的表面积公式 台体的体积公式 24S R π=()112213V h S S S S = 球的体积公式其中12,S S 分别表示台体的上、下底面积, 343V R π=h 表示台体的高 其中R 表示球的半径第 Ⅰ 卷 (选择题,共40分)一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知{}{}1,2,3,4,5,6,3A B y y ==<,则R AC B =( ){}.1,2,3,4,5,6A {}.1,2B {}.3,4,5,6C {}.4,5,6D2.双曲线22154x y -=的焦点坐标为( ) A.(1,0)± B.(0,1)± C.(3,0)± D.(0,3)±3.已知,x y 满足条件350401x y x y y +-≥⎧⎪+-≤⎨⎪≥⎩,则y z x =的取值范围为( )A.(0,7]B.1[,7]3C.[3,7]D.[2,7]4.某几何体的三视图(单位:cm )如图所示,则该几何体的表面积(单位:cm 2)是( ) A.43B.323+C.31515235.设2211,,:log (1)log (1)0,:1a b R p a b q a b∈-+->+<,则p 是q 的( ).A 充分不必要条件 .B 必要不充分条件 .C 充要条件 .D 既不充分也不必要条件6.函数2ln ,0()1sin(2),02xx xx e f x x x π⎧>⎪⎪=⎨⎪-≤⎪⎩的部分图象大致为( )7.随机变量X 的分布列如图所示,则当p 在(0,1)内增大时,2()D X 满足( ) A .先增大后减小 B .先减小后增大 C .增大 D .减小8.设n S 是某个等差数列的前n 项和,若201920202020S S ==,则2021S =( )A.220202019-B. 220202019+C. 120201010-D.120201010+ 9.已知F 为抛物线22(0)y px p =>的焦点,P ,Q 为抛物线上的两个动点,线段PQ 的中点为M ,过M 作y 轴的垂线,垂足为H . 若2pPQ MH -≤,则cos QFP ∠的最小值为( )A.0B.12C.22 310.设函数()3sin 2cos 1f x x x =++. 若实数a ,b ,c 使得()()1af x bf x c +-=对任意实数x 恒成立,则cos b c a 的值等于( )A.12-B.12C.1-D.1第 Ⅱ 卷 (非选择题部分,共110分)注意事项:用钢笔或签字笔将试题卷上的题目做在答题卷上,做在试题卷上的无效. 二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分)11.复数z 满足z+3i=2,则z 的虚部是_______.12.若823901239(21)(1)(1)(1)(1)(1)x x a a x a x a x a x ++=+-+-+-+⋅⋅⋅+-,则0a = ;0123456789a a a a a a a a a a -+-+-+-+-= .13.已知直线1:220l x y --=,直线2:220l mx y m +--=,点P 为圆22:4O x y +=上的一个动点,则直线1l 与圆O 相交所得的弦长为 ;当实数m 变化时,点P 到直线2l 的最大距离为 .14.三边长均不相等的△ABC 满足:2222(sin sin )sin (sin sin )sin()A B C A B A B -=+-,则∠C =_______cos 3cos 3Bx A x+>x 恒成立,则∠A 的范围是_______.15.已知,a b 是空间单位向量,0a b ⋅=,若空间向量c 满足:1,2,10c a c b c ⋅=⋅==,则a b c ++=_______,对于任意,x y R ∈,向量c 与向量xa yb +所成角的最小值为_______.16.已知实数,x y 满足(31)(21)1x y x y +-+-=,则x y +的最小值是________.17.已知函数1()212f x x x =--+,若对于任意实数x ,有()()1()f x t f x t R +-≤∈恒成立, 则实数t 的取值范围为________.三、解答题(本大题共5小题,共74 分. 解答应写出文字说明、证明过程或演算步骤) 18. (本小题满分14分)设函数2()2sin sin(2).6f x x x π=--(1)当[0,]2x π∈时,求()f x 的值域;(2)若函数()f x 的图象向右平移6π个单位后得到()g x 的图象,且存在0[,0]2x π∈-,使02()3g x =,求0cos 2x 的值. 19.(本题满分15分)在三棱锥P ABC -中,2,,,AB BC AB BC CP BC ==⊥⊥,AP AB ⊥060CPA ∠=。
冠词中难度题
1.—Do you think an advertisement is ________ help when you look for a college? —Well, it all depends. Anyway, it gives me more of ________ chance.A. a; aB. 不填; aC. 不填; theD. a; the【答案】A【解析】考查冠词。
第一空help表示具体的人,所以前面加不定冠词,a help表示“一个帮手”;第二空表泛指。
2.Johnson had made up his mind to give it up, but on ________ second thought he determined to try ________ third time.A. /; aB. the; /C. a; aD. the; a【答案】A【解析】考查冠词。
第一空on second thought是固定短语,意为“三思,再三考虑”;第二空序数词前用不定冠词表示“再一,又一”。
句意:约翰逊已经下定决心放弃了,但是思虑再三后,他决定再试一次。
3.(2013·福建卷)The "Chinese Dream" is ____ dream to improve people's well-being and ____ dream of harmony, peace and development.A. the; aB. a; aC. a; theD. the; the【答案】B【解析】考查冠词:第一空填a,泛指“一个提高人们幸福的梦想”第二空还是填a,指“和谐,和平,发展的梦想”,句意:“中国梦”是提高人们幸福的梦想,是和谐,和平,发展的梦想。
所以选B。
【考点定位】考查冠词4.(2013·山东卷) It was ______ cold winter night and the moon was shining brightly across ____ night sky.A. 不填;aB. a; theC. the; aD. the; 不填【答案】B【解析】第一空“一个寒冷的冬夜”,应用不定冠词a;第二空“夜空”,指独一无二的事物用定冠词the。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁波市2014年高考模拟考试 数学(理科)试卷
本试题卷分选择题和非选择题两部分.全卷共4页, 选择题部分1至2页, 非选择题部分3至4页.满分150分, 考试时间120分钟. 请考生按规定用笔将所有试题的答案涂、写在答题纸上.
第Ⅰ卷(选择题部分 共50分) 一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合M={x|1122x},N={x | x2 ≤ x},则M∩N =
(A)1[1,)2 (B)1(,1]2 (C)1[0,)2 (D)1(,0]2 2.设a>1>b>0,则下列不等式中正确的是 (A)(-a)7<(-a)9 (B)b- 9<b- 7
(C)11lglgab (D)11lnlnab 3.已知R,cos3sin5,则tan2= (A)43 (B)34 (C)34 (D)43
4.若某程序框图如图所示,则输出的n的值是 (A)3 (B)4 (C)5 (D)6
参考公式: 如果事件A,B互斥,那么P(A+B)=P(A)+P(B) 如果事件A,B相互独立,那么 P(A·B)=P(A)·P(B) 如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中事件A恰好发生k次的概率 Pn(k)=Cknpk(1-p)n-k (k=0,1,2,…,n) 台体的体积公式:
V=)(312211SSSSh
(其中S1,S2分别表示台体的上、下底面积, h表示台体的高)
柱体的体积公式:ShV (其中S表示柱体的底面积,h表示柱体的高)
锥体的体积公式:ShV31 (其中S表示锥体的底面积,h表示锥体的高) 球的表面积公式:S=4πR2
球的体积公式:343VR(其中R
表示球的半径)
开始 p=1,n=1 n=n+1
p>20 ? 输出n 结束 (第4题图)
是 否 p=p+2n1 5.设,mn是两条不同的直线,,是两个不同的平面,则下列命题中正确..的是 (A)若//,mn且,则mn (B)若,mn且mn,则 (C)若/,/nm且n,则//m (D)若,mn且//mn,则// 6.已知某锥体的三视图(单位:cm )
如图所示,则该锥体的体积为 (A)23cm (B)43cm
(C)63cm (D)83cm 7.251(1)(2)xx的展开式的常数项是 (A)48 (B)﹣48 (C)112 (D)﹣112 8.袋子里有3颗白球,4颗黑球,5颗红球.由甲、乙、丙三人依次各抽取一个球,抽取后不放回.若每颗球被抽到的机会均等,则甲、乙、丙三人所得之球颜色互异的概率是
(A)14 (B)13 (C)27 (D)311 9.已知实系数二次函数()fx和()gx的图像均是开口向上的抛物线,且()fx和()gx均有两个不同的零点.则“()fx和()gx恰有一个共同的零点”是“()()fxgx有两个不同的零点”的 (A)充分不必要条件 (B)必要不充分条件 (C)充分必要条件 (D)既不充分也不必要条件 10.设F1、F2是椭圆Γ的两个焦点,S是以F1为中心的正方形,则S的四个顶点中能落在椭圆Γ上的个数最多有(S的各边可以不与Γ的对称轴平行) (A)1个 (B)2个 (C)3个 (D)4个
(第6题图) 正视图 侧视图 俯视图
2
2 2 1 第Ⅱ卷(非选择题部分 共100分) 二、填空题:本大题共7小题, 每小题4分, 共28分. 11.已知复数z满足22zz= i(其中i是虚数单位),则z ▲ . 12.设25zxy,其中实数,xy满足68xy且20xy,则z的取值范围是 ▲ . 13.已知抛物线23xy上两点,AB的横坐标恰是方程2510xx的两个实根,则直线AB的方程是 ▲ .ks5u
14.口袋中装有大小质地都相同、编号为1,2,3,4,5,6的球各一只.现从中一次性随
机地取出两个球,设取出的两球中较小的编号为X,则随机变量X的数学期望是 ▲ . 15.已知直线10xy及直线50xy截圆C所得的弦长均为10,则圆C的面积 是 ▲ . 16.在△ABC中,∠C=90,点M满足3BMMC,则sin∠BAM的最大值是 ▲ . 17.已知点O是△ABC的外接圆圆心,且AB=3,AC=4.若存在非零实数....x、y,使得AOxAByAC,且21xy,则cos∠BAC = ▲ .
三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. 18.(本题满分14分) 在ABC中,内角,,ABC的对边分别为,,abc,且
23sin5aBc,11cos14B.
(I)求角A的大小;(II)设BC边的中点为D,192AD,求ABC的面积. 19.(本小题满分14分)设等差数列}na的前n项和为nS,且248,40aS. 数列nb的前n项和为nT,且230nnTb,nN. (I)求数列na,nb的通项公式; (II)设为偶数为奇数nbnacnnn , 求数列nc的前n项和nP. 20.(本题满分15分)如图所示,PA⊥平面ABCD, △ABC为等边三角形,PAAB,AC⊥CD,
M为AC中点.
(I)证明:BM∥平面PCD; (II)若PD与平面PAC所成角的正切值 为62,求二面角C-PD-M的正切值.
21.(本题满分15分)已知椭圆Γ:22221(0)xyabab的离心率为12,其右焦点F与椭圆Γ的左顶点的距离是3.两条直线12,ll交于点F,其斜率12,kk满足1234kk.设1l
交椭圆Γ于A、C两点,2l交椭圆Γ于B、D两点. (I)求椭圆Γ的方程; (II)写出线段AC的长AC关于1k的函 数表达式,并求四边形ABCD面积S 的最大值.
22.(本题满分14分)已知R,函数(1)()ln1xfxxx,其中[1,)x. (Ⅰ)当2时,求()fx的最小值; (Ⅱ)在函数lnyx的图像上取点(,ln)nPnn ()nN,记线段PnPn+1的斜率为kn ,
12111nnSkkk.对任意正整数n,试证明:
(ⅰ)(2)2nnnS; (ⅱ)(35)6nnnS.
P A B C
D M (第20题图)
O F
A
C B
D x
y
(第21题图) 宁波市2014年高考模拟试卷 数学(理科)参考答案
说明: 一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容制订相应的评分细则. 二、对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容与难度,可视影响的程度决定后续部分的给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分. 三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数.选择题和填空题不给中间分.
一、选择题:本题考查基本知识和基本运算。每小题5分,满分50分. 1.C 2.D 3.A 4.C 5. B 6.A 7.B 8.D 9.D 10.B
二、填空题:本题考查基本知识和基本运算.每小题4分,满分28分. 11.2 12.[21,31] 13.5310xy 14.73
15.27 16.35 17.23 ks5u
三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. 18.(本题满分14分)
解:(Ⅰ)由11cos14B,得53sin14B, ……………………1分 又23sin5aBc,代入得37ac, 由sinsinacAC,得3sin7sinAC, ……………………3分 3sin7sin()AAB, 3sin7sincos7cossinAABAB ………5分
得tan3A,23A ……………………7分
(Ⅱ)22192cos4ABBDABBDB, ……………………9分 22771119()266144cccc,3c,则7a ……………………11
分 1153153sin3722144SacB ………………14分
(19)(本小题满分14分) 解:(Ⅰ)由题意,1184640adad,得14,44naand. …………3分 230nnTb,113nb当时,,
112230nnnb当时,T,两式相减,得12,(2)nnbbn 数列nb为等比数列,132nnb. …………7分 (Ⅱ)14 32nnnncn为奇数为偶数 . 当n为偶数时, 13124()()nnnPaaabbb
=212(444)6(14)222214nnnnn. ……………10分 当n为奇数时, (法一)1n为偶数,1nnnPPc(1)1222(1)24221nnnnnn
……………13分 (法二)132241()()nnnnPaaaabbb
1221(44)6(14)2221214nnnnnn
. ……………13分
12222,221nnnnnPnnn为偶数
,为奇数 ……………14分
20.(本题满分15分) 解:(Ⅰ)证明:因为M为等边△ABC的AC边的中点,所以BM⊥AC. 依题意CD⊥AC,且A、B、C、D四点共面,所以BM∥CD. …………3分 又因为BM平面PCD,CD平面PCD,所以BM∥平面PCD. …………5分
(Ⅱ)因为CD⊥AC,CD⊥PA, 所以CD⊥平面PAC,故PD与平面 PAC所成的角即为∠CPD. ……………7分
不妨设PA=AB=1,则PC=2.
由于6tan2CDCPDPC,
P A B C
D M (第20题图)
F E
