基于云量子进化算法的SOC测试规划研究

合集下载

【国家自然科学基金】_量子粒子群优化(qpso)_基金支持热词逐年推荐_【万方软件创新助手】_20140802

2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
科研热词粒子群优化算法量子行为粒子群优化滤波器设计预测量子粒子群优化算法量子粒子群优化邻域拓扑遗传算法轮形结构艾尔曼网络流量神经网络早熟微分进化干扰因子变异机制作业车间调度优化设计 iir数字滤波器 fir数字滤波器
全局最优化全局位置变异余弦调制滤波器组代谢途径互信息两通道正交镜像滤波器组 volterra级数 soc powell法 ip核
1 1 1 1 1 1 1 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词推荐指数量子粒子群优化算法 4 量子粒子群优化 3 聚类 2 基因表达数据 2 全局收敛 2 锦标赛选择 1 量子进化算法 1 量子行为粒子群优化 1 量子行为的粒子群算法 1 量子系统 1 量子粒子群算法 1 量子粒子群 1 量子pso 1 重构 1 遗传pso 1 逐步优化策略 1 轮盘赌选择 1 路径规划 1 耗散操作算子 1 网络入侵检测系统 1 组合优化 1 粒子群优化(pso) 1 粒子群优化 1 移动机器人 1 硬件实现 1 现场可编程门阵列 1 模拟退火pso 1 有向无环图 1 支持向量机 1 属性约简 1 多样性引导 1 多agent系统 1 基因调控网络 1 基于量子行为的粒子群优化(qpso)算法 1 图像分割 1 参数估计 1 势阱 1 函数优化 1 全局最好位置 1 任务调度 1 二阶振荡pso 1 二进制编码 1 二维fisher准则函数 1 s-系统 1 agent联盟 1

一种基于智能蚁群算法的SOC芯核测试调度方法

ＡｅｈｄｆｒＩｌｃｅｔａｌｃｔｎｐｉｍａｅｎＳｍｔｏＰｂｏｋｔｓｌａｅａｄｏｔｍｕｂｓｄｏＯＣｏｏ
ＷＡａｊｎＭＡａｇｓｅｇＬＵｉｏｘａ，ＮＧＧｕｎｕ，Ｇｕｎ —ｈｎ，ＩＸａ—ｉＷＡＮＧＭａ— ｏｏｌｉ
一
种基于智能蚁群算法的ＳＣ芯核测试调度方法Ｏ
王冠军，马光胜刘晓晓王茂励，，
（哈尔程大学计算机科学与技术学院，１．滨工黑龙江哈尔５０１２滨１００；．滨工程大学自哈尔动化学院，黑龙江哈尔滨，５０１１００）
摘
要：随着现代半导体技术的发展，将整个系统集成在一个芯片上成为可能．但系统集成芯片ｓｃＵｏ￣试也成为一项越来越
ｍｅｏｄｃｓｈｓｍｅａｄｓｏｏｄｅｆｃｅｃ．ｈｔｄｒｕｅｅｔｔｉ，ｅｔｅｔｎｈｗｓａｇｏｆｉｉｎｙＫｅｗｏｄ：ＯＣ；ｙｒｓＳＡＣＯ；ＡＭ；ｅｔｅｏｒｅａｌｃｔ；ｅｔｅｏｒｅｏｔｚｔｎＴｔｓｒｓｕｃｌａｅｔｓｓｕｃｐｍａｉｏｒｉｉｏ
（ｃｏｌｆＣｏｕｅｃｅｃｎｅｈｏｏｙＨａｂｎＥｎｉｅｒｇＵｎｖｒｉ，ｒｂｎ１００１Ｃｈｎ）ＳｈｏｏｍｐｔｒＳｉｎｅａｄＴｃｎｌｇ，ｒｉｇｎｅｉｉｅｓｙＨａｉ５０，ｉａｎｔ
ＡｂｔａｔＷｉｅｄｖｌｐｎｆｍｏｅＣｃｎｌｇ，ｔＳａａｌｂｅｔｎｅｒｔｅｗｈｌｙｔｍｎａｓｎｌｈｐＩｅｍｅｎｓｒｃ：ｔｔｅｅｏｍｅｔｄｒＩｔｈｏｏｙｉ’ ｖｉｌｉｔｇａｅｔｏｅｓｓｅｏｉｇｅｃｉ．ｎｔａｈｈｏｎｅａｏｈｈｔ，ｅｔｓｉｇｏＯＣｅｏｓａｍｏｅｃｍｐｉａｅｒ．ｎｔｉａｅ，ｅｍｅｈｄｂｓｄｏｎｅｌｅｔａｔｃｌｎｙｔｍｏｉｍｅｔｔｆＳｈｅｎｂｃｍｅｒｏｌｔｄｗｏｋＩｓｐｐｒａｎｗｔｏａｅｎｉｔｌｇｎｏｏｙｓｓｃｈｉｎｅｆｒ

基于量子计数的贝叶斯二元分类算法

Vol. 44 No. 4Dec,2021第44卷第4期2021年12月南京师大学报(自然科学版)JOURNAL OF NANJING NORMAL UNIVERSITY (Natural Science Edition)doi ：10.3969/j.issn.l001-4616.2021.04.015基于量子计数的贝叶斯二元分类算法陆春悦，郭躬德，林耘(福建师范大学计算机与网络空间安全学院，福建福州350117)［摘要］贝叶斯分类算法是一种基于概率统计理论的有监督学习算法,常被用于分类问题中•本文将量子计数与经典贝叶斯分类算法相结合，提出一种新的量子贝叶斯分类算法.通过量子随机访问存储器制备所需的量子态，使用oracle 进行相位翻转并构造与之所对应的操作算子，在操作算子的本征态空间上重新描述量子态，借助辅助粒子进行相位估计，投影测量后即可高效地计算出贝叶斯分类所需的数据，实现量子贝叶斯分类算法.该算法在低维特征空间中与经典算法相比有着指数级加速.［关键词］量子机器学习,贝叶斯分类，二元分类,量子计数，相位估计［中图分类号］TP38；TP181 ［文献标志码］A ［文章编号］1001-4616(2021) 04-0117-05Bayesian Binary Classification Algorithm Based on Quantum CountingLu Chunyue,Guo Gongde,Lin Song(College of Computer and Cyber Security , Fujian Normal University , Fuzhou 350117, China)Abstract : Bayesian classification algorithm is a supervised learning algorithm based on the statistics theory of probability , which is often used in classification problems. In this paper,a new quantum Bayesian classification algorithm is proposed by combining quantum counting with classical Bayesian classification aLgorithm. The required quantum states are prepared by a quantum random access memory ,the oracle is used to phase flip and construct the corresponding operator, the quantum states are redescribed on the eigenstate space of the operator, and phase estimation is performed with the help of auxiliary particles. Then,the data required for Bayesian classification can be efficiently calculated after projection measurements and the quantum Bayesian classification algorithm can be realized. Compared with the classical algorithm , this algorithm has exponential acceleration in the low dimensional feature space.Key words :quantum machine learning ,Bayesian classification ,binary classification ,quantum counting,phase estimation 量子计算利用量子并行、量子纠缠等特性解决一些计算任务,展现出了比经典计算更为优越的计算能力⑴.1994年,Shor ⑵提出用于大数分解的Shor 算法，与经典算法相比,实现了指数级加速.1997年, Grover ⑶提出了针对非结构化数据库的量子搜索算法,时间复杂度为0阿，达到了二次加速.受这些量子算法的启发，人们对量子机器学习进行研究，提出了一系列高效的量子机器学习算法，如量子K 近邻算法、量子决策树同、量子支持向量机、量子关联规则m 等.贝叶斯分类算法是一种常见的机器学习算法,它利用贝叶斯定理与联合概率模型进行分类预测,被广泛应用于文本分类.Shao [11]在2020年提出了基于块编码的量子贝叶斯分类算法(简记为Shao 算法).该算法将块编码与贝叶斯分类相结合，实现了指数级加速.然而，该算法仅仅适用于厄米矩阵.本文针对这 _问题进行研究,提出了_种基于量子计数的贝叶斯二元分类算法.该算法通过量子计数与相位估计，快速得到能够反映待分类数据属于第&类别概率的相关值,获取待分类数据所属类别.本文所提算法在低维特征空间中与经典算法相比有着指数级加速，也可应用于更为普遍的数据集.收積日期:2021-07-12.基金项目：国家自然科学基金项目(61976053,61772134),福建省•高等学校新世纪优秀人才支持计划、福建省§然科学基金项目(2018J01776).通讯作者:林撚，博士，教授，博士生导师，研究方向:量子机器学习.E-mail : lins95@ ——117 —南京师大学报(自然科学版)第44卷第4期(2021年)1背景知识1.1朴素贝叶斯分类算法朴素贝叶斯分类算法是在特征条件独立假设和贝叶斯定理的基础上得出的一种分类算法,它利用贝叶斯公式可以得到待分类数据属于不同类别的概率〔炉⑷.在该问题中,本文假设存在一个由N个有类标签的数据(x“)(i=l,2,・“,N)构成的数据集T,这里=(束",乂严，...,屮丁表示有M个属性的向量，必表示七的类别，其中y^c k,k=l,2,-,K.更多地，叩e｛卯乙表示也的第j个属性，其中号表示第j个属性种类.贝叶斯分类的目的是判断新测试样本数据x所属的类别y,在该模型下,算法是先计算出新数据F属于类别q的概率P(cjx)，然后判断出其最大可能属于的类别.根据贝叶斯定理和联合概率分布,P(cJx)可以表述为：P(c』F)=P(X=x,Y=c k)P(x)MP(y；II P(X F)i=c k)___________j=iP(x)(1)通过式(1)，容易发现对于待分类数据壬,仅需要通过比较P(i,yi=cQ就可得到X所属类别,My=axgmaxP(Y i=c k)P(X卩书I乙=q)."；=i因此，贝叶斯分类过程要求计算概率,⑵P(Y i=c k)==4)——,k=l,2,-K,⑶式中，X/(必=C»)表示在数据集T中”=c»的个数.此外，还需计算，1=1Mp(x=riy；=cQ=JI p(xy)niy；=q).(4)显然，后者是算法的主要步骤.这样，经典贝叶縮分类算法所需的时间复杂度为。

【计算机应用研究】_量子算法_期刊发文热词逐年推荐_20140724

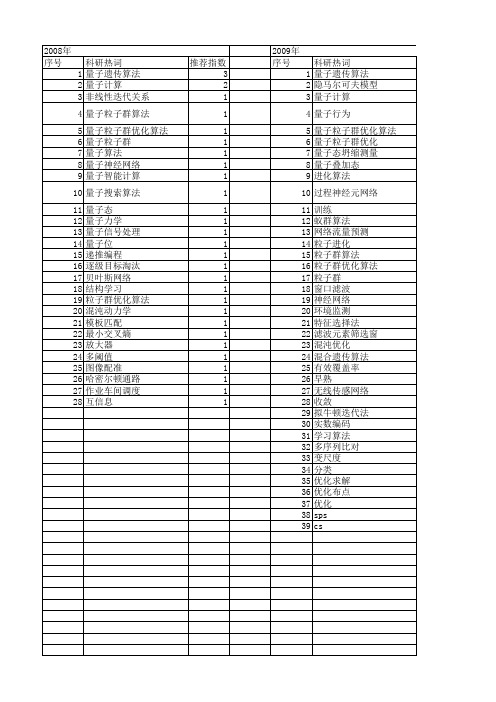
科研热词推荐指数量子遗传算法 4 量子进化算法 3 量子门 2 量子粒子群优化算法 2 量子旋转门 2 隐马尔可夫情感模型 1 量子非门 1 量子遗传 1 量子计算 1 量子行为的粒子群优化(qpso)算法1 量子比特 1 量子概率幅编码 1 量子密码 1 量子叠加态 1 进化阶段 1 近邻ainet 1 边缘检测 1 车辆路径问题 1 要目 1 自适应罚函数 1 自诊断智能结构 1 聚类集成 1 聚类质量 1 聚焦爬虫 1 立即价值 1 移动机器人路径规划 1 生产调度 1 特征选择 1 混沌遗传算法 1 混合算法 1 核函数 1 未来价值 1 无条件安全 1 旋转角 1 方法综述 1 文本分类 1 数学形态学 1 改进 1 成本与效益 1 情感虚拟人 1 强盲签名 1 并行量子遗传神经网络 1 带约束优化 1 多链拓展编码 1 多级量子神经网络 1 多目标优化 1 基因链 1 图像配准 1 变异算子 1 变异概率 1 区域生长 1 动态 1
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
53 s-系统 54 doa估计 55 agent联盟
1 1 1
2011年科研热词推荐指数量子遗传算法 3 粒子群优化 2 量子计算 1 量子行为的粒子群优化算法 1 量子行为 1 量子蚁群算法 1 量子粒子群算法 1 量子粒子群优化算法 1 量子粒子群优化 1 量子比特编码 1 遗传算法 1 路由协议 1 蛋白质折叠 1 蛋白质序列 1 编码方案 1 粮库选址 1 空间聚类 1 矩阵编码 1 直方图 1 树型编码 1 标准函数 1 析取图 1 最大完工时间 1 指标预测 1 带障碍约束 1 实数编码 1 完全重构 1 完全学习策略 1 多约束qos路由 1 多样性变异 1 多样性函数 1 图像对比度增强 1 变换函数 1 变异 1 原型低通滤波器 1 动态聚类 1 函数优化 1 关键路径 1 作业车间调度 1 优化算法 1 云模型 1 二进制编码 1 二进制 1 二维hp模型 1 两通道正交镜像滤波器组 1 t-s推理网络 1 ad hoc网络 1

【计算机应用研究】_量子信息_期刊发文热词逐年推荐_20140725

2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
科研热词量子进化算法隐蔽信道量子门量子遗传算法量子秘密共享量子神经网络量子攻击量子叠加态通信指纹边缘检测辫群聚类集成聚类质量聚焦爬虫纠缠交换立即价值求根问题比特承诺检测未来价值旋转角数学形态学多目标优化启发式可验证秘密共享单向函数共轭搜索问题信息熵信息交互交叉主题相关度一次群签名 xml文档 knn分类 hash运算
推荐指数 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年序号 1 2 3 4 5
2014年科研热词量子隐形传态量子纠缠量子测量辅助驱动型量子计算盲量子计算推荐指数 1 1 1 1 1
科研热词辫群量子遗传算法代理签名高斯扰动量子进化算法量子粒子群优化算法量子粒子群量子算法量子签名量子密码量子多目标进化算法重构逐步优化策略软硬件划分计算复杂度聚类组合优化稀疏表示盲签名测量矩阵求根问题无线视频监控平均位置多重共轭搜索多目标优化基因调控网络同时签名参数估计压缩传感共轭搜索问题共轭搜索全局最优位置入侵检测信号相位匹配不经意传输 soc系统 s-系统 epr态 doa估计

【计算机应用】_量子算法_期刊发文热词逐年推荐_20140727

2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 481 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90
智能优化算法无限脉冲响应无线视频监控旅行商问题文化算法数字滤波器改进量子进化算法异常检测建模并行量子进化算法平均位置局域搜索多目标作业车间调度多目标优化多任务联盟多agent系统基因调控网络压缩传感分类属性分子对接函数优化共轭搜索问题全局最优位置入侵特征库入侵检测信号相位匹配任务调度代谢途径代理签名二阶振荡pso tsp toy模型 soc系统 s-系统 l-缬氨酸 doa估计 autodock3.05 agent联盟
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词推荐指数量子遗传算法 5 量子计算 3 量子粒子群优化算法 2 量子算法 2 非线性迭代关系 1 非线性方程组 1 量子逻辑线路 1 量子进化算法 1 量子粒子群算法 1 量子粒子群优化 1 量子粒子群 1 量子神经网络 1 量子智能计算 1 量子搜索算法 1 量子态 1 量子小波变换 1 量子化学 1 量子力学 1 量子信号处理 1 量子位 1 遗传算法 1 递推编程 1 逐级目标淘汰 1 进化计算 1 运输成本 1 贝叶斯网络 1 网络流量预测 1 结构学习 1 粒子群优化算法 1 神经网络 1 目标函数 1 物流信息系统 1 混沌动力学 1 混合量子遗传算法 1 模糊推理 1 模糊petri网 1 模板匹配 1 最小交叉熵 1 放大器 1 拟牛顿迭代法 1 径向基函数 1 并行进化模型 1 小生境 1 多阈值 1 基组 1 基于量子行为的微粒群优化算法 1 图像配准 1 图像增强 1 哈密尔顿通路 1 分子结构 1 六氨氯化镁 1 免疫算子 1

量子进化和模拟退火的混合优化算法

ＺｈａｎｇＷｅｉｆｅｎｇ１，ＷａｎｇＺｈａｏｈｕｉ１，ＺｈｅｎｇＪｉａｎｇｕｏ２
（１．ＣｏｌｌｅｇｅｏｆＣｏｍｐｕｔｅｒＳｃｉｅｎｃｅａｎｄＴｅｃｈｎｏｌｏｇｙ，ＷｕｈａｎＵｎｉｖｅｒｓｉｔｙｏｆＳｃｉｅｎｃｅａｎｄＴｅｃｈｎｏｌｏｇｙ，Ｗｕｈａｎ４３００８１，Ｃｈｉｎａ；２．ＧｌｏｒｉｏｕｓＳｕｎＳｃｈｏｏｌｏｆＢｕｓｉｎｅｓｓａｎｄＭａｎａｇｅｍｅｎｔ，ＤｏｎｇｈｕａＵｎｉｖｅｒｓｉｔｙ，Ｓｈａｎｇｈａｉ２０００５１，Ｃｈｉｎａ；３．Ｄｅｐｔ．ｏｆＩｎｆｏｒｍａｔｉｏｎＭａｎａｇｅｍｅｎｔ，ＨｕｂｅｉＡｕｔｏｍｏｔｉｖｅＩｎｄｕｓｔｒｉｅｓＩｎｓｔｉｔｕｔｅ，Ｓｈｉｙａｎ４４２００２，Ｃｈｉｎａ）
（５）
当高温时用式（４）产生新解，低温时用式（５）产
生新解，其中Ｐｍ为变异概率，一般取Ｐｍ＝０．３～０．４。! 为学习率，一般取 !＝０．２～０．３，Ｕ为区间内随机数，
ｓＲ为搜索半径，不宜取的太大，一般取ｓＲ＝０．１～０．２，
在本文算法中采用最常用的指数退温函数，即
ｍｉｎｆ（ｘ）
ｘ＝（ｘ１，ｘ２， …，ｘｍ），ｘｉ∈［ａ，ｂ］，ｉ∈（１，２， …，ｍ）其中［ａ，ｂ］为搜索区间，由于!ｉ， "ｉ∈（０，１），因此必须将实数编码按一定规则映射到区间（０，１）
中，本文采用以下方式进行映射：
!ｉ＝
ｘｉ－ｂ－
该文档贡献者很忙什么也没留下
第２０卷第２期２００６年６月
湖北汽车工业学院学报ＪｏｕｒｎａｌｏｆＨｕｂｅｉＡｕｔｏｍｏｔｉｖｅＩｎｄｕｓｔｒｉｅｓＩｎｓｔｉｔｕｔｅ

基于电池等效电路模型和扩展卡尔曼滤波器算法的电池单体soc估计算法和soh估计算法

基于电池等效电路模型和扩展卡尔曼滤波器算法的电池单体soc估计算法和soh估计算法基于电池等效电路模型和扩展卡尔曼滤波器算法的电池单体SOC（State of Charge）和SOH（State of Health）估计算法是一种先进的电池管理系统（BMS）技术。

这种算法结合了电池的物理特性和电化学属性，通过建立等效电路模型来描述电池的内部行为，并利用扩展卡尔曼滤波器进行状态估计，从而实现对电池SOC 和SOH的准确估算。

以下是基于电池等效电路模型和扩展卡尔曼滤波器算法的电池单体SOC和SOH估计算法的基本步骤：1.建立电池等效电路模型：根据电池的电化学特性和物理属性，建立一个适当的等效电路模型。

常用的等效电路模型包括Rint模型、Thevenin模型和PNGV模型等。

这些模型能够描述电池的动态行为和内部电阻、电容等参数。

2.定义状态方程和观测方程：在扩展卡尔曼滤波器中，需要定义状态方程和观测方程来描述电池的动态行为。

状态方程通常包括SOC和电池内部状态变量（如极化电压），而观测方程则描述了可测量的电池特性（如端电压和电流）。

3.初始化参数：根据电池的初始状态和参数，对扩展卡尔曼滤波器的参数进行初始化，包括状态变量、过程噪声协方差、测量噪声协方差和初始估计值等。

4.进行状态估计：在每个采样时刻，根据当前时刻的测量值和等效电路模型，计算卡尔曼增益，并更新状态变量的估计值。

重复此过程，以逐步估计电池的SOC和SOH。

5.数据处理与结果输出：对估计结果进行处理和分析，提取电池的SOC和SOH信息。

这些信息可以用于电池管理系统的其他功能，如充电控制、放电控制、故障诊断等。

基于电池等效电路模型和扩展卡尔曼滤波器算法的电池单体SOC和SOH估计算法具有较高的精度和实时性，能够有效地估计电池的状态并提高电池的性能和使用寿命。

然而，该算法的实现需要深入理解电池的电化学特性和等效电路模型，同时还需要对扩展卡尔曼滤波器进行适当的调整和优化。

【计算机应用研究】_多目标进化算法_期刊发文热词逐年推荐_20140723

2014年序号 1 2 3 4 5 6 7 8 9 10
2014年科研热词鲁棒性鲁棒优化问题非支配解进化算法迁移操作精英保留差分进化算法工程最优性多目标优化坡度推荐指数 1 1 1 1 1 1 1 1 1 1
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
科研热词多目标优化非均匀变异网格 nsga-ⅱ算法 e-占优量子门量子进化算法配送中心选址进化博弈自适应惯性权值聚类排挤组合电路粗糙集粒子群优化核属性染色体本征基因最优搜索方向学习旋转角属性约简层次遗传算法双层规划优化算法人工选择交叉互信息
推荐指数 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
2011年科研热词推荐指数多目标优化 3 多目标进化算法 2 协同进化 2 鲁棒边界域 1 蚁群算法 1 精英保留策略 1 粗糙集理论 1 粒子群算法 1 混沌序列 1 测试函数 1 模拟退火 1 文化 1 多目标 1 协同进化非支配遗传算法 1 soc软硬件划分 1 nsga-ⅱ 1 epsilon支配 1
推荐指数 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
科研热词多目标优化高层次综合隐私保护量子进化算法量子多目标进化算法遗传算法进化算法软硬件划分调度记忆体粒子群优化算法目标空间分割模块分配微粒群算法局域搜索多目标作业车间调度多目标多样性可测性匿名化区间索引免疫克隆偏好区域 soc系统 pbest

量子化学计算方法及应用

量子化学计算方法及应用马建华华侨大学材料学院2009级研究生班学号0900202003摘要：文章概括地介绍了从头算法及一些半经验的量子化学计算方法, 同时简要介绍了国际理论界近年发展起来的组合方法、遗传算法、神经网络等计算方法及其在材料学、生物学、药物学以及配位化学中的应用。

关键词：量子化学；计算方法；应用1、量子化学计算方法简介量子力学是20世纪最重要的科学发现之一。

在量子力学基础上发展起来的理论物理、量子化学及相关的计算, 为我们开辟了通向微观世界的又一个途径。

量子化学研究的电子- 原子核体系可用相应的Schrdinger 方程解的波函数来描述。

原则上,Schrdinger方程的全部解保证了多电子体系中电子结构与相互作用的全面描述。

然而, 由于数学处理的复杂性, 在实践中, 总希望发展和运用量子力学的近似方法, 从而无需进行很繁杂的计算就可以说明复杂原子体系的主要特性, 这就必须在原始量子化学方程中引进一些重要的简化, 以便得到一定程度的近似解。

量子化学发展到现在, 根据为解Schrdinger方程而引入近似程度的不同,大致可分为以下几种方法:1.1、从头计算方法(ab initio calculation)[1- 2]从头计算方法, 即进行全电子体系非相对论的量子力学方程计算。

这种方法仅仅在非相对论近似、Born-Oppenheimer近似、轨道近似这三个基本近似的基础上利用Planck常数、电子质量和电量三个基本物理常数以及元素的原子序数, 对分子的全部积分严格进行计算,不借助任何经验或半经验参数,达到求解量子力学Schrdinger方程的目的。

Roothaan方程是多电子体系Schrdinger方程引入三个基本近似后的基本表达。

原则上,只要合适地选择基函数,自洽迭代的次数足够多,Roothaan方程就一定能得到接近自洽场极限的精确解。

因此这种计算方法在理论和方法上都是比较严格的, 其计算结果的精确性和可靠性都大大优于半经验的一些计算方法。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ｏａｉｒｔｖｅｏｐｔｍｉａｉｉｅＣＳｎｗｅｏｎｓｐｔｏｎｉｉｚｔｏｎｏｆｔｍＯｔａｄｐｏｒｃｕｍｉｎＳＯＣｅｔＦｉｌｙ，ｔｉｕｌｔｏｎｅｅｉｅｓｆｎｔｒｔｓ．ｎａｌｈｅｓｍａｉｘｐｒｍｎｔｏｒｉｅ－ｎｉｎａｔｎｄａｄｃｒｕｔＩａｔｏｌｓａｒｉｃｉＴＣ０ｓｎｃａｋａｅｍａ．Ｅｘｐｒｍｅａｅｕｔｍｏｔａｅｔｔｃｏｕａｕ — ２ＴｅｔＢｅｈｍｒｒｄｅｅｉｎｔｌｒｓｌｓｄｅｎｓｒｔｈａｌｕｄｑｎｔｍｅｖｕｔｏｎａｇｉｈｍａｅｔｒｒｄｕｅＳＯＣｅｔｔｍｅａｏｏｔｈｅＳＯＣｅｔｅｆｃｅｃｏｌｉｌｏｒｔｃｎｂｔｅｅｃｔｓｉｎｄｐｒｍｅｔｔｓｆｉｉｎｙ，ｃｏｍｐａｅｉｈｔｅｅｘｓｉｒｄｗｔｈｉｔｎｇ
滴的随机性和稳定倾向性特点， … ｒ一种新的量ｒ进化算法，算法在量进化算法基础Ｌ，云模型的Ｘ、捉该 … Ｙ条什发器加入杂交操作，ｌ本发ｆ加入变异操作。并将云量ｆ进化算法用于解决Ｓ【ｌ器－ＯＣ测试时间与测试功耗协同优化。最后用同际标准电路Ｉ ’ ２Ｔｅｔｅｃｍａｋ进行实验仿真，已有算法相比，ＴＣ０ｓＢｎｈｒ与云量进化算法能够更好地缩短ＳＣ测试时间、高ＳＣ测试效率。ｏ提０关键词：Ｏ测试；ｆ进化算法；模型；功耗约束ＳＣ量中图分类号：Ｎ４Ｔ７文献标识码：Ａ文章编号：６３８８（００ｄｔｂｌｅｅｙｉｌｕｍｏｌｉｒｒｔｖｅｃｍｅｔｅｓｒｃｉｓｏｆｔｅｔａｔｏｎｌｑｎｔｍｖｌｉｎａｙｎｓａｅｔｎｄｎｃｎｃｏｄｄｅ，ｎｏｄｅｏｏｒｏｈｈｏｔｏｍｎｇｈｒｄｉｉａｕａｕｅｏｕｔｏｒ
ｗｈｃｙｒｄｚｔｎｏｅａｉｎｒｄｅｙＸ＆Ｙｏｄｔｎｌｕｅｅａｏｎｃｏｄｍｏｅ。ａｄｔｅｖｒａｉｎｏｅ．ｉｈｈｂｉｉａｉｐｒｔｓａｅａｄｄｂｏｏｃｎｉｏｓｃｏｄｇｎｒｔｒｉｌｕｄｌｎｈａｉｔｐｒｉｏ
（ｃｏｌｆＥｅｔｏｉＥｎｉｅｒｇａｄＡｕｏｔｎＳｈｏｌｃｒｎｃｏｇｎｅｉｎｔｍａｉ，ＧｕｌｉｅｓｔｆＥｅｔｏｉＴｅｈｏｏｙ，ｕｌ４０４ｎｏｉｎＵｎｖｒｉｏｌｃｒｎｃｉｙｃｎｌｇＧｉｎ５１０，Ｃｈｎ）ｉｉａ
ＴｅｔｓｈｄｌｎｆＳＯＣａｅｎｃｏｄｑｕｎｕｅｏｕｉｎａｇｒｔｍｓｃｅｕｉｇｏｂｓｄｏｌｕａｔｍｖｌｔｏｌｏｉｈ
ＸｕＣｈａｐｉｕｎｅ，ＱｉｈｎｚｏｎＳａｇｈｕ
ａｉｎｂｈａｉｌｕｅｅａｏ．Ｆｕｔｅｍｏｅｌｕｕｎｕｅｏｕｉｎａｇｒｔｍｓｅｌｙｄｔｏｖｅｃｌｂｔｙｔｅｂｓｃｏｄｇｎｒｔｒｏｃｒｈｒｒ，ｃｏｄｑａｔｍｖｌｔｌｏｉｈｉｍｐｏｅｏｓｌｅｔｏｌ — ｏｈａ
第３Ｏ卷
第５期
桂林电子科技大学学报
ＪｕｎｌｆＧｕｌｉｅｓｔｆＥｌｃｒｎｉｃｏｏｙｏｒａｉｉＵｎｖｒｉｙｏｅｔｏｃＴｅｈｎｌｇｏｎ
Ｖｏ１３０，ｏ．Ｎ．５
Ｏｃ．２０ｔ０１
２１００年１｛Ｏ』
基于云量子进化算法的ＳＯＣ测试规划研究
许川佩，覃上洲
（林电子科技大学电子工程与自动化学院，西桂林５１０）桂广４０４
摘要：克服传统量ｊ进化算法Ｉ，移操作和量ｒｆ单一方向更新操作易陷入局部最优解的缺陷，鉴模型为＿：Ｉ迁ｌＪ借
ＡｂｔａｔＡｅｃｏｄｑａｔｍｖｌｔｎａｇｒｔｍｓｐｏｏｅｎｔｉｐｐｒｃｏｄｎＯｃｏｄｄｏｌｔａｄｍｎｓｓｒｃ：ｎｗｌｕｕｎｕｅｏｕｉｌｏｉｏｈｉｒｐｓｄｉｈｓａｅｃｒｉｇｔｌｕｒｐｅｓｒｎｏｅｓａ
ａｇｒｔｍ，ｓｃｓｔａｈｒｎｆｒｏｅａｉｎｎｕｎｕｇｔｎ－ｉｅｔｎｕｄｔｐｒｔｎｒａｉｒｐｅｌｏｉｈｕｈａｈｔｔｅｔａｓｅｐｒｔｓａｄｑａｔｍａｅｏｅｄｒｃｉｐａｅｏｅａｉｓａｅｅｓｌｔａｐｄｏｏｏｙｉｔｏａｐｉｌｏｕｉｎＴｈｌｕｕｎｕｅｏｕｉｎａｇｒｔｍａｅｎｔｅｑａｔｍｖｌｔｏｌｏｉｈ，ｉｎｏｌｃｌｔｏｍａｌｔ．ｓｏｅｃｏｄｑａｔｍｖｌｔｌｏｉｈｉｂｓｄｏｈｕｎｕｅｏｕｉｎａｇｒｍｏｓｔｎ